Open Access Article
Open Access ArticleDirectional actuation and phase transition-like behavior in anisotropic networks of responsive microfibers†
Shiran
Ziv Sharabani
abc,
Elad
Livnat
abc,
Maia
Abuchalja
a,
Noa
Haphiloni
a,
Nicole
Edelstein-Pardo
abc,
Tomer
Reuveni
abc,
Maya
Molco
abc and
Amit
Sitt
 *abc
*abc
aSchool of Chemistry, Faculty of Exact Sciences, Tel Aviv University, Tel Aviv, 6997801, Israel. E-mail: amitsitt@tauex.tau.ac.il
bThe Center for Nanoscience and Nanotechnology, Tel Aviv University, Tel Aviv, 6997801, Israel
cThe Center for Physics & Chemistry of Living Systems, Tel Aviv University, Tel Aviv, 6997801, Israel
First published on 12th February 2024
Abstract
Two-dimensional shape-morphing networks are common in biological systems and have garnered attention due to their nontrivial physical properties that emanate from their cellular nature. Here, we present the fabrication and characterization of anisotropic shape-morphing networks composed of thermoresponsive polymeric microfibers. By strategically positioning fibers with varying responses, we construct networks that exhibit directional actuation. The individual segments within the network display either a linear extension or buckling upon swelling, depending on their radius and length, and the transition between these morphing behaviors resembles Landau's second-order phase transition. The microscale variations in morphing behaviors are translated into observable macroscopic effects, wherein regions undergoing linear expansion retain their shape upon swelling, whereas buckled regions demonstrate negative compressibility and shrink. Manipulating the macroscale morphing by adjusting the properties of the fibrous microsegments offers a means to modulate and program morphing with mesoscale precision and unlocks novel opportunities for developing programmable microscale soft robotics and actuators.
Introduction
Developing shape-morphing materials with anisotropic and directional morphing is a longstanding objective in material programming, with extensive applications in soft robotics and bioinspired engineering.1–4 Among various morphing systems, two-dimensional (2D) films have been widely studied for the formation of directional morphing, owing to the precise control that can be exerted over their physical and chemical attributes and the ease of visualizing different morphing effects.5–8 In recent years, there has been a growing interest in the mechanics of static and dynamic (quasi) 2D meshes and cellular architectures. These are characterized by an array of voids encapsulated by solid walls and offer advantages, including a high surface area-to-volume ratio, low mass-to-volume ratio, and mechanical robustness, making them highly suitable for design and fabrication using additive manufacturing approaches.9–11 Moreover, cellular architectures can be employed to design mechanical metamaterials with unconventional mechanical properties such as auxetic behaviors and negative compressibility.12,13The porous nature of the cellular architecture can introduce mechanical properties and morphing behaviors that significantly differ from continuous 2D sheets.14,15 Additionally, the cellular architecture provides inherent means to create anisotropy in the mechanical properties. The most trivial means is to impart distinct mechanical properties to the cellular walls.16,17 For example, Mueller et al. demonstrated that constructing the cells’ walls of two components, namely active and passive materials, arranged in a triangular network helped achieve anisotropic behavior under compression testing.18 Anisotropy can also be induced by imposing an anisotropic cavity shape along the sample.19
While macroscopic shape morphing cellular structures are typically formed using 3D and 4D printing,20,21 these approaches cannot be usually used for constructing microscale systems, where precise fabrication of the morphing components must be achieved. A common approach for obtaining shape-morphing cellular structures and meshes with microscale precision is lithography.22 For example, soft lithography was used to create capillary-driven cellular structures that change shape and topology,23 and a combination of surface deposition and lithography was employed to construct micro-lattices of 2D bonded films programmed to form curved 3D surfaces.24
Hierarchical networks of soft nano-to-microscale filaments represent another category of microscale shape-morphing cellular structures. Such networks are commonly encountered at the cellular level in biological systems (e.g., microtubules-kinesin and actin-myosin networks) and are used for exerting forces and inducing motility at the microscale level. A common approach for constructing synthetic shape-morphing networks of microscale filaments is spinning microfibers of stimuli-responsive polymers.25–27 Recently, highly structured networks of microfibers have been obtained using the jet-writing approach, in which the spinning is coupled to a collector mounted on an accurate XY stage, enabling the deposition of ordered networks with high control over the network's architecture.28–32 For example, Moon et al. employed jet-writing to form polymer fiber meshes, which exhibited well-defined unidirectional morphing upon heating.28 Javadzadeh et al. used melt-spinning jet-writing to form shape-morphing liquid-crystal elastomers scaffolds.33 The transition to the microscale can affect the morphing behavior of the entire system at the macroscale. In previous work, we utilized the jet-writing approach to fabricate hierarchical networks of thermoresponsive mesoscale filaments that demonstrated two types of morphing: shape-preserving behavior and buckling-governed behavior.29
In this work, we present the development and characterization of responsive Cartesian networks composed of perpendicularly arranged thermoresponsive and non-responsive polymeric microfibers, which exhibit a directional and reversible morphing imposed by the inhomogeneity within the network's architecture. By changing the mesh size and, consequently, the slenderness of the filaments, we observe a transition in the morphing behavior at the single filament level between buckling-governed and linear extension regimes. Based on Landau's theory, we demonstrate that the transition can be interpreted as an athermal second-order phase transition, where the mechanical energy of the system upon swelling is expressed as a function of a buckling-related order parameter, and the reciprocal slenderness serves as an effective temperature. Lastly, we demonstrate the ability to achieve both extensile and contractile regimes within a single network by changing the slenderness of the responsive fibers. This capability gives rise to a phenomenon analogous to “negative compressibility” and showcases these networks' distinctive mechanical and shape-morphing characteristics.
Results and discussions
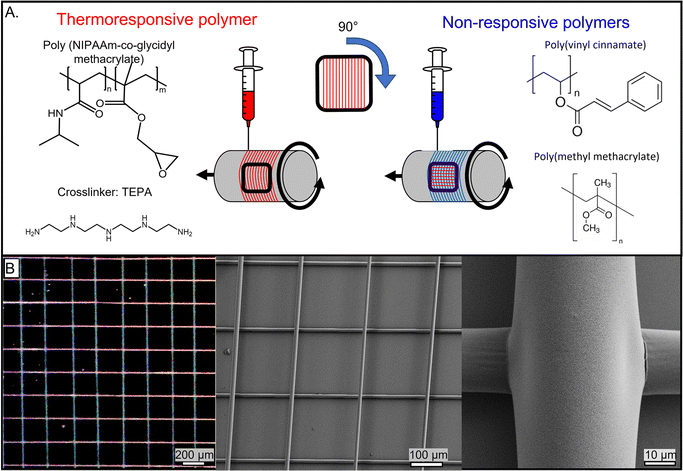
A directionally morphing network was fabricated using the dry-spinning jet-writing approach. The network consisted of two-dimensional (2D) orthogonally arranged microfibers with thermoresponsive and non-responsive microfibers (Fig. 1). The thermoresponsive fibers, made of poly N-isopropyl acrylamide-co-glycidyl methacrylate (PNcG) with a monomer ratio of 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, exhibited a lower critical solution temperature (LCST) of 32 °C in water.34,35 The copolymer fibers were crosslinked post-fabrication with tetraethylenepentamine (TEPA). When immersed in water, crosslinked PNcG undergoes reversible swelling and shrinking below and above LCST, respectively. The non-responsive fibers were made of either polyvinyl cinnamate (PVCi) or poly methyl methacrylate (PMMA), which are hydrophobic and do not change their dimensions upon heating/cooling in the temperature range of the experiments.
1, exhibited a lower critical solution temperature (LCST) of 32 °C in water.34,35 The copolymer fibers were crosslinked post-fabrication with tetraethylenepentamine (TEPA). When immersed in water, crosslinked PNcG undergoes reversible swelling and shrinking below and above LCST, respectively. The non-responsive fibers were made of either polyvinyl cinnamate (PVCi) or poly methyl methacrylate (PMMA), which are hydrophobic and do not change their dimensions upon heating/cooling in the temperature range of the experiments.
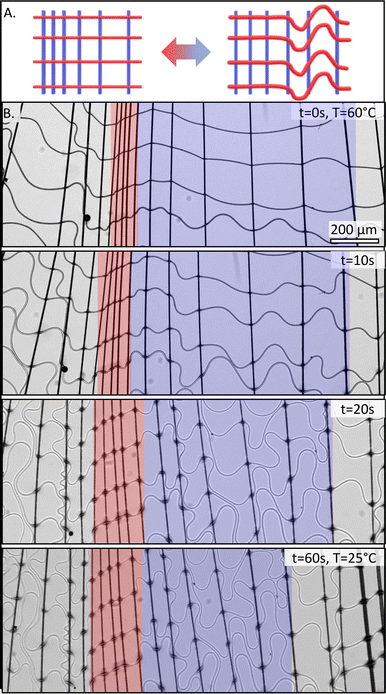
The network was next extracted from the frame, submerged in deionized water, and placed on a heating microscope slide for environmental temperature control. The networks were initially immersed in water at a temperature of 60 °C, above the LCST of PNcG, and retained their as-spun configuration. When cooled below the LCST, the PNcG fibers swelled significantly and elongated. Upon swelling, the fibers displayed two distinct shape-morphing behaviors, as was also demonstrated in our preceding investigations of isotropic networks (see Section S1 in ESI†). The first type of morphing behavior, referred to as shape-preserving morphing (Fig. 2A), was characterized by the PNcG fibers extending linearly and remaining straight throughout their swelling. Consequently, the spacing between the non-responsive fibers increased while the distances between the PNcG fibers remained constant, and the entire network expanded anisotropically along the direction of the PNcG fibers while maintaining its Cartesian structure. Upon reheating the system back above the LCST, the PNcG fibers contracted to their original size, and the network returned to its initial dimensions.
A second typical morphing behavior was observed wherein cooling below the LCST caused the PNcG fibers to swell, forming elastic instabilities and substantial buckling in the fibers (Fig. 2B). Consequently, the original Cartesian network structure was disrupted and not preserved, while the non-responsive fibers and vertical node-to-node distances remained unchanged. Upon reheating, the PNcG fibers contracted, returning to their original linear configuration, and the network regained its Cartesian geometry. Remarkably, in this type of morphing, which we refer to as buckling-governed morphing, the morphing still occurs anisotropically along the responsive axis. Nonetheless, the extent of morphing was significantly lower than in the shape-preserving case, and it was strongly influenced by the buckling behavior of individual fibers. Regardless of the morphing behavior, the networks exhibited memory of the as-spun configuration and returned to it upon heating.
To better characterize the transition between the two morphing behaviors, we constructed an inhomogeneous network architecture in which the distribution of non-responsive fibers varied along the horizontal axis while the responsive fibers were uniformly distributed along the vertical axis (Fig. 3A). In this architecture, the node-to-node distance, L, changes along each responsive PNcG fiber, while the radius and Young modulus of the fiber remain constant. This approach enabled us to change the node-to-node distances along the responsive fibers and effectively isolate the influence of L on the morphing behavior of the same fiber under controlled experimental conditions. Fig. 3B shows a time-lapse sequence of the morphing observed in a representative network of PNcG (horizontal) and PVCi (vertical) fibers with a variable mesh size along the horizontal axis (Movie S1 in ESI†). At t = 0, the network was immersed in water at 60 °C, above the LCST. At this stage, both the responsive and non-responsive fibers remained relatively straight. As the water temperature dropped below 32 °C, the responsive fibers underwent two distinct morphing behaviors depending on the mesh size dictated by the non-responsive fibers. Within dense regions with a small mesh size (indicated in pink), the responsive segments swelled and elongated linearly without buckling, preserving the network's Cartesian structure. However, in regions characterized by a larger mesh size (indicated in blue), the responsive fibers displayed significant in-plane buckling during swelling, diminishing the Cartesian structure. Notably, the non-responsive fibers remained straight through the process. The process was reversible, and the network retained its original shape when the temperature was reset to 60 °C. The morphing behaviors of the segments in all the networks described above and previously examined isotropic networks suggest that the change in morphing behavior can be attributed to dimensions and the mechanical properties of the filament positioned between two neighboring nodes. If the segments are approximated as Euler–Bernoulli beams, then buckling should occur if the segment is exposed to a stress that is equal to or larger than a critical Euler buckling stress, defined as
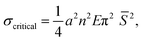 | (1) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) is the reciprocal slenderness defined as
is the reciprocal slenderness defined as 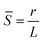 , where r is the beam's radius, and L is its length. The presence of buckling in some segments suggests internal stresses caused by swelling, as no external stresses are imposed on the networks. The internal stresses can be related to inhomogeneities in the swelling throughout the network and geometrical frustrations that occur due to the slow translational response of the entire network compared to the fast swelling of the single fiber. It should also be noted that Euler critical stress is calculated for a static beam, whereas the responsive fiber softens significantly as it swells, and its Young modulus decreases during the process.
, where r is the beam's radius, and L is its length. The presence of buckling in some segments suggests internal stresses caused by swelling, as no external stresses are imposed on the networks. The internal stresses can be related to inhomogeneities in the swelling throughout the network and geometrical frustrations that occur due to the slow translational response of the entire network compared to the fast swelling of the single fiber. It should also be noted that Euler critical stress is calculated for a static beam, whereas the responsive fiber softens significantly as it swells, and its Young modulus decreases during the process. ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) also changes slightly throughout the swelling process due to different swelling along and perpendicular to the fiber's main axis. Unlike the PNcG fibers, the non-responsive fibers of both PMMA and PVCi did not exhibit significant buckling in any of the tested networks, indicating that their critical buckling stress exceeds the network-induced stresses. To further analyze the shape-morphing behavior and its dependence on the filament parameters, a quantitative indicator for the buckling extent is required. A convenient indicator is the maximum deflection of the segment from its original straight configuration, denoted as ψ (Fig. 4A, inset). In the case of a perfectly straight segment, ψ is equal to zero, and as the degree of buckling increases, the value of ψ also increases. ψ can be regarded as an order parameter, indicating the extent of symmetry breaking from the straight configuration, where a value of ψ = 40 μm was arbitrarily determined as the border between the straight and deflected states. Using deflection as a key parameter, we analyzed the morphing behavior of 237 segments from 34 different fibers. Fig. 4A depicts a color map of the order parameter for different segments as a function of the reciprocal slenderness and Young modulus, calculated from the swelling ratio of the fibers using the Flory–Rehner equation (see Section S2 in ESI†). Each segment is marked as a single point in the graph. Segments with low reciprocal slenderness exhibit significant buckling, while those with high reciprocal slenderness maintain their straight configuration. The map indicates a clear border between the two behaviors as a function of
also changes slightly throughout the swelling process due to different swelling along and perpendicular to the fiber's main axis. Unlike the PNcG fibers, the non-responsive fibers of both PMMA and PVCi did not exhibit significant buckling in any of the tested networks, indicating that their critical buckling stress exceeds the network-induced stresses. To further analyze the shape-morphing behavior and its dependence on the filament parameters, a quantitative indicator for the buckling extent is required. A convenient indicator is the maximum deflection of the segment from its original straight configuration, denoted as ψ (Fig. 4A, inset). In the case of a perfectly straight segment, ψ is equal to zero, and as the degree of buckling increases, the value of ψ also increases. ψ can be regarded as an order parameter, indicating the extent of symmetry breaking from the straight configuration, where a value of ψ = 40 μm was arbitrarily determined as the border between the straight and deflected states. Using deflection as a key parameter, we analyzed the morphing behavior of 237 segments from 34 different fibers. Fig. 4A depicts a color map of the order parameter for different segments as a function of the reciprocal slenderness and Young modulus, calculated from the swelling ratio of the fibers using the Flory–Rehner equation (see Section S2 in ESI†). Each segment is marked as a single point in the graph. Segments with low reciprocal slenderness exhibit significant buckling, while those with high reciprocal slenderness maintain their straight configuration. The map indicates a clear border between the two behaviors as a function of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) and of the Young modulus (marked in a dashed line), and can be interpreted as a phase transition diagram.
and of the Young modulus (marked in a dashed line), and can be interpreted as a phase transition diagram.
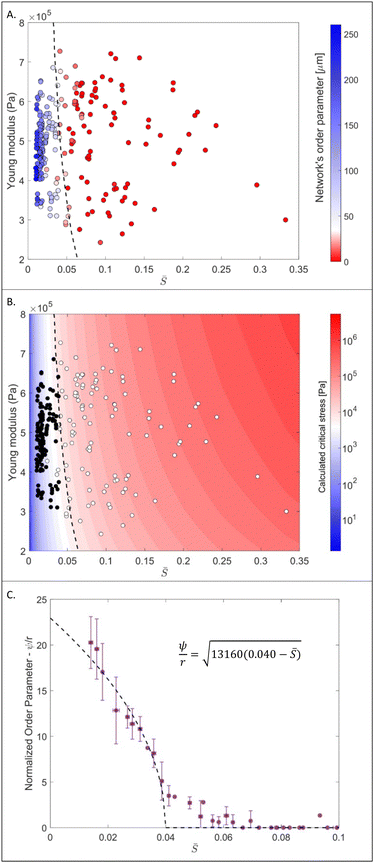 | ||
Fig. 4 (A) A color map of the order parameter as function of the reciprocal slenderness, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , and of the Young modulus indicating the phase transition boundary between the two morphing behaviors. Inset shows an illustration of a buckled beam and its deflection, ψ. (B) A map of the critical buckling stress as a function of , and of the Young modulus indicating the phase transition boundary between the two morphing behaviors. Inset shows an illustration of a buckled beam and its deflection, ψ. (B) A map of the critical buckling stress as a function of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) and the Young modulus. Circles represent the position of the examined segment on the map. Filled circles represent the buckling-governed regime and the empty circles represent the linear extension regime. The dashed black contour line represents critical buckling stresses of 10 kpa. (C) The averaged normalized order parameter for different segments as function of and the Young modulus. Circles represent the position of the examined segment on the map. Filled circles represent the buckling-governed regime and the empty circles represent the linear extension regime. The dashed black contour line represents critical buckling stresses of 10 kpa. (C) The averaged normalized order parameter for different segments as function of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) (purple dots) and the fit according to eqn (7) (dashed line). The critical reciprocal slenderness, (purple dots) and the fit according to eqn (7) (dashed line). The critical reciprocal slenderness, 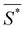 , is 0.040. Error bars represent the standard deviation. , is 0.040. Error bars represent the standard deviation. | ||
Fig. 4B presents a map of the expected Euler critical buckling stress (in logarithmic scale) as a function of the reciprocal slenderness and the Young modulus calculated according to eqn (1). Measured segments are depicted on this map in circles, with filled circles representing segments with ψ ≥ 40 μm that exhibit buckling upon swelling, and empty circles represent segments with ψ < 40 μm that preserve their linear morphology. The map shows that the transition between the morphing behaviors, as indicated by the deflection, occurs for a critical stress of about 10 kPa. Thus, segments with critical stress below that value buckle while those with higher critical stress stay straight. Interestingly, this value is derived from all the segments in different networks and indicates that a similar stress of ∼10 kPa develops throughout the swelling process for all the networks. The transition between morphing behaviors shown in Fig. 4A and B calls for examining the analogy to classical phase transitions. Indeed, several works indicated the resemblance between beam buckling and Landau phase transition.36–38 Here, we derive the analogy following the formalism suggested by Savel’ev and Nori for a beam under external force.36 We show here only the primary outcome of the derivation, which is described in detail in Section S3 of the ESI.† For a segment of length L, radius r, and Young modulus E, the mechanical energy of a segment, F, under an externally applied stress σ*, is given by:
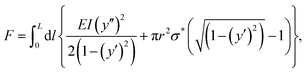 | (2) |
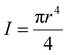 , and y is the contour of the beam with respect to the beam axis coordinate, l. All the derivatives are taken with respect to the beam axis coordinate, l. The first term of the integral provides the energy due to buckling, while the second term is the mechanical work performed by the force. For the sake of simplicity, we assume no moments are exerted on the segments at the initial unswollen state. This is an approximation for the experimental system, in which moments may be formed due to minor network fabrication defects or external factors. However, as can be seen in Fig. 2 and 3 and Movie S1 (ESI†), these primarily affect the segments at the edge of the network yet are relatively small and negligible in controlling the morphing process of the inner segments.
, and y is the contour of the beam with respect to the beam axis coordinate, l. All the derivatives are taken with respect to the beam axis coordinate, l. The first term of the integral provides the energy due to buckling, while the second term is the mechanical work performed by the force. For the sake of simplicity, we assume no moments are exerted on the segments at the initial unswollen state. This is an approximation for the experimental system, in which moments may be formed due to minor network fabrication defects or external factors. However, as can be seen in Fig. 2 and 3 and Movie S1 (ESI†), these primarily affect the segments at the edge of the network yet are relatively small and negligible in controlling the morphing process of the inner segments.
If we assume the segment is regarded as a clamped Euler beam (y = 0 and y′ = 0 at l = 0 and l = L), the beam contour obtained from Euler analysis is:
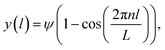 | (3) |
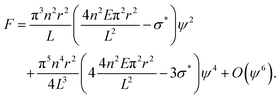 | (4) |
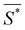 , for which the stress
, for which the stress 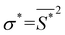 will cause buckling. Substituting this expression into eqn (4) yields:
will cause buckling. Substituting this expression into eqn (4) yields: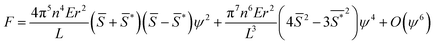 | (5) |
![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , is the driving parameter corresponding to temperature in the standard expression, and the amplitude, ψ, acts as the order parameter.
, is the driving parameter corresponding to temperature in the standard expression, and the amplitude, ψ, acts as the order parameter.
The order parameter that minimizes the energy can be found by solving the equation 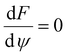 , which yields that the relation between the order parameter and the driving parameter in proximity to the critical reciprocal slenderness (
, which yields that the relation between the order parameter and the driving parameter in proximity to the critical reciprocal slenderness (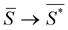 ) is:
) is:
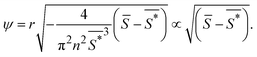 | (6) |
However, this expression depends on the radius of the fiber. To attain a general expression for segments of different radii, the amplitude can be divided by r, generating a normalized order parameter:
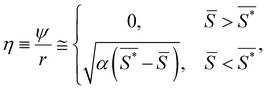 | (7) |
Fig. 4C shows the averaged normalized order parameter for different segments as a function of the reciprocal slenderness, ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , (purple dots) and the fit to these experimental results according to eqn (7) (dashed black line). There is a high level of agreement between the values obtained from the experimental results and the theoretical expression, indicating a critical slenderness of
, (purple dots) and the fit to these experimental results according to eqn (7) (dashed black line). There is a high level of agreement between the values obtained from the experimental results and the theoretical expression, indicating a critical slenderness of 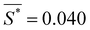 .
.
The change in the morphing behavior occurs on the filament level at the microscale and propagates through the hierarchical network structures to induce morphological changes at the macroscale. Since the network structure is primarily defined by its nodes, the dimensions of the network are determined by the distance between adjacent nodes along the network. Thus, in regions where the filaments undergo shape-preserving morphing and remain straight, as depicted in pink in Fig. 3B, the distance between the nearest neighbor nodes is equal to the length of the connecting filament. Upon swelling of the filaments, the entire network expands, and the local swelling ratio of the network is comparable to that of the single filaments. This outcome is expected because the change in the filament length induces compressive stress that is distributed uniformly along the main axis of the fiber, resulting in the motion of the nodes along this direction, which leads to the swelling of the network.
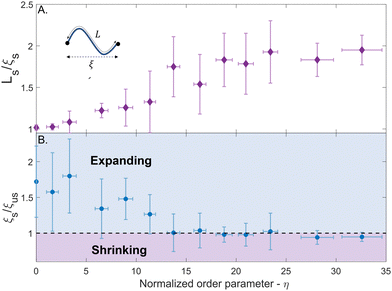
The relationship between the morphing behavior of the network and the filament morphing in the buckling-governed regime is more intricate. Buckling leads to a considerable modification in stress distribution within the filament. The compressive stress in the filament becomes highly concentrated near the points of maximum deflection, whereas the stress in the remaining regions of the filament and near the nodes reduces significantly. Under these conditions, the distance between the nodes is expected to be smaller than the longitudinal swelling of the filaments, and the network will exhibit significantly less swelling compared to the shape-preserving scenario. To examine this, the ratio between the filament length, Ls, and the node-to-node distance, ξs, in the swollen state was measured for 237 segments, and the average value normalized order parameter, η, of the segments, is portrayed in Fig. 5A (errors represent the standard deviation). This ratio equals 1 for linearly extending segments and increases with the normalized order parameter, indicating that the length of the filaments increases more rapidly than the node-to-node distance.
Nevertheless, upon examining the dimensions of the regions in the networks that exhibit buckling-governed morphing, e.g., the area that is depicted in Fig. 3B in blue, a surprising observation arises – not only that the network in this region does not elongate upon swelling of the filaments, but it significantly contracts in length to about 1.5 times less than in the unswollen state. To examine this phenomenon, we compared the distance between the adjacent nodes in the swollen and unswollen networks (ξs and ξus respectively) for the same segments that were measured in Fig. 5A. Fig. 5B illustrates the average ratio ξs/ξus along the PNcG fibers as a function of the normalized order parameter, η (errors represent the standard deviation). For low-order parameters, the ratio is greater than 1, indicating swelling of the network. As the order parameter increases, the ratio decreases, eventually going below 1 for η > 17. The contraction of the network at high-order parameters is counterintuitive and reminiscent of negative compressibility. In most materials, applying a longitudinal force leads to a longitudinal deformation. However, in materials with negative compressibility, the longitudinal deformation opposes the longitudinal applied force. Hence, the system contracts under tension and dilates under pressure. Here, upon longitudinal swelling of the fibers, the network contracts. A plausible explanation for the observed behavior could be attributed to the spontaneous shearing of the network in a direction perpendicular to the axis of the PNcG fibers. Fig. S1 in the ESI,† displays the node-to-node pathways of the PNcG fibers atop the network shown in Fig. 3B. In the buckling-governed regimes, during the progression of the morphing process, several non-responsive fibers (and their associated nodes) exhibit considerable vertical translation along their primary axis. This motion can be interpreted as a shearing of the network. Due to this shearing, the responsive fiber segments that are linked to the moving fiber are pulled, reducing their buckling. This reduction is energetically favorable since it decreases the buckling energy without increasing the stretching energy of the segment. However, the pulling reaction of the responsive fibers leads to the pulling of the non-responsive fibers in the opposite direction, resulting in a decrease in the distance between them and the contraction of the network in a scissors mechanism. Such shearing requires buckling of the fibers and hence cannot occur in the shape-preserving regions where the critical buckling load is high.
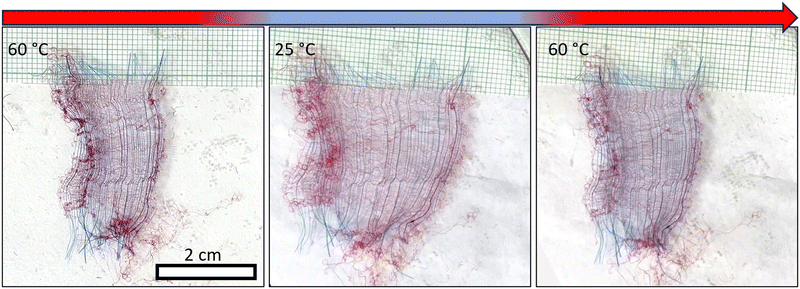
All the findings mentioned above have been examined within the confines of relatively small networks characterized by an area of approximately a square millimeter. This prompts the question of whether controllability over directional deformations and structural changes can be extrapolated to macroscale networks. To investigate this prospect, we meticulously assembled macroscale anisotropic networks measuring 4 centimeters along the inert axis and 2 centimeters along the responsive axis—dimensions spanning three to four orders of magnitude larger than the fiber diameter and length, respectively. Fig. 6 and Movie S2 (ESI†) show the reversible shape-morphing of a macro-network with an average swollen segment length of 450 μm and radius of r = 25 μm, corresponding to an average reciprocal slenderness of ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) = 0.06. Such a network is anticipated to be shape-preserving and extend anisotropically as it swells. Indeed, it manifests a swelling ratio of 1.73, a value consistent with the swelling ratios observed in individual microscale segments, as illustrated in Fig. 5B. In macro-networks with lower
= 0.06. Such a network is anticipated to be shape-preserving and extend anisotropically as it swells. Indeed, it manifests a swelling ratio of 1.73, a value consistent with the swelling ratios observed in individual microscale segments, as illustrated in Fig. 5B. In macro-networks with lower ![[S with combining macron]](https://www.rsc.org/images/entities/i_char_0053_0304.gif) , in which the morphing is governed by fiber buckling, no swelling was observed. Thus, the microscale morphing is maintained also when increasing the size of the networks to centimeters. Notably, larger networks are susceptible to the presence of defects, including loose responsive fibers, which can be easily identified by their constant buckled state in both swollen and unswollen states. Akin buckling behavior is also observed at the periphery of the network in the free ends of the fibers. In addition, larger networks are submerged within a more substantial volume of water, resulting in extended heating and cooling cycles and correspondingly protracted morphing durations compared to their micro-network counterparts.
, in which the morphing is governed by fiber buckling, no swelling was observed. Thus, the microscale morphing is maintained also when increasing the size of the networks to centimeters. Notably, larger networks are susceptible to the presence of defects, including loose responsive fibers, which can be easily identified by their constant buckled state in both swollen and unswollen states. Akin buckling behavior is also observed at the periphery of the network in the free ends of the fibers. In addition, larger networks are submerged within a more substantial volume of water, resulting in extended heating and cooling cycles and correspondingly protracted morphing durations compared to their micro-network counterparts.
Conclusions
In conclusion, we demonstrated the fabrication and characterization of microscale and macroscale anisotropic shape-morphing networks composed of thermoresponsive and non-responsive microfibers. Through a hierarchical construction of the networks and precise positioning of fibers with different responses, we successfully demonstrated the ability to induce directional actuation of the networks. The shape-morphing of individual segments within the network can exhibit one of two distinct behaviors: buckling or linear extension, depending on the radius and length of the segment and the Young modulus of the polymer. The transition between these two morphing behaviors follows a second-order athermal Landau phase transition-like behavior, where the buckling amplitude serves as the order parameter, while the reciprocal slenderness acts as the effective temperature. The disparities in morphing behaviors upon swelling result in significant differences in the macroscale morphing of the network itself, where regions of linear extension preserve their Cartesian structure and exhibit swelling. In contrast, buckling-governed regions experience shrinking compared to the unswollen state and exhibit internal negative compressibility. The hierarchical control of the macroscale morphing through adjustments of the microscale components offers new insights regarding the physical behavior of shape-morphing structures constructed of soft microscale filaments. It also introduces a novel approach for modulating the morphing and programming responsive systems with a mesoscale resolution, thereby enabling innovative applications in tissue engineering, soft robotics, and micro-actuation.Experimental methods
Materials
N-Isopropyl acrylamide (NIPAAm) 99%, glycidyl methacrylate (GMA), and 2,2′-azobis (2-methyl propionitrile) (AIBN) were purchased from Alfa Aesar. Toluene (anhydrous, 99.8%), dimethylformamide (DMF), tetrahydrofuran (THF), chloroform, dichloromethane (DCM), hexane, tetraethylenepentamine (TEPA), polyvinyl cinnamate (PVCi), and poly methyl methacrylate (PMMA) were purchased from Sigma-Aldrich. Diethyl ether was purchased from BioLab. All the materials were used as bought without further purification.Copolymer synthesis
The copolymer poly(N-isopropyl acrylamide-co-glycidyl methacrylate) PNcG was synthesized as was previously reported.29 NIPAAm, GMA, and AIBN were dissolved in toluene, and the monomers were allowed to polymerize for two hours at 70 °C. Then, the copolymer was redissolved in DCM and precipitated by dropwise addition of diethyl ether. The precipitate was removed from the solution by filtration and redissolved in DCM and hexane. Finally, the solution was evaporated, and the product was dried under vacuum overnight.Network fabrication
The 2D Cartesian networks were fabricated via the dry-spinning process, using thermoresponsive fibers in one axis and non-responsive fibers in the orthogonal axis. The dry-spinning was chosen to create stable jetting and accurate structures. In a typical jetting process, the solution was dispensed through a metallic needle. When a drop was formed at the end of the capillary, it was drawn toward a rotating drum. In this process, the solvents evaporated rapidly throughout the drawing until the solidification of a thin fiber. The fiber is attached and drawn by a rotating drum with a radius of Rd and angular velocity of ωd. The drum is positioned on a moving stage with a velocity of Vs perpendicular to the drum rotation. The distance between the adjacent fibers is given by d = Vs/(Rd·ωd), so the velocity of the stage is determined by the angular velocity of the drum and the wanted distance between the fibers. First, the thermoresponsive PNcG fibers were collected on a plastic frame that was attached to a drum; hence, they were collected parallel to the direction of the rotation. Next, the frame was detached from the rotating drum and reattached after rotating it at an angle of 90°. Next, one of the non-responsive solutions was dispensed via a metallic gauge needle.To fabricate thermoresponsive fibers, a 0.50–0.75 g mL−1 solution was prepared by dissolving PNcG in a mixture of chloroform and DMF (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v). 6% of TEPA was added before the jetting process. PVCi and PMMA were chosen to fabricate non-responsive fibers. 0.7 g of PVCi was dissolved in 1 mL of a mixture of THF and DMF (6
1 v/v). 6% of TEPA was added before the jetting process. PVCi and PMMA were chosen to fabricate non-responsive fibers. 0.7 g of PVCi was dissolved in 1 mL of a mixture of THF and DMF (6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4 v/v). 0.3 g of PMMA was dissolved in 1 mL of a mixture of DMF and chloroform (1
4 v/v). 0.3 g of PMMA was dissolved in 1 mL of a mixture of DMF and chloroform (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 v/v).
1 v/v).
For constructing Cartesian networks, the PNcG solution was dispensed via a metallic needle at a flow rate of 0.006–0.020 mL h−1. The rotating speed of the drum was 14–30 mm s−1. A linear stage velocity of 0.05–0.35 mm s−1 was set according to the rotating velocity to obtain the desired gaps. The non-responsive fibers solutions were dispensed via a metallic gauge needle at a flow rate of 0.014 mL h−1 for the PMMA solution and 0.140 mL h−1 for the PVCi solution. The rotating speed of the drum was 7 mm s−1 for the PMMA solution and 14 mm s−1 for the PVCi solution. To create a density gradient, the stage velocity was varied from 0.12 to 0.50 mm s−1 for PMMA fibers and from 0.17 to 2.16 mm s−1 for the PVCi fibers. Finally, the networks were cured post-fabrication at 70 °C overnight in an oven.
Instrumentation
Scanning electron microscopy (SEM) was performed using a Zeiss GeminiSEM 300 in a high vacuum, WD ∼7 mm, 3 kV. All images and videos were taken with an Olympus IX73 microscope equipped with a heating glass slide (LCI, CU-301). The spinning setup included a syringe pump (New Era), a linear motion stage (ILS-200LM, Newport), an eight-axis universal controller (XPS-D8, Newport), and a rotating drum collector.Author contributions
S. Z. S. and A. S. conceived of and designed the project. S. Z. S., N. E. P., and T. R. synthesized the copolymer. S. Z. S. and M. M. carried out SEM measurements. S. Z. S., E. L., M. A., and N. H. prepared the samples, carried out optical microscopy measurements, and analyzed the data. A. S. supervised the research.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was funded by generous support from the Israel Science Foundation (grant no. 1682/22) and the Army Research Office (Grant Number W911NF-23-1-0257). The views and conclusions contained in this document are those of the authors and should not be interpreted as representing the official policies, either expressed or implied, of the Army Research Office or the U.S. Government. The U.S. Government is authorized to reproduce and distribute reprints for Government purposes notwithstanding any copyright notation herein. S. Z. S. and N. E.-P. acknowledge the generous support of The Shulamit Aloni Scholarship for Advancing Women in Exact Science and Engineering, provided by The Ministry of Science Technology, Israel. The authors acknowledge the Chaoul Center for Nanoscale Systems of Tel Aviv University for the use of instruments and staff assistance, and the Mechanical Workshop for Research and Development, School of Chemistry, Tel Aviv University, for their help in constructing the fabrication devices.Notes and references
- J. Wang, D. Gao and P. S. Lee, Adv. Mater., 2021, 33, 2003088 CrossRef CAS PubMed.
- N. Park and J. Kim, Adv. Intell. Syst., 2020, 2, 1900135 CrossRef.
- H. Kim, S. Kyun Ahn, D. M. Mackie, J. Kwon, S. H. Kim, C. Choi, Y. H. Moon, H. B. Lee and S. H. Ko, Mater. Today, 2020, 41, 243–269 CrossRef CAS.
- X. Liu, M. Gao, J. Chen, S. Guo, W. Zhu, L. Bai, W. Zhai, H. Du, H. Wu, C. Yan, Y. Shi, J. Gu, H. J. Qi and K. Zhou, Adv. Funct. Mater., 2022, 32, 2203323 CrossRef CAS.
- J. Wong, A. Basu, M. Wende, N. Boechler and A. Nelson, ACS Appl. Polym. Mater., 2020, 2, 2504–2508 CrossRef CAS.
- B. Yiming, T. Liu, G. Nian, Z. Han, Z. Jia and S. Qu, Extrem. Mech. Lett., 2020, 35, 100643 CrossRef.
- Z. L. Wu, M. Moshe, J. Greener, H. Therien-aubin, Z. Nie, E. Sharon and E. Kumacheva, Nat. Commun., 2013, 4, 1586 CrossRef PubMed.
- E. Siéfert, E. Reyssat, J. Bico and B. Roman, Nat. Mater., 2019, 18, 24–28 CrossRef PubMed.
- L. R. Meza, S. Das and J. R. Greer, Science, 2014, 345, 1322–1326 CrossRef CAS PubMed.
- X. Xia, C. M. Spadaccini and J. R. Greer, Nat. Rev. Mater., 2022, 7, 683–701 CrossRef PubMed.
- M. Kucewicz, P. Baranowski, J. Małachowski, A. Popławski and P. Płatek, Mater. Des., 2018, 142, 177–189 CrossRef.
- X. Yu, J. Zhou, H. Liang, Z. Jiang and L. Wu, Prog. Mater. Sci., 2018, 94, 114–173 CrossRef.
- K. K. Dudek, J. A. I. Martínez, G. Ulliac and M. Kadic, Adv. Mater., 2022, 34, 2110115 CrossRef CAS PubMed.
- A. Nojoomi, J. Jeon and K. Yum, Nat. Commun., 2021, 12, 1–8 CrossRef PubMed.
- Y. Klein, E. Efrati and E. Sharon, Science, 2007, 315, 1116–1120 CrossRef CAS PubMed.
- L. Dong, J. Wang and D. Wang, Addit. Manuf., 2023, 69, 103532 Search PubMed.
- X. Fan, C. Deng, H. Gao, B. Jiao, Y. Liu, F. Chen, L. Deng and W. Xiong, Sci. Adv., 2022, 8, 1–11 Search PubMed.
- J. Mueller, J. A. Lewis and K. Bertoldi, Adv. Funct. Mater., 2022, 32, 2105128 CrossRef CAS.
- M. F. Ashby, Metall. Trans. A, 1983, 14, 1755–1769 CrossRef.
- A. S. Gladman, Elisabetta A. Matsumoto, Ralph G. Nuzzo, L. Mahadevan and J. A. Lewis, Nat. Mater., 2016, 15, 413–419 CrossRef PubMed.
- J. W. Boley, W. M. Van Rees, C. Lissandrello, M. N. Horenstein, R. L. Truby, A. Kotikian, J. A. Lewis and L. Mahadevan, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 20856–20862 CrossRef CAS PubMed.
- A. Gregg, M. F. L. De Volder and J. J. Baumberg, Adv. Opt. Mater., 2022, 10, 2200180 CrossRef CAS.
- S. Li, B. Deng, A. Grinthal, A. Schneider-Yamamura, J. Kang, R. S. Martens, C. T. Zhang, J. Li, S. Yu, K. Bertoldi and J. Aizenberg, Nature, 2021, 592, 386–391 CrossRef CAS PubMed.
- X. Cheng, Z. Fan, S. Yao, T. Jin, Z. Lv, Y. Lan, R. Bo, Y. Chen, F. Zhang, Z. Shen, H. Wan, Y. Huang and Y. Zhang, Science, 2023, 379, 1225–1232 CrossRef CAS PubMed.
- L. Liu, S. Jiang, Y. Sun and S. Agarwal, Adv. Funct. Mater., 2016, 26, 1021–1027 CrossRef CAS.
- S. Jiang, F. Liu, A. Lerch, L. Ionov and S. Agarwal, Adv. Mater., 2015, 27, 4865–4870 CrossRef CAS PubMed.
- Q. He, Z. Wang, Y. Wang, Z. Wang, C. Li, R. Annapooranan, J. Zeng, R. Chen and S. Cai, Sci. Robot., 2021, 6, eabi9704 CrossRef PubMed.
- S. Moon, M. S. Jones, E. Seo, J. Lee, L. Lahann, J. H. Jordahl, K. J. Lee and J. Lahann, Sci. Adv., 2021, 7, eabf5289 CrossRef CAS PubMed.
- S. Ziv Sharabani, N. Edelstein-Pardo, M. Molco, N. Bachar Schwartz, M. Morami, A. Sivan, Y. Gendelman Rom, R. Evental, E. Flaxer and A. Sitt, Adv. Funct. Mater., 2022, 32, 2111471 CrossRef CAS.
- J. H. Jordahl, L. Solorio, H. Sun, S. Ramcharan, C. B. Teeple, H. R. Haley, K. J. Lee, T. W. Eyster, G. D. Luker, P. H. Krebsbach and J. Lahann, Adv. Mater., 2018, 30, 1707196 CrossRef PubMed.
- D. Nahm, F. Weigl, N. Schaefer, A. Sancho, A. Frank, J. Groll, C. Villmann, H. W. Schmidt, P. D. Dalton and R. Luxenhofer, Mater. Horizons, 2020, 7, 928–933 RSC.
- D. J. Wu, N. H. Vonk, B. A. G. Lamers, M. Castilho, J. Malda, J. P. M. Hoefnagels and P. Y. W. Dankers, Eur. Polym. J., 2020, 141, 110099 CrossRef CAS.
- M. Javadzadeh, J. del Barrio and C. Sánchez-Somolinos, Adv. Mater., 2023, 35, 2209244 CrossRef CAS PubMed.
- H. G. Schild, Prog. Polym. Sci., 1992, 17, 163–249 CrossRef CAS.
- A. Halperin, M. Kröger and F. M. Winnik, Angew. Chem., 2015, 54, 15342–15367 CrossRef CAS PubMed.
- S. Savel’ev and F. Nori, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 1–19 CrossRef.
- J. Bobnar, K. Susman, V. A. Parsegian, P. R. Rand, M. Čepič and R. Podgornik, Eur. J. Phys., 2011, 32, 1007–1018 CrossRef.
- D. O. Margaretta, N. Amalia, F. D. Utami, S. Viridi and M. Abdullah, J. Taibah Univ. Sci., 2019, 13, 1128–1136 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Uniform Cartesian network analysis, Flory–Rehner equation, using phase transition formalism for describing buckling of a beam, figure of shearing within buckling-governed morphing regimes, detailed experimental section, Movie S1 of a representative network of PNcG and PVCi fibers, with a variable mesh size along the horizontal axis, Movie S2 of a macroscale network exhibiting swelling and shrinking upon temperature changes. See DOI: https://doi.org/10.1039/d3sm01753b |
| This journal is © The Royal Society of Chemistry 2024 |