Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Impact of anti-coagulant choice on blood elongational behavior
Jorge Eduardo
Fiscina
*a,
Alexis
Darras
b,
Daniel
Attinger
c and
Christian
Wagner
 bd
bd
aSaarland University, Physics Department, 66123 Saarbruecken, Germany. E-mail: j.fiscina@mx.uni-saarland.de
bSaarland University, Physics Department, 66123 Saarbruecken, Germany
cStruo LLC, Ames, Iowa 50010, USA
dUniversity of Luxemburg, Physics and Materials Science Research Unit, 1511 Luxembourg, Luxembourg
First published on 16th May 2024
Abstract
Blood is a highly complex fluid with rheological properties that have a significant impact on various flow phenomena. In particular, it exhibits a non-Newtonian elongational viscosity that is comparable to polymer solutions. In this study, we investigate the effect of three different anticoagulants, namely EDTA (ethylene diamine tetraacetic acid), heparin, and citrate, on the elongational properties of both human and swine blood. We observe a unique two stage thinning process and a strong dependency of the characteristic relaxation time on the chosen anticoagulant, with the longest relaxation time and thus the highest elongational viscosity being found for the case of citrate. Our findings for the latter are consistent with the physiological values obtained from a dripping droplet of human blood without any anticoagulant. Furthermore, our study resolves the discrepancy found in the literature regarding the reported range of characteristic relaxation times, confirming that the elongational viscosity must be taken into account for a full rheological characterization of blood. These results have important implications for understanding blood flow in various physiological, pathological and technological conditions.
1 Introduction
Blood is a complex fluid that exhibits a range of rheological properties, including shear thinning, viscoelasticity, thixotropy, and yield stress, particularly at physiological hematocrit.1–4 Recently, it has been demonstrated that blood also displays a high elongational viscosity.5–9 This behavior arises from the elasticity of plasma proteins, similar to that observed for flexible synthetic polymers.10–15 The presence of an elevated elongational viscosity can have a significant impact on various flow phenomena, such as turbulent drag reduction,16,17 viscoelastic instabilities,18–20 and inhibition of drop splashing.21 Therefore, a quantitative understanding of the magnitude of the elongational viscosity is essential for studying physiological blood flow, including vascular flow instabilities,22 as well as for the design and optimization of biomedical devices, such as cell sorters23 and ventricular assist devices,24 and for forensic investigations of blood stains.9,25,26Measuring the elongational viscosity of low-viscosity fluids is a challenging task. Besides some microfluidic technologies,27 the most established method is the capillary break-up extensional rheometry (CaBER) that involves observing the thinning process of a capillary bridge between two plates that are drawn apart. While the neck of a Newtonian fluid breaks up into self-similar solutions,28 the change of the conformational state of the polymers and the resulting build-up of elastic stresses inhibits breakage. This results typically in the formation of a cylindrical filament with a pure elongational flow29 that thins exponentially over time. Alternatively, one can also observe the capillary thinning of dripping droplets, but in general, CaBER offers better control of the thinning process and better image quality.30,31 Recently the dripping-on-substrate technique was introduced as an alternative method to characterise the elongational properties of low viscous non-Newtoinan fluids.32 The balance of capillary pressure and elastic stresses leads to an exponential thinning behavior, and in some cases the characteristic timescale λC can be indirectly related to the polymer relaxation time via scaling laws.14,33 Additionally, λC is directly proportional to the apparent elongational viscosity, which can be orders of magnitude larger than the shear viscosity measured in standard rheometers.12 It is important to note that the capillary bridge shrinks only due to capillary forces with an elongational rate that is, according to the simple models, exactly 3 times the polymer relaxation time. Consequently, one cannot give any statement on the rate dependent elongational viscosity.13
The shear thinning and (visco-)elastic properties of blood in shear rheology result mostly from the formation of aggregates of red blood cells at low shear rates and stasis, the so-called rouleaux. They form a weak, fragile colloidal gel which leads to a small yield stress and shear thinning at larger shear rates.3,4 The blood cells are suspended in an aqueous buffer solution, the plasma, that contains in average 70 g l−1 of proteins, of which some have a large molecular weight of up to 1.3 Mio amu. The plasma itself has no measurable elastic effect in shear rheometry, only a surface layer of proteins at the plasma-air interface can lead to misleading data and of course such a surface film does not exist in physiological flow.34 It was shown in two independent studies by replacing the surrounding air by oil in a CaBER experiment that such a protein surface film does not play a significant role in capillary thinning experiments of blood.5,7
In pure elongational flow, polymers are aligned with the flow and most efficiently stretched which leads to the high elongational viscosity. Consequently, the plasma proteins are the microscopic constituents that are responsible for the elongational properties of blood and washed red blood cells in a buffer solution without any proteins do not show any viscoelastic filament in capillary thinning experiments,5 but of course the presence of the red blood cells can still alter the pinch-off process of the Newtonian suspending medium.35,36 Of course, the red blood cells experience a strong elongational flow field that might lead to strong deformations or even haemolysis,37,38 but those effects are beyond the scope of this study. While there is now unanimous agreement that plasma and thus also blood have an extensional viscosity, the statements about the characteristic time scale λC vary by more than an order of magnitude.5–9 Even if the specific protocol of the capillary break-up measurement might play a role here, this effect is much too large for being the sole mechanism. We therefore hypothesized that the anticoagulant in use might play an important role.
In this study, we compare the effect of EDTA (ethylene diamine tetraacetic acid), heparin, and citrate on the elongational properties of blood. All three are commonly used anticoagulants in clinical settings and they work by different mechanisms to prevent blood from clotting. Anticoagulation is achieved either by the binding of calcium ions (EDTA, citrate) or by the inhibition of thrombin (heparin). However, the biochemical effects of these substances is far more complex and goes beyond the scope of our study.39–41 To test the generality of our findings and due to its relevance as a replacement fluid for in vitro studies, we performed this study not only on human blood but also on swine blood.9
2 Materials and methods
2.1 Experimental set-up
The capillary break-up extensional rheometer set-up is a lab-made upgrade of the apparatus described in a previous work.31 It consists of two copper discs with a diameter of 4 mm, where the lower disc is fixed and the upper disc can be moved in the z-direction with a linear motor (P01-23 × 80, Linmot, Spreitenbach, Switzerland). A droplet of blood with a specified volume is placed with a micro-pipette between the two plates. The initial gap distance between the disks is 2 mm and the linear motor pulls the upper disk with a constant speed of 0.1 mm s−1, according to the slow retraction method (SRM) that is best suited for low viscous fluids with short relaxation times.30 The pending (dripping) droplet experiments is done by connecting a reservoir filled with the anticoagulant-treated blood to a Teflon nozzle with a diameter of 2 mm or, for the case of the untreated blood, by connecting a Teflon tube from a venous punctured person directly to the nozzle. The dripping frequency is controlled by a manual valve (Discofix 3SC, B. Braun Melsungen AG,Germany) which allows to tune the hydraulic resistance of the Teflon tube. For all experiments, an LED illumination (ZLED CLS 9000, Zett Optics GmbH, Braunschweig, Germany) is used to project a shadow image of the capillary bridge. All experiments were performed at room temperature (22 °C). Due to the small diameter of the Teflon tube, we assume that the untreated blood from the venous punctured person has reached room temperature when it reaches the nozzle. We follow the evolution of the filament with a 10-bit high-speed camera (X-Stream XS-5, IDT, Tallahassee, USA) at up to 1.54 kHz frame rate and down to 0.65 ms shutter time. The camera has 1280 × 1024 pixels with a size of μm × μm, and we use a 10× microscope objective with 4 mm working distance (Plan Apo, Nikon, Minato, Japan) attached to the camera via a tubus lens (InfiniTube, Edmund Optics, Barrington, USA). The minimum radius of the capillary bridge is detected using self-written image analysis software,31 and once the parallel filament is formed, we use the following equation to fit the temporal evolution of the radius h(t):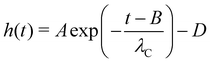 | (1) |
2.2 Materials
Human blood is collected from four healthy donors by venipuncture in EDTA-, heparin- or citrate-containing tubes (S-Monovette, Sarstedt, Nümbrecht, Germany). Only for the blood dripping experiment without any anticoagulant, the venipuncture needle is directly connected via a Teflon tube to the nozzle of one single donor. The human blood collection is performed following the declaration of Helsinki and is approved by the ethics committee of Ärztekammer des Saarlandes, permit number 51/18. Blood from pig is collected in a similar manner from two different animals as waste material during surgery inventions and used for our experimental investigations within 8 hours.3 Results
Fig. 1(a) illustrates the dynamic evolution of a capillary bridge formed by blood treated with citrate in the context of a capillary break-up extensional rheometry (CaBER) experiment. After the initial thinning phase that is primarily governed by the Rayleigh–Plateau instability,43 the bridge's radius progressively transitions into a self-similar finite-time singularity reminiscent of behavior exhibited by Newtonian fluids.28 However, a notable departure from this behavior occurs as the flow rate surpasses the characteristic time scale associated with polymer dynamics. At this juncture, the rapid dynamics undergo an abrupt deceleration, leading to the formation of a parallel filament that undergoes exponential thinning over time (Fig. 1(c)). This distinctive phase commences when the filament reaches a thickness on the order of 100 μm. Intriguingly, an additional unexpected shift in behavior manifests as the filament's thickness approaches approximately 10 μm. At this critical point, a secondary exponential thinning regime emerges, characterized by a notably extended characteristic relaxation time (as detailed in the caption of Fig. 1). Remarkably, the behavior exhibited by swine blood (Fig. 1(a)) closely mirrors that of human blood, with both exhibiting characteristic time scales λC on the order of several milliseconds. However, it is crucial to note the substantial variability observed across different experimental runs, a topic that will be elaborated upon in subsequent discussions.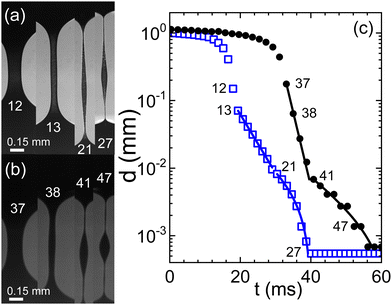 | ||
| Fig. 1 Evolution of a capillary bridge of (a) swine and (b) human blood, both anti-coagulated with citrate. Frame rates are 723 and 520 fps, respectively. (c) The minimal filament diameter extracted from the image sequences; closed circles: human blood, open squares: swine blood; numbers in the graph indicate the frame numbers as referenced in (a) and (b). Lines are fits according to eqn (1) for two consecutive elasto-capillary regimes yielding the relaxation times (a) with on-set at frame 13: λC = 5 ms, and with on-set at frame 21: λC = 13 ms and (b) with on-set at frame 37: λC = 2 ms, and with on-set at frame 41: λC = 11.2 ms. | ||
For both human and swine blood samples, the behavior observed with citrate is remarkably consistent with that observed with heparin as the anticoagulant (Fig. 2). In both cases, a two-stage exponential thinning process unfolds, accompanied by a notable degree of variability among different experimental runs. The resemblance in behavior between the two blood types is striking, with quite comparable elongational properties. However, it is noteworthy that the characteristic time scales λC tend to be shorter when heparin replaces citrate as the anticoagulant.
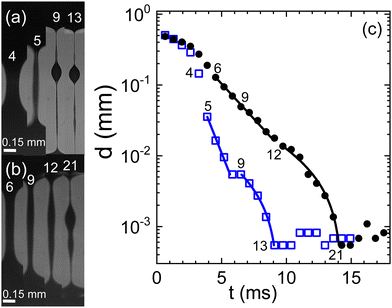 | ||
| Fig. 2 Evolution of a capillary bridge of (a) swine and (b) human blood, both anti-coagulated with heparine. Frame rate is 1540 fps. (c) The minimal filament diameter extracted from the image sequences; closed circles: human blood, open squares: swine blood; numbers in the graph indicate the frame numbers as referenced in (a) and (b). Lines are fits according to eqn (1) for two consecutive elasto-capillary regimes yielding the relaxation times (a) with on-set at frame 5: λC = 0.9 ms, and with on-set at frame 9: λC = 4.7 ms and (b) with on-set at frame 6: λC = 2.2 ms, and with on-set at frame 12: λC = 5.4 ms. | ||
A stark departure from this behavior is observed when EDTA is employed as the anticoagulant (Fig. 3). Under these conditions, the emergence of the two-stage exponential thinning process is conspicuously absent. Instead, the initial exponential thinning regime dominates, characterized by significantly smaller values of the characteristic relaxation time λC. Nevertheless, it is noteworthy that both human and swine blood continue to exhibit remarkably similar behavior in the presence of EDTA.
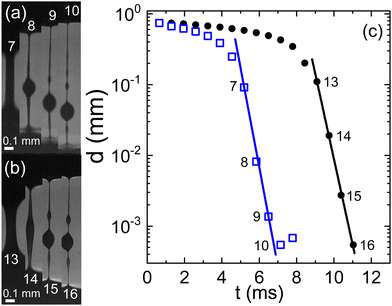 | ||
| Fig. 3 Evolution of a capillary bridge of (a) swine and (b) human blood, both anti-coagulated with EDTA. Frame rates is 1540 fps. (c) The minimal filament diameter extracted from the image sequences; closed circles: human blood, open squares: swine blood; numbers in the graph indicate the frame numbers as referenced in (a) and (b). Lines are fits according to eqn (1) yielding the relaxation times (a) with on-set at frame 7: λC = 0.3 ms and (b) with on-set at frame 13: λC = 0.3 ms. | ||
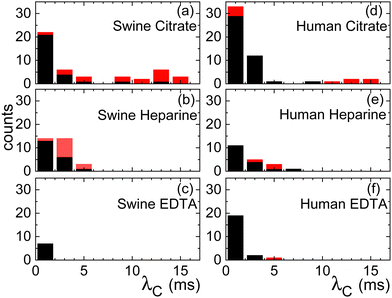
The pronounced variability inherent in our measurements becomes evident upon closer examination of the histogram in Fig. 4. The black bars indicate the characteristic time λC from the first thinning regime and the red bars from the second one. Both for the case of citrate and heparine, the onset of the second thinning is detectable in several cases. While the use of citrate as the anticoagulant yields time scales extending beyond 10 ms, there are instances where measurements hover around the 1 ms mark or even less. A similar trend is observed when heparin is employed, albeit the longest characteristic time scales remain below 10 ms here. In contrast, the use of EDTA results in a consistent observation of λC values below the 1 ms threshold.
To investigate whether the various anticoagulants either delay or expedite the thinning process relative to untreated blood, we conduct a series of exploratory runs using a pending droplet setup. This arrangement enables us to directly connect a Teflon tube from a venous puncture to the nozzle, facilitating the observation of capillary thinning in untreated blood within a matter of seconds after donation. In cases where blood is treated with anticoagulants, a reservoir is attached to the nozzle. Compared to the CaBER, it is much more difficult to obtain data that could be evaluated, because the detachment process induces always strong oscillations and in many cases the droplet drips asymmetrically from the faucet. We therefore present only exemplary runs in Fig. 5. Notably, the relaxation times associated with full blood samples treated with citrate align closely with the relaxation times determined from samples lacking anticoagulants. A comparison of the time scales λC with those obtained from CaBER experiments reveals certain differences, which are typical when comparing CaBER with pending droplet or jet break-up experiments.44 However, both experimental setups consistently reflect qualitatively the trends induced by the chosen anticoagulant.
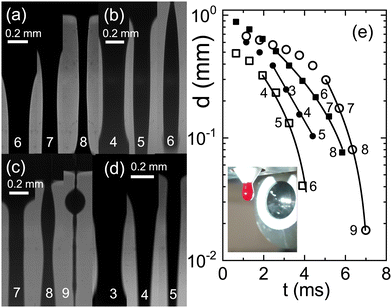 | ||
| Fig. 5 Sequences of images of a falling drop through a nozzle at 1540 fps (a) blood without any anticoagulant directly drawn from a donor, full squares in (e) λC = 3.8 ms; (b) full blood with citrate, open squares, λC = 3.1 ms; (c) full blood with heparine, open circles, λC = 2 ms; (d) full blood with EDTA, full circles, λC = 1.5 ms. (e) Filament thinning and the corresponding fits with eqn (1) (see text). The inset shows a photograph of the pending droplet in front of the microscope lense. | ||
4 Discussion & conclusion
Our findings unequivocally demonstrate that the choice of anticoagulant exerts a profound influence on the elongational properties of blood. In the case of heparin and citrate, we observe a distinctive two-stage exponential thinning behavior, a phenomenon that raises intriguing questions about the underlying mechanisms. Two plausible explanations emerge from our observations: firstly, it might be a consequence of the presence of different relaxation modes in the plasma polymers (proteins), and this phenomena was already observed in numerical simulations of the multi mode Giesekus model (cp. Fig. 2b in ref. 8) Secondly, it is worth noting that when the second thinning regime commences, the filament thickness is on the order of 10 μm, roughly equivalent to the size of red blood cells. It is a well-established fact that the presence of particles can expedite the pinching process.35,45 Consequently, it is conceivable that a filament with a thickness below 10 μm might be entirely devoid of blood cells, potentially contributing to the observed behavior. The strong elongational rates in this regime together with the small dimensions suggests that changes in the aggregability of the red blood cells due to the different anticoagulants does not play a significant role here, a hypothesis that dedicated experiments could investigate.One noteworthy aspect of our results is the significant dispersion in the measured relaxation times for a given set of parameters. This variability presents a less straightforward challenge to interpret. While we can only speculate at this juncture, one plausible explanation could be a substantial heterogeneity in the concentrations of plasma proteins within the blood samples, thereby contributing to the observed dispersion.
To further elucidate the impact of different anticoagulants on the thinning process compared to untreated, non-coagulated blood, we conducted dripping droplet experiments. This approach provided a means to directly compare the elongational properties of blood samples subjected to various anticoagulants with those of untreated blood. Intriguingly, our findings indicate that citrate has a negligible effect on the elongational properties of blood, suggesting that it preserves the intrinsic behavior of blood during the thinning process. In contrast, heparin appears to exert an accelerating effect on the thinning process, leading to shorter characteristic relaxation times λC. Perhaps the most striking observation is associated with the use of EDTA as an anticoagulant, which markedly alters the characteristic relaxation time λC by an order of magnitude, emphasizing the dramatic impact of anticoagulant choice on blood's elongational behavior.
Our data are in overall agreement with what is reported in the literature,5–9 if one considers the reported anticoagulants and our study clarifies the apparent discrepancies. There is quite some need for a replacement fluid for human blood for any type of experimental investigation and any blood replacement fluid46,47 that should reflect the droplet forming or flow properties of blood should also reflect the elongational properties. This may be done, e.g., by adding a tiny amount of long chained polyethylenoxide to the replacement solution.5 In any case, our study also reveals that swine blood is a very good replacement for human blood with respect to the elongational properties.
Author contributions
DA and CW designed research. JEF performed experiments and evaluated the data. AD performed experiments. CW, DA, JEF and AD wrote the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful for the opportunity to carry on this research as a part of the DFG project WA1336/12-2. JEF thanks the Alexander von Humboldt Foundation.References
- S. Chien, S. Usami, R. J. Dellenback and M. I. Gregersen, Science, 1967, 157, 829 CrossRef CAS PubMed.
- E. W. Merrill, C. S. Cheng and G. A. Pelletier, J. Appl. Physiol., 1969, 26, 1–3 CrossRef CAS PubMed.
- A. N. Beris, J. S. Horner, S. Jariwala, M. J. Armstrong and N. J. Wagner, Soft Matter, 2021, 17, 10591–10613 RSC.
- A. Darras, A. K. Dasanna, T. John, G. Gompper, L. Kaestner, D. A. Fedosov and C. Wagner, Phys. Rev. Lett., 2022, 128, 088101 CrossRef CAS PubMed.
- M. Brust, C. Schaefer, R. Doerr, L. Pan, M. Garcia, P. E. Arratia and C. Wagner, Phys. Rev. Lett., 2013, 110, 078305 CrossRef CAS PubMed.
- A. Kolbasov, P. M. Comiskey, R. P. Sahu, S. Sinha-Ray, A. L. Yarin, B. S. Sikarwar, S. Kim, T. Z. Jubery and D. Attinger, Rheol. Acta, 2016, 55, 901–908 CrossRef CAS.
- P. C. Sousa, R. Vaz, A. Cerejo, M. S. N. Oliveira, M. A. Alves and F. T. Pinho, J. Rheol., 2018, 62, 447–456 CrossRef CAS.
- S. Varchanis, Y. Dimakopoulos, C. Wagner and J. Tsamopoulos, Soft Matter, 2018, 14, 4238–4251 RSC.
- S. Kar, A. Kar, K. Chaudhury, T. K. Maiti and S. Chakraborty, ACS Omega, 2018, 3, 10967–10973 CrossRef CAS PubMed.
- M. Goldin, J. Yerushalmi, R. Pfeffer and R. Shinnar, J. Fluid Mech., 1969, 38, 689–711 CrossRef.
- A. V. Bazilevskii, S. I. Voronkov, V. M. Entov and A. N. Rozhkov, Sov. Phys. Dokl., 1981, 26, 333 Search PubMed.
- Y. Amarouchene, D. Bonn, J. Meunier and H. Kellay, Phys. Rev. Lett., 2001, 86, 3558–3561 CrossRef CAS PubMed.
- S. L. Anna and G. H. McKinley, J. Rheol., 2001, 45, 115 CrossRef CAS.
- C. Clasen, J. P. Plog, W.-M. Kulicke, M. Owens, C. Macosko, L. E. Scriven, M. Verani and G. H. McKinley, J. Rheol., 2006, 50, 849 CrossRef CAS.
- J. Eggers, M. A. Herrada and J. H. Snoeijer, J. Fluid Mech., 2020, 887, A19 CrossRef CAS.
- B. A. Toms, Proc. Int. Cong. Rheol., 1949, 135 CAS.
- L. Xi, Phys. Fluids, 2019, 31, 121302 CrossRef.
- D. Samanta, Y. Dubief, M. Holzner, C. Schäfer, A. N. Morozov, C. Wagner and B. Hof, Proc. Natl. Acad. Sci. U. S. A., 2013, 110, 10557–10562 CrossRef CAS PubMed.
- S. S. Datta, A. M. Ardekani, P. E. Arratia, A. N. Beris, I. Bischofberger, G. H. McKinley, J. G. Eggers, J. E. López-Aguilar, S. M. Fielding, A. Frishman, M. D. Graham, J. S. Guasto, S. J. Haward, A. Q. Shen, S. Hormozi, A. Morozov, R. J. Poole, V. Shankar, E. S. G. Shaqfeh, H. Stark, V. Steinberg, G. Subramanian and H. A. Stone, Phys. Rev. Fluids, 2022, 7, 080701 CrossRef.
- F. Mighri, P. J. Carreau and A. Ajji, J. Rheol., 1998, 42, 1477–1490 CrossRef CAS.
- V. Bergeron, D. Bonn, J. Y. Martin and L. Vovelle, Nature, 2000, 405, 772–775 CrossRef CAS PubMed.
- D. Xu, A. Varshney, X. Ma, B. Song, M. Riedl, M. Avila and B. Hof, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 11233–11239 CrossRef CAS PubMed.
- C. W. Shields Iv, C. D. Reyes and G. P. López, Lab Chip, 2015, 15, 1230–1249 RSC.
- Z. Chen, A. Sun, H. Wang, Y. Fan and X. Deng, Med. Nov. Technol. Devices, 2019, 3, 100024 CrossRef.
- P. M. Comiskey, A. L. Yarin and D. Attinger, Phys. Rev. Fluids, 2018, 3, 063901 CrossRef.
- J. Huh, S. Kim, B.-H. Bang, A. Aldalbahi, M. Rahaman, A. L. Yarin and S. S. Yoon, Phys. Fluids, 2024, 36 DOI:10.1063/5.0189094.
- F. D. Giudice, Micromachines, 2022, 13, 167 CrossRef PubMed.
- J. Eggers, Rev. Mod. Phys., 1997, 69, 865 CrossRef CAS.
- S. Gier and C. Wagner, Phys. Fluids, 2012, 24, 053102 CrossRef.
- L. Campo-Deaño and C. Clasen, J. Non-Newtonian Fluid Mech., 2010, 165, 1688–1699 CrossRef.
- J. E. Fiscina, P. Fromholz, R. Sattler and C. Wagner, Exp. Fluids, 2013, 54, 1611 CrossRef.
- J. Dinic and V. Sharma, Proc. Natl. Acad. Sci. U. S. A., 2019, 116, 8766–8774 CrossRef CAS PubMed.
- A. Zell, S. Gier, S. Rafaï and C. Wagner, J. Non-Newtonian Fluid Mech., 2010, 165, 1265–1274 CrossRef CAS.
- A. Jaishankar, V. Sharma and G. H. McKinley, Soft Matter, 2011, 7, 7623 RSC.
- A. Lindner, J. E. Fiscina and C. Wagner, EPL, 2015, 110, 64002 CrossRef.
- V. Thiévenaz and A. Sauret, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2120893119 CrossRef PubMed.
- G. Tomaiuolo, M. Barra, V. Preziosi, A. Cassinese, B. Rotoli and S. Guido, Lab Chip, 2011, 11, 449–454 RSC.
- J. E. Mancuso and W. D. Ristenpart, Phys. Rev. Fluids, 2017, 2, 101101 CrossRef.
- M. Mohri and H. Rezapoor, Res. Vet. Sci., 2009, 86, 111–114 CrossRef CAS PubMed.
- S. Tassi Yunga, A. J. Gower, A. R. Melrose, M. K. Fitzgerald, A. Rajendran, T. A. Lusardi, R. J. Armstrong, J. Minnier, K. R. Jordan, O. J. T. McCarty, L. L. David, P. A. Wilmarth, A. P. Reddy and J. E. Aslan, J. Thromb. Haemostasis, 2022, 20, 1437–1450 CrossRef CAS PubMed.
- A. Merlo, S. Losserand, F. Yaya, P. Connes, M. Faivre, S. Lorthois, C. Minetti, E. Nader, T. Podgorski, C. Renoux, G. Coupier and E. Franceschini, Biophys. J., 2023, 122, 360–373 CrossRef CAS PubMed.
- C. Wagner, L. Bourouiba and G. H. McKinley, J. Non-Newtonian Fluid Mech., 2015, 218, 53–61 CrossRef CAS.
- C. Wagner, Y. Amarouchene, D. Bonn and J. Eggers, Phys. Rev. Lett., 2005, 95, 164504 CrossRef CAS PubMed.
- W. Mathues, S. Formenti, C. McIlroy, O. G. Harlen and C. Clasen, J. Rheol., 2018, 62, 1135–1153 CrossRef CAS.
- W. Mathues, C. McIlroy, O. G. Harlen and C. Clasen, Phys. Fluids, 2015, 27, 093301 CrossRef.
- L. Campo-Deaño, R. P. A. Dullens, D. G. A. L. Aarts, F. T. Pinho and M. S. N. Oliveira, Biomicrofluidics, 2013, 7, 034102 CrossRef PubMed.
- A. Orr, P. Wilson and T. Stotesbury, Soft Matter, 2023, 19, 3711–3722 RSC.
| This journal is © The Royal Society of Chemistry 2024 |