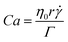Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Combining fracture mechanics and rheology to investigate the impact of micro-aeration on chocolate oral processing
G.
Samaras†
 *a,
D.
Bikos†
*a,
D.
Bikos†
 *a,
P.
Cann
a,
M.
Masen
a,
Y.
Hardalupas
a,
C.
Hartmann
b,
J.
Vieira
c and
M. N.
Charalambides
*a,
P.
Cann
a,
M.
Masen
a,
Y.
Hardalupas
a,
C.
Hartmann
b,
J.
Vieira
c and
M. N.
Charalambides
 a
a
aDepartment of Mechanical Engineering, Imperial College London, UK. E-mail: georgios.samaras17@imperial.ac.uk; d.bikos17@imperial.ac.uk
bNestlé Research, Lausanne, Switzerland
cNestlé Product Technology Centre, York, UK
First published on 31st May 2024
Abstract
This study presents a rigorous mechanical characterisation investigation on milk chocolate with varying porosities, at different temperatures and strain rate levels. Uniaxial compression tests at temperatures varying from 20 °C to 30 °C were performed to measure the bulk properties of chocolate as a function of porosity and temperature. Fracture experiments were also conducted to compute the fracture energy at temperature levels between 20 °C and 30 °C for all tested samples. Additionally, rheological experiments are conducted to compute the viscosity of the different chocolates at 37 °C. This combined experimental analysis of solid mechanics, fracture mechanics, and rheology aims to define the impact of temperature and chocolate's phase change from solid to liquid on its mechanical properties. Moreover, the impact of micro-aeration on the relationship between material properties and temperature is discussed. The results demonstrate a significant impact of both temperature and micro-aeration on the chocolate's material properties; fracture stresses decrease with micro-aeration due to the presence of micro-pores creating weak links in the chocolate matrix, the critical strain energy release rate decreases with micro-aeration at temperatures up to 25 °C and increases at temperatures above 30 °C. Finally, the viscosity at 37 °C increases with increasing porosity due to the obstruction of the flow by micro-pores acting as “solid” particles. The results highlight how the impact of micro-aeration on the material properties of chocolate alters as the testing temperature rises and the material changes phase. The relationships between the micro-aeration and material properties and the dependence of temperature on the different mechanical properties are used to explain the difference in textural attributes as obtained from temporal dominance sensation tests. This study seeks to contribute valuable insights into the field of chocolate technology, emphasizing the need for a combined engineering approach to understand the structural breakdown of chocolate during oral processing as mechanisms such as chewing, melting, mixing and shearing occur.
1. Introduction
A great effort in the food technology field has been demonstrated to shed insight into the structure–property relationship. The aim of this study is to optimise food processes such as industrial manufacturing and/or human oral process. Material properties as defined by engineering analysis are essential for controlling processes that involve mechanical loads. Flow processes are dictated by rheological properties1 and processes which involve fracture, such as cutting and crushing, are dominated by the fracture properties.2–5 However, in processes such as food oral processing which involves simultaneous breakdown mechanisms, such as mastication, melting, and the shearing action of the tongue–palate interface, a combined engineering analysis is necessary to investigate the structure–property relationship. Such a rigorous study is notably missing from the literature.In chocolate, rheological and fracture properties play a key role in the final quality of the product influencing the dispersion characteristics of chocolate's components during the manufacturing process while also affecting sensory characteristics, such as “hardness” and “smoothness” perception, and the characteristic snap.6–9 Understanding and optimising these properties are crucial both for manufacturers, seeking to produce high-quality chocolate, and consumers, expecting a delightful sensory experience.
There is a vast literature performing rheological experiments on chocolate materials attempting to establish the link between the manufacturing steps and rheological properties and also the structure–property relationship.10–12 Servais et al.13 proposed a methodology to measure the rheology of chocolate and related cocoa products using factory grade rheometers. Afoakwa et al.14 provided a detailed review of factors influencing the rheological properties of chocolate, concluding that the processing technique, the ingredients and the particle size distribution are the most important factors. Váscquez et al.15 performed a rheological study on four commercial chocolate samples with similar microstructures and reported a shear thinning behaviour. According to Windhab,16 melted chocolate is a non-Newtonian fluid as the viscosity depends on the temperature, shear rate, and time. The viscosity measurements are linked to sensorial attributes such as the “grittiness” perception, and based on the same study, chocolate is considered as “smooth” for viscosity values within 1.5–3.5 Pa s. These values are recorded at a shear rate of 20 s−1 and at a temperature of 37 °C, i.e., human body temperature. Melted chocolate contains sugar, cocoa and milk particles dissolved in the melted fat matrix. Lannes et al.17 studied the flow behaviour of chocolate drinks at 25 °C and 40 °C and found that Bingham plastic models fit well with the experimental data. The rheological behaviour of coconut flavoured milk with varying fat content (15–30%) was investigated in the study by Simuang et al.18 at temperatures ranging between 70 °C and 90 °C. They reported pseudoplastic behaviour, and the effect of temperature on the apparent viscosity was captured using the Arrhenius equation.
While considerable effort is focused on measuring the rheological properties of chocolate, the literature narrows significantly when the focus shifts to the critical strain energy release rate, Gc, of chocolate. Based on the authors’ knowledge, in a few studies where Gc of chocolate was investigated, a large deviation in the reported values is observed. Namely, Chen et al. utilised wedge-cutting tests on chocolate with different compositions, reporting a wide range of Gc values between 330 and 1189 J m−2.19 Gomez et al. proposed a numerical method to inversely calculate the critical strain energy release rate of chocolate through SENB simulations and reported a value of 2.1 J m−2.20 Even though translating the fracture energy of chocolate from Charpy tests into the critical strain energy release rate might be debatable, Parsons and Goodall reported absorbed energy on fracture which varied from 70% to 78% depending on the type of chocolate. In our previous work on the mechanical properties of chocolate, values of Gc for non-aerated milk chocolate at 20 °C ranged from 8 to 22 J m−2, showing a dependency on the testing speed.21,22
The importance of measuring the critical strain energy release rate of chocolate extends beyond being a key input computational parameter for simulating various processes with industrial significance;2,23,24 it is also intricately linked to consumer perception.4,25,26 Based on previous studies,9,20,21,27 chocolate hardness, affected both by the strength and toughness of the food, is linked to the early stages of oral processing. It guides the subsequent steps of fragmentation, chocolate melting, and the shearing action between the oral surfaces.27–31 However, as the process progresses and a combination of sensations is perceived, rheological properties begin to dominate the process.30,32 The critical point where the shift of dominance is observed is unknown.
Therefore, we believe that the fracture and rheological properties of chocolate should be studied together and as a function of temperature. This approach is essential for understanding the mechanisms occurring during oral processing and their effects on the sensorial attributes perceived at these intermediate steps of oral processing. To unravel the underlying mechanisms in a chocolate system, a rigorous experimental campaign must be undertaken.
To the best of the authors’ knowledge, no such study in the literature has been reported to date. Integrating these two experimental methodologies aims to provide a holistic understanding of the mechanical and rheological aspects governing chocolate quality.
In our previously published work on the effect of micro-aeration, the authors presented a comprehensive experimental analysis to calculate the mechanical properties of chocolate at 20 °C under different loading scenarios and proposed a novel multiscale computational tool to simulate the first bite of chocolate.3,22,33,34 However, the effect of temperature on the mechanical properties of chocolate at temperatures relevant to oral processing conditions, 20–37 °C, which is important after the first bite, remained to be investigated. Additionally, the impact of micro-aeration on the rheological properties of chocolate is lacking in the literature too. While an initial attempt to link the mechanical properties of chocolate to explain the mechanisms happening during oral processing was performed,27 the lack of the dependency of chocolate's mechanical response on the temperature and the coupling to rheological analysis prevent a more comprehensive explanation of the oral processing mechanisms as observed from temporal dominance sensation (TDS) tests.
Therefore, this study delves into the combined exploration of fracture and rheological properties in chocolate and attempts to use this combined analysis to explain the temporal dominance mechanisms occurring during food oral processing of chocolate. More specifically, single-edge notched bending (SENB) tests at 20 °C and 25 °C are performed to study the fracture behaviour of chocolate when it is considered to be in its solid regime. Wire-cutting tests are conducted at 30 °C when the chocolate is in a soft state. On the other hand, when chocolate is considered fully melted, rotational experiments are conducted at shear rates between 0.1 and 1000 s−1. Finally, combined engineering analysis is performed to discuss temporal dominance sensation test data and explain the evolving mechanisms occurring during oral processing.
2. Materials & methods
2.1. Materials
Three milk chocolate materials with typical compositions and different levels of micro-aeration, 0%, 10%, and 15%, were provided by the Nestlé Product Technology Centre (NPTC) in York, UK. The composition of all samples was as follows: 44 wt% of sugar crystals, 27 wt% of cocoa fats, 10 wt% of milk powders, 6 wt% of cocoa solids and a small percentage of sunflower lecithin, i.e. ∼0.3 wt%. Details regarding the manufacturing steps of the chocolate samples and the micro-aeration process are reported in our previous published work.21,22 The chocolate samples used in the uniaxial compression and fracture experiments were provided in the following geometries: cylinders of 20 mm diameter, Do, and 20 mm height, Lo, and rectangular beams of 80 mm length, L, 15 mm width, W, and 8 mm thickness, B, as shown in Fig. 2a and c, respectively.2.2. Chocolate microstructure
The scanning electron microscopy (SEM) micrographs of all chocolate materials with different levels of micro-aeration are shown in Fig. 1, as obtained by Bikos et al.21,22 Based on these figures, the differentiating factor between the chocolate microstructures is the presence of micropores, which, according to our previous published work, have an average diameter of approximately 40–45 μm and can be up to approximately 100 μm. This size is fairly similar (10 –40 μm) to other microscopic features found in chocolate, such as sugar crystals and cocoa solids.35 For further details about the size distribution of pores and the microscope testing parameters, the reader is referred to Bikos et al.21,22 | ||
| Fig. 1 Scanning electron microscopy (SEM) micrographs of the (a) non-aerated, (b) 10%, and (c) 15% micro-aerated chocolate under different magnifications. The red and yellow arrows depict sugar particles and micro-pores, respectively. The images of the micrographs are modified from Bikos et al.22 | ||
2.3. Experimental methods
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0.01 s−1, 0.1 s−1 and 1 s−1. These tests were performed under monotonically increasing applied strain up to fracture. The three temperature thresholds were selected to highlight the change in the chocolate's mechanical behaviour at room temperature, at a temperature just before the phase change, and temperature where the phase change occurred8,36 and correlate the response with rheological experiments under shear when the chocolate is fully melted at 37 °C. The tests were not extended beyond 30 °C because of the response of the chocolate in a liquid state which violates the applicability of the mechanical testing protocols.
= 0.01 s−1, 0.1 s−1 and 1 s−1. These tests were performed under monotonically increasing applied strain up to fracture. The three temperature thresholds were selected to highlight the change in the chocolate's mechanical behaviour at room temperature, at a temperature just before the phase change, and temperature where the phase change occurred8,36 and correlate the response with rheological experiments under shear when the chocolate is fully melted at 37 °C. The tests were not extended beyond 30 °C because of the response of the chocolate in a liquid state which violates the applicability of the mechanical testing protocols.
To control the temperature of the chocolate during the compression tests, a temperature chamber was fitted to the 5584 Instron machine. The chamber (Fig. 2) was able to monitor the temperature within the chamber with an accuracy of 0.1 °C. Due to the relatively low thermal conductivity of the chocolate,37,38 approximately 60 minutes were allowed for the temperature to equilibrate, based on thermocouple indications on a “dummy” chocolate specimen placed inside the chamber.
A thin PTFE film was applied on the compression plates to minimise the friction coefficient at the chocolate–compression plate interface.39 A Logitech HD Pro Webcam C920 was used to monitor the chocolate samples during compression tests and ensure that no “barrelling” mechanism was apparent, which could interfere with the accurate computation of the chocolate's material properties. In addition, preliminary tests on chocolate samples (results not shown) with different aspect ratios showed no significant variations providing further evidence for the accuracy of the calculated material properties. Compliance tests were conducted at the same strain rates by bringing the compression plates in contact with each other to measure the deflection which is not associated with the material deformation. Preliminary results showed no significant machine compliance effect in the computed σ–ε response, i.e. deviations less than 5%.
The true stress, σ, and strain, ε, for a uniaxial compression test are calculated as follows:
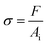 | (1) |
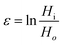 | (2) |
| HiAi = HoAo | (3) |
Uniaxial compression tests were preferred over tensile and bending experiments because they are closely associated with the compressive actions of the teeth against the food during mastication. Previous reports have shown the complex mechanical behaviour of the chocolate, which is dependent on the mode of deformation, i.e., tension, compression, and bending.33 The results of this study highlighted complex microscopic mechanisms that cause differences in the computed stress–strain curve and the bulk mechanical properties of the chocolate depending on the loading scenario. Although loading–unloading experiments are recommended in previous studies to compute an accurate value of Young's modulus, they are not directly relevant here. This study aims to use engineering analysis to explain changes in consumer perception due to micro-aeration during oral processing. The first bite and mastication are a monotonic process, and hence, employing uniaxial unconfined compression is more appropriate.
The Carreau40 and Cross41 models will be used to characterise the flow behaviour of the chocolate samples:
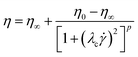 | (4) |
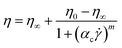 | (5) |
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate, λc and αc are time constants, and p and m are dimensionless exponents for the Carreau and Cross models, respectively.15,40 It is worth noting that the widely used Casson model was also examined and calibrated with the experimental data, but it was not found applicable for the specific chocolate materials.
is the shear rate, λc and αc are time constants, and p and m are dimensionless exponents for the Carreau and Cross models, respectively.15,40 It is worth noting that the widely used Casson model was also examined and calibrated with the experimental data, but it was not found applicable for the specific chocolate materials.
Force–displacement data were recorded at three constant crosshead speeds: 0.02 mm s−1, 0.2 mm s−1 and 2 mm s−1. In addition, force–displacement data obtained from the machine compliance experiments were used to eliminate any indentation or compliance effects from the instrument. To consider these effects, unnotched chocolate specimens (see Fig. 2c) were placed on a three-point bending setup. The support pins were moved together to the mid-span location under the loading pin, and the chocolate was loaded up to the same load level as the SENB experiments. Then, for a given load, the displacement recorded from the machine compliance experiment was subtracted from the one measured from the SENB experiments.42 Four repeats were conducted for each testing speed for all chocolate materials. The same experimental procedure was repeated at 25 °C for all types of chocolate and all applied strain rates. To ensure uniform temperature throughout the samples and control the temperature conditions, the same temperature chamber as the one used in the compression experiments was installed in the testing machine, as shown in Fig. 2c, and the samples were left for an hour for temperature equilibration. Similarly, four repeats were used for each testing condition and all types of chocolate.
Due to the soft nature of the chocolate at elevated temperatures, wire cutting experiments were performed on all materials (0%, 10%, and 15% micro-aeration) at 30 °C and 50% relative humidity to measure the corresponding critical strain energy release rate, Gc. Similar to the other mechanical tests, a temperature chamber was placed in the testing instrument to control the set temperature. The wire was attached to a holder and was adjusted to be tight enough to prevent any significant deflections. The holder with the wire attached to it was placed on a 100 N load cell. The wire cutting test configuration is shown in Fig. 2d.
The cutting force–displacement data were recorded at three constant crosshead speeds of 0.02 mm s−1, 0.2 mm s−1 and 2 mm s−1 using three different wire diameters of 0.5 mm, 0.25 mm, and 0.125 mm for each speed. Preliminary wire cutting experiments ensured that the wire remained straight and tight throughout the cutting process, with no excess material concentrated at the crack tip that could interfere with the force–displacement measurements. Three repeats were performed for each experimental condition, i.e. testing speed, wire diameter, and type of material. This study did not investigate the effect of the sample dimensions, such as width and length, since the current dimensions (L, B > 10d) meet the requirements for reproducible wire cutting forces.2,43 The Gc data and their error bars were obtained using the statistical methodology presented by Williams and Rink.44
The critical strain energy release rate is evaluated by recording the area underneath the force–displacement curve and assuming linear elastic behaviour. Based on Linear Elastic Fracture Mechanics theory, the critical energy release rate Gc is computed from
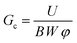 | (6) |
The computation of Gc, performed using eqn (6), was performed as a function of the crosshead speed to highlight potential rate-dependency. The values of Gc in these tests refer to the measurements obtained during crack initiation, i.e., initiation Gc. Due to the challenges associated with measuring accurately crack growth during SENB tests, the propagation critical strain energy release rate was not calculated in this study.
For a direct comparison with the Gc data obtained from the SENB experiments, the Gc measurements from wire cutting tests were plotted as a function of the crack speed, ȧ. For wire cutting experiments, the crack speed equals the wire cutting speed. However, the crosshead speed, ![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) , during the SENB tests is not equal to the crack speed, ȧ, in front of the crack tip. To convert the crosshead speed,
, during the SENB tests is not equal to the crack speed, ȧ, in front of the crack tip. To convert the crosshead speed, ![[u with combining dot above]](https://www.rsc.org/images/entities/i_char_0075_0307.gif) , into the crack speed, ȧ, during SENB experiments, the methodology introduced by Gamonpilas et al. for starch gels is employed.45
, into the crack speed, ȧ, during SENB experiments, the methodology introduced by Gamonpilas et al. for starch gels is employed.45
Assuming that Gc is constant during crack propagation and the crack growth is stable, which is true for large crack lengths (∼a/W > 0.4), the crack speed in front of the crack, ȧ, is measured through
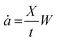 | (7) |
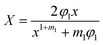 | (8) |
The crack speed values measured from eqn (7) are utilised to highlight the dependency of Gc from the SENB tests on the crack speed, enabling a comparison to Gc data derived from the wire cutting experiments.
The methodology to calculate Gc from wire cutting experiments is based on the assumption that multiple dissipation mechanisms occur in front of the crack tip. These mechanisms include the energy associated with the plastic deformation during cutting, friction energy present during cutting, and energy associated with producing a new surface. The resultant stresses associated with these mechanisms are illustrated in Fig. 3a.
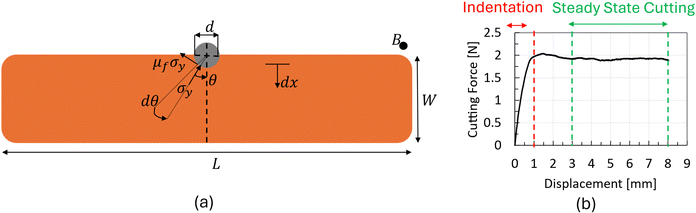 | ||
| Fig. 3 (a) Schematic of the beam specimen showing the cutting parameters from eqn (11) and (b) a typical load–displacement curve extracted from the wire cutting test indicating the indentation and the steady state cutting state. | ||
In a wire cutting process, the applied energy increases with the increasing wire diameter. However, this increase in applied energy is primarily caused by the rise in plastic deformation and friction energy due to the higher volume of material in contact with the wire. By using wires of varying diameters, extrapolating the steady state cutting force per unit thickness (B), corresponding to different wire diameters d, to a zero diameter provides an estimation of the fracture energy, Gc. Typical data extracted from such experiments are summarised in Fig. 3b.
The methodology assumes a material with an elastic-plastic stress–strain response with no strain softening or hardening. However, the methodology has also been successfully applied to other materials with a strain hardening response similar to that shown for the chocolate in this study.46 Assuming yielding occurs at the crack tip, the cutting force (F) is associated with the yield stress (σy), coefficient of friction (μf), and wire diameter (d), as per:46
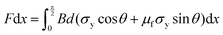 | (9) |
| Fdx = BGcdx | (10) |
Adding eqn (9) and (10), a linear expression between F/B and d is derived. The y-axis intercept of a plot F/B–d would then be equal to Gc.
For a given yield stress, σy, the friction coefficient, μf, can also be estimated through the slope of this linear fit to the experimental data.
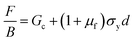 | (11) |
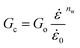 | (12) |
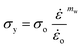 | (13) |
![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) is the strain rate and
is the strain rate and ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) o is a parameter taken to be 1 s−1 and is used to make the ratio
o is a parameter taken to be 1 s−1 and is used to make the ratio 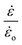 dimensionless. The parameters nw and mw are power law constants. In addition, Go refers to the critical strain energy release rate at the strain rate
dimensionless. The parameters nw and mw are power law constants. In addition, Go refers to the critical strain energy release rate at the strain rate ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) o and σo is the stress responsible for the energies associated with the viscous dissipation and friction at the same strain rate,
o and σo is the stress responsible for the energies associated with the viscous dissipation and friction at the same strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) o.43 Note that the power law constant mw is obtained by creating isometric curves, i.e., stress, σ, vs. strain rate,
o.43 Note that the power law constant mw is obtained by creating isometric curves, i.e., stress, σ, vs. strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , from compression experiments for different strain intervals. Similarly, the constant nw is obtained by extracting the slope from cutting energies, F/B, vs. crack speed, ȧ, plots for different wire diameters.2 Based on preliminary results on the tested materials, nw and mw were found to be approximately 0.04, 0.06, and 0.05 and 0.13, 0.14, and 0.13 for the 0%, 10%, and 15% micro-aerated chocolate, respectively. Goh et al., who investigated the fracture behaviour of different types of cheese, reported that nw = mw. The values of these constants ranged between 0.16 and 0.19 for different types of cheese materials.2
, from compression experiments for different strain intervals. Similarly, the constant nw is obtained by extracting the slope from cutting energies, F/B, vs. crack speed, ȧ, plots for different wire diameters.2 Based on preliminary results on the tested materials, nw and mw were found to be approximately 0.04, 0.06, and 0.05 and 0.13, 0.14, and 0.13 for the 0%, 10%, and 15% micro-aerated chocolate, respectively. Goh et al., who investigated the fracture behaviour of different types of cheese, reported that nw = mw. The values of these constants ranged between 0.16 and 0.19 for different types of cheese materials.2
The strain rate, ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) , is related to the wire diameter, d, and crack speed ȧ, through
, is related to the wire diameter, d, and crack speed ȧ, through
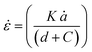 | (14) |
Substituting eqn (12)–(14), into eqn (11) yields:
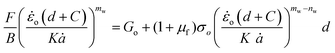 | (15) |
The critical strain energy release rate for different speeds is computed by the intercept of the plot 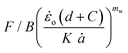 versus
versus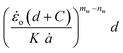 .
.
3. Experimental results
3.1. Uniaxial compression results
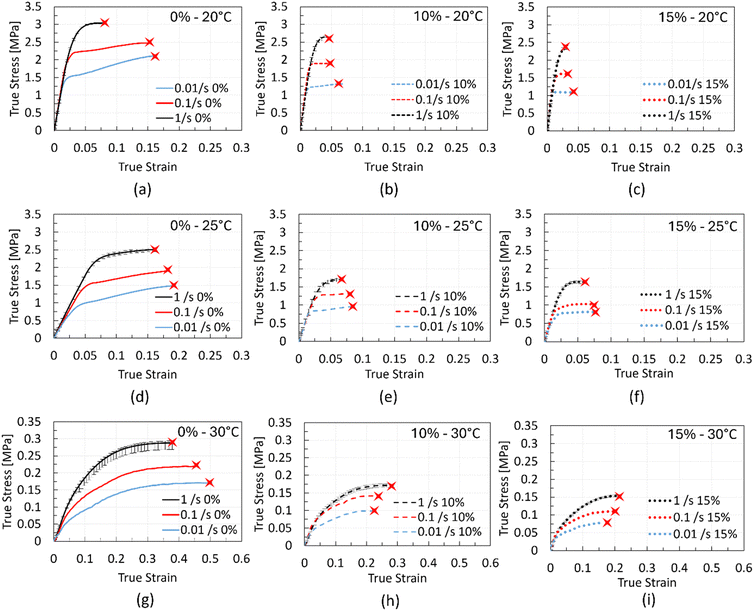
The stress–strain curves for all chocolate materials at temperatures of 20 °C, 25 °C, and 30 °C, under three strain rates, are shown in Fig. 4. Each curve in this figure exhibits a small variability amongst the repeats, with a maximum error of less than 10% (the error bars at the highest strain rate are included). The red cross-shaped marks in the plots signify the strain at ultimate failure. Except for the curves at 30 °C, the strain rate dependency is observed in the nonlinear region, i.e., initiating from the onset of macroscopic yielding. However, at 30 °C, significant rate dependency is observed from the beginning of the material's deformation. As shown in Fig. 4a, a strain hardening effect is present in the stress–strain response of the non-aerated chocolate, i.e., the stresses increase after yielding initiation with increasing applied strain (see the red curve in Fig. 4a). This effect diminishes with increasing porosity and increasing strain rate, see Fig. 4a–c.Assessing the effect of chocolate micro-aeration on its stress–strain response, an overall reduction of stresses with increasing porosity is observed. This is true regardless of the testing conditions such as temperature and strain rate. This observation is consistent with results in the literature, reporting that pores create weaker material structures compared to their solid counterparts.47–49
Similarly, the effect of temperature on the stress–strain curves leads to a reduction in the stresses too, see Fig. 4d, e, and f. Especially at 30 °C (Fig. 4g–i), the stresses are an order of magnitude lower compared to the values at lower temperatures, providing further evidence of the transition of chocolate to a soft solid at these conditions. Interestingly, at 30 °C, and in contrast to the stress–strain behaviour at 20 °C and 25 °C, a non-linear, rate-dependent response is noted without a distinct linear region. In such cases, the computation of the Young's modulus becomes a subjective exercise but not essential too.
For a more quantitative comparison, the macroscopic yield stress, σy, and the fracture stress, σf, are plotted as a function of strain rate for chocolate materials at 20 °C as shown in Fig. 5a and b. According to these figures, both material properties decrease with increasing porosity. For all testing speeds, an average difference of 18% is observed between the yield stress values of the non-aerated chocolate and the 10% micro-aerated chocolate. This difference increases to 27% when comparing the macroscopic yield stress of the non-aerated chocolate to the macroscopic yield stress of the 15% micro-aerated chocolate. Similar decreasing trends are observed for the fracture stress values. These decreasing trends of stresses with increasing porosity are common in porous materials such as porous metals, polymers, and cement.47–49
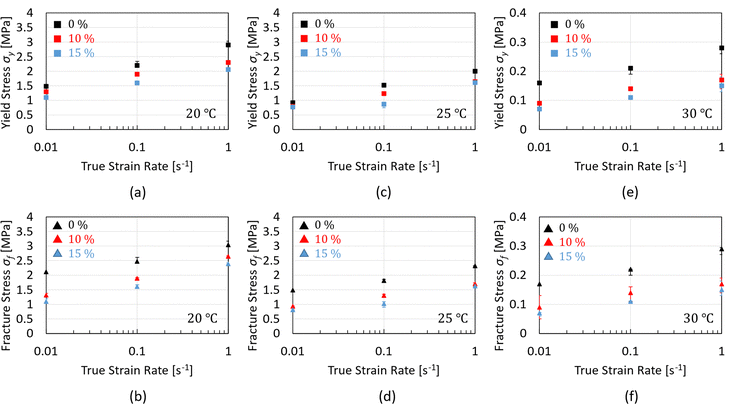 | ||
| Fig. 5 Plots of the compressive macroscopic yield stress, σy, and fracture stress, σf, as a function of strain rate at 20 °C, 25 °C, and 30 °C for all chocolate materials. | ||
Fig. 5c and d summarise the data for the macroscopic yield stress and the fracture stress for the three chocolate materials as a function of strain rate at 25 °C. Both the macroscopic yield stress and the fracture stress exhibit significant rate-dependent response and they also decrease with increasing porosity. A maximum difference of 19% (at ![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0.1 s−1) in macroscopic yield stress is observed when comparing the non-aerated chocolate to the 10% micro-aerated chocolate. The maximum difference increases to 42% when the macroscopic yield stress of the non-aerated chocolate is compared to the macroscopic yield stress of the 15% micro-aerated chocolate, with the maximum difference occurring at a strain rate of 0.1 s−1. Similar comparisons for the fracture stress values result in differences of 22% (
= 0.1 s−1) in macroscopic yield stress is observed when comparing the non-aerated chocolate to the 10% micro-aerated chocolate. The maximum difference increases to 42% when the macroscopic yield stress of the non-aerated chocolate is compared to the macroscopic yield stress of the 15% micro-aerated chocolate, with the maximum difference occurring at a strain rate of 0.1 s−1. Similar comparisons for the fracture stress values result in differences of 22% (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0.1 s−1) and 46% (
= 0.1 s−1) and 46% (![[small epsi, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a1.gif) = 0.1 s−1), respectively.
= 0.1 s−1), respectively.
Assessing the impact of micro-aeration on the macroscopic yield stress, σy, and fracture stress, σf, when the chocolate reaches a temperature of 30 °C, an interesting phenomenon is observed. Based on Fig. 5f, the values of σf at 30 °C indicate no significant difference between the micro-aerated products, i.e., the error bars of these measurements overlap. This is also true for σy at 30 °C at the highest rate, see Fig. 5e. One possible explanation for this phenomenon is that the presence of micro-pores in the soft but not fully melted matrix can still act as weak links, reducing the yield and fracture stresses. However, the presence of more pores might not contribute significantly to any further stress reduction. This might be explained by the fact a portion of the chocolate matrix is melted whilst the rest still remains a solid. The pores in the melted part of the matrix might hinder the deformation and flow of the matrix. Therefore, competing mechanisms might occur at that semi-solid, semi-liquid state.
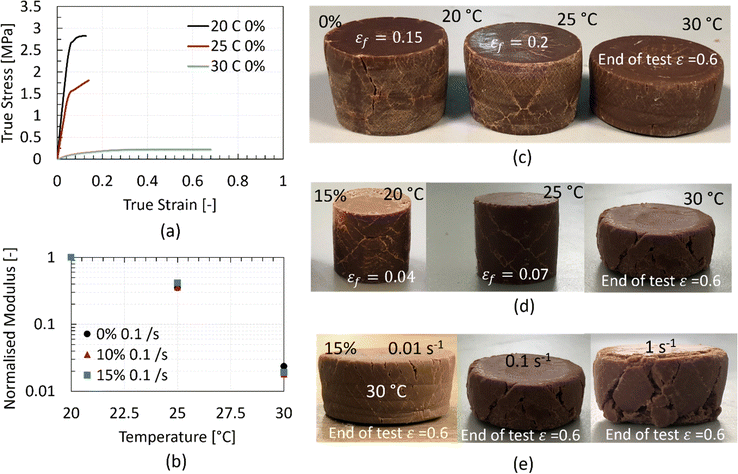
Despite the assumption that the computation of the macroscopic yield stress and Young's modulus might be subjective when the material exhibits such a non-linear stress–strain response, it is crucial to visualise the temperature dependence of these material properties. To visualise this dependence and the drastic reduction of stresses with increasing temperature, the stress–strain response of the non-aerated chocolate at a strain rate of 0.1 s−1 for the three different testing temperatures is plotted in Fig. 6a. It becomes clear that stresses reduce due to the phase change (soft solid to viscous fluid) of the chocolate.
In addition, Fig. 6b summarises the data of the different chocolate materials as a function of temperature at a strain rate of 0.1 s−1. Since the true modulus of elasticity needs to be computed from a loading–unloading experiment,22,33 the values of the apparent modulus in the graph of Fig. 6b are normalised to the modulus of the given material at 20 °C. The graph is plotted on a logarithmic y-scale to distinguish the magnitude of the differences. Based on the same plot, the average values of Young's modulus are two orders of magnitude lower than the reported values at 20 °C, proving further the soft state of the chocolate at a temperature (i.e., 30 °C) close to the phase change of the chocolate, which is reported to be 28–34 °C.8,36,37
Inspecting the fracture behaviour of the chocolate after the completion of the compression tests reveals differences in the shear band formation and the crack patterns for different testing temperatures and porosity levels. The presence of shear bands and the crack initiation and propagation along these bands implies a purely uniaxial compression behaviour for all chocolate samples.
The fractured specimens for the different cases are summarised in Fig. 6c–e. Fig. 6c and d summarise the fracture behaviour of the non-aerated and 15% micro-aerated chocolate materials, respectively, at different temperatures. For both chocolate materials, a decrease in the number of the shear band formation is observed with increasing temperature which is not surprising because the shear band formation is characteristic of brittle materials. The ductility of chocolate is found to increase with temperature (see larger fracture strains shown in Fig. 4 and 5d and f). In addition, no clear rate-dependent effect on shear band formation is reported for the 15% micro-aerated chocolate, see Fig. 6e, and similar effects are observed for the other two chocolate samples, i.e. 0% and 10% (results not shown). Interestingly, the cracks on the surface of the chocolate samples at 30 °C just after the test, as shown in Fig. 6e, imply that the chocolate exhibits characteristics of a solid, (i.e., clear fracture due to the applied deformation) rather than a liquid (i.e., flow due to deformation).
So far, the results from the uniaxial compression tests reveal a drastic dependence of the mechanical response of the non-aerated chocolate on the temperature. Mechanical properties such as the apparent Young's modulus, macroscopic yield stress, and compressive strength exhibit a reduction with increasing temperature. This trend persists even when comparing compression tests at 20 °C and 25 °C, which are both outside the phase change range, i.e., (28–34 °C).8,36 More specifically, the compressive stresses can decrease up to 30% when the temperature elevates by 5 °C, emphasizing the importance of maintaining controlled testing conditions, including temperature, humidity (its effect not studied here), and testing speed, in such complex biological systems like foods. The decrease in stresses and the further decrease in chocolate's stiffness when the temperature rises by 10 °C illustrate the complexity of chocolate's mechanical response, transitioning from a “hard” solid at 20 °C to a very “viscous” fluid at 30 °C. These temperature-dependent mechanisms are also evident when considering the effect of temperature on the two micro-aerated chocolates, highlighting the soft nature of the chocolate at these temperature levels.
3.2. Rheological results
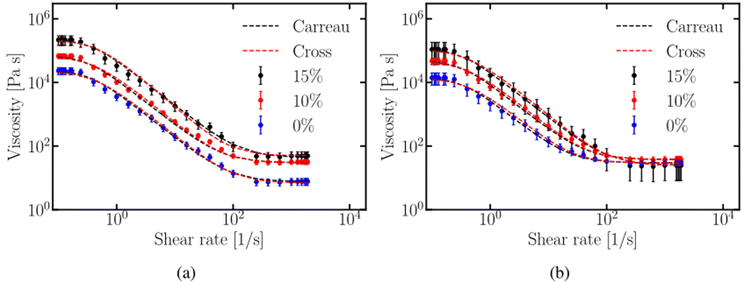
The viscosity–strain rate plots without and with the artificial saliva present, as presented in Fig. 7a and b, respectively, show that the viscosity decreases with increasing shear rate for all samples and increases with the increasing micro-aeration level. Fig. 7a shows the comparison among the viscosity values without artificial saliva for samples with porosities f = 0, 10, and 15 vol%. The trend for all samples is the same, the viscosity is initially steady for low shear rates and reduces for shear rates between 0.2 and 600 s−1 as the shear rate increases until it reaches a constant value at shear rates above![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 600 s−1.
> 600 s−1.
Fig. 7b shows results of viscosity for the different micro-aeration levels with the artificial saliva present. The same trend is observed, although there is no difference in viscosity values, for shear rates above ![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) > 600 s−1. Clear differences were observed in viscosity values for all micro-aeration levels with and without artificial saliva present in both figures. The Carreau and Cross models were fitted to the experimental results and both of them fit well as shown in Fig. 7a and b. Tables 1 and 2 summarise the calibrated parameters of the two models without and with artificial saliva, respectively. The parameter p has a constant value of 0.72 whereas the parameter m ranges between 1.48 and 1.5. The parameter p is higher than the corresponding p value of 0.42 reported by Taylor et al.,50 who examined the rheology of molten crumb chocolate. The constant λc appears to be higher than those reported in the literature for non-aerated chocolate samples, 2.9 vs. 1.9.50 The results showed that the rheological properties of the examined chocolate samples can be modelled well using both the Carreau and Cross models.
> 600 s−1. Clear differences were observed in viscosity values for all micro-aeration levels with and without artificial saliva present in both figures. The Carreau and Cross models were fitted to the experimental results and both of them fit well as shown in Fig. 7a and b. Tables 1 and 2 summarise the calibrated parameters of the two models without and with artificial saliva, respectively. The parameter p has a constant value of 0.72 whereas the parameter m ranges between 1.48 and 1.5. The parameter p is higher than the corresponding p value of 0.42 reported by Taylor et al.,50 who examined the rheology of molten crumb chocolate. The constant λc appears to be higher than those reported in the literature for non-aerated chocolate samples, 2.9 vs. 1.9.50 The results showed that the rheological properties of the examined chocolate samples can be modelled well using both the Carreau and Cross models.
| Parameter | f = 15 vol% | f = 10 vol% | f = 0 vol% |
|---|---|---|---|
| η 0 [Pa s] | 218![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
67![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 191 191 |
23![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 373 373 |
| η ∞ [Pa s] | 44 | 30 | 7.71 |
| λ c [s] | 2.7 | 3.2 | 2.9 |
| α c [s] | 2.1 | 2.5 | 2.4 |
| p [—] | 0.72 | 0.72 | 0.72 |
| m [—] | 1.6 | 1.5 | 1.48 |
| Parameter | f = 15 vol% | f = 10 vol% | f = 0 vol% |
|---|---|---|---|
| η 0 [Pa s] | 109![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
47![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 048 048 |
14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 049 049 |
| η ∞ [Pa s] | 25 | 38 | 29.5 |
| λ c [s] | 3.1 | 3.2 | 3.1 |
| α c [s] | 2.4 | 2.5 | 2.4 |
| p [—] | 0.72 | 0.72 | 0.72 |
| m [—] | 1.6 | 1.5 | 1.48 |
Micro-aeration increases the viscosity of chocolate by modifying its rheology, leading to greater shear-thinning and viscoelastic behaviour. Studies on aerated liquids, like honey and syrup, have shown that air bubbles resist deformation at low shear rates, increasing relative viscosity. Torres et al.51 found that pores in the chocolate matrix influence shear thinning. At low shear rates, micro-pores act as barriers to deformation, increasing viscosity, while at high shear rates, they align with the flow, causing shear thinning. The capillary number (Ca) describes micro-void deformation and is calculated as:
![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) is the shear rate and Γ is the surface tension at the pore–liquid interface. The equilibrium deformation is determined by the balance between the deforming, viscous stress η0
is the shear rate and Γ is the surface tension at the pore–liquid interface. The equilibrium deformation is determined by the balance between the deforming, viscous stress η0![[small gamma, Greek, dot above]](https://www.rsc.org/images/entities/i_char_e0a2.gif) acting on a pore and the restoring stress supplied by surface tension (Γ/r). The shear thinning behaviour of aerated liquids has been reported in the literature initially in the study by Shaw et al.52 who investigated the effect of bubbles in magma viscosity and the later study of Manga et al.53 validated his findings. The capillary number has been related to the magnitude of pore deformation D = (A − B)/(A + B), where A and B are the major and minor axes of the deformed pore, respectively.53 Assuming that the pores in the chocolate matrix are initially undeformed (D = 0), the deformation induced by shear will increase D resulting in higher Ca. The flow streamlines are more distorted in the case of the spherical pore which act as a barrier to the flow, resulting in higher viscosity values. The viscosity reduction of micro-aerated chocolate follows the same trend as the bubble-bearing magmas studied by Rust and Manga.54 This theory can also be used to explain the similar viscosity values obtained for high strain rates when saliva is present in Fig. 7b. The addition of saliva possibly enhances the flow of the melted chocolate around the deformed pores, reducing the effect that micro-aeration has on the viscosity.
acting on a pore and the restoring stress supplied by surface tension (Γ/r). The shear thinning behaviour of aerated liquids has been reported in the literature initially in the study by Shaw et al.52 who investigated the effect of bubbles in magma viscosity and the later study of Manga et al.53 validated his findings. The capillary number has been related to the magnitude of pore deformation D = (A − B)/(A + B), where A and B are the major and minor axes of the deformed pore, respectively.53 Assuming that the pores in the chocolate matrix are initially undeformed (D = 0), the deformation induced by shear will increase D resulting in higher Ca. The flow streamlines are more distorted in the case of the spherical pore which act as a barrier to the flow, resulting in higher viscosity values. The viscosity reduction of micro-aerated chocolate follows the same trend as the bubble-bearing magmas studied by Rust and Manga.54 This theory can also be used to explain the similar viscosity values obtained for high strain rates when saliva is present in Fig. 7b. The addition of saliva possibly enhances the flow of the melted chocolate around the deformed pores, reducing the effect that micro-aeration has on the viscosity.
3.3. Fracture results
Fig. 8 shows the typical load–displacement response for all three chocolate materials under three testing speeds of 0.02 mm s−1, 0.2 mm s−1, and 2 mm s−1 at 20 °C and at 25 °C. The larger error bars compared to the uniaxial compression tests are attributed to the challenge of precisely controlling the length and sharpness of the notch due to the brittle nature of the material. Based on Fig. 8, the load increases nonlinearly, reaching a maximum load followed by a smooth drop to zero load, implying complete fracture of the surfaces. In all cases, the maximum load increases with increasing testing speed, increasing the total area underneath the force–displacement curve. The gradual drop of the load suggests a stable crack growth for all three chocolate materials which progresses almost asymptotically to the zero value (see Fig. 8). The arrows in the plots of Fig. 8 indicate the crack initiation of all tested materials for each testing speed, which is found to be close the maximum points, as observed from video images recorded during the experiments. After the completion of the experiments, separation of the cracked surfaces was not observed regardless of the testing speed and chocolate material. The cracked surfaces remained in contact, implying the presence of an adhesion mechanism that holds the two surfaces together even when the samples returned to the zero-force position.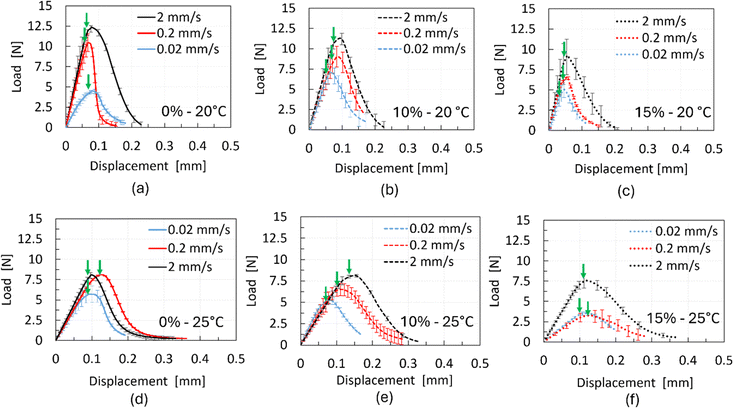 | ||
| Fig. 8 Load–displacement data for chocolate materials of different porosities from the SENB tests under three testing speeds at 20 °C and 25 °C. | ||
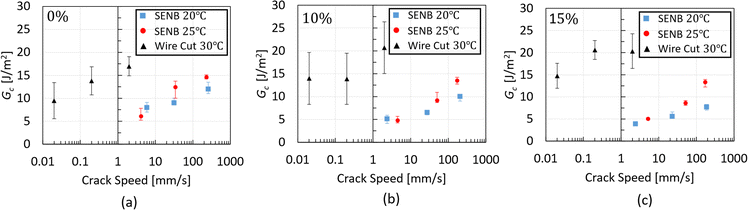
The critical strain energy release rate, Gc, of the three chocolate varieties is summarised in Fig. 9 as a function of crack speed. Based on the plots of this figure, increasing trends of Gc with increasing crack speed are observed for all materials at both testing temperatures. Based on Fig. 9a, the Gc values of the 0%, 10% and 15% micro-aerated chocolate at 20 °C range from 8–12 J m−2, 5.5–10 J m−2 and 4–8 J m−2, respectively. The same ranges at 25 °C change to 6–15 J m−2, 5–13 J m−2 and 5.2–13 J m−2, respectively. The decreasing trend of Gc with increasing micro-aeration is evident at both testing temperatures. Based on these data, it is argued that the micro-pores dispersed in the chocolate microstructure impact Gc of the porous chocolate, enhancing the material's brittle nature, which is aligned with reports in the literature for porous or cellular materials.55,56 The Gc values of chocolate shown in Fig. 9 are found to be somewhat different to Gc of chocolate (∼ 2.1 J m−2) reported by Gomez et al.,20 who inversely calculated the critical strain energy release rate of chocolate using a finite element model. This discrepancy potentially implies variability in the material properties of chocolate depending on its composition or even highlights the need for rigorous mechanical analysis to get an accurate value of fracture toughness.
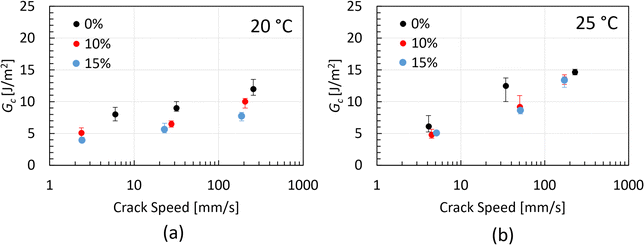 | ||
| Fig. 9 Critical strain energy release rate data obtained from the SENB experiments for all types of chocolates at 20 °C and 25 °C as a function of the crack speed. | ||
Moving to the wire cutting experimental results, Fig. 10 summarises the cutting force versus wire displacement results for all testing conditions and chocolate varieties. Based on Fig. 10, the cutting force increases with growing wire diameter, both in the indentation and the steady state cutting regime. This trend aligns with the analysis presented in Section 2.3.3 assuming that the total energy increases with increasing wire diameter due to other forms of energy present during the cutting process, such as friction energy and plastic deformation local to the crack tip, and not the fracture energy. The macroscopic behaviour of the chocolate during the wire-cutting experiments exhibited characteristics of a solid, i.e., clear cracks forming in front of the wire rather than flowing, as shown in images of Fig. 2d. This observation is consistent with the experimental results from the uniaxial compression tests at 30 °C, where clear cracks and fractures were observed (see Fig. 6e).
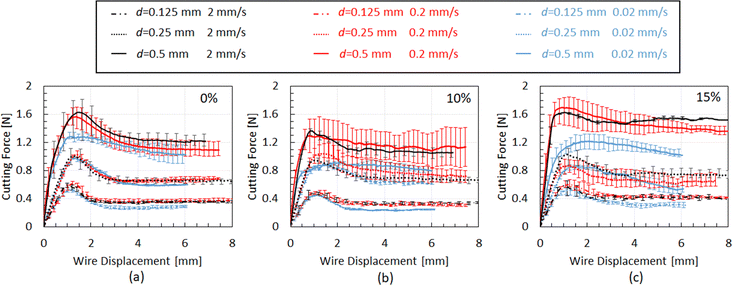 | ||
| Fig. 10 Typical cutting force–wire displacement plots for the (a) non-aerated, (b) 10% micro-aerated, and (c) 15% micro-aerated chocolate for different wire diameters and crack speeds. | ||
For a given wire diameter (see Fig. 10 for a given type of line), the peak force in the cutting force–wire displacement curves does not change with increasing testing speed (shown in Fig. 10 with different colours). Any differences observed among different speeds for the cases with the larger wire diameter of 0.5 might be due to the state of the material, which is only partially melted. The fact that the region in front of the wire might be melted or not in some cases might contribute to these differences and create a variability in the cutting force–wire displacement data. However, focusing on the steady-state regime of the curve (see Fig. 3b), which regards the critical data for the calculation of Gc, rate-dependent effects might be more prominent.
Fig. 11 shows the surface cuts under three wire diameters of 0.5 mm, 0.25 mm, and 0.125 mm for the case of the non-aerated and the 15% micro-aerated chocolate. Note that the surface cuts between the 10% and 15% micro-aerated chocolate samples did not exhibit any distinct differences. In both figures, there are two distinct regions in the fracture surface of the chocolate, as shown in Fig. 11, denoted as “i” and “ii”. The “i” region corresponds to the surface cut by the wire and the second, i.e., “ii”, indicates the natural fracture surface produced after the experiment to inspect the fracture surfaces. The fractured surface “i” indicates a larger degree of damage with increasing wire diameter. In addition, in the surface cuts produced by the wire of 0.5 mm diameter, a tearing effect in the cracked surface is depicted for all types of chocolate. This tearing effect at the cracked surfaces is caused by secondary cracks occurring during the wire cutting experiments at large sizes of wire diameter.2,45 This tearing effect diminishes with decreasing wire diameter to produce a smooth, flat surface, at least macroscopically, at d = 0.125 mm, which was true for all tested materials. The surface cuts shown in Fig. 11 and this tearing effect are consistent with other studies on foods such as cheese and gels.2,45
Comparing the surface cuts between the two chocolate materials, the tearing effect in the case of the 15% micro-aerated chocolate occurs more predominately compared to its solid 0% counterpart. It is evident that micro-aeration affects the damage process that occurs during the wire cutting experiments which potentially correlates with the larger error bars present in cutting force–wire displacement data of these materials, as shown in Fig. 10. This mechanism is expected to have an impact on Gc.
The cutting data in the form of 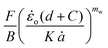 vs.
vs.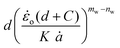 plots are shown in Fig. 12. The Gc values of the different materials, which correspond to d = 0 mm, are shown in the equation of the trend lines (constant term of the equation) and summarised in Fig. 12d for different testing speeds. Considering the relatively large error bars in the bar chart, no clear rate effect on Gc can be suggested for any of the materials. These error bars, reaching up to 50% of the average value in some cases (e.g., non-aerated chocolate at the slowest cutting speed in Fig. 12d), result from the extrapolation process to derive Gc. Even a small variation amongst the repeats, e.g. 3% for a certain wire diameter, could produce significant errors in the average Gc, exceeding 10–15%. Similar magnitudes of error bars are observed in other studies employing the wire cutting technique.45
plots are shown in Fig. 12. The Gc values of the different materials, which correspond to d = 0 mm, are shown in the equation of the trend lines (constant term of the equation) and summarised in Fig. 12d for different testing speeds. Considering the relatively large error bars in the bar chart, no clear rate effect on Gc can be suggested for any of the materials. These error bars, reaching up to 50% of the average value in some cases (e.g., non-aerated chocolate at the slowest cutting speed in Fig. 12d), result from the extrapolation process to derive Gc. Even a small variation amongst the repeats, e.g. 3% for a certain wire diameter, could produce significant errors in the average Gc, exceeding 10–15%. Similar magnitudes of error bars are observed in other studies employing the wire cutting technique.45
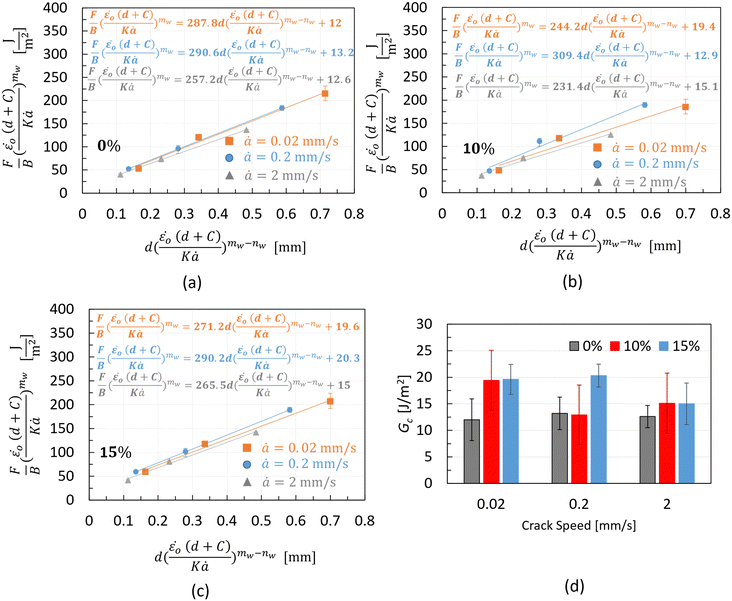 | ||
| Fig. 12 Cutting force over sample's thickness data, using eqn (15), along with the fitted trend lines for three testing speeds and the (a) 0%, (b) 10%, and (c) 15% chocolate. Bar chart (d) summarising the critical strain energy release rate values extracted from the wire cutting tests through the extrapolation method for all types of chocolate, 0%, 10%, and 15%, as a function of the cutting speed. | ||
The results shown in Fig. 12d do not indicate a clear trend in the impact of micro-aeration on Gc. In addition, at the lowest and highest testing speeds, there is no difference between Gc of the 10% and 15% micro-aerated chocolate. However, at the intermediate speed of 0.2 mm s−1, there is a large difference between the two chocolates. This inconsistency might be due to the soft, partially melted, state of the chocolate at this temperature.
Unlike the compression tests, which measure the bulk response of the chocolate sample and the SENB test, where the indenter exhibits significantly larger than the wire (radius: 4 mm vs. 0.25 mm), the wire-cutting experiments test a small region ahead of the wire. The difference in microstructure between the 10% and 15% chocolate in a plane with such dimensions (Fig. 1b and c) might not be sufficient to produce consistent differences in Gc, as opposed to the differences reported from the SENB tests and compression tests.
However, the bar chart results indicate some increase in Gc for the micro-aerated material compared to the non-aerated product, in contrast to the observations from the SENB tests at 20 °C and 25 °C. The same chart shows that the difference in Gc between non-aerated and micro-aerated chocolate is more distinct at the slowest speed compared to the highest testing speed. This suggests a different fracture behaviour for the micro-aerated chocolate depending on the testing rate, consistent with reports in the literature for other multiphase materials.57,58 At slow speeds, fracture occurs in regions with imperfections, micro-cracks, pores, or imperfect interfaces, while at higher speeds, fracture involves a higher stress state that can directly crack the matrix. This argument is believed to explain the results in Fig. 12d for the micro-aerated chocolate.
Assessing the dependency on temperature, as obtained by the different fracture experiments, Gc is plotted against crack speed for all temperature thresholds and materials, and the results are summarised in Fig. 13a–c for the 0%, 10%, and 15% micro-aerated chocolate, respectively. For a valid comparison between the SENB and wire cutting tests, Gc values that fall within the same crack speed region for all testing conditions are only compared. These regions correspond to 1–4 mm s−1, for the comparison of the Gc data at 20 °C and 30 °C, and 180–250 mm s−1, for the comparison of the SENB Gc data at 20 °C and 25 °C.
For all chocolate materials, a significant increase in Gc with temperature is observed. This is evident by comparing the SENB Gc values at 20 °C with the corresponding Gc values at 25 °C at the highest speeds (180–250 mm s−1), and similarly for the SENB Gc at 20 °C and the wire cutting Gc at 30 °C at speeds between 1 mm s−1 and 4 mm s−1. At the highest speeds, the difference between SENB Gc values at 20 °C and 25 °C for the 0%, 10%, and 15% micro-aerated chocolate is approximately 22%, 35%, and 72%, respectively. On the other hand, for the speed range of 1–4 mm s−1, a difference of 60% is observed between SENB Gc at 20 °C and the wire cutting Gc at 30 °C for the non-aerated chocolate.
This difference increases to 75% and 78% for the 10% and 15% micro-aerated, respectively. The increased “jump” in the Gc value at 30 °C of the micro-aerated materials compared to their solid counterpart may be attributed to the presence of the micro-pores in the chocolate matrix. During the wire-cutting test, the presence of micro-pores dispersed in the chocolate matrix might impact the fracture process by creating a larger degree of secondary cracks and a tortuous crack path in front of the wire tip, thereby increasing Gc of the micro-aerated chocolate at 30 °C. This hypothesis is supported by the observation of a greater degree of damage observed in the fracture surfaces of the micro-aerated chocolate (resulting in a “rougher” surface) compared to the non-aerated counterpart, as shown in Fig. 11a and b, as well as by the larger cutting forces observed for the micro-aerated material in Fig. 10. This hypothesis is also supported by the rheological results at 37 °C in this work, which demonstrate an increase of the overall viscosity with increasing level of micro-aeration, see Fig. 7. Based on these observations, the presence of micro-pores in the chocolate system seems to obstruct the flow. A similar effect might also be present at lower temperatures close to 30 °C during the wire cutting experiments.
It is important to highlight that at this temperature, the material exhibits characteristics of both a viscous liquid and a soft solid, questioning the conventional definition of Gc. More specifically, there is a dual argument: one could argue that the material fractures by the action of the wire, creating a crack tip in front of the wire, and concurrently, it may also undergo flow around the wire during the fracture experiments. This dual nature argument was initially introduced by Skamniotis et al.,59 who investigated the fracture behaviour of oatcake biscuits with varying moisture levels. This effect might also be relevant to chocolate at temperatures close to the phase change temperature, i.e., 28–34 °C, where the material becomes softer and potentially Gc measurements increase because the energy dissipation due to deformation ahead of the crack tip becomes significantly higher than the actual energy due to fracture.
Investigating the impact of micro-aeration on mechanical properties at 20 °C reveals a reduction in fracture stresses, strains, and Gc with increasing micro-aeration, consistent with trends observed in engineering materials (pores create weaker structures). However, at 30 °C, the trends begin to shift: (i) fracture toughness starts to increase with micro-aeration, attributed to micro-pores hindering the fracture process, and (ii) fracture stress and fracture toughness do not change significantly with a further 5% increase in micro-aeration. In addition, the viscosity measurements at 37 °C showed that micro-pores hinder the flow process, leading to increasing trends of viscosity with micro-aeration.
The results of these sections highlight how the impact of micro-aeration changes as the testing temperature increases and the material transitions from a soft solid to a viscous liquid. The discussed trends suggest that structural changes in chocolate due to temperature (and partial or complete melting) might induce microstructural movements or mechanisms that affect the material behaviour; micro-aeration, even at the small levels of 10–15%, can in turn significantly affect these mechanisms.
4. Discussion on micro-aeration and its link to consumer perception
This investigation of chocolate proposes a shift from the classical solid and fracture mechanics theory when it is considered as a solid, towards the theory of rheology when the material is considered fluid. The authors suggest that for applications where temperature variations lead to a phase change of chocolate coupling of classical solid and fracture mechanics experiments with rheological experiments could provide a better understanding of the material's behaviour.An example of such a scenario is found in the context of food oral processing, where a progressive structural breakdown of chocolate occurs due to mechanical, thermal, and enzymatic loads.27,28 From our previous published work,27 temporal dominance sensation (TDS) tests offered valuable insights into the processes and sensations perceived during the chocolate's oral processing. A modified version of the TDS graph from that study is presented in Fig. 14 for two chocolate materials with different levels of porosity, 0% and 10%. In these plots, only textural attributes which are statistically dominant, i.e. lying above the significance line (see red dotted line) are shown for both cases. The onset of food oral processing (FOP) is assumed when the first sensation becomes dominant, and swallowing (end of FOP) occurs when the mouthcoating sensation is perceived.
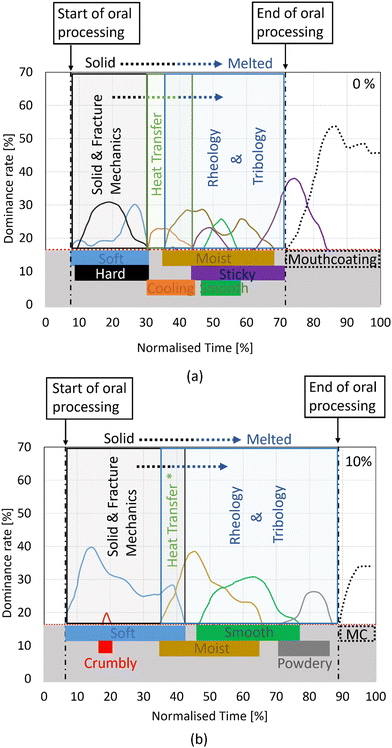 | ||
| Fig. 14 Temporal dominance sensation (TDS) sensory results in the form of a graph for (a) non-aerated (0%) and (b) 10% micro-aerated chocolate. The graph was adapted from Bikos et al.27 and only textural results which are statistically significant, i.e., above the red dotted line, are shown in this graph. The start and end of oral processing are assumed when the first sensation and once the mouth-coating is perceived. Mouthcoating (or “MC” in image b) is a sensation which is assessed after the material is consumed.27 | ||
Based on the results of our previous published work, which focused solely on mechanical measurements at 20 °C, the increased dominance (peak value of the light-blue curve in Fig. 14) in the “soft” perception between the non-aerated and 10% micro-aerated chocolate is justified by the reduction of Young's modulus and fracture stresses at 20 °C.27 Furthermore, the increase in fragmentation, as illustrated in that study by the in vivo mastication tests, with 10% micro-aeration, is linked to the decreased Gc from SENB tests at 20 °C. This increase in fragmentation is also thought to accelerate the melting, thereby increasing dominance and the duration of “smooth” perception (see the green curve in Fig. 14). Lastly, the absence of the sticky attribute as the dominant sensation in the case of the 10% micro-aerated chocolate was attributed to the drop in friction with increasing micro-aeration.
In addition to the above arguments, the new combined engineering approach of this study offers insights into the trends and evolution of certain sensorial attributes. For instance, based on Fig. 14b, the prolonged “soft” sensation in the case of the micro-aerated chocolate is attributed to a synergy of the solid-like behaviour during the early stages of FOP (time: ∼10–15%) and the complex liquid behaviour of the material during later stages when melting is expected to initiate (time: ∼30–40%). The reduced fracture stresses of the micro-aerated chocolate compared to its solid counterpart justify the absence of a “hard” sensation (and the first peak of a “soft” sensation) during FOP times between 10 and 15% as the chocolate remains predominantly solid at this stage. Conversely, the delayed peak of the “soft” sensation curve (FOP time: 30–40%) is believed to be linked to the increased Gc at 30 °C and its flow behaviour at 37 °C, indicating the onset of melting (as implied by the presence of “moist” sensation). The wire cutting experiments at 30 °C revealed higher Gc values with micro-aeration (see Fig. 13) and potentially higher energy dissipation mechanisms due to the larger energy to create a new crack, as well as the presence of secondary cracks (see Section 3.3). The overall increased viscosity with micro-aeration (see Fig. 7) could also create a resistant viscous chewed mass (partially melted) which could contribute to a prolonged “soft” sensation.
The reduction of Gc with micro-aeration at temperatures of 20 °C and 25 °C (see Fig. 13), together with the reduction of the fracture strains (see the change in the lateral position of the red marks in Fig. 4) with micro-aeration, implies a more brittle behaviour for the micro-aerated chocolate. This suggests higher fragmentation of the micro-aerated material, leading to an expedited melting process, as reported in previous literature.27 The expedited melting process could affect the perception of attributes associated with the melting of chocolate,60 such as the “cooling” sensation in this study. In this case, an accelerated melting process might diminish the perceived prominence of the “cooling” sensation compared to other attributes sensed at the same time.
Finally, the increase in the viscosity measurements with micro-aeration at shear rates relevant to FOP (1–20 Hz) results in a more viscous bolus, which may be more coherent and tolerant to the shear actions during the subsequent steps of the FOP, contributing in that way to the increased dominance and duration of the “smooth” perception in the 10% micro-aerated chocolate.
The definition of the textural attributes can reveal the state of the chocolate during food oral processing (FOP).27 For instance, “hardness–softness” and “crumbly” attributes are associated with the solid nature of the chocolate and are perceived in the early stages of FOP, while “cooling” indicates the melting of chocolate and its phase change. Attributes such as “smooth-powdery-gritty”, “dry-moist”, and “sticky” are related to the molten state of chocolate and the bolus formation.
Based on this argument, the authors propose the temporal dominance of engineering analysis including solid and fracture mechanics, heat transfer, and rheology and tribology, each relevant to specific stages of the FOP. The duration of each dominant engineering approach – solid and fracture mechanics, heat transfer, and rheology and tribology – is aligned with the dominance of the corresponding textural attribute. For instance, the regime where the solid and fracture mechanics analysis is dominant aligns with the onset and the end of the “hard/soft” sensation. For heat transfer, the regime coincides with the duration of the “cooling” sensation. Lastly, rheology and tribology27,28 are important to consider when attributes such as “moist” and “sticky” become dominant. These dominant regimes are depicted in the plots of Fig. 14. It is important to note that the absence of the cooling attribute in Fig. 14b does not negate the importance of heat transfer analysis, as chocolate melting is associated with not only textural but also flavour attributes.61
It is important to highlight that these arguments represent the authors’ interpretation based on their rigorous engineering analysis. However, extracting valid correlations between the material properties and the sensory perceptions remains a challenge that requires further investigation.
The material properties defined in this work using various experimental methods as a function of rate, temperature, and level of micro-aeration present an opportunity for advancing numerical models in the literature. One example is the advancement of recent multiscale models that simulate the first bite of chocolate3,34 to incorporate mastication and account for the effect of temperature as the material transitions from solid to liquid. Such computational tools can leverage the mechanical properties established in this study, considering their dependence on temperature and rate, to unravel the mechanisms occurring in these intermediate stages of oral processing. The advantage of such computational models over in vivo or in vitro experiments is that simulating consumer-specific testing conditions such as chewing rate, chewing force and their effect on the breakdown of chocolate is a feasible task. This paper lays the foundation by presenting a detailed methodology for accurately estimating the material properties of chocolate, essential for developing such a computational model.
5. Conclusions
Our study provides a comprehensive experimental methodology that combines fracture and rheological theories to measure the rheological and fracture properties of chocolate with varying micro-aeration levels as a function of rate and temperature. The combined experimental campaign reveals a drastic dependence of the material properties of chocolate on micro-aeration. Specifically, fracture stresses and the critical strain energy release rate, Gc, decrease with micro-aeration when the chocolate is solid, resulting in a more brittle and soft material. However, at 30 °C, Gc is found to increase with micro-aeration due to the obstruction of the fracture process by the micro-pores. Similarly, at 37 °C, the rheological experiments show that the presence of micro-pores leads to a more viscous flow, likely caused by the increased capillary number. These results demonstrate how the microstructure impacts the material properties of chocolate differently during the transition from a solid to a viscous liquid. The relationships between the micro-aeration and material properties and the dependence of temperature on the different mechanical properties as defined by the combined engineering analysis are used to explain the difference in textural attributes observed in micro-aeration during temporal dominance sensation tests. Moreover, these material parameters serve as valuable inputs for computational models that simulate the fracture and the phase change of chocolate during oral processing.Author contributions
G. Samaras and D. Bikos: conception of the idea, investigation, methodology, formal analysis, writing the original draft, writing, review, and editing of the revised manuscript. M. N. Charalambides: conception of the idea, writing the original draft, writing, review, and editing of the revised manuscript, project administration, supervision, funding acquisition. P. Cann, M. Masen, Y. Hardalupas, J. Vieira, C. Hartmann: validation, review and editing the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank the Engineering and Physical Sciences Research Council (EPSRC) for the funding via the Centre for Doctoral Training – Theory and Simulation of Materials (CDT-TSM) and Nestlé PTC York for funding the project and providing the materials for testing. The authors would also like to acknowledge the Imperial College President's PhD scholarship. Lastly, Dr Ruth Brooker and Mr Suresh Viswanathan are acknowledged for their technical guidance and training in mechanical testing.References
- T. M. Deboni, M. Bündchen, C. V. Junior, D. Hotza, R. Piletti and M. G. N. Quadri, Effect of the processing steps on cactus juice production, Food Bioprocess Technol., 2014, 7(4), 990–1000 CrossRef CAS.
- S. M. Goh, M. N. Charalambides and J. G. Williams, On the mechanics of wire cutting of cheese, Eng. Fract. Mech., 2005, 72(6 SPEC. ISS.), 931–946 CrossRef.
- G. Samaras, D. Bikos, C. Skamniotis, P. Cann, M. Masen and Y. Hardalupas, et al., Experimental and computational models for simulating the oral breakdown of food due to the interaction with molar teeth during the first bite, Extreme Mech. Lett., 2023, 62, 102047 CrossRef.
- J. F. V. Vincent, Application of fracture mechanics to the texture of food, Eng. Failure Anal., 2004, 11(5), 695–704 CrossRef.
- P. W. Lucas, J. F. Prinz, K. R. Agrawal and I. C. Bruce, Food Physics and Oral Physiology, Food Qual. Prefer., 2002, 13(4), 203–213 CrossRef.
- S. T. Beckett, L. Info, M. Records and R. S. C. Read, Science of Chocolate. The Science of Chocolate, 2008, 103–124 Search PubMed.
- V. Glicerina, F. Balestra, M. Dalla Rosa and S. Romani, Effect of manufacturing process on the microstructural and rheological properties of milk chocolate, J. Food Eng., 2015, 145, 45–50 CrossRef.
- V. Glicerina, F. Balestra, M. Dalla and S. Romani, Rheological, textural and calorimetric modifications of dark chocolate during process, J. Food Eng., 2013, 119(1), 173–179, DOI:10.1016/j.jfoodeng.2013.05.012.
- H. Zhao, B. Li and B. J. James, Structure-fracture relationships in chocolate systems, LWT, 2018, 96, 281–287 CrossRef CAS.
- E. O. Afoakwa, A. Paterson, M. Fowler and J. Vieira, Effects of tempering and fat crystallisation behaviour on microstructure, mechanical properties and appearance in dark chocolate systems, J. Food Eng., 2008, 89(2), 128–136 CrossRef.
- O. S. Toker, H. R. Pirouzian, I. Palabiyik and N. Konar, Chocolate flow behavior: Composition and process effects, Crit. Rev. Food Sci. Nutr., 2021, 1–15 Search PubMed Available from: https://www.tandfonline.com/doi/full/10.1080/10408398.2021.1993782.
- N. De Clercq, K. Moens, F. Depypere, J. Vila Ayala, G. Calliauw and W. De Greyt, et al., Influence of cocoa butter refining on the quality of milk chocolate, J. Food Eng., 2012, 111(2), 412–419 CrossRef CAS.
- C. Servais, H. Ranc and I. D. Roberts, Determination of chocolate viscosity, J. Texture Stud., 2003, 34(5–6), 467–497 CrossRef.
- E. O. Afoakwa, A. Paterson and M. Fowler, Factors influencing rheological and textural qualities in chocolate – a review, Trends Food Sci. Technol., 2007, 18(6), 290–298 CrossRef CAS.
- C. Vásquez, G. Henríquez, J. V. López, E. K. Penott-Chang, A. J. Sandoval and A. J. Müller, The effect of composition on the rheological behavior of commercial chocolates, LWT, 2019, 111, 744–750 CrossRef.
- E. J. Windhab, What makes for smooth, creamy chocolate?, Phys. Today, 2006, 59(6), 82 CrossRef CAS.
- S. C. da Silva Lannes and M. L. Medeiros, Rheological properties of chocolate drink from cupuassu, Int. J. Food Eng., 2008, 4, 1 Search PubMed.
- J. Simuang, N. Chiewchan and A. Tansakul, Effects of fat content and temperature on the apparent viscosity of coconut milk, J. Food Eng., 2004, 64(2), 193–197 CrossRef.
- Y. Y. Chen, X. Y. Zhou, S. H. Qian and J. H. Yu, Effect of Sugar and Milk Powder Addition on the Mechanical Properties and Texture of Chocolate, J. Oleo Sci., 2022, 71(11), ess22148 Search PubMed.
- F. J. Gómez, A. Salazar, M. Martínez, S. K. Rana and J. Rodríguez, Fracture of notched samples of chocolate, Theor. Appl. Fract. Mech., 2022, 121, 103477 CrossRef.
- D. Bikos, Effect of micro-aeration on mechanical and thermal properties of chocolate and correlation to oral processing [PhD], [London], Imperial College London, 2022.
- D. Bikos, G. Samaras, P. Cann, M. Masen, Y. Hardalupas and C. Hartmann, et al., Effect of micro-aeration on the mechanical behaviour of chocolates and implications for oral processing, Food Funct., 2021, 12, 4864–4886 RSC.
- B. J. Dobraszczy, A. G. Atkins, G. Jeronimidis and P. P. Purslow, Fracture toughness of frozen meat, Meat Sci., 1987, 21(1), 25–49 CrossRef CAS.
- S. Stefan, W. Tilman, S. Carolin, S. Yvonne, N. Thomas and M. Jens-Peter, et al., High-speed cutting of foods: Development of a special testing device, J. Food Eng., 2018, 216, 36–41 CrossRef.
- K. R. Agrawal and P. W. Lucas, The mechanics of the first bite, Proc. R. Soc. B, 2003, 270(1521), 1277–1282 CrossRef . Available from: https://rspb.royalsocietypublishing.org/cgi/doi/10.1098/rspb.2003.2361.
- K. R. Langley, A. Martin and S. L. Ogin, The effect of filler volume fraction on the fracture toughness of a model food composite, Compos. Sci. Technol., 1994, 50, 259–264 CrossRef CAS.
- D. Bikos, G. Samaras, P. Cann, M. Masen, Y. Hardalupas and M. N. Charalambides, et al., Effect of structure on the mechanical and physical properties of chocolate considering time scale phenomena occurring during oral processing, Food Struct., 2021, 31, 100244 CrossRef.
- G. Samaras, D. Bikos, J. Vieira, C. Hartmann, M. N. Charalambides and Y. Hardalupas, et al., Measurement of molten chocolate friction under simulated tongue-palate kinematics: Effect of cocoa solids content and aeration, Curr. Res. Food Sci., 2020, 3, 304–313 CrossRef.
- J. Chen, Food oral processing: Some important underpinning principles of eating and sensory perception, Food Struct., 2014, 1(2), 91–105, DOI:10.1016/j.foostr.2014.03.001.
- J. Chen and J. R. Stokes, Rheology and tribology: Two distinctive regimes of food texture sensation, Trends Food Sci. Technol., 2012, 25(1), 4–12, DOI:10.1016/j.tifs.2011.11.006.
- S. A. Rodrigues, N. Selway, M. P. Morgenstern, L. Motoi, J. R. Stokes and B. J. James, Lubrication of chocolate during oral processing, Food Funct., 2017, 8(2), 533–544 RSC.
- J. R. Stokes, M. W. Boehm and S. K. Baier, Oral processing, texture and mouthfeel: From rheology to tribology and beyond, Curr. Opin. Colloid Interface Sci., 2013, 18(4), 349–359, DOI:10.1016/j.cocis.2013.04.010.
- D. Bikos, G. Samaras, P. Cann, M. Masen, Y. Hardalupas and J. Vieira, et al., Destructive and non-destructive mechanical characterisation of chocolate with different levels of porosity under various modes of deformation, J. Mater. Sci., 2023, 58(11), 5104–5127 CrossRef CAS.
- G. Samaras, D. Bikos, P. Cann, M. Masen, Y. Hardalupas and J. Vieira, et al., A multiscale finite element analysis model for predicting the effect of micro-aeration on the fragmentation of chocolate during the first bite, Eur. J. Mech. – A/Solids, 2024, 104, 105221 CrossRef.
- S. K. Reinke, F. Wilde, S. Kozhar, F. Beckmann, J. Vieira and S. Heinrich, et al., Synchrotron X-Ray microtomography reveals interior microstructure of multicomponent food materials such as chocolate, J. Food Eng., 2016, 174, 37–46 CrossRef.
- M. Sarfarazi and M. Mohebbi, An investigation into the crystalline structure, and the rheological, thermal, textural and sensory properties of sugar-free milk chocolate: effect of inulin and maltodextrin, J. Food Meas. Charact., 2020, 14(3), 1568–1581, DOI:10.1007/s11694-020-00405-4.
- D. Bikos, G. Samaras, M. Charalambide, P. Cann, M. Masen and C. Hartmann, et al., Experimental and numerical evaluation of the effect of micro-aeration on the thermal properties of chocolate, Food Funct., 2022, 13(9), 4993–5010 RSC.
- D. Bikos, G. Samaras, M. N. Charalambides, P. Cann, M. Masen and C. Hartmann, et al., A micromechanical based finite element model approach to accurately predict the effective thermal properties of micro-aerated chocolate, Innovative Food Sci. Emerging Technol., 2023, 83, 103227 CrossRef.
- M. N. Charalambides, S. M. Goh, L. Wanigasooriya, J. G. Williams and W. Xiao, Effect of friction on uniaxial compression of bread dough, J. Mater. Sci., 2005, 40(13), 3375–3381 CrossRef CAS.
- P. J. Carreau and D. De Kee, Review of some useful rheological equations, Can. J. Chem. Eng., 1979, 57(1), 3–15 CrossRef CAS.
- M. M. Cross, Relation between viscoelasticity and shear-thinning behaviour in liquids, Rheol. Acta, 1979, 18(5), 609–614 CrossRef CAS.
- ASTM D5045, Standard Test Methods for Plane-Strain Fracture Toughness and Strain Energy Release, ASTM International Designation: D. 1999.
- S. Meng, An engineering approach to food texture studies [PhD], [London], Imperial College London, 2002.
- J. G. Williams and M. Rink, The standardisation of the EWF test, Eng. Fract. Mech., 2007, 74(7), 1009–1017 CrossRef.
- C. Gamonpilas, M. N. Charalambides and J. G. Williams, Determination of large deformation and fracture behaviour of starch gels from conventional and wire cutting experiments, J. Mater. Sci., 2009, 44(18), 4976–4986 CrossRef CAS.
- I. Kamyab, S. Chakrabarti and J. G. Williams, Cutting cheese with wire, J. Mater. Sci., 1998, 33, 2763–2770 CrossRef CAS.
- S. N. Ahmad, J. Hashim and M. I. Ghazali, The Effects of Porosity on Mechanical Properties of Cast Discontinuous Reinforced Metal–Matrix Composite, J. Compos. Mater., 2005, 39(5), 451–466 CrossRef CAS.
- X. Chen, S. Wu and J. Zhou, Influence of porosity on compressive and tensile strength of cement mortar, Constr. Build. Mater., 2013, 40, 869–874 CrossRef.
- M. I. El Ghezal, Y. Maalej and I. Doghri, Micromechanical models for porous and cellular materials in linear elasticity and viscoelasticity, Comput. Mater. Sci., 2013, 70, 51–70 CrossRef.
- J. E. Taylor, I. Van Damme, M. L. Johns, A. F. Routh and D. I. Wilson, Shear rheology of molten crumb chocolate, J. Food Sci., 2009, 74(2), 55–61 CrossRef.
- M. D. Torres, F. Gadala-Maria and D. I. Wilson, Comparison of the rheology of bubbly liquids prepared by whisking air into a viscous liquid (honey) and a shear-thinning liquid (guar gum solutions), J. Food Eng., 2013, 118(2), 213–228 CrossRef.
- H. R. Shaw, T. L. Wright, D. L. Peck and R. Okamura, The viscosity of basaltic magma; an analysis of field measurements in Makaopuhi lava lake, Hawaii, Am. J. Sci., 1968, 266(4), 225–264 CrossRef CAS.
- M. Manga, J. Castro, K. V. Cashman and M. Loewenberg, Rheology of bubble-bearing magmas, J. Volcanol. Geotherm. Res., 1998, 87(1–4), 15–28 CrossRef CAS.
- A. C. Rust and M. Manga, Bubble shapes and orientations in low Re simple shear flow, J. Colloid Interface Sci., 2002, 249(2), 476–480 CrossRef CAS.
- V. Bernardo, F. Loock, J. Martin-de Leon, N. A. Fleck and M. A. Rodriguez-Perez, Mechanical Properties of PMMA-Sepiolite Nanocellular Materials with a Bimodal Cellular Structure, Macromol. Mater. Eng., 2019, 304(7), 1900041 CrossRef.
- S. K. Maiti, M. F. Ashby and L. J. Gibson, Fracture toughness of brittle cellular solids, Scr. Metall., 1984, 18(3), 213–217 CrossRef CAS.
- J. W. Gillespie, L. A. Carlsson and A. J. Smiley, Rate-dependent mode I interlaminar crack growth mechanisms in graphite/epoxy and graphite/PEEK, Compos. Sci. Technol., 1987, 28(1), 1–15 CrossRef CAS.
- S. W. Koh, J. K. Kim and Y. W. Mai, Fracture toughness and failure mechanisms in silica-filled epoxy resin composites: effects of temperature and loading rate, Polymer, 1993, 34(16), 3446–3455 CrossRef CAS.
- C. G. Skamniotis, C. H. Edwards, S. Bakalis, G. Frost and M. N. Charalambides, Eulerian-Lagrangian finite element modelling of food flow-fracture in the stomach to engineer digestion, Innovative Food Sci. Emerging Technol., 2020, 66, 102510 CrossRef CAS.
- J. Haedelt, S. T. Beckett and K. Niranjan, Bubble-included chocolate: Relating structure with sensory response, J. Food Sci., 2007, 72(3), 138–142 CrossRef.
- G. Mongia and G. R. Ziegler, The role of particle size distribution of suspended solids in defining the flow properties of milk chocolate, Int. J. Food Prop., 2000, 3(1), 137–147 CrossRef CAS.
Footnote |
| † Equally contributing authors. |
| This journal is © The Royal Society of Chemistry 2024 |