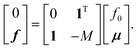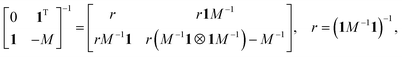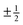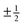DOI:
10.1039/D4SM00586D
(Paper)
Soft Matter, 2024,
20, 6894-6906
Many-defect solutions in planar nematics: interactions, spiral textures and boundary conditions
Received
16th May 2024
, Accepted 5th August 2024
First published on 8th August 2024
Abstract
From incompressible flows to electrostatics, harmonic functions can provide solutions to many two-dimensional problems and, similarly, the director field of a planar nematic can be determined using complex analysis. We derive a closed-form solution for a quasi-steady state director field induced by an arbitrarily large set of point defects and circular inclusions with or without fixed rotational degrees of freedom, and compute the forces and torques acting on each defect or inclusion. We show that a complete solution must include two types of singularities, generating a defect winding number and its spiral texture, which have a direct effect on defect equilibrium textures and their dynamics. The solution accounts for discrete degeneracy of topologically distinct free energy minima which can be obtained by defect braiding. The derived formalism can be readily applied to equilibrium and slowly evolving nematic textures for active or passive fluids with multiple defects present within the orientational order.
I. Introduction
Interactions, dynamics, and orientation of topological defects1 govern the behaviour of materials with liquid crystal-like orientational order. Equilibrium multi-defect textures can be realised by photo patterning of the alignment axis on one of the surfaces2 or by patterning of micro-pillars.3 Such photo-patterned templates can guide the swimming direction of bacteria4,5 and artificial swimmers,6 produce a tuneable photonic response,7 or can be used to study elastic properties and reconfigurations of nematic disclinations.8–11 The applicability of such designed photo-patterned templates generally depends on the shape and orientations of topological defects. Topological defects play a major role also for other symmetries of the orientational order parameter, for example, escaped structure in nematic cells can exhibit defects in the effective two-dimensional polar vector field,12 polar order can emerge in ferroelectric nematics13 and in active biological materials.14 Disclinations in the hexatic phase and their mutual interactions are a key mechanism in the melting of two-dimensional crystals.15 Distinctly out of equilibrium, driven nematic layers16 and active nematics17 are characterized by the proliferation and annihilation of topological defects. In active nematics, defects show disordered dynamics, called active turbulence, or form ordered textures,18 and have biologically-relevant properties.19 One approach towards modelling driven or active defect dynamics are particle-like models,20–23 based on the description of nematic alignment, where the director field is in equilibrium, apart from the positions and orientations of defects. Interactions and self-propagation of defects lead to their movement and reorientations. As shown by the above examples, analytical models of various liquid crystalline textures are needed as initial or boundary conditions and, more importantly, to derive general theorems about emergent orientational structures and their dynamics.
Complex analysis is an important tool to generate solutions of field theories in two dimensions. As all complex analytical functions solve the Laplace equation, models with energy proportional to (∇ϕ)2 can be solved by finding analytical functions that satisfy the boundary conditions. Additionally, conformal mapping can be used to transform the problem to a domain where solution can be readily obtained. A well known example is 2D hydrodynamics of ideal incompressible fluids, with Kutta–Joukowsky theory giving the lift generated by an airfoil by transforming a solution on a unit circle to a realistic airfoil domain.24 Complex analysis is also often used to solve for two-dimensional potentials in electrostatics25 and solitonic solutions in ferromagnets.26 A similar approach can be taken for fluids with an orientational order parameter isomorphic to einϕ, where n describes the polar (n = 1), nematic (n = 2), or higher-order symmetry, and ϕ the polar angle of the orientational order. For example, in the approximation of a single elastic constant, alignment of the nematic liquid crystals restricted to the 2D Euclidean plane can be described by a free energy 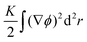 , where K is the elastic constant and
, where K is the elastic constant and ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) = (cos
= (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) is the director field. The equilibrium texture is solved by harmonic functions ϕ and singular points of ϕ correspond to topological defects (disclinations).
ϕ) is the director field. The equilibrium texture is solved by harmonic functions ϕ and singular points of ϕ correspond to topological defects (disclinations).
The conformal description of topological defects is regularly used to generate analytical models of liquid crystalline textures. Solutions for non-trivial planar geometries are often achieved by conformal mapping,27–33 or by stereographic projection for spherical domains,34,35 for describing defects dynamics in active nematics in Q-tensor formalism,36 and active nematic textures in the director formalism.37 Complex field approach can also be used to solve for a shape of nematic domains with a free boundary under different anchoring conditions.28,38 Some of the well known solutions are the core energy of a single nematic defect,39,40 the director field and the interaction energy of a pair of defects,41 and drag force and mobility tensor for moving defects.40,42 These solutions focus on topological defects, where the director field rotates by a multiple of π along a loop circumnavigating the defect core. Another singular solution of the planar Laplace equation is a type of defect, where the director polar angle changes logarithmically with the distance from the defect core.40 Such spiral solutions with a radially varying director naturally occur in, for example, ‘magic’ spiral problems.39,43,44 However, a solution for an arbitrary number of defects with a given orientation and boundary condition has to include a combination of topological defects and logarithmic singularities. No such general framework has yet been formulated.
In this paper, we develop a complete formalism for planar nematic textures involving an arbitrarily large set of point defects with arbitrary winding numbers and logarithmic singularities, quantified with the newly introduced spiral charge. We explore the expression for the director azimuthal angle ϕ in the form of
| | 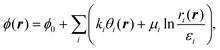 | (1) |
where
ki is the winding number of
i-th defect,
μi its spiral charge,
εi the defect core radial size and (
ri(
r),
θi(
r)) the relative polar positions from
i-th defect to
r. Using complex analysis, we derive the interaction energy between nematic defects. Within the complex analysis, winding number
ki and spiral charge
μi can be joined into a complex winding number
κi =
ki +
iμi. While
ki is topologically quantized to half-integer values,
μi is a continuous variable. We show that constrained energy optimization problems for a set of topological defects and colloidal particle inclusions represented as defects with prescribed surface alignment of the director generally lead to non-zero spiral charge and metastable solutions. Finally, we derive a general expression for forces and torques acting on topological defects and show how spiral charges lead to non-central forces, spiral annihilation trajectories and defect braiding.
II. Conformal formulation of the elastic free energy
In the following sections, we consider planar director fields under the assumption of equal elastic constants. Specifically, we are dealing with equilibrium director fields in the bulk around a set of point defects with fixed positions and orientations, and a prescribed far-field boundary condition. To obtain an analytical description of the director field and the free energy, we express positional coordinate pairs in the form of a complex number, z = x + iy = reiθ. We can express the director field in the complex notation as n = cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + i
ϕ + i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ = eiϕ, where ϕ is the director orientation angle. Local equilibrium corresponds to ∇2ϕ = 0, which we automatically satisfy by writing ϕ as an analytic function. In order to do so, we take ϕ as a real part of a complex-valued functionand define the director orientation angle as ϕ = Re(Φ). While ψ = Im(Φ) has no direct physical meaning, it is connected to ϕ through Cauchy–Riemann equations for analytic expressions of Φ, which as we show in eqn (6) considerably simplifies the evaluations of the free energy integrals. Please note that instead of directly writing an analytic expression for Φ(z), we can deduce it from the construction of the director field as n = w(z)/|w(z)| by introducing
ϕ = eiϕ, where ϕ is the director orientation angle. Local equilibrium corresponds to ∇2ϕ = 0, which we automatically satisfy by writing ϕ as an analytic function. In order to do so, we take ϕ as a real part of a complex-valued functionand define the director orientation angle as ϕ = Re(Φ). While ψ = Im(Φ) has no direct physical meaning, it is connected to ϕ through Cauchy–Riemann equations for analytic expressions of Φ, which as we show in eqn (6) considerably simplifies the evaluations of the free energy integrals. Please note that instead of directly writing an analytic expression for Φ(z), we can deduce it from the construction of the director field as n = w(z)/|w(z)| by introducing| | | w(z) = eiΦ(z) = e−ψ(z)eiϕ(z). | (3) |
The benefit of this approach is that the poles and zeroes of the function w(z) correspond to the defects in the nematic, so we can ensure defect positions and winding numbers by writing w(z) in a factorized form (see Section III). Φ(z) can be directly computed from the expression for w(z) by taking its complex logarithm Φ(z) = −i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(w(z)). Due to the nature of the complex logarithm, the branch cuts in Φ(z) are unavoidable and must be carefully considered when evaluating the free energy.
log(w(z)). Due to the nature of the complex logarithm, the branch cuts in Φ(z) are unavoidable and must be carefully considered when evaluating the free energy.
The nematic elastic energy can be expressed in the regime of one-elastic constant K as
| | 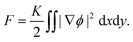 | (4) |
From now on we will omit the constant pre-factor
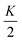
. We can reparameterize the free energy by the use of Green's identity
| | 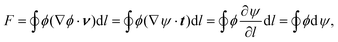 | (5) |
where the integration is performed over the counterclockwise contour, parameterized by the arc length
l, an outward normal
ν, and a tangent
t. We have considered the local equilibrium condition ∇
2ϕ = 0 and the relation ∇
ϕ·
ν = ∇
ψ·
t, which is obtained from Cauchy–Riemann equations for
Φ =
ϕ +
iψ. Considering |∇
ϕ|
2 = |∇
ψ|
2 which follows from Cauchy–Riemann equations, and exchanging the roles of
ψ and
ϕ, we can also derive
| | 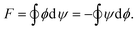 | (6) |
With appropriate choices of contours, and taking into account branch cuts,
eqn (6) is easy to compute, as we show in Section IV. For instance, along the curves of constant
ψ or
ϕ, the integrals in
eqn (6) simply reduce to differences.
III. Spiral charge
We construct point defect solutions as complex functions with a singularity at the coordinate origin in the form of| | | w(z) = eiϕ0(z/ε)k+iμ = (r/ε)k+iμeiθ(k+iμ)+iϕ0, | (7) |
where k and μ are the winding number and the spiral charge, respectively, which we discuss in detail below. To satisfy the nematic symmetry n ∼ −n, the winding number can take any half-integer value. The denominator ε ensures correct dimensions and can be set to the size of the singular defect core, or in case the defect is bound by a larger circular particle inclusion, the size of the particle. From here on, we treat both particle inclusions and real singularities in the nematic director equally as ideal point defects. When μ = 0, eqn (7) leads to the well known ansatz for 2D nematics, expressed as square roots of complex rational functions with poles and zeroes corresponding to the defects with positive and negative winding numbers. The additional rotation ϕ0 corresponds to a rigid rotation of the defect director profiles around the center for k ≠ 1 and to the parametric family of radial and circular defect profiles for k = 1 (Fig. 1b–d).
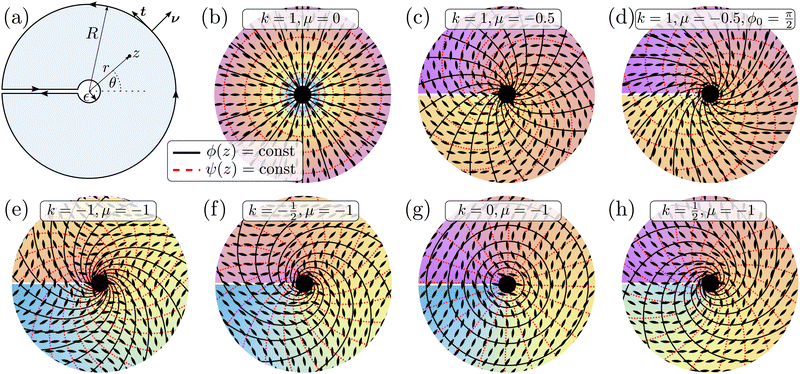 |
| | Fig. 1 Point defects with different complex winding numbers. (a) A schematic showing the integration contour avoiding the branch cut, and the notation for the polar coordinates, and the radii of the outer and inner contour. (b) and (c) A radial defect profile without and with spiral charge. (d) An additional +π/2 rotation induces a tangential anchoring on the central defect. (e)–(h) Defects of other winding numbers with added spiral charge. The colour shading shows ψ(z), which has a branch cut on the negative real axis if μ ≠ 0. The more familiar branch cut in the ϕ(z), which is present at all k ≠ 0, is not shown. Contours of ϕ and ψ form an orthogonal curvilinear grid obeying the conformal properties. Ellipses represent the director field n. | |
We can extract the complex polar angle Φ(z) = ϕ(z) + iψ(z) by taking a logarithm of eqn (7):
| | 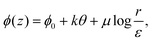 | (8) |
| | 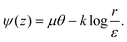 | (9) |
The director polar angle
ϕ matches the standard
μ = 0 defect profile at
r =
ε, and spirals outwards logarithmically (
Fig. 1b–h). Unlike the half-integer restricted winding number
k, the spiral charge
μ can assume any real value, representing the pitch of a logarithmic spiral seen in the contours of constant angle
ϕ(
z) (
Fig. 1). This radius-dependent spiralling is often disregarded in literature unless the geometry explicitly requires it.
39,40 The continuous nature of
μ ensures this quantity is not topologically protected from changing. It can relax to reduce the overall elastic free energy of the system.
The singularity at the origin has a diverging elastic energy, the nematic region is truncated at a finite radius ε, representing the size of the defect core. In the far field, we bound the system at a large radius R, and integrate over the contour in Fig. 1a. The elastic energy
| | 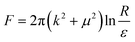 | (10) |
generalizes the well known result at
μ = 0
40 and diverges at
R → ∞. Both the half-integer winding number
k and the spiral charge
μ can be combined into a complex generalisation of the winding number
κ =
k +
iμ, which is a topological invariant in the sense that the quantity
| | 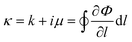 | (11) |
equals the sum of the complex winding numbers of the defects enclosed by the integration path. In the far field, the energy (
eqn (10)) will diverge unless the total
κ equals zero. As such, we expect that the principle of topological charge neutrality in bulk samples extends to the complex winding numbers. In constrained samples, the total real winding number
k can be fixed by the boundary conditions, and the total imaginary winding number
μ can equilibrate at a nonzero value according to free energy minimization. The boundary conditions also set the uniform phase
ϕ0.
IV. Pair interactions
Consider now a pair of topological defects with winding numbers κ1 = k1 + iμ1 and κ2 = k2 + iμ2 at positions z = ±d/2. We allow the core radii to be different, which is reasonable if the winding numbers themselves differ, or if one of the defects is induced by the anchoring on a small circular colloidal inclusion (see Fig. 3 for an example). The complex director angle can be written as a direct sum of two defect profiles:| | 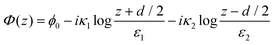 | (12) |
and split into components,| | 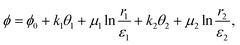 | (13) |
| | 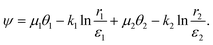 | (14) |
The relative polar positions (r1,θ1) and (r2,θ2) from each defect to the point in question (see Fig. 2a for a schematic) are a useful representation, because the θ1,2 parts control the position of the branch cuts by deciding where along the circle we make the jump by 2π. If the sum of the winding numbers is zero, κ1 + κ2 = 0, the branch cut can be localized to the line between the defects.
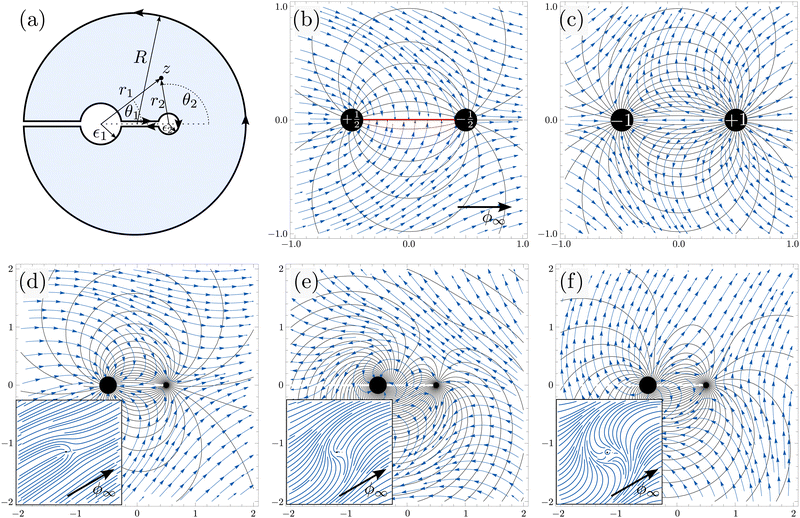 |
| | Fig. 2 Defect pairs with director field streamlines (blue) and contours of a constant orientation ϕ (black). (a) A sketch of the integration contour and the notation for a pair of defects with in principal different core radii. (b) and (c) Well known solutions for a pair of 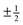 and ±1 defects with core radii ε = 0.1 and zero spiral charge terms. The case of and ±1 defects with core radii ε = 0.1 and zero spiral charge terms. The case of 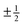 shows a sign discontinuity in the streamlines due to half-integer winding numbers (shown in red). (d)–(f) Three solutions for a pair of fixed position defects with prescribed far field direction ϕ∞, prescribed homeotropic anchoring on the radial defect (left, core radius 0.15), and unconstrained hyperbolic defect (right, core radius 0.05). The solutions differ by an increasing number of nπ windings on the radial defect. The (d) configuration has the lowest energy, but all are local minima. The radius of the outer boundary is set to R = 10. shows a sign discontinuity in the streamlines due to half-integer winding numbers (shown in red). (d)–(f) Three solutions for a pair of fixed position defects with prescribed far field direction ϕ∞, prescribed homeotropic anchoring on the radial defect (left, core radius 0.15), and unconstrained hyperbolic defect (right, core radius 0.05). The solutions differ by an increasing number of nπ windings on the radial defect. The (d) configuration has the lowest energy, but all are local minima. The radius of the outer boundary is set to R = 10. | |
The defect pair free energy is given by integrating eqn (6) along the contour shown in Fig. 2a. Considering the confinement radius R that is much larger than defect–defect separation d, yields the free energy that completely decouples the winding numbers and the spiral charges, F = Fk + Fμ:
| | 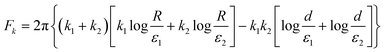 | (15) |
| | 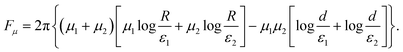 | (16) |
The first term in each part describes the far-field contribution which is positive definite, and vanishes only when the system is charge neutral. This is fulfilled only when the winding numbers are opposite, and when the defects are spiralling in oppositely oriented but equally tight spirals. The second terms describe the pair interaction proportional to the coupling of the winding numbers, and the coupling of the spiral charges, which act as two independent charges that each defect possesses – one quantized and one continuous, with opposite charges feeling an attractive force.
The free energy is the basis for finding equilibrium director configurations at fixed boundaries, or computing forces and torques acting on defects and inclusions. The complete symmetry between winding and spiral charges with no cross terms indicates that the only way for these contributions to couple is through boundary conditions, which we will explore later.
V. Energy minimization
Consider a problem of finding the director solution for fixed boundaries, which corresponds to a fixed far-field and fixed defect positions and orientations. As the winding numbers are topologically protected, the remaining degrees of freedom of the system are the global phase ϕ0 and spiral charges μi. These degrees of freedom are not coupled by the elastic free energy itself, but by additional constraints that may impose relations between them. Boundary conditions are requirements imposed on the orientation ϕ(z) at the outer edge or on the particle surfaces, when they are realized as particle inclusions or fixed by external fields. To apply the boundary conditions, ϕ(z) must be well defined on the boundary, which requires correct handling of branch cuts. In this section, we show energy minimization for a defect pair and a fixed far-field, while in the next section we provide a general formalism for an arbitrary number of defects.
The free energy is a positive definite quadratic form in terms of the spiral charges μ1 and μ2, and in the absence of boundary conditions, reaches a global minimum when all spiral charges are zero. Applying constraints changes that. Consider an example with a k1 = +1 defect enforced by a circular inclusion with a radius ε1 enforcing radial director, an accompanying k2 = −1 defect with core radius ε2 pinned at the distance d along the x axis, and homogeneous far-field in the direction ϕ(R) = ϕ∞.
The boundary condition on the far-field director (eqn (13) under the limit R ≫ d) yields the following constraint:
| | 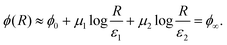 | (17) |
To apply the boundary condition on the radial particle, we decompose the director into the contribution affected by the branch cut, and the rest:
| | 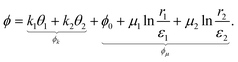 | (18) |
Let both angles
θ1 and
θ2 have an origin pointing to the right, as shown in
Fig. 2a, and range in the interval (−π,π). On the circular path around the radial defect at
r1 =
ε1, the part
ϕk(
θ1) has a value of π +
θ1 on the upper half-space, and −π +
θ1 on the lower half-space. This is consistent with the radial condition on the particle, and it would remain consistent if the branch cuts were chosen in a different way. Note that
ϕk has a constant rate with d
ϕk/d
θ1 =
k1 only in the limit
ε1 → 0, so the boundary condition is not met exactly for finitely sized particles. Due to the nematic symmetry,
ϕμ can be any integer multiple of a half-turn
nπ without violating the boundary condition, so each
n represents a valid local free energy minimum with different director profile. This discrete degeneracy of solutions is true for any defect with a prescribed boundary condition. Note that
ϕμ is not constant on this path in general due to a finite size of the core, but in approximation, we can take the value at the center of the defect:
| | 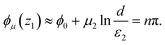 | (19) |
This approximation is valid for
d ≫
ε1, and is useful for our discussion, as it will allow us to draw more general conclusions. As the free energy is a quadratic form, and all the constraints are linear in
ϕ0,
μ1 and
μ2, this is an exactly solvable problem. With two constraints (
eqn (17) and (19)) and three variables (
ϕ0,
μ1 and
μ2), free energy minimization is necessary, and yields the solution
μ1 = (
ϕ∞ −
nπ)/log(
R/
ε1),
μ2 = 0,
ϕ0 =
nπ, shown in
Fig. 2d–f for different values of
n = −1, 0, 1. In the limit
R → ∞, the solution is
μ1 =
μ2 = 0. However, the value of the free energy at the minimum,
F = (
ϕ∞ −
nπ)
2/log(
R/
ε1), shows that the impact of the far-field boundary condition becomes less and less significant with the system size. With enough space, a very slow spiral with negligible elastic cost is enough to match any enforced far-field orientation
ϕ∞. If instead, we assume net neutrality from the start,
μ1 = −
μ2, to ensure asymptotically homogeneous far-field, there are enough constraints to compute all three unknowns, and we obtain the solution
μ1 = −
μ2 = (
ϕ∞ −
nπ)/log(
d/
ε1),
ϕ0 = (
ϕ∞![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log(
d/
ε2) +
nπ
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif)
log(
ε2/
ε1))/log(
d/
ε1). Note that this solution does not depend on
R at all, because charge neutrality ensures far-field homogeneity which adds no elastic energy when system is enlarged. However, at finite
R, this solution has a higher free energy than the previously calculated solution which used the extra degree of freedom of nonzero total spiral charge to diminish the elastic energy even further. Alternatively,
ϕ∞ can be left unconstrained (minimised over), which corresponds to an infinite plane. The way to model infinite systems without imposing an artificial boundary is thus to enforce spiral charge neutrality and minimize over the far-field orientations, in above example, this yields
ϕ∞ =
nπ. This solution then coincides with the bounded solution in the limit
R → ∞.
An important aspect of this problem is that the length scales are hierarchically well separated. The size of the particles or defect cores must be significantly smaller than the separation between them, ε ≪ d, so that the boundary conditions on the circuits of radius ε around the defects can be accurately met. If the particles are too close together, spatial variation of the director field ϕ(z) caused by surrounding particles, cause a deviation from the ideal boundary condition, even though the conditions are still matched in an average sense. Such configuration can still be sufficient to create initial conditions for further numerical simulations. A similar condition applies to the size of the entire system that should be much larger than interparticle separation, R ≫ d. For more tightly confined systems, the method of mirror charges can be used to improve upon our approximation in particular cases that allow it, or an exact solution can be obtained if we can find a conformal mapping from the nematic domain to one where boundary conditions can be met, such as used by Tarnavskyy et al.,29–31 instead of just using point defects represented by simple zeroes and poles.
An important feature of the energy minimisation described above is that we obtain not only a single solution, but a family of local energy minima, enumerated by n, i.e. the number of π turns the director makes to match the boundary condition. Each solution does have a different free energy, but the discrete nature of the solutions means they are metastable, and more than one can be realised in experiments, depending on the initial condition. It may also be possible to switch between them with an appropriate manipulation technique.
VI. Many-body generalisation
The minimal model of two interacting defects, described in the previous section, can be generalised to a general system of N defects. Using the same procedure of contour integration, we arrive at a general form for the free energy (shown for μ-part, k-part being again the same),| | 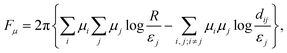 | (20) |
where dij = |zi − zj| are the distances between the defects. However, we also know that the winding number on the outer boundary must match the sum of all the winding numbers on the inside, but with inverted sense of circulation, so we can assign the outer boundary the charge 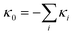 . This form makes it apparent, that the far boundary acts like just another defect, far enough that distances from all other defects can be treated as equal to d0j = R. Möbius transformations can map any of the defects to infinity while preserving the topology of the solution, so the choice of which defect sits at the infinity and represents the outer boundary, is arbitrary and does not affect the form of the free energy. This is helpful for understanding the symmetry behind the system, but for the further discussion, we will not extend the system of equations with κ0. In the limit of a large system size, R → ∞, the first term of eqn (20) dominates the second and they decouple in scale. With the diverging logarithmic terms, the first term can only be finite if
. This form makes it apparent, that the far boundary acts like just another defect, far enough that distances from all other defects can be treated as equal to d0j = R. Möbius transformations can map any of the defects to infinity while preserving the topology of the solution, so the choice of which defect sits at the infinity and represents the outer boundary, is arbitrary and does not affect the form of the free energy. This is helpful for understanding the symmetry behind the system, but for the further discussion, we will not extend the system of equations with κ0. In the limit of a large system size, R → ∞, the first term of eqn (20) dominates the second and they decouple in scale. With the diverging logarithmic terms, the first term can only be finite if 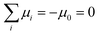 , and thus the second term is minimised within the states with zero total spiral charge. However, this limit converges extremely slowly, so for simulating unbounded systems, it is beneficial to enforce neutrality exactly, and minimise over the far field boundary orientations, as discussed in the previous section for the case of a defect pair. We derive the free energy expression for multiple defects in unbounded unconstrained space under assumption of net neutrality in Appendix B. The formalism below assumes a fixed far-field at a far boundary at distance R from the defects without the assumption of net-neutrality.
, and thus the second term is minimised within the states with zero total spiral charge. However, this limit converges extremely slowly, so for simulating unbounded systems, it is beneficial to enforce neutrality exactly, and minimise over the far field boundary orientations, as discussed in the previous section for the case of a defect pair. We derive the free energy expression for multiple defects in unbounded unconstrained space under assumption of net neutrality in Appendix B. The formalism below assumes a fixed far-field at a far boundary at distance R from the defects without the assumption of net-neutrality.
The free energy expression (eqn (20)) can be rewritten in the matrix form,
| | 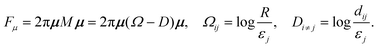 | (21) |
where it is noteworthy that the individual matrices
Ω and
D are not symmetric unless the defect cores are all the same size. On the contrary, the introduced energy matrix
M that contains the information about the entire system composed of the far-field part
Ω and the pair interaction part
D, is symmetric and positive semi-definite, as expected for an energy operator (see Appendix A for proof). It can be rewritten, if convenient, as
Mij = log(
R/
dij), if we define the self-distance
dii ≡
εi. The matrix for the
k part is identical.
To apply the boundary conditions, we take the same steps we took for the two defects, evaluating the director angle on a path around each defect, and neglecting the displacement from the core radius. Eqn (18) rewrites into
| | 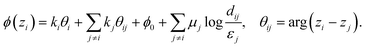 | (22) |
As before, the first term ensures the correct winding number, the second is the contribution of all the rest of the defects where correct branches must be selected for each term, and the last term involves the unknown spiral charges
μj. The first term by itself can be thought of as the defect profile in its “canonical” orientation (when the director at position
θ = 0 points along the
x axis), the remaining terms modify this orientation due to other defects, and together, they must match the orientation (rotation with respect to the canonical orientation) we enforce at the defect – the boundary condition
bi.
The difference fi between the boundary orientation bi and the k-contribution of the rest of the defects equals the angle that must be accumulated by the μ-part, and may be complemented by an arbitrary multiple of π due to rotational symmetries of the director,
| | 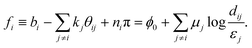 | (23) |
Fig. 3 shows an example of changing
ni at one of the defects. The boundary condition on the outer boundary can be written in a similar way,
| | 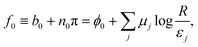 | (24) |
where the
k-contributions of all of the defects in this case simply ensure correct winding. Due to the additional degree of freedom
ϕ0, we can write
eqn (23) and (24) in the form of an extended (
N + 1) × (
N + 1) linear system:
| | 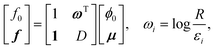 | (25) |
where
1 is a vector with all values equal to 1. The distance matrix
D and the matrix
Ω =
1 ⊗
ω are the same that appear in the expression for the free energy (
eqn (21)).
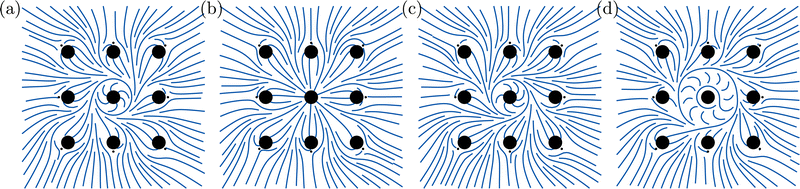 |
| | Fig. 3 Four director field solutions for a regular lattice of 9 fixed homeotropic particles, accompanied by 8 defects with fixed positions. All 8 defects have the real part of the winding number equal to k = −1, and zero spiral charge μ = 0, while the defects that represent particles are constrained and in general have nonzero spiral charges. The solutions shown differ by the amount of extra winding nπ, n = −1, 0, 1, 2, for the central particle. In general, each particle with constrained boundary director has its own discrete index enumerating the local energy minima, although in most cases, extreme spiral charges are not physically plausible. | |
We want to find a free energy minimum corresponding to a constrained orientation of some of the defects. To achieve this, free energy has to be reparameterized in terms of fi terms rather then μi. As some of the defects or the outer boundary might not be necessarily fixed, some of the components fi may be unconstrained “slack variables” that need to be minimized over to find the ground state. We compute the block-wise inverse of the constraint matrix
| | 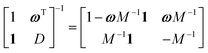 | (26) |
and apply it to
eqn (25). The resulting expression for the spiral charges
can be substituted into
eqn (21), to obtain the free energy, expressed in terms of
fi,
| | 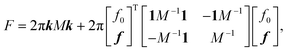 | (28) |
which as a quadratic functional can easily be minimised with respect to any subset of
fi that are not yet constrained by the boundary condition. This procedure can solve for any number of constraints, from a fully constrained case, where inversion of
eqn (25) is the only step, and no minimisable degrees of freedom remain, to the fully unconstrained case with the trivial solution
μi = 0.
For any constraint, there is an infinite discrete set of local minima, parameterized by indices ni, as shown for selected values of ni in Fig. 3. The meaning of these indices reveals that a system of defects with m constraints has m − 1 integer-valued topological indices (excluding one due to the fact that adding the same multiple of π to the entire director changes nothing). Varying the index ni changes the number of relative half-turns the director makes between i-th defect and all other constrained defects. A system of a large number of constrained 2D defects, such as a lattice of micropillars, colloidal inclusions or other topological obstructions with fixed boundary conditions, will thus always be multistable, with a multidimensional lattice of multistable states. Although there will be a practical limit on heavily wound spirals that are hard to create and stabilize, we expect at least a limited number of metastable states. Although this solution was derived for small circular defect-inducing boundaries, the topology and multiplicity of solutions will hold for inclusions of arbitrary shape with topology of a disk, as long as no additional singularities appear on the surface itself.
The values of the indices ni can be set in advance to obtain solutions for each set of indices. Alternatively, we can view the final system of equations as a quadratic minimization problem with m − 1 discrete variables, N − m continuous variables and one zero-mode. In this view, constraining the director on each boundary quantizes one dimension of the parameter space.
VII. Forces and torques
The gradient of the free energy (eqn (28)) with respect to individual defect coordinates zi gives a quasi-static approximation of a force acting on each defect, assuming the director reconfiguration time is much faster than the defect motion. The dependence on inter-particle distances resides both in the matrix M (defined in eqn (21)) and in f terms (defined in eqn (23)) for defects with prescribed boundary conditions. The gradient can thus be symbolically (keeping in mind matrix and vector nature of the variables) written as| | 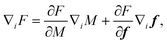 | (29) |
with ∇i representing the derivative with respect to the coordinates zi of i-th defect. The first term reduces to 2πk∇iMk − 2πμ∇iMμ, with the minus sign stemming from the fact, that the free energy is differentiated at constant f, not at constant μ. The second term is zero for unconstrained degrees of freedom, which are minimised over f. After some simplification, we obtain the force on the i-th defect| | 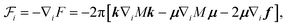 | (30) |
where f was expressed in terms of μ to simplify the expression. The spiral charges μ are the solution of the minimization of eqn (28) and depend on which constraints are imposed.
The first term gives rise to pairwise central forces obeying an inverse distance law:
| | 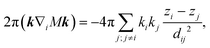 | (31) |
The second term has the same direction and distance scaling for the spiral charge contributions. The final term contains the effect of the boundary condition vector
f, while
f0 is irrelevant, as it does not depend on particle positions. The components with no constraints (the slack variables) do not contribute to this term, while the constrained components differentiate as
| | 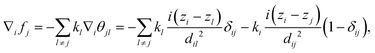 | (32) |
giving a contribution of constraint
j to the force on the particle
i. This term is weighted by the coefficients
μ, so the amount of spiral charge regulates the amount each defect can influence others. The presence of
i multiplied by the distance vector between defect pairs, describes a tangential force that is perpendicular to the distance vector. The first term in
eqn (32) represents the reaction force acted upon a constrained particle itself by all other particles, while the second term in
eqn (32) is the force exerted by a constraint on a different particle.
We illustrate the importance of orientational constraints on the forces acting on the defect pair in Fig. 4. Without orientational contraints, all spiral charges are zero and the forces are central (Fig. 4a). The magnitude and the direction of forces changes if both defects are constrained (Fig. 4b) or if one of them is constrained (Fig. 4c and d). One possibility to prescribe the orientation of a defect profile is to determine the anchoring of nematic molecules at the surface of a colloidal inclusion with winding number k = +1. In Fig. 5, we show how switching between homeotropic and tangential anchoring at the surface of one inclusion alters the forces on each defect within the system.
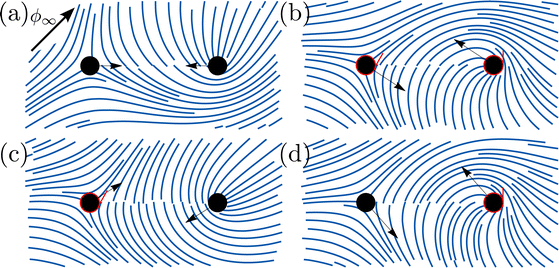 |
| | Fig. 4 Forces acting on a 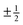 defect pair with different constraints. (a) Without constraints, the forces are radial. (b)–(d) Defects with fixed boundary condition are circled in red, with a red line indicating the preferred direction at θi = 0 position. Presence of boundary conditions induces tangential force components. The far field direction, marked in the corner, is fixed at the distance R = 10, compared to the inter-particle distance d12 = 2 and defect radii ε = 0.15. defect pair with different constraints. (a) Without constraints, the forces are radial. (b)–(d) Defects with fixed boundary condition are circled in red, with a red line indicating the preferred direction at θi = 0 position. Presence of boundary conditions induces tangential force components. The far field direction, marked in the corner, is fixed at the distance R = 10, compared to the inter-particle distance d12 = 2 and defect radii ε = 0.15. | |
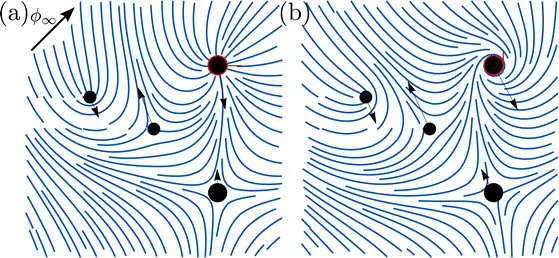 |
| | Fig. 5 Forces acting on a set of 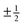 and ±1 defects, with a boundary condition on a single +1 defect, which could represent a micropillar or a colloidal inclusion. Homeotropic and planar alignment results in different forces. The boundary condition is at R = 10, the size is ε = 0.15 for the large defects and ε = 0.1 for the small defects. and ±1 defects, with a boundary condition on a single +1 defect, which could represent a micropillar or a colloidal inclusion. Homeotropic and planar alignment results in different forces. The boundary condition is at R = 10, the size is ε = 0.15 for the large defects and ε = 0.1 for the small defects. | |
In addition to forces, the director field also imparts torques on the particles. Torques reflect energy minimization by changing the boundary condition vector b in eqn (23). However, rotation of the boundary condition is nontrivially connected to rotation of particles. For instance, a particle with k = 1 is invariant to rotation, and for a particle with k = 0, rotation of the particle by some angle results in rotation of the boundary condition by the same angle. Considering the free energy expression in eqn (28), the torque on i-th particle reduces to
| | 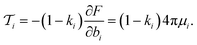 | (33) |
The spiral charge
μi therefore has a direct interpretation as a restoring torque that aims to unwind the spiral.
With forces and torques computable for every configuration, one can write down effective dynamic equations
| | 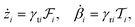 | (34) |
where
γti and
γri are the translational and rotational drag coefficients of the
i-th particle, respectively, and
βi =
bi(1 −
ki)
−1 is the physical rotation angle of the particle.
Fig. 6(a) shows an example, how the constraints on the defect profile orientations lead to spiral trajectories in the case where a ±1/2 defect pair is let to annihilate at fixed defect profile orientations. Without the orientational constraints, the defects would annihilate in a straight line. Using finite translational and orientational drag coefficients, one could in principle observe a range of annihilation trajectories from straight lines to spirals.
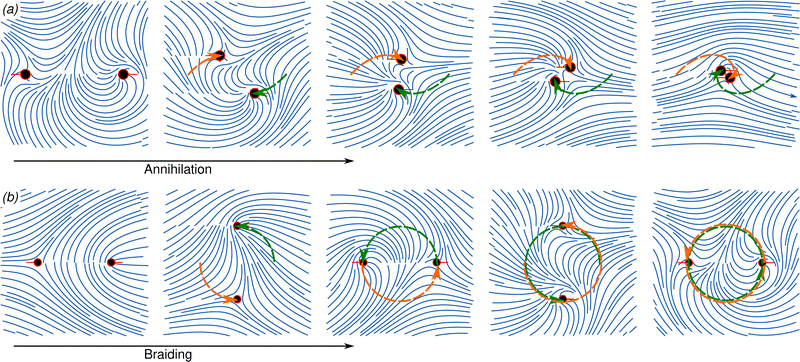 |
| | Fig. 6 Annihilation and braiding of a ±1/2 defect pair with a fixed orientation. Defects have equal core sizes (ε1 = ε2 = ε). (a) Non-central forces lead to spiral annihilation trajectories. The initial separation is set to d12 = 20ε. (b) Defects with the same separation of d12 = 20ε are initiated without any spiral charge (μ1 = μ2 = 0). By braiding the defect pair with a fixed orientation in the counter-clockwise direction around each-other, the +1/2 defect obtains a spiral charge of −π/log(20) and the −1/2 defect obtains a spiral charge of π/log(20), in line with eqn (36). | |
Spiral charge can be modified by not only changing the orientations of defects, but also by changing defect positions. Eqn (23) tells us that the orientation of a defect is determined from the contributions from all other defects through the boundary condition bi:
| | 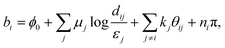 | (35) |
where
ni is an integer. For a fixed defect profile orientation (at constant
bi), a small displacement of defect positions results in the necessary change of the spiral charges
μi. By braiding the
i-th defect with a fixed orientation around the
j-th defect for a full counterclockwise turn around each other, the spiral charges of the two defects change by
| | 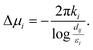 | (36) |
We demonstrate such change of the spiral charges in
Fig. 6(b) by braiding a ±1/2 defect pair for a full loop around each other, while keeping the orientations of both defects fixed.
VIII. Discussion
The presented complex field approach to construction of harmonic solutions in a planar orientational field with polar, nematic, or higher order symmetry, is developed to solve the field around sets of point defects or small enough circular inclusions or boundaries. The solutions allow for an arbitrary number and orientation of disclinations and are represented as a combination of topological charge (winding number k) and spiral charge μ. As shown by Pearce and Kruse, without spiral contributions (called “twisted” in their work), the generated solutions can not be mapped to director fields observed in experiments.45 The benefit of our framework is that the generated fields solve the Laplace equation and correspond to a free energy minimum with a single elastic constant. The forces and torques on the defect structures can also be analytically expressed. Non-central forces and non-zero torques are a direct consequence of the spiral charge. For the simplest configuration of only two defects, the presence of the spiral charge leads to spiral annihilation trajectories in agreement with the literature.41,45 Systems that do not exactly obey the Laplace equation, such as active systems, height-averaged thin samples with inhomogeneous vertical profile, or systems with differing elastic constants, are only solved approximately by our method. Although at given positions and orientations of defects, the director field is considered in equilibrium, the computed forces and alignment torques can still be used to approximate defect dynamics in active and non-equilibrium liquid crystals.46–49 The approximation could possibly be improved upon by calculating corrections to the forces and torques, such as the self-propulsion force in active nematics. The defects act as quasi-particles under the effect of pair interactions, and allow planar nematic simulations at the level of dissipative particle dynamics without the need to model the nematic host. As the spiral charges change in response to motion due to boundary conditions, their motion is collective, and not reducible to a simple pair potential, but the resulting system is linear, and as such is trivial to compute numerically for a moderate number of particles.
We show that movement of defects with a fixed orientation is directly linked to changes of the spiral charge, similarly to how anyonic braiding was shown in k-atic liquid crystals by modulation of the boundary condition.50 Braiding of defects was observed also for spiral waves in living cells51 and in active nematics it was associated with topological entropy and chaos.52–54 Harmonic director fields are of great interest also in three dimensions.55 While our theory considers purely two-dimensional fields, a future challenge would be to address the defect textures also in quasi-two-dimensional layers, where the director is allowed to point out of plane.
Construction of director structures can be extended from simple rational expressions describing finite sets of defects, to any analytical functions with appropriate positioning of poles and zeros to account for infinite sets of defects, such as periodic defect arrays. The formalism remains the same, but the tractability of the elastic energy integrals depends on the function. For example, linear chains of dipoles can be mapped to trigonometric functions while doubly periodic lattices involve Jacobi or Weierstrass elliptic functions.
In this manuscript, we only considered point defect monopoles, which only includes complexified angle functions Φ with logarithmic singularities. Our formalism can be extended to include higher multipoles with singularities of the form z−![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for
for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -th multipole (see ref. 37), which do not require addition of spiral contributions. This would allow to account for particles with more elaborate director profiles, described through a multipolar expansion, at the expense of more convoluted expressions in the interaction matrix M and boundary constraints.
-th multipole (see ref. 37), which do not require addition of spiral contributions. This would allow to account for particles with more elaborate director profiles, described through a multipolar expansion, at the expense of more convoluted expressions in the interaction matrix M and boundary constraints.
Our construction is not directly meant to solve the director field on domains that involve nontrivial boundary shapes or larger inclusions. For such problems, see other works that employ conformal mapping to transform the domain to one that offers a solution in terms of simple analytical functions – such solutions are limited to geometries that have an analytically tractable conformal mapping,27,30,31,56 or can otherwise be solved numerically.28 Our approach is a good approximation for most systems of small, preferably spherical particles. What is lost in exactness of boundary conditions, is offset by the fact that a closed-form solution can be obtained by a routine linear algebra algorithm for an arbitrary number of constrained boundaries. Here, we assume an infinitely strong anchoring, with director at the boundary prescribed exactly. For handling of finite anchoring at arbitrarily shaped boundaries, see Chandler and Spagnolie.33 Finally, the method's ability to handle larger numbers of defects suggests a possibility of developing a numerical scheme capable of handling finite-sized boundaries of arbitrary shapes, akin to methods used in hydrodynamics and electrostatics. We leave this as a future challenge.
Data availability
The code to compute the nematic textures and forces for a set of point defects under specified boundary conditions can be found at https://doi.org/10.5281/zenodo.12664067.
Conflicts of interest
There are no conflicts of interest to declare.
Appendices
Appendix A. Positive semi-definiteness of free energy
We show that the free energy expression| | 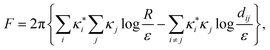 | (A1) |
obtained from eqn (20) for the defect cores of the same size, is always non-negative, provided that the total charge of all N defects sums up to zero:| | 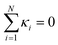 | (A2) |
and that all defects are at least 2ε apart from each other (dij ≥ 2ε for i ≠ j).
The first term in eqn (A1) is directly set to zero once the zero total charge condition is applied. We can rewrite the second term of the free energy expression
| | 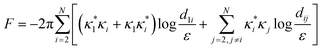 | (A3) |
and set
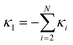
, obtaining
| | 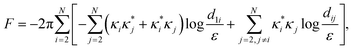 | (A4) |
which can be rewritten in a matrix form as
| | 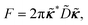 | (A5) |
where
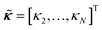
and
| | 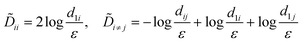 | (A6) |
with
i,
j ∈ {2,…,
N},
| | 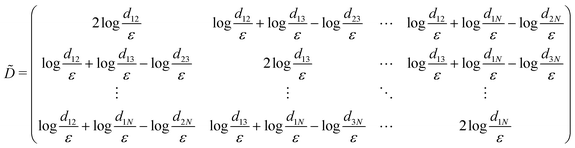 | (A7) |
The free energy is positive for arbitrary
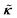
, as long as the real symmetric matrix
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
is positive-definite. We can use the Sylvester's criterion for positive semi-definiteness, which states that
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
is positive semi-definite, if and only if all principal minors of
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
are non-negative.
For k = N − 1, we can construct a simplex with N vertices in a k-dimensional space, where the Euclidean distances between vertices correspond to 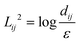 . Note that this is possible because the condition dij ≥ 2ε for i ≠ j leads to non-negative values of
. Note that this is possible because the condition dij ≥ 2ε for i ≠ j leads to non-negative values of 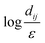 and also to the triangle inequality
and also to the triangle inequality 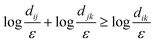 . The k-dimensional volume of the simplex is always non-negative and is given by the Cayley–Menger determinant57
. The k-dimensional volume of the simplex is always non-negative and is given by the Cayley–Menger determinant57
| | 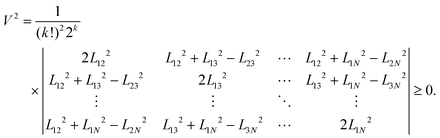 | (A8) |
Using the expression for the simplex volume, we have shown that det(
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
) = (
k!)
22
kV2 ≥ 0. All other principal minors of
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif)
effectively correspond to the same calculation for a smaller number of defects and can be shown to be non-negative using the same arguments. Following the Sylvester's criterion, we can therefore conclude that the free energy is indeed positive semi-definite (
F ≥ 0) for an arbitrary number of defects, provided that total charge of defects is zero and defects are sufficiently spaced from each other.
Appendix B. Solution for an unbounded system
In Section VI, we provided a solution that allows solving for spiral charges in a finite system bound into a circular domain of radius R, with constraints given at any combination of boundary conditions, including at the outer boundary. This requires a mapping between unknown quantities ϕ0, μ and quantities f0, f, which can either be given by boundary conditions or let to vary to minimise the free energy.
An unbounded system does not have an outer boundary and thus also has no boundary condition given there. Instead, the sum of spiral charges must equal zero. To solve for this, we must make f0 an unknown quantity, specifying the far-field orientation, instead of the overall rotation ϕ0, which can be eliminated as an unknown and can be computed from eqn (24) after the calculation. Using eqn (27) together with the zero total charge condition, which can be written as 1·μ = 0, we can write a modified version of eqn (25):
| | 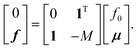 | (B1) |
This matrix does not depend on
R, as we eliminated the outer boundary.
Repeating the block-wise inverse eqn (26), we obtain,
| | 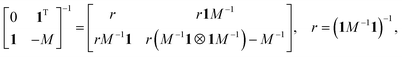 | (B2) |
and reformulate the free energy in the form,
| | | F = 2πkMk + 2πfM−1f − 2πr(fM−11)2. | (B3) |
Dependence of the matrix
M and the fixed boundary conditions
f on defect positions remain unchanged, so their derivatives are unaffected by the changed boundary condition at infinity. The expression for the force (
eqn (30)) remains unchanged, but with different values of
μ, obtained from the solution of
eqn (B1) and minimization of
eqn (B3).
Acknowledgements
The authors acknowledge funding from Slovenian Research and Innovation Agency (ARIS) under contracts P1-0099, J1-50006, and N1-0195.
References
- G. P. Alexander, B. G.-G. Chen, E. A. Matsumoto and R. D. Kamien, Rev. Mod. Phys., 2012, 84, 497 CrossRef CAS.
- C. Meng, J.-S. Wu and I. I. Smalyukh, Nat. Mater., 2023, 22, 64–72 CrossRef CAS PubMed.
- D. S. Kim, S. Čopar, U. Tkalec and D. K. Yoon, Sci. Adv., 2018, 4, eaau8064 CrossRef CAS PubMed.
- C. Peng, T. Turiv, Y. Guo, Q.-H. Wei and O. D. Lavrentovich, Science, 2016, 354, 882–885 CrossRef CAS PubMed.
- P. C. Mushenheim, R. R. Trivedi, H. H. Tuson, D. B. Weibel and N. L. Abbott, Soft Matter, 2014, 10, 88–95 RSC.
- S. Hernàndez-Navarro, P. Tierno, J. A. Farrera, J. Ignés-Mullol and F. Sagués, Angew. Chem., Int. Ed., 2014, 53, 10696–10700 CrossRef PubMed.
- M. Kim and F. Serra, Adv. Opt. Mater., 2022, 10, 2200916 CrossRef CAS.
- I. Nys, B. Berteloot and K. Neyts, J. Mol. Liq., 2023, 386, 122472 CrossRef CAS.
- J. Jiang, K. Ranabhat, X. Wang, H. Rich, R. Zhang and C. Peng, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2122226119 CrossRef CAS PubMed.
- M. Jiang, Y. Guo, R. L. Selinger, O. D. Lavrentovich and Q.-H. Wei, Liq. Cryst., 2023, 1–9 Search PubMed.
-
S. Yi, H. Chen, X. Wang, M. Jiang, B. Li, Q.-H. Wei and R. Zhang, arXiv, 2023, preprint, arXiv:2312.14735 DOI:10.48550/arXiv.2312.14735.
-
P. Pieranski and M. H. Godinho, Liquid Crystals: New Perspectives, 2021, pp. 193–309 Search PubMed.
- N. Sebastián, M. Lovšin, B. Berteloot, N. Osterman, A. Petelin, R. J. Mandle, S. Aya, M. Huang, I. Drevenšek-Olenik, K. Neyts and A. Mertelj, Nat. Commun., 2023, 14, 3029 CrossRef PubMed.
- J. Prost, F. Jülicher and J.-F. Joanny, Nat. Phys., 2015, 11, 111–117 Search PubMed.
- B. Halperin and D. R. Nelson, Phys. Rev. Lett., 1978, 41, 121 CrossRef CAS.
- M. Mur, Ž. Kos, M. Ravnik and I. Muševič, Nat. Commun., 2022, 13, 6855 CrossRef CAS PubMed.
- S. Shankar, A. Souslov, M. J. Bowick, M. C. Marchetti and V. Vitelli, Nat. Rev. Phys., 2022, 4, 380–398 CrossRef.
- S. J. DeCamp, G. S. Redner, A. Baskaran, M. F. Hagan and Z. Dogic, Nat. Mater., 2015, 14, 1110–1115 CrossRef CAS PubMed.
- T. B. Saw, A. Doostmohammadi, V. Nier, L. Kocgozlu, S. Thampi, Y. Toyama, P. Marcq, C. T. Lim, J. M. Yeomans and B. Ladoux, Nature, 2017, 544, 212–216 CrossRef CAS PubMed.
- F. C. Keber, E. Loiseau, T. Sanchez, S. J. DeCamp, L. Giomi, M. J. Bowick, M. C. Marchetti, Z. Dogic and A. R. Bausch, Science, 2014, 345, 1135–1139 CrossRef CAS PubMed.
- A. T. Brown, Soft Matter, 2020, 16, 4682–4691 RSC.
- Y.-H. Zhang, M. Deserno and Z.-C. Tu,
et al.
, Phys. Rev. E, 2020, 102, 012607 CrossRef CAS PubMed.
- L. Giomi, M. J. Bowick, P. Mishra, R. Sknepnek and M. Cristina Marchetti, Philos. Trans. R. Soc., A, 2014, 372, 20130365 CrossRef PubMed.
-
C. Pozrikidis, Introduction to theoretical and computational fluid dynamics, Oxford University Press, 2011 Search PubMed.
-
R. P. Feynman, R. B. Leighton and M. Sands, The Feynman lectures on physics; New millennium ed., Basic Books, New York, 2010, vol. II: Mainly electromagnetism and matter.
- A. Belavin and A. Polyakov, JETP Lett., 1975, 22, 245 Search PubMed.
- A. J. Davidson and N. J. Mottram, Eur. J. Appl. Math., 2012, 23, 99 CrossRef.
- R. M. W. van Bijnen, R. H. J. Otten and P. van der Schoot, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2012, 86, 168 CrossRef PubMed.
- O. Tarnavskyy, M. Ledney and A. Lesiuk, Liq. Cryst., 2018, 45, 641 CrossRef CAS.
- O. S. Tarnavskyy, A. M. Savchenko and M. F. Ledney, Liq. Cryst., 2020, 47, 851 CrossRef CAS.
- O. S. Tarnavskyy and M. F. Ledney, Liq. Cryst., 2023, 50, 21 CrossRef CAS.
- H. Miyazako and T. Nara, R. Soc. Open Sci., 2022, 9, 211663 CrossRef PubMed.
-
T. G. J. Chandler and S. E. Spagnolie, A nematic liquid crystal with an immersed body: equilibrium, stress, and paradox, 2023.
- V. Vitelli and D. Nelson, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2006, 74, 021711 CrossRef CAS PubMed.
- A. T. Brown, Soft Matter, 2020, 16, 4682 RSC.
-
F. Vafa, M. J. Bowick, M. C. Marchetti and B. I. Shraiman, arXiv, 2020, preprint, arXiv:2007.02947 DOI:10.48550/arXiv.2007.02947.
- A. J. Houston and G. P. Alexander, New J. Phys., 2023, 25, 123006 CrossRef.
- J. Rudnick and R. Bruinsma, Phys. Rev. Lett., 1995, 74, 2491 CrossRef CAS PubMed.
-
P. G. de Gennes and J. Prost, Physics of Liquid Crystals [PDF], Clarendon Press, 1993 Search PubMed.
-
M. Kleman and O. Lavrentovich, Soft Matter Physics: An Introduction, Springer, 2003 Search PubMed.
- X. Tang and J. V. Selinger, Soft Matter, 2017, 13, 5481 RSC.
- X. Tang and J. V. Selinger, Soft Matter, 2019, 15, 587 RSC.
- D. R. M. Williams, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1994, 50, 1686 CrossRef CAS PubMed.
- A. H. Lewis, D. G. A. L. Aarts, P. D. Howell and A. Majumdar, Stud. Appl. Math., 2017, 138, 438 CrossRef.
- D. J. G. Pearce and K. Kruse, Soft Matter, 2021, 17, 7408 RSC.
- S. Shankar, S. Ramaswamy, M. C. Marchetti and M. J. Bowick, Phys. Rev. Lett., 2018, 121, 108002 CrossRef CAS PubMed.
- N. Kumar, R. Zhang, J. J. De Pablo and M. L. Gardel, Sci. Adv., 2018, 4, eaat7779 CrossRef CAS PubMed.
- K. Thijssen, M. R. Nejad and J. M. Yeomans, Phys. Rev. Lett., 2020, 125, 218004 CrossRef CAS PubMed.
- R. Zhang, N. Kumar, J. L. Ross, M. L. Gardel and J. J. De Pablo, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E124–E133 CAS.
- A. Mietke and J. Dunkel, Phys. Rev. X, 2022, 12, 011027 CAS.
- J. Liu, J. F. Totz, P. W. Miller, A. D. Hastewell, Y.-C. Chao, J. Dunkel and N. Fakhri, Proc. Natl. Acad. Sci. U. S. A., 2021, 118, e2104191118 CrossRef CAS PubMed.
- A. J. Tan, E. Roberts, S. A. Smith, U. A. Olvera, J. Arteaga, S. Fortini, K. A. Mitchell and L. S. Hirst, Nat. Phys., 2019, 15, 1033–1039 Search PubMed.
- S. A. Smith and R. Gong, Front. Phys., 2022, 10, 880198 Search PubMed.
- K. A. Mitchell, M. M. H. Sabbir, K. Geumhan, S. A. Smith, B. Klein and D. A. Beller, Phys. Rev. E, 2024, 109, 014606 CrossRef CAS PubMed.
- J. Binysh and G. P. Alexander, J. Phys. A: Math. Theor., 2018, 51, 385202 CrossRef.
- F. Vafa, D. R. Nelson and A. Doostmohammadi, Phys. Rev. E, 2024, 109, 064606 CrossRef PubMed.
-
D. M. Y. Sommerville, An Introduction to the Geometry of n Dimensions, Dover Publications, New York, 1958 Search PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *a and
Žiga
Kos
*a and
Žiga
Kos
 *abc
*abc
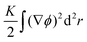 , where K is the elastic constant and
, where K is the elastic constant and ![[n with combining right harpoon above (vector)]](https://www.rsc.org/images/entities/i_char_006e_20d1.gif) = (cos
= (cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ,sin
ϕ,sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ) is the director field. The equilibrium texture is solved by harmonic functions ϕ and singular points of ϕ correspond to topological defects (disclinations).
ϕ) is the director field. The equilibrium texture is solved by harmonic functions ϕ and singular points of ϕ correspond to topological defects (disclinations).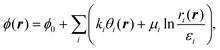
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ + i
ϕ + i![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ϕ = eiϕ, where ϕ is the director orientation angle. Local equilibrium corresponds to ∇2ϕ = 0, which we automatically satisfy by writing ϕ as an analytic function. In order to do so, we take ϕ as a real part of a complex-valued function
ϕ = eiϕ, where ϕ is the director orientation angle. Local equilibrium corresponds to ∇2ϕ = 0, which we automatically satisfy by writing ϕ as an analytic function. In order to do so, we take ϕ as a real part of a complex-valued function![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(w(z)). Due to the nature of the complex logarithm, the branch cuts in Φ(z) are unavoidable and must be carefully considered when evaluating the free energy.
log(w(z)). Due to the nature of the complex logarithm, the branch cuts in Φ(z) are unavoidable and must be carefully considered when evaluating the free energy.
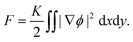
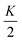 . We can reparameterize the free energy by the use of Green's identity
. We can reparameterize the free energy by the use of Green's identity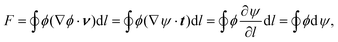
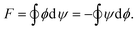
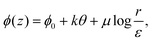
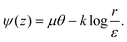
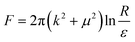
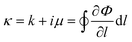
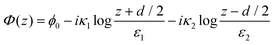
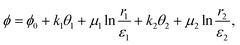
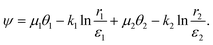
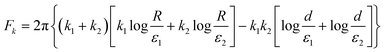
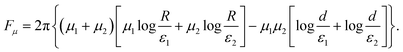
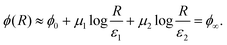
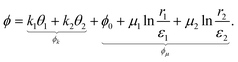
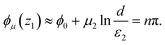
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(d/ε2) + nπ
log(d/ε2) + nπ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) log(ε2/ε1))/log(d/ε1). Note that this solution does not depend on R at all, because charge neutrality ensures far-field homogeneity which adds no elastic energy when system is enlarged. However, at finite R, this solution has a higher free energy than the previously calculated solution which used the extra degree of freedom of nonzero total spiral charge to diminish the elastic energy even further. Alternatively, ϕ∞ can be left unconstrained (minimised over), which corresponds to an infinite plane. The way to model infinite systems without imposing an artificial boundary is thus to enforce spiral charge neutrality and minimize over the far-field orientations, in above example, this yields ϕ∞ = nπ. This solution then coincides with the bounded solution in the limit R → ∞.
log(ε2/ε1))/log(d/ε1). Note that this solution does not depend on R at all, because charge neutrality ensures far-field homogeneity which adds no elastic energy when system is enlarged. However, at finite R, this solution has a higher free energy than the previously calculated solution which used the extra degree of freedom of nonzero total spiral charge to diminish the elastic energy even further. Alternatively, ϕ∞ can be left unconstrained (minimised over), which corresponds to an infinite plane. The way to model infinite systems without imposing an artificial boundary is thus to enforce spiral charge neutrality and minimize over the far-field orientations, in above example, this yields ϕ∞ = nπ. This solution then coincides with the bounded solution in the limit R → ∞.
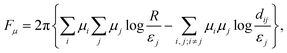
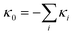 . This form makes it apparent, that the far boundary acts like just another defect, far enough that distances from all other defects can be treated as equal to d0j = R. Möbius transformations can map any of the defects to infinity while preserving the topology of the solution, so the choice of which defect sits at the infinity and represents the outer boundary, is arbitrary and does not affect the form of the free energy. This is helpful for understanding the symmetry behind the system, but for the further discussion, we will not extend the system of equations with κ0. In the limit of a large system size, R → ∞, the first term of eqn (20) dominates the second and they decouple in scale. With the diverging logarithmic terms, the first term can only be finite if
. This form makes it apparent, that the far boundary acts like just another defect, far enough that distances from all other defects can be treated as equal to d0j = R. Möbius transformations can map any of the defects to infinity while preserving the topology of the solution, so the choice of which defect sits at the infinity and represents the outer boundary, is arbitrary and does not affect the form of the free energy. This is helpful for understanding the symmetry behind the system, but for the further discussion, we will not extend the system of equations with κ0. In the limit of a large system size, R → ∞, the first term of eqn (20) dominates the second and they decouple in scale. With the diverging logarithmic terms, the first term can only be finite if 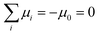 , and thus the second term is minimised within the states with zero total spiral charge. However, this limit converges extremely slowly, so for simulating unbounded systems, it is beneficial to enforce neutrality exactly, and minimise over the far field boundary orientations, as discussed in the previous section for the case of a defect pair. We derive the free energy expression for multiple defects in unbounded unconstrained space under assumption of net neutrality in Appendix B. The formalism below assumes a fixed far-field at a far boundary at distance R from the defects without the assumption of net-neutrality.
, and thus the second term is minimised within the states with zero total spiral charge. However, this limit converges extremely slowly, so for simulating unbounded systems, it is beneficial to enforce neutrality exactly, and minimise over the far field boundary orientations, as discussed in the previous section for the case of a defect pair. We derive the free energy expression for multiple defects in unbounded unconstrained space under assumption of net neutrality in Appendix B. The formalism below assumes a fixed far-field at a far boundary at distance R from the defects without the assumption of net-neutrality.
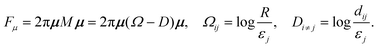
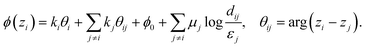
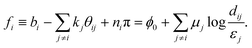
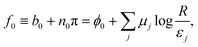
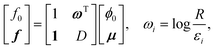
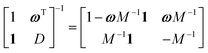
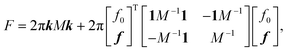
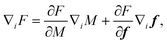
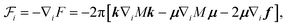
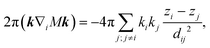
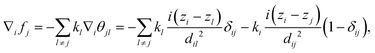
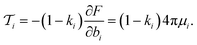
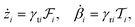

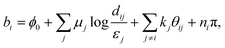
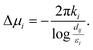
![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) for
for ![[small script l]](https://www.rsc.org/images/entities/char_e146.gif) -th multipole (see ref. 37), which do not require addition of spiral contributions. This would allow to account for particles with more elaborate director profiles, described through a multipolar expansion, at the expense of more convoluted expressions in the interaction matrix M and boundary constraints.
-th multipole (see ref. 37), which do not require addition of spiral contributions. This would allow to account for particles with more elaborate director profiles, described through a multipolar expansion, at the expense of more convoluted expressions in the interaction matrix M and boundary constraints.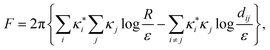
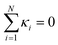
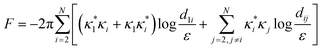
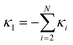 , obtaining
, obtaining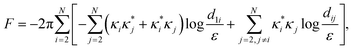
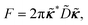
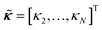 and
and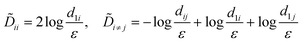
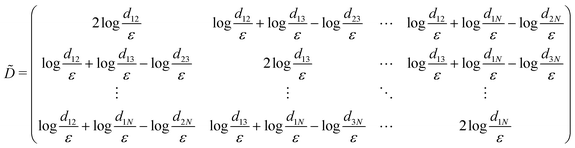
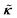 , as long as the real symmetric matrix
, as long as the real symmetric matrix ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) is positive-definite. We can use the Sylvester's criterion for positive semi-definiteness, which states that
is positive-definite. We can use the Sylvester's criterion for positive semi-definiteness, which states that ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) is positive semi-definite, if and only if all principal minors of
is positive semi-definite, if and only if all principal minors of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) are non-negative.
are non-negative.
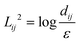 . Note that this is possible because the condition dij ≥ 2ε for i ≠ j leads to non-negative values of
. Note that this is possible because the condition dij ≥ 2ε for i ≠ j leads to non-negative values of 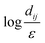 and also to the triangle inequality
and also to the triangle inequality 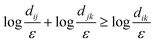 . The k-dimensional volume of the simplex is always non-negative and is given by the Cayley–Menger determinant57
. The k-dimensional volume of the simplex is always non-negative and is given by the Cayley–Menger determinant57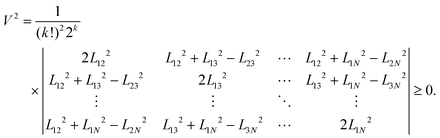
![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) ) = (k!)22kV2 ≥ 0. All other principal minors of
) = (k!)22kV2 ≥ 0. All other principal minors of ![[D with combining tilde]](https://www.rsc.org/images/entities/i_char_0044_0303.gif) effectively correspond to the same calculation for a smaller number of defects and can be shown to be non-negative using the same arguments. Following the Sylvester's criterion, we can therefore conclude that the free energy is indeed positive semi-definite (F ≥ 0) for an arbitrary number of defects, provided that total charge of defects is zero and defects are sufficiently spaced from each other.
effectively correspond to the same calculation for a smaller number of defects and can be shown to be non-negative using the same arguments. Following the Sylvester's criterion, we can therefore conclude that the free energy is indeed positive semi-definite (F ≥ 0) for an arbitrary number of defects, provided that total charge of defects is zero and defects are sufficiently spaced from each other.