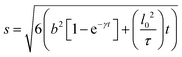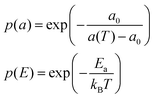Lipid lateral diffusion: mechanisms and modulators
V. K.
Sharma
 *ab,
H.
Srinivasan
ab,
J.
Gupta
ab and
S.
Mitra
*ab,
H.
Srinivasan
ab,
J.
Gupta
ab and
S.
Mitra
 ab
ab
aSolid State Physics Division, Bhabha Atomic Research Centre, Mumbai, 400085, India. E-mail: sharmavk@barc.gov.in; vksphy@gmail.com; Tel: +91-22-25594604
bHomi Bhabha National Institute, Mumbai, 400094, India
First published on 10th September 2024
Abstract
The lateral diffusion of lipids within a membrane is of paramount importance, serving as a central mechanism in numerous physiological processes including cell signaling, membrane trafficking, protein activity regulation, and energy transduction pathways. This review offers a comprehensive overview of lateral lipid diffusion in model biomembrane systems explored through the lens of neutron scattering techniques. We examine diverse models of lateral diffusion and explore the various factors influencing this fundamental process in membrane dynamics. Additionally, we offer a thorough summary of how different membrane-active compounds, including drugs, antioxidants, stimulants, and membrane proteins, affect lipid lateral diffusion. Our analysis unveils the intricate interplay between these additives and membranes, shedding light on their dynamic interactions. We elucidate that this interaction is governed by a complex combination of multiple factors including the physical state and charge of the membrane, the concentration of additives, the molecular architecture of the compounds, and their spatial distribution within the membrane. In conclusion, we briefly discuss the future directions and areas requiring further investigation in the realm of lateral lipid diffusion, highlighting the need to study more realistic membrane systems.
Introduction
A cell serves as the fundamental unit of life, exemplifying the dynamic interplay of complex molecular structures and processes. Central to this complexity is the cell membrane, a natural hydrophobic barrier, which delineates the cytosol from the extracellular environment. The cell membrane is not merely a structural entity but plays pivotal roles in numerous biological processes, encompassing selective permeability, cell defense, recognition, adhesion, and signaling. The fluid mosaic model,1 proposed by Singer and Nicolson in 1972, laid the groundwork for understanding the structural and functional complexity of cell membranes. This model describes each leaflet of the cell membrane as a two-dimensional homogeneous fluid of lipids interspersed with proteins and carbohydrates. Subsequent refinements to this model have incorporated the concept of phase-separated microdomains or rafts within the membrane, each exhibiting distinct composition and dynamics compared to the surrounding fluid phase.2 The lipid raft hypothesis is a specific interpretation of the broader concept of lateral membrane inhomogeneity. In 2006, a consensus operational definition of ‘lipid rafts’ was established, based on available evidence suggesting that rafts are heterogeneous and dynamic (in terms of both lateral mobility and association–dissociation) cholesterol and sphingolipid enriched membrane nano-domains (10–200 nm).3 These nano-domains have potential to form larger microscopic domains (>300 nm) when clustering is triggered by protein–protein and protein–lipid interactions. The enrichment of these hydrophobic components gives lipid rafts unique physical properties, such as increased lipid packing and order, along with reduced fluidity. These domains are present in both the inner and outer leaflets of asymmetric cell membranes, are likely coupled across leaflets, and serve as functional platforms for regulating various cellular processes.4,5 Recent advancements in membrane biophysics have highlighted the heterogeneous nature of cell membranes, with a dynamic interplay between lipids, proteins, and other small molecules, such as carbohydrates.6Fig. 1 provides a general overview of lateral heterogeneity in the plasma membrane. Given the pivotal role of lipid rafts in numerous biological processes, their dynamics are intricately governed by the microscopic behavior of lipids. Specifically, the lateral diffusion of lipids within these membranes, propelled by thermal agitation, significantly influences their distinctive viscoelastic characteristics.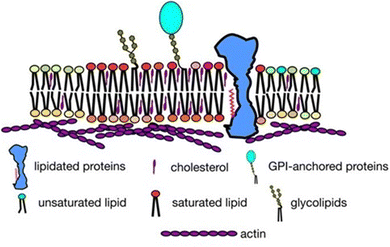 | ||
| Fig. 1 Overview of lateral heterogeneity in the plasma membrane shown in a 2-dimensional view. Adapted from ref. 5 with permission from Springer Nature, copyright 2017. | ||
Despite being only a few nanometers thick, cell membranes possess sufficient elasticity to contain the cytoplasm while retaining fluidity to facilitate the movements of lipids and proteins essential for their functionality.7 The basic matrix of the cell membrane comprises dynamic, fluid self-assemblies of lipids, called the lipid bilayer. This lipid bilayer structure serves as the foundation for the assembly of membrane proteins and the formation of specialized microdomains that regulate various cellular processes.8 In the pursuit of deciphering the intricate biological processes regulated by cell membranes at the molecular level, model membrane systems, such as liposomes and lipid bilayers, have emerged as invaluable tools.9 These model systems enable researchers to probe membrane dynamics, which significantly influence membrane fluidity and viscoelastic behavior, thereby playing pivotal roles in physiological processes such as cell signaling, membrane trafficking, permeability, vesicle fusion, and endo- or exocytosis.5
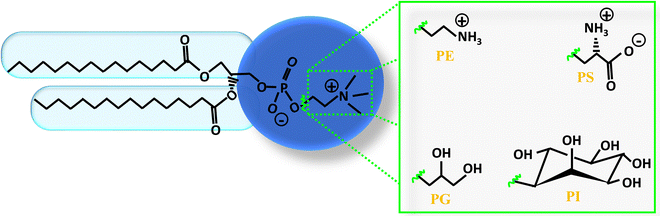
Lipids serve as the foundational components of the lipid bilayer, offering structural integrity and functionality. Lipids are amphiphilic molecules characterized by hydrophilic heads and hydrophobic fatty acid tails. Lipids make up roughly half the mass of most cell membranes, although this ratio can differ depending on the membrane type. For instance, plasma membranes consist of about equal parts of lipids and proteins. Bacterial plasma membranes are often composed of one main type of phospholipid and contain no cholesterol. For example, the plasma membrane of Gram-negative bacteria (e.g., E. coli) consists predominantly of phosphatidylethanolamine (PE), which constitutes 80% of total lipids.10 In contrast, the plasma membrane of Gram positive bacteria (e.g. S. aureus) is mainly composed of phosphatidylglycerol (PG) lipid, which is about 55% of total lipids.10 Mammalian plasma membranes are more complex, containing four major phospholipids—phosphatidylcholine (PC), phosphatidylserine (PS), PE, and sphingomyelin (SM)—which together constitute 50 to 60% of total membrane lipid. In addition to phospholipids, the plasma membranes of mammalian cells contain glycolipids and cholesterol, which generally correspond to about 40% of the total lipid molecules. The diverse class of lipid molecules exhibit variations in the head group, tail length, and tail unsaturation.11 Within cellular environments, lipid structures have evolved to fulfill specific functional needs, resulting in varied concentrations across organelle membranes and cellular tissues.6,12,13 Notably, mammalian membranes boast over thousand unique lipid species, each playing distinct roles in biological processes. Among these lipid classes, phospholipids stand out as a major group, featuring a phosphate headgroup and two hydrophobic fatty acid chains linked by an alcohol residue, typically glycerol. The diversity of phospholipids is evident in their various head groups (Fig. 2), with PC being predominant in over half of mammalian plasma membrane phospholipids.14 By altering the head group, alkyl chain length, and tail unsaturation, a plethora of phospholipid variations emerge. For example, different phospholipids with varying head groups such as PC, phosphatidic acid (PA), PE, PS, PG, and phosphatidylinositol (PI) are shown in Fig. 2. The amphiphilicity of lipids drives their self-assembly into diverse structures such as micelles, vesicles, and bilayers. Additionally, recent research has explored synthetic lipids like dialkyldimethylammonium bromide, which hold promise for application in drug delivery and gene delivery systems.
Lipid membranes are complex and dynamic entities, displaying a hierarchy of dynamics.15–23 This spectrum encompasses individual movements of lipids, such as vibrations, lateral diffusion, flip flop, and rotation. Additionally, these membranes exhibit collective behaviors where multiple lipid molecules synchronize their movements, leading to phenomena like membrane bending and fluctuations in membrane thickness. Fig. 3 illustrates the schematics of these various molecular and collective motions exhibited by lipid membranes. These diverse dynamical motions cover a broad range of time scales, extending over many decades. They range from rapid molecular vibrations occurring within tens of femtoseconds to slower flip flops that unfold over a few hours. Moreover, the characteristic length scales associated with these motions vary from Angstroms for localized molecular movements to several micrometers for macroscopic cellular deformations. To probe these motions, a variety of spectroscopic methods have been employed, including nuclear magnetic resonance (NMR),24–27 fluorescence correlation spectroscopy (FCS),28 dynamic light scattering (DLS),29,30 electron paramagnetic resonance (EPR),31 X-ray photo-correlation spectroscopy (XPCS),32 neutron spin echo (NSE),33–38 Mössbauer time-domain interferometry (MTDI)39 and quasi-elastic neutron scattering (QENS).16,20,21,40–49 However, despite the extensive range of spectroscopic techniques utilized, many are constrained to measuring dynamics within a limited time and length scale. NMR, FCS, and DLS primarily measure diffusion over length scales greater than a micrometer and time scales longer than nanoseconds, making them generally classified as macroscopic methods. On the other hand, QENS probes lipid membrane dynamics on time scales ranging from sub-picoseconds to nanoseconds and length scales spanning from a few Angstroms to nanometers, thus typically falling under the category of microscopic methods. Within these length and time scales in QENS, lipid molecules exhibit long range lateral diffusion of lipids within the leaflet as well as localized internal motion.46,50–54 QENS has been widely used to study the lateral and internal motion of lipids within the membranes.15–17,20,40,43,46,54–58 The spatial-temporal range explored by QENS can be expanded to submicroseconds and several tens of nanometers by utilizing NSE instruments.20,43 NSE has been used to study collective bending and thickness fluctuations of the membranes.15,26,36,59,60 The time and length scales accessible through QENS are highlighted in green in Fig. 3. More information about multiscale membrane dynamics can be found elsewhere.58
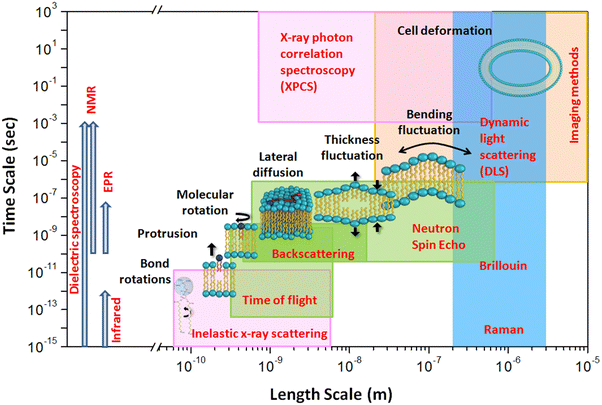 | ||
| Fig. 3 Schematic illustrating dynamical processes observed in typical lipid membranes, along with their corresponding temporal and spatial regimes. The length and time scales accessible by various spectroscopic methods are also depicted. For direct comparison, the regions probed by neutron scattering are represented by green squares, X-ray scattering by magenta squares, light scattering by blue squares, and imaging methods by a yellow square. Other spectroscopic methods shown on the leftmost side, such as electron paramagnetic resonance, nuclear magnetic resonance, infrared, and dielectric spectroscopy, cover a broad temporal regime without specific spatial associations. Reproduced from ref. 20 with permission from American Chemical Society, copyright 2020. | ||
Membrane dynamics are intricately linked to the membrane structure, so it is essential to briefly discuss the lipid bilayer's architecture, which can be effectively studied using various X-ray and neutron scattering techniques.17,20,61–63 These techniques provide valuable insights into key structural parameters, including bilayer thickness, area per lipid, tilt angle, lipid arrangement in the lateral plane, the physical state of the membrane, and the lateral distribution of lipids. It is important to recognize that X-ray and neutron scattering techniques each have distinct sensitivity to various aspects of membrane structure, which can make direct comparisons of their findings challenging. For instance, when measuring bilayer thickness, neutron scattering, which leverages the high contrast between protonated lipids and deuterated water, provides the overall bilayer thickness (db), encompassing both the hydrophobic core (comprising the hydrocarbon acyl chains) and the headgroup region along with the hydrated water. This is often referred to as the Luzzati thickness. On the other hand, X-ray scattering primarily resolves the distance between the peaks in the electron density profile, corresponding largely to the distance between lipid headgroup phosphates (dHH). The primary data obtained from these techniques are various bilayer thicknesses, which allow for the calculation of another crucial structural parameter: the area per lipid. This parameter is derived using the assumptions and inputs such as the volume of lipid molecules and the lipid headgroup volume. The area per lipid is a critical factor influencing the lateral diffusion of lipids; as the area per lipid increases, lateral diffusion typically increases. Moreover, this parameter plays a central role in other membrane properties, such as water permeability. Neutron scattering, with its isotope sensitivity, offers unique advantages in contrast-matching or contrast-variation studies. By selectively deuterating parts of the lipid molecules, specific regions of the membrane can be highlighted. For example, using perdeuterated lipid analogs, where hydrogen atoms in the lipid chains are replaced by deuterium, one can contrast-match the chain region to the deuterated buffer, thereby selectively visualizing the lipid headgroup region. For a comprehensive introduction to lipid bilayer structure using various neutron scattering techniques (e.g., small-angle neutron scattering (SANS), neutron diffraction, neutron reflectivity) and the unique capabilities provided by isotope sensitivity, readers may refer to an excellent article available elsewhere.20
In this review article, we will focus on lateral lipid diffusion, which refers to the long-range movement of entire lipid molecules within the membrane's leaflet, driven by thermal agitation. Lateral diffusion plays a crucial role in modulating membrane fluidity, organization, and functionality and has a central role in various physiological processes including cell signaling, membrane trafficking, membrane protein activity, and energy transduction pathways. Lateral diffusion facilitates the creation of transient microdomains or rafts, which are enriched in specific lipids and play a crucial role in signal transduction and the cellular response to stimuli. Additionally, lateral diffusion facilitates the redistribution of lipids to repair damaged regions in the membrane, thereby preserving its integrity. Lateral motion is essential for maintaining the fluidity of the cell membrane, which in turn regulates its transport properties. Membrane fluidity also plays an important role in endocytosis and exocytosis which facilitate material uptake and waste removal by cells. Alterations in lateral lipid diffusion can impact membrane fluidity, affect the protein–lipid interactions, and modulate cellular responses to external stimuli. Therefore, understanding the mechanisms and regulation of lipid lateral diffusion is crucial for elucidating the complex dynamics of cell membranes and their role in health and disease. Despite extensive research efforts, the determination of lateral diffusion coefficients for lipid molecules within membranes remains a topic of debate. The reported values for these coefficients exhibit significant variability, contingent upon the time and length scales probed by different measurement or computational methods.64 Previous reviews on lateral diffusion, such as those by Vaz, Zalduondo and Jacobson65 Clegg and Vaz,66 Almeida and Vaz,67 Tocanne,68 and Saxton,69 primarily covered studies up to 1999. In these review articles, lateral diffusions were observed mainly through the macroscopic techniques, predominantly based on fluorescence based techniques such as fluorescence recovery after photobleaching (FRAP) and single particle tracking (SPT). In 2009, Lindblom and Oradd reviewed the measurement of lateral diffusion using the pulsed field gradient (PFG)-NMR method.64 In this review article, we concentrate on recent studies concerning lateral lipid diffusion at the nanometer scale, particularly employing microscopic neutron scattering techniques. We explore different models proposed for lateral motion based on QENS experiments and discuss various theories aimed at elucidating lateral diffusion, along with factors influencing this motion. Additionally, we also provide an overview of the impact of various membrane-active compounds on lipid lateral diffusion.
In this article, we begin by exploring various models of lateral motion of lipids discussed in the literature. We then venture into the realm of neutron scattering in particular QENS, a prominent method used to observe the lateral motion of lipids at the microscopic length scale. In the next section, we delve into the theoretical framework of lateral lipid diffusion and examine the multitude of factors that influence this dynamic process. In the following section, we illuminate the effects of various membrane-active compounds on lateral lipid diffusion. In the last section, we summarize our findings with concluding remarks and highlight promising avenues for future research in this intriguing field.
Different models of diffusion
The dynamics of the lipid membrane exhibit a level of complexity beyond that of ordinary liquids. In a simple liquid,70 atoms experience minimal interaction with the surrounding atoms at short times, resulting in ballistic motion where the mean square displacement (MSD) is proportional to the square of time. This ballistic motion transitions to Fickian diffusion at longer times, characterized by an MSD which is proportional to time. However, in dense liquids, a phenomenon known as the caging effect occurs, wherein atoms are temporarily confined by their neighbors, leading to a power-law dependence of MSD on time. In the context of lipid bilayers, the motion of lipid atoms becomes even more intricate due to the high flexibility of the molecules. This flexibility gives rise to a pronounced subdiffusive regime between ballistic and normal Fickian diffusion.71 In this section, we will discuss in brief these different models of motions.Ballistic motion
In the case of ballistic motion, the displacement of the particle (s) can be written as a function of time (t), simply defined by its velocity (v)| s = vt | (1) |
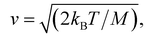 where kB is the Boltzmann constant, T is the temperature and M is the mass of the particle.
where kB is the Boltzmann constant, T is the temperature and M is the mass of the particle.
Brownian motion: continuous diffusion
For a particle diffusing via random Brownian motion, the displacement of the particle can be written as a function of time,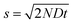 | (2) |
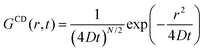 | (3) |
| ICDinc(Q, t) = exp(−DQ2t) | (4) |
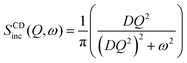 | (5) |
Jump diffusion
In systems where the interactions between particles are strong, often the particles experience transient caging and sudden jumps. These intermittent jumps can be described through the jump-diffusion process, wherein the particle makes sudden jumps interspersed by the particle being caged for an average residence time, τ. Modeling the jump-diffusion involves considering the aspect of caging and jumping which occur alternatively during the process. During the caging, the particles undergo caged diffusion, which essentially can be treated as diffusion within a confined spherical volume with reflecting boundary conditions. In this scenario, the displacement of the particle can be written aswhere b is the radius of confinement, γ denotes the rate of caged diffusion, and l0 is the root mean-squared jump-length. While the MSD or displacement of the particle can be explicitly given, it should be noted that the jump-diffusion process is strongly non-Gaussian in nature and therefore the MSD doesn’t contain sufficient information about the nature of the dynamics. This is because higher moments of displacement (higher than 2), start contributing strongly to the self van Hove correlation function. In fact, a closed form expression for the cage-jump diffusion model doesn’t exist for the self van Hove correlation function. However, at times sufficiently longer than the individual caging times, the jump diffusion can be modeled independently using continuous time random walk (CTRW) models. In this model, the particle executes jumps of certain length, l, sampled from jump-length distribution, ρ(l). The solutions to the CTRW model can be conveniently obtained in Fourier space, in terms of IISF,
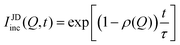 | (6) |
| IJDinc(Q, t) = exp[−Γj(Q)t] | (7) |
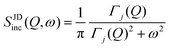 | (8) |
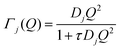 | (9) |
Confined diffusion
As discussed in the previous example of cage-jump diffusion, the confined diffusion model can be described considering the diffusion within a spherical volume of radius b, wherein the spherical walls can be regarded to have reflecting boundary conditions. In this scenario, the displacement is essentially given by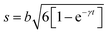 | (10) |
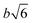 . However, it is important to note that the displacement doesn’t contain complete information about the nature of the diffusion process.
. However, it is important to note that the displacement doesn’t contain complete information about the nature of the diffusion process.
The scattering law for confined diffusion can be written as
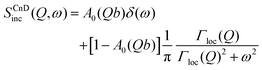 | (11) |
Anomalous diffusion
In the case of anomalous diffusion, displacement of particles can be written as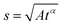 | (12) |
In this case, the scattering law can be written as
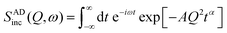 | (13) |
A schematic of different models of diffusion and ballistic motion and the corresponding variation of MSD with time are shown in Fig. 4. It is evident that these different models can be quantitatively differentiated in the traditional plot of MSD with time. For example, ballistic motion will give MSD proportional to square of time but continuous diffusion will give MSD proportional to time. In contrast, in anomalous diffusion, MSD will follow tα, where α is a non-integer value between 0 and 1 and typically takes a value of 0.6 for a variety of lipid bilayer systems.71,72 For jump diffusion, at intermediate time, MSD will be subdiffusive, but at long time, it becomes diffusive, i.e., MSD is proportional to time. Similarly, the dynamic structure factor, S(Q, ω), varies differently with Q and ω for these different motions as evident from the above equations. For example, S(Q, ω) will be a Gaussian, Lorentzian, and Fourier transform of stretched exponentials for the ballistic motion, continuous diffusion, and anomalous diffusion, respectively. This S(Q, ω) can be directly observable with the QENS technique which enables one to identify the exact diffusion mechanism of particles.
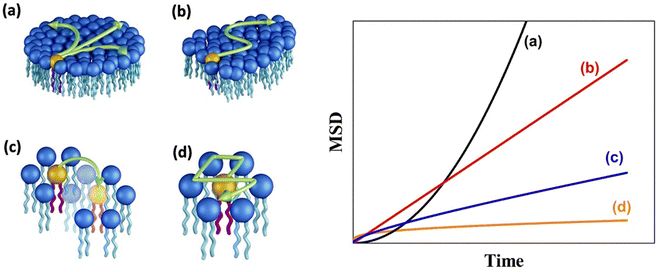 | ||
| Fig. 4 (Left) Different mechanisms for the lateral diffusion of lipids: (a) flow like ballistic motion,54,73 (b) continuous diffusion,50,74 (c) jump diffusion,75 and (d) confined diffusion57 (adapted from ref. 58). (Right) Variation of mean square displacement (MSD) vs. time corresponding to each of these models. | ||
Theoretical frameworks for lateral diffusion
Several theories have been developed to relate the lateral diffusion coefficient to the microscopic properties of the diffusing molecule and the membrane. In the case of planar lipid membranes, two distinct cases are distinguished according to the size of the diffusing molecules with respect to the size of lipids (which are the basic building blocks of the membrane). The first is a continuum hydrodynamic model76–78 for diffusion of particles, the size of which is much larger than that of the lipid. This model is thus best applicable to diffusion of integral membrane proteins in lipid bilayers. The second is the free volume model79,80 which considers the discreteness of the membrane and thus is best suited to explain the diffusion of lipids or molecules similar in size to lipids. Both these models are for the homogeneous lipid membrane system. Since this article primarily focuses on the lateral diffusion of lipids, we will provide a concise overview of the free volume model and related theories to contextualize our discussion.Free volume model
This model is based upon the free volume model proposed by Cohen and Turnbull79 for diffusion in glasses and extended by Galla et al.81 to describe diffusion in the plane of a membrane. According to the free volume model,79,82 diffusion is limited by the occurrence of a free volume greater than a critical size next to a diffusing particle. Free volumes smaller than the critical size do not contribute to diffusion. In the case of a particle performing a random walk in two dimensions, at each diffusion step, the particle needs to have both certain activation energy and a minimum free area to move into. In accordance with Macedo and Litovitz,82 the diffusion coefficient in 2D surface can be written as| Dlat = D′p(a)p(E) | (14) |
where a(T) is the average area per lipid, which is a function of temperature, and a0 is the critical area which is essentially the close-packed cross-sectional molecular area. The average free area per molecule in the plane of the bilayer is af = a(T) − a0. Ea is the activation energy associated with diffusion. D′ can be obtained using the particle performing a random walk in a two dimensional lattice and eqn (14) can be written as
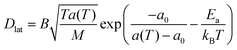 | (15) |
Extended free volume model
The free volume model was further extended by including the influence of viscous force in the aqueous phase (due to its contact with water at the aqueous interface) and at the midplane of the bilayer. Vaz et al.80 have shown that in this model, the diffusion coefficient is given by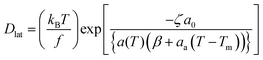 | (16) |
Restricted diffusion or obstruction effects
In a homogeneous membrane system or at zero obstacle concentration, the diffusion of species follows either the free volume model or the continuous hydrodynamic model depending on the size of the species. However, in reality, the cell membrane is a complex heterogeneous mixture of lipids and proteins. Within this heterogeneous environment, obstacles like integral membrane proteins and domains of gel-phase lipids can impede or indirectly influence lipid dynamics, creating barriers to lateral diffusion. Lipid molecules cannot move across these integral proteins or solid domains. Furthermore, these obstacles may decrease the available free volume in the lipid phase, leading to a significant reduction in the diffusion coefficient. Consequently, due to obstruction, the lateral diffusion coefficient can be expressed as a product of multiple factors67,69| Dlat(c) = D0 × Dfv(c) × Dobst(c) × Dhydro(c) | (17) |
Methods
Quasielastic neutron scattering
Thermal and cold neutrons have wavelengths of the order of Å and energies of the order of meV which align closely with the inter-atomic or intra-molecular spacing, as well as the excitation energies within materials. This inherent compatibility renders neutron scattering an effective method for investigating the structure and dynamics of atoms or molecules in condensed matter. The dynamics within materials typically fall into two broad categories: (i) periodic motions, such as atomic vibrations, and (ii) stochastic motions, including diffusion. These motions typically contribute to distinct ranges of energy transfer. For instance, periodic motions associated with oscillations at frequency ω0 result in inelastic peaks at energy transfers E = ±ħω0. Conversely, stochastic motions produce signal broadening near the elastic line position (E = 0), known as quasielastic broadening, which is inversely proportional to the time scale of the motion under scrutiny. Therefore, to observe stochastic motions, measurements are focused on the relatively low energy transfer range (a few μeV to a few meV), centered at the elastic line. In general, this spectrum consists of an elastic and quasielastic contribution. The fraction of the elastic component in the total QENS signal, known as EISF, offers insights into the geometry of molecular motions. Through QENS, both qualitative and quantitative information can be extracted. Qualitative information pertains to the geometric mechanism of the motion, whereas quantitative information relates to the correlation times and length scales of the motion. In the scattering experiments, the intensity of scattered neutrons can be expressed in terms of the double differential scattering cross-section. This cross-section encompasses two distinct contributions arising from coherent and incoherent scattering from the sample, and can be mathematically represented as follows:49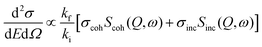 | (18) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) atominc/coh). Consequently, in hydrogenous systems, such as lipid membranes, the scattering intensity is predominantly influenced by the incoherent scattering from hydrogen atoms. In these instances, the observed scattered intensity is primarily attributable to the incoherent scattering function, Sinc(Q, ω), which represents the space-time Fourier transform of the Van Hove self-correlation function, G(r, t). The Van Hove self-correlation function quantifies the probability of finding a particle at position r after a time t, given its initial position at the origin, r = 0, at time t = 0. Therefore, QENS data obtained from hydrogenous systems typically provide valuable insights into the self-diffusion of particles within the system.
atominc/coh). Consequently, in hydrogenous systems, such as lipid membranes, the scattering intensity is predominantly influenced by the incoherent scattering from hydrogen atoms. In these instances, the observed scattered intensity is primarily attributable to the incoherent scattering function, Sinc(Q, ω), which represents the space-time Fourier transform of the Van Hove self-correlation function, G(r, t). The Van Hove self-correlation function quantifies the probability of finding a particle at position r after a time t, given its initial position at the origin, r = 0, at time t = 0. Therefore, QENS data obtained from hydrogenous systems typically provide valuable insights into the self-diffusion of particles within the system.
For studies of lipid membrane dynamics, D2O is generally chosen as the aqueous medium instead of H2O. This substitution enhances the scattering contribution from the lipid because deuterium possesses an incoherent scattering cross-section that is 40 times lower than that of hydrogen. Moreover, in the case of vesicle solutions, the solvent contribution can be assessed by measuring QENS spectra from D2O alone. By comparing the spectra obtained from D2O alone with those obtained from the vesicle solution in D2O, the scattering signal from the lipid membrane can be isolated. This is achieved by subtracting the solvent contribution from the overall scattering signal.
| Smem(Q, ω) = Ssolution(Q, ω) − ϕSsolvent(Q, ω) | (19) |
The resultant solvent subtracted spectra, Smem(Q, ω), are used for data analysis to investigate the diffusion mechanism of the lipids. As mentioned earlier, in the spatial and temporal regime probed by QENS, lipid molecules perform two distinct motions: (i) lateral motion of the whole lipid within the leaflet and (ii) localized internal motions of the lipids.46,51,58,84,85 While both these motions are stochastic in nature and arise due to thermal fluctuations, their relaxation timescales are well separated. Hence, one can assume that these motions are independent of each other. The model scattering function of the membrane can be written as
| Smem(Q, ω) = Slat(Q, ω) ⊗ Sint(Q, ω) | (20) |
Neutron elastic intensity scan
A useful measurement in QENS experiment is the elastic fixed window scan (EFWS) also known as neutron elastic intensity scan. This technique involves monitoring the scattering intensity at zero energy transfer (E = 0), within the instrumental resolution, as a function of temperature. Any microscopic mobility within the sample causes a shift in the scattering signal intensity away from zero energy transfer, rendering the elastic intensity sensitive to the microscopic dynamics. In cases of purely incoherent scattering, the elastic intensity serves as a measure of the extent of dynamics within the system. Moreover, if the system experiences a phase transition accompanied by a change in its dynamical behavior, this transition manifests as a sudden or discontinuous change in the elastic intensity.58,59 Hence, the EFWS serves as a powerful tool for observing phase transitions associated with dynamical changes in the system. It is observed that many phase transitions in lipid membranes, such as pre-transition and main phase transitions, induce significant and sharp changes in neutron elastic scattering intensity, readily detectable through EFWS. Therefore, sudden alterations in elastic scattering intensity suggest that these phase transitions are linked to changes in the microscopic dynamics of lipid membranes, which can be meticulously studied using QENS.Mechanisms of lateral diffusion
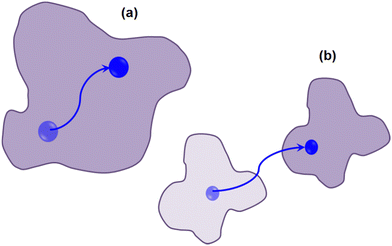
Various techniques have been utilized to explore lateral lipid motion, encompassing both macroscopic methods such as fluorescence-based techniques28 and NMR24–27 and microscopic methods like QENS.40–49 While macroscopic techniques such as fluorescence spectroscopy excel at capturing dynamics occurring over micrometer length scales, QENS offers insights into diffusion over a few lipid diameters (∼20 Å). Although the dynamics of lipid molecules have been extensively investigated, a unified model that consistently describes lipid motion across nanometer to micrometer distances is lacking. Additionally, the diffusion constants determined by these two methods often differ significantly, typically by two to three orders of magnitude. For instance, lateral diffusion coefficients measured by macroscopic fluorescence techniques are approximately on the order of 10−8 cm2 s−1, whereas those from microscopic QENS techniques are around 10−6 cm2 s−1. Different models are employed to explain lipid diffusion in these two experimental approaches. For example, the free volume theory79,86 which originates from glass physics to membranes established that lipid molecules undergo a rattling motion within a cage formed by the surrounding lipid molecules at short timescales (on the order of a few picoseconds). However, over longer timescales, thermal fluctuations create a void or free volume of size similar to that of a lipid molecule, enabling the lipid molecule to engage in long-range jump diffusive motion from one void to another. Macroscopic fluorescence techniques measure such long range diffusive motion whereas microscopic QENS measures the rattling motion of lipids within the cage of surrounding lipid molecules. For years, the widely accepted free volume theory86 effectively reconciled the differences in diffusion coefficients measured through microscopic and macroscopic methods.However, concerns regarding the straightforward mechanistic interpretation of the free volume theory arose upon the discovery, through molecular dynamics (MD) simulations and experimental investigations, that molecular jumps into vacancies were not observed.73,87 This is mostly due to the fact that free volume theory was originally developed for colloid like systems and the basic assumption was that the systems were composed of hard sphere, which may not be true for lipids as the cross-sectional area of lipids is not constant.88 Instead, in jump like motions, neighbouring lipid molecules were found to exhibit highly correlated motions over distances extending up to the nanometre range.73,87 Rheinstädter et al.87,89 have proposed two components of lateral diffusion of lipids: (i) coherent movement of loosely bound clusters of lipid molecules, which have a diameter of approximately 30 Å and (ii) diffusion of individual lipids within the cluster as shown in Fig. 5. The diffusion of such lipid clusters (Fig. 5(b)) is slower compared to that of individual lipids within the cluster (Fig. 5(a)). Consequently, it is conceivable that fluorescence measurements are sensitive to the slower motion of a lipid as part of a coherent cluster over long length scales, while the faster, short length scale dynamics of individual lipids are more effectively probed by neutron scattering experiments. These observations indicate the presence of at least two pertinent length or time scales associated with the lateral diffusion of lipids in a bilayer. Thus, the primary difference in diffusion coefficients from macroscopic and microscopic techniques arises because these methods are sensitive to different length scales, each capturing distinct processes.
Using MD simulation, Flenner et al.71 have shown an extended subdiffusive region in MSD lying between the short time ballistic and longtime Fickian diffusion regimes. Within the subdiffusion model, the lateral diffusivity of the lipid is not a constant but varies as a function of observation timescale. Therefore, they proposed that this extended subdiffusive region is a key factor contributing to the observed disparity in diffusion coefficients obtained from macroscopic and microscopic techniques. Not only do macroscopic and microscopic techniques have different observation length scales, but they also have distinct observation time scales. Microscopic QENS techniques are highly sensitive to sub-nanosecond to picosecond time scales, whereas macroscopic techniques are sensitive to time scales on the order of tens or hundreds of nanoseconds. They proposed that due to the extended regime, the lateral diffusion coefficient obtained through QENS is higher by magnitude than that obtained from macroscopic fluorescence techniques. The primary challenge in reconciling macroscopic and microscopic experiments lies in accurately measuring dynamics over mesoscopic length scales. Both methods leave a significant “blind spot” in the measurement of dynamics occurring over the tens to hundreds of nanometer range. To address this gap, Rheinstädter and coworkers83 have proposed employing incoherent NSE spectroscopy to study lipid diffusion at mesoscopic length scales. NSE in general allows for probing the coherent dynamics of soft matter systems over long timescales (on the order of hundreds of nanoseconds). However, there are challenges associated with this approach, including the need to ensure that the incoherent spin-echo signal is large enough to be detected over the coherent scattering signal. In reconciliation, it is essential to acknowledge that macroscopic fluorescence and microscopic QENS methods observe different diffusion processes, which explains the variations in the measured diffusivity. However, even at short length scales up to a few nanometers, the precise mechanism of lateral diffusion remains highly contentious. Various models, such as jump diffusion,75,90 ballistic flow-like motion,54,73 continuous diffusion,50,74 localized translational motion,57 hopping diffusion,91,92 and sub-diffusive motions,71,72 have been proposed to elucidate lateral lipid motion. Early QENS measurements suggested either continuous Brownian diffusion93 or jump diffusion90 of lipids within the membrane. However, a new perspective on short-time molecular motion emerged when Falck et al.73 analyzed the motion of individual lipids with respect to their neighbours. It was observed that when an individual lipid molecule exhibited rapid movement in a particular direction, its neighbouring molecules also tended to move in the same direction, resulting in the formation of lipid clusters that drifted collectively for a limited time. These clusters transiently formed, lasting only up to nanoseconds,73 before disintegrating and randomly reorganizing elsewhere. This motion is termed as a collective flow-like motion in which lipid molecules move synchronously with their neighbouring molecules, forming loosely bound clusters that move together in a consistent direction for a brief period.
This flow-like motion, depicted in Fig. 4, contrasts with continuous diffusion, which involves the Brownian motion of individual lipid molecules. A subsequent QENS experiment by Busch et al.54 on hydrated lipid powders without solid support suggested that ballistic flow-like motion might be a more efficient search strategy than continuous Brownian motion. Bayesian data analysis has suggested that the fundamental mechanism underlying long-range diffusion in lipid membranes is characterized by flow-like motion. However, Armstrong et al.92 found a different mechanism for lateral diffusion in single lipid bilayers supported by solid substrates. Their study suggested continuous diffusion of lipids rather than the flow-like ballistic motion reported in stacked membrane systems. They also observed hopping diffusion, an enhanced diffusion at the nearest neighbour distance of the lipid molecules, likely attributed to the effect of the supporting substrate on lipid organization. The study of lipid diffusion on very short length scales requires access to high Q values. For this purpose, the thermal backscattering spectrometer IN13 at the Institut Laue-Langevin (ILL) was used, which is capable of probing in the large Q range of 0.2 to 4.9 Å−1. At low Q values, the observed quasielastic broadening is described by a Lorentzian. However, at higher Q values >2.5 Å−1, quasielastic broadening is better described by a Gaussian instead of Lorentzian and the width of Gaussian increases linearly with Q. This revealed a change in dynamics at higher Q values, indicating a shift from continuous diffusion to ballistic like motion. Typical fitted QENS data at higher Q values namely 2.65 Å−1 and 3.59 Å−1 are shown in Fig. 6(a) and (b), respectively. Fig. 6(c) shows the FWHM for all measured Q values as a function of Q2. It is evident that at low Q values <2.5 Å−1 (blue circle), the FWHM is linear with Q2. Then there is a sudden decrease in the quasielastic broadening. This broadening is described using a Gaussian, the width of which increases linearly with Q. From this linear dependence, a lipid velocity of 1.1 m s−1 was extracted, which is notably two orders of magnitude lower than the purely ballistic velocity (87 m s−1) of a free particle with the mass of the lipid molecule. This discrepancy suggests that the short-range lipid motion exhibits characteristics more akin to flow-like behavior rather than purely ballistic motion. Consequently, this prompts consideration of the potential influence of “nano-viscosity” or “nano-friction” on lipid dynamics at length scales smaller than the nearest-neighbour distance. In summary, at the nanometer length scale, lipid molecules exhibit continuous diffusion. However, when examining at length scales shorter than approximately one-third of the lipid nearest neighbor distance, there is a discernible change in the character of motion. At these shorter ranges, lipid motion displays flow-like attributes instead of adhering to continuous diffusion or a rattling-in-the-cage motion. These findings align with QENS results on unilamellar vesicles (ULVs) by Sharma et al.,50 who observed continuous Brownian diffusion of lipids over the nanometer length scale. However, in a contrasting study, Wanderling et al.57 found that QENS results on hydrated supported bilayers revealed lateral lipid diffusion as localized translational motion within a confined cylindrical region.
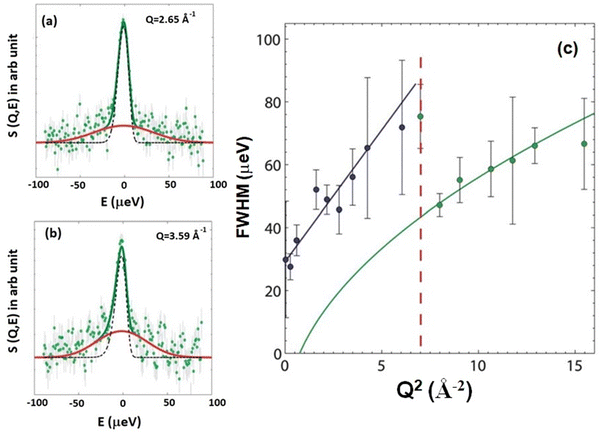 | ||
| Fig. 6 Typical fitted QENS data with an elastic line (black line) and a Gaussian quasielastic broadening (red line) at (a) Q = 2.65 Å−1 and (b) Q = 3.59 Å−1. (c) Full width at half maximum (FWHM) of the quasielastic broadening plotted as a function of Q2. At low Q values (blue circles), the quasielastic broadening is described by a Lorentzian with FWHM linearly dependent on Q2, suggesting continuous diffusion. The corresponding fit is shown by a blue line. The high Q data (green circles) exhibit quasielastic broadening described by a Gaussian, with FWHM increasing linearly with Q. The corresponding fit (green) displays a square root relationship when plotted against Q2. The transition between continuous and ballistic diffusion is marked by the red dashed line. Adapted from ref. 74 with permission from The Royal Society of Chemistry, copyright 2011. | ||
Comparatively, MD simulation studies40,71,72 have shown that the MSD corresponding to the lateral motion of lipids exhibits a power-law dependence of tα (α < 1), suggesting anomalous lateral diffusion. For example, MSD for the DODAB lipid as obtained from MD simulation in both ordered and fluid phases is shown in Fig. 7(a). MSD was found to follow a subdiffusive regime with a dependence of tα in both the ordered and fluid phases. Here α is a sub-diffusive exponent which can be explicitly calculated by the logarithmic time derivative of MSD. Variation of α with time is shown in Fig. 7(b). It is evident that α < 1 (at long time) for both the ordered and fluid phases suggesting that the lateral motion of lipids is subdiffusive. The sub-diffusive motion of lipids in the membrane, associated with crowding of lipids, is described as a non-Markovian diffusion process. The generalized Langevin equation (GLE) with a power-law memory kernel is employed to model the non-Markovian diffusion behavior of lipid molecules.72 This approach is particularly suitable for representing the lateral diffusion of lipids. The power-law memory kernel provides a robust framework for capturing the observed sub-diffusive characteristics of lipid movement, as indicated by MD simulations. By incorporating these findings, the GLE-based model has been refined to accurately interpret QENS data as shown in Fig. 7(c), offering deeper insights into the dynamics of lipid diffusion within membranes. Variation of relaxation rate corresponding to lateral diffusion, Γlat with Q, is shown in Fig. 7(d). For direct comparison, Γlat obtained from MD simulation is also shown in the figure. It is evident that both are consistent with each other. The lines indicate fitting based on the quadratic dependence 1/4AQ2. The value of A obtained from the least-squares fit was found to be 0.42 Å2 ps−α (α = 0.61) and 0.34 Å2 ps−α (α = 0.61) for MD simulation and QENS experiments, respectively.
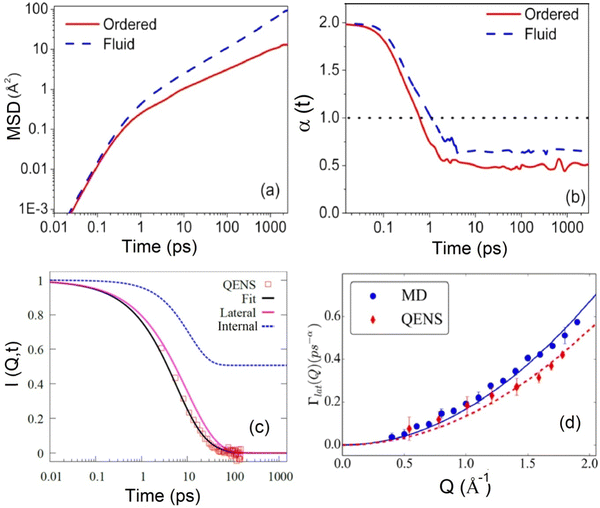 | ||
| Fig. 7 (a) Mean square displacement (MSD) for lateral motion of the DODAB lipid in the ordered (300 K) and fluid (350 K) phases. (b) Variation of the sub-diffusive exponent (α) with time in both ordered and fluid phases. (c) Incoherent intermediate scattering function obtained from the Fourier transform of QENS spectra at Q = 1.2 Å−1 in the fluid phase (345 K). Individual components corresponding to lateral and internal motion are also displayed alongside the fits. (d) Variation of the decay constant (Γlat) corresponding to lateral motion in the fluid phase, obtained from the fits shown in (c). For direct comparison, Γlat obtained from MD simulation is also depicted. Adapted from ref. 72 with permission from American Chemical Society, copyright 2018. | ||
It is evident that the process of lateral diffusion is intricate and not yet fully understood. A meaningful comparison of lateral diffusion in membranes requires consistent measurement techniques, as the diffusion coefficient is highly sensitive to both the observation time and the length scales involved. Generally, macroscopic techniques yield diffusion coefficients that are an order of magnitude slower compared to those obtained from microscopic techniques. Even within the same method, such as microscopic QENS, care must be taken when comparing lateral diffusion coefficients from different instruments. Each QENS instrument has unique instrumental resolution characteristics, hence corresponding distinctive observation time scales, which can significantly affect the measured diffusion values. It has been shown that lower instrumental resolution and longer observation times tend to give slower diffusion coefficients, indicating the importance of understanding the specific measurement context.16,94 Additionally, several factors related to the lipid bilayer (such as area per lipid, molecular structure and charge of lipid, membrane viscosity), solvent viscosity and temperature can influence the lateral diffusion. These factors can either facilitate or hinder the movement of lipids across the membrane, thereby affecting cell membrane dynamics and functions. In the next section, we will examine in detail how these factors impact the lateral diffusion of lipids.
Factors affecting the lateral diffusion
Area per lipid
The area per lipid is an important parameter of any lipid bilayer, representing the average cross-sectional area occupied by each lipid molecule within the bilayer. It can be calculated by dividing the total cross-sectional area of the bilayer, measured along the XY plane (the plane parallel to the bilayer surface), by half the total number of lipid molecules in the bilayer. An increase in area per lipid generally promotes faster lateral diffusion as there is more space for individual lipids to move within the membrane. The area per lipid increases with the increase in temperature.63 In particular, a sharp jump in the area per lipid is observed at the main phase transition of the lipid membrane. For example, in the case of DMPC, the area per lipid molecule increases about 28% from 47 Å2 to 60 Å2, across the gel-to-fluid phase transition.63,95 Sharma et al.50 examined the impact of gel-to-fluid phase transitions on the lateral diffusion of lipids in ULVs. Typical observed QENS spectra for the DMPC membrane in the gel (280 K) and fluid (310 K) at Q = 1.1 Å−1 are shown in Fig. 8(a). For direct comparison, instrument resolution as observed using vanadium is also shown. Significant quasielastic broadening is evident for the DMPC membrane in both gel and fluid phases suggesting the presence of stochastic dynamics of lipids in the membrane. A sharp increase in quasielastic broadening is found when the membrane goes from gel to fluid phase. The QENS spectra can be effectively modeled assuming long range lateral diffusion and localized internal motion of lipids in both gel and fluid phases. Typical fitted QENS spectra for the DMPC membrane in the fluid phase along with the individual components corresponding to the lateral and internal motion are shown in Fig. 8(b). The obtained HWHM of Lorentzian functions associated with lateral motions for both gel (280 K) and fluid (310 K) phases is shown in Fig. 8(c). It is evident that in both the phases, HWHM follows the continuous Fick's diffusion model (HWHM = DlatQ2), with the HWHM for the fluid phase being much higher than that of the gel phase. This is reflected in the respective lateral diffusion coefficients, as in the fluid phase (310 K), Dlat was determined to be (7.7 ± 0.3) × 10−7 cm2 s−1, which was an order of magnitude higher than the value measured in the gel phase (280 K), i.e., (0.7 ± 0.1) × 10−7 cm2 s−1. These observations clearly suggest that the main phase transition is closely linked to the microscopic lateral motion of lipid molecules. As mentioned earlier, at the main phase transition, there is a sharp jump in area per lipid which promotes enhanced lateral diffusion, indicating a close relationship between the mobility of phospholipid molecules and the available area per lipid molecule. The MD simulation snapshot of the DMPC membrane in the gel (280 K) and fluid (310 K) phases is shown in Fig. 8(d). In the gel phase, lipids are organized into a densely packed and orderly array, limiting their conformational, rotational, and translational freedom. However, during the main phase transition, the alkyl chains become disordered, exhibiting numerous gauche defects. This disorder leads to a significant increase in the area per lipid molecule, reducing molecular packing density. Notably, no significant changes in lateral diffusion coefficients were observed during the pre-transition from the gel to ripple phase. Even in the fluid phase, an increase in temperature results in a consistent rise in the area per lipid. For instance, in the fluid phase of DMPC, at 30 °C, the area per lipid measures 60 Å2, increasing to 66 Å2 at 60 °C. Notably, the lateral diffusion coefficient of lipids increases monotonously with temperature in the fluid phase.96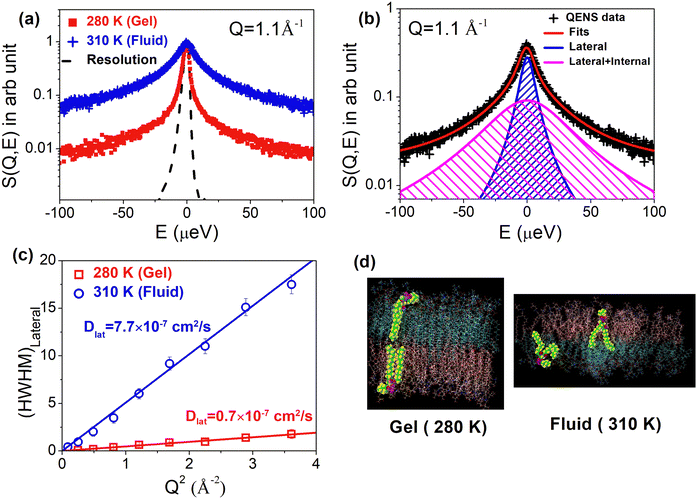 | ||
| Fig. 8 (a) Typical observed QENS spectra for the DMPC membrane in the gel (280 K) and fluid (310 K) phase. Instrument resolution as measured using the vanadium standard is also shown. Spectra are normalized to peak amplitudes for direct comparison. (b) Fitted QENS spectra for the DMPC membrane at 310 K (fluid phase) using a scattering law assuming both lateral and internal motions of the lipid. Individual components corresponding to the lateral (narrower) and internal (broader) motions are also shown. (c) Variation of half width at half maxima (HWHM) of Lorentzian function associated with lateral motion with Q2 at 280 K (gel) and 310 K (fluid). It is evident that in both the phases, the HWHM follows the continuous Fick's diffusion model (HWHM = DlatQ2). (d) MD simulation snapshot of DMPC at 280 K (gel) and 310 K (fluid). It is evident that in the gel phase, lipid molecules are highly ordered with low area per lipid, whereas in the fluid phase, they are highly disordered with high area per lipid. Adapted from ref. 50 with permission from American Chemical Society, copyright 2015. | ||
Hydration
Biological systems predominantly operate in aqueous environments, highlighting the significant influence of hydration levels on their dynamics. Hydration can be precisely regulated in the case of supported lipid multilayers; hence to investigate the effects of hydration, most of the experiments have been carried out on supported multilayers. The main transition temperature and bilayer thickness of model membrane systems tend to decrease with increasing hydration.97,98 This hydration-dependent variation impacts lipid packing density, subsequently modulating the dynamics of lipids in multilayers. König et al.97 explored the hydration-dependent dynamics of DPPC multilayers through QENS, covering hydration levels from 8 to 20 wt%, corresponding to 3–10 water molecules per lipid molecule. In the fluid phase, lipid dynamics involve lipid diffusion within its solvation cage and kink diffusion, whereby the solvation cage size increases as hydration increases. Lateral diffusion has been observed to increase with increasing hydration.62 NMR experiments demonstrated a two-fold increase in DPPC diffusion in the liquid phase when hydration levels were elevated from 15% to 40% (w/w). The results are consistent with the MD simulation study99 which showed that as the hydration increases, the lipid area per head group increases with a decrease in bilayer thickness and lipid order parameters indicating that the bilayer gets disordered. Theoretical calculations suggest that hydration-dependent lipid diffusion largely arises from alterations in bulk water mobility within the multilamellar phospholipid/water system. Trapp et al.98 emphasized hydration-dependent dynamics of head group motion by utilizing tail-deuterated lipids, enabling a focused study on the head group. They observed a pronounced influence of hydration on head group mobility. On the other hand, there is a lot of interest in the hydration dynamics of a lipid membrane.99–102 It has been shown that the interface water hydrogen bonded to lipids shows slower relaxation rates for translational and rotational dynamics compared to that of the bulk water and is found to follow sub-diffusive and non-diffusive behaviors, respectively.99,100 Moreover, as the hydration decreases the interfacial water exhibits dynamical heterogeneity and follows a power law behavior between the diffusion coefficient of water and α relaxation time showing the signature of glass dynamics.99 Two crossovers in the lateral diffusion of interfacial water (IW), associated with the fluid–ripple and ripple–gel phase transitions were observed.101 The activation energy of IW near the gel phase is twice that near the fluid or ripple phase. It was also shown that the size of the membrane's rippling can be obtained from the heterogeneity length scale of IW.102Structure of the membrane system
The lateral diffusion of lipids has been extensively studied across various model membrane systems, including multilamellar vesicles (MLVs),44,103,104 ULVs,20,29,41,45,46,50,52,53,58,59,84,85,96,105–109 supported lipid bilayers,57,74,90,93 unsupported multilamellar stacks (hydrated powder),54,105 and anhydrous lipid powder.110 The dynamics of lipids often vary significantly depending on the structure of the model membrane system, even when composed of the same lipids. For instance, in supported single bilayers, the lipid leaflet in direct contact with the substrate can be influenced by the solid support. This influence may lead to artifact results, such as modulated diffusion at the nearest neighbor distance of lipid molecules or suppression of the main phase transition.42 Busch et al.105 found that the lateral lipid mobility increases from multilayers to single bilayers and then to monolayers. They utilized three different model systems: multibilayers, single bilayers in vesicles, and monolayers in emulsions. Their results showed a 1.3-fold increase in mobility from multibilayers (hydrated powder) to single bilayers (ULVs) and a 2-fold increase from multibilayers to monolayers. Furthermore, they noted that the mobility of lipids in single bilayers (ULVs) increases as the diameter of the ULV decreases. The use of various membrane structures provides distinct advantages for understanding cell membranes. For example, supported membranes allow for the separation of motion within the membrane plane from motion outside of it. This separation can be achieved through in-plane and out-of-plane scattering geometries, assuming that the lipid orientation in the supported membrane samples remains consistent over dimensions commensurate with the incident neutron beam (typically a few centimeters). Additional benefits of supported membranes include their stable surface and smooth morphology, which enable atomic force microscopy to reveal topological features at an atomic scale, such as nanometer-scale domains. These systems hold promise for various applications, including biosensors. On the other hand, studying lipids that self-assemble into vesicles in aqueous environments offers the advantage of closely mimicking the lipid arrangement found in cell membranes. This morphology provides valuable insights into the behavior and properties of lipid membranes in biological contexts.Membrane curvature
The membrane curvature can create local variations in lipid packing and affect lateral diffusion. Regions with higher curvature have slower diffusion compared to flatter regions. Theoretical estimates of the diffusion coefficient of molecules on a curved surface, mimicking the microvilli observed in plasma membranes, revealed a slower diffusion as compared with an ideal planar surface.111Molecular structure of lipids: size and charge of polar head groups, length and degree of unsaturation of alkyl tails
The size and charge of lipid headgroups can affect lateral diffusion by influencing lipid–lipid interactions and packing. For example, DMPG and DMPC have the same alkyl tails and differ only in the head group. DMPC has a zwitterionic PC head group whereas DMPG has an anionic PG head group. Both the lipids have similar main phase transition temperature. Sharma et al. have shown that in the fluid phase, the lateral diffusion coefficient for the zwitterionic DMPC membrane is much higher than that for the charged DMPG membrane.52 Hence, one can infer that higher surface charge density of the membrane or coulombic interactions between the head groups restrict the lateral diffusion of lipids. This is further supported by the fact that addition of NaCl, which reduces surface charge density and screens the coulombic repulsion between the head groups, enhances lateral diffusion.52 Increasing the degree of unsaturation in the acyl chains of the lipids is generally observed to enhance membrane fluidity or lateral diffusion. However, comparing the lateral diffusion coefficients of lipids with varying alkyl chain lengths or degrees of unsaturation poses a significant challenge due to their different melting temperature (Tm) as it is highly sensitive to the acyl chains. Tm tends to increase with longer acyl chain lengths and decrease with higher unsaturation levels in the lipid's acyl chain. To address this challenge, researchers often use a reduced temperature parameter, Tr = (T − Tm)/Tm. Studies have shown an inverse relationship between acyl chain length and lateral diffusion for saturated PC, with the fastest lateral diffusion observed for DSPC and the slowest for DLPC at the same reduced temperature.80Solvent viscosity and ionic strength
In the extended free volume theory, it is evident that solvent viscosity also plays an important role in the lateral diffusion of lipids. The lateral diffusion coefficient is inversely proportional to solvent viscosity. To examine this, Sharma et al. have carried out QENS experiments on the DMPC membrane in two different solvents, namely (i) pure D2O and (ii) a salt solution of (LiCl)0.13(D2O)0.87 or 7.6 m LiCl.85 Using QENS, they found that at 310 K, the lateral diffusion of DMPC in (LiCl)0.13(D2O)0.87 is five times slower than in pure D2O. Their QENS measurements indicated that water translation diffusivity in D2O at 310 K is 2.4 times faster than in (LiCl)0.13(D2O)0.87, suggesting higher viscosity in the latter. Increased solvent viscosity, coupled with salt effects from monovalent cation interaction with lipid carbonyl oxygen atoms, mainly accounts for reduced lipid lateral diffusion in (LiCl)0.13(D2O)0.87. Furthermore, the local diffusivity of lipid tails decreased by a factor of 2.2 in the presence of salt, correlating with increased water viscosity in the LiCl solution. The concentration of ions in the surrounding environment can influence the strength of electrostatic interactions, impacting the diffusion behavior of charged lipids. For example, Sharma et al. examined anionic DMPG vesicles in D2O and 100 mM NaCl D2O.52 DMPG vesicles in D2O exhibit an unusually broad melting range between the gel and fluid phases, characterized by high viscosity due to the increase in vesicle size and ionization. In this anomalous regime, vesicle viscosity is approximately ten times higher than in the ordered and fluid phases. However, our QENS results show no abrupt changes in membrane dynamics, suggesting that macroscopic viscosity measurements do not directly correlate with nanoscale membrane dynamics.52 While the DMPC study85 emphasized the role of solvent viscosity in modulating membrane dynamics, in the case of DMPG, a significant difference in macroscopic vesicle solution viscosity did not markedly affect lateral diffusion. It is worth noting that despite differences in macroscopic vesicle solution viscosity, the viscosities of both D2O and 100 mM NaCl D2O solvents were similar. Our findings suggest that nanoscale lipid lateral motion is largely independent of macroscopic vesicle solution viscosity but is influenced by solvent viscosity.Effects of temperature and pressure
As with any thermally activated motion, lateral diffusion is accelerated by increasing temperature. Temperature also affects other membrane properties, such as the area per lipid and solvent viscosity, both of which influence lateral diffusion. Thus, when considering all these factors, the lateral diffusion coefficient generally increases with increasing temperature. Additionally, if a temperature change leads to a shift in the membrane's physical state—for instance, from an ordered phase to a fluid phase—there can be a substantial increase in lateral diffusion, often by an order of magnitude.The impact of hydrostatic pressure on the dynamics of DMPC MLVs has been studied, revealing distinct effects depending on the membrane phase.103 In the fluid phase, increased pressure significantly impedes lipid mobility, indicating that pressure can affect the fluidity and motion of lipids within the membrane. In contrast, when the membrane is in the gel phase, the dynamics show relatively little change with increasing pressure, suggesting that lipids are already constrained in this more rigid state. Recently, the effects of hydrostatic pressure on membrane dynamics were also studied using NSE.112 It was found that an increase in pressure leads to an increase in membrane rigidity. These findings underscore the role of pressure in modulating membrane dynamics and provide valuable insights into the stability and behavior of lipid membranes under varying conditions.
Membrane composition
It is well-established that alterations in membrane composition can exert significant effects on lipid lateral diffusion. For instance, the inclusion of cholesterol has been demonstrated to diminish the available free area for lipids, resulting in a reduction in lateral diffusion.113 Moreover, the impact of cholesterol on lipid lateral diffusion appears to be concentration-dependent, with higher concentrations further impeding the mobility of lipids within the membrane. Beyond cholesterol, other components of the membrane, such as specific lipid species or membrane proteins, can introduce steric hindrance or alter lipid–protein interactions, thereby impacting lateral diffusion behavior. Changes in the composition of the membrane also modify the interaction between its constituents, thereby modulating the activation energy and consequently affecting the lateral diffusion of lipids. Nickel et al.114 have demonstrated that the composition of cellular membranes exhibits significant variation with temperature, characterized by systematic changes in the distribution of lipids with high and low melting points. This dynamic adjustment in lipid partitioning allows lateral lipid heterogeneities to act as buffers for membrane physical properties, effectively counterbalancing environmental fluctuations through compositional adjustments. Specifically, as temperature increases, there is a greater partitioning of high-melting-point lipids into the fluid phase. This shift enhances the membrane's bending modulus and viscosity, counteracting the thermal effects that would otherwise reduce these properties. The study highlights a buffering effect on both the lateral diffusion coefficient and the bending modulus of the membrane's fluid phase in response to temperature changes. This buffering effect offers a biological advantage by maintaining a more stable physical environment compared to single-component membranes, which are prone to rapid phase transitions. Consequently, complex membrane compositions provide a simple yet effective mechanism for buffering membrane physical properties, based on the thermodynamics of phase separation. This mechanism is notably more responsive than the metabolic adaptations described by the concept of homeoviscous adaptation.In this section, we've explored various factors that influence the lateral diffusion of lipids. All these factors are summarized in Table 1. In the next section, we'll delve into how the presence of membrane-active compounds impacts lipid lateral diffusion.
| S. no | Factor | Effects on Dlat | Ref. |
|---|---|---|---|
| (i) | Area per lipid (APL) | • Dlat increases with the APL | 50 |
| (ii) | Hydration | • Dlat increases with hydration | 68 and 98 |
| (iii) | Structure of the membrane system | • Increase in mobility from multibilayers to single bilayers by a factor of 1.3, and to monolayers by a factor of 2 | 105 |
| • Mobility of the lipid in single bilayers (ULVs) increases with decreasing diameter of ULVs | |||
| • Supported vs. unsupported membrane system; direct contact with the substrate modulates the lateral diffusion | |||
| (iv) | Membrane curvature | • Dlat decreases with the increase in membrane curvature. Hence, highly curved regions have slower diffusion compared to flatter regions | 111 |
| (v) | Molecular structure of the lipid | • Size and charge of head groups affect the lateral diffusion. For example, when comparing charged vs. zwitterionic, lateral diffusion will be slower in charged lipids than in zwitterionic lipids | 52 |
| • Increase in alkyl chain length in the fluid phase, no significant effects on the lateral diffusion | 67 | ||
| • Consistent with the free volume model | |||
| (vi) | Solvent viscosity and ionic strength | • As per the extended free volume model, Dlat should decrease with an increase in solvent viscosity | 85 |
| • Addition of salt affects the lateral diffusion | 52 | ||
| (vii) | Temperature and pressure | • Increase in temperature leads to increase in Dlat | |
| • Dlat increases by an order of magnitude faster when the membrane's physical state changes from an ordered phase to a fluid phase | |||
| • Increase in pressure restricts dynamics significantly in the fluid phase | 50 | ||
| • Relatively small change in Dlat with pressure when the membrane is in the gel phase | 103 | ||
| (viii) | Obstruction effects | • Significant reduction in the diffusion coefficient due to obstacles | 69 |
| (ix) | Membrane composition | • Change in membrane composition affects the free area and Ea which affect Dlat | 114 |
Effects of membrane active compounds on the lateral diffusion
Cell membranes serve as dynamic platforms for signaling, transport, and molecular recognition. However, this dynamic equilibrium can be perturbed by the presence of membrane-active compounds, ranging from therapeutic drugs to stimulants to environmental toxins. Membrane active compounds can impact various membrane properties such as thickness, curvature, main phase transition temperature, and area per lipid, all of which directly influence lipid lateral diffusion, as discussed earlier. Additionally, these compounds can alter interactions between the constituents of the membrane, further affecting lateral diffusion. Studies indicate that long-range repulsive potentials decrease Dlat by effectively expanding particle radii, whereas attractive potentials reduce Dlat by promoting particle clustering or adhesion to obstacles.115 Any alterations in membrane dynamics induced by external compounds can consequently impact these vital cellular functions. Understanding the intricate interplay between these compounds and cellular membranes is paramount, not only for unraveling the mechanisms of their action but also for advancing our knowledge of membrane biophysics and its implications for health and disease. Membrane dynamics also influence the behavior of synthetic membrane systems used in drug delivery, diagnostics, and biomimetic applications, highlighting the importance of understanding how membrane-active compounds affect their functionality and performance. Therefore, investigating the effects of membrane-active compounds on membrane dynamics holds significant implications for both basic research and practical applications in biomedicine and biotechnology. Recently, Kumarage et al.116 discussed the effects of various classes of additives, such as amphiphilic, therapeutic, and industrial compounds, on the structural, thermodynamic, elastic, and dynamic properties of membranes. They explored structure–property relationships that integrate the effects of additives with the design principles of lipid membranes as soft molecular assemblies. To fully understand and harness these interactions, it requires systematic investigation across multiple spatiotemporal scales. In this section, we will summarize the interactions of various membrane-active compounds, including peptides or proteins, drugs, antioxidants, stimulants, and antimicrobials, with lipid membranes at nanometer length scales. We will also discuss their effects on membrane dynamics, particularly the lateral diffusion of lipids.Membrane active peptides
Membrane-active peptides constitute a diverse group of peptides that dynamically interact with cellular membranes, eliciting effects such as disruption or penetration. These peptides are integral to various biological processes, including antimicrobial defense, cellular signaling, and drug delivery. Examples of membrane-active peptides encompass antimicrobial peptides, amyloid peptides, and cell-penetrating peptides. The interaction between these peptides and membranes can be examined by assessing their perturbing effects on the structural, dynamic, and phase behavior of the lipid membrane. In this section, our primary focus will be on elucidating the impact of these peptides on the lateral diffusion of lipids.![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMPS (92
DMPS (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8).117 Their QENS measurements, performed in both the ordered and fluid phases, revealed that this neurotoxic Aβ fragment enhances the lateral diffusion of the lipid membrane in both phases. Moreover, an augmented local mobility of the lipids was noted, with a more pronounced effect observed in the “out-of-plane” direction. Extending this investigation, Barrett et al.94 examined the impact of another Aβ-derived peptide, Aβ (22–40), which has a different amino acid composition and length. Their QENS measurements, carried out on supported DMPC
8).117 Their QENS measurements, performed in both the ordered and fluid phases, revealed that this neurotoxic Aβ fragment enhances the lateral diffusion of the lipid membrane in both phases. Moreover, an augmented local mobility of the lipids was noted, with a more pronounced effect observed in the “out-of-plane” direction. Extending this investigation, Barrett et al.94 examined the impact of another Aβ-derived peptide, Aβ (22–40), which has a different amino acid composition and length. Their QENS measurements, carried out on supported DMPC![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMPS (92
DMPS (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) lipid membranes, revealed intriguing findings. While Aβ (22–40) accelerated the lateral diffusion of lipids in the ordered phase, a contrasting effect was observed near the main phase transition temperature, where the lipid diffusion decreased by 24%. Another study by Buchsteiner et al.118 observed an increase in lateral diffusion in the fluid phase. Our study46 focused on the effects of Aβ (1–40) on the dynamics of anionic DMPG in ULVs. We found that in the fluid phase, Aβ (1–40) accelerates lateral diffusion but does not significantly affect localized internal lipid motion. The addition of Aβ (1–40) in the fluid phase led to effective thinning of the bilayer, as observed by SANS, potentially increasing the area per lipid and hence the lateral diffusion coefficient. Interestingly, no significant effect on lateral diffusion was observed in the ordered phase. In summary, investigations into various Aβ-derived peptides, including Aβ (25–35), Aβ (22–40), and Aβ (1–40), using QENS, have shown that these peptides generally enhance the lateral diffusion of lipid membranes in the fluid phase. However, near the main phase transition temperature, Aβ (22–40) caused a decrease in lipid diffusion, while Aβ (25–35) led to an increase in lipid diffusion in the ordered phase. Conversely, Aβ (1–40) did not significantly impact lipid membrane dynamics in the ordered phase. These findings suggest that the interaction between Aβ peptides and lipid membranes is complex and context-dependent, with potential implications for the pathogenesis of Alzheimer's disease. Further research into the mechanisms underlying these interactions could provide valuable insights into the role of lipid membranes in the development and progression of Alzheimer's disease, potentially paving the way for novel therapeutic approaches targeting membrane-associated pathways.
8) lipid membranes, revealed intriguing findings. While Aβ (22–40) accelerated the lateral diffusion of lipids in the ordered phase, a contrasting effect was observed near the main phase transition temperature, where the lipid diffusion decreased by 24%. Another study by Buchsteiner et al.118 observed an increase in lateral diffusion in the fluid phase. Our study46 focused on the effects of Aβ (1–40) on the dynamics of anionic DMPG in ULVs. We found that in the fluid phase, Aβ (1–40) accelerates lateral diffusion but does not significantly affect localized internal lipid motion. The addition of Aβ (1–40) in the fluid phase led to effective thinning of the bilayer, as observed by SANS, potentially increasing the area per lipid and hence the lateral diffusion coefficient. Interestingly, no significant effect on lateral diffusion was observed in the ordered phase. In summary, investigations into various Aβ-derived peptides, including Aβ (25–35), Aβ (22–40), and Aβ (1–40), using QENS, have shown that these peptides generally enhance the lateral diffusion of lipid membranes in the fluid phase. However, near the main phase transition temperature, Aβ (22–40) caused a decrease in lipid diffusion, while Aβ (25–35) led to an increase in lipid diffusion in the ordered phase. Conversely, Aβ (1–40) did not significantly impact lipid membrane dynamics in the ordered phase. These findings suggest that the interaction between Aβ peptides and lipid membranes is complex and context-dependent, with potential implications for the pathogenesis of Alzheimer's disease. Further research into the mechanisms underlying these interactions could provide valuable insights into the role of lipid membranes in the development and progression of Alzheimer's disease, potentially paving the way for novel therapeutic approaches targeting membrane-associated pathways.
Antimicrobial peptides
Antimicrobial peptides (AMPs) are emerging as promising candidates for combating multidrug-resistant bacteria due to their multifaceted mechanism of action.119 AMPs exist in all living organisms, including plants, animals, and mammals. Some examples of AMPs are melittin, alamethicin, and aurein, which are found in bee venom, the fungus Trichoderma viride, and the Austrian frog, respectively. Cartoon representations of these AMPs are shown in Fig. 9(a). Melittin is a cationic peptide (+5e) consisting of 26 amino acids (AA). Alamethicin and aurein are anionic with 20 AA and cationic with 13 AA, respectively. Sharma et al.51,107 have shown that the inclusion of a minimal quantity of a prototypical cationic AMP, melittin, has a profound impact on the dynamical and phase behavior of membranes. Even at concentrations lower than those necessary for pore formation, melittin induces significant alterations in membrane dynamics, eliminating both pre-transition (gel–ripple) and main (ripple–fluid) transitions of the lipid membrane.51,107 Neutron elastic intensity scans for the DMPC membrane with and without 0.5 mol% melittin are shown in Fig. 9(b). The impact on membrane dynamics is profoundly influenced by the bilayer phase: in the ordered phase, melittin acts as a plasticizer, enhancing membrane dynamics, while in the fluid phase, it acts as a stiffening agent, constraining membrane dynamics.51,107Dlat obtained for the DMPC membrane in the absence and presence of 0.5 mol% melittin at different temperatures is shown in Fig. 9(c). For direct comparison, Dlat obtained for the DMPC membrane in the presence of 0.5 mol% alamethicin at different temperatures is also shown in Fig. 9(c). In the ordered phase, it is evident that alamethicin does not significantly affect lateral motion, whereas melittin enhances it. However, in contrast to these results, in the fluid phase, both AMPs slow down lateral diffusion. Melittin acts as a stronger stiffening agent, more efficiently restricting lateral diffusion compared to alamethicin. These studies suggest that melittin's disruptive effects on lipid lateral motion, even at sub-pore-forming concentrations, could jeopardize cell stability by rendering the membrane more susceptible to additional stress and defects.107 This novel mechanism of action highlights how reduced lateral mobility induced by melittin can lead to changes in membrane properties, impeding membrane-related biological processes and ultimately contributing to bacterial cell death without pore formation or membrane destruction. Selectivity is a crucial characteristic of AMPs, ensuring their efficacy as therapeutic agents while minimizing toxicity to the host. One key distinction between bacterial and mammalian membranes lies in their composition, such as the presence of cholesterol in mammalian membranes but not in bacterial membranes. Sharma et al.51 have shown that the interaction of melittin with the phospholipid membrane strongly relies on the cholesterol content. In the presence of cholesterol, the destabilizing effect of melittin is mitigated.51 Our research demonstrates that these AMPs selectively target bacterial membranes without disrupting mammalian membranes,51,96 a crucial prerequisite for their antibiotic function. Another significant compositional difference is the prevalence of anionic phospholipids, such as PG and cardiolipin, in the bacterial membranes. In contrast, the outer leaflet of mammalian membranes predominantly consists of zwitterionic phospholipids like PC and SM. We investigated the effects of two ubiquicidin (UBI)-derived peptides, UBI (29–41) and UBI (31–38), which possess charges of +6e and +4e, respectively.29 Both peptides were found to restrict lipid lateral diffusion in the fluid phase of the membrane, with UBI (29–41) exhibiting more significant effects, suggesting a stronger interaction with the lipid membrane as confirmed by various biophysical measurements. Furthermore, our study revealed that ubiquicidin-derived peptides selectively bind to anionic phospholipid membranes, resembling bacterial membranes, and predominantly reside on the membrane surface.29,120 This property of the peptides holds potential for their application as in situ infection imaging probes. Sharma et al.96 have also investigated the effects of other AMPs such as aurein 1.2 on the membrane dynamics. While aurein had minimal impact on lateral diffusion in the ordered phase, akin to melittin, it restricted lateral diffusion in the fluid phase. Notably, lateral diffusion decreased consistently with increasing concentration of aurein as shown in Fig. 9(d). Comparative analysis among various AMPs revealed that melittin exhibited the strongest interaction with the membrane and the greatest restriction of lateral diffusion. Furthermore, melittin displayed an exceptional behavior, acting as a plasticizer that enhanced membrane dynamics in the ordered phase. Considering that the cell membrane comprises various lipids, we created a homogeneous mixture of zwitterionic and anionic lipids. Employing the contrast matching SANS technique, Sharma et al. investigated the effects of AMPs, such as aurein 1.2, on the bilayer structure.96 For the first time, their study revealed the induction of lateral lipid segregation in the membrane by an AMP.96 The formation of nanodomains can be attributed to reduced lateral lipid diffusion. The slower lateral diffusion may lead to demixing of lipids or coexistence of phases. Enhanced interaction between charged lipids and peptides could exacerbate this effect, resulting in the observed nanoscopic lateral domains in the contrast matching SANS experiment. The schematics of modulated lateral diffusion and lateral segregation are shown in Fig. 9(e).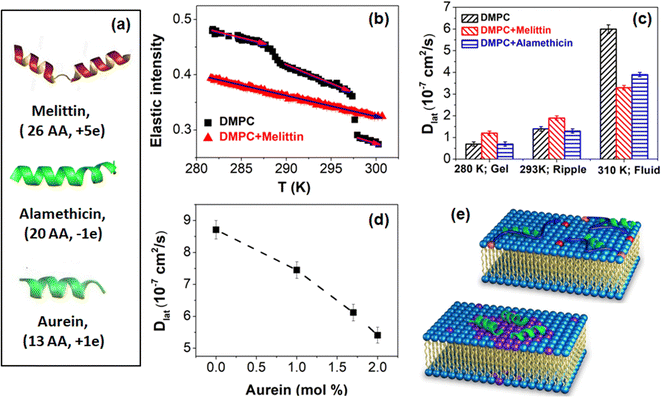 | ||
| Fig. 9 (a) Cartoon representations of different antimicrobial peptides namely melittin (26 amino acid (AA)), alamethicin (20 AA) and aurein (13 AA). (b) Q-averaged elastic intensity scans for DMPC vesicles in the absence and presence of 0.5 mol% melittin in the heating cycle. (c) Lateral diffusion coefficient (Dlat) of the DMPC lipid in the absence and presence of 0.5 mol% melittin and alamethicin at different temperatures. (d) Variation of Dlat of DMPC with aurein concentrations at 320 K. (e) Schematics of lateral diffusion and segregation modulated by an AMP. Adapted from ref. 96 and 107 with permission from American Chemical Society, copyright 2019 & 2016. | ||
Transmembrane peptides
Transmembrane proteins are integral membrane proteins that traverse the entirety of the cell membrane. The impact of a transmembrane sequence from the transferrin receptor (TFRC) protein on the dynamics of DMPC membranes has been investigated.47 TFRC plays a crucial role in iron transport into the cell121 and in regulating cellular iron balance. When coupled with apotransferrin, TFRC accumulates in specialized membrane regions and facilitates iron ion delivery via receptor-mediated endocytosis. To facilitate protein accumulation in specific membrane regions, proteins must exhibit lateral mobility within the membrane plane. To examine protein dynamics, vesicles containing chain-deuterated DMPC-d54 were used.47 QENS experiments were conducted on two sets of samples: pure DMPC vesicles (DMPC and DMPCd54) and analogous samples with an additional 6 mol% of TFRC peptide, at 310 K using IN16B (ΔE = 0.75 μeV).47 This allows for the experimental determination of the lateral self-diffusion coefficient of lipid molecules in the absence and presence of TFRC peptides, as well as the calculation of the self-diffusion coefficient of TFRC peptides. Data analysis utilized models corresponding to both continuous diffusion50,74 and flow-like motion,54,73 with the diffusive motion model demonstrating superior fit, indicating that lipid long-range motion is best described by diffusion processes over observation times as short as tobs ≈ 5 ns (corresponding to ΔE = 0.75 μeV). Deuteration of lipid chains was found to have no impact on the long-range dynamics of lipid molecules, with the lateral diffusion coefficient for DMPC measured at 2 × 10−7 cm2 s−1. However, the presence of TFRC restricted lateral diffusion, reducing the lateral diffusion coefficient to 0.8 × 10−7 cm2 s−1. At 6 mol% TFRC, peptide scattering contribution for chain-deuterated DMPC-d54 ULVs was approximately 50%, providing insight into peptide dynamics. The self-diffusion coefficient of TFRC peptides was determined to be Dpeptide = 0.5 × 10−8 cm2 s−1, approximately 40 times smaller than that of lipids. This finding supports the interpretation of reduced lipid long-range mobility in the presence of TFRC. Transmembrane peptides are hindered in their diffusion not only due to their larger mass compared to lipids but also because of their anchoring in both membrane leaflets. Consequently, neighboring lipid molecules are likely hindered in their long-range mobility, leading to a decrease in their self-diffusion coefficient.Nonsteroidal anti-inflammatory drugs (NSAIDs)
NSAIDs are commonly prescribed for their antipyretic and pain-relieving properties, despite exhibiting a wide range of side effects. The notion that NSAID effects are associated to their interactions at the cellular membrane level has spurred investigations into their membrane interactions. Moreover, given the pivotal role of membrane dynamics in drug encapsulation and intracellular delivery, comprehending the dynamic and structural changes induced by NSAIDs in membranes is imperative for precise targeted delivery strategies. Sharma and co-workers have investigated the impacts of three widely used NSAIDs—aspirin, ibuprofen, and indomethacin—on the biophysical properties of model plasma membranes.59,60,106,122,123 Chemical structures of these NSAIDs are shown in Fig. 10(a). Differential scanning calorimetry (DSC) and neutron elastic intensity scan measurements revealed notable alterations in membrane phase behavior induced by these drugs. Typical observed neutron elastic intensity scans for the DMPC membrane in the absence and presence of 25 mol% NSAIDs are shown in Fig. 10(b). It is evident that incorporation of NSAIDs led to shifts in the main phase transition towards lower temperatures and broadened transitions, indicating an influence on cooperativity.59,106,122,124 QENS data further unveiled enhanced membrane dynamics upon NSAID inclusion, particularly in the ordered phase, where all three NSAIDs enhanced lateral diffusion. Dlat obtained for the DMPC membrane in the absence and presence of 25 mol% NSAIDs at different temperatures is shown in Fig. 10(c). It is evident that at 280 K and 293 K, inclusion of NSAIDs enhances Dlat. Notably, Dlat increased monotonously with NSAID concentration. While the effects on membrane dynamics varied, quantitative differences were noted among the NSAIDs, correlating with their distinct interactions with lipid membranes.106,122 For instance, in the ordered phase, ibuprofen exhibited stronger effects (Fig. 10(c)) on the membrane compared to other NSAIDs, likely due to structural and hydrophobicity differences influencing NSAID–membrane interactions and location within the membrane. NSAIDs primarily interacted with the lipid membrane through a combination of electrostatic interactions with the polar head group and hydrophobic interactions with the nonpolar alkyl tails. Aspirin and ibuprofen, with smaller molecular sizes and polar oxygen atoms, displayed stronger electrostatic interactions with the membrane's headgroup, while indomethacin, despite its charged form, was predominantly influenced by interactions with the hydrophobic tails owing to its larger nonpolar segment. Consequently, indomethacin encountered greater difficulty penetrating the membrane core compared to ibuprofen and aspirin, particularly in the ordered phase.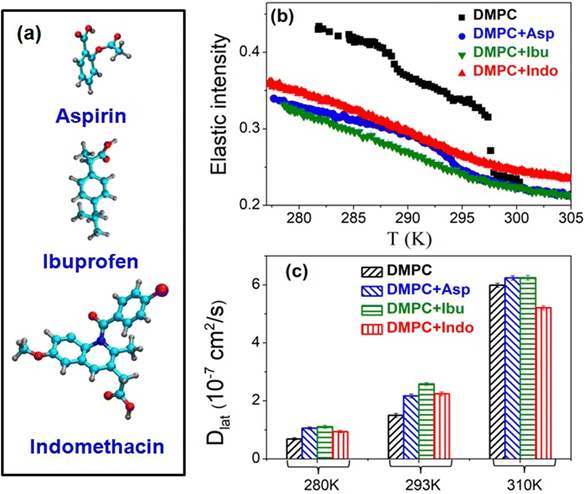 | ||
| Fig. 10 (a) Chemical structures of aspirin, ibuprofen, and indomethacin. (b) Q averaged elastic intensity for the DMPC membrane, neat and with 25 mol% aspirin, ibuprofen or indomethacin in the heating cycle. (c) Lateral diffusion coefficient, Dlat, as obtained using QENS for the DMPC membrane, neat and with 25 mol% aspirin, ibuprofen or indomethacin at different temperatures. Adapted from ref. 59 and 106 with permission from The Royal Society of Chemistry and Elsevier, copyright 2017 & 2020. | ||
In the fluid phase, the effects on membrane dynamics varied depending on the nature and concentration of the NSAIDs. Indomethacin suppressed membrane dynamics, whereas aspirin and ibuprofen slightly enhanced lateral diffusion at equivalent molar concentrations as shown in Fig. 10(c). With increasing aspirin concentration, lateral diffusion coefficients saturated in the fluid phase, whereas higher concentrations of ibuprofen had the opposite effect, restricting lipid lateral diffusion.59,106 These observations underscore the importance of independently scrutinizing each NSAID when analyzing its mechanism of action. A deeper understanding of NSAID–membrane interactions holds promise for informing the development of more effective NSAIDs with reduced side effects.
To gain microscopic insights, we recently conducted MD simulations on DODAB lipid membranes both with and without aspirin, examining both ordered and fluid phases.123 Our simulations revealed that at 298 K and 310 K, the bilayers adopt interdigitated two-dimensional square phases, which become more rugged in the presence of aspirin. As the temperature rises to 345 K, the bilayer transitions to a fluid state, with the disappearance of ripples. Aspirin tends to accumulate near oppositely charged headgroups, creating void spaces that increase interdigitation and order parameters. In the presence of aspirin, although the center of mass of lipids experiences structural arrest, they reach the diffusive regime faster, exhibiting higher lateral diffusion constants.123 These findings align with our QENS studies,122 indicating that aspirin functions as a plasticizer, enhancing lipid lateral diffusion in both ordered and fluid phases. Moreover, the addition of aspirin accelerates the relaxation time scales of bonds along the alkyl tails of DODAB due to increased lipid motions. Our results suggest that aspirin insertion is particularly favourable at physiological temperatures. Consequently, the DODAB bilayer, being ordered, stable, and exhibiting faster dynamics in the presence of aspirin, holds promise as a potential drug carrier for encapsulating aspirin, ensuring protected delivery and facilitating targeted and controlled drug release, potentially with antibacterial activity in the future.
Antioxidants and stimulants
Antioxidants encompass a range of compounds that play a crucial role in neutralizing free radicals and reactive oxygen species that inflict damage upon DNA, cell membranes, and various cellular components. They play pivotal roles in the development of numerous chronic diseases, including cardiovascular diseases, aging, cancer, and inflammation. α-Tocopherol (αToc), the most biologically active form of vitamin E, serves as a crucial lipid-soluble antioxidant, intercepting free radicals diffusing into the membrane from the aqueous phase. Rather than being randomly distributed throughout the lipid membrane, αToc tends to aggregate in domains enriched with this compound. Numerous structural studies have been conducted to pinpoint the precise location of αToc in the lipid membrane. In most lipid environments, it is found near the lipid–water interface, with a perpendicular orientation placing the chromanol ring close to the polar lipid headgroup. However, an intriguing exception arises in the case of DMPC, where αToc is situated deep within the membrane, near the bilayer's center. Sharma et al.45 have investigated the effects of αToc on the dynamics and phase behavior of DMPC membranes. It was found that the inclusion of αToc had a profound impact on the phase behavior of the lipid membrane, notably suppressing the pre-transition and broadening the main phase transition. The increased broadening of the main phase transition suggests that the presence of αToc affects the cooperativity of the transition. Additionally, the main phase transition shifted towards lower temperatures, accompanied by a decrease in associated enthalpy, indicative of a smaller fraction of phospholipid molecules participating in the transition. QENS measurements revealed that αToc influences membrane dynamics. Both lateral and internal motions of lipids were observed to be modulated in the presence of αToc, suggesting a strong interaction between αToc and the lipid membrane. The alteration in membrane dynamics was found to be non-monotonous and dependent on the physical state of the membrane. Specifically, in the ordered phase, αToc acted as a plasticizer, enhancing both lateral and internal motions of the lipid membrane. However, in the fluid phase, it primarily restricted internal motion without significant effects on lateral motion. Recently, the interaction of another antioxidant, chlorophyll, with lipid membranes was investigated using coarse-grained MD simulations.125,126 It was found that certain lipids promote the aggregation of chlorophyll. As the concentration of chlorophyll increases, the area per lipid also increases, leading to a more disordered membrane.Curcumin (diferuloylmethane), the primary compound in turmeric, has been investigated for its effects on membrane dynamics.84 Apart from its antioxidant properties, curcumin demonstrates a wide range of biological effects, including anti-inflammatory, anticancer, and wound-healing properties. Curcumin has been observed to influence the functionality and expression of a wide range of proteins, despite the absence of a definitive binding site for curcumin on any of these proteins. It is hypothesized that curcumin may modulate the functionality of membrane proteins indirectly by altering the physical properties of the host cell's membranes rather than through direct binding to proteins. This hypothesis has spurred investigations into the effects of curcumin on membrane dynamics. Sharma et al. have shown that curcumin significantly impacts the packing arrangement and conformations of DPPC lipids, resulting in enhanced membrane dynamics.84 Specifically, a substantial acceleration of DPPC lateral motion in both the ordered and fluid phases was observed in the presence of curcumin. The effects are particularly pronounced in the ordered phase, where the lateral diffusion coefficient increases by 23%, compared to a 9% increase in the fluid phase.84 These findings provide crucial insights into the molecular mechanisms underlying the heightened lateral diffusion facilitated by curcumin. Interestingly, the localized internal motions of DPPC are minimally affected by curcumin, except for a slight enhancement observed in the ordered phase. When comparing the QENS results of different membrane-active compounds, Sharma et al. have proposed a hypothesis regarding their impact on lipid motion.84 If a membrane-active compound adopts a surface-associated orientation, it is likely to influence the lateral motion of lipids. Conversely, if a membrane-active compound becomes deeply embedded within the membrane, it is expected to affect both the lateral and internal motions of the lipids. This distinction arises primarily due to the nature of lipid motion: lateral motion spans a long range within the membrane, whereas internal motion is confined to localized regions. This suggests that curcumin tends to localize preferentially at the membrane interface rather than adopting a transbilayer configuration. Furthermore, the unequivocal evidence demonstrating curcumin's modulation of membrane dynamics at a molecular level supports a potential action mechanism wherein curcumin acts as an allosteric regulator of membrane functionality. These insights contribute to our understanding of the mechanisms underlying curcumin's biological effects and its potential therapeutic applications.
Stimulants encompass a diverse range of substances known for boosting central nervous system activity. Widely utilized by a substantial portion of the population, these drugs serve various purposes, including enhancing performance, reaping medical benefits, and indulging in recreational activities. Prominent examples of stimulants comprise caffeine, nicotine, and cocaine. Among them, caffeine (1,3,7-trimethylxanthine) stands out as the most globally consumed legal psychoactive compound. Beyond its fatigue-fighting properties, caffeine has garnered attention for its potential antioxidative effects, potentially shielding against ailments like Alzheimer's disease. Various mechanisms have been proposed to elucidate caffeine's action, including the mobilization of intracellular calcium and the inhibition of adenosine and benzodiazepine ligand binding to neuronal membrane-bound receptors. Additionally, caffeine has been observed to interact with lipid membranes.127 Sharma et al.127 explored the effects of caffeine on the microscopic dynamics of lipid membranes. It was shown that caffeine significantly alters the microscopic dynamics of the lipids within the system, with the observed effects contingent upon the lipid phase. Specifically, in the coagel phase, caffeine serves as a plasticizing agent, while in the fluid phase, it constrains both lateral and internal lipid motions. This study sheds light on how caffeine modulates membrane fluidity by influencing the dynamics of constituent lipids, a process intricately linked to the physical state of the bilayer.
Depressants
Depressants stand in contrast to stimulants as they work to decrease central nervous system activity, inducing relaxation, sedation, and diminished alertness. Common examples of depressants encompass alcohol, opioids, and similar substances. Rheinstädter and coworkers128 have carried out a detailed investigation into the interaction between ethanol and DMPC membranes using neutron and X-ray scattering techniques. Their experiments involved DMPC hydrated powder with and without 5 wt% ethanol (equivalent to 2 mol%). It was found that ethanol molecules predominantly reside in the head group region of the bilayers, regardless of whether the membrane is in the gel or fluid phase. Furthermore, the presence of ethanol increases the permeability of the membrane in both phases. Neutron elastic intensity scans were conducted to elucidate the effects of ethanol on the phase behavior of the membrane. DMPC membranes undergo a pre-transition at 286 K and a main phase transition at 296.6 K. Ethanol was found to accentuate both transitions, making them more pronounced. Although the temperature of the main transition remained unchanged, the pre-transition was shifted by approximately 2.5 K towards higher temperatures in the presence of ethanol. Comparing the elastic intensity between pure DMPC and DMPC with ethanol, it was observed that ethanol did not alter the elastic intensity in the fluid phase. However, in the gel phase, the presence of ethanol led to a drastic change in elastic intensity, indicating enhanced order in both the gel and ripple phases. The QENS experiments revealed that ethanol had a moderate effect on the lateral motion of lipids in the fluid phase, resulting in a slight decrease in lateral diffusion. In the gel phase, membranes exhibited a higher degree of order in the presence of ethanol, with lipid lateral diffusion slowing down by a factor of two. Overall, ethanol was found to induce a stiffer and more ordered structure in the ripple and gel phases of the membranes. Importantly, the dynamics of the membrane and hydration water were not significantly affected by the presence of ethanol in the physiologically relevant fluid phase at this alcohol concentration.Sterols
Sterols constitute a vital lipid class pivotal in regulating numerous biological processes. Sterols play a critical role in facilitating the formation of liquid-ordered (Lo) membrane states, or lipid rafts. Sterols have been identified as key molecules responsible for maintaining membranes in a fluid state optimal for proper functionality. Notably, they play a significant role in regulating membrane thickness, facilitating the normal functioning of membrane proteins with diverse hydrophobic region lengths. Different kinds of sterols are found in nature such as cholesterol and ergosterol. Cholesterol predominates in vertebrates, whereas ergosterol is found in fungi and some protists. The chemical structures of ergosterol and cholesterol are shown in Fig. 11. Plants typically exhibit more intricate sterol compositions, featuring compounds like stigmasterol and sitosterol. These plant-specific sterols play pivotal roles in embryonic plant growth.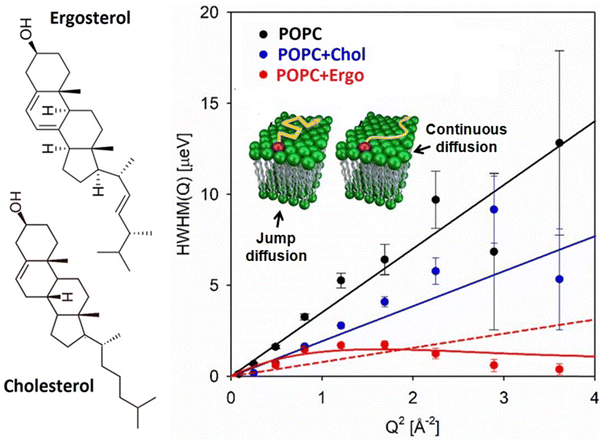 | ||
| Fig. 11 Chemical structure of ergosterol and cholesterol. Variation of half width at half maxima (HWHM) of Lorentzian function associated with lateral diffusion with Q2 for the POPC membrane, neat and in the presence of ergosterol and cholesterol. The best fits (solid lines) are given by the continuous Fickian diffusion model for POPC and POPC + cholesterol and by the jump diffusion model for POPC + ergosterol. For direct comparison, the fits using continuous Fickian diffusion for POPC + ergosterol are shown by a dashed line. Adapted from ref. 75 with permission from American Chemical Society, copyright 2024 (adapted from ref. 75). | ||
Cholesterol
Cholesterol consists of a small polar hydrophilic hydroxyl group and a relatively large hydrophobic steroid ring, lacking inherent ability to self-assemble into distinct structures. Its multifunctional role within cells encompasses modulating various physical properties of the plasma membrane, including mechanical strength (bending and compressibility modules) and fluidity. Extensive investigations into the interaction between cholesterol and lipid membranes have yielded a plethora of intriguing findings. These include condensing effects, reduction in membrane permeability, suppression of the main phase transition of lipids at sufficiently high concentrations, and augmentation of acyl chain ordering in the fluid phase while diminishing ordering in the gel phase, among others.129 Busch et al.130 conducted QENS experiments on DMPC membranes with varying concentrations of cholesterol, employing two different energy resolutions: 60 μeV and 4 μeV, corresponding to observation time scales of 60 ps and 900 ps, respectively. Their findings indicated that above the main phase transition, the inclusion of cholesterol resulted in a reduction in quasielastic broadening, indicative of constrained membrane dynamics. This effect was particularly pronounced at higher energy resolutions (4 μeV) or longer time scales (900 ps), where membrane dynamics exhibited a monotonous decrease with increasing cholesterol concentration. Below the main phase transition, however, the addition of cholesterol did not alter membrane dynamics. In contrast, Sharma et al.51 conducted a comprehensive investigation into the impact of cholesterol on the lateral motion of the membrane. They found that cholesterol significantly restricted lateral motion, particularly above the main phase transition temperature. At 310 K, the addition of 20 mol% cholesterol reduced the lateral diffusion coefficient from 7.7 × 10−7 cm2 s−1 to 2.8 × 10−7 cm2 s−1. The main effect of cholesterol is to decrease the available free area and the observed results can be explained based on eqn (15), free area theory. This restriction can be attributed to cholesterol's ability to promote tight packing of lipid molecules resulting in reduced average area per phospholipid, a(T). Moreover, one also needs to subtract the area occupied by cholesterol from a(T) to obtain the available free area.131 At 280 K, no significant effect of cholesterol on the lateral motion of DMPC was observed, with a lateral diffusion coefficient of 0.7 × 10−7 cm2 s−1.Ergosterol
Fungal infections pose a growing threat to global health, fueled by factors such as climate change and immunocompromised populations. Ergosterol plays a pivotal role in the structure and function of fungal cell membranes, serving as a crucial component that influences membrane fluidity, integrity, and permeability. Moreover, the distinct interactions of ergosterol with therapeutic agents underscore its potential as a target for developing novel antifungal strategies. For example, ergosterol uniquely interacts with amphotericin B, a potent antifungal drug, which distinguishes it from cholesterol and suggests its potential as a specific therapeutic target. Due to their similar chemical structure, ergosterol is thought to modulate the lipid membrane in a manner similar to cholesterol. A recent study has unveiled fundamental differences in the effects of ergosterol and cholesterol on the structure and dynamics of lipid membranes.75 Unlike cholesterol, ergosterol is embedded more shallowly in the lipid bilayer and exhibits a smaller condensation effect, resulting in less significant changes to membrane thickness. Moreover, ergosterol can both rigidify and soften membranes, depending on its concentration, contrasting with cholesterol's consistent role in increasing membrane rigidity. QENS experiments on 1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine (POPC) lipid membranes in the absence and presence of ergosterol and cholesterol have revealed distinct diffusion behaviors. Variations of HWHMs of Lorentzian function associated with lateral diffusion with Q2 for the POPC membrane, neat and in the presence of ergosterol and cholesterol, are shown in Fig. 11. While lateral diffusion in POPC and POPC with cholesterol follows continuous diffusion, POPC with ergosterol requires jump diffusion to describe the observed data. The lateral diffusion coefficients were measured as 5.3 × 10−7 cm2 s−1 for POPC, 2.9 × 10−7 cm2 s−1 for POPC with cholesterol, and 3.8 × 10−7 cm2 s−1 for POPC with ergosterol. Interestingly, in the fluid phase, cholesterol does not alter the continuous Fickian diffusion seen in POPC but significantly reduces its diffusion rate. Conversely, ergosterol's presence results in a moderate reduction in the diffusion rate and transforms the mechanism of POPC dynamics to a distinct jump diffusion process. These findings suggest distinct interactions of ergosterol with membranes compared to cholesterol, highlighting the unique role of ergosterol in membrane dynamics.Ionic liquids
Ionic liquids (ILs) represent a distinctive class of organic salts characterized by their low melting point below 100 °C and unique physicochemical properties. ILs are widely applied across diverse fields, including bio-nanotechnology, where they play pivotal roles in solubilizing drugs, stabilizing biomolecules, and exhibiting antibacterial properties. Despite their broad utility, the precise mechanism underlying their antimicrobial activity remains elusive, impeding their optimized application in bio-nanomedicine. Bakshi et al. have unveiled that ILs induce necrosis-dependent cell death through membrane damage, prompting an exploration into their interaction with model cell membranes.132 Our findings elucidate how IL incorporation modulates the structure, dynamics, and phase behavior of lipid membranes.41,53,108,109,132–137 Our investigation delved into the effects of different ILs, varying in alkyl chain length and anions, on various lipid membranes, including zwitterionic DMPC, DPPC, sphingomyelin, cationic DHDAB, and liver lipid extract.41,53,108,109,132–137 Utilizing X-ray reflectivity, we reveal the formation of interdigitated domains upon IL addition.135 ILs also exert a notable influence on the phase behavior of lipid membranes. They suppress the pre-transition and shift the main transition temperature downward. Additionally, the main phase transition becomes broader, indicating a decrease in the cooperativity of the phase transition. Despite the observed shift in Tm towards lower temperatures and the broadening of the peak, the addition of ILs does not significantly affect the enthalpy (ΔH) associated with the main transition, suggesting no change in the number of lipids participating in the main phase transition. Furthermore, we observe that the interaction between ILs and the membrane depends on the alkyl chain length of ILs.53,108,134 As the alkyl chain length of the IL increases, the binding affinity of the IL with the lipid membrane also increases, indicating that hydrophobic interactions between the IL and the membrane play a crucial role. These results align with dye leakage assay measurements, which suggest that the stronger binding of the DMIM[Br] IL correlates with higher membrane permeability.53 Across all cases, ILs functioned as plasticizers, augmenting membrane dynamics, with their effects contingent on alkyl chain length, which intensified with longer chains. ILs accelerated lateral diffusion in both ordered and fluid phases, with more pronounced effects observed in the ordered phase.53,108 For instance, the inclusion of BMIM[BF4] increased the lateral diffusion of DMPC by 22% in the ordered phase, compared to just 2% in the fluid phase.108 Longer chain ILs displayed enhanced plasticizing effects, highlighting the importance of hydrophobic interactions in their mechanisms of action. For example, in the fluid phase of DMPC, C10MIM[BF4] boosted lateral diffusion by 38%, while C4MIM[BF4] exhibited a modest 2% increase.108 This underscores the significant role of hydrophobic interactions between ILs and lipid membranes. The stronger impact of longer chain length ILs on membrane dynamics correlates with heightened antimicrobial efficacy, as demonstrated by a decrease in MIC, emphasizing the pivotal role of membrane dynamics in influencing membrane fluidity and permeability, thereby impacting cell stability.53 This augmentation in membrane dynamics led to enhanced membrane fluidity and permeability, confirmed through dye leakage and flow cytometry assays, establishing a direct relationship between IL-induced membrane dynamics and antimicrobial activity. These findings underscore the tunability of ILs’ antibacterial properties through the manipulation of alkyl chain length, highlighting the significance of comprehending their effects on membrane dynamics for tailored bio-nanomedicine applications. Interestingly, ILs not only accelerated lateral diffusion in single lipid systems but also in complex liver lipid extracts,109 mimicking cell membranes more closely. This universality of the plasticizing effect suggests that it is independent of membrane composition. QENS data provided a quantitative framework for elucidating the effects of ILs on the dynamical and phase behavior of model cell membranes, essential for understanding their action mechanisms comprehensively.This study also holds broader implications for the development of efficient drug delivery systems. Liposomes have emerged as highly promising carriers for drug delivery, with the stability and release kinetics of liposomes crucially dependent on the phase behavior and membrane fluidity. Our findings highlight the pivotal role of IL incorporation in modulating both the phase behavior and fluidity of the membrane, which in turn influences the balance of electrostatic and hydrophobic interactions and enhances the efficiency of cargo transport. This insight underscores the potential of IL-modified liposomes as effective platforms for advanced drug delivery systems, offering opportunities for improved therapeutic outcomes and targeted delivery strategies.
The impact of DMIM[Br] on the structural, dynamical, and phase behavior of cationic DHDAB vesicles has been thoroughly investigated.133 In the heating cycle, pure DHDAB membranes exhibit two distinct endothermic transitions: the pre-transition occurring at 303 K and the main transition at 318 K.138 The pre-transition marks a solid-to-solid polymorphic shift from the coagel phase to the intermediate crystalline (IC) phase, accompanied by mild disorder in alkyl chains. Conversely, the main transition signifies the transformation from the IC phase to the fluid phase, characterized by decreased packing density, increased head group hydration, and heightened alkyl chain disorder. Notably, a significant hysteresis is observed in the phase behavior during the cooling cycle, with direct transformation from the fluid to coagel phase. Incorporation of DMIM[Br] exerts concentration-dependent effects on DHDAB bilayer phase behavior.133 At 10 and 25 mol%, DMIM[Br] eliminates the pre-transition and lowers the onset temperature of the main transition, while inducing an intermediate gel phase formation during the cooling cycle, akin to observations in DODAB membranes. This phenomenon is attributed to strengthened hydrophobic attraction between tails and enhanced electrostatic repulsion upon DMIM[Br] insertion. However, at 40 mol%, the formation of the intermediate gel phase is suppressed, likely due to self-aggregation of DMIM[Br] into micellar forms, altering the interaction landscape. QENS data reveal enhanced lipid mobility in coagel and fluid phases upon DMIM[Br] addition, suggesting its role as a plasticizer, thereby enhancing membrane fluidity across all phases. These findings underscore the modulation of membrane phase behavior and fluidity by DMIM[Br], pivotal for efficient cargo transport, through control of electrostatic and hydrophobic interactions.
Unsaturated lipids (e.g. monoolein)
Ensuring the flexibility of cell membranes is crucial for numerous cellular processes. In organisms like plants and cyanobacteria, maintaining membrane fluidity becomes particularly vital in colder environments, where fluidity naturally decreases. These organisms counter this by adjusting the composition of their membrane lipids, increasing the number of double bonds in fatty acids and thereby the number of unsaturated lipids in the membrane. Investigating how unsaturated lipids contribute to this maintenance is therefore valuable. Singh et al. explored the impact of monoolein (MO), a significant unsaturated lipid, on the behavior and dynamics of cationic DODAB membranes.56 MO stands out for its non-toxic, biodegradable, and biocompatible properties, making it widely applicable in drug delivery, emulsion stabilization, and protein crystallization. Notably, liposomes formed from DODAB:MO combinations exhibit promise as carriers for gene therapy. These formulations demonstrate reduced toxicity and effectively facilitate cell transfection in in vitro studies. Our neutron elastic intensity scan revealed significant alterations in the phase behavior of DODAB membranes upon incorporation of MO, evident in both heating and cooling cycles. During heating, the transition from the coagel to fluid phase becomes less abrupt and more diffuse, with the phase transition temperature shifting towards lower values. Conversely, in the cooling cycle, the formation of an intermediate gel phase is suppressed, leading DODAB to transition directly from the fluid phase to the coagel phase. This suggests a synchronized ordering of lipid headgroups and tails, contrasting with the nonsynchronous changes observed in pure DODAB membranes. Furthermore, our investigation into membrane dynamics unveiled notable effects of MO. In the coagel phase, MO serves as a plasticizer, enhancing quasielastic broadening and thus increasing membrane flexibility. This disrupts the tightly packed lipid structure characteristic of the coagel phase. Conversely, in the fluid phase, MO acts as a stiffening agent, restricting the lateral diffusion of lipid molecules. The lateral diffusion coefficient decreases from 22 × 10−6 cm2 s−1 to 17 × 10−7 cm2 s−1 in DODAB membranes with MO, attributed to the reduction in available free area per lipid molecule.56 Although the nature of internal motions within the fluid phase remains largely unchanged with MO addition, there is a reduction in the HWHM corresponding to segmental motion, indicating a deceleration of segmental motions.Our research also highlights the pivotal role of the location of guest molecules within the lipid membrane in dictating their effects on membrane dynamics. Alongside factors such as size and the interaction with the membrane, the location of these molecules significantly influences their impact on membrane dynamical behavior. When situated at the interface between the lipid and the aqueous phase, guest molecules predominantly influence lateral motion, leaving internal motion largely unaffected. Conversely, molecules residing deep within the hydrophobic core of the membrane have potential to influence both lateral and internal motions. AMPs provide a pertinent example: at low concentrations, they bind to the surface of the lipid membrane, primarily affecting lateral motion due to the diffusion of lipids within the leaflet. In contrast, compounds like ILs and NSAIDs penetrate deep into the membrane, influencing both lateral and internal motions. Our investigations have revealed that the incorporation of ILs induces disorder within the membrane, thereby enhancing both lateral and internal motion. Furthermore, the behavior of cholesterol within the membrane contrasts with that of ILs: while cholesterol penetrates into the membrane core, it restricts both lateral and internal motions of lipids in the fluidic phase of the membrane. This discrepancy can be attributed to the differing effects of cholesterol and ILs on membrane orderliness: cholesterol enhances membrane order, whereas ILs induce disorder. These findings underscore the sensitivity of membrane dynamics to the presence of membrane-active molecules. Understanding these interactions not only sheds light on fundamental aspects of membrane biology but also holds potential for informing the design of therapeutic agents and elucidating their effects on cellular membranes. The effects of these membrane active compounds on the membrane dynamics are summarised in Table 2.
| S. no. | Compound and concentration | Membrane system | Spectrometer (resolution) | T (phase) | Con. (mol%) | D lat (10−7 cm2 s−1) | Main findings | Ref. |
|---|---|---|---|---|---|---|---|---|
| DMPC: zwitterionic, Tm = 297 K. DPPC: zwitterionic, Tm = 314 K. DMPS: anionic, Tm = 309 K. DMPG: anionic, Tm: 297 K. DPPG: anionic, Tm = 314 K. DHDAB: cationic Tm = 318 K. DODAB: cationic, Tm = 327 K.a Jump diffusion.b wt percentage. | ||||||||
| 1. | Membrane active peptides | |||||||
| 1.1 | Amyloid peptides: amyloid beta (Aβ) | |||||||
| 1.1.1 | Aβ (25–35) 3 mol% | DMPC/DMPS (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) 8) |
NEAT (93 μeV) | 290 K (ordered) | 0 | 6 | (i) Aβ (25–35) accelerates lateral diffusion in both ordered and fluid phases | 117 |
| 3 | 8 | |||||||
| Supported lipid multilayer | 320 K (fluid) | 0 | 18 | (ii) Aβ (25–35) also enhances out of plane motion of lipids | ||||
| 3 | 24 | |||||||
| 1.1.2 | Aβ (22–40) 3 mol% | DMPC/DMPS (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) 8) |
NEAT (93 μeV) | 320 K (fluid) | Aβ (22–40) accelerates lateral diffusion of lipids in the fluid phase | 118 | ||
| Supported lipid multilayer | — | |||||||
| Aβ (22–40) 1.5 mol% | DMPC/DMPS (92![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 8) 8) |
IN16 (1 μeV); | 288 K (ordered) | 0 | 1.02 | In the ordered phase, Aβ (22–40) enhances lateral diffusion. Near the main phase transition temperature (303 K), the trend is reversed, Aβ (22–40) causes a decrease in the lateral diffusion coefficient (Dlat) | 94 | |
| 1.5 | 1.17 | |||||||
| Supported lipid bilayer | IN5 (15 μeV) | 303 K (near the phase transition) | 0 | 2.08 | ||||
| TOFTOF (100 μeV, 25 μeV) | 1.5 | 1.58 | ||||||
| 1.1.3 | Aβ (1–40) 3.3 mol% | DMPG 5 wt% unilamellar vesicles (ULVs) | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 1.1 | Aβ (1–40) mainly affects the long range lateral motion of lipid molecules, especially in the fluid phase, but not the localised internal motion | 46 |
| 3.3 | 0.9 | |||||||
| 310 K (fluid) | 0 | 5.5 | ||||||
| 3.3 | 6.9 | |||||||
| 1.2 | Antimicrobial peptides | |||||||
| 1.2.1 | Melittin 0.2 mol% | DMPC 5 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, melittin acts as a plasticizer, enhancing the lateral motion of lipids. However, in the fluid phase, it acts as a stiffening agent, restricting the lateral motion of lipids | 51 |
| 0.2 | 1.1 | |||||||
| 310 K (fluid) | 0 | 7.7 | ||||||
| 0.2 | 2.4 | |||||||
| DMPC with 20 mol% cholesterol 5 wt% ULVs | BASIS (3.4 μeV) | 280 K | 0 | 0.7 | (ii) No significant effect of melittin on Dlat in the presence of cholesterol | |||
| 0.2 | 0.7 | (iii) Destabilizing effect of melittin on membranes can be mitigated by the presence of cholesterol | ||||||
| 310 K | 0 | 2.8 | ||||||
| 0.2 | 2.8 | |||||||
| 1.2.2 | Alamethicin 0.5 mol% | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, no significant effect of alamethicin on Dlat | 107 |
| 0.5 | 0.7 | (ii) In the fluid phase, alamethicin restricts lateral diffusion of lipids | ||||||
| 310 K (fluid) | 0 | 5.0 | (iii) Effect of cationic (+5e) melittin on lateral diffusion and phase behavior of membranes is stronger than that of anionic (−1e) alamethicin | |||||
| 0.5 | 3.9 | (iv) Proposed a new action mechanism of AMPs in which by modulating lateral motion at very low concentration, AMPs kill the bacterial cells | ||||||
| 1.2.3 | Aurein | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, no significant effect on Dlat | 96 |
| Different molar concentrations (0, 1, 1.7 and 2.5 mol%) | 1.7 | 0.8 | (ii) In the fluid phase, Dlat decreases monotonously with the increase in the concentration of aurein | |||||
| 293 K (ordered) | 0 | 1.6 | (iii) This decrease in lateral diffusion leads to lateral segregation of lipids | |||||
| 1.7 | 1.5 | (iv) Melittin remains as an exception which acts as a plasticizer in the ordered phase and acts oppositely in the fluid phase. Other AMPs (alamethicin, aurein) though restrict lateral motion in the fluid phase do not affect dynamics much in the ordered phase | ||||||
| 310 K (fluid) | 0 | 6.0 | ||||||
| 1.7 | 4.7 | |||||||
| 320 K (fluid) | 0 | 8.7 | ||||||
| 1 | 7.5 | |||||||
| 1.7 | 6.1 | |||||||
| 2. | 5.4 | |||||||
| 1.2.4 | Ubiquicidin (UBI) | |||||||
| 1.2.4.1 | UBI (31–38) 4 mol% | DPPG 5 wt% ULVs | IRIS (17 μeV) | 330 K (fluid) | 0 | 17.4 | UBI (31–38) restricts lateral diffusion of DPPG | 29 |
| 4 | 12.5 | |||||||
| 1.2.4.2 | UBI (29–41) 0, 2 and 4 mol% | DPPG 5 wt% ULVs | IRIS (17 μeV) | 330 K (fluid) | 0 | 17.4 | (i) UBI (29–41) restricts lateral diffusion of DPPG | |
| 2 | 13.8 | (ii) Dlat decreases monotonously with the increase in the concentration of UBI (29–41) | ||||||
| 4 | 10.5 | (iii) UBI (29–41) acts stronger than UBI (31–38) | ||||||
| 2. | Transmembrane peptide | |||||||
| 2.1 | Transferrin receptor (TFRC) protein | DMPC 10 wt% ULVs | IN16 B (0.75 μeV) | 310 K (fluid) | 0 | 2.1 | TFRC protein restricts lateral diffusion of lipids | 47 |
| 6 | 0.8 | |||||||
| 3. | NSAIDs | |||||||
| 3.1 | Aspirin 0, 25 and 50 mol% | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, Dlat increases monotonously with the increase in the concentration of aspirin | 59 |
| 25 | 1.1 | (ii) Effects of aspirin on membrane dynamics are more prominent near the main phase transition temperature, as the main phase transition gets broadened and shifts towards lower temperature | ||||||
| 50 | 1.2 | (iii) In the fluid phase, at lower concentration, addition of aspirin enhances Dlat and then it saturates | ||||||
| 293 K (ordered) | 0 | 1.5 | ||||||
| 25 | 2.2 | |||||||
| 50 | 2.5 | |||||||
| 310 K (fluid) | 0 | 6.0 | ||||||
| 25 | 6.3 | |||||||
| 50 | 6.3 | |||||||
| DODAB 70 mM vesicles | IRIS (17 μeV) | 330 K (fluid) | 0 | 22 | In the fluid phase, Dlat of DODAB increases slightly with 25 mol% aspirin | 122 | ||
| 25 | 24 | |||||||
| 3.2 | Ibuprofen 0, 25 and 50 mol% | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, Dlat increases monotonously with the increase in the concentration of ibuprofen | 106 |
| 25 | 1.1 | (ii) In the fluid phase, Dlat has a non-monotonous dependence on concentration: first it increases at 25 mol% ibuprofen and then it decreases at 50 mol% ibuprofen | ||||||
| 50 | 1.6 | |||||||
| 293 K (ordered) | 0 | 1.5 | ||||||
| 25 | 2.6 | |||||||
| 50 | 3.3 | |||||||
| 310 K (fluid) | 0 | 6.0 | ||||||
| 25 | 6.3 | |||||||
| 50 | 5.4 | |||||||
| 3.3 | Indomethacin 25 mol% | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | (i) In the ordered phase, all NSAIDs generally enhance the membrane fluidity. Among these, ibuprofen affects the dynamics the most compared to others, suggesting stronger interaction with lipids | 106 |
| 25 | 0.9 | (ii) In the fluid phase, 25 mol% indomethacin restricts lateral diffusion which is in contrast with the action of aspirin and ibuprofen. This suggests that the effect of NSAIDs on Dlat depends on the concentration and type of NSAIDs. For example, ibuprofen at 25 mol% enhances but at 50 mol% restricts lateral diffusion of lipids | ||||||
| 293 K (ordered) | 0 | 1.5 | ||||||
| 25 | 2.2 | |||||||
| 310 K (fluid) | 0 | 6.0 | ||||||
| 25 | 5.2 | |||||||
| DODAB 70 mM vesicles | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 22 | In the fluid phase, incorporation of indomethacin restricts lateral diffusion of DODAB. A very similar action was observed for the zwitterionic DMPC membrane | 122 | ||
| 25 | 15 | |||||||
| 4. | Antioxidants and stimulants | |||||||
| 4.1 | Vitamin E | DMPC 7 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | In the ordered phase, aToc enhances both lateral and internal motion. However, in the fluid phase, aToc restricts only internal motion, and no significant effect on lateral motion was observed | 45 |
| α-Tocopherol (aToc) | 10 | 0.8 | ||||||
| 20 | 0.8 | |||||||
| 293 K (ordered) | 0 | 1.4 | ||||||
| 10 | 1.6 | |||||||
| 20 | 1.9 | |||||||
| 310 K (fluid) | 0 | 5 | ||||||
| 10 | 4.9 | |||||||
| 20 | 5 | |||||||
| 4.2 | Curcumin 2 mol% | DPPC 5 wt% ULVs | IRIS (17 μeV) | 310 K (ordered) | 0 | 5.0 | (i) In the ordered and fluid phase, curcumin enhances lateral diffusion about 23% and 9% respectively | 84 |
| 2 | 6.0 | (ii) Effects are more prominent in the ordered phase than in the fluid phase | ||||||
| 330 K (fluid) | 0 | 17.7 | (iii) Curcumin acts as an allosteric regulator | |||||
| 2 | 20.6 | |||||||
| 4.3 | Caffeine 25 mol% | DODAB | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 22 | (i) In the coagel phase, caffeine acts as a plasticizing agent, whereas in the fluid phase, it restricts the lateral and internal motions of the lipids | 127 |
| 70 mM vesicles | 25 | 12 | ||||||
| 5. | Depressants | |||||||
| 5.1 | Ethanol | DMPC | HFBS (0.8 μeV) | 286 K (ordered) | 0 | 0.9 | (i) In the ordered phase, lateral diffusion in the presence of ethanol is slowed down by a factor of 2 as compared to pure DMPC | 128 |
| Hydrated powder | 2 | 0.5 | (ii) Ethanol molecules reside in the head group region of the bilayers and enhance the permeability of the membrane | |||||
| 308 K (fluid) | 0 | 5.2 | ||||||
| 2 | 4.8 | |||||||
| 6. | Sterols | |||||||
| 6.1 | Cholesterol | DMPC 5 wt% ULVs | BASIS (3.4 μeV) | 280 K (ordered) | 0 | 0.7 | Cholesterol restricts lateral diffusion of lipids in the fluid phase | 51 |
| 20 | 0.7 | |||||||
| 310 K (fluid) | 0 | 7.7 | ||||||
| 20 | 2.8 | |||||||
| DMPC 50 wt% hydrated lipid powder | TOFTOF (60 μeV) | 293 K (ordered) | 0 to 40 | — | In the fluid phase, incorporation of cholesterol leads to a decrease in the mobility of lipids, with mobility decreasing with increasing cholesterol content. Effects are more prominent at high energy resolution (4 μeV) or longer observational time | 130 | ||
| 303 K | — | |||||||
| TOFTOF (4 μeV) | 313 K (fluid) | — | ||||||
| POPC | BASIS (3.7 μeV) | 303 K (fluid) | 0 | 5.3 | In the fluid phase, the addition of cholesterol significantly reduces the lateral diffusion coefficient but it does not change the nature of diffusion mechanism which is continuous Fickian diffusion | 75 | ||
| ULVs | 30 | 2.9 | ||||||
| 6.2 | Ergosterol | POPC | BASIS (3.7 μeV) | 303 K (fluid) | 0 | 5.3 | Ergosterol restricts the lateral diffusion moderately but changes the nature of the diffusion process. A jump diffusion is observed in the presence of ergosterol | |
| ULVs | 30 | 3.8a | ||||||
| 7. | Ionic liquids (ILs) | |||||||
| 7.1 | BMIM[BF4] | DMPC 100 mM ULVs | DNA (3.6 μeV) | 283 K (ordered) | 0 | 0.9 | (i) In both ordered and fluid phases, IL accelerates the lateral diffusion | 108 |
| 20 | 1.1 | (ii) Effects are stronger in the ordered phase | ||||||
| 293 K (ordered) | 0 | 1.6 | (iii) Longer chain ILs are found to be a stronger plasticizer suggesting that hydrophobic interaction between ILs and the lipid membrane plays an important role in their action mechanism | |||||
| 20 | 1.7 | |||||||
| 303 K (fluid) | 0 | 4.8 | ||||||
| 20 | 4.9 | |||||||
| 7.2 | DMIM[BF4] | DMPC 100 mM ULVs | DNA (3.6 μeV) | 283 K (ordered) | 0 | 0.9 | 109 | |
| 20 | 1.3 | |||||||
| 293 K (ordered) | 0 | 1.6 | ||||||
| 20 | 3.6 | |||||||
| 303 K (fluid) | 0 | 4.8 | ||||||
| 20 | 6.6 | |||||||
| Liver lipid extract 5 wt% ULVs | IRIS (17.5 μeV) | 310 K | 0 | 11.6 | ILs accelerate lateral diffusion not only for single lipid systems but also for a complex liver lipid extract which is a mixture of various lipids mimicking the cell membrane | |||
| 10b | 13.3 | |||||||
| 330 K | 0 | 18.2 | ||||||
| 10b | 21.5 | |||||||
| 7.3 | DMIM[Br] | DHDAB 70 mM vesicles | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 27 | Incorporation of IL enhances membrane dynamics in both ordered and fluid phases, suggesting that DMIM[Br] acts as a plasticizer | 133 |
| 25 | 30 | |||||||
| DPPC 5 wt% ULVs | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 16.8 | With the increase in the concentration of IL, Dlat increases | 53 | ||
| 25 | 21.3 | |||||||
| 50 | 24.4 | Increase in lateral diffusion ultimately leads to increased permeability and subsequent bacterial death | ||||||
| 7.4 | HMIM[Br] | DPPC 5 wt% ULVs | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 16.8 | 53 | |
| 25 | 19.3 | |||||||
| 8. | Unsaturated lipids | |||||||
| 8.1 | Monoolein (MO) | DODAB 70 mM vesicles | IRIS (17.5 μeV) | 330 K (fluid) | 0 | 22 | In the fluid phase, MO restricts both lateral and internal motions of the lipid | 56 |
| 33 | 17 | |||||||
Concluding remarks and future directions
This article provides an in-depth exploration of the lateral diffusion of lipids within homogeneous membrane systems, highlighting the complexities and sources of heterogeneity that influence this process. Strong emphasis is given to the discussion on significant variability in the lateral diffusion coefficient (Dlat) across different spatial and temporal scales. In particular, the measurement of Dlat at the mesoscopic length scale is essential to reconcile the discrepancies in diffusion coefficients obtained from neutron scattering (microscopic) and macroscopic experimental techniques (fluorescence, PFG-NMR, etc.). Incoherent neutron spin echo (NSE) shows promise in bridging this gap, with early experiments indicating its potential to deepen our understanding of lipid diffusion at mesoscopic length scales. Moreover, molecular dynamics (MD) simulations and preliminary quasielastic neutron scattering (QENS) experiments suggest the presence of sub-diffusive motion of lipids in the membrane, indicating a need for a comprehensive diffusion model across different length scales. This model should address the transitions from continuous to flow-like motion at higher Q-values and incorporate the sub-diffusive behavior noted in MD simulations. Integrating the results from NSE and QENS with macroscopic experiments can potentially provide sufficient data for building such a cohesive model of lipid lateral diffusion. Employing these models can then provide consistent and reliable lateral diffusion coefficients.Several factors influencing lateral diffusion are discussed in detail, including area per lipid, hydration, membrane curvature, temperature, and pressure. We have also explored the impact of membrane-active compounds on Dlat and the various factors influencing the interaction between these compounds and lipid membranes. Key considerations include the size, charge, and location of these compounds, as well as the polarity and composition of the membrane. Understanding these elements is critical for elucidating the mechanisms of action of these compounds in biological systems.
The majority of studies on lipid diffusion have focused on simplified systems, often examining single-component lipid membranes to uncover fundamental mechanisms. However, cell membranes are far more complex, comprising intricate mixtures of lipids, proteins, and various small molecules. This heterogeneity within cell membranes varies across organelles, cell types, organisms, and even in different physiological or pathological states. Various factors such as physical obstructions, binding interactions, the influence of the membrane skeleton, and biological regulation contribute to the complex patterns of diffusion in the plasma membrane. To fully understand these patterns, a comprehensive approach that considers the impact of these factors across different spatial and temporal scales is required.
Moreover, it is essential to analyze obstacles that impede diffusion within the membrane, whether they arise from proteins or other structural components, resulting in heterogeneous environments where movement is constrained. Binding interactions between membrane components, such as lipids and proteins, also play a significant role, potentially forming microdomains or clusters that affect the overall diffusion landscape. Additionally, the membrane skeleton, a network of cytoskeletal elements beneath the membrane, can create barriers or scaffolds that alter diffusion pathways. Biological regulation, which includes cellular signaling and response mechanisms, can further influence the mobility and organization of membrane components.
To gain a more comprehensive understanding of lipid diffusion, it is critical to shift the research focus toward more complex systems that reflect this inherent heterogeneity. This includes exploring membranes formed from natural lipid extracts and studying in vivo membrane dynamics. By doing so, one can better understand how this complexity impacts diffusion processes. Advances in neutron spectrometry, selective deuteration techniques, and sophisticated measurement and analysis methods are making these studies increasingly viable. For example, Sharma et al.,109 in a recent research effort, explored the effects of ionic liquids (ILs) on the lateral diffusion of liver-extract lipids, a blend containing phosphatidylcholine (PC), phosphatidylethanolamine (PE), phosphatidylinositol (PI), and cholesterol. Their study showed that incorporating ILs into liver-extract lipid membranes enhances lateral diffusion, aligning with the results from studies on single-component lipid membranes. Similarly, Paterno et al.139 investigated the impacts of an intramembrane photo-actuator, ZIAPIN2, and its vehicle solvent, dimethyl sulfoxide (DMSO), on the dynamics of both a model membrane (POPC ULV) and intact human embryonic kidney (HEK) cells. They found that while DMSO restricted membrane dynamics, ZIAPIN2 increased them in both model and cellular membranes. These studies underscore the importance of extending research into more complex membrane systems to understand diffusion in realistic biological contexts.
As our capacity to analyze these intricate systems improves, we can expect deeper insights into the mechanisms driving lipid diffusion and how they are influenced by the surrounding environment. This will pave the way for new discoveries in cellular biophysics and membrane dynamics, with potential applications in understanding cell function, disease mechanisms, and targeted drug delivery.
Data availability
No primary research results, software or code have been included and no new data were generated or analysed as part of this review.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We are grateful to our collaborators who contributed to the work discussed in this manuscript.References
- S. J. Singer and G. L. Nicolson, Science, 1972, 175, 720–731 CrossRef PubMed.
- K. Simons and E. Ikonen, Nature, 1997, 387, 569–572 CrossRef.
- L. J. Pike, J. Lipid Res., 2006, 47, 1597–1598 CrossRef.
- R. Raghupathy, A. A. Anilkumar, A. Polley, P. P. Singh, M. Yadav, C. Johnson, S. Suryawanshi, V. Saikam, S. D. Sawant, A. Panda, Z. Guo, R. A. Vishwakarma, M. Rao and S. Mayor, Cell, 2015, 161, 581–594 CrossRef PubMed.
- E. Sezgin, I. Levental, S. Mayor and C. Eggeling, Nat. Rev. Mol. Cell Biol., 2017, 18, 361–374 CrossRef PubMed.
- G. van Meer, D. R. Voelker and G. W. Feigenson, Nat. Rev. Mol. Cell Biol., 2008, 9, 112–124 CrossRef.
- O. G. Mouritsen and M. Bloom, Annu. Rev. Biophys. Biomol. Struct., 1993, 22, 145–171 CrossRef PubMed.
- D. Lingwood and K. Simons, Science, 2010, 327, 46–50 CrossRef PubMed.
- Y.-H. M. Chan and S. G. Boxer, Curr. Opin. Chem. Biol., 2007, 11, 581–587 CrossRef.
- R. M. Epand and R. F. Epand, J. Pept. Sci., 2011, 17, 298–305 CrossRef CAS.
- E. Fahy, S. Subramaniam, H. A. Brown, C. K. Glass, A. H. Merrill, R. C. Murphy, C. R. H. Raetz, D. W. Russell, Y. Seyama, W. Shaw, T. Shimizu, F. Spener, G. van Meer, M. S. VanNieuwenhze, S. H. White, J. L. Witztum and E. A. Dennis, J. Lipid Res., 2005, 46, 839–861 CrossRef.
- T. Harayama and H. Riezman, Nat. Rev. Mol. Cell Biol., 2018, 19, 281–296 CrossRef.
- J. H. Lorent, K. R. Levental, L. Ganesan, G. Rivera-Longsworth, E. Sezgin, M. Doktorova, E. Lyman and I. Levental, Nat. Chem. Biol., 2020, 16, 644–652 CrossRef PubMed.
- M. Eeman and M. J. B. Deleu, Biotechnol. Agron. Soc. Environ., 2010, 14, 719–736 Search PubMed.
- M. Nagao and H. Seto, Biophys. Rev., 2023, 4, 021306 CrossRef PubMed.
- L. Lautner, K. Pluhackova, N. K. H. Barth, T. Seydel, W. Lohstroh, R. A. Böckmann and T. Unruh, Chem. Phys. Lipids, 2017, 206, 28–42 CrossRef PubMed.
- S. Gupta and R. Ashkar, Soft Matter, 2021, 17, 6910–6928 RSC.
- S. Gupta, J. U. D. Mel and G. J. Schneider, Curr. Opin. Colloid Interface Sci., 2019, 42, 121–136 CrossRef CAS.
- H. Srinivasan, V. K. Sharma, V. G. Sakai and S. Mitra, Phys. Rev. Lett., 2024, 132, 058202 CrossRef CAS.
- S. Qian, V. K. Sharma and L. A. Clifton, Langmuir, 2020, 36, 15189–15211 CrossRef CAS.
- V. K. Sharma, S. Mitra and R. Mukhopadhyay, Langmuir, 2019, 35, 14151–14172 CrossRef CAS.
- S. Gupta and G. J. Schneider, Soft Matter, 2020, 16, 3245–3256 RSC.
- S. Gupta, J. U. De Mel, R. M. Perera, P. Zolnierczuk, M. Bleuel, A. Faraone and G. J. Schneider, J. Phys. Chem. Lett., 2018, 9, 2956–2960 CrossRef.
- D. Marquardt, F. A. Heberle, T. Miti, B. Eicher, E. London, J. Katsaras and G. Pabst, Langmuir, 2017, 33, 3731–3741 CrossRef.
- J. Perlo, C. J. Meledandri, E. Anoardo and D. F. Brougham, J. Phys. Chem. B, 2011, 115, 3444–3451 CrossRef.
- S. Chakraborty, M. Doktorova, T. R. Molugu, F. A. Heberle, H. L. Scott, B. Dzikovski, M. Nagao, L.-R. Stingaciu, R. F. Standaert, F. N. Barrera, J. Katsaras, G. Khelashvili, M. F. Brown and R. Ashkar, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 21896–21905 CrossRef.
- G. Orädd and G. Lindblom, Biophys. J., 2004, 87, 980–987 CrossRef.
- R. Machán and M. Hof, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1377–1391 CrossRef PubMed.
- J. B. Mitra, V. K. Sharma, A. Mukherjee, V. G. Sakai, A. Dash and M. Kumar, Langmuir, 2020, 36, 397–408 CrossRef PubMed.
- V. K. Sharma, D. G. Hayes, S. Gupta, V. S. Urban, H. M. O’Neill, S. V. Pingali, M. Ohl and E. Mamontov, J. Phys. Chem. C, 2019, 123, 11197–11206 CrossRef CAS.
- H. M. McConnell and R. D. Kornberg, Biochemistry, 1971, 10, 1111–1120 CrossRef CAS.
- L. Cristofolini, Curr. Opin. Colloid Interface Sci., 2014, 19, 228–241 CrossRef CAS.
- T. Kumarage, J. Nguyen and R. Ashkar, J. Visualized Exp., 2021, 171 DOI:10.3791/62396.
- J. U. De Mel, S. Gupta, S. Harmon, L. Stingaciu, E. W. Roth, M. Siebenbuerger, M. Bleuel and G. J. Schneider, Langmuir, 2021, 37, 9560–9570 CrossRef CAS PubMed.
- E. G. Kelley, M. Nagao, P. D. Butler, L. Porcar and B. Farago, Struct. Dyn., 2020, 7, 054704 CrossRef CAS PubMed.
- M. Nagao, E. G. Kelley, R. Ashkar, R. Bradbury and P. D. Butler, J. Phys. Chem. Lett., 2017, 8, 4679–4684 CrossRef CAS PubMed.
- J. Yu, J. Mao, M. Nagao, W. Bu, B. Lin, K. Hong, Z. Jiang, Y. Liu, S. Qian, M. Tirrell and W. Chen, Soft Matter, 2020, 16, 983–989 RSC.
- P. Kumari, A. Faraone, E. G. Kelley and A. Benedetto, J. Phys. Chem. B, 2021, 125, 7241–7250 CrossRef CAS PubMed.
- M. Nagao, E. G. Kelley, A. Faraone, M. Saito, Y. Yoda, M. Kurokuzu, S. Takata, M. Seto and P. D. Butler, Phys. Rev. Lett., 2021, 127, 078102 CrossRef CAS.
- V. K. Sharma, H. Srinivasan, V. García Sakai and S. Mitra, Struct. Dyn., 2020, 7, 051301 CrossRef CAS PubMed.
- V. K. Sharma and R. Mukhopadhyay, Biophys. Rev., 2018, 10, 721–734 CrossRef CAS.
- C. L. Armstrong, Diffusion and domains: Membrane structure and dynamics studied by neutron scattering, PhD Thesis, McMaster University, 2013 Search PubMed.
- J. S. Gardner, G. Ehlers, A. Faraone and V. G. Sakai, Nat. Rev. Phys., 2020, 2, 103–116 CrossRef.
- S. Mitra, V. K. Sharma, V. G. Sakai, A. Orecchini, T. Seydel, M. Johnson and R. Mukhopadhyay, J. Phys. Chem. B, 2016, 120, 3777–3784 CrossRef PubMed.
- V. K. Sharma, E. Mamontov, M. Tyagi and V. S. Urban, J. Phys. Chem. B, 2016, 120, 154–163 CrossRef PubMed.
- D. K. Rai, V. K. Sharma, D. Anunciado, H. O’Neill, E. Mamontov, V. Urban, W. T. Heller and S. Qian, Sci. Rep., 2016, 6, 30983 CrossRef.
- L. Ebersberger, T. Schindler, S. A. Kirsch, K. Pluhackova, A. Schambony, T. Seydel, R. A. Böckmann and T. Unruh, Front. Cell Dev. Biol., 2020, 8, 579388 CrossRef.
- C.-Z. Xie, S.-M. Chang, E. Mamontov, L. R. Stingaciu and Y.-F. Chen, Phys. Rev. E, 2020, 101, 012416 CrossRef CAS.
- M. Bee, Quasielastic neutron scattering, Adam Hilger, Bristol, 1988 Search PubMed.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O’Neill and V. Urban, J. Phys. Chem. B, 2015, 119, 4460–4470 CrossRef CAS.
- V. K. Sharma, E. Mamontov, D. B. Anunciado, H. O'Neill and V. Urban, Soft Matter, 2015, 11, 6755–6767 RSC.
- V. K. Sharma, J. Gupta and E. Mamontov, Soft Matter, 2023, 19, 57–68 RSC.
- V. K. Sharma, J. Gupta, J. B. Mitra, H. Srinivasan, V. G. Sakai, S. Ghosh and S. Mitra, J. Phys. Chem. Lett., 2024, 15, 7075–7083 CrossRef CAS.
- S. Busch, C. Smuda, L. C. Pardo and T. Unruh, J. Am. Chem. Soc., 2010, 132, 3232–3233 CrossRef CAS.
- P. S. Dubey, H. Srinivasan, V. K. Sharma, S. Mitra, V. G. Sakai and R. Mukhopadhyay, Sci. Rep., 2018, 8, 1862 CrossRef CAS PubMed.
- P. Singh, V. K. Sharma, S. Singha, V. G. Sakai, R. Mukhopadhyay, R. Das and S. K. Pal, Langmuir, 2019, 35, 4682–4692 CrossRef CAS PubMed.
- U. Wanderlingh, G. D'Angelo, C. Branca, V. C. Nibali, A. Trimarchi, S. Rifici, D. Finocchiaro, C. Crupi, J. Ollivier and H. D. Middendorf, J. Chem. Phys., 2014, 140, 174901 CrossRef CAS PubMed.
- V. K. Sharma and E. Mamontov, Prog. Lipid Res., 2022, 87, 101179 CrossRef CAS.
- V. K. Sharma, E. Mamontov, M. Ohl and M. Tyagi, Phys. Chem. Chem. Phys., 2017, 19, 2514–2524 RSC.
- V. K. Sharma, M. Nagao, D. K. Rai and E. Mamontov, Phys. Chem. Chem. Phys., 2019, 21, 20211–20218 RSC.
- A. Seth, D. Kaushik and S. K. Ghosh, Eur. Phys. J.: Spec. Top., 2024 DOI:10.1140/epjs/s11734-024-01189-0.
- J. F. Nagle and S. Tristram-Nagle, Biochim. Biophys. Acta, Rev. Biomembr., 2000, 1469, 159–195 CrossRef CAS PubMed.
- N. Kučerka, M.-P. Nieh and J. Katsaras, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 2761–2771 CrossRef.
- G. Lindblom and G. Orädd, Biochim. Biophys. Acta Biomembr., 2009, 1788, 234–244 CrossRef CAS.
- W. L. C. Vaz, F. G. Zalduondo and K. Jacobson, FEBS Lett., 1984, 174, 199–207 CrossRef CAS.
- J. J. H. H. M. d Pont and A. Watts, Progress in protein-lipid interactions, Elsevier, Amsterdam, 1985 Search PubMed.
- P. F. F. Almeida and W. L. C. Vaz, in Handbook of Biological Physics, ed. R. Lipowsky and E. Sackmann, North-Holland, 1995, vol. 1, pp. 305–357 Search PubMed.
- J.-F. Tocanne, L. D. Cézanne and A. Lopez, Prog. Lipid Res., 1994, 33, 203–237 CrossRef PubMed.
- M. J. Saxton, in Current Topics in Membranes, ed. D. W. Deamer, A. Kleinzeller and D. M. Fambrough, Academic Press, 1999, vol. 48, pp. 229–282 Search PubMed.
- J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, Elsevier, Amsterdam, 2006 Search PubMed.
- E. Flenner, J. Das, M. C. Rheinstädter and I. Kosztin, Phys. Rev. E, 2009, 79, 011907 Search PubMed.
- H. Srinivasan, V. K. Sharma, S. Mitra and R. Mukhopadhyay, J. Phys. Chem. C, 2018, 122, 20419–20430 Search PubMed.
- E. Falck, T. Róg, M. Karttunen and I. Vattulainen, J. Am. Chem. Soc., 2008, 130, 44–45 Search PubMed.
- C. L. Armstrong, M. Trapp, J. Peters, T. Seydel and M. C. Rheinstädter, Soft Matter, 2011, 7, 8358–8362 Search PubMed.
- S. Qian, G. Nagy, P. Zolnierczuk, E. Mamontov and R. Standaert, J. Phys. Chem. Lett., 2024, 15, 4745–4752 Search PubMed.
- P. G. Saffman and M. Delbrück, Proc. Natl. Acad. Sci. U. S. A., 1975, 72, 3111–3113 CrossRef.
- P. G. Saffman, J. Fluid Mech., 1976, 73, 593–602 CrossRef.
- W. L. Vaz, M. Criado, V. M. Madeira, G. Schoellmann and T. M. Jovin, Biochemistry, 1982, 21, 5608–5612 CrossRef.
- M. H. Cohen and D. Turnbull, J. Chem. Phys., 1959, 31, 1164–1169 CrossRef.
- W. L. Vaz, R. M. Clegg and D. Hallmann, Biochemistry, 1985, 24, 781–786 CrossRef CAS PubMed.
- H. J. Galla, W. Hartmann, U. Theilen and E. Sackmann, J. Membr. Biol., 1979, 48, 215–236 CrossRef CAS PubMed.
- P. B. Macedo and T. A. Litovitz, J. Chem. Phys., 1965, 42, 245–256 CrossRef CAS.
- B. J. Balcom and N. O. Petersen, Biophys. J., 1993, 65, 630–637 CrossRef PubMed.
- V. K. Sharma, J. Gupta, H. Srinivasan, H. Bhatt, V. García Sakai and S. Mitra, Langmuir, 2022, 38, 9649–9659 CrossRef PubMed.
- V. K. Sharma and E. Mamontov, J. Appl. Phys., 2022, 132, 074702 CrossRef.
- W. L. Vaz and P. F. Almeida, Biophys. J., 1991, 60, 1553–1554 CrossRef PubMed.
- M. C. Rheinstädter, J. Das, E. J. Flenner, B. Brüning, T. Seydel and I. Kosztin, Phys. Rev. Lett., 2008, 101, 248106 CrossRef PubMed.
- E. Falck, M. Patra, M. Karttunen, M. T. Hyvönen and I. Vattulainen, Biophys. J., 2004, 87, 1076–1091 CrossRef PubMed.
- C. L. Armstrong, L. Toppozini, H. Dies, A. Faraone, M. Nagao and M. C. Rheinstädter, ISRN Biophys., 2013, 2013, 439758 Search PubMed.
- S. König, W. Pfeiffer, T. Bayerl, D. Richter and E. Sackmann, J. Phys. II, 1992, 2, 1589–1615 CrossRef.
- T. Fujiwara, K. Ritchie, H. Murakoshi, K. Jacobson and A. Kusumi, J. Cell Biol., 2002, 157, 1071–1082 CrossRef CAS.
- C. L. Armstrong, M. D. Kaye, M. Zamponi, E. Mamontov, M. Tyagi, T. Jenkins and M. C. Rheinstädter, Soft Matter, 2010, 6, 5864–5867 RSC.
- W. Pfeiffer, H. Th, E. Sackmann, W. Knoll and D. Richter, Europhys. Lett., 1989, 8, 201 CrossRef CAS.
- M. A. Barrett, M. Trapp, W. Lohstroh, T. Seydel, J. Ollivier, M. Ballauff, N. A. Dencher and T. Hauß, Soft Matter, 2016, 12, 1444–1451 RSC.
- S. T. Nagle and J. F. Nagle, Chem. Phys. Lipids, 2004, 127, 3–14 CrossRef PubMed.
- V. K. Sharma and S. Qian, Langmuir, 2019, 35, 4152–4160 CrossRef CAS PubMed.
- S. König, T. M. Bayerl, G. Coddens, D. Richter and E. Sackmann, Biophys. J., 1995, 68, 1871–1880 CrossRef.
- M. Trapp, T. Gutberlet, F. Juranyi, T. Unruh, B. Demé, M. Tehei and J. Peters, J. Chem. Phys., 2010, 133, 164505 CrossRef.
- S. Malik and A. Debnath, J. Chem. Phys., 2021, 154, 174904 Search PubMed.
- A. Srivastava and A. Debnath, J. Chem. Phys., 2018, 148, 094901 CrossRef.
- S. Malik, S. Karmakar and A. Debnath, J. Chem. Phys., 2023, 158, 091103 CrossRef PubMed.
- S. Malik, S. Karmakar and A. Debnath, J. Chem. Phys., 2023, 158, 114503 CrossRef CAS PubMed.
- M. Trapp, J. Marion, M. Tehei, B. Demé, T. Gutberlet and J. Peters, Phys. Chem. Chem. Phys., 2013, 15, 20951–20956 RSC.
- J. Peters, J. Marion, F. J. Becher, M. Trapp, T. Gutberlet, D. J. Bicout and T. Heimburg, Sci. Rep., 2017, 7, 15339 CrossRef CAS.
- S. Busch, L. C. Pardo, C. Smuda and T. Unruh, Soft Matter, 2012, 8, 3576–3585 RSC.
- V. K. Sharma, E. Mamontov and M. Tyagi, Biochim. Biophys. Acta, Biomembr., 2020, 1862, 183100 CrossRef CAS PubMed.
- V. K. Sharma, E. Mamontov, M. Tyagi, S. Qian, D. K. Rai and V. S. Urban, J. Phys. Chem. Lett., 2016, 7, 2394–2401 CrossRef CAS.
- V. K. Sharma, S. Ghosh, P. Mandal, T. Yamada, K. Shibata, S. Mitra and R. Mukhopadhyay, Soft Matter, 2017, 13, 8969–8979 RSC.
- V. K. Sharma, S. K. Ghosh, V. García Sakai and R. Mukhopadhyay, Front. Chem., 2020, 8, 577508 CrossRef CAS.
- M. Doxastakis, V. G. Sakai, S. Ohtake, J. Maranas and J. J. D. Pablo, Biophys. J., 2007, 92, 147–161 CrossRef CAS.
- B. M. Aizenbud and N. D. Gershon, Biophys. J., 1982, 38, 287–293 CrossRef CAS.
- J. G. LoRicco, I. Hoffmann, A. Caliò and J. Peters, Soft Matter, 2023, 19, 6280–6286 RSC.
- A. Filippov, G. Orädd and G. Lindblom, Biophys. J., 2003, 84, 3079–3086 CrossRef CAS PubMed.
- J. D. Nickels, M. D. Smith, R. J. Alsop, S. Himbert, A. Yahya, D. Cordner, P. Zolnierczuk, C. B. Stanley, J. Katsaras, X. Cheng and M. C. Rheinstädter, J. Phys. Chem. B, 2019, 123, 2050–2056 CrossRef CAS PubMed.
- J. R. Abney, B. A. Scalettar and J. C. Owicki, Biophys. J., 1989, 55, 817–833 CrossRef CAS.
- T. Kumarage, N. B. Morris and R. Ashkar, Front. Phys., 2023, 11 DOI:10.3389/fphy.2023.1251146.
- A. Buchsteiner, T. Hauβ, S. Dante and N. A. Dencher, Biochim. Biophys. Acta, Biomembr., 2010, 1798, 1969–1976 CrossRef CAS.
- A. Buchsteiner, T. Hauß and N. A. Dencher, Soft Matter, 2012, 8, 424–429 RSC.
- M. Mahlapuu, J. Håkansson, L. Ringstad and C. Björn, Front. Cell. Infect. Microbiol., 2016, 6, 235805 Search PubMed.
- J. B. Mitra, V. K. Sharma, A. Dash, A. Mukherjee and M. Kumar, AIP Conf. Proc., 2020, 2265, 030026 CrossRef CAS.
- T. Moos and E. H. Morgan, Cell. Mol. Neurobiol., 2000, 20, 77–95 CrossRef.
- P. S. Dubey, V. K. Sharma, H. Srinivasan, S. Mitra, V. G. Sakai and R. Mukhopadhyay, J. Phys. Chem. B, 2018, 122, 9962–9972 CrossRef PubMed.
- S. Sahu, H. Srinivasan, S. E. Jadhav, V. K. Sharma and A. Debnath, Langmuir, 2023, 39, 16432–16443 CrossRef PubMed.
- V. K. Sharma, Hierarchical Dynamics in Biomembrane: Effects of Interaction with Membrane Active Molecules, Phys. News, 2022, 52, 23–30 Search PubMed.
- R. Saini and A. Debnath, J. Phys. Chem. B, 2023, 127, 9082–9094 CrossRef PubMed.
- R. Saini, S. J. Ansari and A. Debnath, Phys. Chem. Chem. Phys., 2023, 25, 11356–11367 RSC.
- V. K. Sharma, H. Srinivasan, V. G. Sakai and S. Mitra, J. Appl. Phys., 2020, 128, 154701 CrossRef CAS.
- L. Toppozini, C. L. Armstrong, M. A. Barrett, S. Zheng, L. Luo, H. Nanda, V. G. Sakai and M. C. Rheinstädter, Soft Matter, 2012, 8, 11839–11849 RSC.
- T. Róg, M. P. Gierula, I. Vattulainen and M. Karttunen, Biochim. Biophys. Acta, Biomembr., 2009, 1788, 97–121 CrossRef PubMed.
- S. Busch and T. Unruh, Biochim. Biophys. Acta, Biomembr., 2011, 1808, 199–208 CrossRef PubMed.
- P. F. Almeida, W. L. Vaz and T. E. Thompson, Biochemistry, 1992, 31, 6739–6747 CrossRef.
- K. Bakshi, S. Mitra, V. K. Sharma, M. S. K. Jayadev, V. Garcia Sakai, R. Mukhopadhyay, A. Gupta and S. K. Ghosh, Biochim. Biophys. Acta, Biomembr., 2020, 1862, 183103 CrossRef.
- J. Gupta, V. K. Sharma, H. Srinivasan, H. Bhatt, V. G. Sakai, R. Mukhopadhyay and S. Mitra, Langmuir, 2024, 40, 504–518 CrossRef.
- S. Mitra, V. K. Sharma, J. B. Mitra, S. Chowdhury, M. K. Mukhopadhyay, R. Mukhopadhyay and S. K. Ghosh, Biochim. Biophys. Acta, Biomembr., 2021, 1863, 183589 Search PubMed.
- R. Gupta, V. K. Sharma, J. Gupta and S. K. Ghosh, Langmuir, 2022, 38, 3412–3421 CrossRef PubMed.
- P. Hitaishi, M. Raval, A. Seth, S. Kumar, V. S. Mithu, V. K. Sharma and S. K. Ghosh, Langmuir, 2023, 39, 9396 CrossRef PubMed.
- N. Kaur, M. Fischer, P. Hitaishi, S. Kumar, V. K. Sharma, S. K. Ghosh, G. K. Gahlay, H. A. Scheidt and V. S. Mithu, Langmuir, 2022, 38, 13803 CrossRef CAS.
- J. Gupta, V. K. Sharma, H. Srinivasan, H. Bhatt, S. Kumar, M. Sarter, V. G. Sakai and S. Mitra, Phys. Rev. Mater., 2022, 6, 075602 CrossRef CAS.
- G. M. Paternò, G. Bondelli, V. G. Sakai, V. Sesti, C. Bertarelli and G. Lanzani, Langmuir, 2020, 36, 11517–11527 CrossRef.
| This journal is © The Royal Society of Chemistry 2024 |