DOI:
10.1039/D4SM00717D
(Paper)
Soft Matter, 2024,
20, 9562-9571
Active droplet driven by collective chemotaxis
Received
12th June 2024
, Accepted 12th November 2024
First published on 14th November 2024
Abstract
Surfactant-laden fluid interfaces of soft colloids, such as bubbles and droplets, are ubiquitously seen in various natural phenomena and industrial settings. In canonical systems where microparticles are driven in hydrodynamic flows, convection of the surfactant changes local surface tension. Subsequently, the interplay of Marangoni and hydrodynamic stresses leads to rich interfacial dynamics that directly impact the particle motions. Here we introduce a new mechanism for self-propelled droplets, driven by a thin layer of chemically active microparticles situated at the interface of a suspended droplet, which is a direct extension of the planar collective surfing model by Masoud and Shelley (H. Masoud and M. J. Shelley, Phys. Rev. Lett., 2014, 112, 128304). These particles can generate chemicals locally, leading to spontaneous Marangoni flows that drive the self-aggregation of microparticles. This process, in turn, creates a polarized surfactant distribution, which induces collective chemotaxis and dipolar bulk flows, ultimately breaking the symmetry. By assuming the local surfactant production to be either proportional to particle density or saturated at a high particle density, we observe that the system can be chemotactically diverging or approach a steady state with constant migration velocity. The system is studied analytically in the linear region for the initial transient dynamics, yielding critical numbers and familiar patterns, as well as numerically for larger amplitudes and over a long time using spectral methods.
1. Introduction
Active fluids define a novel class of non-equilibrium materials composed of self-driven microparticles that consume local fuels to perform mechanical work.1,2 The many-body interactions between suspended microparticles lead to spontaneous collective dynamics whose sizes are much larger than individual microparticles. The unstable dynamics of active fluids encompass a range of phenomena, including pattern formation, instability cascades, density fluctuations, ordering transitions, and anomalous diffusion. When properly manipulated, the non-equilibrium physical properties of active fluids can be used to design novel applications of microfluidic transport and mixing.3–6
Active fluids are varied. Of particular interest here is a class of active interfacial flows where a thin layer of active constituents reside on liquid–liquid or liquid–air interfaces.7,8 The hydrodynamic coupling between the interfacial movements of active microparticles and the resting bulk fluid9–11 effectively produces unstable dynamics that exhibit spatiotemporal features with unique characteristic length and time scales, and can drastically differ from those measured in coherent bulk flows.12 As demonstrated by Masoud and Shelley,13 reciprocal coupling with a chemical concentration field can be achieved by introducing chemically active particles that produce or consume chemical species to alter the local concentration field, which effectively generates Marangoni stresses that drive the flows. The resultant collective aggregation accompanies intriguing critical behaviors of chemotactic collapse predicted by the canonical Keller–Segel model. It is seen that the particle distributions shrink to singular point density “sinks” from which the induced interfacial flows are drained into the bulk.
Given the prevalence of particle-laden fluid interfaces in various natural phenomena and industrial settings, exploring non-equilibrium interfacial dynamics as such may potentially suggest novel mechanisms for manipulating soft colloidal systems, especially for droplets and emulsions. For canonical (passive) systems of surfactant laden droplets, Marangoni flow spontaneously occurs as the surfactant redistributes to change surface tension, which could be either driven by external forces (e.g., gravity14,15) and imposed flows (e.g., shear16,17) or caused by hydrodynamically coupling with another field (e.g., thermocapillarity18,19). More interestingly, in recent times there have been considerable efforts in studying self-propelling droplets that generally exploit the chemo-hydrodynamic coupling for symmetry breaking via Marangoni flows. These active systems take full advantage of the droplet's fluidic nature to carry and encapsulate various kinds of chemical species, which hence facilitate controllable chemical reactions, either on the surface20 or in the bulk,21 to alter surfactant distribution directly, as well as utilizing micellar dissolution to change surface tension.22
In this work, we adopt Masoud and Shelley's model13 on spherical geometries to reveal the mechanism of spontaneous generation of Marangoni flows that may break symmetry and induce droplet migration. Unlike the canonical systems where surfactants are driven out of equilibrium, we consider scenarios of chemically active microparticles that reside on the droplet surface and continuously secrete chemical species, such as bacteria-laden droplets.23–25 Their chemical secretions act as a source of biosurfactants, which in turn lead to collective chemotaxis, altering the surface tension.26 Once these chemical substances are set free, they become affixed to the interface between liquids, facilitating their transport into the bulk volume. Our model exhibits parallels with the active colloid model of De Corato et al.,27 where a spherical, rigid particle with surface-bound enzymes continuously produces surfactants, resulting in steady self-propulsion. In that model, surface advection-diffusion of mobile enzymes leads to spontaneous polarization from a uniform state, inducing Marangoni flows that break symmetry. Notably, the instability in their system is governed entirely by enzyme transport and diffusion at the surface, without being coupling to bulk flow. In contrast, while our model similarly displays axisymmetric polarization of microparticles and the generation of interfacial Marangoni flows, the symmetry-breaking instability arises from the development of swirling bulk flows within the droplet, driven by the surface aggregation of microparticles.
As discussed below, we first examine the Keller–Segel system's diverging chemotactic process where singular solutions form on the surface. Next, we employ a phenomenological chemo-mechanical model to enable localized surfactant saturation, thereby preventing the occurrence of density singularities effectively. This model represents one of the most straightforward approaches for investigating bacteria quorum sensing, which is a signaling mechanism that controls high density during bacterial aggregation.28,29 We have conducted both asymptotic analysis and nonlinear simulation to uncover the underlying rich dynamics. In the linear regime of initial transient, we consider the limit of pure diffusion for the chemical species by neglecting advection. We solve for the analytical solutions of the coupled system using Lamb's fundamental solutions in spherical geometries.30 The late time dynamics are resolved in direct simulations of the full equations using the open-source spectral codes of the Dedalus project.31 Overall, we demonstrate that adjusting local surfactant consumption or depletion regulates the collective interfacial dynamics, which effectively drives swirling flows in the bulk to break symmetry, resulting in entire-body movements. The prevailing pattern within the droplet resembles the classical Hadamard–Rybczynski solution of a moving spherical bubble.32,33 Furthermore, we illustrate that introducing a saturation mechanism for local surfactant production not only prevents divergence but also facilitates steady droplet migration.
The paper is organized as follows. Section 2 presents a model of a droplet immersed in another Newtonian fluid. We introduce the governing equations of the interfacial dynamics of microparticles, which hydrodynamically couple with the Stokes flow and chemical transport inside and outside of the droplet. Section 3 seeks analytical solutions in the linear regime to obtain critical conditions for collective chemotaxis to occur and illustrates how internal flow generation breaks symmetry to drive the whole-body migration. In particular, we examine axisymmetric modes in the diffusion-dominant limit where the chemical Péclet numbers tend to zero. Diverging behavior is seen when the local interfacial chemical production rate is proportional to the local particle density. A comparison is made with the planar geometry in the limit of a large mode number. Section 4 demonstrates that introducing a local surfactant-saturation mechanism effectively prevents chemotactic collapsing and leads to steady-state bulk flow generation and stable droplet migration. Finally, we summarize and draw conclusions in Section 5.
2. Mathematical model
Our mathematical model builds upon and expands the previous investigation of the collective dynamics of immobile, chemically active microparticles on a flat surface,13 extending it to the context of a spherical liquid–liquid interface of a droplet. Consider a spherical droplet of radius R immersed in another fluid, where chemically active particles on the droplet surface (e.g., liquid–liquid interface) continuously produce surfactant. The spherical coordinates are represented by the orthonormal unit vectors (êϕ, êθ, êr). The surface number density of microparticles, ψ(ϕ, θ, t) (0 ≤ ϕ < 2π, 0 ≤ θ ≤ π), is governed by| | 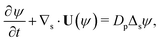 | (1) |
where Dp is the diffusion coefficient and U(ϕ, θ) = (u, v) = uêϕ + vêθ represents the induced Marangoni flow field on the spherical surface. Here we use the subscript “s” to denote the spatial gradient on the surface of a sphere. The particles excrete chemical species whose bulk concentration fields are denoted by Ci/o(ϕ, θ, r, t), where the subscript “i” and “o” denote the solution for the interior of the drop and for the fluid outside, respectively. They satisfy the governing equations| | 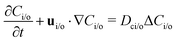 | (2) |
where ui/o(ϕ, θ, r) = (ui/o, vi/o, wi/o) = ui/oêϕ + vi/oêθ + wi/oêr is the 3D fluid velocity field and Dci/o is the diffusion coefficient in the bulk. The chemical field is continuously defined across the domain. On the liquid–liquid interface, the interior and exterior bulk chemicals are directly coupled via| | 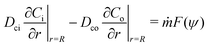 | (3) |
where C represents the surfactant distribution on the interface. Function F(ψ) describes the details of the local surfactant production below| | 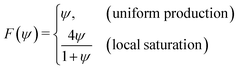 | (5) |
with coefficient ṁ > 0 characterizing the surfactant production per active particle. Here we consider two scenarios. In the first uniform production (UP) model, we choose a linear function F to continuously introduce chemicals at a uniform rate that can cause divergence, similar to the results for the planar Keller–Segel system.13 Alternatively, we allow the chemical flux to saturate locally as the particle density increases following the Michaelis–Menten way (i.e., one of the simplest enzyme kinetic models), which has been used to model quorum sensing regulatory systems such as bacteria aggregation.34–36 Hereinafter, we will term it the local saturation (LS) model. Our results demonstrate that the second model can effectively regulate singularities in the density field.
The corresponding bulk fluid velocity fields inside and outside the droplet satisfy the incompressible Stokes equation:
| | | −∇pi/o + μi/oΔui/o = 0, and ∇·ui/o = 0. | (6) |
where
pi/o is the pressure field and
μi/o is the fluid viscosity. On the surface, we enforce the continuity condition in the tangential direction,
i.e.,
| | | (ui, vi)|r=R = (uo, vo)|r=R = U. | (7) |
Since the spherical shape is fixed and no fluid penetrates the interface, we require the third component (i.e., in the radial direction) to be
The surface tension γ is assumed to be an affine function of the chemical concentration at the surface, γ(ϕ, θ, t) = γ0 + αC|r=R, where γ0 and α are constants. Then the jump condition of the traction force in the tangential direction becomes
| | 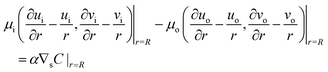 | (9) |
The traction jump condition in the radial (normal) direction is not taken into account since it can be decoupled from the Marangoni-flow-driven system dynamics for a fixed spherical shape. For non-dimensionalization, we rescale particle density, length, chemical concentration, and time, with averaged particle number density
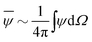
, droplet radius
R, reference concentration
Cref ∼
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) R
R/
Dc, and advection time scale
τ ∼
μDc/(
αṁ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif)
), respectively. Hence, the dimensionless equations read
| | 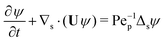 | (10) |
| | 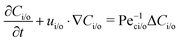 | (11) |
| | | −∇pi/o + Δui/o = 0, ∇·ui/o = 0. | (12) |
where the Péclet numbers are given by Pe
p =
τp/
τ and Pe
ci/o =
τci/o/
τ, with
τp =
R2/
Dp and
τci/o =
R2/
Dci/o being the particles' diffusion time scale and chemical species, respectively. The above governing equations are subjected to the interfacial conditions
| | 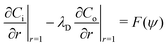 | (13) |
| | 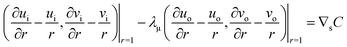 | (15) |
| | | (ui, vi)|r=1 = (uo, vo)|r=1 = U, wi|r=1 = wo|r=1 = 0, | (16) |
where
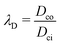
and
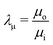
, respectively, represent the ratio of diffusivity and viscosity. Overall, the evolution of the interfacial density of microparticles is governed by an advection-diffusion equation with the induced Marangoni flow being the source of energy, driving fluid fields both inside and outside of the droplet.
To handle the migration of the droplet, we choose the co-moving coordinate with the motile droplet. Then the corresponding far-field conditions in the external flow field read
where
V represents the unknown droplet migration velocity to be solved together with the other variables. The initial condition for the concentration field is
| | | Ci/o(ϕ, θ, r, t = 0) = 0. | (19) |
Besides the linear analysis discussed below, we use the Dedalus project,31 an open-source spectral code, to perform nonlinear simulation for the above coupled equation system. We choose quadrature points with the spatial resolution Nϕ × Nθ × Nr = 128 × 64 × 64 (along with dealiasing) and the time-marching step Δt ≤ 1/400. A third-order Runge–Kutta scheme is used for the time stepping.
3. Linear analysis in the limit of small chemical Péclet numbers
3.1. Axisymmetric modes
To begin, we follow the classical stability analysis of chemically active droplets22,37,38 to seek axisymmetric solutions. The particle density can be constructed using the classical Lamb solution in Stokes flows30 as| | 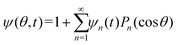 | (20) |
where Pn are Legendre polynomials and ψn(t) are the corresponding coefficients. Note that 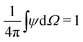 , as required. The modal solutions for the chemical concentration field become
, as required. The modal solutions for the chemical concentration field become| | 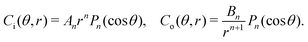 | (21) |
The continuity condition in eqn (14) immediately yields Bn = An. Using the UP model (i.e., F = ψ), eqn (13) requires
| | | (n + λD(n + 1))An = ψn. | (22) |
To solve for the velocity field, we choose the stream function as
| | 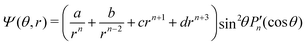 | (23) |
where “,” is the derivative on cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ. The polar (
i.e.,
v) and radial (
i.e.,
w) velocity components can be calculated as
| | 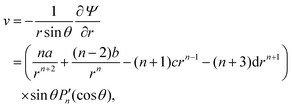 | (24) |
| | 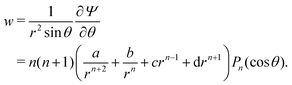 | (25) |
Setting a = b = 0 is automatically determined for solutions inside the sphere (r < 1). Then applying the no-penetration condition (16) for the w component yields d = −c and the expression for the polar angular component becomes
| | 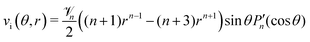 | (26) |
with coefficient
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) n
n. For the flow outside of the droplet (
r > 1), obviously
d = 0 can be chosen, as well as
c = 0 for
n > 1. The polar velocity component becomes
| | 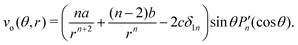 | (27) |
From continuity at the interface, eqn (16), we have
| | 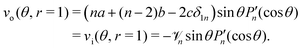 | (28) |
The far-field condition in (18) reads
| | vo(θ, r → ∞) = −2c![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −V θ = −V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ, θ, | (29) |
leading to 2
c =
V. Also, since
wo|
r=1 = 0, we need
a +
b +
cδ1n = 0. Putting it together,
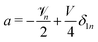
and
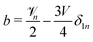
. The polar component of
eqn (15) requires
| | 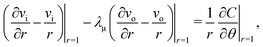 | (30) |
leading to
| | 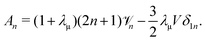 | (31) |
When linearizing
eqn (10), combining
eqn (31) and (22), it is straightforward to obtain
| | 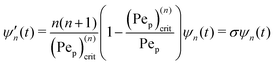 | (32) |
where
| | 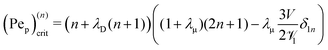 | (33) |
is the critical Péclet number for the
nth-order mode – when Pe
p goes beyond (Pe
p)
(n)crit, the growth rate
σ becomes positive, and hence suggests the
nth mode becomes unstable. To close the system, the Lorentz reciprocal theorem
39,40 gives
| | 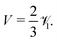 | (34) |
Thus, the critical Péclet numbers for the surface particles finally become
| | | (Pep)(n)crit = (n + λD(n + 1))((1 + λμ)(2n + 1) − λμδ1n). | (35) |
A few examples are given in
Fig. 1. Note that a smaller critical Péclet number, for a given mode
n, not only leads to a lower stability threshold, but also indicates a faster growth. Using
eqn (22) and (31) for
n = 1, together with
(34), the droplet migration speed can be derived as
| | 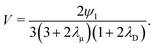 | (36) |
Also, in accordance with linear theory, higher-order modes (with
n > 1), whether symmetric or asymmetric, do not contribute to the droplet's motion. To examine the above result, we perform direct simulation using Dedalus to solve the full governing equation set presented in Section 2. In
Fig. 2, we choose the initial condition
ψ(
θ) = 1 + 0.001
P1(cos
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ
θ) with Pe
p = 50, Pe
c = 0, and
λμ = 1. Excellent agreements are seen between full simulation and
eqn (36). In
Fig. 3, we plot the resultant chemical and flow fields for the first two modes. The first mode
ψ1 induces a donut-shaped vortex ring inside and a source-dipole-like flow field outside of the liquid–liquid interface, which hence effectively breaks symmetry to drive the entire-body migration. The mode exhibits a polar structure with a concentrated region or “hotspot” at the north pole, where micropaticles, for a sufficiently large value of Pe
p, eventually aggregate to form a singularity, and a depletion zone at the south pole. The streamlines of the bulk flow show how the resulting Marangoni force induces the two counter-rotating vortices reminiscent of the classical Hadamard–Rybczynski solution, in which surfactants are driven out of equilibrium by gravity.
32,33 In comparison, the second mode
ψ2 produces symmetric chemical distribution and flow structure, which doesn't produce any net motion. More generally, the
nth surface mode induces
n vortex rings stacked inside the droplet. As the instability grows, the particle density becomes more and more singular and eventually diverges.
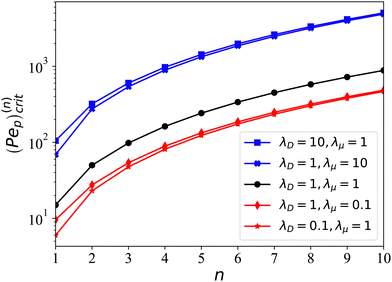 |
| | Fig. 1 Critical Péclet numbers as a function of λD and λμ predicted by eqn (35). | |
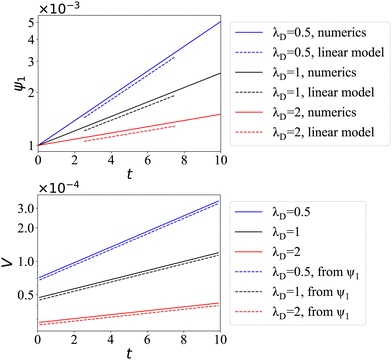 |
| | Fig. 2 Linear growth of particle density fluctuation (top) and migration speed (bottom). (Top) Comparisons are made between numerical simulations when fixing λμ = 1, with Pep = 50 and initial condition ψ(θ) = 1 + 0.001P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), and the slope from the linear theory (given in eqn (32)). (Bottom) Comparisons for the droplet speed V obtained from full simulation and the linear theory in eqn (36). θ), and the slope from the linear theory (given in eqn (32)). (Bottom) Comparisons for the droplet speed V obtained from full simulation and the linear theory in eqn (36). | |
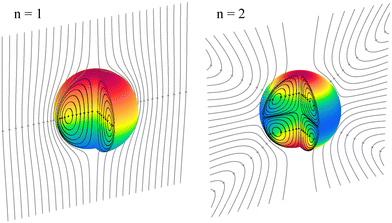 |
| | Fig. 3 Chemical concentration field inside the spherical drop (colors), as well as streamlines for the flow inside (black) and outside (gray), for the first two modes n = 1, 2. | |
In Fig. 4, we perform a long time simulation in the nonlinear regime to reveal the system's diverging behaviors during chemotactic collapsing, via sequential snapshots of surface density distribution and flow patterns. In the top panel, it is evident that the particle density keeps increasing near the north pole, with the maximum value ψmax(t) occurring at θ = 0. From the corresponding time-sequential snapshots shown in the bottom panel, we observe the resultant flow pattern gradually losing fore-aft symmetry, with the vortex center moving closer to the north pole. We highlight that, without using an interfacial advection-diffusion-reaction equation to define surfactant transport, the polar concentration distribution arises solely from the hydrodynamic interaction with the chemical field. As the induced fluid flow intensifies, the passive microparticles are carried by the interfacial flow, acting as a moving surfactant source. Nevertheless, without any regulation mechanism, these microparticles continue to migrate toward the north pole, resulting in the observed diverging behavior.
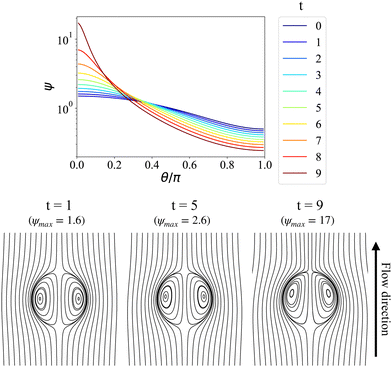 |
| | Fig. 4 Evolution of particle density distribution (top) and flow patterns (bottom) during the chemotactic collapsing, starting from the initial condition ψ(θ, t = 0) = 1 + 0.5P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) (ψmax = 1.5), showing divergent behavior. Pep = 200, λD = λμ = 1. θ) (ψmax = 1.5), showing divergent behavior. Pep = 200, λD = λμ = 1. | |
3.2. Comparison with planar geometry for large n
In this section a comparison is made to the linearized planar case, where a flat 2D interface (at z = 0) separates two fluids occupying the regions −∞ < z < 0 and 0 < z < ∞, respectively. Since the problem doesn't involve a natural length scale, a square region L × L is considered, where the fields are forced to be L-periodic in both directions. The governing equations are nondimensionalized using L instead of R. Its connection to the spherical case is illustrated in Fig. 5. The bulk equations have the same form, with Peclet numbers Pecl/u, where the subscripts “l” and “u” denote the lower (z < 0) and upper solutions (z > 0), respectively. For the UP case, the dimensionless boundary conditions at the interface become| | 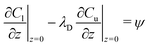 | (37) |
| | 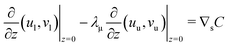 | (39) |
| | | ul|z=0 = uu|z=0 = U, wl|z=0 = wu|z=0= 0, | (40) |
where 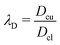 and
and 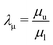 , and the far-field behaviorBy applying analogous linear analysis techniques used for phoretic flows on planar surfaces,13,41,42 and taking the limit as Pecl/u → 0, we employ the 2D Fourier transform
, and the far-field behaviorBy applying analogous linear analysis techniques used for phoretic flows on planar surfaces,13,41,42 and taking the limit as Pecl/u → 0, we employ the 2D Fourier transform| | 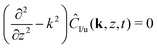 | (45) |
where k = (kx, ky) and k = |k|. The solutions, for k ≠ 0, are| | | Ĉl(k, z, t) = a(k,t)ekz | (46) |
| | | Ĉu(k, z, t) = b(k, t)e−kz | (47) |
where the boundary conditions (37) and (38) require| | 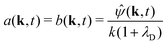 | (48) |
Similarly, solving for the velocity field leads to| | 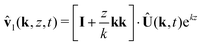 | (49) |
| | | ŵl(k, z, t) = −izk·Û(k, t)ekz | (50) |
| | 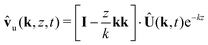 | (51) |
| | | ŵu(k, z, t) = −izk·Û(k, t)e−kz | (52) |
and the Marangoni stress (39) gives| | 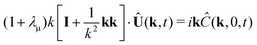 | (53) |
Finally, the Fourier transformed velocity field at the surface becomes| | 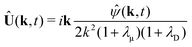 | (54) |
Consider a small disturbance ψ = 1 + εg(x, t), with ε ≪ 1, from eqn (10) giving| | 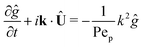 | (55) |
to first order in ε, and therefore| | 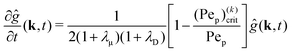 | (56) |
where| | | (Pep)(k)crit = 2(1 + λμ)(1 + λD)k2. | (57) |
For periodicity, we require k = (2πn1, 2πn2) where ni = 0, 1, 2,…, i = 1, 2. To compare with the spherical axisymmetric case, consider fluctuations in only one direction, e.g. n2 = 0. See Fig. 5. For n ≫ 1, eqn (32) becomes| | 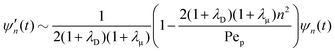 | (58) |
Note that Pep is defined differently in the spherical and planar cases. Set θ = θ0 + θd, for a given 0 < θ0 < π, where θd is sufficiently small. The asymptotic form, n ≫ 1, of the Lagrange polynomials43 is| | 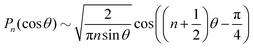 | (59) |
which becomes| | 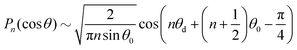 | (60) |
with zeros in steps Δθd = π/n. For the planar case, restoring the length scale L,| | 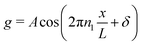 | (61) |
Let L = πR/N, with N ≫ 1, giving| | 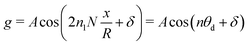 | (62) |
where n = 2n1N and θd = x/R. We thus have| | 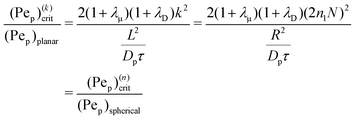 | (63) |
and the growth/decay rates are the same.
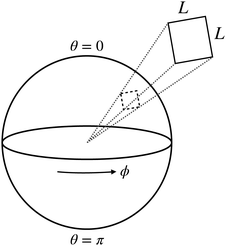 |
| | Fig. 5 Illustration of the planar geometry and its connection to the spherical domain. | |
4. Steady droplet migration due to local surfactant saturation
To motivate the design of robust active droplets driven by Marangoni flows, it is desirable to inhibit the collective chemotactic collapsing behaviors. In this section, we demonstrate that the system dynamics can be stabilized using the LS model. Note that in the linear regime, the LS model predicts the same critical Péclet numbers as the UP model in eqn (35). When going beyond the linear regime, the local value of F may further increase but will eventually saturate to 1. To investigate the full nonlinear dynamics of quorum-sensing driven droplet migration, we choose to initialize ψ using spherical harmonics Ymn according to| | 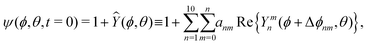 | (64) |
with the values of anm being sampled uniformly on the interval [0, a], where a is chosen so that max(|Ŷ|) = 0.5, and Δϕnm likewise being sampled from [0, 2π]. Note that, since spherical harmonics with n > 0 are used, the restriction ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 1 still holds. As demonstrated in Fig. 6, even though we may choose arbitrary initial fields, they all end up, after a transient period, showing the same axisymmetric dipole-type profile at the steady state.
= 1 still holds. As demonstrated in Fig. 6, even though we may choose arbitrary initial fields, they all end up, after a transient period, showing the same axisymmetric dipole-type profile at the steady state.
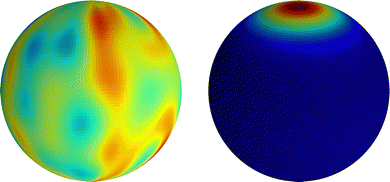 |
| | Fig. 6 Nonlinear simulation of steady droplet migration due to the local surfactant saturation when a quorum-sensing model is used. (Left) Initial microparticle distribution created from a random sampling using eqn (64). (Right) Equilibrium particle distribution during steady droplet migration at a late time (t = 200). | |
In Fig. 6(a), it is seen that unlike the diverging behaviors predicted by the UP model, now the particle density characterized by ψmax gradually saturates at later times when using the LS model, leading to a stable polarized structure and steady migration speed. In contrast, the gray dash-dot line representing the UP model continues to show diverging behavior without reaching a steady state. The shape at saturation of the axisymmetric profile ψ(θ), as well as the peak value ψmax, depends on the value of Pep. Profiles are shown in panel (c). In panel (b), the droplet speed first exhibits an overshoot during the initial transient and then decays to steady-state values as ψ saturates. Also, we see that faster migration occurs when Pep is closer to the critical value (in this case, (Pep)(1)crit = 15). Note that here the migration speed is the magnitude of the projected velocity along the steady droplet migration direction which appears to be random.
Streamlines for the cases Pep = 50 and 250 at late times are shown in Fig. 8. In contrast to the UP case, the stable surfactant surface polarization leads to steady flow patterns. The resultant velocity fields are seen to be stronger further towards the top (θ = 0), where the larger particle densities need to be sustained against the diffusive transport. In order to shed some light on the transient behavior of the droplet speeds in Fig. 7(b), in particular regarding the peaks before saturation, time series of the velocity profiles for the axisymmetric initial condition are displayed at the bottom in Fig. 8. The polar velocity on the surface, i.e., the Marangoni flows, at saturation not only is weaker for the Pep = 250 case, but also deviates more from a sinusoidal shape, suggesting the interactions of higher-order modes. To elucidate the role of the relative properties of the inner and outer fluids, simulations, all using Pep = 50, were carried out for a few different values of λD and λμ. Some typical results for steady migration are collected in Table 1, which reflects the similar trends predicted in the linear regime by eqn (36). Generally speaking, we observe that the droplet speed increases when the diffusion coefficient and viscosity are larger inside the drop. We also see that the speed is more sensitive to the varying values of λD than to λμ. Moreover, as shown in panel (a) and (b), the initial transient time is largely affected by the initial condition – initial randomly-selected modes apparently lead to longer transition times before the system saturates at steady states. In contrast, the particle distribution and migration speed all approach the same steady-state values at late times and hence are independent of the initial conditions.
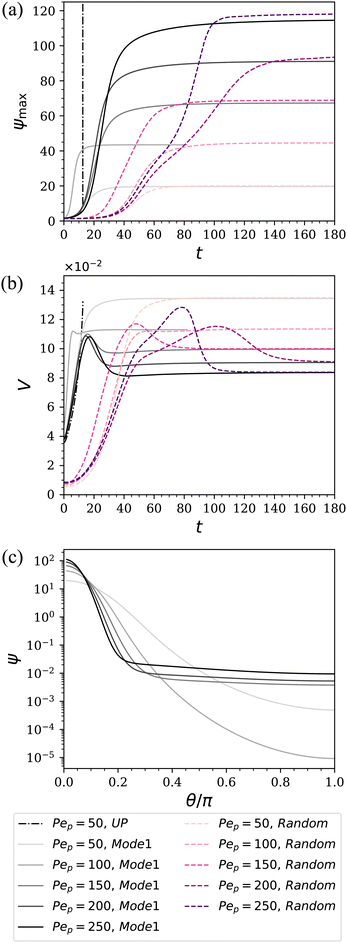 |
| | Fig. 7 Evolution of the particle density field (a) and droplet migration speed (b), along with the axisymmetric profiles of ψ at saturation (c). Here we set λD = λμ = 1, giving critical Péclet number (Pep)(1)crit = 15 from the axisymmetric linear theory. The initial conditions are either ψ = 1 + 0.5P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) or randomized according to eqn (64). θ) or randomized according to eqn (64). | |
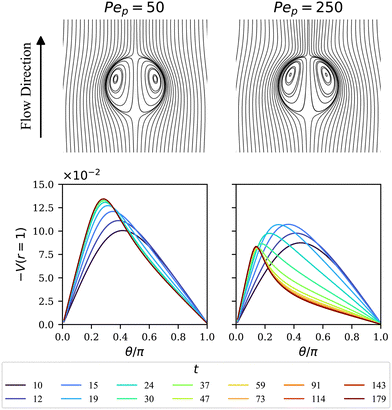 |
| | Fig. 8 (Top) Streamlines for the steady-state velocity fields at a late time (t = 200) when choosing Pep = 50 and 250. (Bottom) Corresponding time evolution of the Marangoni flow (the polar velocity component) at the interface. The initial condition for ψ is chosen as ψ(θ, t = 0) = 1 + 0.5P1(cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ). θ). | |
Table 1 Steady-state values of ψmax and V for different λD and λμ, where Pep= 50
|
λ
D
|
λ
μ
|
ψ
max
|
V
|
| 0.5 |
1 |
20 |
0.134 |
| 1 |
0.5 |
27 |
0.164 |
| 1 |
1 |
20 |
0.134 |
| 1 |
2 |
12 |
0.099 |
| 2 |
1 |
20 |
0.134 |
5. Conclusions
In this work, we present a theoretical model for a prototype of an active droplet powered by assemblies of chemically active microparticles moving on the droplet surface while continuously producing chemical surfactants. Physically, the local surfactant production effectively builds surface tension gradients to spontaneously drive Marangoni flows to redistribute the microparticles. In the meantime, the resultant non-equilibrium interfacial dynamics due to collective chemotaxis induce intriguing fluid flows in the bulk, together with concentration variations of surfactant. Here we present two phenomenological models that describe the chemotactic responses (i.e., the UP and LS model) where we assume the local surfactant production either is proportional to particle density or saturates during particle aggregation. Combining analytical analysis and nonlinear simulations, we investigate the diverging nature of the UP model and illustrate the Hadamard–Rybczynski-like swirling bulk flows due to a polar surface chemical distribution, propelling the droplet in a liquid. Similar flow structures are also seen inside another class of self-propelling droplets that directly encapsulate active suspensions using soft boundaries such as surface tension or elastic membranes.44,45 Furthermore, we show that allowing the local surfactant to saturate using the LS model can effectively prevent system divergence and permit steady-state chemical distributions and migration speeds, which hence can be used to inspire real-world active droplet design. It is straightforward to extend this study to other scenarios, including imposing various types of background flows, droplet–droplet interactions, and additional multiphysics coupling with external fields. We anticipate this model will provide a new angle in studying non-equilibrium interfacial dynamics and will inspire new active droplet designs in experiments.
Data availability
We have presented all the data in the main text. There are no additional supporting data.
Conflicts of interest
There are no conflicts to declare.
Acknowledgements
This work is partially supported by the National Science Foundation grant No. 1943759 and the MSU's Strategic Partnership Grant.
Notes and references
- S. Ramaswamy, Annu. Rev. Condens. Matter Phys., 2010, 1, 323–345 CrossRef.
- M. Marchetti, J. Joanny, S. Ramaswamy, T. Liverpool, J. Prost, M. Rao and R. Simha, Rev. Mod. Phys., 2013, 85, 1143–1189 CrossRef CAS.
- A. Kaiser, A. Peshkov, A. Sokolov, B. ten Hagen, H. Löwen and I. Aranson, Phys. Rev. Lett., 2014, 112, 158101 CrossRef.
- H. Wioland, E. Lushi and R. Goldstein, New J. Phys., 2016, 18, 075002 CrossRef.
- K. Wu, J. Hishamunda, D. Chen, S. DeCamp, Y. Chang, A. Fernández-Nieves, S. Fraden and Z. Dogic, Science, 2017, 355(6331), 1284 CrossRef CAS.
- M. Davies Wykes, X. Zhong, J. Tong, T. Adachi, Y. Liu, L. Ristroph, M. Ward, M. Shelley and J. Zhang, Soft Matter, 2017, 13, 4681–4688 RSC.
- T. Sanchez, D. Chen, S. DeCamp, M. Heymann and Z. Dogic, Nature, 2012, 491, 431–434 CrossRef CAS.
- F. Keber, E. Loiseau, T. Sanchez, S. DeCamp, L. Giomi, M. Bowick, M. Marchetti, Z. Dogic and A. Bausch, Science, 2014, 345, 1135–1139 CrossRef CAS.
- T. Gao, R. Blackwell, M. Glaser, M. Betterton and M. Shelley, Phys. Rev. Lett., 2015, 114, 048101 CrossRef PubMed.
- N. Oppenheimer, D. B. Stein and M. J. Shelley, Phys. Rev. Lett., 2019, 123, 148101 CrossRef CAS PubMed.
- R. Samanta and N. Oppenheimer, Phys. Fluids, 2021, 33, 051906 CrossRef CAS.
- J. Dunkel, S. Heidenreich, K. Drescher, H. Wensink, M. Bär and R. Goldstein, Phys. Rev. Lett., 2013, 110, 228102 CrossRef.
- H. Masoud and M. J. Shelley, Phys. Rev. Lett., 2014, 112(12), 128304 CrossRef PubMed.
- L. S. Chang and J. C. Berg, AIChE J., 1985, 31, 551–557 CrossRef CAS.
- Å. Ervik and E. Bjørklund, Eur. J. Mech. B: Fluids, 2017, 66, 10–19 CrossRef.
- J. A. Hanna and P. M. Vlahovska, Phys. Fluids, 2010, 22, 013102 CrossRef.
- H. Liu, J. Zhang, Y. Ba, N. Wang and L. Wu, J. Fluid Mech., 2020, 897, A33 CrossRef CAS.
- M. L. Ford and A. Nadim, Phys. Fluids, 1994, 6, 3183–3185 CrossRef.
- B. Dai, J. Wang, Z. Xiong, X. Zhan, W. Dai, C.-C. Li, S.-P. Feng and J. Tang, Nat. Nanotechnol., 2016, 11, 1087–1092 CrossRef CAS.
- N. J. Suematsu, K. Saikusa, T. Nagata and S. Izumi, Langmuir, 2019, 35, 11601–11607 CrossRef CAS PubMed.
- S. Herminghaus, C. C. Maass, C. Krüger, S. Thutupalli, L. Goehring and C. Bahr, Soft Matter, 2014, 10, 7008–7022 RSC.
- S. Michelin, Annu. Rev. Fluid Mech., 2023, 55, 77–101 CrossRef.
- M. Grinberg, T. Orevi, S. Steinberg and N. Kashtan, eLife, 2019, 8, e48508 CrossRef CAS PubMed.
- N. K. Dewangan and J. C. Conrad, Soft Matter, 2019, 15, 9368–9375 RSC.
- S. Shyam, S. Misra, S. Mitra and S. K. Mitra, Soft Matter, 2024, 20, 3425–3435 RSC.
- T. E. Angelini, M. Roper, R. Kolter, D. A. Weitz and M. P. Brenner, Proc. Natl. Acad. Sci. U. S. A., 2009, 106, 18109–18113 CrossRef CAS PubMed.
- M. De Corato, I. Pagonabarraga, L. K. E. A. Abdelmohsen, S. Sánchez and M. Arroyo, Phys. Rev. Fluids, 2020, 5, 122001 CrossRef.
- R. Novick and E. Geisinger, Annu. Rev. Genete., 2008, 42, 541–564 CrossRef CAS.
- W. Ng and B. Bassler, Annu. Rev. Genete., 2009, 43, 197–222 CrossRef CAS.
-
J. Happel and H. Brenner, Low Reynolds number hydrodynamics: with special applications to particulate media, Springer, 1983 Search PubMed.
- K. J. Burns, G. M. Vasil, J. S. Oishi, D. Lecoanet and B. P. Brown, Phys. Rev. Res., 2020, 2(2), 023068 CrossRef CAS.
- J. Hadamard, Comp. Rend. Acad. Sci., 1911, 152, 1735–1738 Search PubMed.
- W. Rybzynski, Bull. Acad. Sci. Cracovie, 1911, A, 41–46 Search PubMed.
-
A. Cornish-Bowden, Fundamentals of Enzyme Kinetics, 4th edn, Wiley-Blackwell, Weinheim, 2012 Search PubMed.
- T. Hillen and K. J. Painter, J. Math. Biol., 2009, 58, 183–217 CrossRef CAS PubMed.
- M. R. Myerscough and J. D. Murray, Bull. Math. Biol., 1992, 54(1), 77–94 CrossRef CAS PubMed.
- S. Michelin, E. Lauga and D. Bartolo, Phys. Fluids, 2013, 25, 061701 CrossRef.
- Z. Izri, M. N. van der Linden, S. Michelin and O. Dauchot, Phys. Rev. Lett., 2014, 113, 248302 CrossRef PubMed.
- M. Schmitt and H. Stark, Phys. Fluids, 2016, 28(1), 012106 CrossRef.
- H. Masoud and H. A. Stone, J. Fluid Mech., 2019, 879 Search PubMed.
- S. Michelin, S. Game, E. Lauga, E. Keaveny and D. Papageorgiou, Soft Matter, 2020, 16(5), 1259–1269 RSC.
- Y. Chen, K. L. Chong, L. Liu, R. Verzicco and D. Lohse, J. Fluid Mech., 2021, 919, A10 CrossRef CAS.
-
H. Bateman and A. Erdélyi, Higher Transcendental Functions, McGraw-Hill Book Company, 1953, vol. 1 Search PubMed.
- E. Tjhung, D. Marenduzzo and M. Cates, Proc. Natl. Acad. Sci. U. S. A., 2012, 109, 12381–12386 CrossRef CAS.
- T. Gao and Z. Li, Phys. Rev. Lett., 2017, 119, 108002 CrossRef PubMed.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article *ab
*ab
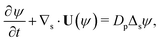
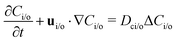
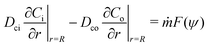
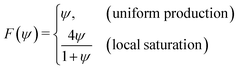
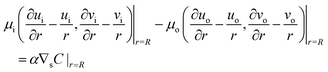
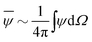 , droplet radius R, reference concentration Cref ∼
, droplet radius R, reference concentration Cref ∼ ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) R/Dc, and advection time scale τ ∼ μDc/(αṁ
R/Dc, and advection time scale τ ∼ μDc/(αṁ![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) ), respectively. Hence, the dimensionless equations read
), respectively. Hence, the dimensionless equations read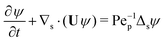
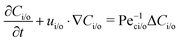
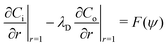
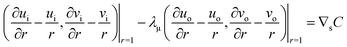
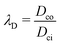 and
and 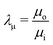 , respectively, represent the ratio of diffusivity and viscosity. Overall, the evolution of the interfacial density of microparticles is governed by an advection-diffusion equation with the induced Marangoni flow being the source of energy, driving fluid fields both inside and outside of the droplet.
, respectively, represent the ratio of diffusivity and viscosity. Overall, the evolution of the interfacial density of microparticles is governed by an advection-diffusion equation with the induced Marangoni flow being the source of energy, driving fluid fields both inside and outside of the droplet.
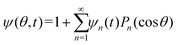
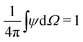 , as required. The modal solutions for the chemical concentration field become
, as required. The modal solutions for the chemical concentration field become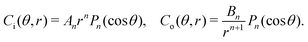
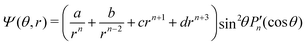
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ. The polar (i.e., v) and radial (i.e., w) velocity components can be calculated as
θ. The polar (i.e., v) and radial (i.e., w) velocity components can be calculated as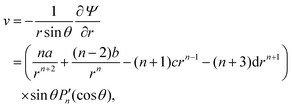
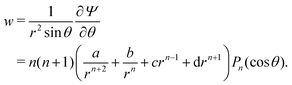
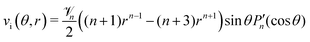
![[scr V, script letter V]](https://www.rsc.org/images/entities/char_e149.gif) n. For the flow outside of the droplet (r > 1), obviously d = 0 can be chosen, as well as c = 0 for n > 1. The polar velocity component becomes
n. For the flow outside of the droplet (r > 1), obviously d = 0 can be chosen, as well as c = 0 for n > 1. The polar velocity component becomes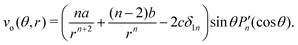
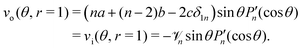
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ = −V
θ = −V![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) sin
sin![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ,
θ,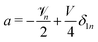 and
and 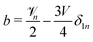 . The polar component of eqn (15) requires
. The polar component of eqn (15) requires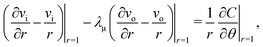
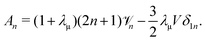
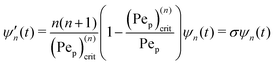
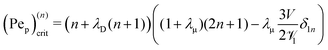
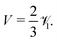
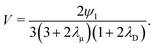
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) with Pep = 50, Pec = 0, and λμ = 1. Excellent agreements are seen between full simulation and eqn (36). In Fig. 3, we plot the resultant chemical and flow fields for the first two modes. The first mode ψ1 induces a donut-shaped vortex ring inside and a source-dipole-like flow field outside of the liquid–liquid interface, which hence effectively breaks symmetry to drive the entire-body migration. The mode exhibits a polar structure with a concentrated region or “hotspot” at the north pole, where micropaticles, for a sufficiently large value of Pep, eventually aggregate to form a singularity, and a depletion zone at the south pole. The streamlines of the bulk flow show how the resulting Marangoni force induces the two counter-rotating vortices reminiscent of the classical Hadamard–Rybczynski solution, in which surfactants are driven out of equilibrium by gravity.32,33 In comparison, the second mode ψ2 produces symmetric chemical distribution and flow structure, which doesn't produce any net motion. More generally, the nth surface mode induces n vortex rings stacked inside the droplet. As the instability grows, the particle density becomes more and more singular and eventually diverges.
θ) with Pep = 50, Pec = 0, and λμ = 1. Excellent agreements are seen between full simulation and eqn (36). In Fig. 3, we plot the resultant chemical and flow fields for the first two modes. The first mode ψ1 induces a donut-shaped vortex ring inside and a source-dipole-like flow field outside of the liquid–liquid interface, which hence effectively breaks symmetry to drive the entire-body migration. The mode exhibits a polar structure with a concentrated region or “hotspot” at the north pole, where micropaticles, for a sufficiently large value of Pep, eventually aggregate to form a singularity, and a depletion zone at the south pole. The streamlines of the bulk flow show how the resulting Marangoni force induces the two counter-rotating vortices reminiscent of the classical Hadamard–Rybczynski solution, in which surfactants are driven out of equilibrium by gravity.32,33 In comparison, the second mode ψ2 produces symmetric chemical distribution and flow structure, which doesn't produce any net motion. More generally, the nth surface mode induces n vortex rings stacked inside the droplet. As the instability grows, the particle density becomes more and more singular and eventually diverges.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ), and the slope from the linear theory (given in eqn (32)). (Bottom) Comparisons for the droplet speed V obtained from full simulation and the linear theory in eqn (36).
θ), and the slope from the linear theory (given in eqn (32)). (Bottom) Comparisons for the droplet speed V obtained from full simulation and the linear theory in eqn (36).
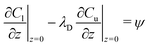
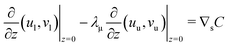
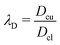 and
and 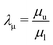 , and the far-field behavior
, and the far-field behavior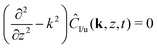
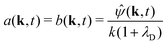
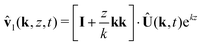
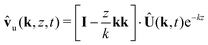
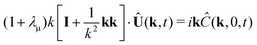
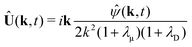
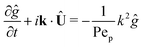
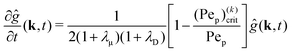
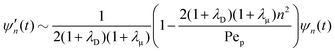
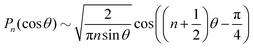
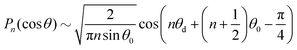
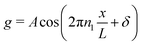
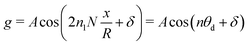
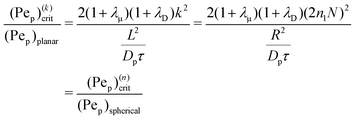
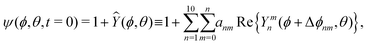
![[small psi, Greek, macron]](https://www.rsc.org/images/entities/i_char_e0d9.gif) = 1 still holds. As demonstrated in Fig. 6, even though we may choose arbitrary initial fields, they all end up, after a transient period, showing the same axisymmetric dipole-type profile at the steady state.
= 1 still holds. As demonstrated in Fig. 6, even though we may choose arbitrary initial fields, they all end up, after a transient period, showing the same axisymmetric dipole-type profile at the steady state.


![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ) or randomized according to eqn (64).
θ) or randomized according to eqn (64).


