Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Features of heterogeneously charged systems at their liquid–liquid critical point
Daniele
Notarmuzi†
*a and
Emanuela
Bianchi†
 *ab
*ab
aInstitut für Theoretische Physik, TU Wien, Wiedner Hauptstraße 8-10, A-1040 Wien, Austria. E-mail: daniele.notarmuzi@tuwien.ac.at; emanuela.bianchi@tuwien.ac.at
bCNR-ISC, Uos Sapienza, Piazzale A. Moro 2, 00185 Roma, Italy
First published on 19th August 2024
Abstract
Recently synthesized colloids and biological systems such as proteins, viruses and monoclonal antibodies are heterogeneously charged, i.e., different regions of their surfaces carry different amounts of positive or negative charge. Because of charge inhomogeneity, electrostatic interactions between these units through the surrounding medium are intrinsically anisotropic, meaning that they are characterized not only by the attraction between oppositely charged regions but also by the repulsion between like-charged areas. Recent experiments have shown that the liquid–liquid phase separation of these systems can be driven by anisotropic electrostatic interactions, but it is not clear how the emerging aggregates are affected by charge imbalance and charge patchiness. The ability to experimentally control these two quantities calls for a theoretical understanding of their interplay, which we address here at the critical point. We consider a coarse-grained model of anisotropically charged hard spheres whose interaction potential is grounded in a robust mean field theory and perform extensive numerical Monte Carlo simulations to understand the aggregation behavior of these units at the critical point. Stemming from the simplicity of the model, we address the interplay between charge imbalance and charge patchiness with the use of three parameters only and fully rationalize how these features impact the critical point of the model by means of thermodynamic-independent pair properties.
1 Introduction
Colloidal particles featuring engineered surface patterns serve both as self-assembling units for crafting new materials with target structures and properties1–4 and as simple models to shed light on the aggregation behaviors observed in biological systems, such as globular proteins, viral capsids and antibodies.5–9Particle models with built-in directional attraction, often referred to as patchy colloids, have shown a plethora of diverse collective behaviours, such as the formation of finite clusters with well-defined geometries, the assembly of exotic two- and three-dimensional crystals and the emergence of disordered networks with incessantly rearranging topology, to name just a few examples.10–16 In the context of the liquid–liquid phase separation (LLPS), i.e., the separation into a dilute and a dense disordered phase, patchy colloid models have provided insight into the stability of the LLPS, with particular reference to globular proteins:17–21 when the particle bonding valence is limited (due to the built-in particle functionality), then the LLPS becomes metastable with respect to the liquid–crystal transition and a large region of the phase diagram is dominated by a homogeneous, low-density liquid (often referred to as empty liquid) and, on gradually reducing the temperature, by a disordered arrested network (also referred to as an ideal/equilibrium gel).8,22–24
Particle models with directional repulsion on the top of the built-in directional attraction have been recently put forward to take into account the possibility of charge heterogeneity on the particle surface25–33 for charged patchy colloids34–38 as well as globular proteins.39–41 Models aiming at elucidating the role of charge patchiness have been used to investigate a variety of phenomena spanning from the bulk aggregation of charged Janus and patchy colloids42–44 to the protein adsorption on polyelectrolyte chains or brush layers.45,46 The competition between attractive and repulsive charge–charge interactions has also been investigated in the context of the LLPS:47,48 in particular, we have recently shown that the interplay between the net particle charge and the surface patchiness controls the critical parameters of the LLPS in systems of model particles with a null dipole moment and a linear quadrupole moment.47 We consider here a broader and more systematic selection of systems with the aim of fully elucidating the trends of all thermodynamic parameters at the critical point on smoothly varying the surface anisotropy and the charge imbalance.
The paper is organized as detailed in the following. In Section 2, we introduce the coarse-grained model, its microscopic background, features and parameters. In Section 3, we briefly discuss the details of our Monte Carlo simulations and the methods used to determine the critical points. In Section 4, we present our results. Namely in Section 4.1, we discuss the critical parameters and fields on varying the interplay between directional repulsion and directional attraction as well as on changing the surface patchiness; we then relate the behaviour of the observed critical temperatures to (i) a thermodynamic-independent pair quantity that estimates the particles' availability to form bonds (Section 4.2) and (ii) the reduced second virial coefficient at the estimated critical points (Section 4.3); moreover, we relate the behaviour of the observed critical density to the morphology of the aggregates at the critical point by (i) comparing the energy distributions of random versus simulated pairs of particles (Section 4.4) and (ii) evaluating the number of bonds formed in the systems (Section 4.5). We draw our conclusions in Section 5.
2 The model
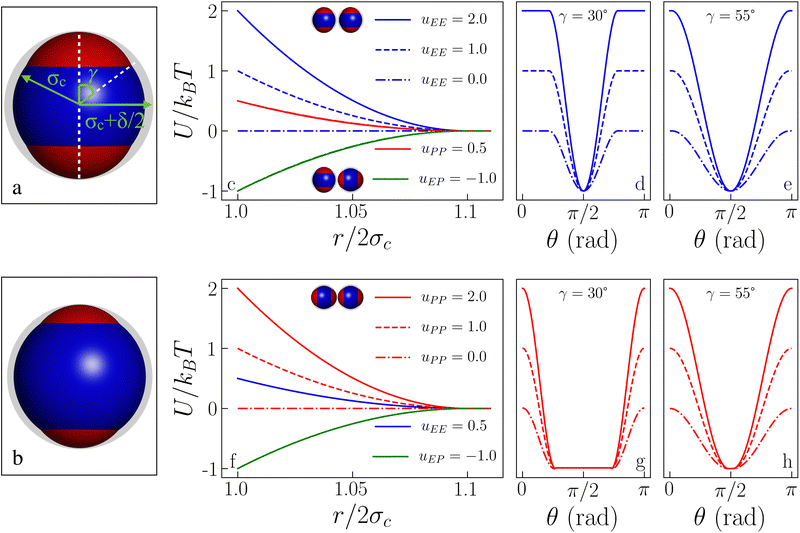
We consider a dielectric sphere containing three point charges, a negative one positioned at the center of the sphere and two positive ones, equally charged and symmetrically placed at a distance a from the center. This distribution of charges gives rise to a linear, axially symmetric quadrupole. The resulting electrostatic pair interaction is thus anisotropic and, given a set of microscopic parameters, it can be explicitly computed under linear approximation within a mean-field approach.27,49 We refer to this potential as “DLVO-like” as in the limit of a single, central charge such a mean-field interaction coincides with the well-known DLVO potential between homogeneously charged spheres. The inverse patchy particle (IPP) model discussed in the following represents the coarse-grained version of the aforementioned DLVO-like potential and as such can be regarded as representative of the effective interactions in heterogeneously charged systems such as globular proteins and patchy colloids.27,49Within the IPP model, each particle has a radius σc = 0.5 > a, which sets the units of length and is endowed with three interaction sites, positioned exactly as the three charges of the mean-field description. Each interaction site is the center of an interaction sphere. The off-center spheres emerge from the surface of the central sphere, thus defining the polar patches and the complementary equatorial belt, which is the part of the particle surface not covered by the patches. This geometry mimics the heterogeneous pattern of the surface charge distribution of the mean field model: the equatorial regions of two different IPPs as well as two patches of two IPPs mutually repel each other, while a patch of one IPP is attracted to the equatorial region of different IPPs. This consideration also explains the use of the “inverse” patchy particles notion: unlike conventional patchy systems, the patches of IPPs cannot bond to each other but rather repel each other.
The sphere associated with the central site has a radius σc + δ/2, while the off-center spheres have a radius σp constrained by σp + a = σc + δ/2. The above constraint, which is a direct consequence of the screening conditions of the solvent, forces the off-center spheres to extend exactly up to the extension of the central sphere, i.e., δ is the sole parameter characterizing the interaction range of the model: if the center-to-center distance between two IPPs is r, then r < 2σc implies an infinite, hard-sphere repulsion, while r > 2σc + δ implies that the two particles do not interact at all. The geometry of an IPP is hence specified by two parameters, δ and a, given the constraint on σp. An alternative way to characterize the model is to replace a with the semi-opening angle of the off-center spheres, γ, which quantifies the surface area covered by a patch. The constraint on σc translates in the expression γ = arccos[(σc2 + a2 − σp2)/2aσc]. See Fig. 1 (panels a and b) for a detailed representation of the geometric parameters of the model. Note that the patch size, γ, and the interaction range, δ, can be directly related to physical quantities, namely to the measured surface extension of experimental IPPs and to the Debye screening length of their dispersion media.27,49
As our coarse-grained description aims at accurately reproducing the DLVO-like description while being computationally efficient, the distance- and orientation-dependent pair interaction energy is written in the form27,49
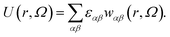 | (1) |
In the above expression, r is the center-to-center distance between two IPPs, Ω is their mutual orientation, α and β identify the three interaction sites of the two particles, i.e., they run over the central site and both the off-center sites, εαβ characterizes the energy strength of the αβ interaction, i.e., the interaction strength between the α site of one particle and the β site of the other particle, and finally, wαβ takes into account the interaction geometry of the specific pair configuration. While the values of εαβ are constant and characterize a specific set of microscopic parameters, the functions wαβ characterize the dependence on the mutual orientation and distance of the specific pair configuration. Such a dependence is chosen to be represented by the relative overlap volume between the interaction spheres associated with the interaction sites α and β of the two particles.27,49 From an operational point of view, given a distance 2σc ≤ r ≤ 2σc + δ and a relative orientation Ω, the summation in eqn (1) accounts for (i) the relative overlap between the spheres of radius 2σc + δ associated with the two central sites, weighted by εc,c, where c,c stands for center–center; (ii) the relative overlap between the four spheres of radius σp associated with the off-center sites of one particle and the two spheres associated with the central sites of the other particle, weighted by εc,oc, where c,oc stands for center-off center; (iii) the relative overlap between the spheres associated to the off-center sites of the two different particles, weighted by εoc,oc, where oc,oc stands for off-center-off-center; the relative overlap stands for the overlap volume between two spheres, normalized by the maximum possible overlap volume, i.e., the volume of the smallest sphere.
ε αβ can be directly related to the charge balance between the different regions of the particle surface by a mapping between the IPP potential resulting from eqn (1) and the mean field, DLVO-like potential derived for a dielectric sphere with a given set of point charges.27,47,49 Here, however, instead of mapping the IPP model to specific parameter sets of the DLVO-like description, we explore the role played by the net particle charge in a systematic fashion by varying the energy strengths arbitrarily. To this aim, we fix the value of the interaction potential U when the particles are in contact (r = 2σc) and in one of three specific reference configurations, named EE, EP, and PP (Fig. 1 shows the three reference configurations in the legend of panels c and f): in the EE configuration, the symmetry axes of the particles are parallel; in the EP configuration, they are orthogonal, and in the PP configuration, they are coincident. Once the desired energy strength of these configurations is defined and stored in an array u = {uEE,uEP,uPP}, the array ε = {εc,c,εc,oc,εoc,oc} can be computed by solving
| W−1u = ε | (2) |
 | (3) |
To clarify with an example, given two particles i and j, the element WEPc,oc is the sum of the overlap volumes between all possible combinations of center–off center interaction sites, i.e., the overlap between the interaction spheres associated with the first and second off-center sites of particle i(j) and the interaction sphere of the central site of particle j(i), given that the particles are in the EP configuration, for a total of four contributions. The other elements of the matrix are computed in the same way: given one of the reference configurations, there is a single contribution for the center–center elements and four contributions for the off-center–off-center elements. Once the matrix is constructed, the multiplication of it with one of the arrays ε or u is made by suppressing the indices shared between the array and the matrix, i.e., the product WABαβε is made by suppressing the indices α,β (resulting into the array u, with indices AB) and vice versa. Taking again the configuration EP as an explicit example, uEP = WEPc,cεc,c + WEPc,ocεc,oc + WEPoc,ocεoc,oc.
In this work, we fix the interaction range to δ = 0.2σc and systematically vary the patch size and the net particle charge of the particles in order to assess the effect of the interplay between the geometry of the patches and the strength of the electrostatic interactions on the liquid–liquid critical point. In particular, we vary γ in the range [30°,55°] in steps of 5°, while we create a regular grid of values for uEE and uPP, where uEP = −1.0 sets the energy scale: we vary uEE and uPP independently in steps of 0.5 within the range [0,2]; we also add – for all γ values and selected uEE (namely, 0, 1 and 2) – two values of uPP (namely, 4 and 6) to bridge towards IPPs with charge imbalances already studied in the literature.50 Note that a few data points (at large patch sizes and large uEE values) are missing due to the emergence of crystallization in the sample.
3 Methods
3.1 Grand Canonical Monte Carlo simulations
We perform Grand Canonical (GC) Monte Carlo (MC) simulations with a code adapted from the publicly available code published with ref. 51. Our code as well as the analytics tools used to produce the data presented in this paper are available at ref. 52. In a GCMC simulation, the system energy![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and the particle number N are allowed to fluctuate so as to estimate their probability distributions, while the volume of the cubic simulation box is fixed by its linear size L = 8. An MC step corresponds to Nmax MC moves, where Nmax is the maximum number of particles allowed in the simulation box. The moves used in an MC step are insertion/deletion of a particle, and a single particle rototranslational (RT) move, i.e., the contemporary translation and rotation of a single particle.51 An insertion/deletion move is attempted with a probability of 0.01, while an RT move with a probability of 0.99. The maximum translation length (0.05) and maximum rotation angle (0.1) are chosen to result in an average acceptance rate of the RT move of about 30% around the critical point. The average acceptance rate strongly fluctuates between high values in the diluted phase and low values in the dense phase.
and the particle number N are allowed to fluctuate so as to estimate their probability distributions, while the volume of the cubic simulation box is fixed by its linear size L = 8. An MC step corresponds to Nmax MC moves, where Nmax is the maximum number of particles allowed in the simulation box. The moves used in an MC step are insertion/deletion of a particle, and a single particle rototranslational (RT) move, i.e., the contemporary translation and rotation of a single particle.51 An insertion/deletion move is attempted with a probability of 0.01, while an RT move with a probability of 0.99. The maximum translation length (0.05) and maximum rotation angle (0.1) are chosen to result in an average acceptance rate of the RT move of about 30% around the critical point. The average acceptance rate strongly fluctuates between high values in the diluted phase and low values in the dense phase.
3.2 Identification of the critical point
For each model, we first perform a large number of short simulations at different values of the temperature T and of the chemical potential μ, so as to approximately locate the phase separation region. We then select a few values of T and μ and perform 12 independent GCMC simulations per state point. Each simulation begins with N0 = 180 particles and equilibrates for 2.5 × 106 MC steps, a value that is a posteriori checked to guarantee a sufficiently large equilibration time for all systems. The total run time per simulation is set to 5 × 107 MC steps, during which the values of N and![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) are collected every 103 MC steps and a configuration is saved every 5 × 104 MC steps, thus resulting in a total of 57 × 104 values of
are collected every 103 MC steps and a configuration is saved every 5 × 104 MC steps, thus resulting in a total of 57 × 104 values of ![[scr E, script letter E]](https://www.rsc.org/images/entities/char_e140.gif) and N per state point and 11
and N per state point and 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 400 configurations.
400 configurations.
At each state point, we calculate the scaling variable 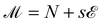 , where s is a fitting parameter with non-universal values. As, at the critical point, the probability distribution of
, where s is a fitting parameter with non-universal values. As, at the critical point, the probability distribution of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) coincides (up to vanishing second order corrections) with the distribution of the magnetization of the Ising model,53 the histograms produced by a simulation of the state point (T,μ) are reweighted,54 so to identify new values of (T′,μ′) and an optimal value of s such that the distribution of
coincides (up to vanishing second order corrections) with the distribution of the magnetization of the Ising model,53 the histograms produced by a simulation of the state point (T,μ) are reweighted,54 so to identify new values of (T′,μ′) and an optimal value of s such that the distribution of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) , rescaled to have unit variance, matches the Ising magnetization distribution, computed as in ref. 55. We perform simulations until the norm of the difference between the reweighted distribution of
, rescaled to have unit variance, matches the Ising magnetization distribution, computed as in ref. 55. We perform simulations until the norm of the difference between the reweighted distribution of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) and the Ising magnetization distribution is lower than 0.140. The final values of T′ and μ′ are then defined to be the critical ones, Tc and μc. We then define the critical density, ρc, and the critical energy density, uc, as the average of their respective distributions at (Tc,μc), computed via histogram reweighting. After the identification of (Tc,μc), for some selected systems we also perform simulations at the critical point, in order to gather data for the structural properties of the critical phases. To verify whether a simulation is sufficiently close to the critical point we check that the distribution of
and the Ising magnetization distribution is lower than 0.140. The final values of T′ and μ′ are then defined to be the critical ones, Tc and μc. We then define the critical density, ρc, and the critical energy density, uc, as the average of their respective distributions at (Tc,μc), computed via histogram reweighting. After the identification of (Tc,μc), for some selected systems we also perform simulations at the critical point, in order to gather data for the structural properties of the critical phases. To verify whether a simulation is sufficiently close to the critical point we check that the distribution of ![[scr M, script letter M]](https://www.rsc.org/images/entities/char_e145.gif) coincides with the Ising magnetization distribution without any reweighting. The structural properties of the models characterized by (uEE, uPP) = (0.0, 0.0) and (uEE, uPP) = (0.5, 2.0) are computed by using configurations sampled at the critical point.
coincides with the Ising magnetization distribution without any reweighting. The structural properties of the models characterized by (uEE, uPP) = (0.0, 0.0) and (uEE, uPP) = (0.5, 2.0) are computed by using configurations sampled at the critical point.
4 Results
4.1 The critical point
The behaviour of Tc, μc, ρc and uc is shown in Fig. 2 for all investigated IPP systems, where the critical temperature and the critical density of four sets of systems – listed in the figure caption – are reported from ref. 47 for completeness.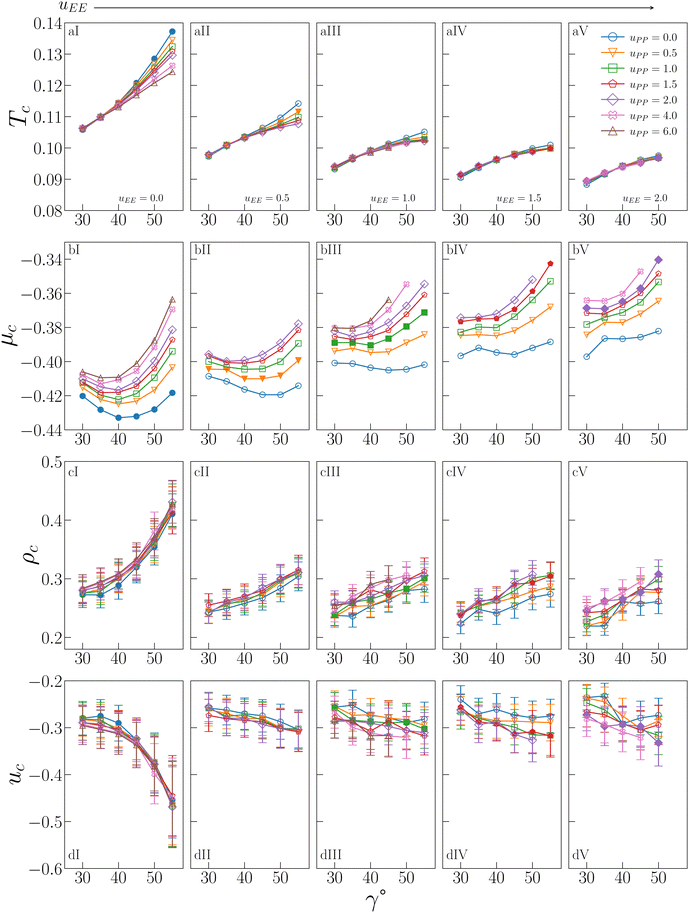 | ||
| Fig. 2 Critical behaviour of all investigated IPP systems. From top to bottom: Critical temperature Tc (row a), critical chemical potential μc (row b), critical density ρc (row c), critical energy density uc (row d). From left to right: Values of uEE increase from uEE = 0.0 to uEE = 2.0 in steps of 0.5 per panel (labeled I to V). Different colors and symbols refer to different values of uPP as reported in the legend of panel (aIV). Note that four sets of data are reported from ref. 47 for completeness, namely: (uEE, uPP) = (0, 0) (filled blue circles in panels aI and cI, referred to as ro (“repulsions off”) in ref. 47), (uEE, uPP) = (0, 0.5) (empty downward orange triangles in panels aI and cI), (uEE, uPP) = (2, 0) (empty blue circles in panels aV and cV) and (uEE, uPP) = (2, 0.5) (empty downward orange triangles in panels aV and cV, referred to as ref (“reference”) in ref. 47). | ||
As already suggested from the selection of systems studied in ref. 47, the critical temperature (a-panels of Fig. 2) monotonically increases with γ for any combination (uEE, uPP) of the electrostatic repulsion, where uEE and uPP have nonetheless a different quantitative impact on Tc. The repulsion between the equators has in fact the strongest effect: on increasing uEE (from panel aI to aV of Fig. 2), Tc significantly decreases for each given γ. It must be noted that, as uEE increases, the increase in Tc with γ becomes less and less pronounced at any fixed uPP and we observe a change in the curvature in the γ-dependence of Tc from convex to concave. In contrast, the repulsion between the polar regions plays a significant role only when the EE repulsion is small and, even in that case, only at large γs (panels aI–aIII of Fig. 2). On increasing uEE, the effect of uPP at large γs reduces until it becomes negligible (panels aIV and aV of Fig. 2). Overall, the interplay between geometry and electrostatics leads to strong variations in Tc, from a minimum of 0.0883 to a maximum of 0.1372, a value that is 55% larger than the minimum.
The critical chemical potential (b-panels of Fig. 2) shows qualitatively different trends. In particular, μc displays a more pronounced dependence on the PP repulsion: an increase in uPP implies an increase in μc, meaning that all curves are shifted upward, regardless of uEE and γ. The dependence on uEE is also monotonic, with μc increasing on increasing uEE, where the EE repulsion has nonetheless a smaller effect with respect to the PP repulsion. In contrast to Tc, μc does not increase monotonically with γ at all values of the EE repulsion: while for large values of uEE, μc monotonically increases with γ (see e.g. panel bV of Fig. 2), as uEE diminishes, μc shows instead a non-monotonic γ-dependence (see e.g. panels bI of Fig. 2). A minimum of μc at an intermediate γ implies that inserting a particle with a smaller or larger patch in the system is more costly. In the purely attractive case (i.e. uEE = uPP = 0), the curve is almost symmetrical with respect to its minimum, suggesting that particles with intermediate γs can be inserted at a lower cost due to geometric reasons. On increasing only the PP repulsion, the minimum does not move in γ, but it becomes increasingly costly to insert a particle with a large patch compared to one with a small patch, confirming that it is the number of unfavorable configurations due to the PP repulsion to determine μc: the larger and more repulsive the patches are, the more costly it is to insert the particles on average. When uEE also increases, μc gradually returns to being monotonic, as the EE repulsion outweighs the PP repulsion. The distinct behavior of the chemical potential compared to the other critical parameters and fields is thus an effect of the increased sensitivity of μc to the PP repulsion.
Similar to Tc, the critical density (c-panels in Fig. 2) is a monotonically increasing function of γ for any combination (uEE,uPP) of the electrostatic repulsion, consistently with the trends observed in ref. 47 for a small selection of IPP systems. Again like Tc, the increase is more pronounced when uEE is small and it flattens as the EE repulsion increases, while the increase of uPP weakly affects ρc, regardless of uEE or γ. The remarkable changes in ρc caused by the interplay between electrostatic repulsion and patch geometry imply that the largest value of the critical density, 0.430 (obtained for uEE = 0.0, uPP = 2.0 and γ = 55°), is 98% larger than the smallest value, 0.219 (obtained for uEE = 2.0, uPP = 0.0 and γ = 35°).
The critical energy (d-panels in Fig. 2) mirrors the behaviour of ρc, which comes as no surprise given the strong correlation between these variables at the critical point.56 For uEE = 0.0, uc rapidly decreases as γ increases, reaching a minimum value −0.469 for uEE = 0.0, uPP = 2.0 and γ = 55 (the system with the largest ρc). The maximum value is −0.232 for uEE = 2.0, uPP = 0.0 and γ = 35 (the system with the smallest ρc). Again in analogy to the critical density, uc is weakly affected by the PP repulsion at any γ and uEE, while it increases with the EE repulsion at any γ.
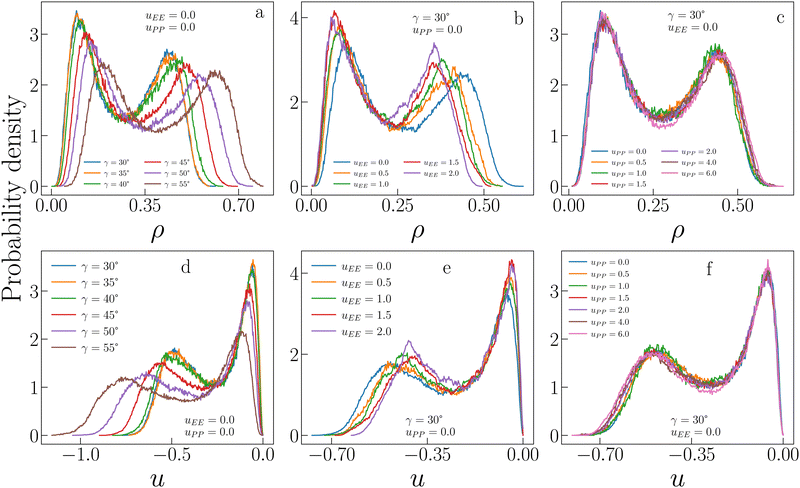
Fig. 3 allows a better understanding of the behaviour of ρc and uc by displaying the critical distributions of these variables, as obtained after histogram reweighting. For small values of uEE and uPP (for instance uEE = uPP = 0), the distributions become wider and wider on increasing γ, with the weight of extremely large densities increasing systematically with the patch size, subtracting weight to regions of low density (panel a of Fig. 3). This behaviour is mirrored by the increase in the weight of very low-energy regions and by the contemporary reduction of weight associated with regions of relatively high energy (panel d in Fig. 3). In contrast, when the opening angle and the PP repulsion are kept fixed and small, but the EE repulsion increases, we observe the opposite trend (panels b and e in Fig. 3). In this case, the weight moves toward regions of low density (high energy) with increasing uEE, implying a decrease (growth) in ρc (uc). Finally, variations in uPP are substantially ineffective in altering the probability distributions of ρ and u for a given set of γ and uEE values (panels c and f in Fig. 3) and indeed their average weakly depends on the PP repulsion.
As further confirmation that the behavior of the critical energy can be explained by the strong correlation between uc and ρc at the critical point, we show in Fig. 4 the joint probability density function of particle and energy density, computed from simulations at the critical point. The shape of the distributions confirms the existence of a strong correlation between these variables: regardless of γ, the distributions are extremely narrow along a slightly curved line, so that the value of one variable is almost entirely determined by the value of the other, with extremely small fluctuations around the conditioned average. Moreover, the distributions clearly show that low values of u are systematically associated with large values of ρ and vice versa, hence confirming that the two opposite monotonic trends (with γ and on increasing uEE) shown in Fig. 2 are due to the strong correlation between the critical fields.
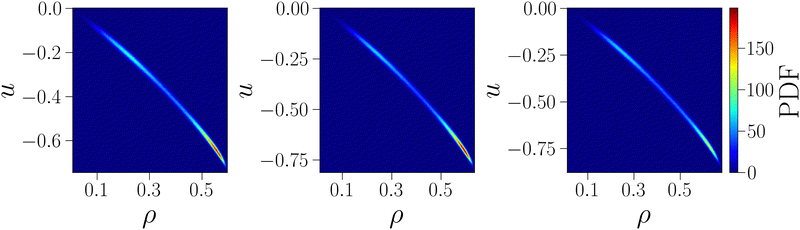 | ||
| Fig. 4 Joint probability density functions of energy density u and particle density ρ at the critical point for uEE = uPP = 0.0 and three different values of γ = 30, 40, 50 from left to right. | ||
4.2 Bonding volume versus critical temperature
A well-established result in the study of the critical point of patchy systems is that the critical temperature can be related to the amount of physical space around a single particle that is available for bonding. This quantity is referred to as bonding volume Vb and can be defined as57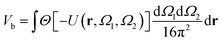 | (4) |
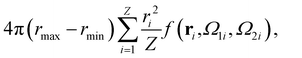 | (5) |
Fig. 5 displays Vb for the systems considered in Fig. 2. As expected, the behaviour of Vb reproduces the same trends observed for Tc: it strongly decreases on increasing uEE (from panel a to e) and it is always a monotonically growing function of γ; furthermore, it is weakly affected by uPP. In contrast to Tc, the curvature of Vb goes from concave to convex on increasing uEE. Moreover, again in contrast to Tc, Vb still decreases on increasing uPP at large values of uEE and γ.
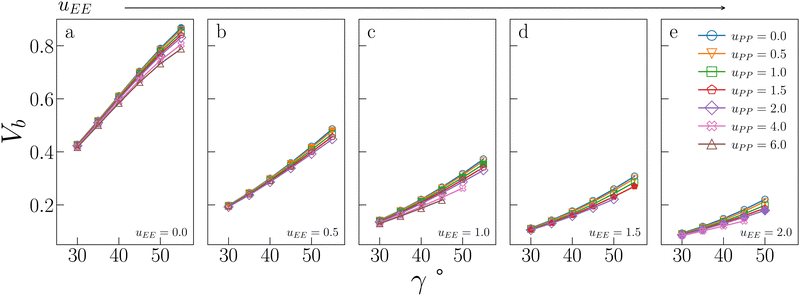 | ||
| Fig. 5 Bonding volume Vb for all systems studied in Fig. 2. The value of uEE increases from uEE = 0.0 to uEE = 2.0 in steps of 0.5 per panel (from a to e). Different colors and symbols refer to different values of uPP, as shown in the legend of panel (e). Markers are filled when uEE = uPP and empty otherwise. Note that four sets of data are reported from ref. 47 for completeness, namely: (uEE, uPP) = (0, 0) (filled blue circles in panel a, referred to as ro (“repulsions off”) in ref. 47), (uEE, uPP) = (0, 0.5) (empty downward orange triangles in panel a), (uEE, uPP) = (2, 0) (empty blue circles in panel e) and (uEE, uPP) = (2, 0.5) (empty downward orange triangles in panel e, referred to as ref (“reference”) in ref. 47). | ||
It is worth noting that while in conventional patchy colloids, Vb is in a straightforward relation with the number and size of the attractive patches,23,24 in IPP systems Vb emerges as a consequence of the interplay between electrostatics and geometry, both of which contribute to control the particle bonding valence. As complex as this interplay may be, Vb represents a powerful tool to estimate the critical temperature behaviour of sets of IPPs, since it is a thermodynamic-independent parameter based on pair properties.
4.3 Second virial coefficient and effective particle's valence
The second virial coefficient, b2(T), is defined as60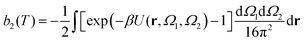 | (6) |
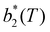 , has been proposed by Noro and Frenkel as a scaling variable to extend the van der Waals law of corresponding states to systems with variable attraction range60 and, since then, it has been used to map phase diagrams of different models in a large variety of systems, from proteins61 to colloids.62 The reduced second virial coefficient is defined as
, has been proposed by Noro and Frenkel as a scaling variable to extend the van der Waals law of corresponding states to systems with variable attraction range60 and, since then, it has been used to map phase diagrams of different models in a large variety of systems, from proteins61 to colloids.62 The reduced second virial coefficient is defined as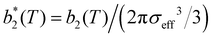 | (7) |
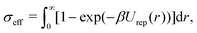 | (8) |
A generalized law of corresponding states for conventional patchy systems has been proposed under the observation that systems with the same number of patches tend to display similar values of 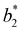 at the critical temperature.63 A natural question to ask is whether the generalized law of corresponding states holds for IPP systems. To answer this question, we must calculate b2 and σeff. For the first one, one can rely on the observation that eqn (6) has the same form as eqn (4), thus, if the Heavyside function is replaced by the Meyer function [1 − exp(−βU)], we can use eqn (5) for measuring b2. Eqn (8), however, does not have the same form of eqn (4) and hence a different strategy is required. The difficulty arises in front of the observation that the potential of IPP systems has a repulsive component that is not radial but rather depends on the relative orientation between the particles and hence the radial integral in eqn (8) is not appropriate to quantify σeff: an evaluation of Urep necessarily requires the exploration of the whole configuration space, i.e., an integration with respect to dΩ1dΩ2dr, with the consequence that the resulting integral has the dimension of a volume. Simply replacing the integration with respect to r in eqn (8) with one over the configuration space and then taking the cubic root of the resulting integral is clearly inappropriate, as for isotropic potentials it would not yield the same result of eqn (8). Hence, we generalize the definition of σeff as
at the critical temperature.63 A natural question to ask is whether the generalized law of corresponding states holds for IPP systems. To answer this question, we must calculate b2 and σeff. For the first one, one can rely on the observation that eqn (6) has the same form as eqn (4), thus, if the Heavyside function is replaced by the Meyer function [1 − exp(−βU)], we can use eqn (5) for measuring b2. Eqn (8), however, does not have the same form of eqn (4) and hence a different strategy is required. The difficulty arises in front of the observation that the potential of IPP systems has a repulsive component that is not radial but rather depends on the relative orientation between the particles and hence the radial integral in eqn (8) is not appropriate to quantify σeff: an evaluation of Urep necessarily requires the exploration of the whole configuration space, i.e., an integration with respect to dΩ1dΩ2dr, with the consequence that the resulting integral has the dimension of a volume. Simply replacing the integration with respect to r in eqn (8) with one over the configuration space and then taking the cubic root of the resulting integral is clearly inappropriate, as for isotropic potentials it would not yield the same result of eqn (8). Hence, we generalize the definition of σeff as
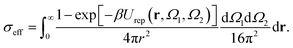 | (9) |
The comparison of the second virial coefficients of different IPP systems, however, is not straightforward even once the measures of b2 and σeff are well-defined. The observation made in ref. 63 relates the second virial coefficient of different patchy systems to the number of patches per particle. Under the single bond per patch condition, such a quantity corresponds to the maximum number of energetic bonds per particle,63 often referred to as particle functionality. As in IPP systems the particle functionality is not a built-in feature of the model, we need to determine the maximum number of bonds that an IPP can in principle form. For the purpose of our discussion in Sections 4.4 and 4.5, we distinguish between geometric and energetic bonds: a geometric bond, Gb, forms between two particles when their distance r is 2σ ≤ r ≤ 2σ + δ; an energetic bond, Eb, is a geometric bond with pair energy U < 0. Note that in conventional patchy systems, all bonds are energetic bonds. While the maximum number of geometric bonds that an IPP can form is 12, the so-called kissing number in three dimensions, the maximum number of energetic bonds is the particle functionality, which we thus label fmaxE. To infer fmaxE, we devise a specific MC sampling with 12 particles positioned around a central particle along the vertices of a regular icosahedron, where each of the external particles is within a distance r < 2σc + δ from the central one. These 12 particles are roto-translated by selecting one at random and moving its center of mass by a vector with three different random components between −Δ/2 and Δ/2. The move is accepted if the particle remains within the interaction range of the central particle and if no overlap is created, nor with the central particle nor with the 11 remaining external particles. Basically, any move that keeps the number of geometric bonds equal to 12 without creating overlaps is accepted. Δ = 0.17 is selected so as to have an average acceptance rate of the move around 30%. In this way, we create a large number of random configurations where the central particle has 12 possibly bonded neighbours. Note that this first stage of the MC is not concerned with the specific interaction potential of IPP systems and can simply be seen as a way to sample configurations where the kissing number of the central sphere is 12 given a square well potential with interaction range δ. In particular, the value Δ = 0.17 is independent of the interaction potential of the IPP model for which the measure is being performed. In the second stage of the MC, the IPP potential is activated and the measure of fmaxE is performed. In this second stage, external particles are first moved in the same exact way as they were moved in the first stage, so as to have again an average acceptance rate of around 30%. Moves are accepted according to the same criterion described earlier. If a move is accepted, a random orientation is assigned to the newly positioned particle and the IPP potential between it and the central particle is computed, so to evaluate if the new position and orientation of the moved particle forms an energetic bond with it. This scheme allows the monitoring of the evolution of the total number of energetic bonds formed by the central particle as the remaining 12 are roto-translated (with respect to it) and acquire a random orientation. fmaxE is estimated as the largest number of bonds formed by the central particle along the simulation. In principle, this measure provides a lower bound on the quantity of interest, so we attempted to move a random particle for a total of 4 × 1011 times, corresponding to having successfully moved each of the 12 external particles 1010 times each. This large number of measures makes us confident that our estimator of fmaxE well captures the maximum number of energetic bonds a particle can form. Note, in particular, that two successive configurations of the simulation are clearly correlated, but we are not interested in the probability distribution of the number of energetic bonds formed by the central particle, rather our focus is on the maximum number of energetic bonds that have non-zero probability. Hence, there is no reason to disregard any sampled configuration because of correlations: in principle, the measure becomes exact if the entire configuration space is sampled, even if the sampling is made of a series of strongly correlated configurations.
Fig. 6 shows the reduced second virial coefficient at the critical point as a function of fmaxE for the IPP systems under investigation in this work. The behavior of the latter is clearly correlated with the bonding volume: fmaxE diminishes as uEE increases (from panel a to e) and is rather insensitive to uPP. Interestingly, the variability of 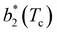 against variations of uPP depends on uEE. At small EE repulsion the patch–patch interaction seems to weakly affect
against variations of uPP depends on uEE. At small EE repulsion the patch–patch interaction seems to weakly affect 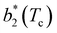 , while changes in uPP become more relevant in determining
, while changes in uPP become more relevant in determining 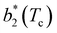 for large equator–equator repulsion, meaning that the charge imbalance strongly impacts the behavior of
for large equator–equator repulsion, meaning that the charge imbalance strongly impacts the behavior of 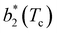 for a given geometry. Despite the spectrum of values spanned by
for a given geometry. Despite the spectrum of values spanned by 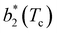 of IPP systems being consistent with the values observed for conventional patchy systems,63 it is not possible to apply the generalized law of corresponding states proposed by Foffi and Sciortino,63 meaning that it is not possible to identify classes of IPP systems with the same corresponding states a priori on the basis of their bonding functionality. However, the larger values of
of IPP systems being consistent with the values observed for conventional patchy systems,63 it is not possible to apply the generalized law of corresponding states proposed by Foffi and Sciortino,63 meaning that it is not possible to identify classes of IPP systems with the same corresponding states a priori on the basis of their bonding functionality. However, the larger values of 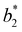 , observed for small values of uEE, are consistent with experimental measurements on monoclonal antibodies,64,65 globular proteins61,66 and folded domains of intrinsically disordered proteins.67
, observed for small values of uEE, are consistent with experimental measurements on monoclonal antibodies,64,65 globular proteins61,66 and folded domains of intrinsically disordered proteins.67
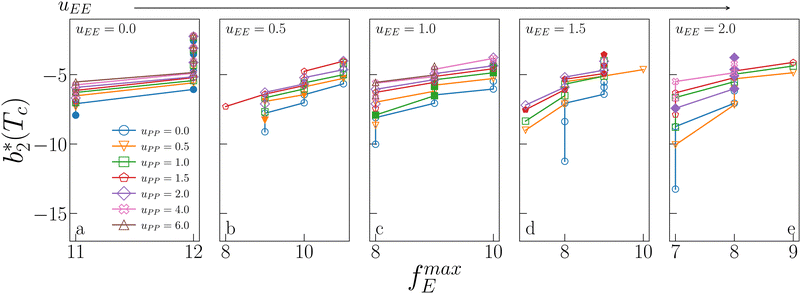 | ||
Fig. 6 Reduced second virial coefficient at the critical temperature, 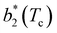 , as a function of the maximal functionality, fmaxE, for all systems studied in Fig. 2. Values of uEE increase from uEE = 0.0 to uEE = 2.0 in steps of 0.5 per panel (from a to e). Different colors and symbols refer to different values of uPP as shown in the legend of panel (a). Markers are filled when uEE = uPP and empty otherwise. For each uEE and uPP, the smallest , as a function of the maximal functionality, fmaxE, for all systems studied in Fig. 2. Values of uEE increase from uEE = 0.0 to uEE = 2.0 in steps of 0.5 per panel (from a to e). Different colors and symbols refer to different values of uPP as shown in the legend of panel (a). Markers are filled when uEE = uPP and empty otherwise. For each uEE and uPP, the smallest 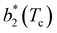 corresponds to γ = 30° and then γ increases by 5° pointwise, up to γ = 55°, when corresponds to γ = 30° and then γ increases by 5° pointwise, up to γ = 55°, when 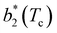 reaches its largest value. reaches its largest value. | ||
In the following, we focus on the microscopic characterization of the aggregates at the critical point to better understand the behaviour of the described critical quantities.
4.4 The role of the patch–patch repulsion
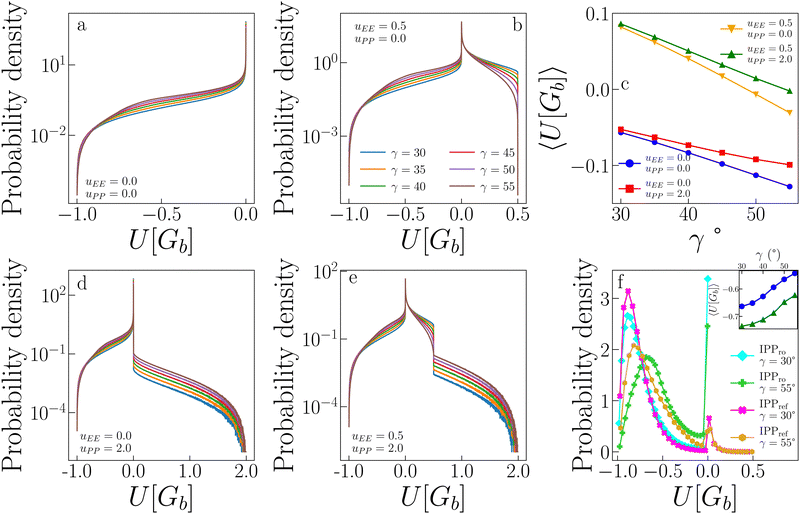
The above discussion leads to the observation that the parameter uPP is less relevant for the critical behaviour of our systems. The reason for this is rooted in the ability of the particles to self-organize into configurations where the PP repulsion is completely avoided. To show this, we calculate the probability distribution of the interaction energy of random pairs of bonded particles and compare it to the probability distribution of the pair interaction energy measured in the simulations at the critical point for several systems.Fig. 7 shows the probability distribution of the pair energy of geometric bonds for a variety of systems. Distributions in panels a, b, d, and e for the systems (uEE, uPP) = (0.0, 0.0), (0.5, 0.0), (0.0, 2.0), (0.5, 2.0) (and all γs), respectively, are computed by creating random geometric bonds. Specifically, while one IPP is fixed in its position and orientation, the other is assigned a random position within the interaction distance and a random orientation. Panel c shows the average of these distributions as a function of γ, while panel f reports the distribution for the systems (uEE, uPP) = (0.0, 0.0) and (0.5, 2.0) at the two extreme values of γ = 30° and 55°. For consistency with ref. 47, the system with (uEE, uPP) = (0.0, 0.0) is referred to as IPPro, where the subscript stands for “repulsion off”, and the system with (uEE, uPP) = (0.5, 2.0) is named IPPref, where the subscript stands for “reference”, as these values of the electrostatic repulsion have been observed in previously studied IPP systems.27,49,50,68
The probability distributions of randomly generated configurations estimate the number of possible pair configurations with a given energy. In the absence of any electrostatic repulsion (panel a in Fig. 7), the probability of a given energy is higher, the greater (less negative) the value of the energy U[Gb] is: while perfect EP configurations (with U[Gb] = − 1) are relatively rare, the distributions show a long regime of exponential growth at intermediate energies (with −1 < U[Gb] < 0, where the amplitude is higher for larger γs) and a peak at U[Gb] = 0. When either the EE (panel b) or the PP (panel e) repulsion is present, configurations with U[Gb] > 0 become possible: the largest energies can be reached only if either the EE or the PP interaction, respectively, contributes to U. While configurations where the EE repulsion contributes to the bond energy are relatively abundant (with 0 < U[Gb] < uEE), configurations where the PP repulsion plays a role are exceedingly rare: as soon as U[Gb] > 0, the probability has a substantial drop, larger for small γs, and then exponentially decays (note the log-lin scale) with a rate that seems γ-independent. This behaviour is confirmed also when both uEE ≠ 0 and uPP ≠ 0 (panel d), where the significant drop in the probability occurs as soon as U[Gb] > uEE.
In summary, configurations that provide a large PP contribution to U[Gb] are not numerous, meaning that it is relatively simple for a pair of IPPs to avoid such configurations when forming a geometric bond in a simulation. This speculation is confirmed by the distributions shown in panel f: for IPPref systems, the probability that U[Gb] > 0.5 is very close to zero, thus explaining why PP repulsion rarely impacts the critical parameters and fields. From comparing IPPro and IPPref systems in panel f, we further note that the presence of electrostatic repulsion facilitates the formation of low energy bonds both at large and small γs and greatly reduces the probability of configurations with zero energy. The weight in the distributions of those configurations that have zero energy in IPPro is partially transferred to configurations with U[Gb] > 0, but a large fraction of this weight is actually moved to configurations with very low energy.
As a result of the described differences between randomly generated pair configurations and pairs measured in simulations, the average energies of a geometric bond, 〈U[Gb]〉, (reported in panel c for random pairs and in the inset in panel f for pairs in simulations) show opposite trends: while 〈U[Gb]〉 decreases with γ for random pairs, it instead increases with γ in the simulations. In particular, panel c shows that the EE repulsion has the largest effect on the average energy of a geometric bond: when this repulsion is off, then 〈U[Gb]〉 <0, while a very mild EE repulsion causes a shift of 〈U[Gb]〉 to higher and mostly positive values. In contrast, the PP repulsion mainly tunes the rapidity with which the average energy decreases as γ increases. In contrast, the inset in panel f shows that 〈U[Gb]〉 is always negative in simulations of both IPPro and IPPref and increases with γ; on increasing γ, bonds become thus weaker. Moreover at any fixed γ, the average energy of the system with only directional attraction is always higher than the average energy of the system with directional attraction and directional repulsion; this is due to additional morphological constraints introduced by the electrostatic repulsion leading to more optimized EP configurations.47
4.5 Geometric versus energetic bonds
We now compare the probability that a particle forms n geometric bonds to the probability that a particle forms n energetic bonds. Fig. 8 (panels a, b and d, e) displays these probabilities for IPPro (top) and IPPref (bottom) systems. In the absence of electrostatic repulsion (panels a and b), the distributions of both n[Gb] and n[Eb] show a remarkable dependence on γ, with large patches allowing more (geometric as well as energetic) bonds than small patches. Only a fraction of geometric bonds is also energetic: the probability of having a small number of energetic bonds is slightly higher than that of having the same number of geometric bonds, while for a large number of bonds, the probability is higher that they are geometric rather than energetic (see the difference between the two cases reported in panel c). This trend is suppressed as γ increases, when the two distributions become increasingly similar, suggesting that large patches allow for a greater ability to form energetic bonds. Note that, on increasing γ, the numerous energetic bonds formed tend to be weaker as shown in the inset in panel f in Fig. 7. The presence of electrostatic repulsion significantly alters the described scenario: the dependence on γ is almost entirely suppressed, meaning that for large patches, the electrostatic repulsion acts against the formation of many energetic bonds. In other words, the fraction of geometric bonds which is also energetic does not significantly vary with γ due to electrostatic repulsion (see also panel f).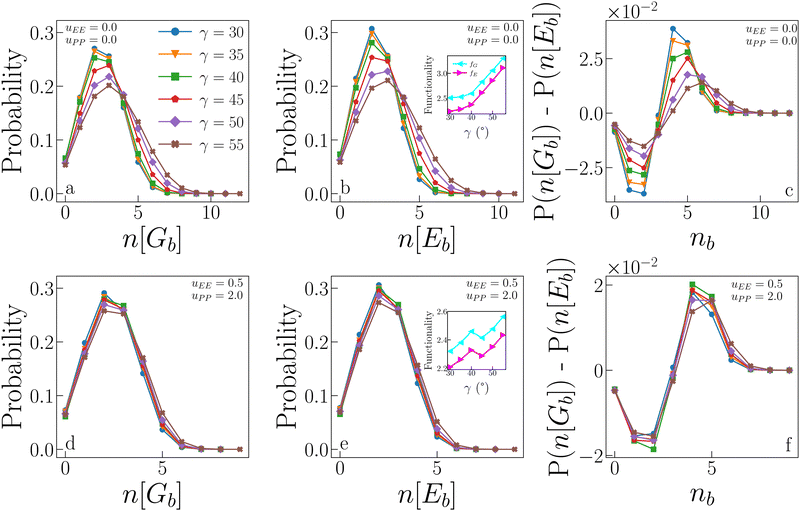 | ||
| Fig. 8 Statistics of geometric and energetic bonds from samples collected at the critical point. (a) Probability that n[Gb] geometric bonds are formed for systems with uEE = uPP = 0.0 and different values of γ. (b) Probability that n[Eb] energetic bonds are formed for the same systems as in panel (a). Inset: Average functionality, i.e., the average number of bonds (geometric and energetic, fG and fE respectively) as a function of γ, for the same systems as in panels (a) and (b), data reported from ref. 47. (c) Difference between the probability of forming n[Gb] geometric bonds and the probability of forming n[Eb] energetic bonds for the same systems as in panels (a) and (b). (d), (e) and (f) Same as in (a), (b) and (c) respectively, but for systems with uEE = 0.5 and uPP = 2.0. | ||
The insets of panels b and e in Fig. 8 show the average functionality of IPPro and IPPref systems at criticality. In conventional patchy systems, the functionality f of a particle is defined as the maximum number of bonds that a particle can form, and it corresponds to the number of patches per particle when the single bond per patch condition is satisfied. In IPP systems, however, the single bond per patch condition is not guaranteed, and hence, we define the functionality as the average number of bonds per particle actually formed in simulations. As we distinguish between geometric and energetic bonds, we also distinguish between geometric and energetic functionalities, fG and fE, respectively. Both quantities can be measured by averaging (over the whole system) the number of bonds each particle forms. Importantly, this definition implies that f depends on the thermodynamic conditions under which the system is. Data show that both functionalities increase with γ for both systems, but in the absence of repulsion (inset in panel b), the increase is such that the gap between fG and fE becomes smaller as γ increases; this behaviour reflects the fact that the distributions of n[Gb] and n[Eb] become increasingly similar as γ increases. In the presence of electrostatic repulsion (inset in panel e), the average functionalities have a systematically smaller value if compared to the case where the electrostatic repulsion is absent, namely 2.2 ≤ fG/E ≤ 3.4 for IPPro systems and 2.2 ≤ fG/E ≤ 2.6 for IPPro systems; moreover, the gap between fG and fE remains constant as the patch size increases. This is easily understood considering that identical configurations can have much larger energy when uEE and/or uPP are non-zero: two repulsive equatorial regions of two IPPs surely interact as soon as the two particles are within their interaction distance, hence giving a positive contribution to the pair energy, regardless of γ. That the reduced growth of the functionality with γ is a consequence of mostly the EE repulsion is an obvious consequence of the fact that configurations dominated by patch–patch repulsion are avoided, as already discussed.
It is worth noting that the average (geometric and energetic) functionality can be related to the compactness of the aggregates. Smaller functionalities imply more branched structures, as discussed in ref. 47. In particular, IPPro systems with small patches have on average a small number of bonds, most of which are energetic, which give rise to branched structures, as observed in ref. 47. These branched structures allow the system to condense into the liquid phase even at relatively low densities. In contrast, IPPro systems with large patches have, on average, a larger number of bonds, but a fraction of these are only geometric, which is due to the compact structures formed in the absence of directional repulsion. These compact structures require a large density for the liquid phase to condense, which explains the behaviour of ρc with γ in IPPro systems. In summary, low fG/E values imply branched structures, which in turn lead to low ρc values. The same paradigm is observed for IPPref systems: as their fG/E values are systematically lower than those observed in IPPro systems and do not increase significantly with γ, their ρc is also significantly lower over the whole γ-range, confirming that the electrostatic repulsion is a key factor in reducing the particle's connectivity.
5 Conclusions
In this work, we numerically study the effect of electrostatic anisotropy on the LLPS of heterogeneously charged particles, referred to as IPPs, which represent charged patchy colloids or protein systems. By taking advantage of a relatively simple coarse-grained model, we are able to investigate the critical behaviour of a large selection of IPP systems via robust MC simulations. Our model reproduces the features of a directional screened Coulomb interaction for spherical particles with simple charge heterogeneity and allows the control of the competition between surface patchiness and charge imbalance by means of a few parameters. We stress that, despite our model being more suitable for colloids and globular rather than disordered proteins, estimates of the reduced second virial coefficient of our systems at the critical point are in the range reported not only for globular proteins but also for disordered proteins and antibodies. This supports the speculation that our modeling approach has predictive power beyond the spherical approximation.We show that anisotropic electrostatics results in a limited bonding valence, a feature that is usually associated only with site-specific interactions. In particular, we show that the directional attraction stemming from the interactions between oppositely charged regions is not the only responsible for such limited functionality: the directional repulsion stemming from like-charged regions is in fact crucial in controlling the bonding valence, thus implying that both charge patchiness and charge imbalance control the ability of a particle to form bonds. As an effect of the limited bonding functionality, the LLPS critical point shifts towards extremely low temperatures and densities. In particular, consistent with the LLPS behaviour of systems with site-specific interactions, the directional nature of the attractive interactions shifts the critical point towards lower temperatures and densities, where smaller patches disfavour the condensation of the dense liquid phase with respect to larger patches. Electrostatic directional repulsion further reduces the critical parameters, where the impact of the electrostatic repulsion on the critical point varies with the size of the patches, highlighting the complex interplay between charge imbalance and charge patchiness.
We rationalize the behaviour of the critical parameters in terms of thermodynamic-independent pair properties such as the particle bonding volume and the probabilities for a particle to form a given number of bonds or have a given energy. The collection of these quantities provides additional insight into the morphological features of the aggregates. In particular, while in systems with only directional attraction, the number of possibly bonded pair configurations is controlled only by the patch size, when the directional repulsion is also present, the number of possibly bonded pair configurations is controlled by the complex interplay between patch size and charge imbalance. As a consequence, we observe the emergence of branched rather than compact structures not only in small patches – as it is for IPPs with only directional attraction – but also at large patches. This outcome highlights the potential of anisotropic electrostatics to control LLPS by tuning the charge patchiness of the systems by means of, e.g., pH changes or, specifically for protein systems, mutagenesis.
We note that a broader understanding of the phase separation of IPP systems would also require the determination of the binodal lines to estimate the width and shape of the phase coexistence region. Nonetheless, the Grand Canonical Monte Carlo simulations presented here are difficult to equilibrate at temperatures significantly lower than the critical one, while the behavior of the binodal line in such a regime is of particular interest. We are thus currently calculating the binodal lines of a selection of IPP systems via Successive Umbrella Sampling (SUS) simulations, which can reach equilibrium in a reasonable amount of time even at very low temperatures.51 In a future work, we plan to in fact address the interplay between phase separation and networking in a broad region of the phase diagram around the critical points. To this aim, we are also combining SUS with NVT simulations to determine the properties of IPP aggregates in large systems.69 A comprehensive picture of how charge patchiness affects the whole LLPS region and the properties of the IPP fluid/liquid will allow the control of such a phenomenon leveraging only on heterogeneous electrostatics.
Data availability
Numerical simulations of the Inverse Patchy Particle (IPP) model have been performed by adapting the publicly available code published with [L. Rovigatti, J. Russo, F. Romano, How to simulate patchy particles, Eur. Phys. J. E, 41, 2018, 137]. The resulting code, together with data analytics tools to reproduce the results presented in this paper is available at https://github.com/DaniMuzi/IPPs-critical-point. All data are available under request.Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
DN and EB acknowledge support from the Austrian Science Fund (FWF) under proj. no. Y-1163-N27. Computation time at the Vienna Scientific Cluster (VSC) is also gratefully acknowledged.References
- Q. Chen, E. Diesel, J. K. Whitmer, S. C. Bae, E. Luijten and S. Granick, J. Am. Chem. Soc., 2011, 133, 7725 CrossRef CAS.
- M. He, J. P. Gales, É. Ducrot, Z. Gong, G.-R. Yi, S. Sacanna and D. J. Pine, Nature, 2020, 585, 524–529 CrossRef CAS PubMed.
- G. Posnjak, X. Yin, P. Butler, O. Bienek, M. Dass, I. D. Sharp and T. Liedl, Science, 2024, 384, 781–785 CrossRef CAS.
- H. Liu, M. Matthies, J. Russo, L. Rovigatti, R. P. Narayanan, T. Diep, D. McKeen, O. Gang, N. Stephanopoulos, F. Sciortino, H. Yan, F. Romano and P. Šulc, Science, 2024, 384, 776–781 CrossRef CAS.
- L. Cademartiri and K. J. M. Bishop, Nat. Mater., 2015, 14, 2–9 CrossRef CAS PubMed.
- V. Schubertová, F. J. Martinez-Veracoechea and R. Vácha, Sci. Rep., 2017, 7, 11689 CrossRef PubMed.
- A. Stradner and P. Schurtenberger, Soft Matter, 2020, 16, 307–323 RSC.
- J. R. Espinosa, J. A. Joseph, I. Sanchez-Burgos, A. Garaizar, D. Frenkel and R. Collepardo-Guevara, Proc. Natl. Acad. Sci. U. S. A., 2020, 117, 13238–13247 CrossRef CAS PubMed.
- N. Skar-Gislinge, M. Ronti, T. Garting, C. Rischel, P. Schurtenberger, E. Zaccarelli and A. Stradner, Mol. Pharmaceutics, 2019, 16, 2394–2404 CrossRef CAS PubMed.
- A. J. Williamson, A. W. Wilber, J. P. K. Doye and A. A. Louis, Soft Matter, 2011, 7, 3423–3431 RSC.
- A. Pawar and I. Kretzschmar, Macromol. Rapid Commun., 2010, 31, 150 CrossRef CAS PubMed.
- E. Bianchi, R. Blaak and C. N. Likos, Phys. Chem. Chem. Phys., 2011, 13, 6397 RSC.
- F. Romano and F. Sciortino, Nat. Commun., 2012, 3, 975 CrossRef.
- F. Smallenburg, L. Leibler and F. Sciortino, Phys. Rev. Lett., 2013, 111, 188002 CrossRef PubMed.
- E. Bianchi, B. Capone, I. Coluzza, L. Rovigatti and P. D. J. van Oostrum, Phys. Chem. Chem. Phys., 2017, 19, 19847–19868 RSC.
- D. Morphew, J. Shaw, C. Avins and D. Chakrabarti, ACS Nano, 2018, 12, 2355–2364 CrossRef CAS.
- J. A. Thomson, P. Schurtenberger, G. M. Thurston and G. B. Benedek, Proc. Natl. Acad. Sci. U. S. A., 1987, 84, 7079–7083 CrossRef CAS.
- P. Schurtenberger, R. A. Chamberlin, G. M. Thurston, J. A. Thomson and G. B. Benedek, Phys. Rev. Lett., 1989, 63, 2064–2067 CrossRef CAS.
- Q. Chen, P. G. Vekilov, R. L. Nagel and R. E. Hirsch, Biophys. J., 2004, 86, 1702–1712 CrossRef CAS.
- O. Annunziata, A. Pande, J. Pande, O. Ogun, N. H. Lubsen and G. B. Benedek, Biochemistry, 2005, 44, 1316–1328 CrossRef CAS PubMed.
- T. Gibaud, F. Cardinaux, J. Bergenholtz, A. Stradner and P. Schurtenberger, Soft Matter, 2011, 7, 857–860 RSC.
- R. P. Sear, J. Chem. Phys., 1999, 111, 4800–4806 CrossRef CAS.
- N. Kern and D. Frenkel, J. Chem. Phys., 2003, 118, 9882–9889 CrossRef CAS.
- E. Bianchi, J. Largo, P. Tartaglia, E. Zaccarelli and F. Sciortino, Phys. Rev. Lett., 2006, 97, 168301 CrossRef PubMed.
- N. Hoffmann, C. N. Likos and J.-P. Hansen, Mol. Phys., 2004, 102, 857 CrossRef CAS.
- N. Boon, E. Carvajal Gallardo, S. Zheng, E. Eggen, M. Dijkstra and R. van Roij, J. Phys.: Condens. Matter, 2010, 22, 104104 CrossRef CAS PubMed.
- E. Bianchi, G. Kahl and C. N. Likos, Soft Matter, 2011, 7, 8313–8323 RSC.
- J. de Graaf, N. Boon, M. Dijkstra and R. van Roij, J. Chem. Phys., 2012, 137, 104910 CrossRef PubMed.
- C. Yigit, J. Heyda and J. Dzubiella, J. Chem. Phys., 2015, 143, 064904 CrossRef.
- R. Hieronimus, S. Raschke and A. Heuer, J. Chem. Phys., 2016, 145, 064303 CrossRef.
- N. E. Brunk, J. Kadupitiya and V. Jadhao, Phys. Rev. Lett., 2020, 125, 248001 CrossRef CAS PubMed.
- R. A. Mathews Kalapurakal and E. Mani, Mol. Simul., 2022, 48, 176–184 CrossRef CAS.
- A. Popov and R. Hernandez, J. Phys. Chem. B, 2023, 127, 1664–1673 CrossRef CAS PubMed.
- P. D. J. van Oostrum, M. Hejazifar, C. Niedermayer and E. Reimhult, J. Phys.: Condens. Matter, 2015, 27, 234105 CrossRef CAS PubMed.
- M. M. Virk, K. N. Beitl and P. D. J. van Oostrum, J. Phys.: Condens. Matter, 2023, 35, 174003 CrossRef CAS PubMed.
- M. Sabapathy, R. A. Mathews and E. Mani, Phys. Chem. Chem. Phys., 2017, 19, 13122–13132 RSC.
- K. Lebdioua, M. Cerbelaud, A. Aimable and A. Videcoq, J. Colloid Interface Sci., 2021, 583, 222–233 CrossRef CAS.
- F. N. Mehr, D. Grigoriev, N. Puretskiy and A. Böker, Soft Matter, 2019, 15, 2430 RSC.
- A. L. Božič and R. Podgornik, Biophys. J., 2017, 113, 1454–1465 CrossRef.
- M. Lund, Colloids Surf., B, 2016, 137, 17–21 CrossRef CAS.
- H. Nakamura and A. Wada, J. Phys. Soc. Jpn., 1985, 54, 4047–4052 CrossRef CAS.
- J. M. Dempster and M. O. de la Cruz, ACS Nano, 2016, 10, 5909 CrossRef CAS.
- B. C. Rocha, S. Paul and H. Vashisth, J. Phys. Chem. B, 2021, 125, 3208–3215 CrossRef CAS PubMed.
- J. L. B. de Araújo, F. F. Munarin, G. A. Farias, F. M. Peeters and W. P. Ferreira, Phys. Rev. E, 2017, 95, 062606 CrossRef.
- C. Yigit, J. Heyda, M. Ballauff and J. Dzubiella, J. Chem. Phys., 2015, 143, 064905 CrossRef PubMed.
- C. Yigit, M. Kanduć, M. Ballauff and J. Dzubiella, Langmuir, 2017, 33, 417 CrossRef CAS PubMed.
- D. Notarmuzi and E. Bianchi, arXiv, 2024, preprint, arXiv:2401.10655 DOI:10.48550/arXiv.2401.10655.
- M. A. Blanco and V. K. Shen, J. Chem. Phys., 2016, 145, 155102 CrossRef.
- M. Stipsitz, E. Bianchi and G. Kahl, J. Chem. Phys., 2015, 142, 114905 CrossRef.
- S. Ferrari, E. Bianchi and G. Kahl, Nanoscale, 2017, 9, 1956 RSC.
- L. Rovigatti, J. Russo and F. Romano, Eur. Phys. J. E: Soft Matter Biol. Phys., 2018, 41, 59 CrossRef PubMed.
- https://github.com/DaniMuzi/IPPs-critical-point .
- A. D. Bruce and N. B. Wilding, Phys. Rev. Lett., 1992, 68, 193–196 CrossRef PubMed.
- A. M. Ferrenberg and R. H. Swendsen, Phys. Rev. Lett., 1988, 61, 2635–2638 CrossRef CAS PubMed.
- M. M. Tsypin and H. W. J. Blöte, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 2000, 62, 73–76 CrossRef CAS.
- N. B. Wilding and M. Müller, J. Chem. Phys., 1995, 102, 2562–2573 CrossRef CAS.
- F. Sciortino, E. Bianchi, J. F. Douglas and P. Tartaglia, J. Chem. Phys., 2007, 126, 194903 CrossRef PubMed.
- M. S. Wertheim, J. Chem. Phys., 1986, 85, 2929–2936 CrossRef CAS.
- Recalling that
where the numbers xi are sampled from a uniform distribution over [a,b], an integral of the form appearing in the right hand side of eqn (4) can be estimated as in eqn (9): the factor rmax − rmin comes from the sampling of the distance, while each of the integrals over Ω1, Ω2 and over the pair (θ, ϕ) requires to sample the unitary sphere, introducing a factor 4π for each of these integration variables. - M. G. Noro and D. Frenkel, J. Chem. Phys., 2000, 113, 2941–2944 CrossRef CAS.
- F. Platten, N. E. Valadez-Pérez, R. Castañeda-Priego and S. U. Egelhaaf, J. Chem. Phys., 2015, 142, 174905 CrossRef.
- P. J. Lu, E. Zaccarelli, F. Ciulla, A. B. Schofield, F. Sciortino and D. A. Weitz, Nature, 2008, 453, 499–503 CrossRef CAS PubMed.
- G. Foffi and F. Sciortino, J. Phys. Chem. B, 2007, 111, 9702–9705 CrossRef CAS PubMed.
- N. Sibanda, R. K. Shanmugam and R. Curtis, Mol. Pharmaceutics, 2023, 20, 2662–2674 CrossRef CAS.
- P. Singh, A. Roche, C. F. van der Walle, S. Uddin, J. Du, J. Warwicker, A. Pluen and R. Curtis, Mol. Pharmaceutics, 2019, 16, 4775–4786 CrossRef CAS.
- F. Zhang, R. Roth, M. Wolf, F. Roosen-Runge, M. W. A. Skoda, R. M. J. Jacobs, M. Stzucki and F. Schreiber, Soft Matter, 2012, 8, 1313–1316 RSC.
- J. Kim, S. Qin, H.-X. Zhou and M. K. Rosen, J. Am. Chem. Soc., 2024, 146, 3383–3395 CrossRef CAS.
- E. G. Noya, I. Kolovos, G. Doppelbauer, G. Kahl and E. Bianchi, Soft Matter, 2014, 10, 8464 RSC.
- D. Notarmuzi and E. Bianchi, in preparation.
Footnote |
| † Both authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |