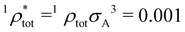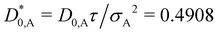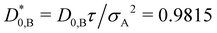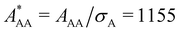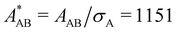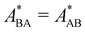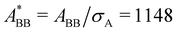Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Coupled dynamics in binary mixtures of model colloidal Yukawa systems†
Daniel
Weidig
 and
Joachim
Wagner
and
Joachim
Wagner
 *
*
Institut für Chemie, Universität Rostock, 18051 Rostock, Germany. E-mail: joachim.wagner@uni-rostock.de
First published on 1st November 2024
Abstract
The dynamical behavior of binary mixtures consisting of highly charged colloidal particles is studied by means of Brownian dynamics simulations. We investigate differently sized, but identically charged particles with nearly identical interactions between all species in highly dilute suspensions. Different short-time self-diffusion coefficients induce, mediated by electrostatic interactions, a coupling of both self and collective dynamics of differently sized particles: the long-time self-diffusion coefficients of a larger species are increased by the presence of a more mobile, smaller species and vice versa. Similar coupling effects are observed in collective dynamics where both time constant and functional form of intermediate scattering functions' initial decay are influenced by the presence of a differently sized species. We provide a systematic analysis of coupling effects in dependence on the ratio of sizes, number densities, and the strength of electrostatic interactions.
1 Introduction
Dynamical processes in strongly interacting systems and their relation to the time-averaged structure are since decades in the focus of scientific interest. Understanding of freezing processes, where correlations covering orders of magnitude in time are crucial, is still a challenge both from the viewpoint of experiment and theory. With evolving photon correlation spectroscopy1 as a quasielastic scattering method accessing timescales from microseconds to hours, colloidal suspensions gained interest as model systems on, compared to atomic or molecular systems, enlarged scales of lengths and times: the availability of highly defined particles with tailored interactions establishes a fruitful combination of experiment and theory to investigate structure–dynamics relations in interacting systems self-organizing to analogues of imperfect gases, liquids, glasses and even colloidal crystals.2,3 Colloidal suspensions have become relevant model systems for an experimental test of mode coupling theory describing slow dynamic processes such as, e.g., the glass transition.4–8Opposite to model hard-sphere colloids interacting via their mutual excluded volume, highly charged colloidal particles interact via the long-range electrostatic repulsion of equally charged macroions. Hence, these systems form at volume fractions as low as φ = 10−3 colloidal crystals.9 According to DLVO theory,10 charged colloids interact via a screened Coulomb- or Yukawa-potential while the mutual excluded volume and van der Waals interactions are not relevant in dilute systems.
Binary mixtures of charged colloidal particles have previously been studied in two dimensions.11–15 In three dimensions, studies are so far limited to hard-sphere systems16–22 while only few works investigate mixtures of charged particles.23–28 The vast majority of existing studies focuses on the self-dynamics of identical particles employing both, theoretical29–35 and experimental36–38 methods. Collective dynamics are up to now only rarely analyzed.39–45 Investigations of self- and collective diffusion processes in binary mixtures are up to now reported using systems with hard-sphere interactions.46–49
We demonstrate that employing highly parallelized code it is feasible to calculate distinct, time-dependent van Hove functions from trajectories of comparatively large systems consisting of 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 particles. By spatial Fourier transform, finally, dynamic structure factors are obtained. These quantities can, in principle be obtained via quasielastic scattering experiments in the time domain, e.g., photon correlation spectroscopy. In multi-component systems of differently sized particles consisting of the same material, an average dynamic structure factor as a weighted sum of the partial structure factors is obtained by these experiments. Partial structure factors are experimentally accessible with index-matching experiments, if particles with different refractive indices are available. Even if such particles are available, for charged colloids, however, tuning the suspending medium's refractive index affects the protolysis of functional groups and thus their number of effective charges and interactions.50 Typically, assuming a constant surface charge density, the number of effective charges is proportional to the particle surface. A possible experimental access to differently sized, but equally charged particles is the combination of particles stabilized via differently acidic functional groups: small particles with highly acidic functional groups and large particles with less acidic groups can, controlled by the suspending medium's pH provide equal number of effective charges. Since the preparation of such a system is highly challenging, we investigate in a first approach using computer experiments possible dynamic coupling effects in such binary mixtures.
000 particles. By spatial Fourier transform, finally, dynamic structure factors are obtained. These quantities can, in principle be obtained via quasielastic scattering experiments in the time domain, e.g., photon correlation spectroscopy. In multi-component systems of differently sized particles consisting of the same material, an average dynamic structure factor as a weighted sum of the partial structure factors is obtained by these experiments. Partial structure factors are experimentally accessible with index-matching experiments, if particles with different refractive indices are available. Even if such particles are available, for charged colloids, however, tuning the suspending medium's refractive index affects the protolysis of functional groups and thus their number of effective charges and interactions.50 Typically, assuming a constant surface charge density, the number of effective charges is proportional to the particle surface. A possible experimental access to differently sized, but equally charged particles is the combination of particles stabilized via differently acidic functional groups: small particles with highly acidic functional groups and large particles with less acidic groups can, controlled by the suspending medium's pH provide equal number of effective charges. Since the preparation of such a system is highly challenging, we investigate in a first approach using computer experiments possible dynamic coupling effects in such binary mixtures.
We investigate, how different mobilities of equally charged particles with identical time-averaged interactions influence the non-Gaussian diffusion of interacting systems. The wave-vector resolved, distinct partial correlation functions can be a valuable test for theoretical predictions of structure–dynamics relations in charged multi-component systems.
In this paper, we investigate structure–dynamics relations in dilute, binary mixtures of equally charged but differently sized particles by means of Brownian dynamics simulations. Since the strength of electrostatic interactions essentially depends on the number of effective charges, the interactions in such systems are practically identical between all species. Different particle sizes, however, lead to different Stokes–Einstein diffusion coefficients as short-time self-diffusion coefficients with impact both on long-time self and collective diffusion coefficients: mediated by electrostatic interactions, the long-time dynamics of a larger species is influenced by the presence of a smaller, more mobile species. We investigate long-time self-diffusion coefficients and, to quantify collective diffusion in mixtures of highly charged colloids, partial intermediate scattering functions where the influence of both size- and number density ratios is systematically assessed.
For metastable, supercooled liquids, we compare different static and dynamic freezing criteria such as the Hansen–Verlet criterion51 based on the maximum total structure factor, the dynamic Löwen criterion52 based on the ratio of long- to short-time self-diffusion coefficient and the Debye–Waller factor as long-time limit of the dynamic structure factor. We demonstrate using Brownian dynamics that the long-time dynamics in binary mixtures is significantly influenced by different short-time mobilities of its constituents.
2 Theoretical background
2.1 Charged colloidal particles
The interaction between charged colloidal macroions can, according to the DLVO theory,10 at relevant distances rij be written as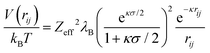 | (1) |
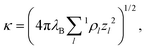 | (2) |
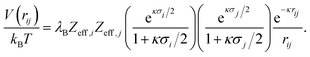 | (3) |
Suspensions consisting of highly charged colloidal particles, due to the long-range electrostatic repulsion, self-organize to liquid-like ordered and even crystalline structures at extremely low densities9 with particle distances as large as ten times the particle diameter. For such highly dilute systems, the pairwise additive approximation of the interactions is an adequate assumption53 neglecting hydrodynamic interactions as a consequence of their extremely small volume fraction. Typical pair correlation functions g(r) show, that distances comparable to the particle size do not occur: collisions of these electrostatically interacting particles are not observed and the mutual excluded volume, unlike in hard-sphere systems, does not play a role for the self-organization.
2.2 Brownian dynamics simulation
Relevant time scales for the Brownian motion of colloidal macroions are orders of magnitude larger than those of the suspending medium particles. The rapidly varying degrees of freedom of the suspending medium can be eliminated employing a projection operator formalism54–57 leading to a generalized Fokker–Planck equation. Restricting to times larger than momentum relaxation times with typically τp ≈ 10−8 s, such particles' equation of motion can be described as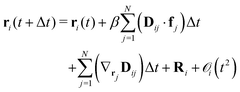 | (4) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) BT)−1 the inverse thermal energy, and Dij the diffusion tensor. The force acting on particle j is denoted as fj and Ri is a random displacement caused by the rapidly fluctuating interactions between the suspending medium and the colloidal macroions with the properties
BT)−1 the inverse thermal energy, and Dij the diffusion tensor. The force acting on particle j is denoted as fj and Ri is a random displacement caused by the rapidly fluctuating interactions between the suspending medium and the colloidal macroions with the properties| 〈Ri(τ)〉 = 0 | (5) |
| 〈Ri(τ)·Ri(τ + Δt)〉 = 6D0Δt | (6) |
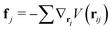 | (7) |
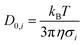 | (8) |
2.3 Dynamic properties
The time-dependent self-diffusion coefficient DS,i(t) of a particle i is accessible via its mean-square displacement as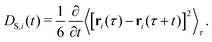 | (9) |
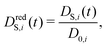 | (10) |
In an alternative way, the time-dependent self-diffusion of particle i is accessible from the van Hove function61
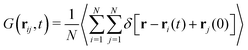 | (11) |
| = GS(rii, t) + GD(rij, t) | (12) |
In a mixture of NC species for each species α a self correlation function GS,α(rii, t) exists which obeys the differential equation
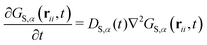 | (13) |
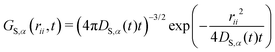 | (14) |
In such a mixture, NC(NC + 1)/2 different, distinct van Hove functions GD,αβ(rjβ − riα, t)
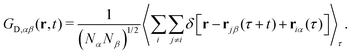 | (15) |
Analogously to eqn (13), the distinct part of the van Hove function obeys the differential equation
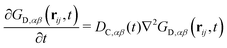 | (16) |
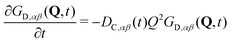 | (17) |
| Sαβ(Q, t) = GD,αβ(Q, t) + δαβ | (18) |
In a binary mixture, three partial intermediate scattering functions are accessible from the trajectories. Normalizing by the static structure factors Sαβ(Q, 0) = Sαβ(Q, t = 0), reduced intermediate scattering functions
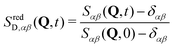 | (19) |
To identify a freezing transition in interacting systems, different criteria are described in the literature. The Hansen–Verlet criterion51 is based on the maximum of the static structure factor and identifies a frozen state for systems with max[S(Q)] ≳ 2.85. Löwen et al. suggest a dynamical freezing criterion based on the reduced long-time self-diffusion coefficient, to identify a frozen state when D(L)S/D0 ≲ 0.098.52,62 A frequently used criterion to characterize the glass transition is a non-zero Debye–Waller factor S(Q, t → ∞)/S(Q, 0) indicating a frustrated α-process.5,63–66
2.4 Computational details
We performed Brownian dynamics simulations employing the previously described and well known Ermak–McCammon algorithm,60 neglecting hydrodynamic interactions in three dimensional space employing a cubic box with periodic boundary conditions. The mean-square displacement 〈Δri2(t)〉 and partial distinct van Hove functions are calculated from the simulation trajectories. By Fourier transform, from the latter quantities intermediate scattering functions S(Q,t) are obtained. The parameters used for Brownian dynamics simulations are compiled in Tables 1 and 2.| Parameter | SI units |
|---|---|
| Temperature | T = 298.15 K |
| Box length | L B = 2.52 × 10−5 m |
| Total number density | 1 ρ tot = 1 × 1018 m−3 |
| Time base | τ = 1 × 10−3 s |
| Time step | Δt = 2.0 × 10−6 s |
| Viscosity | η = 8.9 × 10−4 Pa s |
| Relative permittivity | ε r = 78.3 |
| Bjerrum length | λ B = 7.160 × 10−10 m |
| Particle number |
N
P = 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 000 |
The diameter σA = 100 nm is kept constant during all simulations, while σB is varied from 100 nm to 20 nm to obtain binary mixtures including a virtually binary mixture with σA = σB = 100 nm. The number of effective charges of both species is varied in the range of Zeff,A = Zeff,B = 300–600. To investigate the influence of relative particle number densities 1ρB/1ρA, three different ratios 1ρB/1ρA = {1, 2, 4} are simulated. Additionally, in Table 2 the reduced interaction parameters
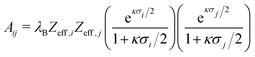 | (20) |
Starting from a bcc structure, in ten successive simulations, each with 104 time steps, with drastically reduced number of effective charges of Zeff,A = Zeff,B = 50, a gaseous configuration is prepared. Using this disordered configuration, in ten successive simulation runs of each 104 time steps liquid-like ordered systems consisting of particles with the respective number of effective charges are prepared. The convergence of equilibration is monitored by comparison of static pair correlation functions and the time-dependence of self-diffusion coefficients computed in each run. After equilibration, a production run of 2 × 106 time steps is performed.
From its trajectory, the mean-square displacement and the distinct van Hove functions are computed. To estimate uncertainties of the results, twelve independent production runs are evaluated for each system. The uncertainties are given as triple standard deviations of the results.
3 Results and discussion
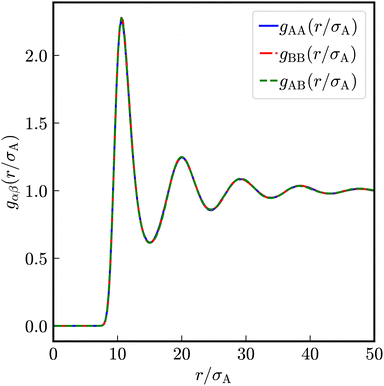
In the present work, we investigate binary colloidal suspensions of equally charged, but differently sized particles, interacting via a repulsive, screened electrostatic or Yukawa-potential. The interaction is primarily governed by the number of effective charges of the particles, the permittivity of the suspending medium, the temperature, and the mean interparticle distance depending on the total number density. Therefore, the interaction only slightly depends on the particles' size and is neglectable. Due to practically identical interactions between all species in time average, as visible in Fig. 1, the partial pair correlation functions gAA(r), gAB(r), and gBB(r) are identical.3.1 Self dynamics
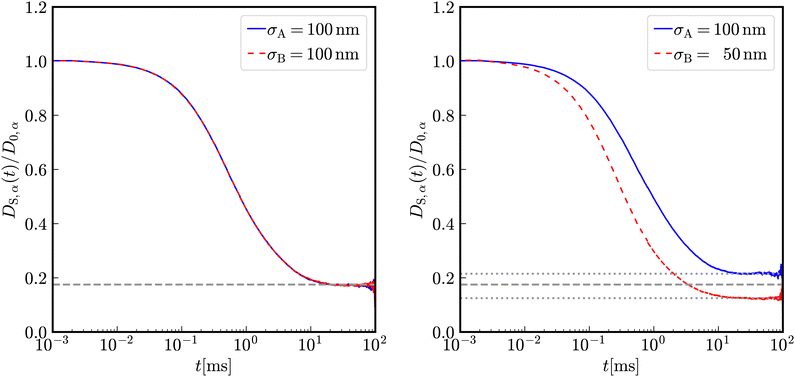
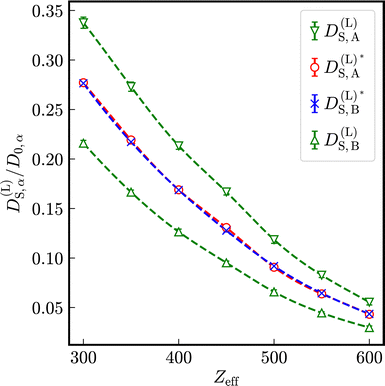
In Fig. 2, the reduced time-dependent self-diffusion coefficients in a virtually binary mixture of identical particles (lhs) and differently sized, but equally charged particles (rhs) are displayed. In the virtually binary mixture of identical particles, the time-dependence of the self-diffusion coefficients is identical. Opposite, in presence of a differently sized, smaller species, the reduced long-time self-diffusion coefficient D(L)S,A/D0,A is enhanced while that D(L)S,B/D0,B is reduced. In the short-time limit, consistently, the respective Stokes–Einstein diffusion coefficients are approached. For intermediate times, a subdiffusive motion leading to formal time-dependent self-diffusion coefficients is observed.In contrast to the effective one-component system, different Stokes–Einstein diffusion coefficients of a mixture's constituents lead to a different time-dependence of their self-diffusion coefficients: in the short-time limit, both self-diffusion coefficients approach the respective Stokes–Einstein diffusion coefficient, while in the long-time limit different reduced long-time self-diffusion coefficients D(L),redS,α are observed. The influence of the identical number of effective charges Zeff,A = Zeff,B is visible in Fig. 3 for a binary suspension consisting of particles with diameter σA = 100 nm and σB = 50 nm at identical particle number densities 1ρA = 1ρB = 5 × 1017 m−3. For comparison, the self-diffusion coefficients in a virtually binary mixture of identical particles, i.e., an effective one-component system, is depicted as well. With increasing number of effective charges and therewith increasing interactions, the long-time self-diffusion coefficient non-linearly decreases.
Generally, the long-time self-diffusion coefficients of a larger species with smaller Stokes–Einstein diffusion coefficient are enhanced by the presence of a smaller species with correspondingly larger Stokes–Einstein diffusion coefficients and vice versa. The differences of long-time self-diffusion coefficients decrease at identical ratios of sizes and number densities with increasing strength of electrostatic interaction.
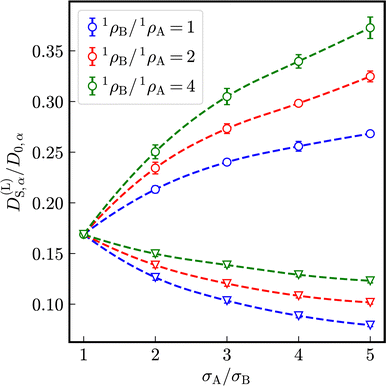
As visible in Fig. 4, with increasing particle-size ratio, the enhancement and reduction of reduced long-time self-diffusion coefficients increases, too. In suspensions with different number densities 1ρA ≠ 1ρB, reduced long-time self-diffusion coefficients of the minority component change more than those of the majority component. The numerical values of reduced long-time self-diffusion coefficients in virtually binary, as well as binary mixtures are compiled in Tables S1 and S2 of the ESI.†
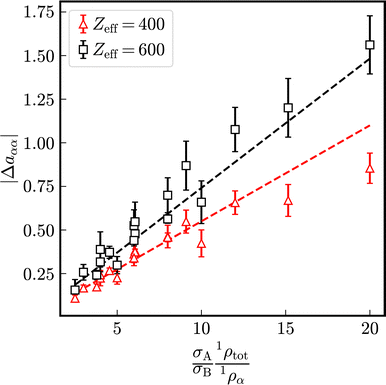
Let us define a reduced excess long-time self-diffusion coefficient
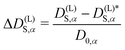 | (21) |
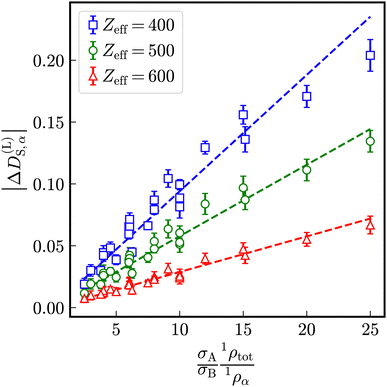 | ||
| Fig. 5 Modulus of the reduced excess long-time self-diffusion coefficient in dependence on the ratio (σA1ρtot)/(σB1ρα). The dashed lines are linear fits to the data. | ||
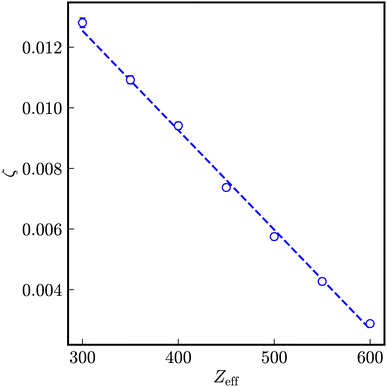 | ||
| Fig. 6 Dependency of the coupling constant ζ on the number of effective charges Zeff. The dashed line is a linear fit to the data. | ||
3.2 Collective dynamics
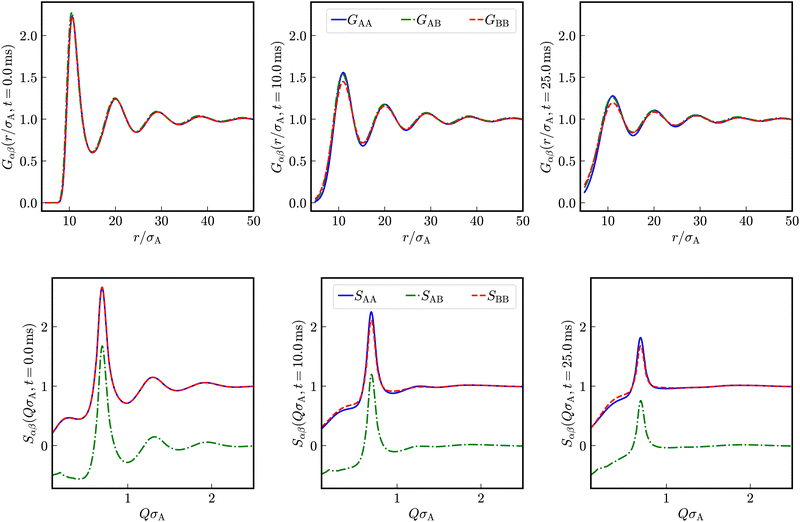
In addition to the self-dynamics, we investigate the collective dynamics employing intermediate scattering functions obtained by Fourier transform of distinct van Hove functions. The partial, distinct time-dependent pair correlation functions are calculated from simulation trajectories employing eqn (15). In Fig. 7, distinct, time-dependent partial pair correlation functions Gαβ(r/σA, t) and the corresponding partial dynamic structure factors Sαβ(QσA, t) for t = 0, t = 10.0 ms and t = 25.0 ms are displayed for a binary mixture with Zeff,A = Zeff,B = 400, diameters σA = 100 nm and σB = 50 nm at identical number densities 1ρA = 1ρB = 5 × 1017 m−3.In the here investigated liquid-like systems, all partial time-dependent structure factors decay to zero in the long-time limit. We quantify the collective short-time behavior by stretched exponentials exp(−at)b as a heuristic approach at the wave-vector Qmax at the maximum of the static structure factor.
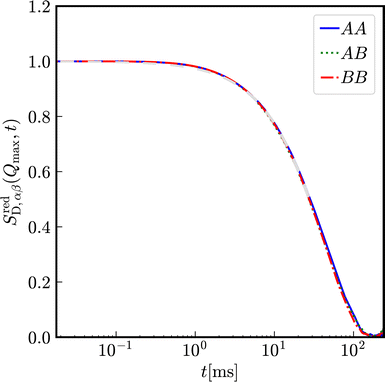
Let us first consider a virtually binary suspension consisting of identical particles. In Fig. 8, the reduced partial, distinct intermediate scattering functions SredD,αβ(Qmax, t) are shown for a suspension of colloidal macroions with diameter σA = σB = 100 nm, Zeff,A = Zeff,B = 400 effective charges at identical number densities 1ρA = 1ρB = 5 × 1017 m−3. Here, the functional form of decay is identical for all partial intermediate scattering functions.
The relaxation rates a and stretching exponents b of stretched exponentials of virtually binary mixtures are extracted from fits covering correlation times until Sαβ(Qmax, t) = Sαβ(Qmax, 0)/2 is reached.
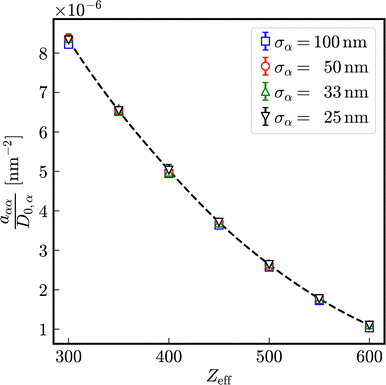
In Fig. 9, the relaxation rates a in effective one-component systems are displayed in dependence on the number of effective charges Zeff for different diameters. Normalized to the respective Stokes–Einstein diffusion coefficients D0,α a universal reduced relaxation rate, decreasing with the number of effective charges Zeff is obtained. The exponent b decreases in first approximation linearly with increasing number of effective charges and is independent of the particle size.
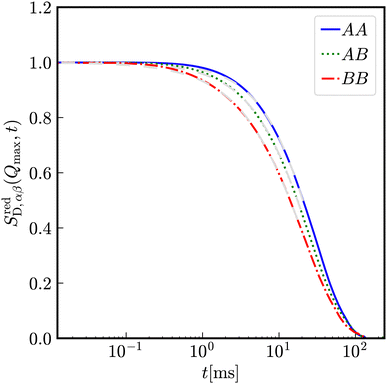
In a binary mixture of differently sized but still equally charged particles, the time-dependence of partial intermediate scattering functions differs as shown in Fig. 10 for particles with diameters σA = 100 nm and σB = 33 nm with Zeff,A = Zeff,B = 400 effective charges at identical number densities 1ρA = 1ρB = 5 × 1017 m−3. As expected, the decay of SAA(Q, t) is the slowest and that of SBB(Q, t) the fastest. The relaxation of the correlation between both species SAB(Q, t) is in between SAA(Q, t) and SBB(Q, t).
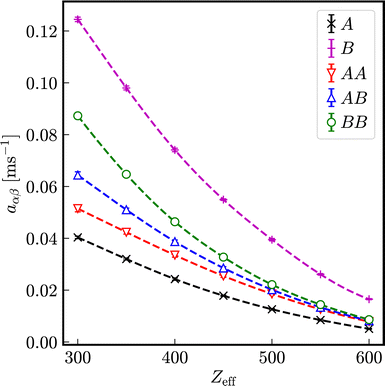
The relaxation rates aαβ in binary mixtures of particles with σA = 100 nm and σB = 33 nm at the same number densities 1ρA = 1ρB = 5 × 1017 m−3 in dependence on the number of effective charges Zeff = Zeff,A = Zeff,B is displayed in Fig. 11. For comparison, those of effective one-component systems consisting of particles with diameters σA = 100 nm and σB = 33 nm, respectively, are depicted as well. The values of the relaxation rates and the stretching exponents are compiled in the Tables S3–S6 of the ESI.† In analogy to self-diffusion, also the decay of intermediate scattering functions is influenced by the presence of a differently sized species: the relaxation rates of the correlation between the larger particles are enhanced in the presence of more mobile smaller particles and vice versa. As expected, the relaxation rates of correlations between different species aAB are in between the relaxation rates aAA and aBB of correlations between identical particles. With increasing number of effective charges Zeff = Zeff,A = Zeff,B, a nonlinear decay of relaxation rates is observed, approaching a common limit in the case of very strong electrostatic interactions.
Defining an excess relaxation rate as
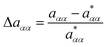 | (22) |
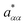 denoting the relaxation rate in a one-component system and aαα that in a binary mixture at identical total number densities. Analogously to self-diffusion, the modulus of excess relaxation rates of correlations between identical particles depend in first approximation linearly on the ratio (σA1ρtot)/(σB1ρα) for sufficiently strong electrostatic interaction as visible in Fig. 12.
denoting the relaxation rate in a one-component system and aαα that in a binary mixture at identical total number densities. Analogously to self-diffusion, the modulus of excess relaxation rates of correlations between identical particles depend in first approximation linearly on the ratio (σA1ρtot)/(σB1ρα) for sufficiently strong electrostatic interaction as visible in Fig. 12.
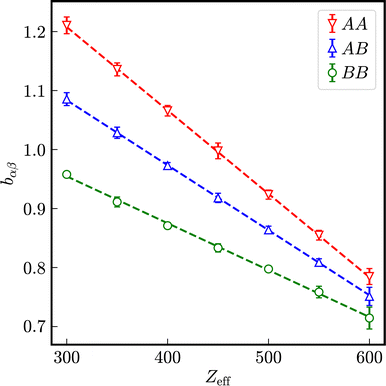
Opposite to one-component systems, the stretching exponents bαβ differ in binary mixtures of equally charged particles with different sizes as shown in Fig. 13 for a mixture of particles with σA = 100 nm and σB = 33 nm at identical number densities 1ρA = 1ρB = 5 × 1017 m−3. The stretching exponents bAB of the partial intermediate scattering functions SredD,AB(Qmax, t) are for all investigated numbers of effective charges practically identical to one-component systems consisting either of the larger species A or the smaller species B at the same total number density. In presence of a smaller species B, the stretching exponent bAA is larger than bAB indicating a more compressed relaxation. The stretching exponent bBB of the intermediate scattering function SBB(Qmax, t) is reduced by the presence of a larger species A indicating a more stretched relaxation.
With increasing number of effective charges and thus electrostatic repulsion, a linear decrease of all stretching exponents bαβ is observed, where the differences bAA–bBB also decrease with Zeff.
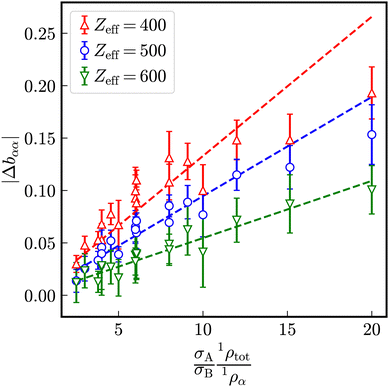
Let us analogously to the excess relaxation rate Δaαα define an excess stretching exponent
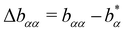 | (23) |
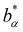 indicating the stretching exponent in a one-component system with the same total number density. For sufficiently strong electrostatic interaction, similar as for the reduced excess long-time self-diffusion coefficient, a nearly linear dependence on the ratio (σA1ρtot)/(σB1ρα) (Fig. 14) is observed where the slope decreases with the number of effective charges Zeff.
indicating the stretching exponent in a one-component system with the same total number density. For sufficiently strong electrostatic interaction, similar as for the reduced excess long-time self-diffusion coefficient, a nearly linear dependence on the ratio (σA1ρtot)/(σB1ρα) (Fig. 14) is observed where the slope decreases with the number of effective charges Zeff.
3.3 Comparison of freezing criteria
The Hansen–Verlet criterion51 uses the mean structure factor as freezing criterion. Since in our case all partial structure factors are identical, also the mean structure factor 〈Sαβ(Q)〉αβ is identical to the partial ones. We found that with a number of effective charges larger than Zeff ≳ 450 the Hansen–Verlet criterion max[〈Sαβ(Q)〉αβ] ≳ 2.85 is exceeded, predicting a frozen state for the entire binary mixture (Table 3).| Z eff | max[〈Sαβ(Q)〉αβ] |
|---|---|
| 300 | 2.107(23) |
| 350 | 2.363(24) |
| 400 | 2.65(4) |
| 450 | 2.885(25) |
| 500 | 3.14(4) |
| 550 | 3.38(4) |
| 600 | 3.57(5) |
Löwen et al.52 proposed a reduced long-time self-diffusion coefficient D(L)S,a/D0,α ≲ 0.098 as a dynamic freezing criterion for species α. For an effective one-component system with Zeff = 450, opposite to the Hansen–Verlet criterion, the dynamic freezing criterion predicts a non-frozen state. Due to the reduced long-time self-diffusion coefficient of particles with σB = 50 nm in presence of particles with σA = 100 nm at identical number densities 1ρA = 1ρB, this dynamic freezing criterion predicts a selectively frozen state of the more mobile subsystem B and a non-frozen state of the less mobile species A in a binary mixture. (cf. Tables S1 and S2 in the ESI.†)
Both for one-component systems and binary mixtures, the long-time limits of reduced partial intermediate scattering functions Sredαβ(Q, t → ∞) decay to zero indicating a liquid-like state for all here investigated systems. At a total number density of 1ρtot = 1 × 1018 m−3, systems with Zeff ≳ 450 effective charges do not melt starting from a bcc-structure. Hence, liquid-like ordered systems with Zeff ≳ 450 are metastable, supercooled liquids. Also for these systems, the Debye–Waller factors vanish, indicating a non-arrested state with still complete structural relaxation. Comparing the here discussed freezing criteria, only the Debye–Waller factor reliably distinguishes between a supercooled liquid and a colloidal glass.
4 Conclusion
In this paper, we investigate structure and dynamics of binary Yukawa systems. Preserving the strength of electrostatical interaction, i.e., the number of effective charges, we study the influence of different mobilities quantified by Stokes–Einstein short-time diffusion coefficients of differently sized particles. Due to practically identical interactions between all species, also the partial correlation functions are identical. Mediated by the electrostatic interaction, however, coupling effects both in long-time self-diffusion and collective diffusion are observed.The long-time self-diffusion coefficients of a less mobile species are enhanced by the presence of a more mobile, smaller species and vice versa. A dynamic coupling is also visible in collective dynamics in the relaxation rates as well as the functional form of the correlation decay in partial intermediate scattering functions calculated from time-dependent, partial correlation functions. These coupling effects are quantified by respective excess quantities using pure systems with the same interactions and total number densities as reference systems. For sufficiently strong electrostatic interactions, in first approximation a linear dependence of excess quantities on the ratio (σA1ρtot)/(σB1ρα) is identified.
Furthermore, we compare different freezing criteria for metastable liquid-like structures. Despite for systems with Zeff ≳ 450 effective charges at a total number density of 1ρ = 1 × 1018 m−3 the static Hansen–Verlet criterion indicates a completely frozen state and the dynamic Löwen criterion a selectively frozen state, all intermediate scattering functions asymptotically decay to zero in the long-time limit. Hence, a structural arrest is not observed in the here investigated systems.
We have demonstrated the feasability to calculate distinct van Hove functions for considerably large systems including mixtures giving access to partial, time-dependent pair correlation functions using massive parallel computing either on CPUs or GPUs. Due to correlation functions up to large correlation lengths intermediate scattering functions as spatial Fourier transforms are accessible with high accuracy as well. Intermediate scattering functions are valuable data for comparison either with experimental data resulting from quasielastic scattering experiments in the time domain or theoretical approaches such as mode coupling theory.
Including hydrodynamic interactions is a remaining task especially at higher volume fractions where a glass transition is expected. Using the available partial static structure factors as an input, multi-component mode coupling theory is capable to predict time-dependent processes such as self- and collective diffusion. The comparison of the here provided simulation data with multi-component mode coupling theory is a promising test for the latter approach.
Author contributions
Daniel Weidig: conceptualization (equal); funding acquisition (minor); investigation (equal); software (equal); validation (equal); visualization (equal); writing – original draft; writing – editing and revision (equal). Joachim Wagner: conceptualization (equal); funding acquisition (major); investigation (equal); software (equal); supervision; validation (equal); visualization (equal); writing – editing and revision (equal).Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors have no conflict to disclose.Acknowledgements
D. W. gratefully acknowledges financial support by “Stiftung Stipendien-Fonds des Verbandes der Chemischen Industrie” within their PhD scholarship program.Notes and references
- B. J. Berne and R. Pecora, Dynamic light scattering: with applications to chemistry, biology, and physics, Dover Publications Inc., New York, 2000 Search PubMed.
- P. N. Pusey, Liquids, freezing and glass transition, Elsevier Science Pub. Co., Amsterdam, 1991 Search PubMed.
- B. V. R. Tata, Curr. Sci., 2001, 80, 948–958 CAS.
- G. Szamel and H. Löwen, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 44, 8215–8219 CrossRef CAS PubMed.
- W. Götze and L. Sjögren, Rep. Prog. Phys., 1992, 55, 241 CrossRef.
- W. van Megen, S. M. Underwood and P. N. Pusey, Phys. Rev. Lett., 1991, 67, 1586–1589 CrossRef CAS PubMed.
- W. van Megen and P. N. Pusey, Phys. Rev. A: At., Mol., Opt. Phys., 1991, 43, 5429–5441 CrossRef CAS PubMed.
- J. Diaz Maier and J. Wagner, Phys. Rev. E, 2024, 109, 064605 CrossRef PubMed.
- M. O. Robbins, K. Kremer and G. S. Grest, J. Chem. Phys., 1988, 88, 3286–3312 CrossRef CAS.
- E. J. W. Verwey and J. T. G. Overbeek, Theory of the stability of lyophobic colloids, Elsevier Science Pub. Co., Amsterdam, 1948 Search PubMed.
- L. Assoud, R. Messina and H. Löwen, J. Chem. Phys., 2008, 129, 164511 CrossRef PubMed.
- T. Ott and M. Bonitz, Phys. Rev. Lett., 2009, 103, 195001 CrossRef CAS PubMed.
- G. J. Kalman, P. Hartmann, Z. Donkó, K. I. Golden and S. Kyrkos, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 043103 CrossRef PubMed.
- T. Ott, H. Löwen and M. Bonitz, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2014, 89, 013105 CrossRef CAS PubMed.
- P. Mishra, M. Mukherjee and S. Kumar, Mol. Phys., 2016, 114, 741–756 CrossRef CAS.
- J. M. Lynch, G. C. Cianci and E. R. Weeks, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 78, 031410 CrossRef PubMed.
- T. Narumi, S. V. Franklin, K. W. Desmond, M. Tokuyama and E. R. Weeks, Soft Matter, 2011, 7, 1472–1482 RSC.
- N. H. P. Nguyen, D. Klotsa, M. Engel and S. C. Glotzer, Phys. Rev. Lett., 2014, 112, 075701 CrossRef PubMed.
- K. Yeo, E. Lushi and P. M. Vlahovska, Phys. Rev. Lett., 2015, 114, 188301 CrossRef PubMed.
- T. Sentjabrskaja, A. R. Jacob, S. U. Egelhaaf, G. Petekidis, T. Voigtmann and M. Laurati, Soft Matter, 2019, 15, 2232–2244 RSC.
- M. Medina-Noyola, Phys. Rev. Lett., 1988, 60, 2705 CrossRef CAS PubMed.
- H. Acuña-Campa and M. Medina-Noyola, J. Chem. Phys., 2000, 113, 869–875 CrossRef.
- R. Krause, G. Nägele, J. Arauz-Lara and R. Weber, J. Colloid Interface Sci., 1992, 148, 231–240 CrossRef CAS.
- E. Arrieta, C. Je drzejek and K. N. Marsh, J. Chem. Phys., 1987, 86, 3607–3626 CrossRef CAS.
- O. Vázquez, J. Herrera and L. Blum, Phys. A, 2003, 325, 319–332 CrossRef.
- E. Schöll-Paschinger, D. Levesque, J.-J. Weis and G. Kahl, J. Chem. Phys., 2004, 122, 024507 CrossRef PubMed.
- P. Hopkins, A. J. Archer and R. Evans, J. Chem. Phys., 2008, 129, 214709 CrossRef PubMed.
- G. J. Kalman, Z. Donkó, P. Hartmann and K. I. Golden, Phys. Rev. Lett., 2011, 107, 175003 CrossRef PubMed.
- J. Méndez-Alcaraz and O. Alarcón-Waess, Phys. A, 1999, 268, 75–88 CrossRef.
- S. A. Khrapak, O. S. Vaulina and G. E. Morfill, Phys. Plasmas, 2012, 19, 034503 CrossRef.
- S. Khrapak, B. Klumov and L. Couedel, J. Phys. Commun., 2018, 2, 045013 CrossRef.
- H. Ohta and S. Hamaguchi, Phys. Plasmas, 2000, 7, 4506–4514 CrossRef CAS.
- J. G. Wang, Q. Li, X. Peng, G. B. McKenna and R. N. Zia, Soft Matter, 2020, 16, 7370–7389 RSC.
- E. Sanz and D. Marenduzzo, J. Chem. Phys., 2010, 132, 194102 CrossRef CAS PubMed.
- K. N. Dzhumagulova, T. S. Ramazanov and R. U. Masheeva, Phys. Plasmas, 2013, 20, 113702 CrossRef.
- A. Van Blaaderen, J. Peetermans, G. Maret and J. Dhont, J. Chem. Phys., 1992, 96, 4591–4603 CrossRef CAS.
- J. Wagner, W. Härtl and H. Walderhaug, J. Chem. Phys., 2001, 114, 975 CrossRef CAS.
- C. Lellig, J. Wagner, R. Hempelmann, S. Keller, D. Lumma and W. Härtl, J. Chem. Phys., 2004, 121, 7022–7029 CrossRef CAS PubMed.
- A. Rahman, Phys. Rev., 1964, 136, A405–A411 CrossRef.
- K. J. Gaylor, I. K. Snook, W. J. van Megen and R. O. Watts, J. Phys. A: Math. Gen., 1980, 13, 2513 CrossRef CAS.
- L. Yeomans-Reyna, H. Acuña-Campa, F. de Jesús Guevara-Rodríguez and M. Medina-Noyola, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2003, 67, 021108 CrossRef PubMed.
- M. A. Chávez-Rojo and M. Medina-Noyola, Phys. A, 2006, 366, 55–78 CrossRef.
- A. M. Leshansky, J. F. Morris and J. F. Brady, J. Fluid Mech., 2008, 597, 305–341 CrossRef CAS.
- A. J. Banchio, G. Nägele and J. Bergenholtz, J. Chem. Phys., 2000, 113, 3381–3396 CrossRef CAS.
- R. Higler, J. Krausser, J. van der Gucht, A. Zaccone and J. Sprakel, Soft Matter, 2018, 14, 780–788 RSC.
- A. Imhof and J. K. G. Dhont, Phys. Rev. E: Stat. Phys., Plasmas, Fluids, Relat. Interdiscip. Top., 1995, 52, 6344–6357 CrossRef CAS PubMed.
- G. Nägele, J. Bergenholtz and J. K. G. Dhont, J. Chem. Phys., 1999, 110, 7037–7052 CrossRef.
- G. Foffi, W. Götze, F. Sciortino, P. Tartaglia and T. Voigtmann, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2004, 69, 011505 CrossRef CAS PubMed.
- A. L. Thorneywork, D. G. A. L. Aarts, J. Horbach and R. P. A. Dullens, Phys. Rev. E, 2017, 95, 012614 CrossRef PubMed.
- M. Tamashiro, V. B. Henriques and M. Lamy, Langmuir, 2005, 21, 11005–11016 CrossRef CAS PubMed.
- J.-P. Hansen and L. Verlet, Phys. Rev., 1969, 184, 151–161 CrossRef CAS.
- H. Löwen, T. Palberg and R. Simon, Phys. Rev. Lett., 1993, 70, 1557–1560 CrossRef PubMed.
- D. Thirumalai, J. Phys. Chem., 1989, 93, 5637–5644 CrossRef CAS.
- R. Zwanzig, J. Chem. Phys., 1960, 33, 1338–1341 CrossRef CAS.
- R. Zwanzig, Phys. Rev., 1961, 124, 983 CrossRef CAS.
- H. Mori, Prog. Theor. Phys., 1965, 33, 423–455 CrossRef.
- H. Mori, Prog. Theor. Phys., 1965, 34, 399–416 CrossRef.
- D. L. Ermak, J. Chem. Phys., 1975, 62, 4189–4196 CrossRef CAS.
- D. L. Ermak, J. Chem. Phys., 1975, 62, 4197–4203 CrossRef CAS.
- D. L. Ermak and J. A. McCammon, J. Chem. Phys., 1978, 69, 1352–1360 CrossRef CAS.
- P. Hopkins, A. Fortini, A. J. Archer and M. Schmidt, J. Chem. Phys., 2010, 133, 224505 CrossRef PubMed.
- A. Torres-Carbajal, F. J. Sevilla, L. A. Nicasio-Collazo, M. Medina-Noyola and R. Castañeda-Priego, Mol. Phys., 2023, e2292749 CrossRef.
- F. J. Bermejo, M. García-Hernández, B. FÅk, J. Alonso, J. L. Martínez and T. Mason, Europhys. Lett., 1993, 24, 545 CrossRef CAS.
- W. Götze, Complex dynamics of glass-forming liquids: A mode-coupling theory, Oxford University Press, New York, 2009 Search PubMed.
- K. Amann-Winkel, F. Löw, P. H. Handle, W. Knoll, J. Peters, B. Geil, F. Fujara and T. Loerting, Phys. Chem. Chem. Phys., 2012, 14, 16386–16391 RSC.
- A. Ghosh, J. Phys. Chem. B, 2023, 127, 5162–5168 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical values of reduced long-time self-diffusion coefficients, relaxation rates and stretching exponents for binary Yukawa-systems. See DOI: https://doi.org/10.1039/d4sm01123f |
| This journal is © The Royal Society of Chemistry 2024 |