Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Solvent-free confinement of ordered microparticle monolayers: effect of host substrate and pattern symmetry†
Ignaas S. M.
Jimidar‡
 *ab,
Mitch T. J.
de Waard‡
*ab,
Mitch T. J.
de Waard‡
 ab,
Gijs
Roozendaal
bc and
Kai
Sotthewes
ab,
Gijs
Roozendaal
bc and
Kai
Sotthewes
 *c
*c
aDepartment of Chemical Engineering CHIS, Vrije Universiteit Brussel, Brussels 1050, Belgium. E-mail: ignaas.jimidar@vub.be
bMesoscale Chemical Systems, MESA+ Institute, University of Twente, 7500AE Enschede, The Netherlands. E-mail: i.s.m.jimidar@utwente.nl
cPhysics of Interfaces and Nanomaterials, MESA+ Institute, University of Twente, 7500AE Enschede, The Netherlands. E-mail: k.sotthewes@utwente.nl
First published on 8th November 2024
Abstract
The self-organisation of individual suspended colloids into ordered structures that can be mediated by confinement has garnered interest recently. Despite the push for solvent reduction for sustainability reasons, the comprehension and development of solvent-free assembly methods remain largely unaddressed. In this study, we explore the effect of confinement without rigid geometrical constraints, i.e., wall-less confinement on the assembly of monodisperse PMMA powder microspheres (diameters of 3 μm and 10 μm) on fluorocarbon-patterned heterogeneous substrates using a solvent-free rubbing assembly approach. Our findings reveal that the PMMA microspheres self-align on the fluorocarbon patterns, adapting to various geometrical shapes of these patterns through symmetry matching. The assembly process is driven by triboelectric charging and elastic properties of the microspheres and substrates. Moreover, we observe that the host substrate and the particle and pattern size ratio significantly influence the ordering of the microparticles on the fluorocarbon patterns. Ultimately, we demonstrate the successful use of fluorocarbon patterns to assemble tunable crystal patterns on rigid substrates, which typically do not exhibit any ordering.
1 Introduction
The self-organisation of individual building blocks into organized large collective structures is ubiquitous in nature at different length scales, e.g., molecules, living cells, colloidal particles, granular matter, a flock of animals, pedestrians, robots, and even objects in space.1–4 In particular, the controlled assembly and crystallisation of colloids and granular matter into ordered structures is appealing from fundamental perspective,5–10 but can also be advantageous for a sustainable society as these structures unlock many industrial applications, e.g., photonics, smart materials and sensors, surface coatings, robust light-weight materials, and miniaturized devices.11–14 As such, the literature on colloidal assembly is extensive.8,11,14Another approach gaining attention within the soft matter community is steering the self-organisation of individual building blocks through the confinement of different natures, e.g., inside microfluidic chips or simply using an evaporating suspension droplet.2,8,15,16 By spatially confining colloids, their translational and rotational degrees of freedom are restricted, altering possible configurations or system order.
Research on colloidal self-assembly phenomena into ordered structures has been primarily devoted to colloidal particles in suspension, using so-called “wet assembly” techniques. However, the impetus for reducing solvent waste towards more sustainable processes elucidates the necessity of comprehending solvent-free assembly, i.e., “dry assembly” methods.17 To achieve this anticipated transition, a handful of dry assembly methods have been proposed on different length scales (size of building blocks) over the last decades as recently surveyed by Sotthewes and Jimidar,17 including shaking,18–20 acoustic-driven,21 vacuum-assisted techniques,22,23 and rubbing.24–27
The rubbing method has recently emerged as an advanced solvent-free assembly approach to rapidly (<20 s) attain large areas of ordered crystals, spherical colloids and cubic particles,28 using polydimethylsiloxane (PDMS). Recently, Sotthewes et al.26 have reported the assembly of tunable hexagonal closely packed (HCP) arrays driven by triboelectrification and contact mechanics. Triboelectrification or contact electrification is the process of spontaneous electrical charge exchange when two bodies are in frictional contact.29,30 The exact mechanism at the onset of triboelectric charging has not been resolved yet, as many factors can play a role.29,30 A few of the mechanisms include electron transfer,30 material transfer and bond scission in polymers,31 mechanochemistry,32–34 and water or humidity in ambient air.30,35–37 In particular, understanding the role of ambient humidity or water in contact electrification charging/discharging has garnered interest in the context of improving the performance of triboelectric nanogenerators (TENGs) and other green energy harvesting applications.34,36
Besides the tribocharging-driven rubbing assembly proposed by Jimidar and co-workers,25,26 the Whiteside group explored the agitation concept to self-assemble millimetre-size polymer beads19,20 into closely packed crystals of different symmetry structures using the triboelectrification mechanism. On the other hand, Jimidar et al.18 reported that agitation was not commensurate with the scale to achieve a closely packed monolayer of silica and polystyrene microspherical particles (3–10 μm).
The solvent-free rubbing method offers significant control over the order and positioning of a broad spectrum of particles (size and material), enabling the assembly of ordered crystals on any desired pattern.26 By utilizing a fluorocarbon-patterned (heterogeneous) substrate, microparticles are laterally confined to the patterns, despite the fluorocarbon pads being at least 50 nm higher than the host substrate. This confinement occurs without physical boundaries or rigid walls, referred to as wall-less confinement. The driving mechanism underpinning this confinement is the differences in triboelectric charging and contact mechanics forces between the fluorocarbon coating and the host substrate. However, the effect of the host substrate and size of the fluorocarbon patterns on the ordering of the particles remains unaddressed.
In this study, we leverage the solvent-free rubbing method to investigate the self-alignment of poly(methyl methacrylate) (PMMA) powder into hexagonal closely packed (HCP) monolayer arrays on fluorocarbon-patterned substrates. Using the Voronoi tessellation approach, we quantify the order of the assembled monolayers composed of monodisperse PMMA microspheres (3 and 10 μm) on the wall-less confined fluorocarbon patterns. Their effect on particle orderings is examined by varying the shape and size of the fluorocarbon pattern and the type of host substrate (glass and SiO2). Our findings show that particles are confined to the CFx and match the geometrical shape of the pattern, affecting the local ordering of the particles. Additionally, the edge between the fluorocarbon pattern and host substrate plays a crucial role in the order achieved using the rubbing assembly process. The insights gained in this study will impact our understanding of reaching and tuning structural ordering using solvent-free (dry) assembly methods, addressing the need for designing greener assembly processes.
2 Experimental and analysis section
2.1 Materials and methods
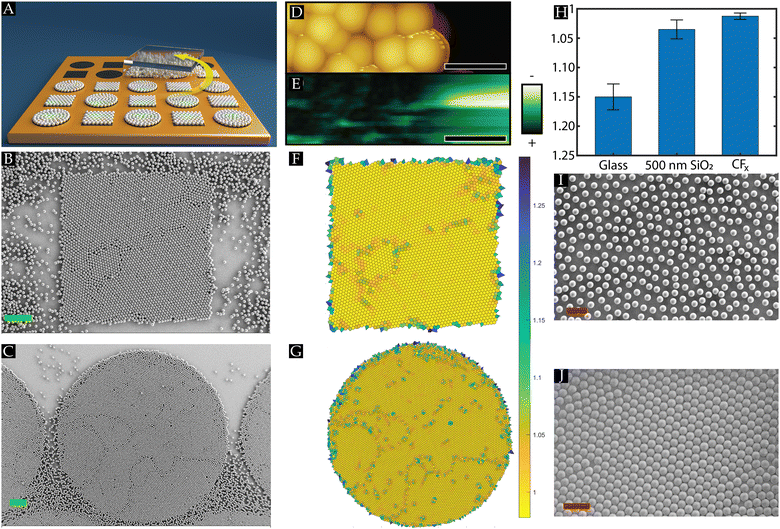
The rubbing experiments, illustrated in Fig. 1(A), were performed using monodisperse dry PMMA powder (15 ± 3 mg) with a diameter of (3.04 ± 0.11) μm, and (9.95 ± 0.22) μm that were purchased from microParticles GmbH. The manufacturer provided the standard deviations on the particle diameter. Note that the rubbing assembly (cf.Fig. 1(A)) is a dynamic process, and concomitantly time-dependent. Since only the final result can be microscopically examined, we repeated the process at least 6 times to gain sufficient statistics. All experiments were performed under standard lab conditions (T = 21 ± 1 °C and RH = 40–55%). The temperature and humidity are measured with a Digital Professional Thermo-Hygrometer KLIMA BEE, TFA, Germany.The substrates are patterned using plasma polymerisation using a 50–75 nm thick fluorocarbon (CFx with 2 ≤ x ≤ 3) coating. The manufacturing process of these patterned substrates is described in detail in our previous studies,25,26 to which the interested reader is kindly referred.
Kelvin probe force microscopy (KPFM) measurements are performed using a Bruker icon atomic force microscope (AFM) under ambient conditions with RH = 45–50% (measured with a TFA Digital Professional Thermo-Hygrometer KLIMA BEE). A heavily boron-doped diamond cantilever with a resonance frequency of 100 kHz and a force constant of 8 Nm−1 (FM-LC, Adama Innovations) was used. The FM-KPFM mode is utilized to detect the electrostatic gradient through the frequency shift of the cantilever oscillation. During the KPFM measurement, the tip was grounded, allowing the determination of the contact potential difference (VCPD) using the following equation:
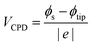 | (1) |
2.2 Structure analysis of particle monolayer arrays
After rubbing the particles onto the substrates, optical microscopy images were captured using a Leica DM2500 MH microscope connected to a ZWO ASI294MC Pro camera, while in some instances, scanning electron microscopy (SEM) images were taken using a ZEISS Merlin high-resolution scanning electron microscope.Voronoi diagrams were constructed from the images using MATLAB routines to characterize the structure of the PMMA monolayers. A Voronoi diagram is constructed by using the centres of the microspheres to partition the space into polygonal cells comprising points closer to one microsphere centre than to all the others, as elaborated in Sections S1 and S2 of the ESI.†![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 38,39 The shape of each obtained Voronoi cell i can be described by computing a dimensionless quantity ϑi, called shape factor:
38,39 The shape of each obtained Voronoi cell i can be described by computing a dimensionless quantity ϑi, called shape factor:
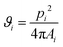 | (2) |
The orientational order of the obtained monolayers can be quantified by computing the local 6-fold bond-orientation, or hexatic, order parameter ψ for each particle, which is defined as:10,40
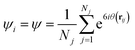 | (3) |
One can also compute the spatially averaged orientational order parameter ψav of an ensemble of N particles as:
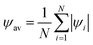 | (4) |
3 Results and discussion
3.1 Initial observations on rubbing-induced assembly
Dry monodisperse PMMA powder sandwiched between a PDMS stamp and another fluorocarbon-patterned substrate is manually rubbed for approximately 20 seconds in a circular motion across the substrates to assemble a monolayer array of hexagonal closely packed (HCP) crystal structures, as depicted in Fig. 1(A). We vary the geometrical shape and size of the confined CFx patterns (height of 50–75 nm) on the heterogeneous host substrates. During the rubbing motion, the operator applies a pressure P, which can be adjusted to assemble a monolayer array depending on two extreme cases: when the applied pressure is too high, the assembled monolayer of particles is disturbed, whereas, at low pressures, the powder is not spreading across the substrate, hindering the assembly process.26 It has been reported that soft-elastomeric substrates, like PDMS, induce a rolling motion on the spherical particles confined between the PDMS stamp and the substrate, which promotes the formation of the closely packed monolayer, i.e., HCP crystal structures.24,26Initial rubbing experiments were performed on a fluorocarbon-patterned SiO2 substrate using 10 μm PMMA powder microspheres. It is striking to observe from Fig. 1(B) and (C) that despite the circular rubbing motion, the PMMA microspheres self-aligned into HCP crystal monolayers matching the geometrical shapes, square or circular, of the wall-less confined CFx patterns. This result indicates that the spherical PMMA powder particles have a strong preference to remain and stick to the fluorocarbon coating rather than the SiO2 substrate, highlighting that a key aspect for assembling HCP crystals on the substrates is the presence of sufficient adhesion between the microspheres and underlying substrate. Our team recently reported that the main drivers for sufficient adhesion between the PMMA microspheres and the fluorocarbon coating are the contact mechanics force due to elastic deformations of the particles and the underlying surface and the triboelectric charging phenomenon.26 The latter is induced as the microspheres and substrates get into frictional contact during the rubbing motion.
The triboelectric charging is supported by KPFM measurements performed on the PMMA particles and the fluorocarbon coating. The contact potential difference VCPD on the PMMA particles and the CFx coating is measured, and it can be observed from Fig. 1(D) and (E) that the particle mainly acquired a positive polarity, whereas the fluorocarbon coating was negatively charged. It should be noted that prior to the rubbing experiments, the PMMA particles were negatively charged.25 This implies that as the particles roll across the substrate, charge is exchanged from the particles to the fluorocarbon coating, which aligns with the triboelectric series.29 Thus, a tribocharging-induced electrostatic attraction exists between the PMMA particles and the coating. It is remarkable that although most of the PMMA particles have the same polarity, a closely packed monolayer is present, as one would expect that Coulombic repulsion between the particles would counter crystal formation. As such, it is elucidated that the electrostatic attraction between the PMMA microspheres and the fluorocarbon coating is sufficiently strong to overcome the repulsive force, enabling the assembly of HCP crystals. We want to point out that humidity effects may also influence the triboelectric charging between the PMMA particles and CFx coating, particularly due to their difference in hydrophobicity.35,37 However, to exclude humidity effects, experiments were performed only under ambient conditions.
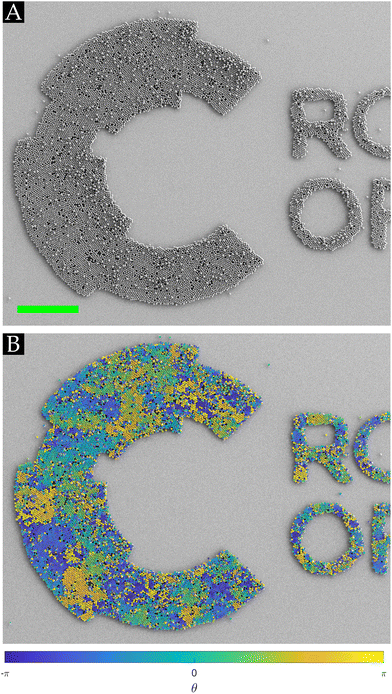
As noticed before, the area of the conspicuously present closely packed monolayers matches the geometrical shape of the confined coating patterns exhibiting symmetry structures and defects, e.g., a few excess particles on top, voids and grain boundaries, even though the rubbing direction is performed randomly. These symmetry structures and defects can be identified and quantified using Voronoi decomposition,39,41 as showcased in Fig. 1(F) and (G). Since our interest is in hexagonal symmetries, each cell in the Voronoi diagrams is coloured according to its normalized shape factor ϑ, such that a perfect hexagonal cell ϑnorm,hex = 1. A feature that can be readily observed from Fig. 1(F) and (G) is that seemingly at the edge of the wall-less confined patterns, the symmetry structures in the monolayers were distorted, indicating that interactions of the particles on the edge (interface) between the coated and uncoated part of the host substrate were altered. Furthermore, defects associated with the misalignment of grains, e.g., square symmetry structures between two grains, indicate that grains with different orientations were assembled during the rubbing motion. This implies that several nucleation sites grow into larger HCP crystal structures as the rubbing process is performed. The assembled crystals then move as a single entity on the surface during the rubbing motion, as shown by Park et al.24. Since no geometrical constraint exists in the system, the attained crystals can leave the confined CFx spaces during the rubbing assembly process, which changes the interaction forces acting on them when entering the uncoated areas on the heterogeneous substrate. When the particles slide instead of rolling, they also tend to disturb already assembled crystal structures due to their high kinetic energy, causing voids in the crystal domains.24 Therefore, Section 3.2 will elaborately discuss the effects of the geometrical shape and size of the fluorocarbon patterns, as well as the properties of the host substrate on the defects and the symmetrical order present within the assembled monolayers.
Next to the HCP crystals on the CFx coating, Fig. 1(B) and (C) show PMMA microspheres, mostly single particles, on the uncoated SiO2 substrate. It is noteworthy that mostly the uncoated areas between the fluorocarbon patterns also contained HCP crystal structures, i.e., the assembly of HCP crystals was not limited to the fluorocarbon layers. This can be corroborated by our earlier reported findings26 in which it was shown that similar to the fluorocarbon coating, the adhesion on the SiO2 substrate was also promoted due to the contact mechanics and tribocharging mechanism. However, on the SiO2 substrate, it was observed that the assembled monolayers were less stable as these could be disturbed during the rubbing motion, and more powder supply was needed to form these monolayers.26 This observation ascertains distinct interactions on the coated and uncoated areas, i.e., the adhesion on CFx was stronger than the SiO2 substrate, which is ascribed to the lower Young's modulus26 and the stronger triboelectrification property of the CFx layer.35 This explains why certain areas on the substrate were still visible where we could distinguish between the fluorocarbon patterns covered with closely packed monolayers and the uncoated substrate (cf.Fig. 1(B) and (C)).
The above discussion underscores that by tuning the interactions induced during the rubbing motion between the microspheres and surface (triboelectric charging and contact mechanics), the structural order can be laterally confined on the CFx patterns. The confinement is achieved without the use of physical boundaries or rigid walls, i.e. wall-less confinement. The properties of the chosen materials (coating surface as well as the host surface) determine the efficiency of the lateral confinement. This underlines the necessity of a host substrate on which the formation of HCP crystals is not promoted such that we can examine the effect of the confined CFx pattern geometry and size on the assembled symmetry structures. This implies that the PMMA powder particles should clearly discriminate between the fluorocarbon layer and the surrounding host substrate. To select such a substrate, we first compare two available substrates that we have, namely SiO2 and borosilicate glass substrates, on which the fluorocarbon patterns can be applied. This comparison is performed by assembling closely packed monolayers on 8 smaller samples (14 × 14 mm2) of these homogeneous substrates. Subsequently, the quality of these monolayers can be quantified by determining the average normalized shape factor (ϑnorm,av = 1).
Fig. 1(H) displays the normalized shape factor (ϑnorm,av) values obtained on the bare SiO2 and glass substrate and a uniformly fluorocarbon-coated SiO2 substrate. Given the discussion above, it is unsurprising that the best results with closely packed monolayers were attained on the fluorocarbon-coated substrates. As mentioned, the closely packed monolayers are present on the SiO2 substrates but can be disturbed, as the particles experience a lower adhesion than on the fluorocarbon coating. This results in a lower ϑnorm,av with a lower reproducibility. In contrast, on the glass substrate, it can be readily observed that HCP crystal structures were scarcely present. It should be remarked that similar to the other surfaces, glass is also an insulator and is also shown to become tribocharged.25 On the other hand, the glass substrate is stiffer (Y = 89 ± 5 GPa) compared to the SiO2 (Y = 54 ± 5 GPa) and the fluorocarbon coating (Y = 21 ± 5 GPa),26 resulting in smaller elastic deformations on the glass surface. This leads to a lower contact mechanics force and, concomitantly, to less adhesion between the PMMA particles and glass substrate, impeding the assembly of HCP crystals (cf.Fig. 1(I)).
On the other hand, we could observe regions, albeit relatively small domains, of HCP crystals on a full glass wafer (cf.Fig. 1(J)). Like the small samples (Fig. 1(I)), the full glass wafer was also covered with single PMMA microspheres. This elucidates that assembled crystals are less stable on the uncoated glass wafer. Furthermore, these results support the notion that nucleation sites are needed to promote the assembly of the HCP crystals, and a larger substrate inherently contains more available sites than a sample with a smaller area. Moreover, on a smaller sample, the PDMS rubbing stamp moves more frequently past the same region, increasing the chances of disturbing any HCP crystallized seeds compared to larger wafers. Thus, HCP crystals are demoted on the glass wafer, i.e., the poor ordering on glass.
These results highlight that changing the substrate properties and concomitant interactions between them and the PMMA microspheres can change the system's order. As such, the confined CFx pattern were applied on two different host substrates (SiO2 and glass) on which distinct structural ordering was expected from the data shown in Fig. 1(H). Consequently, the following sections will give us insights into how the geometrical shape and size of the wall-less confined CFx patterns combined with the host substrate affect the order of the assembled monolayer arrays on respective patterns.
3.2 Fluorocarbon squares: influence of the host substrate and pattern size
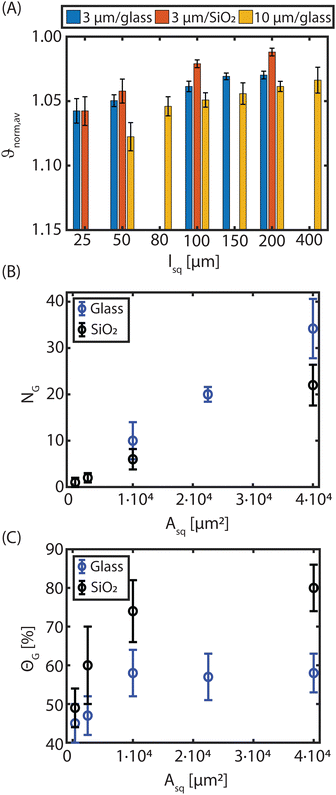
To further investigate the influence of the host substrate on the ordering of the assembled monolayer arrays, square fluorocarbon patterns of different dimensions are made on glass and SiO2 host substrates. The order of the assembled arrays, particularly HCP crystals, on the wall-less confined fluorocarbon squares, is quantified by determining the normalised shape factor ϑnorm,av.The result is shown in Fig. 2(A) and reveals a clear decrease of the shape factor as the square area increases. This holds for all three investigated cases on the CFx patterns: (i) 3 μm PMMA on the glass host substrate (blue bars), (ii) 3 μm PMMA on SiO2 as a host substrate (red bars) and (iii) 10 μm PMMA on glass as a host substrate (yellow bars). In the case of the 3 μm PMMA particles, it can be readily observed that for small square sizes, no difference is observed between a glass and a SiO2 surface, whereas distinct results are obtained on larger CFx squares to the extent that significantly better ordered monolayers comprising HCP crystals are attained when the SiO2 surface is utilized as the host substrate. This result agrees with previous studies.25,26 When 10 μm PMMA particles are used on glass, a similar trend is observed as for the 3 μm particles, the ordering is improved (lower ϑnorm,av values) with increasing pattern size. In contrast to the 3 μm sized spheres, the highest possible packing density (lowest ϑnorm,av) is not yet reached on the largest square sizes26 and ϑnorm,av is higher for similar square sizes. Altogether, these observations elucidate that a combined effect of particle size, the interface between patterns and host substrate, and the pattern size affects the ordering of the arrangements on the wall-less confined CFx patterns.
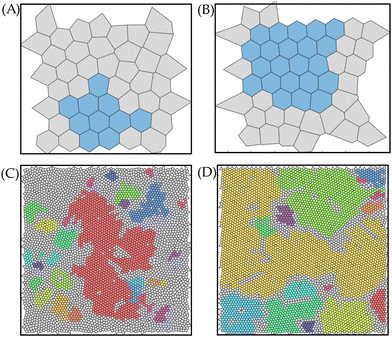
As noted before, deviations from ϑnorm,av = 1 (HCP crystals) are mainly caused by grain boundaries, defects, second layer particles and/or poor ordering of particles at the edges. From Fig. 1(F) and (G), it was already inferred that HCP crystal domains with different orientational order, i.e. various grains, were attained during the rubbing assembly on the CFx patterns. As such, we examine the rotational order to identify the assembled crystal structures on the CFx squares, as elaborately discussed in Section S3 of the ESI.†Fig. 3 shows that on the large squares, poly-crystalline monolayers were attained, whereas a single crystal, albeit relatively small, were attained on the smallest CFx square. In addition, Fig. 3 suggests that larger grains can be obtained on these square patterns when the SiO2 substrate is utilized as a host. Therefore, we quantified the number of grains (NG), i.e. HCP particles with a specific rotational orientation and their corresponding size on the fluorocarbon squares on the glass and SiO2 substrate. Fig. 2(B) shows that the number of grains present on the confined CFx squares is lower for the SiO2 substrate than the glass host, while the grain size on the larger squares is relatively larger on the SiO2 host compared to glass (cf.Fig. 3).
To explain the observations, two-dimensional (2D) classical nucleation theory (CNT) is used as the microspheres are confined between the surface and the stamp during the rubbing assembly process. The CNT uses two terms to obtain an expression for the free energy of the formation of a nucleus.42–45 Particles at the perimeter add a positive energy term through the edge line tension and particles in the bulk add a negative term due to the free energy gained from bonding to a crystal (cf.eqn (5)). For a circular flat grain of size A, the Gibbs free energy (G) is given by
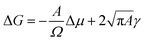 | (5) |
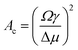 ) tend to decay, while grains that are larger have the tendency to grow.
) tend to decay, while grains that are larger have the tendency to grow.
The CNT explains the roughly linear increase of NG with increasing square size (Fig. 2(B)). As the available area of the confined CFx squares doubles, the number of critical nuclei that can occupy this area also doubles. Hence, a linear dependence is expected between the number of grains and the area. Eqn (5) also accounts for the observation with larger microspheres. For the 10 μm PMMA spheres, a larger critical nucleus size is expected (large Ω, thus a larger Ac is needed), resulting in fewer nuclei per square. Since the critical nucleus size scales with Ω2, the squares need to be approximately 10 times larger (>1 × 1 mm2) for 10 μm particles compared to 3 μm particles to achieve low ϑnorm,av, i.e., highly ordered monolayers comprising HCP crystals. In a previous study, we demonstrated that 10 μm microspheres can be assembled in HCP crystals using larger pattern dimensions of fluorocarbon-coated areas.26 This is further supported by the data presented in Fig. 1(H) compared to Fig. 2(A), as low ϑnorm,av was attained on the uniformly coated fluorocarbon-coated substrates (14 × 14 mm2) compared to significantly smaller confined squares in the latter case.
From the slopes of the curves in Fig. 2(B), the average areas (particles and surrounding spaces) per grain (AG, not to be confused with the grain size) are extracted, which are approximately 30 × 30 μm2 for glass and 45 × 45 μm2 for SiO2 (when projected on a square grain). Thus, the smallest squares in this study (25 × 25 μm2) are smaller than AG and indeed, only one grain (and sometimes even no grain) is present on an average on these squares (Fig. 2(B)). However, the average normalized shape factor is large, indicating poor overall ordering.
The relatively high-shape factor for small square sizes is reflected in the total grain coverage (ΘG, relative to the square area), shown in Fig. 2(C). For the small confined CFx squares, coverage of <50% is obtained regardless of the host surface. This is due to the small grain sizes (much smaller than AG) that result in ill-defined grain boundaries and poor ordering of the microspheres.
As the wall-less confined squares on the heterogeneous substrates become larger, the grain coverage also increases, decreasing the shape factor (Fig. 2). Larger grains imply that the proportion of grain boundaries and defects on the overall ordering decreases, reducing the average shape factor. For large CFx squares, the difference between the glass and SiO2 host substrates becomes more pronounced. The coverage on the CFx squares is twice as large on SiO2 compared to glass, even though the number of grains is less (Fig. 2(B) and (C)). This is attributed to the much larger grain sizes obtained when a SiO2 host substrate is involved (see Fig. 3(C) and (D) and Fig. S5 in ESI†). In addition, it is observed that on the 200 μm CFx squares on the SiO2 host substrate, the normalized shape factor coincides with the value obtained on uniformly fluorocarbon-coated samples (cf.Fig. 1), implying the order enhancement effect that the SiO2 substrate has on the formation of HCP monolayers.
The above observations underscore a combined effect of the confined CFx squares and the host substrate on the order of the attained monolayer arrays using the solvent-free rubbing assembly process. As elaborated in the previous section (Section 3.1), rolling particles are needed during the rubbing process to attain ordered structures.17,24,26 Due to the wall-less confinement, the microspheres can enter, leave or stay on the CFx patterns, affecting their assembly behaviour. Those that are located and stay on the CFx pattern are arranged into ordered structures, as shown in Fig. 1(B) and (C) and previous studies.17,26
Assembled grains attained on the CFx layer, which cross the edge towards the host substrate may remain intact or be disturbed, depending on the host substrate's properties, as was noted in Section 3.1. Due to the higher contact mechanics force and the better triboelectric charging, particles tend to roll more easily on SiO2 (resulting in a lower shape factor, see Fig. 1(H)) compared to glass,26 making them less likely to be disturbed when crossing the edge. This promotes grain formation. Additionally, the formation of closely packed monolayers will be promoted on SiO2 (see Fig. 1(H)), increasing the likelihood that an ordered monolayer can cross the edge to the CFx layer as a grain, further enhancing grain formation and ordering on the CFx layer. This is reflected in the values found for AG, which are higher for SiO2 compared to glass. Therefore, the grain size and the ordering heavily depend on the host substrate and pattern material. As noted before, glass is a poor performing host substrate, significantly affecting the grains on the CFx squares. Thus, as the host substrate's properties improve, AG and ΘG will increase, while NG will decrease as the host substrate aids in the formation of larger grains.
Altogether, the results elucidate that particle arrangement on the confined CFx square patterns is significantly affected by the host substrate in two main ways: (i) the formation of grains on the host substrate that are transferred to the CFx squares, and (ii) the disturbance of pre-existing grains that cross the wall-less edge towards the host substrate. The quality of particle ordering is determined by both the contact mechanics force and the triboelectric charging strength of the host surface.17,26 In addition, larger patterns exhibit better particle arrangement (for the same particle size) due to the reduced influence of the host substrate, leading to larger grains (cf. Fig. S5, ESI†) and relatively fewer grain boundaries or defects. However, the edge and its geometry have not been considered in this analysis, which is investigated in the next section.
3.3 Fluorocarbon geometrical shapes: edge effect
As briefly pointed out in Section 3.1, the geometrical shape of the confined CFx patterns seemingly affected the order, particularly at the edge. Therefore, the influence of the edge confinement on the particle ordering is explored in this section, focusing on the geometrical shape and symmetry. To make a fair comparison between the different patterns, a form factor is introduced, which is defined as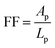 with Ap being the pattern area and Lp being the pattern perimeter. A higher form factor indicates a larger surface area of the confined CFx pattern with a relatively small edge (perimeter) contribution.
with Ap being the pattern area and Lp being the pattern perimeter. A higher form factor indicates a larger surface area of the confined CFx pattern with a relatively small edge (perimeter) contribution.
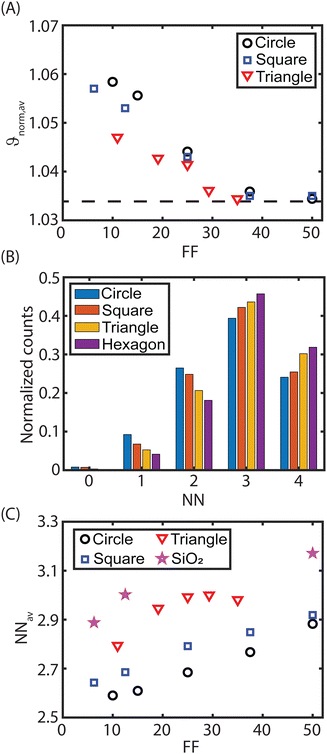
Fig. 4(A) presents the normalized average shape factor as a function of the form factor for different geometries of the CFx patterns on the glass substrate. Similar to the squares in Fig. 2(A), ϑnorm,av decreases for circles and right-angle triangles as the form factor increases (or larger pattern sizes), and ϑnorm,av saturates at higher FFs. For all three geometries on the heterogeneous glass substrate, the shape factor converges to approximately the same shape factor, suggesting that for large patterns, geometry has a minor to negligible effect on the order of the assembled monolayers. However, as soon as the different geometrical patterns become smaller, distinctive packing orders are attained on the various patterns.
The local ordering of particles at the edge is analysed to further examine the geometrical effect of the CFx pattern on the quality of the assembled packing. As such, this analysis focuses solely on particles located at the edge of the pattern, i.e., the interface between the CFx pattern and host substrate. Using this analysis, the number of nearest neighbours (NNs) is quantified for each individual particle at the edge (cf. Section S4 in ESI†), which can range from zero (no neighbours) to four (the maximum number of neighbours). A distribution of the number of the nearest neighbours for different geometrical shapes is shown in Fig. 4(B) and Fig. S4 (ESI†) for various form factors. Across all geometries (and form factors), the contribution of particles at the edge with three neighbours is most common, but their relative distribution varies. Circular patterns host more edge particles with two neighbours than four neighbours, while this trend is reversed for right-angle triangular and hexagonal geometries.
From the neighbours’ distribution shown in Fig. 4(B), the average number of the nearest neighbours is calculated by 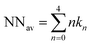 with n being the number of the nearest neighbours and kn being the percentage of particles with the nearest neighbours n. In Fig. 4(C), the average number of the nearest neighbours is plotted as a function of the form factor. As expected based on Fig. 4(B), the right-angle triangular geometry exhibits the best particle ordering at the edge. For the triangular pattern NNav remains constant for large form factors, unlike the square and circular geometries, where NNav continues to increase with larger FF.
with n being the number of the nearest neighbours and kn being the percentage of particles with the nearest neighbours n. In Fig. 4(C), the average number of the nearest neighbours is plotted as a function of the form factor. As expected based on Fig. 4(B), the right-angle triangular geometry exhibits the best particle ordering at the edge. For the triangular pattern NNav remains constant for large form factors, unlike the square and circular geometries, where NNav continues to increase with larger FF.
The quality of particle arrangement at the edge follows the order: circle < square < right-angle triangle for all form factors. This sequence is also observed in ϑnorm,av for small form factors (FF < 30, Fig. 4(A)). This observation can be directly attributed to a discrepancy in the symmetry of the CFx pattern and the packing symmetry of the assembled PMMA microspheres. When the microspheres are arranged in an HCP orientation, a three-fold symmetry is present, matching the three-fold symmetry of triangular patterns. On small right-angle triangular patterns, a single grain of HCP-assembled particles can align with two of the three edges. However, in the 90° corner of the right-angle triangle, the ordering is locally disrupted due to the mismatch in symmetry. On the other hand, for square patterns, only two of the four edges would match the grain symmetry. Especially, at the corners of the pattern, disordered particle assembly is obtained, resulting in fewer neighbouring particles (Fig. 4(C)). Regarding the circular patterns, it is obvious that straight edges are absent, preventing alignment with HCP grain symmetry, which leads to even lower local ordering compared to the other geometries. Thus, the results highlight that the edges influence the ordering, while perfect ordering is unequivocally also affected by the host substrate (Section 3.2). Perfect ordering is occasionally achieved on small patterns, particularly on equilateral triangles, where the 60° angles align perfectly with the three-fold symmetry of the HCP-arranged particles.
As the form factor increases, the impact of the geometrical shape of the pattern and its symmetry on the overall particle ordering diminishes, as shown in Fig. 4(A). This reduction is caused by two factors: (i) the larger pattern-to-particle ratio and (ii) the reduced edge influence on the ordering. With larger patterns, the pattern-to-particle ratio increases, reducing the influence of the CFx pattern corners that define their symmetry. More particles experience straight edges, which simplifies the particle arrangement through grain rotation compared to alignment in corners. This is particularly true for larger circles, where the edge becomes locally straighter, enhancing edge ordering and increasing the average number of nearest neighbours (NNav). Additionally, the influence of the edge is reduced on the total ordering, as shown in Fig. 2 and 4(A). For FF > 40, the ordering is primarily dictated by the presence and properties of the host substrate, even though the ordering at the edge of the triangular and hexagonal patterns remains superior compared to square and circular patterns (cf.Fig. 4(B)). While the local symmetry of the pattern still affects particle ordering near the edge, it no longer influences particles away from the edge where grain boundaries and defects become dominant factors consistent with the observations in Fig. 2. This is further confirmed by the average nearest neighbour data of square CFx patterns on SiO2 (stars in Fig. 4(C)). The obtained NNav values on SiO2 are higher than for any pattern on glass. Thus, these results emphasize the importance of the host substrate on the HCP monolayer ordering on the confined CFx patterns.
3.4 Enhancing particle assembly using nucleation sites
From the previous sections, it is understood that poor ordering of HCP crystals on the confined CFx patterns on the glass substrate is attained (cf.Fig. 2). To improve the ordering on this host substrate, we performed an experiment in which the surface density of confined CFx squares was higher than the previous patterns on glass, i.e., the separation between subsequent squares became smaller.Fig. 5 shows the result of the 3 μm PMMA microspheres on 200 μm squares (A) and (B) and 50 μm squares. It can be readily observed that assembled HCP crystals are predominantly present in Fig. 5(A)–(C). In particular, it is challenging in Fig. 5(C) to distinguish the confined coated areas from the uncoated glass regions on squares of only 50 μm. This implies that the assembled crystals do not discriminate between the two areas on the heterogeneous substrate. As the spacing on the uncoated areas is less (on the order of 10–50 μm), the crystal has limited time to experience the uncoated areas of the glass substrate. Consequently, the weaker interactions between the PMMA microspheres and the glass surface have an insufficient chance to disturb already assembled crystals, leading to stable crystals that can move across the heterogeneous glass substrate (almost 80% covered with CFx pattern overall). Additionally, it is implied that the particle–particle interactions are sufficiently strong to keep the assembled crystals intact. On the other hand, Fig. 5(D) shows that when the distance between subsequent CFx squares of 50 μm becomes larger (coverage <10%), poor ordering is achieved on the confined patterns, which aligns with preceding results in Sections 3.2 and 3.3. Thus, these results signify that a local high density of nucleation sites is needed to achieve long-range ordering on a host substrate unfavourable (low elasticity and tribocharging) for HCP crystal formation.
As inferred from the previous sections, SiO2 is an ideal host to form HCP crystals on the wall-less confined fluorocarbon patterns. To demonstrate the merit of the solvent-free rubbing assembly technique, we performed an experiment that highlights the point that the HCP crystals self-align to match any arbitrary geometry of the CFx confinement on a SiO2 substrate, as showcased in Fig. 6(A). Fig. 6(B) corroborates the notion that several nucleation sites exist, which grow into grains, as different orientations of the particles can be identified.
As the assembled HCP crystals comprising PMMA microspheres match the geometry of the confined fluorocarbon patterns, Fig. 6 shows that the shape of the ordered monolayer array patterns can be tuned, which can open avenues in photonics,17,24,26 (bio-)analytics,17,46 anti-counterfeiting,47 sensing,17 and (flexible) microelectronics.48
4 Conclusions
This study demonstrates that PMMA microspheres (3 and 10 μm) can be rapidly (<20 s) assembled into highly ordered, closely packed monolayers on various substrates using the solvent-free rubbing method. These microspheres can be confined laterally into any desired shape without physical barriers, attributed to the different contact mechanics force and triboelectrification of the materials. The ordering process of dry powder into HCP crystals was examined by taking two distinct host substrates and various pattern geometries and sizes. In agreement with previous studies on homogeneous substrates, we found that the best ordering is achieved on CFx patterns, whereas poor ordering was attained on glass substrates due to the lower contact mechanics force and triboelectrification. The tribocharging is corroborated through KPFM measurements, and elastic properties explain the contact mechanics contribution.26The critical nucleation theory effectively describes the ordering process using the rubbing method. The results show that HCP ordering on the wall-less confined geometrical patterns is primarily influenced by two factors: (i) the ratio between the pattern and particle size and (ii) the host substrate properties (the uncoated surface surrounding the pattern). In particular, larger patterns promote the formation of grains and reduce the amount of grain boundaries and defects, leading to better overall ordering. The ability of the host substrate to support grain formation, determined by the aforementioned contact mechanics force and triboelectrification, further enhances ordering.
For smaller patterns with a form factor FF ≤ 25, pattern symmetry affects particle assembly. Geometrical shapes that match the symmetry of the particle grains (three-fold symmetry) result in better edge and overall ordering. For larger patterns, edge influence on ordering diminishes and is mainly determined by the host substrate, such that conspicuous HCP monolayer arrays are attained on the SiO2 substrate. However, even for large patterns, those with matching symmetry, e.g., triangles, exhibit better edge ordering.
Ultimately, it is elucidated that with a high density of pattern distribution, highly ordered closely packed monolayers can be formed on hard and non-elastomeric surfaces. The patterns act as nucleation points, promoting the growth of ordered monolayers.
This solvent-free rubbing technique unlocks the potential of reducing solvent waste in a more sustainable assembly era to create fully ordered monolayers and patterned arrays of HCP crystals on wall-less confined areas. The assembly of such tunable patterned arrays can hold promising applications in fields such as (bio-)analytics, photonics and electronic/sensing technologies.17 Additionally, from a fundamental perspective, the system can function as an assembly toolbox to study grain formation on various patterns, geometries, and substrates with different colloids, which can be supported by numerical modelling.49 From recent experiments,26 we already know that under the right environmental conditions, HCP monolayers of 500 nm colloids (silica and PMMA) can be assembled using the rubbing method. But, more research is needed to understand what the size limit is to obtain ordered arrays and how surface interaction forces influence the ordering and which surface forces become dominant.18,50 Furthermore, by changing the wettability properties of the particles, we will explore in the near future the effect of humidity conditions on the achieved order in the system (see e.g., our work25,26 on silica microspheres at different humidity levels), as ambient humidity levels may affect triboelectric charging and other surface force interactions, e.g., capillary forces, among the particles themselves and between the particles and substrates.25,26,35
Author contributions
ISMJ and KS conceptualised and supervised the work. ISMJ and GR performed the experiments. MTJW was involved in sample fabrication and data analysis. ISMJ and KS wrote the initial draft of the manuscript. All authors reviewed the manuscript.Data availability
The data and detection code are accessible via DOI: https://doi.org/10.4121/01365bbe-72ba-47fb-8044-505e1aee0e29 after submitting a request to the corresponding authors.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
The authors gratefully acknowledge funding from the VUB Methusalem grant (METH 7). ISMJ acknowledges financial support from the VUB (OZR4311) and support from Gert Desmet and Han Gardeniers. The authors thank Stefan Schlautmann for sample fabrication and Mark Smithers for his time in taking SEM images.Notes and references
- G. M. Whitesides and B. Grzybowski, Science, 2002, 295, 2418–2421 CrossRef CAS PubMed.
- N. A. Araújo, L. M. Janssen, T. Barois, G. Boffetta, I. Cohen, A. Corbetta, O. Dauchot, M. Dijkstra, W. M. Durham and A. Dussutour, et al. , Soft Matter, 2023, 19, 1695–1704 RSC.
- T. Vicsek and A. Zafeiris, Phys. Rep., 2012, 517, 71–140 CrossRef.
- G. Volpe, C. Bechinger, F. Cichos, R. Golestanian, H. Löwen, M. Sperl and G. Volpe, npj Microgravity, 2022, 8, 54 CrossRef PubMed.
- B. Li, D. Zhou and Y. Han, Nat. Rev. Mater., 2016, 1, 1–13 Search PubMed.
- J. Schockmel, E. Mersch, N. Vandewalle and G. Lumay, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2013, 87, 062201 CrossRef CAS PubMed.
- J. Menath, R. Mohammadi, J. C. Grauer, C. Deters, M. Böhm, B. Liebchen, L. M. Janssen, H. Löwen and N. Vogel, Adv. Mater., 2023, 35, 2206593 CrossRef CAS PubMed.
- C. P. Royall, P. Charbonneau, M. Dijkstra, J. Russo, F. Smallenburg, T. Speck and C. Valeriani, arXiv, 2023, preprint, arXiv:2305.02452 DOI:10.48550/arXiv.2305.02452.
- E. Locatelli and E. Bianchi, Soft Matter, 2018, 14, 8119–8136 RSC.
- P. Digregorio, D. Levis, L. F. Cugliandolo, G. Gonnella and I. Pagonabarraga, Soft Matter, 2022, 18, 566–591 RSC.
- N. Vogel, M. Retsch, C.-A. Fustin, A. Del Campo and U. Jonas, Chem. Rev., 2015, 115, 6265–6311 CrossRef CAS PubMed.
- S. Jiang, A. Van Dyk, A. Maurice, J. Bohling, D. Fasano and S. Brownell, Chem. Soc. Rev., 2017, 46, 3792–3807 RSC.
- Y. Hu, Z. Tian, D. Ma, C. Qi, D. Yang and S. Huang, Adv. Colloid Interface Sci., 2024, 103089 CrossRef CAS PubMed.
- V. Lotito and T. Zambelli, Adv. Colloid Interface Sci., 2017, 246, 217–274 CrossRef CAS PubMed.
- M. Schelling, T. Verouden, T. Stevens and J.-M. Meijer, Soft Matter, 2024, 20, 6343–6352 RSC.
- C. O. Solano-Cabrera, P. Castro-Villarreal, R. E. Moctezuma, F. Donado, J. C. Conrad and R. Castañeda-Priego, Annu. Rev. Condens. Matter Phys., 2024, 16 DOI:10.1146/annurev-conmatphys-041124-120513.
- K. Sotthewes and I. S. Jimidar, Small, 2024, 2405410, DOI:10.1002/smll.202405410.
- I. S. Jimidar, K. Sotthewes, H. Gardeniers, G. Desmet and D. van der Meer, Soft Matter, 2022, 18, 3660–3677 RSC.
- B. A. Grzybowski, A. Winkleman, J. A. Wiles, Y. Brumer and G. M. Whitesides, Nat. Mater., 2003, 2, 241–245 CrossRef CAS PubMed.
- S. Battat, D. A. Weitz and G. M. Whitesides, Soft Matter, 2023, 19, 3190–3198 RSC.
- M. X. Lim, A. Souslov, V. Vitelli and H. M. Jaeger, Nat. Phys., 2019, 15, 460–464 Search PubMed.
- W. Van Geite, I. S. Jimidar, K. Sotthewes, H. Gardeniers and G. Desmet, Mater. Des., 2022, 216, 110573 CrossRef CAS.
- W. Van Geite, I. S. Jimidar, H. Gardeniers and G. Desmet, Powder Technol., 2023, 415, 118177 CrossRef CAS.
- C. Park, T. Lee, Y. Xia, T. J. Shin, J. Myoung and U. Jeong, Adv. Mater., 2014, 26, 4633–4638 CrossRef CAS PubMed.
- I. S. Jimidar, K. Sotthewes, H. Gardeniers and G. Desmet, Langmuir, 2020, 36, 6793–6800 CrossRef CAS PubMed.
- K. Sotthewes, G. Roozendaal, A. Sutka and I. S. Jimidar, ACS Appl. Mater. Interfaces, 2024, 16, 12007–12017 CrossRef CAS PubMed.
- D. Park, H. Kwak, S. Kim, H. Choi, I. Lim, M. Kwak, I.-S. Kim, H. Park, I.-Y. Eom and J.-W. Lee, et al. , Adv. Funct. Mater., 2024, 2408902 CrossRef.
- D. N. t Napel, J.-M. Meijer and A. V. Petukhov, Appl. Sci., 2021, 11, 5117 CrossRef.
- K. Sotthewes, H. J. Gardeniers, G. Desmet and I. S. Jimidar, ACS Omega, 2022, 7, 41828–41839 CrossRef CAS PubMed.
- D. J. Lacks and T. Shinbrot, Nat. Rev. Chem., 2019, 3, 465–476 CrossRef CAS.
- A. Šutka, K. Mālnieks, L. Lapčinskis, P. Kaufelde, A. Linarts, A. Bērziņa, R. Zābels, V. Jurkāns, I. Gorņevs and J. Blūms, et al. , Energy Environ. Sci., 2019, 12, 2417–2421 RSC.
- L. B. da Silveira Balestrin, D. Del Duque, D. S. da Silva and F. Galembeck, Faraday Discuss., 2014, 170, 369–383 RSC.
- E.-C. Shin, J.-H. Mun, S. Baek, J. Jung and Y.-H. Kim, Chem. Phys. Rev., 2023, 4, 031305 CrossRef CAS.
- F. Galembeck, T. A. Burgo, L. B. Balestrin, R. F. Gouveia, C. A. Silva and A. Galembeck, RSC Adv., 2014, 4, 64280–64298 RSC.
- I. S. Jimidar, W. Kwiecinski, G. Roozendaal, E. S. Kooij, H. J. Gardeniers, G. Desmet and K. Sotthewes, ACS Appl. Mater. Interfaces, 2023, 15, 42004–42014 CrossRef CAS PubMed.
- S. Lin, X. Chen and Z. L. Wang, Chem. Rev., 2021, 122, 5209–5232 CrossRef PubMed.
- F. Galembeck, L. P. Santos, T. A. Burgo and A. Galembeck, Chem. Soc. Rev., 2024, 53, 2578–2602 RSC.
- V. Lotito and T. Zambelli, Langmuir, 2018, 34, 7827–7843 CrossRef CAS PubMed.
- V. Lotito and T. Zambelli, Adv. Colloid Interface Sci., 2020, 284, 102252 CrossRef CAS PubMed.
- P. Dillmann, G. Maret and P. Keim, Eur. Phys. J.: Spec. Top., 2013, 222, 2941–2959 Search PubMed.
- A. T. Gray, E. Mould, C. P. Royall and I. Williams, J. Phys.: Condens. Matter, 2015, 27, 194108 CrossRef PubMed.
- R. Becker and W. Döring, Ann. Phys., 1935, 416, 719–752 CrossRef.
- X. C. Zeng, J. Chem. Phys., 1996, 104, 2699–2704 CrossRef CAS.
- D. Schwarz, R. van Gastel, H. J. W. Zandvliet and B. Poelsema, Phys. Rev. Lett., 2012, 109, 016101 CrossRef PubMed.
- S. Karthika, T. K. Radhakrishnan and P. Kalaichelvi, Cryst. Growth Des., 2016, 16, 6663–6681 CrossRef CAS.
- M. Serra, D. Ferraro, I. Pereiro, J.-L. Viovy and S. Descroix, Lab Chip, 2017, 17, 3979–3999 RSC.
- X. Li, L. Chen, Y. Ma, D. Weng, Z. Li, L. Song, X. Zhang, G. Yu and J. Wang, Adv. Funct. Mater., 2022, 32, 2205462 CrossRef CAS.
- R. Pan, W. Zhang, H. Cheng, J. Yang, Y. Gong, R. Hu, Y. Zhuo, J. Ding, X. Zhang and L. Chen, et al. , Adv. Mater. Technol., 2023, 8, 2300514 CrossRef CAS.
- E. B. Lindgren, H. Avis, A. Miller, B. Stamm, E. Besley and A. J. Stace, J. Colloid Interface Sci., 2024, 663, 458–466 CrossRef CAS PubMed.
- J. N. Israelachvili, Intermolecular and surface forces, Academic Press, 2011 Search PubMed.
Footnotes |
| † Electronic supplementary information (ESI) available: Analysis of quality of monolayer arrays, grain detection, and additional data. See DOI: https://doi.org/10.1039/d4sm01196a |
| ‡ These authors contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |