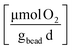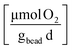Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The optimization of poly(vinyl)-alcohol-alginate beads with a slow-release compound for the aerobic cometabolism of chlorinated aliphatic hydrocarbons†
Conor G.
Harris
 ,
Hannah K.
Gedde
,
Hannah K.
Gedde
 ,
Audrey A.
Davis
,
Lewis
Semprini
,
Audrey A.
Davis
,
Lewis
Semprini
 ,
Willie E.
Rochefort
and
Kaitlin C.
Fogg
,
Willie E.
Rochefort
and
Kaitlin C.
Fogg
 *
*
School of Chemical, Biological, and Environmental Engineering, Oregon State University, Corvallis, OR 97331, USA. Tel: +541-737-1777E-mail: kaitlin.fogg@oregonstate.edu
First published on 14th March 2024
Abstract
Chlorinated aliphatic hydrocarbons (CAHs), such as cis-1,2-dichloroethylene (cDCE), are prevalent in groundwater at many locations throughout the United States. When immobilized in hydrogel beads with slow-release compounds, the bacteria strain Rhodococcus rhodochrous ATCC 21198 can be used for the in situ bioremediation of cDCE. These hydrogel beads must exhibit high mechanical strength and resist degradation to extend the lifetime of slow-release compounds and bioremediation. We engineered poly(vinyl)-alcohol – alginate (PVA-AG) beads to immobilize ATCC 21198 with the slow-release compound, tetrabutoxysilane (TBOS) that produces 1-butanol as a growth substrate, for high mechanical strength. We optimized three inputs (concentration of PVA, concentration of AG, and the crosslinking time) on two responses (compressive modulus and rate of oxygen utilization) for batch incubation experiments between 1 and 30 days using a design of experiments approach. The predictive models generated from design of experiments were then tested by measuring the compressive strength, oxygen utilization, and abiotic rates of hydrolysis for a predicted optimal bead formulation. The result of this study generated a hydrogel bead with immobilized R. rhodochrous ATCC 21198 and TBOS that exhibited a high compressive modulus on day 1 and day 30, which was accurately predicted by models. These hydrogel beads exhibited low metabolic activity based on oxygen rates on day 1 and day 30 but were not accurately predicted by the models. In addition, the ratio between oxygen utilization and abiotic rates of hydrolysis were observed to be roughly half of what was expected stoichiometrically. Lastly, we demonstrated the capability to use these beads as a bioremediation technology for cDCE as we found that, for all bead formulations, cDCE was significantly reduced after 30 days. Altogether, this work demonstrates the capability to capture and enhance the material properties of the complex hydrogel beads with predictive models yet signals the need for more robust methods to understand the metabolic activity that occurs in the hydrogel beads.
Sustainability spotlightChlorinated volatile organic compounds (VOCs) are one of the most commonly detected pollutants in public supply wells and pose a threat to human and environmental health. Chlorinated VOCs have diffused into saturated low permeability zones within aquifers that require long-term passive techniques. Our work explores the long-term passive and economical remediation technique of in situ aerobic cometabolic bioremediation with immobilized bacteria and slow-release compounds in hydrogel beads. This work specifically evaluates and optimizes the material properties of the hydrogel bead based on the mechanical strength of the bead and the oxygen utilization of the microbe to extend the time for bioremediation. Our work aligns with the UN sustainable development goals: Clean Water and Sanitation6 and Industry, Innovation, and Infrastructure.9 |
1. Introduction
A subset of chlorinated aliphatic hydrocarbons (CAHs) persist as contaminants in groundwater aquifer systems.1–3 Actually, these chlorinated hydrocarbon compounds are some of the most common groundwater contaminants globally.4 One of the most abundant CAHs found in groundwater is cis-1,2-dichloroethylene (cDCE).5 Currently, the EPA regulates cDCE at a maximum contaminant level goal and maximum contaminant level (MCL) of 0.07 mg L−1 due to potential health effects such as liver and kidney problems, drowsiness and nausea, and cardiovascular problems.6 The release of cDCE into the environment has propagated from the use of chloroethylenes as solvents and synthetic feedstocks.7 Specifically, groundwater contamination by cDCE occurs due to the reductive dechlorination of more highly chlorinated compounds, such as tetrachloroethylene and trichloroethylene.6 When aquifers lack Dehalococcoides or Dehalogenimonas microbes that can reduce dichloroethylenes (DCEs) to ethene, DCEs accumulate in the groundwater, known as a DCE stall.8–10 Instead, the process of aerobic cometabolism generates metabolites of epoxides and alcohols that can be degraded into carbon dioxide and can degrade contaminants to concentrations below the thresholds needed to support direct metabolism.8 This study focused on the bacterium Rhodococcus rhodochrous ATCC 21198 (ATCC 21198) that has been previously validated to aerobically cometabolize a wide range of CAHs and 1,4-dioxane, which was used as a stabilizer in CAHs and is typically found as a co-contaminant where CAHs are measured.11,12 Therefore, it is advantageous to treat such zones in situ with the use of aerobic cometabolic bioremediation.13Currently, the most common implementation of bioremediation for CAHs is biostimulation, where the induction of an enzyme occurs through the continuous sparging of a gaseous substrate.14 Either native microbes capable of aerobic cometabolism exist in aquifer systems or aquifers receive injections of non-native microbes, known as bioaugmentation. While sparging can stimulate or enhance aerobic biodegradation by microorganisms, the volatilization of contaminates can occur and present hazardous atmospheres.15 In contrast, permeable reactive bio-barriers are in situ permeable treatment zones that contain materials to enhance or stimulate microorganisms to transform contaminants.16 These permeable reactive bio-barriers have the potential to reduce costs and eliminate the need for continuous injections of substrates.17
We and others have successfully developed passive treatment systems that can be used in permeable reactive bio-barriers to transform CAHs.18,19 Specifically, we developed a passive cometabolic system consisting of gellan gum hydrogel beads with immobilized ATCC 21198 and a slow-release compound, tetrabutoxysilane (TBOS), that hydrolyzes gradually over time to generate 1-butanol, a carbon source used to stimulate ATCC 21198.20 We demonstrated the use of the gellan gum immobilization system in column studies, with results of more than 99% removal of cDCE and with 1-butanol concentrations below detection at a hydraulic residence time of one day.12 While this system was successful in demonstrating the capability to encapsulate both ATCC 21198 and a slow-release compound, the gellan gum hydrogel beads exhibited poor mechanical strength and degraded rapidly, greatly reducing the permeability of the column packing. This presented a challenge, as the hydrogel provides protection to the immobilized bacteria against the harsh soil macroenvironment, helping to extend the metabolic activity of cells.21 Consequently, hydrogels must resist compression from the weight of the packed column and remain intact such that the packed column maintains a high permeability to allow contaminants to flow through and into beads. Therefore, the hydrogel beads designed for permeable bio-barriers must be engineered with high mechanical strength.
Poly(vinyl)-alcohol (PVA) is a synthetic, yet biocompatible polymer that is resistant to degradation and has high mechanical strength.22–24 Alginate (AG) is a natural polysaccharide produced from brown algae that is highly biocompatible and is frequently used in biomedical applications.25 Many crosslinking techniques exist for both PVA and AG, however with the long-term goal of mass production of these hydrogel beads, this study focuses on chemical crosslinking where the polymer linkage occurs through the introduction of free ions to polymer solutions. Boric acid forms bonds with the oxygen groups occurring on the diol linkages in PVA, whereas divalent cations, such as calcium chloride, bind AG between its polymeric α-L-guluronate units. Hydrogels formed from both PVA and AG create semi-interpenetrating polymer networks, where the polymer chains interlace between each other but do not bond.22,24 Together, PVA-AG hydrogels offer wide applicability and possess key characteristics that enable the entrapment of whole cells.26–29
In this study, we optimized PVA-AG hydrogel beads to immobilize ATCC 21198 and TBOS with high compressive moduli. The optimization objectives were to simultaneously maximize the mechanical strength of the hydrogel bead and minimize the rate of substrate utilization based on oxygen utilization over the course of 30 days. This was attempted using Design of Experiments (DOE), a powerful statistical optimization technique that provided the experimental design to empirically model and optimize the immobilization method while reducing the number of experiments required compared to a traditional scientific method approach. Using DOE, we generated predictive models of the output variables measured as a function of the input variables. The predictive models were then tested by measuring the compressive strength, oxygen utilization, and abiotic rates of hydrolysis for a predicted optimal bead formulation.
2. Materials and methods
2.1. Cell culture
Dr Michael Hyman (NC State) provided us with ATCC 21198. Additionally, the American Type Culture Collection (ATCC) (Manassas, Virginia, United States) maintains a commercial stock of ATCC 21198. Details on growth of ATCC 21198 in batch reactors for immobilization in PVA-AG hydrogel beads are provided in the ESI (Section ESI1–3†).2.2. Immobilizing ATCC 21198 and TBOS with PVA – AG beads
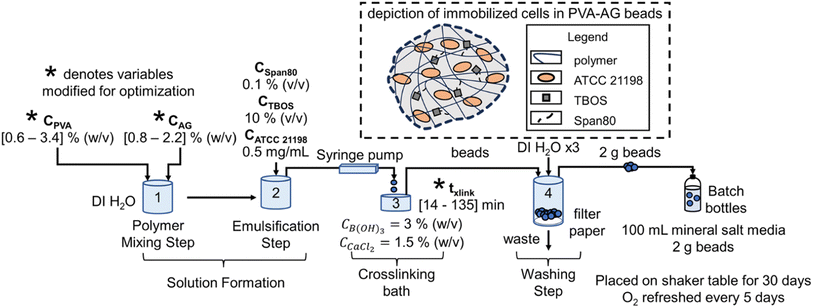
ATCC 21198 was immobilized with a slow-release compound in PVA-AG hydrogel beads using an entrapment method, where cells are trapped in the pores of crosslinked polymers (Fig. 1).30,31 99+% hydrolyzed PVA (molecular weight distribution: 85–124 kDa) (Sigma-Aldrich St. Louis, Missouri, United States) solutions were prepared by dissolving the appropriate amount of PVA in autoclaved water at 80 °C. Sodium alginate (Cape Crystal Brands, Summit, New Jersey, United States) solutions were prepared by dissolving the appropriate amount of sodium alginate in autoclaved water at room temperature. Using a 4-Bladed, IKA 0741300 Propeller Stirrer (Cole-Parmer, Vernon Hills, Illinois, United States) attached to an IKA RW 20 Digital Dual-Range mixer (Cole-Parmer), the polymer solutions, Span80 (Ohio Valley Specialty Company, Marietta, Ohio, United States), tetrabutoxysilane (TBOS) (90% purity) (United Chemical Technologies, Levittown, Pennsylvania, United States), and suspended ATCC 21198 (in its late exponential growth state) were mixed until the solution was emulsified and homogeneous. Note, for optimal beads, we used higher purity TBOS (98% purity) (VWR International, Radnor, Pennsylvania, United States). The final suspension of cells contained [0.6–3.4] % (w/v) PVA, [0.8–2.2] % (w/v) AG, 0.1% (v/v) Span80, 10% (v/v) TBOS, and 0.5 mg mL−1 of ATCC 21198. The concentrations of PVA and AG were selected based on their capability to crosslink and the total viscosity of the solution. Below 0.6 and 0.8% (w/v) of PVA and AG, respectively, gels would not form; yet at concentrations higher than 3.4 and 2.2% (w/v) of PVA and AG, respectively, the mixed polymer solution would be too difficult to extrude. 10% (v/v) was used for TBOS as this was determined by preliminary studies as a high concentration that could be successfully emulsified into all pre-gel solutions. Span80 is a nonionic surfactant used to emulsify TBOS into the pre-gel solution with polymers and cells. The amount of cell inoculum was added to beads with the intention to grow cells in the hydrogel beads during a 30 day incubation period.Beads were generated using a IPS-14S syringe pump (Inovenso Technology Inc, Cambridge, Massachusetts, United States) to extrude the polymer solution dropwise through an 16-gauge metal blunt point needle (Hamilton Company, Reno, Nevada, United States) into a crosslinking bath comprised of approximately 100 mL of 3% (w/v) boric acid (Honeywell International Inc., Charlotte, North Carolina, United States) and 1.5% (w/v) calcium chloride (Merck KGaA, Darmstadt, Germany) in a 150–250 mL Pyrex beaker with a magnetic stir rod placed on a magnetic stir plate. To reduce the degree of elongation in beads, we adjusted the solution flow rate between 10 and 20 mL h−1. To crosslink the beads, they remained in the crosslinking bath between 14 and 135 min, timed from when the last bead dropped into solution. After crosslinking, the crosslinking solution with beads was poured into a Coors Buchner funnel laid with qualitative Grade 1 filter paper (Whatman, Maidstone, United Kingdom). They were then washed with deionized water up to 3 times under vacuum at approximately 15 inHg of vacuum using a vacuum filtering side-arm flask attached to a lab vacuum spigot using vacuum tubing.
2.3. Incubation of immobilized ATCC 21198 in 150 mL batch reactors
Batch reactors were used to evaluate both the performance of the cometabolic transformation by immobilized ATCC 21198 with TBOS and the durability of the hydrogel beads at days 1 and 30. The two time points, days 1 and 30, were used to evaluate the performance of beads to select a bead formula for column studies that can last up to two years. Batch reactors consisted of 125 mL Wheaton serum bottles (DWK Life Sciences Wheaton, Stoke-on-Trent, United Kingdom) with nominal volumes of 155 mL sealed with screw on caps fitted with gray butyl rubber septa as were previously described in Rasmussen et al.20 Batch reactors contained 100 mL of phosphate-buffered 1X MSM with an addition of immobilized cells to achieve an initial cell concentration of 1 mg cells per L which was 2 g of beads per batch bottle. The headspace of the batch reactor (55 mL) contained air as the source of oxygen. Batch reactors were mixed constantly on a New Brunswick Scientific G10 Gyratory shaker table (Eppendorf, Hamburg, Germany) at 100 RPM at 20 °C.2.4. Cometabolic and metabolic analytical methods
The performance of cometabolism by immobilized strain ATCC 21198 was evaluated by using cDCE as a surrogate for cometabolism based on the ability of ATCC 21198 to cometabolize cDCE, as well as 1,1,1-TCA and 1,4-D that was observed in past studies.20 This is due to the fast rates of cDCE transformation compared to other CAHs observed in prior cometabolic transformation experiments when using ATCC 21198.12,20 The reactors used for metabolic and cometabolic transformation experiments received additions of environmentally relevant aqueous concentrations (250 ppb) of cDCE (Tokyo Chemical Industry, Tokyo, Japan) at days 1 and 30 after beads were added to batch reactors. Oxygen served as the electron accepter for the metabolic utilization of 1-butanol product from TBOS and the cometabolic transformation. Batch reactors received oxygen every 5 days by opening the reactors in a sterile biosafety cabinet to replenish oxygen used in metabolism through the exchange of air to the batch reactor headspace. cDCE was not present when batch reactors were opened.We measured volatile compounds in batch reactors as was previously described by Rasmussen et al.20 Samples of headspace were taken from batch reactors using a 100 μL Hamilton Gastight Syringe and were injected into either a 5890 or 6890 Series HP Gas Chromatograph (GC). 5890 Series HP GCs was equipped with a thermal conductivity detector to measure O2, whereas the 6890 Series HP GC was equipped an electron capture detector to measure cDCE. See gas chromatography details in the ESI (Section ESI4†) The total mass (mT) in the batch reactors was calculated as follows:
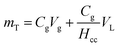 | (1) |
H
CC values, taken as the dimensionless ratio between gas- and aqueous-phase concentration were 31.5 and 0.16 for O2 and cDCE, respectively at 20 °C.32,33mT values were normalized with negative control batch reactors to remove variability in instrument measurements. Normalization was applied by dividing the negative control total mass mT− by the initial mass at time, t = 1 [d], mT−,0, such that 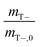 , and multiplying the inverse of this value,
, and multiplying the inverse of this value, 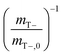 , to active batch reactor mT values. The values of
, to active batch reactor mT values. The values of 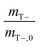 ranged from 0.63 to 1.2, and 0.78 to 1.1 for O2 and cDCE, respectively. Negative control batch reactors consisted of batch reactors with 3 mL of 2% (w/v) sodium azide injected into medium to inhibit microbial activities.
ranged from 0.63 to 1.2, and 0.78 to 1.1 for O2 and cDCE, respectively. Negative control batch reactors consisted of batch reactors with 3 mL of 2% (w/v) sodium azide injected into medium to inhibit microbial activities.
Zero-order rate laws applied to the total mass measured over time, t, were used to obtain the rates for cDCE (kcDCE) and oxygen (kO2). Sample data is provided in the ESI (Section ESI5: Fig. S1A and B†). Further, rates were normalized by the weight of the beads added to batch reactors to account for the cells that can grow within the beads, such that:
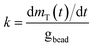 | (2) |
A transformation yield, TY, was calculated for days 1 and 30 as ratio between the amount of cDCE transformed and the amount of O2 consumed to provide how efficient the cells immobilized in different hydrogel formulations were with respect to the primary substrate, 1-butanol, such that:
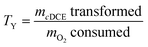 | (3) |
Paired t-tests were used to evaluate the significance between rates and the transformation yields at days 1 and 30.
2.5. Unconfined compression tests for individual beads
The durability of individual beads in batch bottles between 1 and 30 days was evaluated using unconfined compression tests. For these batch reactors, we decided against injecting cDCE to remove potential hazards with handling cDCE. Unconfined compression tests on an ARG2 rheometer (TA Instruments, New Castle, Delaware, United States) were used to obtain compressive modulus data for individual beads. Individual beads were centered on the bottom Peltier plate and the top 25 mm diameter plate was lowered until contact was achieved with the bead such that the normal force read 0.01 N. The gap at initial contact was set as the undeformed diameter, D, of each bead. The compression of all beads proceeded at a constant strain rate (ε = 0.005 s−1) while collecting the resultant normal force data and the axial displacement data. Termination of the procedure occurred once the gap fell below 50 μm to obtain the entire stress–strain curve. For all measurements, beads were irreversibly deformed during the experiment (Section ESI6: Fig. S2†).The compressive modulus refers to the stiffness of a material determined from the slope in the linear region of a stress–strain curve obtained from compression tests. We used the stress–strain relationship derived by Hertz for the compressive modulus for spherical particles: as a function of the force F and the deformation ΔD:34
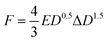 | (4) |
| ΔD = D − D′ | (5) |
Typical stress–strain data for hydrogel beads is included in the ESI (Section ESI7: Fig. S3†). The elastic loss (ΔE) refers to the percent loss of the compressive moduli between day 1 and day 30 used to quantify the degradability of hydrogel beads:
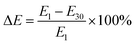 | (6) |
Paired t-tests were used to evaluate the significance between rates at day 1 and day 30.
2.6. Performance evaluation for the abiotic hydrolysis of TBOS
The rates of hydrolysis of TBOS were determined using methods described in Rasmussen et al.20 3 mL of 2% (w/v) sodium azide (Spectrum Chemical, Gardena, California, United States) was added into batch reactors to poison cells and to stop the utilization of the hydrolysis product, 1-butanol. The complete hydrolysis of TBOS is as follows as we previously described in Vancheeswaran et al.:35| Si(OC4H7)4 + 4H2O → 4C4H8 + Si(OH)4 | (7) |
2.7. Abiotic hydrolysis analytical methods
The release of 1-butanol (1-BuOH) was used to determine the rate of hydrolysis from TBOS. Samples were prepared for injection using a Tekmar Lumin heated purge and trap concentrator with an Aqua Tek 70 Liquid Autosampler (Teledyne Tekmar, Mason, Ohio, United States). Samples were injected into a HP 6890 Series Gas Chromatograph with a 5973 Agilent Mass Selective Detector (GC-MS). The GC-MS was fitted with a Restek Rtx-VMS capillary column (Restek, Bellefonte, Pennsylvania, United States) to separate compounds. The GC-MS received injections of diluted aqueous samples from batch bottles while in the single-ion monitoring mode for m/z of 56 to measure 1-BuOH in the samples.2.8. Central composite orthogonal design
A Design of Experiments (DOE) statistical method was used to design experiments due to its prevalence of use in biomaterials research and due to the successful optimization of other immobilization methods using DOE.28,36,37 The application of a central composite orthogonal design (CCO) established the experimental matrix for this study. Details on the DOE method are provided in the ESI (Section ESI8†). The concentration of PVA CPVA [% (w/v)], the concentration of alginate CAG [% (w/v)], and cross-linking time txlink [min] were set as the three independent variables. The variables CPVA, CAG, and txlink are coded by the equations: | (8) |
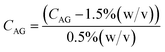 | (9) |
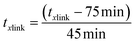 | (10) |
In coded units, the low, medium, and high values correspond to −1, 0, +1, respectively. The number of runs equaled a total of 17 runs with 3 replicates at the design center (Experiment No. 15) to assess the pure error (Table 1). The experimental levels for each variable were determined based on preliminary tests. The rate of transformation of cDCE kcDCE, rate of oxygen utilization kO2, and compressive modulus E after 1 day after immobilization and 30 days after immobilization constituted the dependent variables (responses) in this study. The rate of cDCE utilization kcDCE on day 1 and day 30 was measured for each batch reactor and evaluated with DOE but was excluded from the main text as the primary goal for that data was to show that immobilized cells in all bead types were capable of transforming cDCE. Models for predicting cDCE can be found in the ESI (Section SI9†).
| No. | C PVA [% (w/v)] | C AG [% (w/v)] | t xlink [min] | E 1 [kPa] | E 30 [kPa] | ΔE [%] | k O2,1 | k O2,30 | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Exp. | Pred. | Exp. | Pred. | Exp. | Pred. | Exp. | Pred. | Exp. | Pred. | ||||
| 1 | 1.0 | 1.0 | 30.0 | 23 ± 0.8 | 28 | 5.5 ± 3.3 | 0.58 | 76 ± 15 | 94 | 30 ± 2.8 | 28 | 12 ± 2.1 | 11 |
| 2 | 3.0 | 1.0 | 30.0 | 60 ± 7.3 | 56 | 29 ± 10 | 29 | 52 ± 18 | 58 | 17 ± 1.6 | 15 | 5.1 ± 1.2 | 4.6 |
| 3 | 1.0 | 2.0 | 30.0 | 75 ± 11 | 78 | 13 ± 5.7 | 21 | 82 ± 8.1 | 83 | 23 ± 2.5 | 24 | 6.2 ± 1.3 | 6.1 |
| 4 | 3.0 | 2.0 | 30.0 | 96 ± 1.5 | 106 | 51 ± 6.6 | 49 | 47 ± 6.9 | 48 | 10 ± 0.9 | 11 | 2.8 ± 1.2 | 3.0 |
| 5 | 1.0 | 1.0 | 120.0 | 70 ± 7.3 | 55 | 17 ± 11 | 21 | 75 ± 16 | 69 | 23 ± 1.6 | 22 | 5.7 ± 2.4 | 5.1 |
| 6 | 3.0 | 1.0 | 120.0 | 71 ± 20 | 83 | 30 ± 6.8 | 27 | 57 ± 15 | 60 | 17 ± 1.5 | 17 | 2.2 ± 0.7 | 1.9 |
| 7 | 1.0 | 2.0 | 120.0 | 103 ± 10 | 105 | 45 ± 22 | 42 | 56 ± 4.7 | 59 | 17 ± 3.2 | 18 | 5.9 ± 1.1 | 6.0 |
| 8 | 3.0 | 2.0 | 120.0 | 127 ± 14 | 134 | 26 ± 7.6 | 47 | 79 ± 6.4 | 49 | 13 ± 2.1 | 13 | 5.9 ± 0.8 | 6.2 |
| 9 | 0.6 | 1.5 | 75.0 | 95 ± 14 | 31 | 23 ± 5.4 | 20 | 76 ± 6.7 | 79 | 18 ± 2.9 | 28 | 5.2 ± 0.8 | 5.6 |
| 10 | 3.4 | 1.5 | 75.0 | 89 ± 5.2 | 69 | 40 ± 16 | 43 | SS ± 18 | 49 | 24 ± 1.5 | 16 | 1.9 ± 0.7 | 1.4 |
| 11 | 2.0 | 0.8 | 75.0 | 70 ± 7.1 | 73 | 8 ± 1.7 | 11 | 88 ± 2.8 | 89 | 15 ± 1.1 | 18 | 5.9 ± 1.5 | 7.3 |
| 12 | 2.0 | 2.2 | 75.0 | 155 ± 23 | 40 | 41 ± 13 | 39 | 74 ± 9.5 | 74 | 16 ± 1.4 | 13 | 7.4 ± 0.7 | 6.9 |
| 13 | 2.0 | 1.5 | 14.1 | 70 ± 13 | 31 | 13 ± 4.0 | 5.9 | 81 ± 6.6 | 77 | 21 ± 4.5 | 23 | 3.5 ± 17 | 4.4 |
| 14 | 2.0 | 1.5 | 135.9 | 62 ± 16 | 68 | 22 ± 3.9 | 19 | 64 ± 11 | 61 | 21 ± 1.6 | 21 | 2.2 ± 0.7 | 2.6 |
| 15 | 2.0 | 1.5 | 75.0 | 48 ± 8.0 | 50 | 8.7 ± 7.8 | 12 | 82 ± 16 | 81 | 22 ± 1.3 | 22 | 4.0 ± 0.3 | 3.5 |
| Opt | 3.2 | 2.0 | 110.0 | 121 ± 10 | 126 | 51 ± 11 | 50 | 58 ± 9.9 | 48 | 7.0 ± 1.0 | 13 | 1.2 ± 0.2 | 5.4 |
3. Results
3.1. Cometabolic and metabolic transformation after cell immobilization
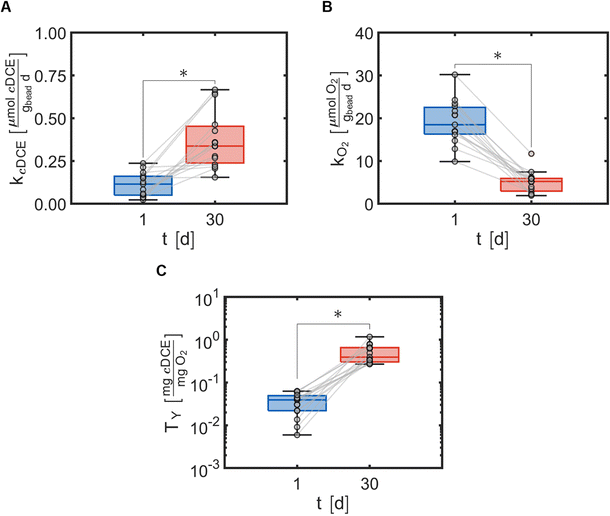
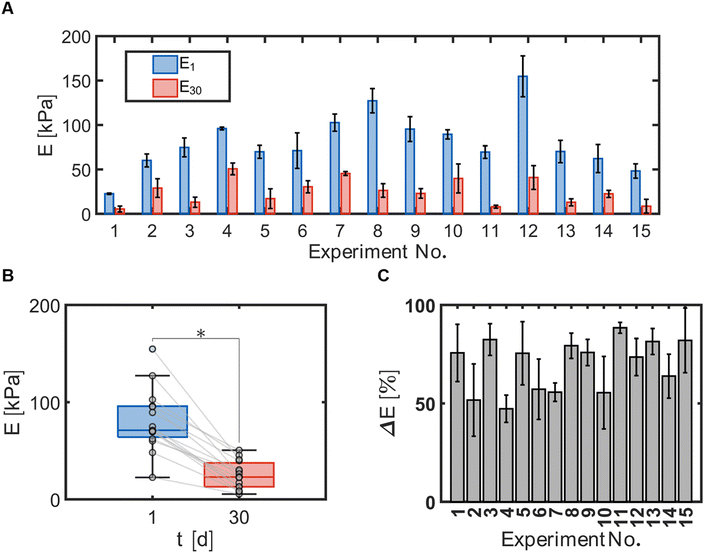
Cometabolic transformation experiments were used to evaluate the capability for ATCC 21198 to perform cometabolism on day 1 and day 30 (Fig. 2A). For all experiments, the rate of cDCE transformation increased between day 1 and day 30 indicated by the positive slopes of the lines drawn between kcDCE,1 and kcDCE,30. Values of kcDCE,1 ranged between 0.02 and 0.24 [μmol cDCE gbead−1 d−1] for all bead formulations. Values of kcDCE,30 ranged between 0.15 and 0.67 [μmol cDCE gbead−1 d−1] for all bead formulations.Metabolic utilization experiments were used to evaluate the activity of strain ATCC 21198 between day 1 and day 30 (Fig. 2B). For all experiments, the rate of O2 utilization decreased between day 1 and day 30 indicated by the negative slopes of the lines drawn between kO2,1 and kO2,30. Values of kO2,1 ranged between 9.9 and 30 [μmol O2 gbead−1 d−1] for all bead formulations. Values of kO2,30 ranged between 1.9 and 12 [μmol O2 gbead−1 d−1] for all bead formulations.
Transformation yield calculations were used to evaluate the efficiency of the immobilized cells in different formulations of hydrogels with respect to the primary substrate (Fig. 2C). For all experiments, the transformation yield, TY, increased between day 1 and day 30 indicated by the positive slopes of the lines drawn between TY,1 and TY,30. Values of TY,1 ranged between 0.0059 and 0.063 [mg cDCE/mg O2] for all bead formulations. Values of TY,30 ranged between 0.27 and 1.2 [mg cDCE/mg O2] for all bead formulations.
3.2. Compressive modulus of hydrogel beads after cell immobilization
Hydrogel bead durability was assessed by quantifying the compressive modulus of the hydrogel beads with immobilized cells and TBOS at day 1 and day 30 using the Hertz equation (eqn (3)). The compressive moduli measured for each experiment number (Table 1) at day 1 and day 30 indicated significant differences between bead formulae (Fig. 3A). Comparison of E1 and E30 revealed that the compressive modulus decreased for all bead formulae, indicated by the negative slope of the fitted lines between E1 and E30 (Fig. 3B). Values for E1 ranged between 23 and 155 [kPa] for all bead formulations. Values for E30 ranged between 5.5 and 51 [kPa] for all bead formulations.Hydrogel bead degradability was characterized by the elastic loss, ΔE, or the change in the compressive modulus between day 1 and day 30 with respect to the modulus measured at day 1. The elastic loss demonstrates that beads underwent different degrees of degradation with positive values ranging between 47 and 88 [%] (Fig. 3C).
3.3. DOE model fitting and parameters
The central composite design (CCD) is an empirical design that relates the input factors and their combinatorial effects to the responses measured using second-order polynomial response surface equations. We fit second order multivariate regression models for each response and eliminated the terms that were not statistically significant determined from ANOVA tests (p < 0.05). Note that lower order insignificant terms must remain in the model if higher order terms or interaction terms involving these terms were deemed significant. The statistical significance of each model was then evaluated with ANOVA tests, with a p-value of < 0.05 indicating a significant model and a p-value > 0.10 for lack of fit indicating a model with a negligible pure error. For all responses, the models were statistically significant and had negligible pure error (Table 2). The unscaled models obtained for each response variable are as follows:| E1 = 201 + 14CPVA − 320CAG + 0.3txlink + 123CAG2 | (11) |
| E30 = 41 − 24CPVA − 61CAG + 0.4txlink + 11CPVA2 + 27CAG2 − 0.1CPVAtxlink | (12) |
| ΔE = 94 + 17CPVA − 12CAG + 0.1txlink − 9.6CPVA2 − 0.003txlink2 + 0.1CPVAtxlink | (13) |
| kO2,1 = 14 ± 7.9CPVA + 37CAG − 0.1txlink − 14CAG2 + 0.04CPVAtxlink | (14) |
| kO2,30 = 41 − 5.4CPVA − 33CAG − 0.2txlink + 8.0CAG2 + 1.7CPVACAG + 0.02CPVAtxlink + 0.06CAGtxlink | (15) |
| Response | E 1 | E 30 | ΔE | k O2,1 | k O2,30 |
|---|---|---|---|---|---|
| p-values | |||||
| Model | <0.0001 | 0.0008 | <0.0001 | <0.0001 | <0.0001 |
| C PVA | 0.0037 | 0.0009 | 0.0003 | <0.0001 | 0.0001 |
| C AG | <0.0001 | 0.0003 | 0.0173 | 0.0161 | 0.5301 |
| t xlink | 0.0045 | 0.0251 | 0.0148 | 0.2484 | 0.0176 |
| C PVA 2 | — | 0.0009 | 0.0019 | — | — |
| C AG 2 | 0.0001 | 0.0121 | — | 0.0061 | 0.0001 |
| t xlink 2 | — | — | 0.0133 | — | — |
| C PVA C AG | — | — | 0.0147 | ||
| C PVA t xlink | — | 0.0281 | 0.0211 | 0.0386 | 0.0165 |
| C AG t xlink | — | — | |||
| Lack of fit | 0.2079 | 0.1283 | 0.6447 | 0:1697 | 0.1309 |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) |
|||||
| Validation metrics | |||||
| Total sample size (N) | 15 | 16 | 15 | 15 | 17 |
| Degree of freedom (DF) | 10 | 9 | 8 | 9 | 9 |
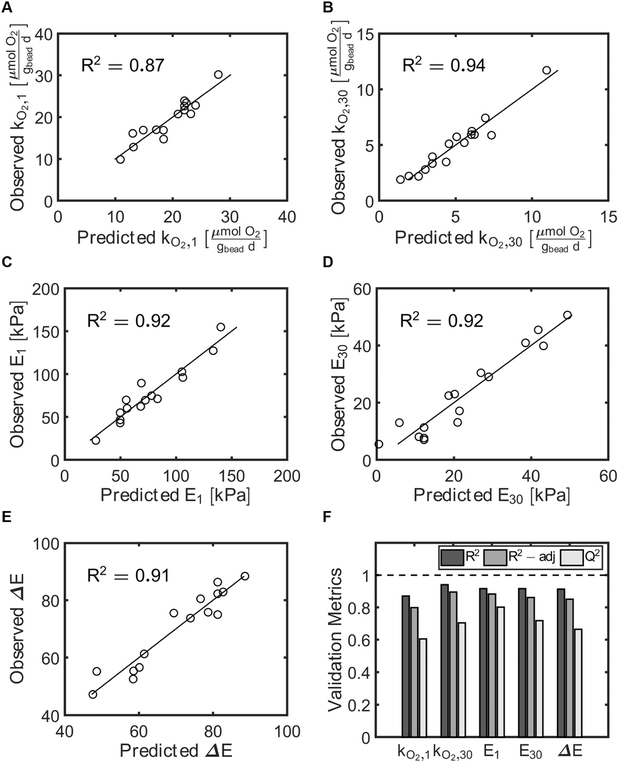
| R 2 | 0.92 | 0.92 | 0.91 | 0.87 | 0.94 |
| R 2-adjusted | 0.88 | 0.86 | 0.85 | 0.80 | 0.90 |
| Q 2 | 0.80 | 0.72 | 0.66 | 0.60 | 0.70 |
The model performance was further assessed using the coefficients of determination validation metrics: R2, adjusted R2, and Q2 (Table 2, Fig. 4F). R2 describes the percent of the variation of the response explained by the model for every variable. Adjusted R2 describes the percent of variation of the response explained by the model only for the variables that affect the response. Q2 describes the percent of the variation of the response predicted by the model for new data. R2 and adjusted R2 values close to 1.0 signal a high correlation between observed and predicted values. Q2 above 0.50 and the difference between R2 and Q2 values lower than 0.30 validates that the model works independently of the specific data used to train the model. We found that all of our models fit the validation metrics criteria, indicating significant correlations between the input variables and the responses. Lastly, the observed response values were compared to those predicted using the second order multivariate regression models (Table 1, Fig. 4A–E). For all responses the observed and predicted values were very close to each other, as indicated by the observed = predicted lines on each of the observed vs. predicted plots.
3.4. Factor effects and predictions for the rate of oxygen utilization at day 1 (kO2,1) and day 30 (kO2,30)
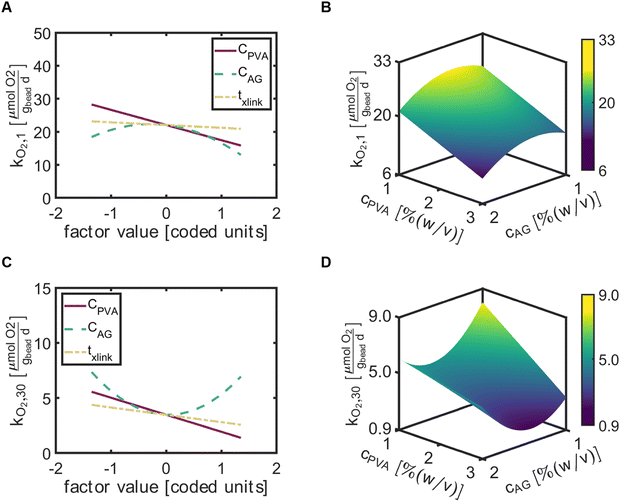
The factor effect plot of rate of oxygen utilization at day 1 (kO2,1) indicated CAG most significantly influenced kO2,1, with a negative quadratic function centered about CAG = 0 [coded units] (Fig. 5A). Thus, relatively high values of CAG would result in decreased values of kO2,1. The influence of CPVA generated a gentle negative linear slope on the rate of O2 utilization. The time for crosslinking had the least impact, with a slight negative slope. The 3D response surface map demonstrates the interactions between CPVA and CAG on kO2,1 with a constant txlink = 75 [min] (Fig. 5B). The predicted minimum value of kO2,1 occurred at high values of CPVA and CAG.At 30 days, the rate of oxygen utilization at day 30 (kO2,30) depended most significantly on CAG (Fig. 5C). Interestingly, a positive quadratic curve for the rate of oxygen utilization with respect to CAG occurred centered at CAG = 0 [coded units] and suggested that both low and high values of CAG can provide greater respiration rates. The factor effects CPVA and txlink on kO2,30 revealed linear lines with negative slopes near the same values, indicating that a reduction of the apparent metabolic activity of ATCC 21198 occurred as CPVA and txlink increased. Similar to the response surface map of kO2,1, the predictive plots of kO2,30 suggested that increased values of CPVA and CAG would result in decreased values of kO2,30 (Fig. 5D). However, the minimum kO2,30 was predicted to occur at CAG = 1.6% (w/v) due to the positive parabolic curve exhibited for kO2,30 in response to the factor CAG.
3.5. Factor effects and predictions for the compressive modulus at day 1 and day 30 and the elastic loss
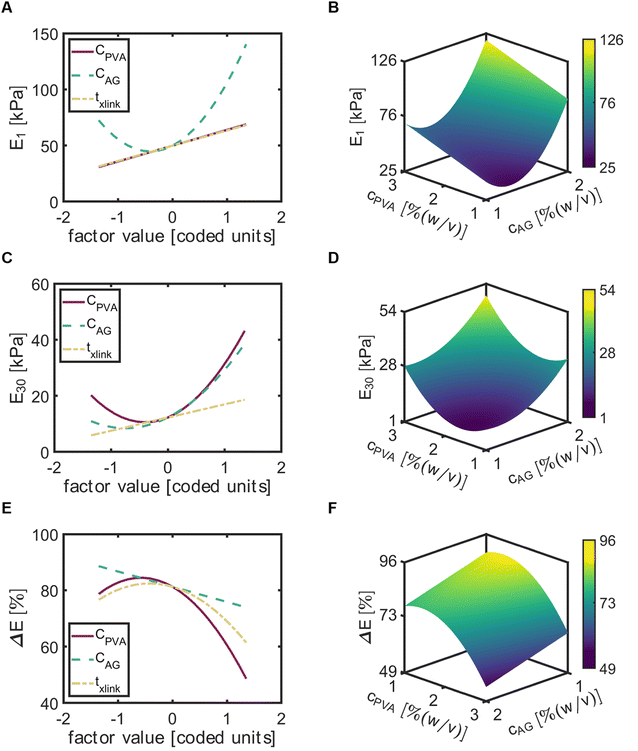
For the compressive modulus at day 1 (E1), CAG exhibited a positive quadratic relationship and txlink exhibited a positive linear relationship. Of the three input variables, CAG exhibited the most significant effect (Fig. 6A). The maximum of E1 with respect to CAG occurred at the maximum of AG, while the minimum occurred near the center point (factor value = 0). Both CPVA and txlink factors led to a near similar trend of E1, with a linear increase in E1 with increased factors. The response surface map of E1 indicated that increases in CPVA and CAG would increase E1 to a maximum value of 122 [kPa] at CPVA = 3% (w/v) and CAG = 2% (w/v) (Fig. 6B).The input variables had similar effects on the compressive modulus at day 30 (E30). However, in contrast to E1, CPVA exhibited the most significant effect on E30 and was found to be a quadratic term in the model for E30 (Fig. 6C). The effects of CAG was similar to CPVA, but with slightly lower values of E30. The response map of E30 demonstrated predictions of E30 would increase with increased values of CPVA and CAG (Fig. 6D). Here, the maximum value of E30 was equal to 62.3 [kPa] at CPVA = 3% (w/v) and CAG = 2% (w/v).
To better decipher the roles of each factor on the decrease of the compressive modulus, we then examined elastic loss (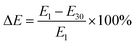 ) (Fig. 5E). Interestingly, txlink exhibited a negative quadratic relationship with ΔE, with the maximum ΔE observed at a crosslinking time near the center point. A negative quadratic relationship was also observed for CPVA, with a slight increase in ΔE from the minimum to the midpoint yet a steep decline in ΔE from the midpoint to the maximum of CPVA. A negative linear relationship was observed between ΔE and CAG. The response surface map of the ΔE revealed that the predicted minimum (ΔE = 51%) occurred at CPVA = 3% (w/v) and CAG = 2% (w/v) (Fig. 6F).
) (Fig. 5E). Interestingly, txlink exhibited a negative quadratic relationship with ΔE, with the maximum ΔE observed at a crosslinking time near the center point. A negative quadratic relationship was also observed for CPVA, with a slight increase in ΔE from the minimum to the midpoint yet a steep decline in ΔE from the midpoint to the maximum of CPVA. A negative linear relationship was observed between ΔE and CAG. The response surface map of the ΔE revealed that the predicted minimum (ΔE = 51%) occurred at CPVA = 3% (w/v) and CAG = 2% (w/v) (Fig. 6F).
3.6. Validation of predictive models to enhance bioremediation potential of ATCC 21198
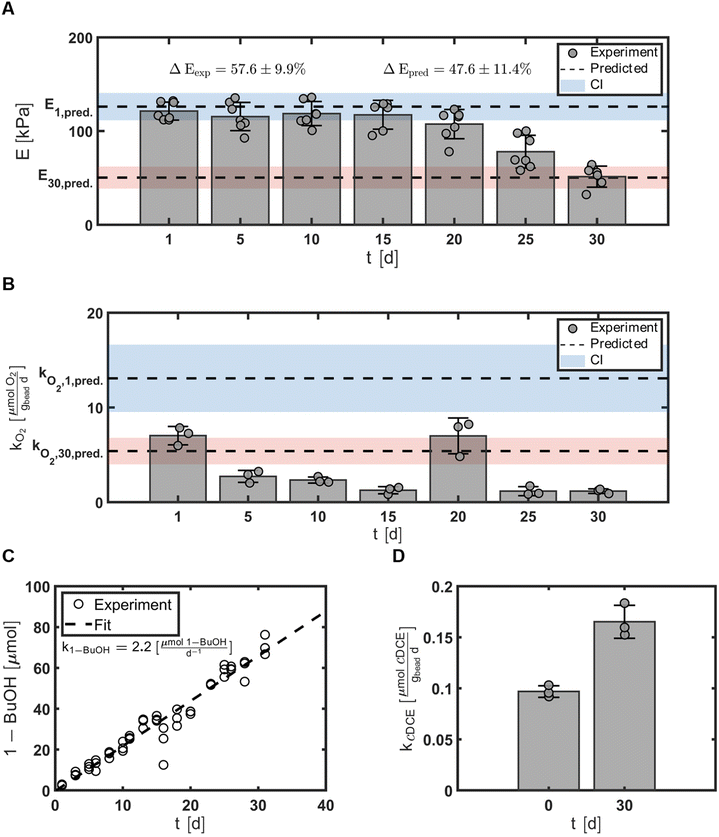
Our overall engineering objective was to use the second order multivariate regression models to identify the hydrogel formulation that maximized the mechanical strength of the hydrogel beads while simultaneously minimizing the respiration rates of the entrapped microbes. Thus, to validate these models, we generated a hydrogel bead formulation (optimal bead) predicted to fulfill the optimization parameters that was not included in the original CCO design and tested it against model predictions with a confidence at 95% (Table 1). The optimal bead was specified as 3.2% (w/v), 2.0% (w/v), and 110 min for cPVA, cAG, and txlink, respectively.The mechanical strength of the hydrogel beads was evaluated by measuring the compressive moduli, E, every five days for 30 days, t ∈ {1, 5, 10, 15, 20, 25, 30}\[d], that resulted in average values of E = {121, 115, 119, 117, 107, 78, 51}\[kPa], respectively (Fig. 7A). E1 was 121 ± 10 and 126 kPa for the measured and predicted values, respectively. E30 was 51 ± 11 and 50 kPa for the measured and predicted values, respectively. The optimal bead experienced an elastic loss, ΔE, of 58 ± 9.9% compared to the predicted value at of 48%. For moduli data, the experimental mean or standard deviation overlapped the prediction interval with confidence at 95%.
The metabolic activity of the entrapped microbes was evaluated by measuring the oxygen consumption rates every five days for 30 days, t ∈ {1, 5, 10, 15, 20, 25, 30}\[d], that resulted in average values of kO2 = {7.0, 2.7, 2.3, 1.3, 7.0, 1.2, 1.2}\[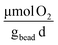 ], respectively (Fig. 7B). On day 1, rates of oxygen utilization kO2,1 measured with the optimal bead was 7.0 ± 1.0, whereas the predicted value was 13 (Fig. 7A). The rate of oxygen utilization at day 30, kO2,30, was measured at 1.2 ± 0.2
], respectively (Fig. 7B). On day 1, rates of oxygen utilization kO2,1 measured with the optimal bead was 7.0 ± 1.0, whereas the predicted value was 13 (Fig. 7A). The rate of oxygen utilization at day 30, kO2,30, was measured at 1.2 ± 0.2 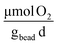 compared to the predicted value of 5.4
compared to the predicted value of 5.4 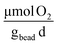 (Fig. 7B).
(Fig. 7B).
3.7. Rate of abiotic hydrolysis of TBOS for optimized beads
Abiotic hydrolysis tests were performed to evaluate the behavior of the slow-release compound without cells present. The abiotic hydrolysis of TBOS exhibits a zero-order rate, with the amount of 1-butanol increasing linearly over time, and serves as a proxy for how 1-butanol hydrolyzes within the bead in the absence of microbial utilization (Fig. 7C). This data can elucidate how well the rate of oxygen utilization data can predict hydrolysis rates based on a stoichiometric balance between 1-butanol and oxygen. For the optimal bead, we observed an abiotic hydrolysis rate at 1.1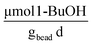 .
.
3.8. Rate of transformation of cDCE for optimized beads
Cometabolic activity was evaluated by measuring the transformation of cDCE at times, t = 1 and t = 30 [d] (Fig. 7D). The rate of cDCE was measured at 0.10 ± 0.01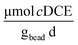 at day 1, and increased to 0.17 ± 0.02
at day 1, and increased to 0.17 ± 0.02 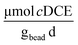 at day 30.
at day 30.
3.9. Transformation yields for optimized beads
The transformation yield TY was calculated at days 1 and 30 to evaluate the efficiency of the immobilized cells in the optimal beads. TY was 0.084 ± 0.016 and 0.86 ± 0.21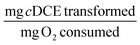 at day 1 and 30, respectively.
at day 1 and 30, respectively.
4. Discussion
Measurements of the transformation of cDCE between day 1 and day 30 demonstrated the capability for ATCC 21198 to perform cometabolism when immobilized in different compositions of PVA-AG hydrogel beads. Statistical modeling with DOE suggested that the compressive modulus (E), the elastic loss (ΔE) of the hydrogel beads, and the oxygen utilization rates of ATCC 21198 (kO2), could be modeled as functions of all three of the input variables that composed the hydrogel formulation, CPVA, CAG, and txlink. The hydrogel composition directly affected E at day 1 and day 30, such that the maximum value of E would occur at the maximum levels of CPVA, CAG, and txlink. Additionally, the models predicted that the minimum values of ΔE and kO2 at day 1 and day 30 would result from the maximum values of all three input variables. The validation of the optimal hydrogel formulation demonstrated the capability for the second order multivariate regression models to capture the material properties based on compressive moduli data after initially making the beads and 30 days after an incubation period with cells. The biological response used throughout this study, kO2, needs further investigation as the models could not predict kO2 at day 1 or day 30 observed in the optimal batch study. Still, these models are a first attempt to empirically optimize the material properties and biological cues based on hydrogel formulae for this in situ bioremediation strategy.Transformation of cDCE measurements ensured that cometabolic transformations were possible across all bead formulations. Further, rates of cDCE transformation (kcDCE) increased during the 30 day incubation across all bead formulations. Murnane et al. reported minimal induction of the monooxygenase enzyme used to transform cDCE with a 1-butanol substrate for ATCC 21198.38 We postulate that kcDCE increased over a 30 day period due to an increase in ATCC 21198 population between day 1 and day 30 (Fig. 2A); yet recognize that the monooxygenase enzyme may be stimulated in the presence of cDCE.20 Our previous works have demonstrated that ATCC 21198 can also cometabolize other CAHs and co-contaminants, such as 1,1,1-trichloroethane, and 1,4-dioxane.12,20 We intended to use cDCE as a surrogate for cometabolism, and due to the capability for ATCC 21198 to transform cDCE throughout all bead formulations, we have demonstrated that this immobilization method could be extended to treat other CAHs, and 1,4-dioxane in column studies.39,40
The rates of oxygen (O2) utilization, kO2, were used to estimate the metabolic activity that corresponded with the utilization of 1-butanol (1-BuOH), the product of hydrolyzed TBOS (Fig. 2B). Unlike cDCE transformation data, kO2 decreased over a 30 day period. Due to the environmental changes the cell undergoes (from growth medium to hydrogel precursor solution to crosslinking bath and finally back to medium), the increased oxygen rate at day 1 could occur from environmental stress. The crosslinking bath is naturally acidic (pH ∼4.5) due to the boric acid that crosslinks PVA, and could damage cells during the crosslinking process. Thus, the rate of oxygen utilization on day 1 may be partially linked to cell repair. Second, the low pH of the crosslinker bath could rapidly hydrolyze TBOS and flood the hydrogel with plenty of 1-BuOH to initiate a high rate of oxygen utilization. The abiotic hydrolysis tests performed for the optimal bead trial suggests that the latter is less likely as the amount of 1-BuOH present in batch bottles at day 1 is approximately zero; however, it should be noted that the TBOS used for optimal beads was of higher purity (98% purity) compared to the CCO experiments (90% purity) and the residual could contain pure 1-BuOH. Indeed, a spike in 1-BuOH at day 1 would promote greater respiration rates and could lend reasoning behind missed predictions for the optimal bead trials. This information heavily warrants that the amount of substrate should be accounted for in future models.
While uncertainties in the behavior of kO2 exist, we attempted second order multivariate modeling for kO2,1 and kO2,30 to identify trends, and found these dependent variables significantly depended on all three factors as well as interaction terms. We found that in general, increasing values of CPVA would result in decreased responses of kO2,1 (Fig. 5A and B) and kO2,30 (Fig. 5C and D). Kumar et al. describe PVA as an oxygen barrier, which may explain the factor effect behavior of CPVA on kO2.41 Further, the significant decrease of kO2,1 could occur due to an increase in the total polymer volume fraction.42 The polymer volume fraction can be thought as the amount of volume the polymer takes up in the gel in comparison to free volume for diffusion. Higher amounts of polymer content could cause tighter gel networks and decrease cells capability to proliferate and reduce the total respiration rate. A negative quadratic slope was predicted for kO2,1 with respect to CAG and contributes to the lowest kO2,1 value at a maximized factor value CAG = 1.4 [coded units] (Fig. 5B). Similar to the reasoning for the kO2 values in respect to CPVA, greater polymer content could lead to lower oxygen utilization rates due to the incapability for cells to proliferate. kO2,30 was modeled as a positive quadratic curve with respect to CAG, suggesting that high concentrations of alginate would indeed increase kO2,30 (Fig. 5D). Differences in cell density could tend to drive higher oxygen rates, and due to characteristic biocompatibility that alginate possesses, beads with higher amounts of alginate could yield a greater population of cells at day 30.
The crosslinking time (txlink) exhibited a significant negative linear effect on both kO2,1 and kO2,30 (Fig. 5A–D). This may be due to the fact that during crosslinking the cells are exposed to boric acid and the longer cells interact with the acidic crosslinker, the more cells could undergo cell death.43 As more cells perish, the respiration rates would be lower for hydrogels with longer crosslinking times compared to shorter time, assuming equal amounts of cells are immobilized. An additional consideration, and more closely related to total polymer content, is that as txlink increases, the gels proceed toward equilibrium and more available crosslink sites are inhabited by ions. A gel with more crosslinked sites would have, on average, smaller pore sizes, and lower effective diffusivity that would limit cell proliferation.44,45
The statistical models for kO2,1 and kO2,30 could suggest trends between the factors related to the bead formulae. However, these models must be used with caution when predicting values of oxygen rates. Specifically, we found that the optimal bead validation tests resulted in kO2 values that did not overlap with predicted values. An analysis of the rates of oxygen utilization for an alginate only hydrogel positive control (CPVA = 0 [% (w/v)], CAG = 1.5 [% (w/v)], and txlink = 75 [min]) demonstrates the differences in respiration rates with different batches of cells (Section ESI10: Fig. S5†). This suggests that the differences are not necessarily due to the bead formula. Instead, the differences could occur from differences in the number of cells per bead. The cell inoculum concentration is set in the bead precursor solution, and cells may not be evenly distributed amongst the beads. Secondly, the quantity of live versus dead cells is not known. Without methods to determine live versus dead cells before cells are added to the bead precursor solution or after the cells are inoculated in beads, we cannot account for differences in the quantity of live cells present for each batch of beads. Potential live/dead staining techniques used to determine cell counts and live/dead ratios in beads could be available to use for our Rhodococcus strain similar to the work of Veeranagouda et al.;46 however, that methodology has yet to be determined for our bacteria strain in a hydrogel system. Note that due to the unknown quantity of cells in the beads means that we cannot compare either kcDCE or kO2 between this study and others.
Stoichiometric analysis of the O2 consumption compared to the abiotic rates of hydrolysis from TBOS forces us to reconsider the interactions between the cells and the slow-release compound. We consider the stoichiometric balance: 6 μmol of O2 is required to oxidize 1 μmol 1-BuOH to carbon dioxide and water. Altogether, the total amount of oxygen consumed for the optimal batch beads and the total amount of 1-BuOH liberated from abiotic beads over the 30 days was 215 μmol O2 and 66 μmol 1-BuOH. The ratio between oxygen consumed and 1-BuOH produced equals 3.3 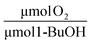 , 1.8 times less than stoichiometrically expected. In our previous works, we found that cells in our gellan gum matrix coupled with TBOS consumed nearly twice the expected oxygen.20 The discrepancy between this work and our previous work is likely a consequence of the use of 1-BuOH for cell synthesis.
, 1.8 times less than stoichiometrically expected. In our previous works, we found that cells in our gellan gum matrix coupled with TBOS consumed nearly twice the expected oxygen.20 The discrepancy between this work and our previous work is likely a consequence of the use of 1-BuOH for cell synthesis.
To consider the efficiency of immobilized cells in different hydrogel formulations with respect to the primary substrate, 1-butanol, we calculated TY at days 1 and 30. For the optimal beads, TY is equal to 0.084 ± 0.016 and 0.86 ± 0.21 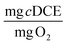 at days 1 and 30. In our previous work with ATCC 21198 immobilized in gellan gum, we obtained TY values of 0.012 ± 0.005 and 0.015 ± 0.02
at days 1 and 30. In our previous work with ATCC 21198 immobilized in gellan gum, we obtained TY values of 0.012 ± 0.005 and 0.015 ± 0.02 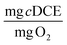 at days 2 and 32.20 While the values for TY found in our previous work were an order of magnitude less than the optimal beads studied in this work, the reactors in our previous work were subjected to injections of 1,1,1-trichloroethane, 1,4-D, and cDCE at concentrations ranging approximately between 250 and 1000 μg L−1, which were also transformed to a great extent. Therefore, we would expect the values of TY to be greater for the beads tested in this study. In this study, we saw significant increases between the values of TY measured at day 1 and 30, whereas Rasmussen et al. did not see a significant increase in TY. Therefore, we suspect that more growth was observed in this study and is likely due to a difference in the structure of PVA-AG beads compared to gellan gum hydrogels beads.47 Based on the assumption that the consumed oxygen serves as the surrogate for 1-butanol, we use the value for the ratio between oxygen consumed and 1-BuOH produced to calculate TY based on 1-BuOH. This results in TY equal 0.06 ± 0.011 and 0.61 ± 0.15
at days 2 and 32.20 While the values for TY found in our previous work were an order of magnitude less than the optimal beads studied in this work, the reactors in our previous work were subjected to injections of 1,1,1-trichloroethane, 1,4-D, and cDCE at concentrations ranging approximately between 250 and 1000 μg L−1, which were also transformed to a great extent. Therefore, we would expect the values of TY to be greater for the beads tested in this study. In this study, we saw significant increases between the values of TY measured at day 1 and 30, whereas Rasmussen et al. did not see a significant increase in TY. Therefore, we suspect that more growth was observed in this study and is likely due to a difference in the structure of PVA-AG beads compared to gellan gum hydrogels beads.47 Based on the assumption that the consumed oxygen serves as the surrogate for 1-butanol, we use the value for the ratio between oxygen consumed and 1-BuOH produced to calculate TY based on 1-BuOH. This results in TY equal 0.06 ± 0.011 and 0.61 ± 0.15 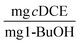 . Tejasen studied an aerobic mixed culture grown on TBOS and observed a TY of 0.24
. Tejasen studied an aerobic mixed culture grown on TBOS and observed a TY of 0.24 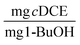 .48 The values for TY likely differ due to the differences of the microorganisms between the different studies.
.48 The values for TY likely differ due to the differences of the microorganisms between the different studies.
In regard to the material properties of the hydrogels, depletion of hydrogel bead mechanical properties was observed. Significant differences were found between the compressive modulus, E, at day 1 and day 30 (Fig. 3B) for all bead types. The decrease in the compressive modulus, E, and the increase in the elastic loss, ΔE, over time likely occurred due to a loss of crosslinking between polymer chains. Several possibilities can describe the potential loss of crosslinking: (1) calcium ions could transfer from alginate linkages to phosphate ions in solution to form calcium phosphate.49 The MSM used in the incubation batch reactors contains excess phosphate ions that could reduce the crosslinks between calcium and alginate polymers. (2) Crosslinks between PVA and boric acid could be reduced as they are labile bonds. Casassa et al. discuss the dynamic equilibrium of a PVA hydrogel due to the labile hydrogen bonds that must form between PVA and boric acid, thus these crosslinks could have been reduced due to long periods of shaking.50 (3) Cell proliferation could reduce crosslinking. With enough pressure within the hydrogel matrix due to cell growth promoted with the use of TBOS, the increase of cell population could have broken the crosslinks in the polymer network (reduced the crosslink density) and further reduced the compressive modulus. Comparison between the CCO center point experiment (Experiment No 15) and an abiotic experiment with beads with the same formulation demonstrates that hydrogels with cells that can proliferate will undergo greater elastic loss (Section 11: Fig. S6†). The data observed for our optimal bead formulation demonstrates the change in E over time in and suggests good stability of hydrogels for at least 20 days (Fig. 7A). While there is a decline in the compressive moduli over time, additional studies performed outside the scope of this work demonstrated that these hydrogel beads would retain their shape and provide the capability for 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 to transform contaminants for over one year in column studies.39,40
198 to transform contaminants for over one year in column studies.39,40
The accurate models used to predict the compressive moduli could be used to describe the effects of the input factors on E1, E30 and ΔE. In general, the models suggest that increases in txlink, CPVA, and CAG result in increased compressive moduli for both days (Fig. 6A–D). This is in line with many other studies that have demonstrated that increasing polymer concentration and crosslinking time increases compressive moduli across a wide range of hydrogels.51,52 Evaluation of factors on the elastic loss demonstrated how hydrogel degradation occurred over the 30 day incubation period. We observed that beads with greater mechanical strength, obtained from high polymer content and crosslinking time, degraded less compared to the other formulae over the 30 day incubation period. Additionally, the squared term CAG2 is significant in E1, E30 and ΔE, and CPVA2 is significant in E30 and ΔE. These squared terms are expected as hydrogel systems have been shown to exhibit a power law behavior for the compressive modulus.53 However, the response surface map of ΔE demonstrates that both CPVA and CAG at high concentrations alone do not support gel structure (Fig. 6E–F). Only when CPVA and CAG values appear at the maximums together does the response of elastic loss significantly decreases. This behavior indicates synergy between PVA and AG blends that reduces the capability for chemical crosslinks to dissociate in aqueous solutions. As mentioned above, bead degradation could occur through abiotic processes.49,50 In the case of PVA polymers, due to the continual breaking and reforming of chains, the structure can be supported by alginate crosslinks where PVA could reform in the gel without losing polymer content. Overall, the synergistic interactions between PVA and AG promote a more durable hydrogel.54–56
Here we discuss the interaction terms found in eqn (11)–(15). The interaction term CPVAtxlink was found to be significant for kO2,1, kO2,30, E30, and ΔE. We find that at high concentrations of CPVA, increases in txlink increases kO2,1, kO2,30 and ΔE, but decreases E30. At low concentrations of CPVA, increases in txlink results in a decrease in kO2,1, kO2,30 and ΔE, but increases E30. Liao et al. evaluated the morphology of PVA beads crosslinked with boric acid and observed an internal porous structure with many irregular pores, yet found no obvious pores on the surface of the beads.57 Their explanation is that gelation is quick at the surface which reduces the permeability of the individual beads. An increase in txlink increases the time for ions to diffuse through the highly crosslinked surface and generate the internal porous structure. At high CPVA, the viscosity of the pre-gel solution is higher which reduces diffusion. Further, higher concentrations of PVA lead to more entanglements available to crosslink, and more ions will be taken up as they diffuse into the bead. Thus, at high CPVA, increasing txlink allows more ions to populate the dense number of crosslink sites and create an internal structure further inside the bead. This in turn allows for better transport of 1-butanol, which increases the respiration rate, and decreases the compressive modulus similar to a sponge. At low CPVA, increases in txlink promotes further crosslinking to create a denser network. Since diffusion is not as affected at low CPVAvs. high CPVA, we expect that the pores get smaller at txlink increases due to more crosslinks. As pores get smaller, respiration rates decrease, and the compressive modulus increases. Interestingly, the model for kO2,30 also included the interactions CPVACAG and CAGtxlink. CPVACAG was found to have a positive interaction on kO2,30, which could be due to the synergy described before. CAGtxlink was also positive, which could be due to more time for calcium ions to saturate the gel and provide a better structure for cells over the 30 day incubation period.
A critical finding established in this work elucidates the capability to predict mechanical properties of a hydrogel bead with immobilized 21![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 198 and slow-release compounds based on the hydrogel composition. We demonstrated that the optimal bead formula exhibited a relatively high compressive modulus, low elastic loss, and low rate of oxygen utilization for both 1 and 30 days. The optimal bead formula determined from this study would promote longer periods of bioremediation and reduce the frequency that beads would need to be replenished in permeable reactive bio-barriers. The use of statistical designs and response surface plots can help investigate the interactions between tunable variables and the cell response that occurs in cell–hydrogel interactions;47 however, we have shown that respiration data cannot be described by hydrogel formulations alone. Of course, this finding is due to the interactions between cells and hydrogels that obscure our understanding of the mechanisms that exist, which suggests that models need more and more experimental and computational validation.47
198 and slow-release compounds based on the hydrogel composition. We demonstrated that the optimal bead formula exhibited a relatively high compressive modulus, low elastic loss, and low rate of oxygen utilization for both 1 and 30 days. The optimal bead formula determined from this study would promote longer periods of bioremediation and reduce the frequency that beads would need to be replenished in permeable reactive bio-barriers. The use of statistical designs and response surface plots can help investigate the interactions between tunable variables and the cell response that occurs in cell–hydrogel interactions;47 however, we have shown that respiration data cannot be described by hydrogel formulations alone. Of course, this finding is due to the interactions between cells and hydrogels that obscure our understanding of the mechanisms that exist, which suggests that models need more and more experimental and computational validation.47
Lastly, batch reactors with mineral salt medium (MSM) may not capture the effects that groundwater composition and conductivity can impose on the beads. MSM provides excess nutrients to the microorganisms that promote growth but can potentially reduce the number of crosslinks in hydrogels due to the concentration of phosphate ions that exist in the MSM (760 mg L−1 PO4−3). Groundwater typically possesses significantly less phosphate than the MSM (<10 mg L−1 PO4−3).58 With lower amounts of nutrients for cells and significantly less phosphate, we expect cell growth would be slower and the reduction of crosslink sites would occur less. Thus, we expect cells would exhibit lower rates of metabolic activity and that beads would experience less elastic loss over time when compared to the values observed throughout this study.
5. Conclusions
We have demonstrated the capability of poly(vinyl)-alcohol – alginate beads for the immobilization of ATCC 21198 with a slow-release compound, tetrabutoxysilane. With the use of a Design of Experiments approach, we were able to elucidate factors of the hydrogel formulation that provide high mechanical strength but were unable to accurately predict oxygen utilization rates. While more in-depth measurements on the interactions between the slow-release compound, oxygen rates, and hydrogel formula are needed, these beads would provide cells with a stable, durable microenvironment and a constant carbon source. These beads have already been applied in long-term column studies and could be applied as an in situ bioremediation technique to reduce CAHs, and 1,4-dioxane in groundwater aquifers.39,40Future studies will consist of scaling-up the production of hydrogel beads that control the size and output using a coaxial air and piezoelectric ring set-up, as well as characterizing the hydrogel structure with molecular and structural characterization techniques. There is still a need to determine the number of cells that develop within the beads over time and how the hydrogel structure responds to changes in cell density. Additionally, future studies will be conducted with actual groundwater samples to demonstrate the durability and bioremediation capability of immobilized cells and support the feasibility of this approach.
Data availability
All data are available on the https://github.com/fogg-lab/.Conflicts of interest
The authors have no conflicts to declare.Acknowledgements
This research was funded by the National Institute of Environmental Health Sciences under grant NIH R01 ES032707. The authors thank Mohammad Azizian for his support of the analytical methods; Dara Coon, Celia H'Almeida, Casey Johnson, and Brontë S Mckinnis for assisting in data collection; and Dr Michael Hyman for helping understand the microbial processes.References
- Chlorinated Solvent Source Zone Remediation [Internet], ed. Kueper B. H., Stroo H. F., Vogel C. M. and Ward C. H., Springer New York, New York, NY, 2014, DOI:10.1007/978-1-4614-6922-3.
- Waste USEPAO of S and Response E, Engineered Approaches to in situ Bioremediation of Chlorinated Solvents: Fundamentals and Field Applications, DIANE Publishing, 2000 Search PubMed.
- M. Grindstaff, Bioremediation of Chlorinated Solvent Contaminated Groundwater, US Environmental Protection Agency, Office of Solid Waste and Emergency Response, Technology Innovation Office, 1998 Search PubMed.
- G. B. Davis, Reviewing the Bioremediation of Contaminants in Groundwater: Investigations over 40 Years Provide Insights into What's Achievable, Front. Biosci., 2023, 15(3), 16 CrossRef PubMed.
- K. R. Schmidt, T. Augenstein, M. Heidinger, S. Ertl and A. Tiehm, Aerobic biodegradation of cis-1,2-dichloroethene as sole carbon source: stable carbon isotope fractionation and growth characteristics, Chemosphere, 2010, 78(5), 527–532 CrossRef CAS PubMed.
- U.S. EPA, IRIS Toxicological Review of Cis-& Trans-1,2-Dichloroethylene (Final Report), US Environmental Protection Agency, Washington, DC, 2010, EPA/635/R-09/006F Search PubMed.
- N. V. Coleman, T. E. Mattes, J. M. Gossett and J. C. Spain, Biodegradation of cis -Dichloroethene as the Sole Carbon Source by a β-Proteobacterium, Appl. Environ. Microbiol., 2002, 68(6), 2726–2730 CrossRef CAS PubMed.
- C. Clark and L. K. Rhea, Cometabolism of Chlorinated Volatile Organic Compounds and 1,4-Dioxane in Groundwater, Water, 2023, 15(22), 3952 CrossRef CAS PubMed.
- S. W. Chapman, B. L. Parker, J. A. Cherry, R. Aravena and D. Hunkeler, Groundwater–surface water interaction and its role on TCE groundwater plume attenuation, J. Contam. Hydrol., 2007, 91(3–4), 203–232 CrossRef CAS PubMed.
- N. Blázquez-Pallí, M. Rosell, J. Varias, M. Bosch, A. Soler and T. Vicent, et al., Multi-method assessment of the intrinsic biodegradation potential of an aquifer contaminated with chlorinated ethenes at an industrial area in Barcelona (Spain), Environ. Pollut., 2019, 244, 165–173 CrossRef PubMed.
- H. M. Rolston, M. R. Hyman and L. Semprini, Aerobic cometabolism of 1,4-dioxane by isobutane-utilizing microorganisms including Rhodococcus rhodochrous strain 21198 in aquifer microcosms: experimental and modeling study, Sci. Total Environ., 2019, 694, 133688 CrossRef CAS PubMed.
- M. F. Azizian and L. Semprini, Aerobic cometabolism of chlorinated Solvents and 1,4-dioxane in continuous-flow columns packed with gellan-gum hydrogels coencapsulated with ATCC strain 21198 and TBOS or T2BOS as slow-release compounds, ACS EST Eng., 2022 DOI:10.1021/acsestengg.2c00023.
- C. C. Azubuike, C. B. Chikere and G. C. Okpokwasili, Bioremediation techniques–classification based on site of application: principles, advantages, limitations and prospects, World J. Microbiol. Biotechnol., 2016, 32(11), 180 CrossRef PubMed.
- D. Frascari, G. Zanaroli and A. S. Danko, In situ aerobic cometabolism of chlorinated solvents: a review, J. Hazard. Mater., 2015, 283, 382–399 CrossRef CAS PubMed.
- B. Groundwater, Introduction to In Situ Bioremediation of Groundwater [Internet], Office of Solid Waste and Emergency Response, 2013, (Preparation of this report has been funded by the U.S. Environmental Protection Agency Office of Superfund Remediation and Technology Innovation (OSRTI) under Contract Number EP-W-07-078 to Tetra Tech EM Inc.), Report No.: 542-R-13–018, available from, https://semspub.epa.gov/work/HQ/171054.pdf Search PubMed.
- S. Upadhyay and A. Sinha, Role of microorganisms in Permeable Reactive Bio-Barriers (PRBBs) for environmental clean-up: A review, Global Nest Journal, 2018, 269–280 CAS.
- Z. Madzin, F. M. Kusin, M. S. Md Zahar and S. M. Nurjaliah, Passive in situ remediation using permeable reactive barrier for groundwater treatment, Pertanika Journal of Scholarly Research Reviews, 2016, 2(2), 1–11 Search PubMed.
- R. C. Borden, Concurrent bioremediation of perchlorate and 1,1,1-trichloroethane in an emulsified oil barrier, J. Contam. Hydrol., 2007, 94(1–2), 13–33 CrossRef CAS PubMed.
- W. Wang and Y. Wu, A multi-path chain kinetic reaction model to predict the evolution of 1,1,1-trichloroethane and its daughter products contaminant-plume in permeable reactive bio-barriers, Environ. Pollut., 2019, 253, 1021–1029 CrossRef CAS PubMed.
- M. T. Rasmussen, A. M. Saito, M. R. Hyman and L. Semprini, Co-encapsulation of slow release compounds and Rhodococcus rhodochrous ATCC 21198 in gellan gum beads to promote the long-term aerobic cometabolic transformation of 1,1,1-trichloroethane, cis -1,2-dichloroethene and 1,4-dioxane, Environ. Sci.: Processes Impacts, 2020, 22(3), 771–791 RSC.
- M. B. Cassidy, H. Lee and J. T. Trevors, Environmental applications of immobilized microbial cells: a review, J. Ind. Microbiol., 1996, 16(2), 79–101 CrossRef CAS.
- M. An and K. V. Lo, Activated sludge immobilization using the PVA-alginate-borate method, J. Environ. Sci. Health, Part A, 2001, 36(1), 101–115 CrossRef CAS PubMed.
- S. Hashimoto and K. Furukawa, Immobilization of activated sludge by PVA-boric acid method, Biotechnol. Bioeng., 1987, 30(1), 52–59 CrossRef CAS PubMed.
- N. A. M. Zain, M. S. Suhaimi and A. Idris, Development and modification of PVA–alginate as a suitable immobilization matrix, Process Biochem., 2011, 46(11), 2122–2129 CrossRef CAS.
- T. Andersen, P. Auk-Emblem and M. Dornish, 3D Cell Culture in Alginate Hydrogels, Microarrays, 2015, 4(2), 133–161 CrossRef CAS PubMed.
- K. Y. A. Wu and K. D. Wisecarver, Cell immobilization using PVA crosslinked with boric acid, Biotechnol. Bioeng., 1992, 39(4), 447–449 CrossRef CAS PubMed.
- D. V. Pham and L. Tho Bach, Immobilized bacteria by using PVA (Polyvinyl alcohol) crosslinked with Sodium sulfate, Int. J. Sci. Eng., 2014, 7(1), 41–47 Search PubMed.
- S. P. Sam, R. Adnan and S. L. Ng, Statistical optimization of immobilization of activated sludge in PVA/alginate cryogel beads using response surface methodology for p-nitrophenol biodegradation, J. Water Process Eng., 2021, 39, 101725 CrossRef.
- Y. Dong, Y. Zhang and B. Tu, Immobilization of ammonia-oxidizing bacteria by polyvinyl alcohol and sodium alginate, Braz. J. Microbiol., 2017, 48(3), 515–521 CrossRef CAS PubMed.
- A. Dzionek, D. Wojcieszyńska and U. Guzik, Natural carriers in bioremediation: a review, Electron. J. Biotechnol., 2016, 23, 28–36 CrossRef.
- M. J. Lapponi, M. B. Méndez, J. A. Trelles and C. W. Rivero, Cell immobilization strategies for biotransformations, Curr. Opin. Green Sustainable Chem., 2022, 33, 100565 CrossRef CAS.
- P. Warneck, A review of Henry's law coefficients for chlorine-containing C1 and C2 hydrocarbons, Chemosphere, 2007, 69(3), 347–361 CrossRef CAS PubMed.
- P. Warneck and J. Williams, The Atmospheric Chemist's Companion: Numerical Data for Use in the Atmospheric Sciences [Internet], Springer Netherlands, Dordrecht, 2012, DOI:10.1007/978-94-007-2275-0.
- F. Topuz and O. Okay, Macroporous hydrogel beads of high toughness and superfast responsivity, React. Funct. Polym., 2009, 69(5), 273–280 CrossRef CAS.
- S. Vancheeswaran, R. U. Halden, K. J. Williamson, J. D. Ingle and L. Semprini, Abiotic and biological transformation of tetraalkoxysilanes and trichloroethene/cis -1,2-dichloroethene cometabolism driven by tetrabutoxysilane-degrading microorganisms, Environ. Sci. Technol., 1999, 33(7), 1077–1085 CrossRef CAS.
- T. Keskin Gündoğdu, İ. Deniz, G. Çalışkan, E. S. Şahin and N. Azbar, Experimental design methods for bioengineering applications, Crit. Rev. Biotechnol., 2016, 36(2), 368–388 CrossRef PubMed.
- M. Darnell and D. J. Mooney, Leveraging advances in biology to design biomaterials, Nat. Mater., 2017, 16(12), 1178–1185 CrossRef CAS PubMed.
- R. A. Murnane, W. Chen, M. Hyman and L. Semprini, Long-term cometabolic transformation of 1,1,1-trichloroethane and 1,4-dioxane by Rhodococcus rhodochrous ATCC 21198 grown on alcohols slowly produced by orthosilicates, J. Contam. Hydrol., 2021, 240, 103796 CrossRef CAS PubMed.
- K. Bailey, Aerobic cometabolism of cis-dichloroethylene, 1,1,1-trichloroethane, and 1,4-dioxane by polyvinyl alcohol/sodium alginate hydrogel beads that co-entrapped rhodococcus rhodochrous strain ATCC 21198 and slow-release growth substrates: column studies, Master's thesis, Oregon State University, 2023, available from, https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/3j333994k?locale=en.
- S. P. Conway, Aerobic cometabolism of 1,4-dioxane and cis-dichloroethylene by gellan gum and polyvinyl alcohol/sodium alginate hydrogel beads co-encapsulated with rhodococcus rhodochrous strain ATCC 21198 and slow-release growth substrates: batch, column, and toxicity studies, Master's thesis, Oregon State University, 2022, available from, https://ir.library.oregonstate.edu/concern/graduate_thesis_or_dissertations/rv0432149.
- A. Kumar, A. Sood and S. S. Han, Poly (vinyl alcohol)-alginate as potential matrix for various applications: a focused review, Carbohydr. Polym., 2022, 277, 118881 CrossRef CAS PubMed.
- J. Li and D. J. Mooney, Designing hydrogels for controlled drug delivery, Nat. Rev. Mater., 2016, 1(12), 16071 CrossRef CAS PubMed.
- N. Guan and L. Liu, Microbial response to acid stress: mechanisms and applications, Appl. Microbiol. Biotechnol., 2020, 104(1), 51–65 CrossRef CAS PubMed.
- Y. Wu, S. Joseph and N. R. Aluru, Effect of cross-linking on the diffusion of water, ions, and small molecules in hydrogels, J. Phys. Chem. B, 2009, 113(11), 3512–3520 CrossRef CAS PubMed.
- S. Bhusari, S. Sankaran and A. Del Campo, Regulating bacterial behavior within hydrogels of tunable viscoelasticity, Advanced Science, 2022, 9(17), 2106026 CrossRef PubMed.
- Y. Veeranagouda, E. J. Lim, D. W. Kim, J. K. Kim, K. Cho and H. J. Heipieper, et al., Formation of specialized aerial architectures by Rhodococcus during utilization of vaporized p-cresol, Microbiology, 2009, 155(11), 3788–3796 CrossRef CAS PubMed.
- F. J. Vernerey, S. Lalitha Sridhar, A. Muralidharan and S. J. Bryant, Mechanics of 3D cell–hydrogel interactions: experiments, models, and mechanisms, Chem. Rev., 2021, 121(18), 11085–11148 CrossRef CAS PubMed.
- S. Tejasen, Aerobic biotransformation of trichloroethylene, cis-dichloroethylene and vinyl chloride by a mixed culture grown on a non-toxic substrate: benzyl alcohol, J. Sci. Technol., 2004, 26(1), 117–129 Search PubMed.
- C. K. Kuo and P. X. Ma, Maintaining dimensions and mechanical properties of ionically crosslinked alginate hydrogel scaffoldsin vitro, J. Biomed. Mater. Res., 2008, 84(4), 899–907 CrossRef PubMed.
- E. Z. Casassa, A. M. Sarquis and C. H. Van Dyke, The gelation of polyvinyl alcohol with borax: a novel class participation experiment involving the preparation and properties of a “slime.”, J. Chem. Educ., 1986, 63(1), 57 CrossRef CAS.
- P. M. Kharkar, K. L. Kiick and A. M. Kloxin, Designing degradable hydrogels for orthogonal control of cell microenvironments, Chem. Soc. Rev., 2013, 42(17), 7335–7372 RSC.
- S. Barbon, M. Contran, E. Stocco, S. Todros, V. Macchi and R. D. Caro, et al., Enhanced Biomechanical properties of polyvinyl alcohol-based hybrid dcaffolds for cartilage tissue engineering, Processes, 2021, 9(5), 730 CrossRef CAS.
- H. M. Wyss, T. Franke, E. Mele and D. A. Weitz, Capillary micromechanics: measuring the elasticity of microscopic soft objects, Soft Matter, 2010, 6(18), 4550 RSC.
- X. Li, M. Shu, H. Li, X. Gao, S. Long and T. Hu, et al., Strong, tough and mechanically self-recoverable poly(vinyl alcohol)/alginate dual-physical double-network hydrogels with large cross-link density contrast, RSC Adv., 2018, 8(30), 16674–16689 RSC.
- Y. J. Kim and J. Min, Property modulation of the alginate-based hydrogel via semi-interpenetrating polymer network (semi-IPN) with poly(vinyl alcohol), Int. J. Biol. Macromol., 2021, 193, 1068–1077 CrossRef CAS PubMed.
- S. Sanjeev Kumar, M. S. Kumar, D. Siddavattam and T. B. Karegoudar, Generation of continuous packed bed reactor with PVA–alginate blend immobilized Ochrobactrum sp. DGVK1 cells for effective removal of N,N-dimethylformamide from industrial effluents, J. Hazard. Mater., 2012, 199–200, 58–63 CrossRef CAS PubMed.
- H. Liao, Y. Liu, Q. Wang and W. Duan, Structure and properties of porous poly(vinyl alcohol) hydrogel beads prepared through a physical–chemical crosslinking method, J. Appl. Polym. Sci., 2018, 135(26), 46402 CrossRef.
- J. L. Domagalski and H. Johnson, phosphorus and groundwater: establishing links between agricultural use and transport to streams, US Geological Survey Fact Sheet, 2012, vol. 3004, p. 4 Search PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3su00409k |
| This journal is © The Royal Society of Chemistry 2024 |