Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Advancements and assessment of compressed carbon dioxide energy storage technologies: a comprehensive review
Hailing
Ma
 ab,
Yao
Tong
ab,
Yao
Tong
 *a,
Xiao
Wang
*a,
Xiao
Wang
 *c and
Hongxu
Wang
*b
*c and
Hongxu
Wang
*b
aHoffmann Institute of Advanced Materials, Shenzhen Polytechnic University, 7098 Liuxian Boulevard, Shenzhen, Guangdong 518055, China. E-mail: yao_tong@szpt.edu.cn
bSchool of Engineering and Technology, The University of New South Wales, Canberra, ACT 2600, Australia
cChongqing Institute of Green and Intelligent Technology, Chinese Academy of Sciences, Chongqing 400714, China. E-mail: wangxiao@cigit.ac.cn
First published on 28th August 2024
Abstract
Compressed carbon dioxide energy storage (CCES) emerges as a promising alternative among various energy storage solutions due to its numerous advantages, including straightforward liquefaction, superior energy storage density, and environmental compatibility. This review delves into the recent advancements, economic viability, technological feasibilities, and operational aspects of CCES systems comprehensively. It encapsulates the evaluation methodologies, examines the intricacies of compressed carbon dioxide storage, and explores the avenues for performance optimization within CCES technology. A comparative analysis reveals that among trans-critical, supercritical, and liquid CCES systems, the supercritical variant exhibits enhanced thermodynamic properties and a more straightforward configuration, positioning it as the preferred choice for large-scale applications. Additionally, this review incorporates recent advancements in CO2-related conversion technologies, such as photocatalytic and photothermal CO2 reduction, which further enhance the potential of CCES systems. The review highlights the future direction for CCES development, emphasizing the need for optimal compression–expansion ratios, refined analytical models, and integrated multi-disciplinary approaches. This discussion aims to serve as a foundational reference for the effective design and implementation of CCES systems.
Sustainability spotlightGlobal energy storage demands are rising sharply, making the development of sustainable and efficient technologies critical. Compressed carbon dioxide energy storage (CCES) addresses this imperative by utilizing CO2, a major greenhouse gas, thus contributing directly to climate change mitigation. This review explores CCES as a high-density, environmentally friendly energy storage option that aligns with the United Nations Sustainable Development Goals (SDGs), specifically SDG 7 (Affordable and Clean Energy) and SDG 13 (Climate Action). By enhancing the efficiency and scalability of CCES technologies, this work supports the transition towards more sustainable energy systems. It demonstrates significant advancements in the thermodynamic properties of supercritical CO2 systems, offering a sustainable alternative to traditional energy storage methods and paving the way for reduced carbon footprints in industrial applications. |
1 Introduction
In response to the increasingly severe climate change, Carbon Capture and Storage (CCS) technology has emerged as a vital solution. Over the past few decades, compressed carbon dioxide energy storage (CCES) technology has seen significant advancements. Initial research primarily focused on fundamental theories and laboratory tests. However, as technology progressed, the scale and application scope of CCES systems have gradually expanded. Current research efforts are directed towards optimizing compression–expansion ratios, developing refined analytical models, and promoting multidisciplinary integration methods. Optimizing compression–expansion ratios can enhance the thermodynamic efficiency of the system and reduce energy losses. Refined analytical models facilitate more accurate simulation and prediction of system performance. Additionally, multidisciplinary integration methods can combine CCES technology with other energy technologies, further enhancing its application potential.Countries worldwide have adopted various measures to minimize greenhouse gas emissions. Developed countries like the United States, which have reached their carbon peak, have implemented CCS technology as a strategy to reduce greenhouse gas emissions. Carbon capture and sequestration technology mainly consist of the following steps: CO2 capture, which means that CO2 is separated from fossil fuels before or after combustion and can be reduced by compression; CO2 transportation, which means that the captured CO2 is transported to the storage site through pipelines or other means of transportation. CO2 storage refers to the injection of CO2 into storage space, such as an underground saltwater layer, waste gas mining, and other geological structures or geological structures below the seabed.1–4 Pre-combustion capture, post-combustion capture, and oxygen-enriched combustion are the three primary carbon capture methods now in use.5,6 Due to the high expense of directly injecting CO2 into the ground and geological storage, some researchers have expanded the attention of CO2 oil displacement in the carbon capture and storage process and proposed the concept of carbon capture, utilization, and storage (CCUS). How to use this captured CO2 has also become one of the research directions of scholars. Compared with CCS technology, the CCUS proposed in recent years has more obvious advantages. It purifies the captured CO2 and then puts it into the new production process to become raw material recycling rather than simple storage. Compared with CCS, CCUS can turn CO2 in waste gas into a useable resource, resulting in economic benefits.7–10 According to the 2017 CCS Global Status Report,11 there are 39 large-scale CCS devices in use globally as of September 2017, with 21 projects in operation or under development, capturing a total of 38 million tons of CO2 per year. For such a big amount of CO2 captured every year, the most common treatment method is to store it underground. If this portion of CO2 can be employed instead of air as an energy storage system, the pressure to deal with the CO2 gathered each year will be reduced.
Simultaneously, renewable energy sources such as wind and solar can help improve power system structure, reduce the amount of primary energy used in grid power generation, and minimize carbon emissions. However, due to natural conditions' limitations, like wind and solar power generation, the objective of renewable energy power generation is to effectively utilization these renewable energies and safely connect to the grid during periods of no wind or at night. Additionally, it aims to enhance the benefits of renewable energy power generation technology.12 Consequently, with renewable energy poised for large-scale adoption, energy storage technology is being integrated into renewable energy generation systems, such as wind power generation and photovoltaic power generation, as peak shaving equipment in the power grid. This technology is required for the widespread and successful deployment of renewable energy systems. Renewable energy sources, like wind power and photovoltaic power generation, are stored during low power consumption periods. The energy storage device adjusts the unit's output curve, mitigating the risks associated with the randomness and unpredictability of renewable energy power generation on stable power generation in the power grid. By converting stored energy into electric energy output during peak power consumption periods, the energy storage device can effectively eliminate the risk of power supply shortages during peak periods, act as a peak load shaving mechanism, and reduce the power grid's reserve demand for peak-shaving power stations.13,14
The current electric energy storage technology, as illustrated in Table 1, is fairly advanced. The current electric energy storage technologies mainly include three categories: physical energy storage technologies represented by pumped hydro energy storage, compressed air energy storage, and flywheel energy storage; chemical energy storage technologies represented by battery energy storage, superconducting energy storage technologies, and electromagnetic energy storage technology represented by supercapacitors.19–22 Electrochemical energy storage systems generally have relatively small capacities and high costs. At present, only pumped storage technology and compressed air energy storage technology can match the grid and realize large-scale energy storage. The single unit power of a compressed air energy storage power station can reach more than 350 MW, and the maximum capacity of a pumped storage power station can reach 2.1 GW.23 Although the technology of pumped storage power stations has matured, and the cycle efficiency is high and the cycle is long, the site selection of pumped storage power station has strict requirements: it must be a reservoir with a large drop and a corresponding dam. Therefore, the sites suitable for the construction of pumped storage power plants will decrease year by year. Compressed air energy storage technology is another technology that can realize large-scale energy storage. Compared with pumped hydro storage, it has more flexible site selection requirements, so this technology has also received extensive attention.24,25 Research on compressed air energy storage systems provides a theoretical foundation for increasing the energy utilization of compressed air energy storage systems, making them more useful in renewable energy, power grid peak cutting, and valley filling. However, there are still several issues with compressed air energy storage. CO2 has good physical qualities compared to air and is a type of energy storage system with significant development potential, allowing for large-scale deployment of CCES technology.
| Energy storage mode | Initial investment dollar/kW h | Rated power/MW | Discharge duration | Cycle efficiency/% | Cycle life/year | |
|---|---|---|---|---|---|---|
| Physical energy storage | Pumping energy storage (PES) | 10.6–21.2 | 10–1000 | Minute level–hour level | 65–80 | 30–50 |
| Flywheel energy storage (FES) | 1000–5000 | 0.01–20 | Seconds–minutes | 75–90 | 20–50 | |
| Compressed air energy storage (CAES) | 3.18–5.3 | 10–300 | Minute level–hour level | 42–73 | 30–40 | |
| Liquid air energy storage (LAES) | 7.6 | 10–500 | Minute level–hour level | 61.6 | 30–40 | |
| CCES | 2.88 | 10–300 | Minute level–hour level | 64–67 | 30–40 | |
| Electromagnetic energy storage | Supercapacitor | 20000 | 0.05–0.1 | Seconds–minutes | 65–90 | 8–17 |
| Superconducting electromagnetism | — | 1–100 | Millisecond–second | 80–95 | 20 | |
| Electrochemical energy storage | Vanadium flow battery | 600 | 0.2–12 | Hour class | 65–75 | 12–20 |
| Zinc bromine flow battery | 450 | 0.1–15 | Hour class | 60–70 | 15 | |
| Sodium–sulfur battery | 450 | 0.05–30 | Hour class | 75–87 | 12–20 | |
| Lead-acid battery | 50–100 | 0.05–10 | Minute level–hour level | 70–90 | 5–15 | |
| Lithium-ion battery | 900–1300 | — | Minute level–hour level | 80–95 | 10–20 | |
| Hydrogen fuel cell | 2–15 | 0.01–50 | Minute level–hour level | 20–50 | 5–20 | |
The energy storage working system using air has the characteristic of low energy storage density. Although the energy storage density can be increased by converting air into a liquid or supercritical state, it will increase the technical difficulty and economic cost accordingly.24,26,27 So, researchers began to explore the gas energy storage system with high density and can be used as the compressed energy storage system. Because supercritical carbon dioxide has the characteristics of low viscosity, low diffusion coefficient, and high density, using it as the energy storage system for compressed gas energy storage can obtain higher energy storage density and greatly reduce the energy storage volume needed by container/reservoir.28–30 As a result, many professionals and academics have been interested in compressed-gas energy storage technology based on carbon dioxide in recent years.
In conclusion, as compared to air, carbon dioxide has several distinct benefits as an energy storage system. Pumps, rather than compressors, may be applied to enhance storage pressure since it has a higher dew point temperature and is easier to condense than air. On either hand, it enables large-scale carbon dioxide consumption, which aids in the reduction of carbon dioxide emissions. Due to the advantages of easy access to carbon dioxide and good physical properties, CCES technology is developing rapidly at present. The research work on the refrigeration cycle and Brayton cycle with carbon dioxide as the working system has been paid attention to, and the research on the carbon dioxide system has been more mature.31 However, there is still a big deficiency in the research on using carbon dioxide as the working system of compressed-gas energy storage systems. Therefore, it is necessary to research on the expansion of a new type of energy storage system with carbon dioxide as the working system, especially paying attention to the performance improvement of carbon dioxide heat exchanger and compression expander in the supercritical state, which is helpful to further improve the cycle efficiency of the system and expound the utilization field of carbon dioxide.
The advancement of carbon dioxide compression energy storage system research is evaluated and addressed in this study. The thermodynamic techniques of CCES are outlined first, followed by a discussion of the development of the CCES system, as well as its economic and technical viability and system operation. This review also addresses cycle efficiency, energy storage efficiency, energy storage density, and system structure complexity, which are commonly used to assess the overall performance of CCES systems. Finally, the challenges faced by the current compressed carbon dioxide energy storage system are summarized, and its future research directions are prospected.
2 Principle of CCES system
The operational strategy of CCES systems includes multi-stage compression, thermal energy storage, high-pressure gas storage, and expansion processes. During the energy storage phase, the system uses excess electrical energy to drive compressors, compressing carbon dioxide to a supercritical state, while the heat generated during compression is stored in thermal storage devices. The high-pressure carbon dioxide is then stored in high-pressure gas storage tanks. During the energy release phase, the high-pressure gas absorbs the stored heat through a heat exchanger and enters an expansion turbine to perform work, with the released electrical energy being output through a generator. Optimizing the parameters for multi-stage compression and expansion processes can further improve the system's cycle efficiency and energy storage density.Carbon dioxide has a melting point of 194.7 K and a boiling point of 216.6 K, making it denser than air (under ordinary circumstances) and somewhat soluble in water. Carbon dioxide is chemically inactive, exhibits great thermal stability (only 1.8% degradation at 2000 °C), cannot burn, does not generally assist combustion, and low quantities of carbon dioxide are non-toxic. The critical temperature of carbon dioxide is 304.1 K, with an equivalent pressure of 7.38 MPa, making it relatively simple for it to reach the critical state. When the temperature and pressure of carbon dioxide exceed the critical threshold, it is termed supercritical carbon dioxide (SC-CO2). Transcritical carbon dioxide (TC-CO2) occurs when the pressure of carbon dioxide undergoes supercritical and subcritical transitions and cycles around the critical point. Studies on transcritical carbon dioxide heat pumps and supercritical carbon dioxide Brayton cycles have indicated that carbon dioxide can be used as a natural working system. SC-CO2 combines some properties of gaseous and liquid CO2 but also exhibits new properties, such as lower viscosity, greater diffusion coefficient, and higher density.32–34 Under current technical conditions, carbon dioxide can easily reach the supercritical state through pressurization, leading to extensive research on thermodynamic cycles based on carbon dioxide, including carbon dioxide refrigeration cycles,35–38 carbon dioxide Brayton cycles,39,40 carbon dioxide Rankine cycles,41 carbon dioxide heat pump cycles,42 carbon dioxide energy storage cycles,30,43,44 and more.
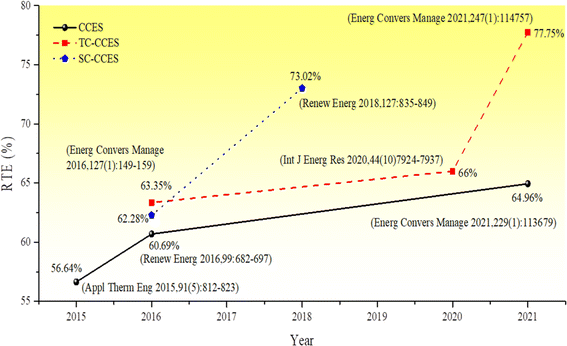
Liu et al.45 proposed an electrothermal energy storage system that utilizes CO2 as the working fluid and converts energy through heat engine and heat pump cycles. Depending on the physical state of carbon dioxide at the outlet of the expansion unit, the energy storage system is categorized as either a transcritical energy storage system (Transcritical CCES, TC-CCES) when the pressure of carbon dioxide at the outlet is below the critical pressure, or as a supercritical compressed carbon dioxide energy storage system (Supercritical CCES, SC-CCES) when the temperature and pressure at the exit of the expansion unit exceed the critical values of carbon dioxide. Fig. 1 and 2 illustrate the significant advancements in CCES, TC-CCES, and SC-CCES, showcasing notable enhancements in system round-trip efficiency (RTE) across various operational scenarios. The working principle of the electrothermal energy storage system involves the excess electric energy input driving the compressor to compress CO2 during the energy storage process. This conversion process transforms the electric energy into internal energy and pressure energy of CO2, which is stored in the high-temperature accumulator. The pressure energy is then converted into cold energy through the expansion turbine and stored in the cold accumulator. Subsequently, after increasing the pressure, CO2 absorbs heat energy in the accumulator, warms up, and enters the expansion turbine to perform work. The CO2 exiting the turbine is cooled by the cold source before being cycled back to the beginning of the process, thereby converting heat and cold energy into electric energy.
 | ||
| Fig. 2 A schematic of the carbon dioxide electrothermal energy storage system's cycle.43 | ||
On the basis of classic compressed air energy storage technology, a CCES system has been developed. The system incorporates multi-stage compression, inter-stage cooling, multi-stage expansion, inter-stage reheat, and other operational options. Nevertheless, there are notable structural differences between the two systems. This section provides an overview of the principles and development progress of the compressed carbon dioxide energy storage system to elucidate its development trajectory.
Because carbon dioxide is a greenhouse gas that significantly impacts global temperature change, the process of capturing and collecting carbon dioxide is complex. The CCES system uses closed technology, meaning there is no material exchange with the outside world during the entire energy storage process, only energy exchange. Fig. 3 depicts the CCES device in action. The working principle of the system is as follows: when storing energy, surplus electric energy compresses the carbon dioxide, which is then stored after heat exchange by the heat storage device. The high-pressure carbon dioxide is stored in the storage tank, and the compressed heat is stored in the heat storage device. During energy release, the high-pressure carbon dioxide is heated by heat exchange, driving the expander to perform work, and generates electric energy. The carbon dioxide, after the work is done, is cooled to its initial state for storage.47,48
 | ||
| Fig. 3 Schematic diagram of CCES system.46 | ||
To maintain the liquid or supercritical state of carbon dioxide working fluid in the gas storage chamber in the existing CCES system, a specially manufactured gas storage tank must be used to ensure the temperature and pressure of the gas storage chamber.46 A heat accumulator is required in the system to recover and utilize the heat created by the energy storage process. The presence of artificial gas storage tanks and heaters adds to the existing CCES system's complexity and manufacturing expense. The compression of carbon dioxide into subterranean fluids or porous rock formations that formerly held fluids, such as natural gas, oil, or deep saline water layers, exhausted oil and gas reservoirs, unexploitable coal seams, and so on, is known as carbon dioxide geological storage. The rise in temperature per unit distance down the normal of the subsurface isothermal surface to the core of the earth is defined as a geothermal gradient,49 also known as the “geothermal gradient.” The geothermal gradient is usually about 30 °C km−1. As a result, when carbon dioxide is kept underground for 2–3 kilometers, geothermal energy may be used to heat high-pressure carbon dioxide, eliminating the need for a heat accumulator in the CCES system.
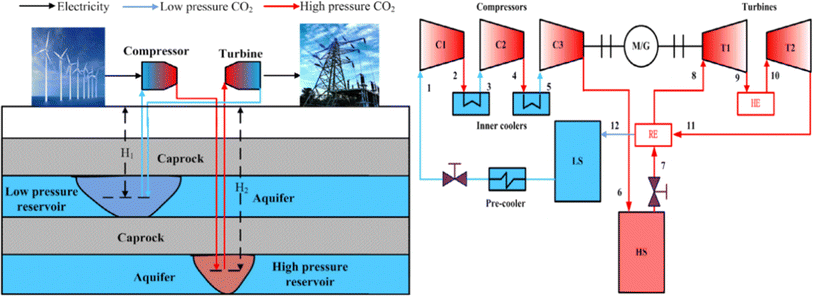
The CCES system utilizes two subterranean gas storage chambers. One chamber stores high-pressure carbon dioxide emitted by the compressor to prevent its release into the atmosphere. The other chamber stores low-pressure carbon dioxide from the expansion turbines, creating a closed CCES system.47 The heat accumulator may be excluded from the system due to the geothermal gradient's impact on the subterranean gas storage chamber. The carbon dioxide from the compressor can be directly injected into the gas storage chamber for storage. The CCES system consists of a compressor, high-pressure gas storage chamber, low-pressure gas storage chamber, heater, expansion turbine, regenerator, and other components, all based on subterranean gas storage technology.
The CCES system, based on the underground gas storage chamber, operates on the following principle: during periods of low power consumption, the compressor uses excess electric energy to supercritically reduce the carbon dioxide in the low-pressure gas storage chamber and then stores it in the high-pressure gas storage chamber.50 The supercritical carbon dioxide stored in the high-pressure gas storage chamber is released at the peak of power consumption, where it heats up in the heater and enters the expansion turbine to perform work. This work is then converted into electricity through the generator, and the carbon dioxide is subsequently stored in the low-pressure gas storage chamber after the work is completed, ready to be utilized in the next cycle of energy storage.51
3 Research progress of CCES
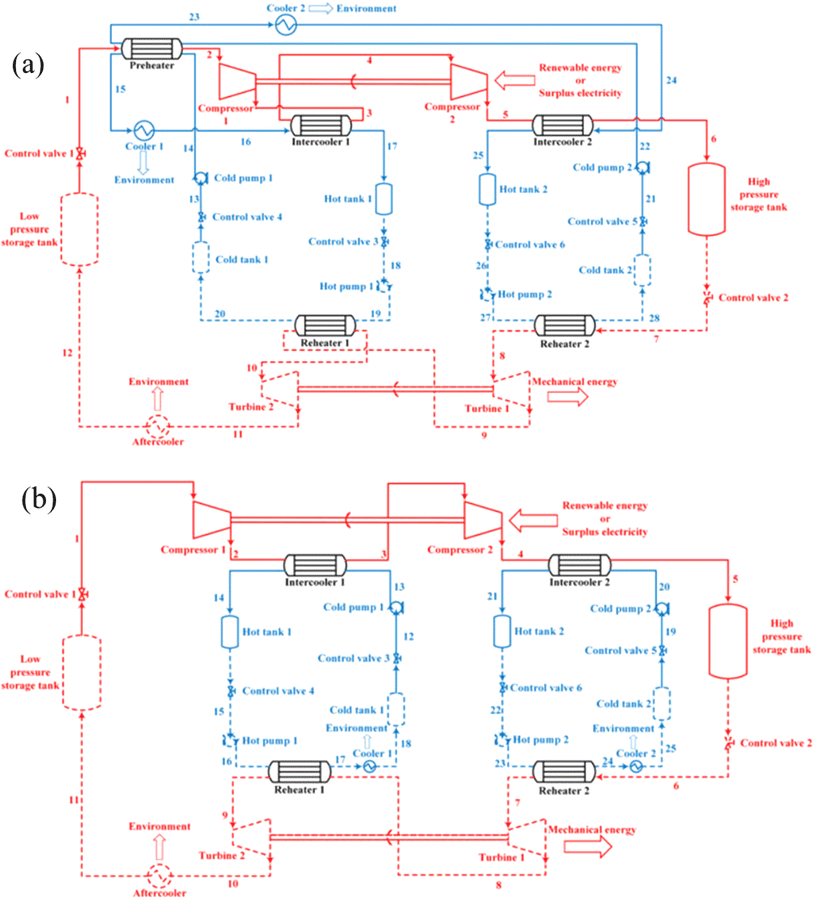
In past studies, compressed carbon dioxide energy storage (CCES) technology has achieved many significant advancements. Recent research focuses on optimizing compression–expansion ratios, developing refined analytical models, and promoting multidisciplinary integration methods. For example, optimizing compression–expansion ratios can significantly improve the thermodynamic efficiency of the system and reduce energy losses. Refined analytical models can more accurately simulate and predict system performance, while multidisciplinary integration methods can help combine CCES technology with other energy technologies, enhancing its application potential. Additionally, recent studies have also addressed CO2-related conversion technologies. For example, Fang et al.52 developed efficient photocatalytic CO2 reduction using molecular polypyridyl Zn(II) complexes through ligand-based electron transfer. Zhang et al.53 explored photothermal catalytic CO2 reduction over nanomaterials, demonstrating significant advancements in this area. Li et al.54 investigated one-dimensional copper-based heterostructures for photo-driven CO2 reduction to sustainable fuels and feedstocks. Yuan et al.55 proposed a coupling strategy for CO2 valorization integrated with organic synthesis by heterogeneous photocatalysis. Ren et al.56 introduced host–guest assemblies of molecular catalysts onto CuInS2/ZnS quantum dots for robust photocatalytic syngas production in water. Lastly, Jia et al.57 developed a Z-scheme heterostructure of Cu2O/Pt/NH2-MIL-125 (Ti) for photocatalytic CO2 reduction. These studies have further advanced CCES technology, providing new insights for future applications.A liquid CO2 energy storage system based on the Brayton cycle was firstly proposed by Zhang et al.58 Through the storage of liquid CO2 for energy storage, while using the organic Rankine cycle to absorb the waste heat generated in the process of power generation, it finally achieves the storage and release of electric energy, as shown in Fig. 3. The operational principle of the liquid compression CO2 energy storage system is that during the energy storage process, the CO2 in the gas storage tank releases cold energy in the accumulator after being regulated by the throttle valve, and then enters the compressor. The compressor uses excess electric energy to compress the CO2. The high temperature and high-pressure CO2 is cooled to a liquid to be stored in the gas storage tank, and thermal energy is stored in the tank simultaneously. During the energy release process, the liquid CO2 in the gas storage tank is pressurized by the CO2 pump, absorbs the heat energy in the heat accumulator, and then enters the expansion turbine to perform work. The waste heat discharged by the turbine enters the Rankine cycle to perform work, and the CO2 is cooled to a liquid in the heat accumulator before entering the gas storage tank. Thermodynamic analysis shows that compared with the advanced adiabatic air compression energy storage system (advanced adiabatic compressed air energy storage, AA-CAES), the liquid compression CO2 energy storage system has a higher energy storage density (approximately 12 times that of the AA-CAES system), but its cycle efficiency is lower.
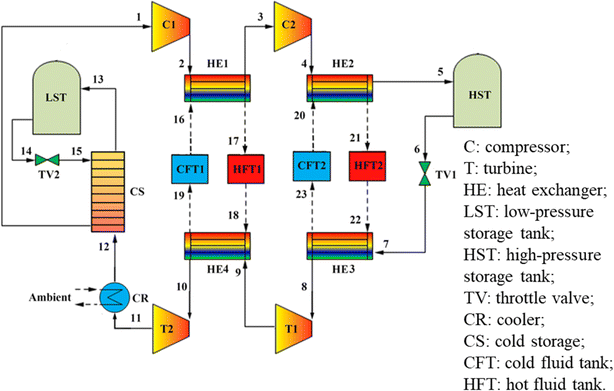
On the basis of the electrothermal energy storage system proposed, by He et al.59 introduced the supercritical (transcritical) CO2 energy storage system based on the Rankine cycle and the integrated energy storage system combining the CO2 Rankine cycle and voltage shrinking refrigeration cycle, as illustrated in Fig. 4(a). Additionally, the supercritical (transcritical) compression CO2 energy storage system is founded on the Brayton cycle,60 as depicted in Fig. 4(b). The cycle characteristics, optimal design, system and cycle analysis, and the relationship between components and parameters of the thermoelectric energy storage system utilizing CO2 as a working fluid are thoroughly examined. The operational principle of the compressed CO2 energy storage system based on the Brayton cycle involves several stages. In the energy storage phase, liquid CO2 in the low-pressure gas tank releases cold energy, transforming into low-pressure gaseous CO2. The vaporized CO2 is then compressed to a supercritical state in the compressor before releasing heat energy through the accumulator and entering the high-pressure gas storage tank. During the energy release phase, the high-pressure gas storage tank discharges CO2, absorbs heat energy via the accumulator, and proceeds to the expansion turbine to perform work. The CO2 from the turbine goes through the air cooler, cold accumulator, and expansion turbine successively, eventually liquefying into the low-pressure liquid storage tank. In the calculation process, a packed bed serves as the heat storage device, absorbing heat during the system's compression process to reduce temperature differences in heat transfer and enhance system efficiency from 56.3% to 60.69%. Sensitivity analysis reveals the relationship between system efficiency, energy density, and compressor, expander, and turbine efficiencies. Exergy analysis of the system provides insights into the exergy loss distribution of each component, indicating that turbines contribute to 47.15% of exergy loss, which decreases with improved turbine efficiency. Enhancing turbine mechanical component efficiency can elevate system performance and reduce exergy losses. Prioritizing turbine optimization is crucial as it can potentially increase the system's energy density. Additionally, changes in pressure at different process points can be utilized to assess variations in exergy loss, system efficiency, and energy density of individual components.
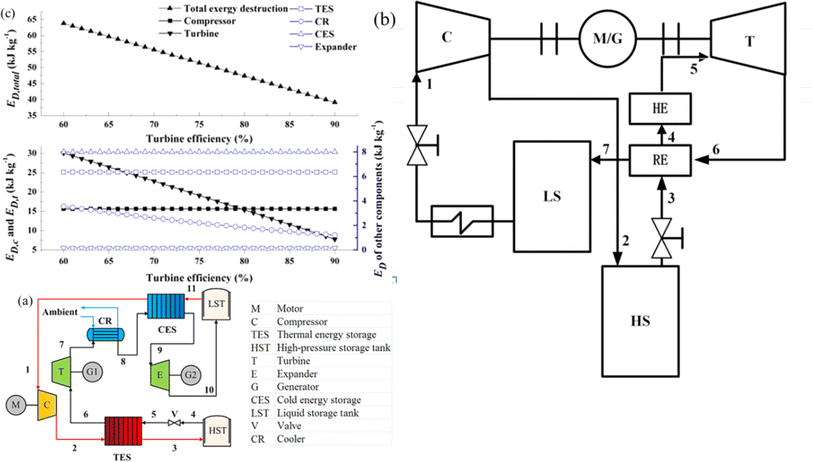 | ||
| Fig. 4 (a) Compressed CO2 energy storage system based on Brayton cycle;59 (b) integrated energy storage system of supercritical (transcritical) CO2 Rankine cycle and voltage shrinking refrigeration cycle;60 (c) effect of turbine efficiency on exergy.59 | ||
Following that, a hybrid system was created that combined carbon dioxide energy storage with other energy storage methods. Fig. 5(a) shows a carbon dioxide energy storage system with phase change devices developed by Liu et al.61 The system compresses carbon dioxide using wind energy and power grid surplus electric energy, then employs a phase change device to absorb the compression heat created by compressed carbon dioxide in the energy storage stage and heat high-pressure carbon dioxide in the energy release stage. The device has high energy storage density and can realize large-scale energy storage. Liu et al.61 combine the characteristics of easy liquefaction of carbon dioxide, use wind energy to compress carbon dioxide, and propose a combination system of wind energy and carbon dioxide energy storage technology, as shown in Fig. 5(b). Double-tank liquid storage is utilized in the energy storage process, which considerably decreases storage volume while increasing energy density. The technology has the maximum efficiency in the first-stage compression and first-stage expansion when compared to multi-stage compression. At the same time, instead of using water as a heat storage system, it employs heat conduction oil, which makes better use of compression heat in the energy storage stage and lowers the heat transfer temperature difference. Finally, the system is combined with the organic Rankine cycle to absorb the waste heat from the tail gas of the last stage expander in the energy release stage, and the efficiency of the system is improved by nearly 10% on the basis of 41.2% in the process of system optimization.
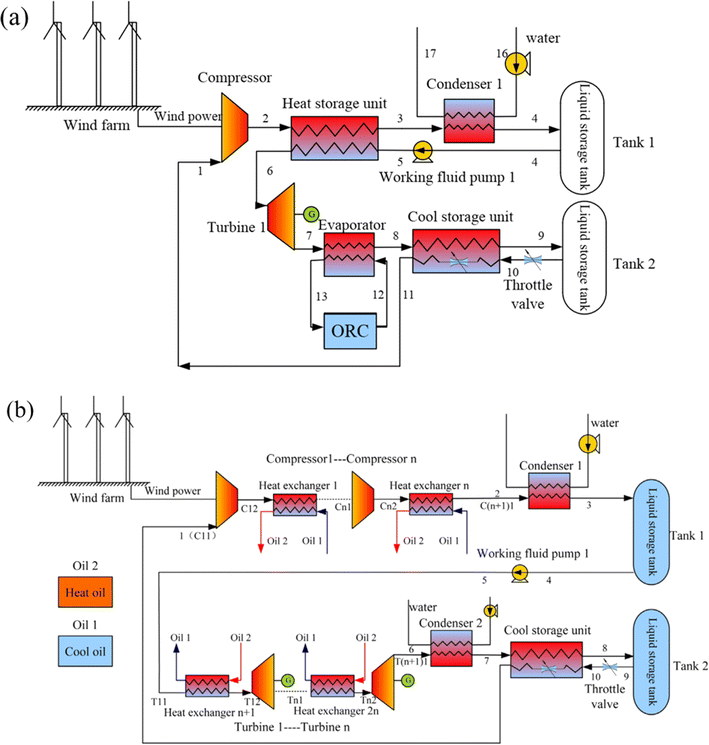 | ||
| Fig. 5 Various compressed CO2 energy storage systems: (a) a carbon dioxide energy storage system with a phase transition device;61 (b) an energy storage system with a combination of wind energy and carbon dioxide.61 | ||
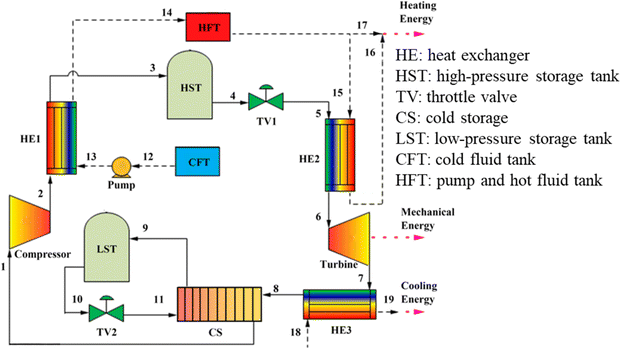
Koohi-Kamali et al.62 proposed a new triple generation system based on a transcritical Brayton cycle and carbon dioxide energy storage, as shown in Fig. 6. The CCHP system operates in the charging phase during off-peak hours. The liquid CO2 (stream 10) provided is initial expanded by TV2 to ensure the functionality of the CS. The resulting gas–liquid mixture (stream 11) transforms into gaseous CO2 (stream 1) after the phase transition, during which the cold energy from CO2 is stored in CS. Subsequently, using the excess and inexpensive electricity from the power grid, the CO2 is compressed into a supercritical phase (stream 2). Following the cooling process in HE1, it is ultimately stored in HST as a supercritical phase (stream 3). The heat from compression is absorbed by the heat storage system and stored in HFT for future use.
 | ||
| Fig. 6 A new triple production system based on transcritical Brayton cycle and carbon dioxide energy storage.62 | ||
Zhang et al.47 proposed a carbon dioxide energy storage system that combines underground strata of different depths, as illustrated in Fig. 7. The system maintains the temperature of carbon dioxide relatively constant based on the temperature characteristics of rock strata at various depths. During the energy release stage, in conjunction with natural gas combustion, the inlet carbon dioxide of the expander is heated, enhancing the energy grade of carbon dioxide.63 A natural gas combustion supporting system is integrated into the system, resulting in a higher temperature of carbon dioxide at the outlet of the last stage expander. This portion of energy is used to heat the carbon dioxide before the expander stage, effectively utilizing the waste heat of the tail gas. Additionally, the transcritical carbon dioxide energy storage system and supercritical carbon dioxide energy storage system under different pressures are examined. The study investigates the impact of key parameter variations on the supercritical carbon dioxide energy storage system, as well as the distribution of losses in each component and how they change with the key parameters. A natural gas supplementary combustion device is introduced in front of the expander stage in the system to enhance the working capacity of carbon dioxide. However, this setup raises concerns regarding tail gas treatment and reliance on underground strata.
 | ||
| Fig. 7 A carbon dioxide energy storage system with underground rock strata.47 | ||
He et al.59 proposed transcritical and supercritical carbon dioxide energy storage systems based on the Brayton cycle, as shown in Fig. 8(a) and (b), respectively. To limit the loss caused by hot water mixing, the system employs water as the working fluid for heat storage and stores the compression heat produced in the compression stage in distinct hot tanks. The impacts of critical factors on system cycle efficiency, expansion efficiency, expander power output, and energy density are determined via sensitivity analysis. Transcritical carbon dioxide energy storage systems and supercritical carbon dioxide energy storage systems have a maximum efficiency of 60% and 70%, respectively, and both exhibit high energy density. However, due to the enormous storage pressure of the two energy storage systems, it is challenging to detect, and the equipment has concealed risks.
 | ||
| Fig. 8 (a) A cross-carbon dioxide energy storage system based on Brayton cycle;59 (b) an ultra-carbon dioxide energy storage system based on Brayton cycle.59 | ||
Supercritical fluid technology is a new green chemical technology that has rapidly developed in recent decades worldwide. Supercritical carbon dioxide is currently the most commonly used supercritical fluid. The physical and chemical properties of supercritical fluids are unique, as they exhibit characteristics between those of liquids and gases. They do not strictly belong to either state. Table 2 compares the differences in density, viscosity, and diffusion coefficient of working fluids in gaseous, liquid, and supercritical states. It is evident that the density of supercritical fluid is similar to that of a liquid, while its viscosity is akin to that of a gas. Therefore, the supercritical state is recognized as a distinct third phase state separate from gas and liquid states. Moreover, supercritical fluids possess excellent flow and transfer properties, with a strong ability to dissolve low-volatile substances. Their physical properties significantly depend on temperature and pressure near the critical region. The critical temperature of carbon dioxide is 31.1 °C, and the pressure is 7.38 MPa. Gaseous carbon dioxide can be liquefied by increasing the pressure to about 6 MPa at room temperature. Liquid carbon dioxide can store a large amount of energy in a very compact tank space, maintaining stable pressure as long as the temperature remains constant during the gasification process. Zhang et al.35 introduced a novel transcritical carbon dioxide refrigeration cycle incorporating a vortex tube expansion structure, optimizing key cycle parameters to enhance system efficiency. Wright et al.66 investigated the carbon dioxide transcritical (subcritical) refrigeration cycle, analyzing its thermodynamic characteristics and optimizing cycle parameters based on thermodynamic principles. Pickard et al.67 explored the application of carbon dioxide in the Brayton cycle, considering the unique characteristics of carbon dioxide in the supercritical state and assessing its potential future applications. Building on the first law of thermodynamics, Zhang et al.35 examined the carbon dioxide Brayton cycle across different states, using thermal efficiency, power generation efficiency, and irreversibility as evaluation criteria. They analyzed the thermodynamic properties of carbon dioxide under subcritical, transcritical, and supercritical conditions, summarizing the advantages, disadvantages, and suitable conditions of carbon dioxide cycle systems in various states.
| Fluid category | Density (kg m−3) | Viscosity (g cm−3 s−1) | Diffusion coefficient (cm2 s−1) |
|---|---|---|---|
| Gaseous | 1 | 10−4 | 10−1 |
| Liquid | 1000 | 10−2 | 10−5 |
| Super | 300–800 | 10−4 | 10−4 |
A significant number of scholars have conducted innovative research to advance the carbon dioxide energy storage system. However, the system currently lacks high output power, eco-friendliness, and the ability for comprehensive and flexible application of new energy sources. Most of the existing CO2 energy storage systems are designed with low compression and expansion ratios to maintain transcritical or supercritical conditions. Consequently, due to the low temperature trend of system heat compression, limited power capacity, and low energy density are anticipated. These factors will inevitably result in increased system size and cost.
In the aforementioned compressed carbon dioxide energy storage system, the thermal parameters of the system are set during the design process. The design scheme adopts an equal distribution of compression ratios and expansion ratios at all levels for both the step-by-step compression and expansion processes. However, the effects of changes in the physical properties of carbon dioxide on the thermodynamic parameters of the system's compression and expansion processes were not fully considered. As a result, there is significant potential for enhancing the thermal performance of the compressed carbon dioxide energy storage system.
4 Evaluation for the characterization of CCES systems
4.1 Economic and technical feasibility
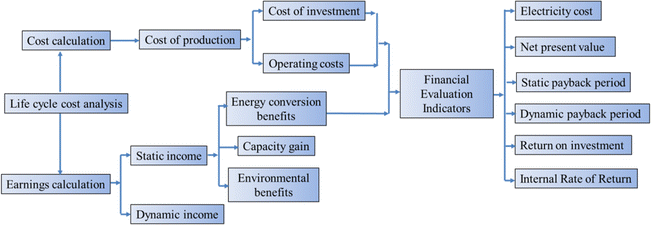
As a new type of electric energy storage system, the compressed carbon dioxide energy storage system has a long construction period and an operating income period of more than ten years to several decades, which prolongs the project's break-even period and does not have obvious economic benefits in the short term. To analyze and evaluate the technical and economic characteristics of the system comprehensively and accurately, it is necessary to study the economic status of the compressed carbon dioxide energy storage system in its entire life cycle, and to compare and analyze the technical and economical aspects of the compressed carbon dioxide energy storage system. Sensitivity analysis and critical point impact analysis are carried out on the economic factors that have a greater impact on the power generation cost and profit and loss of the energy storage system project, and the impact trend of the technical and economic indicators of the energy storage system and the corresponding critical point value are found. The whole life cycle analysis method is an analysis method to obtain the best overall equipment efficiency at an economical life cycle cost, and is the core of equipment management.68 Life Cycle Cost (LCC) refers to the synthesis of all costs that may occur in the process of equipment from investment, operation, maintenance to scrapping during the equipment life cycle.69 The whole life cycle analysis method can effectively solve the contradiction between equipment development and shortage of funds, and it is a strategic measure to effectively improve the profit of equipment life cycle.70Fig. 9 shows the specific calculation flow of the full life cycle method. For system investment projects, the calculation of the whole life cycle model can predict the direct and indirect economic benefits of project investment to a certain extent, comprehensively analyze the technicality and economy of system investment projects, and provide reasonable decision-making basis for system project investors.71Wang et al.51 evaluate the economy of a new CCES system that combines the storage of carbon dioxide in underground coal seams with the compression and storage of carbon dioxide above ground. The results show that reducing the compression stage and increasing the expansion stage can enhance the system's performance. By considering factors such as carbon tax and carbon income price, the study identifies the economic conditions necessary for the energy storage system to achieve economic benefits. The system can generate a profit under most electricity prices during the energy storage process. In comparison to the integrated system and the independent carbon dioxide storage system, the independent energy storage system demonstrates economic advantages only when the carbon tax is below $47 per ton and $68 per ton, respectively.
4.2 System operability
In the realm of dynamic simulation of CCES systems, Alami et al.72 introduced a novel hybrid compressed supercritical carbon dioxide energy storage system. This system utilizes an electric heater powered by a wind farm's high-frequency magnetoresistive power to harness wind energy. Dynamic simulation is conducted to evaluate the system's dynamic characteristics under stable wind generation conditions and actual wind generation scenarios. With a round-trip efficiency (RTE) of 57.55% and an energy density of 84.1 kW h m−3, the system can store wind power during off-peak hours and seamlessly release it to the grid. Uncertainty quantification indicates that the system can operate normally with an RTE standard deviation ranging from 55.72% to 58.16% and an energy density uncertainty between 83.7 kW h m−3 and 86.5 kW h m−3. In experimental research on the CCES system, Alirahmi et al.73 explored the use of carbon dioxide as the working fluid in a low-pressure compressed gas energy storage system. They gathered experimental data on key thermal parameters of the CCES system by constructing a test-bed. The pressure regulator and heater are employed to manage the pressure and temperature of the carbon dioxide entering the cylinder, maintaining the carbon dioxide at initial pressures of 2 bar, 2.5 bar, and 3 bar, respectively. The experimental findings demonstrate that heat transfer losses during the charge–discharge cycle can be minimized, and safety can be improved when the system operates at a maximum starting pressure of 3 bar. The system's cycle efficiency is approximately 79%.It is vital to study the thermodynamic properties of a thermal system while developing, optimizing, and integrating it to understand the transfer, transformation, and loss of energy within the system. According to the theory of thermodynamics, there are various methods for analyzing thermodynamic systems, such as the “energy balance method” based on the first law of thermodynamics, the “heat balance method, “entropy analysis method, and the “exergy analysis method” based on the second law of thermodynamics. Additionally, there is the exergy economic analysis method based on thermodynamic analysis (exergy economic analysis).74,75
4.3 Exergy analysis
Energy exhibits the characteristic of mutual transformation, yet not all forms of energy can be converted into useful work. This indicates variations in the capacity to convert different energy forms into useful work. Consequently, energy embodies both the concept of “quantity” and the aspect of “quality.” The first law of thermodynamics, which is the foundation of energy analysis, primarily focuses on the attribute of energy.Exergy is defined as the maximum work that can be obtained from a specific type of energy when a particular environmental condition is used as the reference state. Consequently, exergy exhibits both “quantity” and “quality” characteristics. The classical analysis method, which is grounded in the first and second laws of thermodynamics, is an energy system analysis technique based on the concept of exergy. In practical applications, exergy losses occur due to the irreversibility of processes. Exergy analysis can uncover the inefficiencies of a thermodynamic system under specific thermal conditions, and the efficiency of a thermodynamic process can be assessed by the extent of exergy loss. A high exergy loss indicates irreversibility in the thermodynamic process. Typically, during exergy analysis, the ratio of input exergy to output exergy is utilized to gauge exergy utilization. Through exergy analysis, the efficiency of energy utilization in the energy conversion system can be assessed, identifying any inefficiencies in energy use and providing a foundation for optimizing the energy system.76
The exergy analysis method is based on the exergy equilibrium equation. In thermodynamics, the exergy equilibrium equation is:77
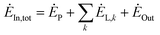 | (4-1) |
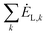 -the sum of exergy losses of components (k) in the system, kW.
-the sum of exergy losses of components (k) in the system, kW.
For any part of the system, the exergy loss is:77
| ĖL,k = ĖIn,k − ĖP,k | (4-2) |
The exergy loss of the internal components of the compressed carbon dioxide energy storage system can be categorized as two parts: internal exergy loss and external exergy loss. It can also be divided into avoidable exergy loss and unavoidable exergy loss.78 The exergy loss of components in the system can be expressed as:
ĖL(i) = ELĖN(i) + ELĖX(i) = ELȦV(i) + EL![[U with combining dot above]](https://www.rsc.org/images/entities/char_0055_0307.gif) N(i) N(i) | (4-3) |
![[U with combining dot above]](https://www.rsc.org/images/entities/char_0055_0307.gif) N(i) is the unavoidable exergy loss of any component in the system, kW.
N(i) is the unavoidable exergy loss of any component in the system, kW.
To analyze the interrelationship between the various operating components in the energy storage system, the exergy loss of the i-th component is divided into internal exergy loss and external exergy loss.79 The internal exergy loss refers to the exergy loss caused by the structure of the part in the system when the other parts in the system, except the part, are in an ideal state. The calculation formula is:
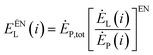 | (4-4) |
The external exergy loss of the i-th component in the system is the exergy loss caused by the structural defects of other components (excluding this component) under the non-ideal state, and its calculation formula is:79
| ELĖX(i) = ĖL(i) − ELĖN(i) | (4-5) |
The external exergy loss of the system is:79
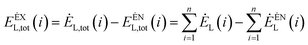 | (4-6) |
To effectively reduce the exergy loss of the internal components of the system, it can be achieved by optimizing the structure of the components or optimizing the cooperation between the various components within the system. The avoidable exergy loss of any component in the system means that the loss is reduced by optimizing the structure of the components and optimizing the cooperation between the components in the system under the unavoidable working conditions of the remaining components in the system except the component. The inevitable exergy loss is:80
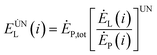 | (4-7) |
![[U with combining dot above]](https://www.rsc.org/images/entities/char_0055_0307.gif) N(i) is the unavoidable Hata loss of the i-th component in the system, kW.
N(i) is the unavoidable Hata loss of the i-th component in the system, kW.
Inevitable exergy loss refers to the exergy loss that cannot be reduced by optimizing the structure of other components or optimizing the operating conditions of the system under unavoidable working conditions except for the i-th component. The avoidable exergy loss is:80
ELȦV(i) = ĖL(i) − EL![[U with combining dot above]](https://www.rsc.org/images/entities/char_0055_0307.gif) N(i) N(i) | (4-8) |
The avoidable exergy loss of the system is:80
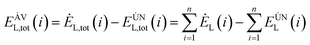 | (4-9) |
Liu et al.81–84 conducted an advanced and economic analysis of the new liquid CCES system. They calculated the thermal efficiency of the system by considering “loss cost” and “investment cost”. Provided energy management strategies for system components to offer technical guidance for optimizing and enhancing the system. The analysis revealed that the avoidable internal system loss accounted for only 42.1% of the total consumption, 43.42% of the total consumption cost, and 55.43% of the total investment cost. Traditional tank analysis indicated that the compressor had the most significant impact on overall consumption. However, advanced economic evaluation suggested that the expander, being the most crucial component, should be prioritized for improvement.
4.4 Exergy economic analysis
The conclusions obtained through exergy analysis are all considered from the perspective of improving energy utilization efficiency. However, these conclusions are often limited by economic factors and may not be feasible. This presents a contradiction between “saving energy” and “saving money”. Therefore, in engineering practice, it is essential to combine thermodynamic analysis with economic analysis to make practical decisions. This integration of thermodynamics and economics has led to the development of a new analysis method known as thermoeconomic analysis, or exergy economic analysis method. The concept of exergy economics was introduced in the 1960s by Tribus and Evans. R. A. Gaggidi optimized the thickness of the thermal insulation layer in a power plant using exergy economics and proposed a method for calculating the cost of steam exergy. In recent years, with the increasing environmental concerns, there has been a growing focus on the system's impact on the environment. Building upon thermoeconomics and considering environmental factors, there has been a shift towards an integrated approach that combines thermodynamics, economics, and environmental protection, resulting in environmental economics based on exergy economics.At present, thermodynamic analysis methods include: enthalpy analysis method; entropy analysis method; exergy analysis method; and exergy economic analysis method. The enthalpy analysis method follows the first law of thermodynamics, which is the law of conservation of energy. This method considers heat loss, kinetic energy loss, and total energy loss as the analysis criteria. The thermodynamic efficiency of the system is assessed using thermal efficiency as the evaluation standard. The entropy analysis method considers both the “quantity” and “quality” of energy and adheres to the second law of thermodynamics. In this method, the analysis criteria are the rate of entropy increase and entropy yield, with the reversible coefficient used as the evaluation standard to assess the system's performance. The exergy analysis method evaluates the thermodynamic efficiency of the system by examining the exergy loss and exergy efficiency during energy transfer or conversion within the system. This approach helps identify inefficiencies in energy utilization and enables further enhancement of energy efficiency. The goal is to uncover the essence of energy transfer or transformation. Exergy-economic analysis integrates both thermodynamic and economic aspects. Its primary objective is to assess the effective energy utilization of the system and propose solutions to enhance exergy efficiency while minimizing system costs. To comprehensively understand the similarities and differences among these four methods, they are summarized from various perspectives in Table 3.
| Enthalpy analysis | Entropy analysis | Exergy analysis | Exoeconomic analysis | |
|---|---|---|---|---|
| Theoretical basis | The first law of thermodynamics | The second law of thermodynamics | The first and second laws of thermodynamics | The first and second laws of thermodynamics; economics; cost accounting, etc. |
| Evaluation standard | Energy efficiency | Irreversible coefficient | Exergy efficiency | Economic isometrics such as exergy efficiency, cost difference, and exergy economic factors |
| Essence | Conservation of energy in “quantity” | Pay more attention to the level of energy “quality” | Taking into account the “quantity” and “quality” of energy | Balance the thermodynamic and economic properties of energy |
| Environment | Benchmark | Benchmark | Physical environment | Physical and economic environment |
| Content | Quantity | Quality | Quantity and quality | The relationship between exergy and economy |
| Purpose | Analyze external losses | Reveal the irreversibility of the system | Internal and external losses | Revealing the weak links in the exergy economy |
| Scope of application | Suitable for short-term decisions | Suitable for mid-term decisions | Suitable for mid-term decisions | Focus on ideals and apply strategic decisions |
From the above analysis, the exergy economic analysis method is an approach that considers both thermodynamic and economic performance. The fundamental concept of this method involves placing the system under analysis in two environments: one is the physical environment, which includes parameters like pressure, density, and temperature that adhere to the law of conservation of energy. The other is the economic environment, which includes costs, benefits, and other economic parameters. When applying exergy economic analysis to address practical issues, it is common to establish a thermodynamic model (exergy equilibrium model, eqn (4-1)) and an economic model (exergy cost conservation model, eqn (4-11)).85
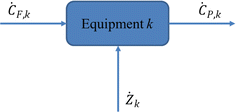
In the thermoeconomic analysis of energy systems, the unit price or value of various exergies is involved. Therefore, in addition to the mass conservation equation, the energy conservation equation, and the commission balance equation, it is also necessary to add an economic balance equation, also known as the exergy cost equation. The so-called exergy cost equation is a capital balance formula that lists the product cost of any energy system (unit, equipment), including one-time initial investment and operating costs (energy consumption, maintenance, wages, and management costs). According to the exergy economic model shown in Fig. 10, the exergy cost balance equation can be obtained as:86
| ĊP,k = ĊF,k + Żk | (4-10) |
In part k, due to factors such as the equipment itself and operating conditions, exergy losses will occur in the equipment, and the cost of equipment exergy losses due to exergy losses is:86
| Ċk = cF,kĖk | (4-11) |
For the combined operation system of compressed carbon dioxide energy storage and new energy power generation, there are two distinct forms of energy input: electric energy converted from new energy input into the energy storage system, and heat energy added to enhance the output work during the energy release process of the energy storage system. The diverse sources of input electrical energy and thermal energy in the energy storage system result in variations in input location and energy levels, making the performance evaluation of the compressed carbon dioxide energy storage system complex.
To accurately measure the thermoeconomic properties of compressed carbon dioxide energy storage systems, Xu et al.87 proposed a relationship between the unit exergy cost of a polygeneration energy system product and the “energy quality factor” of the product based on the principle of “high quality and high price”. The unit exergy cost of electricity and heat of the polygeneration energy system is calculated through an example. By comparing the unit exergy cost per unit of electricity and heat production with the unit exergy cost obtained by the equivalent distribution of products, it is found that according to the “energy quality factor”. It is more appropriate to determine the unit exergy cost of the product. Petrakopoulou et al.88 applied exergy economic theory to a wind power-compressed air energy storage system and proposed the evaluation index of exergy and cost “proportional coefficient”. The cost of storing wind energy and the factors that affect cost growth are revealed. Wen-Yi et al.89 improved the exoeconomics framework by considering environmental factors when building the exoeconomics model. By dividing system losses into avoidable and unavoidable exergy losses, it is demonstrated that system improvement potential and cost interact. Keshavarzian et al.90 based on the theory of exergy economics and considering environmental costs, established an exergy economic model including environmental cost variables and optimized the system. However, the modeling time is long and cannot reflect the performance of a single component. On this basis, Succar et al.91 proposed a “functional analysis method”, which divides the system into multiple subsystems for analysis one by one. The experimental results show that the more detailed the system is divided, the more stable the economy of a single component is. With the continuous development of exotics, the limitations of exergy analysis are addressed.
4.5 Cycle efficiency of energy storage system
Because electric energy is used as both an input and an output in most energy storage systems, the cycle efficiency of the system is described as the ratio of output electric energy to input electric energy. To improve the output electric energy of a compressed gas energy storage system, an additional component of thermal energy is normally provided to heat the high-pressure gas entering the expansion turbine during the energy release phase, to boost the turbine's output work. To compare compressed gas energy storage systems to other types of energy storage systems, the additional thermal energy must first be converted to electrical energy, and then the cycle efficiency must be computed.As a result, the compressed gas energy storage system's cycle efficiency is:92
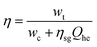 | (4-12) |
The adiabatic efficiency of the compressor increases as the number of stages of the compressor unit increases. On the one hand, this leads to a compression process that is closer to the isothermal adiabatic process, reducing the power consumption of the compressor unit. On the other hand, the compression heat temperature of the system decreases gradually, resulting in a decrease in the temperature of the carbon dioxide working medium at the inlet of the expander and a decrease in the output power of the expansion unit. When the reduction in output power of the expansion unit exceeds the reduction in power consumption of the compressor unit increases, leading to a decrease in cycle efficiency decreases when the system output power is generated.
4.6 Energy storage density
he energy storage density is defined as the amount of useable energy stored per unit space or mass of matter.87 In a compressed gas energy storage system, energy is stored in the gas storage chamber using the gas working system as the carrier. Therefore, the electrical energy stored in a single gas storage chamber represents the energy storage density of a compressed gas energy storage system:92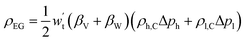 | (4-13) |
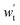 -output work for expansion turbine, kW; Δph-pressure change in the high-pressure gas storage chamber, MPa; Δpl-pressure change in low-pressure gas storage chamber, MPa; ρh,C-carbon dioxide density in the high-pressure gas storage chamber, kg cm−3; ρl,C-carbon dioxide density in the low-pressure gas storage chamber, kg cm−3; βV-void compression coefficient, βW-coefficient of density variation of an underground aquifer.
-output work for expansion turbine, kW; Δph-pressure change in the high-pressure gas storage chamber, MPa; Δpl-pressure change in low-pressure gas storage chamber, MPa; ρh,C-carbon dioxide density in the high-pressure gas storage chamber, kg cm−3; ρl,C-carbon dioxide density in the low-pressure gas storage chamber, kg cm−3; βV-void compression coefficient, βW-coefficient of density variation of an underground aquifer.
To compare the performance of compression systems using air and CO2 as working fluids, exergy, system cycle efficiency, heat storage efficiency, and energy storage density are widely used as thermodynamic evaluation indices. Exergy analysis and sensitivity analysis can help explain the causes of exergy loss in the CCES system from the perspective of system components and topology. Subsequently, the exergy cost analysis method is employed to assess the thermal efficiency of the system.
The energy and exergy of the system can be analyzed using a thermodynamic model to compare the effects of key factors on the system's performance, laying the groundwork for further system enhancements. Liquid carbon dioxide energy storage system (LCES) and liquid air energy storage system (LAES) were assessed through thermodynamic analysis to evaluate their performance. Zhang et al.93 proposed a new LCES with two artificial storage tanks based on the Rankine cycle. Fig. 11 illustrates the impact of turbine inlet temperature on component exergy loss. The turbine inlet temperature significantly affects the net output power and energy generated per unit volume (EVR) of both systems. The exergy loss of the heater increased by 1.9%, while the co-current heat exchanger and turbine exergy damage rose by 1.9% and decreased slightly with a reduction in turbine inlet temperature. In the LAES system, the cooler, heater, and throttle valve are the main sources of exergy loss. Exergy damage to heat exchangers and heaters is more pronounced in the LCES system.
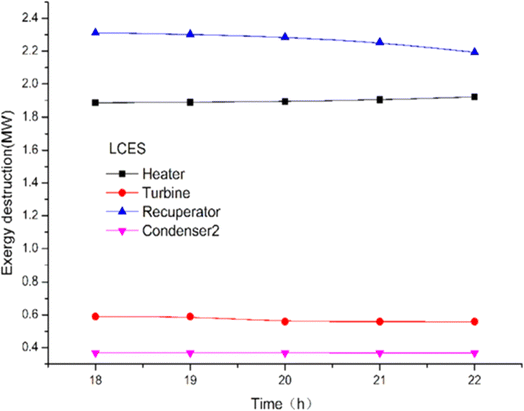 | ||
| Fig. 11 The effect of turbine inlet temperature on the damage of LCES components.93 | ||
Most of the relevant work has been conducted in the past using traditional exergy analysis methods to identify the energy-saving potential sources of each component and to compare the thermodynamic properties of different systems. However, traditional exergy analysis is unable to reveal the thermodynamic interactions between components. To assess the performance of CAES and SC-CCES, Liu et al.80 apply both traditional and advanced exergy analysis methods. The improvement techniques for different energy storage systems vary significantly based on sophisticated exergy analysis, as illustrated in Fig. 12a and b. In SC-CCES, the energy-saving potential of the entire system and individual components align with their exergy loss, while in CAES, they are not in balance with exergy loss. The interaction between different components is crucial for SC-CCES to reduce exergy loss, whereas the internal structure of CAES has the most significant impact on preventable exergy loss.
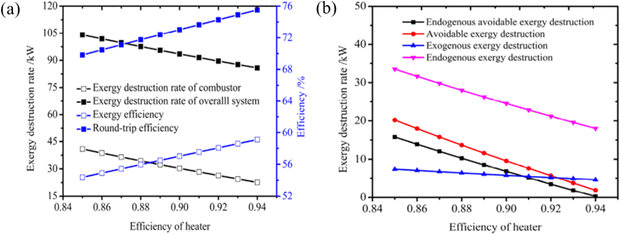 | ||
| Fig. 12 (a) The effect of turbine efficiency on SC-CCES under traditional turbine analysis; (b) the effect of turbine efficiency on SC-CCES under advanced turbine analysis.80 | ||
Improved turbine and compressor efficiency, as well as a smaller temperature differential between hot and cold refrigerants, can significantly minimize the system's unnecessary exergy loss. Yang et al.94 designed and investigated a CCES system based on the Brayton cycle and using hot water as the heat storage system. The study of energy and exergy is done by creating a thermodynamic model of the system, as illustrated in Fig. 13a and b. Then, to expose the influence of various factors on system performance and to seek improvement possibilities, a sensitivity analysis is performed. The cycle pressure is quite high, despite the fact that the RTE and exergy efficiency are relatively excellent and steady with changes in operating parameters under supercritical operation circumstances. Even the lowest pressure is higher than the critical pressure to maintain the post-input cooler's temperature higher than the output temperature. As a result, rather than a high compression ratio and isentropic efficiency of compressors and turbines, the path of system optimization is toward a relatively high heat transfer efficiency and the lowest water temperature.
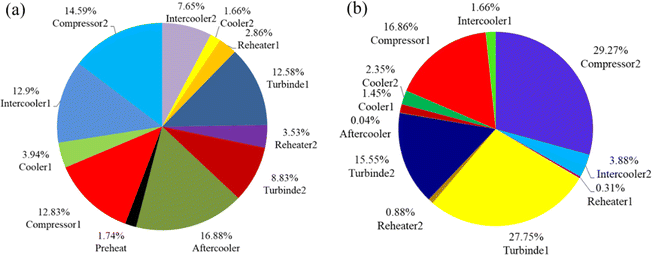 | ||
| Fig. 13 (a) The scale diagram of CCES system components under supercritical condition; (b) the scale diagram of CCES system components under supercritical condition.94 | ||
Several compressed gas energy storage technologies have been subjected to exergy studies. Traditional exergy analysis, however, can only reveal the location, magnitude, and cause of exergy loss in an energy conversion system, not the energy-saving potential of a single component or the thermodynamic interaction between several components.95 For the combined operation of compressed carbon dioxide energy storage and new energy power generation, there will be two different forms of energy input in the system. On the one hand, it is the electric energy converted from new energy that is input into the energy storage system. On the other hand, it is the heat energy added to increase the output work of the energy release system during the energy release process of the energy storage system. Due to the different sources of input electrical energy and thermal energy in the energy storage system, the input location and energy level are also different, which makes the performance evaluation of the compressed carbon dioxide energy storage system complicated. Therefore, enhanced exergy analysis that focuses on identifying causes and decreasing exergy losses is required.96–98 Exergy loss is split into internal/external and inevitable/avoidable portions in advanced exergy analysis, which substantially increases exergy analysis accuracy and comprehension of thermodynamic inefficiency.99
5 Summary and outlook
Future research should focus on the following aspects: first, improving the overall efficiency and economic viability of the system; second, reducing energy losses; and third, optimizing system components and structural design. Through these efforts, CCES technology is expected to play a more significant role in energy storage and utilization in the future.Furthermore, the development of CCES systems should also emphasize the following areas: (a) optimizing the distribution of compression and expansion ratios. During the energy storage process, carbon dioxide is gradually compressed, and the working fluid state changes from transcritical to supercritical; during the energy release process, carbon dioxide is gradually expanded, and the working fluid state changes from supercritical to transcritical. Due to the unique physical properties of supercritical carbon dioxide, as temperature and pressure increase, the power consumption during the compression process decreases, while the output work during the expansion process increases. Therefore, it is necessary to optimize the distribution of compression and expansion ratios in transcritical CCES systems to achieve energy savings and efficiency improvements. (b) Combining surface equipment and underground energy storage to simulate the entire system. Although existing studies have proposed using underground saline aquifers for gas storage, these studies only focus on the thermodynamic analysis of surface equipment and lack thermodynamic analysis and research on the underground energy storage part of deep aquifer CCES systems. (c) Simulating thermo-hydro-mechanical-chemical coupling. During the compression of carbon dioxide for underground storage, chemical reactions may occur between carbon dioxide and formation rocks and minerals, and changes in pressure and temperature can cause mechanical effects. The fatigue damage effect of rocks during cyclic pumping should also be considered, thus further improving multi-field coupling methods to make simulations closer to actual conditions.
With these improvements, CCES technology is expected to achieve more efficient, economical, and environmentally friendly energy storage and utilization in the future. as follow:
(1) Develop a compressed carbon dioxide (CO2) system model for gaseous or liquid fluid, and implement coupling and innovation based on application scenarios, energy-saving requirements, etc.
(2) After analyzing the economy and maneuverability of CCES through thermodynamic analysis, the economic and technological advantages of CCES can be clarified.
(3) The energy-saving potential of individual components and the thermodynamic interaction between different components are discussed through advanced analysis. The source of damage is further analyzed to optimize the system structure and components. To ensure transcritical or supercritical operating conditions, most of the carbon dioxide energy storage systems mentioned above are designed with low compression and expansion ratios.
However, given the system's low compression ratio for producing low-pressure heat, it's safe to assume that the system's restricted power capacity and poor energy density will unavoidably lead to a size and cost increase. In addition, the design scheme of equal distribution of compression ratio and expansion ratio is employed in the process of step-by-step compression and step-by-step expansion while determining the thermal parameters of the above-CCES system. The effect of changes in carbon dioxide's physical properties on the thermodynamic parameters of the system's compression and expansion processes is not fully taken into consideration. As a result, there is significant room for improvement in the CCES system's thermal performance. Presently, research on CCES systems focuses on the variations in carbon dioxide storage states, and then the system is built based on these different storage states, but there is a lack of comparative analysis of CCES systems in different storage states. Simultaneously, there is a scarcity of studies on system losses. The upcoming large-scale CCES system will concentrate on developing a more precise analysis and system model. For multi-stage compression and multi-stage expansion processes, the design strategies involving the average distribution of compression ratio and expansion ratio of compressors at all stages were used in previous CCES system designs and studies. To advance the CCES system, attention should be directed towards the following areas:
(a) Optimize the compression and expansion ratio distributions. On the contrary, during the energy storage process, carbon dioxide is gradually compressed, and the state of the working fluid changes from transcritical to supercritical; during the energy release process, carbon dioxide is gradually expanded, and the state of the working fluid changes from supercritical to transcritical. With increasing temperature and pressure, the power consumption of the compression process decreases while the output work of the expansion process increases due to the specific physical properties of supercritical carbon dioxide. Consequently, as the power consumption capacity of carbon dioxide differs between each stage compressor and expander, it is essential to optimize the compression and expansion ratio distributions in the operation process of a transcritical CCES system to achieve the objectives of energy savings and efficiency enhancement.
Combined surface devices and underground energy storage to simulate the entire system. The thermodynamic analysis of CCES systems of underground gas storage tanks is currently being utilized in research on CCES systems. Although Cao et al.99 proposed using an underground saltwater aquifer for gas storage, their research only focuses on the thermodynamic analysis of a portion of the compressor, regenerator, and expansion permeability of surface equipment. There is a lack of thermodynamic analysis and research on the underground energy storage component of the deep aquifer CCES system (wellbore-aquifer). Due to the pressure involved in underground gas storage, gas energy storage technology requires a broad range of expertise, including energy engineering, electric power engineering, groundwater engineering, geotechnical engineering, and more. Currently, research on pressure gas energy storage of underground gas storage often examines surface devices and underground energy storage separately. The thermodynamic analysis of the above-ground compressor, heat exchanger, and turbine idealizes the process of underground energy storage. Similarly, the study of the underground energy storage process idealizes the surface device, making it impossible to conduct a comprehensive thermodynamic analysis of the entire system in the research.
(c) Simulation of thermal-hydro-mechanical-chemical coupling is essential. During the compression of carbon dioxide for underground storage, chemical reactions may occur between carbon dioxide and formation rocks and minerals. Moreover, changes in pressure and temperature can lead to mechanical effects. It is crucial to consider the fatigue damage effect on rocks during cyclic pumping. Therefore, the multi-field coupling method requires further enhancement in the future to improve the accuracy of simulations and align them more closely with real-world conditions.
Abbreviations
| AA | Advanced adiabatic |
| AV | Avoidable exergy loss |
| Ċ | Exergy cost ($ per s) |
| c | Compressor |
| C | Carbon dioxide |
| C | Compressor |
| CAES | Compressed air energy storage |
| CCES | Compressed carbon dioxide energy storage |
| CCS | Carbon capture and storage |
| CCUS | Carbon capture, utilization and storage |
| CES | Cold energy storage |
| CFT | Cold fluid tank |
| CR | Cooler |
| CS | Cold storage |
| E | Expander |
| Ė | Exergy (kW) |
| EG | Energy |
| EN | Internal exergy loss |
| EX | External exergy loss |
| EVR | Energy generated per unit volume |
| FES | Flywheel energy storage |
| F | Fuel |
| G | Generator |
| h | High-pressure |
| he | Heat |
| HE | Heat exchanger |
| HFT | Hot fluid tank |
| HST | High-pressure storage tank |
| In | Input |
| k | System components |
| l | Low-pressure |
| L | Loss |
| LAES | Liquid air energy storage |
| LCES | Liquid carbon dioxide energy storage |
| LST | Low-pressure storage tank |
| M | Motor |
| Out | Output |
| P | Produce |
| P | Pressure (MPa) |
| PES | Pumping energy storage |
| Q | Heat absorption (kJ) |
| RTE | Round-trip efficiency |
| sg | Standard gas power plant |
| SC | Supercritical |
| t | Turbine |
| tot | Total |
| T | Turbine |
| TC | Transcritical |
| TES | Thermal energy storage |
| TV | Throttle valve |
| UN | Unavoidable exergy loss |
| V | Value |
| V | Void compression |
| W | Underground aquifer |
| W | Work (kW) |
| Ż | Equal annual amortization cost ($ per s) |
| η | Efficiency (%) |
| ρ | Density (kg m−3) |
| β | Coefficient |
Data availability
No new data were created or analyzed in this study.Author contributions
Conceptualization, Hailing Ma and Yao Tong; methodology, Hailing Ma; software, Hongxu Wang; validation, Hailing Ma, Yao Tong, and Xiao Wang; formal analysis, Xiao Wang; investigation, Xiao Wang; resources, Hailing Ma; data curation, Hailing Ma; writing—original draft preparation, Hailing Ma; writing—review and editing, Yao Tong; visualization, Xiao Wang; supervision, Yao Tong; project administration, Xiao Wang; funding acquisition, Yao Tong. All authors have read and agreed to the published version of the manuscript.Conflicts of interest
The authors declare no conflict of interest.Acknowledgements
This work was supported by the National Natural Science Foundation of China (No. 52272096).References
- K. Van Alphen, Q. v. V. tot Voorst, M. P. Hekkert and R. E. Smits, Energy Policy, 2007, 35, 4368–4380 CrossRef.
- R. Golombek, M. Greaker, S. A. Kittelsen, O. Røgeberg and F. R. Aune, Energy J., 2011, 32(3), 209–237 Search PubMed.
- A. B. Rao and E. S. Rubin, Environ. Sci. Technol., 2002, 36, 4467–4475 CrossRef CAS PubMed.
- P. Baskar and A. Senthilkumar, J. Eng. Sci. Technol., 2016, 19, 438–443 Search PubMed.
- S. Yadav and S. Mondal, Fuel, 2022, 308, 122057 CrossRef CAS.
- X. Zhang, J.-L. Fan and Y.-M. Wei, Energy Policy, 2013, 59, 536–550 CrossRef CAS.
- B. Smit, A.-H. A. Park and G. Gadikota, Front. Energy Res., 2014, 2, 122224 Search PubMed.
- R. W. Edwards and M. A. Celia, Proc. Natl. Acad. Sci. U. S. A., 2018, 115, E8815–E8824 CAS.
- K. Jiang, P. Ashworth, S. Zhang, X. Liang, Y. Sun and D. Angus, Renewable Sustainable Energy Rev., 2020, 119, 109601 CrossRef.
- B. Page, G. Turan, A. Zapantis, L. Beck, C. Consoli, I. Havercroft, H. Liu, P. Loria, A. Schneider and E. Tamme, Global Status of CCS 2019, Technical Report, Global CCS Institute, Melbourne, Australia, 2019 Search PubMed.
- C. Zhang, Y.-L. Wei, P.-F. Cao and M.-C. Lin, Renewable Sustainable Energy Rev., 2018, 82, 3091–3106 CrossRef CAS.
- P. Denholm and G. L. Kulcinski, Energy Convers. Manage., 2004, 45, 2153–2172 CrossRef CAS.
- A. Shahmohammadi, R. Sioshansi, A. J. Conejo and S. Afsharnia, Energy Convers. Manage., 2018, 162, 307–320 CrossRef.
- J. Liu, C. Hu, A. Kimber and Z. Wang, J. Energy Storage, 2020, 32, 101731 CrossRef.
- R. Lueken and J. Apt, Energy Syst., 2014, 5, 677–704 CrossRef.
- S. Ruester, S. Schwenen, M. Finger and J.-M. Glachant, Int. J. Energy Technol. Pol., 2013, 9, 160–174 CrossRef.
- G. Oriti, A. L. Julian and N. J. Peck, IEEE Trans. Power Electron., 2015, 31, 452–460 Search PubMed.
- E. Bazdar, M. Sameti, F. Nasiri and F. Haghighat, Renewable Sustainable Energy Rev., 2022, 167, 112701 CrossRef.
- E. Bullich-Massagué, F.-J. Cifuentes-García, I. Glenny-Crende, M. Cheah-Mañé, M. Aragüés-Peñalba, F. Díaz-González and O. Gomis-Bellmunt, Appl. Energy, 2020, 274, 115213 CrossRef.
- M. M. Rahman, A. O. Oni, E. Gemechu and A. Kumar, Energy Convers. Manage., 2020, 223, 113295 CrossRef CAS.
- Y. Cao, S. B. Mousavi and P. Ahmadi, Fuel, 2022, 324, 124495 CrossRef CAS.
- S. Rehman, L. M. Al-Hadhrami and M. M. Alam, Renewable Sustainable Energy Rev., 2015, 44, 586–598 CrossRef.
- S. M. Alirahmi, A. R. Razmi and A. Arabkoohsar, Renewable Sustainable Energy Rev., 2021, 142, 110850 CrossRef CAS.
- Z. Tong, Z. Cheng and S. Tong, Renewable Sustainable Energy Rev., 2021, 135, 110178 CrossRef.
- M. H. Nabat, S. Sharifi and A. R. Razmi, J. Energy Storage, 2022, 45, 103711 CrossRef.
- A. Olabi, T. Wilberforce, M. Ramadan, M. A. Abdelkareem and A. H. Alami, J. Energy Storage, 2021, 34, 102000 CrossRef.
- M. Qi, J. Park, R. S. Landon, J. Kim, Y. Liu and I. Moon, Renewable Sustainable Energy Rev., 2022, 153, 111732 CrossRef CAS.
- Z. Liu, X. Liu, W. Zhang, S. Yang, H. Li and X. Yang, Energy, 2022, 238, 121759 CrossRef CAS.
- A. Skorek-Osikowska, Ł. Bartela, D. Katla and S. Waniczek, Fuel, 2021, 304, 120764 CrossRef CAS.
- P. Zhao, W. Xu, S. Zhang, F. Gou, J. Wang and Y. Dai, Energy Convers. Manage., 2021, 229, 113679 CrossRef CAS.
- C. H. Pentland, R. El-Maghraby, S. Iglauer and M. J. Blunt, Geophys. Res. Lett., 2011, 38(6) DOI:10.1029/2011GL046683.
- M. S. A. Perera, P. Ranjith and D. R. Viete, Appl. Energy, 2013, 110, 73–81 CrossRef CAS.
- B. A. Isaka, P. Ranjith and T. Rathnaweera, Sustainable Energy Technol. Assess., 2019, 36, 100547 CrossRef.
- J. Sarkar, Int. J. Therm. Sci., 2009, 48, 1823–1828 CrossRef CAS.
- F. Zhang, P. Jiang, Y. Lin and Y. Zhang, Appl. Therm. Eng., 2011, 31, 432–438 CrossRef CAS.
- B. Yu, J. Yang, D. Wang, J. Shi and J. Chen, Energy, 2019, 189, 116147 CrossRef CAS.
- F. E. Manjili and M. Cheraghi, Appl. Therm. Eng., 2019, 156, 402–409 CrossRef.
- P. Garg, P. Kumar and K. Srinivasan, J. Supercrit. Fluids, 2013, 76, 54–60 CrossRef CAS.
- P. Wu, Y. Ma, C. Gao, W. Liu, J. Shan, Y. Huang, J. Wang, D. Zhang and X. Ran, Nucl. Eng. Des., 2020, 368, 110767 CrossRef CAS.
- J. Meng, M. Wei, P. Song, R. Tian, L. Hao and S. Zheng, Energy Convers. Manage., 2020, 215, 112931 CrossRef CAS.
- D. Yang, Y. Song, F. Cao, L. Jin and X. Wang, Int. J. Refrig., 2016, 72, 156–170 CrossRef CAS.
- Z. Liu, Z. Liu, X. Xin and X. Yang, Appl. Energy, 2020, 269, 115067 CrossRef CAS.
- Y. Hao, Q. He, Q. Zhou and D. Du, J. Energy Storage, 2020, 28, 101273 CrossRef.
- M. Morandin, F. Maréchal, M. Mercangöz and F. Buchter, Energy, 2012, 45, 375–385 CrossRef CAS.
- H. Liu, Q. He, A. Borgia, L. Pan and C. M. Oldenburg, Energy Convers. Manage., 2016, 127, 149–159 CrossRef CAS.
- A. Tanaka, M. Yamano, Y. Yano and M. Sasada, Earth, Planets Space, 2004, 56, 1191–1194 CrossRef.
- Y. Zhang, E. Yao, X. Zhang and K. Yang, Int. J. Energy Res., 2020, 44, 6531–6554 CrossRef CAS.
- Z. Liu, B. Liu, J. Guo, X. Xin and X. Yang, Energy Convers. Manage., 2019, 198, 111807 CrossRef CAS.
- M. Xu, X. Wang, Z. Wang, P. Zhao and Y. Dai, Appl. Therm. Eng., 2021, 183, 116153 CrossRef CAS.
- Z. Cao, J. Deng, S. Zhou and Y. He, Energy Convers. Manage., 2020, 211, 112788 CrossRef CAS.
- M. Wang, P. Zhao, Y. Wu and Y. Dai, Appl. Therm. Eng., 2015, 91, 812–823 CrossRef CAS.
- Y. Fang, X. Hong, Y. Fu, Y. Li and D. Chao, Mol. Catal., 2023, 551, 113610 CrossRef CAS.
- F. Zhang, Y. H. Li, M. Y. Qi, Y. M. Yamada, M. Anpo, Z. R. Tang and Y. J. Xu, Chem Catal., 2021, 1, 272–297 CrossRef CAS.
- J.-Y. Li, L. Yuan, S.-H. Li, Z.-R. Tang and Y.-J. Xu, J. Mater. Chem. A, 2019, 7, 8676–8689 RSC.
- L. Yuan, M.-Y. Qi, Z.-R. Tang and Y.-J. Xu, Angew. Chem., Int. Ed., 2021, 133, 21320–21342 CrossRef.
- Y.-Y. Ren, W. Xia, B.-Y. Deng, J. Liu and F. Wang, Mol. Catal., 2022, 520, 112168 CrossRef CAS.
- Q. Jia, J. Zhou, L. Gong, L. Wang, X. Ma and Y. Zhao, Mol. Catal., 2022, 530, 112599 CrossRef CAS.
- Y. Zhang, K. Yang, H. Hong, X. Zhong and J. Xu, Renewable Energy, 2016, 99, 682–697 CrossRef CAS.
- Q. He, Y. Hao, H. Liu and W. Liu, PLoS One, 2018, 13, e0195614 CrossRef PubMed.
- M. Wang, P. Zhao, Y. Yang and Y. Dai, Energy, 2015, 93, 1931–1942 CrossRef CAS.
- Z. Liu, F. Cao, J. Guo, J. Liu, H. Zhai and Z. Duan, Energy Convers. Manage., 2019, 188, 151–161 CrossRef CAS.
- S. Koohi-Kamali, V. Tyagi, N. Rahim, N. Panwar and H. Mokhlis, Renewable Sustainable Energy Rev., 2013, 25, 135–165 CrossRef.
- M. Yari and S. Mahmoudi, Energy, 2011, 36, 6839–6850 CAS.
- Y. Ahn, S. J. Bae, M. Kim, S. K. Cho, S. Baik, J. I. Lee and J. E. Cha, Nucl. Eng. Technol., 2015, 47, 647–661 CrossRef.
- R. Madlener and J. Latz, Appl. Energy, 2013, 101, 299–309 CrossRef.
- S. A. Wright, P. S. Pickard, R. Fuller, R. F. Radel and M. E. Vernon, ASME Power Conf., Proc., 2009, 573–583 CAS.
- S. A. Wright, R. F. Radel, M. E. Vernon, P. S. Pickard and G. E. Rochau, Operation and Analysis of a Supercritical CO2 Brayton Cycle (No. SAND2010-0171), Sandia National Laboratories (SNL), Albuquerque, NM, and Livermore, CA (United States), 2010 Search PubMed.
- L. Huang, Y. Liu, G. Krigsvoll and F. Johansen, J. Cleaner Prod., 2018, 173, 151–159 CrossRef CAS.
- K. Lu, X. Jiang, J. Yu, V. W. Tam and M. Skitmore, J. Cleaner Prod., 2021, 285, 125438 CrossRef.
- Ł. Bartela, A. Skorek-Osikowska, S. Dykas and B. Stanek, Energy Convers. Manage., 2021, 241, 114297 CrossRef.
- F. Chaychizadeh, H. Dehghandorost, A. Aliabadi and A. Taklifi, Energy Convers. Manage., 2018, 166, 500–511 CrossRef CAS.
- A. H. Alami, A. A. Hawili, R. Hassan, M. Al-Hemyari and K. Aokal, Renewable Energy, 2019, 134, 603–611 CrossRef CAS.
- S. M. Alirahmi, M. Rostami and A. H. Farajollahi, Int. J. Hydrogen Energy, 2020, 45, 15047–15062 CrossRef CAS.
- P. Zhao, J. Wang and Y. Dai, Energy Convers. Manage., 2015, 98, 161–172 CrossRef.
- G. P. Hammond and A. Stapleton, Proc. Inst. Mech. Eng., Part A, 2001, 215, 141–162 CrossRef.
- L. Wang, Y. Yang, T. Morosuk and G. Tsatsaronis, Energies, 2012, 5, 1850–1863 CrossRef CAS.
- T. Morosuk and G. Tsatsaronis, Energy, 2008, 33, 890–907 CrossRef CAS.
- G. Tsatsaronis, Thermodynamic Optimization of Complex Energy Systems, Springer, 1999, pp. 93–100 Search PubMed.
- Q. He, H. Liu, Y. Hao, Y. Liu and W. Liu, Renewable Energy, 2018, 127, 835–849 CrossRef CAS.
- Z. Liu, Z. Liu, X. Yang, H. Zhai and X. Yang, Energy Convers. Manage., 2020, 205, 112391 CrossRef CAS.
- C. Breyer, D. Bogdanov, K. Komoto, T. Ehara, J. Song and N. Enebish, Jpn. J. Appl. Phys., 2015, 54, 08KJ01 CrossRef.
- M. Ehyaei, A. Ahmadi and M. A. Rosen, Energy Convers. Manage., 2019, 183, 369–381 CrossRef.
- G. Luderer, V. Bosetti, M. Jakob, M. Leimbach, J. C. Steckel, H. Waisman and O. Edenhofer, Clim. Change, 2012, 114, 9–37 CrossRef.
- M. L. Elsayed, O. Mesalhy, R. H. Mohammed and L. C. Chow, Energy, 2019, 166, 552–568 CrossRef.
- C. Torres and A. Valero, Energies, 2021, 14, 1594 CrossRef CAS.
- Q. He, H. Liu and W. Liu, Thermoelectr. Power Gener., 2016, 45, 34–39 Search PubMed.
- M. Xu, P. Zhao, Y. Huo, J. Han, J. Wang and Y. Dai, J. Cleaner Prod., 2020, 242, 118437 CrossRef CAS.
- F. Petrakopoulou, G. Tsatsaronis, T. Morosuk and C. Paitazoglou, Energy, 2012, 45, 23–30 CrossRef.
- Y. Y.-P. L. Wen-Yi and G. X.-Y. L. Xiang, J. Eng. Thermophys., 2004, 25(1), 5–8 Search PubMed.
- S. Keshavarzian, M. V. Rocco, F. Gardumi and E. Colombo, Energy Convers. Manage., 2017, 150, 532–544 CrossRef.
- S. Succar and R. H. Williams, Compressed air energy storage: theory, resources, and applications for wind power, Princeton Environmental Institute Report, 2008, vol. 8, p. 81 Search PubMed.
- R. Wang, F. Wang, D. Boroyevich, R. Burgos, R. Lai, P. Ning and K. Rajashekara, IEEE Trans. Power Electron., 2010, 26, 1430–1443 Search PubMed.
- X. R. Zhang and G. B. Wang, Int. J. Energy Res., 2017, 41, 1487–1503 CrossRef CAS.
- Y. Yang, L. Wang, C. Dong, G. Xu, T. Morosuk and G. Tsatsaronis, Appl. Energy, 2013, 112, 1087–1099 CrossRef.
- A. Vatani, M. Mehrpooya and A. Palizdar, Energy Convers. Manage., 2014, 78, 720–737 CrossRef.
- G. Tsatsaronis and T. Morosuk, Energy, 2010, 35, 820–829 CrossRef CAS.
- F. Petrakopoulou, G. Tsatsaronis, T. Morosuk and A. Carassai, Energy, 2012, 41, 146–152 CrossRef.
- Y. Zhang, E. Yao, Z. Tian, W. Gao and K. Yang, Appl. Therm. Eng., 2021, 185, 116421 CrossRef CAS.
- Y. Cao, S. B. Mousavi and P. Ahmadi, Fuel, 2022, 324, 124495 CrossRef CAS.
| This journal is © The Royal Society of Chemistry 2024 |