Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Conjugated microporous polymer frameworks for sustainable energy materials – elucidating the influence of solvents on the porosity properties for future design principles†
Catherine
Mollart
 and
Abbie
Trewin
and
Abbie
Trewin
 *
*
Department of Chemistry, Lancaster University, Lancaster, LA1 4YB, UK. E-mail: a.trewin@lancaster.ac.uk
First published on 16th January 2024
Abstract
Since 2010 the influence of reaction solvent choice on the porosity of conjugated microporous polymers (CMPs) has been known, but never fully understood. This means that the current approach to find the optimal conditions for CMP synthesis relies heavily on the empirical knowledge of the researcher and costly solvent screening processes. This approach risks overlooking CMP systems with exceptional properties due to not being synthesised using the optimal solvent. In this work, we have artificially synthesised CMP-1 as a model system in multiple solvents of varying polarities to assess the influence of the reaction solvent choice on the CMP-1 structure. The full synthetic conditions and catalytic pathway were modelled, and we hypothesise that the solvent choice has little to no impact on the micro-structure of the polymer core, but does influence the ratios of meso- to microporosity in the edge regions surrounding the core of the polymer particles due to differences in the phase separation of the polymer from the solvent depending on the solvent polarity. This offers a strategy to explore this structural tuning effect for future CMP materials pre-real-world synthesis, allowing us to identify the optimal conditions for a material with the best opportunity to perform for a target application.
Introduction
In the current digital era, there is increased demand for clean, renewable energy sources to power electronic devices.1 By 2050, the global energy demand is expected to double.2 Hence, the search for new materials that can store or generate energy is imperative.Crystalline porous materials, such as zeolites,3 metal–organic frameworks (MOFs)4–6 and covalent organic frameworks (COFs)7–9 have a range of interesting energy applications due to their ‘ultra-high’ surface areas (e.g., MOF-210 has a surface area of 6240 m2 g−1),4 resulting from their clearly defined pore structures, but some suffer due to a lack of stability, removing them from the line-up of potential new, renewable energy materials.10,11
An alternative to the crystalline MOFs and COFs is the class of conjugated microporous polymers (CMPs), which have applications in a range of areas, e.g., organically synthesised porous carbon (OSPC)-1 (OSPCs are a subset of CMPs) shows promise as a battery anode material,12 hypercrosslinked polymers can be used for gas uptake,13 porous aromatic framework (PAF)-1 (PAFs are a subset of CMPs) has been used as a solid-state electrolyte for fuel cell technologies,14 and aza-CMP has the potential to act as a nanoporous supercapacitor.15,16 CMPs have an amorphous interpenetrated three dimensional framework structure, where porosity arises from inefficient space filling by the polymer. The porosity is intrinsically linked to their ability to perform as energy materials. For example, the capacitance of aza-CMP changes drastically between 549 and 945 F g−1, with this maximum value being linked to a compromise between high overall surface area and a larger diameter of the pores.15
Due to the hypercrosslinked nature of these polymers, they are typically much more stable than MOFs and COFs, however, the materials currently reported often don't yield the same ‘ultra-high’ surface areas as the crystalline alternatives.7,11 This often means that depending on the application of choice for a new material, a decision must be made whether to prioritise the stability or the porosity.
The amorphous nature of porous polymers like CMPs, which are made up of a fully π-conjugated polymer backbone,11 with a three-dimensional arrangement of micropores throughout the structure, means that they are highly dependent on the synthetic conditions employed, including the reaction solvent and catalyst.11,17 The lack of a defined unit cell due to the absence of order within the system also makes characterisation challenging and the synthetic chemist must rely on a toolkit of techniques to piece together a picture of what the atomic structure looks like. This toolkit includes solid-state nuclear magnetic resonance spectroscopy to assess the extent of bonding and chemical environments, Fourier Transform Infrared spectroscopy, elemental analysis, and X-ray photoelectron spectroscopy to identify the functional groups within the material, and porosity analysis including pore size distribution and Brunauer–Emmett–Teller surface area calculations to inform about the pore size range, surface area, and adsorption isotherm type.11,18,19
Since the initial discovery of CMP-1 (Fig. 1(a)), the first CMP material reported from the Sonogashira–Hagihara reaction of 1,4-dibromobenzene (DBB) or 1,4-diiodobenzene with 1,3,5-triethynylbenzene in the presence of a Pd(PPh3)4 catalyst, solvent, and triethylamine (TEA) in 2007,20 the field of CMPs has grown rapidly due to the flexibility in monomer building blocks and synthetic strategies used to prepare them,11,21,22 making it possible to tailor the properties of the polymer towards an application of interest. However, in order to be able to design novel energy materials with exceptional properties, it is important to first understand how the external influences such as reaction solvent choice affect the polymer structure, so that only those materials that would appear to have promising applications in theory are synthesised experimentally, saving time and money through the reduction of solvent-screening processes, which are expensive due to the palladium-based catalyst.
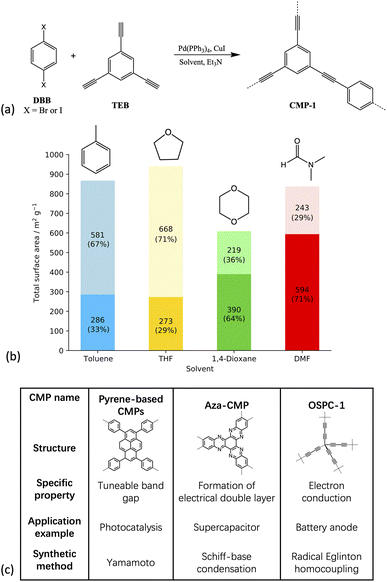 | ||
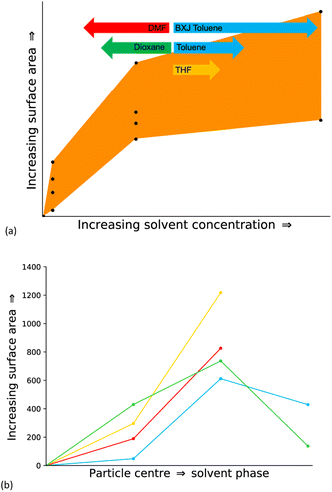
| Fig. 1 (a) Scheme showing the synthesis of CMP-1 (b) plot of the resulting experimental surface areas when synthesised in the respective solvent. Dark shades show the micropore surface area and light shades show the mesopore surface area with the percentage of the total surface area shown in brackets (c) table showing some example CMP materials, all of which are chemically and thermally stable, fully pi-conjugated frameworks with permanent three-dimensional microporosity. Each CMP shown has a different application arising due to additional properties specific to each, and a wide variety of synthetic methods are used to prepare these, as shown in the table.12,15,16,29 | ||
Chen et al. have previously reported a new method of CMP synthesis, initially designed to make CMPs using the Buchwald–Hartwig catalytic method,23 and then adapted to synthesise CMPs using other methods including the Sonogashira–Hagihara reaction used to synthesise CMP-1.24 Their new approach, termed Bristol–Xi'an Jiaotong (BXJ), involves the addition of inorganic salts to the reaction mixture during the synthesis to optimise the surface area and pore size distribution of the material without changing the chemical composition or introducing any crystallinity into the polymer network.23,24
Adding inorganic salts to the material enhances the solubility of the monomers in the solvent by altering the Hansen solubility parameters (HSPs, see ESI section 2† for more information)25 of the solvent, in particular the polar and hydrogen bonding contributions, which should increase with the electronegativity of the salt.24 This better match between the HSPs of the solvent and polymer then leads to a later phase separation of the polymer from the solvent and an increase in the surface area by narrowing the pores within the network to the micropore region only.23,24 This approach could then be used to identify which solvent and salt composition would give the maximum surface area for each CMP network.
Maximising the surface area within the polymer framework is vital when considering the applications of the material. An increased surface area gives a higher volume within the material for guest molecules to be adsorbed onto, which can lead to an increased uptake of gas molecules.21 Additionally, an enhanced porosity can also give an increased power density within electrodes for renewable batteries and facilitate easier diffusion of the ions throughout the battery.26,27 Examples of CMPs with high porosities leading to applications within the energy sector include OSPC-1 (surface area = 766 m2 g−1, lithium ion capacity = 748 mA h g−1, current density = 200 mA g−1),12 CON-16 (surface area = 300 m2 g−1, sodium ion capacity = 250 mA h g−1, current density = 100 mA g−1),28 aza-CMP@500 (surface area = 1227 m2 g−1, specific capacitance = 946 F g−1, current density = 0.1 A g−1),16 and TCNQ-CTF (surface area = 4000 m2 g−1, specific capacitance = 383 F g−1, current density = 0.2 A g−1).27,30
Simulation is also a vital tool to assess the structure at the atomic level, but it is important to follow the chemistry of the reaction to generate structures that are representative of the overall CMP network.10 We previously reported the artificial synthesis of CMP-1 synthesised using N,N-dimethylformamide (DMF) solvent, where we modelled the structure using our in-house Ambuild code, which allows us to mimic the full synthetic procedure, including the Sonogashira–Hagihara catalytic pathway (Fig. SI.1†) and using the experimental stoichiometry of reagents.10
We followed the experimental network formation mechanism proposed for CMP-1 by Laybourn et al. (Fig. SI.2†),31 which begins with the reaction of monomers to form soluble oligomers, that continue to react and grow until they reach a point where they become insoluble clusters and precipitate out of solution into a gel-like phase, reacting further through alkyne–alkyne homocoupling – which requires similar synthetic conditions to the Sonogashira–Hagihara pathway – in the absence of 1,4-dibromobenzene. These clusters then combine to form the final CMP-1 product.31
In our previous work, we found that the only way to rationalise the porosity data reported by Laybourn et al. in our simulated models was to consider a series of spherical polymer particles that would fuse together on desolvation, each with a dense core, which we modelled using a small amount of solvent relative to the number of monomers and catalyst molecules, surrounded by two outer ‘edge’ regions with increasing pore size (and modelled using increasing numbers of solvent molecules) going out from the central core towards the edge of the spherical particles.10,31
Following on from our previous work,10 here we explore the influence of reaction solvent on the structure and porosity of CMPs to rationalise why the reaction solvent choice influences the porosity of the resulting materials. Whilst it has previously been postulated that the differences in CMP porosity when synthesised in different solvents arise due to phase separation,17 this has never been confirmed until the present work. It is anticipated that the methods reported within this study will enable the rational design of new CMP materials with exceptional applications within the real-world energy sector and without the need for costly solvent screening processes. There is very little reported research on the impact of solvent choice on the porosity of CMP materials,17,23,24,32 and so it is therefore necessary to choose from these, which experimental data is most appropriate for computational assessment in terms of the CMP system, the number of solvents assessed, and consistency of synthetic approach.
In this work, we have mimicked the synthetic conditions reported by Dawson et al. (Fig. 1(b), Table SI.1, SI.3†),17 who reported the experimental synthesis of CMP-1 within four different solvents to enable direct comparison between simulation and experiment. This experimental report was chosen due to the quantity of experimental data for CMP-1 to which we can compare our simulation results.17 Additionally, CMP-1 was chosen due to the existing ability of Ambuild to model the Sonogashira–Hagihara catalytic mechanism, which is commonly used to artificially synthesise CMPs,11,22 within Ambuild.10
The solvents used in the experimental work by Dawson et al.17 and studied artificially here – DMF, toluene, tetrahydrofuran (THF) and 1,4-dioxane – are all commonly used in CMP synthesis.17,20,23,24 Toluene was the original solvent used to prepare the first CMP, CMP-1,20 and over time the reaction solvent choice has evolved through the empirical knowledge that solvents such as DMF tend to yield a CMP with a higher surface area compared to the same network prepared in toluene.17,31 THF and 1,4-dioxane often give CMP networks with similar properties, with the networks synthesised in THF resulting in a slightly higher average surface area, whilst the networks synthesised in 1,4-dioxane give a slightly higher average degree of microporosity, shown in Fig. 1(b).17
Organic bases such as triethylamine, piperidine and diisopropylamine have also been used as the solvent in Sonogashira–Hagihara reactions,33 however, there is no experimental evidence of CMP-1 being synthesised using these bases as the solvent, and so it was not possible to include these within this study.
The solvents studied have varying polarities, with a range of polarity index and Hildebrand solubility parameters (see Table SI.2† for the values).25,34 DMF is the most polar of the solvents studied, followed by 1,4-dioxane, THF, and finally, toluene is the least polar.25,34 Whilst the overall CMP-1 surface area does not differ greatly depending on the reaction solvent choice compared to other CMPs, the percentages of micro- to mesoporosity for the network synthesised in each solvent are sensitive to the reaction solvent choice (Table SI.2, Fig. SI.4†).16 For example, CMP-1 prepared in DMF has the largest microporous surface area of those reported by Dawson et al., at 594 m2 g−1, and the lowest mesoporous surface area, whilst when synthesised in THF, CMP-1 has the lowest microporous surface area, at 273 m2 g−1, and the highest mesoporous surface area,17 suggesting that the solvent does influence the formation of the polymer network.
Methodology
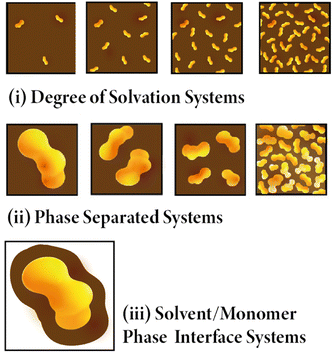
The structural models presented in this work were generated using the Ambuild code.10 More information about Ambuild is available in the SI, but in summary, Ambuild is a GPU-based simulation code written in Python that is specifically designed to model amorphous porous polymers.10 Ambuild integrates with HOOMD-blue,35,36 which was used as our geometry optimisation and molecular dynamics (MD) engine throughout, and Poreblazer,37,38 used to calculate the porosity properties of our models. This code in particular was chosen as the full synthetic pathway and catalytic mechanism can be mimicked, giving a better match between the experimental and computational materials studied.10 The Polymer Consistent Forcefield (PCFF)39 has been used previously by both our own group and by others to model microporous polymers.10,40,41 It was used throughout this work as it is an appropriate forcefield to model materials like CMP-1 due to being designed to model the interactions within polymers.39 Again, this leads to a better comparison between simulation and experiment on choosing an appropriate forcefield.Three sub-classes of systems were generated as part of this work, each artificially synthesised in each of the four solvents studied. They are referred to throughout this work as: (i) Degree of Solvation Systems – where the CMP synthesis is modelled with various quantities of solvent fully mixed with the CMP monomer throughout the respective simulation cell, keeping the number of CMP monomers the same for each system modelled (ii) Phase Separated Systems – where we model varying degrees of phase separation between the CMP monomer and solvent modelled, keeping the number of solvent and CMP monomers the same, and (iii) Solvent/Monomer Phase Interface Systems. These are shown in Fig. 2. More information about the Ambuild methodology for each system type is given in ESI section 3,† and a summary is presented below.
The (i) degree of solvation system models (ESI section 4†), (ii) phase separated systems (ESI section 5†) and (iii) solvent/monomer phase interface system models (ESI section 6†) were simulated by firstly seeding the required number of building blocks to the unit cell in the correct configuration depending on the system type (Tables SI.5 and SI.10†). Once the seed step was complete, a loop was undertaken to allow any building blocks within a pre-determined bond and angle distance that meet the specified bonding rules, which allows us to mimic the Sonogashira–Hagihara catalytic cycle, to react. Geometry optimisation and NVT (constant number of molecules, cell volume, and temperature) MD were also carried out to allow the structure to find a lower energy configuration and to allow the building blocks to diffuse throughout the simulation cell. Once each network had finished reacting and was therefore complete, it was desolvated and the porosity properties were calculated using Poreblazer.37,38
Before the network formation process, the (ii) phase separated systems and (iii) solvent/monomer phase interface system models were also analysed by seeding the required quantities of monomers, catalyst, and solvent to the simulation cell (Table SI.10†), then running a loop containing geometry optimisation and NPT (constant number of molecules, cell pressure, and temperature) MD to assess the diffusion of building blocks within each system.
Results and discussion
Degree of solvation systems
We firstly took the same approach we have taken in our previous work,10 modelling the synthesis of CMP-1 using various quantities of solvent and triethylamine (TEA). We generated models with 1%, 33%, 67% and 100% of the experimental stoichiometry, whilst keeping the quantities of monomers and catalyst constant throughout. We generated four repeat models of each structure to increase the statistical sampling of the amorphous CMP-1 material.As reported previously for CMP-1 synthesised using DMF as the solvent,10 some solvent is required to be present to allow diffusion of monomers and catalyst throughout the simulation cell, but on increasing the quantity of solvent past a certain point, polymer formation is inhibited as the increased volume of solvent reduces the likelihood of monomers and catalyst being in close contact and thus being able to react. A similar effect is observed here for all solvents (Fig. SI.5 and Tables SI.6–SI.9†), indicating that this trend is common across the different solvent systems.
Predicting degrees of solvation is challenging and not possible within the scope of this study. However, we can elucidate the relative solubility of the polymer building blocks in each solvent using their respective polarity index and Hildebrand solubility parameters, shown in Table SI.2.† As the monomers used in the synthesis of CMP-1 (1,4-dibromobenzene and 1,3,5-triethynylbenzene) are non-polar,42 the higher these values are, the less soluble we expect the monomers to be in the respective solvent. This suggests that the monomers will be least soluble (fully co-phase separated) in DMF, followed by 1,4-dioxane (partially co-phase separated), THF (partially co-phase separated to a lesser extent than CMP-1 synthesised in 1,4-dioxane), and most soluble in toluene.42
Fig. 3(a) shows the surface area of the obtained models against the degree of solvation for all solvents. There is a broadly logarithmic relationship between the degree of solvation and the surface area of the resulting polymer formed, no matter which solvent is used and with no clear trend between solvents. We therefore expect that solvents that have a high polarity, and thus a bad match to the HSP of the monomers, will feature have lower solvent concentrations in the reaction mixture leading to polymers with lower surface area. Whereas solvents with low polarity, and thus a good match to the monomer HSP, will have higher concentrations in the reaction mixture and hence lead to higher surface areas.
Interestingly, Chen et al.24 used their BXJ method to increase the solubility of the CMP-1 monomers in toluene and achieved an increase in the total surface area from 886 m2 g−1 to 1148 m2 g−1. An increase in pore volume and in pores in the micropore region were observed which was rationalised as being due to changes in the phase separation and an accompanying increase in the degree of polymerisation. This aligns with the expected outcomes here, where an increase in solubility should result in more mixing of the monomer/solvents and thus a more homogenous resulting polymer structure and a smaller range of resulting pores.
Previously, we have rationalised the surface area properties of CMP-1 through the formation of spherical particles that have a dense non-porous core and increasing porosity as the particle edge is approached as a result of phase separation of the monomer from the solvent. Similarly, here we see that with zero solvent present a non-porous structure is obtained mimicking the centre of a phase separated spherical region. We expect that as we move out from the centre of the phase separated sphere, the solvent concentration will increase. Fig. 3(b) shows the expected pathway through the solvent concentrations modelled here and the relevant desolvation strategy required. We see that in general the surface area increases for each solvent as expected. However, for toluene and 1,4-dioxane the surface area of the respective final solvent concentration model is lower than the previous. We believe that this is due to the highly open mesoporous structure formed that collapses upon desolvation to form a more densely packed and therefore less porous structure. The models generated using equivalent solvent concentrations for THF and DMF produced oligomers only that are removed as part of the desolvation process. This suggests that there are some differences between solvents and the influence upon resulting structure. However, we cannot determine from these models the relative ratios of each region in the different solvents. To explore this further, we assess the phase separation behaviour.
Phase separated systems
To explore the relative phase separation behaviour, we generated a range of models with different degrees of phase separation. We kept the quantity of monomers, catalyst, solvent, and TEA constant at 100% of the experimental stoichiometry, and instead changed the configuration of building blocks within the unit cell, giving us a range of phase separation within our models.The models include a fully mixed cell, where all of the monomer and catalyst building blocks, solvent, and TEA were randomly added into the simulation cell, a cell with four regions into which we added the building blocks, a cell with two regions into which we added the building blocks, and a cell where the building blocks were added into a central region. Once the monomer and catalyst building blocks were added to their respective regions, the solvent and TEA were added into the remaining cell volume. As with the fully mixed systems modelled with varying quantities of solvent, four repeat models per structure were generated to increase statistical sampling. We also simulated a one large cluster model for the Solvent/Monomer Phase Interface Systems to allow us to study the interface between monomers and solvent, where the number of monomer and catalyst building blocks were increased by a factor of 15, whilst keeping the quantity of solvent and TEA the same as for the other models generated in our varying phase separation series. The Solvent/Monomer Phase Interface Systems were then analysed alongside the phase separated systems. Fig. 4(a) shows a comparison of each phase separated system model type, and ESI section 5† has full details about the modelling approach taken.
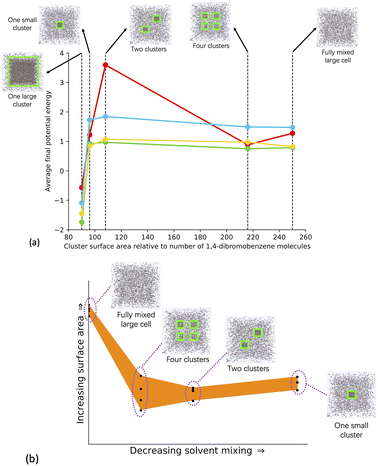 | ||
| Fig. 4 (a) Average final potential energy relative to the number of DBB molecules for models generated in different solvents. Key: toluene – blue, THF – yellow, 1,4-dioxane – green, DMF – red. (b) Plot of the surface area against the solvent mixing for all the models generated for the phase separated systems. The different structural configurations modelled in the phase separated systems are shown as insets. The yellow boxes around each cluster are present for clarity. In each model the number of respective solvent molecules and cell size is the same. The one large cluster Solvent/monomer phase interface system has 15× more monomer and catalyst units than the phase separated system models. See Table SI.10† for full details. | ||
Solvent/monomer phase interface systems
To assess the solvent/monomer interface, we analysed the set of solvent/monomer phase interface system models in detail (ESI section 6†). These models, which have a large, scaled-up region of monomers and catalyst surrounded by a solvent region, are the closest we have modelled to the experimental CMP-1 particles, which, from the experimental SEM data,17,31,43 appear to have diameters in the range of 150–450 nm. Ideally, larger models that have full cell solvation would enable us to fully assess the solvent diffusion behaviour. However, we are currently limited by the computational expense of such model systems. To assess these, fully atomistic approaches will not be possible with current technologies and so a coarse grain approach will need to be taken, which is beyond the scope of this work.From looking back at the polarity index and HSP values, we would expect to see that as toluene has the closest polarity match to the monomers, the models should be fully miscible, meaning that we would expect a high quantity of toluene throughout the cluster with increasing values towards the centre. We would then expect the models generated in THF and 1,4-dioxane, which have higher polarities and would therefore make the monomers less soluble, would have fewer and more isolated regions of solvent away from the monomers. DMF, as the most polar solvent studied, would have very discrete regions of solvent that is fully co-phase separated from the monomers and should have a lower concentration of solvent molecules in the centre of the cluster.25,34
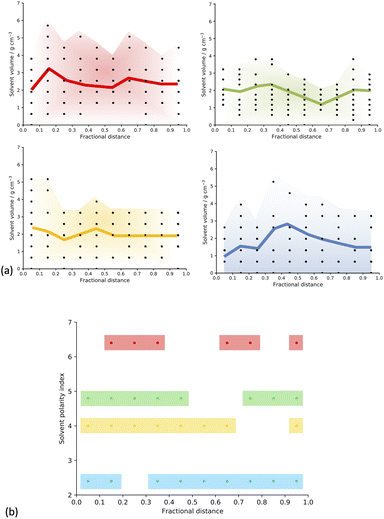
To test this hypothesis, we took a series of slices through the centre of our material going from one edge to the other in each of the three xyz directions (more details in ESI section 6†) and counted the number of solvent molecules in each fragment sampled, generating a concentration profile, shown in Fig. 5(a).
In all models, we can see that the solvent is able to reach the centre of the simulation cell, suggesting that the solvated regions in the experimental CMP-1 particles are larger than the 200 Å simulation cell length modelled here. We therefore propose that in order to model the entire CMP-1 particle in one system, a much larger model size would be required.
The concentration profiles appear to be different for each solvent, and broadly in-line with expectations given their respective polarity index and HSP values.25,34 At the extremes of the solvents assessed here, we can see that DMF shows a distinct decrease in concentration in the centre of the cluster, whereas toluene shows an even more distinct increase in concentration at the centre of the cluster.
Further, we calculated the fractional distance corresponding to the largest number (maximum count) of solvent molecules in each of the concentration profiles we obtained for our solvent/monomer phase interface system models and plotted it as a function of solvent polarity index (Fig. SI.19,† and 5(b)).34 We can see that when the solvent is DMF, the maximum counts present as an approximate bimodal distribution, with the solvent centred around a fractional distance of 0.3 and 0.7 from the edge of the cell, with no maximum solvent counts in the centre of the cell, suggesting phase separation from the monomer and catalyst building blocks. When the solvent is 1,4-dioxane, we also see a bimodal distribution, but this is broadened, giving maximum counts spanning closer to the centre of the simulation cell, but still not exactly in the centre, with no maximum solvent counts observed in the fractional distance range of 0.5–0.7 from the edge of the cell. In the next solvent, THF, we see an almost unimodal distribution of maximum counts, spanning a fractional distance range of 0.0–0.7 from the edge of the cell, with just one point that is not in this range, occurring at 0.95, but it is important here to remember the periodic nature of the simulated models, meaning that this point is just across the periodic boundary from the next unimodal region. Finally, when the solvent is toluene, the least polar of those studied and therefore the best polarity match to the monomers,42 we observe an almost uniform distribution of maximum solvent counts throughout the simulation cell.
This suggests that our hypothesis is correct. As the solvent polarity increases, there is a less uniform distribution of solvent throughout the simulation cell, indicating that the solvent is more isolated from the polymer cluster (Fig. SI.19,† and 5(b)). This shows that we can observe differences in the phase separation of our solvent/monomer phase interface system models depending on the polarity of the solvent, where a higher solvent polarity, quantified by a larger solvent polarity index and HSP,25,34 such as when the solvent is DMF, corresponds to a larger degree of phase separation within the structure; and a lower solvent polarity, corresponding to a smaller solvent polarity index and HSP,25,34 such as when the solvent is toluene, leads to more miscibility within the system, a larger quantity of solvent within the reaction mixture, and a more homogenous resulting polymer. We suggest that these differences in the phase separation of the structures, caused by the polarity of the reaction solvent choice, causes the observed differences in the porosity properties of the CMP-1 material by changing the percentages of meso- and microporosity in the structure.
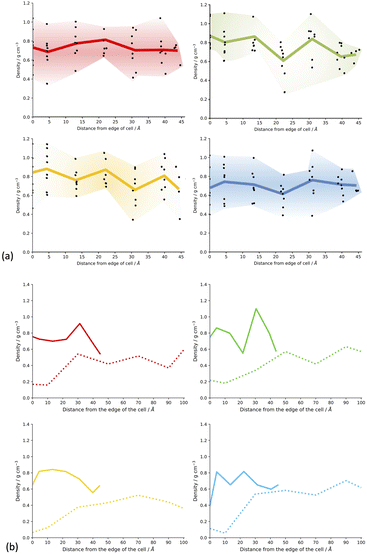
Fig. SI.20† shows slices through the solvent/monomer phase interface system models after network generation but before desolvation. We can see that as expected, the models all have very similar overall densities throughout the structure of the cluster as the space is filled efficiently. No distinct overall trends can be seen in the overall density of the respective models when compared to each other. Upon desolvation, the system is allowed to relax fully and hence fill the void space remaining after solvent removal efficiently as the network will allow. Regions where large numbers of solvent molecules resided will result in less dense regions of the resulting polymer due to the rigidity of the framework and hence inability to fill the void space. Fig. 6(a) shows the density of the CMP-1 network as a function of the distance from the edge of the cell for the systems synthesised in the respective solvents. In general, the density of the resulting model systems is approximately 0.8 g cm−3, in line with bulk densities determined for CMP-1 previously.17,31,43 For each set of model systems a range of densities is observed depending upon the location within the slice of the respective CMP-1 cluster. These broadly follow the inverse trend of the respective solvent concentration profiles shown in Fig. 5(a). Interestingly, the edges of the cluster appear to act as ‘crumple zones’ after desolvation, where the volume of the cells are allowed to change and thus the system can reach a minimal cell volume, shown in Fig. 6(b). The regions that are high CMP-1 density before desolvation become higher in density so that the overall effect is that the density profile is condensed into a smaller distance but remains the same overall shape. The CMP-1 density of the central regions of the cluster appear to not increase in density as much as the edge regions and so have not crumpled. This suggests that the density profiles of the solvated regions of the CMP-1 concentration at the centre of the cluster for DMF and 1,4-dioxane clusters do not increase linearly towards the centre but change in a heterogenous manner that is highly dependent upon the degree of solvation and location within the cluster.
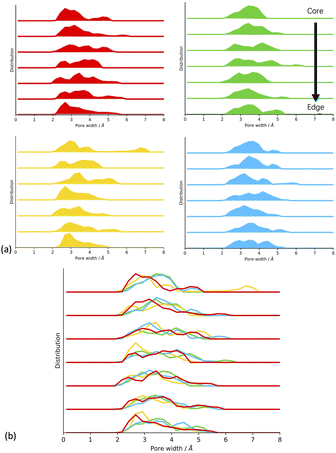
From looking at the experimental data (Fig. 1),17 we expect that the CMP-1 models artificially synthesised in toluene and THF will have a high degree of mesoporosity, whereas those synthesised in DMF and 1,4-dioxane will have a high degree of microporosity. Our hypothesis is that the solvent influences the ratio of meso- to microporous regions which result from the respective solvent concentration profiles within the cluster. The solvent concentration profiles, shown in Fig. 5(a), suggest that this hypothesis is correct as we see a drop in solvent for DMF and 1,4-dioxane, but the inverse is true for toluene and THF. However, the response of the network structure to desolvation and homocoupling is complex and results in crumple zones that have fluctuating densities relating to their solvated as-synthesised structure. Fig. 7 shows the pore size distributions obtained after network generation, desolvation and homocoupling stacked as a function of distance from the edge of the cluster, with the lowest stack being at the edge of the cell and the upper stack being at the centre of the cell. The centre of the cell may not correspond to the centre of the cluster after network generation and desolvation and so this analysis can only tell us the range of pore sizes within the models.
We can see that for CMP-1 synthesised in all solvents the pore size diameters are small, being less than 8.0 Å. This is an artefact of the small cluster size used to model these systems in comparison to the much larger particle sizes observed experimentally. While this cannot tell us the pore size distributions that we would see experimentally, it can show the relative ability of each network to pack efficiently and hence inform us about the structural effects that may influence the real-world synthesis in each solvent.
For DMF, 1,4-dioxane and toluene we can see that the pore size diameter ranges between 2.0 Å and 6.5 Å. This is consistent for each plot as we move through the cell, with only small increases or decreases in pore size diameter. For THF, we see the largest range between 2.0 Å and up to 7.0 Å. We rationalise these trends as being due to the respective abilities of the CMP-1 framework to pack efficiently upon desolvation.
For DMF, the structure is more microporous throughout the cluster at the point of network generation due to the lower concentration of solvent within the cluster. Therefore, upon desolvation, the structure is not able to pack much more efficiently, and we retain the micropore structure throughout the cluster. For 1,4-dioxane and THF, we expect to see a small shift to higher pore size diameter values as the solvent concentration within the cluster during network generation increases with the respective decrease in polarity index and HSP. The pore size distributions for 1,4-dioxane and THF do show this shift to larger pore sizes as expected.
For toluene, we expect that there will be a shift to larger pore diameters as it has the smallest polarity index and therefore the highest concentration of solvent within the cluster. However, we do not see this in the obtained pore size distributions which appears similar to that of 1,4-dioxane. We postulate that at the point of network generation we do see this trend but that after desolvation and homocoupling the pore sizes of toluene are decreased due increased flexibility of the framework resulting from the larger and more open structure at this point. Thus, THF has optimum solvent behaviour for maintaining pores as the pore sizes are not too flexible to collapse upon desolvation and homocoupling. This agrees with the trend in experimental surface areas determined where CMP-1 synthesised in THF shows the largest degree of mesoporosity with 71% of the surface area being mesoporous compared to 67%, 36%, and 29% for toluene, 1,4-dioxane, and DMF respectively. However, the effects observed here are small and so larger system sizes will be required to confirm.
To test this hypothesis, we assessed the structure of the CMP-1 framework after network generation but before desolvation and homocoupling, shown in Fig. SI.21.† We can see that for DMF the solvent filled regions are small and well-spaced. This spacing increases slightly for 1,4-dioxane and again for THF. However, for toluene we see larger regions of solvent volume and the CMP-1 polymer regions being clumped closer together. The large voids resulting from removing the solvent will be unstable and the flexibility of the polymer will result in these voids being more likely to collapse upon desolvation.
Conclusions
In this work, we have artificially synthesised CMP-1 in four solvents of varying polarities, following the full synthetic pathway and modelling each step of the Sonogashira–Hagihara catalytic cycle. Through modelling the CMP-1 structure generation in various quantities of solvation and various phase separation configurations, we have found that the differences in the surface area of the CMP-1 framework when synthesised in different reaction solvents arise from changes in the phase separation observed within the reaction mixture, leading to different ratios of meso- and microporosity within the edge regions surrounding the polymer particles, whilst the central microporous polymer core region will be unaffected by solvent.Assessing the monomer/solvent interface through a one large cluster model, and the respective polymer structure synthesised, enables us to explore the trends in micro/mesoporosity with respect to the solvent. This offers a strategy to explore this structural tuning effect for future CMP materials pre-real-world synthesis, allowing us to identify the optimal synthetic conditions for a material with the best opportunity to perform for a target application. It also means that existing CMP systems can be identified that have great potential that would otherwise not be discovered due to having less than optimal porosity properties as synthesised in standard solvents.
Author contributions
All authors contributed to conceptualisation, data analysis, and draft preparation. Catherine Mollart: data collection. Abbie Trewin: editing and supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to thank Professor Jamshed Anwar for his advice and expertise. We would also like to thank the High End Computing facility at Lancaster University, which was used to run all of the Phase Separated System and Solvent/Monomer Phase Interface System simulations discussed here.Notes and references
- Energy Trends: June 2023, https://www.gov.uk/government/statistics/energy-trends-june-2023, accessed 07 August 2023 Search PubMed.
- B. Dunn, H. Kamath and J.-M. Tarascon, Science, 2011, 334, 928–935 CrossRef CAS PubMed.
- M. Moshoeshoe, M. S. Nadiye-Tabbiruka and V. Obuseng, Am. J. Mater. Sci., 2017, 7, 196–221 Search PubMed.
- H. Furukawa, N. Ko, Y. B. Go, N. Aratani, S. B. Choi, E. Choi, A. Ö. Yazaydin, R. Q. Snurr, M. O'Keeffe, J. Kim and O. M. Yaghi, Science, 2010, 329, 424–428 CrossRef CAS PubMed.
- A. E. Baumann, D. A. Burns, B. Liu and V. S. Thoi, Commun. Chem., 2019, 2, 86 CrossRef.
- O. K. Farha, I. Eryazici, N. C. Jeong, B. G. Hauser, C. E. Wilmer, A. A. Sarjeant, R. Q. Snurr, S. T. Nguyen, A. Ö. Yazaydın and J. T. Hupp, J. Am. Chem. Soc., 2012, 134, 15016–15021 CrossRef CAS PubMed.
- S. Das, P. Heasman, T. Ben and S. Qiu, Chem. Rev., 2017, 117, 1515–1563 CrossRef CAS PubMed.
- A. P. Côté, A. I. Benin, N. W. Ockwig, M. O'Keeffe, A. J. Matzger and O. M. Yaghi, Science, 2005, 310, 1166–1170 CrossRef PubMed.
- H. Wang, L. Huang and D. Cao, in Porous Polymers: Design, Synthesis and Applications, ed. S. Qiu and T. Ben, The Royal Society of Chemistry, 2015, pp. 121–150, 10.1039/9781782622260-00121.
- J. M. H. Thomas, C. Mollart, L. Turner, P. Heasman, P. Fayon and A. Trewin, J. Phys. Chem. B, 2020, 124, 7318–7326 CrossRef CAS PubMed.
- R. Dawson and A. Trewin, in Porous Polymers: Design, Synthesis and Applications, ed. S. Qiu and T. Ben, The Royal Society of Chemistry, Cambridge, 2015, ch. 7, pp. 155–185 Search PubMed.
- Z. Zhao, S. Das, G. Xing, P. Fayon, P. Heasman, M. Jay, S. Bailey, C. Lambert, H. Yamada, T. Wakihara, A. Trewin, T. Ben, S. Qiu and V. Valtchev, Angew. Chem., Int. Ed., 2018, 57, 11952–11956 CrossRef CAS PubMed.
- A. Liu, C. Mollart, A. Trewin, X. Fan and C. H. Lau, ChemSusChem, 2023, 16, e202300019 CrossRef CAS PubMed.
- C. Wang, T. Yan, G. Xing, S. Bailey, C. Lambert, P. Fayon, A. Trewin and T. Ben, J. Solid State Chem., 2022, 308, 122903 CrossRef CAS.
- P. Fayon, J. M. H. Thomas and A. Trewin, J. Phys. Chem. C, 2016, 120, 25880–25891 CrossRef CAS.
- Y. Kou, Y. Xu, Z. Guo and D. Jiang, Angew. Chem., Int. Ed., 2011, 50, 8753–8757 CrossRef CAS PubMed.
- R. Dawson, A. Laybourn, Y. Z. Khimyak, D. J. Adams and A. I. Cooper, Macromolecules, 2010, 43, 8524–8530 CrossRef CAS.
- M. F. De Lange, T. J. H. Vlugt, J. Gascon and F. Kapteijn, Microporous Mesoporous Mater., 2014, 200, 199–215 CrossRef CAS.
- S. Brunauer, P. H. Emmett and E. Teller, J. Am. Chem. Soc., 1938, 60, 309–319 CrossRef CAS.
- J.-X. Jiang, F. Su, A. Trewin, C. D. Wood, N. L. Campbell, H. Niu, C. Dickinson, A. Y. Ganin, M. J. Rosseinsky, Y. Z. Khimyak and A. I. Cooper, Angew. Chem., Int. Ed., 2007, 46, 8574–8578 CrossRef CAS PubMed.
- Y. Xu, S. Jin, H. Xu, A. Nagai and D. Jiang, Chem. Soc. Rev., 2013, 42, 8012–8031 RSC.
- J.-S. M. Lee and A. I. Cooper, Chem. Rev., 2020, 120, 2171–2214 CrossRef CAS PubMed.
- J. Chen, W. Yan, E. J. Townsend, J. Feng, L. Pan, V. Del Angel Hernandez and C. F. J. Faul, Angew. Chem., Int. Ed., 2019, 58, 11715–11719 CrossRef CAS PubMed.
- J. Chen, T. Qiu, W. Yan and C. F. J. Faul, J. Mater. Chem. A, 2020, 8, 22657–22665 RSC.
- A. F. M. Barton, Handbook of Solubility Parameters and Other Cohesion Parameters, CRC Press, Boca Raton, 2nd edn, 1991 Search PubMed.
- J. Xie, P. Gu and Q. Zhang, ACS Energy Lett., 2017, 2, 1985–1996 CrossRef CAS.
- K. Amin, N. Ashraf, L. Mao, C. F. J. Faul and Z. Wei, Nano Energy, 2021, 85, 105958 CrossRef CAS.
- M.-S. Kim, W.-J. Lee, S.-M. Paek and J. K. Park, ACS Appl. Mater. Interfaces, 2018, 10, 32102–32111 CrossRef CAS.
- J.-X. Jiang, A. Trewin, D. J. Adams and A. I. Cooper, Chem. Sci., 2011, 2, 1777–1781 RSC.
- Y. Li, S. Zheng, X. Liu, P. Li, L. Sun, R. Yang, S. Wang, Z.-S. Wu, X. Bao and W.-Q. Deng, Angew. Chem., Int. Ed., 2018, 57, 7992–7996 CrossRef CAS PubMed.
- A. Laybourn, R. Dawson, R. Clowes, T. Hasell, A. I. Cooper, Y. Z. Khimyak and D. J. Adams, Polym. Chem., 2014, 5, 6325–6333 RSC.
- D. Tan, W. Fan, W. Xiong, H. Sun, Y. Cheng, X. Liu, C. Meng, A. Li and W.-Q. Deng, Macromol. Chem. Phys., 2012, 213, 1435–1440 CrossRef CAS.
- C. D. Varnado and C. W. Bielawski, in Polymer Science: A Comprehensive Reference, ed. K. Matyjaszewski and M. Möller, Elsevier, Amsterdam, 2012, ch. 5.08, pp. 175–194, DOI:10.1016/B978-0-444-53349-4.00138-2.
- L. R. Snyder, J. Chromatogr. A, 1974, 92, 223–230 CrossRef CAS.
- J. A. Anderson, C. D. Lorenz and A. Travesset, J. Comput. Phys., 2008, 227, 5342–5359 CrossRef.
- J. Glaser, T. D. Nguyen, J. A. Anderson, P. Lui, F. Spiga, J. A. Millan, D. C. Morse and S. C. Glotzer, Comput. Phys. Commun., 2015, 192, 97–107 CrossRef CAS.
- L. Sarkisov, R. Bueno-Perez, M. Sutharson and D. Fairen-Jimenez, Chem. Mater., 2020, 32, 9849–9867 CrossRef CAS.
- L. Sarkisov and A. Harrison, Mol. Simul., 2011, 37, 1248–1257 CrossRef CAS.
- H. Sun, Macromolecules, 1995, 28, 701–712 CrossRef CAS.
- C. Mollart, B. Ciborowski and A. Trewin, Mol. Syst. Des. Eng., 2023, 8, 1456–1461 RSC.
- A. Wang, R. Tan, C. Breakwell, X. Wei, Z. Fan, C. Ye, R. Malpass-Evans, T. Liu, M. A. Zwijnenburg, K. E. Jelfs, N. B. McKeown, J. Chen and Q. Song, J. Am. Chem. Soc., 2022, 144, 17198–17208 CrossRef CAS PubMed.
- C. Mollart and A. Trewin, Phys. Chem. Chem. Phys., 2020, 22, 21642–21645 RSC.
- R. Dawson, A. Laybourn, R. Clowes, Y. Z. Khimyak, D. J. Adams and A. I. Cooper, Macromolecules, 2009, 42, 8809–8816 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta04866g |
| This journal is © The Royal Society of Chemistry 2024 |