Direct measurement of the hydrogen adsorption entropy on shape-controlled Pt nanoparticles using electrochemical microcalorimetry

Abstract

Platinum nanoparticles are indispensable in electrochemical applications, e.g., for the generation and usage of green hydrogen. Therefore, understanding the properties of these materials before and during operation is of crucial research interest. However, their investigation is complicated by the variety of adjustable parameters under operating conditions. Researchers thus often revert to studying model systems, like single crystal Pt surfaces, yet it is not always clear how gained insights translate to actual applications. Conducting comprehensive physico-chemical studies on nanoparticles with preferential shapes could help bridge this gap. In this contribution, we use electrochemical microcalorimetry to investigate hydrogen adsorption on different shape-controlled platinum nanoparticles (quasi-spheres, cubes and octahedrons). From this method, we obtain the entropy of the adsorbed hydrogen on the different particles, which we aim to relate to its binding condition with the surface. This quantity often serves as a descriptor for the catalytic performance in the hydrogen evolution reaction. We show that the entropy of adsorption on the particles with different geometries is in good agreement with the adsorption on the single crystal sites related to the respective faces of the particles, by a comparison with entropy values obtained on platinum single crystals using the electrocapillary equation. The consistency between both methods opens possibilities for further research on analogous surfaces. The study is completed by investigating the effect of roughening of the particle surface by continuously cycling the potential into the platinum oxidation region. This enables the investigation of adsorbed hydrogen under more realistic conditions.

---

1 Introduction

Pt nanoparticles (NPs) with a specific shape and size exhibit not only enhanced catalytic properties compared to bulk materials, but also tuneable characteristics like selectivity and stability,^1,2 making them one of the most researched nanomaterials.^3–5 To understand the unique properties of nanomaterials, it is important to distinguish between the effects of the surface sites and effects stemming from the particle size.⁶ Recent research has demonstrated that the electrochemical properties of nanoparticles with clearly defined facets can be correlated with the electrochemistry observed in single crystals cut to expose the same dominant orientation.⁷ This allows for the investigation of surface sensitive processes in cases where single crystals cannot be used and helps to bridge the gap between fundamental studies and applications.

This research field benefits from many years of research into single crystal platinum electrodes, in which it was established that the different configurations of atoms of a surface have a profound effect on the catalytic properties.⁸ The hydrogen adsorption on these Pt surfaces from perchloric or sulfuric acid solution is one of the most prominent examples of an electrochemical system, where a nearly complete picture of the composition of the interfacial layer has been reached.

Following the pioneering work of Clavilier on the preparation of well defined Pt single crystals,⁹ a rigorous thermodynamic,^10–12 spectroscopic^13,14 and theoretical^15–17 description of this interface was achieved (a recent review of the history of Pt electrochemistry can be found e.g. in ref. 18). Among the mentioned studies, García-Araez et al. investigated the enthalpic and entropic effects of hydrogen adsorption on Pt basal planes first by using a generalized isotherm and later by developing a method based on the electrocapillary equation (ECE);^19–22 they found that the standard molar entropy of the adsorbed hydrogen depends on the geometric arrangement of atoms on the surface.²¹ Both methods show a good agreement²³ and can be used to ultimately determine the entropy of formation of the interface, a quantity introduced by Harrison et al. to study the interfacial thermodynamic properties at Hg electrodes.²⁴ The method based on the ECE determines the temperature coefficient of the interfacial potential 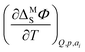to obtain the entropy of formation of the interface. On the other hand, the method using the generalized isotherm determines the coverage as a function of the potential to access the standard Gibbs energy of adsorption. Finally, the standard entropy of adsorption is derived from the temperature dependence of the Gibbs energy.²⁰ In the second approach, the determination of the entropy of the adlayer with respect to the number of moles of adsorbed species, i.e., coverage, then necessitates assuming an isotherm to correct for the coverage dependence of the standard entropy.²²

In general, the approach using the ECE is more precise and provides the advantage that double-layer contributions to the entropy of formation of the interface can be corrected by using the temperature coefficient of the potential drop across the double-layer 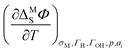. This temperature coefficient can be obtained by temperature-jump experiments.²⁰ Nevertheless, this method comes with the downside of being experimentally very challenging. On the other hand, the method using the generalized isotherm is experimentally better accessible, but brings about the intrinsic downside of assuming a Langmuir isotherm.²⁰ Using more sophisticated statistical mechanics models for the treatment of the H-coverage on steps, this approach can also be extended to stepped or kinked surfaces.²³

Another method to obtain the entropy of formation of the interface is electrochemical microcalorimetry (ECM), which measures the reversibly exchanged heat at the working electrode, the so called Peltier heat. The Peltier heat is directly linked to the reaction entropy of all surface processes referred to moles of electrons, i.e., to the reaction variable of the overall interface formation, including the adsorption itself as well as e.g. double-layer charging.²⁵ This method comes with the advantage that no model considerations are necessary to account for the H-coverage on steps. However, the disadvantage is that entropic contributions stemming from the double-layer formation cannot be separated directly and corrections for the entropy of transfer have to be considered.

In this work, we use ECM to determine the reaction entropy of hydrogen adsorption from sulfuric acid solution on three differently shaped NPs that exhibit polyoriented (spherical NPs), {100}-oriented (cubic NPs) and predominantly {111}-oriented surfaces (octahedral NPs). To analyse whether the thermodynamics of the NPs are comparable to those of single crystal surfaces corresponding to their respective geometry, we compare the results with the entropy of adsorption on the basal planes obtained using the ECE. As the entropy of the adsorbed hydrogen is obtainable from both methods, we chose to discuss the results based on this quantity; in addition this allows for a comparison with calculations of the entropy of adsorbed hydrogen based on simple statistical mechanics models.^20,26

2 Experimental

We used the calorimeter presented in previous contributions, e.g. ref. 27, which measures the temperature change at the backside of the working electrode (WE). An electrochemical cell made out of Kel-F allowing for the usage of a three-electrode setup is placed on top of the WE. The Pt NPs used as the WE were applied by casting a 4 μl droplet of a NP suspension on top of a 250 nm Au(111) film, which was evaporated on 50 μm sapphire glass coated with a 2 nm adhesion layer of chromium. The counter electrode was a flame annealed platinum wire and the reference electrode was a palladium-hydride electrode;²⁸ for a better comparison, all reported potentials were converted to the RHE scale. Spherical, octahedral and cubic platinum NPs with highly developed {111} and {100} facets respectively were employed in this study. The octahedral NPs were synthesized by the method published by Moglianetti et al.²⁹ and the cubic NPs were prepared following the method published by Arán-Ais et al.³⁰ The spherical NPs were prepared with the method described by López-Cudero et al.,³¹ adapted from the synthesis of gold NPs. After their synthesis, the NPs were cleaned once with a 0.5 M sodium hydroxide solution and then washed and stored in ultrapure water. The NPs used in this work were taken from previously synthesized batches; for details on their characterization refer to their respective publications.^29–31 A representative transmission electron microscopy (TEM) image for each of the nanoparticles mentioned before is presented in Fig. S7.†

The solutions were prepared from 96% sulfuric acid and 70% perchloric acid (Merck Suprapur). For cleaning, all materials were first submerged in a 3 : 1 mixture of 96% sulfuric acid and 30% hydrogen peroxide and later rinsed with boiling ultrapure water (Milli-Q, 18.2 MΩ cm).

The procedure of the calorimetric measurements was described in detail, e.g. in ref. 27. In brief, the electrochemical reaction was driven by applying 10 ms potential pulses of 40 mV, 60 mV, 80 mV and 100 mV with negative and positive amplitudes from a constant rest potential. The temperature change of the electrode upon application of the potential pulse was measured by using a pyroelectric sensor. For each set of potential pulse measurements, the rest potential was changed step-wise by 25 mV between 0.1 and 0.35 V vs. RHE in one direction. After cleaning of the NPs, the direction was reversed. At the end of every experiment, the calorimeter was calibrated, using the established Peltier heat of the [Fe(CN)₆]³⁻/[Fe(CN)₆]⁴⁻ redox reaction in equimolar 0.1 M solution, which amounts to −45.1 kJ mol⁻¹.³² Additionally, the thermal response function of the setup was obtained by probing the cell with a 2 ms laser pulse to reconstruct the heat flux (for more details about the experimental setup c.f. (ref. 27) and about the experimental procedure c.f. (ref. 33)). In order to remove traces of contaminants from the NP surface, an electrochemical cleaning protocol was developed. Before every set of the aforementioned potential pulse measurements, the system was cycled between −0.05 and 0.75 V for around 5 min at 200 mV s⁻¹. The hydrogen produced at the surface at negative potentials helps in the reductive removal of surface contaminants. Subsequent oxidation ensures that there is no excess hydrogen in solution. The potential was kept below 0.75 V to avoid roughening of the NPs by surface oxidation.^34,35 To ensure that any excess hydrogen was removed from the cell, the potential was cycled for 3 additional minutes with the same upper limit but increasing the negative limit to 0.05 V. A detailed discussion of the cleaning procedure is given in the ESI,† where the effect of the cleaning procedure is demonstrated in Fig. S2.† The electrochemically active surface area of the NPs was determined from the charge of the under-potential deposition of hydrogen. We used a charge density of 230 μC cm⁻² after subtraction of the double layer charge, which was determined from the minimum current measured in the double-layer region of the voltammetric profiles and considered constant over the whole potential range.³⁶

3 Results and discussion

The typical voltammetric profiles of the spherical, cubic and octahedral NPs in 0.1 M sulfuric acid are presented in Fig. 1. All three cyclic voltammograms (CVs) coincide well with previously reported CVs for the respective NPs.³⁷ Note that the CVs were recorded in the O-Ring sealed EC cell of the calorimeter, where the features of voltammetric profiles in general appear less sharp in comparison with those obtained in glass cells with hanging meniscus configuration. Nevertheless, the profiles are not only reproducible but their characteristic peaks are in excellent agreement with the profiles published in the literature.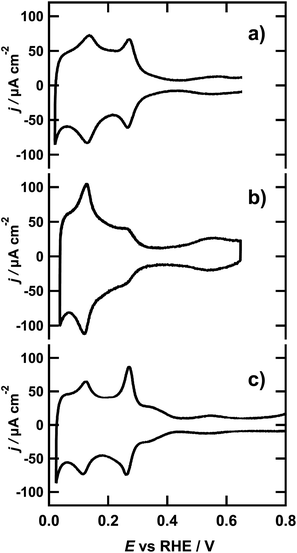

Fig. 1 Cyclic voltammograms of (a) spherical NPs, (b) octahedral NPs and (c) cubic NPs at a scan rate of 50 mV s⁻¹ in 0.1 M H₂SO₄.

As the spherical NPs do not have any preferential surface orientation and the number of low coordinated atoms with different geometric arrangements is high, the CV is a superposition of the different signals associated with the adsorption of hydrogen on the sites of every possible orientation. The resulting shape of the CV, as can be seen in Fig. 1a, is reminiscent of the classic voltammetric profile of the polycrystalline platinum electrode.³⁸ The voltammetric profile of the octahedral NPs seen in Fig. 1b is distinctively different and lacks the peak and wave around 0.27 V and 0.37 V respectively, which generally are assigned to hydrogen adsorption on {100} step sites (facets with local {100} orientation at the edges) and {100} terrace sites from the faces of the cube. However, these features are not completely absent in the voltammogram of Fig. 1b, since the octahedral nanoparticles contain a small proportion of truncated octahedrons that contain {100} terrace sites, although they are sufficiently small to be considered negligible in this case. The typical wave in the potential region below 0.30 V is associated with the adsorption of hydrogen on the {111} terraces. The peak at 0.1 V corresponds to the hydrogen adsorption on {110} steps and appears sharper than in Fig. 1a due to the well defined steps located on the edges of the octahedral geometry of the NPs.³⁹ This assignment is further corroborated by comparing the voltammetric profile to the CV of a Pt(554) single crystal in the same solution, presented in Fig. S3 of the ESI.† This CV exhibits a similar voltammetric profile to that of the octahedral NPs, stemming from adsorption on {111} terraces and {110} steps.⁷ In addition, there is a clear current wave between 0.4 and 0.65 V in the CVs of both octahedral NPs and Pt(554), which is associated with sulfate adsorption on {111} terraces.⁴⁰ The voltammetric profile of the cubic NPs, presented in Fig. 1c, is dominated by a prominent peak at 0.27 V, which is ascribed to the H-adsorption on {100} step sites. This, peak is even larger for cubic NPs than for octahedral and spherical ones. Moreover, the additional wave observed around 0.37 V signals the existence of extended, well-ordered {100} terraces, expected from the cubic shape of the nanoparticles.³⁰ Since the NPs where cast on a gold substrate, the Au surface might also contribute to the current in the CV and ultimately the microcalorimetric measurements. Therefore, we additionally measured the voltammetric response of the bare gold surface, which is presented in Fig. S4 of the ESI.† Considering that the current is at least 10 times lower than the smallest current measured in the presence of NPs, the influence of the gold surface on the CV is regarded as negligible. Similarly, we compared the evolved heat at the bare gold sample, with that of the NP loaded surface, resulting from the same polarization, in Fig. S5 of the ESI.† The heat resulting from the hydrogen adsorption on the NPs is at least 50 times higher than the heat resulting from polarization of the gold substrate, which is in line with the small current contribution of the Au surface to the CV of the NP covered Au. Hence, we are confident that the calorimetric response of the NP loaded sample in the investigated potential region can be assigned solely to hydrogen adsorption/desorption.

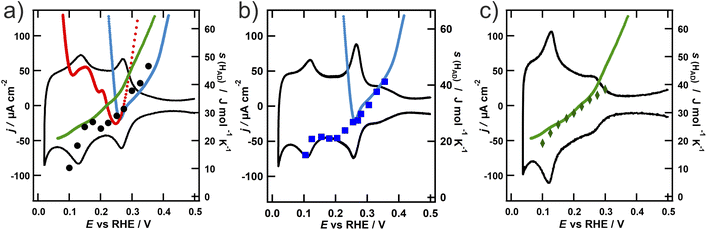
The results of the calorimetric measurements are shown in Fig. 2 together with the respective CV, to support the assignment of the entropy data to the respective voltammetric features. All of the calorimetric measurements are originally obtained as heat generated per unit of charge transferred, which is equivalent to a normalization of the heat generated per moles of hydrogen reacting. However, as explained in the Introduction, the calorimetric results of the hydrogen adsorption on the different NPs are more straightforwardly comprehensible and comparable in terms of the entropy of the adsorbed hydrogen. Therefore, we converted the reaction entropy, which we obtained from the calorimetric measurements, to the entropy of the adsorbed hydrogen s(H_ad), which is depicted in Fig. 2 (for details about this process c.f. the ESI†).

Fig. 2 (a) Entropy of the adsorbed hydrogen on (a) octahedral (green), (b) cubic (blue) and (c) spherical (black) platinum NPs from 0.1 M H₂SO₄. Additionally, the entropy of the adsorbed hydrogen adsorption derived by the ECE on Pt(111) (light green), Pt(100) (light blue) and Pt(110) (red) in 0.1 M HClO₄ is shown.

In Fig. 2, there are slight but important differences in the tendencies of s(H_ad) for each NP geometry: s(H_ad) on the octahedral NPs (Fig. 2a) presents mostly a monotonic decrease with decreasing potential, i.e., increasing hydrogen coverage. On the other hand, s(H_ad) on the cubic NPs (Fig. 2b) exhibits a stronger decrease between 0.35 and 0.25 V, followed by a plateau until 0.15 V, before it further decreases at potentials close to the onset of the hydrogen evolution reaction (HER). s(H_ad) on the spherical NPs (Fig. 2c) follows the same tendency as on the cubic ones, but with overall slightly higher values. In particular, in the region of the plateau between 0.25 and 0.15 V, s(H_ad) values are closer to the values of the octahedral NPs. A common feature of all NPs is a decrease of s(H_ad) at higher surface coverage, a trend that has also been observed in the aforementioned analysis of the hydrogen adsorption on platinum single crystals using the ECE.²¹ To allow for a comparison of s(H_ad) on the NPs with the results from Garcia-Araez et al., we added the entropy of the adsorbed hydrogen on the respective basal plane, based on the assignment of the voltammetric peaks, as a function of potential to Fig. 2. Note that the steep increase of s(H_ad) for Pt(110) and (100) at potentials below 0.1 V and 0.27 V is a consequence of the coverage reaching values close to θ → 1 on the respective single crystal surface. This behaviour is not observed on the NPs due to the existence of adsorption states at lower potentials. Another important aspect is that the ECE measurements were conducted in 0.1 M HClO₄, while for the measurements on the NPs presented in this contribution 0.1 M H₂SO₄ was used. As the standard entropy of adsorption of hydrogen on Pt(111) is not affected by the anion,⁴¹ this should not influence the obtained results. To verify this assumption, we conducted further microcalorimetric measurements using the octahedral NPs in perchloric acid. The obtained entropy of the adsorbed hydrogen depicted in Fig. S6 of the ESI† nicely coincides with the values obtained in sulfuric acid and therefore validates our comparison between the data from the ECE and ECM.

The magnitude of s(H_ad) obtained by both methods is in good agreement. The shape of the Pt(100) curve has a remarkable similarity to the curve obtained from cubic NPs in the potential region, where H adsorbs on the {100} terraces. At potentials down to 0.27 V, where the adsorption on the {100} step sites takes place, the entropy continues to decrease. This clearly indicates that the thermodynamic state of the hydrogen adsorbed on facets with a square {100} geometry of the cubic NPs is comparable to that of the adsorbed hydrogen on the {100} terraces of a single crystal. Although at first glance this result might look obvious, since analogous adsorption sites are occupied, our results show that neither the limited size of the faces nor the cubic geometry of the NPs plays a decisive role in the thermodynamic state of adsorbed species and that the local orientation has the strongest influence.

Furthermore, a similar trend of the entropy values obtained from the ECE on Pt(111) and those from ECM on the octahedral NPs can be observed. The biggest difference appears in the potential region below 0.15 V, where contributions from the {110} steps are expected. This is contradictory at first, as the adsorption entropy on the {110} single crystal surface displayed in Fig. 2c (red curve) is evidently higher at low potentials than the values for the other basal planes. However, the steps oriented along the {110} direction on Pt(111) feature a local hexagonal {111} geometry,⁴² which might explain why the adsorption entropy is closer to the value found from the ECE on {111} than on {110} single crystals. The spherical NPs exhibit contributions from all orientations, and thus the entropy of the adsorbed hydrogen is as expected from the voltammetric profile composed of contributions from all three basal planes.

Our results therefore show that the thermodynamic state of the hydrogen adsorbed on the NP facets is comparable to the hydrogen adsorbed on the corresponding single-crystal surfaces. We additionally observe that the entropy of the hydrogen adsorbed on the edges of a particle resembles that on a single crystalline surface with the corresponding local structure of the step edges.

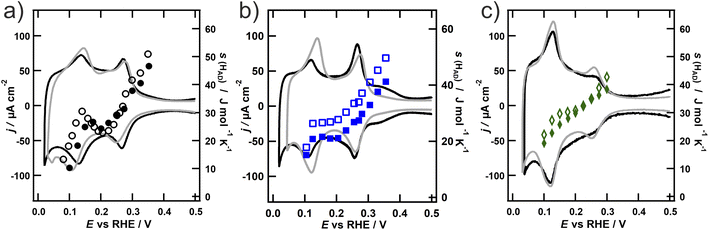
As mentioned in the Introduction, Pt NPs not only show promising electrocatalytic behaviour, but are also often used to increase the surface area and mass transport properties of catalysts.⁴³ Under intense reaction conditions however, the electrode surface might undergo significant changes,⁵ eventually leading to a loss of activity as shown e.g. for the oxygen reduction reaction on carbon supported Pt NPs.^44,45 It is therefore necessary to investigate surface changes of NPs under reactive conditions to understand possible degradation processes. Two main degradation processes proposed for Pt NPs are surface roughening and Pt dissolution. The latter one might also result in coarsening. Therefore, the NPs were subjected to surface roughening by cycling the potential between −0.05 V and 1.25 V for at least 100 cycles at a scan speed of 200 mV s⁻¹.

The entropy of the adsorbed hydrogen on the roughened NPs (open symbols) is depicted in Fig. 3 together with the entropy on the NPs prior to roughening (closed symbols) and the corresponding CVs in the hydrogen adsorption region after the roughening procedure of the particles (grey). It is apparent from Fig. 3 that the entropy generally increases upon roughening on all three NPs, although not in a similar fashion. The entropy on the spherical NPs increases strongly in the region below 0.2 V, but stays unaltered at more positive potentials. The entropy on the octahedral particles likewise increases in the region below 0.2 V, but also above 0.3 V. In contrast, the entropy on the cubic particles increases evenly in the whole potential region. The entropy values of all three particles are getting very close below 0.15 V. Concurrent with the entropy data, also the voltammetric peak in this potential region substantially grows upon roughening, while other features like the charge contribution from the adsorption of hydrogen on the {100} terraces of the cubic NPs or the sulfate adsorption on the {111} terraces vanish. This region is generally associated with the adsorption of hydrogen on {110} terraces and steps.⁷ Indeed, several studies investigating the roughening of Pt surfaces show that upon oxidation the contribution of {110} steps increases. These steps additionally undergo a step-edge roughening process upon increased cycling.^17,42,46 These newly formed adsorption sites are therefore not as well defined as regular step edges⁴² and therefore offer a different adsorption environment. The higher entropy of the adsorbed hydrogen observed after roughening in this potential region could therefore be explained by these adsorption sites, whose local geometry resembles that of the Pt(110) single crystal. It is apparent from Fig. 2a that in contrast to Pt(111) and Pt(100) the entropy on Pt(110) increases with the hydrogen coverage, even exceeding the values for the other two facets. However, this alone cannot explain the additionally observed increase of the entropy on the cubic and octahedral NPs at higher potentials. This additional change of s(H_ad) is concurrent with the potential regions, where the charge contribution from the terraces in the voltammetric response in Fig. 3a and b decreases, while the contribution from the steps increases (0.15–0.35 V for the cubic and 0.25–0.3 V for the octahedral NPs). This behaviour is line with thermodynamic studies of the standard entropy of electrochemically adsorbed hydrogen on two stepped platinum surfaces Pt(776) and Pt(544).²³ They found that the entropy of hydrogen on the terrace sites of the stepped surfaces is higher compared to the entropy of hydrogen on the theoretically infinite terrace of Pt(111).²¹ This would explain the increase of the entropy on the roughened faces of the particles. In addition, the standard entropy of electrochemically adsorbed hydrogen was found to be higher on steps than on terrace sites, which would explain the higher entropy in the potential regions attributed to adsorption on the steps.

Fig. 3 Cyclic voltammograms and entropy of the adsorbed hydrogen from 0.1 M H₂SO₄ on (a) octahedral (green), (b) cubic (blue) and (c) spherical (black) platinum NPs before (closed symbols/black) and after roughening (open symbols/grey); scan speed 50 mV s⁻¹.

To analyze the entropy of the adsorbed hydrogen we need to consider its degrees of freedom. For a single-atom adsorbate we have to consider 3 different contributions, namely from the in-plane translation s_trans, the out-of-plane vibration s_vib and from the configurations of different adsorbates on the limited area s_config. Conway et al.²⁶ and later Garcia-Araez et al.²¹ found the vibrational contributions to be negligible and thus combined the latter two contributions by considering the adsorbed hydrogen in between two extreme cases. In this model, the adsorbed hydrogen is either immobile and thus retains only the configurational entropy of an ideal lattice-gas or fully mobile and thereby resembles an ideal 2D-gas on a restricted surface. As the entropy of the mobile adlayer is generally higher, a higher entropy value implies a higher mobility in this model. With the hindered translator model Sprowl et al. introduced a possibility to calculate the transition between both cases, by calculating s_trans as a function of the diffusion barrier height.⁴⁷ In the case of a high diffusion barrier, the model reduces to the lattice gas and for a low diffusion barrier, the model corresponds to the ideal 2D-gas. Thus, this model can help to describe the adsorbed hydrogen between the above-mentioned limiting cases. Although diffusion barriers are scarcely reported in the literature and vary between different experimental approaches, the experimentally found diffusion barriers of H on Pt(111) (68 meV (ref. 48) to 157 meV (ref. 49)) are always lower than the theoretically calculated barrier of H on Pt(100) (200 meV (ref. 50)). Thus, the lower entropy on Pt(100) than on Pt(111) single crystals would indeed result from a lower mobility. Extrapolating the values in Fig. 6 of ref. 47 to the roughly 10 times lighter hydrogen showed that we expect this difference to be between 3 and 12 J mol⁻¹ K⁻¹ and thus in the order of magnitude of the observed difference. However, although the diffusion barrier is also dependent on the coverage,⁴⁹ the small change of 30 meV from θ = 0 to θ = 0.6 cannot account for the experimental change of s(H_ad) with coverage. The observed decrease is caused by s_config, which changes by at least 30 J mol⁻¹ K⁻¹ over the same coverage range. Unfortunately, values for the hydrogen diffusion barrier on rough surfaces necessary to evaluate the entropy changes introduced by the roughening of the surface are missing. However, for flat surfaces the diffusion barrier height scales with the adsorption energy.⁴⁷ As DFT studies of the hydrogen adsorption energy on stepped Pt surfaces^17,51,52 find generally lower adsorption energy on steps than on terraces, this could explain the higher entropy of the adsorbed hydrogen upon roughening. Another effect that could affect the entropy is the coarsening of the particles upon cycling. While the extent of coarsening in the recent experiments can hardly be estimated based on the voltammetric response alone, previous experiments by Arán-Ais et al. using Identical location-TEM (IL-TEM) indicated that the amount of area loss accounts to only around 11% after 1000 cycles from coalescence and Pt dissolution together.⁵³ In comparison, in the present contribution only between 100 and 200 roughening cycles were employed, upon which the particles even experienced a small surface area increase. Additionally, the IL-TEM experiments show how drastic the loss of faceted edges and the rounding of the corners is, already after 50 cycles.⁵³ We therefore expect the effect of the different adsorption sites to be the dominant contribution. Ultimately, contributions from possible contaminants, which might be removed by the oxidation procedures performed during the roughening,⁵⁴ but not by the employed hydrogen cleaning procedure, cannot be excluded completely (see the Experimental section). Since these contaminants would block surface sites, the mobility of the adsorbed hydrogen would decrease. This effect could cause the small decrease of the reaction entropy observed when discussing the cleaning procedure in Fig. S1 of the ESI.† However, from the discussion regarding the effectiveness of the employed cleaning procedure it is evident that the effect of contaminants on the selected data of the pristine NPs should be very small, definitely smaller than the effect seen upon roughening.

The sensitivity to distinguish minute modifications of the thermodynamic state of adsorbed hydrogen found in this contribution, implies that the ECM could help in understanding the HER, where adsorbed hydrogen is the key intermediate. The paramount importance of this reaction has led researchers to define different physicochemical attributes that allow predictions of the reaction kinetics, which are commonly called descriptors. A prime example is the use of the hydrogen binding energy (HBE)^55,56 to the metal surface as a descriptor, which changes with solution pH.⁵⁷ The argument follows Sabatier's principle and predicts an optimal HBE exhibiting the fastest kinetics, while a stronger or weaker interaction will result in a diminished catalytic activity. This argument is closely related to the entropy of the adsorbed intermediate, whose magnitude in this contribution was associated with its mobility and therefore the binding strength. The entropy of formation of the interface further provides information on the structure, order and composition of the interface,⁵⁸ properties which are closely related to other previously proposed descriptors like the interfacial water structure, the potential of zero charge or the potential of maximum entropy.^59–62 Nonetheless, assigning only one descriptor might oversimplify the real situation and the interplay between different descriptors must be understood to correctly predict catalytic behaviour.^63–67 As the ECM provides direct access to the thermodynamic state of species on the surface, the expansion of this research line to the reactivity of different NPs towards the HER or other reactions, with clearly distinguishable intermediate states, could lead to new insight into the surface dependence of these reactions. A prominent example would be ammonia oxidation⁶⁸ and nitrate reduction,⁶⁹ which have shown an enhanced catalytic response for {100} surface orientations and cubic NPs compared to the other surface orientations.

4 Conclusions

In this study, the entropy of hydrogen adsorption on different shape-controlled Pt nanoparticles was investigated using electrochemical microcalorimetry. We obtained results precise enough to detect the minute entropy differences from the adsorption on the differently faceted NPs. We could allocate the entropy of the adsorbed hydrogen to the corresponding particle geometry, by a comparison to results obtained from the temperature coefficient of the interfacial potential on Pt single crystals. This was the first time that these two methods were employed to a comparable electrochemical system, showing how both methods can complement each other. It further shows how shape-controlled nanoparticles can be used to study electrochemically analogous surfaces with techniques where single crystals are not applicable. We additionally investigated the hydrogen adsorption entropy on the NPs after roughening, representing a more realistic surface state for applications in electrocatalysis. After the roughening, a slight increase of the entropy was observed, which we attributed to an increased hydrogen mobility on step sites and edges, as well as to the adsorption on an increasing number of {110} steps. The presented results demonstrate the importance of a complete understanding of the adsorption environment of reaction intermediates, which can be drastically altered under reaction conditions. We think that by expanding the current study to catalytically relevant conditions, the ECM can provide further information on the thermodynamic state of reaction intermediates.

Author contributions

L. E. B. conceptualization, data curation, formal analysis, investigation, visualization, and writing – original draft; M. S. data curation, formal analysis, and methodology, investigation, visualization, and writing – original draft; J. S. G. resources, validation, visualization, and writing – review & editing; V. C. conceptualization, data curation, resources, supervision, validation, visualization, and writing – review & editing; J. M. F. resources, supervision, and writing – review & editing; R. S. methodology, resources, supervision, validation, and writing – review & editing.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

L. E. B., J. M. F and V. C. acknowledge Ministerio de Ciencia e Innovación (Spain) grant number PID2019-105653GB-I00. L. E. B. also acknowledges the Escuela de Doctorado of the Universidad de Alicante for the travel grant. M. S and R. S acknowledge funding from the Deutsche Forschungsgemeinschaft (SCHU 958/7-2). The authors thank Laurin Derr for participating in the early stages of this study.

Notes and references

1. B. Roldán Cuenya, Acc. Chem. Res., 2013, 46, 1682–1691.
2. I. Lee, F. Delbecq, R. Morales, M. A. Albiter and F. Zaera, Nat. Mater., 2009, 8, 132–138.
3. L. García-Cruz, V. Montiel and J. Solla-Gullón, Phys. Sci. Rev., 2019, 4, 20170124.
4. Y. Kang, P. Yang, N. M. Marković and V. R. Stamenkovic, Nano Today, 2016, 11, 587–600.
5. Y. Zhou, C. Jin, Y. Li and W. Shen, Nano Today, 2018, 20, 101–120.
6. M. T. M. Koper, Nanoscale, 2011, 3, 2054–2073.
7. Q.-S. Chen, F. J. Vidal-Iglesias, J. Solla-Gullón, S.-G. Sun and J. M. Feliu, Chem. Sci., 2012, 3, 136–147.
8. V. Climent and J. M. Feliu, J. Solid State Electrochem., 2011, 15, 1297–1315.
9. J. Clavilier, R. Faure, G. Guinet and R. Durand, J. Electroanal. Chem. Interfacial Electrochem., 1980, 107, 205–209.
10. N. García-Araez, V. Climent and J. M. Feliu, Interfacial Phenomena in Electrocatalysis, Springer, New York, NY, 2011, pp. 1–105.
11. N. M. Marković, T. J. Schmidt, B. N. Grgur, H. A. Gasteiger, R. J. Behm and P. N. Ross, J. Phys. Chem. B, 1999, 103, 8568–8577.
12. A. Zolfaghari and G. Jerkiewicz, J. Electroanal. Chem., 1999, 467, 177–185.
13. V. Climent, R. Gómez, J. M. Orts, A. Rodes, A. Aldaz and J. M. Feliu, Interfacial Electrochemistry, CRC Press, Boca Raton and London and New York, 1999, pp. 463–476.
14. V. Komanicky, K. C. Chang, A. Menzel, N. M. Markovic, H. You, X. Wang and D. Myers, J. Electrochem. Soc., 2006, 153, B446.
15. V. Briega-Martos, A. Ferre-Vilaplana, E. Herrero and J. M. Feliu, Electrochim. Acta, 2020, 354, 136620.
16. A. Ferre-Vilaplana, R. Gisbert and E. Herrero, Electrochim. Acta, 2014, 125, 666–673.
17. I. T. McCrum, C. J. Bondue and M. T. M. Koper, J. Phys. Chem. Lett., 2019, 10, 6842–6849.
18. V. Climent and J. Feliu, Annu. Rev. Anal. Chem., 2020, 13, 201–222.
19. N. García-Araez, V. Climent and J. M. Feliu, J. Solid State Electrochem., 2008, 12, 387–398.
20. N. García-Araez, V. Climent and J. M. Feliu, J. Phys. Chem. C, 2009, 113, 19913–19925.
21. N. García-Araez, V. Climent and J. M. Feliu, J. Electroanal. Chem., 2010, 649, 69–82.
22. N. García-Araez, J. Phys. Chem. C, 2011, 115, 501–510.
23. A. M. Gómez-Marín and J. M. Feliu, Surf. Sci., 2016, 646, 269–281.
24. J. A. Harrison, J. E. B. Randles and D. J. Schiffrin, J. Electroanal. Chem. Interfacial Electrochem., 1973, 48, 359–381.
25. R. Schuster, Curr. Opin. Electrochem., 2017, 1, 88–94.
26. B. E. Conway, H. Angerstein-Kozlowska and W. B. A. Sharp, J. Chem. Soc., Faraday Trans. 1, 1978, 74, 1373–1389.
27. S. Frittmann, V. Halka, C. Jaramillo and R. Schuster, Rev. Sci. Instrum., 2015, 86, 064102.
28. M. J. Vasile and C. G. Enke, J. Electrochem. Soc., 1965, 112, 865.
29. M. Moglianetti, J. Solla-Gullón, P. Donati, D. Pedone, D. Debellis, T. Sibillano, R. Brescia, C. Giannini, V. Montiel, J. M. Feliu and P. P. Pompa, ACS Appl. Mater. Interfaces, 2018, 10, 41608–41617.
30. R. M. Arán-Ais, F. J. Vidal-Iglesias, J. Solla-Gullón, E. Herrero and J. M. Feliu, Electroanalysis, 2015, 27, 945–956.
31. A. López-Cudero, J. Solla-Gullón, E. Herrero, A. Aldaz and J. M. Feliu, J. Electroanal. Chem., 2010, 644, 117–126.
32. P. Boudeville, Inorg. Chim. Acta, 1994, 226, 69–78.
33. K. R. Bickel, K. D. Etzel, V. Halka and R. Schuster, Electrochim. Acta, 2013, 112, 801–812.
34. J. Clavilier, D. Armand and B. L. Wu, J. Electroanal. Chem. Interfacial Electrochem., 1982, 135, 159–166.
35. S. Motoo and N. Furuya, J. Electroanal. Chem. Interfacial Electrochem., 1984, 172, 339–358.
36. Q.-S. Chen, J. Solla-Gullón, S.-G. Sun and J. M. Feliu, Electrochim. Acta, 2010, 55, 7982–7994.
37. F. J. Vidal-Iglesias, R. M. Arán-Ais, J. Solla-Gullón, E. Herrero and J. M. Feliu, ACS Catal., 2012, 2, 901–910.
38. M. W. Bretter, J. Electroanal. Chem., 1964, 8, 230–236.
39. J. Solla-Gullón, P. Rodríguez, E. Herrero, A. Aldaz and J. M. Feliu, Phys. Chem. Chem. Phys., 2008, 10, 1359–1373.
40. J. M. Feliu, J. M. Orts, R. Gómez, A. Aldaz and J. Clavilier, J. Electroanal. Chem., 1994, 372, 265–268.
41. N. García-Araez, V. Climent and J. M. Feliu, Russ. J. Electrochem., 2012, 48, 271–280.
42. L. Jacobse, Y.-F. Huang, M. T. M. Koper and M. J. Rost, Nat. Mater., 2018, 17, 277–282.
43. E. Roduner, Chem. Soc. Rev., 2006, 35, 583–592.
44. L. Braunwarth, C. Jung and T. Jacob, Top. Catal., 2020, 63, 1647–1657.
45. Y. Shao-Horn, W. C. Sheng, S. Chen, P. J. Ferreira, E. F. Holby and D. Morgan, Top. Catal., 2007, 46, 285–305.
46. M. Wakisaka, S. Asizawa, H. Uchida and M. Watanabe, Phys. Chem. Chem. Phys., 2010, 12, 4184–4190.
47. L. H. Sprowl, C. T. Campbell and L. Árnadóttir, J. Phys. Chem. C, 2016, 120, 9719–9731.
48. A. P. Graham, A. Menzel and J. P. Toennies, J. Chem. Phys., 1999, 111, 1676–1685.
49. C. Z. Zheng, C. K. Yeung, M. M. T. Loy and X. Xiao, Phys. Rev. B: Condens. Matter Mater. Phys., 2004, 70, 205402.
50. E. d. V. Gómez, S. Amaya-Roncancio, L. B. Avalle, D. H. Linares and M. C. Gimenez, Appl. Surf. Sci., 2017, 420, 1–8.
51. I. T. McCrum and M. J. Janik, ChemElectroChem, 2016, 3, 1609–1617.
52. M. J. Kolb, A. L. Garden, C. Badan, J. A. Garrido Torres, E. Skúlason, L. B. F. Juurlink, H. Jónsson and M. T. M. Koper, Phys. Chem. Chem. Phys., 2019, 21, 17142–17151.
53. R. M. Arán-Ais, Y. Yu, R. Hovden, J. Solla-Gullón, E. Herrero, J. M. Feliu and H. D. Abruña, J. Am. Chem. Soc., 2015, 137, 14992–14998.
54. B. E. Conway, H. Angerstein-Kozlowska, W. B. A. Sharp and E. E. Criddle, Anal. Chem., 1973, 45, 1331–1336.
55. J. Zheng, W. Sheng, Z. Zhuang, B. Xu and Y. Yan, Sci. Adv., 2016, 2, e1501602.
56. J. Zheng, J. Nash, B. Xu and Y. Yan, J. Electrochem. Soc., 2018, 165, H27–H29.
57. S. A. Giles, J. C. Wilson, J. Nash, B. Xu, D. G. Vlachos and Y. Yan, J. Catal., 2018, 367, 328–331.
58. M. Schönig and R. Schuster, Phys. Chem. Chem. Phys., 2023, 25, 5948–5954.
59. I. Ledezma-Yanez, W. D. Z. Wallace, P. Sebastián-Pascual, V. Climent, J. M. Feliu and M. T. M. Koper, Nat. Energy, 2017, 2, 17031.
60. A. Auer, F. J. Sarabia, D. Winkler, C. Griesser, V. Climent, J. M. Feliu and J. Kunze-Liebhäuser, ACS Catal., 2021, 11, 10324–10332.
61. X. Ding, B. Garlyyev, S. A. Watzele, T. Kobina Sarpey and A. S. Bandarenka, Chem. – Eur. J., 2021, 27, 10016–10020.
62. B. Huang, R. R. Rao, S. You, K. Hpone Myint, Y. Song, Y. Wang, W. Ding, L. Giordano, Y. Zhang, T. Wang, S. Muy, Y. Katayama, J. C. Grossman, A. P. Willard, K. Xu, Y. Jiang and Y. Shao-Horn, JACS Au, 2021, 1, 1674–1687.
63. Y. Cong, B. Yi and Y. Song, Nano Energy, 2018, 44, 288–303.
64. L. Rebollar, S. Intikhab, N. J. Oliveira, Y. Yan, B. Xu, I. T. McCrum, J. D. Snyder and M. H. Tang, ACS Catal., 2020, 10, 14747–14762.
65. L. Rebollar, S. Intikhab, S. Zhang, H. Deng, Z. Zeng, J. D. Snyder and M. H. Tang, J. Catal., 2021, 398, 161–170.
66. A. R. Zeradjanin, G. Polymeros, C. Toparli, M. Ledendecker, N. Hodnik, A. Erbe, M. Rohwerder and F. La Mantia, Phys. Chem. Chem. Phys., 2020, 22, 8768–8780.
67. E. Santos, Curr. Opin. Electrochem., 2023, 37, 101194.
68. F. J. Vidal-Iglesias, J. Solla-Gullón, P. Rodríguez, E. Herrero, V. Montiel, J. M. Feliu and A. Aldaz, Electrochem. Commun., 2004, 6, 1080–1084.
69. M. C. Figueiredo, J. Solla-Gullón, F. J. Vidal-Iglesias, V. Climent and J. M. Feliu, Catal. Today, 2013, 202, 2–11.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta04937j

---