Open Access Article
Open Access ArticleThermo-mechanical characterization and stress engineering of Lipon solid electrolyte†
Truong
Cai
 a,
Andrew
Westover
b,
Sergiy
Kalnaus
b,
Christos E.
Athanasiou
ac,
Nancy
Dudney
b and
Brian W.
Sheldon
a,
Andrew
Westover
b,
Sergiy
Kalnaus
b,
Christos E.
Athanasiou
ac,
Nancy
Dudney
b and
Brian W.
Sheldon
 *a
*a
aSchool of Engineering, Brown University, 182 Hope Street, Providence, RI 02912, USA. E-mail: brian_sheldon@brown.edu
bEnergy Storage Group, Oak Ridge National Lab, TN 37831-6069, USA
cDaniel Guggenheim School of Aerospace Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
First published on 9th January 2024
Abstract
A high temperature multibeam-optical-stress sensor (HTMOSS) was used to characterize the coefficient of thermal expansion (CTE) and yield stress of 1-micron thick Lipon films. Fully dense, amorphous films were deposited on glass and sapphire substrates. The films were then annealed at temperatures ranging from 80 to 200 °C for 3 hours. The CTE of Lipon is found to be approximately 4.1 × 10−6. This value did not vary appreciably with the substrate type, and was similar in tension and compression. With this intermediate CTE value, the films heated on the two different substrates imposed either tension or compression due to the thermal expansion mismatch. We observed further that the yield stress of the film is approximately 60–100 MPa. Using constant-load holds at and beyond the yield point, the stress developed during heating was relaxed via visco-plastic deformation. A permanent residual stress then evolved during cooling, up to 120 MPa in either tension or compression depending on substrate type. This ability to engineer stress into Lipon films also suggests a strategy for creating a protective layer on other solid electrolytes with higher ionic conductivities (e.g., LLZO and sulfides), which is a potentially effective approach for mitigating lithium dendrite penetration. In addition, Lipon lost ductility at an annealing temperature above 140 °C. Thismay be associated with composition changes that were observed in XPS measurements.
1 Introduction
Solid electrolytes (SEs) are attracting increased attention for next generation batteries, primarily because they promote battery safety,1,2 operate over wide temperature and electrochemical stability ranges, and can potentially provide improved energy density by enabling lithium metal anodes.1–3 The relatively high modulus of ceramic and glass electrolytes can mechanically stabilize the interface with Li metal,4–8 however, short circuits due to lithium filament propagation at sufficiently high current densities are a critical problem.3,9–13As one of the most successful SEs, Lipon has enabled an all-solid-state thin film battery with a lithium metal anode and a high-voltage LiNi0.5Mn1.5O4 (LNMO) cathode to achieve capacity retention of 90% over 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 cycles.14 An extremely stable interface between Lipon and electrode materials is one reason for its superior electrochemical performance. Because Lipon is vapor deposited, these interfaces are also relatively homogeneous (i.e., smooth and chemically uniform, with minimal defects). This generally mitigates crack formation,11,15 and recent evidence also indicates that Lipon has high fracture resistance.14 The current investigation explores mechanical behavior in Lipon more broadly, by monitoring thermally induced stresses during heating and cooling on two different substrates. These treatments create residual tensile and compressive stress of 100 to 200 MPa in the Lipon films, and these measurements also provide values for the Lipon CTE. This work also provides information about plasticity, a potentially valuable mechanism for effective local stress relief during fracture. Recent work also suggests that plastic deformation of glass SEs can occur upon contact with pressurized lithium filaments, and thus mitigate dendrite propagation.6,15,16
000 cycles.14 An extremely stable interface between Lipon and electrode materials is one reason for its superior electrochemical performance. Because Lipon is vapor deposited, these interfaces are also relatively homogeneous (i.e., smooth and chemically uniform, with minimal defects). This generally mitigates crack formation,11,15 and recent evidence also indicates that Lipon has high fracture resistance.14 The current investigation explores mechanical behavior in Lipon more broadly, by monitoring thermally induced stresses during heating and cooling on two different substrates. These treatments create residual tensile and compressive stress of 100 to 200 MPa in the Lipon films, and these measurements also provide values for the Lipon CTE. This work also provides information about plasticity, a potentially valuable mechanism for effective local stress relief during fracture. Recent work also suggests that plastic deformation of glass SEs can occur upon contact with pressurized lithium filaments, and thus mitigate dendrite propagation.6,15,16
The experiments reported here demonstrate that thermal treatments can be used to engineer residual stresses of 100's of MPa into Lipon, as a means for controlling and potentially improving its performance. In particular, compressive stresses will generally improve fracture resistance, and recent work also indicates that these stresses can impede Li metal dendrites. For example, modeling and experiments with Li7La3Zr2O12 (LLZO)13,17,18 indicate that compressive residual stresses on the order of 100 MPa are large enough to deflect dendrite propagation, and can thus be employed to mitigate the resulting short circuits. In principal, our approach to engineering residual stresses can also be extended to enhance the performance of other solid electrolytes.
2 Experimental
2.1 Materials
Lipon samples were prepared by radio frequency magnetron sputtering of a 2-inch diameter ceramic target, with film deposition on a polished sapphire wafer facing the target at a distance of 6 cm. The chamber base pressure was 0.3 μT; deposition was conducted at a N2 flow rate of 40 sccm, a deposition pressure of 20 mT, a power of 75 W and a bias of 136 V. The deposition rate was 2.5 nm m−1. The films for the substrate curvature measurements were approximately 1 μm thick, and the films for nanoindentation were ≈8 μm thick after a long deposition. The substrate materials were used to deposit upon were highly pure fused quartz glass (350 μm thickness, from University Wafer) and sapphire disc-shape substrate (350 μm thickness, from Semiconductor Wafer). Both of these materials were tested in the as-received condition. From previous works,47 the average roughness of the film was no more than 10 nm. More details about roughness characterization are provided in the ESI.†2.2 Curvature measurement
High-temperature Multi-beam Optical Sensor (HTMOS) measurements were conducted in a custom-made furnace that permits optical access.48 This technique measures wafer curvature changes during thermal treatment, by monitoring the spacing between reflected laser beams.21,27,482.3 Post-mortem imaging
After the experiment, the surface was examined with Scanning Electron Microscopy (SEM) (FEI HELIOS 600). X-ray photoelectron spectrometer (XPS) was performed (K-Alpha, Thermo Scientific) to obtain chemical information of the surface and subsurface. XPS spectra were collected using a monochromatized Al Kα radiation (hy = 1486.7 eV) under a base pressure of 10−9 torr. All XPS measurements were collected with a 400 μm spot size. Survey scans used a pass energy of 50 eV, followed by a high-resolution scan with 0.1 eV resolution, for Li 1s, O 1s, N 1s, and P 2p regions. A 5 keV Ar plasma etching source was used for depth profiling with a pre-etching for 5 s, etching for 60 s and post-etching for 10 s. All spectra were calibrated with adventitious carbon 1s (284.6 eV) and analyzed by CasaXPS software. All the handling materials and the polyacetal surface were cleaned with analytical grade isopropanol and rubbed dry with clean paper before contact with the host material.2.4 Data analysis
Raw data were collected and stored in CSV or Excel file formats. Data processing was done using the custom-made MATLAB script. For fitting of the CTE, a RANSAC49 algorithm was used to prevent adverse effects of outliers.2.5 Nanoindentation
Nanoindentation of Lipon films was performed using the InForce 1000 actuator from NanoMechanics Inc (KLA Instruments), which has 1 N maximum load and 6 nN nominal load resolution. The actuator, attached to the frame, was installed inside the Tescan Mira 3 SEM, and the shallow tilt was applied to the stage to allow in situ observation of the surface approach and nanoindentation process. The Lipon samples were indented in as-deposited condition, and after the heat treatment. The latter was performed under flowing Ar and consisted of a heating ramp at a rate of 1 °C![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min−1 from room temperature to 170 °C, hold at 170 °C for 8 hours, and a cooling ramp at approximately the same rate of 1 °C
min−1 from room temperature to 170 °C, hold at 170 °C for 8 hours, and a cooling ramp at approximately the same rate of 1 °C ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) min−1. The nanoindentation was performed using Berkovich (65.27° angle) nanoindenter tip. The experiments were performed in continuous stiffness measurement mode19 which allows collecting modulus and hardness data as a function of nanoindentation depth. Standard instrument calibration19 was performed using a fused silica sample before the experiments. 16 nanoindentations were performed for calibration and tip area function fit. In addition, nanoindentation with the sharp cube corner (35.26° angle) was performed to estimate resistance to crack formation in as-deposited Lipon. A matrix containing 25 nanoindentations was applied to each sample to estimate the scatter of data. The indentations were placed 40 μm apart in the matrix. The thermal drift was measured before each experiment and, in addition, a small constant load hold (one-tenth of the maximum load) was applied in the unloading segment to check for thermal drift. The target thermal drift value was 0.1 nm s−1. All of the experiments were done at the nominal strain rate of 0.2 s−1.
min−1. The nanoindentation was performed using Berkovich (65.27° angle) nanoindenter tip. The experiments were performed in continuous stiffness measurement mode19 which allows collecting modulus and hardness data as a function of nanoindentation depth. Standard instrument calibration19 was performed using a fused silica sample before the experiments. 16 nanoindentations were performed for calibration and tip area function fit. In addition, nanoindentation with the sharp cube corner (35.26° angle) was performed to estimate resistance to crack formation in as-deposited Lipon. A matrix containing 25 nanoindentations was applied to each sample to estimate the scatter of data. The indentations were placed 40 μm apart in the matrix. The thermal drift was measured before each experiment and, in addition, a small constant load hold (one-tenth of the maximum load) was applied in the unloading segment to check for thermal drift. The target thermal drift value was 0.1 nm s−1. All of the experiments were done at the nominal strain rate of 0.2 s−1.
3 Results and discussion
3.1 Observation of visco-plasticity and stress relaxation under constant load
Lipon films were deposited on one face of either a quartz glass or sapphire substrate. The film deposition and measurement techniques are described in the Methods section and in previous work.20–26 The film thickness (1 micron) is more than two orders of magnitude thinner than the substrates that were used, and thus it is reasonable to assume that only in-plane bi-axial stress is present.27–29 The measured curvatures obtained in situ during heating and cooling are then interpreted with the Stoney equation27–29 to obtain spatially averaged bi-axial stress values: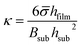 | (1) |
The film thickness is assumed to be approximately constant throughout the experiments.27–29
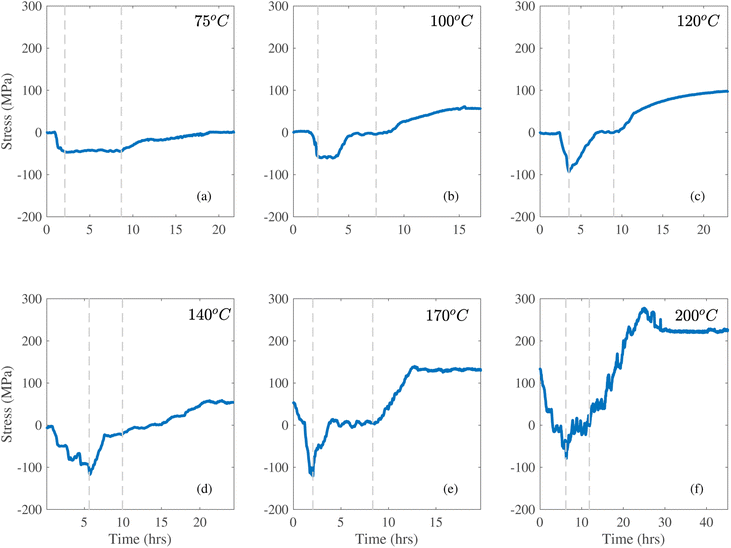
Fig. 1a–c shows results for three samples subjected to heat treatments where the temperature was raised at a fixed rate to a set temperature and subsequently held for approximately four hours. Because the quartz glass CTE is very small, the substrate imposed a compressive membrane force on these films during heating. In Fig. 1a, the initial and final stress values are very small (close to zero). This similarity indicates that the thermal stress is fully reversible. During the hold at 75 °C, the constant stress of −40 MPa indicates that there was no inelastic mechanism in the film capable of relieving the stress. In contrast, during the 100 °C hold in Fig. 1b, the stress remains constant at about −60 MPa for approximately 1.5 hours, and then gradually relaxes to zero. This can be attributed to plastic flow in the Lipon, which has also been observed during nanoindentation at ambient temperature.14,30 In addition, when the temperature is subsequently decreased, Fig. 1b shows that there is a net residual stress of 60 MPa at the end of the cool-down. This indicates that the thermal mismatch stress imposes net tension in the film, and demonstrates that there is permanent deformation in the Lipon structure. When the hold temperature is increased to 120 °C, the film relaxes the thermal stress immediately upon reaching this temperature, and exhibits a sharp yield point of approximately −90 MPa. In this case the stress remains zero until the end of the high temperature hold segment, Fig. 1c. This suggests that the relaxation behavior is load dependent, which is characteristic of visco-plasticity.6,27 Similar to the 100 °C sample, upon cooling the thermal mismatch stress imposes residual tension on the film.
Fig. 1d–f shows results at higher holding temperatures of 140, 170, and 200 °C, respectively. By using one sample to perform this series of three experiments, it was possible to determine if multiple steps can be used to impose additional stress. In Fig. 1d, note that before raising the temperature to 140 °C the sample was held at 75 °C for one hour, resulting in approximately −50 MPa. This approach provided better temperature control during relatively fast heating to the target temperature of 140 °C (i.e., at 1.5 °C min−1). We note further that there's significant noisy features in the stress profile during the heating. This is due to the temperature control of this experiment. In the supplementary section Fig. S1,† we overlay the stress and temperature profile to illustrate our stress variation corresponds well with the temperature variation. This indicates that such noisy features are not experimental artifacts. In this experiment the stress starts to relax at about 90 MPa during heating, which is consistent with the observation in Fig. 1c. Because the temperature is still changing here, the stress relaxation is quickly altered by additional thermal mismatch strains, such that compressive stress builds up in the film. Upon reaching 140 °C, the compressive stress of about −110 MPa relaxes immediately. However, even after 4 hours at temperature, the stress does not fully relax to the zero stress seen in the previous experiments. Instead, it remains in compression at approximately −25 MPa, which suggests that the plastic relaxation is limited. This could be due to composition or structural changes that occur at higher temperature, based on additional observations which are described below. Upon cooling, the thermal mismatch imposes approximately 80 MPa of tensile residual stress. This lower value of residual stress in comparison with Fig. 1c is consistent with the incomplete relaxation during the constant load hold.
In Fig. 1e, the initial stress is approximately 80 MPa, which is the final state observed in Fig. 1d. During heating there are two slopes for the heating curve, because the sample was first heated at 1 °C min−1 and then at 2 °C min−1. Curiously, at about −90 MPa, we no longer observe the immediate yielding behaviors. This suggests that the previous plastic flow expanded the yield surface, consistent with classical plasticity theory.31 Upon reaching 170 °C, about −110 MPa, the film exhibits immediate relaxation and reaches a stress-free state. This load-dependent and history-dependent behavior further affirms that the behavior is visco-plastic.31,32 After complete stress relaxation, cooling leads to residual stress of approximately 140 MPa (tensile).
To further investigate the inelastic behavior of Lipon and to further increase residual stress in the film, the holding temperature was raised to 200 °C, Fig. 1f. Note that before reaching 200 °C, the sample was held for 1 hour at 100 °C and 140 °C which is reflected by the two plateaus during the heating portion at 50 MPa and −20 MPa, respectively. During these two holds the stress is below the yield point and thus there was no relaxation. This is perhaps due to the fact that the sample relaxes the residual stress imposed by the previous trial, so it is not under any net compression. We note that during this relaxation plastic deformation is not expected because yielding from the previous cycle extends the elastic regime beyond the initial yield point.31 When the sample reaches approximately −80 MPa at 200 °C, relaxation occurs, but the behavior is rather erratic and incomplete (stress fully relaxes like Fig. 1c–e). Upon cooling the thermal mismatch stress is highly non-linear. This suggests that the material may undergo phase and composition changes via reaction with the ambient trace nitrogen, oxygen, and water vapor, which is consistent with previous observations15,33. This incomplete relaxation is also consistent with our observation of crackings (Fig. 5 and 6b) at 170 °C. This suggests that at much higher temperature than 170 °C, the film would show significant crackings. Because our method tracks the average stress-thickness through samples' curvature variation, and thus incapable to fully determine the stress-state at 200 °C where significant fracture happens.
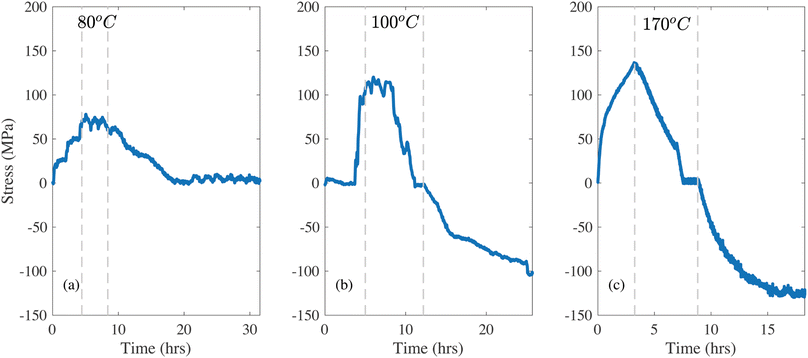
For Lipon films deposited on sapphire, the high CTE of the substrate (∼6.3 × 10−6 K−1)34 imposes compressive residual strains during cooling. This is seen in the in situ stress measurements in Fig. 2, where a separate sample was used for each thermal cycling procedure. The overall behavior is similar to that observed in the films deposited on quartz substrates, where the heating ramp now induces tension in the Lipon. In Fig. 2a the stress level remains constant at 60 MPa when the sample is held at 80 °C. Upon cooling, the sample returns to the initial stress state (close to 0 MPa), which indicates that the yield stress in tension is higher than 60 MPa. When the sample is subjected to a 100 °C hold, Fig. 2b, the tensile stress relaxes (similar to the behavior observed with the quartz substrate, where compressive stress relaxes at this temperature). With tensile stress of approximately 100 MPa, the stress again does not relax immediately. This only occurs after approximately 1 hour, and here again it eventually reaches a stress-free state. Upon cooling, the thermal mismatch led to approximately −100 MPa of residual stress. To further investigate this effect, the hold temperature was increased to 170 °C as shown in Fig. 2c. The hold at 170 °C imposes a maximum tensile stress of approximately 145 MPa, and here the stress relaxation starts immediately upon reaching the maximum temperature. Similarly to the quartz case, the plastic flow leads to the imposed tension of the film completely relaxed. Upon cooling the film reaches about 140 MPa of residual compression.
3.2 The values of the coefficients of thermal expansion and yield stress
As discussed in great detail in the previous section, Lipon exhibits visco-plastic behavior which makes the yield surface temperature and rate dependent6,15,31. Therefore, a single yield stress value is not enough to capture the entire inelastic behavior of this material. The complete characterization of the yield surface is beyond the scope of this study. However from the experimental observations reported here, it is reasonable to state that the yield stress is approximately 60–100 MPa under conditions that do not introduce significant composition changes.In our experiments only the heating is controlled at fixed rate, so the heating profile is linear while the cooling profile is non-linear.35 Nevertheless, the thermal mismatch stress from both parts of the cycle can be computed as:
| σ = Bfilm(αsub − αfilm)ΔT | (2) |
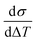 will give an estimate for the αfilm. The results for the quartz-substrate and sapphire-substrate samples are summarized in Tables 1 and 2. The CTE values reported for both substrates across the temperature range studied here are generally consistent. Furthermore, for lower temperature, below about 120 °C the CTE values computed from the heating curve and the cooling curve are also consistent. From this we estimate that the intrinsic CTE for these samples are about 4.1 × 10−6. We note that consistent with the drastic changes in mechanical response of the film, the CTE values at higher processing temperature deviate significantly versus the lower temperature ones (5 × 10−6vs. 4.1 × 10−6 for quartz and 4.7 × 10−6vs. 4.1 × 10−6). Notably there is also a discrepancy between the values estimated by fitting the heating and cooling portion of the data at higher temperature for the quartz-substrate sample. This further indicates that at higher processing temperature, the film changes its composition which affects its thermo-mechanical properties.
will give an estimate for the αfilm. The results for the quartz-substrate and sapphire-substrate samples are summarized in Tables 1 and 2. The CTE values reported for both substrates across the temperature range studied here are generally consistent. Furthermore, for lower temperature, below about 120 °C the CTE values computed from the heating curve and the cooling curve are also consistent. From this we estimate that the intrinsic CTE for these samples are about 4.1 × 10−6. We note that consistent with the drastic changes in mechanical response of the film, the CTE values at higher processing temperature deviate significantly versus the lower temperature ones (5 × 10−6vs. 4.1 × 10−6 for quartz and 4.7 × 10−6vs. 4.1 × 10−6). Notably there is also a discrepancy between the values estimated by fitting the heating and cooling portion of the data at higher temperature for the quartz-substrate sample. This further indicates that at higher processing temperature, the film changes its composition which affects its thermo-mechanical properties.
| Hold temp. (°C) | Linear fit heating | Linear fit cooling |
|---|---|---|
| 75 | 4.0 × 10−6 | 4.1 × 10−6 |
| 100 | 4.1 × 10−6 | 4.1 × 10−6 |
| 120 | 4.1 × 10−6 | 4.2 × 10−6 |
| 140 | 5.0 × 10−6 | 4.9 × 10−6 |
| 170 | 5.0 × 10−6 | 4.0 × 10−6 |
| Hold temp. (°C) | Linear fit heating | Linear fit cooling |
|---|---|---|
| 80 | 4.1 × 10−6 | 4.2 × 10−6 |
| 100 | 4.0 × 10−6 | 4.1 × 10−6 |
| 170 | 4.7 × 10−6 | 4.7 × 10−6 |
3.3 Mechanical behavior of Lipon examined by nanoindentation
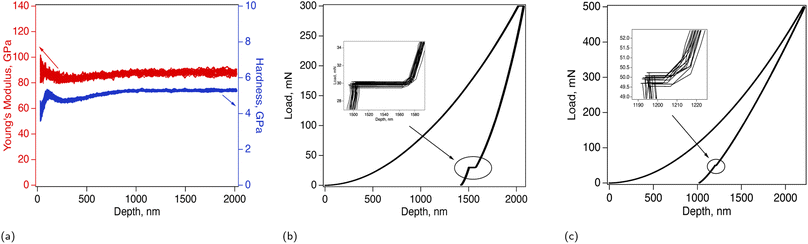
Nanoindentation was performed to obtain the elastic properties of these films and to further explore the creep and strain relaxation behavior of Lipon at the nanoscale. The results for Lipon in the as-deposited condition, together with the load-depth curves collected from the calibration of fused silica sample, are presented in Fig. 3. High consistency of the data indicates that the material is homogeneous. This is observed in Fig. 3a and b where the load-depth curves from twenty five nanoindentations overlap each other. Fig. 3a shows the modulus and hardness as functions of the nanoindentation depth, as obtained from the continuous stiffness measurement experiments at room temperature (see Methodology section for details). Some fluctuations at shallow depths less than 200 nm are observed, but the mechanical properties become consistent as indentation progresses, with a small increase in the property values with increasing indentation depth. We do not expect this to be a substrate effect, since the Lipon deposited for nanoindentation was ≈8 μm thick and the maximum indentation depth was 2 μm. Such stiffening and hardening could rather be a manifestation of continuous densification of Lipon in response to the hydrostatic pressure under the nanoindenter tip. The average value of the Young's modulus determined from the nanoindentation depths greater than 500 nm was 85 ± 0.9 GPa, and the corresponding value of hardness was 4.968 ± 0.039 GPa. It's important to note these values is quite stable after indentation depth of 700 nm up to 2000 nm. According to classical indentation models,37–39 this observation implies that the substrate effect is not too prominent. Moreover it should be mentioned, that these values are only slightly higher than previous reports.14,30The nanoindentation experiments were conducted with a ε = 0.2 s−1 constant strain rate loading period to the maximum load, ten-second hold at the maximum load level, unloading to ten percent of the maximum load, and finally an eighty-second hold at that minimum load before the final unload and tip withdrawal. The hold at the peak load provides evidence of creep behavior, while the hold at the Pmin = 0.1Pmax is designed to estimate thermal drift in comparison to that measured at the beginning of the experiment. As can be seen from Fig. 3b, Lipon shows evidence of time-dependent behavior, manifested by creep under constant maximum load, as well as strain relaxation under minimum load hold. This is especially evident in comparison with the nanoindentation curve from fused silica, Fig. 3c. The values of the thermal drift, measured before the nanoindentation were between 0.02 nm s−1 and 0.08 nm s−1, and the displacements collected during the 80 s hold in fused silica are within the range of anticipated total displacements at such drift rate and as such can be attributed almost entirely to thermal drift. The displacements in Lipon, both positive, due to creep, and negative, due to strain relaxation, are much larger. Calculated over the 80 second hold at Pmin, the displacement rate is on average 0.82 nm s−1, which is an order of magnitude greater than the thermal drift rate measured before the experiment. Therefore, this behavior is predominantly driven by a strain relaxation, rather than thermal drift.
The mechanical behavior of Lipon, described above suggests a combination of time-dependent behavior (creep and relaxation) with pressure-dependent yielding, characteristic of cohesion-friction materials. The applicability of the corresponding traditional plasticity models based on the deviatoric stress space to such materials remains an open question. It should be mentioned, that while the dependence of elastic properties (modulus and Poisson's ratio) on glass network connectivity has been reported, the investigations of yield and post-yield behavior in ionic glasses are lacking. It is reasonable to assume, that the traditional elasto-plastic and viscoplastic models are not applicable to glassy materials due to the ability of the latter to densify under pressure. Drucker-Prager type models account well for the hydrostatic pressure dependent yielding, as they are designed for cohesive-friction materials, but they do not incorporate time- and rate-dependent processes, such as creep or stress relaxation. Determination of yield point in glass is thus rather elusive as there is no dislocation coordinated motion to create the visible pop-in event on the load-depth curve that is characteristic of metallic materials.
The ability of Lipon to develop inelastic strain due to densification and isochoric shear results in its remarkable ability to resist fracture under sharp nanoindentation. Among different compositions, the tendency towards shear deformation apparently increases with increasing Li content, as has been demonstrated via MD simulations in.14 This is associated with break up of the covalent bonded network of phosphate tetrahedra, which yields a more ductile material with lower degree of compressibility. At the optimal ratio of Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P equal to 3
P equal to 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Lipon represents the typical inverted glass, where the amount of network modifying component (lithium) is greater than the content of network formers. Such high content of lithium ions in the composition is hard to achieve by traditional glass processing, but can be accomplished via the physical vapor deposition techniques employed here. The ability of Lipon to resist nanoindentation induced cracking was confirmed here in as-sputtered films via sharp cube corner tip nanoindentation, following.40 The residual hardness impressions of Lipon are shown in Fig. 4. A significant amount of shear-driven pileup can be observed in the residual hardness impression created by the cube corner nanoindenter tip, Fig. 4b. The residual hardness impression from the Berkovich tip, Fig. 4a, shows no specific features, neither pile-up, nor sink-in, rendering the measured values of modulus and hardness reliable. Neither scenario resulted in fracture of Lipon, confirming that this material exhibits high resistance to cracking.
1, Lipon represents the typical inverted glass, where the amount of network modifying component (lithium) is greater than the content of network formers. Such high content of lithium ions in the composition is hard to achieve by traditional glass processing, but can be accomplished via the physical vapor deposition techniques employed here. The ability of Lipon to resist nanoindentation induced cracking was confirmed here in as-sputtered films via sharp cube corner tip nanoindentation, following.40 The residual hardness impressions of Lipon are shown in Fig. 4. A significant amount of shear-driven pileup can be observed in the residual hardness impression created by the cube corner nanoindenter tip, Fig. 4b. The residual hardness impression from the Berkovich tip, Fig. 4a, shows no specific features, neither pile-up, nor sink-in, rendering the measured values of modulus and hardness reliable. Neither scenario resulted in fracture of Lipon, confirming that this material exhibits high resistance to cracking.
3.4 Strain engineering from residual stress upon cooling
The residual stress induced in Lipon during thermal annealing is induced by the thermal mismatch between the relaxed glassy material and the underlying substrate. The experiments reported here demonstrate that with processing temperatures above 100 °C, it is possible to engineer significant tensile or compressive stresses in the Lipon (with the two types of substrates that were used). Recent work17 demonstrates that compressive stresses of this magnitude can deflect and potentially mitigate the propagation of Li metal dendrites. Thus the thermal annealing approach employed here demonstrates that a single thermal processing step can be used to engineer such stress into a Lipon film, by using a primary solid electrolytes with sufficiently high CTE. For example, high compressive stresses can be created by depositing Lipon on LLZO, which has a CTE that is significantly higher than the sapphire substrates (about 6.3 × 10−6 across the given temperature range34). This is expected to improve its long-term cycling performance by suppressing dendrite penetration. In general, for relevant solid-electrolyte materials like LLZO where the CTE mismatch is large. In general, for relevant solid-electrolyte materials like LLZO, which exhibit a large CTE mismatch (with αLLZO reported to be 15.5 × 10−6, which is significantly larger than the measured αLiPON of approximately 4 × 10−6), it is feasible to engineer compressive residual stresses. These stresses can be considerably larger than those observed on sapphire substrates, potentially reaching or exceeding 400 MPa for LLZO. Such high compressive stresses are expected to enhance long-term cycling performance by suppressing dendrite penetration, offering a substantial improvement in dendrite resistance, which is crucial since these values are well above those needed to deflect dendrites.17The thermal treatment outlined in this work could potentially be extended to other glassy solid electrolyte such as sulfide glasses,6 oxysulfides,41 and lithium thiosilicophosphate glasses.42 Some sulfide glasses also exhibit plasticity,6 such that stress relaxation is expected to occur during constant-load holds at elevated temperatures. Moreover varying the substrate material and the hold temperature makes it possible to control the amount of CTE mismatch. This should permit precise residual strain engineering. In general, the single step approach presented here can provide a platform for precise engineering of residual strain into wide range of plastically-deformable materials.
The results in Fig. 1d–f also indicate that repeated thermal cycling could potentially be used to further increase the residual stress in the film. This approach requires that the material have excellent thermal chemical stability. For relevant materials like LLZO or glassy solid electrolytes, engineering such properties is an intriguing topic for further studies.
3.5 Modification of Lipon mechanical properties at higher processing temperature
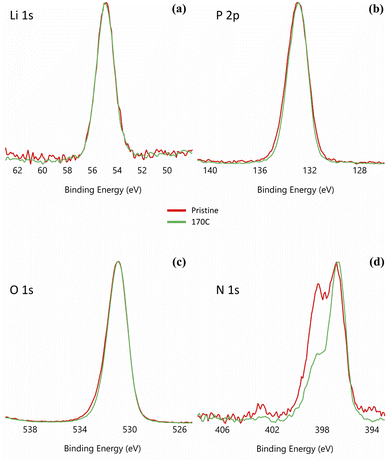
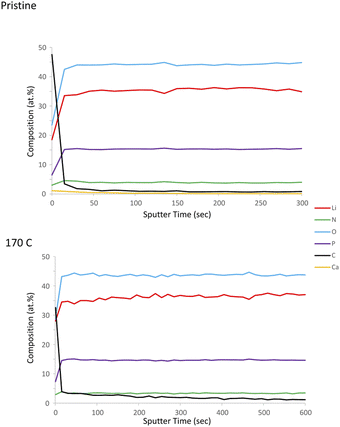
As indicated in previous sections, LiPON is unable to plastically relax all of the built-up stress during heating at higher processing temperatures. This is evident from Fig. 1e showing 100/150 relief and Fig. 1f depicting 40/160 relief. To further demonstrate the loss of plasticity in the LiPON/quartz system, we performed a series of nanoindentations on both pristine and heat-treated samples at 170 °C. The nanoindentation results for the as-deposited films, which were not subjected to heat treatment, have been discussed previously in Section 3.3. None of the nanoindentations resulted in fracture events, and the representative residual hardness impressions are shown in Fig. 4. Fig. 5 shows the remarkable change in the material's ability to resist cracking after the thermal treatment. All of the nanoindentations with the Berkovich tip resulted in development of long radial cracks. This indicates substantial increase in brittleness when the material departs from its ideal high-alkali composition due to lithium loss after heat treatment. Overall such change certainly indicates that there's a processing temperature upper bound around 140 °C for Lipon.To investigate the correlation between this effect and Lipon composition, we performed XPS on the surface of the film (Fig. 6) and the sub-surface of the film (Fig. 7) by etching the surface with Ar ion sputtering. In these measurements, we chose to investigate all four constituting elements of Lipon, namely Li, P, O, and N. We choose to contrast the signals between pristine and 170 °C processing temperatures, because under this temperature the films undergo significant plastic deformation. Overall from Fig. 7, there was no essential difference in the composition versus depth for the 170 °C sample compared to the pristine film.
From Fig. 6 the local bonding environment appears to be comparable between the two samples. However, there is noticeable differences in the proportion of the two peaks in the N 1s spectra. From previous investigation,43 these two peaks are associated with Nd: a nitrogen atom linked to two phosphorus atoms (–N![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) ) with binding energy at around 397 eV, and Nt: a nitrogen atom linked to three phosphorus atoms (–N<) with binding energy at around 400 eV. If there is significant nitrogen bonding rearrangements of Nt turning into Nd as implied in Fig. 6d, we anticipate that the excess phosphorous must either evaporates or bonds to other species. But from Fig. 6a–c, there is no significant changes in the bonding environment of other species. Moreover from Fig. 7, the phosphorous percentage remains similar between the pristine and 170 °C samples, so there's no evidence of phosphorous escaping. Therefore, it is difficult to conclude there is significant differences in the nitrogen bonding between the samples.
) with binding energy at around 397 eV, and Nt: a nitrogen atom linked to three phosphorus atoms (–N<) with binding energy at around 400 eV. If there is significant nitrogen bonding rearrangements of Nt turning into Nd as implied in Fig. 6d, we anticipate that the excess phosphorous must either evaporates or bonds to other species. But from Fig. 6a–c, there is no significant changes in the bonding environment of other species. Moreover from Fig. 7, the phosphorous percentage remains similar between the pristine and 170 °C samples, so there's no evidence of phosphorous escaping. Therefore, it is difficult to conclude there is significant differences in the nitrogen bonding between the samples.
Based on the previous investigations,14 high ductility and toughness of Lipon are a direct result of its high alkali content with lithium cations disrupting the network of the phosphate tetrahedra. With the Li![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) P ratio of 3
P ratio of 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, Lipon can plastically deform under shearing while also allowing for some degree of densification. Therefore it is reasonable to hypothesize that the alternation of mechanical properties at elevated temperature is related to loss of Li. Yet from the XPS data above, we can rule out the possibility of Li loss as the driving mechanism.
1, Lipon can plastically deform under shearing while also allowing for some degree of densification. Therefore it is reasonable to hypothesize that the alternation of mechanical properties at elevated temperature is related to loss of Li. Yet from the XPS data above, we can rule out the possibility of Li loss as the driving mechanism.
These indicate that the observed loss of plasticity at high processing temperature is unlikely due to composition changes, but perhaps due to mechanics. We note that the principal differences between the pristine and 170 °C samples prior to nano-indentation is the residual stress state, with the 170 °C sample under higher residual stress. It is reasonable to hypothesize that the loss of ductility (Fig. 4vs.5) is due to plastic deformation modes deactivated because of residual stress.31
In addition to the observed cracking in nano-indentation, we report also that we can directly observe extensive cracking on the sapphire sample during the MOSS experiments Fig. 8. We first note such cracking was be seen at elevated temperature (170 °C). There were no obvious flaws in the pristine sample. Moreover we can observe that the cracks are extensive across the surface as seen from the optical image. Using classical theory of cracks in thin film,27 specifically
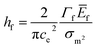 | (3) |
Using a stereological approach,44 we can estimate the crack spacing to be 1 per 100 microns. From the treatment of classical crack in thin-film,27 given the film thickness in the order of 5 microns, we can surmise that the change in curvature versus the uncracked film about 5–10%. The implication of this is that at elevated temperature, the film has an additional stress relief mechanism which makes CTE values analysis at high temperature (more than 120 °C) much more challenging. This explains the different CTE values at high annealing temperature versus lower temperature (Tables 1 and 2).
This is also consistent with the MOSS results earlier (Fig. 1d and 2c) where the Lipon shows incomplete plastic relaxation which possibly due to the stress being relief through crack formation. However the detail analysis is out of the scope of this study and will be left for a future study.
4 Conclusion
Using the HT-MOSS approach, controlled thermal strains were applied to Lipon thin films on quartz glass and sapphire substrates. The in situ stress measurements provide important information about the Lipon mechanical behaviour. Based on these measurements, CTE values were obtained over the temperature range from 75 °C to 170 °C. Furthermore at temperatures above 140 °C, there is a modification in the Lipon structure leading to changes in CTE values and loss of ductility. XPS measurements confirm that this modification is due to the loss of nitrogen and lithium.Initial plastic yield occurs at approximately 60–100 MPa. In addition to plastic flow under constant strain, the Lipon plastic yielding behaviour exhibits a strong dependence on heating rate (hence strain rate) and processing temperature. This indicates that the material is visco-plastic.
It was possible to create large residual stresses in the Lipon by annealing the material at elevated temperatures. During holds at a constant temperature (and hence applying a fixed thermal mismatch strain on the film), the measurements show plastic flow relaxes the CTE mismatch stress during heating which allows strain engineering upon cooling. With a CTE mismatch strain of 2 × 10−6 it was possible to engineer about ∼100 MPa of residual compressive/tensile strain. This suggests that the larger mismatch with LLZO (∼12 × 10−6) can potentially lead to ∼400 MPa of residual compression upon cooling. Engineering this on a solid electrolyte is potentially beneficial for mitigating dendrite penetration. We note that in a practical device, the LLZO thickness is expected to be about 50 microns, while that of PVD LiPON will be a micron or less. Thus, the maximum residual stress in the LLZO is far lower than that in the LiPON. Furthermore the relatively low yield stress may also prevent crack formation by allowing the structure to relax stress concentrations locally in the vicinity of the dendrite.6 This and Lipon's ionic conductivity indicate that Lipon is an excellent candidate as a thin coating on another solid electrolyte with higher conductivity.
The work reported here is also relevant because of growing interest in miniaturized batteries (i.e., microbatteries) with a small footprint ≤1 cm2 and uncompromised energy densities for a wide range of microelectronic applications including medical implants, hearing aids, and wireless sensor networks.45 Lipon is often chosen as the electrolyte in microbatteries because of it can be deposited as a thin-film.46 Hence the properties measured here are of direct interest to this community as they are relevant to both device manufacturing and cycling performance.
Data availability
The data that support the findings of this study are available from the corresponding author upon reasonable request.Author Contributions
T. Cai and B. Sheldon conceived the scientific ideas and planned the project. B. Sheldon supervised all aspects of the research. N. Dudney, A. Westover grew the LiPON films. A. Westover conducted the XPS measurements. S. Kalnaus conducted the nano-indentation measurements. T. Cai and C. Athanasiou conducted the SEMs. The manuscript was written by T. Cai and B. Sheldon and was revised by other co-authors. All the authors contributed to the discussions.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The work at Brown University was supported by U.S. Department of Energy, Office of Energy Efficiency and Renewable Energy (EERE), under Award Number DE-EE0008863, and by the National Science Foundation, under Award Number DMR-1832829. Andrew Westover, Sergiy Kalnaus, and Nancy Dudney were sponsored by the US Department of Energy (DOE), Office of Energy Efficiency and Renewable Energy for the Vehicle Technologies Office's Advanced Battery Materials Research Program (S. Thompson, Program Manager).Notes and references
- P. Albertus, S. Babinec, S. Litzelman and A. Newman, Nat. Energy, 2018, 3, 16–21 CrossRef CAS.
- R. J. Y. Park, C. M. Eschler, C. D. Fincher, A. F. Badel, P. Guan, M. Pharr, B. W. Sheldon, W. C. Carter, V. Viswanathan and Y.-M. Chiang, Nat. Energy, 2021, 6, 314–322 CrossRef CAS.
- F. Han, A. S. Westover, J. Yue, X. Fan, F. Wang, M. Chi, D. N. Leonard, N. J. Dudney, H. Wang and C. Wang, Nat. Energy, 2019, 4, 187–196 CrossRef CAS.
- X. Liu, R. Garcia-Mendez, A. R. Lupini, Y. Cheng, Z. D. Hood, F. Han, A. Sharafi, J. C. Idrobo, N. J. Dudney, C. Wang, C. Ma, J. Sakamoto and M. Chi, Nat. Mater., 2021, 20, 1485–1490 CrossRef CAS PubMed.
- Z. Ning, D. S. Jolly, G. Li, R. De Meyere, S. D. Pu, Y. Chen, J. Kasemchainan, J. Ihli, C. Gong, B. Liu, D. L. R. Melvin, A. Bonnin, O. Magdysyuk, P. Adamson, G. O. Hartley, C. W. Monroe, T. J. Marrow and P. G. Bruce, Nat. Mater., 2021, 20, 1121–1129 CrossRef CAS PubMed.
- C. E. Athanasiou, X. Liu, M. Y. Jin, E. Nimon, S. Visco, C. Lee, M. Park, J. Yun, N. P. Padture, H. Gao and B. W. Sheldon, Cell Rep. Phys. Sci., 2022, 3, 100845 CrossRef CAS.
- R. Armstrong, T. Dickinson and J. Turner, Electrochim. Acta, 1974, 19, 187–192 CrossRef CAS.
- C. E. Athanasiou, M. Y. Jin, C. Ramirez, N. P. Padture and B. W. Sheldon, Matter, 2020, 3, 212–229 CrossRef.
- J. Zhao, Y. Tang, Q. Dai, C. Du, Y. Zhang, D. Xue, T. Chen, J. Chen, B. Wang, J. Yao, N. Zhao, Y. Li, S. Xia, X. Guo, S. J. Harris, L. Zhang, S. Zhang, T. Zhu and J. Huang, Energy Environ. Mater., 2022, 5, 524–532 CrossRef CAS.
- A. Sharafi, H. M. Meyer, J. Nanda, J. Wolfenstine and J. Sakamoto, J. Power Sources, 2016, 302, 135–139 CrossRef CAS.
- E. Kazyak, R. Garcia-Mendez, W. S. LePage, A. Sharafi, A. L. Davis, A. J. Sanchez, K.-H. Chen, C. Haslam, J. Sakamoto and N. P. Dasgupta, Matter, 2020, 2, 1025–1048 CrossRef.
- T. Swamy, R. Park, B. W. Sheldon, D. Rettenwander, L. Porz, S. Berendts, R. Uecker, W. C. Carter and Y.-M. Chiang, J. Electrochem. Soc., 2018, 165, A3648 CrossRef CAS.
- Y. Qi, C. Ban and S. J. Harris, Joule, 2020, 4, 2599–2608 CrossRef CAS.
- S. Kalnaus, A. Westover, M. Kornbluth, E. Herbert and N. J. Dudney, J. Mater. Res., 2021, 36, 787–796 CrossRef CAS.
- A. S. Westover, N. J. Dudney, R. L. Sacci and S. Kalnaus, ACS Energy Lett., 2019, 4, 651–655 CrossRef CAS.
- C. E. Athanasiou, X. Liu, B. Zhang, T. Cai, C. Ramirez, N. P. Padture, J. Lou, B. W. Sheldon and H. Gao, J. Mech. Phys. Solids, 2023, 170, 105092 CrossRef.
- C. D. Fincher, C. E. Athanasiou, C. Gilgenbach, M. Wang, B. W. Sheldon, W. C. Carter and Y.-M. Chiang, Joule, 2022, 6, 2794–2809 CrossRef CAS.
- H. D. Jagad, S. J. Harris, B. W. Sheldon and Y. Qi, Chem. Mater., 2022, 34, 8694–8704 CrossRef CAS.
- W. Oliver and G. Pharr, J. Mater. Res., 2004, 19, 3 CrossRef CAS.
- W. Zhang, T. H. Cai and B. W. Sheldon, Adv. Energy Mater., 2019, 9, 1803066 CrossRef.
- J. H. Cho, X. Xiao, K. Guo, Y. Liu, H. Gao and B. W. Sheldon, Energy Storage Mater., 2020, 24, 281–290 CrossRef.
- J. H. Cho, K. Kim, S. Chakravarthy, X. Xiao, J. L. M. Rupp and B. W. Sheldon, Adv. Energy Mater., 2022, 12, 2200369 CrossRef CAS.
- M. Y. Jin, K. Guo, X. Xiao, M. W. Verbrugge, H. Gao and B. W. Sheldon, Adv. Funct. Mater., 2021, 31, 2010640 CrossRef CAS.
- M. Tokur, M. Y. Jin, B. W. Sheldon and H. Akbulut, ACS Appl. Mater. Interfaces, 2020, 12, 33855–33869 CrossRef CAS PubMed.
- Q. Wang, C. Ramírez, C. S. Watts, O. Borrero-López, A. L. Ortiz, B. W. Sheldon and N. P. Padture, Acta Mater., 2020, 186, 29–39 CrossRef CAS.
- R. Kumar, P. Lu, X. Xiao, Z. Huang and B. W. Sheldon, ACS Appl. Mater. Interfaces, 2017, 9, 28406–28417 CrossRef CAS PubMed.
- L. B. Freund and S. Suresh, Thin Film Materials: Stress, Defect Formation and Surface Evolution, Cambridge University Press, 2004 Search PubMed.
- H. Haftbaradaran, S. K. Soni, B. W. Sheldon, X. Xiao and H. Gao, J. Appl. Mech., 2012, 79, 031018 CrossRef.
- H. Haftbaradaran, X. Xiao and H. Gao, Modell. Simul. Mater. Sci. Eng., 2013, 21, 074008 CrossRef.
- E. G. Herbert, W. E. Tenhaeff, N. J. Dudney and G. M. Pharr, Thin Solid Films, 2011, 520, 413–418 CrossRef CAS.
- S. Govindjee, Continuum Mechanics of Solids, Oxford University Press, 2020 Search PubMed.
- T. Courtney, Mechanical Behavior of Materials, Waveland Press, 2nd edn, 2005 Search PubMed.
- V. Lacivita, A. S. Westover, A. Kercher, N. D. Phillip, G. Yang, G. Veith, G. Ceder and N. J. Dudney, J. Am. Chem. Soc., 2018, 140, 11029–11038 CrossRef CAS PubMed.
- G. K. White and M. L. Minges, Int. J. Thermophys., 1997, 18, 1269–1327 CrossRef CAS.
- T. Bergman, A. Lavine, F. Incropera and D. DeWitt, Introduction to Heat Transfer, Wiley, 2011 Search PubMed.
- J. M. Wheeler and J. Michler, Rev. Sci. Instrum., 2013, 84, 101301 CrossRef CAS PubMed.
- W. C. Oliver and G. M. Pharr, J. Mater. Res., 1992, 7, 1564–1583 CrossRef CAS.
- G. Huajian, C. Cheng-Hsin and L. Jin, Int. J. Solids Struct., 1992, 29, 2471–2492 CrossRef.
- J. Hay and B. Crawford, J. Mater. Res., 2011, 26, 727–738 CrossRef CAS.
- D. S. Harding, W. C. Oliver and G. M. Pharr, MRS Proc., 1994, 356, 663 CrossRef.
- X. Chi, Y. Zhang, F. Hao, S. Kmiec, H. Dong, R. Xu, K. Zhao, Q. Ai, T. Terlier, L. Wang, L. Zhao, L. Guo, J. Lou, H. L. Xin, S. W. Martin and Y. Yao, Nat. Commun., 2022, 13, 2854 CrossRef CAS PubMed.
- R. Zhao, S. Kmiec, G. Hu and S. W. Martin, ACS Appl. Mater. Interfaces, 2020, 12, 2327–2337 CrossRef CAS PubMed.
- B. Fleutot, B. Pecquenard, H. Martinez, M. Letellier and A. Levasseur, Solid State Ionics, 2011, 186, 29–36 CrossRef CAS.
- K. M. Nemati and P. Stroeven, Mater. Struct., 2001, 34, 486–494 CrossRef.
- N. A. Kyeremateng and R. Hahn, ACS Energy Lett., 2018, 3, 1172–1175 CrossRef CAS.
- V. Chaudoy, F. Pierre, A. Ghosh, M. Deschamps, F. T. Van and F. Ghamouss, Batteries Supercaps, 2021, 4, 1351–1362 CrossRef CAS.
- L. Li, S. Liu, X. Xue and H. Zhou, Ionics, 2018, 24, 351–362 CrossRef CAS.
- S Bhatia and B.W. Sheldon, J. Am. Ceram. Soc., 2008, 91(33), 3986–3993 CrossRef CAS.
- M.A. Fischler and R.C. Bolles, Random sample consensus: a paradigm for model fitting with applications to image analysis and automated cartography, Communications of the ACM, 1981, 24(6) CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta06386k |
| This journal is © The Royal Society of Chemistry 2024 |