Direct observation of phase transitions between delta- and alpha-phase FAPbI₃via defocused Raman spectroscopy

Abstract

The ability to characterise perovskite phases non-destructively is key on the route to ensuring their long-term stability in operando. Raman spectroscopy holds the promise to play an important role in this task. Among all perovskites, formamidinium lead iodide (FAPbI₃) has emerged as one of the most promising candidates for single-junction photovoltaic cells. However, Raman spectroscopy of FAPbI₃ remains challenging as is evidenced by conflicting reports in the literature. Here, we demonstrate that due to the vulnerability of FAPbI₃ to laser-induced degradation, the detected Raman spectrum depends strongly on the experimental conditions. This can lead to conflicting results and is revealed as the origin of discrepancies in the literature. We overcome this issue by deploying defocused Raman spectroscopy, preventing laser-induced damage to the sample and simultaneously improving the signal-to-noise ratio, allowing us to furthermore resolve much weaker Raman modes than was previously possible. We offer step-by-step instructions on how to apply this technique to a given spectrometer. Non-destructive characterisation of the FAPbI₃ phases further enables us to quantify the phase stability of pristine FAPbI₃ crystals and FAPbI₃ grown with the high-performance additive methylenediammonium chloride (MDACl₂). This shows that the neat crystals fully degrade within two weeks, whereas in samples grown with the additive only about 2% of the crystal bulk is in the δ-phase after 400 days. This establishes defocused Raman spectroscopy as a powerful tool for the characterisation of FAPbI₃ and other perovskite materials.

---

1 Introduction

Hybrid organic–inorganic metal–halide perovskites have emerged as a promising class of semiconductor materials. Their tuneable bandgaps,¹ high absorption coefficients² and long charge-carrier diffusion lengths³ make them attractive for a range of optoelectronic applications. For single-junction photovoltaic cells, FAPbI₃ (FA⁺ is formamidinium, HC(NH₂)₂⁺) is the most promising candidate out of all the ABX₃ lead-halide perovskites reported to date⁴ since FAPbI₃ has the narrowest achievable bandgap (E_g ≈ 1.45 eV) for a Pb-based halide perovskite.⁵ This allows for the highest theoretical photovoltaic power conversion efficiency (PCE) for a lead halide perovskite in a single-junction architecture⁶ and is reflected in the majority of recent world record PCE perovskite PV devices employing FAPbI₃-based materials as their photo-absorbing layer.^7–10

The main challenge with the use of FAPbI₃ is the thermodynamic instability of the cubic α-phase in ambient conditions which tends to transform into a photo-inactive hexagonal 2H δ-phase. This hexagonal phase has a wider band gap, larger defect density and poor quantum efficiency and is hence unsuitable for photovoltaic applications.^11–13

Several approaches aiming to stabilise the α-phase have been investigated, including the synthesis of low dimensional perovskite materials, compositional engineering, and the addition of external additives.^7,14,15

To study FAPbI₃'s phase instability it is necessary to isolate the effect of the intended adaptation from other processing variables. For this purpose, single crystalline materials are most suitable, as the properties of thin film and powder samples are highly dependent on their fabrication conditions. Moreover, FAPbI₃ single crystals have several advantages over polycrystalline films, such as lower defect densities, longer carrier diffusion lengths, and better-defined structure since the influence of interfaces and grain boundaries can be eliminated.^16–19 Therefore, single crystals provide a more reliable platform to study phase transitions as well as the optoelectronic properties of FAPbI₃.^20,21

The ability to quantify the phase stability of single crystalline FAPbI₃ under operational ageing is a critical tool for these investigations. Characterisation of single crystals by X-ray techniques either requires single crystal X-ray diffraction (SCXRD) or powder X-ray diffraction (PXRD). SCXRD of mixed-phase materials is often highly complex, and moreover cannot be used to quantify sample phase composition. On the other hand, PXRD requires single crystals to be powdered, thus destroying the sample and potentially artificially inducing changes in phase composition. Moreover, both techniques are sensitive only to bulk crystalline phases, and are insensitive to either amorphous phases or crystalline nanodomains. Thus, although instructive, neither is suitable for operational phase stability studies, which requires a technique that can be applied many times to the same FAPbI₃ single crystal without affecting its properties.

The different symmetries of the δ- and α-phases of FAPbI₃ suggest Raman spectroscopy as a powerful characterisation tool. The Raman activity of lead halide perovskites can be divided into two regions. The low wavenumber region (<500 cm⁻¹) contains modes of the inorganic framework and coupled modes, whereas the individual molecular modes of the organic part are represented in the higher wavenumber region (500–3000 cm⁻¹).²² Consequently, only wavenumbers below 500 cm⁻¹ have to be considered to distinguish the δ and α-phase of FAPbI₃.

The hexagonal space group of the δ-phase gives rise to four expected Raman modes in the low-frequency region: octahedral distortion (35 cm⁻¹), molecular in-plane rotation around a corner H (63 cm⁻¹), molecular out-of-plane rotation around the N–N axis (90 cm⁻¹) and molecular translation (108 cm⁻¹).²³ These four distinct modes make the δ-phase straightforward to identify.

However, the literature is inconsistent in the assignment of Raman modes to the α-phase. Han et al. were the first to report Raman signatures for both phases, assigning peaks at 111 cm⁻¹ and 135 cm⁻¹ to the δ- and α-phase, respectively.¹³ This assignment has been used in numerous studies^24–26 since, even though the cubic Pm3̄m symmetry of the α-phase is predicted to be Raman inactive by group theory. Two recent reports by Driscoll et al.²⁷ and Ibaceta-Jana et al.²⁸ dissent from these previous assignments and provide experimental data supporting the assignment of the α-phase as Raman inactive.

This discrepancy in the literature is surprising, as FAPbI₃ crystals can, once degraded into the δ-phase, be transformed back into the α-phase via heating to temperatures above the phase transition (observed at 145 °C under 3 K min⁻¹ heating, see Fig. S1†) and α-phase Raman peaks should therefore be straightforward to identify. The origin of this controversy can be found in the experimental details of the Raman measurements.

2 Experimental

2.1 Materials

γ-Butyrolactone (GBL, Alfa Aesar), formamidinium iodide (HC(NH₂)₂I, Greatcell Solar), methylenediammonium dichloride (H₂C(NH₃)₂Cl₂, Sigma Aldrich), lead iodide (PbI₂, TCI). All chemicals were used as received and without any further purification.

2.2 Synthesis of single crystals

All single crystals were fabricated in N₂ from a seed crystal following a previously published experimental protocol.^29,30 FAPbI₃ single crystals are prepared by dissolving equimolar FAI and PbI₂ in GBL. The solution is then stirred at 60 °C for 4 h. Then the solution is filtered with a 25 mm diameter 0.45 μm GMF filter. 4 mL of the filtrate is then placed in a vial that contains a seed FAPbI₃ crystal, and the vial is kept in an oil bath undisturbed at 95 °C for 12 h. The crystals were then dried in a vacuum oven at 180 °C for 45 min. For the FAPbI₃-M single crystals, alongside equimolar FAI and PbI₂ 3.8 mol% MDACl₂ is added. Then the same procedure as for the FAPbI₃ crystals was followed.

2.3 Raman spectroscopy

Raman spectra were acquired with a Jobin Yvon T64000 triple spectrometer and an Andor DU420A-OE CCD. The spectrometer was calibrated with the 520.7 cm⁻¹ line of a silicon wafer. Samples were excited with a Ventus solo Nd:YAG laser (λ = 532 nm) and the incident laser irradiation of the samples was strictly monitored.

3 Results and discussion

3.1 Raman spectroscopy of FAPbI₃

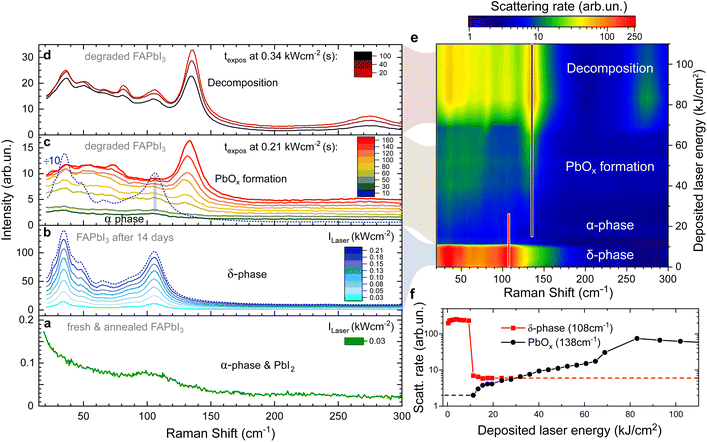
The high absorption coefficient (1 × 10⁵ cm⁻¹ at E_laser = 2.33 eV)³¹ and low thermal conductivity³² of α-FAPbI₃ make it sensitive to laser-induced heating. In the presence of oxygen, this has been shown to cause the formation of Raman active PbO_x compounds with a peak at 138 cm⁻¹ and a wider two-phonon peak at 276 cm⁻¹.^33,34

Chemical decomposition of FAPbI₃ single crystals is thought to occur first through abstraction of H⁺ from FA⁺ to produce formamidine (FA), which is volatile, leading to the formation of lead iodide (PbI₂), polyiodides (I_x⁻) and molecular iodine (I₂) which have low wavenumber peaks in the range of 40–110 cm⁻¹.^34,35

Here, we demonstrate all of these degradation stages on a single FAPbI₃ crystal in Fig. 1 as a function of laser intensity and deposited laser energy. Initially, the freshly grown and vacuum annealed sample is in the α-phase (Fig. 1a) as is confirmed by X-ray scattering data (Fig. S2†). Apart from the laser line background, there is only a small shoulder present at 110 cm⁻¹ which we attribute to the presence of traces of PbI₂ which can be formed as a side effect of annealing.³⁴ No peak is observed at 138 cm⁻¹ and we conclude that the α-phase of FAPbI₃ is Raman inactive as predicted by theory.

Fig. 1 Raman spectra of a FAPbI₃ single crystal at different degradation stages. Raman spectra were taken at E_laser = 2.33 eV with denoted laser intensities. (a) In the α-phase, no Raman peaks are present. The wide peak at 110 cm⁻¹ is caused by residual PbI₂. (b) After 14 days of ambient exposure, the crystal shows a strong δ-phase Raman signature, increasing linearly with the laser intensity. (c) At a threshold laser intensity of I_laser = 0.21 kW cm⁻², the Raman intensity is strongly reduced after 10 s as the crystal surface layer transforms into the α-phase (dotted blue spectrum is the same in b and c). With continuous exposure at the same laser intensity, the formation of a PbO_x related peak at 138 cm⁻¹ can be observed and the PbO_x peak continues to grow over time at 0.21 kW cm⁻2. (d) The laser intensity is further increased to 0.34 kW cm⁻². The PbO_x peak intensity decreases as the crystal decomposes and the crystal surface moves out of focus. Further decomposition peaks emerge. (e) False colour map of the Raman scattering rate summarising the data shown in (b–d). The Raman shift is plotted against the cumulative deposited laser energy. (f) Raman scattering rate of the strongest δ-phase and PbO_x peaks plotted against the cumulative deposited laser energy.

Raman spectra of the same crystal after ambient exposure for 14 days are given in Fig. 1b. The surface of the FAPbI₃ crystal has now degraded into the δ-phase and shows the characteristic four peaks. Upon increasing the laser intensity, the Raman intensity of the δ-phase peaks grows linearly. However, after 10 s at a threshold laser intensity of 0.21 kW cm⁻², we observe a 50-fold intensity drop of the Raman modes (Fig. 1b and c) that happens faster than the 5 s acquisition time used. We assign this to laser-induced heating causing a δ-to α-phase transition.

The rapid nature of the switch (see also Fig. 1f) can be explained by the much higher absorption coefficient of the α-phase, resulting in the laser energy being deposited in a smaller volume of the crystal. About 90% of the laser energy is deposited in the first 200 nm of an α-phase crystal (using α = 10⁵ cm⁻¹), resulting in a rapidly increasing temperature in this surface layer and formation of PbO_x begins. Note that due to the low thermal conductivity of FAPbI₃ (ref. 32) this is a local effect and limited to a small area around the laser spot on the surface (see next section).

The weak remaining peaks at 35 cm⁻¹ and 108 cm⁻¹ (bottom of Fig. 1c) originate from the remaining δ-phase in the periphery of the laser spot on the crystal surface that has not reached the phase transition temperature. Besides these, there are no modes visible, as expected for the α-phase.

Under continuing exposure at the same laser intensity, the PbO_x mode at 138 cm⁻¹ becomes visible within 60 seconds of the phase transition (Fig. 1c).

At even higher laser intensities (0.34 kW cm⁻²), additional modes arise at 36, 50, 67, 82 and 106 cm⁻¹ (Fig. 1d) caused by the formation of PbI₂, I_x⁻ and I₂ upon decomposition.^34,36 The overall signal intensity decreases over time, a clear indication of decomposition which results in the crystal surface moving out of focus.

Fig. 1e provides a visualisation of the laser-induced phase transition and consecutive degradation of the Raman data in Fig. 1b–d. In the false-colour map, the Raman shift is plotted against the cumulative laser energy deposited into the single crystal while the colour indicates the Raman scattering rate. This demonstrates that the Raman scattering cross-section of the α-phase is at least two orders of magnitude weaker than the δ-phase.²⁴

The peak scattering rates of the δ-phase peak at 108 cm⁻¹ and the PbO_x peak at 138 cm⁻¹ are plotted against the cumulative deposited laser energy in Fig. 1f. The peak at 108 cm⁻¹ was picked over the stronger peak at 35 cm⁻¹ as it is less affected by the laserline background. Tracking the peak intensity of these two peaks highlights the drop in Raman intensity when the surface of the crystal is transformed from the δ-into the α-phase, even on a logarithmic scale.

3.2 Defocused Raman spectroscopy

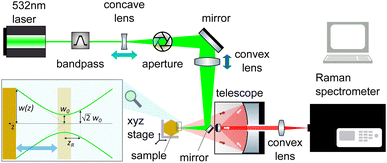
The sensitivity of FAPbI₃ to laser-induced degradation demonstrated above requires the laser intensity to be reduced as far as possible. This can be realised by reducing the laser power or, alternatively, increasing the laser spot size on the sample. Lowering the laser power is accompanied by a proportional decrease in Raman signal intensity, such that longer acquisition times are required to maintain sufficient signal-to-noise ratios (SNRs). This is not an ideal solution, as the longer laser exposure at a lower intensity might still degrade the crystal surface. Therefore, increasing the laser spot size is the better approach. This can be achieved in two ways, either by increasing the beam radius at the focal point or by moving the sample out of the focal plane.

The spot size at the focal point can be calculated for a Gaussian beam in the paraxial approximation as 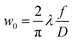with the focal length of the focusing lens f and the diameter D of the beam at the focusing lens, which is controlled by the aperture. Adjusting the optical system so the sample is not in the focal plane requires a more complex approach. Raman spectrometers typically consist of two separate optical systems, one to focus the laser onto the sample (green rays in Fig. 2) and the second to collect and focus the scattered light onto the detector (red rays in Fig. 2). This means that simply moving the sample out of focus is not a good option, as the detection system would have to be adjusted simultaneously. Instead, de-focusing the excitation system by repositioning either of the two lenses (see Fig. 2) in the direction of the beam is the better option. This moves the focal point of the excitation beam away from the sample surface while keeping the alignment of the detection system intact.

Fig. 2 Schematic of a typical Raman spectroscopy setup. The setup consists of two optical systems, both focused on the surface of the sample. The excitation system (green rays) consists of the laser source with a bandpass filter to produce monochromatic light and a concave lens followed by an aperture to control the beam diameter at the focusing lens. The detection system (red rays) comprises a telescope collecting the scattered photons and a convex lens focusing them on the entrance slit of the Raman spectrometer. The light and dark blue arrows indicate the two options for defocusing the Raman setup by moving either of the two lenses. The inset illustrates the propagation of a Gaussian beam.

The beam radius at a given distance to the focal point w(z) can be calculated via the Raleigh length z_R = πw₀²/λ as 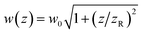(see Fig. 2). In combination with the equation for the focal length, this allows us to calculate how far a given lens has to be moved to achieve a given spot size at the sample position.

Since the FAPbI₃ samples investigated are all single crystals, the outcome of the Raman measurement is not affected by the spot size. We have increased the spot size from a diameter of d = 10 ± 3 μm to d = 65 ± 5 μm by repositioning the concave lens (light blue arrow in Fig. 2). This simple adjustment allows us to retain 50% of the original SNR. Since the area of the defocused spot is about 40 times larger than before, the defocused Raman setup produces a 20-fold increase in the SNR at the same laser intensity. The spot sizes were measured by moving the spot across the edge of a Silicon wafer with a micrometre stage, see Fig. S3.†

The defocused Raman setup, therefore, allows us to resolve much weaker Raman modes than was previously possible. To demonstrate this, we reported the molecular modes of the organic cation FA⁺ in a recent study³⁷ (see also Fig. S4†) which have previously only been detected in FAPbI₃ with laser energies below the band gap.^24,25

3.3 Spatially resolved laser-induced phase changes and degradation

In addition to reducing the laser intensity required for a given Raman measurement, the defocused Raman setup also gives us access to new experimental techniques.

At very high laser powers, the defocused spot can be used to intentionally change the sample surface. Subsequently, the laser power is strongly reduced and the laser spot focused, which means it can be used as a probe to resolve the spatial variation of the laser-induced changes which now happen on a larger scale.

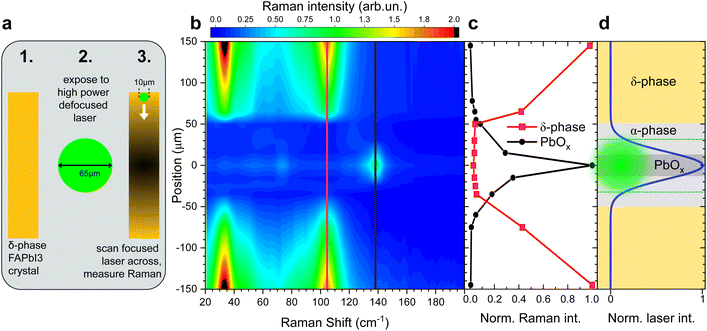
To demonstrate this, we performed Raman measurements on a FAPbI₃ crystal, in the δ-phase, in the defocused setting (65 μm spot size) and gradually increased the laser power, until the Raman response indicated a phase transition into the α-phase, similar to the experiment described in Fig. 1b and c.

As soon as the phase change was observed, the laser power was strongly reduced and the setup returned to the focused setting (10 μm spot size). The smaller laser spot can now act as a probe and be scanned across the crystal surface that was previously irradiated with the larger high-power spot, see illustration in Fig. 3a.

Fig. 3 Spatial resolution of laser-induced FAPbI₃ phase transition via dual focus Raman spectroscopy. (a) Working principle: A δ-phase FAPbI₃ single crystal (1) is exposed to a high-power laser with a defocused focal spot of diameter d = 65 μm (2). The laser-induced changes are detected with a low-power focused laser spot via Raman measurements with a spatial resolution (3). (b) False-colour plot of the resulting Raman data. Coloured lines highlight the position of modes used in (c). (c) Raman peak intensities as shown in (b) for a δ-phase and a PbO_x mode. (d) Laser intensity profile of a Gaussian beam with d = 65 μm and the predominant FAPbI₃ phases at different laser intensities: δ-phase (orange), α-phase (light grey) and PbO_x (dark grey).

This allows us to sample the Raman response across the large spot on the crystal surface. Since the intensity distribution across a focal spot follows a Gaussian distribution, we can observe the effect of a continuum of laser intensities on the δ-phase FAPbI₃ crystal. The false-colour map in Fig. 3b reflects the Raman scattering intensity across the defocused laser spot. Far away from the laser spot, the crystal is still entirely in the δ-phase. Starting at about 150 μm from the spot centre, the δ-phase Raman intensity decreases until it vanishes entirely at 50 μm from the centre.

Towards the centre of the large spot, from about 20 μm out, a strong PbO_x peak emerges at 138 cm⁻¹ and the iodine peaks indicative of crystal decomposition are detected.

The position-dependent Raman peak intensities of the best resolved δ-phase and PbO_x peaks are displayed in Fig. 3c.

The intensity profile of a Gaussian beam with d = 65 μm and the predominant crystal phases are illustrated in Fig. 3d. Since the α-phase is Raman inactive, the absence of Raman scattering in the range of 20 up to 50 cm⁻¹ from the centre suggests that the crystal surface is converted into the α-phase there. The size of the defocused spot is highlighted in green in Fig. 3d. The surface area partially transformed into the α-phase is much larger than the irradiated area, suggesting laser-induced heating rather than photodegradation as the driving mechanism behind the phase transition, in accordance with previous observations on MAPbI₃.³²

The presence of the PbO_x peak (138 cm⁻¹) on a δ-phase crystal that was just briefly exposed to a higher intensity laser shows that the presence of the PbO_x peak is uncorrelated to the phase of the FAPbI₃ sample prior to the Raman measurement. At sufficient laser intensity, it can be observed in both α-phase and δ-phase crystals, either, via degrading the α-phase sample directly, or, by first transforming the δ-into the α-phase and then degrading it. The PbO_x peak is thus not suited as an indicator for the presence of the α-phase.

Even so, the fraction of the crystal that is in the δ-phase can be estimated from the intensity of the δ-phase peaks compared to a purely δ-phase crystal. In the absence of degradation-related peaks like PbO_x, the missing fraction of the δ-phase peak intensity can be assumed to be in the α-phase. This insight will be used for tracking the phase stability of FAPbI₃ single crystals in the following.

3.4 Quantifying the phase stability of FAPbI₃

To quantitatively track the phase stability of FAPbI₃ crystals, we compare pristine FAPbI₃ crystals and crystals grown with the methylenediammonium (MDA) additive which has been shown to improve stability.^7,9,10 We have reported the mechanism of the stability improvement and early Raman results elsewhere,³⁷ here we provide an instructive description of the evolved approach.

In Fig. 1 we have shown that the Raman scattering cross-section of α-phase FAPbI₃ is at least two orders of magnitude weaker than for the δ-phase (Fig. 1). The overall Raman response of any given FAPbI₃ sample will consequently be dominated by δ-phase peaks as soon as a small fraction of the probed layer is transformed into the δ-phase.

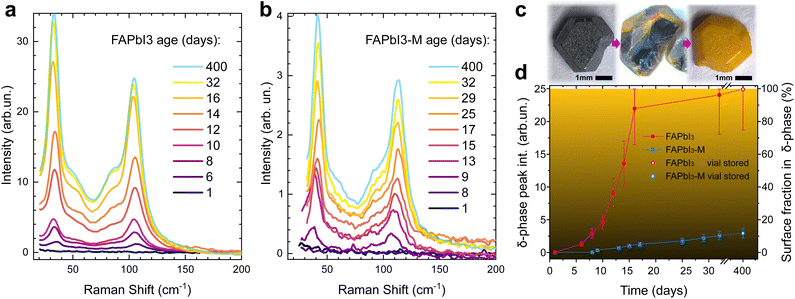
The enhanced SNR of the defocused Raman setup thus allows us to track the degraded fraction of the probed surface layer by monitoring the δ-phase peak intensities, even if the crystal is predominantly in the α-phase. We note that peak area is always proportional to the amount of δ-phase present in the crystal and, as is the case here, if peak width is constant then peak height correlates directly with peak area. We monitor the absolute Raman intensity of the best resolved δ-phase peak at a Raman shift of 108 cm⁻¹ under ambient conditions, see Fig. 4.

Fig. 4 Phase stability of FAPbI₃ single crystals. (a) Raman spectra of neat FAPbI₃ crystals and (b) crystals grown with MDACl₂ (FAPbI₃-M) additive taken at increasing exposure time to open-air ambient conditions. Crystals were used directly after growth and consecutive annealing. Spectra up to day 32 were taken on the same crystal and are representative of multiple spots on the crystal surface. Spectra after 400 days were taken on additional crystals from the same batches stored in air-filled vials. (c) Photographs of pristine FAPbI₃ crystals at different degradation stages after 0, 8 and 250 hours of ambient exposure. The picture in the centre was taken directly after cleaving the crystal. (d) The peak intensity of the best resolved δ-phase peak at 108 cm⁻¹ is plotted against the ambient exposure time.

Crystals were used directly after growth and consecutive vacuum annealing. All spectra were taken on the same crystal and are representative of multiple spots on the crystal surface. Crystals were kept in the sample holder of the Raman spectrometer under exposure to ambient air for the duration of the experiment to ensure consistent experimental conditions. We observed the formation of the PbO_x Raman peak at laser intensities as low as 25 W cm⁻². The defocused Raman setup allows us to keep the laser intensity in our Raman measurements strictly below 5 W cm⁻² while maintaining a good SNR.

Neat FAPbI₃ (Fig. 4a) undergoes detectable δ-phase formation after 6 days of open ambient exposure. This onset occurs after 8 days for FAPbI₃-M (Fig. 4b). After 32 days, the δ-phase peak intensity of neat FAPbI₃ stabilises at 24 ± 6, which means the probed crystal volume is fully degraded into the δ-phase. The δ-phase peak intensity is about 10 times smaller for FAPbI₃-M after 32 days, suggesting that only about 10% of the probed surface layer has degraded into the δ-phase (Fig. 4d).

Raman spectra of fully degraded FAPbI₃ crystals from the same batch that were stored in air-filled vials for 400 days show an intensity of 25 ± 5 which we thus use as reference for a 100% δ-phase crystal. FAPbI₃-M shows an intensity of 3.0 ± 0.7 in the same experiments, demonstrating that only about 12% of the probed surface layer is in the δ-phase.

Fig. 4c shows a FAPbI₃ crystal cleaved after 8 hours of ambient exposure, demonstrating that our FAPbI₃ crystals degrade from the surface inwards. We verify that this surface degradation does not correspond to regions probed during defocused Raman analysis, and thus confirm that surface-initiated phase transformation is the general mechanism for degradation of α-FAPbI₃. The thickness of the probed layer for α-phase FAPbI₃ is estimated to be 100 nm via the absorption coefficient (α = 10⁵ cm⁻¹ at the Raman laser wavelength of 532 nm).³¹

Since the absorption coefficient is much lower in the δ-phase, this does not affect the accuracy of the measurement. The estimated δ-phase fraction of the crystal is limited to the probed surface layer. However, the technique can be expanded to the crystal bulk by probing freshly cleaved crystals of a given age. Performing this on our vial stored crystals after 400 days yields an intensity ratio of I_bulk/I_surface = 0.15 ± 0.04 for FAPbI₃-M. Combined with our measurements on the surface, this suggests that merely a thin surface layer is degraded while the bulk remains largely in the α-phase (compare centre of Fig. 4c) with only about 0.15 × 0.12 = 2% δ-phase detected. By contrast, the neat FAPbI₃ is fully degraded into the δ-phase and the intensity ratio of bulk and surface is close to unity.

4 Conclusions

Non-destructive phase determination of perovskites is a crucial step in assessing and improving their stability. Raman spectroscopy holds the promise to play a key role in this task. Here, we demonstrate the challenges involved in Raman experiments on perovskites with the example of FAPbI₃. The vulnerability of metal halide perovskites to laser-induced degradation means that depending on prior history and the experimental conditions used virtually any result can be produced for the same sample. Defocused Raman spectroscopy offers a solution which eliminates this problem while simultaneously improving the SNR. We offer step-by-step instructions on how to apply this technique to a given spectrometer.

Applying this allows us to resolve the weak molecular FA⁺ modes of FAPbI₃ for the first time with standard visible laser energies above the band gap. Non-destructive characterisation of the FAPbI₃ phase further enables us to quantify the phase stability of neat FAPbI₃ crystals and FAPbI₃ grown with the high-performance additive MDACl₂. This shows that the neat crystals fully degrade within two weeks, whereas in samples grown with the additive only about 12% of the crystal surface and 2% of the crystal bulk are in the δ-phase after 400 days. Overall, this work establishes defocused Raman spectroscopy as a powerful tool for the characterisation of FAPbI₃ and opens the door for a better characterisation of other perovskite materials.

Author contributions

B. K. S. performed Raman experiments and wrote the manuscript. B. K. S., M. W. vdL, and R. J. N. conceptualised the defocused Raman setup. B. K. S., P. H., and R. J. N. curated and analysed the Raman data. B. M. G. and E. A. D. synthesised the samples. H. C. S. performed and analysed single crystal XRD measurements. H. J. S., M. K. R., and R. J. N. supervised the work. All authors reviewed and commented on the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

B. K. S. acknowledges University College, Oxford, for the Oxford-Radcliffe scholarship and thanks EPSRC for the funding through the Centre for Doctoral Training in New and Sustainable PV (EP/L01551X/1). This work was supported through UKRI-STFC Grants (ST/P002048/1 and No. ST/V001655/1). H. C. S. thanks EPSRC for support under the EPSRC Prosperity Partnership EP/S004947/1. This project was supported by the Processable Electronics Centre for Doctoral Training.

Notes and references

1. M. Saliba, J. P. Correa-Baena, M. Grätzel, A. Hagfeldt and A. Abate, Angew. Chem., Int. Ed., 2018, 57, 2554–2569.
2. S. De Wolf, J. Holovsky, S. J. Moon, P. Löper, B. Niesen, M. Ledinsky, F. J. Haug, J. H. Yum and C. Ballif, J. Phys. Chem. Lett., 2014, 5, 1035–1039.
3. J. Lim, M. T. Hörantner, N. Sakai, J. M. Ball, S. Mahesh, N. K. Noel, Y. H. Lin, J. B. Patel, D. P. McMeekin, M. B. Johnston, B. Wenger and H. J. Snaith, Energy Environ. Sci., 2019, 12, 169–176.
4. G. E. Eperon, S. D. Stranks, C. Menelaou, M. B. Johnston, L. M. Herz and H. J. Snaith, Energy Environ. Sci., 2014, 7, 982–988.
5. L. Chen, J. W. Yoo, M. Hu, S. U. Lee and S. I. Seok, Angew. Chem., Int. Ed., 2022, 61, 1–7.
6. W. Shockley and H. Queisser, J. Appl. Phys., 1961, 32(3), 510–519.
7. H. Min, M. Kim, S. U. Lee, H. Kim, G. Kim, K. Choi, J. H. Lee and S. I. Seok, Science, 2019, 366, 749–753.
8. G. Kim, H. Min, K. S. Lee, D. Y. Lee, S. M. Yoon and S. I. Seok, Science, 2020, 370, 108–112.
9. H. Min, D. Y. Lee, J. Kim, G. Kim, K. S. Lee, J. Kim, M. J. Paik, Y. K. Kim, K. S. Kim, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2021, 598, 444–450.
10. J. Park, J. Kim, H.-S. Yun, M. J. Paik, E. Noh, H. J. Mun, M. G. Kim, T. J. Shin and S. I. Seok, Nature, 2023, 616, 724–730.
11. C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038.
12. F. Ma, J. Li, W. Li, N. Lin, L. Wang and J. Qiao, Chem. Sci., 2016, 8, 800–805.
13. Q. Han, S. H. Bae, P. Sun, Y. T. Hsieh, Y. Yang, Y. S. Rim, H. Zhao, Q. Chen, W. Shi, G. Li and Y. Yeng, Adv. Mater., 2016, 28, 2253–2258.
14. S. Masi, A. F. Gualdrón-Reyes and I. Mora-Seró, ACS Energy Lett., 2020, 5, 1974–1985.
15. S. P. Dunfield, L. Bliss, F. Zhang, J. M. Luther, K. Zhu, M. F. van Hest, M. O. Reese and J. J. Berry, Adv. Energy Mater., 2020, 10, 1–35.
16. D. Shi, V. Adinolfi, R. Comin, M. Yuan, E. Alarousu, A. Buin, Y. Chen, S. Hoogland, A. Rothenberger, K. Katsiev, Y. Losovyj, X. Zhang, P. A. Dowben, O. F. Mohammed, E. H. Sargent and O. M. Bakr, Science, 2015, 347, 519–522.
17. Q. Dong, Y. Fang, Y. Shao, P. Mulligan, J. Qiu, L. Cao and J. Huang, Science, 2015, 347, 967–970.
18. Z. Chen, Q. Dong, Y. Liu, C. Bao, Y. Fang, Y. Lin, S. Tang, Q. Wang, X. Xiao, Y. Bai, Y. Deng and J. Huang, Nat. Commun., 2017, 8, 1–7.
19. M. T. Weller, O. J. Weber, J. M. Frost and A. Walsh, J. Phys. Chem. Lett., 2015, 6, 3209–3212.
20. T. Chen, B. J. Foley, C. Park, C. M. Brown, L. W. Harriger, J. Lee, J. Ruff, M. Yoon, J. J. Choi and S. H. Lee, Sci. Adv., 2016, 2, 1–7.
21. Z. A. Nan, L. Chen, Q. Liu, S. H. Wang, Z. X. Chen, S. Y. Kang, J. B. Ji, Y. Y. Tan, Y. Hui, J. W. Yan, Z. X. Xie, W. Z. Liang, B. W. Mao and Z. Q. Tian, Chem, 2021, 7, 2513–2526.
22. A. M. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodríguez-Martínez, O. J. Weber, A. Pallipurath, M. I. Alonso, M. Campoy-Quiles, M. T. Weller, J. Nelson, A. Walsh and P. R. Barnes, Phys. Chem. Chem. Phys., 2016, 18, 27051–27066.
23. J. Ibaceta-Jaña, R. Muydinov, P. Rosado, H. Mirhosseini, M. Chugh, O. Nazarenko, D. N. Dirin, D. Heinrich, M. R. Wagner, T. D. Kühne, B. Szyszka, M. V. Kovalenko and A. Hoffmann, Phys. Chem. Chem. Phys., 2020, 22, 5604–5614.
24. J. A. Steele, H. Yuan, C. Y. Tan, M. Keshavarz, C. Steuwe, M. B. Roeffaers and J. Hofkens, ACS Nano, 2017, 11, 8072–8083.
25. A. G. Kontos, G. K. Manolis, A. Kaltzoglou, D. Palles, E. I. Kamitsos, M. G. Kanatzidis and P. Falaras, J. Phys. Chem. C, 2020, 124, 8479–8487.
26. U. Erkılıç, H. G. Ji, E. Nishibori and H. Ago, Phys. Chem. Chem. Phys., 2020, 22, 21512–21519.
27. E. H. Driscoll, A. Orera, P. A. Anderson, M. L. Sanjuán and P. Slater, Dalton Trans., 2021, 3315–3323.
28. J. Ibaceta-Jaña, R. Muydinov, P. Rosado, S. H. B. Vinoth Kumar, R. Gunder, A. Hoffmann, B. Szyszka and M. R. Wagner, Phys. Chem. Chem. Phys., 2021, 3, 9476–9482.
29. P. K. Nayak, D. T. Moore, B. Wenger, S. Nayak, A. A. Haghighirad, A. Fineberg, N. K. Noel, O. G. Reid, G. Rumbles, P. Kukura, K. A. Vincent and H. J. Snaith, Nat. Commun., 2016, 7, 1–8.
30. B. Wenger, P. K. Nayak, X. Wen, S. V. Kesava, N. K. Noel and H. J. Snaith, Nat. Commun., 2017, 8, 1–10.
31. J. Chang, L. Jiang, G. Wang, Y. Huang and H. Chen, New J. Chem., 2021, 45, 4393–4400.
32. Y. Zhou, H. F. Garces and N. P. Padture, Front. Optoelectron., 2016, 9, 81–86.
33. E. Climent-Pascual, B. C. Hames, J. S. Moreno-Ramírez, A. L. Álvarez, E. J. Juarez-Perez, E. Mas-Marza, I. Mora-Seró, A. De Andrés and C. Coya, J. Mater. Chem. A, 2016, 4, 18153–18163.
34. N. N. Udalova, A. S. Tutantsev, Q. Chen, A. Kraskov, E. A. Goodilin and A. B. Tarasov, ACS Appl. Mater. Interfaces, 2020, 12, 12755–12762.
35. S. B. Sharp and G. I. Gellene, J. Phys. Chem., 1997, 101(11), 2192–2197.
36. S. Wang, Y. Jiang, E. J. Juarez-Perez, L. K. Ono and Y. Qi, Nat. Energy, 2017, 2, 1–8.
37. E. A. Duijnstee, B. M. Gallant, P. Holzhey, D. J. Kubicki, S. Collavini, B. K. Sturdza, H. C. Sansom, J. Smith, M. J. Gutmann, S. Saha, M. Gedda, M. I. Nugraha, M. Kober-Czerny, C. Xia, A. D. Wright, Y. H. Lin, A. J. Ramadan, A. Matzen, E. Y. Hung, S. Seo, S. Zhou, J. Lim, T. D. Anthopoulos, M. R. Filip, M. B. Johnston, R. J. Nicholas, J. L. Delgado and H. J. Snaith, J. Am. Chem. Soc., 2023, 145, 10275–10284.

---

Footnote

† Electronic supplementary information (ESI) available. CCDC 2299142 and 2299143. For ESI and crystallographic data in CIF or other electronic format see DOI: https://doi.org/10.1039/d3ta06411e

---