On the influence of the coherence length on the ionic conductivity in mechanochemically synthesized sodium-conducting halides, Na_3−xIn_1−xZr_xCl₆

Abstract

The Na⁺ ionic conductivity of ball milled Na_3−xIn_1−xZr_xCl₆ rises with increasing Zr content, while that in the subsequently annealed Na_3−xIn_1−xZr_xCl₆ compounds reaches a maximum conductivity at an intermediate substitution degree (x = 0.5). To clarify the underlying mechanism causing the differing trends, the local structure and coherence length of the ball milled Na_3−xIn_1−xZr_xCl₆ solid solutions were investigated by pair distribution function analyses. The structural evolution in the ball milled Na_3−xIn_1−xZr_xCl₆ series resembles those found in their annealed counterpart, however, its structural coherence length decreases with higher Zr content. By further investigating the transport properties using impedance spectroscopy, this work uncovers a correlation between the coherence length and the ionic conductivity in ball milled Na_3−xIn_1−xZr_xCl₆, in which lower structural coherence leads to higher ionic transport. This work indicates an influence of the microstructure beyond unit cell scale onto macroscopic transport properties in these sodium-conducting halide solid electrolytes.

---

Introduction

Owing to the earth-abundance of sodium and expected superior safety, sodium solid-state batteries are viewed as a promising alternative for conventional lithium-ion batteries employing liquid electrolytes, as numerous low-cost and reliably safe batteries are demanded nowadays.^1,2 As the core component of solid-state batteries, the properties of the solid electrolytes are critical for sodium solid-state battery performance, requiring a high ionic conductivity, an ultralow electronic conductivity, a wide electrochemical stability window as well as chemical and mechanical compatibility with the active materials.³ A wide range of sodium ionic conductors have been investigated, such as β-Al₂O₃ based oxides,^4,5 NASICON-type (e.g. NaZr₂(PO₄)₃),^6,7 Na₃PnCh₄ (Pn = P, Sb, Ch = S, Se),^8–10 Na₁₁Sn₂PS₁₂-type^11–13 and sodium closo-borate (e.g. Na₂B₁₂H₁₂).^14,15 For instance, tungsten substituted sodium thioantimonate Na_2.9Sb_0.9W_0.1S₄ shows an ionic conductivity of up to 41 mS cm⁻¹ at room temperature.^16,17 However, the narrow electrochemical stability window of these sulfide solid electrolytes may result in an incompatibility against the high-voltage cathode active materials or sodium metal anode.^18–21 In contrast, oxide-based Na⁺ conductors seem to show wider electrochemical stability. For example, the sodium solid-state battery employing Sc-substituted NASICON Na_3.4Sc_0.4Zr_1.6(SiO₄)₂(PO₄) against the cathode Na_xCoO₂ can be operated at a voltage up to 4.2 V vs. Na⁺/Na.²² Nevertheless, the high sintering temperatures, undesirable mechanical properties and significant grain boundary resistances do not favor their practical application in room-temperature solid-state batteries.²³

Recently, halide-based ionic conductors have stimulated a growing interest as promising candidates for the use as solid catholytes because of their oxidation stability and deformability.²⁴ These halides, especially when synthesized by the conventional solid-state reaction, suffer from low ionic conductivities.^2,25 However, in 2018, Asano et al. developed a high energy ball milling assisted synthesis procedure that allows room-temperature ionic conductivities of Li₃YCl₆ and Li₃YBr₆ to reach as high as 0.5 and 1.7 × 10⁻³ S cm⁻¹ respectively, which enhanced the transport about three orders of magnitude in comparison to that of fluorite- or spinel-type halides.²⁶ Likewise, sodium metal halides (e.g. Na₂ZrCl₆ and NaAlCl₄) synthesized via ball-milling exhibit better transport performance in comparison to their subsequently annealed counterparts.^27,28 It was suggested that disorder phases prepared by high energy ball milling facilitate Na⁺ movement, while highly crystalline phases formed under subsequent annealing result in drastically reduced ionic conductivity.²⁹ In addition, the synthesis procedure further seems to influence the crystal structure of sodium metal halides. For instance, Na₃InCl₆, exclusively synthesized by ball milling, can be stabilized in the cryolite (Na₃AlF₆) structure-type in space group P2₁/n; while upon subsequent annealing, Na₃InCl₆ transforms into a trigonal phase (space group P3̄1c) with a reduction in ionic conductivity.³⁰ To develop more conductive sodium halides, Zr⁴⁺ was introduced in Na₃InCl₆ and both via ball milling and also by subsequent annealing.^31,32 However, it is interesting that the trend of ionic conductivity as a function of the Zr content is different between the series of Na_3−xIn_1−xZr_xCl₆ (0.1 ≤ x ≤ 0.9) with and without subsequent annealing, even though both adopt the monoclinic polymorph (space group P2₁/n). For the subsequently annealed Na_3−xIn_1−xZr_xCl₆ series, the intermediate substituted Na_2.5In_0.5Zr_0.5Cl₆ shows the highest ionic conductivity, which is analogous with the Na_3−xY_1−xZr_xCl₆ and Na_3−xEr_1−xZr_xCl₆ series of solid solutions.^33,34 However, for the ball milled Na_3−xIn_1−xZr_xCl₆ series, the ionic conductivity keeps increasing with higher Zr content when x ≤ 0.9.³²

To clarify the underlying mechanism causing the differing trends of ionic conductivity against Zr content (schematically illustrated in Fig. S1†) and to better understand the relationship between the synthesis, structure, and transport properties in the Na_3−xIn_1−xZr_xCl₆ series, pair distribution function (PDF) analyses were performed. These analyses are meant to counterbalance the challenges in refinement and crystallite size analyses using Bragg diffraction data that may be not accurate for low crystalline materials usually coming from a ball-milling synthesis. PDF analyses allow to determine the local structure and coherence length of the ball milled Na_3−xIn_1−xZr_xCl₆ series with low crystallinity. By combining the structural results with impedance spectroscopy, this work reveals a decreasing coherence length with higher Zr content in ball milled Na_3−xIn_1−xZr_xCl₆, which significantly impacts the transport behavior. Thereby, it leads to the observed difference in the relationship between ionic conductivity and Zr content in differently synthesized Na_3−xIn_1−xZr_xCl₆. This work highlights the significant effect of the coherence length on the sodium ion transport in sodium metal halides and the importance of structure optimization beyond the lattice unit cell scale for ion conductor design.

Experimental methods

Synthesis of ball milled Na_3−xIn_1−xZr_xCl₆

Stoichiometric amounts of NaCl (Merck, 99.5%, pre-dried at 200 °C for 48 h under vacuum), ZrCl₄ (Merck, 99.99%), and InCl₃ (Alfa Aesar, 99.99%) were transferred into ball mill cups (80 mL) in an argon atmosphere. The volumetric filling of the ball mill cups was less than 30%. The mass ratio between precursors and milling media (ZrO₂, 5 mm diameter) was 1 : 30. Planetary ball milling was performed utilizing a Fritsch Pulverisette 7 at 100 rpm and subsequently 300 rpm for 10 minutes in each step, to preliminarily mix the precursors uniformly. Afterwards, planetary ball-milling was conducted for 99 cycles in reverse mode, with one cycle including milling at 500 rpm for 15 minutes and resting for 5 minutes to cool down.

X-ray diffraction

All samples were sealed in 0.5 mm-diameter glass capillaries in an argon atmosphere for X-ray diffraction measurements due to their air sensitivity. X-ray diffraction of ball milled samples was carried out using a STOE STADI P diffractometer (Ag Kα₁ radiation, λ = 0.5594 Å; curved Ge(111) monochromator, Mythen4K detector) in Debye–Scherrer scan mode at room temperature. Data collection was carried out for every sample in 0.015° steps for 64 hours. To get rid of additional background resulting from the fluorescence of Zr in the samples, the detector threshold was set as 20 keV. An empty capillary was measured as the background with the same procedure for further processing to obtain the pair distribution function, instrumental parameters were obtained using a LaB₆ standard as described below.

Pair distribution function analyses (PDF)

The X-ray diffraction data (λ(Ag Kα₁)) were background subtracted and then converted to a pair distribution function by Fourier-transforming the obtained normalized structure function S(Q) using PDFgetX3.³⁵ A Q-range cutoff of 13 Å⁻¹ was chosen. The fits were conducted using TOPAS Academic V7 software package.³⁶ The instrumental resolution parameters q_damp (0.011) and q_broad (0.010) were determined using NIST® SRM ® 660c LaB₆.³⁷ The fitting of the pair distribution function was performed in the wide range of 2 to 60 Å to obtain more precise coherence lengths, and includes: (1) scale factor and atomic correlated motion factor, (2) lattice parameters, (3) site fractional coordinates and occupancies, (4) atomic displacement parameters and (5) sphere particle diameter (spdiameter). At last, all variable parameters were allowed to fit simultaneously to achieve the best possible fit.

Electrochemical impedance spectroscopy

About 200 mg of each sample was initially pelletized by a custom-made manual screw press and then isostatically pressed under 330 MPa for 40 min. Subsequently, the pellets with a thickness of ∼0.15 cm and diameter of ∼0.9 cm were coated with thin gold electrodes using sputter deposition and enclosed in pouch cells. The impedances were measured with a SP-300 potentiostat (Biologic) under excitation with a sinusoidal alternating voltage of 10 mV amplitude and frequencies from 7 MHz to 100 mHz in a temperature range of −40 °C to 60 °C. Some spectra measured at low temperatures were excluded from evaluation because the samples were too resistive at low temperatures to have their complex impedances resolved. The spectra were analyzed employing RelaxIS 3 (rhd instruments) and with the inbuilt Kramers–Kronig testing the ultrahigh or ultralow frequency range was discarded to stay within less than 2% relative residuals ensuring the validity of the evaluated data.

Results and discussions

X-ray diffraction and pair distribution function of ball milled Na_3−xIn_1−xZr_xCl₆

The structure and transport properties of ball milled Na₃InCl₆ have been discussed in-depth in previous reports.^30,32 Meanwhile, ball milled Na₂ZrCl₆ is a phase mixture of the trigonal and monoclinic polymorphs,³² which makes it difficult to distinguish the contributions of each phase. Hence in this work, we focus on the cation-mixed Na_3−xIn_1−xZr_xCl₆ solid solutions only, excluding the endmembers from the discussion. Compounds of nominal Na_3−xIn_1−xZr_xCl₆ (0.1 ≤ x ≤ 0.95) were successfully synthesized by ball milling.³² An additional smaller step composition (i.e. x = 0.95) was included to push the series closer to the Na₂ZrCl₆ endmember. Representative powder X-ray diffraction patterns of the ball milled Na_3−xIn_1−xZr_xCl₆ (x = 0.1; 0.5; 0.9) are shown in Fig. 1a and all collected powder X-ray diffraction patterns of ball milled Na_3−xIn_1−xZr_xCl₆ samples are shown in Fig. S2a.† The X-ray diffraction patterns seem analogous with those of annealed compounds in Na_3−xIn_1−xZr_xCl₆ and ball milled Na₃InCl₆ with a monoclinic phase (space group P2₁/n).^30,31 However, nominal Na_2.05In_0.05Zr_0.95Cl₆ is an exception, where an additional reflection at ∼1.47 Å⁻¹ (Fig. S2†) is observed in its X-ray diffraction pattern. This may indicate already a presence of a secondary phase with the trigonal Na₂ZrCl₆-like polymorph (in space group P3̄m1) as previously observed in nominal Na₂ZrCl₆.³³ For the rest of the Na_3−xIn_1−xZr_xCl₆ compounds with 0.1 ≤ x ≤ 0.9, reflections shift to higher q values with increasing Zr content which indicates the shrinkage of the unit cell. Furthermore, the reflections of the ball milled Na_3−xIn_1−xZr_xCl₆ samples broaden and merge when increasing the Zr content, as shown in Fig. 1a and S2a.† This implies that higher degrees of Zr substitution result in changes in the microstructure which lies within the resolution range of the measurement. Using mechanical alloying syntheses of, for instance, lithium metal halide solid electrolytes, strain as well as stacking faults up to reduced domain sizes of coherency or full amorphization have been observed.^38,39 This may also extend in the compounds of Na_3−xIn_1−xZr_xCl₆ with stoichiometry. Previous work identified the structure of ball milled Na_3−xIn_1−xZr_xCl₆ samples by Rietveld refinements against X-ray diffraction data,³² but the apparent low crystallinity of the Zr-rich samples may mislead the refinement result. When considering the complex X-ray diffraction patterns of these ball milled Na_3−xIn_1−xZr_xCl₆ samples, broad and merged reflections can be observed. Thus, it is impossible to accurately extract the peak width as well as calculate the crystallite size by the Scherrer equation or strain influences using the Williamson–Hall method. Therefore, pair distribution function analysis is a useful tool to investigate the crystal structures and coherence lengths of the ball milled Na_3−xIn_1−xZr_xCl₆ series, since it can be used to determine the average local structure of materials whose coherence extends even only over a few atom–atom distances.⁴⁰ So it not only can counter the shortcoming of Rietveld refinements to identify the local structure of ball milled Na_3−xIn_1−xZr_xCl₆ series, but also overcomes the limitations of the Scherrer equation and Williamson–Hall methods to determine the coherent degrees of ball milled Na_3−xIn_1−xZr_xCl₆ compounds, as some of which seem to exhibit low crystallinity. The representative X-ray pair distribution functions of the ball milled Na_3−xIn_1−xZr_xCl₆ (x = 0.1; 0.5; 0.9) are shown in Fig. 1b. These pair distribution functions exhibit similar features; however, different damping profiles are prevalent indicated by the schematic envelope lines (dashed lines). The damping properties of the pair distribution function signal is related to the structural coherence length (often referred to as crystallite or domain size).⁴¹ As illustrated in Fig. 1c, samples with high coherence consist of large ordered domains; while for samples with low coherence, there are only small ordered domains potentially embedded in an amorphous matrix. Therefore, the probability of finding atom pair correlations at a larger distance r in a highly coherent sample is greater than that of its lower coherent counterpart, so the pair distribution function of samples with low coherence length dampens more significantly at high distances r. Here, the pair distribution functions of the ball milled Na_2.1In_0.1Zr_0.9Cl₆ attenuates strongly with increasing distance r between the atom pair correlations, while the dampening is less expressed for the samples with increased indium content. This phenomenon implies that the structural order degree of Na_3−xIn_1−xZr_xCl₆ degrades when incorporating more zirconium, which is in line with the observation of X-ray diffraction patterns.

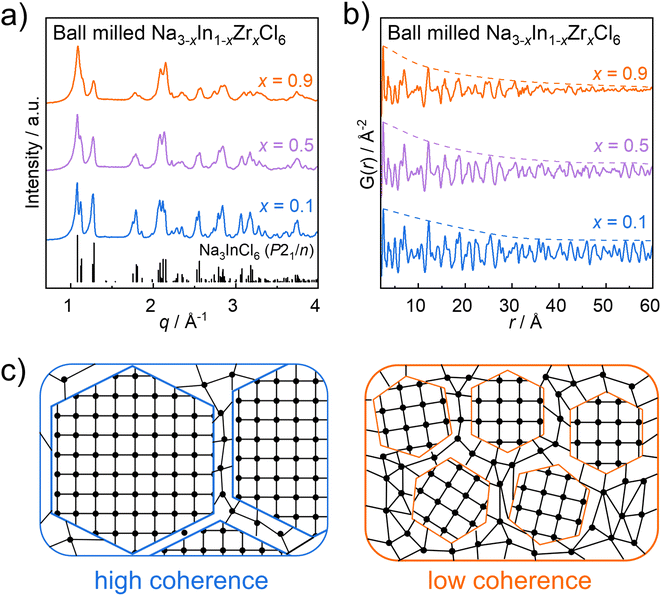Fig. 1 (a) X-ray diffraction patterns under Ag Kα₁ radiation of ball milled Na_3−xIn_1−xZr_xCl₆ (x = 0.1; 0.5; 0.9) and reference reflections of ball milling synthesized Na₃InCl₆ with a monoclinic phase (space group P2₁/n).³⁰ (b) Pair distribution functions of ball milled Na_3−xIn_1−xZr_xCl₆ (x = 0.1; 0.5; 0.9). The envelope curves (dashed lines) are only representing guides-to-the-eye. (c) Schematic of samples with high coherence and low coherence.

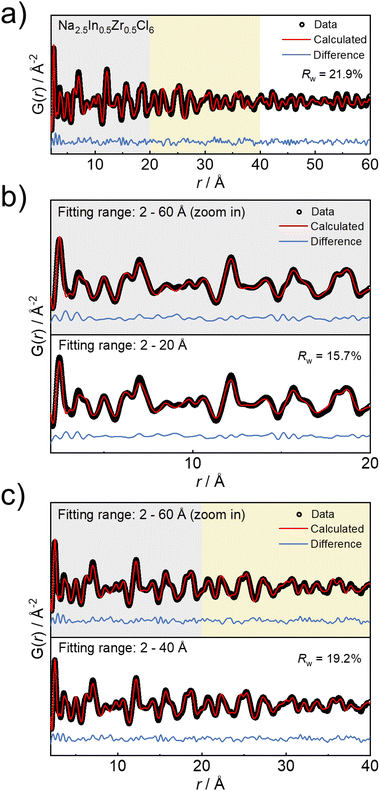
To further uncover the structural details of the ball milled Na_3−xIn_1−xZr_xCl₆ series, the obtained pair distribution functions were fitted. For the bulk materials synthesized by ball milling, the sphere particle diameter parameter as a variable in the fitting of the pair distribution function is used herein as a measure of structural coherence length.^41,42 The representative pair distribution function fitting result of Na_2.5In_0.5Zr_0.5Cl₆ is displayed in Fig. 2a and other fitting results of pair distribution functions are shown in Fig. S3–S5 and Tables S2–S11.† To get a more precise measure of coherence length that is strongly correlated to the envelope function of the pair distribution functions, a wide fitting range of 2 Å to 60 Å was analyzed. Within this wide range, the resulting statistic weighted residual (R_w) achieves around 20% and fitting quality is still satisfactory from visual inspection. To further verify the reliability of the long-range fitting procedure, the results using different evaluated ranges are compared. When performing the fitting in the range from 2 Å to 20 Å, R_w results in 15.7% (Fig. 2b), comparable with the previously reported R_w of the pair distribution function fit within the same evaluated range,^29,43 demonstrating the reliability of fitting in the range from 2 Å to 20 Å. Even though R_w grows with the extension of the evaluated range up to 60 Å, the resulting structural parameters do not show significant differences compared to those obtained from fitting against data in the limited range up to 20 Å (Fig. 2b, Tables S6 and S12†). Moreover, the comparison with the pair distribution function fitting from 2 Å to 40 Å shows a similar case (Fig. 2c, Tables S6 and S13†). These comparisons demonstrate the negligible influence of the r range considered for fitting on the determined crystal structure and the reliability of the wide-range fitting from 2 to 60 Å. However, in the sample of nominal Na_2.05In_0.05Zr_0.95Cl₆, the presence of a side phase prevents obtaining reliable pair distribution function fitting results in the wider r range and is therefore excluded from further structure analysis.

Fig. 2 (a) Representative pair distribution function fitting of ball milled Na_2.5In_0.5Zr_0.5Cl₆. (b) Comparison of pair distribution function fittings of ball milled Na_2.5In_0.5Zr_0.5Cl₆ fitted in the range of 2 to 60 Å and 20 Å. (c) Comparison of pair distribution function fittings of ball milled Na_2.5In_0.5Zr_0.5Cl₆ fitted in the range of 2 to 60 Å and 40 Å.

Crystal structure of ball milled Na_3−xIn_1−xZr_xCl₆

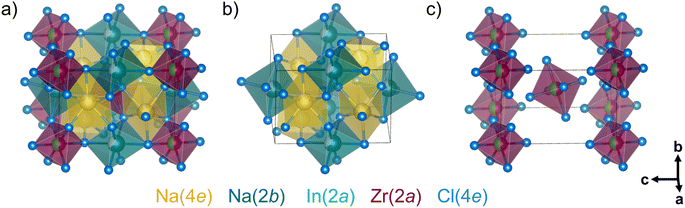
As the average structure determined by X-ray diffraction refinement, the local structure of Na_3−xIn_1−xZr_xCl₆ determined from the pair distribution function is also described in a deficient, monoclinic cryolite-type structure (space group P2₁/n), as shown in Fig. 3, represented by Na_2.5In_0.5Zr_0.5Cl₆. It consists of two In³⁺/Zr⁴⁺ ions (Wyckoff 2a), the stoichiometry-dependent Na⁺ ions (Wyckoff 4e and 2b), and twelve Cl⁻ ions (on three different Wyckoff 4e sites) per unit cell. Na⁺ ions at the Wyckoff 4e positions are prismatically coordinated while Na⁺ ions at the Wyckoff 2b sites are octahedrally coordinated each by chloride anions (Fig. 3b). The In_1−xZr_xCl₆^(3−x)− octahedra (magenta) locate at the corner and center of the unit cell (Fig. 3c). NaCl₆⁵⁻ prisms (yellow) share corners or edges with NaCl₆⁵⁻ octahedra (cyan) and In_1−xZr_xCl₆^(3−x)− octahedra. Otherwise, NaCl₆⁵⁻ octahedra and In_1−xZr_xCl₆^(3−x)− octahedra are connected by shared corners.

Fig. 3 Crystal structure of ball milled Na_3−xIn_1−xZr_xCl₆ in space group P2₁/n represented by Na_2.5In_0.5Zr_0.5Cl₆. (a) The full structure. (b) The building units of NaCl₆⁵⁻ octahedra and prisms. (c) The building units of In_1−xZr_xCl₆^(3−x)− octahedra.

Structure evolution of ball milled Na_3−xIn_1−xZr_xCl₆

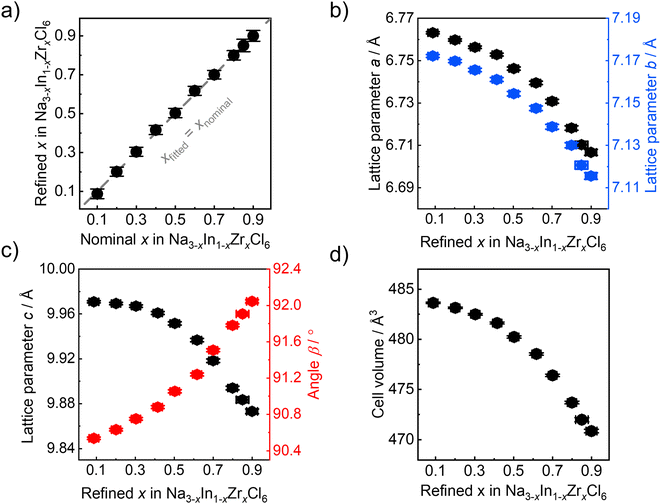
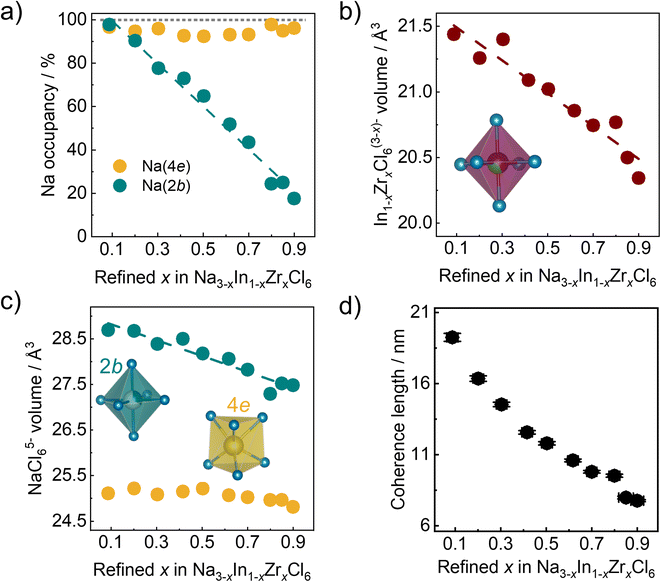
The refined Zr⁴⁺ fraction on the Wyckoff 2a site as a function of the nominal Zr content in ball milled Na_3−xIn_1−xZr_xCl₆ compounds follows a linear behavior (Fig. 4a). This finding is in accordance with the formation of solid solutions in Na_3−xIn_1−xZr_xCl₆ synthesized only by ball milling and further validates the reliability of results obtained by fitting against the pair distribution functions. The lattice parameters of ball milled Na_3−xIn_1−xZr_xCl₆ compounds determined by the pair distribution function fitting are shown in Fig. 4b and c. The obtained lattice parameters a, b, and c sharply decrease with the increase of Zr content in the Zr-rich region (x > 0.5), while the reduction flattens in the Zr-poor region (x < 0.5). The angle β between a and c increases with refined x in Na_3−xIn_1−xZr_xCl₆, diverging further from a right angle and opposing the lattice length change. These changes are in line with the structural changes in the annealed Na_3−xIn_1−xZr_xCl₆ solid solutions.³¹ The unit cell volume shows a similar trend, which slowly declines first and then a faster decrease occurs with increasing Zr content (Fig. 4d), because the Zr⁴⁺ ionic radius (72 pm) is lower than that of In³⁺ (80 pm) in 6-fold coordination.⁴⁴

Fig. 4 (a) Refined Zr⁴⁺ content against nominal Zr⁴⁺ content of ball milled Na_3−xIn_1−xZr_xCl₆ series. (b) Lattice parameters a and b of ball milled Na_3−xIn_1−xZr_xCl₆ series against refined Zr⁴⁺ content. (c) Lattice parameters c and angle β of ball milled Na_3−xIn_1−xZr_xCl₆ series against refined Zr⁴⁺ content. (d) Unit cell volume of ball milled Na_3−xIn_1−xZr_xCl₆ series against refined Zr⁴⁺ content. The uncertainties shown correspond to 1σ.

Further structural evolution details of ball milled Na_3−xIn_1−xZr_xCl₆ are displayed in Fig. 5a–c. The Na⁺ occupancy at the Wyckoff 4e site fluctuates between 90% and 100%, remaining highly occupied. In contrast, the Na⁺ occupancy at the Wyckoff 2b position exhibits a negative linear correlation with the zirconium substitution degree, showing that the Na⁺ site of Wyckoff 2b is depopulated first when less Na⁺-ions are present. Because of the smaller radius and higher valence of Zr⁴⁺ compared to In³⁺, a quasi-linear reduction of the In_1−xZr_xCl₆^(3−x)− octahedral volume with Zr content increase is observed. Besides the volume change of In_1−xZr_xCl₆^(3−x)− octahedral, its rotation was also investigated. As shown in Fig. S6a and b,† the M1–M2–Cl1 angle decreases upon increased substitution degree while the M1–M2–Cl2 angle increases, as M1–M2 direction parallel to the b axis, indicating the rotation of the In_1−xZr_xCl₆^(3−x)− octahedra when the Zr content is increasing (M1, M2 = In; Zr). The angle between the a axis and the M–Cl bond (M = In; Zr) also increases upon increased substitution degree (Fig. S6c and d†), corroborating that the In_1−xZr_xCl₆^(3−x)− octahedra rotate along the b axis. The complex behavior of the In_1−xZr_xCl₆^(3−x)− octahedra impacts the angle β change. Considering that Na_3−xIn_1−xZr_xCl₆ is not a simple binary-cation system a non-linear change of the structure is not surprising. When the average cation radius at Wyckoff 2a sites declines as In³⁺ is replaced by Zr⁴⁺, Na⁺ is also depopulated from Wyckoff 2b site. Here, the average cation radius, sodium occupancy, and octahedra rotation may have a synergistic impact on the lattice parameters and volume change, which results in their complex non-linear manner. As shown in Fig. 5c, the NaCl₆⁵⁻ octahedra (Na⁺ at Wyckoff 2b site) shrink with increasing the Zr content, alongside their average Na–Cl distance declining (Fig. S7a†), which may result from the decreased unit cell volume upon Zr⁴⁺ substitution compressing the NaCl₆⁵⁻ octahedra (Fig S7b†), or the reduced Na⁺ occupation on that site. In case of the NaCl₆⁵⁻ prism (Na⁺ at Wyckoff 4e site), no major systematic change to their volume and average Na–Cl distance is observed (Fig. 5c and S7a†), likely because of the central Wyckoff 4e site being almost fully occupied by Na⁺, leading to strong Na–Cl local interactions, which does not allow NaCl₆⁵⁻ prism to dramatically deform. The structural evolution details of ball milled Na_3−xIn_1−xZr_xCl₆ shown in Fig. 5a–c are similar to its subsequent annealed counterpart.³¹

Fig. 5 (a) Na⁺ occupancies at Wyckoff 2b and 4e sites, (b) the In_1−xZr_xCl₆^(3−x)− octahedral volumes and (c) the NaCl₆⁵⁻ octahedral and prism volumes along the series of ball milled Na_3−xIn_1−xZr_xCl₆. Dashed lines correspond to linear behavior as guides-to-the-eye. (d) Coherence lengths of ball milled Na_3−xIn_1−xZr_xCl₆. The uncertainties, where shown, correspond to 1σ.

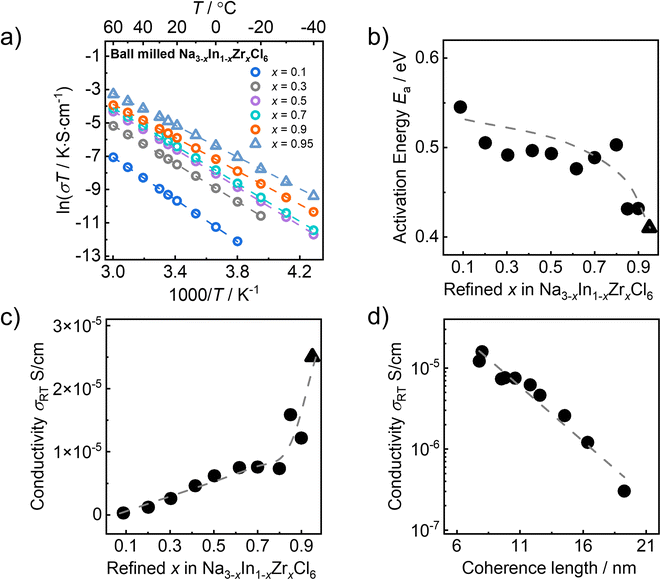
As discussed above, the coherence length can be approximated by fitting the pair distribution functions. As shown in Fig. 5d, there is a negative correlation between the obtained coherence length and Zr content for the ball milled Na_3−xIn_1−xZr_xCl₆ series. The more Zr⁴⁺ is incorporated into the structure, the smaller the coherence length. The reason for this is unclear, however we may speculate the following: (1) the increased Zr content leads to more strain, which causes the lattice deformation and partial amorphization; (2) the rising vacancy concentration due to aliovalent substitution results in a less stable crystal structure prone to form low coherence order structures; (3) the general composition leads to changes in energy transfer during the ball milling (as the mechanical properties of the solid change) and with it lower crystallization during the milling.³⁹ Considering that low coherence is not found when annealing these compositions,³¹ the third option seems more reasonable at this stage.

Ionic transport properties

The Na⁺ ion transport of the ball milled Na_3−xIn_1−xZr_xCl₆ series is evaluated by electrochemical impedance spectroscopy. The collected room-temperature (25 °C) impedance spectra are shown in Fig. S8† in Nyquist representation. All impedance spectra of the ball milled Na_3−xIn_1−xZr_xCl₆ samples were fit with an equivalent circuit model (the inset of Fig. S8a†) consisting of a parallel resistor-constant phase element (CPE) combination, in series with another CPE representing the ion-blocking electrodes. As the contributions of grain bulk and grain boundary cannot be deconvoluted from the collected impedance spectra and the fitted capacitances (∼10⁻¹¹ F) do not allow the exclusion of grain boundary contributions,⁴⁵ the obtained resistances (see Table S14†) are evaluated to total ionic conductivities. The sodium ionic conductivities of ball milled Na_3−xIn_1−xZr_xCl₆ samples exhibit linear Arrhenius behavior in the measured temperature ranges (Fig. 6a and S9†). The activation energies (E_a) were extracted from the linear Arrhenius fitting, as shown in Fig. 6b, which fluctuates around 0.5 eV and drops to ∼0.43 eV when x > 0.8. The ball milled Na_3−xIn_1−xZr_xCl₆ compounds show steadily rising room-temperature ionic conductivity (σ_RT) along the substitution degree x = 0.1 to 0.8. Beyond x > 0.8 a sharper increase in room-temperature ionic conductivity can be observed as displayed in Fig. 6c, in line with the previous report.³² Contrary to these two regimes, the fitting of the pair distribution functions suggest a predominantly continuous changes in the structural parameters within the ball milled Na_3−xIn_1−xZr_xCl₆ compounds. This implies that structural changes beyond the lattice unit cell scale may play a role here. Employing the determined coherence length, an approximately negative logarithmic correlation with the room-temperature ionic conductivity in the ball milled Na_3−xIn_1−xZr_xCl₆ compounds with 0.1 ≤ x ≤ 0.9 is observed (see Fig. 6d). Here, Na_2.05In_0.05Zr_0.95Cl₆ (x = 0.95) remains excluded as the coherence length could not reliably be obtained from fitting because of the side phase present, see above.

Fig. 6 (a) Arrhenius plots from the temperature dependent impedance of ball milled Na_3−xIn_1−xZr_xCl₆ series (x = 0.1; 0.3; 0.5; 0.7; 0.9; 0.95). (b) Activation energies of ball milled Na_3−xIn_1−xZr_xCl₆ series. The dashed line is guides-to-the-eye. (c) Room-temperature ionic conductivities of ball milled Na_3−xIn_1−xZr_xCl₆ series. The dashed line is guides-to-the-eye. For Na_2.05In_0.05Zr_0.95Cl₆, its activation energy and room-temperature ionic conductivity are against nominal x because its Zr content cannot be properly refined. To emphasize the difference, the symbol of Na_2.05In_0.05Zr_0.95Cl₆ is a triangle. (d) Room-temperature ionic conductivities of ball milled Na_3−xIn_1−xZr_xCl₆ as a function of coherence length.

To rule out a coincidence in the correlation between the coherence length and ionic conductivity, the local structures, coherence lengths, and ionic conductivities of Na_2.1In_0.1Zr_0.9Cl₆ synthesized by ball milling and subsequent one hour annealing at 200 °C and 330 °C, respectively, were compared to the milled compound. Pair distribution fitting results suggest that there is no significant change in the unit cell structure of Na_2.1In_0.1Zr_0.9Cl₆ after annealing (Tables S11, S15 and S16†), but the coherence length shows an obvious difference. As shown in Fig. S11a,† with the increase of the annealing temperature, the coherence length of Na_2.1In_0.1Zr_0.9Cl₆ increases. Moreover, the increased coherence length leads to a drop in ionic conductivity of Na_2.1In_0.1Zr_0.9Cl₆ (Fig. S11b†), as other structural changes are not observed here.³¹ This comparison strongly suggests that the coherence length does influence the macroscopic transport properties of sodium metal halides. Nevertheless, the coherence length of Na_2.1In_0.1Zr_0.9Cl₆ annealed at 200 °C is similar to that of ball milled Na_2.3In_0.3Zr_0.7Cl₆, but its ionic conductivity is only half that of milled Na_2.3In_0.3Zr_0.7Cl₆ (Fig. S11c†). As Na_2.1In_0.1Zr_0.9Cl₆ has less Na⁺ for movement, other structural features such as crystal geometry, diffusion pathway size, Na⁺/vacancy ratio, etc. cannot be neglected.

According to our previous work, the Na_3−xIn_1−xZr_xCl₆ series with subsequent annealing expresses a different trend of ionic conductivity against composition x (see Fig. S1†).³¹ The measured room-temperature ionic conductivity of subsequently annealed Na_3−xIn_1−xZr_xCl₆ series initially increases and subsequently decreases with higher Zr contents, reaching the maxima at x = 0.5,³¹ analogous to subsequently annealed Na_3−xEr_1−xZr_xCl₆ solid solutions.³³ Since high temperatures promote crystallization and grain growth of low coherent samples (Fig. S11a†), we can speculate that the influence of the coherence length difference observed after ball milling is considerably weakened. Hence, the ionic transport of subsequently annealed Na_3−xIn_1−xZr_xCl₆ solid solutions is dominantly driven by the Na⁺/vacancy ratio, contrary to those of ball milled Na_3−xIn_1−xZr_xCl₆ series of solid solutions.³¹ The discrepancy of the relationship between σ_RT and the Zr content x in Na_3−xIn_1−xZr_xCl₆ solid solutions with and without annealing further corroborates the existence of the influence of coherence length on the ionic conductivity in ball milled solid solutions of Na_3−xIn_1−xZr_xCl₆.

While a low coherence length in this series leads to better ionic transport, the underlying reason remains elusive. Less ordered compounds in this class of halides often lead to a higher ionic conductivity,^27–29,31 however, the root cause has not been fully revealed yet. A recent theoretical work suggests that large-amplitude vibrations of Li⁺ and Cl⁻ ions enable the fast Li-ion transport in glassy LiTaCl₆,⁴⁶ and low coherent sodium metal halides may follow a similar mechanism. Nevertheless, more experimental and computational work is needed to understand the complex ionic transport behavior of halide-based Na⁺ conductors with low coherence.

Conclusion

In this work, we investigated the local structure and coherence length of ball milled Na_3−xIn_1−xZr_xCl₆ utilizing pair distribution function analyses. The structure evolution of the ball milled Na_3−xIn_1−xZr_xCl₆ series of solid solutions is similar to that of its subsequently annealed counterpart, however, its coherence length reduces with increasing Zr content. By investigating the ionic transport using impedance spectroscopy, this work reveals that the ionic conductivity of the ball milled Na_3−xIn_1−xZr_xCl₆ solid solutions increases when increasing the Zr content. Here, the ionic conductivity seems to be significantly impacted by the coherence length with faster transport found in lower coherency samples. Therefore, the trend of ionic conductivity in the ball milled Na_3−xIn_1−xZr_xCl₆ series against the Zr substitution degree is different from that of its subsequently annealed counterpart. This work suggests an influence of the coherence length in sodium metal halides on their ionic transport properties and emphasizes the significance of multi-scale (micro-)structural design beyond the structural parameters for further development of fast ionic conductors.

Author contributions

Tong Zhao: conceptualization, methodology, investigation, experiments, analyses, writing – original draft, review & editing. Alexander N. Sobolev: experiments, analyses, writing – review & editing. Xabier Martinez de Irujo Labalde and Marvin A. Kraft: analyses, writing – review & editing. Wolfgang G. Zeier: supervision, conceptualization, analyses, resources, writing – review & editing, funding acquisition.

Conflicts of interest

The authors declare no conflict of interest.

Acknowledgements

This work is funded by the Ministry of Culture and Science of the State North Rhine Westphalia in course of the International Graduate School of Battery Chemistry, Characterization, Analysis, Recycling and Application (BACCARA). The authors acknowledge financial support from the NATTER project, funded by Bundesministerium für Bildung und Forschung (BMBF, project 03XP0525B). We further acknowledge funding from the Deutsche Forschungsgemeinschaft under project number 459785385.

References

1. P. K. Nayak, L. Yang, W. Brehm and P. Adelhelm, Angew Chem. Int. Ed. Engl., 2018, 57, 102–120.
2. J. Janek and W. G. Zeier, Nat. Energy, 2023, 8, 230–240.
3. F. Zheng, M. Kotobuki, S. Song, M. O. Lai and L. Lu, J. Power Sources, 2018, 389, 198–213.
4. G. Zhang, Z. Wen, X. Wu, J. Zhang, G. Ma and J. Jin, J. Alloys Compd., 2014, 613, 80–86.
5. D. Xu, H. Jiang, M. Li, O. Hai and Y. Zhang, Ceram. Int., 2015, 41, 5355–5361.
6. M. Guin and F. Tietz, J. Power Sources, 2015, 273, 1056–1064.
7. J.-M. Winand, A. Rulmont and P. Tarte, J. Solid State Chem., 1991, 93, 341–349.
8. Z. Zhu, I.-H. Chu, Z. Deng and S. P. Ong, Chem. Mater., 2015, 27, 8318–8325.
9. T. Krauskopf, S. Muy, S. P. Culver, S. Ohno, O. Delaire, Y. Shao-Horn and W. G. Zeier, J. Am. Chem. Soc., 2018, 140, 14464–14473.
10. T. Krauskopf, C. Pompe, M. A. Kraft and W. G. Zeier, Chem. Mater., 2017, 29, 8859–8869.
11. M. A. Kraft, L. M. Gronych, T. Famprikis, S. Ohno and W. G. Zeier, Chem. Mater., 2020, 32, 6566–6576.
12. Z. Zhang, E. Ramos, F. Lalère, A. Assoud, K. Kaup, P. Hartman and L. F. Nazar, Energy Environ. Sci., 2018, 11, 87–93.
13. M. Duchardt, U. Ruschewitz, S. Adams, S. Dehnen and B. Roling, Angew. Chem., Int. Ed., 2018, 57, 1351–1355.
14. M. Matsuo, S. Kuromoto, T. Sato, H. Oguchi, H. Takamura and S.-I. Orimo, Appl. Phys. Lett., 2012, 100, 203904.
15. R. Moury, Z. Lodziana, A. Remhof, L. Duchene, E. Roedern, A. Gigante and H. Hagemann, AcCrB, 2019, 75, 406–413.
16. T. Fuchs, S. P. Culver, P. Till and W. G. Zeier, ACS Energy Lett., 2020, 5, 146–151.
17. A. Hayashi, N. Masuzawa, S. Yubuchi, F. Tsuji, C. Hotehama, A. Sakuda and M. Tatsumisago, Nat. Commun., 2019, 10, 5266.
18. J. A. S. Oh, L. He, B. Chua, K. Zeng and L. Lu, Energy Storage Mater., 2021, 34, 28–44.
19. Y. Wang, S. Song, C. Xu, N. Hu, J. Molenda and L. Lu, Nano Mater. Sci., 2019, 1, 91–100.
20. S. Wenzel, T. Leichtweiss, D. A. Weber, J. Sann, W. G. Zeier and J. Janek, ACS Appl. Mater. Interfaces, 2016, 8, 28216–28224.
21. L. E. Goodwin, P. Till, M. Bhardwaj, N. Nazer, P. Adelhelm, F. Tietz, W. G. Zeier, F. H. Richter and J. Janek, ACS Appl. Mater. Interfaces, 2023, 15, 50457–50468.
22. P. Kehne, C. Guhl, Q. Ma, F. Tietz, L. Alff, R. Hausbrand and P. Komissinskiy, J. Power Sources, 2019, 409, 86–93.
23. C. Li, R. Li, K. Liu, R. Si, Z. Zhang and Y.-S. Hu, Interdiscip. Mater., 2022, 1, 396–416.
24. X. Li, J. Liang, X. Yang, K. R. Adair, C. Wang, F. Zhao and X. Sun, Energy Environ. Sci., 2020, 13, 1429–1461.
25. K. Yamada, K. Kumano and T. Okuda, Solid State Ionics, 2005, 176, 823–829.
26. T. Asano, A. Sakai, S. Ouchi, M. Sakaida, A. Miyazaki and S. Hasegawa, Adv. Mater., 2018, 30, 1803075.
27. H. Kwak, J. Lyoo, J. Park, Y. Han, R. Asakura, A. Remhof, C. Battaglia, H. Kim, S.-T. Hong and Y. S. Jung, Energy Storage Mater., 2021, 37, 47–54.
28. J. Park, J. P. Son, W. Ko, J.-S. Kim, Y. Choi, H. Kim, H. Kwak, D.-H. Seo, J. Kim and Y. S. Jung, ACS Energy Lett., 2022, 7, 3293–3301.
29. R. Schlem, S. Muy, N. Prinz, A. Banik, Y. Shao-Horn, M. Zobel and W. G. Zeier, Adv. Energy Mater., 2020, 10, 1903719.
30. T. Zhao, M. A. Kraft and W. G. Zeier, Inorg. Chem., 2023, 62, 11737–11745.
31. T. Zhao, A. N. Sobolev, R. Schlem, B. Helm, M. A. Kraft and W. G. Zeier, ACS Appl. Energy Mater., 2023, 6, 4334–4341.
32. Y. Okada, T. Kimura, K. Motohashi, A. Sakuda and A. Hayashi, Electrochemistry, 2023, 91, 077009–077009.
33. R. Schlem, A. Banik, M. Eckardt, M. Zobel and W. G. Zeier, ACS Appl. Energy Mater., 2020, 3, 10164–10173.
34. E. A. Wu, S. Banerjee, H. Tang, P. M. Richardson, J.-M. Doux, J. Qi, Z. Zhu, A. Grenier, Y. Li, E. Zhao, G. Deysher, E. Sebti, H. Nguyen, R. Stephens, G. Verbist, K. W. Chapman, R. J. Clément, A. Banerjee, Y. S. Meng and S. P. Ong, Nat. Commun., 2021, 12, 1256.
35. P. Juhás, T. Davis, C. L. Farrow and S. J. L. Billinge, J. Appl. Cryst., 2013, 46, 560–566.
36. C. L. Farrow, P. Juhas, J. W. Liu, D. Bryndin, E. S. Božin, J. Bloch, T. Proffen and S. J. L. Billinge, J. Phys.: Condens. Matter, 2007, 19, 335219.
37. S. L. J. Thomae, N. Prinz, T. Hartmann, M. Teck, S. Correll and M. Zobel, Rev. Sci. Instrum., 2019, 90, 043905.
38. E. Sebti, H. A. Evans, H. Chen, P. M. Richardson, K. M. White, R. Giovine, K. P. Koirala, Y. Xu, E. Gonzalez-Correa, C. Wang, C. M. Brown, A. K. Cheetham, P. Canepa and R. J. Clément, J. Am. Chem. Soc., 2022, 144, 5795–5811.
39. R. Schlem, C. F. Burmeister, P. Michalowski, S. Ohno, G. F. Dewald, A. Kwade and W. G. Zeier, Adv. Energy Mater., 2021, 11, 2101022.
40. S. J. L. Billinge, Philos. Trans. R. Soc., A, 2019, 377, 20180413.
41. M. W. Terban and S. J. L. Billinge, Chem. Rev., 2022, 122, 1208–1272.
42. F. M. Michel, S. M. Antao, P. J. Chupas, P. L. Lee, J. B. Parise and M. A. A. Schoonen, Chem. Mater., 2005, 17, 6246–6255.
43. O. Maus, M. T. Agne, T. Fuchs, P. S. Till, B. Wankmiller, J. M. Gerdes, R. Sharma, M. Heere, N. Jalarvo, O. Yaffe, M. R. Hansen and W. G. Zeier, J. Am. Chem. Soc., 2023, 145, 7147–7158.
44. R. Shannon, AcCrA, 1976, 32, 751–767.
45. J. T. S. Irvine, D. C. Sinclair and A. R. West, Adv. Mater., 1990, 2, 132–138.
46. M. Lei, B. Li, H. Liu and D.-E. Jiang, Angew. Chem., Int. Ed., 2023, e202315628.

---

Footnote

† Electronic supplementary information (ESI) available: The ESI includes X-ray diffraction patterns of ball milled Na_3−xIn_1−xZr_xCl₆ series, pair distribution function fitting results, analysis of the In_1−xZr_xCl₆^(3−x)− and NaCl₆⁵⁻ polyhedral, Arrhenius plots from the temperature dependent impedance of ball milled Na_3−xIn_1−xZr_xCl₆ series and the room-temperature impedance data. See DOI: https://doi.org/10.1039/d3ta07209f

---