Securing cation vacancies to enable reversible Mg insertion/extraction in rocksalt oxides

Abstract

Oxide cathode materials have promising applications in rechargeable magnesium batteries (RMBs) due to their high redox potential, which allows the exploitation of the low potential of Mg metal anodes and the eventual realization of RMBs with high energy densities. However, the capacity and cyclability of oxide cathodes, such as spinel oxides, are frequently limited by the irreversible formation of rocksalt oxides during discharging because the rocksalt structure with densely packed cations hinders subsequent facile Mg extraction by charging, eventually leading to electrode deterioration. It is, therefore, of great importance to reveal a mechanism that realizes reversible Mg extraction/intercalation in rocksalt oxides to enhance the conventional oxide cathodes and exploit the rocksalt oxides as novel cathode materials for RMBs. Herein, we show an activation mechanism of rocksalt oxides as a cathode material for RMBs by exemplifying Li-extracted defect disordered rocksalt oxide obtained from Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O, which is capable of reversible Mg insertion/extraction. Extracting the Li cations in the first charging leads to a substantial amount of cation vacancies in the rocksalt structure, facilitating Mg diffusion in subsequent cycles. This vacancy is secured even after fully discharging the material by inserting Mg into the structure because of the lowest possible valence states of the constituent transition metal cations, contributing to the reversible charging/discharging of this material.

---

Introduction

Rechargeable magnesium batteries (RMBs) have been of great interest as next-generation energy storage devices beyond Li-ion batteries (LIBs) due to their potentially high energy density and the abundance of elemental Mg in the earth's crust.^1–3 The high energy density of RMBs derives from the availability of Mg metal anodes that have a high specific capacity of 2205 mA h g⁻¹, a relatively low redox potential of −2.38 V vs. SHE, and preferable plating morphology in contrast to alkaline-metal anodes, which are prone to formation of unfavorable dendrites. RMBs, therefore, have the potential to become an alternative option for safe and economical rechargeable batteries in a variety of applications, including electric vehicles. However, it has also been challenging to realize practical RMBs that are superior to LIBs since the RMB prototype was first proposed in 2000,⁴ mainly because of the lack of appropriate cathode materials. On the basis of a systematic study of chalcogenide cathode materials,⁵ such as oxides, sulfides, and selenide, several sulfide cathode materials have been proposed,^6–8 including a Chevrel phase compound employed in the first RMB prototype,⁴ because Mg diffusion is relatively fast due to weaker coulombic interactions between guest Mg cations and anion lattices compared to that in oxides. However, sulfides inherently tend to yield low redox potentials of 1–2 V vs. Mg²⁺/Mg due to the low electronegativity of sulfur. Oxide materials are therefore generally advantageous for achieving high energy density due to their intrinsically high redox potential (2–3 V vs. Mg²⁺/Mg), which enables the exploitation of the low potential of Mg.

The first challenge in developing oxide cathode materials is to overcome the inherently sluggish Mg diffusion, which is attributed to the stronger affinity between the guest cations of divalent Mg and the oxygen lattice, compared to that in alkaline-metal oxides, such as Li and Na diffusion. This was partially resolved by employing an appropriate structure, such as spinel structures,^9–11 in which the energy barrier of Mg hopping is relatively low (400–800 meV).^12–15 Moderately elevated temperatures of 150 °C can sufficiently activate substantial Mg-cation migration in these materials. Consequently, spinel oxides can accommodate Mg ions at vacant octahedral sites, accompanied by a phase transition into a rocksalt structure (spinel–rocksalt transition).⁹ Another solution was to employ layered oxides such as V₂O₅ (ref. 16–18) and δ-MnO₂ (ref. 19) due to the inherent interlayer space, which can accommodate Mg cations. In δ-MnO₂,¹⁹ Mg cations chelated by amines, which screen the strong coulombic interactions between Mg and the oxygen lattice by coinsertion, enable reversible Mg insertion/extraction. However, compositional flexibility is usually limited in these structural frameworks because the unique properties of the elements V and Mn yield various polymorphs including layered oxides. Furthermore, it was also demonstrated that oxides, such as spinel oxides and polymorphs of MnO₂ (α-,²⁰ γ-, δ-, and λ-MnO₂), became intrinsically metastable after fully inserting Mg into the structures,²¹i.e., Mg oxide itself preferred to form the rocksalt structure as a stable phase, so that they eventually transformed into the rocksalt structure by cycling,⁹ which posed the second challenge for RMB oxide cathodes.

Rocksalt structure formation generally deteriorates battery cyclability due to the sluggish Mg diffusion that occurs in the densely packed cations of the rocksalt structure. For instance, the energy barrier of Mg hopping in pure MgO was reported to be as high as 1900–2400 meV,²² at which Mg diffusion hardly occurs under ordinary battery operating conditions. Thus, oxide cathode materials have been developed by improving the reversibility of the spinel–rocksalt transition or by suppressing the transition itself by utilizing defect structures. The former was achieved by adding Zn to the spinel structure,¹² which improved the reversibility of the rocksalt-to-spinel transition because Zn prefers the tetrahedral oxygen coordination that exists only in the spinel structure. The latter was realized by precisely introducing cation defects into the spinel structure,²³ which yielded Mg insertion sites and eventually suppressed the phase transition into the rocksalt structure within a limited Mg composition. A similar approach was also employed for rutile structures,²⁴ in which Mg was inserted into preliminarily formed defects. However, excessive Mg insertion still induced the rocksalt transition in various oxide materials, in which the number of defect or Mg accommodation sites in the initial structures limited the reversible capacity. Elucidating a mechanism to achieve reversible Mg extraction/insertion in rocksalt oxides is, therefore, a method for improving the oxide cathodes, whose capabilities are limited by the irreversible rocksalt transition. Moreover, the remarkable compositional flexibility of the rocksalt framework will expand the frontier of candidate cathode materials since various 3d and 4d transition metals form rocksalt or its derivative structures, such as layered rocksalt and spinel structures.

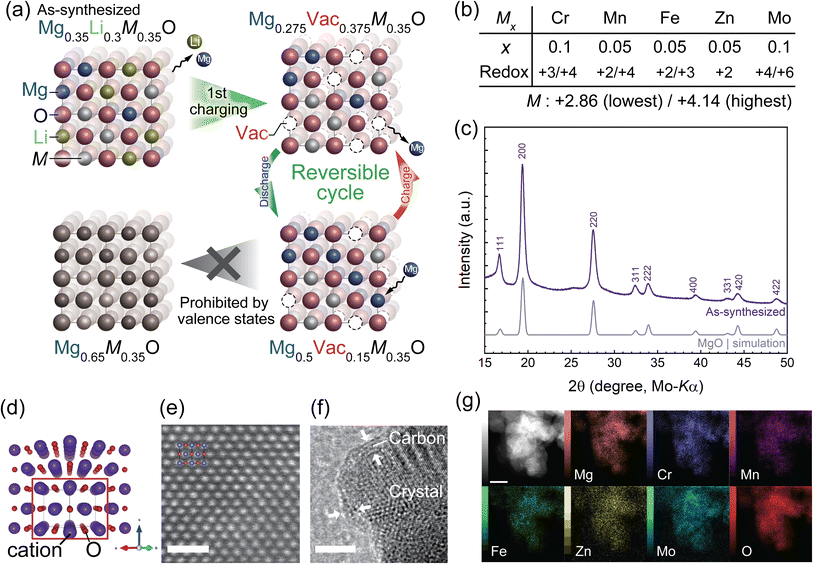
In this study, we reveal a mechanism to activate reversible Mg extraction/insertion in rocksalt oxides by exemplifying a novel high-entropy (HE) defect rocksalt oxide^25–27 of Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O (M7O). To the best of our knowledge, this is the first HE disordered rocksalt (DRX) oxide cathode material for RMBs showing substantial Mg extraction/insertion at 90 °C, which is fairly lower than the operating temperature of 150 °C for the previously reported spinel oxides.^9–11 Heating the cell is, however, still required to facilitate inherently sluggish Mg diffusion in the oxide cathode for the RMBs, which are currently under development in contrast to well-established lithium-ion batteries. The theoretical reversible capacity, potential, and energy density of M7O are 240.4 mA h g⁻¹, ∼2.3 V vs. Mg²⁺/Mg (Fig. S1 in the ESI†), and 553 W h kg⁻¹, respectively.

The composition of the present material is designed based on the following principles. The initial composition contains Li to form cation vacancies (Vac in Fig. 1a) after the first charging cycle, which can expectedly facilitate Mg diffusion in subsequent cycles, as well as induce concerted interactions of coexisting Mg and Li that reduce the energy barrier of Mg hopping.²⁸ The formed vacancy is preserved even after inserting Mg into the structure as much as possible because the lowest average valence state of the constituent transition metals, M, is +2.86 (Fig. 1b), while the average valence state of the cations in stoichiometric rocksalt oxide must be +2. Namely, a vacancy fraction of 0.15 at the cation site is conserved even at the fully discharged state so that the average valence state of the cations is maintained at +2 (Fig. 1a, bottom right). This vacancy secured at the discharged state is expected to yield diffusion paths for Mg in the subsequent charging process and eventually facilitate reversible cycling. A theoretical capacity of 240.4 mA h g⁻¹ was therefore derived from the amount of vacancies formed by Li extraction, which can accommodate Mg, as well as the initial Mg composition, i.e., the composition change between Mg_0.275M_0.35O to Mg_0.5M_0.35O (Fig. 1a), where M refers to other constituent transition metals.

Fig. 1 Design strategy and characterization of Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O (M7O). (a) Charge/discharge process of disordered rocksalt oxide cathodes for RMBs. (b) Composition of constituent transition metals, M, and expected valence changes during charging and discharging. (c) XRPD profiles for the as-synthesized M7O. (d) Perspective view of the rocksalt oxide structure along the [110] direction. (e) HAADF-STEM image along the [110] direction of a typical particle with a diameter of tens of nm. A superimposed atomic illustration showing the positions of the atomic columns. (f) Bright-field TEM image of a particle surface. The white arrows indicate the carbon coating on the particle. (g) STEM-EDS element mapping of primary particles. The scale bars in (e–g) are 1 nm, 5 nm, and 10 nm, respectively.

The amount of vacancies that enables Mg diffusion in the whole particles is discussed based on the percolation theory. A high-entropy strategy^26,29–34 is also employed to finely tune the redox range of the transition metals and obtain a homogeneous DRX structure with multiple guest cations and transition metals, some of which do not solely form rocksalt oxide as a stable phase. Additionally, the high configurational entropy of the present material is expected to ensure the solid-solution reaction after Mg/Li extraction because of its stabilization effect. In contrast, low-entropy materials are prone to transformation into a different structure by the insertion/extraction of guest cations.

Results and discussion

The single-phase M7O material with a rocksalt structure was successfully synthesized by the modified Pechini method, followed by ball milling and carbon coating. All the diffraction peaks in the X-ray powder diffraction (XRPD) pattern of the as-synthesized material were successfully indexed with the single-phase rocksalt structure (Fig. 1c). Atomic-resolution scanning transmission electron microscopy (STEM)-observations with a high-angle annular dark-field (HAADF) detector confirmed the rocksalt structure in real space, in which each cation column showed quite a similar brightness (Fig. 1e). This manifested that the constituent cations occupied virtually the same crystalline cation site and the occupying cations were disordered in the single cation site. The structure was further confirmed by the selected-area electron diffraction pattern, Fourier transform of the HAADF-STEM image (Fig. S2†), and extended X-ray absorption fine structure (EXAFS) spectra, which were successfully fitted by using a model structure of the disordered rocksalt oxide (Fig. S3 and Table S1 in the ESI†) while very weak peaks in the XRPD and STEM observations of a small particle implied the formation of a slight middle-range order of the cations (Fig. S4 and S5†). A carbon coating was employed to ensure sufficient electrical conductivity and suppress the dissolution of the constituent elements,³⁵ as confirmed by transmission electron microscopy (TEM, Fig. 1f). Energy-dispersive spectroscopy (EDS) images taken from the STEM (Fig. 1g) and scanning electron microscopy (SEM, Fig. S6†) images indicated that the constituent elements were homogenously distributed in different spatial scales of nm to μm, i.e., inside and among the particles. Inductively-coupled plasma optical emission spectroscopy (ICP-OES) analyses showed that the composition of the synthesized material was in good agreement with that of the target material (Table S2†), which was further confirmed by the quantitative EDS analyses (Table S3†) of the SEM image shown in Fig. S6.†

The electrode properties were evaluated by several electrochemical techniques, for which a well-established three-electrode beaker cell^9,12,23 was employed and operated in an Ar-filled glove box. The cell was homogenously heated to 90 °C to facilitate Mg diffusion within the cathode material. We chose an electrolyte of Mg(TFSA)₂/G3 with a 1 : 2 mol ratio (TFSA: bis(trifluoromethanesulfonyl)amide; G3 (triglyme): triethyleneglycol dimethyl ether) because its high salt concentration, i.e., low amount of free solvent, reportedly improved the electrolyte stability sufficiently for cathode evaluation in the present temperature and electrochemical window.^36–38 The reference electrode (RE) was Li foil immersed in 0.5 M LiTFSA/DEME-TFSA electrolyte (DEME: N,N-diethyl-N-methyl-N-(2-methoxyethyl)ammonium) separated from the main bath by a ceramic filter rather than Mg metal, which hardly works as a reference electrode because of the passivation in the present electrolyte (Fig. S7†).³⁹ The counter electrode (CE) was a Mg ribbon. The working-electrode (WE) potential, which was converted to V vs. Mg²⁺/Mg as shown in Fig. 2 by using the experimentally determined potential difference of 0.7 V between Li⁺/Li and Mg²⁺/Mg in the present system, was therefore monitored and controlled based on the Li RE (Fig. S7†).³⁶ A large anodic current was observed in a cyclic voltammogram (CV, Fig. 2a) on sweeping toward a high potential in the first cycle, indicating mainly Li extraction because neither the corresponding cathodic current in the low potential region in the 1st cycle nor a comparable anodic current in subsequent cycles was observed. It should be noted that Li was hardly reinserted into the cathode material after the first charging cycle because the electrolyte initially contained no Li cations, and the Li cations extracted from the cathode material were immediately diffused and diluted in the electrolyte bulk such that the Li/Mg molar ratio of the electrolyte was typically <0.003. Indeed, replacing the electrolyte with a pristine one that contained no Li cations after the first charging hardly affected the charge/discharge curves (Fig. S8†), indicating that Li reinsertion after the first charging was negligibly small in the present cell configuration. The almost identical CV profiles from the 2nd to 30th cycles indicated that there was virtually no degradation in the electrode material during these cycles, implying a superior cyclability compared to that of conventional spinel oxide materials, such as MgCo₂O₄.^40,41 On the other hand, the current observed in the CV (Fig. 2a) was substantially attributed to the diffusion-limited redox reaction rather than the electrochemical capacitor reaction, as revealed by the scan-rate dependence of the CV profiles (Fig. S9†).

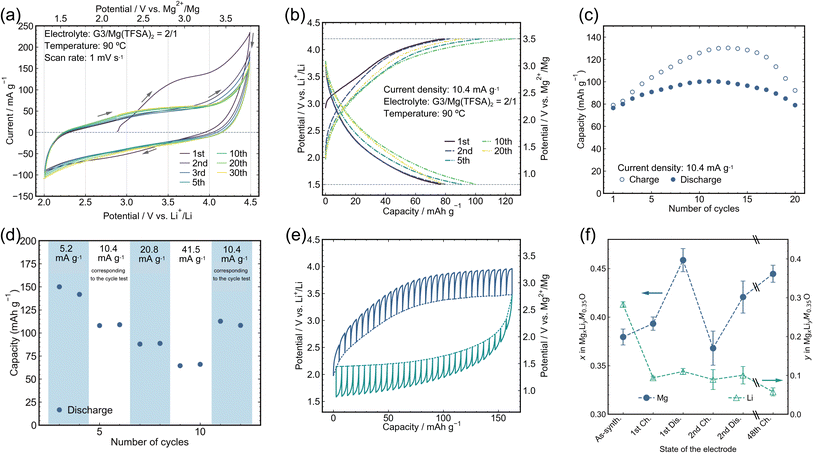Fig. 2 Electrochemical analyses and charge/discharge capabilities. (a) CV of the M7O cathode material between 2.0 and 4.5 V vs. Li⁺/Li with a scanning speed of 1 mV s⁻¹ at 90 °C. (b) Charge and discharge profiles of M7O at 90 °C with a current density of 10.4 mA g⁻¹ within the potential window of 4.2 and 1.5 V for charging and discharging, respectively. See Fig. S8† for the charging/discharging test by replacing the electrolyte with a virgin one after the 1st charging. (c) Capacity retention corresponding to (b). (d) Rate capability from 5.2 mA g⁻¹ to 41.5 mA g⁻¹ evaluated after two conditioning cycles at 10.4 mA g⁻¹. (e) Potential profiles from the GITT obtained by charging (blue lines) and discharging (green lines) at 10.4 mA g⁻¹ for 0.5 h followed by 3 h of rest. The GITT measurement was conducted during the 2nd cycle of the pristine electrode. The solid and dotted lines represent the experimentally measured potential and the potential achieved after 3 h of rest at each step, respectively. (f) Mg and Li composition changes analyzed by ICP-OES after charging/discharging cycles at 10.4 mA g⁻¹. The scale break lines (\\) indicate a large gap in the cycle number.

Charge/discharge tests were conducted using a constant current density of 10.4 mA g⁻¹ at 90 °C with cutoff potentials of 1.5 and 4.2 V vs. Li RE (Fig. 2b). The upper potential limit was decreased from 4.5 V during CV to 4.2 V for the charge/discharge tests to reduce excessive electrolyte decomposition above 4.2 V, as seen in the CV, while the lower potential limit was expanded to 1.5 V to clarify the Mg insertion reaction. A reversible discharge capacity of >∼80 mA h g⁻¹ was constantly observed (Fig. 2c), which is comparable to that of the state-of-the-art defect spinel oxide cathode material for RMBs,²³ while the reversible capacity suddenly decreased after 20 cycles (Fig. S10†), which will be discussed in the subsequent section in detail. A charge capacity larger than the discharge capacity would partially be attributed to the oxidation decomposition of the electrolyte, which became prominent in the high potential region of ∼4 V (Fig. S7†). The change in this capacity discrepancy, i.e., coulombic efficiency, with the cycle number would reflect the evolution of the active material surface condition and area. Still, these details are beyond the scope of this article. The average charge and discharge potentials were in good agreement with those predicted by the ab initio calculations (Fig. S1†). The reversible discharge capacity even increased to as high as 150 mA h g⁻¹ (Fig. 2d) on halving the current density, which strongly indicated that the present material potentially has a large capacity, whereas the available capacity was limited by the slow kinetics, mainly by the inherently sluggish Mg diffusion in the oxide material. Indeed, an overpotential as high as ∼0.5 V was observed during both charging and discharging by the galvanostatic intermittent titration technique (GITT) at a current density of 10.4 mA g⁻¹ (Fig. 2e). The discharge capacity inevitably decreased with increasing current density. Nevertheless, a capacity of >60 mA h g⁻¹ was retained at a current density of 41.5 mA g⁻¹, which was four times larger than that used in the cycle tests.

The origin of the electrochemical capacities observed in the beaker cell at 90 °C was carefully studied through ICP-OES analyses and further electrochemical tests. The ICP-OES analyses (Fig. 2f and S11†) strongly indicated that the Mg composition substantially changed after the 1st discharge and subsequent cycles, whereas the Li composition hardly changed, which demonstrates that the observed electrode capacity in the cycle test (Fig. 2b) was predominantly attributed to Mg extraction/insertion rather than Li extraction/insertion. The substantial capacity of >∼80 mA h g⁻¹ rigorously verified as due to Mg extraction/insertion by the composition analyses stands out from the previously reported DRXs for RMBs, Mg–Ni–O⁴² and Mg–Ni–Co–O⁴³ systems, which showed limited capacity without composition confirmation. Mg extraction/insertion in the present material was also demonstrated by an additional experiment, in which almost identical charge/discharge behavior was observed even on replacing the electrolyte with a pristine one and washing the composite electrode after the 1st charging cycle to eliminate the contribution from the extracted Li cations in the electrolyte (Fig. S8†). On the other hand, a charge capacity of 80 mA h g⁻¹ in the 1st cycle (Fig. 2b) was predominantly attributed to Li extraction from M7O according to the ICP-OES analyses (Fig. 2f), which is quantitatively in excellent agreement with the Li and Mg composition changes. The decrease in 0.18 Li and increase in 0.01 Mg during the 1st charging cycle yielded a charge capacity of 85 mA h g⁻¹ by considering that one electron transfer is equivalent to 534 mA h g⁻¹ per unit Mg_0.35Li_0.3M_0.35O. The slight increase in Mg after the 1st charging cycle was ascribed to the competition between the electrochemical Mg extraction and spontaneous ion exchange from constituent Li to Mg in the electrolyte, where the latter does not accompany current flow in an outer electric circuit. The ion-exchange reaction was separately confirmed to occur by simply immersing the electrode in the electrolyte without any electrochemical operation followed by ICP-OES analysis (Fig. S12†).

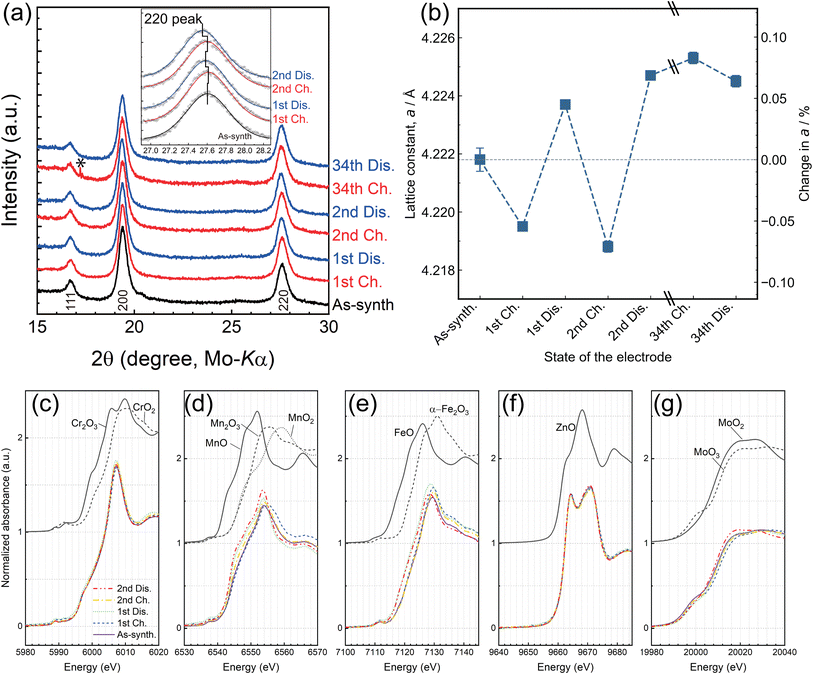
The crystalline and electronic structures of M7O after cycling were analyzed by XRPD and X-ray absorption spectroscopy (XAS), respectively. All profiles of M7O before and after cycling were successfully indexed with the rocksalt oxide structure with neither a phase transition nor the formation of a new phase during cycling (Fig. 3a), while a peak shift was clearly observed depending on the charge/discharge states (inset of Fig. 3a). This result demonstrates that the Mg insertion/extraction in the present system proceeded in a topotactic manner rather than by a two-phase reaction or conversion reaction. The superlattice peaks observed in the as-synthesized state became weaker after cycling (Fig. S13†), which implies that repetitive Mg extraction/insertion disordered the cations, including the transition metals.

Fig. 3 Structure change and redox mechanism of M7O. (a) XRPD profiles of the as-synthesized and cycled M7O materials. The peak indicated by an asterisk is from the Al current collector. The inset shows the magnified 220 peak profiles of the first two cycles. The black circles and solid lines indicate the data and best-fit curves of the peaks, respectively. (b) Change in the lattice constant a of the rocksalt oxide structure during cycles. The scale break lines (\\) indicate a large gap in the cycle number. (c–g), XANES spectra at the K-edge of (c) Cr, (d) Mn, (e) Fe, (f) Zn, and (g) Mo. The purple solid, blue dashed, green dotted, yellow dash-dot, and red dash-dot-dot lines indicate the as-synthesized, 1st charged, 1st discharged, 2nd charged, and 2nd discharged states, respectively, as denoted in the legend in (c).

The magnitude of the peak shifts was further quantitatively evaluated by the Rietveld method (Fig. 3b, S14, and Table S4†), indicating that the lattice shrunk and expanded on charging and discharging, respectively, whose magnitude was as small as 0.43%. The volume change during charging and discharging is rationalized by a general trend where charging oxide cathodes decreases the M–O distances as a result of the smaller ionic radii of M at their higher valence states,⁴⁴ which is attained by the charge compensation that coincides with Mg/Li extraction. It was also demonstrated by the Rietveld method that the occupancy of Mg at the various charge/discharge states (Fig. S15a†) was in excellent agreement with that estimated from the ICP-OES results (Fig. 2f). Furthermore, a substantial amount of vacancies was formed in the first charging and retained in the structure in the subsequent Mg insertion to the structure (Fig. S15b†).

This valence change was also evidenced in the X-ray absorption near edge structure (XANES) spectra of each constituent transition metal ion (Fig. 3c–g), and their local structures at the initial state were analyzed by fitting the EXAFS spectra (Table S1†). Mn, Fe, and Mo exhibited an absorption-edge shift in XANES by charging and discharging, while Cr and Zn did not, indicating that the former elements were redox active in M7O under the present charge/discharge conditions. The valence states of Mn and Fe were close to 2.5+ in the as-synthesized state according to the edge and white line energies, shifting toward 3+ and 2+ on charging and discharging, respectively. The initial valence state of Mo was 4+, shifting between 4+ and 6+ on charging/discharging. Cr is generally known as a “redox active” element in cathode materials.^45,46 However, its absorption-edge energy hardly changed in the present study, which indicated that the potential region was too low to activate the redox reaction between Cr³⁺/Cr⁴⁺. Zn is intrinsically redox inactive such that only its divalent state is generally observed in oxides. Indeed, little valence change of Zn was observed judging from the absorption-edge shift.

The discrepancy between the theoretical (240.4 mA h g⁻¹) and observed (∼150 mA h g⁻¹ at 5 mA g⁻¹ in Fig. 2d) capacities can be explained by the practically available valence changes of the constituent transition metals. For instance, the redox pairs of Cr^3+/4+ and Mn^3+/4+ were expected to be active when estimating the theoretical capacity of M7O, whereas the XANES observation revealed that these redox pairs were not activated within the potential range we examined in the present study, which could yield the discrepancy between the theoretical and experimental capacities. The potential range for the charge/discharge test was limited by the electrochemical window of the electrolyte as well as the large overpotential on the electrode, which is mainly due to the sluggish Mg diffusion. The experimental capacity is expected to approach the theoretical capacity by improving these factors.

The electrode capacity seemed to suddenly decrease after 20 cycles (Fig. S10†) in the present system. Note that the CV measurements, which showed little degradation within 30 cycles, do not necessarily ensure equivalent cyclability in the charge/discharge tests. The duration time for 30 cycles of CV was significantly shorter than that of 20 cycles of the charge/discharge test (42 h and 400 h for CV and the charge/discharge test, respectively). Namely, the shorter duration time of CV decreased the amount of adverse side reactions. The ICP-OES analyses indicate that the Mg compositions of the 34th-cycle samples were similar to that at the 2nd discharge (Fig. 2f). Also, the crystalline structure after 34 cycles remained the disordered rocksalt structure, whose lattice constant was close to that of the 2nd discharge judging from the XRPD profile (Fig. 3a and b). However, the Debye–Waller (DW) factor of the transition metals (TMs) increased from 1.68 Ų at the 2nd discharge to ∼2.05 Ų after 34 cycles, indicating that the dynamic and/or static disorder of the TMs from the ideal cation position increased as a consequence of the structural relaxation accompanied by the Mg insertion/extraction cycles. On the other hand, the XANES spectra (Fig. S16 and S17†) indicate that the absorption edges of Cr, Mn, and Zn after 34 cycles were almost identical to those at the 2nd discharged state, whereas the absorption edges of Fe and Mo slightly shifted toward a higher energy after 34 cycles. This indicates that the Fe–O and Mo–O distances decreased after cycling, presumably because of the structural relaxation observed on the increase in the DW factor rather than their ordinal oxidation judging from the other observations of the lattice constants and ICP-OES results. The charge/discharge cycles induced slight changes in the internal structure. However, it was still unclear if such structural changes directly account for the substantial degradation of the cyclability in light of the bulk-sensitive analyses of XRPD, XAS, and ICP-OES.

Other reasons for the degradation of the cyclability of the present M7O would be attributed to changes at the particle surface: the loss of electric and ionic contact of the electrode material. These can be further ascribed to the irreversible crystalline structure change near the particle surface and/or accumulation of the electrolyte-decomposition products on the particle surface. The former was frequently observed in the conventional layered rocksalt cathodes for LIBs, in which the inactive rocksalt structure is formed near the particle surface,⁴⁷ eventually impeding the facile insertion/extraction of guest ions. The latter would also be critical in the present system. For instance, G3 (solvent) and Mg(TFSA)₂ (salt) in the present electrolyte could slightly decompose on the electrode in high (>4 V) and low (<2 V) potential regions.^36,48 Indeed, the SEM observation after cycling confirmed that the decomposition products covered the surface of the electrode material (Fig. S18†). Besides, electron-induced soft X-ray emission spectroscopy (EXES) indicated that the decomposition products contained sulfur, the only constituent element from the electrolyte. The thickness of the decomposition products was roughly estimated to be less than a few hundred nm, judging from the penetration depth of the 15 kV electron beam, which excited the X-ray fluorescence of sulfur derived from the decomposed electrolyte. Such decomposition products would impede electrochemical reactions on the electrode surface, resulting in capacity decay after cycling.

The decomposition of the electrolyte would also affect the electrochemical capacities. The capacity difference between charging and discharging increased in the first 15 cycles, while it decreased in subsequent cycles (Fig. 2c). The excessive charging capacity could be attributed to the electrolyte decomposition, which increased due to the increase in the active surface of the cathode material due to electrolyte infiltration and/or cracks of the particles. Then, the excessive charging capacity decreased after the electrode surface was covered with the decomposition products of the electrolytes. However, note that the plateau-like potential profiles were not necessarily derived from the electrolyte decomposition judging from the consistently observed capacities in the cycle tests and ICP-OES, and the potential profile of the GITT (Fig. 2e). Developing durable electrolytes should, therefore, be one of the challenges to solve in order to harness the potential capabilities of the present material and ultimately realize practical RMBs. However, detailed electrode-degradation mechanisms are beyond the scope of this article.

The constituent transition metals of M7O were chosen according to the following principles. We chose the early transition metals in their lowest valence state (Cr(III), Mn(II), Fe(II), and Mo(IV)) except for Zn, because of their relatively low redox potentials, which is advantageous for demonstrating the reversible Mg insertion/extraction in the limited electrochemical window of the currently available electrolyte even with the large overpotential. Cr(III) and Mo(IV) also contribute to incorporating Li(I) into DRX, whose average valence state of the constituent cations should be divalent. The function and behavior of Mn(II) and Fe(II) were expected to be similar. However, it was divided into two different elements for the sake of configurational entropy. For instance, the valence states of both Mn and Fe changed between 2+ and 3+ during charging and discharging, contributing to the electrochemical capacity of the electrode (Fig. 3d and e). Likewise, Cr(III) and Mo(IV) were simultaneously incorporated as the higher valence state cations, originally expected to contribute to the charge compensation in charging and discharging like Mn and Fe. However, it was experimentally demonstrated that Cr(III) was not further oxidized at the present low cut-off potential for charging (Fig. 3c). On the other hand, the valence state of Mo changed between 4+ and 6+ during charging and discharging, contributing to the electrochemical capacity (Fig. 3g). In contrast to the other transition metal cations, Zn(II) is an inherently redox-inactive element. However, it can be used as a “spectator cation” in an HE DRX material because Zn strongly prefers tetrahedral coordinates in oxides,¹² as seen for ZnO, which has a wurtzite structure and consequently does not solely form a rocksalt oxide structure, and whose local structure consists entirely of octahedral coordinates. Therefore, Zn(II) was a good indicator that M7O was stable enough to incorporate Zn in the DRX structure at its octahedral site, in addition to the contribution to the configurational entropy. Indeed, the distinctively different XANES spectrum shapes of M7O and a ZnO reference sample (Fig. 3g) indicated that even Zn was incorporated into the rocksalt oxide partially due to the high configurational entropy in the present material. All TM cations hardly migrated to another site, e.g., a tetrahedral site, on charging and discharging judging from the STEM (Fig. S19†) and XANES spectra (Fig. 3c–g), which indicate that TM supports the structural framework of the rocksalt oxide, enabling Mg/Li insertion/extraction in a topotactical manner.

The present study employed the high-entropy strategy^26,29–34 to synthesize a DRX cathode for RMBs containing Li cations that yield vacancies after the first charging and eventually facilitate Mg diffusion. Generally, Li-containing transition metal oxides tend to form cation-ordered structures such as a layered rocksalt structure and a spinel structure.⁴⁹ In addition to these Li-containing ordered structures, combinations of the other elements potentially form a number of cation-ordered structures such as FeCr₂O₄ (spinel structure). It is, therefore, not trivial whether it is possible to synthesize pristine DRX materials containing essential elements such as Mg, Li, and transition metals with the target composition. The present result implies that the large configurational entropy obtained by mixing multiple cations in the present composition thermodynamically contributes to stabilizing the single phase⁵⁰ of DRX M7O over the numerous competing phases mentioned above. The coexistence of the many elements would also ensure the solid-solution reaction after Mg/Li extraction, as shown in the XRD measurements after cycling (Fig. 3a), whereas extraction of the guest cations potentially induces the phase transition to other structures in the other low entropy materials. For instance, it was demonstrated that Mg extraction from the disordered rocksalt oxide of (Mg, Co)O yields the spinel structure of MgCo₂O₄.⁹ However, quantitative evaluations of the entropy-stabilization effect are still challenging even in the relatively simple composition and structure.^29,51 On the other hand, the high entropy composition might facilitate Mg migration in the material.⁵² The Debye–Waller factor of the transition metal cations in M7O determined by the Rietveld analyses (Fig. S15b and Table S4†) was significantly large in comparison with that of the rocksalt monoxides. This indicated that the cations were loosely bonded in the oxygen sublattice because of the shallow interatomic potential and/or static displacements from the ideal cation sublattice, both of which can be ascribed to the coexistence of the various elements with different ionic radii. Such a lattice is expected to decrease the activation energy of Mg migration because the energy increase for locally distorting the lattice for Mg hopping would be smaller in a loosely bonded “flexible” lattice than that in a rigid lattice.

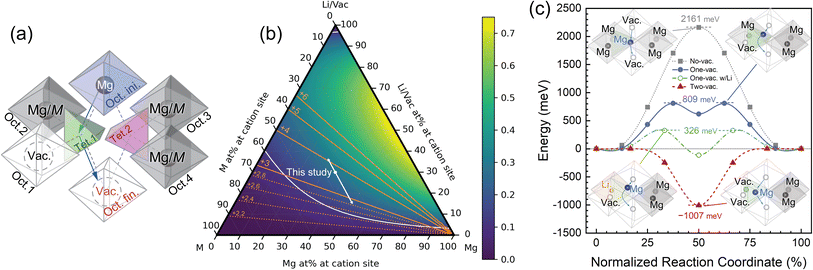
It is of great importance to alleviate the energy barrier of Mg diffusion in order to realize reversible Mg insertion/extraction in rocksalt oxides. To this end, the diffusion mechanism of the present DRX is further discussed from a theoretical perspective. An elementary process of bulk diffusion of guest cations, such as Li/Mg, in the rocksalt structure is hopping from the initial octahedral site (Oct. ini. in Fig. 4a) to an adjacent vacant octahedral site (Oct. fin.) via either one of two tetrahedral sites (Tet. 1 and Tet. 2), each of which has four face-sharing octahedral sites. Two octahedral sites out of four (e.g., Oct. 1 and 2 for Tet.1.) do not directly relate to Mg hopping but possibly affect the corresponding energy barrier. Hereafter, we therefore regard Oct. 1–4 as interfering octahedral sites. The other two octahedral sites are trivial such that each of them is regarded as the guest cation (Oct. ini.) and vacancy (Oct. fin). The distances between the centers of an intermediate tetrahedral site (e.g., Tet. 1) and its face-shared interfering octahedral sites (e.g., Oct. 1 and 2) are so close (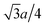 with a lattice constant of a., e.g., 1.82 Å in MgO) that the occupancy state of the interfering octahedral sites significantly affects the energy barrier of ion hopping.

Fig. 4 Energy barriers at the one-vacancy path and percolation probability. (a) Diffusion path via a tetrahedral site facing one vacancy (Oct. 1) at interfering octahedral sites (Oct. 1–4) in the rocksalt structure (one-vacancy path). (b) Probability of the one-vacancy path as a function of composition. (c) Energy barriers of Mg hopping at the different paths in MgO predicted by NEB calculations. In (a), each polyhedron is defined by oxygen atoms at their vertices. Oct. ini. and Oct. fin. are the octahedral sites for a given hopping Mg atom and destination vacancy, respectively, where Tet. 1 and 2 are the intermediate tetrahedral sites for Mg hopping. The gray broken lines connecting two polyhedra represent their face-sharing geometry. The solid blue arrows indicate expected hopping paths whose probabilities are visualized in (b). In (b), the white solid lines are contour curves of a critical bond-percolation probability of 0.120 for opening one-vacancy channels throughout entire particles. The orange lines indicate the average valence state of the constituent metal elements, M, other than guest Mg/Li, after complete delithiation. The white points and arrows represent the initial composition and possible composition range determined by the expected valence change of M, respectively. In (c), the gray dotted, blue solid, and red dashed lines indicate the minimum energy paths (MEPs) of the no-, one-, and two-vacancy paths, respectively. The green dashed-dotted line indicates the MEP of the one-vacancy path, but with Li occupying Oct. 1. The insets represent the atomic configurations of the saddle points or local minimum as well as the path environments.

A pioneering study on DRX for LIBs³⁵ revealed that the “0-TM diffusion channel”, in which no TM occupies the interfering octahedral sites, has an adequately small energy barrier for Li migration. The DRX materials for LIBs are therefore available when the Li fraction in the cation site is high enough to percolate only through 0-TM diffusion channels. Similarly, other previous studies^53–55 using a layered rocksalt structure revealed that the transition metal vacancy, i.e., the absence of TM at the interfering octahedral sites, facilitates Li/Na diffusion in LIBs and Na-ion batteries (NIBs). In these previous studies, the effect of Li occupation on the energy barrier at the interfering octahedral sites was ignored, presumably due to the intrinsically small interactions between the Li cations in Li-containing compounds. For instance, the Li diffusion barriers in Li₂O, Li₂CO₃, and LiF were reported to be as low as 220, 120, and 40 meV, respectively.⁵⁶ However, this is not the case for Mg in DRX because the diffusion barrier of Mg hopping in the simplest MgO was reported to be as high as 1900–2400 meV.²² Furthermore, though the TM vacancy effects studied in the layered rocksalt structure potentially provide essential clues for understanding the diffusion mechanism in the present system, the significant differences regarding the interactions between guest cations themselves and the structural frameworks highlight the need to develop a unique DRX diffusion model for RMBs.

In the present study, we therefore regard the Mg atoms at the interfering octahedral sites as hindering elements of Mg hopping in addition to the transition metals, in contrast to the case of Li diffusion in the previous study.³⁵ A one-vacancy path (Fig. 4a) is defined as a path in which the intermediate tetrahedral site has one vacancy in the interfering octahedral sites (Oct. 1–4). Likewise, a two-vacancy path has two vacancies in the interfering octahedral site adjacent to an intermediate tetrahedral site (Fig. S20a†). The corresponding energy barriers of Mg hopping were calculated by the climbing image-nudged elastic band (NEB) method^57,58 (Fig. 4c), in which the MgO structure was used to semiquantitatively evaluate the effect of the vacancy on the energy barrier in a simplified toy model. Given the complexity and variety of the local structures at Mg in the present high-entropy M7O material, the energy barriers calculated from the MgO model structure would admittedly be too simplified. Nevertheless, we believe that the effects of the constituent vacancies and Li on the hopping barrier in the present calculations are semiquantitatively plausible clues for understanding the diffusion mechanism in the present M7O material.

The energy barrier of Mg hopping drastically decreased to 809 meV for the one-vacancy path (vacancy at Oct. 1) from 2161 meV for the no-vacancy path. This indicates that vacancies, which are formed by prior Li extraction in M7O, facilitate Mg diffusion in the subsequent charging/discharging cycles. An additional vacancy at one of the other interfering octahedral sites (Oct. 3 and 4) was confirmed to slightly affect the energy barrier of the one-vacancy path (Fig. S21†), but its effect was much smaller than the energy differences among the no-, one-, and two-vacancy paths. Also, the elements occupying Oct. 2 affect the energy barrier. For instance, higher-valence cations of Cr and Mo yield energy barriers of 1641 and 2177 meV, respectively, while a lower-valence cation of Zn yields 743 meV (Table 1). Interestingly, the energy barrier of Mg hopping via the one-vacancy path further decreased to 326 meV when Li occupied the interfering octahedral site (Oct. 2), which is comparable to that of Li in cathode materials for LIBs.⁵⁹ This indicated that Li itself facilitated Mg diffusion in addition to vacancy formation by its extraction in the present system. Moreover, this implies the significant advantage of utilizing DRX materials in dual-salt batteries⁶⁰ as well as in RMBs. Similar phenomena were observed both in Chevrel compounds for RMBs²⁸ and layered rocksalt cathodes for Na-ion batteries.⁶¹ Since the Li component remained in the cycled electrode (Fig. 2f), Mg diffusion would also be enhanced to some extent in the present material. These mechanisms to facilitate Mg diffusion enabled battery operation at room temperature, whereas the still sluggish Mg diffusion at this temperature limited the reversible capacity (Fig. S22†). However, a more sophisticated synthesis to yield hierarchically structured ultrasmall particles⁶² would enhance the capabilities of the present material at room temperature. On the other hand, the energy barrier of the two-vacancy path was virtually negligible, whereas there was a local minimum at the tetrahedral site, whose energy was −1007 meV compared to the original octahedral site. Mg atoms in the two-vacancy path would therefore be spontaneously drawn into the tetrahedral site and stabilized until the next hopping event and/or the occupation of the other atoms at the surrounding vacant octahedral sites. The diffusion paths with low energy barriers should be connected throughout the entire particle to allow Mg atoms to percolate from the particle to the electrolyte and vice versa. Since each type of diffusion path randomly exists with a probability determined by a given composition in the ideal defect rocksalt structure, the probabilities of each path were evaluated and discussed from the perspective of percolation theory.

Table 1 Energy barriers of Mg hopping in the one-vacancy path with various cations occupying the Oct. 2 site in Fig. S21b

Element at the Oct. 2 site	Li	Mg	Cr	Mn	Fe	Zn	Mo
Energy barrier (meV)	326	809	1640	1421	1059	743	2177

---

The percolation probabilities of the one- and two-vacancy paths were analytically calculated and are shown in the ternary diagrams (Fig. 4b and S20b†), for which it was assumed that Li was completely extracted and the vacancies were randomly distributed as per the composition. The critical percolation probability for the bond process, i.e., 0.120,⁶³ is shown as a contour curve by using a white solid line, indicating that Mg can diffuse in an infinite medium by hopping only in the corresponding paths above this probability. Hereafter, percolation via the one-vacancy path is mainly discussed because the percolation probability of the two-vacancy path would be negligibly small in the material (see Fig. S20b† and its discussion), and Mg at the tetrahedral site, which could be yielded in the two-vacancy path, was hardly observed by STEM (Fig. S19†).

The first criterion for activating DRX materials for RMBs is the vacancy formation by Li extraction from the structure in the first charging cycle. The Li composition should therefore be greater than 0.198, which is the critical percolation probability for the site process. We consider the site process for Li in contrast to that for Mg, which is referenced by the bond process in percolation theory, because Li should be extracted via the no-vacancy path due to the low amount of cation vacancies, especially at the beginning of the first charging cycle, while the Mg-hopping behavior should be affected by the path environment, i.e., “bonds” in percolation theory, in the subsequent charging/discharging cycles. The energy barrier of Li hopping via the no-vacancy path in MgO was as low as 957 meV (Fig. S23†), which is less than half that of Mg hopping, because of the intrinsically weak coulombic interaction of Li in the oxide. The elevated temperature of 90 °C in the present study would therefore sufficiently activate Li hopping even via the no-vacancy path. Indeed, most Li was extracted after the first charging cycle in the present Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O (Fig. 2f), whose Li composition was above the percolation limit of 0.198 but less than ∼0.55, which is a proposed threshold value for activating DRX materials for LIBs at room temperature.³⁵

The second criterion is that the percolation probability at the initial composition must be above the critical values of the one-vacancy path. Namely, the initial composition should lie inside the white contour line in the ternary plots of the probabilities shown in Fig. 4b. This ensures that the constituent Mg can migrate from the bulk to the surface and vice versa only through the one-vacancy path, while the critical value decreases in finite particles depending on their size.

The third criterion concerns the possible Mg composition range during charging and discharging, which is shown as white arrows in Fig. 4b and S20b† for the present system. The possible range of the Mg component should be within the percolative region. Otherwise, once Mg fills vacancies to block the percolation path, subsequent Mg extraction is extremely difficult. This would be a reason for the limited cyclability of conventional spinel materials, for which Mg extraction is challenging once Mg is inserted into the pristine spinel structure. Also, for instance, Mg_0.5Li_0.1Cr_0.1Mn_0.1Fe_0.1Zn_0.1O, whose composition matches the critical value in Fig. 4b, showed much less capacity and fast degradation (Fig. S24†) due to the inadequate amount of vacancies formed by Li extraction. The Mg composition range can be controlled by the available valence state of the transition metals in addition to the amount of vacancies, which was actually taken advantage of in the present study. The orange lines in Fig. 4b represent the valence state of M after complete delithiation. For example, designing the M composition so that the lowest valence state is higher than 2.6+ ensures that the one-vacancy path can yield a percolation network during battery cycling in theory when the cation fraction of M is 0.35, while the lowest valence state of the present M7O is 2.86+, which satisfies this criterion.

The existence of the one- and two-vacancy paths was further confirmed by the model structure constructed based on the DFT calculation because it is challenging to directly observe the diffusion paths, i.e., the configuration of the cation vacancies, experimentally. The configuration of Mg and vacancies in the present M7O model structure was optimized to minimize the formation energy calculated by the DFT at each Mg composition (Fig. S1b†). The interaction between Mg and vacancies (attractive or repulsive) was, therefore, reflected in the optimized structure. The probabilities of the one- and two-vacancy paths were numerically evaluated in this optimized structure and compared with the analytical values statistically estimated in the randomly distributed Mg and vacancies (Fig. S25†). The path probabilities obtained from the model structure demonstrated that the one-vacancy path and the two-vacancy path substantially exist in the structure, whose probabilities were in good agreement with those analytically estimated within the error bars. This indicates that Mg and vacancies are distributed virtually in a random manner from an energetic perspective. Note that such a random distribution should be more enhanced at battery-operation temperature and coincides more with the analytical value because of the entropy contribution to the Mg-vacancy configuration.

Conclusions

The mechanisms for activating reversible Mg insertion/extraction in the rocksalt oxides were proposed by studying a DRX material of Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O, which was the first DRX cathode capable of reversible Mg insertion/extraction to the best of our knowledge. The present material yielded a reversible capacity of ∼90 mA h g⁻¹ at a current density of 10.4 mA g⁻¹ with a potential of ∼2.0 V vs. Mg²⁺/Mg at 90 °C, which was a relatively low temperature in comparison with that for the previously reported spinel-oxide cathodes operated at 150 °C.^9–11 The reversible capacity was even further increased to ∼150 mA h g⁻¹ by halving the current density, which implies that kinetics is a key factor in improving this type of material. The present study revealed that including Li in the initial composition of the DRX oxide enabled the reversible Mg insertion/extraction for the following reasons: (1) yielding the vacancies necessary for subsequent Mg migration after Li extraction at the first charging, (2) controlling the valence state of the other transition metal cations, and (3) enhancing Mg diffusion through concerted interactions.²⁸ Thus, these criteria were further semi-quantitatively manifested based on the theoretical considerations of ab initio CI-NEB calculations and percolation theory. The CI-NEB calculations showed that the one-vacancy path significantly alleviated the energy barrier of Mg hopping to 809 meV in the rocksalt structure, which was significantly decreased from that of the no-vacancy path by ∼1300 meV. To exploit the advantage of the one-vacancy path in DRX materials, the amount of vacancies must always be greater than a value defined by the critical percolation probability during charging and discharging (Fig. 4b). The vacancies formed after Li extraction should be preserved after Mg insertion, which can be realized particularly by controlling the lowest valence state of the constituent transition metal cations. The high-entropy strategy employed in the present study enabled us to control the compositions that satisfy the target range of the valence state finely and to ensure the solid-solution reaction within the defect rocksalt structure because of the stabilization effect of the configurational entropy.

At the nascent research stage of oxide cathodes for RMBs, it has been debated whether or not Mg is genuinely inserted into the structures of many oxide materials.⁵ The spinel–rocksalt transition, clearly detectable by XRPD, was firm evidence that Mg can be surely inserted into the oxide materials semitopotactically, in which the guest cations are inserted into the structure by maintaining the oxygen sublattice, while the cation configuration changes.⁹ However, rocksalt structure applications have been unfortunately circumvented^12,23 because of its slow kinetics and the limited reversibility of the phase transition back into the spinel structure, which leads to insufficient cyclability. Eventually, the rocksalt structure was considered a “grave” structure, into which most of the Mg-inserted oxides for RMBs are thermodynamically drawn.^20,21,40 Nevertheless, the present study sheds light on rocksalt oxide cathode materials for RMBs to reveal the criteria for utilizing this structure framework and ultimately expands the design opportunities of oxide cathodes for RMBs in general, which become possible due to the compositional flexibility of high-entropy oxides.^29,30 The present study and revealed criteria pave the way for exploring novel DRX materials and other oxide materials that potentially transition into rocksalt oxides, ultimately contributing to the future realization of practical RMBs.

Experimental

Synthesis

The active material Mg_0.35Li_0.3Cr_0.1Mn_0.05Fe_0.05Zn_0.05Mo_0.1O was synthesized by the Pechini process⁶⁴ followed by carbon coating. Stoichiometric amounts of Mg(NO₃)₂·6H₂O (Wako, 99%), LiNO₃ (Wako), Cr(NO₃)₃·9H₂O (Strem Chemicals, 99%), Mn(NO₃)₂·6H₂O (Wako, 98%), Fe(NO₃)₃·9H₂O (Wako, 99.9%), Zn(NO₃)₂·6H₂O (Nacalai Tesque, 99%), and (NH₄)₆Mo₇O₂₄·4H₂O (Wako, 99%) were dissolved in propylene glycol C₃H₈O₂ (Wako, 98%) with citric acid anhydrous (Wako, 98%) so that the molar ratio of [metal element] : [propylene glycol] : [citric acid] was 1 : 3 : 3. Deionized water was added to facilitate dissolution, whose typical amount was ∼300 ml for a single batch of 200 mmol of the final product. The solution was stirred at 80–120 °C for 4 h until all the reagents were thoroughly dissolved, then heated up to and held at 200 °C to initiate polymerization for 20 h, followed by firing at 450 °C for 2 h in air to remove excess propylene glycol. The resulting powder was ball-milled in ethanol and calcined at 600 °C for 10 h under a 5% H₂–Ar gas flow. The obtained black powder was ball milled and mixed with sucrose (Wako, ≤100%) at an 8 : 2 weight ratio of [powder] : [sucrose]. Approximately 5 ml water was added to dissolve 0.25 g of sucrose. The mixture was hand milled using an alumina mortar and pestle for 10 minutes, followed by drying at 130 °C and firing at 600 °C for 4 hours under a 5% H₂–Ar gas flow. The final products were again hand-milled for characterization.

Electrochemical test

Composite electrodes for the electrochemical measurements were prepared by mixing the active material, carbon black (Super C65, Timcal), and polyvinylidene difluoride (PVDF, Kureha) with a weight ratio of 8 : 1 : 1. The obtained slurry was applied to a piece of Al foil and dried in a vacuum at 120 °C for 12 h. Note that Al metal was confirmed to be stable enough in the present electrochemical system and potential region (Fig. S26†). Typically, 2–3 mg of the active material was loaded on the ∼10 × 10 mm² area out of the 10 × 30 mm² Al foil. Three-electrode beaker cells, which were assembled and operated in Ar-filled glove boxes, were employed for all the electrochemical measurements. The details of the beaker cell are described elsewhere.^9,12,23 The cells were embedded in an Al-metal block and homogenously heated to 90 °C by using a hot plate. An electrolyte of Mg(TFSA)₂/triglyme with a 1 : 2 mol ratio (TFSA: bis(trifluoromethanesulfonyl)amide; triglyme: triethyleneglycol dimethyl ether) was used. As a counter electrode (CE) and reference electrode (RE), a Mg ribbon (Kojundo Chemical Laboratory) and Li foil (Honjo Metal) immersed in 0.5 M LiTFSA/DEME-TFSA electrolyte (DEME: N,N-diethyl-N-methyl-N-(2-methoxyethyl) ammonium) separated from the main bath by a ceramic filter were used. Mg(TFSA)₂ and LiTFSA were provided by Kishida Chemical (battery grade). DEME-TFSA was provided by Kanto Chemical. Triglyme was provided by Tokyo Chemical Industry and dried using 3 Å molecular sieves before use. The electrochemical measurements were conducted using VMP3, VSP-300, and VSP apparatus (Biologic). Cyclic voltammetry was performed between 2.0 and 4.5 V vs. Li RE with a scanning rate of 1 mV s⁻¹. Galvanostatic charge/discharge tests were carried out at a current density of 10.4 mA g⁻¹ in a potential window of 1.5–4.2 V vs. Li RE, while rate capability tests were performed with different current densities every two cycles after two conditioning cycles at 10.4 mA g⁻¹ at the beginning of the tests.

Sample characterization

X-ray powder diffraction (XRPD) measurements were performed using a Smartlab (Rigaku) equipped with a Mo X-ray source and 1D detector (D/teX, Rigaku). The as-synthesized sample was measured using Bragg–Brentano geometry. The electrode samples before and after the electrochemical tests were encapsulated in a Lindeman glass capillary with a diameter of 500 μm in Ar-filled glove boxes to avoid exposure to an air atmosphere, and were measured using Debye–Scherrer geometry. Scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) were conducted using a JSM-7200F (JEOL) operated at 15 kV, for which the samples were transferred from the glove boxes by using a transfer vessel without exposure to the air atmosphere. Scanning transmission electron microscopy (STEM) and EDS analyses were carried out using a spherical-aberration corrected microscope JEM-ARM200F (JEOL) operated at 200 kV. The samples for the STEM observation were suspended on molybdenum-mesh grids covered with thin perforated carbon. X-ray absorption spectroscopy (XAS) was performed in transmission mode at BL5S1 in the Aichi Synchrotron Radiation Center, Japan. The washed composite electrodes were mixed with BN, pelletized into 6 mm diameter disks, sealed with polyimide film tape, and measured without exposure to the air atmosphere. The chemical compositions of the metal elements and carbon were analyzed by the inductively-coupled plasma optical emission spectroscopy (ICP-OES) and infrared absorption methods after combustion, respectively. The electrochemically cycled samples for the characterization studies mentioned above were prepared by charging/discharging the electrodes at a current density of 10.4 mA g⁻¹ in a potential window of 1.5–4.2 V vs. Li RE at 90 °C, washing them with acetonitrile, removing them from the Al current collector, and processing them for each analysis in Ar-filled glove boxes.

Structural analyses by XRPD and EXAFS

Rietveld analyses were performed using Rietan-FP⁶⁵ based on the MgO rocksalt structure (space group: Fm3̄m, #225). Lattice constants, peak profiles, instrument functions, and background were refined, along with the structure parameters of the rocksalt oxide. For the cation 4a sites, disordered occupation of the constituent cations was assumed, in which the Debye–Waller (DW) factors of Mg and Li were set to 0.31 and 1.8, respectively, according to the reported values for each element.^66,67 For the as-synthesized sample, the DW factor of a virtual chemical species of Mg/Li was set to 1.0 based on the mol fraction of Mg/Li in the present material. The occupancy of Mg was refined for the electrochemically cycled samples, in which the occupancy of Li was fixed to 0.1 as per the ICP-OES results because of Li's small X-ray scattering power.

EXAFS analyses were performed by using the IFEFFIT program code.⁶⁸ The rocksalt structure was assumed for the FEFF simulation to calculate backscattering amplitudes and phase shifts. Only the spectra of Cr, Mn, Fe, and Zn were analyzed because spectra of the other cations, i.e., Li, Mg, and Mo, were not measured (Li and Mg) or of inadequate data quality (Mo). Scattering paths for the fit were then obtained by averaging individually calculated paths, which were simulated from simple rocksalt oxides containing a single cation, i.e., MgO, MnO, etc., according to the cation fraction of M7O. The first and second coordination shells were analyzed by the least-square method in radial space, while the background was co-refined as needed. A single inner potential shift parameter, ΔE₀, was used for each fit. Amplitude reduction terms of each element were determined from preliminary analyses of reference samples.

DFT calculations

Density functional theory (DFT) calculations were performed using the Vienna ab initio software package (VASP),^69,70 which implements a projector-augmented-wave (PAW) approach⁷¹ and the exchange-correlation effects described with the Perdew–Burke–Ernzerhof (PBE) generalized gradient approximation (GGA).⁷² The Hubbard U parameters for correction of on-site Coulomb interactions for Cr, Mn, Fe, and Mo were set to 3.5, 3.9, 4.0, and 4.38 eV, respectively, according to a previous study.⁷³ The ionic positions, lattice parameters, and angles were relaxed so that the energy converged to less than 10⁻⁴ eV per MO. Special quasirandom structures (SQSs) of MO were produced with 40 atoms based on cation correlations obtained from the cluster expansion lattice model implemented in the alloy-theoretic automated toolkit (ATAT).^74,75 For the electrode potential calculation as a function of Mg composition, possible Mg-vacancy configurations were optimized within the original Mg and Li sites followed by the energy calculation that accompanies the structure relaxation.

The Mg migration barrier was evaluated by the climbing image-nudged elastic band (CI-NEB) method.^57,58 The 2 × 2 × 2 supercell of a cubic MgO cell was used as a model structure. For the NEB calculations, the atomic force tolerance was set to 0.05 eV Å⁻¹. In the case where a local minimum was found in the minimum energy path (MEP), its energy was individually evaluated by relaxing the structure and used to interpolate the MEP plot.

Percolation probability

The probabilities of the one-vacancy and two-vacancy paths were analytically derived based on the polyhedral networks shown in Fig. 4. The probability of the one-vacancy path, P_one, was derived as a product of a probability regarding the initial/final octahedral sites and that regarding the interfering octahedral sites. Here, we define P_Mg, P_M and P_Vac as the probabilities of occupation at the cation site by Mg, transition metals M, and vacancies, respectively, for the following derivation. Namely, P_M + P_Vac + P_Mg = 1 is always true by definition, and each probability is equivalent to the molar fraction of the cation site. The probability regarding the initial/final octahedral sites was calculated as (1 − P_M)² because both initial and final octahedral sites have to be occupied by Mg or vacancies so that the transition metals do not block the path. The probability regarding the interfering octahedral sites was calculated by summing the exclusive probabilities at each number of vacancies occupying the interfering octahedral sites. For example, the probability that only one vacancy occupies one of the interfering octahedral sites was calculated as 4P_Vac(1 − P_Vac)³. A factor of four was derived from the possible configuration of the vacancies at the four octahedral sites. By calculating the probabilities of the different numbers of vacancies and summing them, P_one was derived as 4(1 − P_M)²P_Vac(1 − P_Vac)(1 − P_Vac + P_Vac²). Likewise, the probability of the two-vacancy path was derived as P_two = (1 − P_M)²P_Vac²(2 − P_Vac²).

Author contributions

Conceptualization: TK, TI; funding acquisition: TK, TI; investigation: TK, MY, NN, KS, NLO, HL; supervision: TK, TI; visualization: TK, MY, NLO; methodology: TK; writing – original draft: TK; writing – review & editing: TK, MY, NN, KS, HL, NLO, TI.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors thank Dr Takuya Hatakeyama and Dr Hiroshi Tanimura for the fruitful discussions and technical support. The work by TK was supported by JSPS KAKENHI Grant numbers 19K15307, 21H01646, and 22KK0068. The work by TI was partially supported by JSPS KAKENHI Grant numbers 18H05249 and 23H05452. The ICP-OES analyses were supported by F. Sakamoto, K. Nakayama, and Y. Kabasawa at the Analytical Research Core for Advanced Materials, IMR, Tohoku University. The authors acknowledge the Center for Computational Materials Science, Institute for Materials Research, Tohoku University for the use of MASAMUNE-IMR (Project no. 2012SC0401 and 2112SC0401). The crystalline structure was drawn by Vesta.⁷⁶

Notes and references

1. Y. Liang, H. Dong, D. Aurbach and Y. Yao, Nat. Energy, 2020, 5, 646–656.
2. C. You, X. Wu, X. Yuan, Y. Chen, L. Liu, Y. Zhu, L. Fu, Y. Wu, Y.-G. Guo and T. van Ree, J. Mater. Chem. A, 2020, 8, 25601–25625.
3. Y. Wang, Y. Sun, W. Ren, D. Zhang, Y. Yang, J. Yang, J. Wang, X. Zeng and Y. NuLi, Energy Mater., 2022, 2, 200024.
4. D. Aurbach, Z. Lu, A. Schechter, Y. Gofer, H. Gizbar, R. Turgeman, Y. Cohen, M. Moshkovich and E. Levi, Nature, 2000, 407, 724–727.
5. P. Canepa, G. Sai Gautam, D. C. Hannah, R. Malik, M. Liu, K. G. Gallagher, K. A. Persson and G. Ceder, Chem. Rev., 2017, 117, 4287–4341.
6. L. Blanc, C. J. Bartel, H. Kim, Y. Tian, H. Kim, A. Miura, G. Ceder and L. F. Nazar, ACS Mater. Lett., 2021, 3, 1213–1220.
7. X. Sun, P. Bonnick, V. Duffort, M. Liu, Z. Rong, K. A. Persson, G. Ceder and L. F. Nazar, Energy Environ. Sci., 2016, 9, 2273–2277.
8. K. Shimokawa, T. Furuhashi, T. Kawaguchi, W.-Y. Park, T. Wada, H. Matsumoto, H. Kato and T. Ichitsubo, J. Mater. Chem. A, 2021, 9, 16585–16593.
9. S. Okamoto, T. Ichitsubo, T. Kawaguchi, Y. Kumagai, F. Oba, S. Yagi, K. Shimokawa, N. Goto, T. Doi and E. Matsubara, Adv. Sci., 2015, 2, 1500072.
10. D. C. Hannah, G. Sai Gautam, P. Canepa and G. Ceder, Adv. Energy Mater., 2018, 8, 1–12.
11. I. D. Johnson, A. N. Mistry, L. Yin, M. Murphy, M. Wolfman, T. T. Fister, S. H. Lapidus, J. Cabana, V. Srinivasan and B. J. Ingram, J. Am. Chem. Soc., 2022, 144, 14121–14131.
12. K. Shimokawa, T. Atsumi, M. Harada, R. E. Ward, M. Nakayama, Y. Kumagai, F. Oba, N. L. Okamoto, K. Kanamura and T. Ichitsubo, J. Mater. Chem. A, 2019, 7, 12225–12235.
13. G. Sai Gautam, P. Canepa, A. Urban, S.-H. Bo and G. Ceder, Chem. Mater., 2017, 29, 7918–7930.
14. Z. Rong, R. Malik, P. Canepa, G. Sai Gautam, M. Liu, A. Jain, K. Persson and G. Ceder, Chem. Mater., 2015, 27, 6016–6021.
15. M. Liu, Z. Rong, R. Malik, P. Canepa, A. Jain, G. Ceder and K. A. Persson, Energy Environ. Sci., 2014, 8, 964–974.
16. J. L. Andrews, A. Mukherjee, H. D. Yoo, A. Parija, P. M. Marley, S. Fakra, D. Prendergast, J. Cabana, R. F. Klie and S. Banerjee, Chem, 2018, 4, 564–585.
17. H. D. Yoo, J. R. Jokisaari, Y. S. Yu, B. J. Kwon, L. Hu, S. Kim, S. D. Han, M. Lopez, S. H. Lapidus, G. M. Nolis, B. J. Ingram, I. Bolotin, S. Ahmed, R. F. Klie, J. T. Vaughey, T. T. Fister and J. Cabana, ACS Energy Lett., 2019, 4, 1528–1534.
18. X. Zhang, D. Li, Q. Ruan, L. Liu, B. Wang, F. Xiong, C. Huang and P. K. Chu, Mater. Today Energy, 2023, 32, 101232.
19. S. Hou, X. Ji, K. Gaskell, P. F. Wang, L. Wang, J. Xu, R. Sun, O. Borodin and C. Wang, Science, 2021, 374, 172–178.
20. C. Ling, R. Zhang, T. S. Arthur and F. Mizuno, Chem. Mater., 2015, 27, 5799–5807.
21. T. Hatakeyama, H. Li, N. L. Okamoto, K. Shimokawa, T. Kawaguchi, H. Tanimura, S. Imashuku, M. Fichtner and T. Ichitsubo, Chem. Mater., 2021, 33, 6983–6996.
22. F. Zhang, A. M. Walker, K. Wright and J. D. Gale, J. Mater. Chem., 2010, 20, 10445–10451.
23. K. Shimokawa, T. Atsumi, N. L. Okamoto, T. Kawaguchi, S. Imashuku, K. Wagatsuma, M. Nakayama, K. Kanamura and T. Ichitsubo, Adv. Mater., 2021, 33, 2007539.
24. T. Koketsu, J. Ma, B. J. Morgan, M. Body, C. Legein, W. Dachraoui, M. Giannini, A. Demortière, M. Salanne, F. Dardoize, H. Groult, O. J. Borkiewicz, K. W. Chapman, P. Strasser and D. Dambournet, Nat. Mater., 2017, 16, 1142–1148.
25. P. Barnes, Y. Zuo, K. Dixon, D. Hou, S. Lee, Z. Ma, J. G. Connell, H. Zhou, C. Deng, K. Smith, E. Gabriel, Y. Liu, O. O. Maryon, P. H. Davis, H. Zhu, Y. Du, J. Qi, Z. Zhu, C. Chen, Z. Zhu, Y. Zhou, P. J. Simmonds, A. E. Briggs, D. Schwartz, S. P. Ong and H. Xiong, Nat. Mater., 2022, 21, 795–803.
26. Z. Lun, B. Ouyang, D.-H. H. Kwon, Y. Ha, E. E. Foley, T.-Y. Y. Huang, Z. Cai, H. H. Kim, M. Balasubramanian, Y. Sun, J. Huang, Y. Tian, H. H. Kim, B. D. McCloskey, W. Yang, R. J. Clément, H. Ji and G. Ceder, Nat. Mater., 2021, 20, 214–221.
27. Q. Wang, A. Sarkar, D. Wang, L. Velasco, R. Azmi, S. S. Bhattacharya, T. Bergfeldt, A. Düvel, P. Heitjans, T. Brezesinski, H. Hahn and B. Breitung, Energy Environ. Sci., 2019, 12, 2433–2442.
28. H. Li, N. L. Okamoto, T. Hatakeyama, Y. Kumagai, F. Oba and T. Ichitsubo, Adv. Energy Mater., 2018, 8, 1801475.
29. C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 8485.
30. T. Kawaguchi, X. Bian, T. Hatakeyama, H. Li and T. Ichitsubo, ACS Appl. Energy Mater., 2022, 5, 4369–4381.
31. Z. Gu, J. Guo, J. Cao, X. Wang, X. Zhao, X. Zheng, W. Li, Z. Sun, H. Liang and X. Wu, Adv. Mater., 2022, 34, 2110108.
32. A. Sarkar, Q. Wang, A. Schiele, M. R. Chellali, S. S. Bhattacharya, D. Wang, T. Brezesinski, H. Hahn, L. Velasco and B. Breitung, Adv. Mater., 2019, 31, 1806236.
33. T. Jin, X. Sang, R. R. Unocic, R. T. Kinch, X. Liu, J. Hu, H. Liu and S. Dai, Adv. Mater., 2018, 30, 1–5.
34. L. Lin, K. Wang, A. Sarkar, C. Njel, G. Karkera, Q. Wang, R. Azmi, M. Fichtner, H. Hahn, S. Schweidler and B. Breitung, Adv. Energy Mater., 2022, 2103090, 2103090.
35. J. Lee, A. Urban, X. Li, D. Su, G. Hautier and G. Ceder, Science, 2014, 343, 519–522.
36. K. Shimokawa, H. Matsumoto and T. Ichitsubo, J. Phys. Chem. Lett., 2018, 9, 4732–4737.
37. T. Kimura, K. Fujii, Y. Sato, M. Morita and N. Yoshimoto, J. Phys. Chem. C, 2015, 119, 18911–18917.
38. K. Hashimoto, S. Suzuki, M. L. Thomas, T. Mandai, S. Tsuzuki, K. Dokko and M. Watanabe, Phys. Chem. Chem. Phys., 2018, 20, 7998–8007.
39. M. Oishi, T. Ichitsubo, S. Okamoto, S. Toyoda, E. Matsubara, T. Nohira and R. Hagiwara, J. Electrochem. Soc., 2014, 161, A943.
40. K. Shimokawa, T. Hatakeyama and T. Ichitsubo, in Rechargeable Batteries for Electric Vehicles, ed. K. Kanamura, Elsevier, 2022.
41. K. Shimokawa and T. Ichitsubo, Curr. Opin. Electrochem., 2020, 21, 93–99.
42. N. Kitamura, Y. Konishi, W. Ma, N. Ishida, T. Mandai, C. Ishibashi and Y. Idemoto, Sci. Rep., 2022, 12, 1–8.
43. Y. Idemoto, T. Takahashi, N. Ishida, M. Nakayama and N. Kitamura, Inorg. Chem., 2019, 58, 5664–5670.
44. R. D. Shannon, Acta Crystallogr., 1976, A32, 751–767.
45. J. Huang, P. Zhong, Y. Ha, D. Kwon, M. J. Crafton, Y. Tian, M. Balasubramanian, B. D. McCloskey, W. Yang and G. Ceder, Nat. Energy, 2021, 6, 706–714.
46. N. Yabuuchi, K. Yamamoto, K. Yoshii, I. Nakai, T. Nishizawa, A. Omaru, T. Toyooka and S. Komaba, J. Electrochem. Soc., 2013, 160, A39–A45.
47. F. Lin, I. M. Markus, D. Nordlund, T. C. Weng, M. D. Asta, H. L. Xin and M. M. Doeff, Nat. Commun., 2014, 5, 3529.
48. L. Suo, O. Borodin, T. Gao, M. Olguin, J. Ho, X. Fan, C. Luo, C. Wang and K. Xu, Science, 2015, 350, 938–943.
49. T. Kim, W. Song, D.-Y. Son, L. K. Ono and Y. Qi, J. Mater. Chem. A, 2019, 7, 2942–2964.
50. S. J. McCormack and A. Navrotsky, Acta Mater., 2021, 202, 1–21.
51. M. Fracchia, M. Coduri, M. Manzoli, P. Ghigna and U. A. Tamburini, Nat. Commun., 2022, 13, 2977.
52. Y. Zeng, B. Ouyang, J. Liu, Y. Byeon, Z. Cai, L. J. Miara, Y. Wang and G. Ceder, Science, 2022, 378, 1320–1324.
53. T. Wang, J. Yang, H. Wang, W. Ma, M. He, Y. He and X. He, Adv. Energy Mater., 2023, 13, 2204241.
54. X. Li, C. Ma and Y. Zhou, Chem.–Eur. J, 2023, 29, e202203586.
55. M.-S. Kwon, S. G. Lim, Y. Park, S.-M. Lee, K. Y. Chung, T. J. Shin and K. T. Lee, ACS Appl. Mater. Interfaces, 2017, 9, 14758–14768.
56. L. Benitez and J. M. Seminario, J. Electrochem. Soc., 2017, 164, E3159–E3170.
57. G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904.
58. G. Henkelman and H. Jónsson, J. Chem. Phys., 2000, 113, 9978–9985.
59. M. S. Islam and C. A. J. Fisher, Chem. Soc. Rev., 2014, 43, 185–204.
60. T. Ichitsubo, S. Okamoto, T. Kawaguchi, Y. Kumagai, F. Oba, S. Yagi, N. Goto, T. Doi and E. Matsubara, J. Mater. Chem. A, 2015, 3, 10188.
61. J. E. Wang, W. H. Han, K. J. Chang, Y. H. Jung and D. K. Kim, J. Mater. Chem. A, 2018, 6, 22731–22740.
62. H. Kobayashi, Y. Fukumi, H. Watanabe, R. Iimura, N. Nishimura, T. Mandai, Y. Tominaga, M. Nakayama, T. Ichitsubo, I. Honma and H. Imai, ACS Nano, 2023, 17, 3135–3142.
63. D. Stauffer and A. Aharony, Introduction to Percolation Theory, Taylor & Francis, London, 2nd edn, 2018.
64. T. Hatakeyama, N. L. Okamoto, K. Shimokawa, H. Li, A. Nakao, Y. Uchimoto, H. Tanimura, T. Kawaguchi and T. Ichitsubo, Phys. Chem. Chem. Phys., 2019, 21, 23749–23757.
65. F. Izumi and K. Momma, IOP Conf. Ser.: Mater. Sci. Eng., 2011, 18, 022001.
66. V. G. Tsirelson, A. S. Avilov, Y. A. Abramov, E. L. Belokoneva, R. Kitaneh and D. Feil, Acta Crystallogr., Sect. B: Struct. Sci., 1998, 54, 8–17.
67. N. Douakha, M. Holzapfel, E. Chappel, G. Chouteau, L. Croguennec, A. Ott and B. Ouladdiaf, J. Solid State Chem., 2002, 163, 406–411.
68. B. Ravel and M. Newville, J. Synchrotron Radiat., 2005, 12, 537–541.
69. G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
70. G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775.
71. P. E. Blöchl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
72. J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868.
73. A. Urban, I. Matts, A. Abdellahi and G. Ceder, Adv. Energy Mater., 2016, 6, 1600488.
74. A. Van De Walle and G. Ceder, J. Phase Equilib., 2002, 23, 348–359.
75. A. Van de Walle, M. Asta and G. Ceder, CALPHAD: Comput. Coupling Phase Diagrams Thermochem., 2002, 26, 539–553.
76. K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta07942b

---