Open Access Article
Open Access ArticleRapid in situ growth of high-entropy oxide nanoparticles with reversible spinel structures for efficient Li storage†
Siyu
Zhu‡
a,
Wei
Nong‡
ab,
Lim Jun Ji
Nicholas
 a,
Xun
Cao
a,
Xun
Cao
 a,
Peilin
Zhang
c,
Yu
Lu
a,
Mingzhen
Xiu
a,
Peilin
Zhang
c,
Yu
Lu
a,
Mingzhen
Xiu
 d,
Kang
Huang
e,
Gang
Wu
d,
Kang
Huang
e,
Gang
Wu
 b,
Shuo-Wang
Yang
b,
Shuo-Wang
Yang
 b,
Junsheng
Wu
e,
Zheng
Liu
b,
Junsheng
Wu
e,
Zheng
Liu
 a,
Madhavi
Srinivasan
*a,
Kedar
Hippalgaonkar
a,
Madhavi
Srinivasan
*a,
Kedar
Hippalgaonkar
 *af and
Yizhong
Huang
*af and
Yizhong
Huang
 *a
*a
aSchool of Materials Science and Engineering, Nanyang Technological University, 50 Nanyang Avenue, Singapore 639798, Singapore. E-mail: madhavi@ntu.edu.sg; kedar@ntu.edu.sg; yzhuang@ntu.edu.sg
bInstitute of High Performance Computing, Agency for Science, Technology and Research, 1 Fusionopolis Way, Connexis, Singapore 138632, Singapore
cSchool of Mechanical and Electrical Engineering, Jiaxing Nanhu University, Jiaxing 314001, China
dEnergy Research Institute, Interdisciplinary Graduate Programme, Nanyang Technological University, Singapore
eInstitute for Advanced Materials and Technology, University of Science and Technology Beijing, 30 Xueyuan Road, Beijing 100083, China
fInstitute of Materials Research and Engineering, Agency for Science, Technology and Research, Singapore 138634, Singapore
First published on 16th April 2024
Abstract
High-entropy oxides (HEOs) are considered promising electrode materials as they have great potential to provide much higher energy density and cyclability than their conventional electrode counterparts such as graphite. In the present work, nanostructured HEOs were fabricated on the surface of conductive carbon black using laser beam irradiation, which generally implements the rapid bottom-up carbothermal process. Furthermore, electrochemical performances of Co-free and Co-incorporated HEO nanoparticles in comparison with bulk-HEO counterparts were investigated. In particular, the Co-free (LiFeNiMnCuZn)3O4 nanoparticle electrode showed the best capability presenting both the highest cycling value of 866 mA h g−1 (100% capacity retention) after 800 cycles at 0.5 A g−1 and rate performances of 585 at 2.0 A g−1 and 436 mA h g−1 at 5.0 A g−1 without decay. The long cycling performance of Co-free HEOs could be derived from the reversible spinel structure, according to the in situ X-ray diffraction (XRD) results, as well as the strong thermal stability of high-entropy mixing phases, as indicated by a large positive decomposition enthalpy according to density functional theory (DFT) calculations. Additionally, the assembled full cell (LiFeNiMnCuZn)3O4‖LiNi0.6Co0.2Mn0.2O2 delivered a power density of 670 W h kg−1 with a high discharge voltage around 3.7 V based on the 0.1C discharge profile. As manifested by the DFT calculations, the low anode voltage of HEOs measured here is due to the electron-sufficient Zn, which favors the Ni2+/Ni3+ redox couple. This work is expected to provide a guideline for the development of advanced high-entropy nanostructured electrode materials for efficient batteries.
Introduction
At present, lithium-ion batteries (LIBs) are commonly used in our daily life activities due to their stable charge/discharge capacity, long cycle life, and cost effectiveness.1–3 The traditional graphite anode plays an important role in the application and research of LIBs. However, relatively low theoretical specific capacity (372 mA h g−1), sluggish Li-ion transport, and death-Li metal deposition of graphite hamper the development of LIBs, particularly in the field of fast-charge batteries.4,5 These shortcomings motivated researchers to search for more effective alternative electrode materials.The emerging high-entropy materials (HEMs) are considered potential candidates for use as electrodes in rechargeable batteries.6–8 By the combination of over five transition metal elements, this group of materials share unique properties such as high-entropy stabilization and cocktail effect.9–11 Other than these, HEOs can also be regarded as a type of transition metal oxides (TMOs), which have already been proven as LIB anodes with multi-electron transfer reactions.12,13 This property confers a higher theoretical capacity of over 1000 mA h g−1. The relatively high electrochemical potential of this type of material may provide less power but has less risk of forming metallic Li. However, when applied in energy storage devices, TMOs might suffer from structural destruction due to their phase changes during the charge/discharge processes.14 In contrast, the accommodation of five or more elements with different ion volumes in HEOs causes the distortion of crystal structures that may protect them from serious structural damage during lithiation and delithiation.15–17 Therefore, efforts have been made to integrate HEOs into the LIBs in recent years. A (FeCoNiCrMn)3O4 HEO material18 was reported to exhibit cycling stability and a reversible capacity of 596.5 mA h g−1 with a capacity retention of 86.2% after 1200 cycles at 2.0 A g−1. Some researchers focused on removing Co elements. The single-phase (CrNiMnFeCu)3O4 material without Co exhibited a rate capacity of 480 mA h g−1 when subjected to a current density of 2000 mA g−1.19 However, the absolute capacities reported in this research cannot exceed the ones with cobalt.
When it comes to the electrode design of rechargeable batteries, nanoparticles are one of the best choices, which can improve the ion/electron transport. High-entropy materials in combination with nanoparticles show high potential in battery applications. However, the HEO nanoparticle electrodes for LIBs reported in previous works were mostly prepared by ball milling or hydrothermal methods.20,21 The nanoparticle size distributions by these traditional top-down methods can be hardly minimized down below 100 nm. Moreover, the extra heat produced during ball milling may undermine some potential active structures.18 In contrast, laser and microwave were used as effective approaches to fabricate high-entropy nanoparticles known as the carbothermal methods.22 Among them, the laser-based carbothermal method implements both rapid heating in nanosecond shocking followed by fast quenching of the carbon substrate with high thermal conductivity. It enables the formation of single-phase high-entropy nanomaterials.23 Furthermore, the laser-based method only needs up to 30 min for a batch of samples, while the traditional solid sintering process needs up to 12 h in a high-temperature environment, which costs more heat and time. However, the mass-loading ratios of the prepared samples in previous studies were much low (approximately 22 wt%),24,25 which are insufficient for the electrodes of LIBs. Therefore, this work is also aimed to increase the concentration of nanostructured active materials to meet the requirements of battery electrodes.
In the current study, we used a scaled-up (up to 51% mass ratio) and bottom-up laser-based method to fabricate HEO nanoparticles on a conductive carbon surface at high speed. The carbon black substrate not only functions as the conductive network in the electrode material but also provides favorable conditions for rapid heating and cooling to synthesize nanoparticles. Based on the literature, we applied the advanced carbothermal method using a laser to fabricate HEO nanoparticle composite electrodes in batteries at the very beginning. Furthermore, the Co-free and Li-involved nanoparticle electrode material (LiFeNiMnCuZn)3O4 (abbreviated as LFNM-CuZn) was focused on. The chosen Li, Fe, Ni, Mn, Cu and Zn elements are based on the principle of similar ionic radii to facilitate the formation of HEOs. Among them, Li would improve the compatibility with lithium ions. Fe, Ni and Mn are classic anode elements, which can provide high specific capacity.26 Cu and Zn can not only provide capacity in anodes but also improve material stability and reaction reversibility.27 To investigate the influence of Co elements in HEO nanoparticle electrodes, two other HEO nanoparticle anode materials were synthesized using the same method. They were denoted as (LiFeNiMnCoZn)3O4 (abbreviated as LFNM-CoZn) and (LiFeNiMnCoCu)3O4 (abbreviated as LFNM-CoCu). Furthermore, a bulk-HEO sample was fabricated by annealing the LFNM-CoZn sample to compare the electrochemical performance between HEO nanoparticles and HEO blocks.
Results and discussion
In this research, the HEO electrode was prepared by a laser-based carbothermal method, which enables the in situ growth of HEO nanoparticles on the surface of conductive carbon subject to the rapid heating and cooling processes under laser irradiation.18,28–30 Carbon black was first acid-treated and mixed with a nitrate solution prepared according to the molar ratio. The as-prepared precursor was then sonicated and vacuum-dried in a tungsten crucible. In the next step, HEO nanoparticles spontaneously grew on the carbon substrate through laser radiation sintering within a short time. Fig. 1 shows the schematic diagram illustrating the synthesis process of the HEO nanoparticle electrode material, where HEO nanoparticles are uniformly dispersed over the surface of carbon black. A representative on-site photo is displayed in Fig. S1a† and a corresponding video was recorded, showing the scanning processes of laser radiation (please refer to the ESI†). During the process, the precursor became more compact after the irradiation process.Structure and morphology
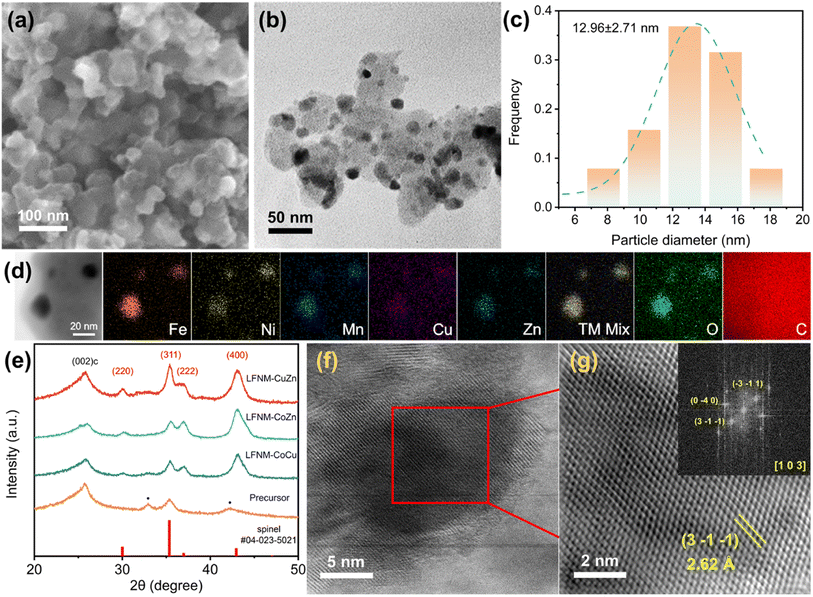
The decoration of HEO spherical nanoparticles over the surface of conductive carbon black is shown in Fig. 2a, a secondary electron image acquired using a scanning electron microscope (FESEM 7600F). Fig. 2b shows the corresponding bright-field image of LFNM-CuZn acquired using a JEOL 2100F transmission electron microscope (TEM). The particles were measured to be around 13 nm from the size distribution in Fig. 2c, analyzed from Fig. 2b. The uniform distribution of all metal elements across the C substrate is verified by energy-dispersive X-ray spectroscopy (EDX) mapping (Fig. 2d). The TEM images of LFNM-CoCu and LFNM-CoZn are presented in Fig. S2.†Fig. 2f presents the high-resolution transmission electron microscopic (HRTEM) image of an HEO nanoparticle with a diameter of approximately 10 nm taken along the [1 0 3] zone axis. It was performed by indexing the FFT pattern (inset) obtained from Fig. 2g, a magnified lattice structure of the squared area (marked in Fig. 2f). The d-spacing of the (3−1−1) lattice plane was calculated to be 2.62 Å, which is consistent with the XRD analysis.XRD technique was used to reveal the phase structures of HEOs. The obtained patterns of HEOs and their precursor are shown in Fig. 2e. Among them, the XRD spectrum of the precursor mainly consists of three peaks. Carbon black shows an identical peak at 25.8°, ascribed to the (0 0 2) plane of carbon, and metal nitrate peaks at 32.9° and 42.3°. After the laser shock process in air, the peaks at 32.9° and 42.3° become invisible, while five new diffraction peaks appear as marked in red. They are indexed to be spinel characteristic peaks (refer to PDF#04-023-5021) at around 30.0°, 35.3°, 36.8° and 43.1° ascribed to the (2 2 0), (3 1 1), (2 2 2) and (4 0 0) planes of the HEO crystal, respectively. These indicate the complete decomposition of metal nitrates and the formation of spinel HEO phases after laser irradiation. Meantime, the relatively broad peaks in these spectra result from the fact that the HEOs are in the form of nanoparticles.31 In order to clarify the size effect of HEOs on the properties, bulk-HEO counterparts were grown by the aggregation of HEO nanoparticles during annealing at 800 °C. They were measured to be around 150 nm in diameter (Fig. S3†). In summary, the high-entropy nanoparticles were successfully fabricated on the acid-treated carbon black with the spinel structure.
Composition analysis
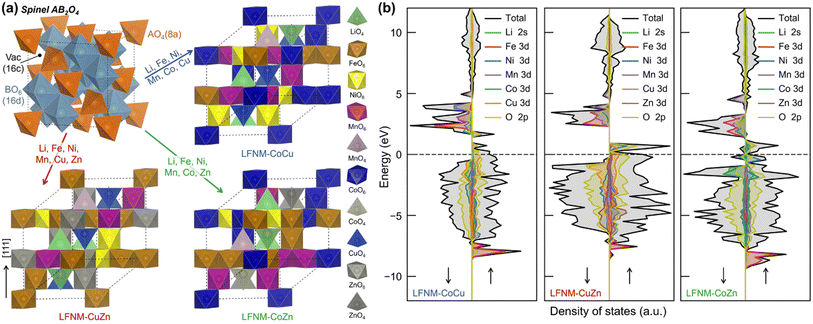
Inductively coupled plasma-mass spectroscopy (ICP-MS) was used to investigate the elemental distribution of HEOs. The pristine mass concentration data of HEOs acquired by the ICP-MS method are listed in the Table S1.† In order to directly present the elements' amount of substance, the data are normalized in Table S1.† Generally, the elemental contents of Ni, Fe, Cu, Zn, Li, and Mn remain almost identical. The slight reduction of Zn and Li elements may result from their evaporation during the laser heating process due to their fairly low boiling points of 907 °C and 1340 °C at standard pressure.32As illustrated in Fig. 3a, the spinel oxide AB2O4 contains two types of metal–oxygen (M–O) polyhedra, AO4 tetrahedron and BO6 octahedron, forming two repeating layers along the [111] direction. One repeating layer is constructed with pure edge-sharing octahedral, while another one repeating layer with octahedra and tetrahedra mixed. To model the HEOs, the composition of metals from ICP-MS measurements was fitted into the spinel formula (Table S1†), as follows: (Li0.4Mn0.1Cu0.5)[Mn0.25Fe0.3Zn0.2Ni0.25]2O4, (Li0.4Mn0.1Co0.1Zn0.4)[Mn0.25Fe0.25Co0.25Ni0.25]2O4 and (Li0.4Mn0.1Cu0.5)[Mn0.25Fe0.25Co0.25Ni0.25]2O4 for LFNM-CuZn, LFNM-CoZn and LFNM-CoCu, respectively. The configuration entropies of HEOs were estimated using eqn (1) of ESI.† As listed in Table S2,† the entropy of LFNM-CoZn is 3.97 R/formula, where R is the gas constant, slightly higher than those of LFNM-CoCu (3.71 R/formula) and LFNM-CuZn (3.70 R/formula). This arises from one more metal element occupying at the tetrahedral A site.
Thermal stability and electronic properties
Thermogravimetric analysis-differential scanning calorimetry (TGA-DSC) coupling technique was used to measure the mass loading ratios of HEOs on the carbon black substrate as well as the thermal stability. The experiments were performed from 30 °C to 800 °C under a synthetic air atmosphere (N2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) O2 = 80
O2 = 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 20) to remove the carbon content. All samples showed main mass reduction around 400 °C due to the oxidation of carbon black (Fig. S4a†). The corresponding mass loadings of LFNM-CuZn, LFNM-CoZn, and LFNM-CoCu are 51.38%, 39.23%, and 40.18% calculated from the TG results, indicating that the mass loadings of some HEO nanoparticles can reach over 50% by the advanced laser synthesis method. After the electrodes were assembled, the active mass ratio was calculated to be approximately 46.24%, 35.31%, and 36.16%, respectively without additional conductive carbon. These active mass ratio values are closer to 0.6–0.7 in agreement with that reported in the literature.33 This allows carbothermal-made nanomaterials to be used as electrodes in batteries. Moreover, all three TG curves are very smooth above 400 °C, indicating the excellent thermal stability of HEO samples (Fig. S4b†). The current density and specific capacity used in the electrochemical experiments were calculated based on the TG results.
20) to remove the carbon content. All samples showed main mass reduction around 400 °C due to the oxidation of carbon black (Fig. S4a†). The corresponding mass loadings of LFNM-CuZn, LFNM-CoZn, and LFNM-CoCu are 51.38%, 39.23%, and 40.18% calculated from the TG results, indicating that the mass loadings of some HEO nanoparticles can reach over 50% by the advanced laser synthesis method. After the electrodes were assembled, the active mass ratio was calculated to be approximately 46.24%, 35.31%, and 36.16%, respectively without additional conductive carbon. These active mass ratio values are closer to 0.6–0.7 in agreement with that reported in the literature.33 This allows carbothermal-made nanomaterials to be used as electrodes in batteries. Moreover, all three TG curves are very smooth above 400 °C, indicating the excellent thermal stability of HEO samples (Fig. S4b†). The current density and specific capacity used in the electrochemical experiments were calculated based on the TG results.
To determine the stabilization mechanism and electronic properties of HEOs, extensive density functional theory (DFT) calculations were performed (see Methodology for details). Given the compositions as obtained from ICP-MS measurements as well as the site occupations of each metal, the special quasi-random structure (SQS)34 was adopted to simulate the disordering of HEOs. The representative SQS cells were generated and selected as described in Methodology (results illustrated in Fig. S5†). The structures are demonstrated in Fig. 3a, where the metal ions are dispersed randomly for the simulation of the disordered cationic arrangement. The calculated equilibrium lattice constants of LFNM-CoCu, LFNM-CuZn and LFNM-CoZn are 8.20, 8.23 and 8.24 Å, respectively (Table S3†). To determine the stabilization mechanism of the prepared HEOs, the decomposition energies (enthalpies), ΔHd, were calculated according to eqn (S2) and summarized in Table S4.† The resulting ΔHd values for LFNM-CuZn, LFNM-CoZn and LFNM-CoCu, are all in positive 1.99, 1.10 and 0.33 eV/formula, respectively. This indicates that HEOs are thermodynamically (enthalpy) stable without the tendency to decomposing or phase-separating into mono-oxides, well consistent with the observed mixed elements in scanning transmission electron microscopy (STEM)-EDX mappings (Fig. 2d). The stability of the HEOs was also confirmed by DSC measurement, where no decomposition of HEOs was observed up to 800 °C. Additionally, the highest ΔHd value (thermal stability) of LFNM-CuZn amongst the HEOs might facilitate the long cycling performance during the charge–discharge process.
The battery performance is contributed by the intrinsic electronic properties of electrode materials. Then, the density of states (DOS) of HEOs were calculated at the DFT+U level, as shown in Fig. 3b. Overall, all the DOS of HEOs are dominated by the metal 3d and O 2p bands from −12 to 12 eV (vs. Fermi level). For metal ions with U applied, their upper Hubbard band (UHB) is well separated from the lower Hubbard band (LUB), as illustrated in Fig. S6,† which are similar to the cases in the respective mono-metal oxides (Fig. S7†), whereas one can note that the band widths and positions of Ni 3d UHB significantly differ from one HEO to another (Fig. S6†), and this key difference could have effect on the performance of HEO anodes.
To study the valence states of elements, X-ray photoelectron spectroscopy (XPS) technique was performed against the LFNM-CuZn sample. In the Li 1s spectra, the peak at 55.6 eV is assigned to Li+, which verifies the existence of Li (Fig. S8a†), as proven by ICP-MS results. There is only one Mn 2p3/2 characteristic peak at 641.8 eV in the Mn 2p spectra (Fig. S8b†). According to the XPS database, Mn4+ is likely the valence here.35 The Mn 2p1/2 peak is positioned at 653.8 eV. Fe components are separated into two valence states in the Fe 2p spectra (Fig. S8c†). The peaks at 710.6 and 713.5 eV are attributed to Fe2+ and Fe3+, respectively.36 Their 2p1/2 peaks are visible at 724.6 and 727.7 eV. There are also two valence states in the Ni spectra. The Ni 2p3/2 characteristic peak is convoluted into the Ni2+ and Ni3+ peaks located at 854.9 eV and 856.2 eV respectively (Fig. S8d†).37 The Ni 2p1/2 spectra generate two peaks at 873.0 and 874.6 eV. Cu and Zn in the LFNM-CuZn sample present single valences. Two peaks of 934.0 and 954.0 eV are assigned as Cu 2p3/2 and 2p1/2, while 1021.6 and 1044.7 eV peaks are associated with Zn 2p3/2 and 2p1/2 (Fig. S8e and S8f†).38
Lithium storage and diffusion in half-cell batteries
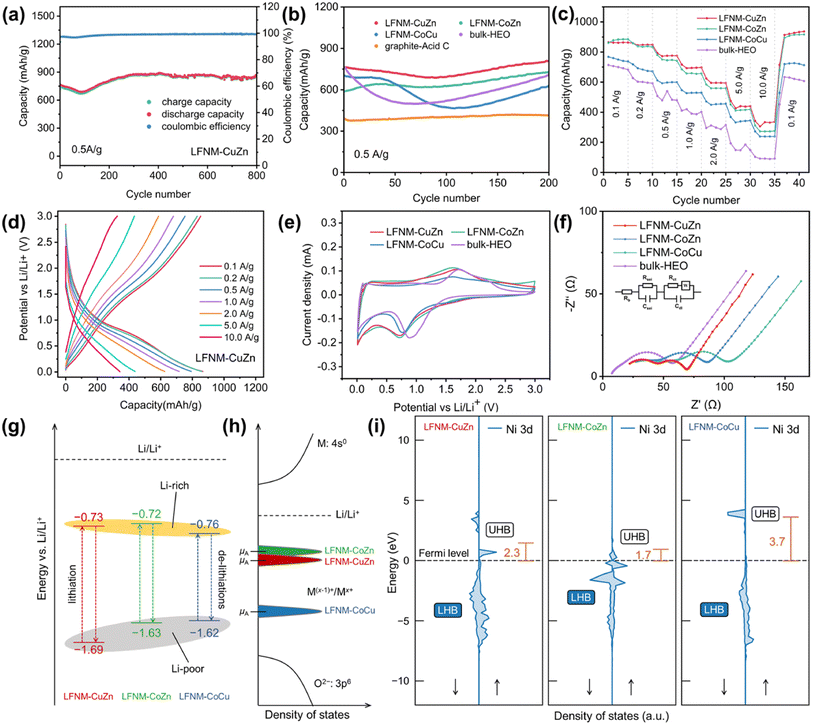
In Fig. 4a, galvanostatic charge–discharge tests were conducted to evaluate the Li+ storage of the as-prepared samples. The initial discharge/charge of LFNM-CuZn was 1217.5/857.7 mA h g−1 at 0.1 A g−1, delivering an initial coulombic efficiency (ICE)39 of 70.4%. At 0.5 A g−1, the initial specific capacity of LFNM-CuZn electrode is 759 mA h g−1, which then slowly decays till 93 cycles followed by an increase. This phenomenon is commonly agreed in the literature due to the phase transformation.26,40 After charge/discharge of 800 cycles, the capacity retention of the Co-free HEO electrode remains 100% and the reversible capacity reaches a value of 866 mA h g−1. This is the highest cycle specific capacity among HEO anodes to our best knowledge27,41–46 with alkali metal and Co-free HEOs, as shown in Table S5 and Fig. S9.† Moreover, the high-capacity retention of LFNM-CuZn after long charge–discharge cycles might be associated with its materials' stability, as indicated by the highest decomposition enthalpy (Table S4†) that could contribute to the phase stability of HEO.Fig. 4b shows the comparison of the cycling performances of the as-prepared electrodes before 200 cycles. The LIB half-cell assembled with LFNM-CuZn provides the best cyclic charge/discharge capacity and stability. Other HEO electrodes show a relatively low initial capacity at 0.5 A g−1. They are 589, 700, and 762 mA h g−1 for LFNM-CoZn, LFNM-CoCu, and bulk-HEO, respectively. The specific capacity values decline at around the 100th cycle and then continuously increase until the 200th cycle. Afterwards, the capacities of three samples are stabilized at 726, 623, and 713 mA h g−1, respectively. In comparison with the LFNM-CoZn nanoparticle electrode, the LIB assembled with bulk-HEO presents a high initial capacity at 762 mA h g−1 but subject to the fastest drop. The lowest value was down to 497 mA h g−1, indicating a rapid phase transformation during cycling. Concerning the utilization of acid for treating carbon black, a cell with graphite and acid-treated carbon black (abbreviated as graphite-acid-C) was assembled. During 200 cycles at 0.5 A g−1, the reference sample remains at a low capacity around 390 mA h g−1, which is close to the theoretical capacity of graphite. The gravimetry capacity of graphites theoretically is 372 mA h g−1.47 The ratio of conductive carbon to active material in HEO nanoparticle electrodes is nearly identical to that of the reference graphite electrodes with similar mass loadings. It is believed that the conductive carbon in the HEO electrodes contributes approximately 18 mA h g−1 of specific capacity (at 0.5 A g−1).
To investigate the lithiation/delithiation capability of HEO nanoparticle-based electrodes at different specific currents, rate performance experiments were evaluated. The Co-free electrode LFNM-CuZn delivers (Fig. 4c) capacities of 436 mA h g−1 at 5.0 A g−1 and 342 mA h g−1 at 10.0 A g−1, the highest among the reported HEO anodes according to the literature. The highly stable crystal structure of HEOs and the alternating structure of active material nanoparticles with a conductive network facilitate the efficient transportation of massive current.48,49 In contrast, the LFNM-CoZn/LFNM-CoCu electrodes with cobalt afford relatively low capacities, which are 418/344 and 275/238 mA h g−1 at 5.0 and 10.0 A g−1. In the previous works, cobalt was considered as the key to improving the capacity of LIBs but highly expensive and environmentally detrimental50 even in HEO electrodes. Hereby, the results illustrate that cobalt is not a compulsory part to boost the rate capacity among the HEO nanoparticle electrodes, which is beneficial for its large-scale applications. The bulky counterpart of HEO nanoparticles shows shows the weakest in the comparisons of rate performance as the unstable trends lasted over 0.5 A g−1 and the capacity of only 91 mA h g−1 delivered at 10 A g−1. These results indicate that HEO nanomaterial electrodes are obviously advantageous in rate capacity over HEO bulk electrodes.
Fig. 4d shows the charge–discharge curve of LIBs assembled with LFNM-CuZn nanoparticle electrodes at different rates. Due to the kinetic limitation in electrochemical reactions,51 the specific capacities inevitably declined from 865 to 624/437/342 mA h g−1, as the current rate rose from 0.1 A g−1 to a relatively high rate of 2.0/5.0/10.0 A g−1. Nonetheless, the attenuation of capacity in the LFNM-CuZn-based electrode was not large as the capacity retention maintained at outstanding levels of 72.1%/50.5%/39.5%. Significantly, even at an ultrahigh rate of 10.0 A g−1, the LFNM-CuZn high-entropy nanoparticle electrode could deliver a considerable capacity of 342 mA h g−1, which can still meet the requirements of commercial cathodes. The inclined discharge and charge platforms of HEO anodes are at around 0.72 and 1.65 V. Among them, the plateau of the LFNM-CuZn electrode was most stable and longest in the low voltage area.
The cyclic voltammetry (CV) technique was used to better understand the electrochemical properties of HEOs. In Fig. 4e, reduction peaks in the negative scan at 0.729/0.715/0.763/0.890 V for LFNM-CuZn/LFNM-CoZn/LFNM-CoCu/bulk-HEO were evident, indicating the main discharge plateaus of conversion reactions. In the following positive scan of CV, broad peaks at 1.689/1.625/1.616/1.727 V were observed as the occurrence of a re-conversion reaction. The operating voltage window52 widths are ranked as LFNM-CuZn > LFNM-CoZn > LFNM-CoCu. This trend is also consistent with the stability results presented in Table S4† calculated by DFT. These results indicate that the Co-free sample is not only the most stable material but also has the largest window between the Li-rich and Li-poor area, which most probably leads to a higher specific capacity.
Electrochemical impedance spectroscopy (EIS) was conducted to investigate the resistance in LIBs. Fig. 4f shows the EIS spectra of HEO nanoparticle electrodes after 200 cycles. After fitting through the equivalent circuit, the Rs, Rsei and Rct values of HEO nanoparticles are presented in Table S6.†53 Among them, Rs indicates the ohmic impedance by the electrode itself and the electrolyte. Rsei denotes the impedance by the solid electrolyte interphase (SEI). Rct stands for the charge-transfer resistance in the battery. Besides, the W values of three electrodes are almost the same as they represent for the concentration polarization impedance. Compared to the bulk sample, there were inevitable increases in Rsei of HEO nanoparticle electrodes, on the one hand, due to the generation of more SEI layer.54 On the other hand, this indicates that nanomaterials have a larger electric double layer effect area, which is similar to a supercapacitor and therefore evidently conducive to high-rate charge and discharge.55 In addition, the LFNM-CuZn electrode shows the lowest Rct value of 17.8 Ω. This indicated the best charge transfer property at the electrode interface among all the as-prepared samples. Since Rct and DLi+ values are strongly related to the high-rate performance of the oxide electrodes.19,56 This result may also provide the evidence why the LFNM-CuZn electrode can produce the outstanding specific capacities in rate performance experiments.
The morphology of the HEO nanoparticle electrodes after cycling for 200 cycles in 0.8 V was investigated by field emission scanning electron microscopy (FESEM). Interestingly, the surface of the materials turned into relatively uniform microflakes instead of accumulating in the form of spheres after lithiation process. As shown in Fig. S10a,† some of the regions in the deeper part circled in yellow remained in the pristine state, which is the proof that most part of the electrodes changed. EDX analysis results are shown in Fig. S10b.† It is worth noting that this conversion of morphology brought about tremendous volume change. During the long-term charge and discharge process, a detrimental impact on the performance of the bulk electrode would take place as the expansion intensifies,57 while the design of nanoparticle electrodes will be more conducive to resisting this structural change.
The energy levels of redox peaks vs. Li/Li+ are depicted in Fig. 4g, illustrating the lithiation/de-lithiation process between Li-poor and Li-rich HEOs. The values are consistent with the results obtained by charge and discharge curves. Notably, the nanoparticle samples with Zn show a lower voltage during the reduction reaction while bulk-HEO always the highest. This may be because the presence of Cu and Zn provides additional valence electrons, which stabilizes the lattice structure and enhances the anti-bonding state.58,59 Furthermore, the injection of Zn into the anti-bonding orbitals of the spinel structure provides more electrons, thus reducing the energy level of the anti-bonding orbitals.60 These factors thereby reduce the discharge voltage. Moreover, bulk samples exhibit more pseudocapacitive properties, as they only featured higher currents in the redox peaks.61 On the contrary, the HEO nanoparticle samples also have higher current values at the lowest voltage (0.01 V) of discharge and the highest voltage (3.0 V) of charge, indicating a stronger double layer effect in the nanoparticle electrodes.62 This may explain why nanomaterials have better performance at higher currents.
The open circuit voltage of a battery is determined by the difference in electrochemical potential (μ) between the anode (μA) and the cathode; therefore, in a battery where the cathode is fixed, a μA as close as possible to that of Li metal is preferred. The electrochemical potential of electrode materials are determined by many factors, and one critical is the relative position of the metal redox couple.63 The CV measurements shows a trend of reduction (lithiation) peaks for HEOs, e.g., LFNM-CoCu > LFNM-CuZn > LFNM-CoZn (Fig. 4f), indicating that for Li-rich anodes, the energy levels of redox couples in Zn-containing HEOs could have been closer to Li/Li+ than in LFNM-CoCu (Fig. 4h). The discrepancy of electrochemical potentials among the three HEO nanoparticles as observed in CV measurement could originate from the difference in Ni 3d Hubbard bands, as discussed previously (Fig. S6†). It is probable that many metal ion species are involved in the redox process of HEOs, while they would be dominated by the Ni2+/Ni3+ couple. As indicated in Fig. 4i, the UHB center of Ni 3d were evaluated. One can note that the Ni 3d UHBs in LFNM-CuZn and LFNM-CoZn are far closer to the Fermi level than in the case of LFNM-CoCu, which follows LFNM-CoZn < LFNM-CuZn < LFNM-CoCu. The position of the Ni2+/Ni3+ couple could be associated with the UHB center (conduction band), for the UHB center from the Fermi level gives the position of the corresponding redox couple relative to the bottom of conduction band, which determines the intrinsic voltage limit vs. Li/Li+ of the anode.63 The calculated UHB centers of the HEOs follow the voltage limit trend of the anode HEOs, as observed from CV measurements (Fig. 4g).
Moreover, the two zincous HEOs (LFNM-CuZn and -CoZn) show lower UHB centers of Ni 3d than that of the Zn-free HEO (LFNM-CoCu), consistent with the experimental results of voltage limits, indicating that the Zn element has an effect on the anode voltage through the compositional and electronic interplay with the rest of the metals, particularly with Ni. This interplay is highly beneficial for the specific capacity of the two zincous HEOs, even if the anode is Co-free. This can be clearly observed from the rate capacity results shown in Fig. 4c; the capacity for the zincous, Co-free LFNM-CuZn and the zincous LFNM-CoZn far outperform the cobaltic but Zn-free LFNM-CoCu anode. Yet, for the long cycling performance of the anode that requires a favorable material stability, the zincous, Co-free LFNM-CuZn is more prominent than the other two HEOs, as shown in Fig. 4b. This originates from its highest thermal stability as revealed by its decomposition energy (Table S4†).
In conclusion, the battery assembled with LFNM-CuZn shows the excellent overall performances in terms of high specific capacity, good rate performance, improved capacity retention, low ion transportation resistance, and large voltage window according to the electrochemical experimental data. Those high-performance features resulted from the material stability, unique electronic properties, and low ion transport resistance it exhibits.
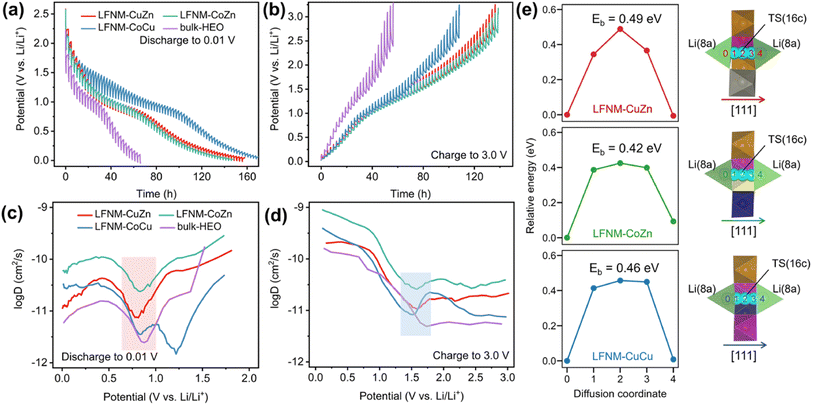
In order to investigate the Li ion diffusion in the LIBs with HEO nanoparticle electrodes, galvanostatic intermittent titration technique (GITT)64 was performed using battery test equipment between 0.01 V and 3.0 V. The lithium-ion diffusion coefficient DLi+ during lithiation/delithiation processes of the batteries was calculated using eqn (1) and plotted against the potentials. The DLi+ values were pre-converted into log![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) D for easier observation and comparison in Fig. 5a–d. Then, local minimum/maximum data points near the redox voltage (marked by color blocks) were focused on because they represent the coefficients near the main discharge (0.73 V) and charge (1.69 V) plateaus. LFNM-CuZn and LFNM-CoZn share a similar trend regarding DLi+versus potential during discharging. Their relative minimum DLi+ values in the low-voltage region were witnessed at around 0.78 V, which are 7.53 × 10−12 and 2.38 × 10−11 cm2 s−1, higher than the records of approximately 5 × 10−12 cm2 s−1 in previous works.19,65 During the charge process, the maximum DLi+ data are at approximately 1.60 V which are 1.07 × 10−11 and 2.59 × 10−10 cm2 s−1, respectively. Specifically, the efficient lithium-ion diffusion performances of LFNM-CuZn and LFNM-CoZn electrodes illustrate the rapid lithium-ion migration process during the charge/discharge processes in these electrodes.66 In contrast, bulk-HEO and LFNM-CoCu though show similar trends of DLi+versus potential but lower local maximum/minimum DLi+, indicating less efficient charge/discharge procedures. These experiment results illustrate that a smaller particle size is very significant for the improvement of lithium-ion transport efficiency, and Zn maybe more important for the improvement of HEO nanoparticle electrode performances than Cu and Co.
D for easier observation and comparison in Fig. 5a–d. Then, local minimum/maximum data points near the redox voltage (marked by color blocks) were focused on because they represent the coefficients near the main discharge (0.73 V) and charge (1.69 V) plateaus. LFNM-CuZn and LFNM-CoZn share a similar trend regarding DLi+versus potential during discharging. Their relative minimum DLi+ values in the low-voltage region were witnessed at around 0.78 V, which are 7.53 × 10−12 and 2.38 × 10−11 cm2 s−1, higher than the records of approximately 5 × 10−12 cm2 s−1 in previous works.19,65 During the charge process, the maximum DLi+ data are at approximately 1.60 V which are 1.07 × 10−11 and 2.59 × 10−10 cm2 s−1, respectively. Specifically, the efficient lithium-ion diffusion performances of LFNM-CuZn and LFNM-CoZn electrodes illustrate the rapid lithium-ion migration process during the charge/discharge processes in these electrodes.66 In contrast, bulk-HEO and LFNM-CoCu though show similar trends of DLi+versus potential but lower local maximum/minimum DLi+, indicating less efficient charge/discharge procedures. These experiment results illustrate that a smaller particle size is very significant for the improvement of lithium-ion transport efficiency, and Zn maybe more important for the improvement of HEO nanoparticle electrode performances than Cu and Co.
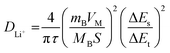 | (1) |
For better understanding on the Li diffusion, the energy barriers (Eb) in the Li-poor HEOs were calculated by the climbing image nudged elastic band (CI-NEB) method.67 The calculated Eb corresponds to the activation energy of the temperature (T) dependence of the diffusion coefficient DLi+ = D0![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Eb/kBT), where D0 is a material- and diffusion mechanism-dependent pre-exponential factor and kB is the Boltzmann constant. Previous experiments and calculations established that the Li ions hop between 8a sites through the 16c void (8a–16c–8a pathway) along the [111] direction in the spinel crystal.68–72 Hence, the diffusion mechanism in our calculations is selected to be the same. As depicted in Fig. 5e, the transition states (TS) for Li diffusion were found located exactly at 16c sites, resulting in energy barriers of 0.49, 0.42 and 0.46 eV for LFNM-CuZn, LFNM-CoZn and LFNM-CoCu, respectively. The results reveal the Li+ diffusion coefficients DLi+: LFNM-CoZn > LFNM-CoCu > LFNM-CuZn, giving the discrepancy from GITT-derived results for Li-poor anodes during the charge process (Fig. 5d), where the delithiation peaks occur at different potentials (varying from 1.52 to 1.57 V for GITT curves). The potential difference (vs. Li/Li+) implies that HEOs have various Li contents that differ from the very initial Li-poor anodes (molar content of 0.4 per spinel formula as obtained from the ICP-MS measurements). The various Li contents may lead to D0 varying slightly from one HEO to another, deviating the measured Li diffusion coefficients DLi+. However, the calculated energy barriers are still valid for the Li-poor cases with the same low Li content of same discharge potential at ∼1.7 V. As demonstrated in Fig. 5d, when DLi+ in LFNM-CoCu near the charge potential of 1.7 V exceeds that of LFNM-CuZn, leading to the Li diffusion coefficients follow LFNM-CoZn > LFNM-CoCu > LFNM-CuZn at 1.7 V. This is well consistent with the calculated CINEB results.
exp(−Eb/kBT), where D0 is a material- and diffusion mechanism-dependent pre-exponential factor and kB is the Boltzmann constant. Previous experiments and calculations established that the Li ions hop between 8a sites through the 16c void (8a–16c–8a pathway) along the [111] direction in the spinel crystal.68–72 Hence, the diffusion mechanism in our calculations is selected to be the same. As depicted in Fig. 5e, the transition states (TS) for Li diffusion were found located exactly at 16c sites, resulting in energy barriers of 0.49, 0.42 and 0.46 eV for LFNM-CuZn, LFNM-CoZn and LFNM-CoCu, respectively. The results reveal the Li+ diffusion coefficients DLi+: LFNM-CoZn > LFNM-CoCu > LFNM-CuZn, giving the discrepancy from GITT-derived results for Li-poor anodes during the charge process (Fig. 5d), where the delithiation peaks occur at different potentials (varying from 1.52 to 1.57 V for GITT curves). The potential difference (vs. Li/Li+) implies that HEOs have various Li contents that differ from the very initial Li-poor anodes (molar content of 0.4 per spinel formula as obtained from the ICP-MS measurements). The various Li contents may lead to D0 varying slightly from one HEO to another, deviating the measured Li diffusion coefficients DLi+. However, the calculated energy barriers are still valid for the Li-poor cases with the same low Li content of same discharge potential at ∼1.7 V. As demonstrated in Fig. 5d, when DLi+ in LFNM-CoCu near the charge potential of 1.7 V exceeds that of LFNM-CuZn, leading to the Li diffusion coefficients follow LFNM-CoZn > LFNM-CoCu > LFNM-CuZn at 1.7 V. This is well consistent with the calculated CINEB results.
In situ structural transition
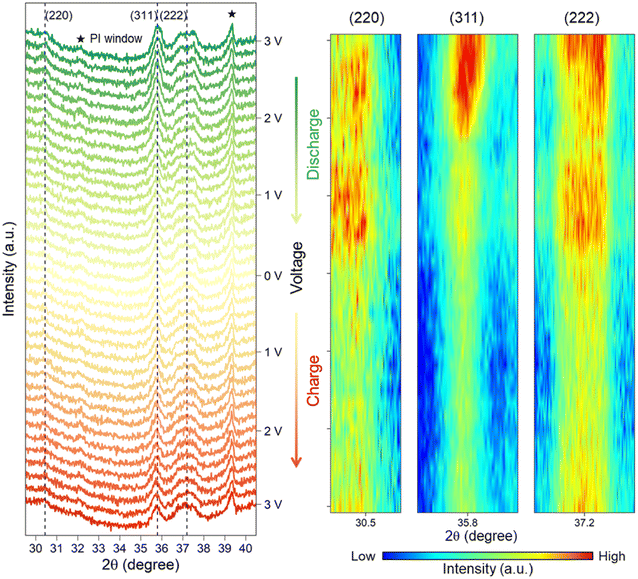
Operando XRD analysis was performed to reveal the phase transition of the LFNM-CuZn electrode during the first lithiation/delithiation process in an in situ cell. Fig. 6 shows the raw XRD patterns and their corresponding heatmaps generated from three reflected lattice planes. Polyimide (PI) windows at 32.1° and 39.4° along with other background peaks are indexed in the figure. With the decrease in voltage from 3 V to 0 V during the discharging process, intensities of spinel characteristic peaks at 30.5°, 35.8° and 37.2° are seen to be sequentially declined. All the peaks, in particular at around 0.33 V to 0.16 V, fall down to the lowest intensities, suggesting the weakening of the long-range spinel periodic lattice order. It is the intercalation of lithium in the spinel structure that may be responsible for the long-range order reduction of spinel phases. However, the spinel peaks are still visible, and no new characteristic peaks are detected at 0 V. During the subsequent charging process, all intensities of peaks remain almost the same initially followed by ramping up in the intensity of spinel structure at a high voltage from 2.32 V to 3 V. This indicates the reversibility of the lattice structure to the long-range ordered spinel phase. Overall, the weakened spinel lattice of the HEO nanoparticle electrode at low voltages can partially recover through the deintercalation of lithium during the whole discharge/charge process. The previous operando XRD experiments18,19 only recorded the diminished peak of the spinal structure after the intercalation process. In the present work, perhaps due to the nanoparticle morphology of LFNM-CuZn which can directly display microscopic changes in unit crystals, this reversible phenomenon of spinel phase can be vividly interpreted.Full-cell batteries
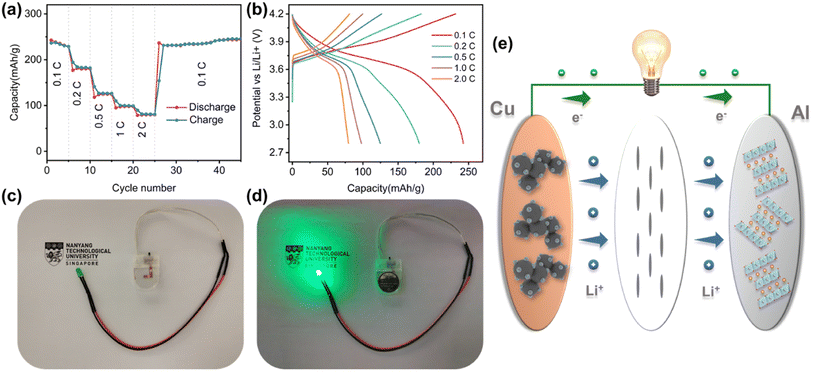
To verify the feasibility of HEOs in practical LIBs, the LFNM-CuZn‖LiNi0.6Co0.2-Mn0.2O2 full cell was assembled and evaluated by electrochemical methods.73 The rate capacities and charge–discharge curves measured at different C-rates (1C = 275 mA h g−1 based on the cathode mass) are shown in Fig. 7a and b. The specific capacities calculated based on the mass of cathode active materials are 242, 180, 125, 98, and 80 mA h g−1 at 0.1, 0.2, 0.5, 1, and 2C, respectively. There was no decay trend after 20 more cycles at 0.1C. Moreover, the capacity releases of discharge profiles are concentrated at approximately 3.7 V plateau, indicating stable and uniform discharge processes at the high voltage. With the mass ratio of anode to cathode materials to be only 1 to 3.7, the energy density of the full cell was calculated to be about 670 W h kg−1 according to the 0.1C discharge profile (based on the total mass of anode and cathode active materials). It is worth noting that the relatively high voltage of around 0.72 V in half cells does not reduce the practical high voltage of 3.7 V in the LIB full cell since the cathode is probably charged to a higher delithiation state. It may lead to irreversible phase change of cathode material,74 but there was no capacity decay after 20 more cycles at 0.1C in this work. Fig. 7d shows the example of a full cell, which is connected to a LED light with a nominal voltage of 3.7 V, and delivers the significant illumination. Therefore, the potential application of HEO nanoparticle electrodes in commercial LIBs is feasible.Conclusions
HEO nanoparticles decorated on the conductive carbon surface were grown by a laser-irradiation method. The laser shocking approach enables the fabrication of uniform Li-containing HEO nanoparticles that present both of more efficient electron conductivity and improved lithium storage capacity in comparison with the bulky counterpart. First, the Co-free HEO nanoparticle sample LFNM-CuZn was assessed to exhibit better capacity, particularly at a higher rate in this system. Second, the long cycling performance with a capacity retention of 100% after 800 cycles at 0.1 A g−1 of Co-free HEO indicates the thermal stability of the high-entropy phase, as revealed by the DFT+U calculations. The operando XRD experiment demonstrates a partially reversible spinel phase transition process during the lithiation/delithiation process of the LFNM-CuZn electrode. Moreover, a full cell formed by LFNM-CuZn (anode) and LiNi0.6Co0.2Mn0.2O2 (cathode) displays an exciting high voltage plateau at about 3.7 V almost identical to the half-cell of the positive electrode material. The low anode voltage of zincous HEOs is benefitted from the electron-sufficient Zn, which favors the Ni2+/Ni3+ redox couple as evidenced by the DFT+U calculations. Finally, coupled with the high material stability, the zincous, Co-free HEO nanoparticle anode (LFNM-CuZn) performs with high specific capacity as well as long-term cycling. This advanced bottom-up material preparation strategy of high-entropy nanostructures subject to laser irradiation can shed light on the relationship of the LIB performances with HEO nanoparticle electrode materials.Methodology
Synthesis of HEO nanoparticles
In a typical synthesis process, Fe(NO3)3·9H2O, Ni(NO3)2·6H2O, Mn(NO3)2·4H2O and LiNO3 (purchased from Sigma-Aldrich) were dissolved in 99.8% ethanol with the same molar concentration (100 mmol L−1) as solution S1. Cu(NO3)2·3H2O, ZnNO3·6H2O, or Co(NO3)2·6H2O according to the diverse energy storage systems were dissolved in ethanol or deionized water (100 mmol L−1), respectively as solution S2. Then, a mixture of S1 and S2 was prepared according to the calculation of the targeted mass loading (50%) of metal elements as solution S3.The commercial super C65 carbon black for Li-ion batteries (from TIMCAL) was chosen to serve as the substrate material. Before use, the carbon black was milled and sour-boiled in concentrated nitric acid (70%) for 8 h. This meant producing plenty of hydrophilic groups on the surface to anchor metal ions by hydrogen bonds in larger quantities. During preparation, the acid-treated carbon black with a certain quality was mixed with S3, stirred and then sonicated for 2 h. The obtained slurry was dropped into a tungsten crucible and vacuum-dried overnight. Then, the precursors were irradiated under a commercial laser source (JPT-M7-100W). The parameters used in the laser source are as follows: 900 kHz frequency, 20 ns pulse width, 1064 nm wavelength, 2 W power, laser spot diameter, 30 μm line space, and 40 mm s−1 movement speed. The duration of the laser spot on a point of the sample is approximately 0.75 ms. With less duration time but a smaller energy focus, the central temperature can reach above 1600 K according to our previous work.23 The laser spot size was determined by using photosensitive paper (JPT Electronics). After the laser shock, the samples were washed in ethanol, dried before characterization and assembled in the batteries. The bulk-HEO sample for comparison was fabricated by further annealing in air at 800 °C for 1 h.
Material characterization methods
FESEM images were acquired using a JEOL JSM-7600F. XRD spectra were recorded using XRD Shimadzu Powder equipment with a Cu Kα source (40 kV 30 mA, and 0.154 nm wavelength). XPS spectrum was recorded using a Kratos AXIS Supra spectrometer. TEM, HRTEM and STEM with EDX images were acquired using a JEOL 2100F-A. Cs-corrected annular bright-field (ABF) images were acquired using a JEOL ARM-200F CF with a spherical aberration corrector. TG-DSC curves were collected using a STA Netzsch STA44.Electrochemical experiments
The lithium storage behaviors of the as-prepared samples were measured by assembling CR2016-type half-cells in a glove box filled with Ar. Herein, 90 wt% HEO-based electrode composite material (including HEO nanoparticles and the carbon black substrate) and 10 wt% polyvinylidene fluoride (PVDF) binder were mixed and stirred with NMP for 5 h and then evenly painted on the current collector (copper foil). After heated at 70 °C overnight under vacuum, the coating electrode was tailored into round pieces with a diameter of 12 mm and a loading weight of ≈ 0.53 mg cm−2 (according to the HEO mass). In order to assemble the LIB half-cell, lithium metal and Celgard 2400 were selected as the counter electrode and separator. Between them, the electrolyte contained 1.0 m LiPF6 in ethylene carbonate (EC) and dimethyl carbonate (DMC) in a volume ratio of 1/1 with 5.0 wt% fluoroethylene carbonate (FEC). Moreover, the LIB full cell of LFNM-CuZn versus LiNi0.6Co0.2Mn0.2O2 was also assembled. The fabrication of the LiNi0.6Co0.2Mn0.2O2 cathode was similar to the half-cell electrodes except the fact that the mass ratio of active material/Super C65/PVDF was 7/2/1 on aluminum foil as the current collector. The mass loadings of the anode and cathode are 0.568 and 2.084 mg cm−2. The N/P ratio was calculated to be 1.24. The assembled half-cells and full-cells were tested in the NEWARE battery testing system according to the regular procedures of galvanostatic charge/discharge (GCD), rate performance and GITT. The GCD and rate performance experiments were conducted in the potential range between 0.01 and 3.0 V at the required currents. The specific capacity was calculated by the measured charge/discharge capacity divided by the mass of the HEO nanomaterial in electrodes, and the C rates of LFNM-CuZn, LFNM-CoZn, and LFNM-CoCu at 0.5 A g−1 were 0.421C, 0.428C, and 0.428C respectively. GITT was tested at a discharging/charging current density of 50 mA g−1 for 25/20 min, followed by a relaxation process of 2 h. The CV and EIS were measured using an electrochemical workstation (Metrohm Autolab). Operando XRD experiments were conducted using an XRD Rigaku SmartLab with 9 kW power between 0.01 and 3.00 V (vs. Li/Li+). To investigate the relationship between phase transitions and voltage variations, the chronopotentiometry method was performed to control the voltage within a specific range (∼0.16 V) through pulsed charge/discharge cycles, for example, 3.00 V–2.84 V. The in situ XRD curves were collected every time after stabilizing the voltage within the set range for 2 minutes.Density functional theory (DFT) calculations
The spin-polarized DFT calculations were performed using the Vienna Ab initio Simulation Package (VASP.5.4) with the plane-wave basis set.75 The electron–ion interaction is described by the projector augmented wave (PAW) pseudo-potentials.76 The exchange-correlation of valence electrons was treated by the Perdew–Burke–Ernzerhof (PBE) functional within the generalized gradient approximation (GGA).77 The valence configurations of Li: 2s1, O: 2s2 2p4, Mn: 3p6 3d5 4s2, Fe: 3d7 4s1, Co: 3d8 4s1, Ni: 3d9 4s1, Cu: 3d10 4s1, and Zn: 3d10 4s2 were adopted, and the electrons in transition metals were initialized in ferromagnetic high-spin configurations. An energy cutoff of 520 eV for the plane wave basis set was used. The simplified (effective) DFT+U approach78 was employed to describe the strongly correlated d electrons of Co (U = 3.32 eV), Fe (U = 5.3 eV), Mn (U = 3.9 eV), and Ni (U = 6.2 eV). The U values in the Materials Project are referenced.79–81 The tetrahedron method with Blöchl corrections was employed for orbital occupancy.82 The Γ-centered Monkhorst–Pack scheme was used to sample k-points in the Brillouin zone,83 and the spacing between k-points was set as 0.35 Å−1 for structure relaxations, 0.3 Å−1 for self-consistent field calculations, and 0.2 Å−1 for non-self-consistent calculations. The convergence threshold for force per atom and total energy were set as 0.05 eV Å−1 and 10−5 eV, respectively. The atomic positions were relaxed by the conjugate gradient algorithm.Disordered structure modeling and lithium diffusion
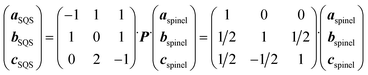
The disordered arrangement of metals in spinel HEOs is represented by SQS.34 A cubic normal spinel AB2O4 (Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m, No. 227) was used as the prototype for SQS generation. There are two equivalent sets of Wyckoff positions for the spinel:84 A at 8a (0, 0, 0), B at 16d (5/8, 5/8, 5/8) for the origin at −43 m (setting 1), or A at 8b (3/8, 3/8, 3/8), B at 16c (0, 0, 0) for the origin at −3 m (setting 2), and O at 32e (x, x, x), x = 0.111. The SQS was generated using the ICET python package,85 with which the simulated annealing from 1, 000 K to 300 K with 120, 000 Monte Carlo steps was performed. The cutoff for pair, triplet and quadruplet cluster correlations was chosen as 1.6, 0.8 and 0.4 times of the spinel lattice constant, respectively, resulting in 298, 650 and 15 correlations for pair, triplet and quadruplet clusters. The object cluster functions were then minimized to be as close as that of fully disordered structures. The lattice vectors of the SQS unit cell (aSQS, bSQS, cSQS) was obtained by the following transformation based on the lattice vectors of spinel (aspinel, bspinel, cspinel):
m, No. 227) was used as the prototype for SQS generation. There are two equivalent sets of Wyckoff positions for the spinel:84 A at 8a (0, 0, 0), B at 16d (5/8, 5/8, 5/8) for the origin at −43 m (setting 1), or A at 8b (3/8, 3/8, 3/8), B at 16c (0, 0, 0) for the origin at −3 m (setting 2), and O at 32e (x, x, x), x = 0.111. The SQS was generated using the ICET python package,85 with which the simulated annealing from 1, 000 K to 300 K with 120, 000 Monte Carlo steps was performed. The cutoff for pair, triplet and quadruplet cluster correlations was chosen as 1.6, 0.8 and 0.4 times of the spinel lattice constant, respectively, resulting in 298, 650 and 15 correlations for pair, triplet and quadruplet clusters. The object cluster functions were then minimized to be as close as that of fully disordered structures. The lattice vectors of the SQS unit cell (aSQS, bSQS, cSQS) was obtained by the following transformation based on the lattice vectors of spinel (aspinel, bspinel, cspinel):where
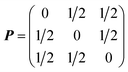 is the transform matrix from the conventional face-centered cubic cell to the corresponding primitive cell. The transformation gives a volume for SQS with five-fourth times that of the conventional cell of spinel, or five times that of the primitive cell. The derived SQS has 5/4 × (8 + 16 + 32) = 70 atoms per cell. For each HEO we initiated four candidates (SQS1–4), and then their atomic positions and cell volumes are relaxed, however, with the cell shape fixed for symmetry preservation. The equilibrium lattice constant was found when the lowest total energy was reached. The lowest-energy SQS cell in each HEO set was employed as the representative structure for subsequent calculations (the corresponding atomic coordinates of input structures can be found in the Appendix of ESI†). To explore the lithium diffusion mechanism in the HEO, a vacancy was introduced into the representative SQS cell on the 8a site (as the initial diffusion state), and then an adjacent lithium metal was moved to occupy the 8a vacancy (as the final state). The CI-NEB method67 was used to find the minimum energy path and transition state for lithium diffusion. Vibrational analysis was performed to confirm the TS with only a single imaginary frequency.
is the transform matrix from the conventional face-centered cubic cell to the corresponding primitive cell. The transformation gives a volume for SQS with five-fourth times that of the conventional cell of spinel, or five times that of the primitive cell. The derived SQS has 5/4 × (8 + 16 + 32) = 70 atoms per cell. For each HEO we initiated four candidates (SQS1–4), and then their atomic positions and cell volumes are relaxed, however, with the cell shape fixed for symmetry preservation. The equilibrium lattice constant was found when the lowest total energy was reached. The lowest-energy SQS cell in each HEO set was employed as the representative structure for subsequent calculations (the corresponding atomic coordinates of input structures can be found in the Appendix of ESI†). To explore the lithium diffusion mechanism in the HEO, a vacancy was introduced into the representative SQS cell on the 8a site (as the initial diffusion state), and then an adjacent lithium metal was moved to occupy the 8a vacancy (as the final state). The CI-NEB method67 was used to find the minimum energy path and transition state for lithium diffusion. Vibrational analysis was performed to confirm the TS with only a single imaginary frequency.
Conflicts of interest
There are no conflicts of interest to declare.Acknowledgements
The authors gratefully acknowledge the financial support from MOE Tier 1 RG193/17, MOE Tier 1 RG 79/20 (2020-T1-001-045). Some of the data presented are collected with the help of Facility for Analysis, Characterisation, Testing and Simulation (FACTS)'s staff. We acknowledge the A*STAR Computational Resource Centre (A*CRC) of Singapore through the use of its high-performance computing facilities.References
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- Y. Liu, Y. Zhu and Y. Cui, Nat. Energy, 2019, 4, 540–550 CrossRef.
- S. Li, K. Wang, G. Zhang, S. Li, Y. Xu, X. Zhang, X. Zhang, S. Zheng, X. Sun and Y. Ma, Adv. Funct. Mater., 2022, 32, 2200796 CrossRef CAS.
- M. V. Reddy, G. V. Subba Rao and B. V. R. Chowdari, Chem. Rev., 2013, 113, 5364–5457 CrossRef CAS PubMed.
- S. Chu, Y. Cui and N. Liu, Nat. Mater., 2017, 16, 16–22 CrossRef PubMed.
- X. Wang, X. Li, H. R. Fan, M. Miao, Y. M. Zhang, W. Guo and Y. Z. Fu, J. Energy Chem., 2022, 67, 276–289 CrossRef CAS.
- Q. Wang, A. Sarkar, Z. Li, Y. Lu, L. Velasco, S. S. Bhattacharya, T. Brezesinski, H. Hahn and B. Breitung, Electrochem. Commun., 2019, 100, 121–125 CrossRef CAS.
- Z. Y. Lun, B. Ouyang, D. H. Kwon, Y. Ha, E. E. Foley, T. Y. Huang, Z. J. Cai, H. Kim, M. Balasubramanian, Y. Z. Sun, J. P. Huang, Y. S. Tian, H. Kim, B. D. McCloskey, W. L. Yang, R. J. Clement, H. W. Ji and G. Ceder, Nat. Mater., 2021, 20, 214 CrossRef CAS PubMed.
- A. Amiri and R. Shahbazian-Yassar, J. Mater. Chem. A, 2021, 9, 782–823 RSC.
- Y. Ma, Y. Ma, Q. Wang, S. Schweidler, M. Botros, T. Fu, H. Hahn, T. Brezesinski and B. Breitung, Energy Environ. Sci., 2021, 14, 2883–2905 RSC.
- C. M. Rost, E. Sachet, T. Borman, A. Moballegh, E. C. Dickey, D. Hou, J. L. Jones, S. Curtarolo and J.-P. Maria, Nat. Commun., 2015, 6, 8485 CrossRef CAS.
- S. Fang, D. Bresser and S. Passerini, Adv. Energy Mater., 2020, 10, 1902485 CrossRef CAS.
- Y. Z. Jiang, M. J. Hu, D. Zhang, T. Z. Yuan, W. P. Sun, B. Xu and M. Yan, Nano Energy, 2014, 5, 60–66 CrossRef CAS.
- J. Cabana, L. Monconduit, D. Larcher and M. R. Palacín, Adv. Mater., 2010, 22, E170–E192 CrossRef CAS PubMed.
- R. Zhang, C. Wang, P. Zou, R. Lin, L. Ma, L. Yin, T. Li, W. Xu, H. Jia, Q. Li, S. Sainio, K. Kisslinger, S. E. Trask, S. N. Ehrlich, Y. Yang, A. M. Kiss, M. Ge, B. J. Polzin, S. J. Lee, W. Xu, Y. Ren and H. L. Xin, Nature, 2022, 610(7930), 67–73 CrossRef CAS PubMed.
- C. Zhao, F. Ding, Y. Lu, L. Chen and Y.-S. Hu, Angew. Chem., Int. Ed., 2020, 59, 264–269 CrossRef CAS PubMed.
- K. Huang, B. Zhang, J. Wu, T. Zhang, D. Peng, X. Cao, Z. Zhang, Z. Li and Y. Huang, J. Mater. Chem. A, 2020, 8, 11938–11947 RSC.
- B. Xiao, G. Wu, T. Wang, Z. Wei, Y. Sui, B. Shen, J. Qi, F. Wei and J. Zheng, Nano Energy, 2022, 95, 106962 CrossRef CAS.
- J. Patra, T. X. Nguyen, C.-C. Tsai, O. Clemens, J. Li, P. Pal, W. K. Chan, C.-H. Lee, H.-Y. T. Chen, J.-M. Ting and J.-K. Chang, Adv. Funct. Mater., 2022, 32, 2110992 CrossRef CAS.
- T. X. Nguyen, J. Patra, J.-K. Chang and J.-M. Ting, J. Mater. Chem. A, 2020, 8, 18963–18973 RSC.
- Y. Wei, X. Liu, R. Yao, J. Qian, Y. Yin, D. Li and Y. Chen, J. Alloys Compd., 2023, 938, 168610 CrossRef CAS.
- Y. Yao, Q. Dong, A. Brozena, J. Luo, J. Miao, M. Chi, C. Wang, I. G. Kevrekidis, Z. J. Ren, J. Greeley, G. Wang, A. Anapolsky and L. Hu, Science, 2022, 376, eabn3103 CrossRef CAS PubMed.
- Y. Lu, K. Huang, X. Cao, L. Zhang, T. Wang, D. Peng, B. Zhang, Z. Liu, J. Wu, Y. Zhang, C. Chen and Y. Huang, Adv. Funct. Mater., 2022, 32, 2110645 CrossRef CAS.
- Y. G. Yao, Z. N. Huang, P. F. Xie, S. D. Lacey, R. J. Jacob, H. Xie, F. J. Chen, A. M. Nie, T. C. Pu, M. Rehwoldt, D. W. Yu, M. R. Zachariah, C. Wang, R. Shahbazian-Yassar, J. Li and L. B. Hu, Science, 2018, 359, 1489–1494 CrossRef CAS.
- T. Li, Y. Yao, B. H. Ko, Z. Huang, Q. Dong, J. Gao, W. Chen, J. Li, S. Li, X. Wang, R. Shahbazian-Yassar, F. Jiao and L. Hu, Adv. Funct. Mater., 2021, 31, 2010561 CrossRef CAS.
- S. Hao, B. Zhang, S. Ball, M. Copley, Z. Xu, M. Srinivasan, K. Zhou, S. Mhaisalkar and Y. Huang, J. Power Sources, 2015, 294, 112–119 CrossRef CAS.
- C. Duan, K. Tian, X. Li, D. Wang, H. Sun, R. Zheng, Z. Wang and Y. Liu, Ceram. Int., 2021, 47, 32025–32032 CrossRef CAS.
- M. Moździerz, K. Świerczek, J. Dąbrowa, M. Gajewska, A. Hanc, Z. Feng, J. Cieślak, M. Kądziołka-Gaweł, J. Płotek, M. Marzec and A. Kulka, ACS Appl. Mater. Interfaces, 2022, 14, 42057–42070 CrossRef.
- B. Petrovičovà, W. Xu, M. G. Musolino, F. Pantò, S. Patanè, N. Pinna, S. Santangelo and C. Triolo, Appl. Sci., 2022, 12, 5965 CrossRef.
- Y. Zheng, X. Wu, X. Lan and R. Hu, Processes, 2022, 10, 49 CrossRef CAS.
- S. R. Nalage, S. T. Navale and V. B. Patil, Measurement, 2013, 46, 3268–3275 CrossRef.
- D. Kong, C. Dong, Z. Zheng, F. Mao, A. Xu, X. Ni, C. Man, J. Yao, K. Xiao and X. Li, Appl. Surf. Sci., 2018, 440, 245–257 CrossRef CAS.
- T. M. Gür, Energy Environ. Sci., 2018, 11, 2696–2767 RSC.
- A. Zunger, S. H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- M. C. Biesinger, B. P. Payne, A. P. Grosvenor, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2011, 257, 2717–2730 CrossRef CAS.
- X. Li, X. Liu, C. Lin, Z. Zhou, M. He and W. Ouyang, Chem. Eng. J., 2020, 382, 123013 CrossRef CAS.
- M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Phys. Chem. Chem. Phys., 2012, 14, 2434–2442 RSC.
- M. C. Biesinger, L. W. M. Lau, A. R. Gerson and R. S. C. Smart, Appl. Surf. Sci., 2010, 257, 887–898 CrossRef CAS.
- W.-J. Zhang, J. Power Sources, 2011, 196, 13–24 CrossRef CAS.
- S. Hao, B. Zhang, S. Ball, J. Wu, M. Srinivasan and Y. Huang, J. Mater. Chem. A, 2016, 4, 16569–16575 RSC.
- B. Xiao, G. Wu, T. Wang, Z. Wei, Y. Sui, B. Shen, J. Qi, F. Wei, Q. Meng, Y. Ren, X. Xue, J. Zheng, J. Mao and K. Dai, Ceram. Int., 2021, 47, 33972–33977 CrossRef CAS.
- T. X. Nguyen, J. Patra, C.-C. Tsai, W.-Y. Xuan, H.-Y. T. Chen, M. S. Dyer, O. Clemens, J. Li, S. B. Majumder, J.-K. Chang and J.-M. Ting, Adv. Funct. Mater., 2023, 2300509 CrossRef CAS.
- X. Liu, Y. Xing, K. Xu, H. Zhang, M. Gong, Q. Jia, S. Zhang and W. Lei, Small, 2022, 18, 2200524 CrossRef CAS PubMed.
- H. Chen, N. Qiu, B. Wu, Z. Yang, S. Sun and Y. Wang, RSC Adv., 2020, 10, 9736–9744 RSC.
- T. X. Nguyen, C.-C. Tsai, J. Patra, O. Clemens, J.-K. Chang and J.-M. Ting, Chem. Eng. J., 2022, 430, 132658 CrossRef CAS.
- E. Lökçü, Ç. Toparli and M. Anik, ACS Appl. Mater. Interfaces, 2020, 12, 23860–23866 CrossRef.
- E. Peled, C. Menachem, D. Bar-Tow and A. Melman, J. Electrochem. Soc., 1996, 143, L4 CrossRef CAS.
- S. Akrami, P. Edalati, M. Fuji and K. Edalati, Mater. Sci. Eng. R Rep., 2021, 146, 100644 CrossRef.
- D. Wang, R. Kou, D. Choi, Z. Yang, Z. Nie, J. Li, L. V. Saraf, D. Hu, J. Zhang, G. L. Graff, J. Liu, M. A. Pope and I. A. Aksay, ACS Nano, 2010, 4, 1587–1595 CrossRef CAS PubMed.
- B. Liu, A. Abouimrane, D. E. Brown, X. Zhang, Y. Ren, Z. Z. Fang and K. Amine, J. Mater. Chem. A, 2013, 1, 4376–4382 RSC.
- A. Grenier, P. J. Reeves, H. Liu, I. D. Seymour, K. Märker, K. M. Wiaderek, P. J. Chupas, C. P. Grey and K. W. Chapman, J. Am. Chem. Soc., 2020, 142, 7001–7011 CrossRef CAS PubMed.
- X. Z. Sun, X. Zhang, K. Wang, Y. B. An, X. H. Zhang, C. Li and Y. W. Ma, Electrochim. Acta, 2022, 428, 140972 CrossRef CAS.
- D. Andre, M. Meiler, K. Steiner, C. Wimmer, T. Soczka-Guth and D. U. Sauer, J. Power Sources, 2011, 196, 5334–5341 CrossRef CAS.
- A. P. Wang, S. Kadam, H. Li, S. Q. Shi and Y. Qi, npj Comput. Mater., 2018, 4, 15 CrossRef.
- H. S. Kim, T. H. Kim, W. Kim, S. S. Park and G. Jeong, ACS Appl. Mater. Interfaces, 2023, 15(7), 9212–9220 CrossRef CAS PubMed.
- M. Yao, K. Okuno, T. Iwaki, M. Kato, K. Harada, J. J. Park, S. Tanase and T. Sakai, J. Electrochem. Soc., 2007, 154, A709–A714 CrossRef CAS.
- J. B. Goodenough and K. S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- X. F. Tan, S. D. McDonald, Q. Gu, L. Wang, S. Matsumura and K. Nogita, J. Power Sources, 2019, 440, 227085 CrossRef CAS.
- R. Vidya, P. Ravindran and H. Fjellvag, J. Appl. Phys., 2012, 111, 123713 CrossRef.
- M. S. Liao and S. Scheiner, J. Chem. Phys., 2001, 114, 9780–9791 CrossRef CAS.
- A. G. Dylla, G. Henkelman and K. J. Stevenson, Acc. Chem. Res., 2013, 46, 1104–1112 CrossRef CAS PubMed.
- E. Frackowiak and F. Beguin, Carbon, 2001, 39, 937–950 CrossRef CAS.
- J. B. Goodenough and Y. Kim, Chem. Mater., 2010, 22, 587–603 CrossRef CAS.
- A. V. Churikov, A. V. Ivanishchev, I. A. Ivanishcheva, V. O. Sycheva, N. R. Khasanova and E. V. Antipov, Electrochim. Acta, 2010, 55, 2939–2950 CrossRef CAS.
- W. Zhao, S. Yuan, S. Lei, Z. Zeng, J. Dong, F. Jiang, Y. Yang, W. Sun, X. Ji and P. Ge, Adv. Funct. Mater., 2023, 2211542 CrossRef CAS.
- Z. M. Xu, X. Chen, R. H. Chen, X. Li and H. Zhu, npj Comput. Mater., 2020, 6, 47 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- M. Nakayama, M. Kaneko and M. Wakihara, Phys. Chem. Chem. Phys., 2012, 14, 13963–13970 RSC.
- B. Xu and S. Meng, J. Power Sources, 2010, 195, 4971–4976 CrossRef CAS.
- C. Y. Ouyang, S. Q. Shi, Z. X. Wang, H. Li, X. J. Huang and L. Q. Chen, Europhys. Lett., 2004, 67, 28 CrossRef CAS.
- V. W. J. Verhoeven, I. M. de Schepper, G. Nachtegaal, A. P. M. Kentgens, E. M. Kelder, J. Schoonman and F. M. Mulder, Phys. Rev. Lett., 2001, 86, 4314–4317 CrossRef CAS PubMed.
- J. B. Goodenough and K.-S. Park, J. Am. Chem. Soc., 2013, 135, 1167–1176 CrossRef CAS PubMed.
- Y. Zhang, Z. B. Wang, F. D. Yu, L. F. Que, M. J. Wang, Y. F. Xia, Y. Xue and J. Wu, J. Power Sources, 2017, 358, 1–12 CrossRef CAS.
- R. A. House, J. J. Marie, M. A. Pérez-Osorio, G. J. Rees, E. Boivin and P. G. Bruce, Nat. Energy, 2021, 6, 781–789 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B: Condens. Matter Mater. Phys., 1998, 57, 1505–1509 CrossRef CAS.
- S. P. Ong, Hubbard U Values, https://docs.materialsproject.org/methodology/materials-methodology/calculation-details/gga+u-calculations/hubbard-u-values, (accessed 2023/7/22).
- A. Jain, S. P. Ong, G. Hautier, W. Chen, W. D. Richards, S. Dacek, S. Cholia, D. Gunter, D. Skinner, G. Ceder and K. A. Persson, APL Mater., 2013, 1, 011002 CrossRef.
- L. Wang, T. Maxisch and G. Ceder, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 195107 CrossRef.
- P. E. Blöchl, O. Jepsen and O. K. Andersen, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 49, 16223–16233 CrossRef PubMed.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- M. I. Aroyo, International Tables for Crystallography: Space-Group Symmetry, International Union of Crystallography, Chester, England, 2nd edn, 2016 Search PubMed.
- M. Ångqvist, W. A. Muñoz, J. M. Rahm, E. Fransson, C. Durniak, P. Rozyczko, T. H. Rod and P. Erhart, Adv. Theory Simul., 2019, 2, 1900015 CrossRef.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ta08101j |
| ‡ Siyu Zhu and Wei Nong contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2024 |