Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Leveraging machine learning in porous media†
Mostafa
Delpisheh
 *a,
Benyamin
Ebrahimpour
*a,
Benyamin
Ebrahimpour
 b,
Abolfazl
Fattahi
b,
Abolfazl
Fattahi
 c,
Majid
Siavashi
c,
Majid
Siavashi
 d,
Hamed
Mir
d,
Hamed
Mir
 d,
Hossein
Mashhadimoslem
d,
Hossein
Mashhadimoslem
 e,
Mohammad Ali
Abdol
e,
Mohammad Ali
Abdol
 e,
Mina
Ghorbani
e,
Mina
Ghorbani
 f,
Javad
Shokri
f,
Javad
Shokri
 g,
Daniel
Niblett
g,
Daniel
Niblett
 a,
Khabat
Khosravi
a,
Khabat
Khosravi
 h,
Shayan
Rahimi
h,
Shayan
Rahimi
 i,
Seyed Mojtaba
Alirahmi
i,
Seyed Mojtaba
Alirahmi
 j,
Haoshui
Yu
j,
Haoshui
Yu
 j,
Ali
Elkamel
j,
Ali
Elkamel
 ke,
Vahid
Niasar
ke,
Vahid
Niasar
 *g and
Mohamed
Mamlouk
*g and
Mohamed
Mamlouk
 *a
*a
aSchool of Engineering, Newcastle University, Newcastle Upon Tyne, NE1 7RU, UK. E-mail: m.delpisheh2@ncl.ac.uk; mohamed.mamlouk@ncl.ac.uk
bSchool of Mathematics and Physics, University of Portsmouth, Portsmouth, UK
cDepartment of Mechanical Engineering, University of Kashan, Kashan, Iran
dSchool of Mechanical Engineering, Iran University of Science and Technology, Iran
eDepartment of Chemical Engineering, University of Waterloo, Waterloo, N2L3G1, Canada
fSchool of Metallurgy and Materials Engineering, College of Engineering, University of Tehran, Tehran, Iran
gDepartment of Chemical Engineering, University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: vahid.niasar@manchester.ac.uk
hSchool of Climate Change and Adaptation, University of Prince Edward Island, Charlottetown, PEI, Canada
iDepartment of Chemical Engineering & Materials Science, University of Southern California, USA
jDepartment of Chemistry and Bioscience, Aalborg University, Niels Bohrs Vej 8A, Esbjerg 6700, Denmark
kDepartment of Chemical and Petroleum Engineering, Khalifa University, Abu Dhabi, UAE
First published on 19th July 2024
Abstract
The emergence of artificial intelligence (AI) and, more particularly, machine learning (ML), has had a significant impact on engineering and the fundamental sciences, resulting in advances in various fields. The use of ML has significantly enhanced data processing and analysis, eliciting the development of new and improved technologies. Specifically, ML is projected to play an increasingly significant role in helping researchers better understand and predict the behavior of porous media. Furthermore, ML models will be able to make use of sizable datasets, such as subsurface data and experiments, to produce accurate predictions and simulations of porous media systems. This capability could help optimize the design of porous materials for specific applications and improve the effectiveness of industrial processes. To this end, this review paper attempts to provide an overview of the present status quo in this context, i.e., the interface of ML and porous media in six different applications, namely, heat exchanger and storage, energy storage and combustion, electrochemical devices, hydrocarbon reservoirs, carbon capture and sequestration, and groundwater, stressing the advances made in the application of ML to porous media and offering insights into the challenges and opportunities for future research. Each section also entails a supplementary database of the literature as a spreadsheet, which includes the details of ML models, datasets, key findings, etc., and mentions relevant available online datasets that can be used to train ML models. Future research trends include employing hybrid models by combining ML models with physics-based models of porous media to improve predictions concerning accuracy and interpretability.
1. Introduction
Porous media play an important role in many natural and engineered systems, including subsurface reservoirs for energy resources such as oil, natural gas, and geothermal heat, as well as aquifers that store water for drinking and irrigation. In addition, porous media play a critical role in a variety of environmental and industrial processes, such as carbon capture and sequestration (CCS), water treatment, heat transfer, etc. which underscores the significance of porous media in diverse applications. The study of porous media is interdisciplinary, combining elements of physics, chemistry, mechanics, and geology. It involves understanding the transport and exchange of fluid, heat, and mass in porous media and the interactions between fluid, solid, and thermal components.1Current research on porous media covers various aspects of physics, chemistry, and engineering. In terms of transport phenomena, the transport of fluid, heat, and mass in porous media and the impact of fluid–fluid, fluid-solid, and solid–solid interactions on these processes are investigated. In materials science, researchers are developing new materials with improved properties, such as higher permeability, better mechanical strength, and improved thermal conductivity, for use in an assorted range of applications. In the context of energy resources such as oil and natural gas, researchers are studying the behavior of subsurface reservoirs and developing tools and techniques to improve the extraction of these resources.2
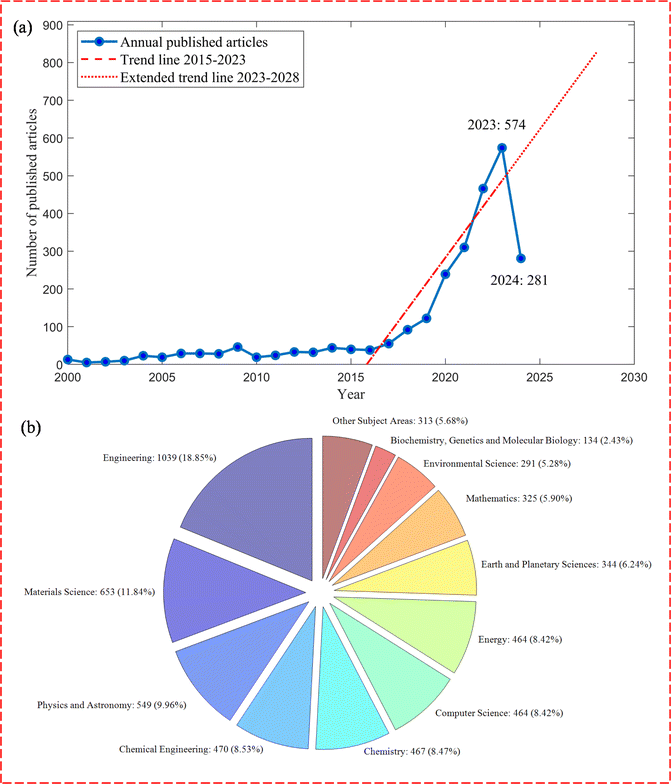
Over recent years, there has been a marked increase in interest in employing ML and data analysis techniques to uncover and elucidate the underlying mechanisms and interactions within porous media, thereby enhancing the ability to both understand and predict their behavior. Researchers are attempting to develop models that capture the composite interactions between fluid, solid, and thermal components and use these models for optimizing processes and augmenting predictions. In particular, ML techniques can particularly assist in cases where traditional modeling methods are limited by the complexity of the system or the availability of data.3Fig. 1 depicts the occurrences of the published research on the keywords “machine learning” (ML) and “porous media” over the past two decades together with the relevant fields. This rapport between the interface of ML and porous media is conspicuous to grow even more over the coming years, signposting the present review paper's direction.
Chapter two provides a comprehensive description of different ML models employed in the study of porous media such as supervised and unsupervised learning methods. Additionally, it gives instances of particular models that have been deployed, such as decision trees, random forests, support vector machines, and neural networks, followed by evaluation metrics.
In chapter three, the review paper applies the different applications of ML to porous media, stratified in different sections, namely, heat exchanger and storage, energy storage and combustion, electrochemical devices, hydrocarbon reservoirs, CCS, and groundwater. In each section, the different variables involved are scrutinized which include fluid flow prediction and characterization of porous media, i.e., permeability, porosity, pore size distribution, wettability, and transport properties. Furthermore, it underscores examples of particular applications, such as the prediction of permeability, pinpointing the optimal production and injection methods, and flood optimization.
A common and essential component of many porous media applications is heat transfer. The contribution of the various geometrical shapes, governing parameters, materials, and micro/macroscale flow in different forms (convection, conduction, and radiation) elicits challenges in analyzing, optimizing, and predicting such physics. In the field of heat exchanger and storage, ML allows for optimizing heat transfer processes and thermal management of porous media. In this scope, key thermal properties, such as thermal conductivity, diffusivity, and heat capacity, are crucial for ensuring efficient and safe heat transfer in thermal systems, especially high flux systems such as electronics, chemical reactors, etc. ML models can assist in interpreting large thermal data sets generated by monitoring these systems and provide critical information that will ultimately lead to the identification and mitigation of potential risks and better decision-making to ensure the desired operation.
ML models are commonly used in the energy storage field to predict and improve the performance of various energy storage systems, including thermal, electrochemical, hydrogen gas, and hybrid energy storage methods.4–6 This includes identifying optimal charging and discharging approaches for batteries and thermal storage systems, as well as controlling the operation of energy storage equipment such as inverters and charge controllers. Furthermore, ML models can predict and diagnose the state of energy storage systems, including identifying factors responsible for battery degradation. The use of ML models helps improve the performance and reliability of energy storage systems. These models can analyze data from weather forecasts, energy usage, and energy production to predict energy demand. This information is then used to optimize the use of energy storage systems and balance the energy grid through grid integration. Thermal energy storage (TES) systems, such as thermal batteries, can be improved using ML models. These models analyze data from experiments and monitoring systems, such as temperature and heat flux, to optimize the design and operation of TES systems. This results in improved efficiency for the system. In general, implementing ML in energy storage can enhance the effectiveness, functionality, and dependability of energy storage systems. This can also lead to the optimization of energy storage systems to manage the balance between energy supply and demand. The incorporation of ML models into combustion has led to many discoveries, particularly in the field of optimizing and controlling combustion systems used in power generation, industrial heating, and transportation. These models are utilized to forecast and improve the performance of various combustion systems, such as by identifying the optimal fuel-air ratios and combustion conditions for maximum efficiency. They also help in controlling the operation of combustion equipment, such as burners and boilers, by considering factors such as ignition, flame propagation, and burnout. An important field of study involves the creation of fresh combustion technologies, specifically those that produce low levels of emissions. Using ML models, data from experiments and simulations can be analyzed to discover innovative strategies and technologies that can enhance performance while also reducing emissions. Finally, ML models can aid in predicting combustion-related problems. For instance, they can identify the root cause of combustion instability, leading to enhanced performance and reliability of combustion systems.
In the field of electrochemical devices, ML models have found various applications to analyze experimental data and improve the understanding and optimization of electrochemical processes. For electrocatalyst experiments, ML models are used to assess stability and activity, aiding in the development of more efficient catalysts for reactions such as the hydrogen evolution reaction (HER) and oxygen evolution reaction (OER).7 ML models are also valuable for battery research, predicting the performance and behavior of different battery types such as lithium-ion, alkaline, carbon zinc, redox flow, and zinc air. This information can guide battery design and optimization. Supercapacitors can also benefit from ML modeling. ML models are used in corrosion prediction to analyze experimental data and forecast the corrosion rate of various materials, contributing to corrosion mitigation strategies. Additionally, ML models can be employed in electrodeposition processes to control the microstructure of metal coatings, leading to improved properties. In the field of electrolysis, ML models explored the relationship between electrocatalyst synthesis conditions, structural properties, and catalytic performance.8,9 Specifically, in the PEM water electrolyzer, ML highlighted the key variables that influence current/power density and polarization of the electrolyzers. In fuel cells, both PEM and solid oxide, ML helps design porous media such as gaseous diffusion layers (GDLs) and catalyst layers (CLs) by optimizing porosity and pore size distribution and their impacts on fuel cell performance.10 Finally, ML models are employed in pore-scale modeling to predict electrochemical transport and reactions within porous media, providing accurate predictions of the behavior of charged species.
The review paper focuses on the ML models in hydrocarbon porous media, as a complex and dynamic system, to foremost raise the understanding and thereafter provide an overview of ways that optimize the recovery of hydrocarbons from the reservoir.11 In reservoir characterization, ML models are used for analyzing data from reservoir cores, including porosity and permeability, for creating more accurate reservoir models. To this end, the location of wells can be optimized to improve the recovery of hydrocarbons from the reservoir. ML models in reservoir history matching are used for matching production data from oil or gas reservoirs to numerical models, which allows for more accurate predictions of future production and its changes over time. In enhanced oil recovery (EOR), ML models may be employed for optimizing EOR methods including CO2 injection and waterflooding,12 by analyzing data from the reservoirs. In rock physics modeling, ML models are used for introducing rock physics models, whereby the connection between rock's physical properties, such as porosity and permeability, and the fluids' properties in the rock, such as oil and water are described. Here, pore-scale fluid flow and transport are also appraised allowing for better predictions of oil and gas behavior in porous media. Furthermore, in the subfield of fracture characterization, ML models can be used to analyze data from seismic surveys and well logs to eventually identify and characterize fractures in the reservoir, which are critical to the fluids' flow. Finally, by analyzing data from log measurements, i.e., resistivity, porous media properties can be determined.
Many key applications of ML can be applied to CCS porous media. ML models can be used for analyzing data from experiments on the CCS process, for instance, porosity, pore structure, and permeability, and using this to discern the CO2 behavior and thereafter optimize the CCS process.13 ML models in predictive modeling can be used for predicting CO2 behavior in introducing a new framework for calculating the normalized effective permeability resulting from hydrate formation. Furthermore, ML models can be introduced for optimizing the CO2-EOR process, by analyzing experimental data and optimizing the CO2 injection rate, timing, and location in the reservoir. ML can make it possible to provide algorithms for developing new materials and has attracted a great deal of interest for its ability to accurately predict chemical and physical properties, establish structure–property relationships, synthesize activated carbon and porous materials adsorbents via several types of biomasses, and navigate the chemical space to direct chemical synthesis. To determine structure–performance correlations and choose the top descriptors that can precisely predict the CO2 adsorption capacity, efficiency, and selectivity, ML is applied to discover different porous materials for carbon capture technologies. Furthermore, ML models could predict highly accurate process condition prediction allowing for quantifying the influence of CO2 capacity variations on material ranking in adsorption process technologies.14 Nowadays, researchers present cases of ML algorithm development in various CO2 capture, storage, transport, and utilization (CCSTU) systems. Adsorption, absorption, chemical looping, membranes, sequestration, and hydrates are a few examples of carbon capture or separation technology (CCST). Modeling and simulating solvent-based carbon capture would be a progressive effort towards the complicated governing processes of absorption, particularly chemical absorption, involving mass transfer and chemical reactions.15
The paper reviews ML models that can be applied to groundwater porous media to optimize the management of water resources and ensure water is used sustainably. The ML models are utilized for aquifer characterization, namely, analyzing experimental data on aquifers, which include their porosity, pore structure, and permeability, to understand the aquifer water behavior and attempt to promote groundwater management. Parameters such as recharge, flow, and storage of aquifers can be studied over some time through ML models to better manage groundwater resources through predictive modeling. Concerning water quality, by analyzing data from water quality sensors in monitoring systems, the ML models can detect changes in water quality and therefore predict issues such as heavy metal removal, nitrates, pH variations, and contamination, aimed at mitigating potential risks. Data-driven decision-making is also addressed in this field. Regarding groundwater recharge prediction, ML models can examine parameters such as temperature, precipitation, and evapotranspiration and predict the groundwater recharge rate and hence identify optimal conditions for recharge. Finally, further assessments such as optimal pumping rate and drought prediction, i.e., predicting the onset and severity of droughts, and flood prediction, by analyzing data from weather forecasts and water level monitoring systems, can be made using ML models for water management decisions.
The review paper sums up by addressing the challenges and outlook of ML in porous media. The article recollects the challenges and relevant limitations associated with using ML on porous media grounded on the findings of the prior section. With the authors' prior knowledge in this field, this may include issues such as the requirement for powerful computing, lack of data, the complexity of studying porous media, dimensionality, scaling, and validation and interpretability. The review paper attempts to signpost new techniques to overcome these challenges and to improve the accuracy and robustness of ML models for porous media. It additionally culminates future research outlook for the application of ML to porous media, such as integrating ML with other technologies such as simulation and imaging and developing state-of-the-art ML methods especially designed for porous media systems. Finally, as a further reading and better comprehension of the scope of the review, a list of available online databases that can be used as an exercise to train ML models and all the reviewed literature in the manuscript as a spreadsheet are given in the ESI.†
2. Background on machine learning and porous media
The integration of ML with porous media has been addressed extensively during the past 10 years and, as evidenced by the number of publications in this field, the field will be even more focused on in the years to come. The review synthesizes recent advancements and interdisciplinary applications by providing a detailed analysis of how different ML models can improve and innovate these applications, each of which is crucial to resource management and sustainable technology advancements. Additionally, the review enjoys the addition of a supplemental database of literature and datasets and discussions on current challenges and future outlook. Dynamic research in ML for porous media primarily focuses on data-based methods for predicting the characteristics of complex porous substances in transportation and chemical reactions. This area finds utility in various sectors, including subsurface contaminant transport,16 geothermal power utilization,17 CO2 and H2 containment in geological formations,18 water purification,19 and lithium-ion batteries.20One of the main challenges in this domain involves accurately capturing the physical properties of pore-scale pores, dealing with the heterogeneity and uncertain nature of porous substances, and extrapolating these predictions to a larger scale. By employing ML techniques to learn from different types of data, such as visual representations or computer simulations of porous media, we can overcome these obstacles and provide rapid and accurate evaluations of relevant factors such as pore volume, flow capacity, pathway complexity, and reaction rates.
ML can extract insights from various data sources, including two or three-dimensional images, pore structure characteristics, computational fluid dynamics (CFD), or experimental findings.21,22 It can also incorporate fundamental physical constraints or existing knowledge into the learning process to enhance accuracy and applicability. The field of ML applied to porous media represents an innovative and stimulating area, offering fresh perspectives and solutions to numerous scientific and technical challenges related to fluid movement and distribution in complex materials. The following section briefly provides an overview various ML methods applicable to porous media.
2.1. Principles of porous media
Porous substances are characterized by two primary attributes: (1) the presence of unfilled voids or pores within the solid material that can be occupied by liquids such as air, water, oil, or a combination of different fluids and (2) the ability to allow various fluids to pass through at specific pressure differentials.232.1.1.1. Permeability. Permeability, which refers to the flow of liquids through materials containing pores or cavities such as rocks, soils, or filtration devices, has been extensively studied by researchers and experts in porous media. Factors influencing permeability include pore volume, pathway complexity, pore shape and size, and other porous medium characteristics. Various methods exist to determine permeability, such as core analysis, interpretation of well logs, and well assessments. Permeability is commonly expressed in units of Darcy or milli-Darcy.24
2.1.1.2. Porosity. Within the context of porous media, porosity represents the proportion of empty spaces within the material. It significantly influences the movement of liquids, heat, and solutes within the porous medium. Porosity is generally quantified as a dimensionless ratio or percentage. Furthermore, porosity can be categorized into different types: total porosity, effective porosity, primary porosity, and secondary porosity.25
2.1.1.3. Capillarity. Capillarity refers to the phenomenon where fluids are drawn into tiny pores or porous materials due to surface tension driven by capillary pressure. The capillary pressure, influenced by interfacial tension, pore size and shape, and the wetting characteristics of the liquids and solid structure, is used to determine the pressure difference at the interface of two immiscible liquids. Capillarity plays a crucial role in governing the flow, spreading, and confinement of liquids within porous media, with applications in areas such as oil extraction, CO2 storage, groundwater decontamination, and fuel cells.26
2.1.1.4. Sorption. Sorption, in the context of porous media, refers to the process by which a porous material adsorbs or absorbs a substance. This phenomenon significantly impacts the movement and fate of pollutants in soil and groundwater, as well as the sequestration and retrieval of gases such as CO2 and CH4. The properties of the substance, the porous material, and the environmental conditions all play a crucial role in influencing sorption. Sorption can exhibit nonlinearity, meaning that the sorbed substance amount does not correspond linearly to its concentration in the liquid phase. This nonlinearity arises from the heterogeneous nature of the porous material, the arrangement of sorption sites, and competition among different substances for the same sites. Additionally, sorption can exhibit disequilibrium, where the equilibrium between the solid and liquid phases is delayed or hindered in rate. This phenomenon is due to substance diffusion within the pores, mass transfer between distinct pore regions, and the kinetics of sorption reactions.27
2.1.1.5. Fluid–solid interactions. The interaction between fluids and solids in porous media, known as fluid–solid interaction, explores the interplay at the pore scale and its implications for the macroscopic properties of the porous material. This interaction encompasses fluid flow, solid deformation, mass transfer, chemical reactions, and phase transitions. Fluid–solid interaction has significant applications and consequences in fields such as geomechanics, hydrology, petroleum engineering, environmental engineering, and biomedicine.28
2.1.2.1. Darcy's law. Darcy's law, which serves as the foundational model, relates the fluid velocity to the pressure gradient within the porous medium. According to this law, the volumetric flow rate of the fluid is directly related to the cross-sectional area of the porous medium, its hydraulic conductivity, and the hydraulic gradient (pressure or head difference per unit length) along the flow direction. Mathematically, Darcy's law can be expressed as:29
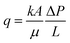 | (1) |
In this equation, q represents the Darcy flux, k denotes the permeability, A is the cross-sectional area (m2), ΔP signifies the pressure difference, and L corresponds to the length of the porous medium. Darcy's law is applicable for low Reynolds number flows in homogeneous and isotropic porous media.
2.1.2.2. Brinkman's equation. Regarding porous substrates, the concept of Brinkman characterizes an advancement of Darcy's law, encompassing the influence of fluid thickness on the flow through the porous material. An extension of Darcy's law, the Brinkman equation integrates a component reflecting the Laplacian of velocity in accordance with the Stokes equation for viscous movement. The Brinkman equation is expressed as follows:30
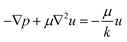 | (2) |
In this equation, p represents pressure, μ denotes the dynamic viscosity of the fluid, and u signifies Darcy's velocity. The first term on the left symbolizes the pressure gradient, the second term represents the Brinkman viscosity factor, and the resistance term of Darcy is depicted on the right side.
This Brinkman equation proves effective in modeling fluid movement within porous substances exhibiting low porosity, reduced permeability, or high velocity, where viscosity impacts are more evident. The Brinkman equation can also be combined with other elements to account for supplementary influences such as inertia, reactions, diffusion, and heat transfer within porous substances.
2.1.2.3. Forchheimer equation. In relation to porous substrates, the Forchheimer equation denotes a notion that encompasses a modification of Darcy's law, incorporating the inertial effects of fluid motion through the porous material. The Forchheimer equation, an expansion of Darcy's law, encompasses a term signifying the squared relationship between the pressure gradient and velocity, akin to the Bernoulli equation for non-viscous motion. The Forchheimer equation can be formulated as follows:31
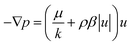 | (3) |
In this equation ρ refers to the density of the fluid, β is the Forchheimer coefficient and u denotes Darcy's velocity.
The Forchheimer equation proves valuable in modeling the movement of fluid within porous substances featuring high porosity, increased permeability, or high velocity, where inertial effects become noticeable.
2.1.2.4. Richards' equation. In the case of porous substrates, Richards' equation represents a concept that encompasses a partial differential equation elucidating the movement of water in unsaturated soils, where gravitational and capillary effects play a significant role. This equation is based on the Darcy–Buckingham law, representing water flow in porous substances under varying saturation conditions, and the law of mass conservation for an incompressible porous substance with consistent liquid density. The equation can be formulated as follows:32
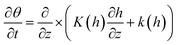 | (4) |
In this equation, θ represents the volume-based water content, t denotes time, K represents the hydraulic conductivity, h signifies the pressure head of the liquid, and z symbolizes the unit vector in the vertical direction.
Richards' equation proves effective in modeling the movement of water in the vadose zone, which is the region between the atmosphere and the aquifer, where saturated and unsaturated conditions can coexist. The equation can also be employed to investigate various phenomena such as water infiltration, drainage, evaporation, irrigation, plant transpiration, soil erosion, pollutant transportation, and heat transfer in porous substances.
2.1.2.5. Navier–Stokes. The Navier–Stokes equation is a crucial mathematical model that characterizes the motion of fluids by considering the conservation of mass, momentum, and energy. It can be expressed in the general form below:
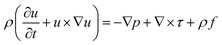 | (5) |
To address these challenges, ML techniques can be employed to enhance the modeling of fluid flow in porous media. ML can be utilized to approximate the solution of the Navier–Stokes equation in porous media. For instance, ML can predict steady-state velocity fields and permeability in porous media.33
2.2. Types of learning
Fundamentally, ML operates by utilizing encoded instructions to analyze and evaluate input data, generating predictions within a permissible range. As new information is introduced, these algorithms adapt, improve their functionality, and gradually acquire knowledge, becoming more effective over time.ML algorithms can be classified into four categories: supervised learning, semi-supervised learning, unsupervised learning, and reinforcement learning.
(1) Classification: during categorization functions, the ML application must deduce the group of fresh instances using the data.
(2) Segmentation: it is the process of classifying a given set of data into different groups. It is used in machine learning applications to determine similarities and differences in the data and to identify patterns and trends.
Reservoir simulations pose a significant computational challenge due to their complexity. In this situation, semi-supervised learning offers a promising solution to this problem. By utilizing high-resolution simulations from a limited number of samples and combining them with lower-resolution data from a larger set, semi-supervised learning enables more efficient upscaling of simulations for reservoir characterization. Another application of semi-supervised learning in porous media is its use in identifying anomalous flow patterns. By training on labeled data containing examples of normal and anomalous flow patterns, a semi-supervised learning model can leverage unlabeled data to detect potential anomalies in new datasets.
(1) Clustering groups of similar datasets based on specific criteria allows for data segmentation into multiple groups to identify patterns within each group.
(2) Dimension reduction simplifies the consideration of variables by reducing their number, aiming to reveal the essential data required.
Unsupervised learning enables the analysis of unlabeled images of porous materials, allowing the quantification of pore network complexity metrics such as connectivity and tortuosity. Moreover, unsupervised learning algorithms can detect anomalies in flow data, identifying deviations from typical flow patterns within large datasets. This capability is particularly useful for early detection of issues such as preferential flow paths or blockages, which can significantly impact porous media behavior. Overall, unsupervised learning has proven to be a promising tool for studying porous media, with various potential applications in both research and industry.
2.3. Machine learning models
ML models can be seen as software programs designed to identify patterns in new data and make predictions. These models are represented as mathematical functions that take input queries, make conjectures, and produce corresponding outputs. Initially, the models are trained on a dataset, and an algorithm is applied to reason over the data, extract patterns, and acquire knowledge from it. Once trained, these models can be used to predict unseen data.Decision trees' merits lie in their simplicity and ease of implementation, but they fall short in precision. They find extensive application in operational research, especially in decision analysis, strategic planning, and primarily in ML.
In relation to porous substances, decision trees can aid in determining the crucial features influencing CO2 adsorption, such as textural characteristics, compositional properties, and adsorption parameters.37
A random forest model is versatile, being applicable to both regression and classification tasks. For classification tasks, the outcome from the random forest is derived from the majority voting. Conversely, the outcome in regression tasks originates from the mean or average of predictions produced by each tree.
Numerous varieties of neural networks exist, each with varying complexity levels. All aim to emulate the human brain's functionality to tackle complex problems or tasks. The configuration of each neural network type somewhat mirrors neurons and synapses. However, they differ in complexity, applications, and structure. The differences extend to modeling artificial neurons within each type of neural network and the connections between each node. Other distinctions include the way data navigate through the neural network and the density of the nodes. The most common types of neural networks used in porous media are detailed in the following.
2.3.4.1. Multi-layer perceptron. A multi-layer perceptron (MLP) falls under the category of feedforward neural network (FFNN).41 It is a versatile and commonly used architecture for supervised learning tasks such as classification and regression. MLPs are the most fundamental deep neural network, consisting of a sequence of fully interconnected layers (an input layer, one or more hidden layers, and an output layer). Each neuron within the network processes input data using weighted connections and activation functions. MLPs can be utilized to circumvent the need for extensive computational resources required by modern deep learning frameworks.
2.3.4.2. Convolutional neural networks. Convolutional neural networks (CNNs) constitute a variant of neural networks predominantly utilized for processing image and visual data. They are designed to autonomously learn and extract hierarchical patterns and features from input images. CNNs encompass convolutional layers that apply filters to input data, followed by pooling layers for downsampling and fully connected layers intended for classification or regression tasks.
2.3.4.3. Recurrent neural networks. A recurrent neural network (RNN) represents another category of ANNs that leverages sequential data input. RNNs were conceived to tackle the time-series challenge posed by sequential input data. An RNN's input comprises the current input along with prior samples. As a result, the connections between nodes form a directed graph that follows a chronological order. Additionally, every neuron in an RNN possesses an internal memory that preserves computational information from prior instances.
2.3.4.4. Physics-informed neural networks. Physics-informed neural networks (PINNs) are a groundbreaking fusion of artificial intelligence and mathematical physics, specifically tailored to address the complexities of partial differential equations (PDEs). Their modus operandi involves projecting solutions to these PDEs through the fine-tuning of a neural network aimed at minimizing a meticulously designed loss function. This loss function is imbued with critical elements representing the initial and boundary conditions within the space-time domain and the residual of the PDE at specific loci, known as collocation points. As PINNs function under the umbrella of deep learning models, they deliver a calculated approximation of a differential equation's solution at a specific point within the computational domain after completing their training. A revolutionary stride in the field of PINNs is the incorporation of a residual network that envelops the primary physics equations. In essence, the PINN's training process is viewed as an unsupervised learning approach, eliminating the necessity for pre-labeled data that typically originate from prior simulations or experiments.
The PINN algorithm is a grid-independent method that procures solutions to PDEs by recasting the task of directly solving governing equations into an optimization challenge for the loss function. This transformation becomes feasible by weaving the mathematical model into the fabric of the network and enriching the loss function with a residual term extracted from the governing equation. This residual term acts as a constraint that focuses on the range of acceptable solutions, ensuring more precise and reliable results.
2.4. Evaluation metrics
Evaluation metrics serve as tools to quantify the performance level of an algorithm or model. They offer a numerical indication of the model's success in meeting its objectives, such as precise prediction of results or data categorization. Diverse types of tasks might necessitate the application of different evaluation metrics.37,423. Applications of machine learning to porous media
This section presents a thorough review of the interface of ML and porous media in the six subsections, namely, heat exchanger and storage, energy storage and combustion, electrochemical devices, hydrocarbon reservoirs, CCS, and groundwater. Scientific research on porous media has traditionally been dominated by empirical and semi-empirical models which, while useful, often fail to capture the complex inherent interactions in such materials. In recent years, applications of porous media have been pronounced, especially in energy applications, including electrochemical devices43,44 (i.e., batteries, fuel cells,45 supercapacitors,46etc.), enhanced oil recovery, different energy storage technologies, and also environmental applications, such as carbon capture and water filtration. The advent of ML offers transformative potential in this regard, providing tools that can improve data processing, integrate large datasets, and uncover patterns that are not immediately discernable. ML's capability to adaptively learn from data without explicit programming leads to the assessment of porous media in exceptional detail. This facilitates a more refined understanding of physics such as flow and transport phenomena, adsorption and absorption, phase changes, and reactive dynamics within porous structures, which are critical for optimizing applications and poised to address some of the most important challenges in engineering and environmental science today. This discussion aims to engage readers by linking theoretical advancements in ML with practical, impactful applications in porous media, highlighting how these integrated approaches are transforming the assessments of porous media.3.1. Heat exchanger and storage
Heat transfer represents a pivotal and foundational issue within thermal science, holding absolute significance in today's global economic and energy landscape. The efficiency of heat transfer systems is influential in mitigating energy waste and protecting the current fossil fuel reservoirs. It is conducted using energy recovery systems, such as economizers, and enhancing heat transfer methods, such as extended surfaces, turbulators, microchannels, and phase change materials (PCMs). Moreover, the optimization of thermal systems, encompassing the extraction, transportation, and utilization of energy sources, particularly those facing challenges in temporal and spatial production, is imperative. Efficient heat transfer is needed using the methods of heat transfer increment, as well as the optimal input conditions. Another positive outcome of effective heat exchangers and storage devices is the reduction of pollution, contributing to improving adverse environmental impacts and climate change, especially for those systems that apply combustion flue gases.The pursuit of a heat exchange system with superior thermo-hydraulic performance necessitates the use of tools for optimization and prediction. ML approaches, which initially emerged over half a century ago for pattern recognition, have evolved into sophisticated and professional methods. Consequently, tools for optimizing and predicting thermal system parameters are now readily available. The combined capabilities of optimization and prediction empower a thermal system to operate in a tuned mode, facilitating control systems a process that would be time-consuming with traditional analytical approaches. As well as the prediction of steady conditions, ML now takes advantage of transient estimation, enabling us to predict and respond to changes in real-time. This is particularly crucial in scenarios where thermal systems experience rapid variations, such as during startup and shutdown, or when subjected to varying external conditions. The ability to estimate transients allows ML models to adapt quickly and optimize control strategies, leading to enhanced energy efficiency, improved system performance, and increased reliability in thermal processes.
Accurately determining the conditions for the efficient operation of thermal systems requires handling large volumes of data, a task that becomes slow and hard without the aid of ML methods. This is because thermal systems are affected by both thermal and hydrodynamic conditions as well as the ambient status and energy resource quality. Recognizing the potential of ML, it emerges as a key tool not only in setting a thermal system at its desired operational point but also in the design phase. It is such that the optimum dimensions of the geometry can be determined using ML. This section aims to explore previous endeavors that utilized ML models in thermal systems and porous media. As the chronological trend indicates continuous improvement in prediction and optimization methods, there is confidence that future ML methods will reshape the current engineering system trends.
Moreover, recent studies have emphasized the role of ML in assessing the characteristics of convection heat transfer, especially within porous media. Fig. 2 provides a visual representation, illustrating the integration of ML techniques to analyze and optimize the features of convection heat transfer processes in porous media. The incorporation of ML not only enhances our understanding of heat transfer phenomena but also paves the way for more efficient and targeted approaches to optimizing heat transfer characteristics within porous media.
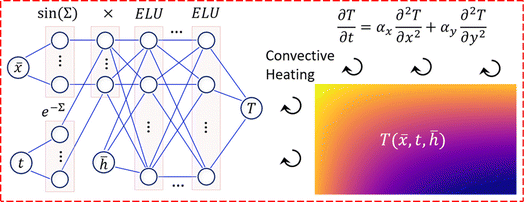 | ||
| Fig. 2 Application of ML in the prediction of temperature using spacial and temporal parameters as independent variables in transient convection of a porous medium, Zobeiry and Humfeld,47 reproduced with permission from Elsevier. | ||
Keykhah et al.48 numerically simulated a tube with porous zone inserts filled with water–silver nanofluid, which is a suspension of a liquid and nanoparticles. The Darcy number left an increment and mitigation effect on the Nusselt number and friction factor, respectively. Furthermore, the nanofluid volume fraction made the heat transfer increase and the friction factor decrease. Particle swarm optimization (PSO) was applied to find the optimum conditions considering the Nusselt number and friction factor as the objectives in the tube of a heat exchanger. TOPSIS, LINMAP, and Shannon entropy were used to select the optimum point; however, Shannon entropy was the best decision-maker. It is worth noting that TOPSIS, LINMAP, and Shannon entropy are called decision-makers to find the best point of working conditions among the Pareto frontiers, showing the set of solutions having the best trade-off among the whole objectives.
Selimefendigil et al.49 proposed a 3D channel equipped with porous blocks for dehumidification and heat transfer of wet air. The constrained optimization by the linear approximation (COBYLA) method was used to optimize the geometrical features of the blocks concerning heat transfer. COBYLA is a derivative-free optimization method used to solve problems with bound and general constraints. It approximates the objective function and constraints using linear models and iteratively finds solutions that minimize the approximations while satisfying the constraints. The full simulation includes unsteady heat and mass transfer. The flow behavior between the blocks caused the temperature difference in the domain. A transient ANN was introduced using Levenberg–Marquardt (LM) with backpropagation (BP) by feeding the time and drying temperature as dependent variables and the liquid saturation as the output. However, the author recommended generating an ANN with time-dependent variables as the model inlet.
Khan et al.50 numerically simulated porous fins with various shapes, called trapezoidal, rectangular, and dovetail, by considering convective and radiative heat transfer. Applying 1001 datasets, a neural network was constructed using the LM algorithm and cascade feedforward back-propagated approach. Using the inlet parameters, such as the inclination angle, tip tapering, and porosity, the temperature profile throughout the fins was predicted. A comparison between the captured results and those obtained by PSO and gray wolf optimization was accompanied and a negligible disparity was found. The results indicated that, in terms of having higher heat transfer, the fin shapes could be ranked as dovetail and rectangular followed by the trapezoidal fin profile.
Liu and Liu51 numerically simulated a heat-transferring tube involving porous ring inserts. The CFD results were coupled with an online multi-objective process, which was a non-dominating sorting genetic algorithm (NSGA-II), to find the optimum working conditions considering the Nusselt number and friction factor. The tube's radii, Damkohler number, and porosity were set as independent parameters. To reduce the undesirable populations in the genetic algorithm, they applied a penalty function, which removed the results with a higher friction factor. TOPSIS was used as a decision maker, showing more than a 40% increment in the Nusselt number and an 80% decrement in the friction factor.
Butt et al.52 tested an inverse multiquadric radial basis neural network for the problem of Casson nanofluid, which is a non-Newtonian fluid inherently, on a stretchable porous surface under an affecting magnetic force. The genetic algorithm was used for training and the solution method resulted in ODEs. The Casson parameter, Brownian motion parameter, Prandtl number, stretching parameter, and porosity parameter were some parameters to feed, and the velocity, temperature, and nanofluid concentration were predicted with an absolute error lower than 10−4. However, the ability of the current method is required to test for stiff sets of equations.
Ahmad et al.53 investigated a porous fin model through an analytical-numerical analysis. Two different porous types, which were silicon nitride and alumina, were compared and the prediction and optimization process was conducted respectively using an ANN and GA. It was concluded that silicon nitride had higher heat transfer than alumina. Therefore, alumina was highlighted with a higher temperature in the porous fin. The hybrid ANN-GA with the interior-point technique (IPT) showed more accurate and efficient optimum results.
Su et al.54 performed high-performance computing (HPC) coupled with an ANN for a double-diffusive problem, including mass and thermal diffusion. Furthermore, a multi-objective optimization for the functions of the Nusselt and Sherwood numbers was performed. The authors tried to solve the problem that needed a large volume of data to feed the ANN by applying the weighted objective functions, and aid from an HPC is required. The macroscopic porous properties and thermal features were fed to the ANN. It was shown that the random ordering of training data helped the accuracy of prediction when a sparse set of data is available, as the ANN's precision depended on the data distribution as well as the volume of data to feed.
Raja et al.55 considered a three-dimensional hybrid nanofluid flow over a stretching/shrinking porous surface including radiative heat transfer using an analytical-numerical approach. The solution approach converted the PDEs to ODEs. The ANN was constructed using the input parameters of mass flux parameter, thermal relaxation parameter, stretching/shrinking parameter, and Prandtl number. The prediction was made on a hydrothermal field. The stretching/shrinking parameter changed the mass flow rate and velocity profile, while the variation in the radiation heat flux affected the temperature gradient. The author proposed a solution using AI based on infrastructure for future studies.
Ahmad et al.56 used an ANN involving the Levenberg–Marquardt backpropagation to predict the temperature distribution of a fin attached to the heat sink. The fin was made of a functionally graded porous material to decrease the thermal gradient and three mechanisms of conduction, convection, and radiation heat transfer were considered through an analytical-numerical solution procedure. It was illustrated that the non-homogeneity of the fin increased heat transfer and the temperature gradient along the fin. It was such that the functionally graded materials made the temperature gradient negligible throughout the fin compared to the homogeneous materials.
Sajjad et al.57 proposed an ANN to predict convective heat transfer for pool boiling with R2 > 0.97 and MAE = 5.74%. Owing to the involvement of various parameters in problem physics, the prediction was hard using traditional methods. Therefore, a neural network could be beneficial and precise for predicting various fluids. Some input parameters were porosity, coating thickness, and particle size. Three hidden layers with neuron numbers of respectively 30, 15, and 1 were chosen.
The onset of convection cooling considering the rotation and magnetic field was studied in a horizontal bidispersive porous layer by Singh et al.58 using a neural network with SVM type. The network was applied to find the marginal state and instability mode. Having the targets of the Taylor number, the Hartman number, and the Vadasz number, defined as the ratio of the thermal diffusivity of the base fluid to that of the nanoparticles, to determine the stationary zone, it was found that the rotation, inertia, and magnetic field postponed the instability beginning, and therefore, steady working conditions could be extended. The two hidden layers worked better than the neural network with only one hidden layer. The Hartmann number could motivate the instability mode from the stability mode critically.
Increasing heat transfer in a proton exchange membrane fuel cell was simulated by Pourrahmani et al.59 A series of wave-like porous ribs made of aluminum were mounted in the gas flow channel to increase heat transfer. The results indicated that the height of the first porous layer played a critical role in the Nusselt number and PEC. The latter indicates the ratio of the heat transfer improvement to the cost of the pumping. An ANN was also applied to produce a large amount of data to analyze the effects of the geometrical parameters on heat transfer and friction loss. The results showed the salient role of the friction factor in the investigated system. Furthermore, it was illustrated that the PEC could be an influential parameter in design geometry.
Alizadeh et al.60 proposed an accurate estimator for the transport phenomena of a nanofluid passing through a cylinder in a porous medium using a support-vector regression (SVR) ANN. The semi-similarity technique by considering the local thermal non-equilibrium assumption was applied to find the results for training the ANN. As the problem involved a dozen parameters, the ANN decreased the time for a response by more than 90%. The correlations for the Nusselt number and shear stress using the PSO algorithm were derived.
Alhadri et al.61 analyzed a hybrid nanofluid flow with water base fluid over a stretching porous surface. The governing PDEs were converted into ODEs and then solved numerically using the shooting method. An ANN was produced to predict the Nusselt number and friction factor using the input parameters of porosity, Hartmann number, inertia coefficient, and suction/injection parameter. The coefficient of determination was found to be greater than 0.98. An optimization analysis was indicated using the response surface methodology (RSM). The main goal of RSM is to optimize a response variable, such as maximizing yield or minimizing cost, by exploring the relationship between this response and the input variables. RSM uses statistical models, often based on polynomial equations, to approximate the behavior of the response variable.
Mohebbi Najm Abad et al.62 instigated heat and mass transfer of a hybrid nanofluid in a porous medium. As the problem involves many parameters, conventional approaches to solving it might be complex and prone to failure. Therefore, they used an ANN. Furthermore, a PSO was also applied to derive some correlation to estimate the Nusselt and Sherwood numbers. Stemming from the dependency of the targets on various parameters, the feature selection process was performed. The results showed that the correlation involved at least five parameters that could reach an acceptable accuracy. Porous properties and the nanofluid volume fraction were among the most important ones.
Rajabi et al.63 analyzed the accuracy and robustness of a deep learning method for the problem of natural convection. The porous media was selected as a heterogeneous type. The encoder–decoder convolutional neural network (ED-CNNs) was applied for image-to-image processing as the input-to-target for a porous cavity. The training was conducted through high-resolution imaging and the output generally showed good accuracy. The zone with lower precision was found in the middle of the cavity where the temperature gradient fell. The training using a heat map in this method needed a large quantity of data, as they used 1000 samples. The method was beneficial for the uncertainty analysis of the meta-model.
The Brownian and thermophoresis effects were studied by Khan et al.64 in a fluid flow passing through two parallel porous plates. Brownian motion refers to the random movement of particles suspended in a fluid (liquid or gas) due to collisions with the molecules of the fluid. Thermophoresis is the movement of particles in a fluid medium due to a temperature gradient. The governing PDEs were transformed into ODEs using the homotopy analysis method. Viscosity, porosity, Prandtl number, and some other parameters were used as input parameters to the ANN applied to predict the concentration and temperature profile. The accuracy of the method showed well as the MSE fell between 10−14 and 10−7. The authors would like to test the applied ANN, which was a back-propagated neural network with the Levenberg–Marquard system to predict other fluid flow problems.
The subsequent focus involves advancements in manufacturing technologies targeting the fabrication of micro and nanoscale structures, particularly within miniature channels filled with porous media relevant to heat and mass transfer. This exploration is detailed in the next section. Surprisingly, the integration of ML into micro/nanoscale heat transfer with porous media has not been extensively explored, as indicated in Fig. 3. It should include data set creation, which is expensively hindered in experiments as well as feature selection methods and data training. The last part of this section reviews earlier studies on solar applications where porous media play a crucial role. Recognizing the significant role of heat exchangers in renewable energy production, the final section explores the application of ML in heat exchangers within solar systems equipped with porous parts.
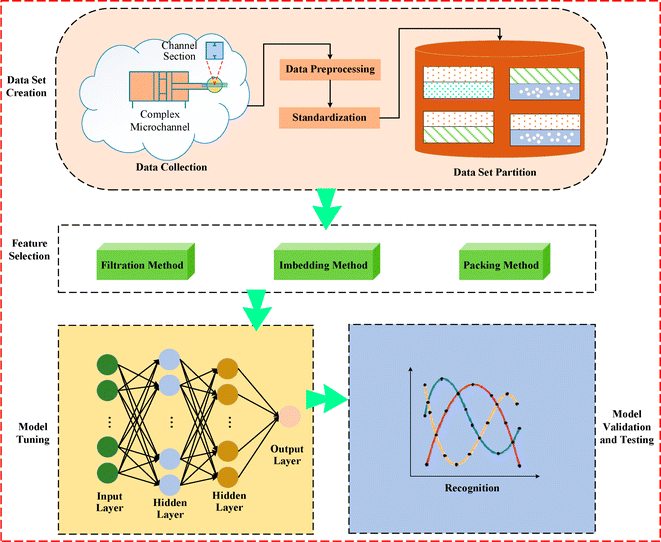 | ||
| Fig. 3 The schematic diagram for application of the feed-forward algorithm in microchannel flows; the first step includes data preprocessing and normalization, the second one is feature selection for removing the weak related parameters, and the final step involves model tuning and validation for having an accurate prediction, Yang et al.,65 reproduced with permission from MDPI. | ||
3.1.2.1. Conventional types. Siavashi et al.66 numerically studied heat transfer augmentation and pressure loss increment in a tube of a heat exchanger by inserting gradient and multilayer porous media and applying the water-alumina nanofluid. Six different porous types, including linear increasing particle size (LIPS), linear decreasing particle size (LDPS), stepwise increasing particle size (SIPS), stepwise decreasing particle size (SDPS), constant minimum particle size (CMIPS), and constant maximum particle size (CMAPS) were used. In LIPS structures, the pore size increases linearly and gradually along the length or depth of the material, while LDPS has a linear decrease in pore size. SIPS structures have discrete steps where the pore size increases abruptly rather than gradually; however, SDPS shows a similar structure when pore sizes decrease. CMIPS (CMAPS) structures maintain a constant minimum (maximum) pore size throughout the material. The maximum value of PEC (performance evaluation criteria) was captured by the PSO algorithm considering the independent parameters of porosity and grain size. The optimization for simultaneously considering particle size and porosity led to the same arrangement for independent parameters when considering each of them separately. Applying the nanofluid made the PEC three times higher.
Meng et al.67 used porous fins to increase heat transfer in a heat exchanger equipped with thermoelectric modules by a numerical simulation. An NSGA-II algorithm along with the TOPSIS decision maker was employed to increase heat transfer and decrease pressure drop by feeding the variables of the position, number, and relative distance of porous fins. A higher power generation and lower pressure drop by respectively about 79% and 21% was achieved by introducing porous pin fins. The dense downstream distribution for pin fins was shown to have the best performance compared to other distributions. A novel index was introduced to aid in picking up the optimum solution from the Pareto frontiers, meaning the electrical power generated by considering the pressure drop penalty. The velocity profile in the solution was reduced by increasing the porosity factor, the volumetric concentration, and the magnetic field amplitude.
Abbasi et al.68 numerically simulated a shell-and-tube heat exchanger with some segmental porous baffles. Inserting more baffles increased heat transfer, while it upgraded the pressure loss penalty. An ANN was trained to predict the crucial functions, which were the heat transfer rate and pressure drop to calculate the system performance. Furthermore, a multi-objective optimization along with a TOPSIS decision maker was performed to find the best values for baffles' features by minimizing the pressure drop and maximizing the heat transfer. The process recommended 10 porous baffles, a baffle angle of 111.9°, and a thickness of 16.69 mm, which led to a heat transfer rate and pressure drop respectively of 523.81 kW and 48.87 kPa.
Athith et al.69 numerically simulated a heat exchanger partially filled with high porosity metal foams, made of aluminum, copper, and nickel with two pore densities, 20 pores per inch (PPI) and 40 PPI. The authors intended to find the best performance of the heat exchanger by maximizing heat transfer and minimizing the pressure drop. Therefore, a multi-objective optimization using the NSGA-II algorithm was performed linking with an ANN to predict the objectives, which were the heat transfer rate and pressure loss. Although the porous inserts increased pressure drop, they could improve heat transfer significantly more than 5 times compared to the case without obstacles.
Chen et al.70 conducted a transient numerical simulation for a vertical geothermal heat exchanger. Soil was considered a porous medium. The borehole depth was predicted through a three-layer ANN using the input parameters of the soil thermal conductivity, grout thermal conductivity, inlet water temperature, underground water velocity, and heat flux. They concluded that the porosity of soil and volumetric heat capacity had an insignificant effect on the results. The ANN worked with 10 neurons and R2 > 0.9999; however, without using the Levenberg–Marquardt algorithm, the prediction error was critically enhanced.
Zheng et al.71 optimized the porosity of a multi-layer porous medium, ranging from 0.5 to 1.0, by coupling the ANSYS Fluent and MATLAB software. The application of their study was in the tubes of shell-and-tube heat exchangers. The multi-objective optimization found the appropriate porosity to have maximum performance evaluation criteria (PEC). The number of porous layers was also determined.
Mohammadi et al.72 numerically simulated a shell and tube heat exchanger equipped with porous baffles. An ANN was conducted coupled with an NSGA-II algorithm to find the optimum values of the porosity, permeability, and baffle cut for the objectives of heat transfer and pressure drop; each dependent parameter took six values. Additionally, the ANN was applied for sensitivity analysis, which showed that the baffle cut mostly contributed to the heat transfer enhancement and pressure drop decrement, respectively by 88% and 71%. The permeability was set in the next rank. The authors declared that, owing to steady state assumption, the fouling phenomenon was not considered a limitation of the simulation.
Baiocco et al.73 numerically evaluated a heat exchanger using aluminum metal foam, electrically deposited with copper for increasing conductivity. A neural network was applied to predict the characteristics of the heat exchanger with a general error of less than 1%. Input temperature, airflow speed, and foam material were the inputs, while the outlet temperature was the output. An electroplating process increased heat transfer and enhanced efficiency by about 10%. The numerical simulation was performed considering non-local thermal equilibrium.
Deshamukhya et al.74 used PSO to find the optimum design variables for a rectangular fin attached to a heat exchanger. The fin was made of porous materials and the porosity, the Damkohler number, and the ratio of thickness to length were selected as input parameters to find the maximum value of the heat transfer rate. PSO had a higher convergence speed, as it has a derivative-free nature. The tip temperature decreased by increasing the Damkohler number, while heat transfer increased. PSO elicited higher heat transfer while increasing the porosity decreased the heat transfer.
3.1.2.2. Micro/mini channels. Microchannels and mini channels are small-scale conduits through which fluids flow. Microchannels have dimensions in the range of micrometers to millimeters and exhibit a high surface-to-volume ratio, enabling enhanced heat transfer and fluid flow properties. They are employed in applications such as microfluidics and electronics cooling. Mini channels are slightly larger, ranging from millimeters to centimeters, and are used in areas such as compact heat exchangers and cooling systems. Both micro and mini channels offer unique fluid dynamics and heat transfer characteristics due to their reduced size compared to conventional channels.
Wang et al.75 performed a multi-objective optimization for finding a higher thermal resistance and a lower pumping power for a double-layered porous microchannel. Geometrical features were chosen as independent parameters. The numerical simulations showed an inverse trend for both objectives. The NSGA-II algorithm optimization results showed that the cooling performance increased by about 14% and pumping power decreased by nearly 16% compared to the reference case. The numerical results indicated that the upper channel was involved more in the pumping power and the lower channel was critical for improving heat transfer. The importance of various geometrical variables was derived.
Bayer et al.76 presented a microchannel with wavy double-layered porous walls to increase heat transfer as well as solve the problem of high-pressure loss. More than 3000 numerical tests were conducted to build an ANN based on the Levenberg–Marquardt backpropagation algorithm. The eight geometrical scales were used as independent parameters and convective heat transfer and pressure loss were the outputs of the ANN. Six neurons guaranteed the precision of the prediction. After validation of the proposed ANN using 30% of the data, the three best performers were introduced. The introduced patterns not only increased heat transfer but also decreased the temperature uniformity on the heat sink. The thermal efficiency factor was shown increase if the top wall became wavy and the bottom was straight instead of making a wavy shape on both walls.
Khosravi et al.77 applied an ANN to predict entropy generation in a microchannel under a constant thermal flux with porous fins filled with the water–silver/graphene hybrid nanofluid. A neural network was constructed using the parameters, such as different porous medium thicknesses, nanoparticle concentrations, and inlet mass flow rates. Various neuron numbers for the ANN were tested and it was found that the ANN could be accurate with two hidden layers having 12 and 20 neurons. The Bejan number was reported to be 0.944, showing that the thermal irreversibility was salient. An increase in the inlet mass flow rate and nanofluid concentration diminished the strength of thermal entropy generation.
3.1.2.3. Solar systems. Solar systems utilize the principles of conduction, convection, and radiation to transfer heat from solar radiation to useful applications. Solar radiation is absorbed by solar collectors, which convert it into heat energy. This heat is then transferred through conduction within the system's components, such as metal tubes or fluid-filled panels. Convection allows for the movement of heated fluids, such as water or air, which carry thermal energy to desired locations. Additionally, radiation is involved in both the absorption and emission of heat. By combining these heat transfer processes in porous media, solar systems efficiently harness solar energy for various applications such as heating water or spaces.
Ghritlahre and Prasad78 experimentally studied a solar air heater by inserting a porous bed. The prediction of thermal performance using a neural network using a multi-layer perceptron (MLP), generalized regression neural network (GRNN), and radial basis function (RBF) was conducted and compared with multiple linear regression (MLR) statistical models. The input parameters to the models were mass flow rate, wind speed, atmospheric temperature, inlet fluid temperature, fluid mean temperature, and solar intensity, collected during 96 tests. It was concluded that the neural models could predict better than the MLR. Furthermore, the GRNN was highlighted as the best predictive neural method; the MLP was set in the next rank.
Du et al.79 investigated a porous volumetric solar receiver by considering silicon carbide as the fluid flow medium. Furthermore, non-equilibrium assumption was involved with convective-radiative heat transfer. A multi-objective optimization by coupling ANSYS Fluent and MATLAB was performed. The pressure drop and thermal efficiency were selected as objective functions. Although the pareto front was derived, decision-maker strategies were not investigated. Nonetheless, the single objective optimization showed that the higher the porosity and flow velocity, the larger the thermal performance would be.
Zheng et al.80 evaluated a parabolic solar system by inserting porous fins in the shape of circular sectors and implementing a non-uniform heat flux on the tube. The Nusselt number, synergy angle, entransy dissipation, and exergy loss were the indices to appraise the heat transferring system. The porosity, thermal conductivity, and Reynolds number were the input parameters for the single objective genetic algorithm, while the Nusselt number was the target function. The results elucidated that optimum porous inserts made the receiver more efficient compared to the reference case with a lower exergy loss at the same pumping power.
Hosseini and Siavashi81 numerically scrutinized the steam reforming process to produce hydrogen gas in a thermo-chemical reactor aiding solar energy. A novel idea using a two-layer porous medium with different porosities was applied. Some parameters, such as permeability, pore size, and reactor length were chosen as input parameters for an ANN, coupled with the PSO algorithm, to find the optimum conditions. The objective was hydrogen production. The results showed that the optimization could enhance hydrogen production more than all the investigated cases. Additionally, the two-layer porous medium made an increment in hydrogen production.
Grosjean et al.82 optimized a glass with porous SiO2 anti-reflective coating to enhance solar transmittance using GA. The porosity and angle were the inputs. The performance was found to be drastically dependent on the glass type. The optimization process showed that the angle below 30 degrees had no effect on the objective, while values higher than 45 degrees made it critically different. A low refractive index and high Abbe number were introduced for an acceptable glass for solar applications.
Du et al.83 presented that a porous layer with small pore diameters was beneficial for uniform radiation heat flux in a solar receiver in terms of higher convective heat transfer. However, it had an undesirable effect on the radiation penetration, such as having overheating zones. Therefore, they optimized the pore scales using a GA to have the highest thermal efficiency. The proposed radial-graded porous increased the thermal efficiency by 4.1% and decreased the flow resistance by 8.6%. It was made of super-alloy Inconel 718 and passed mythological post-processing.
The thermal efficiency of an air heater equipped with a porous bed was predicted using an ANN by Ghritlahre and Prasad.84 Four training functions, such as one-step secant backpropagation, conjugate gradient backpropagation with Polak–Ribiere, and Levenberg–Marquardt were tested and it was illustrated that the latter performed the best. Thermal efficiency, heat gain, and temperature difference were chosen as targets for the input parameters of inlet velocity/temperature of the air, ambient temperature, and solar irradiance.
The application of ML in the cooling systems of electrical devices further contributes to a more efficient design, enabling a swifter and more resilient control system capable of responding adeptly to sudden thermal fluctuations. Moreover, the strategic use of porous media enhances the overall effectiveness of the thermal management system, providing a more stable operating environment for compact electrical systems. Additionally, as the diminished performance of vehicle batteries can compromise the power system's efficacy and competitiveness, maintaining precise temperature control within the desired range becomes crucial. This goal is easily attainable through optimization based on ML, as illustrated in Fig. 4, with the added advantage of porous media integration ensuring enhanced thermal regulation and reliability in challenging operational conditions.
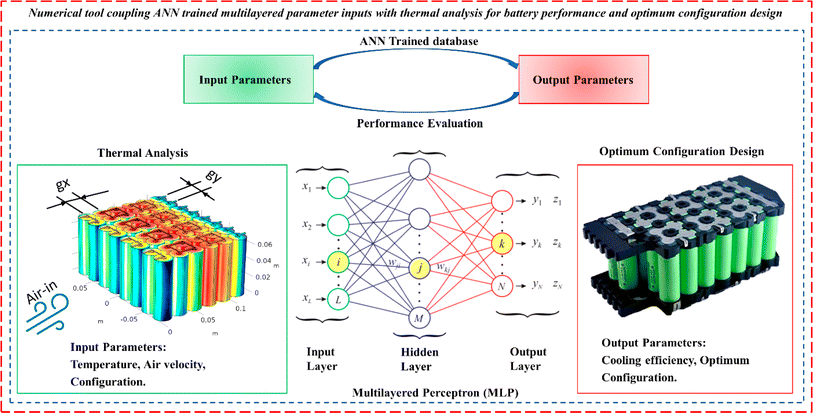 | ||
| Fig. 4 Schematic view for applying combined CFD-ANN for battery cooling; temperature, air velocity, and geometrical features as input parameters and cooling efficiency as the output parameter in an MLP network aiming for prediction, Li et al.,85 reproduced with permission from MDPI. | ||
Duan and Li86 investigated transient heat transfer in a metal foam filled with a phase change material, applied for cooling electrical devices or batteries. An ANN was trained to predict the liquid fraction, temperature, and average Nusselt number using lab-based experimental data. The input data were the time series and the porous medium characteristics. However, the effects of geometrical features and environmental conditions were not considered. The importance of the porosity parameter on the changes in the melting process speed with passing time was reported. The latter was dependent on the temperature-dependent thermal features of the metal foam.
Tikadar and Kumar87 predicted the thermo-hydraulic performance of a heat sink in conjugation with a metal foam using five ML algorithms, called k-nearest neighbors (KNN), random forest (RF), extreme gradient boosting (XGBoost), SVR, and ANN. The average Nusselt number and friction factor were chosen as the dependent parameters, while the porous zone density, porosity, two geometrical indices, and the Reynolds number were picked as the input parameters. SVR and the ANN showed a minimum mean absolute percent error of 3.1%. A data size of 1000 points was numerically collected, and the results indicated that the ML methods could capture the thermo-hydraulic performance of the heat sink well, despite its nature as a ‘black box’.
Ilyas et al.88 in an analytical-numerical study scrutinized the fluid flow and heat transfer of a hybrid nanofluid, as alumina–copper–water, over a rotating disk where a porous medium was attached and a magnetic field was imposed. Scaling group transformation converted the PDEs to ODEs. The thermo-hydraulic field was predicted by the Levenberg–Marquardt backpropagation neural network. The porosity factor, inertia coefficient, Prandtl number, Brinkman number, radiation parameter, magnetic parameter, and concentration of nanoparticles were selected as the feeding parameters for prediction. The validation performance was reported to be precisely a value lower than 10−10.
Butt et al.89 presented an amalgam procedure involving the inverse multiquadric (IMQ) radial basis neural networks (RBNNs) and a genetic algorithm, i.e., IMQ-RBNN-GA. The hybrid proposed method was validated through the problem of cooling a wedge by passing a nanofluid in a porous medium considering the radiation, viscous effect, and magnetic field. The absolute error for the neural procedure was lower than 10−10 by comparing it with the Adams solution method. The dynamic properties of the nanofluid were the objective. The Eckert number and Brownian motion made the nanofluid temperature higher, while the radiation subsided it.
Bianco et al.90 numerically simulated a cooling system for a heat sink involving finned and non-finned metal foams. As the heat transfer and pressure drop act in opposite directions, optimization was conducted in the study by linking the COMSOL Multiphysics and MATLAB modules. The results indicated a higher heat transfer by inserting fins about 3.3–3.5 times than that of simple configuration with constant pressure loss. In this case, the optimization could enhance the heat transfer by a factor of 3. The optimization concluded that a porosity of 0.85, 40 PPI and a number of fins of 8 were appropriate. Furthermore, correlations for Pareto fronts were provided.
Deshamukhya et al.91 studied the optimal heat transfer rate for stepped, convex and triangular porous fins attached to a heat sink. PSO and the firefly algorithm (FA) were employed to achieve optimal heat transfer versus the geometrical parameters, as well as the Damkohler number, Rayleigh number and porosity, keeping the fin volume constant. The stepped profile showed the highest heat transfer compared to the triangular and convex profiles by nearly 2% and 40%, respectively. PSO illustrated marginally better performance, while the FA indicated more acceptable suboptimal points. A porosity of 20% at a lower length ratio addressed optimal heat transfer.
A layered porous heat sink was scrutinized numerically for heat sink by Dathathri and Balaji.92 An ANN was used to predict the temperature and pressure drop using the input parameters of inlet velocity and pore scale. The applied ANN was fed to a multi-objective genetic algorithm (NSGA-II) to find a maximum temperature and minimum pressure drop. The results elucidated that neglecting pressure drop could result in a major deviation from reality in genetic algorithm optimization.
Shoaib et al.93 investigated double-diffusive, free convective nanofluid flow in a porous medium numerically for cooling a hot plate. The prediction was performed using a Levenberg–Marquardt scheme in a backpropagation algorithm, in a novel application. Different cases with changing the Grashof number and various scenarios with varying variables, such as the Brownian motion parameter and thermophoresis parameter were studied. Various parameters, such as the Brownian parameter, inclination angle, and Dufour, Grashof, and Lewis number as well as magnetic strength were evaluated. The non-dimensional temperature and concentration were among the target parameters. The effect of governing parameters on the volume fraction of the nanofluid was critically investigated.
Integration of porous media becomes particularly significant in enhancing the performance of these systems. The incorporation of porous media in terms of geometry, foam distribution, and flow path optimizes heat storage mechanisms, ensuring a more effective utilization of undemanding energy. This approach not only addresses the energy crisis but also promotes sustainable practices in energy management. Furthermore, the application of ML extends its benefits by enabling the prediction of thermal energy storage system performance under various operating conditions. This predictive capability enhances the overall efficiency of energy management strategies, providing valuable insights into system behavior under diverse circumstances. In summary, the synergy between ML and porous media contributes to the development of advanced heat storage systems that are not only more sustainable but also adept at meeting the evolving demands of energy consumption.
Yang et al.94 tried to solve the problem of the low heat transfer rate and low thermal efficiency of a latent heat storage unit using metal foams, made of aluminum, nickle, and copper. A quasi-stationary approximation was considered to have a simple and accurate solution. A simplified model predicted the phase change time and a genetic algorithm optimized the metal foam distribution. The effect of various parameters on the porosity distribution and graded layer number was numerically found to be negligible. Thermal performance was the objective function sought to find the best value with an average accuracy of 5–6%. Considering economical and engineering requirements, four metal foam layers were recommended.
Cui et al.95 numerically and experimentally analyzed an inclined container equipped with a hybrid structure of metal foam and metal foam-fin hybrid. The metal foam-fin system aided in having more heat transfer. Furthermore, an increment in the fin number accelerated the phase change material (PCM) melting and heat accumulation. Using a proposed ANN, the melting time was predicted using the input parameters of the fin number, inclined angle, and melting time with an R2 of about 0.9990. Applying the metal foam fin could make the melting process up to 60% quicker.
Anand et al.96 used numerical results to feed a self-organizing map (SOM) to predict gas and solid phase temperature profiles in a porous medium including a PCM. The extinction coefficient and convective coupling were applied as inputs. Four pairs of temperature profiles were fed to the SOM, and it could predict various regimes correctly. The algorithm also succeeded in estimating precisely the PCM regime when it was trained using 1% noisy data. The proposed procedure could aid in the design process of thermal systems including porous PCMs, such as those working in a combustive aperture.
 | ||
| Fig. 5 A flow work to predict porous properties of porosity (ϕ), specific surface area (SSA), and average pore size (APS) by a CNN using image acquisition, visually/experimentally input parameter extraction, and construction of a tuned neural network for prediction, Alqahtani et al.,97 reproduced with permission from Elsevier. | ||
Eghtesad et al.98 applied an ANN to predict the radiation properties of a porous medium at a high temperature. The model could mitigate the burden of the numerical simulation of radiative models. Transmission and reflection were selected as the outputs. The authors introduced coupled geometrical and physical features, such as porosity, the void's refractive index, the particle's refractive index, and the particle radius. Three predictive categories, namely, whole-size, wall-wise, and point-wise were also considered by involving random overlapping and non-overlapping packed porous media; the latter was shown to be more accurate. The point-wise class, predicted independently from the emission angle, was of the least accuracy. It showed a promising prediction needed involving directional features of the porous media.
Wei et al.99 tried to derive an ML method to predict porous thermal properties, considering morphology properties, owing to the high expense of numerical simulations. The effects of some parameters, such as the shape factor and channel factor, on the thermal conductivity were studied using an ANN. Then, the SVR could predict the anisotropy features of the pores and involve them in effective thermal conductivity. The results showed that the selected inputs were critical to have an accurate estimation of conductivity. The resultant ML could present an intuitive insight into the conductivity values out of the normal range.
Mishra et al.100 used a global search algorithm (GSA) and GA to predict some thermal properties in a 2D rectangular porous matrix considering conduction, convection, and radiation. Scattering albedo, emissivity, solid conductivity, and heat transfer coefficient were tried to predict by capturing the solid and gas temperature distribution. Both direct and indirect approaches were applied using the finite volume method for solving energy equations. The results indicated that the GSA showed faster prediction with higher accuracy compared to the GA. However, the run time was affected by the starting points and the error.
Singh et al.101 tried to predict the effective thermal conductivity using six feedforward backpropagation ANN models for a moist porous medium by feeding the thermal conductivity and volume fraction. The complex structure and different thermal features of the substances in a moist porous material pushed the authors to use artificial intelligence. The model showed good accuracy against the experimental data. It was concluded that the fluid phase played a critical role in the prediction. The derived model could be used for complex moist porous structures.
3.2. Energy storage and combustion
As time passes, humans are facing a growing energy demand.102 Meeting the growing energy demand can be achieved by utilizing combustion systems such as boilers and gas turbines and renewable sources of energy, such as solar and wind energies, which are viable solutions.103 In addition to addressing the growing energy demand, it is crucial to consider the storage of generated energy.104 The industrial sector frequently stores energy to guarantee a consistent and uninterrupted power supply, as well as to regulate fluctuations in energy demand. Thermal energy storage (TES),105 electrochemical energy storage (EES),106 hydrogen gas energy storage,107 and hybrid energy storage108 are some prevalent methods for energy storage in industry. Optimal storage technology selection is performed using various factors, including the scale of storage required, the duration of storage needed, the specific energy demands, and the economic feasibility of the system.Porous media can indeed be used for energy storage in various ways. For instance, metal–organic frameworks (MOFs) have found diverse applications as a porous medium across multiple industries such as solar cells, fuel cells, supercapacitors, white light emitting diodes, and lithium-ion batteries.105 The porous nature of these materials provides a large surface area, which can enhance storage capacity and facilitate the movement of fluids or gases. Energy storage systems consist of various components that use porous media, including porous electrodes for batteries,106 porous adsorbents for gas storage,107 and porous phase change materials (PCMs) for thermal energy storage.108
The application of ML techniques in energy storage with porous media has gained significant attention.109,110 These techniques offer valuable tools to understand and optimize various aspects of energy storage systems based on porous media. ML has several applications in this field, such as the characterization of porous materials,111 material design,112 and optimization of energy storage systems.113 Through ML, researchers and engineers can analyze complex data, optimize system performance, and advance the field of energy storage with porous media. By leveraging these techniques, they can enhance the efficiency, reliability, and overall performance of energy storage systems based on porous media. Fig. 6 depicts several studies on energy storage systems utilizing porous materials, aided by ML.
 | ||
| Fig. 6 (a) Determining achievable volumetric targets for adsorption-based hydrogen storage in porous crystals using ML,114 reproduced with permission from American Chemical Society, (b) predicting hydrogen storage in MOFs through ML techniques,115 reproduced with permission from Cell Press, (c) a computational framework that utilizes ML techniques to predict the work function of MXenes,116 reproduced with permission from IOP Publishing Ltd, (d) the construction of a hybrid framework that combines ANNs and genetic algorithms for optimizing capacitance in supercapacitors,117 reproduced with permission from Elsevier, (e) the process of utilizing ML for rechargeable battery materials involves four major stages,118 reproduced with permission from Elsevier, and (f) predicting the adsorption energies of hydrogen, carbon, and oxygen using online databases, density functional theory (DFT) calculations, and ML regression models,119 reproduced with permission from the AIDIC-Italian Association of Chemical Engineering. | ||
In the upcoming section, we will delve into various processes of energy storage utilizing porous media and ML. We will present diverse thermal energy storage and electrochemical energy storage methods. Also, hydrogen gas energy storage, hybrid energy storage, and combustion will be reviewed. Fig. 7 illustrates some research on energy storage and combustion using porous media aided by ML.
 | ||
| Fig. 7 (a) The temperature behavior of the walls of pore scale porous media (PSPM) changes with the use of PCM encapsulation influenced by variations in porosity, (1) without and (2) with optimization,120 reproduced with permission from Elsevier, and (b) the wetting of an electrode using real and predicted visualization of the electrolyte over time in a lithium-ion (Li-ion) battery. The electrolyte enters through the yz plane at x = 0. Refer to the web version for color explanations,121 reproduced with permission from Elsevier, and (c) comparing actual and predicted capacitance values for a supercapacitor during training and test phases. Circles represent real values and triangles represent predicted values,243 reproduced with permission from Elsevier, (d) performance of an ML model in predicting ln Poeq (the equilibrium pressure of H2 at room temperature) in (1) training and (2) test processes, in which each plot contains overlaid data from 10-fold validation experiments,123 reproduced with permission from ACS Publications, (e) comparing estimated and measured values of liquid fraction, entropy generation rates, and thermal management in battery systems using a gradient boosting decision tree (GBDT) model and scatter plots,124 reproduced with permission from Elsevier, and (f) comparison of research results and experimental data for combustor wall temperature and reformer CH4 conversion,125 reproduced with permission from Elsevier. | ||
3.2.1.1. Phase change materials (PCMs). PCMs can be effectively combined with porous materials for energy storage applications.128 The integration of PCMs with porous media enhances the storage and release of thermal energy. The combination of PCMs and porous materials offers advantages such as high energy storage density, improved thermal conductivity, and enhanced heat transfer characteristics. These hybrid systems have the potential to contribute to more efficient and sustainable energy storage solutions in various fields, including building and construction, renewable energy integration, and thermal management.129 Furthermore, the combination of PCMs with porous materials for energy storage can be further enhanced through the application of ML techniques. In a study, Saboori et al.120 utilized multi-layer calculation loops based on ML to examine the flow pattern and thermal behavior of pore scale porous media (PSPM) walls, which incorporated PCMs in Trombe walls. They introduced a new approach for predicting and optimizing the concentration of PCMs in Trombe walls, considering factors such as porosity, solar radiation, heat flux, and time. Based on the findings, the use of PCMs can lower the temperature of the outer side of the PSPM wall by 5.2% compared to not using PCMs during the day and night. In another study conducted by Selimefendigil and Öztop,130 they explored the impact of a porous disk on the dynamic aspects of the phase change process. The study focused on a circular pipe with PCM integration during nano-liquid forced convection in discharging operation mode using the finite element method for various values of porous disk permeability, radius, and height. The disk achieves its best permeability value at a Darcy number of 5 × 10−3, resulting in the shortest discharging time. In this research, a feed-forward neural network (FFNN) predictive model is utilized to provide precise results on the impact of a porous disk on the dynamic characteristics of the phase change process.
It's important to note that the integration of ML into PCM and porous material systems for energy storage is an emerging research area, and these are potential avenues where ML techniques can provide valuable insights, optimization, and control for enhancing the performance and efficiency of energy storage systems utilizing PCMs and porous materials.
3.2.1.2. Adsorption cooling and heating systems. Adsorption cooling and heating systems that utilize porous media can benefit from the integration of ML techniques. ML can aid in optimizing and improving the performance and energy efficiency of adsorption-based systems for cooling and heating.131 In a study conducted by Skrobek et al.,132 three deep learning techniques (long short-term memory (LSTM), bidirectional long short-term memory (BiLSTM), and gated recurrent unit (GRU)) were employed to predict the mass of an adsorption bed in both fixed and fluidized beds. The purpose of utilizing this particular bed was to optimize the efficiency of adsorption cooling systems by enhancing heat and mass transfer via fluidization. The algorithms developed for the LSTM, BiLSTM, and GRU networks produced results that were highly consistent with experimental tests, with coefficient of determination (R2) values exceeding 0.97. In the field of adsorption-driven heat pumps and chillers, Shi et al.133 conducted a study on selecting effective adsorbents and working fluids. They utilized a high-throughput computational screening of 6013 computation-ready experimental MOFs to determine the best candidates for methanol-MOF pairs. The research resulted in the identification of the top 10 MOFs with the highest working capacity (ΔW) and coefficient of performance (COP) under the heat pump's operating conditions, which were found to be 512.86 mg g−1 and 1.83, respectively. They also applied four ML algorithms (back propagation neural networks (BPNNs), decision trees (DTs), random forest (RF), and SVMs to predict the relative significance of each MOF descriptor. Based on the comparisons, it has been determined that both RF and BPNNs can produce the most accurate predicted results. Using high-throughput screening and ML techniques, this computational work serves as a reliable guide for the development and design of MOF adsorbents in adsorption-driven heat pumps and chillers.
3.2.1.3. Thermochemical energy storage (TCES). Thermochemical energy storage (TCES) with porous media involves utilizing chemical reactions within porous materials to store and release heat. It is a promising approach for high-density and long-duration energy storage. The reactions occur within the porous structure, allowing the storage and release of thermal energy.134 TCES systems that utilize porous media can benefit from the integration of ML techniques which can aid in optimizing performance, improving control strategies, and enhancing system efficiency. A study by Chen et al.135 has shown that calcium carbonate and calcium oxide (CaCO3/CaO) can be excellent materials for storing thermochemical energy and can be used in renewable energy sources due to their high energy storage density and long storage time. This research delves into the impact of complex pore structures and different operating conditions on micro-flow diffusion mass transfer performance within CaO materials. The study discovered that the effective gas diffusion coefficient increases with porosity but decreases with fractal dimension. Moreover, an ML-based prediction model was proposed, with an average error rate of approximately 12% and a root mean square error (RMSE) of 0.04138. This model can be valuable in designing Ca-based materials with high performance, as well as in reactor design or system thermodynamic investigations. According to a study by Praditia et al.,136 the TCES system using calcium oxide and calcium hydroxide (CaO/Ca(OH)2) is a promising energy storage technology due to its relatively high energy density and low cost. They implemented a PINN to predict the dynamics of the TCES internal state. They performed numerical simulations on an ensemble of system parameters to obtain synthetic data to train the network. The suggested approach provides results with an error of 3.96 × 10−4, which is in the same range as the result without physical regularization but is superior compared to conventional ANN strategies because it ensures the physical plausibility of the predictions, even in a highly dynamic and nonlinear problem. A recent study by Tasneem et al.137 discovered that reversible thermochemical reactions have significant potential for use in thermochemical energy storage systems. In this study, five powerful ML algorithms, including KNN, least absolute shrinkage and selection operator (LASSO), XGBoost, SVM, and Bayesian ridge, were utilized to develop accurate models that predict the dynamic behavior of a reversible thermochemical reaction-based system. The research utilized these ML algorithms to create the best formula and model for NH4NO3 and KOH. The study discovered that the polynomial regression degree 4 for the NH4NO3 temperature with KOH and water temperatures provides the best R2 of 0.938, with an MSE of 3.898504. The KNN (K = 5) is ideal for creating a model with polynomial regression degree 2, with an R2 of 0.999 and an MSE of 0.009042. The KNN (K = 5) degree 3 had an R2 of 0.984, with an MSE of 5.355852, making it the best method for creating a model. As KOH also has a time series dataset, XGBoost was used to compute the future KOH temperature.
3.2.2.1. Battery energy storage. A battery stores electrical energy for later use. It has gained significant attention and adoption in various applications, including renewable energy integration, grid stabilization, electric vehicles, and backup power systems in the different types of Li-ion batteries,140 lead-acid batteries,141 and so on. Battery energy storage systems typically do not utilize porous media directly in their operation. However, there are certain aspects where porous media can indirectly affect battery energy storage such as electrode structures.142 Ongoing research focuses on improving battery performance and durability through the design and optimization of porous electrode structures, advanced porous separators, and thermal management systems. These advancements aim to enhance energy storage capacity, cycling stability, and safety of battery systems. The integration of ML techniques with battery energy storage systems can enhance their performance, control, and optimization.143 While the direct involvement of porous media in battery operation is limited, ML can be applied in several areas to improve battery energy storage. ML can aid battery energy storage systems in terms of state-of-charge (SoC) and state-of-health (SoH) estimation,144 battery material design and optimization,145 battery performance and lifetime prediction,146 and optimal control and energy management.147
Some researchers have utilized ML techniques in conjunction with battery energy storage. In a study, Ishikawa et al.148 examined the structural characteristics of positive and negative electrodes in lithium-ion batteries. Using an ML model, they formulated a correlation equation for effective ion conductivity by considering the unique features of each electrode layer. The negative electrode is made up of graphite particles that have a flat shape, which means their aspect ratio is a significant factor in determining tortuosity. On the other hand, the positive electrode is a secondary aggregate, and the tortuosity is dependent on particle morphology, which makes it difficult to determine relevant parameters. Using the SVM, they predicted the tortuosity of the negative electrode in terms of the particle aspect ratio through nonlinear regression. All in all, this study sheds light on the relationship between tortuosity and other structural properties or images and can be applied in various fields related to porous materials to help optimize structural designs. In a study by Weber et al.,149 they efficiently approximate the macroscopic response of batteries. Some approaches, such as direct numerical simulations of transport at the pore-scale on reconstructed or synthetically generated images of electrodes that include detailed topological information about the pore structure, were employed. High-fidelity simulations have also been used to train CNNs to estimate effective battery properties directly from images of porous electrodes. In addition, they combined CNN methods with homogenization theory to take advantage of effective medium formulations and reduce the computational cost associated with individual pore-scale simulations. A noise sensitivity analysis is conducted to evaluate CNN's robustness, and it is shown to accurately predict the effective properties of real battery electrodes using both 2D and 3D images. Jiang et al.150 presented a study to understand the behavior of battery particles in a lithium-ion battery which is a complex challenge. The microstructure of a composite electrode plays a crucial role in determining how these particles are charged and discharged. To tackle this challenge, they used a combination of experimental approaches, statistical analysis aided by ML, and mathematical modeling. They also explored the potential of using electron density as a proxy for SoC.
3.2.2.2. Supercapacitor energy storage. Supercapacitors, also known as ultracapacitors or electrochemical capacitors, store energy through the electrostatic adsorption of ions on the surface of electrodes. They have high power density, fast charge and discharge rates, and long cycle life. Supercapacitors are often used in applications requiring rapid energy storage and release, such as regenerative braking systems and power buffering in renewable energy systems.151 Porous media can play a crucial role in the design and performance of supercapacitors. Research efforts in supercapacitor technology often focus on optimizing the pore structure, pore size distribution, and surface area of the porous media to improve the energy density, power density, and cycling stability of supercapacitors.152 ML and computational modeling techniques are also employed to predict and optimize the performance of supercapacitors by considering the complex interactions between porous media, electrolyte, and electrode materials. ML can aid supercapacitors with porous media in different ways such as electrode material design, performance prediction, state of health monitoring, control, energy management, and material characterization.153
Researchers have used ML techniques along with supercapacitors. In a study by Saad et al.,154 they presented graphene-based nanocomposites that have emerged as promising active components for high-capacity supercapacitor electrodes in energy storage systems. For the sake of predictions, the ML models (KNN, decision tree regression (DTR), Bayesian ridge regression (BRR), and ANN) utilized various electrochemical measurements such as electrolyte ionic conductivity and electrolyte concentration and physicochemical features such as atomic percentages, pore size, and pore-volume. Among these, the ANN model demonstrated the highest accuracy, with RMSE and R2 values of 60.42 and 0.88, respectively. Rahimi et al.122 mentioned that the multi-physio-chemical features of the activated carbon (AC) material play a synergistic role in enhancing the capacitance performance of supercapacitors. A multi-layer perceptron neural network (MLP-NN) model predicts the in-operando performance of N/O co-doped AC, using electrode materials. The results show that the training algorithms in the MLP-NN model have high feasibility in predicting AC performance with minimal error. The model provides valuable insights into possible procedures for fabricating N/O co-doped porous carbon electrodes with maximized specific capacitance. Finally, the genetic algorithm predicts the optimal AC in 6 M KOH in a three-electrode system with a specific capacitance of 550 F g−1 at 1 A g−1, which can be used for practical applications. In another study by Gosh et al.,155 a combinatorial approach that leverages value and grade prediction ML models was used to predict the performance of a novel material, cerium oxynitride, for use in supercapacitor applications. The model predicts that this material will have a specific capacity of approximately 26.6 mA h g−1 and a capacity retention of over 90%. Experimental results have validated this predictive approach, with an observed specific capacity of approximately 26 mA h g−1 and 100% capacity retention. Lu et al.156 introduced a novel ML approach for both electrochemical sensors and supercapacitors using a carbonized metal–organic framework (C-ZIF-67). An ANN algorithm is employed as a powerful tool to achieve intelligent analysis of niclosamide (NA) and incorporates theoretical calculations to optimize the structure of the sensing material and predict its adsorption and binding energy. Results show that the developed sensor exhibits excellent electrochemical response, with a 196.6-fold improvement compared to bare GCE for NA, wider linear ranges of intelligent analysis from 1 nm to 9 μm, and a low limit of detection of 0.3 nm. The ML model with the ANN algorithm is also utilized to predict the performance of the supercapacitor, which exhibits a capacitance of 336.67 F g−1 at a current density of 2 A g−1 and shows excellent prediction accuracy.
3.2.2.3. Fuel cell energy storage. Fuel cells are electrochemical devices that convert the chemical energy of a fuel, typically hydrogen, into electrical energy through an electrochemical reaction. While fuel cells themselves do not directly use porous media, they often incorporate porous materials to facilitate efficient reactions and enhance performance.157 Research and development efforts in fuel cell technology often focus on optimizing the design and performance of porous media within fuel cell components. The combination of fuel cell energy storage and porous media with ML techniques offers several potential benefits for performance optimization, control, and system integration. ML can aid fuel cell energy storage systems utilizing porous media in terms of performance prediction and optimization, optimal control and energy management, design and material optimization, and system integration and sizing.158 The application of ML to fuel cell energy storage systems with porous media is an active area of research and development.159 Designing the flow field is crucial in proton exchange membrane (PEM) fuel cells as it greatly affects gas transfer, water discharge, electron conductance, and heat transfer. The use of porous media flow fields, such as metal foam, shows potential for enhancing cell performance by providing uniform distributions of oxygen, liquid, current density, and temperature, particularly in the concentration polarization regime.
Scientists have employed ML methods in conjunction with fuel cells. Zhang et al.159 utilized a data-driven surrogate model, supported by the SVM, to optimize the geometry of the porous media flow field. Results demonstrate that the SVM-based data-driven surrogate model yields similar predictions to the 3D physical model. Furthermore, the genetic algorithm (GA) is utilized for optimization, and the optimized values obtained from the surrogate model are validated using the 3D physical model, confirming the effectiveness of the proposed data-driven surrogate model in the design and optimization of the porous media flow field. In a study by Liu et al.,160 they utilized the deep convolutional generative adversarial network (DCGAN) deep learning method to reconstruct the three-dimensional (3D) porous structure of the fuel cell catalyst layer using microstructure graphs obtained from focused ion beam scanning electron microscopy (FIB-SEM) as training data. The DCGAN with interpolation in latent space generates spatial-continuous microstructure graphs that are used to construct a unique 3D microstructure of the CL without the need for real FIB-SEM data. Different interpolation conditions in the DCGAN are also explored to optimize the ultimate structure by incorporating real data such as porosity, particle size distribution, and tortuosity. Additionally, the comparison between real and generated structural data shows that the data generated by the DCGAN have an adjacency relationship with real data, indicating its potential applicability in the field of electrochemical simulation with reduced costs.
Scientists have employed ML methods in combination with hydrogen energy storage with porous materials. Gopalan et al.165 developed a highly efficient and accurate method for predicting hydrogen adsorption in porous materials. Their approach involves calculating the amount of adsorption at any given temperature and pressure by integrating the energy density of the adsorption sites (guest–host interactions) and adding an average guest–guest term. To calculate guest–host interaction energy, they use a classical force field with hydrogen modeled as a single-site probe. For guest–guest interaction energy, they approximate an average coordination number using Gaussian process regression (GPR). Their method was tested on 933 MOFs, ranging from 10−5 to 100 bar at 77 K. Their analysis showed that 13 MOFs exceeded the Department of Energy target of 50 g L−1 for adsorption at 100 bar, 77 K, and desorption at 5 bar, 160 K. In a study by Bucior et al.,166 they developed a data-driven approach that accelerates material screening and learns structure–property relationships. They created new descriptors for gas adsorption in MOFs based on the energetics of MOF–guest interactions. The model parameters demonstrate that a slightly weak attraction between hydrogen and the framework is ideal for cryogenic storage and release. As a case study, they applied this method to screen a database of more than 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 experimental MOF structures and identified MFU-4l as one of the top candidates. Rahimi et al.167 constructed and tested three ML models to predict the hydrogen adsorption of ACs. The data-based modeling considers crucial properties of ACs' structural characteristics, such as micropore surface area, pore volume, and pore-size distribution, as inputs for hydrogen adsorption. They found that the proposed models were highly feasible for predicting hydrogen uptake, with RMs ranging from 0.06 to 0.19. Among them, the SVM model demonstrated the highest accuracy in predicting hydrogen adsorption on ACs. Using the SVM-based GA technique, they optimized the effects of microstructure properties on hydrogen storage. By using the optimal structural properties obtained from GA, they were able to increase hydrogen uptake by 2.5 wt%.
000 experimental MOF structures and identified MFU-4l as one of the top candidates. Rahimi et al.167 constructed and tested three ML models to predict the hydrogen adsorption of ACs. The data-based modeling considers crucial properties of ACs' structural characteristics, such as micropore surface area, pore volume, and pore-size distribution, as inputs for hydrogen adsorption. They found that the proposed models were highly feasible for predicting hydrogen uptake, with RMs ranging from 0.06 to 0.19. Among them, the SVM model demonstrated the highest accuracy in predicting hydrogen adsorption on ACs. Using the SVM-based GA technique, they optimized the effects of microstructure properties on hydrogen storage. By using the optimal structural properties obtained from GA, they were able to increase hydrogen uptake by 2.5 wt%.
3.2.4.1. Thermal-electrical hybrid energy storage. This hybrid system combines thermal energy storage (TES) with electrical energy storage (EES) using porous media. Excess electricity is first converted into thermal energy and stored in a porous medium, such as PCMs or hot water/steam in a thermal storage tank.171 When electricity demand is high, the stored thermal energy is converted back into electricity using a thermodynamic cycle or through a heat exchanger. This approach enables the efficient utilization of both electrical and thermal energy, making it suitable for applications such as combined heat and power (CHP) systems or district heating and cooling. The integration of porous media and ML techniques in thermal-electrical hybrid energy storage systems holds great potential for achieving enhanced energy storage performance, efficient energy management, and optimized system control. Ongoing research and development efforts aim to further advance these technologies and improve the scalability, reliability, and cost-effectiveness of thermal-electric hybrid energy storage systems.124
3.2.4.2. Electrochemical-thermal hybrid energy storage. In this hybrid system, electrochemical energy storage, such as batteries or supercapacitors, is combined with thermal energy storage using porous media. Excess electrical energy is first stored in the electrochemical storage system. When there is a demand for thermal energy, the stored electrical energy is converted into heat using resistive heating or other means and stored in a porous medium, such as high-temperature PCMs or solid-state materials. The stored thermal energy can later be utilized for heating applications or power generation. This hybrid approach can provide a more flexible and efficient utilization of energy for both electrical and thermal requirements.172 Electrochemical-thermal hybrid energy storage systems that incorporate porous media, aided by ML techniques, offer promising solutions for efficient energy storage and management and hold great potential for achieving enhanced energy storage performance, efficient energy management, and optimized system control. Ongoing research and development efforts aim to further advance these technologies and improve the scalability, reliability, and cost-effectiveness of electrochemical-thermal hybrid energy storage systems.173
Researchers have utilized ML techniques to enhance the efficiency of combustion systems. In a study by Pourali and Esfahani,125 they developed an innovative approach that combines ML for data generation (pre-processing), analytical techniques for processing, and response surface methodology for post-processing to investigate an integrated hydrogen production system. They used the decision tree algorithm to establish appropriate correlations for the species' net rate, mixture properties, and heat of reactions based on a detailed reaction mechanism of methane steam reforming and combustion in the pre-processing step. The findings suggest that wall thickness is the most influential parameter in CH4 conversion and system efficiency, while combustor height is the most critical parameter for sustaining combustion in the integrated system. Lastly, they propose five optimized designs of the integrated system for constructing experimental prototypes. In another study, Jiang et al.175 utilized wheat straw, corn straw, and sorghum straw as raw materials. Using KOH and NaOH as catalysts, they prepared straw pyrolytic carbon (SPC) and analyzed the characteristics of combustion activation energy (AE) through thermogravimetric analysis. They proposed predictive models of combustion AE based on linear regression (LR), SVR, and random forest regression (RFR) and compared their results. In the LR, SVR, and RFR models, R2 values reached 0.8531, 0.9048 and 0.9834, respectively. The RFR model was found to be more suitable for the AE prediction of alkali-catalyzed SPC compared to the LR and SVR models.
3.3. Electrochemical devices
The advancement of porous electrocatalytic materials primarily depends on empirical approaches, involving extensive trial-and-error methods.178 Discovering optimal solutions for multicomponent catalysts across diverse reaction conditions demands substantial investments of time and effort. However, in recent years, the landscape has undergone a revolutionary transformation with the emergence of ML techniques. These powerful ML tools have revolutionized the development and exploration of materials designed for electrochemical devices.179 This section presents a comprehensive review of ML-based techniques for discovering and developing porous media for electrochemical devices. It also highlights practical applications in various fields such as electrocatalysts, proton exchange membrane water electrolyzers (PEMWEs), PEM fuel cells (PEMFCs), solid oxide fuel cells (SOFCs), batteries, and supercapacitors.Fig. 8a depicts design parameters in an ANN for the prediction of SOFC cell performance. Fig. 8b shows a schematic of a PEMWE, Fig. 8c shows an SOFC voltage prediction using an ANN model, and Fig. 8d displays a PEMFC catalyst layer with SVM polarization curve prediction. In electrochemical reactions, two half-reactions take place: one at the anode, such as the oxygen evolution reaction (OER), and the other at the cathode, encompassing reactions such as carbon dioxide reduction, hydrogen evolution reaction (HER), nitrogen reduction, and the oxygen reduction reaction (ORR).178 These reactions are powered by the flow of electrons. Effective catalysts play a crucial role in optimizing efficiency and minimizing overpotential during these processes.178
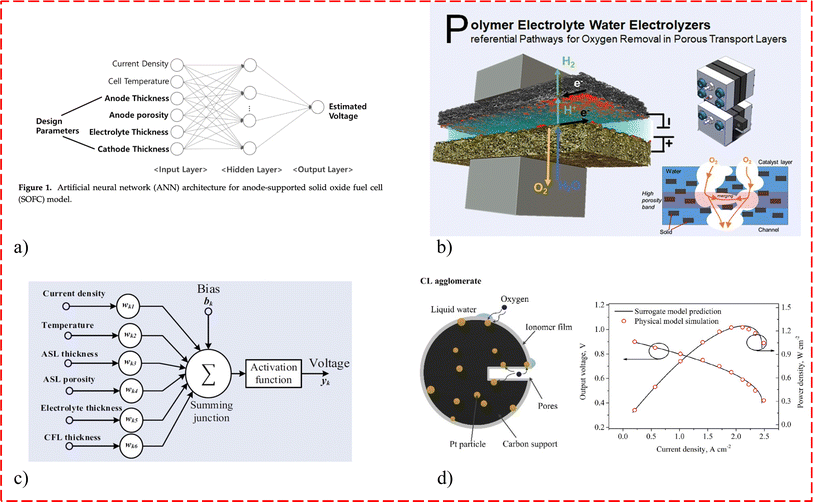 | ||
| Fig. 8 (a) The optimization of multiple parameters such as anode and cathode thickness, anode porosity, and electrolyte thickness included in an ANN for the prediction of voltage of an SOFC and improve its performance,180 reproduced with permission from MDPI. (b) In order to distinguish oxygen within the PTL, machine learning was utilized to analyze the amount of oxygen present in the PTL of the electrolyzers at varying flow rates and current densities which is shown in 3D representation of a conventional PEWE,181 reproduced with permission from Cell Press, (c) prediction of cell voltage in the SOFC using an ANN model using current density, temperature, anode, cathode, and electrolyte thickness,182 reproduced with permission from Elsevier, and (d) schematic of distribution of water, platinum, ionomer, and carbon support in the PEMFC catalyst layer, including prediction of the SVM for the polarization curve compared against a physical model,183 reproduced with permission from Elsevier. | ||
The composition and microstructure of the catalyst layer (CL), which serves as the central electrochemical reaction region in PEMFCs, play a pivotal role in determining the output performance of PEMFCs. Wang et al.183 established an SVM model combined with a GA to globally optimize multiple variables and enhance the maximum power density of PEMFCs. The database was formed using simulation results from a CFD model coupled with a CL agglomerate model. After the surrogate model was developed, prediction performance was assessed using RMSE, R2, mean percentage error, and maximum percentage error to evaluate model performance. For verification, the optimal CL composition was returned to the physical model and a good agreement was achieved. Additionally, the porous structure of the CL in PEMFCs is crucial for oxygen transfer resistance and charge/discharge performance. Using microstructure graphs acquired from focused ion beam scanning electron microscopy (FIB-SEM), Liu et al.201 employed a deep convolutional generative adversarial network (DCGAN) to reconstruct the 3D porous structure of the CL in PEMFCs. Different interpolation conditions in the DCGAN were explored to optimize the generated structure, aligning it with real data in terms of particle size distribution, porosity, and tortuosity. Comparisons between generated structural and real data demonstrated the adjacency relationship, suggesting the potential application of DCGAN-generated data in electrochemical simulations with reduced costs. The cathode catalyst layer (CCL) in PEMFCs plays a crucial role in facilitating mass, charge, and heat transfer. Traditional methods are insufficient for a comprehensive understanding of the CCL. As a new approach, Lou et al.202 employed an ML model to investigate the structure of the CCL. By integrating the XGBoost algorithm with the PEMFC physical model, this model effectively established a relationship between nine adjustable parameters (such as Pt loading, agglomerate radius, pore diameters, and CCL thickness) and optimization goals (power density, current density, and temperature uniformity of the CCL). The model achieved high accuracy, with an R2 value greater than 0.95 and an RMSE value less than 0.05, indicating its strong predictive capabilities. Their results indicated that the critical parameters for multi-objective optimization are the Pt loading, agglomerate radius, ratio of Pt to carbon, and CCL thickness. Implementing an optimized CCL leads to improvements in power density and current density and a reduction in Pt loading. Vaz et al.203 employed an MLP model for multi-objective optimization analysis to assess the impacts of different compositions in the CCL on single-cell voltage and stack cost. Four important parameters of the cathode CL, namely Pt loading, ionomer to carbon weight ratio, Pt to carbon weight ratio, and cathode CL porosity, were treated as design variables. The 85 CFD simulation database from a comprehensive three-dimensional, multi-scale, two-phase PEMFC model was utilized to train and validate the MLP model. The accuracy of the MLP model was verified using metrics such as RSME and adjusted R2. The optimization process led to significant cost reduction by minimizing Pt usage and simultaneously resulted in noteworthy improvements in single-cell voltage.
Solid oxide electrochemical cells (SOCs) are versatile energy conversion devices that can function as either fuel cells or electrolysis cells. In the fuel cell mode (SOFC), they produce electricity by oxidizing fuel, while in the electrolysis mode (SOEC), they convert electricity into chemical energy stored as fuel. Wang et al.209 introduced a data-driven surrogate model that utilized the SVM regression algorithm to establish a relationship between fabrication parameters (including volume fractions of NiO, YSZ, and pore former phases, as well as initial average particle size) and electrode overpotentials. The model demonstrated fast and accurate prediction of the electrochemical performance of heterogeneous porous electrodes. Specifically, the volume fractions of YSZ were identified as a crucial factor influencing the overall overpotential.
The optimization of electrode microstructures has been investigated in the literature using a combination of ML methods, lattice Boltzmann method (LBM) simulations,210 and pore network modeling (PNM).211 In one study, artificial fibrous electrode microstructures were generated using stochastic reconstruction methods and morphological algorithms, and their hydraulic permeability was evaluated using the LBM.210 ML models such as linear regression, ANN, and random forests (RF) were utilized, along with the genetic algorithm NSGA-II, to identify microstructures with high specific surface area and hydraulic permeability. The workflow resulted in the discovery of microstructures exhibiting microstructures with significant improvements compared to commercial carbon felt electrodes. However, limitations were noted regarding assumptions made during microstructure generation, which may impact the realism of the optimized microstructures.210 Another study employed PNM to optimize the pore and throat size distributions of an artificially generated microstructure using a genetic algorithm.211 The optimized microstructures showed a bimodal pore size distribution, leading to improved flow pathways and enhanced electrochemical performance. However, challenges were identified regarding the realism and manufacturability of the optimized microstructures, as well as the consideration of pore coordinate relocation during the optimization process.211
Furthermore, a multi-scale model was employed to investigate the relationship between pore-scale electrode structure reactions and device-scale electrochemical reaction uniformity.212 The study combined a deep neural network with a partial differential equation solver and utilized 128 pore-scale simulations to train and validate the deep neural network. The findings revealed that optimizing the electrolyte inlet velocity over time led to a significant reduction in pump power consumption while maintaining surface reaction uniformity, while the impact on electric power output during discharging was minimal.212 It is important to note that the limited number of simulations conducted in this study may restrict the generalizability of the results. Additionally, the characterization of electrode microstructure plays a crucial role in understanding its behavior. In another investigation,213 a custom Weka three-dimensional segmentation technique214 was employed to study the permeability and mass transport processes in various carbon electrodes. This segmentation approach provided improved control over the known fiber thickness, potentially leading to more accurate estimations of specific surface area and porosity. However, it is worth mentioning that the disadvantage of the workflow was the small sample size used for training the classifier and the use of scanning electron microscope (SEM) images as the ground truth for adjusting fiber thickness.213
The laser reduction process of poly(acrylonitrile) (PAN) membranes has been investigated using Bayesian optimization.215 A dataset of 204 samples, including laser scan speed, laser power, focal point height, and image density, was utilized for this study. The results demonstrated the successful synthesis of laser-reduced PAN membranes in a single lasing step, leading to materials with low sheet resistance (6.5 Ω sq−1). The suitability of these materials as membrane electrodes for vanadium RFBs was confirmed through electrochemical testing.215 However, challenges were encountered, such as the system-specific nature of the optimized parameter set and the limitation imposed by electrode thickness. In another study,216 an ANN was employed to develop polybenzimidazole (PBI) membranes with high ion selectivity, proton conductivity, and low cost through solvent treatment. The dataset comprised 49 samples, with solvent properties and experimental parameters used as inputs. The predicted performance of the PBI membranes in vanadium RFBs, in terms of voltage efficiency (VE) and energy efficiency (EE), achieved a mean absolute prediction error (MAPE) within 1% of the experimental data as highlighted between the comparisons in chemicals (hexane, ethanol, etc.) as shown in Fig. 9a. Nonetheless, the relatively small dataset and the limited exploration of solvents could impact the generalizability of the model.216
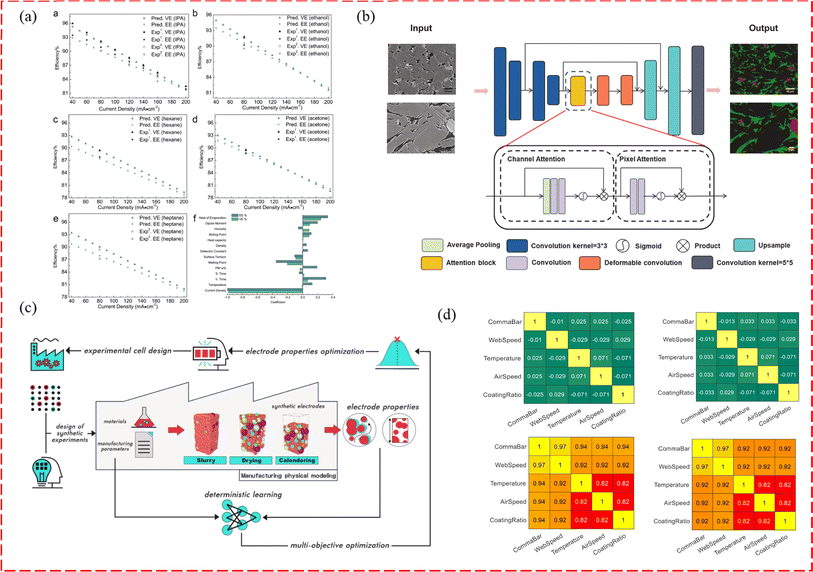 | ||
| Fig. 9 (a) Predictable membrane performance of the ML model and membrane structure,216 reproduced with permission from the Royal Society of Chemistry, (b) U-Net neural network used to enhance the quality of extracted microstructures from X-ray tomography images,217 reproduced with permission from Elsevier, (c) coupled physical models for battery electrode manufacturing processes (drying and calendering) to a deterministic learning method and subsequent property optimization,218 reproduced with permission from Elsevier, and (d) correlation analysis between control variables for the cathode and anode,219 reproduced with permission from Elsevier. | ||
Microstructure characterization plays a vital role in optimizing manufacturing processes and predicting the long-term performance of LIBs. In a recent study, researchers focused on LiNi0.33Co0.33Mn0.33O2 as the active material and employed coarse-grained molecular dynamics simulations and X-ray micro-computed tomography to investigate changes in electrode heterogeneity and the deformation of secondary particles during manufacturing.220 To analyze the obtained tomographic data, ML techniques, including the Weka plugin214 and fast random forest class, were trained on real particle shapes. However, further improvements and validations are necessary to enhance the accuracy and applicability of the model in real-world scenarios. In a similar study, to minimize variation in quantifying the volume fraction of the active material, researchers utilized the open-source software Ilastik221 and employed an iterative, manual training approach.222 This method achieved reduced variation compared to unsupervised techniques, but additional refinements and validations were required to enhance accuracy and applicability when quantifying the active material volume fraction in LIB cathode tomograms. Moreover, researchers employed a DL-based U-Net architecture and StarDist223 for active particle segmentation, enabling rapid and accurate characterization of the electrode microstructure.224 Geometric analysis of the segmented data provided valuable information on particle size distribution, porosity, tortuosity, and particle system connectivity. Additionally, a stochastic reconstruction methodology was presented to generate statistically equivalent virtual microstructure designs. It is important to note that the limitations of this approach include its reliance on previously published tomographic data and the challenge of accurately representing non-spherical particle morphology.
For microstructure extraction from 2D scanning electron microscopy (SEM) images, researchers used a modified U-Net architecture223 based on the CNN217 with an input to segmented output process on the images shown in Fig. 9b. They examined the relationship between porosity and thickness at different states of charge, demonstrating the effectiveness of the image segmentation method in improving microstructure extraction quality. Another investigation focused on the rapid characterization of microstructural effective properties of LIB graphite anode electrodes using ML models.225 Different supervised learning models, including linear, decision-tree, and ensemble-based models, were employed and trained on input parameters such as composition, active material shape, mean pore size, and particle orientation and alignment. The results exhibited high prediction accuracy for estimating effective properties, but the limitations included the use of artificially constructed porous electrodes and the complexity of accurately estimating the properties of real electrodes.
To estimate the tortuosity of the cathode and anode in LIBs, researchers used a combination of a CNN and support vector regression (SVR).226 Three-dimensional porous structures were employed as input, and the study revealed a correlation between tortuosity and the particle aspect ratio, expanding the understanding beyond porosity alone. However, the limitations included the use of simulated electrode structures that may not fully represent real microstructures and the neglect of carbon black and binder in the models. Researchers developed a CNN model to predict the microstructural properties of a graphite|LiMn2O4 electrode based on voltage–capacity curves.227 Training the model on a large dataset allowed successful prediction of Bruggeman's exponent and shape factor. This study highlighted the potential of deep learning approaches for rapidly inferring microstructural properties for battery design optimization and performance evaluation. Limitations included the challenges of capturing particle–particle effects at high current densities and predicting the performance of highly aligned platelets with morphological anisotropy.
Advancements in 3D microstructure reconstruction have also been explored. One study developed a method using ANNs and the scaled conjugate gradient (SCG) method to construct 3D microstructures from limited morphological information obtained from 2D cross-sectional images.228 The results demonstrated that the workflow preserved statistical characteristics, geometrical irregularities, long-distance connectivity, and anisotropy observed in the 2D images. However, further research is needed to address and validate the limitations and challenges related to accuracy and efficiency. Another study focused on the reconstruction and analysis of anode and cathode electrodes using a neural network-based approach.229 The study employed an autoencoder–decoder framework for microstructure reconstruction and feature extraction. While the findings showed promise in optimizing microstructure reconstruction, incorporating additional computational layers such as pooling, batch normalization, and regularization, the model's inability to produce realistic reconstructions indicated the need for more data to enhance its performance. Additionally, researchers utilized CNNs to build 3D models of nickel–manganese–cobalt cathodes.230 This approach aimed to overcome the challenges associated with accessing 3D images by utilizing readily available 2D images and capturing the granular-like morphology of the battery system. The findings demonstrated the ability of the proposed method to generate synthetic 3D models that exhibited good agreement with the original models. However, differences in pore size distribution, permeability, and thermal conductivity compared to the original models indicated a limitation of the approach.
Researchers have explored the optimization of manufacturing parameters in LIBs using ML techniques. A combination of ML methods with physics-based simulations was employed for multi-objective optimization and inverse design of LIB electrode properties and manufacturing parameters218 as shown in the flow chart in Fig. 9c. The ML-assisted pipeline utilized a synthetic dataset generated from physics-based simulations to train ML models, to find a balance between minimizing the electrode tortuosity factor and maximizing effective electronic conductivity, active surface area, and density, all crucial factors influencing Li+ (de-) intercalation kinetics and transport properties. The study revealed the interconnected nature of these properties and their impact on optimal electrode performance. However, limitations include reliance on simulation data, limited dataset volume impacting generalizability, and exclusion of certain manufacturing steps in the simulation process. Nonetheless, the successful experimental fabrication of an electrode based on the model's predictions validated the physical relevance of the modeling pipeline.218 In predicting electrolyte infiltration in LIB electrodes, a multi-layer perceptron (MLP) approach was used.231 The model was trained on a database generated from a 3D-resolved physical model based on the LBM and X-ray micro-computer tomography. The MLP model accurately predicted the rate of saturation, filling time, and direction of electrolyte flow in porous electrodes. It enabled quick and accurate predictions, facilitating the screening of different conditions to optimize the infiltration process. However, limitations of the model included the exclusion of certain geometrical parameters influencing the fluid distribution and the reliance on simulated data that may not fully capture the complexity of real-world systems.231
In another study, to optimize electrolyte infiltration conditions, random forest (RF), neural network, and SVM models were employed.232 Exploratory data analysis (EDA) identified influential electrolyte parameters affecting saturation descriptors. Lower kinematic viscosity led to higher wetting degrees and rates, while higher inlet applied pressure reduced the electrolyte filling time. The study showcased the potential of ML as a surrogate model for optimizing multi-parameter processes in battery manufacturing. However, the computational cost associated with physics-based approaches such as the LBM poses a limitation.232 Gradient-boosted trees and random forest models were used to identify key parameters in the manufacturing process of LIB electrodes.219 Coating process factors such as the comma bar gap, coating speed, and the coating ratio were considered input parameters. The study demonstrated a data-driven approach to predicting electrode quality and identified key parameters and control variables affecting the manufacturing process as shown in Fig. 9d. A systematic design of experiments was proposed to generate representative data for ML activities, reducing waste and resource demand. However, the limited number of experiments and consideration of only a subset of parameters restricted the general applicability of the model.219
A deep-learning-based prediction algorithm combines adaptive dropout long short-term memory-Monte Carlo (ADLSTM-MC), for early prediction of battery remaining useful life (RUL) in LiFePO4/graphite and LiNi0.8Co0.15Al0.05O2/graphite batteries,233 with reduced degradation data. The method achieves precise early prediction with only 25% of the degradation data, outperforming existing models. The proposed method demonstrates high accuracy with an R2 value of 0.957–0.982 for capacity prediction and low prediction errors (RMSE and MAE). However, the computational efficiency of the LSTM network needs improvement for real-time battery management systems. Moreover, the Bayesian optimization (BO) strategy was employed to optimize rapid charging protocols in graphite/LiCoO2 batteries.234 The goal was to reduce charging time while limiting battery degradation. The probability-of-improvement acquisition function showed the best performance. Limitations include computational cost, limited applicability of the electrochemical model used, simplified assumptions, and a lack of experimental validations. Another study employed particle swarm optimization (PSO) to optimize highly ordered laser-patterned electrode (HOLE) architectures for fast-charging LIBs.235 The study used experimentally obtained voltage vs. capacity data for galvanostatic charging at different C-rates as input. The optimal spacing between channels for improved fast-charging performance was identified, with the Damkohler number (Da) serving as a metric. The optimal configuration maintained a Da ≈ 1 throughout charging. Limitations include the oversight of pore-scale changes due to continuum modeling and the small dataset used in the study.
Ions must flow from the separator region towards or away from the electrodes which is influenced by diffusion and migration, where the electrode structure may facilitate or resist each transport mechanism as shown in Fig. 10a. To determine the optimal properties for supercapacitor electrodes (typically activated carbon-based materials as shown in the figure, where the performance metrics are often specific capacitance (F g−1),236–243 ML tools using experimental data can be used.
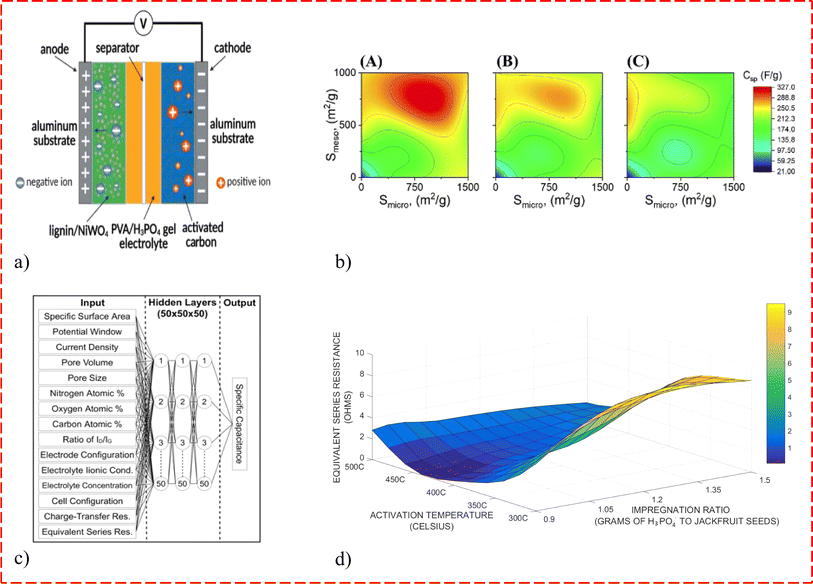 | ||
| Fig. 10 (a) Schematic of an asymmetric supercapacitor showing different materials that can be used for the anode (lignin/NiWO4) and cathode (activated carbon),242 reproduced with permission from American Chemical Society, (b) specific capacitance design maps predicted by ANNs, allowing meso and micropore surface area to be optimized at different scan rates,237 reproduced with permission from Elsevier, (c) selection of input variables taken from 200 experimental publications allowing for prediction of specific capacitance of graphene doped electrodes,238 reproduced with permission from Elsevier, and (d) ANN used along with particle swarm optimization to predict and optimize specific capacitance (color bar) based on activation temperature and the impregnation ratio,241 reproduced with permission from Elsevier. | ||
ML models are empirical, meaning that high-quality datasets are needed for the models generated to be predictive outside of the experimental region of interest. For example, in one case243 400 raw datasets were condensed to 259 defect-free results. The inclusion of inaccurate experimental data could bias the prediction of the ML models.
In the literature on supercapacitors, it is stated that theoretical models are not reliable enough to predict the state of supercapacitors away from equilibrium so to optimize the electrode structure currently, ML techniques must be used.237,242 The ML methods that have been used for supercapacitor optimization have used ANNs, MLP, LR, XGBoost, RF, and DTs236–243 to name a few; however, of these the ANN and XGBoost are often the more accurate performance models. The evaluation metrics used to study the predictive capability of the models include R2, RMSE, and MAPE.
As shown in Fig. 10b, the ANN can be used to create material design operating maps which provide a design space to choose specific surface area for mesoscale and microscale pores237,242 allowing for next-generation material design.
Some of these studies have used ML to optimize the chemical composition or preparation structure for bio-mass-derived electrodes for supercapacitors, including jackfruit-derived.241 Here, using a design of experiment (Box-Behnken design), 15 experimental datasets were extracted and an ANN was trained on this limited dataset. The ANN model was able to predict and optimize the amount of phosphoric acid and activation temperature required, obtaining a maximum specific capacitance of 56.12 F g−1. However, in this scenario, the microstructural properties were not used as inputs to the trained model.241 As shown in Fig. 10d, this method was able to provide the response of specific capacity as a function of activation temperature, impregnation ratio, and series resistance, which could lead to improvements in specific capacitance of over 9 times. Similarly, lignin-based electrodes have been investigated via ML methods (LR, SVG, and ANN) using an 80/20 training/test split on cycle data, where performance data did not use microstructure data but could predict specific capacitance change over time.242
Other studies, where BET data for surface area have been acquired, have looked at using microstructural properties as inputs for ML models. This can include the surface area for the micro and macroporous structure237,239,240,243 or operating parameters such as electrolyte conductivity, cell configuration, and charge transfer resistance238 as shown by the inputs to the neural network in Fig. 10c.
The impact of ML models on the development of next-generation electrode materials was highlighted by Rahimi et al.243 They used 259 defect-free datasets for experimental values in 6 M KOH and with three electrode configurations to train an ANN. The surrogate model was used for a genetic algorithm to optimize the input parameters which could predict the optimal properties of an AC supercapacitor electrode to reach 550 F g−1.
ML approaches using empirical data as input may miss some critical features as the relationships between parameters may be highly non-linear. However, without this, there has been some success in optimizing input parameters or macroscopic parameters. However, there is still no approach that considers a mix of theoretical models, ML, perhaps as surrogate models to the theory (which contains no noise), leading to ML algorithms for optimization.
ML applied to electrochemical engineering has been shown to be able to predict the complex interaction between operating and material parameters that a physical-based model is currently unable to resolve. There are readily available data regarding the manufacturing methods that lead to certain electrode microstructures, and these could be leveraged by ML methods through surrogate modeling or optimization strategies to choose optimal manufacturing conditions. Generally, between fuel cells, electrolyzers, batteries, and supercapacitors, the role of the microstructure of electrodes, separators, and electrolytes plays a key role in performance and durability.
3.4. Hydrocarbon reservoirs
Central to the efficacy of oil and gas reservoirs is the intricate matrix of porous media, a labyrinthine network of interconnected spaces within rock formations that house hydrocarbons. These porous structures, comprising varying permeabilities and porosities, act as repositories for vital resources. ML algorithms play a pivotal role in unraveling the mysteries held within these porous domains. By harnessing ML models, the characterization and understanding of these porous media undergo a profound transformation.244ML is a subset of artificial intelligence that enables computers to learn from data without being explicitly programmed. It involves developing algorithms to identify patterns in large datasets and make predictions based on those patterns. In oil and gas reservoirs, ML can analyze geological data, well logs, seismic surveys, production data, and other relevant information to enhance reservoir characterization, improve production efficiency, and reduce costs. One of the key benefits of ML in the oil and gas industry is its ability to handle large amounts of complex data. Traditional methods for analyzing geological data involve manual interpretation by geologists or engineers. However, this process can be time-consuming and prone to errors. ML methods can quickly analyze vast amounts of data from multiple sources to identify patterns that may not be apparent to human analysts. Another advantage of ML is its ability to make accurate predictions based on historical data.245
As technology continues to evolve, we will likely see more widespread adoption of ML in the exploration and production of oil and gas reservoirs. However, it is essential to note that ML is not a silver bullet solution and requires careful consideration of data quality, model accuracy, and ethical considerations. Nonetheless, the benefits of ML in the oil and gas industry are clear, and its application will undoubtedly continue to grow in the years to come.
This section focuses on the ML models in oil and gas porous media, as a complex and dynamic system, to foremost raise the understanding and thereafter provide an overview of ways that optimize the recovery of hydrocarbons from the reservoir. In reservoir characterization, ML models are used for analyzing data from reservoir cores, including porosity and permeability, for creating more accurate reservoir models. To this end, the location of wells can be optimized and improve the recovery of hydrocarbons from the reservoir. ML models in reservoir history matching are used for matching production data from oil or gas reservoirs to numerical models, which allows for more accurate predictions of future production and its changes over time. In EOR, ML models may be employed for optimizing EOR methods including CO2 injection and waterflooding, by analyzing data from the reservoirs. Towards rock physics modeling, ML models are used for introducing rock physics models, whereby the connection between rock's physical properties, such as porosity and permeability, and the fluids' properties in the rock, such as oil and water is described. Here, pore-scale fluid flow and transport are also appraised allowing for better predictions of oil and gas behavior in porous media. Furthermore, in the subfield of fracture characterization, ML models can be used to analyze data from seismic surveys and well logs to eventually identify and characterize fractures in the reservoir, which are critical to the fluids' flow. Finally, by analyzing data from log measurements, i.e., resistivity, the porous media properties can be determined.
In this section, the application of ML techniques in hydrocarbon reservoirs is described in four subsections: pore-scale modeling, reservoir characterization, reservoir modeling, and reservoir management (Fig. 11).
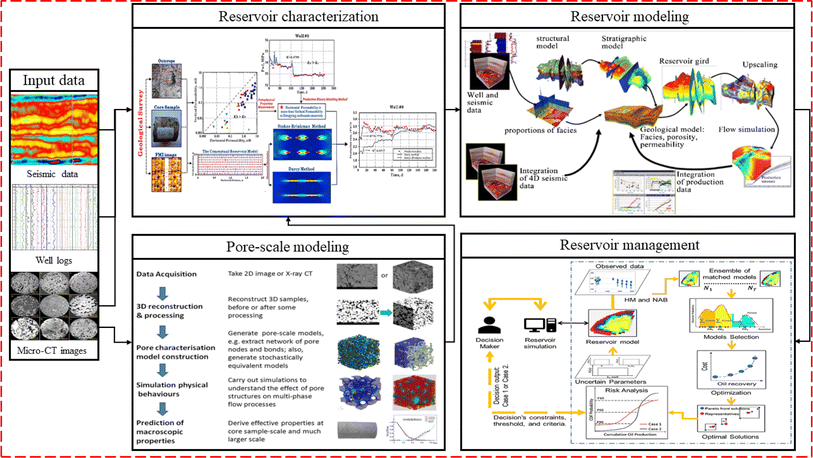 | ||
| Fig. 11 The workflow of the hydrocarbon reservoir engineering section. The input data, such as seismic, well logs and micro-CT images, are used for reservoir characterization, Xie et al.,246 reproduced with permission from Elsevier, and petrophysical property prediction through pore-scale modeling, Ma,247 reproduced with permission from Elsevier, and then static and dynamic models are constructed for reservoir simulation, Fornel and Estublier,248 reproduced with permission from Elsevier. The final step is reservoir management, where production strategies, optimization, and EOR selection are conducted, Hutahaean et al.,249 reproduced with permission from Elsevier. | ||
 | ||
| Fig. 12 A depiction of ML approach utilization in pore-scale imaging and modeling workflow. Gray-scale images obtained from scanners can undergo segmentation or super-resolution through CNNs, while GANs enable synthetic image reconstruction from latent or 2D/3D information. Petrophysical property prediction in pore-scale modeling can be enhanced using ANNs and CNNs to forecast parameters such as permeability and fluid phase distributions, Wang et al.,251 reproduced with permission from Elsevier. | ||
3.4.1.1. Image resolution enhancement. One of the primary applications of ML in pore-scale modeling is image resolution enhancement. Due to hardware constraints, pore images obtained from micro-CT scans or other imaging techniques are often limited by low resolution and size. There is a trade-off between image resolution and field-of-view (FOV), meaning that a wider FOV covers a larger area but reduces the pixel density (low resolution) and vice versa. ML algorithms can be trained for image resolution enhancement by using deep learning techniques while capturing a larger FOV, which improves realistic fluid flow simulation, and estimating rock-effective properties at desired scales.252 Super-resolution (SR) reconstruction methods have shown outstanding performance in converting low-resolution (LR) images to high-resolution (HR) images by lowering the difference error between these two types of images. As mentioned earlier, deep learning approaches such as generative adversarial networks (GANs) and CNNs are utilized regularly with SR for tackling problems. Jackson et al.253 used an enhanced deep-super resolution (EDSR) convolutional neural network to generate high-quality images from low-resolution (LR) images. This methodology reduces the common flaws in micro-CT imaging and generates realistic HR images for pore network modeling (PNM) and continuum modeling. In the image resolution enhancement field, two types of image data are used as input variables for the ML models, paired and unpaired images. In paired images, input and the ground-truth image domains are aligned, while the unpaired image refers to the data collected from various sample locations. Although paired images usually produce better results, they are challenging to acquire. The convolutional neural network (CNN) requires paired data as input, but methods based on generative adversarial networks (GANs) use unpaired images. Niu et al.254 probed the performance of these two approaches utilizing a micro-CT sample for creating HR images from LR images. They concluded that the unpaired GAN method performs the same as the paired CNN approach in creating HR images, but the unpaired GAN does not require image registration in the data processing stage. Compared to the paired CNN method, this feature reduces computational costs by up to 22.5%. In another study,255 the enhanced deep super-resolution generative adversarial network (EDSRGAN) showed remarkable visual similarity in texture regeneration over other approaches. Also, it reconstructs high-frequency texture, while the super-resolution convolutional neural network (SRCNN) retrieves large-scale edge features. Also, Liu and Mukerji256 utilized style-based GAN and cycle-consistent GAN to regenerate high-resolution images with a large FOV, which is the ultimate purpose of using ML for digital rock resolution enhancement. Their study used the style-based GAN to tackle the overfitting problem and cycle-consistent GAN for integrating the unpaired image data from various sources.
3.4.1.2. Pore geometry generation. Another important application of ML in pore-scale modeling is generating realistic pore geometries. Traditional methods for generating pore geometries involve manual segmentation or random generation based on statistical parameters. However, these methods may need to capture real-world porous media's complex geometry and heterogeneity accurately. ML methods can be conducted on large datasets of micro-CT scans to learn the statistical distribution of pores' shapes and sizes. This information can then be used to generate realistic 3D models that accurately represent the geometry and heterogeneity of porous media. Due to the high cost of 3D microscopy imaging, 3D microstructure reconstruction from 2D cross-sectional images using deep learning approaches is recommended as a cost-effective and accurate solution. Fu et al.257 used a supervised ML procedure for 3D pore reconstruction purposes. The proposed method showed superior results to conventional approaches, such as stochastic optimization-based reconstruction and Gaussian random field, regarding the accuracy and maintaining microstructural complexities within 2D images. Zheng and Zhang258 proposed a deep learning-based method called RockGPT to generate several types of rocks simultaneously using a single 2D image. Hybrid superposition approaches have shown promising performance in reconstruction problems, but they are complex, and both low and high-resolution images are required as the input images. Hence, Yang et al.259 utilized a cGAN-based method to overcome the complexity of the proposed approach and prevent human factors that may cause severe problems. This method used low-resolution core images as the input for multi-scale digital rock reconstruction, while high-resolution images with a narrow FOV opted for the training stage. In another study, Zhang et al.260 introduced a framework named LGCNN based on the GAN and CNN for 3D porous media reconstruction. The LGCNN approach proved to be faster and more precise compared to traditional reconstruction methods with a higher construction speed (6003 voxels) and lower time (10 min).
3.4.1.3. Pore-scale simulation. ML has also been applied to simulate fluid flow and transport properties at the pore scale. Conventional numerical simulations involve solving partial differential equations (PDEs) that describe fluid flow through porous media. Direct numerical simulation (DNS) and pore network modeling (PNM) are the primary approaches for flow simulation at the pore-scale. DNS solves Navier–Stokes equations on the realistic 3D pore geometry reconstructed from high-resolution micro-CT images of rock samples. Using DNS leads to accurate but computationally expensive results. However, PNM uses a simplified ball-and-stick network obtained from real pore geometry to reduce the model complexity and computational costs of the DNS approach. However, the main drawback of PNM is that it may not accurately capture complex phenomena such as fluid–solid interactions and pore-scale heterogeneity as DNS. ML methods are also used in numerical simulations to learn the relationship between input parameters and output properties. This information can then be used to develop surrogate models that accurately predict fluid flow and transport properties such as temperature, pressure, and permeability at a fraction of the computational cost of traditional simulations. Ting et al.261 applied a convolutional neural network (CNN) in a fluid flow simulation through the fracture problem. The priority of the researchers was avoiding simplified assumptions used in PNM, as it neglects the realistic geometry of the fractures and, consequently, the effect of capillary phenomena at the pore scale. However, the computational demands of DNS methods were also a significant challenge. Hence, they suggested using a data processing algorithm and CNN to tackle the disadvantages of the DNS method (LBM). The results illustrated that the accelerated LBM effectively simulated multiphase flow through 3D fractures in a shorter time. Ishola and Vilcáez262 utilized a stochastic pore-scale simulation method for permeability estimation, and then they used the gradient boosting algorithm to reduce the number of simulations. The outcomes exhibited that using the gradient boosting algorithm reduced the number of simulations from 4400 to 28 while achieving the same results of rock core data with an MAE of 10%. Sun et al.263 proposed a deep learning-based approach for estimating permeability as a substitute for conventional pore-scale simulation and experimental methods, which are assumed to be time-consuming. They concluded that the proposed framework was 100 times faster than DNS. Tian et al.264 evaluated the performance of six different ML algorithms in a permeability prediction study. These algorithms were optimized by using particle swarm optimization (PSO) to enhance the performance of the ML algorithms. The results showed that PSO's hyperparameter tuning of the ML algorithm improved their performance. Among all the ML algorithms, the ANN-PSO approach exceeded other algorithms regarding permeability prediction accuracy (R-value of 0.9985). Also, the application of feature selection in ML algorithms improved their performance and proved their supremacy over the empirical equations in permeability prediction. Bu et al.265 used five different linear regression algorithms for permeability prediction from CT images of core samples. The outcomes revealed that the Gaussian process regression (GPR) models achieved the highest R-squared values (minimum of 0.87), outperforming other methods in estimating permeability accurately. In addition, using ML-based methods overcomes the computational cost issues, which makes them an excellent alternative approach to conventional pore-scale simulation methods such as PNM.
 | ||
| Fig. 13 Workflow for S-wave velocity prediction, utilizing a petrophysical model and employing a long short-term memory (LSTM) model based on wireline logs, Zhang et al.,276 reproduced with permission from Elsevier. The LSTM model begins by analyzing relationships between conventional wireline logs and measured S-wave velocity, selecting sensitive logs for prediction. Subsequently, an optimal LSTM model is established to predict the S-wave velocity. Then, the two models are compared based on factors such as rock mineral content and wireline log combinations, with the most accurate method selected for elastic modulus calculation. | ||
In several types of research, well-logging data are used as input since data obtained from core samples highly rely on core experiments and have limitations in uncored areas.277 Yang et al.278 used a deep learning approach based on the combination of a 1-D convolutional neural network (CNN) and bidirectional LSTM network to predict reservoir parameters such as permeability and porosity from logging data. In their study, optimization algorithms and self-attention mechanisms were conducted to find the optimum network architecture and weights for accuracy enhancement. The results showed that the proposed framework accurately predicts despite using input data from various reservoir regions. Masroor et al.279 established the supremacy of a novel multiple-input deep residual convolutional neural network (MIRes CNN) with single-input deep residual CNN methods and baseline methods such as random forest (RF) in the permeability estimation task. Two types of data, numerical well-logs (NWLs) and graphical feature images (GFIs) were fed to the network. It was concluded that the MIRes CNN's ability to handle mixed data as input features reduced the overfitting issue and computational costs compared to conventional methods. The computational costs and convergence problems related to ANNs have been addressed in some studies. Matinkia et al.280 suggested that MLP neural network-heuristic hybrid approaches optimize the network architecture for predicting rock permeability. They compared the effectiveness of the social ski-driver (SSD) algorithm-MLP combination with two commonly used hybrid methods, such as particle swarm optimization (PSO)-MLP and genetic algorithm (GA)-MLP. It was illustrated that SSD-MLP had the highest accuracy with a correlation coefficient (R) of 0.9928, while GA-MLP converged faster than the other two approaches. Chao et al.281 proposed a new ML model that can predict the stress-dependent gas permeability of shales with different moisture contents. The model combines the mind evolutionary algorithm (MEA) and adaptive boosting algorithm-back propagation ANN (ADA-BPANN) and has higher prediction accuracy and shorter training time than traditional ML algorithms. In another study, Pan et al.282 used a grid search approach and genetic algorithm for hyperparameter tuning and optimizing the XGBoost algorithm in a porosity prediction problem. The proposed method illustrated excellent generalization performance and adaptability, and compared to the five other approaches, it showed the most accurate porosity estimation. Wang and Cao283 combined the 1-D CNN and bidirectional gated recurrent unit (BiGRU) neural network to take advantage of both models and overcome their drawbacks for porosity prediction from well-logging data. The CNN network was used for learning hierarchical local features, and the BiGRU neural network was used to learn global features. The porosity prediction results proved that the novel integrated neural network outperformed other models, such as LSTM and RNN. Despite the efficiency of the ML models in reservoir property prediction, the “black box” nature of these models hinders their enhancement in some points. Water saturation, a crucial property in reservoir characterization, can be determined using various correlations. However, there are several obstacles, such as the faultiness of presumptions and high computational demand, to using these equations. Ibrahim et al.284 fed various types of well-logs to ML approaches, such as random forest (RF), function network (FN), and SVM, for the training and testing of a model that forecasts water saturation. Compared to empirical correlations, the introduced models showed excellent performance in water saturation determination, with an average absolute percentage error (AAPE) of less than 8%.
Some other researchers fed data from rock samples and micro-CT images to ML models for training and testing. Zhao et al.285 introduced a digital quantum mechanism-based neural network (DQNN) to estimate rock permeability and pore-scale variables are opted as input variables. The results showed that pore length, size, and throat size are more important variables than the coordinate number and porosity for predicting permeability. Also, the evaluation results of the DQNN were compared with those of the classical ANN and experimental permeability in terms of computational costs and accuracy. dos Anjos et al.286 utilized a CNN and CNN with spatial pyramid pooling (CNN-SPP), two convolutional neural network models, to predict petrophysical properties such as permeability from micro-CT images. Also, an easy-to-implement model, named the ImageNet pre-trained model, was tested and compared with the CNN models. It was shown that the pre-trained model could achieve the most accurate prediction, although CNN models reached satisfactory results. In addition, by using the prediction tools, absolute permeability was obtained 100 times faster than the Swanson method. Yet, the authors declared that the major problem for model training was not only the quality of the input data but also the quantity and amount of data. Alqahtani et al.287 conducted CNN models to estimate reservoir properties, such as specific surface area, porosity, and average pore size. These are the most crucial in permeability calculation using 2D slices generated from rock sample images. The model training and testing images are categorized as binary and greyscale images. The outcomes indicate that model training based on binary images leads to the minimum value of average relative error and maximum accuracy.
 | ||
| Fig. 14 AI-assisted history matching workflow for reservoir property tuning. First a high-resolution model with suitable grid cells, zones, and layers is constructed from seismic data. Then the facies model was built using the SGS technique to select the most suitable fluvial channel distribution. After that, an ANN is employed to optimize the selection of seismic attributes for porosity and permeability prediction. Through multiple trials and testing iterations, ANNs rank the attributes based on their correlation with well-log values. Finally, the efficiency of the integrated ANN technique and object-based modeling is evaluated through history matching, Thanh and Sugai,288 reproduced with permission from Elsevier. | ||
3.4.3.1. Upscaling. Upscaling refers to converting fine-scale properties, such as permeability and porosity, into coarser-scale data that can be used for reservoir simulation. The main goal of upscaling is to conserve the crucial properties and effects of heterogeneity at a lower computational cost and shorter time, which is necessary because simulating a reservoir at high resolution requires significant computational resources. Traditionally, flow-based methods are used to simulate fine-scale grids corresponding to the coarse cell and extract the property value that imitates the same flow value. However, this method highly relies on boundary conditions, and it is also considered to be time-consuming. ML algorithms can identify which parts of the model are most important for accurate predictions and simplify those areas while maintaining accuracy in other areas. Pal et al.289 presented an ML approach called the neural upscaling method that is more accurate than traditional analytical and numerical upscaling methods. They proved the superiority of the mentioned method over analytical and numerical upscaling methods. Also, they discussed the limitation of the neural upscaling method, which is the need for a substantial amount of training data. To overcome this limitation, the authors generated pseudo-training data using classical upscaling approaches. Wang et al.290 used an ML-assisted upscaling (MLAU) approach to reduce the computational cost of two-phase upscaling for large-scale reservoir models. The procedure involves using a CNN-based clustering model to select representative coarse blocks and a regression algorithm to predict two-phase upscaled functions for the rest of the blocks. They showed that the MLAU method can reach the same coarse-scale outcomes as accurately as the full flow-based upscaling while achieving significant speedups compared to flow-based upscaling and fine-scale simulations. In another study by Wang et al.,291 an ML-assisted relative permeability upscaling method was utilized to quickly compute upscaled relative permeability functions for coarse blocks using ML algorithms. The method was tested for generic flow problems using 2D models and showed similar accuracy to full numerical upscaling while achieving significant speedups. The outcomes suggest that the mentioned approach can be a promising alternative to traditional upscaling methods for subsurface uncertainty quantification or optimization. Santos et al.292 proposed an artificial intelligence approach for upscaling geological properties in reservoir simulation models. The method uses ML to apprehend patterns from a portion of datasets and extrapolate them to all other scenarios, resulting in faster and more accurate upscaling. They concluded that the introduced method outperformed other conventional approaches since it reached the same results as the fine model with less computational effort. Siavashi et al.293 presented an upscaling method using CNNs and downsampling techniques to predict low-resolution model properties. The results showed a significant reduction in computational cost and time while maintaining a close match between the dynamic behavior of the upscaled model through CNNs and high-resolution properties. The proposed method can be used for predicting multiphase flow characteristics in low-resolution large-scale models.
3.4.3.2. History matching. History matching is a crucial step in reservoir modeling that involves adjusting the uncertain parameters of a model to match observed data. It is a challenging and time-consuming task that requires expertise and experience. History matching can be performed using the computer assistant, known as automatic history matching (AHM). ML algorithms can automate this process by identifying which parameters need to be adjusted to match historical data and reducing the problem's computational costs. Alolayan et al.294 introduced a new approach for solving the history matching problem in reservoir simulation using reinforcement learning. They introduced a Markov decision process formulation of the problem, which allows an artificial deep neural network agent to collaborate with the simulator and speed up the process considerably. Jo et al.295 used a deep-learning-based history-matching method in fluvial channel reservoirs without conventional calibration processes. The method outperforms non-convolution-based methods regarding geological constraints and computational resources. The convolutional denoising autoencoder (CDAE) as a post-processor of the proposed method enhances the uncertainty assessment of posterior production behaviors. Ma et al.296 exploited a hybrid recurrent convolutional network (HRCN) model for surrogate modeling conducted in automatic history matching (AHM). The proposed model significantly reduces the computational cost of AHM. They illustrated that the introduced surrogate model can obtain reliable predictions, and the surrogate-based AHM workflow can considerably reduce the computational cost. Ma et al.297 utilized a history-matching method using a recurrent neural network (RNN) surrogate model to estimate the parameters of spatially varying geological properties in large-scale reservoirs. The proposed multilayer RNN surrogate model with the gated recurrent unit (GRU) is used to estimate mapping from the feature vector of geological realizations to the production data. Numerical experiments on a 2D reservoir model and the Brugge benchmark model demonstrate the performance of the proposed surrogate model and history matching method. Xiao et al.298 proposed an efficient surrogate-assisted deterministic inversion framework for large-scale history matching problems in reservoir modeling. The framework uses a deep neural network surrogate to approximate the gradient and stochastic gradient optimizers for quick convergence. The proposed method is compared and evaluated with a previously submitted projection-based subdomain called the proper orthogonal decomposition and trajectory piecewise linearization (POD-TPWL) approach regarding computational costs and accuracy. Both models have illustrated outstanding capacity in carrying out history-matching problems.
3.4.3.3. Reservoir simulation. Dynamic modeling involves simulating the flow of fluids through the reservoir over time, which requires considering factors such as pressure change, fluid movement, and production rates. ML algorithms can optimize these simulations by predicting how different variables will affect the behavior of the reservoir. For example, neural networks can be trained on historical production rates based on changes in pressure or fluid properties. Qubian et al.299 discussed using a hybrid reservoir simulation model that combines artificial intelligence and numerical models. The study uses a neural network called LSTM to learn order dependence in sequence prediction problems. The study results suggest that the hybrid model can be a valuable tool in reservoir simulation. Behl and Tyagi300 explored using data-driven reduced-order models (ROMs) as an alternative to detailed physics-based simulations for reservoir simulation. The study found that the case with stateless LSTM achieved the most accurate forecasting. Also, by applying a walk-forward validation strategy, the proposed framework decreased estimation error by 95% on average with less computational costs compared to the conventional simulation. The physical realism was also enhanced by adding a capacitance resistance model (CRM) constraint, demonstrating the ROM's ability to detect spatial irregularities. Huang et al.301 proposed an improved E2C model for faster predictions of subsurface flow in complex reservoirs with many wells. The proposed model significantly enhances the deep-learning network structure, well quantity calculation, and loss function specification, resulting in highly accurate predictions with substantial speedups. The results proved the accuracy of the improved E2C model, with a median average error of 3.1% for production, 1.0% for saturation, and 5.9% for pressure. Saberali et al.302 introduced a new method for constructing a grid-based surrogate reservoir model (SRM) using a hybrid data source based on finite differences and streamline data. The outcomes showed that the mentioned hybrid database allows the SRM to be utilized by fast-supply inputs from streamline data and generate results as accurate as the finite difference-based simulation. The fidelity of the introduced approach was also approved by testing it on the 10th SPE model. Shuaibi et al.303 discussed testing a new tool on a brownfield with over 30 years of production history. The tool can potentially improve brownfield development and optimization for future developments. The paper concluded that the AI simulator, which utilizes an AI-physics hybrid reservoir simulator, could generate a reasonable production forecast for the tested brownfield. The AI simulation results were compared to the actual field data, and it was found that the predictions from the AI simulator compared better than the reference case conventional simulator forecast. Manasipov et al.304 presented different approaches that follow the concepts of physics-informed models. They found that incorporating physics into ML models can increase their accuracy and predictive power. However, in cases where physics-based models perform poorly, history matching or tuning of the model should be performed in a globally constrained optimization formulation. The study also found that generalized additive models (GAMs) can produce comparable results to popular ML methods such as neural networks and gradient boosting. GAMs offer flexibility in considering inter-well connectivity, inter-well distances, production and injection rates, and average reservoir properties.
3.4.4.1. Production forecasting. Production forecasting is critical to reservoir management as it helps companies plan their operations, estimate reserves, and optimize production. ML algorithms can examine substantial amounts of data from various sources, such as well-logs, seismic data, production history, and geological models, to generate accurate production forecasts. ML models can also optimize production by identifying the best operating conditions for wells. These models can analyze real-time data from sensors installed in wells to predict the optimal flow rate, pressure, and temperature for maximum output. Kong et al.305 used a hybrid prediction model for oil production based on two-stage decomposition, sample entropy reconstruction, and LSTM forecasts. The model performed more accurately than traditional approaches and proved to be a useful tool for reservoir evaluation and oilfield management. Chu et al.306 utilized a data-driven proxy model using deep learning to assess the production performance of horizontal wells with complex fracture networks in shale gas reservoirs. The model considers production time, variable bottom hole pressure, and fracture network properties as input variables to forecast production for the future period. Ibrahim et al.307 introduced a new approach to estimating the estimated ultimate recovery (EUR) for oil production wells in the Niobrara shale formation using ML techniques. The study shows that ML tools can accurately predict EUR from completion design parameters and initial well production rates. Although conventional empirical decline curve analysis (DCA) models need multiple months of production to estimate the EUR, the developed models demand only an initial flow rate and the completion design for EUR prediction with high certainty. Osah and Howell308 investigated the use of supervised ML methods to forecast the performance of oil fields on the United Kingdom continental shelf. The study tests five different algorithms and finds that support vector regression is the most effective method for predicting recovery factor and the maximum field rate. Al-Ali and Horne309 discussed using a transformer-based deep learning model called the temporal fusion transformer (TFT) to predict the oil production rates of wells in the Norwegian Volve field. It was concluded that the TFT model is a promising approach for accurate oil rate prediction. The model was more precise than traditional block recurrent neural network architectures (BlockRNNs) in predicting complex trends in oil rates. The ability of the TFT model to provide a range of forecasting uncertainty using quantile regression is vital for making critical decisions in well intervention and field development. Liu et al.310 presented a new approach for evaluating the complex characteristics and production optimization of shale oil reservoirs using an ANN. The introduced quantitative evaluation approach is based on source-reservoir assemblage types, source rock quality, reservoir quality, migration dynamics, and conduit conditions. The study concludes that increased liquid hydrocarbon, mud gas, total organic carbon (TOC), and normal fault percentage positively affects shale oil production. In contrast, the increase in reverse fault percentage negatively affects shale oil production. Ullah et al.311 proposed using ML models to predict bio-oil yield from microalgae pyrolysis. The best-performing model was GPR-GA with a high R-squared value and low RMSE, and an interface was developed for predicting bio-oil yield. Du et al.312 proposed an ensemble framework for coalbed methane (CBM) production forecasting using supervised and unsupervised learning. An LOF-Xgboost governance system autonomously detects outliers and supplies missing values. At the same time, the improved Bi-LSTM method establishes a forecasting model of CBM production for both long-term and short-term prediction. The experimental analysis shows that the proposed framework improves the short-term prediction performance and considerably increases the long-term estimation capability.
3.4.4.2. Operational parameters and well placement optimization. Optimal well placement and operating conditions are other critical aspects of reservoir management that determine the success of oil and gas operations. ML algorithms can analyze geological data to identify the best locations for drilling new wells and optimum operating parameters, such as pressure, rate, and temperature. These algorithms can also predict the impact of drilling on existing wells by analyzing data from nearby wells. Tang and Durlofsky313 presented an optimization framework for well placement in 3D models using low-fidelity (LF) models and ML error correction. LF models are constructed using a global transmissibility upscaling procedure and tree-based ML methods to predict the error in the net present value (NPV) associated with the LF models. In the offline stage, preliminary optimizations are conducted using LF models, and a clustering approach is used to opt for a representative set of well configurations for training. In the online stage, optimization with LF models, with the ML correction, is performed using differential evolution. The results show that the proposed method provides a significant speedup factor compared to optimization using high-fidelity (HF) models, with the best-case NPV within 1% of the HF result. Using ML algorithms, Bertini et al.314 explored a methodology to efficiently estimate the NPV of oil production strategies. The proposed methodology considers binary data representation, indicating the presence or absence of a given well in a production strategy, reducing data dimensions and model complexity. The simulations conducted in a benchmark case, based on a real field, showed that some regression algorithms could be used as a surrogate model to the simulator to perform well placement optimization considering binary data efficiently. The best results were obtained with MLP, whose estimations covered a wide range of NPV with a small and constant error. Zhou et al.315 utilized an efficient multi-objective optimization framework for well placement and hydraulic fracture parameter optimization. The framework uses a novel hierarchical surrogate-assisted evolutionary algorithm and multi-fidelity modeling technology. The NPV and cumulative gas production (CGP) are the bi-objective functions to be optimized. The proposed approach is validated on a naturally fractured shale gas reservoir and is found to be accurate and efficient. The ML model used in the approach only needs to run 100 or 500 reservoir numerical simulations, making it highly efficient. Nasir and Durlofsky316 proposed a closed-loop reservoir management framework that uses deep reinforcement learning to train control policies for optimal well settings. The framework incorporates operational and economic constraints, including relative-change requirements and project life optimization. The purpose is to maximize the NPV while ensuring the practical applicability of the control policy results. The framework is applied to waterflooding cases involving 2D and 3D geological models. The results show that the control-policy approach provides comparable or superior solutions to deterministic and robust optimization approaches. The optimal well settings provided by the control policy display gradual ramping, consistent with operational requirements. Chen et al.317 presented a new method called InterOpt for optimizing operational parameters in petroleum exploration and development. This method uses interpretable ML to assess the impact and importance of various parameters. The experiment showed that by modifying operational parameters, InterOpt presented various optimization scenarios and attained an average cost reduction of 9.7%. The transferability and scalability of InterOpt to different optimization objectives are also verified based on the optimization of test production. Yao et al.318 discussed using surfactants to enhance oil recovery by altering the wettability of carbonate rock surfaces. ML models are used to predict and optimize surfactant performance. The Shapley additive explanations approach is used to interpret the results and provide insights into the effects of different parameters on surfactant performance. Fabbri et al.319 discussed a screening code that helps reservoir engineers identify potential locations for new oil wells. The code uses data from existing wells, production and pressure data, and geological information to create polygons representing areas with high potential for oil production. The code was tested by comparing the results to a base case with no new wells and a case with a combination of hand-picked and code-identified locations for new wells. The results showed that the code-identified locations provided additional value compared to the hand-picked locations alone. Overall, the paper suggests that the screening code can be a useful tool for optimizing oil well placement.
3.4.4.3. Screening for IOR/EOR technique selection. Improved oil recovery (IOR) and enhanced oil recovery (EOR) are techniques used to increase recovery rates from hydrocarbon reservoirs. ML algorithms can screen potential IOR/EOR techniques by analyzing geological data to identify suitable candidates for these techniques. ML models can also predict the effectiveness of IOR/EOR techniques by analyzing historical data from similar projects. Screening potential IOR/EOR techniques increases recovery rates while costs associated with unsuccessful projects are reduced. Pirizadeh et al.320 proposed a novel method for ranking EOR processes based on predicting the EOR-PR values. EOR-PR is a new production rate that represents the performance of EOR processes on particular reservoir characteristics. The proposed approach uses multi-gene genetic programming (MGGP), a practical ML approach, to predict EOR-PR values and rank EOR methods based on their efficiency under specific reservoir conditions. The results show that MGGP has a significant performance in predicting EOR-PR values, and it can be used for EOR decision-making strategies. Pavan et al.321 proposed a PIML approach to forecasting the performance of the in situ microbial-enhanced oil recovery process and screening suitable microbe-nutrient combinations based on inadequate experimental data. The method evaluates the impact of microbial kinetic, operational, and reservoir parameters as input variables on oil recovery and assesses their weightage factors to screen a suitable microbe–nutrient–reservoir combination. Mahdaviara et al.322 aimed to study potential EOR scenarios for low permeability reservoirs. The databank included essential parameters such as permeability, porosity, API, viscosity, lithology, depth, and temperature for each reservoir. They developed EOR screening tools based on statistical and intelligent procedures such as RF, GBM, XGBoost, and gene expression programming (GEP). The introduced EOR screening tools were valuable for this study's scope, with RF outperforming the alternatives.
3.5. Carbon capture and sequestration
Several porous organic, inorganic, and chemical-organic composites have been suggested for adsorptive CO2 collection.332–335 In addition to activated carbons (ACs), MOFs, and zeolites, porous organic polymers (POPs) have also been used as porous materials for CO2 capture, as depicted in Fig. 15a–e. The selectivity of an adsorbent for CO2 in the presence of other gases, the adsorbent's CO2 swing capacity during adsorption–desorption cycling, the kinetics of adsorption and desorption, the energy needed to cycle or regenerate the adsorbent, the adsorbent's resistance to mechanical and chemical stresses during recycling, and the adsorbent's economic and environmental potential are important metrics for evaluating its utility. In Fig. 15e, radar plots for important sorbent criteria for choosing are shown. The key performance indicators for selecting materials in carbon capture applications have been qualitatively evaluated.
 | ||
| Fig. 15 (a) Activated carbons (ACs), Palmer et al.,332 reproduced with permission from Elsevier, (b) IRMOF-5, Cai et al.,336 reproduced with permission from American Chemical Society, (c) Zeolites Rho, Lozinska et al.,337 reproduced with permission from American Chemical Society, (d) porous organic polymers (POPs), Bandyopadhyay et al.,338 reproduced with permission from American Chemical Society, and (e) radar plot for evaluation of adsorbent selection in CO2 adsorption applications using various material class features. The radar plot is depicted in terms of different scores for adsorption of gases through porous adsorbents, Mashhadimoslem et al.,339 reproduced with permission from Elsevier. | ||
The development of adsorbents for carbon capture has seen significant advancements in the materials community. Nevertheless, more resources are required to meet requirements along the way to industrialization. In general, lifespan issues require more focus, and as materials move along in their development, more thorough evaluations must be undertaken.340–342 In particular, suggested synthetic methods must be scalable and safe, with few steps and good space-time yields, and starting materials must be feasible at the goal scale (especially for MOFs, given restricted extraction rates and deposits of specific metals).343 It is also important to consider how easily biomass can be recycled, utilizing both experimental and computational waste streams.344–347 ML, which makes it possible to provide algorithms for developing new materials,348 has attracted a great deal of interest recently for its ability to accurately predict chemical and physical properties, establish structure–property relationships,349,350 synthesize AC adsorbents via various types of biomass,351 and navigate the chemical space to direct chemical synthesis.352,353 Designing and implementing process strategies that successfully extract CO2 from a gas composition with a minimal energy cost is the main objective of ML for carbon capture deployment.
At both the molecular and process levels, ML techniques have been effectively used in absorption and adsorption-based processes to address the issues that these techniques are now experiencing.356 A schematic of the ML implementation at different resolutions for a carbon capture technology based on multiple sources is shown in Fig. 16a. Fig. 16a illustrates the application of ML for carbon capture techniques in several stages, from adsorbent syntheses through adsorption steps, using experimental and computational data. External (published papers/databases) or internal sources (experimental/computational data) are used as feeds for ML algorithms. One of the applications of gas (air) separation in the power plant industry is oxyfuel, one of several solutions that reduce the percentage of CO2 released from the combustion chamber output. Additional carbon cannot be produced if the air is separated, and additional oxygen is injected into the combustion chamber. One technique used in this industry to select the right adsorbent for gas separation technology is the prediction of the adsorption process using ML algorithms. To forecast gas absorption using porous carbon adsorbents, Fig. 16b depicts the architecture of the gray wolf multilayer perceptron optimizer meta-heuristic algorithm.
 | ||
| Fig. 16 (a) Schema of ML deployment for carbon capture systems, Rahimi et al.,354 reproduced with permission from Cell Press, (b) schema structure of the gray wolf-multilayer perceptron optimizer (GWO-MLP) meta-heuristic ML algorithm for predicting gas absorption using porous carbon adsorbents, Mashhadimoslem et al.,355 reproduced with permission from The Canadian Journal of Chemical Engineering. | ||
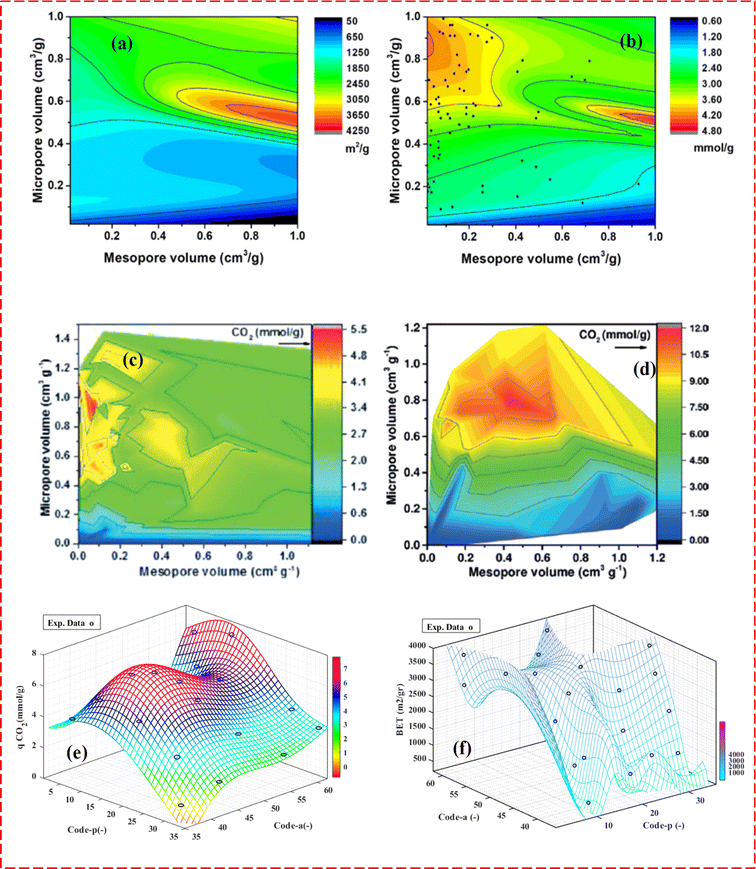 | ||
| Fig. 17 Contour maps of (a) SBET (m2 g−1), and (b) CO2 adsorption capacities (mmol g−1) at 298 K and 1 bar,359 reproduced with permission from the American Chemical Society, the contour maps of CO2 capture and micropore and mesopore volume under the same adsorption conditions, (c) at 298 K and 1 bar and (d) at 5 bar,358 reproduced with permission from Wiley, (e) 3D response surface of CO2 adsorption prediction using the MLP from different precursor biomass and activators and, and (f) prediction of SBET (m2 g−1) synthesized from different biomass materials and activators at different temperatures using RBF algorithms,346 reproduced with permission from American Chemical Society. | ||
Wang et al.359 developed an ML model using the DNN algorithm and trained the algorithm using experimental data on CO2 and N2 uptakes in porous carbons. The training algorithm was based on textural features such as micropore volume, mesopore volume, SBET, temperature, and pressure adsorption conditions. The trained DNN model was then used to screen porous carbons and predict their CO2 and N2 uptakes and CO2/N2 selectivity. In this study, 2500 hypothetical combinations of micropore volume (Vmicro) and mesopore volume (Vmeso), ranging from 0.02 to 1.00 cm3 g−1, were created. The trained DNN-3 model was then employed to predict their SBET. Additionally, another neural network (DNN-3) was trained to predict SBET from Vmicro and Vmeso and was used to generate 2D maps of adsorption uptakes and selectivity (see Fig. 17a and b). The results of this analysis suggest that introducing more mesopores in microporous carbons can disrupt and decrease N2 adsorption, ultimately leading to better CO2/N2 selectivity. Their research results discovered that the highest CO2/N2 gas selectivity is not necessarily obtained in the regions with the highest CO2 uptake, but rather in the regions with the lowest N2 uptake where mesopores can disrupt N2 adsorption. Moreover, it was found that the best features for high CO2 uptake may not necessarily be optimal for achieving high CO2/N2 selectivity.
Zhang et al.358 developed an ML model using SBET, Vmicro, Vmeso, temperature, and pressure parameters for CO2 adsorption prediction. In this study, a DNN was trained as a generative model to establish the relationship between the CO2 adsorption of porous carbons and their corresponding textural properties. Then, the neural network was utilized as an implicit model to evaluate its ability to predict the CO2 adsorption capacity of unknown porous carbons. It was found that when the Vmicro,Vmeso, and SBET are used as input neurons simultaneously, the trained neural network was able to achieve a remarkable agreement between experimental and predicted CO2 adsorption capacity values (see Fig. 17c and d). The investigations confirmed that Vmeso is important in controlling gas uptake, contrary to the previous belief that Vmicro is the only parameter. Additionally, SBET is an independent textural parameter that can work with other parameters to determine gas-uptake capacities. Finally, gas uptake in solid adsorbents depends on the complex interplay of textural parameters, and the sensitivity of each parameter can be estimated.
A further interesting possibility for carbon capture, separation, and storage is MOF adsorbents, which have a variety of porosities, high SBET, low densities, and an extensive variety of pore size diameters.363,364 To determine structure–performance correlations and choose the top descriptors that can precisely predict the CO2 adsorption capacity, efficiency, and selectivity, ML is applied in MOFs for carbon capture technologies.365,366 Deep generative models, such as the supramolecular variational autoencoder (SmVAE), were created by Yao et al.366 for the converse design of MOFs exhibiting improved CO2 capacity selectivity and separation from other gases. The autoencoder, which was jointly trained on several top adsorbent materials found for better gas separation, demonstrated promising optimization potential in this study.
Over 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 new CoRE MOF 2014 database structures have been proposed, and the MOF's structure came from several types of sources. By compiling the new structure data to feed the database, the full set of structures for the presence of open metal sites (OMSs), examining the impact of bound energy on the calculated geometric attributes, and considering real MOFs that could be discovered in a set of computer-generated, hypothetical MOFs, the understanding of the molecular fingerprint strategy was illustrated. With the aid of the distribution of data from experiments, the mentioned model could begin to produce a new dataset.367 Given the assistance of data from experiment distribution, this model could begin to produce new data. Using the 372 MOF edges acquired through CoRE MOF identification, this study produced an edge dataset of over 300
000 new CoRE MOF 2014 database structures have been proposed, and the MOF's structure came from several types of sources. By compiling the new structure data to feed the database, the full set of structures for the presence of open metal sites (OMSs), examining the impact of bound energy on the calculated geometric attributes, and considering real MOFs that could be discovered in a set of computer-generated, hypothetical MOFs, the understanding of the molecular fingerprint strategy was illustrated. With the aid of the distribution of data from experiments, the mentioned model could begin to produce a new dataset.367 Given the assistance of data from experiment distribution, this model could begin to produce new data. Using the 372 MOF edges acquired through CoRE MOF identification, this study produced an edge dataset of over 300![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000. When simultaneously trained using several top suggestions for improved gas separation and verified by atomistic Monte Carlo (MC) simulations, this model demonstrated excellent predicting and optimizing capabilities.
000. When simultaneously trained using several top suggestions for improved gas separation and verified by atomistic Monte Carlo (MC) simulations, this model demonstrated excellent predicting and optimizing capabilities.
Researchers provide cases of ML development in various CO2 capture, storage, transport, and utilization (CCSTU) systems. Adsorption, absorption, chemical looping, membranes, sequestration, and hydrates are a few examples of carbon capture or separation technology (CCST). Any research project incorporates a synergistic approach (sequestration plus absorption).368 Modeling and simulating solvent-based carbon capture requires extensive effort and time owing to the complicated governing processes of absorption, particularly chemical absorption, involving mass transfer and chemical reactions.356,369 The measurement of parameters such as the mass flow rate using differential pressure-based flowmeters is unable to attain adequate precision in the measurement of mass flow, and their substantial complexity and cost limit their use in carbon capture, utilization, and storage (CCUS) industries. Recently, low-cost sensing methods that include ML techniques to increase the accuracy of flowmeters have been developed.368 In oxyfuel combustion for CO2 collection, ML is also used in applications including forecasts of combustion characteristics and pollutants' emissions, as well as controlling the process of combustion using flame images.370 The use of ML algorithms for chemical looping combustion for CO2 capture has been investigated in a few investigations, although this subject still needs further research.371 The novel modeling and analysis work that has been performed to examine various elements of the CO2 adsorption, absorption, and separation processes in porous media is the main topic of our review study. Adsorbent materials, the adsorption process, optimization, and simulation of the process are all included.
Zhang et al.372 developed ML techniques using experimental and simulation datasets that revealed the most significant factors affecting CO2/N2 selectivity and CO2 permeability in the MOF composite. The RF model revealed that AV is a key factor in predicting membrane selectivity and GASA is a key factor in predicting CO2 permeability. Guan et al.373 developed RF models trained on literature experimental data for CO2/CH4 separation to identify suitable MOFs for constructing Mixed Matrix Membranes (MMMs). The resulting membranes showed CO2 separation performance beyond the 2008 Robeson upper bound and agreed well with model predictions. Moosavi et al.2 developed and trained the ML model (using the XGBoost algorithm) using DFT simulations to predict the heat capacity of solid nanoporous sorbents, including MOFs, zeolites, and COFs. The ML model's highly accurate heat capacity prediction allows for quantifying the influence of heat capacity variations on material ranking in a TSA process. Yao et al.366 developed a platform using experimental data for nanoporous material discovery using a super molecular variational autoencoder (SMVAE) to create reticular frameworks with optimized properties. The MOF structures generated using the SMVAE model showed significant competitiveness against some of the best-performing MOFs/zeolites reported to date. The platform was employed to design new MOFs with improved CO2/N2 and CO2/CH4 separation capacity and selectivity. The developed platform has wide-ranging applicability for various materials, such as COFs, metal–organic polyhedra (MOP), hydrogen-bonded organic frameworks, and coordination polymers. It serves as a basis for creating reticular frameworks for diverse applications. Gao et al.374 employed ML using XGBoost, RF, Gradient Boosting Machine (GBM), and MLP algorithms and simulation datasets to gain a comprehensive understanding of the adsorption behaviors, and an ML-assisted analysis was employed to pinpoint the preferred CO2 adsorption sites for each framework at various four distinct temperatures. The center-of-mass coordinates of 800 CO2 molecules were randomly selected and labeled with their corresponding binding site types. Various well-known ML algorithms were applied to learn the relationship between the CO2 molecule's C atom coordinates and the corresponding adsorption site types. Krokidas et al.375 for the first time used the ML using DFR and DTR algorithms to investigate how the substitution of basic MOF building blocks affects the pore structure and molecular diffusivity. While the ML approach is general, the focus was specifically on ZIFs with SOD topology. Due to the lack of a relevant ZIF database, an ensemble of 72 new and existing ZIFs has been created through systematic sub-unit replacement. Forcefields were developed for each structure, and fully flexible MD simulations were conducted to determine the framework properties and molecular diffusivity of various molecules.
Another study was presented by Yang et al.376 which used ML-assisted MC computational screening to identify optimal secondary building units (SBUs) for wet flue gas separation using COFs. They used the DT, RF, XGBoost, and CatBoost algorithms for the training of the experimental dataset. It has been found that tetraphenyl porphyrin units enhanced CO2 adsorption uptake, while functional groups improved CO2/N2 selectivity. Based on these findings, 1233 COFs were assembled using the optimal SBUs. This research analyzed the quantitative relationship between input descriptors and COF separation performance. Their results showed that the IS and SBET features had the greatest impact on CO2 uptake, whereas the IS and DF features had the most significant impact on CO2/N2 selectivity. Cheng et al.377 proposed a multi-scale design framework using an MD simulation dataset for CO2/CH4 separation via MOF-based membranes. In this research, ANN prediction models were created and trained using MD and GCMC simulations to characterize the adsorption capacity and self-diffusivity of MOF membranes. The models were subsequently employed to determine permeability. The tanks-in-series model of a hollow fiber membrane separation process was combined with the ANN models and simulated using the finite volume method. Zhu et al.378 using the DFT calculations dataset developed ML models that were employed to predict the ΔG and pressure of all possible reaction intermediates and products, including methanol, methane, and formaldehyde, during the reduction of CO2 on 26 single-atom catalysts (SACs) in zeolites. The multi-ML models proposed using XGBoost, gradient boosting regression (GBR), extra trees, KNN, DT, ANNs, SVR, multi-linear regression (MLR), linear ridge (LR), and least absolute shrinkage and selection operator (LASSO) algorithms exhibited good transferability and can be utilized to predict the performance of MOFs, 2D materials, and molecular complexes. After a comparison of the selected algorithms, the XGBoost algorithm demonstrated the strongest performance with an MAE of 0.36 eV and an R2 value of 0.87. Kriesche et al.379 integrated a new ML model, the ANI-2 neural network potential (NNP) with an MD framework to model the behavior of two COF systems, HEX COF1 and 3D-HNU-5, which share the same linking unit. Their results indicated that the ANI-2x NNP could accurately describe the structures of macromolecules such as COFs and their interactions with CO2 guest molecules. The main innovation of this research was the use of a DFT-based neural network approach and a suitable MD simulation protocol to simulate a relatively large system over an extended period. This approach provides access to correlated properties within the long-time limit, with a particular focus on estimating the system's diffusion coefficient. The exceptional efficiency of this approach was demonstrated by the extensive total simulation time of over 0.4 μs, which cannot be achieved using traditional DFT methods. The use of minimum distance distribution functions (MDDFs) can provide valuable insights into the nature of interactions between host–gas molecule systems. In this study, MDDFs were employed to identify similarities and differences in the host-CO2 interactions of HEX-COF1 and 3D-HNU5. Feng et al.380 created an intelligent system for materials, which utilized the DeepFM approach to predict multiple adsorption properties of the hMOF database by integrating descriptors. The mentioned research investigated the importance of various descriptors on the CO2 capture capabilities of MOFs. Their results revealed that MOFID is an extremely crucial descriptor. Excluding MOFID, the top five important descriptors for CO2 uptake and CO2/N2 selectivity were the same, which included topology, metal linker, functional group, SBET, and porosity, although their ranking differed slightly. The DM model presented in this study was used to predict 28 adsorption properties of 8206 screened hMOFs database. Sturluson et al.381 proposed a COF recommendation system that matches COFs with specific adsorption tasks. This model was achieved by training a low-rank model of an incomplete COF-adsorption-property matrix constructed from simulated uptakes of CH4, H2O, H2S, Xe, Kr, CO2, N2, O2, and H2 using experimental data under various conditions. This model was developed by fitting a model of the COF-adsorption-property matrix to the observed (COF, adsorption property) values. The mentioned research results were able to provide predictions for missing (COF, adsorption property) values. Additionally, this approach generated a “map” of COFs, where COFs were represented as points and those with similar or dissimilar adsorption properties congregated or separated, respectively. The COF recommendation system developed in this research was found to be capable of effectively ranking COFs for most adsorption properties. However, the imputation performance of the system decreased significantly when the fraction of missing entries in the COF-adsorption-property matrix exceeded 60%. A knowledge engineering technology was utilized by Kondinski et al.382 to automate the development of MOP formulations using existing knowledge as a database. In this study, an ontological MOP was created to establish a clear definition of MOP and its essential properties. Raji et al.383 developed ML models, which use experimental temperature and pressure CO2 adsorption. The main goal of this study was to develop efficient prediction models using soft computing methods, specifically hybrid-ANFIS, particle swarm optimization-adaptive neuro-fuzzy inference system (PSO-ANFIS), and least-squares support vector machine (LSSVM), for estimating CO2 adsorption on five distinct types of zeolite adsorbents (5A, 13X, T-Type, SSZ-13, and SAPO-34). This research aimed to provide an alternative to the costly and time-consuming laboratory experiments currently used for this purpose. Based on the results, it was demonstrated that all the proposed models are reliable and precise for estimating CO2 adsorption on various types of zeolites. Zhang et al.384 utilized the ML using RF, XGBoost, and SHAP algorithms to investigate the correlation between the CO2 adsorption performance of amine-functionalized adsorbents and input descriptors. It was found that amine loading was the most crucial factor affecting CO2 adsorption capacity, followed by pore volume. Pore size was the primary factor influencing amine efficiency, while the cycle stability of the adsorbent was mainly related to the type of amine used. This research illustrated, that to attain the highest possible CO2 adsorption capacity for the adsorbents, the pore volume required for amine loading should account for 40–50% of the support's pore volume for TEPA (Tetraethylenepentamine) and 65–75% for PEI (polyethyleneimine). Yan et al.385 presented a deep learning (DL) workflow for predicting the pressure evolution of fluid flows in large-scale 3D heterogeneous porous media. This research developed an efficient feature technique to extract the most representative information for DL training and prediction at the coarse scale. The mentioned technique also allowed for the recovery of resolution at a fine scale through spatial interpolation. By using a predefined stride, feature coarsening was employed to extract the most representative information about geology and well controls, resulting in reduced memory consumption of feature arrays and improved training efficiency. The effect of feature coarsening on DL performance was investigated, and it was discovered that it not only cut training time by more than 74% and memory consumption by more than 75% but also maintained an average temporal error of 0.63%. Another research study focused on the gas permeability database, to address missing values in the database. Yuan et al.386 utilized the ML model to impute or fill in the missing data. For systems with limited experimental data, sparse feature ML was utilized. The study suggests that once the permeability of CO2 and/or O2 for a polymer has been measured, most other gas permeabilities and selectivity, including those for CO2/CH4 and CO2/N2, can be quantitatively estimated through ML techniques. The research results suggested that KAUST-PI-1 may exhibit potentially high CO2/CH4 selectivity and good CO2/N2 selectivity. This prediction was later confirmed by experimental work that was not originally recorded in the database. The multivariate imputation by chained equations (MICE), Bayesian linear regression (BLR), and extremely randomized tree (ERT) algorithms were used to simulate datasets (1387 datasets). The ERT algorithm showed the best results in predicting CO2/CH4 and CO2/N2 adsorption selectivity, based on the CO2 permeability data.
3.6. Groundwater
Finding proper, cost-effective, and efficient models in hydrology and groundwater is always challenging. On the one hand, hydrologic cycle phenomena such as flood and streamflow, evapotranspiration, precipitation, infiltration, groundwater modeling, etc., have a complex process on a catchment scale and cannot be predicted using simple/linear models.390 On the other hand, developing and implementing a model that involves all catchment phenomena, such as distributed and semi-distributed hydrologic models/physically-based models i.e., MIKE-SHE and SWAT (soil and water assessment tool) is time-consuming and needs a vast amount of high-quality input data according to ref. 391–393. Owing to substantial advancements in computational power, ML algorithms have recently achieved notable breakthroughs in managing and processing intricate and voluminous datasets. Due to high computational power, user-friendliness, handling big data, handling data with different dimensions, not needing a vast amount of data like numerical models, and high prediction/forecasting power of any complicated process such as water resource phenomena by formulating the relationship between inputs and output variables,394–396 application of ML/DL algorithms has recently been increasing, especially in the field of hydrology and groundwater resources. In addition, by expanding the application of big data, which is available from numerous sources such as satellite images, reanalysis data, drones, sensors, and geophysical data,397 the use of ML/DL model has significantly increased. Within this context, groundwater issues have consistently been a focal point for researchers seeking to harness these technological strides for diverse applications. These applications encompass areas such as hydrological modeling, fluid flow and transport in porous media, and the characterization of geo-systems. Consequently, there exists pervasive interest in the development of ML techniques tailored to capitalize on the burgeoning availability of substantial datasets from the varied above-mentioned sources. Khosravi et al.398 compared the prediction accuracy of hybrid ML models, including random forest (RF) and Dagging-RF (DA-RF), simple and well-known approaches of sediment rating curve (SRC), and the SWAT model for prediction of suspended sediment load at Talar catchment, in the north of Iran. They revealed that the Dagging-RF model outperformed traditional and physically based models. Therefore, complicated models such as distributed and semi-distributed models don't guarantee higher prediction power, and their results confirm the higher performance of ML models in groundwater.Groundwater resource management on a catchment scale can be divided into two main classes, namely, surface water hydrology (precipitation, streamflow, flood, infiltration, soil moisture, and wetland/lake water level) and groundwater hydrology. Surface water hydrology is not well matched by porous media, but all relevant groundwater applications are in the area of porous media. Overall, modeling of fluid flow in porous media has numerous applications, from the micro-scale (cell membranes, filters, and rocks) to macro-scale (groundwater, hydrocarbon reservoirs, and geothermal) and beyond, and in the current review macro-scale application, which is more relevant to groundwater resources, has been reviewed and discussed. In natural science, soil and rocks are prominent examples of porous media. Fluid flow which goes through porous media (i.e., ground/soil) is a fascinating subject and has a significant impact on other hydrologic cycles.399 DL algorithms employing CNNs have been used to analyze porosity, permeability, and tortuosity in porous media through fluid flow, yielding accurate results. In groundwater resource management, regression and classification-based methods can be applied, depending on the context and objective. Generally, a regression-based approach is used for time series prediction (i.e., streamflow, rainfall, etc.), while classification-based methods are used for spatial modeling (i.e., flood, groundwater, etc.).
The data inherent to porous media and subsurface systems exhibit distinctive attributes that differentiate them from commonplace datasets in other domains. In contrast to conventional data encountered in fields such as image recognition within computer science, the data associated with porous media adhere to physical laws. Consequently, the direct application of ML techniques to such data is often impractical, necessitating reformulation and customization of these techniques to align with the inherent characteristics of the dataset. The burgeoning influx of data-sensing tools, coupled with the continuous evolution of advanced computational algorithms, underscores the imperative to develop ML and automated methods capable of addressing the complexities posed by such data.
Effectively unlocking the potential of big data in geosciences and making informed decisions mandates the development of advanced techniques adept at identifying intricate dependencies and patterns within the dataset. This involves overcoming inherent challenges that make traditional methods difficult or nearly impossible. As elucidated in this review, ML techniques emerge as a highly efficient alternative for discerning patterns within vast and multidimensional datasets. The adaptability of ML allows for the discovery and extraction of linear and nonlinear correlations among various physical parameters. Such capabilities of ML techniques have proven instrumental in unveiling the potential inherent in big data, thereby advancing our comprehension of complex phenomena within porous media, spanning scales from the minuscule to the expansive in GeoMedia.397
Panahi et al.400 applied an optimized DL of a CNN using gray wolf optimization (GWO), a genetic algorithm (GA), and independent component analysis (ICA) for the prediction of two important soil characteristics, cumulative infiltration and the infiltration rate. They considered time of measuring, sand, clay, and silt percent, bulk density and soil moisture percent from field survey as inputs. They showed that metaheuristic algorithms enhance the CNN model's prediction power and that they can accurately predict cumulative infiltration and infiltration rates. In addition, their findings revealed that time had the most effective impact on cumulative infiltration, while silt content was the most correlated variable with the infiltration rate. Rehman et al.401 implemented ML-based intelligent modeling of sandy soils' hydraulic conductivity (k) considering a wide range of grain sizes. They considered and involved a comprehensive array of input parameters delineating geological characteristics, including but not limited to variations in grain sizes encompassing large, medium, and small dimensions (D), gradation parameters, and dry density (γd). This deliberate inclusion aims to address the inherent limitations of prevailing k-value predictive models, ensuring a more robust coverage of output variability across diverse combinations of D-values within a sandy soil deposit. They applied the ANN, multi-expression programming (MEP), and genetic expression programming (GEP) on a large dataset. They revealed that the GEP model is the superior model. Lu and Mei402 applied a DL approach for predicting excess pore water pressure of two-dimensional soil consolidation using PINN. The effectiveness of the developed approach was evaluated by comparison with the numerical solution of the partial differential equation (PDE) for two-dimensional consolidation. They depicted that the excess pore water pressure could be predicted efficiently using this developed approach. Pandhiani403 applied different ML models, including SVM, M5 Prime (M5P), Gaussian process (GP), RF, and multiple linear regression (MLR) for infiltration rate prediction and compared the result with those of some empirical models such as the Kostiakove model using different error indicators. They revealed that time is the most influential parameter on the infiltration rate compared with sand, silt, density, initial moisture content, etc. In addition, they showed that the RF model outperforms other models.
Prakash et al.404 developed and compared the prediction accuracy of MLP, SVM, and RNN for predicting soil moisture 1, 2, and 7 days ahead. Their finding revealed that the MLP model outperforms other models by a mean square error (MSE) and coefficient of determination (R2) of 0.14 and 0.975 for one day ahead, 0.353 and 0.939 for two days early, and 1.59 and 0.786 for seven days on, respectively. Singh and Gaurav405 compared the prediction accuracy of different ML/DP models for the prediction of surface soil moisture from multi-sensor satellite images. They developed an ANN, a generalized regression neural network (GRNN), a radial basis network (RBN), exact RBN (ERBN), Gaussian process regression (GPR), SVR, RF, boosting ensemble learning (boosting EL), RNN, binary decision tree (BDT), and an automated ML (AutoML) model. Finally, they stated that the ANN model outperforms other models. More papers and information about this subject can be found in Uthayakumar et al.406
Globally, groundwater constitutes a primary drinking water source for approximately 2 billion individuals,420 while in the agricultural sector, around 278.8 million hectares of land are irrigated by groundwater.421 With population and economic growth, the future demand for groundwater is expected to rise.422 However, recognizing that groundwater is a finite resource underscores the imperative of understanding its potential for sustainable utilization. One of the most effective methodologies for managing groundwater resources is the delineation of groundwater potential zones.423
Numerous methodologies exist for groundwater potential mapping, with traditional techniques such as drilling, geological, geophysical, and hydrogeological methods being widely employed.424 However, these methods are often time-consuming and financially burdensome, particularly for expansive areas. In recent years, the integration of geographic information systems (GIS) and remote sensing has been proven instrumental in groundwater potential mapping,425 owing to their capacity to efficiently handle extensive spatial datasets. A sample methodology is given in Fig. 18. This methodology has been used in other fields of study such as groundwater recharge area delineation, groundwater vulnerability assessment, and even flood modeling, landslide occurrences evaluation, and land subsidence spatial mapping.
 | ||
| Fig. 18 Groundwater potential mapping approach using ML models, Khosravi et al.,426 adopted with permission from Copernicus Publications. The flowchart outlines a method involving data collection, analysis, model development, and validation. Initially, groundwater samples are divided into training (70%) and testing (30%) datasets. Key impacting parameters are identified through data correlation and multicollinearity analysis. ML models are then developed using metaheuristic optimization techniques such as invasive weed optimization, differential evolution, the firefly algorithm, PSO, and the bees algorithm. Model performance is evaluated using metrics such as MSE and RMSE, followed by statistical tests (Friedman and Wilcoxon signed-rank) to ensure accuracy. The final goal was to select the optimal model for mapping groundwater spring locations. | ||
Khosravi et al.426 optimized the ANFIS model with five metaheuristic models, including weed optimization (IWO), differential evolution (DE), firefly algorithm (FA), particle swarm optimization (PSO), and the bee's algorithm (BA) for delineating potential groundwater mapping through 2463 spring locations in Koohdasht–Nourabad plain, Iran. They revealed that based on the result of ANFIS–DE as a superior model, 39.33% of the study area has a high and very high groundwater potential north of the plain. In addition, they depicted that based on the finding of the information gain ratio (IGR) technique, land use/land cover, lithology, rainfall, and TWI are among the most efficient factors in groundwater occurrence. Hakim et al.427 compared the prediction accuracy of the CNN and LSTM models to delineate a potential groundwater map in Anseong, South Korea. To meet the aim, a total of 295 well locations were separated using the median value of transmissivity data (T) and assigned “1” as high groundwater productivity data and “0” as the point with low groundwater productivity. Finally, they stated that both models under a receiver operating characteristics (ROC) curve (AUC) of more than 0.80 show good accuracy. Morgan et al.428 applied RF models to delineate potential groundwater zones in the desert fringes of the East Esna-Idfu area, Nile Valley, Egypt. They revealed that the soil type factor has the highest impact on groundwater occurrences. In addition, they showed that the RF model, with an accuracy of 97%, selectivity (recall) of 92%, and F1-score of 94%, has an excellent prediction power in delineating potential groundwater areas.
Khosravi et al.431 modified the DRASTIC model using four statistical/ML models, weights-of-evidence (WOE), Shannon entropy (SE), logistic model tree (LMT), and bootstrap aggregating (BA) to generate a groundwater vulnerability map for the Sari-Behshahr plain, Iran. In addition, they investigated the effectiveness of eight additional factors, including distance to fault, fault density, distance to a river, river density, land use, soil order, geological time scale, and altitude, to improve groundwater vulnerability assessment for the first time as displayed in Fig. 19. They stated that additional factors could enhance the result of groundwater vulnerability assessment. They demonstrated that all models have improved the modeling performance of the original DRASTIC model. Their results showed that considering the input variable for groundwater, vulnerability directly depends on the plain characteristics and the input variable in original models may lead to higher error and need to be removed from the modeling. In another study, Khosravi et al.396 implemented metaheuristic (DE and BBO) and multi-attribute decision-making (MADM), stepwise weight assessment ratio analysis (SWARA), and statistical index (SI) methods to improve the GALDIT model at the Gharesoo-Gorgan Rood coastal aquifer in Iran. Metaheuristic models were used to improve weight, while MADM models were applied to enhance the rating of the GALDIT model. Based on the findings, all models improved the prediction power of GALDIT, while the GALDITSI-DE model outperformed all other models. Their finding showed that integrating intelligent ML-based models can improve the results of empirical models. Ijlil et al.430 developed five hybrid ML models of DRASTIC-RF, DRASTIC-SVM, DRASTIC-MLP, DRASTIC-RF-SVM, and DRASTIC-RF-MLP, for groundwater pollution assessment in the Saiss basin, in Morocco. DRASTIC-RF-MLP (AUC = 0.953) and DRASTIC-RF-SVM (AUC = 0.901) showed higher performance, followed by DRASTIC-RF (AUC = 0.852), DRASTIC-SVM (AUC = 0.802), and DRASTIC-MLP (AUC = 0.763).
 | ||
| Fig. 19 Flowchart of the methodology for groundwater vulnerability assessment, Khosravi et al.,431 adopted with permission from Elsevier. This flowchart outlines a systematic method to analyze nitrate levels in groundwater, focusing on data segmentation, model building, and verification. It starts by evaluating key factors such as groundwater depth, recharge rates, aquifer and soil media, and topography. The DRASTIC method is used to evaluate potential groundwater contamination. Data are divided into two categories based on the nitrate concentration: above and below 50 PPM, with each category split into 70% training and 30% testing datasets for modeling and validation. Model effectiveness is verified through the ROC curve for model performance evaluation and comparison. | ||
4. Challenges and future outlook
This section presents the challenges and future outlook pertinent to the previous chapter. In the field of heat exchanger and storage, research has a rich history dating back to the application of thermal systems in various industries. The extensive volume of currently available data, accumulated over the years, provides a valuable resource for categorization and future predictions through the application of ML approaches. The rapid development of ML technology sparks optimism and enthusiasm for leveraging more sophisticated tools in research, aiming to predict target functions and optimize thermal systems. An exciting avenue for advancement lies in the development of image-processing systems complementing ML methods. Such systems can potentially create online optimization tools on a real scale, reducing reliance on time-consuming numerical modeling. However, a significant challenge arises from the limited availability of comprehensive data, particularly for complex thermal systems or those involving hazardous fluids, posing a potential threat to the reliability of ML outputs. To address this challenge, the deployment of accurate thermal and hydrodynamical sensors is imperative, along with meticulous avoidance of random errors in experiments. Additionally, conducting high-fidelity numerical simulations becomes crucial to prevent the incorporation of noisy and imprecise data into ML models. The careful consideration of feature selection further contributes to refining the accuracy of predictions.One notable concern in ML applications for thermal systems with simple physics is the risk of underfitting. Reliance on heavy numerical simulations and expensive experiments currently hampers the ability to feed a sufficiently large volume of data to ML models, impacting the precision of their outputs. Furthermore, as thermal systems become increasingly integrated into daily life, it becomes crucial to balance ML optimization with customer-friendly necessities, such as appearance and space occupation, to avoid potential adverse effects on marketing. A noteworthy aspect of current ML versions is their lack of interpretability and discussion on the outputs, potentially leading to incorrect interpretations. Despite these challenges, the outlook for ML in thermal science remains optimistic, with the potential for higher precision, reduced data feeding requirements, and improved identification and elimination of noisy input values. The realization of these advancements will largely depend on the continuous development of hardware capabilities.
When it comes to energy storage and combustion using porous media and ML, there are a few challenges and future outlooks to keep in mind. The first challenge is the availability and quality of data. ML algorithms require large amounts of data for training and validation, but obtaining comprehensive and high-quality data for some of the energy storage processes and combustion systems using porous media can be difficult. Limited data availability can affect the accuracy and generalizability of ML models. According to the literature, there is limited research on the integration of ML and geothermal energy storage, thermo-chemical energy storage, natural gas energy storage, and combustion using porous media. Thermochemical energy storage with porous media offers several advantages, including high energy density, long-term storage capability, and reduced heat losses compared to some other storage technologies. However, there are also challenges associated with material selection, reaction kinetics, heat and mass transfer, and system design. Efficient utilization of porous media and optimal reaction conditions are crucial for achieving high storage capacity and fast heat transfer rates. Apart from lithium-ion batteries, experimental data for other batteries such as sodium-ion batteries and potassium-ion batteries are limited and it is hard to use ML to design and characterize battery materials.
Additionally, there are available hybrid energy storage options, such as electrical-gas hybrid energy storage and electrical-gravitational systems. This hybrid system combines electrical energy storage, such as batteries, with hydrogen gas storage using porous media. Excess electricity generates hydrogen through electrolysis and is stored in porous media, such as metal hydrides or adsorbents. When there is an electricity demand, the stored hydrogen can be utilized in a fuel cell to generate electricity. This hybrid storage system allows for the storage of electrical energy in the form of hydrogen, providing longer-duration energy storage and enabling the use of hydrogen as an energy carrier. In another hybrid system, electrical energy storage is combined with gravitational potential energy storage using porous media. Excess electricity is used to lift heavy masses, such as concrete blocks or weights, against gravity, storing the energy as gravitational potential. When electricity demand is high, the potential energy is released, and the weight is lowered, driving a generator to produce electricity. Porous media can be used to support and control the movement of the weights, ensuring efficient energy storage and retrieval. An effective way to overcome this issue is through physics-informed ML (PIML). This approach combines principles from physics-based modeling with ML techniques to enhance the modeling, prediction, and understanding of complex physical systems. By incorporating domain knowledge, physical constraints, and governing equations into the ML framework, PIML recognizes that physical laws and governing equations provide valuable insights into the behavior of physical systems. This approach allows for more robust and interpretable models compared to purely data-driven ML models, as ML models can learn from limited data more effectively and make predictions that align with the underlying physical laws. Overall, PIML aims to leverage the strengths of both disciplines to provide more accurate and insightful predictions for complex physical systems.
Interpretability is also a challenge, especially with deep learning approaches that can be considered black boxes. It's crucial to understand the underlying physical phenomena within the porous media for gaining insights, optimizing system performance, and ensuring safe and reliable operation. Some challenges associated with thermal energy storage using porous media include heat transfer limitations, thermal degradation of the porous media, system efficiency, and economic viability. Overcoming these challenges requires advancements in materials science, system design, and optimization techniques. Another challenge is the complex and nonlinear dynamics of these systems. Modeling and understanding them accurately can be difficult due to the intricate interplay between fluid flow, heat transfer, chemical reactions, and porous media properties. Finally, ensuring the generalization and transferability of ML models across different scenarios and applications is a challenge that needs to be addressed. Energy storage and combustion systems using porous media can exhibit significant variations due to factors such as material properties, operating conditions, and system configurations.
Looking ahead, there are several exciting developments in the field of energy storage and combustion using porous media that are being facilitated by ML techniques. First, ML can greatly enhance the accuracy and optimization of these processes. Advanced algorithms such as deep learning and reinforcement learning can capture complex relationships and improve system performance. Secondly, by extracting valuable insights from large datasets, ML can help us better understand the intricate phenomena that occur within porous media. This understanding can then be used to improve materials, develop better system designs, and optimize operational strategies. Thirdly, ML algorithms can enable real-time control and monitoring of energy storage and combustion systems, allowing for informed decisions and optimized performance. Fourthly, combining ML with experimental and computational methods can lead to more robust and reliable solutions. Finally, ML can also contribute to the development of safer and more sustainable energy storage and combustion systems by identifying potential risks and optimizing safety protocols. Overall, the future of energy storage and combustion using porous media aided by ML is bright. This technology can greatly improve system performance while advancing the adoption of sustainable energy technologies.
In the field of electrochemical devices, although ML has shown practical achievements, its application in porous media in electrochemical devices is still in its early stages, presenting several unexplored research prospects. There is ample opportunity for further advancements in the utilization of ML and DL to enhance the exploration of porous electrocatalysts for electrochemical devices. Additional efforts should be dedicated to advancing novel approaches that can enhance the efficiency and precision of ML in the identification of prospective porous electrocatalysts. Due to the intricate nature of the fuel cell system, current ML algorithms fall short of meeting the demands for both superior performance and cost-effectiveness. Consequently, there is a need for new ML methodologies to enhance the overall system performance. Supervised learning currently dominates the field of ML applications, requiring researchers to gather extensive sets of annotated data to train ML models. Whether obtained through resource-intensive high-throughput experiments or computationally demanding numerical simulations, the associated costs are significant. To tackle this challenge, new approaches need to be proposed. The integration of AI technologies is expected to enable the targeted design of porous media, provide guidance for experimental synthesis, validate predicted outcomes, and greatly advance the field of electrocatalysis.
Research into the manufacturing steps of LIBs, including electrolyte infiltration, formation, and electrochemical performance, continues to be a dynamic field where ML has demonstrated its potential. However, several challenges persist that necessitate further exploration and innovation. Notably, the robustness and adaptability of ML models for real-world applications need ongoing refinement and validation. These models must evolve to improve the accuracy of quantifying active material volume fractions, accommodate non-spherical particle morphologies, and address intricacies related to estimating the properties of actual electrodes, particularly in scenarios involving highly aligned platelets and high current densities. Bridging the gap between simulated and real microstructure data remains an important endeavor. To this end, the integration of additional data sources and the creation of accurate representations for reconstructed models are imperative. Furthermore, enhancing the computational efficiency of deep learning models for real-time battery management systems is paramount. As we look to the future, addressing these challenges will contribute to elevating the performance, longevity, and safety of LIBs across various applications.
Research in RFBs has made significant strides in optimizing various components, aided by the application of ML techniques. However, several challenges persist, and the path forward is marked by ongoing exploration and innovation. One critical challenge is the need for more realistic and manufacturable microstructures in electrode optimization. The assumptions made during microstructure generation, though helpful in discovering superior microstructures, may impact the practicality of their implementation. Future research should focus on bridging the gap between idealized designs and real-world manufacturability. Additionally, the generalizability of results in studies involving a limited number of simulations or small datasets needs to be addressed to ensure the applicability of findings to diverse scenarios. Furthermore, the characterization of electrode microstructure remains an essential aspect, and improvements in control and accuracy are vital for more precise estimations of specific surface area and porosity. In terms of future work, the optimization of manufacturing parameters, especially in designing porous materials for enhanced ion transport, remains a primary focus. ML offers the potential to revolutionize the design of porous materials to achieve specific transport characteristics. Moreover, the mechanical strength, heat transfer, and electron transfer properties of microstructures play pivotal roles in RFB performance. ML applications are well-suited to fine-tuning microstructure designs for improved strength, heat management, and electron transfer efficiency, thus advancing the overall capabilities of redox flow batteries.
ML techniques have been successfully applied to use existing literature data to optimize the properties of supercapacitor electrodes. Although there is still some scope for improvement in material performance by first creating accurate and valid physics-based models and then subsequently training neural networks on the performance metrics of those models to create fast surrogate-based models, these models should then be free of experimental error, noise, or inconsistency in experimental data reporting, allowing the microstructure of supercapacitor electrodes to be optimized. ML will likely be an invaluable tool for screening chemical compositions and structures for more durable cycle lifetimes and specific capacitance.
The oil and gas industry has always been at the forefront of technological advancements. With the advent of ML, the industry has been presented with new challenges that need to be addressed before ML can be fully integrated into the industry. One of the challenges of using ML in reservoir engineering is the lack of physical nature of ML algorithms. ML algorithms are data-driven and rely on finding patterns and correlations in data to make predictions. However, these algorithms do not inherently incorporate the underlying physical principles that govern the behavior of reservoirs. This can result in models that are not able to accurately capture the complex phenomena that occur in subsurface reservoirs. In contrast, traditional reservoir simulation models are based on physical equations that describe the flow of fluids through porous media. While these models can be computationally expensive and require a high level of expertise to develop and use, they can accurately capture the underlying physics of reservoir behavior. The lack of physical nature of ML algorithms can result in models that are less accurate and less reliable than traditional simulation models. To address this challenge, it is suggested to work on developing hybrid approaches, such as PIML, that combine ML with traditional simulation methods. These approaches aim to leverage the strengths of both methods to develop more accurate and reliable models for reservoir engineering.
Data quality and quantity are other issues mentioned in previous research. ML algorithms rely on large amounts of high-quality data to make accurate predictions. Data quality refers to the accuracy and reliability of the data used to train machine learning models. In reservoir engineering, data are often collected from sensors and instruments that are deployed in the field. These sensors can be subject to various sources of error, such as measurement noise, calibration errors, and environmental interference. As a result, the data collected may not accurately reflect the true state of the reservoir. One way to improve data quality is by implementing rigorous data validation and cleaning processes to help identify and correct errors in the data. Furthermore, data is often collected at discrete points in time and space. This can result in sparse datasets that do not provide enough information to accurately capture the complex behavior of subsurface reservoirs. Using data augmentation techniques to produce synthetic data can increase data quantity. These techniques use existing data to generate new data that are similar but not identical to the original data. This can help enlarge the size of the dataset and enhance the accuracy of ML models.
Transfer learning has the potential to address some of the challenges associated with using ML in reservoir engineering, such as data scarcity. By leveraging knowledge gained from other reservoirs, transfer learning can help improve the accuracy and reliability of ML models in reservoir engineering. Transfer learning is an ML technique that allows the knowledge gained from one task to be applied to another related task. This can help enhance the performance of ML models when there is limited data available for the new task. Transfer learning could be used to apply knowledge gained from one reservoir to another similar reservoir. In other words, if a machine learning model has been trained on data from one reservoir to predict production rates, transfer learning could be used to apply this knowledge to another reservoir with similar characteristics. This could help enhance the accuracy of the model and lower the amount of data needed to train the model on the new reservoir. In a nutshell, solving ML challenges in hydrocarbon reservoirs requires a combination of domain expertise and technical skills in areas such as data science and reservoir engineering. By leveraging advanced analytics tools, it is possible to gain valuable insight into reservoir behavior that can help improve production and efficiency and reduce costs over time.
For carbon capture and sequestration, there are still certain obstacles to be overcome, despite the recent successes, for the field to reach new levels. Prospects would be illustrated for investigation in using ML to create porous materials, adsorption techniques, and carbon capture optimization, as well as potential solutions to these problems. Despite the feasible extraction of meaningful experimental data from the literature's papers, the calculating techniques would result in a significant amount of information being lost. It is recommended that they be standardized in order to disseminate the technique, basic information, and outcomes more effectively in detail. A different recommendation is to digitize lab notes in ML-code formats for future research and extensive data communication. This approach would be helpful and extend the rapid expansion of materials science data communities. Large-scale, high-quality experimental and computational data are necessary for developing ML models that function robustly and generally. Getting enough data in the field of materials science, particularly for computational and experimental purposes, requires a cost impact. To deal with the lack of data, new approaches have been developed, such as transfer learning, data wrapping, augmentation, and dimension transformation. Traditionally, finding, gathering, and interpreting literature takes a lot of effort and time. Natural language processing (NLP) has recently made it feasible to automatically gather data for creating a materials database so that it can be more effectively incorporated into ML workflows for material design and experimental mechanization. Therefore, autonomous literature extraction of porous media for carbon capture using NLP will be an exciting approach. The last issue is that gathering experimental data is expensive because training ML models with adequate prediction accuracy often necessitates a large volume of data. To overcome the issues outlined above, researchers have recently begun to merge physics-based principles with ML models. These methods embed physical limitations, cutting-edge physics-based normalization, symmetries, invariances, and equivariants into ML models, which could improve generalizing, speed up training, and improve transparency. Advancements in materials research and adsorption/absorption process optimization for carbon capture are expected to be fueled by the field's research developments.
In the field of groundwater resources, modeling natural resources and water-related issues using ML is very popular. Based on the literature review for all aspects of water science, several items and steps significantly impact the modeling performance of ML models. These are data quality, length, splitting ratio, hyperparameter tuning, optimum input variables, hybridization/ensemble, and model prediction power (model structure). Also, in each literature review, authors stated that their models are robust and have high accuracy; therefore, selection of an optimum model is challenging. Data quality has a significant impact on other models (numerical, physically based, etc.) and has a meaningful effect on ML models. Involving poor-quality data can bring about degradation in the findings and have further consequences when decisions are made on those results. The length of the dataset is another important and influential factor in modeling prediction power. The larger the data, the higher the probability of extracting trends, and finally, the higher the prediction power of models.
ML models are attracting the interest of researchers, and their implementation is on the rise. The issue with ML models is that they need to consider the physics underlying catchment modeling, which must still be addressed. In addition, the implementation of need-based physical models and the vast quantity of data persist. In certain situations, their integration is highly recommended, such as the prediction of missing data and the prediction of unavailable data (e.g., inadequate data capture) or the prediction of some input parameters such as effective rainfall via Identification of unit Hydrographs and Component flows from Rainfall, Evaporation and Streamflow data (IHACRES) model and feed to ML models.
It is worth mentioning that for further knowledge and reading, a list of available online databases in the six fields of the review is given in Table S1 of the ESI,† which can be used as an exercise to train ML models with the relevant data given in these databases. Also, all the reviewed literature in the manuscript is displayed as spreadsheets containing relevant information on each of the references in the ESI.†
5. Conclusion
The review paper provided an overview of the present status quo of the interface of ML and porous media in six different applications, namely, heat exchanger and storage, energy storage and combustion, electrochemical devices, hydrocarbon reservoirs, CCS, and groundwater resources. A comprehensive elaboration of different ML models employed in the study of porous media such as supervised learning, unsupervised learning, and deep learning methods was carried out. Additionally, particular models that have been deployed, such as decision trees, random forests, support vector machines, and neural networks, followed by evaluation metrics, were noted. The advances made in the application of ML to porous media were stressed and insights into the challenges and opportunities for future research were offered. In the realm of heat transfer research, ML holds promise for predicting target functions and optimizing thermal systems through the extensive available data. Challenges arise in image processing systems due to limited comprehensive data for complex thermal systems, urging the deployment of accurate sensors and high-fidelity numerical simulations to enhance ML reliability. In energy storage and combustion, ML faces challenges such as limited data availability for various storage processes and combustion systems. PIML models are proposed to address complexities in material selection and reaction kinetics. Electrochemistry applications of ML are in the early stages, with opportunities for enhancing the exploration of porous electrocatalysts, and challenges include the need for new ML methodologies to improve fuel cell system performance. ML in hydrocarbon reservoirs encounters challenges due to its lack of inherent physical principles, supporting hybrid approaches such as PIML. CCS faces obstacles related to data standardization, digitization, and the cost impact of obtaining high-quality experimental data. In the groundwater resources framework, there are challenges and crucial considerations, including data quality and dataset length. It is concluded that the application of ML in a spectrum of fields holds promise for optimizing systems and processes, but it also faces challenges. These challenges include the need for high-quality data, addressing the lack of physical nature in ML algorithms, and finding ways to overcome data scarcity. Despite these obstacles, there is an opportunity to improve accuracy and efficiency through hybrid approaches that combine ML with physics-based principles. The outlook for ML in these domains is optimistic, with a focus on enhancing precision, reliability, and sustainability, as well as addressing ongoing issues related to data quality and the integration of physical principles, contingent on continuous hardware processing development. Ongoing research and innovation are essential to harness the full potential of machine learning in these fields.Abbreviations
| AAPE | Average absolute percentage error |
| AC | Activated carbon |
| ADLSTM | Adaptive dropout long short-term memory |
| AE | Activation energy |
| AEM | Anion exchange membrane |
| AHM | Automatic history matching |
| AI | Artificial intelligence |
| ANN | Artificial neural network |
| APS | Average pore size |
| ARM | Association rule mining |
| ASL | Airway surface liquid |
| BET | Brunauer, Emmett, and Teller |
| BiLSTM | Bidirectional long short-term memory |
| BLR | Bayesian linear regression |
| BP | Back-propagation |
| BPNNs | Back propagation neural networks |
| BRR | Bayesian ridge regression |
| BWDPCs | Biomass waste-derived porous carbons |
| CBM | Coalbed methane |
| CCL | Cathode catalyst layer |
| CCS | Carbon capture and sequestration |
| CCST | Carbon capture or separation technology |
| CCSTU | Carbon capture, storage, transport, and utilization |
| CCUS | Carbon capture, utilization, and storage |
| CFD | Computational fluid dynamics |
| CGP | Cumulative gas production |
| CHP | Combined heat and power |
| CL | Catalyst layer |
| CNN | Convolutional neural network |
| COBYLA | Constrained optimization by linear approximation |
| COFs | Covalent organic frameworks |
| COP | Coefficient of performance |
| CT | Computed tomography |
| Da | Damkohler number |
| DCA | Decline curve analysis |
| DCGAN | Deep convolutional generative adversarial network |
| DFT | Density functional theory |
| DL | Deep learning |
| DNN | Deep neural network |
| DNS | Direct numerical simulation |
| DT | Decision tree |
| DTR | Decision tree regression |
| ECPEM | Evaluation criterion of the proton exchange membrane |
| EES | Electrochemical energy storage |
| EOR | Enhanced oil recovery |
| ERT | Extremely randomized tree |
| FFNN | Feed-forward neural network |
| FIB-SEM | Focused ion beam scanning electron microscopy |
| FOV | Field-of-view |
| GA | Genetic algorithm |
| GAN | Generative adversarial network |
| GBDT | Gradient boosting decision tree |
| GBR | Gradient boosting regression |
| GBM | Gradient boosting machine |
| GCMC | Grand canonical Monte Carlo |
| GDL | Gas diffusion layer |
| GPR | Gaussian process regression |
| GRNN | Generalized regression neural network |
| GRU | Gated recurrent unit |
| HER | Hydrogen evolution reaction |
| HDPCs | Heteroatom-doped porous carbons |
| HOLE | Highly ordered laser-patterned electrode |
| HPC | High-performance computing |
| HVAC | Heating, ventilation, and air conditioning |
| IGWO | Improved gray wolf optimizer |
| IOR | Improved oil recovery |
| IPCC | Intergovernmental panel on climate change |
| KELM | Kernel extreme learning machines |
| KNN | k-Nearest neighbors |
| KNR | k-Nearest neighbor regression |
| LASSO | Least absolute shrinkage and selection operator |
| LBM | Lattice Boltzmann method |
| LGB | Light gradient boosting |
| LIBs | Lithium-ion batteries |
| LIME | Local interpretable model-agnostic explanations |
| LINMAP | Linear programming technique for multidimensional analysis of preference |
| LM | Levenberg–Marquardt |
| LR | Linear regression |
| LSSVM | Least-squares support vector machine |
| LSTM | Long short-term memory |
| M&V | Monitoring and verification |
| MAE | Mean absolute error |
| MAPE | Mean absolute prediction error |
| MC | Monte Carlo |
| MDDFs | Minimum distance distribution functions |
| MFO | Moth-flame optimizer |
| MICE | Multivariate imputation by chained equations |
| ML | Machine learning |
| MLP | Multi-layer perceptron |
| MLR | Multi linear regression |
| MLP-NN | Multi-layer perceptron neural network |
| MMMs | Mixed matrix membranes |
| MMP | Minimum miscible pressure |
| MOF | Metal–organic framework |
| MPV | Micropore volume |
| MSE | Mean squared error |
| NDCs | Nitrogen-doped catalysts |
| NLP | Natural language processing |
| NNP | Neural network potential |
| NPV | Net present value |
| NSGA | Non-dominating sorting genetic algorithm |
| ODE | Ordinary differential equation |
| OER | Oxygen evolution reaction |
| OMSs | Open metal sites |
| ORR | Oxygen reduction reaction |
| PBI | Polybenzimidazole |
| PCA | Principal component analysis |
| PCM | Phase change material |
| PDE | Partial differential equation |
| PEC | Performance evaluation criteria |
| PEI | Polyethyleneimine |
| PEM | Proton exchange membrane |
| PEMFC | Proton exchange membrane fuel cell |
| PEMWE | Proton exchange membrane water electrolyzer |
| PIML | Physics-informed machine learning |
| PINN | Physics-informed neural network |
| PLS | Partial least squares |
| PNM | Pore network modeling |
| POD-TPWL | Proper orthogonal decomposition and trajectory piecewise linearization |
| PSA | Pressure swing adsorption |
| PSO | Particle swarm optimization |
| PSPM | Pore-scale porous media |
| PTL | Porous transport layer |
| RBF | Radial basis function |
| REPT | Reduced error pruning trees |
| RF | Random forest |
| RFR | Random forest regression |
| RMSE | Root mean squared error |
| RNN | Recurrent neural network |
| ROM | Reduced order models |
| RPCs | Regular porous carbons |
| RSM | Response surface methodology |
| RUL | Remaining useful life |
| SACs | Single-atom catalysts |
| SBUs | Secondary building units |
| SCG | Scaled conjugate gradient |
| SCR | Selective catalytic reduction |
| SDGs | Sustainable development goals |
| SHAP | Shapley additive explanations |
| SML | Supervised machine learning |
| SmVAE | Supramolecular variational autoencoder |
| SoC | State-of-charge |
| SOFCs | Solid oxide fuel cells |
| SoH | State-of-health |
| SOM | Self-organizing map |
| SPC | Straw pyrolytic carbon |
| SRM | Surrogate reservoir model |
| SSA | Specific surface area |
| SVM | Support vector machine |
| SVR | Support vector regression |
| TCES | Thermochemical energy storage |
| TEPA | Tetraethylenepentamine |
| TES | Thermal energy storage |
| TOC | Total organic carbon |
| TOPSIS | Technique for order of preference by similarity to ideal solution |
| TSA | Temperature swing adsorption |
| VE | Voltage efficiency |
| VSA | Vacuum swing adsorption |
| XGBoost | Extreme gradient boosting |
Author contributions
Writing – original draft: 1. Introduction: M.D.; 2. Background on machine learning and porous media: S. M. A & H. Y.; 3.1. Heat exchanger and storage: A. F.; 3.2. Energy storage and combustion: B. E.; 3.3. Electrochemical devices: M. G., J. S., & D. N.; 3.4. Hydrocarbon reservoirs: M. S. & H. M.; 3.5. Carbon capture and sequestration: H. M., M. A. A., & A. E.; 3.6. Groundwater: K. K. & S. R. Writing – review & editing: M. D., B. E., V. N. & M. M. Funding acquisition: M. D. & M. M. Conceptualization, methodology, supervision, & project administration: M. D.Conflicts of interest
The authors declare there are no conflicts of interest.Acknowledgements
The authors would like to acknowledge the UK Engineering and Physical Sciences Research Council (EPSRC) Project through the project number EP/W005204/1.References
- Z. Niu, V. J. Pinfield, B. Wu, H. Wang, K. Jiao, D. Y. C. Leung and J. Xuan, Energy Environ. Sci., 2021, 14, 2549–2576 RSC.
- S. M. Moosavi, B. Á. Novotny, D. Ongari, E. Moubarak, M. Asgari, Ö. Kadioglu, C. Charalambous, A. Ortega-Guerrero, A. H. Farmahini, L. Sarkisov, S. Garcia, F. Noé and B. Smit, Nat. Mater., 2022, 21, 1419–1425 CrossRef CAS.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- N. Heinemann, J. Alcalde, J. M. Miocic, S. J. T. Hangx, J. Kallmeyer, C. Ostertag-Henning, A. Hassanpouryouzband, E. M. Thaysen, G. J. Strobel, C. Schmidt-Hattenberger, K. Edlmann, M. Wilkinson, M. Bentham, R. Stuart Haszeldine, R. Carbonell and A. Rudloff, Energy Environ. Sci., 2021, 14, 853–864 RSC.
- Y. Wang, Y. Pang, H. Xu, A. Martinez and K. S. Chen, Energy Environ. Sci., 2022, 15, 2288–2328 RSC.
- M. Bastos-Neto, C. Patzschke, M. Lange, J. Möllmer, A. Möller, S. Fichtner, C. Schrage, D. Lässig, J. Lincke, R. Staudt, H. Krautscheid and R. Gläser, Energy Environ. Sci., 2012, 5, 8294–8303 RSC.
- L. Bu, F. Ning, J. Zhou, C. Zhan, M. Sun, L. Li, Y. Zhu, Z. Hu, Q. Shao, X. Zhou, B. Huang and X. Huang, Energy Environ. Sci., 2022, 15, 3877–3890 RSC.
- P. P. Mukherjee, Q. Kang and C. Y. Wang, Energy Environ. Sci., 2011, 4, 346–369 RSC.
- S. Haussener, C. Xiang, J. M. Spurgeon, S. Ardo, N. S. Lewis and A. Z. Weber, Energy Environ. Sci., 2012, 5, 9922–9935 RSC.
- X. Lu, T. Li, A. Bertei, J. I. S. Cho, T. M. M. Heenan, M. F. Rabuni, K. Li, D. J. L. Brett and P. R. Shearing, Energy Environ. Sci., 2018, 11, 2390–2403 RSC.
- Q. Lyu, J. Tan, L. Li, Y. Ju, A. Busch, D. A. Wood, P. G. Ranjith, R. Middleton, B. Shu, C. Hu, Z. Wang and R. Hu, Energy Environ. Sci., 2021, 14, 4203–4227 RSC.
- F. M. Orr, Energy Environ. Sci., 2009, 2, 449–458 RSC.
- S. L. Candelaria, R. Chen, Y. H. Jeong and G. Cao, Energy Environ. Sci., 2012, 5, 5619–5637 RSC.
- R. S. Middleton, G. N. Keating, P. H. Stauffer, A. B. Jordan, H. S. Viswanathan, Q. J. Kang, J. W. Carey, M. L. Mulkey, E. J. Sullivan, S. P. Chu, R. Esposito and T. A. Meckel, Energy Environ. Sci., 2012, 5, 7328–7345 RSC.
- Y. Yan, T. N. Borhani, S. G. Subraveti, K. N. Pai, V. Prasad, A. Rajendran, P. Nkulikiyinka, J. O. Asibor, Z. Zhang, D. Shao, L. Wang, W. Zhang, Y. Yan, W. Ampomah, J. You, M. Wang, E. J. Anthony, V. Manovic and P. T. Clough, Energy Environ. Sci., 2021, 14, 6122–6157 RSC.
- W. Zhi, D. Feng, W.-P. Tsai, G. Sterle, A. Harpold, C. Shen and L. Li, Environ. Sci. Technol., 2021, 55, 2357–2368 CrossRef CAS PubMed.
- A. M. Norouzi, M. Babaei, W. S. Han, K. Y. Kim and V. Niasar, Chem. Eng. J., 2021, 425, 130031 CrossRef CAS.
- L. Hashemi, M. Blunt and H. Hajibeygi, Sci. Rep., 2021, 11, 8348 CrossRef CAS PubMed.
- S. Caré, R. Crane, P. S. Calabrò, A. Ghauch, E. Temgoua and C. Noubactep, Clean, 2013, 41, 275–282 Search PubMed.
- Md. S. Hossain, L. I. Stephens, M. Hatami, M. Ghavidel, D. Chhin, J. I. G. Dawkins, L. Savignac, J. Mauzeroll and S. B. Schougaard, ACS Appl. Energy Mater., 2020, 3, 440–446 CrossRef CAS.
- J. Lin, Z. Liu, Y. Guo, S. Wang, Z. Tao, X. Xue, R. Li, S. Feng, L. Wang, J. Liu, H. Gao, G. Wang and Y. Su, Nano Today, 2023, 49, 101802 CrossRef.
- T. Yasuda, S. Ookawara, S. Yoshikawa and H. Matsumoto, Chem. Eng. J., 2023, 453, 139540 CrossRef CAS.
- D. A. Nield and A. Bejan, in Convection in Porous Media, Springer International Publishing, Cham, 2017, pp. 1–35 Search PubMed.
- N. Nishiyama and T. Yokoyama, J. Geophys. Res.: Solid Earth, 2017, 122, 6955–6971 CrossRef.
- J. M. McKinley, Encyclopedia of Mathematical Geosciences: Encyclopedia of Earth Sciences Series, ed. B. S. Daya Sagar, Q. Cheng, J. McKinley and F. Agterberg, 2022, pp. 1–3 Search PubMed.
- C. Wang, Y. Mehmani and K. Xu, Proc. Natl. Acad. Sci. U. S. A., 2021, 118 DOI:10.1073/pnas.2024069118.
- S. Bakhshian, Z. Shi, M. Sahimi, T. T. Tsotsis and K. Jessen, Sci. Rep., 2018, 8, 8249 CrossRef.
- S. Fagbemi, P. Tahmasebi and M. Piri, Water Resour. Res., 2018, 54, 6336–6356 CrossRef.
- M. E. Rosti, S. Pramanik, L. Brandt and D. Mitra, Soft Matter, 2020, 16, 939–944 RSC.
- M. Kohr and G. P. R. Sekhar, Eng. Anal. Bound. Elem., 2007, 31, 604–613 CrossRef.
- A. Lenci, F. Zeighami and V. Di Federico, Transp. Porous Media, 2022, 144, 459–480 CrossRef.
- K.-K. Phoon, T.-S. Tan and P.-C. Chong, Geotech. Geol. Eng., 2007, 25, 525–541 CrossRef.
- Y. Da Wang, T. Chung, R. T. Armstrong and P. Mostaghimi, Transp. Porous Media, 2021, 138, 49–75 CrossRef.
- M. R. M. Talabis, R. McPherson, I. Miyamoto, J. L. Martin and D. Kaye, in Information Security Analytics, Elsevier, 2015, pp. 1–12 Search PubMed.
- H. Huo, Z. Rong, O. Kononova, W. Sun, T. Botari, T. He, V. Tshitoyan and G. Ceder, npj Comput. Mater., 2019, 5, 62 CrossRef.
- K. M. Jablonka, D. Ongari, S. M. Moosavi and B. Smit, Chem. Rev., 2020, 120, 8066–8129 CrossRef CAS PubMed.
- J. Abdi, F. Hadavimoghaddam, M. Hadipoor and A. Hemmati-Sarapardeh, Sci. Rep., 2021, 11, 24468 CrossRef CAS PubMed.
- A. Banerjee, S. Pasupuleti, K. Mondal and M. M. Nezhad, Int. J. Heat Mass Transfer, 2021, 179, 121650 CrossRef.
- D. Thakur, A. Chandel and V. Shankar, Water Pract. Technol., 2022, 17, 2625–2638 CrossRef.
- S. M. Alirahmi, S. F. Mousavi, P. Ahmadi and A. Arabkoohsar, Energy, 2021, 236, 121412 CrossRef.
- A. C. Cinar, Arabian J. Sci. Eng., 2020, 45, 10915–10938 CrossRef.
- S. M. Alirahmi and A. Ebrahimi-Moghadam, Appl. Energy, 2022, 323, 119545 CrossRef CAS.
- K. Kim, W. H. Lee, J. Na, Y. J. Hwang, H. S. Oh and U. Lee, J. Mater. Chem. A, 2020, 8, 16943–16950 RSC.
- R. Ding, Y. Ding, H. Zhang, R. Wang, Z. Xu, Y. Liu, W. Yin, J. Wang, J. Li and J. Liu, J. Mater. Chem. A, 2021, 9, 6841–6850 RSC.
- Ş. Neaţu, F. Neaţu, I. M. Chirica, I. Borbáth, E. Tálas, A. Tompos, S. Somacescu, P. Osiceanu, M. A. Folgado, A. M. Chaparro and M. Florea, J. Mater. Chem. A, 2021, 9, 17065–17128 RSC.
- S. Jha, M. Yen, Y. S. Salinas, E. Palmer, J. Villafuerte and H. Liang, J. Mater. Chem. A, 2023, 11, 3904–3936 RSC.
- N. Zobeiry and K. D. Humfeld, Eng. Appl. Artif. Intell., 2021, 101, 104232 CrossRef.
- S. Keykhah, E. Assareh, R. Moltames, M. Izadi and H. M. Ali, Phys. A, 2020, 545, 123804 CrossRef CAS.
- F. Selimefendigil, S. O. Coban and H. F. Öztop, Int. J. Therm. Sci., 2022, 172, 107286 CrossRef.
- N. A. Khan, M. Sulaiman and F. S. Alshammari, Struct. Multidisc. Optim., 2022, 65, 1–14 CrossRef.
- Y. Ge, Z. Liu and W. Liu, Int. J. Heat Mass Transfer, 2016, 101, 981–987 CrossRef.
- Z. I. Butt, I. Ahmad, H. Ilyas, M. Shoaib and M. A. Z. Raja, Int. J. Hydrogen Energy, 2023, 48, 16100–16131 CrossRef CAS.
- I. Ahmad, H. Zahid, F. Ahmad, M. A. Z. Raja and D. Baleanu, Chin. J. Phys., 2019, 59, 641–655 CrossRef.
- Y. Su, T. Ng, Z. Li and J. H. Davidson, Chem. Eng. J., 2020, 397, 125257 CrossRef CAS.
- M. A. Z. Raja, M. Shoaib, Z. Khan, S. Zuhra, C. A. Saleel, K. S. Nisar, S. Islam and I. Khan, Ain Shams Eng. J., 2022, 13, 101573 CrossRef.
- I. Ahmad, H. Ilyas, M. A. Z. Raja, Z. Khan and M. Shoaib, Surf. Interfaces, 2021, 26, 101403 CrossRef.
- U. Sajjad, I. Hussain, K. Hamid, S. A. Bhat, H. M. Ali and C. C. Wang, J. Therm. Anal. Calorim., 2021, 145, 1911–1923 CrossRef CAS.
- M. Singh, R. Ragoju, G. Shiva Kumar Reddy and C. Subramani, Phys. Fluids, 2023, 35, 34103 CrossRef CAS.
- H. Pourrahmani, M. Moghimi, M. Siavashi and M. Shirbani, Appl. Therm. Eng., 2019, 150, 433–444 CrossRef.
- R. Alizadeh, J. M. N. Abad, A. Ameri, M. R. Mohebbi, A. Mehdizadeh, D. Zhao and N. Karimi, J. Taiwan Inst. Chem. Eng., 2021, 124, 290–306 CrossRef CAS.
- M. Alhadri, J. Raza, U. Yashkun, L. A. Lund, C. Maatki, S. U. Khan and L. Kolsi, J. Indian Chem. Soc., 2022, 99, 100607 CrossRef CAS.
- J. Mohebbi Najm Abad, R. Alizadeh, A. Fattahi, M. H. Doranehgard, E. Alhajri and N. Karimi, J. Mol. Liq., 2020, 313, 113492 CrossRef CAS.
- M. M. Rajabi, M. R. Hajizadeh Javaran, A. oury Bah, G. Frey, F. Le Ber, F. Lehmann and M. Fahs, Int. J. Heat Mass Transfer, 2022, 183, 122131 CrossRef.
- R. A. Khan, H. Ullah, M. A. Z. Raja, M. A. R. Khan, S. Islam and M. Shoaib, Int. Commun. Heat Mass Transfer, 2021, 126, 105436 CrossRef CAS.
- B. Yang, X. Zhu, B. Wei, M. Liu, Y. Li, Z. Lv and F. Wang, Energies, 2023, 16, 1500 CrossRef.
- M. Siavashi, H. R. Talesh Bahrami and E. Aminian, Appl. Therm. Eng., 2018, 138, 465–474 CrossRef CAS.
- J. H. Meng, Y. Liu, X. H. Zhu, Z. J. Yang, K. Zhang and G. Lu, Energy Convers. Manage., 2022, 273, 116404 CrossRef.
- H. R. Abbasi, E. Sharifi Sedeh, H. Pourrahmani and M. H. Mohammadi, Appl. Therm. Eng., 2020, 180, 115835 CrossRef.
- T. S. Athith, G. Trilok, P. H. Jadhav and N. Gnanasekaran, Mater. Today: Proc., 2022, 51, 1642–1648 CAS.
- S. Chen, J. Mao, F. Chen, P. Hou and Y. Li, Int. J. Heat Mass Transfer, 2018, 117, 617–626 CrossRef.
- Z. J. Zheng, M. J. Li and Y. L. He, Int. J. Heat Mass Transfer, 2015, 87, 376–379 CrossRef.
- M. H. Mohammadi, H. R. Abbasi, A. Yavarinasab and H. Pourrahmani, Appl. Therm. Eng., 2020, 170, 115005 CrossRef.
- G. Baiocco, V. Tagliaferri and N. Ucciardello, Procedia CIRP, 2017, 62, 518–522 CrossRef.
- T. Deshamukhya, D. Bhanja, S. Nath and S. A. Hazarika, J. Mech. Sci. Technol., 2018, 32, 4495–4502 CrossRef.
- T. H. Wang, H. C. Wu, J. H. Meng and W. M. Yan, Int. J. Heat Mass Transfer, 2020, 149, 119217 CrossRef.
- Ö. Bayer, S. Baghaei Oskouei and S. Aradag, Int. Commun. Heat Mass Transfer, 2022, 134, 105984 CrossRef.
- R. Khosravi, M. Zamaemifard, S. Safarzadeh, M. Passandideh-Fard, A. R. Teymourtash and A. Shahsavar, Eng. Anal. Bound. Elem., 2023, 150, 259–271 CrossRef.
- H. K. Ghritlahre and R. K. Prasad, Therm. Sci. Eng. Prog., 2018, 6, 226–235 CrossRef.
- S. Du, Y. L. He, W. W. Yang and Z. Bin Liu, Int. J. Heat Mass Transfer, 2018, 122, 383–390 CrossRef.
- Z. J. Zheng, Y. Xu and Y. L. He, Sci. China: Technol. Sci., 2016, 59, 1475–1485 CrossRef CAS.
- F. Hosseini and M. Siavashi, Sol. Energy, 2021, 230, 208–221 CrossRef CAS.
- A. Grosjean, A. Soum-Glaude, P. Neveu and L. Thomas, Sol. Energy Mater. Sol. Cells, 2018, 182, 166–177 CrossRef CAS.
- S. Du, T. Xia, Y. L. He, Z. Y. Li, D. Li and X. Q. Xie, Appl. Energy, 2020, 275, 115343 CrossRef.
- H. K. Ghritlahre and R. K. Prasad, Energy Procedia, 2017, 109, 369–376 CrossRef.
- A. Li, A. C. Y. Yuen, W. Wang, T. B. Y. Chen, C. S. Lai, W. Yang, W. Wu, Q. N. Chan, S. Kook and G. H. Yeoh, Batteries, 2022, 8, 69 CrossRef CAS.
- J. Duan and F. Li, J. Energy Storage, 2021, 33, 102160 CrossRef.
- A. Tikadar and S. Kumar, Int. J. Heat Mass Transfer, 2022, 199, 123438 CrossRef CAS.
- H. Ilyas, I. Ahmad, M. A. Z. Raja, M. B. Tahir and M. Shoaib, Int. J. Hydrogen Energy, 2021, 46, 28298–28326 CrossRef CAS.
- Z. I. Butt, I. Ahmad, M. Shoaib, H. Ilyas and M. A. Z. Raja, Int. Commun. Heat Mass Transfer, 2023, 140, 106516 CrossRef CAS.
- N. Bianco, M. Iasiello, G. M. Mauro and L. Pagano, Appl. Therm. Eng., 2021, 182, 116058 CrossRef.
- T. Deshamukhya, D. Bhanja and S. Nath, Neural Comput. Appl., 2021, 33, 12605–12619 CrossRef.
- S. Dathathri and C. Balaji, Int. Commun. Heat Mass Transfer, 2015, 60, 32–36 CrossRef.
- M. Shoaib, T. Rafia, M. A. Z. Raja, W. A. Khan and M. Waqas, J. Braz. Soc. Mech. Sci. Eng., 2022, 44, 1–21 CrossRef.
- C. Yang, Y. Xu, X. Cai and Z. J. Zheng, Int. J. Heat Mass Transfer, 2022, 196, 123309 CrossRef.
- W. Cui, T. Si, X. Li, X. Li, L. Lu, T. Ma and Q. Wang, Energy Reports, 2022, 8, 10203–10218 CrossRef.
- K. Anand, A. Bhardwaj, S. Chaudhuri and V. K. Mishra, Arabian J. Sci. Eng., 2022, 47, 15175–15194 CrossRef.
- N. Alqahtani, F. Alzubaidi, R. T. Armstrong, P. Swietojanski and P. Mostaghimi, J. Pet. Sci. Eng., 2020, 184, 106514 CrossRef CAS.
- A. Eghtesad, F. Tabassum and S. Hajimirza, Int. J. Heat Mass Transfer, 2023, 205, 123890 CrossRef.
- H. Wei, H. Bao and X. Ruan, Int. J. Heat Mass Transfer, 2020, 160, 120176 CrossRef.
- V. K. Mishra, S. C. Mishra and D. N. Basu, Numer. Heat Transfer, Part A, 2017, 71, 677–692 CrossRef CAS.
- R. Singh, R. S. Bhoopal and S. Kumar, Build. Environ., 2011, 46, 2603–2608 CrossRef.
- M. Laimon, T. Yusaf, T. Mai, S. Goh and W. Alrefae, Int. J. Thermofluids, 2022, 15, 100161 CrossRef.
- B. Ebrahimpour and M. Behshad Shafii, Sol. Energy, 2022, 247, 453–467 CrossRef.
- A. G. Olabi, C. Onumaegbu, T. Wilberforce, M. Ramadan, M. A. Abdelkareem and A. H. Al-Alami, Energy, 2021, 214, 118987 CrossRef CAS.
- D. Ranjan Parida, N. Dani and S. Basu, Sol. Energy, 2021, 227, 447–456 CrossRef CAS.
- Y. Liu, B. Guo, X. Zou, Y. Li and S. Shi, Energy Storage Mater., 2020, 31, 434–450 CrossRef.
- A. Gopalan, B. J. Bucior, N. S. Bobbitt and R. Q. Snurr, Mol. Phys., 2019, 117, 3683–3694 CrossRef CAS.
- Z. Wen, P. Fang, Y. Yin, G. Królczyk, P. Gardoni and Z. Li, J. Energy Storage, 2022, 49, 104072 CrossRef.
- G. Yan, B. Teng, D. H. Elkamchouchi, T. Alkhalifah, F. Alturise, M. Amine Khadimallah and H. E. Ali, Fuel, 2023, 348, 128253 CrossRef CAS.
- P. Roy, L. Rekhi, S. W. Koh, H. Li and T. S. Choksi, J. Phys.: Energy, 2023, 5, 034005 Search PubMed.
- A. Rabbani, M. Babaei, R. Shams, Y. Da Wang and T. Chung, Adv. Water Resour., 2020, 146, 103787 CrossRef.
- A. Chen, X. Zhang and Z. Zhou, InfoMat, 2020, 2, 553–576 CrossRef CAS.
- L. Abualigah, R. A. Zitar, K. H. Almotairi, A. M. Hussein, M. A. Elaziz, M. R. Nikoo and A. H. Gandomi, Energies, 2022, 15, 578 CrossRef CAS.
- G. Anderson, B. Schweitzer, R. Anderson and D. A. Gómez-Gualdrón, J. Phys. Chem. C, 2019, 123, 120–130 Search PubMed.
- A. Ahmed and D. J. Siegel, Patterns, 2021, 2, 100291 CrossRef CAS.
- P. Roy, L. Rekhi, S. W. Koh, H. Li and T. S. Choksi, J. Phys.: Energy, 2023, 5, 034005 Search PubMed.
- D. Kaya, D. Koroglu, E. Aydın and B. Uralcan, J. Power Sources, 2023, 568, 232987 CrossRef CAS.
- Y. Liu, B. Guo, X. Zou, Y. Li and S. Shi, Energy Storage Mater., 2020, 31, 434–450 CrossRef.
- J. G. T. Tomacruz, K. E. S. Pilario, M. F. M. Remolona, A. A. B. Padama and J. D. Ocon, Chem. Eng. Trans., 2022, 94, 733–738 Search PubMed.
- T. Saboori, L. Zhao, M. Mesgarpour, S. Wongwises and O. Mahian, J. Build. Eng., 2022, 54, 104505 CrossRef.
- A. Shodiev, M. Duquesnoy, O. Arcelus, M. Chouchane, J. Li and A. A. Franco, J. Power Sources, 2021, 511, 230384 CrossRef CAS.
- M. Rahimi, M. H. Abbaspour-Fard and A. Rohani, J. Power Sources, 2022, 521, 230968 CrossRef CAS.
- M. Witman, S. Ling, D. M. Grant, G. S. Walker, S. Agarwal, V. Stavila and M. D. Allendorf, J. Phys. Chem. Lett., 2020, 11, 40–47 CrossRef CAS PubMed.
- A. Shahsavar, A. Goodarzi, I. Baniasad Askari, M. Jamei, M. Karbasi and M. Afrand, Eng. Anal. Bound. Elem., 2022, 140, 432–446 CrossRef.
- M. Pourali and J. A. Esfahani, Energy, 2022, 255, 124553 CrossRef CAS.
- M. M. A. Khan, N. I. Ibrahim, I. M. Mahbubul, H. M. Ali, R. Saidur and F. A. Al-Sulaiman, Sol. Energy, 2018, 166, 334–350 CrossRef CAS.
- L. Miró, J. Gasia and L. F. Cabeza, Appl. Energy, 2016, 179, 284–301 CrossRef.
- B. Liu, G. Lv, T. Liu, M. Liu, J. Bian, Q. Sun and L. Liao, J. Mater. Chem. A, 2024, 12, 8663–8682 RSC.
- K. Swaminathan Gopalan and V. Eswaran, Int. J. Therm. Sci., 2016, 104, 266–280 CrossRef.
- F. Selimefendigil and H. F. Öztop, J. Taiwan Inst. Chem. Eng., 2021, 124, 381–390 CrossRef CAS.
- N. Tonekaboni, M. Feizbahr, N. Tonekaboni, G. J. Jiang and H. X. Chen, Math. Probl. Eng., 2021, 2021, 9984840 Search PubMed.
- D. Skrobek, J. Krzywanski, M. Sosnowski, A. Kulakowska, A. Zylka, K. Grabowska, K. Ciesielska and W. Nowak, Adv. Eng. Softw., 2022, 173, 103190 CrossRef.
- Z. Shi, H. Liang, W. Yang, J. Liu, Z. Liu and Z. Qiao, Chem. Eng. Sci., 2020, 214, 115430 CrossRef CAS.
- A. Malley-Ernewein and S. Lorente, Int. J. Heat Mass Transfer, 2020, 158, 119975 CrossRef CAS.
- X. Chen, Z. Dong, L. Zhu and X. Ling, Renewable Energy, 2023, 205, 340–348 CrossRef CAS.
- T. Praditia, T. Walser, S. Oladyshkin and W. Nowak, Energies, 2020, 13, 3873 CrossRef CAS.
- S. Tasneem, H. S. Sultan, A. A. Ageeli, H. Togun, W. M. Alamier, N. Hasan and M. R. Safaei, J. Taiwan Inst. Chem. Eng., 2023, 104926 CrossRef CAS.
- L. Mao, X. Zhao, H. Wang, H. Xu, L. Xie, C. Zhao and L. Chen, Chem. Rec., 2020, 20, 922–935 CrossRef CAS PubMed.
- A. Shodiev, M. Duquesnoy, O. Arcelus, M. Chouchane, J. Li and A. A. Franco, J. Power Sources, 2021, 511, 230384 CrossRef CAS.
- H. Chun, J. Kim and S. Han, in IFAC-PapersOnLine, Elsevier B.V., 2019, vol. 52, pp. 129–134 Search PubMed.
- M. Shi, J. Yuan, L. Dong, D. Zhang, A. Li and J. Zhang, Electrochim. Acta, 2020, 353, 136567 CrossRef CAS.
- F. Wang, X. Li, J. Tan, X. Hao and B. Xiong, Int. J. Heat Mass Transfer, 2022, 183, 122085 CrossRef CAS.
- G. Cho, M. Wang, Y. Kim, J. Kwon and W. Su, IEEE Access, 2022, 10, 88117–88126 Search PubMed.
- E. Galiounas, T. G. Tranter, R. E. Owen, J. B. Robinson, P. R. Shearing and D. J. L. Brett, Energy AI, 2022, 10, 100188 CrossRef.
- H. Xu, J. Zhu, D. P. Finegan, H. Zhao, X. Lu, W. Li, N. Hoffman, A. Bertei, P. Shearing and M. Z. Bazant, Adv. Energy Mater., 2021, 11, 2003908 CrossRef CAS.
- A. Aitio and D. A. Howey, Joule, 2021, 5, 3204–3220 CrossRef.
- M. Boujelbene, M. Goodarzi, M. A. Ali, I. M. T. A. Shigidi, R. A. Pashameah, R. Z. Homod, E. Alzahrani and M. R. Safaei, J. Energy Storage, 2023, 58, 106331 CrossRef.
- S. Ishikawa, X. Liu, T. H. Noh, M. So, K. Park, N. Kimura, G. Inoue and Y. Tsuge, J. Power Sources Adv., 2022, 15, 100094 CrossRef CAS.
- R. M. Weber, S. Korneev and I. Battiato, Transp. Porous Media, 2022, 145, 527–548 CrossRef.
- Z. Jiang, J. Li, Y. Yang, L. Mu, C. Wei, X. Yu, P. Pianetta, K. Zhao, P. Cloetens, F. Lin and Y. Liu, Nat. Commun., 2020, 11, 2310 CrossRef CAS.
- A. González, E. Goikolea, J. A. Barrena and R. Mysyk, Renewable Sustainable Energy Rev., 2016, 58, 1189–1206 CrossRef.
- S. Nanda, S. Ghosh and T. Thomas, J. Power Sources, 2022, 546, 231975 CrossRef CAS.
- J. Wang, X. Zhang, Z. Li, Y. Ma and L. Ma, J. Power Sources, 2020, 451, 227794 CrossRef CAS.
- A. G. Saad, A. Emad-Eldeen, W. Z. Tawfik and A. G. El-Deen, J. Energy Storage, 2022, 55, 105411 CrossRef.
- S. Ghosh, G. R. Rao and T. Thomas, Energy Storage Mater., 2021, 40, 426–438 CrossRef.
- X. Lu, P. Liu, K. Bisetty, Y. Cai, X. Duan, Y. Wen, Y. Zhu, L. Rao, Q. Xu and J. Xu, J. Electroanal. Chem., 2022, 920, 116634 CrossRef CAS.
- W. C. Tan, L. H. Saw, H. S. Thiam, J. Xuan, Z. Cai and M. C. Yew, Renewable Sustainable Energy Rev., 2018, 96, 181–197 CrossRef.
- R. Ding, S. Zhang, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, X. Wang, J. Li and J. Liu, Energy AI, 2022, 9, 100170 CrossRef.
- G. Zhang, L. Wu, K. Jiao, P. Tian, B. Wang, Y. Wang and Z. Liu, Energy Convers. Manage., 2020, 226, 113513 CrossRef CAS.
- X. Liu, K. Park, M. So, S. Ishikawa, T. Terao, K. Shinohara, C. Komori, N. Kimura, G. Inoue and Y. Tsuge, J. Power Sources Adv., 2022, 14, 100084 CrossRef CAS.
- F. Zhang, P. Zhao, M. Niu and J. Maddy, Int. J. Hydrogen Energy, 2016, 41, 14535–14552 CrossRef CAS.
- E. M. Thaysen, S. McMahon, G. J. Strobel, I. B. Butler, B. T. Ngwenya, N. Heinemann, M. Wilkinson, A. Hassanpouryouzband, C. I. McDermott and K. Edlmann, Renewable Sustainable Energy Rev., 2021, 151, 111481 CrossRef CAS.
- T. Hai, F. A. Alenizi, A. H. Mohammed, B. S. Chauhan, B. Al-Qargholi, A. S. M. Metwally and M. Ullah, Int. Commun. Heat Mass Transfer, 2023, 145, 106848 CrossRef CAS.
- G. Anderson, B. Schweitzer, R. Anderson and D. A. Gómez-Gualdrón, J. Phys. Chem. C, 2019, 123, 120–130 CrossRef CAS.
- A. Gopalan, B. J. Bucior, N. S. Bobbitt and R. Q. Snurr, Mol. Phys., 2019, 117, 3683–3694 CrossRef CAS.
- B. J. Bucior, N. S. Bobbitt, T. Islamoglu, S. Goswami, A. Gopalan, T. Yildirim, O. K. Farha, N. Bagheri and R. Q. Snurr, Mol. Syst. Des. Eng., 2019, 4, 162–174 RSC.
- M. Rahimi, M. H. Abbaspour-Fard and A. Rohani, J. Cleaner Prod., 2021, 329, 129714 CrossRef CAS.
- D. P. Dubal, O. Ayyad, V. Ruiz and P. Gómez-Romero, Chem. Soc. Rev., 2015, 44, 1777–1790 RSC.
- F. Zhang, T. Zhang, X. Yang, L. Zhang, K. Leng, Y. Huang and Y. Chen, Energy Environ. Sci., 2013, 6, 1623–1632 RSC.
- T. Gao and W. Lu, iScience, 2021, 24, 101936 CrossRef CAS.
- N. Variji, M. Siavashi, M. Tahmasbi and M. Bidabadi, J. Energy Storage, 2022, 50, 104690 CrossRef.
- M. M. Heyhat, S. Mousavi and M. Siavashi, J. Energy Storage, 2020, 28, 101235 CrossRef.
- M. Boujelbene, M. Goodarzi, M. A. Ali, I. M. T. A. Shigidi, R. A. Pashameah, R. Z. Homod, E. Alzahrani and M. R. Safaei, J. Energy Storage, 2023, 58, 106331 CrossRef.
- M. Krishnamoorthi, R. Malayalamurthi, Z. He and S. Kandasamy, Renewable Sustainable Energy Rev., 2019, 116, 109404 CrossRef CAS.
- W. Jiang, X. Xing, X. Zhang and M. Mi, Renewable Energy, 2019, 130, 1216–1225 CrossRef CAS.
- A. Banerjee and D. Paul, Energy, 2021, 221, 119868 CrossRef CAS.
- L. Zhou, Y. Song, W. Ji and H. Wei, Energy AI, 2022, 7, 100128 CrossRef.
- H. Mai, T. C. Le, D. Chen, D. A. Winkler and R. A. Caruso, Chem. Rev., 2022, 122, 13478–13515 CrossRef CAS.
- A. Mistry, A. A. Franco, S. J. Cooper, S. A. Roberts and V. Viswanathan, ACS Energy Lett., 2021, 6, 1422–1431 CrossRef CAS.
- C. Song, S. Lee, B. Gu, I. Chang, G. Y. Cho, J. D. Baek and S. W. Cha, Energies, 2020, 13, 1621 CrossRef CAS.
- P. Satjaritanun, M. O'Brien, D. Kulkarni, S. Shimpalee, C. Capuano, K. E. Ayers, N. Danilovic, D. Y. Parkinson and I. V Zenyuk, iScience, 2020, 23, 101783 CrossRef CAS.
- A. M. Nassef, A. Fathy, E. T. Sayed, M. A. Abdelkareem, H. Rezk, W. H. Tanveer and A. G. Olabi, Renewable Energy, 2019, 138, 458–464 CrossRef.
- B. Wang, B. Xie, J. Xuan and K. Jiao, Energy Convers. Manage., 2020, 205, 112460 CrossRef CAS.
- S. N. Steinmann, Q. Wang and Z. W. Seh, Mater. Horiz., 2023, 10, 393–406 RSC.
- W. Xia, Z. Hou, J. Tang, J. Li, W. Chaikittisilp, Y. Kim, K. Muraoka, H. Zhang, J. He, B. Han and Y. Yamauchi, Nano Energy, 2022, 94, 106868 CrossRef CAS.
- W. Zhou, L. Yang, X. Wang, W. Zhao, J. Yang, D. Zhai, L. Sun and W. Deng, JACS Au, 2021, 1, 1497–1505 CrossRef CAS.
- E. O. Ebikade, Y. Wang, N. Samulewicz, B. Hasa and D. Vlachos, React. Chem. Eng., 2020, 5, 2134–2147 RSC.
- A. Zheng, Y. Wang, F. Zhang, C. He, S. Zhu and N. Zhao, iScience, 2021, 24, 103430 CrossRef CAS.
- M. Pourali, J. A. Esfahani, H. Jahangir, A. Farzaneh and K. C. Kim, J. Energy Storage, 2022, 55, 105804 CrossRef.
- Y. Chen, J. Feng, X. Wang, C. Zhang, D. Ke, H. Zhu, S. Wang, H. Suo and C. Liu, Environ. Sci. Technol., 2023, 57(46), 18080–18090 CrossRef CAS PubMed.
- R. Ding, Y. Chen, Z. Rui, K. Hua, Y. Wu, X. Li, X. Duan, J. Li, X. Wang and J. Liu, J. Power Sources, 2023, 556, 232389 CrossRef CAS.
- M. E. Günay, N. A. Tapan and G. Akkoç, Int. J. Hydrogen Energy, 2022, 47, 2134–2151 CrossRef.
- M. E. Günay and N. A. Tapan, Energy AI, 2023, 13, 100254 CrossRef.
- Y. Zhang, Y. Tao, H. Ren, M. Wu, G. Li, Z. Wan and J. Shao, J. Power Sources, 2022, 543, 231847 CrossRef CAS.
- G. Zhang, L. Wu, K. Jiao, P. Tian, B. Wang, Y. Wang and Z. Liu, Energy Convers. Manage., 2020, 226, 113513 CrossRef CAS.
- J. Wang, H. Jiang, G. Chen, H. Wang, L. Lu, J. Liu and L. Xing, Energy AI, 2023, 14, 100261 CrossRef.
- H. Pourrahmani and J. Van herle, Energy, 2022, 256, 124712 CrossRef CAS.
- H. Pourrahmani and J. Van herle, Appl. Therm. Eng., 2022, 203, 117952 CrossRef CAS.
- H. W. Li, B. X. Qiao, J. N. Liu, Y. Yang, W. Fan and G. L. Lu, Energy Convers. Manage., 2022, 271, 116338 CrossRef CAS.
- T. Cawte and A. Bazylak, Electrochem. Sci. Adv., 2023, 3, e2100185 CrossRef CAS.
- X. Liu, K. Park, M. So, S. Ishikawa, T. Terao, K. Shinohara, C. Komori, N. Kimura, G. Inoue and Y. Tsuge, J. Power Sources Adv., 2022, 14, 100084 CrossRef CAS.
- Y. Lou, M. Hao and Y. Li, J. Power Sources, 2022, 543, 231827 CrossRef CAS.
- N. Vaz, J. Choi, Y. Cha, J. kong, Y. Park and H. Ju, J. Energy Chem., 2023, 81, 28–41 CrossRef CAS.
- G. Xu, Z. Yu, L. Xia, C. Wang and S. Ji, Energy Convers. Manage., 2022, 268, 116026 CrossRef CAS.
- X. Liu, S. Zhou, Z. Yan, Z. Zhong, N. Shikazono and S. Hara, Energy AI, 2022, 7, 100122 CrossRef.
- A. Fathy, H. Rezk and H. S. Mohamed Ramadan, Energy, 2020, 207, 118326 CrossRef CAS.
- A. Sciazko, Y. Komatsu, A. Nakamura, Z. Ouyang, T. Hara and N. Shikazono, Chem. Eng. J., 2023, 460, 141680 CrossRef CAS.
- M. H. Golbabaei, M. Saeidi Varnoosfaderani, A. Zare, H. Salari, F. Hemmati, H. Abdoli and B. Hamawandi, Materials, 2022, 15, 7760 CrossRef CAS.
- Y. Wang, C. Wu, S. Zhao, Z. Guo, M. Han, T. Zhao, B. Zu, Q. Du, M. Ni and K. Jiao, Sci. Bull., 2023, 68, 516–527 CrossRef CAS.
- S. Wan, X. Liang, H. Jiang, J. Sun, N. Djilali and T. Zhao, Appl. Energy, 2021, 298, 117177 CrossRef CAS.
- R. van Gorp, M. van der Heijden, M. Amin Sadeghi, J. Gostick and A. Forner-Cuenca, Chem. Eng. J., 2023, 455, 139947 CrossRef CAS.
- J. Bao, V. Murugesan, C. J. Kamp, Y. Shao, L. Yan and W. Wang, Adv. Theory Simul., 2020, 3, 1900167 CrossRef CAS.
- B. A. Simon, A. Gayon-Lombardo, C. A. Pino-Muñoz, C. E. Wood, K. M. Tenny, K. V. Greco, S. J. Cooper, A. Forner-Cuenca, F. R. Brushett, A. R. Kucernak and N. P. Brandon, Appl. Energy, 2022, 306, 117678 CrossRef CAS.
- I. Arganda-Carreras, V. Kaynig, C. Rueden, K. W. Eliceiri, J. Schindelin, A. Cardona and H. Sebastian Seung, Bioinformatics, 2017, 33, 2424–2426 CrossRef CAS PubMed.
- J. J. Patil, C. T. C. Wan, S. Gong, Y. M. Chiang, F. R. Brushett and J. C. Grossman, ACS Nano, 2023, 17, 4999–5013 CrossRef CAS.
- T. Li, W. Lu, Z. Yuan, H. Zhang and X. Li, J. Mater. Chem. A, 2021, 9, 14545–14552 RSC.
- Y. Yang, N. Li, B. Wang, N. Li, K. Gao, Y. Liang, Y. Wei, L. Yang, W. L. Song and H. Chen, Electrochem. Commun., 2022, 136, 107224 CrossRef CAS.
- M. Duquesnoy, C. Liu, D. Z. Dominguez, V. Kumar, E. Ayerbe and A. A. Franco, Energy Storage Mater., 2023, 56, 50–61 CrossRef.
- M. F. Niri, K. Liu, G. Apachitei, L. A. A. Román-Ramírez, M. Lain, D. Widanage and J. Marco, Energy AI, 2022, 7, 100129 CrossRef.
- J. Xu, A. C. Ngandjong, C. Liu, F. M. Zanotto, O. Arcelus, A. Demortière and A. A. Franco, J. Power Sources, 2023, 554, 232294 CrossRef CAS.
- C. Sommer, C. Straehle, U. Kothe and F. A. Hamprecht, in Proceedings – International Symposium on Biomedical Imaging, 2011, pp. 230–233 Search PubMed.
- J. J. Bailey, A. Wade, A. M. Boyce, Y. S. Zhang, D. J. L. Brett and P. R. Shearing, J. Power Sources, 2023, 557, 232503 CrossRef CAS.
- A. F. Frangi, J. A. Schnabel, C. Davatzikos, C. Alberola-López and G. Fichtinger, Medical Image Computing and Computer Assisted Intervention – MICCAI 2018, 21st International Conference, Springer International Publishing, Granada, Spain, 2018, vol. 11071 Search PubMed.
- V. Nagda, A. Kulachenko and S. B. Lindström, Comput. Mater. Sci., 2023, 223, 112139 CrossRef CAS.
- V. Kabra, B. Birn, I. Kamboj, V. Augustyn and P. P. Mukherjee, J. Phys. Chem. C, 2022, 126, 14413–14429 CrossRef CAS.
- S. Ishikawa, X. Liu, T. H. Noh, M. So, K. Park, N. Kimura, G. Inoue and Y. Tsuge, J. Power Sources Adv., 2022, 15, 100094 CrossRef CAS.
- Y. Sun, S. M. Ayalasomayajula, A. Deva, G. Lin and R. E. García, Sci. Rep., 2022, 12, 1–11 CrossRef.
- J. Fu, D. Xiao, D. Li, H. R. Thomas and C. Li, Comput. Methods Appl. Mech. Eng., 2022, 390, 114532 CrossRef.
- M. Faraji Niri, J. Mafeni Mase and J. Marco, Energies, 2022, 15, 4489 CrossRef CAS.
- S. Kamrava and H. Mirzaee, Phys. Rev. E, 2022, 106, 055301 CrossRef CAS.
- A. Shodiev, M. Duquesnoy, O. Arcelus, M. Chouchane, J. Li and A. A. Franco, J. Power Sources, 2021, 511, 230384 CrossRef CAS.
- A. El Malki, M. Asch, O. Arcelus, A. Shodiev, J. Yu and A. A. Franco, J. Power Sources Adv., 2023, 20, 100114 CrossRef CAS.
- Z. Tong, J. Miao, S. Tong and Y. Lu, J. Cleaner Prod., 2021, 317, 128265 CrossRef CAS.
- B. Jiang, M. D. Berliner, K. Lai, P. A. Asinger, H. Zhao, P. K. Herring, M. Z. Bazant and R. D. Braatz, Appl. Energy, 2022, 307, 118244 CrossRef CAS.
- V. Goel, K. H. Chen, N. P. Dasgupta and K. Thornton, Energy Storage Mater., 2023, 57, 44–58 CrossRef.
- S. Mishra, R. Srivastava, A. Muhammad, A. Amit, E. Chiavazzo, M. Fasano and P. Asinari, Sci. Rep., 2023, 13, 6494 CrossRef CAS.
- M. Zhou, A. Gallegos, K. Liu, S. Dai and J. Wu, Carbon, 2020, 157, 147–152 CrossRef CAS.
- A. G. Saad, A. Emad-Eldeen, W. Z. Tawfik and A. G. El-Deen, J. Energy Storage, 2022, 55, 105411 CrossRef.
- S. Ghosh, G. R. Rao and T. Thomas, Energy Storage Mater., 2021, 40, 426–438 CrossRef.
- P. Liu, Y. Wen, L. Huang, X. Zhu, R. Wu, S. Ai, T. Xue and Y. Ge, J. Electroanal. Chem., 2021, 899, 115684 CrossRef CAS.
- S. Mathew, P. B. Karandikar and N. R. Kulkarni, Chem. Eng. Technol., 2020, 43, 1765–1773 CrossRef CAS.
- S. Jha, S. Bandyopadhyay, S. Mehta, M. Yen, T. Chagouri, E. Palmer and H. Liang, Energy & Fuels, 2021, 36, 1052–1062 Search PubMed.
- M. Rahimi, M. H. Abbaspour-Fard and A. Rohani, J. Power Sources, 2022, 521, 230968 CrossRef CAS.
- M. Seyyedattar, S. Zendehboudi and S. Butt, Nat. Resour. Res., 2019, 29, 2147–2189 CrossRef.
- Z. Tariq, M. S. Aljawad, A. Hasan, M. Murtaza, E. Mohammed, A. El-Husseiny, S. A. Alarifi, M. Mahmoud and A. Abdulraheem, J. Pet. Explor. Prod. Technol., 2021, 11, 4339–4374 CrossRef.
- X. Xie, H. Lu, H. Deng, H. Yang, B. Teng and H. A. Li, J. Pet. Sci. Eng., 2019, 182, 106243 CrossRef CAS.
- J. Ma, Unconventional Oil and Gas Resources Handbook: Evaluation and Development, 2016, pp. 127–150 Search PubMed.
- A. Fornel and A. Estublier, Energy Procedia, 2013, 37, 4902–4909 CrossRef CAS.
- J. Hutahaean, V. Demyanov and M. Christie, J. Pet. Sci. Eng., 2019, 175, 444–464 CrossRef CAS.
- T. Ramstad, C. F. Berg and K. Thompson, Transp. Porous Media, 2019, 130, 77–104 CrossRef CAS.
- Y. Da Wang, M. J. Blunt, R. T. Armstrong and P. Mostaghimi, Earth-Sci. Rev., 2021, 215, 103555 CrossRef.
- M. Liu and T. Mukerji, Leading Edge, 2022, 41, 591–598 CrossRef.
- S. J. Jackson, Y. Niu, S. Manoorkar, P. Mostaghimi and R. T. Armstrong, Phys. Rev. Appl., 2022, 17, 054046 CrossRef.
- Y. Niu, S. J. Jackson, N. Alqahtani, P. Mostaghimi and R. T. Armstrong, Transp. Porous Media, 2022, 144, 825–847 CrossRef.
- Y. Da Wang, R. T. Armstrong and P. Mostaghimi, Water Resour. Res., 2020, 56, e2019WR026052 CrossRef.
- M. Liu and T. Mukerji, Geophys. Res. Lett., 2022, 49, e2022GL098342 CrossRef.
- J. Fu, D. Xiao, D. Li, H. R. Thomas and C. Li, Comput. Methods Appl. Mech. Eng., 2022, 390, 114532 CrossRef.
- Q. Zheng and D. Zhang, Comput. Geosci., 2022, 26, 677–696 CrossRef.
- Y. Yang, F. Liu, J. Yao, S. Iglauer, M. Sajjadi, K. Zhang, H. Sun, L. Zhang, J. Zhong and V. Lisitsa, J. Nat. Gas Sci. Eng., 2022, 99, 104411 CrossRef.
- H. L. Zhang, H. Yu, S. W. Meng, M. C. Huang, M. Micheal, J. Su, H. Liu and H. A. Wu, J. Pet. Sci. Eng., 2022, 217, 110937 CrossRef CAS.
- A. K. Ting, J. E. Santos and E. Guiltinan, Energies, 2022, 15, 8871 CrossRef.
- O. Ishola and J. Vilcáez, Fuel, 2022, 321, 124044 CrossRef CAS.
- H. Sun, L. ZHOU, D. Fan, L. Zhang, Y. Yang, K. Zhang and J. Yao, Phys. Fluids, 2023, 35, 032014 CrossRef CAS.
- J. W. Tian, C. Qi, K. Peng, Y. Sun and Z. Mundher Yaseen, J. Comput. Civ. Eng., 2022, 36, 983 CrossRef.
- X. Bu, H. Saleh, M. Han and A. AlSofi, presented in SPE Reservoir Characterisation and Simulation Conference and Exhibition, Society of Petroleum Engineers, 2023 Search PubMed.
- J. Lee and D. E. Lumley, J. Pet. Sci. Eng., 2023, 220, 111231 CrossRef CAS.
- T. Ore and D. Gao, Comput. Geosci., 2023, 171, 105266 CrossRef.
- C. M. Saporetti, D. L. Fonseca, L. C. Oliveira, E. Pereira and L. Goliatt, Int. J. Environ. Sci. Technol., 2023, 20, 1585–1596 CrossRef.
- H. Zhang, W. Wu and H. Wu, Geoenergy Sci. Eng., 2023, 221, 111271 CrossRef.
- A. Bemani, A. Kazemi and M. Ahmadi, J. Pet. Sci. Eng., 2023, 220, 111162 CrossRef CAS.
- M. Rajabi, O. Hazbeh, S. Davoodi, D. A. Wood, P. S. Tehrani, H. Ghorbani, M. Mehrad, N. Mohamadian, V. S. Rukavishnikov and A. E. Radwan, J. Pet. Explor. Prod. Technol., 2023, 13, 19–42 CrossRef.
- B. Shen, S. Yang, X. Gao, S. Li, K. Yang, J. Hu and H. Chen, Eng. Appl. Artif. Intell., 2023, 118, 105687 CrossRef.
- C. Huang, L. Tian, J. Wu, M. Li, Z. Li, J. Li, J. Wang, L. Jiang and D. Yang, Fuel, 2023, 337, 127194 CrossRef CAS.
- Q. Lv, R. Zheng, X. Guo, A. Larestani, F. Hadavimoghaddam, M. Riazi, A. Hemmati-Sarapardeh, K. Wang and J. Li, Sep. Purif. Technol., 2023, 310, 123086 CrossRef CAS.
- B. Liu, Z. Wang, Y. Jin, Z. Ge, C. Xu, H. Liu and H. Chen, Energy and Fuels, 2023, 37, 935–944 CrossRef CAS.
- Y. Zhang, H. R. Zhong, Z. Y. Wu, H. Zhou and Q. Y. Ma, J. Pet. Sci. Eng., 2020, 192, 107234 CrossRef CAS.
- X. Zhao, X. Chen, Q. Huang, Z. Lan, X. Wang and G. Yao, J. Pet. Sci. Eng., 2022, 214, 110517 CrossRef CAS.
- L. Yang, S. Wang, X. Chen, W. Chen, O. M. Saad, X. Zhou, N. Pham, Z. Geng, S. Fomel and Y. Chen, IEEE Trans. Neural Netw. Learn. Syst., 2023, 34, 3429–3443 Search PubMed.
- M. Masroor, M. Emami Niri and M. H. Sharifinasab, Geoenergy Sci. Eng., 2023, 222, 211420 CrossRef CAS.
- M. Matinkia, R. Hashami, M. Mehrad, M. R. Hajsaeedi and A. Velayati, Petroleum, 2023, 9, 108–123 CrossRef.
- Z. Chao, Y. Dang, Y. Pan, F. Wang, M. Wang, J. Zhang and C. Yang, Geomech. Energy Environ., 2023, 33, 100435 CrossRef.
- S. Pan, Z. Zheng, Z. Guo and H. Luo, J. Pet. Sci. Eng., 2022, 208, 109520 CrossRef CAS.
- J. Wang and J. Cao, Arabian J. Sci. Eng., 2022, 47, 11313–11327 CrossRef.
- A. F. Ibrahim, S. Elkatatny, Y. Abdelraouf and M. Al Ramadan, J. Energy Resour. Technol. Trans. ASME, 2022, 144, 083009 CrossRef CAS.
- Z. Zhao, X. P. Zhou and Q. H. Qian, Sci. China: Technol. Sci., 2022, 65, 458–469 CrossRef.
- C. E. M. dos Anjos, T. F. de Matos, M. R. V. Avila, J. de, C. V. Fernandes, R. Surmas and A. G. Evsukoff, Geoenergy Sci. Eng., 2023, 222, 211335 CrossRef.
- N. Alqahtani, F. Alzubaidi, R. T. Armstrong, P. Swietojanski and P. Mostaghimi, J. Pet. Sci. Eng., 2020, 184, 106514 CrossRef CAS.
- H. V. Thanh and Y. Sugai, Upstream Oil and Gas Technology, 2021, 6, 100027 CrossRef.
- M. Pal, P. Makauskas and S. Malik, Processes, 2023, 11, 601 CrossRef CAS.
- Y. Wang, H. Li, J. Xu, S. Liu, Q. Tan and X. Wang, Appl. Energy, 2023, 337, 120854 CrossRef.
- Y. Wang, H. Li, J. Xu, S. Liu and X. Wang, Energy, 2022, 245, 123284 CrossRef.
- A. Santos, H. F. A. Scanavini, H. Pedrini, D. J. Schiozer, F. P. Munerato and C. E. A. G. Barreto, J. Pet. Sci. Eng., 2022, 211, 110071 CrossRef CAS.
- J. Siavashi, A. Najafi, M. Ebadi and M. Sharifi, Fuel, 2022, 211, 110071 Search PubMed.
- O. S. Alolayan, A. O. Alomar and J. R. Williams, Energies, 2023, 16, 860 CrossRef.
- S. Jo, H. Jeong, B. Min, C. Park, Y. Kim, S. Kwon and A. Sun, J. Pet. Sci. Eng., 2022, 208, 109247 CrossRef CAS.
- X. Ma, K. Zhang, J. Zhang, Y. Wang, L. Zhang, P. Liu, Y. Yang and J. Wang, J. Pet. Sci. Eng., 2022, 210, 110109 CrossRef CAS.
- X. Ma, K. Zhang, H. Zhao, L. Zhang, J. Wang, H. Zhang, P. Liu, X. Yan and Y. Yang, J. Pet. Sci. Eng., 2022, 214, 110548 CrossRef CAS.
- C. Xiao, H. X. Lin, O. Leeuwenburgh and A. Heemink, J. Pet. Sci. Eng., 2022, 208, 109287 CrossRef CAS.
- A. Qubian, M. A. Zekraoui, S. Mohajeri, E. Mortezazadeh, R. Eslahi, M. Bakhtiari, A. Al Dabbous, A. Al Sagheer, A. Alizadeh and M. Zeinali, in Society of Petroleum Engineers – SPE Symposium: Leveraging Artificial Intelligence to Shape the Future of the Energy Industry, AIS 2023, Society of Petroleum Engineers, 2023 Search PubMed.
- M. V. Behl and M. Tyagi, SPE Reservoir Eval. Eng., 2023, 1–15 Search PubMed.
- H. Huang, B. Gong, Y. Liu and W. Sun, Geoenergy Sci. Eng., 2023, 222, 211418 CrossRef CAS.
- B. Saberali, N. Golsanami, K. Zhang, B. Gong and M. Ostadhassan, Geoenergy Sci. Eng., 2023, 222, 211415 CrossRef CAS.
- F. A. Shuaibi, M. M. Hadhrami, A. H. Sheheimi, B. Agarwal, Q. M. Riyami, M. Ruqaishi, N. Habsi, E. Mortezazadeh and S. Mohajeri, in Society of Petroleum Engineers - SPE Reservoir Characterisation and Simulation Conference and Exhibition 2023, RCSC 2023, Society of Petroleum Engineers, 2023 Search PubMed.
- R. Manasipov, D. Nikolaev, D. Didenko, R. Abdalla and M. Stundner, in Society of Petroleum Engineers - SPE Reservoir Characterisation and Simulation Conference and Exhibition 2023, RCSC 2023, Society of Petroleum Engineers, 2023 Search PubMed.
- X. Kong, Y. Liu, L. Xue, G. Li and D. Zhu, Energies, 2023, 16, 1027 CrossRef CAS.
- H. Chu, P. Dong and W. J. Lee, Adv. Geo-Energy Res., 2023, 7, 49–65 CrossRef.
- A. F. Ibrahim, S. A. Alarifi and S. Elkatatny, J. Pet. Explor. Prod. Technol., 2023, 13, 1123–1134 CrossRef.
- U. Osah and J. Howell, Pet. Geosci., 2023, 19, 071 Search PubMed.
- Z. A.-A. H. Al-Ali and R. Horne, presented in Gas & Oil Technology Showcase and Conference, Society of Petroleum Engineers (SPE), Dubai, UAE, 2023 Search PubMed.
- Y. Liu, J. Zeng, J. Qiao, G. Yang, S. Liu and W. Cao, Appl. Energy, 2023, 333, 120604 CrossRef CAS.
- H. Ullah, Z. U. Haq, S. R. Naqvi, M. N. A. Khan, M. Ahsan and J. Wang, J. Anal. Appl. Pyrolysis, 2023, 170(105879) CAS.
- S. Du, J. Wang, M. Wang, J. Yang, C. Zhang, Y. Zhao and H. Song, Energy, 2023, 263, 126121 CrossRef CAS.
- H. Tang and L. J. Durlofsky, Comput. Geosci., 2022, 26, 1189–1206 CrossRef.
- J. R. Bertini, S. F. Ferreira Batista, M. A. Funcia, L. O. Mendes da Silva, A. A. S. Santos and D. J. Schiozer, J. Pet. Sci. Eng., 2022, 208, 109208 CrossRef CAS.
- J. Zhou, H. Wang, C. Xiao and S. Zhang, Energies, 2023, 16, 303 CrossRef CAS.
- Y. Nasir and L. J. Durlofsky, SPE J., 2023, 1–14 Search PubMed.
- Y.-T. Chen, D.-X. Zhang, Q. Zhao and D.-X. Liu, Pet. Sci., 2023, 20, 1788–1805 CrossRef CAS.
- Y. Yao, Y. Qiu, Y. Cui, M. Wei and B. Bai, Chem. Eng. J., 2023, 451, 138022 CrossRef CAS.
- C. Fabbri, N. Reddicharla, W. Shi, A. Al Shalabi, S. Al Hashmi and S. Al Jaberi, in Society of Petroleum Engineers - SPE Reservoir Characterisation and Simulation Conference and Exhibition 2023, RCSC 2023, Society of Petroleum Engineers, 2023 Search PubMed.
- M. Pirizadeh, N. Alemohammad, M. Manthouri and M. Pirizadeh, Pet. Sci. Technol., 2023, 41, 64–85 CrossRef CAS.
- P. S. Pavan, K. Arvind, B. Nikhil and P. Sivasankar, Bioresour. Technol., 2022, 351, 127023 CrossRef CAS.
- M. Mahdaviara, M. Sharifi and M. Ahmadi, Fuel, 2022, 325, 124795 CrossRef CAS.
- R. K. Pachauri, M. R. Allen, V. R. Barros, J. Broome, W. Cramer, R. Christ, J. A. Church, L. Clarke, Q. Dahe and P. Dasgupta, Climate Change 2014: Synthesis Report. Contribution of Working Groups I, II and III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change, Ipcc, 2014 Search PubMed.
- Climate Change 2022: Impacts, Adaptation and Vulnerability - Contribution of Working Group II to the Sixth Assessment Report of the Intergovernmental Panel on Climate Change, ed. H.-O. Pörtner, D. C. Roberts, E. S. Poloczanska, K. Mintenbeck, M. Tignor, A. Alegría, M. Craig, S. Langsdorf, S. Löschke, V. Möller and A. Okem, Cambridge University Press, Cambridge, UK, New York, NY, USA, 2022, p. 3 Search PubMed.
- G. Luderer, Z. Vrontisi, C. Bertram, O. Y. Edelenbosch, R. C. Pietzcker, J. Rogelj, H. S. De Boer, L. Drouet, J. Emmerling and O. Fricko, Nat. Clim. Change, 2018, 8, 626–633 CrossRef CAS.
- R. Cavicchioli, W. J. Ripple, K. N. Timmis, F. Azam, L. R. Bakken, M. Baylis, M. J. Behrenfeld, A. Boetius, P. W. Boyd and A. T. Classen, Nat. Rev. Microbiol., 2019, 17, 569–586 CrossRef CAS.
- M. Bui, C. S. Adjiman, A. Bardow, E. J. Anthony, A. Boston, S. Brown, P. S. Fennell, S. Fuss, A. Galindo and L. A. Hackett, Energy Environ. Sci., 2018, 11, 1062–1176 RSC.
- D. W. Keith, G. Holmes, D. S. Angelo and K. Heidel, Joule, 2018, 2, 1573–1594 CrossRef CAS.
- H. Azarabadi and K. S. Lackner, Environ. Sci. Technol., 2020, 54, 5102–5111 CrossRef CAS.
- O. S. Bushuyev, P. De Luna, C. T. Dinh, L. Tao, G. Saur, J. van de Lagemaat, S. O. Kelley and E. H. Sargent, Joule, 2018, 2, 825–832 CrossRef CAS.
- B. Smit, J. A. Reimer, C. M. Oldenburg and I. C. Bourg, Introduction to Carbon Capture and Sequestration, World Scientific, 2014, vol. 1 Search PubMed.
- J. C. Palmer, A. Llobet, S. H. Yeon, J. E. Fischer, Y. Shi, Y. Gogotsi and K. E. Gubbins, Carbon, 2010, 48, 1116–1123 CrossRef CAS.
- P. Ugliengo, M. Sodupe, F. Musso, I. J. Bush, R. Orlando and R. Dovesi, Adv. Mater., 2008, 20, 4579–4583 CrossRef CAS.
- J. M. H. Thomas and A. Trewin, J. Phys. Chem. C, 2014, 118, 19712–19722 CrossRef CAS.
- G. Férey, C. Mellot-Draznieks, C. Serre, F. Millange, J. Dutour, S. Surblé and I. Margiolaki, Science, 2005, 309, 2040–2042 CrossRef.
- S. Cai, L. Yu, E. Huo, Y. Ren, X. Liu and Y. Chen, Langmuir, 2024, 40, 6869–6877 CrossRef CAS.
- M. M. Lozinska, E. Mangano, J. P. S. Mowat, A. M. Shepherd, R. F. Howe, S. P. Thompson, J. E. Parker, S. Brandani and P. A. Wright, J. Am. Chem. Soc., 2012, 134, 17628–17642 CrossRef CAS PubMed.
- S. Bandyopadhyay, A. G. Anil, A. James and A. Patra, ACS Appl. Mater. Interfaces, 2016, 8, 27669–27678 CrossRef CAS.
- H. Mashhadimoslem, A. Ghaemi, A. Maleki and A. Elkamel, J. Environ. Chem. Eng., 2023, 11, 109300 CrossRef CAS.
- N. Von Der Assen, P. Voll, M. Peters and A. Bardow, Chem. Soc. Rev., 2014, 43, 7982–7994 RSC.
- R. M. Cuéllar-Franca and A. Azapagic, J. CO2 Util., 2015, 9, 82–102 CrossRef.
- S. Deutz and A. Bardow, Nat. Energy, 2021, 6, 203–213 CrossRef CAS.
- R. Sathre and E. Masanet, RSC Adv., 2013, 3, 4964–4975 RSC.
- M. Vafaeinia, M. S. Khosrowshahi, H. Mashhadimoslem, H. B. M. Emrooz and A. Ghaemi, RSC Adv., 2022, 12, 546–560 RSC.
- M. S. Khosrowshahi, M. A. Abdol, H. Mashhadimoslem, E. Khakpour, H. B. M. Emrooz, S. Sadeghzadeh and A. Ghaemi, Sci. Rep., 2022, 12, 1–19 CrossRef PubMed.
- H. Mashhadimoslem, M. Safarzadeh Khosrowshahi, M. Jafari, A. Ghaemi and A. Maleki, ACS Omega, 2022, 7, 18409–18426 CrossRef CAS.
- M. S. Khosrowshahi, H. Mashhadimoslem, H. B. M. Emrooz, A. Ghaemi and M. S. Hosseini, Diamond Relat. Mater., 2022, 109204 CrossRef CAS.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj Comput. Mater., 2016, 2, 1–7 CrossRef.
- Y. Dong, C. Wu, C. Zhang, Y. Liu, J. Cheng and J. Lin, npj Comput. Mater., 2019, 5, 26 CrossRef.
- A. O. Oliynyk, L. A. Adutwum, B. W. Rudyk, H. Pisavadia, S. Lotfi, V. Hlukhyy, J. J. Harynuk, A. Mar and J. Brgoch, J. Am. Chem. Soc., 2017, 139, 17870–17881 CrossRef CAS.
- H. Mashhadimoslem, M. Vafaeinia, M. Safarzadeh, A. Ghaemi, F. Fathalian and A. Maleki, Ind. Eng. Chem. Res., 2021, 60, 13950–13966 CrossRef CAS.
- P. Raccuglia, K. C. Elbert, P. D. F. Adler, C. Falk, M. B. Wenny, A. Mollo, M. Zeller, S. A. Friedler, J. Schrier and A. J. Norquist, Nature, 2016, 533, 73–76 CrossRef CAS.
- D. T. Ahneman, J. G. Estrada, S. Lin, S. D. Dreher and A. G. Doyle, Science, 2018, 360, 186–190 CrossRef CAS.
- M. Rahimi, S. M. Moosavi, B. Smit and T. A. Hatton, Cell Rep. Phys. Sci., 2021, 2, 100396 CrossRef CAS.
- H. Mashhadimoslem, V. Kermani, K. Zanganeh, A. Shafeen and A. Elkamel, Can. J. Chem. Eng., 2023, 25060 CrossRef.
- H. Pashaei, H. Mashhadimoslem and A. Ghaemi, Sci. Rep., 2023, 13, 4011 CrossRef CAS.
- D. M. D'Alessandro, B. Smit and J. R. Long, Angew. Chem., Int. Ed., 2010, 49, 6058–6082 CrossRef PubMed.
- Z. Zhang, J. A. Schott, M. Liu, H. Chen, X. Lu, B. G. Sumpter, J. Fu and S. Dai, Angew. Chem., 2019, 131, 265–269 CrossRef.
- S. Wang, Z. Zhang, S. Dai and D. Jiang, ACS Mater. Lett., 2019, 1, 558–563 CrossRef CAS.
- X. Yuan, M. Suvarna, S. Low, D. Dissanayake, K. B. Lee, J. Li, X. Wang and Y. S. Ok, Environ. Sci. Technol., 2021, 55, 11925–11936 CrossRef CAS PubMed.
- X. Ma, W. Xu, R. Su, L. Shao, Z. Zeng, L. Li and H. Wang, Sep. Purif. Technol., 2023, 306, 122521 CrossRef CAS.
- C. Xie, Y. Xie, C. Zhang, H. Dong and L. Zhang, J. Environ. Chem. Eng., 2023, 11, 109053 CrossRef CAS.
- A. Ahmed, S. Seth, J. Purewal, A. G. Wong-Foy, M. Veenstra, A. J. Matzger and D. J. Siegel, Nat. Commun., 2019, 10, 1568 CrossRef PubMed.
- D. Alezi, Y. Belmabkhout, M. Suyetin, P. M. Bhatt, Ł. J. Weseliński, V. Solovyeva, K. Adil, I. Spanopoulos, P. N. Trikalitis and A.-H. Emwas, J. Am. Chem. Soc., 2015, 137, 13308–13318 CrossRef CAS.
- P. G. Boyd, A. Chidambaram, E. García-Díez, C. P. Ireland, T. D. Daff, R. Bounds, A. Gładysiak, P. Schouwink, S. M. Moosavi and M. M. Maroto-Valer, Nature, 2019, 576, 253–256 CrossRef CAS PubMed.
- Z. Yao, B. Sánchez-Lengeling, N. S. Bobbitt, B. J. Bucior, S. G. H. Kumar, S. P. Collins, T. Burns, T. K. Woo, O. K. Farha and R. Q. Snurr, Nat. Mach. Intell., 2021, 3, 76–86 CrossRef.
- Y. G. Chung, E. Haldoupis, B. J. Bucior, M. Haranczyk, S. Lee, H. Zhang, K. D. Vogiatzis, M. Milisavljevic, S. Ling and J. S. Camp, J. Chem. Eng. Data, 2019, 64, 5985–5998 CrossRef CAS.
- Q. Li, S. Gupta, L. Tang, S. Quinn, V. Atakan and R. E. Riman, Front. Energy Res., 2016, 3, 53 Search PubMed.
- S. Babamohammadi, A. Shamiri, T. N. G. Borhani, M. S. Shafeeyan, M. K. Aroua and R. Yusoff, J. Mol. Liq., 2018, 249, 40–52 CrossRef CAS.
- J. Krzywanski, T. Czakiert, T. Shimizu, I. Majchrzak-Kuceba, Y. Shimazaki, A. Zylka, K. Grabowska and M. Sosnowski, Energy & fuels, 2018, 32, 6355–6362 CrossRef CAS.
- Y. Yan, T. Mattisson, P. Moldenhauer, E. J. Anthony and P. T. Clough, Chem. Eng. J., 2020, 387, 124072 CrossRef CAS.
- Z. Zhang, X. Cao, C. Geng, Y. Sun, Y. He, Z. Qiao and C. Zhong, J. Membr. Sci., 2022, 650, 120399 CrossRef CAS.
- J. Guan, T. Huang, W. Liu, F. Feng, S. Japip, J. Li, X. Wang and S. Zhang, Cell Rep. Phys. Sci., 2022, 3, 100864 CrossRef CAS.
- W. Gao, S. Wang, W. Zheng, W. Sun and L. Zhao, Sep. Purif. Technol., 2023, 313, 123469 CrossRef CAS.
- P. Krokidas, S. Karozis, S. Moncho, G. Giannakopoulos, E. N. Brothers, M. E. Kainourgiakis, I. G. Economou and T. A. Steriotis, J. Mater. Chem. A, 2022, 10, 13697–13703 RSC.
- S. Yang, W. Zhu, L. Zhu, X. Ma, T. Yan, N. Gu, Y. Lan, Y. Huang, M. Yuan and M. Tong, ACS Appl. Mater. Interfaces, 2022, 14, 56353–56362 CrossRef CAS.
- X. Cheng, Y. Liao, Z. Lei, J. Li, X. Fan and X. Xiao, J. Membr. Sci., 2023, 672, 121430 CrossRef CAS.
- Q. Zhu, Y. Gu, X. Liang, X. Wang and J. Ma, ACS Catal., 2022, 12, 12336–12348 CrossRef CAS.
- B. M. Kriesche, L. E. Kronenberg, F. R. S. Purtscher and T. S. Hofer, Front. Chem., 2023, 11, 210 Search PubMed.
- M. Feng, M. Cheng, X. Ji, L. Zhou, Y. Dang, K. Bi, Z. Dai and Y. Dai, Sep. Purif. Technol., 2022, 302, 122111 CrossRef CAS.
- A. Sturluson, A. Raza, G. D. McConachie, D. W. Siderius, X. Z. Fern and C. M. Simon, Chem. Mater., 2021, 33, 7203–7216 CrossRef CAS.
- A. Kondinski, A. Menon, D. Nurkowski, F. Farazi, S. Mosbach, J. Akroyd and M. Kraft, J. Am. Chem. Soc., 2022, 144, 11713–11728 CrossRef CAS PubMed.
- M. Raji, A. Dashti, M. S. Alivand and M. Asghari, J. Environ. Manage., 2022, 307, 114478 CrossRef CAS PubMed.
- S. Zhang, H. Dong, A. Lin, C. Zhang, H. Du, J. Mu, J. Han, J. Zhang and F. Wang, ACS Sustain. Chem. Eng., 2022, 10, 13185–13193 CrossRef CAS.
- B. Yan, D. R. Harp, B. Chen and R. J. Pawar, Sci. Rep., 2022, 12, 20667 CrossRef CAS.
- Q. Yuan, M. Longo, A. W. Thornton, N. B. McKeown, B. Comesana-Gandara, J. C. Jansen and K. E. Jelfs, J. Membr. Sci., 2021, 627, 119207 CrossRef CAS.
- A. J. Yamaguchi, T. Sato, T. Tobase, X. Wei, L. Huang, J. Zhang, J. Bian and T.-Y. Liu, Fuel, 2023, 334, 126678 CrossRef.
- J. C. Pashin and R. L. Dodge, Carbon Dioxide Sequestration in Geological Media: State of the Science, AAPG Studies in Geology, 2010, vol. 59, p. 59 Search PubMed.
- H. V. Thanh, Q. Yasin, W. J. Al-Mudhafar and K.-K. Lee, Appl. Energy, 2022, 314, 118985 CrossRef.
- F. Pappenberger, P. Matgen, K. J. Beven, J.-B. Henry, L. Pfister and P. Fraipont, Adv. Water Resour., 2006, 29, 1430–1449 CrossRef.
- J. Teng, A. J. Jakeman, J. Vaze, B. F. W. Croke, D. Dutta and S. Kim, Environ. Model. Softw., 2017, 90, 201–216 CrossRef.
- P. Hamel, D. Riveros-Iregui, D. Ballari, T. Browning, R. Célleri, D. Chandler, K. P. Chun, G. Destouni, S. Jacobs, S. Jasechko, M. Johnson, J. Krishnaswamy, M. Poca, P. V. Pompeu and H. Rocha, in Ecohydrology, John Wiley and Sons Ltd, 2018, vol. 11 Search PubMed.
- K. Khosravi, R. Barzegar, S. Miraki, J. Adamowski, P. Daggupati, M. R. Alizadeh, B. T. Pham and M. T. Alami, Groundwater, 2020, 58, 723–734 CrossRef CAS.
- Z. Abdulelah Al-Sudani, S. Q. Salih, A. sharafati and Z. M. Yaseen, J. Hydrol., 2019, 573, 1–12 CrossRef.
- D. T. Bui, K. Khosravi, J. Tiefenbacher, H. Nguyen and N. Kazakis, Sci. Total Environ., 2020, 721, 137612 CrossRef CAS PubMed.
- K. Khosravi, M. Bordbar, S. Paryani, P. M. Saco and N. Kazakis, Sci. Total Environ., 2021, 767, 145416 CrossRef CAS PubMed.
- P. Tahmasebi, S. Kamrava, T. Bai and M. Sahimi, Adv. Water Resour., 2020, 142, 103619 CrossRef.
- K. Khosravi, A. Golkarian, P. M. Saco, M. J. Booji and A. M. Melesse, Geocarto Int., 2022, 37(27), 18520–18545 CrossRef.
- W. Brutsaert, Hydrology, Cambridge University Press, 2005 Search PubMed.
- M. Panahi, K. Khosravi, S. Ahmad, S. Panahi, S. Heddam, A. M. Melesse, E. Omidvar and C. W. Lee, J. Hydrol. Reg. Stud., 2021, 35, 100825 CrossRef.
- Z. U. Rehman, U. Khalid, N. Ijaz, H. Mujtaba, A. Haider, K. Farooq and Z. Ijaz, Eng. Geol., 2022, 311, 106899 CrossRef.
- Y. Lu and G. Mei, Mathematics, 2022, 10, 2949 CrossRef.
- S. Muhammed Pandhiani, Arabian J. Geosci., 2022, 15, 1068 CrossRef.
- S. Prakash and S. S. Sahu, Int. J. Adv. Res. Sci. Eng. Technol., 2020, 11(6), 426–435 Search PubMed.
- A. Singh and K. Gaurav, Sci. Rep., 2023, 13, 2251 CrossRef CAS.
- A. Uthayakumar, M. P. Mohan, E. H. Khoo, J. Jimeno, M. Y. Siyal and M. F. Karim, Sensors, 2022, 22, 5810 CrossRef PubMed.
- C. Hulbert, B. Rouet-Leduc, P. A. Johnson, C. X. Ren, J. Rivière, D. C. Bolton and C. Marone, Nat. Geosci., 2019, 12, 69–74 CrossRef CAS.
- C. Kadow, D. M. Hall and U. Ulbrich, Nat. Geosci., 2020, 13, 408–413 CrossRef CAS.
- C. Marone, Nat. Geosci., 2018, 11, 301–302 CrossRef CAS.
- S. Sahour, M. Khanbeyki, V. Gholami, H. Sahour, I. Kahvazade and H. Karimi, Environ. Sci. Pollut. Res., 2023, 30, 46004–46021 CrossRef CAS.
- F. Sajedi-Hosseini, A. Malekian, B. Choubin, O. Rahmati, S. Cipullo, F. Coulon and B. Pradhan, Sci. Total Environ., 2018, 644, 954–962 CrossRef CAS.
- M. Zhu, J. Wang, X. Yang, Y. Zhang, L. Zhang, H. Ren, B. Wu and L. Ye, Eco-Environment & Health, 2022, 1, 107–116 Search PubMed.
- S. Kumar and J. Pati, J. Water Health, 2022, 20, 829–848 CrossRef CAS PubMed.
- A. O. Meray, S. Sturla, M. R. Siddiquee, R. Serata, S. Uhlemann, H. Gonzalez-Raymat, M. Denham, H. Upadhyay, L. E. Lagos, C. Eddy-Dilek and H. M. Wainwright, Environ. Sci. Technol., 2022, 56, 5973–5983 CrossRef CAS PubMed.
- B. Berhanu, Y. Seleshi and A. M. Melesse, in Nile River Basin: Ecohydrological Challenges, Climate Change and Hydropolitics, Springer International Publishing, 2014, pp. 97–117 Search PubMed.
- C. R. Fitts, Groundwater Science, Elsevier, 2nd edn, 2012 Search PubMed.
- M. K. Jha, A. Chowdhury, V. M. Chowdary and S. Peiffer, Water Resour. Manage., 2007, 21, 427–467 CrossRef.
- S. Mukherjee, Hydrogeol J., 1996, 19, 53–64 Search PubMed.
- H. P. Patra, S. K. Adhikari and S. Kunar, Groundwater Geology and Geological Prospecting, in Groundwater Prospecting and Management, Springer Hydrogeology, Springer, Singapore, 2016, pp. 47–51 Search PubMed.
- A. S. Richey, B. F. Thomas, M. H. Lo, J. T. Reager, J. S. Famiglietti, K. Voss, S. Swenson and M. Rodell, Water Resour. Res., 2015, 51, 5217–5238 CrossRef.
- S. Siebert, V. Henrich, K. Frenken and J. Burke, Update of the Digital Global Map of Irrigation Areas to Version 5, 2013 Search PubMed.
- A. E. Ercin and A. Y. Hoekstra, Environ. Int., 2014, 64, 71–82 CrossRef PubMed.
- A. Ozdemir, J. Hyd., 2011, 405, 123–136 CrossRef.
- M. Israil, M. Al-hadithi and D. C. Singhal, Hydrogeol J., 2006, 14, 753–759 CrossRef CAS.
- O. A. Fashae, M. N. Tijani, A. O. Talabi, • Oluwatola and I. Adedeji, Appl. Water Sci., 2013, 4, 19–38 CrossRef.
- K. Khosravi, M. Panahi and D. Tien Bui, Hydrol. Earth Syst. Sci., 2018, 22, 4771–4792 CrossRef.
- W. L. Hakim, A. S. Nur, F. Rezaie, M. Panahi, C.-W. Lee and S. Lee, J. Hydrol. Reg. Stud., 2022, 39, 100990 CrossRef.
- H. Morgan, A. Madani, H. M. Hussien and T. Nassar, Geosci. Lett., 2023, 10(9) DOI:10.1186/s40562-023-00261-2.
- L. Aller, T. Bennett, J. H. Lehr, R. J. Petty and G. Hackett, Robert S. Kerr Environmental Research Laboratory, Office of Research and Development, US Environmental Protection Agency, 1987 Search PubMed.
- S. Ijlil, A. Essahlaoui, M. Mohajane, N. Essahlaoui, E. M. Mili and A. Van Rompaey, Remote Sens., 2022, 14, 2379 CrossRef.
- K. Khosravi, M. Sartaj, F. T. C. Tsai, V. P. Singh, N. Kazakis, A. M. Melesse, I. Prakash, D. Tien Bui and B. T. Pham, Sci. Total Environ., 2018, 642, 1032–1049 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta00251b |
| This journal is © The Royal Society of Chemistry 2024 |