Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Rethinking the existence of hexagonal sodium zirconate CO2 sorbent†
Ribooga
Chang
 a,
Ashok S.
Menon
a,
Ashok S.
Menon
 b,
Erik
Svensson Grape
b,
Erik
Svensson Grape
 c,
Peter
Broqvist
d,
A. Ken
Inge
c,
Peter
Broqvist
d,
A. Ken
Inge
 c and
Ocean
Cheung
c and
Ocean
Cheung
 *a
*a
aDivision of Nanotechnology and Functional Materials, Department of Materials Science and Engineering, Uppsala University, Ångström Laboratory, Box 35, Uppsala SE-751 03, Sweden. E-mail: ocean.cheung@angstrom.uu.se
bWMG, University of Warwick, Coventry CV4 7AL, UK
cDepartment of Materials and Environmental Chemistry, Stockholm University, SE-10691, Sweden
dDepartment of Chemistry – Ångström Laboratory, Uppsala University, Box 538, 75121 Uppsala, Sweden
First published on 20th May 2024
Abstract
Sodium zirconate (sodium zirconium oxide; Na2ZrO3) is a widely investigated carbon dioxide (CO2) sorbent. Since it was first discussed in the 1960s, Na2ZrO3 has been reported to adopt monoclinic, hexagonal, and cubic structures, and it is widely believed that the CO2 capture performance of Na2ZrO3 is related to its crystal structure. Researchers have relied on the differences in the relative intensities of two peaks (2θ ∼16.2° and 38.7°) in the powder X-ray diffraction (PXRD) pattern to determine the phase of this compound. However, to date, a defined crystal structure of hexagonal Na2ZrO3 has remained elusive. Our findings show that the current literature discussion on the structure of Na2ZrO3 is misleading. With the use of 3D electron diffraction (3D ED), and PXRD, we prove that hexagonal Na2ZrO3 does not exist. The so-called hexagonal Na2ZrO3 is actually Na2ZrO3 with three different types of disorder. Furthermore, the two PXRD peaks (2θ ∼16.2° and 38.7°) cannot be used to distinguish the different phases of Na2ZrO3, as the change in the PXRD pattern is related to the extent of structure disorder. Finally, we also show that the CO2 uptake properties of Na2ZrO3 are not related to the differences in crystal structures, but rather to the Na+ site occupancy differences in different Na2ZrO3 samples. In order to further develop applications of Na2ZrO3, as well as other mixed-metal oxides, their structures, and the existence of any disorder, need be understood using the methods shown in this study.
Introduction
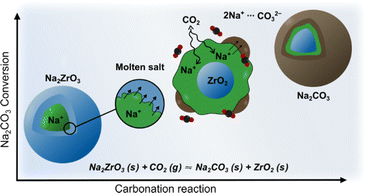
Sodium zirconate (sodium zirconium oxide; Na2ZrO3) is a widely investigated mixed-metal oxide carbon dioxide (CO2) sorbent.1 It has a theoretical maximum CO2 uptake of 23.8 wt% and good cyclic stability,2,3 it can also take up CO2 across a wide temperature range (150 °C to 800 °C).4–7 Generally, Na2ZrO3 is produced by solid-state synthesis using Na2CO3 and ZrO2, neither of which react with CO2 individually. The resulting Na2ZrO3 captures CO2 using the molten salt effect (Fig. 1),8–10 which arises from the mobility of Na+ within Na2ZrO3. Once the Na+ on the surface of the particle reacts with CO2, a carbonate layer forms. The high mobility of Na+ within the particle allows for further reactions between the carbonate layer and the inner core. The carbonate layer can then “migrate” toward the core of the particle to enable further reaction between CO2 and Na+ on the surface.7,11,12 Previous literature suggests that the CO2 uptake and thermodynamic stability of the different phases of Na2ZrO3 vary depending on their crystal structures.7,13,14 For high-temperature (>650 °C) CO2 capture, it is generally believed that hexagonal Na2ZrO3 has the highest carbonation/calcination cyclic stability, while monoclinic Na2ZrO3 possesses the highest CO2 uptake.14,15The different phases of Na2ZrO3 reported in the literature are monoclinic (ICDD 00-035-0770 and 04-009-1070), hexagonal (ICDD 00-021-1179) and cubic (ICDD 04-006-4959, 04-011-5935, and 04-011-5936). Monoclinic and cubic Na2ZrO3 obtained by solid-state synthesis were reported by Claverie et al. in 1966.16 In 1968, Ampian17 indexed the PXRD pattern of Na2ZrO3 to a unit cell with a = b = 18.612 Å, c = 10.965 Å, α = β = 90°, γ = 120° with extinction conditions consistent with the hexagonal space groups P63, P63/m or P6322 (although no structure was reported then or has been since). This form is referred to as “hexagonal Na2ZrO3” as discussed above. The monoclinic and hexagonal forms of Na2ZrO3 are often considered to have very similar peak positions in their PXRD patterns.7,18 However, Na2ZrO3 with a hexagonal space group should yield extra PXRD peaks over the monoclinic Na2ZrO3, but this is not discussed in the literature. Until now, researchers have solely relied upon the differences in the relative peak intensities of two PXRD peak to distinguish between monoclinic and hexagonal Na2ZrO3.7,14,15,18 It is believed that for monoclinic Na2ZrO3, the PXRD peak at 2θ ∼38.7° (d = ∼2.3 Å, Cu Kα radiation) has the highest relative intensity, while for the hexagonal Na2ZrO3 the PXRD peak at 2θ ∼16.2° (d = ∼5.4 Å) has the highest relative intensity.7,14,15,18 The intensities of other peaks have not been considered in phase identification. Furthermore, there are inconsistencies in the literature regarding the relative intensities of the two peaks at 2θ ∼16.2° and 38.7°, as well as on how the Na2ZrO3 phases can be identified.7,14,15,18 For example, Na2ZrO3 samples from different studies have been identified as hexagonal simply because the highest relative peak intensity was observed at 2θ ∼16.2° (relative intensity ratio: I/Imax = 1), even though the peak at 2θ ∼38.7° showed a range of different relative intensities, i.e. I/Imax ranging from 0.52 to 0.98.14,15,18
Despite the wide consensus about the phase identification of Na2ZrO3 using PXRD peak intensities, surprisingly little information is available on (1) why the expected extra PXRD peaks for the hexagonal Na2ZrO3 are not observed nor discussed and (2) how the differences of these phases relate to their CO2 uptake properties. Through the use of a wide range of characterization techniques, we provide some crucial new understanding about the structure–property relationships of different variants of Na2ZrO3 that are commonly discussed in the literature.
Results and discussion
We synthesized two Na2ZrO3 samples by solid-state synthesis (Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZrO2 = 1.5
ZrO2 = 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
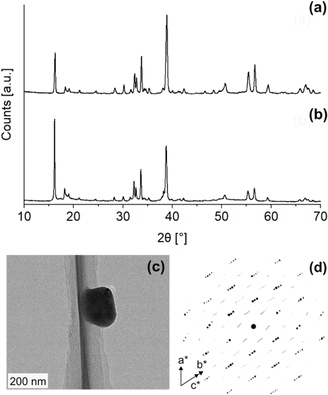
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 at 900 °C under 100% N2 for two and five hours) according to literature procedures and obtained two samples that had highest relative PXRD peak intensities at different 2θ (Fig. 2a and b): one sample at 2θ = 16.2° (d = ∼5.4 Å, Cu Kα radiation) and the other at 2θ = 38.7° (d = ∼2.3 Å). As per the existing literature, these two samples were identified as monoclinic (Fig. 2a, NZO-M) and hexagonal (Fig. 2b, NZO-H).7,15,18 Note that the PXRD patterns showed that the samples did not contain other peaks apart from Na2CO3, ZrO2 and Na2ZrO3. The excess Na
1 at 900 °C under 100% N2 for two and five hours) according to literature procedures and obtained two samples that had highest relative PXRD peak intensities at different 2θ (Fig. 2a and b): one sample at 2θ = 16.2° (d = ∼5.4 Å, Cu Kα radiation) and the other at 2θ = 38.7° (d = ∼2.3 Å). As per the existing literature, these two samples were identified as monoclinic (Fig. 2a, NZO-M) and hexagonal (Fig. 2b, NZO-H).7,15,18 Note that the PXRD patterns showed that the samples did not contain other peaks apart from Na2CO3, ZrO2 and Na2ZrO3. The excess Na![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) Zr ratio (1.5
Zr ratio (1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) used in the synthesis of Na2ZrO3 here is in-line with synthesis methods presented in various literature (with up to 2
1) used in the synthesis of Na2ZrO3 here is in-line with synthesis methods presented in various literature (with up to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 reported earlier).18–21 To the best of our knowledge, there is no literature evidence that suggests the excess Na changes the inherent structure of Na2ZrO3. Also note that the syntheses were repeated a number of times to ensure reproducibility of the representative PXRD patterns. In order to investigate the structure of the hexagonal Na2ZrO3, 3D electron diffraction (3D ED) was performed on NZO-H as shown in Fig. 2c. Surprisingly, the reconstructed 3D ED data of NZO-H, as depicted in Fig. 2d, exhibited a combination of distinct reflections, as well as lines of clear diffuse scattering along c*. The presence of diffuse scattering indicates structural disorder, specifically stacking faults in the structure that may arise from the non-periodic arrangement of Na+ and Zr4+ in alternating layers along the stacking direction. The distinct 3D ED reflections alone were indexed with the unit cell parameters a = b = 3.393 Å, c = 17.029 Å, α = β = 90°, γ = 120°, and systematic absences suggested R
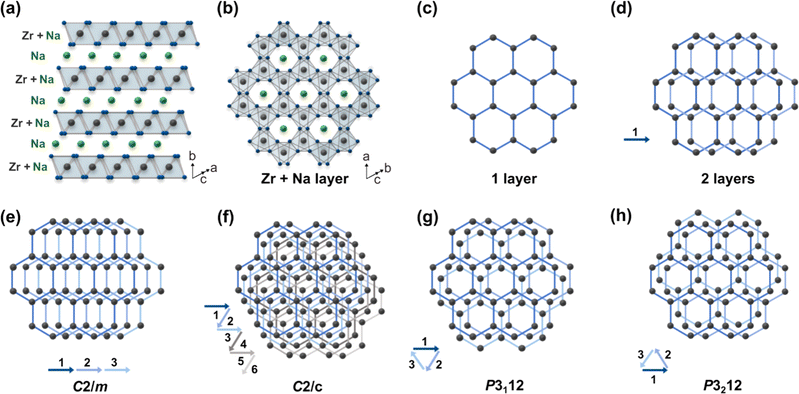
1 reported earlier).18–21 To the best of our knowledge, there is no literature evidence that suggests the excess Na changes the inherent structure of Na2ZrO3. Also note that the syntheses were repeated a number of times to ensure reproducibility of the representative PXRD patterns. In order to investigate the structure of the hexagonal Na2ZrO3, 3D electron diffraction (3D ED) was performed on NZO-H as shown in Fig. 2c. Surprisingly, the reconstructed 3D ED data of NZO-H, as depicted in Fig. 2d, exhibited a combination of distinct reflections, as well as lines of clear diffuse scattering along c*. The presence of diffuse scattering indicates structural disorder, specifically stacking faults in the structure that may arise from the non-periodic arrangement of Na+ and Zr4+ in alternating layers along the stacking direction. The distinct 3D ED reflections alone were indexed with the unit cell parameters a = b = 3.393 Å, c = 17.029 Å, α = β = 90°, γ = 120°, and systematic absences suggested R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry. Generally, stacking disorder affects relative PXRD peak intensities and peak shapes.22 The presence of disorder also meant that structure solutions of these samples could not be determined using the 3D ED data. The distinct reflections and lines of diffuse scattering in the 3D ED data prompted us to further investigate these structures. Based on the 3D ED data, the structure was able to be established using three elements of Na, Zr, and O. The Na+ and Zr4+ cations are octahedrally coordinated to O2− anions, and the structure is composed of alternating Na+ and Na+ + Zr4+ cation layers. The existence of mixed-metal cation layers is common in mixed-metal oxides with a general formula of A21+B4+O3 (A+ = Li+, Na+, K+, etc.; B4+ = Mn4+, Ti4+, etc.).22–25 In the Na+ + Zr4+ mixed-metal layers, the Na+ and Zr4+ cations form a hexagonal arrangement to minimize the coulombic repulsion between the cations (Fig. 3a and b).26
m space group symmetry. Generally, stacking disorder affects relative PXRD peak intensities and peak shapes.22 The presence of disorder also meant that structure solutions of these samples could not be determined using the 3D ED data. The distinct reflections and lines of diffuse scattering in the 3D ED data prompted us to further investigate these structures. Based on the 3D ED data, the structure was able to be established using three elements of Na, Zr, and O. The Na+ and Zr4+ cations are octahedrally coordinated to O2− anions, and the structure is composed of alternating Na+ and Na+ + Zr4+ cation layers. The existence of mixed-metal cation layers is common in mixed-metal oxides with a general formula of A21+B4+O3 (A+ = Li+, Na+, K+, etc.; B4+ = Mn4+, Ti4+, etc.).22–25 In the Na+ + Zr4+ mixed-metal layers, the Na+ and Zr4+ cations form a hexagonal arrangement to minimize the coulombic repulsion between the cations (Fig. 3a and b).26
This ordered arrangement gives rise to superstructure reflections in the 3D ED and PXRD patterns that cannot be indexed by hexagonal R![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m space group symmetry. The crystallographic sites in this layer are occupied by Na+ and Zr4+ with a ratio of 1
m space group symmetry. The crystallographic sites in this layer are occupied by Na+ and Zr4+ with a ratio of 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2. The Na+ + Zr4+ layers can be stacked in the ways as shown in Fig. 3e–h (arrows show the layer numbers) with no other stacking possibilities. These stacking sequences, if they were to be perfectly ordered throughout a material, would have the monoclinic space groups C2/m and C2/c and the trigonal space groups P3112 and P3212. Some of these Na2ZrO3 stacking sequences and space groups have been observed previously for other mixed-metal oxides, such as C2/c in Li2TiO3 and C2/m in Li2MnO3.27 However, none of the simulated PXRD patterns of these four idealized Na2ZrO3 structures exhibit its highest relative peak intensity at 2θ = 16.2° (ESI Fig. S1†). We therefore considered if stacking faults (or disorder) could play a role in the relative peak intensities of these two peaks. Previous studies have reported the presence of stacking faults in similar mixed-metal oxides, such as Na2HfO3 and Li2MnO3.22–24,28 Indeed, the streaks seen in the 3D ED data of NZO-M and NZO-H (Fig. 2d) point to disorder in the stacking of the Na+ + Zr4+ layers. As a first step, we simulated the diffraction pattern of Na2ZrO3 with 0 to 100% stacking faults using the software DIFFaX (sections in SI2.1 and SI2.2†).29,30 We observed changes in the peak shapes and relative intensities of the superstructure reflections with different levels of stacking faults as shown in Fig. 4a and b, especially for the five peaks at 2θ = 18.2°, 19.0°, 21.2°, 24.4°, and 28.4° (020, −110, −111, 0−21, and 1−11, as per the C2/m symmetry, respectively). Increased stacking faults generally led to broadening of these peaks, with the 020 reflection showing a distinct asymmetric character. In the experimental PXRD patterns of NZO-M and NZO-H (Fig. 1), the peaks at 18.2° and 19.0° show noticeable peak asymmetry.
2. The Na+ + Zr4+ layers can be stacked in the ways as shown in Fig. 3e–h (arrows show the layer numbers) with no other stacking possibilities. These stacking sequences, if they were to be perfectly ordered throughout a material, would have the monoclinic space groups C2/m and C2/c and the trigonal space groups P3112 and P3212. Some of these Na2ZrO3 stacking sequences and space groups have been observed previously for other mixed-metal oxides, such as C2/c in Li2TiO3 and C2/m in Li2MnO3.27 However, none of the simulated PXRD patterns of these four idealized Na2ZrO3 structures exhibit its highest relative peak intensity at 2θ = 16.2° (ESI Fig. S1†). We therefore considered if stacking faults (or disorder) could play a role in the relative peak intensities of these two peaks. Previous studies have reported the presence of stacking faults in similar mixed-metal oxides, such as Na2HfO3 and Li2MnO3.22–24,28 Indeed, the streaks seen in the 3D ED data of NZO-M and NZO-H (Fig. 2d) point to disorder in the stacking of the Na+ + Zr4+ layers. As a first step, we simulated the diffraction pattern of Na2ZrO3 with 0 to 100% stacking faults using the software DIFFaX (sections in SI2.1 and SI2.2†).29,30 We observed changes in the peak shapes and relative intensities of the superstructure reflections with different levels of stacking faults as shown in Fig. 4a and b, especially for the five peaks at 2θ = 18.2°, 19.0°, 21.2°, 24.4°, and 28.4° (020, −110, −111, 0−21, and 1−11, as per the C2/m symmetry, respectively). Increased stacking faults generally led to broadening of these peaks, with the 020 reflection showing a distinct asymmetric character. In the experimental PXRD patterns of NZO-M and NZO-H (Fig. 1), the peaks at 18.2° and 19.0° show noticeable peak asymmetry.
Qualitatively, the PXRD patterns of NZO-M and NZO-H suggest that these two samples had 30–50% and over 60% stacking faults, respectively. Similar asymmetric PXRD peaks have been observed in other studies on Na2ZrO3, suggesting that stacking faults were also present in Na2ZrO3 in those studies.2–7,13–15,18,19,25,31 Despite obvious changes with the PXRD patterns due to stacking faults, the relative intensities of the peaks at 2θ = 16.2° and 38.7° were unaffected in the simulated PXRD patterns of Na2ZrO3 with different degrees of stacking faults.
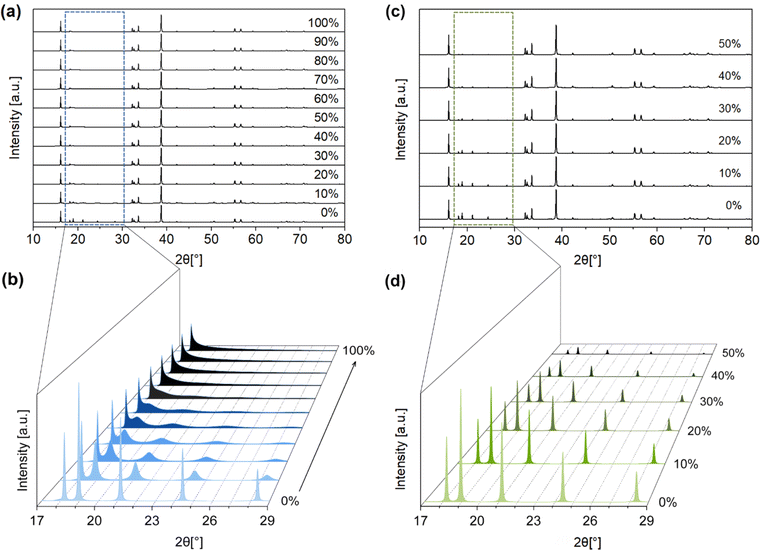
Apart from stacking faults, we considered two other types of disorder that may affect the PXRD pattern of Na2ZrO3. The first type of disorder is the effect of cation site mixing, where the Na+ and Zr4+ occupancies of the two sites (in the mixed-metal layer) are interchanged. We systematically simulated the PXRD patterns of Na2ZrO3 with 10% to 50% site mixing (Fig. 4c and d) using DIFFaX. Again, changes in the intensities of the five peaks between 2θ = 18.2° and 28.4° (the same 2θ range as for stacking faults) were observed. The peak intensities decreased with increased cation site mixing. However, no change in the peak shape was observed, in contrast to what was observed for stacking faults.
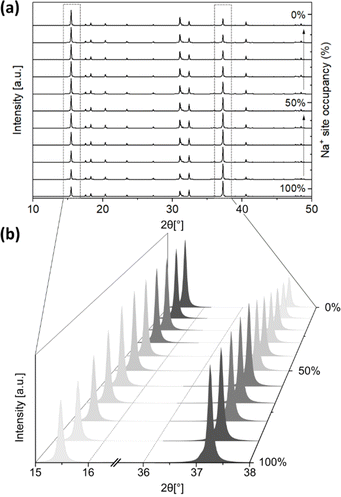
The second type of disorder is related to Na+ site occupancy (along with O2− site occupancy, with the Na+ and O2− site vacancy ratio set to 2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1), which is influenced by the presence or formation of Na2CO3 during the solid-state synthesis, and the product of carbonation. The simulated PXRD patterns of monoclinic Na2ZrO3 (C2/m) with varied Na+ occupancies were obtained using the software Diamond. The location of the Na+ site has two possibilities: Na+ sites in the Na layer, and Na+ sites in the Na+ + Zr4+ layer. We varied the Na+ site occupancy of these two sites independently in our simulations, but we are aware that changes in Na+ site occupancy are likely to happen simultaneously at both sites. The Na+ site occupancy of the Na layer had a noticeable effect on the relative intensity of the PXRD peak at 2θ ∼16.2° and 38.7°. As shown in Fig. 5a and b, when the Na+ site occupancy of the Na layer was reduced from 100% to 0%, the relative intensity of the peak at 2θ ∼16.2° increased and the opposite was true for the peak at 2θ ∼38.7° (Fig. S19–S29†). At below 50% Na+ site occupancy of the Na layer, the relative intensity of the peak at 2θ ∼16.2° became higher than the peak at 2θ ∼38.7° (Table 1). These simulations suggested that when the Na+ site occupancy of the Na layer is below 50%, the PXRD pattern of Na2ZrO3 would resemble what is typically considered as hexagonal Na2ZrO3 in the literature (according to the relative intensities of these two peaks). On the other hand, varying the Na+ site occupancy of the Na+ + Zr4+ layer did not affect the relative intensity of the peaks at 2θ ∼16.2° and 38.7° (Fig. S30–S41†).
1), which is influenced by the presence or formation of Na2CO3 during the solid-state synthesis, and the product of carbonation. The simulated PXRD patterns of monoclinic Na2ZrO3 (C2/m) with varied Na+ occupancies were obtained using the software Diamond. The location of the Na+ site has two possibilities: Na+ sites in the Na layer, and Na+ sites in the Na+ + Zr4+ layer. We varied the Na+ site occupancy of these two sites independently in our simulations, but we are aware that changes in Na+ site occupancy are likely to happen simultaneously at both sites. The Na+ site occupancy of the Na layer had a noticeable effect on the relative intensity of the PXRD peak at 2θ ∼16.2° and 38.7°. As shown in Fig. 5a and b, when the Na+ site occupancy of the Na layer was reduced from 100% to 0%, the relative intensity of the peak at 2θ ∼16.2° increased and the opposite was true for the peak at 2θ ∼38.7° (Fig. S19–S29†). At below 50% Na+ site occupancy of the Na layer, the relative intensity of the peak at 2θ ∼16.2° became higher than the peak at 2θ ∼38.7° (Table 1). These simulations suggested that when the Na+ site occupancy of the Na layer is below 50%, the PXRD pattern of Na2ZrO3 would resemble what is typically considered as hexagonal Na2ZrO3 in the literature (according to the relative intensities of these two peaks). On the other hand, varying the Na+ site occupancy of the Na+ + Zr4+ layer did not affect the relative intensity of the peaks at 2θ ∼16.2° and 38.7° (Fig. S30–S41†).
| Na+ site occupancy (%) | 2θ peak position [°] | |
|---|---|---|
| 16.2 | 38.7 | |
| 100% | 0.56 | 1.00 |
| 90% | 0.64 | 1.00 |
| 80% | 0.74 | 1.00 |
| 70% | 0.85 | 1.00 |
| 60% | 0.98 | 1.00 |
| 50% | 1.00 | 0.89 |
| 40% | 1.00 | 0.68 |
| 30% | 1.00 | 0.78 |
| 20% | 1.00 | 0.59 |
| 10% | 1.00 | 0.52 |
| 0% | 1.00 | 0.45 |
As demonstrated, a number of factors could affect the PXRD pattern, and especially the relative peak intensities and peak shapes of Na2ZrO3. We therefore propose that the commonly adopted method for phase identification of Na2ZrO3 (by comparing the relative peak intensities of the two peaks) should be reconsidered for two reasons: (1) disordered Na2ZrO3, which has superstructure reflections, cannot be indexed using a hexagonal space group (2) the changes in the relative peak intensities of the peaks at 2θ ∼16.2° and 38.7° are, in fact, related to the Na+ site occupancy of the Na layer, rather than the existence of hexagonal Na2ZrO3. In addition, when examining the PXRD patterns of Na2ZrO3 samples, the relative peak intensities and shapes of the peaks between 2θ = 18.2° and 28.4° provide an indication of the number of stacking faults and the level of cation site mixing disorder. According to our findings, these types of disorders are common in Na2ZrO3, especially as the common synthesis method for Na2ZrO3 is high-temperature solid-state synthesis, which can yield metastable or non-equilibrium structures. Even though solid-state synthesis has several advantages, such as low cost, simplicity, and low by-product production, obtaining a homogeneous product is often challenging. Furthermore, various synthesis conditions such as the Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZrO2 ratio, synthesis temperature and time, could affect the magnitude of disorder.18 Solid-state synthesis has been frequently adopted in previous studies on Na2ZrO3 CO2 sorbents where the differences between “monoclinic” and “hexagonal” Na2ZrO3 has been often discussed. In this study, we have repeated the synthesis a number of times to ensure that the presented PXRD patterns are reproducible.
ZrO2 ratio, synthesis temperature and time, could affect the magnitude of disorder.18 Solid-state synthesis has been frequently adopted in previous studies on Na2ZrO3 CO2 sorbents where the differences between “monoclinic” and “hexagonal” Na2ZrO3 has been often discussed. In this study, we have repeated the synthesis a number of times to ensure that the presented PXRD patterns are reproducible.
Based on disorder simulations, we show that the presumption that monoclinic and hexagonal Na2ZrO3 are distinct crystal structures is not accurate. The difference in relative peak intensities in the PXRD pattern of the so-called hexagonal Na2ZrO3 is in fact related to Na+ site occupancy of the Na layer and varying levels of disorder. Our findings also support the fact that the monoclinic and the hexagonal structures cannot have the same reflections. If the monoclinic and the hexagonal Na2ZrO3 were to exist as distinct structures, there would be a different number of peaks in PXRD patterns for each structure due to the different number of reflections.
We further examined the effect of disorder on the CO2 uptake properties of the NZO-M and NZO-H we synthesized (Fig. 2). After synthesis, both NZO-M and NZO-H underwent a single CO2 carbonation/calcination cycle. After the sample had gone through one carbonation/calcination cycle, we noted a mass increase of 8 wt% on the calcined sample (Fig. S42†). This mass increase suggests that some minor amounts of the Na2CO3 formed during the initial carbonation step could not be calcined, regardless of the calcination time. The presence of Na2CO3 on the calcined NZO samples implies that the Na+ and O2− contents in the Na2ZrO3 part of the sorbent (Fig. 1) decreased (i.e. to give reduced Na+ and O2− site occupancy) and calcination at 900 °C and extended calcination times were unable to fully reverse the carbonation reaction. Interestingly, the relative peak intensities of the peaks at 2θ ∼16.2° and 38.7° on NZO-M changed after one carbonation/calcination cycle (Fig. S43†). The PXRD pattern of NZO-M after the carbonation/calcination cycle resembled the PXRD pattern of NZO-H, or the so-called hexagonal Na2ZrO3 (calcined NZO-H). The changes in relative peak intensities of the two PXRD peaks suggested that after one cycle, there was a decrease in Na+ and O2− site occupancy in NZO-M due to the formation of Na2CO3. We observed the same minor weight increase related to Na2CO3 as well as the same changes in the PXRD pattern after carbonation/calcination cycles for calcined Na2ZrO3 synthesised with Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZrO2 ratios varying from 0.75, 1, 1.25 and 1.5, all of which showed similar PXRD pattern to NZO-M directly after solid-state synthesis (Fig. S44 and S45†).
ZrO2 ratios varying from 0.75, 1, 1.25 and 1.5, all of which showed similar PXRD pattern to NZO-M directly after solid-state synthesis (Fig. S44 and S45†).
NZO-M and NZO-H underwent 20 carbonation/calcination cycles (at 750 °C and 900 °C, respectively, with one hour equilibrium time) as shown in Fig. 6. These experiments were carried out under pure gas conditions with no contact to ambient air or moisture. The CO2 uptake of NZO-M and NZO-H at the end of the first cycle was 11.35 and 13.25 wt% (2.58 and 3.01 mmol g−1), respectively. This confirms that NZO-M (i.e., the monoclinic phase in the literature) does indeed have higher CO2 uptake than the disordered NZO-H at the first cycle. However, the CO2 uptake for both samples fluctuated at the end of the subsequent few cycles. Above 13th cycles, the CO2 uptake appeared to have stabilized. At the 20th cycle, the CO2 uptake of NZO-M and NZO-H was comparable at 16.90 and 17.87 wt% (3.84 and 4.06 mmol g−1), respectively (note that small difference in the CO2 uptake was also related to synthesis batch variations, which was previously discussed24).
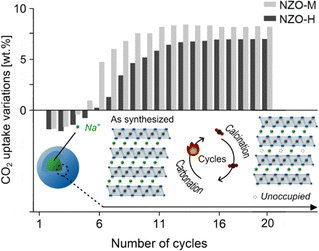 | ||
| Fig. 6 CO2 capture properties over 20 carbonation/calcination cycles on the synthesized NZO-M and NZO-H. | ||
These observations could be explained as follows:
(1) Directly after synthesis, different degrees of Na+ and O2− site occupancies were available to NZO-M and NZO-H, with NZO-H having a lower Na+ and O2− site occupancy than NZO-M. Consequently, NZO-M had more Na+ and O2− available to react with CO2 to form Na2CO3 than NZO-H.
(2) After the first cycle, the Na+ and O2− site occupancies of both samples decreased, due to the formation of Na2CO3 that did not revert after calcination as discussed earlier – evident from the changes in relative intensities of the PXRD peaks at 2θ ∼16.2° and 38.7°. This may also be the reason for the fluctuating CO2 uptake of NZO-M and NZO-H up to 10 cycles.
(3) After a number of cycles (i.e. ∼13), the decrease in the Na+ and O2− site occupancies stabilized for both NZO-H and NZO-M and therefore, the CO2 uptake also stabilized. The two sorbents both stabilized to the same level of Na+ and O2− site occupancy.
(4) According to Fig. 6, the CO2 uptake over 20 cycles exhibited less variation for NZO-H than NZO-M, likely due to a lower Na+ and O2− site occupancy on NZO-H than NZO-M before the first carbonation/calcination cycle. In other words, NZO-H began as a compound more similar to the stabilized form of Na2ZrO3 than NZO-M.
In particular, point 4 above echoes the general conclusion from other studies that the “hexagonal” Na2ZrO3 has higher cyclic stability than monoclinic Na2ZrO3. Other changes, such as increased levels of stacking faults or cation site mixing disorder could also take place during the carbonation/calcination cycles, but such changes could not be easily identified with the analysis done in this study. Energy-dispersive X-ray spectroscopy of scanning transmission electron microscopy (STEM-EDS) on a single particle of the Na2ZrO3, or particles of comparable size and chemical compositions, may provide information at an atomic scale that will be valuable for the further development of Na2ZrO3 as a CO2 sorbent. However, the variations in the chemical composition between different batches of the same synthesis may make accurate estimates of the elemental compositions of the samples challenging. In order to confirm that the difference in the initial CO2 capture capacities of NZO-H and NZO-M was related mainly to Na+ and O2− site occupancy and less likely be related to the differences in layer stacking sequences, we performed density functional theory (DFT) calculations (see computational details in ESI†) to investigate the thermodynamic stability of the different space groups with different layer stacking sequences using a 2 × 3 × 2 supercell with 144 atoms (24 formula units). The lattice constants of the created supercell were optimized with all distances in Ångstrom (Å) and angles in degrees (°). The calculated formula unit energies (EDFT) at 0 K of C2/c, C2/m, P3112, and P3212 were −41.676, −41.675, −41.676, and −41.676 eV, respectively. The values were all very close to each other, indicating that the differences in thermodynamic stability between the perfectly monoclinic C2/c (or C2/m) and other possible structures of Na2ZrO3 is minimal. The similar EDFT of these four different models also suggests that the formation of defect structures is neither energetically demanding nor favourable. The similar predicted EDFT of the various idealized structures with the different space groups, as well as the inhomogeneous nature of solid-state synthesis, even under identical synthesis conditions, would explain why stacking faults commonly exist in Na2ZrO3. In addition, sol–gel and soft chemistry methods also reveal similar PXRD patterns to those from solid-state synthesis, influenced by the disordered stacking faults.19,20
Conclusion
Despite the general assumption that the Na2ZrO3 CO2 sorbent exists with monoclinic, hexagonal and cubic crystal structures, hexagonal Na2ZrO3 does not exist, according to our investigation. The so-called hexagonal Na2ZrO3 (and also to a certain extent the monoclinic Na2ZrO3) is in fact disordered Na2ZrO3 with (1) stacking faults, (2) cation site mixing disorder, and (3) incomplete Na+ and O2− site occupancies. The typically observed variations in the CO2 uptake and cyclic stability between samples of Na2ZrO3 are related to differences in Na+ and O2− site occupancies, and not differences in crystal structure. In this study of Na2ZrO3, the Na+ and O2− site occupancies changed during initial carbonation/calcination cycles and stabilized at a certain level (approximately 50%) after 13 cycles and the CO2 uptake also stabilized. Na2ZrO3 with low Na+ and O2− initial site occupancies (considered previously “hexagonal Na2ZrO3”) is closer to the stabilized form and shows lower variation in the cyclic CO2 uptake than Na2ZrO3 with high Na+ and O2− initial site occupancies. This increased understanding of Na2ZrO3 is essential for not only reducing efforts to control structures, but also further development of these sorbents, as well as a greater understanding of the properties of similar mixed-metal oxide materials.Experimental
Synthesis of sodium zirconate (sodium zirconium oxide; Na2ZrO3)
Zirconium oxide (ZrO2, 98%) and sodium carbonate (Na2CO3, anhydrous for analysis EMSURE®ISO) were purchased from Sigma-Aldrich. Na2ZrO3 was synthesized via a solid-state reaction using a Mettler Toledo thermogravimetric analyzer (Schwerzenbach, Switzerland). In order to produce the so-called monoclinic phase (NZO-M), the Na2CO3: ZrO2 molar ratio was fixed at 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the synthesis mixture was heated to 900 °C at a heating rate of 5 °C min−1 under a 100 mL min−1 flow of 100% nitrogen (N2) for two hours. In the case of the so-called hexagonal phase (NZO-H), the Na2CO3
1 and the synthesis mixture was heated to 900 °C at a heating rate of 5 °C min−1 under a 100 mL min−1 flow of 100% nitrogen (N2) for two hours. In the case of the so-called hexagonal phase (NZO-H), the Na2CO3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ZrO2 ratio was fixed at 1.5
ZrO2 ratio was fixed at 1.5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the same synthesis conditions were used but the synthesis time was increased to five hours. Slight variations from the stated stoichiometry is expected on different samples due to experimental errors and the nature of solid-state synthesis, as discussed previously.24
1 and the same synthesis conditions were used but the synthesis time was increased to five hours. Slight variations from the stated stoichiometry is expected on different samples due to experimental errors and the nature of solid-state synthesis, as discussed previously.24
Characterization of sodium zirconate (sodium zirconium oxide; Na2ZrO3)
PXRD patterns of the synthesized Na2ZrO3 were collected using a Bruker D8 powder diffractometer (Karlsruhe, Germany with Cu Kα radiation (λ = 1.54 Å), 40 mA, and 40 kV) at a 2θ range between 10 and 60° with a 0.01° step size at ambient temperature. The synthesized Na2ZrO3 was examined using a JEOL JEM-2100 TEM equipped with a Timepix detector from Amsterdam Scientific Instruments at 98 K. Scanning electron microscopy (SEM) images of NZO-M and NZO-H were collected on a Zeiss Merlin Field Emission Scanning Electron Microscope (Oberkochen, Germany) with an acceleration voltage of 2.5 kV and a probe current of 80 pA. The samples were coated by gold/palladium sputter coater (Polaron SC7640, Thermo VG Scientific) for 20 s under 20 mA before imaging.Author contributions
Ribooga Chang: material synthesis, formal analysis, investigation, disorder simulation, visualization, writing – original draft. Ashok S. Menon: disorder simulation, writing. Erik Svensson Grape: 3D ED analysis, writing. Peter Broqvist: DFT calculation, writing. A. Ken Inge: disorder simulation, investigation, writing. Ocean Cheung: writing & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
E. S. G. and A. K. I. acknowledge support from the Swedish Foundation for Strategic Research (SSF). RC and OC acknowledge support from the Swedish Research Council (Grant no. 2020-04029), Swedish Research Council for Sustainable Development (FORMAS, Grant No. 2018-00651), and the Swedish Foundation for Strategic Environmental Research (Mistra) (Project Name: Mistra TerraClean, Project number 2015/31). Funding from the National Strategic e-Science program eSSENCE is greatly acknowledged (P. B.) The simulations were performed on resources provided by the Swedish National Infrastructure for Computing (SNIC) at UPPMAX and NSC. A. S. M. would like to acknowledge to Faraday Institution FutureCat consortium for their support (FIRG017).References
- R. Chang, X. Wu, O. Cheung and W. Liu, J. Mater. Chem. A, 2022, 10, 1682–1705 RSC.
- F. Bamiduro, G. Ji, A. P. Brown, V. A. Dupont, M. Zhao and S. J. Milne, ChemSusChem, 2017, 10, 2059–2067 CrossRef CAS PubMed.
- H. G. Jo, H. J. Yoon, C. H. Lee and K. B. Lee, Ind. Eng. Chem. Res., 2016, 55, 3833–3839 CrossRef CAS.
- P. Sánchez-Camacho, I. C. Romero-Ibarra and H. Pfeiffer, J. CO2 Util., 2013, 3–4, 14–20 CrossRef.
- I. Alcérreca-Corte, E. Fregoso-Israel and H. Pfeiffer, J. Phys. Chem. C, 2008, 112, 6520–6525 CrossRef.
- J. A. Mendoza-Nieto, H. Martínez-Hernández, H. Pfeiffer and J. F. Gómez-García, J. CO2 Util., 2022, 56, 101862 CrossRef CAS.
- G. Ji, M. Z. Memon, H. Zhuo and M. Zhao, J. Chem. Eng., 2017, 313, 646–654 CrossRef CAS.
- K. Zhang, X. S. Li, H. Chen, P. Singh and D. L. King, J. Phys. Chem. C, 2016, 120, 1089–1096 CrossRef CAS.
- Y. Xia, Z. Z. Fang, P. Sun, Y. Zhang, T. Zhang and M. Free, J. Mater. Sci., 2017, 52, 4120–4128 CrossRef CAS.
- K. Baek, W. C. Jeon, S. Woo, J. C. Kim, J. G. Lee, K. An, S. K. Kwak and S. J. Kang, Nat. Commun., 2020, 11, 456 CrossRef CAS PubMed.
- T. Zhao, M. Rønning and D. Chen, J. Energy Chem., 2013, 22, 387–393 CrossRef CAS.
- I. Alcérreca-Corte, E. Fregoso-Israel and H. Pfeiffer, J. Phys. Chem. C, 2008, 112, 6520–6525 CrossRef.
- M.-d. Lorena and P. Heriberto, J. Phys. Chem. C, 2012, 116, 9675–9680 CrossRef.
- T. Zhao, E. Ochoa-Fernández, M. Rønning and D. Chen, Chem. Mater., 2007, 19, 3294–3301 CrossRef CAS.
- H. R. Radfarnia and M. C. Iliuta, Sep. Purif. Technol., 2012, 93, 98–106 CrossRef CAS.
- J. Claverie, C. Foussier and P. Hagenmuller, Bull. Soc. Chim. Fr., 1966, 244 10.1039/c6ee00633g.
- S. G. Ampian, J. Am. Ceram. Soc., 1968, 51, 607–608 CrossRef CAS.
- S. Munro, M. Åhlén, O. Cheung and A. Sanna, Chem. Eng. J., 2020, 388, 124284 CrossRef CAS.
- D. Zhou, Y. Wang, M. Z. Memon, W. Fu, Z. Wu, S. Sheng, H. Zhang and G. Ji, Carbon Capture Sci. Technol., 2022, 3, 100050 CrossRef CAS.
- G. Ji, M. Z. Memon, H. Zhuo and M. Zhao, Chem. Eng. J., 2017, 313, 646–654 CrossRef CAS.
- K. M. Ooi, S. P. Chai, A. R. Mohamed and M. Mohammadi, Asia-Pac. J. Chem. Eng., 2015, 10, 565–579 CrossRef CAS.
- A. S. Menon, D. O. Ojwang, T. Willhammar, V. K. Peterson, K. Edström, C. P. Gomez and W. R. Brant, ACS Appl. Mater. Interfaces, 2020, 12, 5939–5950 CrossRef CAS PubMed.
- G. Lang, Z. Anorg. Allg. Chem., 1966, 348, 246–256 CrossRef CAS.
- R. Chang, E. Svensson Grape, T. Clairefond, E. Tikhomirov, A. K. Inge and O. Cheung, J. Mater. Chem. A, 2023, 11, 7617–7628 RSC.
- A. López-Ortiz, N. G. P. Rivera, A. R. Rojas and D. L. Gutierrez, Sep. Sci. Technol., 2005, 39, 3559–3572 CrossRef.
- G. M. Kanyolo, T. Masese, N. Matsubara, C.-Y. Chen, J. Rizell, Z.-D. Huang, Y. Sassa, M. Månsson, H. Senoh and H. Matsumoto, Chem. Soc. Rev., 2021, 50, 3990–4030 RSC.
- K. Kataoka, Y. Takahashi, N. Kijima, H. Nagai, J. Akimoto, Y. Idemoto and K.-i. Ohshima, Mater. Res. Bull., 2009, 44, 168–172 CrossRef CAS.
- T. J. Bastow, M. E. Hobday, M. E. Smith and H. J. Whitfield, Solid State Nucl. Magn. Reson., 1994, 3, 49–57 CrossRef CAS PubMed.
- M. M. J. Treacy, J. M. Newsam and M. W. Deem, Proc. R. Soc. London, Ser. B, 1991, 433, 499–520 Search PubMed.
- M. M. J. Treacy, J. M. Newsam and M. W. Deem, DIFFaX v 1.812, http://www.public.asu.edu/%7Emtreacy/DIFFaX.html Search PubMed.
- J. A. Mendoza-Nieto, S. Tehuacanero-Cuapa, J. Arenas-Alatorre and H. Pfeiffer, Appl. Catal., B, 2018, 224, 80–87 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta01681e |
| This journal is © The Royal Society of Chemistry 2024 |