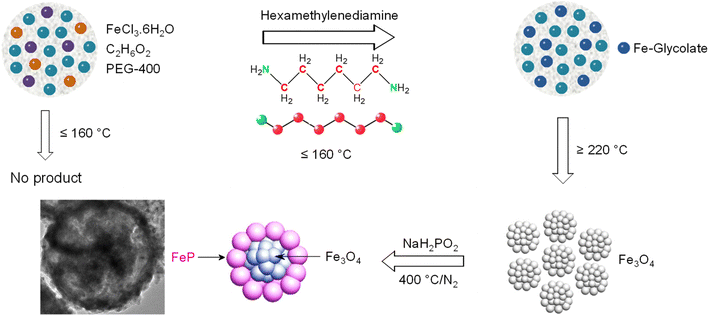
Ultrathin carbon layer-coated mesoporous core–shell-type FeP/Fe₂O₃/C for the hydrogen evolution reaction

Abstract

Due to their low cost and high abundance, iron-based electrocatalysts are considered a promising alternative to platinum for the hydrogen evolution reaction (HER). Herein, we synthesized and evaluated a mesoporous core–shell-type iron phosphide/iron oxide (FeP/Fe₃O₄) coated with few ultrathin carbon layers as an electrocatalyst for the HER. FeP/Fe₃O₄ was produced through the partial phosphidation of Fe₃O₄ mesoporous microspheres. Our findings indicate that even partial phosphidation activates the surface of Fe₃O₄ for the HER and that FeP/Fe₃O₄ outperforms pure FeP. Although FeP/Fe₃O₄ exhibited higher electrochemical impedance and charge-transfer resistance compared to FeP, the FeP/Fe₃O₄ electrode demonstrated superior performance in both acidic and basic electrolytes. In acidic solution, the η₁₀ values for FeP/Fe₃O₄/C and FeP/C were approximately 90 and 135 mV_RHE, respectively, while in basic medium, they were approximately 303 and 261 mV_RHE. In addition, the specific activity of the FeP/Fe₃O₄ electrode, normalized to the electrochemically active surface area, surpassed that of the FeP electrode. The superior performance of FeP/Fe₃O₄ was linked to its active centers and turnover frequency (TOF). Specifically, the number of active sites in FeP/Fe₃O₄ was 1.58 × 10⁻⁸ mol, whereas in FeP, it was 1.2 × 10⁻⁸ mol. At η = 90 mV_RHE, the TOF of the FeP/Fe₃O₄ electrode was estimated to be 0.47 s⁻¹, approximately 2-fold higher than that of FeP (0.47 s⁻¹). Estimation of the exchange current density (i_o) and Tafel slopes indicated faster HER kinetics at the catalytic interface of FeP/Fe₃O₄ (0.18 mA cm⁻², 62 mV dec⁻¹) compared to FeP (0.12 mA cm⁻², 89 mV dec⁻¹). In addition, the FeP/Fe₃O₄ electrode maintained a stable current density (20 mA cm⁻²) for 24 h of continuous operation. Two spin-polarized DFT models were used to obtain information on the Gibbs free energy (ΔG_H) and the corresponding adsorption energy (ΔE_H). These models included a FeP surface with and without carbon layers, as well as a surface consisting of FeP and Fe₃O₄. In addition, the calculations offered insights into the stability of the phosphide surface, both with and without carbon layers.

---

Introduction

The drive to develop clean energy technologies is intensifying in response to increasing energy demands and growing environmental concerns.^1,2 With the declining cost of electrical energy generated from dedicated renewable sources, hydrogen (H₂) production through water electrolysis is emerging as a more promising technological alternative to the steam methane reforming (SMR) process,^3–5 which emits considerable amount of carbon dioxide (CO₂). Before water electrolysis becomes fully realized commercially, several challenges associated with its production costs, safety, storage, etc. remain to be addressed. The idea behind renewably driven electrolysis is to dedicate the energy production or alternatively to store the surplus electrical power, as there tends to be intermittency in energy production as well as a mismatch between demand and supply, in the form of chemicals. As H₂ has well-established markets, which are projected to expand further in the near future, the conversion of electrical energy into H₂ through water electrolysis is a promising opportunity. In the polymer electrolyte membrane electrolysis process, surface-adsorbed H₂O first oxidizes at the anode, generating oxygen molecules, electrons (e⁻), and protons (H⁺). Both e⁻ and H⁺ move toward the other half-cell (cathode compartment), whereby e⁻ travels through an external electrical circuit, while the H⁺ migrates through the polymer electrolyte membrane. The reduction of protons occurs at the cathode surface, leading to the formation of H₂ gas. Although the thermodynamic requirement for complete water electrolysis is 1.23 V, the sluggish reaction kinetics (multistep H₂O oxidation and O₂ formation in particular) can demand a substantially high-energy input. The additional energy needed can have a significant impact on the production costs. To address the challenge of an overpotential requirement, electrocatalysts with a tailored microstructure with high catalytic activity are required by the electrolyzers.

In the conventional commercial PEM-based electrolyzer, the electrodes generally consist of noble metals, such as platinum (Pt) and iridium oxide (IrO₂) as electrocatalysts.⁶ However, the extremely high cost and the limited abundance of these metals are viewed as a significant challenge for the adoption of large-capacity electrolyzers and their widespread installation. As a result, extensive research has been carried out recently with the aim to design and develop both cathode and anode materials, as alternatives to Pt and Ir, with low cost, high activity (close to Pt and Ir), and good stability.^7–19 The main transition metals that have been the focus of most research to date are nickel (Ni),²⁰ cobalt (Co),²¹ and iron (Fe).²² As a cathode material, the electrocatalytic performance of the phosphides of these transition metals is now approaching that of Pt-based electrocatalysts for the HER and therefore such electrocatalysts have great potential. A wide variety of electrodes consisting of nonprecious transition metals, including carbides,^7–9,23,24 sulfides,^10,11,25 nitrides,²⁶ phosphides,^12–14 and borides,^15,27 have been explored. Because of the low cost (the most abundant transition metal) and high activity of iron (Fe), iron monophosphide (FeP) is one potential electrocatalyst that has been investigated for the HER.

In pursuit of high-performance electrocatalysts, efforts are ongoing to further improve the electrocatalytic performance of FeP, mainly by modifying the electronic structure to decrease the catalytic reaction time constant and, at the same time, increase the density of accessible functional sites. The former can be achieved by various methods, including heteroatom doping, both by metal (e.g., Ni, Co, Mn, etc.)^28–31 and nonmetal doping (e.g., N),^32,33 modulating the defect/vacancy, and designing heterostructures.

The availability of a wide variety of metal and nonmetal elements brings a unique opportunity to custom-tailor the electronic properties, and hence the performance, of any specific chemical composition. The electronic structure of bimetallic or multimetallic compounds is likely to allow improved inter-charge transfer, which can have a direct impact on the kinetic energy barriers of electrocatalytic reactions.^34,35 For instance, Chen et al. prepared cobalt iron phosphide (CoFeP) nanotubes and showed that the presence of Co in the structure significantly increased the total density of states (DOS) near the Fermi level.³¹ Such structural modulations led to the faster charge-transfer kinetics and better HER performance. The presence of Co also added to the HER performance of FeP by reducing the hydrogen adsorption free energy. In addition to metal cations, nonmetals can also be used to modulate the chemical and electronic attributes of electrocatalysts. For instance, Yang and colleagues reported an improvement in the HER performance of FeP after introducing nitrogen into the structure.³² It was asserted that the N atoms could modulate the bond strength between FeP and O, which rendered better intrinsic activity of FeP. Similarly, Zhang and coworkers showed coupled H₂ evolution and sulfur generation in the presence of N-doped CoP electrodes.³⁶ Their findings were correlated to the difference in electronegativity of nitrogen and phosphorous. Specifically, nitrogen, being more electronegative than phosphorous, lowered the d-band of CoP more effectively and weakened H adsorption on the electrocatalyst surface. Similarly, intramolecular electronic coupling in iron cobalt (oxy)phosphide nanoboxes accounted for the enhanced oxygen evolution reaction.³⁷

Furthermore, the density of accessible functional sites of FeP can be amplified by improving its surface area,^38,39 introducing porosity,^40,41 creating a hollow morphology,^42,43 supporting on carbon,^44,45 and so forth. Developing nanostructured electrodes with mesoporous surfaces would address several issues; specifically, by increasing (1) the real surface area as well as the electrochemically active surface area, (2) promoting an abundance of accessible active sites, and (3) facilitating the facile penetration of electroactive species and the diffusion of H₂ from the electrode's surface. In addition to chemical composition and surface texture, the shape and morphology can also have a significant impact on the electrocatalytic performance of electrode materials. For instance, He and colleagues found that iron oxide with a microsphere-like morphology possessed much higher catalytic activity and reaction stability than nanocubes and nanorods for the catalytic destruction of ethane.⁴⁶ The superior performance of the microspheres was attributed to the oxygen vacancies and lattice defects.

The stability of electrode materials under harsh electrochemical conditions (0.5 M H₂SO₄ or 1.0 M KOH) is an important metric in assessing their application potential. Earlier findings showed that the catalytic activity of FeP deteriorates because of surface oxidation.⁴⁷ Coating with carbon thin layers can protect FeP from oxidation, and make it a highly stable electrocatalyst for the HER. Also, the durability of FeP can be substantially improved by encapsulation within carbon. Furthermore, carbon thin layers can provide an efficient electrical pathway for facilitating charge transfer.

Herein, we report the synthesis of core–shell-type FeP/Fe₃O₄ microspheres endowed with several advantageous features for the HER reaction both in acidic and alkaline conditions. The surface is partially phosphidized, having a unique bonding configuration consisting of Fe, P, and O to boost the HER kinetics. Furthermore, the surface of the FeP/Fe₃O₄/C is mesoporous, which can render more exposed active sites per unit geometric area to facilitate the diffusion of electroactive species and maximize their interaction with active sites. In addition to its unique chemical composition and mesoporous surface, the morphology of the FeP/Fe₃O₄/C has hollow features, which can further render large electrode–electrolyte contact areas or large accessible active sites for surface protons. Endowed with such unique features, the FeP/Fe₃O₄/C exhibited a much higher HER performance compared to FeP/C. In addition, two spin-polarized density functional theory (DFT) models were employed to collect information about the Gibbs free energy (ΔG_H) and the related adsorption energy (ΔE_H). The models consisted of an FeP surface with and without carbon layers, along with a surface composed of FeP and Fe₃O₄. The DFT calculations showed that presence of an ultrathin carbon layer on the surface was beneficial for H₂ adsorption/desorption, electrochemical stability, and improved charge transfer. Moreover, the calculations offer valuable insights into the stability of the phosphide surface, both in the presence and absence of carbon layers. The performance-dictating features, such as specific and electrochemically active surface area, number of catalytic active sites, electrochemical impedance, charge-transfer resistance, and Tafel slopes, of FeP/Fe₃O₄/C and FeP/C were investigated, compared, and correlated to their electrocatalytic activities. In addition, the intrinsic activities of FeP/Fe₃O₄/C and FeP/C were compared by determining their specific HER activity and turnover frequency (TOF).

Experimental

Details of the materials' synthesis, characterization, electrode preparation, and activity evaluation are supplied in the ESI.† Briefly, iron oxide (Fe₃O₄) microspheres were obtained by a solvothermal process conducted at 220 °C for 12 h. The synthesis was carried out in anhydrous ethylene glycol, using iron trichloride hexahydrate (FeCl₃·6H₂O) as an Fe source and polyethylene glycol and hexamethylenediamine as morphology-directing agents. The as-synthesized Fe₃O₄ microspheres were then heated in the presence of NaH₂PO₂ at 400 °C to obtain FeP/Fe₃O₄. For comparison, iron monophosphide (FeP) nanoparticles were prepared following a synthesis procedure reported elsewhere.⁴⁴ The desired amount of the electrocatalysts were deposited on a glassy carbon electrode for electrochemical evaluation.

Results and discussion

The different synthesis steps followed for the preparation of mesoporous FeP/Fe₃O₄ microspheres are summarized in Scheme 1. First, monodispersed Fe₃O₄ microspheres, utilized as a precursor for FeP/Fe₃O₄, were obtained in the presence of iron chloride hexahydrate, hexamethylenediamine (HMDA), polyethylene glycol (PEG), and anhydrous ethylene glycol (EG) by a solvothermal method. The EG served as a solvent as well as a morphology-directing agent. Upon the addition of HMDA to the synthesis solution, EG reduced some of the ferric into ferrous ions, producing glycolic acid in alkaline conditions. The glycolate groups subsequently coordinated to the central metal ions to form an iron glycolate complex, with a chemical formula similar to Fe^III_3:3Fe^II (C₂H₃O₃)₁₂·4H₂O.⁴⁸ Note, however, that in the absence of HMDA, no precipitates were obtained after the solvothermal processing. This suggests the role of alkaline HMDA is important to activate the reduction reaction of iron(III) by EG. Meanwhile, the formation of a relatively stable complex intermediate could serve (1) as a secondary iron reservoir/or precursor to deaccelerate the release rate of the iron cations, and (2) to control the growth of nanoparticles during the self-assembly of the Fe₃O₄, which thermodynamically seems to favor the formation of microspheres. At elevated temperature, particularly at 220 °C, the iron glycolate complex thermally decomposed to Fe³⁺ and Fe²⁺ cations, which simultaneously co-precipitated to form the structured assemblies of iron oxide nanoparticles. Meanwhile, the structured assemblies could experience a fast rotation of the primary nanoparticles to reduce the surface energy. Yet, the selective binding of an organic motif or carboxylate groups with the high-energy facets of Fe³⁺ and Fe²⁺ cations could presumably control the growth rate of these surfaces, forming highly uniform microspheres. Moreover, the nanoparticles could further undergo the digestive inside-out Ostwald ripening process to eventually form iron oxide microspheres. Finally, FeP/Fe₃O₄ was obtained by the phosphidization of glycolate-derived Fe₃O₄ under phosphine (PH₃) vapor generated from the thermal decomposition of sodium hypophosphite (NaH₂PO₂) under the N₂ atmosphere in the tube furnace.

Scheme 1 Schematic summarizing the different steps involved in the preparation of FeP/Fe₃O₄.

Formation of the iron glycolate precursor and its transformation into the oxide (Fe₃O₄) form at a higher synthesis temperature was verified by XRD (Fig. 1a). The diffractions of the sample prepared at 160 °C were in good agreement with those reported for iron glycolate.⁴⁹ The formation of iron glycolate was further supported by the FTIR analysis (Fig. S1†). Specifically, the vibration bands centered at 3437 and 1632 cm⁻¹ were due to the stretching and bending modes of –OH groups, while the C–H vibrational bands (at 2927 and 2860 cm⁻¹) and C–O (1087 cm⁻¹) peak were in good agreement with those reported earlier. Further, the bands at 1592 and 1384 cm⁻¹ corresponded to symmetric and antisymmetric vibration modes of –COO–, respectively, while the intense band at 485 cm⁻¹ in the low-frequency region accounted for the vibration mode of Fe–O.⁴⁸ These results suggested that the formation of the Fe–glycolate complex had taken place through the iron-carboxylate bonds. When the synthesis temperature was increased from 160 °C to 180 °C, iron glycolate partially transforms into magnetite form, in which both iron glycolate and Fe₃O₄ co-existed. Further increasing the temperature to 220 °C led to the complete decomposition of iron glycolate and the formation of Fe₃O₄, in addition to a crystallinity improvement of Fe₃O₄. The formation of any other phase of iron was not discerned. The XRD pattern of the product obtained after the phosphidation of Fe₃O₄ is shown in Fig. 1b, in addition to the standard XRD reflections of Fe₃O₄ and FeP provided for comparison. The reflections at 32.8° (011), 37.2° (111), 46.9° (202), 48.31° (211), 50.4° (103), 56.1° (212), and 59.6° (020) corresponded to the orthorhombic lattice of the FeP phase (JCPDS, 01-078-1443).⁴⁴ The other diffractions that appeared at 2θ = 30.1° (220), 35.5° (311), 43.1° (400), 53.5° (422), 57.0° (511), and 62.6° (440) were indexed to the cubic phase of Fe₃O₄ (JCPDS, 03-065-3107). The diffractions clearly indicated the presence of both FeP and Fe₃O₄, suggesting a partial phosphidation of Fe₃O₄.

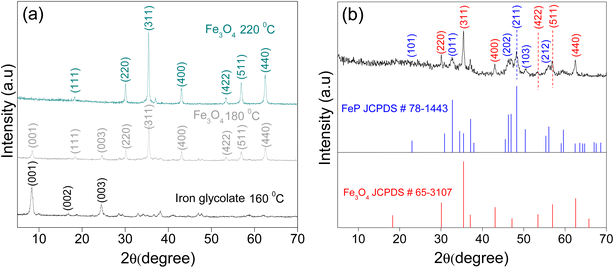Fig. 1 XRD patterns showing the (a) temperature-dependent evolution of iron glycolate into Fe₃O₄, and (b) transformation of Fe₃O₄ into FeP/Fe₃O₄ after phosphidation.

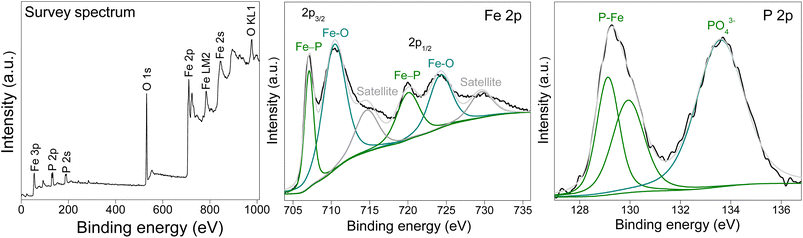
The surface elemental composition and the oxidation states of FeP and FeP/Fe₃O₄ were determined by high-resolution X-ray photoelectron spectroscopy (XPS). The spectra of FeP/Fe₃O₄ are shown in Fig. 2. The survey spectrum confirmed the presence of iron (Fe), phosphorous (P), and oxygen (O) elements. In the deconvoluted spectrum of iron, the signals recorded at 707.1 eV (Fe 2p_3/2) and 720.0 eV (Fe 2p_1/2) accounted for the iron coordinated with phosphorous in FeP, while relatively more intense peaks appeared at 710.4 and 724.3 eV corresponding to iron bonded to oxygen. Two additional peaks centered at 714.6 and 729.6 eV were considered to be satellite peaks of the oxidized iron.⁵⁰ In the case of the P 2p spectrum, two signals were recorded at 129.1 and 129.9 eV corresponding to the phosphorous anion bonded to iron. Besides, a broad peak appeared at 133.6 eV, ascribed to the phosphorous bonded to oxygen (PO₄³⁻).^51,52 The surface oxidation of FeP during sample handling can lead to the formation of phosphate. It may be noted that the Fe 2p peak appeared at a higher binding energy (707.1 eV) compared to the binding energy of metallic iron (706.8 eV), whereas the P 2p peak was recorded at a lower binding energy (129.1 eV) compared to the binding energy of elemental phosphorous (130.2 eV). Such a variation in binding energy indicated electronic interactions between Fe and P atoms in the crystal of FeP. The shifts in binding energies imply a cationic state of iron atoms in the presence of the anionic state of phosphorous atoms created due to the transport of electronic density from iron to phosphorous in the FeP system.⁵³ The deconvoluted spectra of Fe 2p and P 2p analyzed from FeP are shown in Fig. S2 and S3.† Phosphide surfaces are highly susceptible to oxidation when exposed to air. In the case of pure FeP, the phosphide surface appeared to endure severe oxidation in the form of oxides or phosphates. This explains the presence of a very weak signal for Fe coordinated to P (Fig. S2 and S3†). Previous reports have documented comparable FeP spectra.^54–57 In the case of FeP/Fe₃O₄, the presence of oxides can somewhat passivate or stabilize the surface, and hence phosphide surfaces are relatively less susceptible to oxidation. This explains the presence of a relatively stronger signal for Fe coordinated to P (Fig. 2).

Fig. 2 XPS signatures of FeP/Fe₃O₄.

Microscopic details of the as-prepared Fe₃O₄ and FeP/Fe₃O₄ were collected by field emission electron microscopy (FESEM) and transmission electron microscopy (TEM) analyses. A typical FESEM image of glycolate-derived Fe₃O₄ is shown in Fig. 3a. As is evident in the figure, Fe₃O₄ was spherical in shape, and highly uniform (monodisperse) in size (approximately 390 nm). Some microspheres were discerned to have a hollow morphology, which was further corroborated by the TEM images (Fig. 3b and c). In addition, these microspheres appeared to consist of small nanocrystals. The corresponding selected area electron diffraction patterns (the inset of Fig. 3c) verified the monocrystalline nature, indicating that the Fe₃O₄ spheres were formed by the self-assembled and oriented aggregation of nanocrystals. To further confirm that these spheres were Fe₃O₄, the d-spacings were calculated using HRTEM (Fig. 3d). The interplanar value was calculated to be 0.25 nm, which corresponded to the most prominent diffraction plane (311) of Fe₃O₄. The images of FeP/Fe₃O₄, obtained after the phosphidation of Fe₃O₄, are shown in Fig. 3e–k. As can be seen, the overall features (shape, size, and morphology) of Fe₃O₄ were largely maintained after the phosphidation reaction. Yet, a clear contrast in the outer and inner parts of the spheres could be discerned. The interface between the FeP and carbon layers (Fig. 3h), and FeP and Fe₃O₄ (Fig. 3i) was studied by HRTEM. To examine the composition of these two layers, the interplanar distance is calculated. The d-spacing of the outer and thicker layer was calculated to be 1.88 Å (Fig. 3h and j), which corresponded to the (211) plane of the orthorhombic FeP phase.⁵⁸ Note that we attempted to calculate the d-spacings at different spots of the samples. The calculated d-spacings corresponded to either the (011) or (211) plane, predominantly (211). Normally, low index surfaces are more stable than high index surfaces. Thus, FeP with (011) and (211) planes were selected for the DFT analysis. The interplanar spacing of the inner layer at the interface was calculated to be 2.53 Å (Fig. 3k), indicating that it corresponded to the (311) diffraction plane of Fe₃O₄. The thickness of the FeP layer was not uniform in all the microspheres, and was estimated to vary between 5 and 20 nm. In addition, thin layers (∼2 nm) of carbon, as indicated by the arrows in Fig. 3h, appeared to encompass the outer (FeP) surface. The SAED patterns indicated the polycrystalline nature of FeP/Fe₃O₄ (Fig. 3l). The d-spacings calculated from the SAED patterns were 2.73, 2.53, 1.93, 1.88, and 1.48 Å, corresponding to FeP (011), Fe₃O₄ (311), FeP (202), FeP (211), and Fe₃O₄ (440), respectively. The presence and homogeneous distribution of Fe, P, C, and O were further corroborated by EDS elemental mapping, as shown in Fig. S4.† The microscopic image suggests that the surface of FeP/Fe₃O₄ was porous in nature. This notion was corroborated by the BET surface area analysis. The nitrogen adsorption–desorption isotherms of the FeP nanoparticles and FeP/Fe₃O₄ spheres are shown in Fig. S5 and S6.† It is evident that the isotherm of FeP/Fe₃O₄ was a classical type IV isotherm, characteristic of a mesoporous surface. The absence of such a characteristic isotherm in the case of the FeP nanoparticles clearly suggested that the surface of FeP was nonporous.

Fig. 3 FESEM and TEM/HRTEM images of Fe₃O₄ (a–d) and FeP/Fe₃O₄ (e–k), and SAED patterns of FeP/Fe₃O₄ (l).

The performance of the as-prepared electrode materials was investigated by monitoring the electrocatalytic hydrogen evolution reactions. The measurements were carried out in aqueous solutions of 0.5 M H₂SO₄ or 1.0 M KOH. Note that FeP tended to agglomerate due to its nanostructured and semi-metallic nature. Agglomeration may have a detrimental impact on the HER performance. It is evident from the earlier studies that the performance of electrocatalysts can be substantially improved after their dispersion on an electrically conductive and high surface area support, carbon for instance. With this in mind, during electrode/slurry preparation, both FeP and FeP/Fe₃O₄ were also dispersed on carbon black and their HER performance was evaluated. The ratio of FeP or FeP/Fe₃O₄ wt% : carbon was adjusted to 80 : 20. The electrocatalysts FeP and FeP/Fe₃O₄ dispersed on carbon black were denoted as FeP/C and FeP/Fe₃O₄/C, respectively. The enhanced HER performance observed in FeP/C and FeP/Fe₃O₄/C could be attributed to the carbon support's ability to distribute the active sites more uniformly. Carbon did not act as a source of active sites in this study.

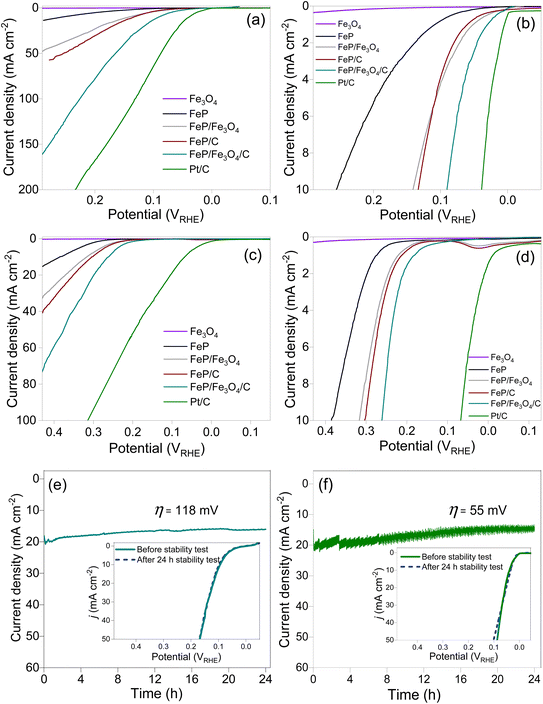
The polarization curves of Fe₃O₄, FeP, FeP/Fe₃O₄, FeP/C, and FeP/Fe₃O₄/C recorded at two different pH levels are compared in Fig. 4. The absolute current was normalized with the geometric area of the electrode to obtain the current density. The current density is presented after iR compensation. In all the experiments, the mass of all the electrocatalysts and the other electrochemical conditions were kept identical, unless otherwise specified. For comparison, the HER results for commercial Pt/C (20 wt% Pt on carbon) are also included. It is evident that Fe₃O₄ did not exhibit any discernible performance in either acidic or alkaline media. The HER performance of FeP/Fe₃O₄ was much better than that of FeP, and the performance of the phosphide-based electrodes improved noticeably after dispersion on the carbon support. The performance patterns were similar both in acidic and basic media. Comparison of the overpotential (η) at 10 mA cm⁻², recommended as the benchmark current density, is usually considered as a performance indicator for electrocatalysts. The linear sweep voltammograms of the electrodes against 10 mA cm⁻² are compared in Fig. 4b and d. In 0.5 M H₂SO₄ electrolyte, the respective η₁₀ values of FeP, FeP/Fe₃O₄, FeP/C and FeP/Fe₃O₄/C were calculated to be ∼254, ∼141, ∼135, and ∼90 mV. The HER performance of FeP/Fe₃O₄ was approximately 1.8 times higher than that of the FeP electrode. In addition, the onset potentials (noted at 1 mA cm⁻²) of FeP/C and FeP/Fe₃O₄/C were 61 and 29 mV. Such small onset potentials and overpotentials clearly suggest that the mesoporous FeP/Fe₃O₄ (or FeP/Fe₃O₄/C) electrocatalyst was endowed with a high catalytic ability, and its activity toward the HER compared favorably with other recently reported Fe-based phosphide electrocatalysts (Table S1†). Similarly, under a basic medium, the respective η₁₀ values of FeP, FeP/Fe₃O₄, FeP/C, and FeP/Fe₃O₄/C electrodes were calculated to be ∼385, ∼317, ∼303, and ∼261 mV. The higher overpotential requirement in basic medium could be attributed to thermodynamic and kinetic restrains, caused by water reduction followed by proton reduction and H₂ evolution. As expected, both under acidic (η₁₀ = 41 mV) and basic (η₁₀ = 65 mV) media, commercial Pt/C exhibited the highest HER performance.

Fig. 4 Polarization curves of Fe₃O₄, FeP, FeP/Fe₃O₄, carbon-supported FeP and FeP/Fe₃O₄, and Pt/C in acidic (a and b) and basic (c and d) media. Current–time profile and polarization curves (figure inset) recorded before and after stability tests of the FeP/Fe₃O₄/C (e) and commercial Pt/C (f). Stability was evaluated in 0.5 M H₂SO₄ aqueous solution.

The electrochemical stability of the FeP/Fe₃O₄/C electrode was evaluated under identical experimental conditions in acidic electrolyte. Also, the loading of FeP/Fe₃O₄/C was kept identical to that employed to evaluate the performance and the other electrochemical evaluations. The stability was assessed by monitoring any change in the current density for 24 h continuous operation at constant η = 118 mV. At η = 118 mV, the electrode produced 20 mA cm⁻². The results (current–time curve) of the potentiostatic measurements are shown in Fig. 4e. Similarly, the electrochemical stability test results of the commercial Pt/C carried out at η = 55 mV (or 20 mA cm⁻²) are also shown in Fig. 4f. For the FeP/Fe₃O₄/C, there was a slight drop in the current density in the initial 8 h, and then the current production became almost stable without any considerable drop in the current density. After completion of the potentiostatic measurement, the spent electrode was re-polarized and linear sweep voltammograms were recorded. The inset in Fig. 4e compares the polarization curves of FeP/Fe₃O₄/C obtained before and after the stability test. It is clear that the LSVs were comparable, suggesting the excellent electrochemical stability of the FeP/Fe₃O₄/C electrode. Also, quantification of the evolved hydrogen gas indicated a near 100% faradaic efficiency (Fig. S7†). A similar drop in the current density in the early stage of reactions has also been noticed in other studies. The decrease in the current density in 0.5 M H₂SO₄ solution was correlated to dissolution of the catalytic composition, caused by the generation of H₂ on the glassy electrode surface.⁵⁹ For CoP electrode, ICP analysis of the electrolyte solution collected after the stability test confirmed the presence of Co and P.⁵⁹ Similar stability and performance trends for FeP and CoP have also been observed in earlier studies.^59–61 To gain a deeper understanding of the structural and chemical stability of the FeP/Fe₃O₄/C electrode, the spent electrode, which was obtained after the durability test, was analyzed by TEM and XPS. Fig. S8 and S9† show the results. The analyses confirmed the structural and chemical stability of the electrode. The retention of the morphological features was confirmed by the TEM images, while the retention of the chemical interface (FeP and Fe₃O₄) was confirmed by HRTEM. Upon comparing the XPS results of the fresh and spent electrodes, the only discernible distinction was the enhanced intensity of the broad peak at 133.6 eV (Fig. S9†). This increase in peak intensity suggested an increase in the phosphate (PO₄³⁻) amount on the electrode surface. In addition, after the durability test, the electrolyte solution was collected and analyzed by ICP-MS. Before the analysis, the electrolyte solution was diluted by a factor of 1000 using deionized water, i.e., 0.1 mL of electrolyte solution mixed with 100 mL of deionized water. The Fe concentration was determined to be 1.4 ppm.

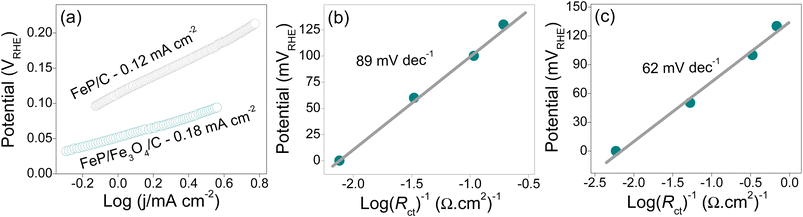
Since the kinetics of the HER reaction is not complicated by the selectivity of the products unlike the OER reaction, the efficiency of electrocatalysts can be demonstrated by two important metrics: the exchange current density (i_o) and the Tafel slope. The estimated values of i_o are shown in Fig. 5a. Here, i_o is essentially indicative of the rate of reaction between H⁺ and H₂ occurring at equilibrium. A larger i_o suggests a faster reaction rate or high inherent performance of an electrode, and vice versa. The i_o values of FeP/C and FeP/Fe₃O₄/C were determined to be 0.12 and 0.18 mA cm⁻², respectively. These values indicate the higher inherent activity of FeP/Fe₃O₄, followed by the FeP electrode. Another important metric that can be used to explain the activity of electrocatalysts is the Tafel slope. While estimation of the Tafel slope for the OER can be complex due to multielectron transfer reactions, its calculation is relatively simple for the HER and can provide important mechanistic and kinetic details. Under acidic conditions, the process of H₂ evolution occurs through two distinct pathways, which entail three possible reactions (HER steps): (step I) Volmer reaction (adsorption), (step II) Tafel reaction (chemical desorption), and (step III) Heyrovsky reaction (electrochemical desorption), as presented below.

Fig. 5 Exchange current density (a) and Tafel slopes of FeP/C (b) and FeP/Fe₃O₄/C (c).

Step I:

M + H₃O⁺ + e⁻ → M–H_ads + H₂O (Volmer reaction)

Step II:

M–H_ads + M–H_ads → H₂ + M (Tafel reaction, chemical desorption)

Step III:

M–H_ads + H⁺ + e⁻ → H₂ + M (Heyrovsky reaction, electrochemical desorption)

where M represents the electrocatalysts active sites. The theoretical Tafel slopes for the HER are 120, 40, and 30 mV dec⁻¹, respectively, which correspond to the Volmer–Heyrovsky step, Heyrovsky step, and Tafel step. A kinetic process that is more rapid is indicated by a smaller Tafel slope, which suggests that the catalyst can attain the necessary current at a lower overpotential.^22,62

As the electrode kinetics of charge transport can have a significant impact on the catalytic mechanism, Tafel slopes are calculated using an electrochemical impedance spectroscopic (EIS) technique. Here, potential-dependent Nyquist plots were recorded and the Tafel values were then derived. The measurements were conducted in 0.5 M H₂SO₄ in a three-electrode cell configuration. Calculation of the semi-logarithmic values of the inverse of R_ct against η resulted in a linear relationship with a gradient, which accounted for the Tafel slope. The results are shown in Fig. 5b and c. The slope value of the FeP/C electrode was found to be higher (89 mV dec⁻¹) than that of FeP/Fe₃O₄/C (62 mV dec⁻¹). The Tafel value correlates the faradaic current with η; whereby a smaller value suggests faster charge-transfer kinetics. In addition, the value is indicative of the HER reaction mechanism. The slopes for both electrodes implied that the HER reaction proceeds through the Volmer–Heyrovsky mechanism, in which electrochemical desorption is likely to be the rate-determining step.

In addition to the exchange current density and the Tafel slopes, the electrochemical impedance, turnover frequency (TOF), and electrochemically active surface area of the FeP/C and FeP/Fe₃O₄/C electrodes were studied and correlated with the variation in the performance. In a number of prior investigations, the overpotential calculated for 10 mA cm⁻² current density was used to compare the performance of electrocatalysts. In the case of smooth and planar surfaces, this approach can be acceptable; however, in the case of rough and porous surfaces, the reactive surface area is likely to be different than the electrode area. In addition, the mass of the electrocatalyst can further alter the catalytic active surface area. The intrinsic catalytic activity of electrocatalysts estimated using electrode geometric area, therefore, remains uncertain. To address this challenge in a somewhat fair and reliable way, the turnover frequency (TOF) should be calculated. By definition, the TOF takes the number of catalytic active sites (or catalytically active surface) into account – it is calculated as the number of molecules reacted per active site per unit time. Information about the intrinsic catalytic abilities of the FeP/C and FeP/Fe₃O₄/C electrodes was obtained by estimating the TOF. The number of active sites (N) was estimated following the electrochemical method recommended earlier.⁶³ First, CVs were recorded in phosphate buffer electrolyte (pH ∼ 7) by sweeping the potential between −0.2 V and +0.6 V_RHE. The CVs of the FeP/C and the FeP/Fe₃O₄/C electrodes are shown in Fig. 6a. The voltammetric charge (Q) integrated over the entire potential range was obtained using the area under the CV curves. Here, N should be proportional to Q, and was calculated using eqn (1) as follows;

N = Q/2F (1)

where F is the Faraday constant (∼96 485 C mol⁻¹).

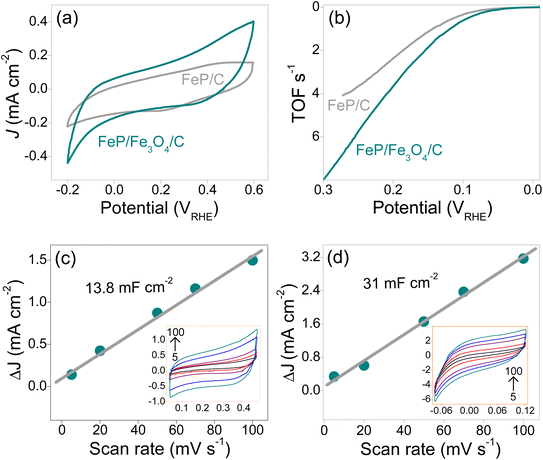Fig. 6 CVs (a) and TOF profiles (b), plots of the current density (and CVs, inset figure) of FeP/C (c) and FeP/Fe₃O₄/C (d) vs. the scan rate.

The respective number of active sites of FeP/C and FeP/Fe₃O₄/C were calculated to be 1.2 × 10⁻⁸ and 1.58 × 10⁻⁸ mol. The higher N of FeP/Fe₃O₄ could be attributed to its mesoporous surface, which seemed to render more active sites accessible to H⁺. The value of N can then be incorporated in eqn (2), as follows, to obtain the TOF.

TOF = JA/2FN (2)

where J is the geometric current density (A cm⁻², determined by LSV measurements), A is the geometric area of the working electrode, 1/2 corresponds to the two electrons that are involved in the formation of one H₂ gas molecule, and F is the Faraday constant.

The TOF profile vs. overpotential is shown in Fig. 6b. At η = 90 mV_RHE, as 90 mV was required to produce a geometric current density of 10 mA cm⁻², the TOF of the FeP/Fe₃O₄/C electrode was estimated to be higher (0.47 s⁻¹) than that of the FeP/C electrode (0.24 s⁻¹). The TOF calculation clearly supports the findings from the exchange current density and Tafel slopes analyses, which indicated that the kinetics of the HER reaction is more favorable on the surface of FeP/Fe₃O₄/C than the FeP/C electrode.

Since the HER is a surface-dictated reaction, any variation in the real surface area, which is the surface area exposed to the electrolyte, can lead to a difference in the electrocatalytic performance. An attempt was thus made to measure the electrochemically active surface area (ECSA) of the FeP/C and the FeP/Fe₃O₄/C electrodes, and to correlate this to their performance. Different techniques, such as electrical double-layer capacitance (C_dl), redox peak, hydrogen underpotential deposition (H-UPD), and carbon monoxide (CO) stripping, have been suggested for calculation of the ECSA.⁶⁴ It may be noted that the value of ECSA can vary with the applied technique. Moreover, these techniques are sensitive toward the nature of the materials under investigation. For instance, H-UPD and CO stripping techniques are recommended for the ECSA measurement of noble metals, such as platinum (Pt) and palladium (Pd). Herein, the electrical double-layer capacitance method was employed to collect the information about the ECSA of the electrodes, as FeP/C and the FeP/Fe₃O₄/C are likely to have similar chemical and physicochemical attributes. The C_dl was estimated by recording CVs with different scan rates between 5 and 100 mV s⁻¹, as shown in the insets in Fig. 6c and d. The corresponding plots of ΔJ vs. scan rate for the FeP/C and the FeP/Fe₃O₄/C electrodes are shown in Fig. 6c and d. The C_dl values of the FeP/C and the FeP/Fe₃O₄/C electrodes were measured to be 13.8 and 31 mF cm⁻². The higher C_dl observed in the case of the FeP/Fe₃O₄/C electrode was attributed to its porous surface texture, which can render more charge storage. A higher C_dl corresponds to a higher ECSA, which usually translates into better electrocatalytic performance. Although the calculation of the ECSA can suggest a possible trend for the performance of electrocatalysts, it does not provide information about the intrinsic activity of electrodes. A fair estimation of the inherent activity can be obtained by normalizing the current density with the ECSA. The potentiodynamic curves of the FeP/C and the FeP/Fe₃O₄/C electrodes obtained after normalization with the real surface area (ECSA) are shown in Fig. S10.† It is evident that the specific activity of FeP/Fe₃O₄ was better than that of FeP, which implies that FeP/Fe₃O₄ was endowed with superior intrinsic activity.

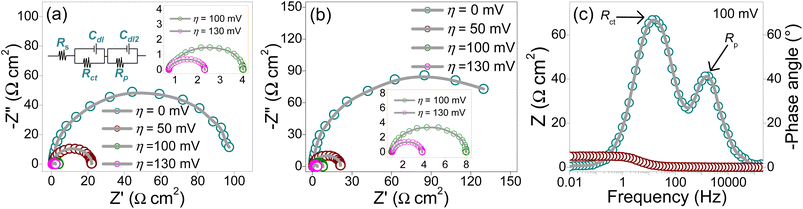
The electrochemical impedance spectroscopy (EIS) technique was employed to investigate the electrical resistance and interfacial charge-transfer resistance (R_ct) between the FeP/Fe₃O₄ surface and H⁺. The measurements were performed at different overpotentials (η = 0–130 mV_RHE) in the frequency range of 10⁵ to 0.01 Hz with 10 mV sinusoidal perturbation. The experimental conditions were kept identical to those applied to perform other electrochemical measurements. The potential-dependent Nyquist plots on the complex plane (real vs. imaginary part) of the FeP/C and the FeP/Fe₃O₄/C electrodes are shown in Fig. 7a and b, respectively. On the basis of the Nyquist plots and Bode (Fig. 7c) results, the two-time constant parallel model (Fig. 7a inset) was used to fit the EIS data, which gave an excellent fitting. As per this circuit model, R_s represents the combined resistance or series resistance, which comprises the resistance from the wire (R_wiring), carbon support if any (R_carbon), resistance of electrocatalytic materials (e.g., FeP, FeP/Fe₃O₄), and the solution resistance (R_soln);⁶⁵R_ct represents the charge-transfer resistance; and R_p represents the resistance induced by surface porosity.⁴⁴ As an example, Nyquist plots of the FeP/Fe₃O₄/C electrode highlighting experimental and fitted EIS results are shown in Fig. S11.† Moreover, Table S1† presents the electrochemical impedance parameters derived from the fitting.

Fig. 7 Nyquist plots of (a) FeP/C and (b) FeP/Fe₃O₄/C, and (c) Bode plot of FeP/Fe₃O₄/C.

In Nyquist plots, the radius of the semicircle is indicative of surface resistance at the interface, solid electrode and liquid electrolyte in the study. A shorter radius implies smaller interfacial electron-transfer resistance or smaller R_ct, and vice versa. It is clear from earlier and current findings that the R_ct decreased with increasing the potential. In the case of the FeP/C electrode, when η was increased from 0 to 130 mV, R_ct decreased from ∼100 to ∼1.6 Ω cm². Similarly, for the FeP/Fe₃O₄/C electrode, a significant drop in R_ct was discerned with increasing η. When the R_ct of both the electrodes were compared, it was clear that the FeP/C electrode had a smaller R_ct than that of the FeP/Fe₃O₄/C electrode for all the applied η values. For instance, at η = 100 and 130 mV, the R_ct values of the FeP/C were calculated to be ∼3.4 and ∼1.6 Ω cm², while for FeP/Fe₃O₄/C the R_ct values were ∼7.2 and ∼3 Ω cm². These findings clearly suggest that FeP/C has faster charge-transfer kinetics. The likely reason for the slightly higher resistance in FeP/Fe₃O₄ could be attributed to the presence of oxygen and a porous (discontinuous) surface. Oxygen, which is much more electronegative than phosphorous, can add to the localization of electrons. Despite the higher R_ct, the FeP/Fe₃O₄/C electrode exhibited better performance. Typically, electrocatalysts with lower charge-transfer resistance demonstrate superior electrocatalytic activity. Nevertheless, the activity of the electrocatalysts can also be influenced by additional parameters, such as the surface structure, morphology, density of active sites, TOF, ECSA, and change in Gibbs free energy. Earlier,⁴⁵ we showed that the electrical conductivity and charge-transfer resistance are important variables that have an impact on the electrocatalytic performance. However, the ECSA and TOF also affect the electrocatalysts activity. The catalytic ability per unit area and time (TOF), ECSA, and inherent activity of FeP/Fe₃O₄/C were more favorable than those of FeP/C. In addition, the change in Gibbs free energy for FeP/Fe₃O₄/C was more favorable compared to that for FeP/C (discussed in following section). Prior studies have reported comparable findings.^66,67

Fig. 7c shows the Bode plot of FeP/Fe₃O₄/C, which confirmed the existence of two-time constants. The semicircle recorded at a higher frequency could be attributed to the presence of surface porosity, while the other semicircle observed at a lower frequency was related to the charge-transfer process of the HER reaction. The resistance (R_p) induced by the high-frequency semicircle was found to be unaffected by the applied potential, indicating that the surface had a porous characteristic. This was additionally supported by conducting measurements in the presence of a potassium cyanide (KCN) concentration of 5 × 10⁻² M in the electrolytic solution. The experiment was conducted in an alkaline solution to prevent the interaction between KCN and H₂SO₄, which would produce hydrogen cyanide (HCN). Nyquist plots were recorded both before and after the addition of KCN. The results indicated that the diameter of both semicircles increased when KCN was present, suggesting a correlation between these resistances and the electrode kinetics.⁶⁸

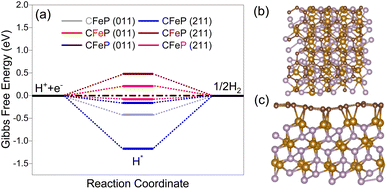
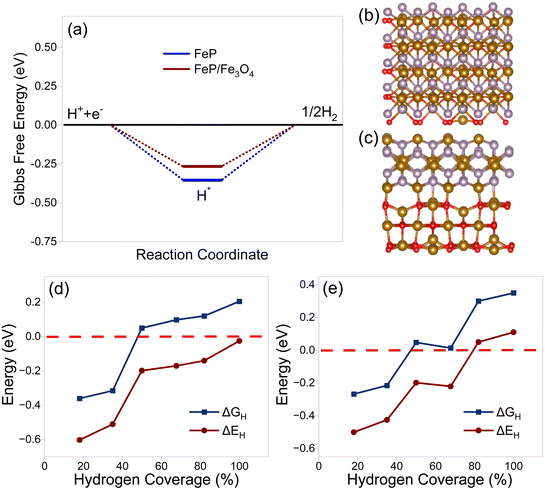
On the basis of the characterization results from the XRD, XPS, and microscopy analyses, it seems reasonable to infer that the surface of the electrocatalyst primarily consisted of FeP and an ultrathin carbon layer. Nevertheless, it was possible that there might be certain oxides on the surface along with phosphides. With this in mind, two density functional theory models were constructed to gain a comprehensive understanding of the electrocatalytic performance. The models included (1) an FeP surface with and without carbon layers, as well as a surface consisting of (2) FeP and Fe₃O₄ (composite model). The model with carbon layers was designated as CFeP, while the one without carbon was referred to as FeP. Surfaces with (011) and (211) facets were considered for the calculations. Before performing the catalytic activity calculations, the atomic structures of the experimentally synthesized CFeP with the (011) and (211) planes were optimized to identify its fundamental structural features. To establish consistency with the XRD findings, we split the FeP bulk structures into (011) and (211) surfaces. The free-energy diagram along with top and side views of the hydrogen adsorption for CFeP are shown in Fig. 8. By applying eqn (S1),† the cohesive energies of CFeP (011), CFeP (211), FeP (011), and FeP (211) were determined to be −5.89, −5.84, −4.83, and −4.96 eV per atom, respectively. These values suggest that CFeP exhibited significant thermodynamic stability in the presence of carbon layers. The predicted binding energies between FeP and C, using eqn (S2),† were −4.54 and −2.43 eV for the CFeP (011) and (211) surfaces, respectively. These values suggest the presence of covalent bonding between C and Fe, as shown in Fig. 8c. A well-established premise is that an effective HER catalyst should exhibit a Gibbs free energy shift that is as close to zero as feasible.⁶⁹ To conduct thorough HER experiments, we considered all the potential active sites on the CFeP surfaces, including Fe, P, and C. The C–H bond length was turned to 1.12 Å, the Fe–H bond length optimized to 1.54 Å, and the P–P bond length optimized to 1.43 Å. The ΔG_H values for the C, Fe, and P active sites on the (011) surface of CFeP were determined to be −0.42, 0.21, and −0.16 eV, respectively. On the other hand, on the (211) surface, the ΔG_H values for the same active sites were −1.17, 0.48, and −0.08 eV, respectively. A significant difference in the hydrogen adsorption energies on all the catalytic active sites was thus noticeable. The ΔG_H values of a hydrogen atom on the (011) and (211) surfaces are shown in Fig. 8a, and were found to be closer to zero. The calculated ΔG_H, as determined by eqn (S3),† suggest that the adsorbed hydrogen did not exhibit either extremely weak or strong binding to the (011) and (211) surfaces. This characteristic boosts the HER reaction. Furthermore, the ΔG_H values indicated that the HER occurs spontaneously on both the P and C sites; however it is non-spontaneous on the Fe sites. According to the Pauling electronegativity scale, both C and P have higher electronegativity than Fe. This causes a reduction in the charges on Fe and an increase in the charges on C and P. This leads to a redistribution of the charges, whereby C and P become more active sites on CFeP surfaces for the HER.⁷⁰ The partial density of states shown in Fig. S12† suggests that the Fermi levels of both (011) and (211) surfaces were mostly influenced by the d-states of Fe. As a result, these d-states play a significant role in facilitating charge transfer between the adsorbate and adsorbent.

Fig. 8 (a) Free-energy diagram for hydrogen evolution on the carbon-coated FeP surface. Top (b) and side (c) views of hydrogen adsorption. Black, blue, red, and green balls represent C, Fe, P, and H atoms, respectively.

Similarly, a double-layered model composed of FeP and Fe₃O₄ was also constructed. The free-energy diagram along with top and side views of hydrogen adsorption for the bare FeP and composite (FeP/Fe₃O₄) are shown in Fig. 9a–c. In addition, the calculated ΔG_H values and the corresponding adsorption energy (ΔE_H) on bare FeP as well as the composite surface with various hydrogen coverages are compared in Fig. 9d and e. On the pristine surface of FeP, the binding was so strong that it could prevent the release of H₂. As the coverage increased, the binding strength weakened, which led to the promotion of hydrogen evolution. With hydrogen coverage ranging from 50% to 66.7%, the ΔG_H value approached zero, indicating excellent activity toward the HER. When Fe₃O₄ was included, the excessive binding energy was much reduced, resulting in a ΔG_H value that was even closer to zero within the coverage range of 50% to 66.7%. Therefore, the HER process could occur with a broader spectrum of hydrogen coverage, which correlates with the enhanced catalytic efficiency of the composite layer. According to Bader charge analysis,⁷¹ an average of 1.77 electrons per square nanometer were transferred from FeP to the Fe₃O₄ layer. The depletion of electrons in the FeP layer of the composite structure weakened the interaction between the pristine surface and hydrogen. On the other hand, with the hydrogen coverage of 50% or 66.7%, the adsorbed hydrogen received 0.77/0.87 electron from FeP, and 0.81/0.91 electron from the composite layer, respectively. Herein, the composite layer could provide more electrons to the adsorbed hydrogen atoms with the optimal coverage, facilitating the following reduction and evolution of hydrogen. Moreover, the density of electronic states (DOS) of each model is plotted Fig. S13† to aid understanding the electronic structure. Both models were metallic with no band gap, indicating the good electronic conductivity and potential electrocatalytic activity. The DOS spectra of Fe₃O₄ and FeP/Fe₃O₄ slab models are compared in Fig. S14.† Fe₃O₄ is widely recognized as a magnetic substance. The surface model also exhibited typical magnetic properties. The inclusion of the Fe₃O₄ layer in the composite model resulted in a substantial enhancement of spin polarization. However, the addition of the FeP layer resulted in an increase in the density of states around the Fermi level. This increase in density may improve the material's electrical conductivity and thus boost its electrocatalytic characteristics.

Fig. 9 (a) Free-energy diagram for the HER on bare FeP and FeP/Fe₃O₄ surfaces, (b) top and (c) side views of hydrogen adsorption. The relationship between the differential adsorption energy (ΔE_H), adsorption free energy (ΔG_H), and hydrogen coverage on the (d) FeP surface and (e) FeP/Fe₃O₄ composite layer.

Conclusions

In summary, we report that phosphidation of the Fe₃O₄ surface leads to the formation of a highly active surface for the HER reaction. To heighten such a phosphidation effect, we proposed a route to obtain uniform microspheres of FeP/Fe₃O₄ with a mesoporous surface by the partial phosphidation of Fe₃O₄. Although the electrical conductivity and the charge-transfer resistance of FeP/Fe₃O₄ were less favorable, presumably due to the presence of oxygen, which tends to localize the electrons, it exhibited better HER performance than FeP. The superior performance of FeP/Fe₃O₄ could be correlated to both (1) the unique bonding configuration in FeP/Fe₃O₄, which boosted the kinetics of the HER reaction, and (2) the mesoporous surface, which offered a higher surface area, facile penetration of H⁺ into the pores and their maximum interaction with the active sites, and favored the diffusion of H₂ from the electrode's surface. The distinct surface quality of FeP/Fe₃O₄ had a favorable impact on some performance-dictating metrics, such as the specific surface area, electrochemically active surface area, exchange current density, Tafel values, active sites, and turnover frequency. As a result, the FeP/Fe₃O₄ electrode exhibited a ∼1.8-fold higher HER performance compared to the FeP electrode. Moreover, the FeP/Fe₃O₄ electrode showed good initial (20 mA cm⁻² for 24 h) electrochemical and structural stability. Moreover, the experimental results were confirmed by DFT calculations, demonstrating that the presence of carbon ultrathin layers could improve the stability of FeP. Furthermore, the redistribution of charges among Fe, C, and P facilitated the activation of P as active sites for the HER on both the (011) and (211) surfaces. In the case of the FeP/Fe₃O₄ model, the binding energy was decreased significantly compared to pristine FeP, leading to a ΔG_H value that approached zero even more closely within the H₂ coverage range of 50% to 66.7%. Thus, the HER process could take place with a wider range of hydrogen coverage, leading to the improved catalytic efficiency of FeP/Fe₃O₄. The findings of this investigation offer fresh impetus for designing and developing high-performance and cost-effective electrodes for the HER.

Data availability

The data supporting this article are included in the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number DRI 598.

References

1. R. Daiyan, I. MacGill and R. Amal, ACS Energy Lett., 2020, 5(12), 3843–3847.
2. S. Carley and D. M. Konisky, Nat. Energy, 2020, 5, 569–577.
3. G. He, J. Lin, F. Sifuentes, X. Liu, N. Abhyankar and A. Phadke, Nat. Commun., 2020, 11, 2486.
4. Z. Yan, J. L. Hitt, J. A. Turner and T. E. Mallouk, Proc. Natl. Acad. Sci. U.S.A., 2020, 117, 12558–12563.
5. R. Amore-Domenech and T. J. Leo, ACS Sustainable Chem. Eng., 2019, 7, 8006–8022.
6. A. Mayyas, R. Mark, P. Bryan, B. Guido and W. Keith, NREL/TP-6A20-72740, 2018.
7. M. Liu, Y. Jiang, Z. Cao, L. Liu, H. Chen and S. Ye, J. Energy Chem., 2024, 96, 464–471.
8. Y. Huang, X. Li, P. K. Shen, C. Yang and J. Zhu, ACS Mater. Lett., 2024, 6(5), 1678–1685.
9. H. Wu, Z. Zhao, M. Wang, W. Zheng, Y. Zhang, Y. Wang, T. Ma, Z. Zeng, C. Cheng and S. Li, J. Mater. Chem. A, 2024, 12, 10755–10763.
10. Y. Zhang, H. Xu, S. Shi, Y. Bao and Y. Chen, J. Mater. Chem. A, 2024, 12, 16592–16604.
11. A. Fathollahi, T. Shahrabi and G. B. Darband, J. Mater. Chem. A, 2024, 12, 9038–9054.
12. M. H. Suliman, A. Adam, L. Li, Z. Tian, M. N. Siddiqui, Z. H. Yamani and M. Qamar, ACS Sustainable Chem. Eng., 2019, 7, 17671–17681.
13. A. Adam, M. H. Suliman, M. N. Siddiqui, Z. H. Yamani, B. Merzougui and M. Qamar, ACS Appl. Mater. Interfaces, 2018, 10, 29407–29416.
14. A. Adam, M. H. Suliman, H. Dafallah, A. R. Al-Arfaj, M. N. Siddiqui and M. Qamar, ACS Sustainable Chem. Eng., 2018, 6, 11414–11423.
15. L. Chen, L. R. Zhang, L. Y. Yao, Y. H. Fang, L. He and Z. P. Liu, Energy Environ. Sci., 2019, 12, 3099–3105.
16. M. I. Díez-García, A. A. G. Blanco, S. Murcia-López, M. Botifoll, J. Arbiol, M. Qamar and J. R. Morante, ChemElectroChem, 2023, 10, e202201152.
17. S. Kong, P. Singh, A. Sarkar, G. Viswanathan, Y. V. Kolen'ko, Y. Mudryk, D. D. Johnson and K. Kovnir, Chem. Mater., 2024, 36, 1665–1677.
18. Z.-Z. Liu, N. Yu, R.-Y. Fan, B. Dong and Z.-F. Yan, Nanoscale, 2024, 16, 1080–1101.
19. W. Gao, Y. Wu, X. Wan, J. Gao and D. Wen, J. Mater. Chem. A, 2023, 11, 18126–18134.
20. V. Vij, S. Sultan, A. M. Harzandi, A. Meena, J. N. Tiwari, W.-G. Lee, T. Yoon and K. S. Kim, ACS Catal., 2017, 7, 7196–7225.
21. S. Li, X. Hao, A. Abudulac and G. Guan, J. Mater. Chem. A, 2019, 7, 18674–18707.
22. S. Xu, H. Zhao, T. Li, J. Liang, S. Lu, G. Chen, S. Gao, A. M. Asiri, Q. Wu and X. Sun, J. Mater. Chem. A, 2020, 8, 19729–19745.
23. A. Adam, M. H. Suliman, M. Awwad, M. N. Siddiqui, Z. H. Yamani and M. Qamar, Int. J. Hydrogen Energy, 2019, 44, 11797–11807.
24. C. Yang, R. Zhao, H. Xiang, J. Wu, W. Zhong, W. Li, Q. Zhang, N. Yang and X. Li, Adv. Energy Mater., 2020, 10, 2002260.
25. S. Chandrasekaran, L. Yao, L. Deng, C. Bowen, Y. Zhang, S. Chen, Z. Lin, F. Peng and P. Zhang, Chem. Soc. Rev., 2019, 48, 4178–4280.
26. N. Han, P. Liu, J. Jiang, L. Ai, Z. Shao and S. Liu, J. Mater. Chem. A, 2018, 6, 19912–19933.
27. S. Gupta, M. K. Patel, A. Miotello and N. Patel, Adv. Funct. Mater., 2020, 30, 1906481.
28. G. Cho, Y. Park, H. Kang, Y.-k. Hong, T. Lee and D.-H. Ha, Appl. Surf. Sci., 2020, 510, 145427.
29. R.-Q. Li, B.-L. Wang, T. Gao, R. Zhang, C. Xu, X. Jiang, J. Zeng, Y. Bando, P. Hu, Y. Li and X.-B. Wang, Nano Energy, 2019, 58, 870–876.
30. H. Li, Y. Wang, W. Zhu and Z. Zhuang, Int. J. Hydrogen Energy, 2019, 44, 22806–22815.
31. J. Chen, J. Liu, J.-Q. Xie, H. Ye, X.-Z. Fu, R. Sun and C.-P. Wong, Nano Energy, 2019, 56, 225–233.
32. M. Yang, J.-Y. Xie, Z.-Y. Lin, B. Dong, Y. Chen, X. Ma, M.-L. Wen, Y.-N. Zhou, L. Wang and Y.-M. Chai, Appl. Surf. Sci., 2020, 507, 145096.
33. J. Cai, Y. Song, Y. Zang, S. Niu, Y. Wu, Y. Xie, X. Zheng, Y. Liu, Y. Lin, X. Liu, G. Wang and Y. Qian, Sci. Adv., 2020, 6, eaaw8113.
34. L. H. Baydoun, C. N. Verani and S. L. Brock, J. Am. Chem. Soc., 2016, 138, 4006.
35. A. Mendoza-Garcia, H. Zhu, Y. Yu, Q. Li, L. Zhou, D. Su, M. J. Kramer and S. Sun, Angew. Chem., Int. Ed., 2015, 54, 9642.
36. Q. Zhou, Z. Shen, C. Zhu, J. Li, Z. Ding, P. Wang, F. Pan, Z. Zhang, H. Ma, S. Wang and H. Zhang, Adv. Mater., 2017, 30, 1800140.
37. H. Zhang, W. Zhou, J. Dong, X. F. Lu and X. W. D. Lou, Energy Environ. Sci., 2019, 12, 3348–3355.
38. J. Chen, J. Liu, J.-Q. Xie, H. Ye, X.-Z. Fu, R. Sun and C.-P. Wong, Nano Energy, 2019, 56, 225–233.
39. M. Wang, R. Zhao, X. Li, X. Zhao and L. Jiang, ChemNanoMat, 2019, 5, 593–598.
40. C. Lin, Z. Gao, J. Yang, B. Liu and J. Jin, J. Mater. Chem. A, 2018, 6, 6387–6392.
41. X. J. Wang, W. Xia, Z. Peng, Z. Wu, W. Lei, K. Xia, H. L. Xin and D. Wang, ACS Appl. Mater. Interfaces, 2017, 9, 26134–26142.
42. Z. Peng, X. Qiu, Y. Yu, D. Jiang, H. Wang, G. Cai, X. Zhang and Z. Dong, Carbon, 2019, 152, 16–23.
43. F.-X. Ma, C.-Y. Xu, F. Lyu, B. Song, S.-C. Sun, Y. Y. Li, J. Lu and L. Zhen, Adv. Sci. Lett., 2019, 6, 1801490.
44. M. H. Suliman, A. Adam, M. N. Siddiqui, Z. H. Yamani and M. Qamar, Carbon, 2019, 144, 764–771.
45. M. H. Suliman, A. Adam, M. N. Siddiqui, Z. H. Yamani and M. Qamar, Catal. Sci. Technol., 2019, 9, 1497–1503.
46. Y. Jian, T. Yu, Z. Jiang, Y. Yu, M. Douthwaite, J. Liu, R. Albilali and C. He, ACS Appl. Mater. Interfaces, 2019, 11, 11369–11383.
47. D. Y. Chung, S. W. Jun, G. Yoon, H. Kim, J. M. Yoo, K. S. Lee, T. Kim, H. Shin, A. K. Sinha, S. G. Kwon, K. Kang, T. Hyeon and Y. E. Sung, J. Am. Chem. Soc., 2017, 139, 6669–6674.
48. G. Tong, Y. Liu, T. Wu, Y. Ye and C. Tong, Nanoscale, 2015, 7, 16493.
49. S. Yang, J. Jiang, C. Xu, Y. Wang, Y. Xu and L. Cao, Sci. Rep., 2017, 7, 45480.
50. C. Y. Son, I. H. Kwak, Y. R. Lim and J. Park, Chem. Commun., 2016, 52, 2819–2822.
51. X. Liang, B. Zheng, L. Chen, J. Zhang, Z. Zhuang and B. Chen, ACS Appl. Mater. Interfaces, 2017, 9, 23222–23229.
52. Y. Zhang, X. Gao, L. Lv, J. Xu, H. Lin and Y. W. C. Ding, Electrochim. Acta, 2020, 341, 136029.
53. Z. Zhang, J. Hao, W. Yang, B. Lu and J. Tang, Nanoscale, 2015, 7, 4400–4405.
54. D. Xiong, X. Wang, W. Li and L. Liu, Chem. Commun., 2016, 52, 8711–8714.
55. X. F. Lu, L. Yu and X. W. D. Lou, Sci. Adv., 2019, 5, eaav6009.
56. B. Wei, G. Xu, J. Hei, L. Zhang and T. Huang, Int. J. Hydrogen Energy, 2021, 46, 2225–2235.
57. K. Wang, X. Liu, Q. Yu, X. Wang, J. Zhu, Y. Li, J. Chi, H. Lin and L. Wang, Small, 2024, 20, 2308613.
58. S. Yao, V. Forstner, P. W. Menezes, C. Panda, S. Mebs, E. M. Zolnhofer, M. E. Miehlich, T. Szilvási, N. A. Kumar, M. Haumann, K. Meyer, H. Grützmacher and M. Driess, Chem. Sci., 2018, 9, 8590–8597.
59. Y. Pan, Y. Lin, Y. Chen, Y. Liu and C. Liu, J. Mater. Chem. A, 2016, 4, 4745–4754.
60. C. Zhang, M. S. Xia, Z. P. Liu, G. Q. Huang, S. S. Yuan, J. Ai, N. Li and X. T. Li, ChemCatChem, 2020, 12, 2589–2594.
61. C. Lin, P. Wang, H. Jin, J. Zhao, D. Chen, S. Liu, C. Zhang and S. Mu, Dalton Trans., 2019, 48, 16555–16561.
62. T. Shinagawa, A. T. Garcia-Esparza and K. Takanabe, Sci. Rep., 2015, 5, 13801.
63. J. Wang, F. Xu, H. Jin, Y. Chen and Y. Wang, Adv. Mater., 2017, 29, 1605838–1605875.
64. C. Wei, S. Sun, D. Mandler, X. Wang, S. Z. Qiao and Z. J. Xu, Chem. Soc. Rev., 2019, 48, 2518–2534.
65. W. Cui, C. Ge, Z. Xing, A. M. Asiri and X. Sun, Electrochim. Acta, 2014, 137, 504–510.
66. C. Cheng, S. S. A. Shah, T. Najam, X. Qi and Z. Wei, Electrochim. Acta, 2018, 260, 358–364.
67. B. Lai, S. C. Singh, J. K. Bindra, C. S. Saraj, A. Shukla, T. P. Yadav, W. Wu, S. A. McGill, N. S. Dalal, A. Srivastava and C. Guo, Mater. Today Chem., 2019, 14, 100207.
68. L. Birry and A. Lasia, J. Appl. Electrochem., 2004, 34, 735.
69. X. Zhao, Z. H. Levell, S. Yu and Y. Liu, Chem. Rev., 2022, 122, 10675–10709.
70. A. L. Allred, J. Inorg. Nucl. Chem., 1961, 17, 215–221.
71. W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens.Matter, 2009, 21, 084204.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta02746a

---