Overcoming the limitations of atomic-scale simulations on semiconductor catalysis with changing Fermi level and surface treatment†
Seulgi
Ji
a,
Dong Won
Jeon
bc,
Junghyun
Choi
d,
Haneol
Cho
e,
Bo-In
Park
f,
Ilpyo
Roh
g,
Hyungil
Choi
g,
Chansoo
Kim
el,
Jung Kyu
Kim
 h,
Uk
Sim
h,
Uk
Sim
 i,
Danlei
Li
j,
Hyunseok
Ko
*k,
Sung Beom
Cho
i,
Danlei
Li
j,
Hyunseok
Ko
*k,
Sung Beom
Cho
 *bc and
Heechae
Choi
*bc and
Heechae
Choi
 *aj
*aj
aInstitute of Inorganic Chemistry, University of Cologne, Greinstr. 6, Cologne, 50939, Germany. E-mail: heechae.choi@xjtlu.edu.cn
bDepartment of Materials Science and Engineering, Ajou University, Suwon, 16499, Republic of Korea. E-mail: csb@ajou.ac.kr
cDepartment of Energy Systems Research, Ajou University, Suwon, 16499, Republic of Korea
dSchool of Chemical, Biological and Battery Engineering, Gachon University, Seongnam-si, Gyeonggi-do 13120, Republic of Korea
eAI, Information and Reasoning (AI/R) Laboratory, Korea Institute of Science and Technology (KIST), Hwrangro 14Gil 5, Seoul, Republic of Korea
fDepartment of Mechanical Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA
gMO R&D Center, M.O.P Co., Ltd, Seoul, 07281, Republic of Korea
hSchool of Chemical Engineering, Sungkyunkwan University (SKKU), Suwon, 16419, Republic of Korea
iHydrogen Energy Technology Laboratory, Korea Institute of Energy Technology (KENTECH), Naju, 58330, Republic of Korea
jDepartment of Chemistry, Xi'an Jiaotong-Liverpool University, Suzhou, 215123, China
kCenter of Material Digitalization, Korea Institute of Ceramic Engineering and Technology (KICET), Jinju, Gyeongnam 52851, Republic of Korea. E-mail: hko@kicet.re.kr
lAI-Robot Department, University of Science and Technology (UST), Republic of Korea
First published on 29th August 2024
Abstract
Wide band gap metal oxide semiconductor catalysts mostly exhibit very huge variations of catalytic reaction activities and pathways depending on the preparation conditions, unlike metallic catalyst materials. Atomic-scale modeling and ab initio calculations are extremely challenging for metal oxide semiconductor catalysts because of two main reasons: (i) large discrepancies between computational predictions and experiments, (ii) typical cell size limitations in modeling for dilute level doping (<1020 cm−3) cocatalyst size-dependency (diameter >3 nm). In this study, as a new groundbreaking methodology, we used a combination of density functional theory (DFT) calculations and a newly derived analytical model to systematically investigate the mechanisms of catalytic methane (CH4) oxidation activity change of CeO2. The key hypothesis that the catalytic methane oxidation reaction can be followed by the Fermi level change in CeO2 was well demonstrated via comparison with our multi-scale simulation and several literature reports. Our new method was found to give predictions in the catalytic activity of wide band gap semiconductors for variations in defect concentrations and cocatalyst coverage with advanced efficiency and accuracy, overcoming the typical model size limitation and inaccuracy problems of DFT calculations.
Introduction
To boost and optimize the methane (CH4) oxidation reaction catalyzed by CeO2-based catalysts in solid oxide fuel cell (SOFC) anodes, a number of materials engineering strategies and mechanism studies have been performed.1 As the most widely used routes to improve the catalytic activity of CeO2 in methane oxidation, cocatalyst deposition and impurity doping methods have been intensively used.2–4 Atomic scale modeling based computational studies have been performed along with experiments to understand how the catalytic methane oxidation activities of CeO2 are highly enhanced by up to several orders even with only very low cocatalyst coverage via cocatalyst nanoparticle (NP) deposition and/or dilute-limit impurity doping.5–7 However, it is extremely challenging to investigate the mechanism by experiments and density functional theory calculation based analysis on wide band gap CeO2 (ref. 6) because the catalytic activity of CeO2 catalysts greatly varies with the deposited NP size and the doping concentration.8–11In previous theoretical studies, the dopant sites on the CeO2 surface or the cocatalyst surfaces were commonly regarded as the main active sites due to the significantly increased catalytic activities.12–14 For example, in theoretical studies on silver- and copper-doped CeO2 systems, surface-doping was assumed in the catalytic reaction modeling.15,16 However, experimental studies proved that the intrinsic n-type characteristic of CeO2 was even enhanced with Ag- and Cu-doping, as the dopants are mostly segregated in the CeO2 grain boundaries.17,18 Therefore, it is a more appropriate assumption that the doped metal impurities in CeO2 do not participate in the surface reaction directly, as demonstrated by several previous experimental studies;19,20 the main roles of metal element doping in CeO2 are not the formation of new kinds of active sites.
For the NP-decorated CeO2 catalyst case, the synergistic effects in the methane oxidation of metallic Ni/CeO2 heterojunctions were explained using adsorption energy calculations and the Mars–Van Krevelen (MvK) mechanism at the interface.21,22 However, the assumption that the main contributions to catalytic reactions are made by the active sites of cocatalyst NPs deposited on CeO2 cannot support mechanism analysis for many other cases. For example, the catalytic CH4 reactivity of cocatalyst deposited CeO2 peaks only with very low coverage of cocatalysts.23 Furthermore, some research revealed that the dominant surface orientations,24 morphology,12,25,26 terminations,22 or the atomic percentages of cocatalyst NP elements on CeO2 largely determine the catalytic activity of metal NP decorated CeO2.27,28 Such findings contradictory to the conventional assumptions in the modeling schemes imply that the cocatalyst deposition and impurity doping contribute to the changed activity of the CeO2 surface in different ways which were never discussed. To advance the rational engineering of the wide band gap CeO2 catalyst, further mechanism study is necessary.
In most of the previous experimental and computational studies, the possibility that the surface electronic structure of CeO2 is tuned by cocatalyst NPs and dopants was hardly considered even though only low coverage of NPs improves the catalytic activity of CeO2 in methane oxidation.2,23,29 Recent semiconductor photochemistry studies revealed that the surface activities of wide band gap oxide materials can be tuned via surface Fermi level modifications with metal deposition or dopant segregation.30–32 An experimental and computational study on the nickel nitride decorated CeO2 catalyst reported that the electron transferred from the cocatalyst to the CeO2 support affects the catalytic activity of CeO2.33
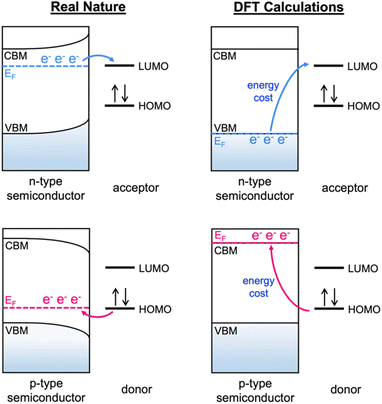
In recent experimental and computational research works on wide band gap oxide materials, we demonstrated that catalytic reactions on the oxide surface were greatly altered via manipulation of the Fermi level either by doping or surface treatment,34,35 whereas the importance of the Fermi level in the catalytic reactions of CeO2 has never been discussed. Heterovalent dopants in CeO2 or point defects can change the bulk Fermi level due to the changed charge carrier concentration and accordingly band bending occurs near the surface because the bulk Fermi level (εF(bulk)) and surface Fermi level (εF) deviate from each other (Fig. 1).36,37 Therefore, the surface Fermi level can be modulated by the difference between εF(bulk) and the degree of band bending (ΔVBB) (eqn (1)); when cocatalyst NPs are loaded on the CeO2 surface, the surface Fermi level can be directly altered by the energy band alignment with the work function of the decorated cocatalyst NPs (∅cocat) at the equilibrium state as shown in Fig. 1.38
| εF = εF(bulk) − ΔVBB | (1) |
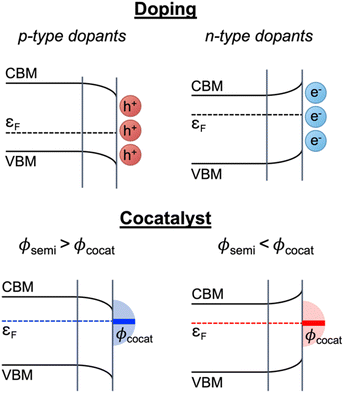 | ||
| Fig. 1 Schematic illustration of surface Fermi level modification strategies: doping and cocatalyst. | ||
According to the theoretical model described above, a variation of the surface Fermi level of a semiconductor determines the favorable charge states of adsorbed species and the adsorption energies. Since an electron transfer between a semiconductor surface and the highest occupied molecular orbital (HOMO) or lowest unoccupied molecular orbital (LUMO) of adsorbates contributes to the Gibbs free energy change by chemisorption, the Fermi level of a semiconductor catalyst must be taken into account for an adsorption energy calculation (Fig. 1).39,40 In our recent previous theoretical–experimental combinational works, we introduced a new theoretical method for better understanding of the relationships between the surface Fermi level and the adsorption energy on wide band gap semiconductors.34,35,41 We successfully controlled the surface reaction kinetics by manipulating the surface Fermi level and theoretically elucidated the influence of surface Fermi level engineering on the adsorption energy.
In this study, we investigate the mechanism of methane oxidation and the promoting effect of doping/cocatalyst decoration on the catalytic activity of CeO2 with a key hypothesis: catalytic methane oxidation reaction activity of the CeO2 catalyst is determined by the surface Fermi level. By using DFT calculations and our new analytical models, we proved that the catalytic methane oxidation reactions on CeO2 are highly dependent on the surface Fermi level. In comparison to our new theoretical predictions with many experimental studies in the literature, the dopant–cocatalyst synergies and cocatalyst coverage effects were successfully explained.
Results and discussion
Theory
As a method to resolve the inevitable discrepancy between the charge transfer energetics of a semiconductor in real life and the DFT electronic structure predictions (Fig. 2), we express the adsorption energy of adsorbates on a semiconductor as a function of the Fermi level. In the conventional method, the Gibbs free energies of adsorbates on catalytic surfaces have been calculated by using the computational hydrogen electrode (CHE) model proposed by Norskov et al.42 In this work, a Gibbs free adsorption energy (ΔGads) of a methane oxidation intermediate adsorbate on a CeO2 surface was expressed as| ΔGads = ΔE0 + q(εF + EVBM) + Eiso − Eper + qΔV + ΔZPE + ∫CpdT − TΔS | (2) |
 | ||
| Fig. 2 A schematic illustration of the inevitable error of adsorption energy between real life and DFT calculations. | ||
Fermi level dependent reaction pathway and energy barrier
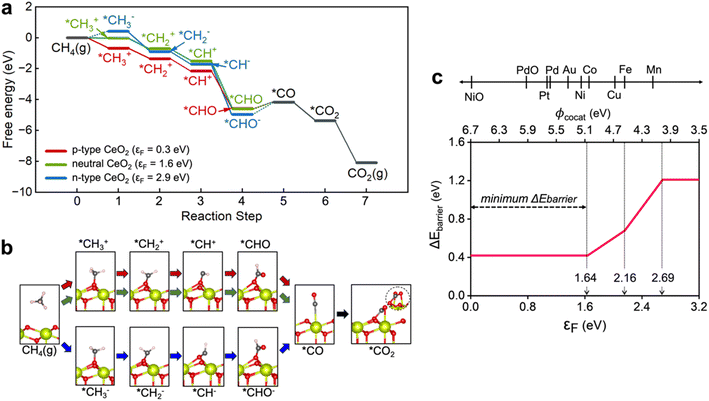
In Fig. 3, we present how the surface Fermi level of CeO2 can alter the methane oxidation reaction pathway and change the reaction energy barrier. We considered the methane oxidation reaction at 923 K (650 °C), a typical reaction temperature of SOFC, in the reaction intermediate free energy calculations.43 Concerning the adsorption of a CH4 molecule on a CeO2 (111) for an initiation of the CH4 oxidation reaction, the positive value of the adsorption energy (2.75 eV) of a CH4 molecule on a CeO2 (111) surface (*CH4 formation) is not energetically favored, as shown in Fig. S1.† On the other hand, the calculated adsorption free energies in Fig. S2† show that negatively charged *O (*O2−) can significantly occupy the active sites of CeO2 when the Fermi level of CeO2 is above 1.58 eV, as the adsorption free energy becomes negative and competes with the adsorbate of reaction step 1 (*CH3 formation). Therefore, the methane oxidation reactant oxygen reservoir is O2(g) (*O2−) with the Fermi level below (above) 1.58 eV. The descriptions of reaction steps, reaction pathways, and the optimized configurations of adsorbates are presented in Scheme S1, ESI 4, and Fig. S3.†The free energy diagrams of the methane oxidation reactions catalyzed by neutral (εF = 1.6 eV), extreme p-type (εF = 0.3 eV), and n-type (εF = 2.9 eV) CeO2 with the thermodynamically preferred intermediates and the atomic structure of each reaction step are presented in Fig. 3a and b to examine whether the Fermi level can affect the reaction pathway and energy barriers. The detailed free energy diagrams of methane oxidation on CeO2 with all possible intermediates are depicted in Fig. S4†. All the excessive charges in the models were localized on intermediates on the CeO2 surface. (Fig. S5†) We additionally calculated the density of states (DOS) of each intermediate (CH3, CH2, CH, and CHO), which can be charged during methane oxidation, to see the effect on the change to the electronic states of CeO2. Fig. S6† shows that the adsorption of the charged CH2 and CH resulted in the formation of gap states, while there is no gap state formation by CH3 and CHO adsorption. According to the calculated free energy diagram in Fig. 3a, CH2 and CH are expected not to bind residually to the CeO2 surface for so long but to form CHO, showing the free energy downhill in reaction step 4. Therefore, we reason that the change to the surface Fermi level position due to the generated gap state by CH2 and CH adsorption can be negligible.
The charge state of *CH3 in reaction step 1 is positive (CH3+) on the p-type (εF = 0.3 eV) and the neutral (εF = 1.6 eV) CeO2, and turns negative (CH3−) on the n-type (εF = 2.9 eV) CeO2. Since the adsorbed *O2− is stabilized on the n-type CeO2 surface due to the stronger binding to the surface Ce ion, the formation of *CH3− is suppressed. According to the calculated energy diagram in Fig. 3a, dehydrogenation reactions are all energy downhill from the reaction steps 1 to 4, regardless of the surface Fermi level position of CeO2. Our theoretical prediction of energy downhills for reaction steps 1 to 4 is well consistent with the experimental in situ observations in the CeO2 catalyst that the CH2 group was not detected due to the too short lifetime.21 For reaction step 4 in Fig. 3a, our calculations predicted that *C adsorption on CeO2 was not thermodynamically stable (Fig. S3†). Instead, *CHO formation is expected to be favored with neutral charge (q = 0) on the p-type CeO2 and negative charge (q = −1) on the n-type CeO2. Since the adsorption energy of *CHO− becomes more negative with the higher Fermi level of CeO2, the energy uphill becomes larger with the CeO2 surface Fermi level. The formation of the *CHO− adsorbate on CeO2 catalyst surfaces during methane oxidation reactions is consistent with the experimental observations of significant stretching vibration frequencies of CHO− groups at 1735, 1715, and 1704 cm−1.44,45
General methods to control the surface Fermi level of wide band gap semiconductors include (i) impurity doping,46 (ii) grain size control,47 and (iii) deposition of other NPs on the surface.48 However, it is extremely challenging to lower the Fermi level of CeO2via impurity doping or grain size control because even metal dopants having a smaller valence preserve the intrinsic n-type characteristic of CeO2, as the dopants are segregated at grain boundaries,17,18 and the size effects on surface band bending can be valid only when the grain radius is smaller than the charge depletion region width (<30 nm).47 However, most of the CeO2 catalysts have grain size greater than 50 nm.12,28,49 Therefore, surface NP deposition is the only available methods. To give a quantitative insight, the total energy barrier, the summation of the energy barriers of the endothermic reaction steps for methane oxidation on CeO2 (Fig. S7†), was plotted with respect to the surface Fermi level of CeO2 (εF) as shown in Fig. 3c.
To enhance the reactivity of methane oxidation on CeO2, the Fermi level of CeO2 should be controlled in the following ways: (i) hindering the strong adsorption of the O atom, so that *CH3 can dominantly occupy the active site of CeO2 and (ii) the total energy barrier including two endothermic reaction steps for *CH3 and *CO formation should be minimized. The adsorption free energy diagram at where the Fermi level is in a range between 0 eV and 1.64 eV is depicted in Fig. S8†. Our theoretical prediction that cocatalysts have work functions between 5.06 eV and 6.70 eV is consistent with many experimental findings such as for CeO2 decorated with Ni,21,26,28 Pt,50,51 Pd,1,12,52 and Au.22
When a cocatalyst is placed on a semiconductor surface, due to the work function difference, a quadratic change in the surface Fermi level on the semiconductor side is induced by band bending. Then, accordingly, the reaction energy barriers and the resultant reaction rate are also changed with the radial distance from the interface between the cocatalyst NP and the semiconductor as the total energy barrier of methane oxidation is assumed to have linearity with the Fermi level (Fig. 3c). Hence, in order to make an accurate prediction of the overall reaction rate, it is necessary to utilize analytical models integrating the changes in the reaction rates with distance from the cocatalyst.
Analytical models for the combinatorial effect of cocatalyst dispersion and work function
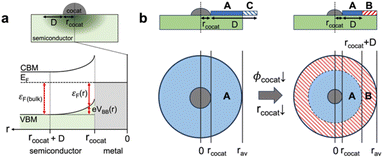
We built the analytical model for precise prediction of the reaction rates for methane oxidation catalyzed by cocatalyst-decorated CeO2 as shown in Fig. 4. Given that the work functions of the predicted cocatalyst candidates are larger than that of CeO2, we considered Schottky contact between a cocatalyst NP and CeO2 (Fig. 4a). In the cocatalyst–CeO2 junction, the surface Fermi level (εF(r)) and the degree of band bending (VBB(r)) vary with the distance from the loaded cocatalyst (r), which is presented as eqn (3) below,| εF(r) = εF(CeO2) − eVBB(r) | (3) |
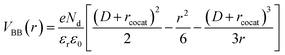 | (4) |
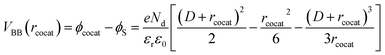 | (5) |
The equation of reaction rate constant (R) can be employed to compare the surface reaction activity of cocatalyst/CeO2 and bare CeO2 for methane oxidation, which can be written as55
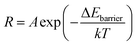 | (6) |
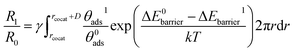 | (7) |
Given that the functionality and selectivity of catalysts are governed by the coverage and dispersion of a cocatalyst on a semiconductor,56,57 the effect of cocatalyst coverage and dispersion on the reaction rate was considered by adding the γ term in eqn (7), which is the ratio of the active site on the CeO2 surface and can be represented by eqn (8),
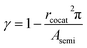 | (8) |
Fig. 4b shows two cases of depletion region formation on a cocatalyst-loaded CeO2 surface. If the band bending occurs at a wider area in the depletion region than half of the average distance between cocatalysts, the band bending area (blue color area A in Fig. 4b) can be distributed in all areas of the exposed CeO2 surface, where the reaction ratio can be obtained using eqn (7) above. On the other hand, with a decrease in the work function and/or radius of a cocatalyst, band bending occurs at a narrower area than half of the average distance between cocatalysts; therefore, a flat band area (red-hatched area B in Fig. 4b) can exist on the CeO2 surface. The ratio of reaction rate constant on the flat band area ranging from rcocat+D to rav can be calculated by using eqn (7).
In previous studies, without the assumptions of the band bending dependency of the methane oxidation reaction on CeO2, cocatalyst coverage effects were not fully understood.36,58 The reaction rate of methane oxidation in the band bending area is approximately 9 times higher than that of the flat band area of CeO2 for Nd = 1019 cm−3 (Fig. 4b and S10†). This indicates that the considerations of cocatalyst dispersion (coverage) are a crucial factor due to the changed band bending and Fermi level positions with radial distance from a cocatalyst.
Hence, the contour maps of the surface reaction rate constant ratio (R1/R0) as a function of the cocatalyst work function and the active sites ratio (γ) were calculated using eqn (9) and (10):
(i) rcocat + D is narrower than rav,
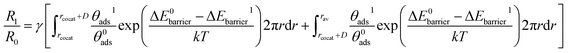 | (9) |
(ii) rcocat + D is wider than rav,
 | (10) |
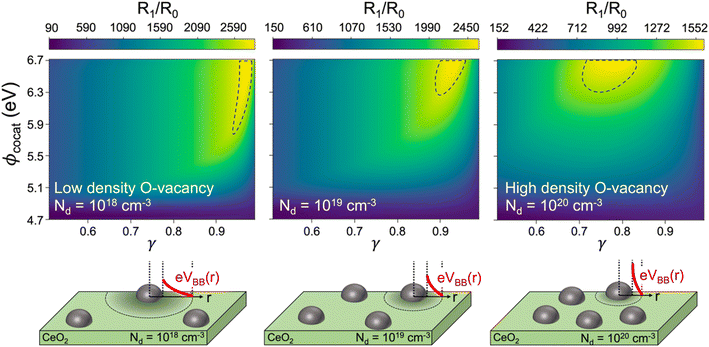
Optimum cocatalyst coverage and space charge density predictions
In most experimental studies on cocatalyst-deposited CeO2 catalysts, the methane oxidation reaction activities are sensitively changed with the combination of many factors, such as cocatalyst species, dispersion distance, size, and impurity concentrations in CeO2 supports.8 To further verify our hypothesis of the Fermi level dependent methane oxidation reaction rate of the CeO2 catalyst, we plotted the ratio of the reaction rate by the use of a cocatalyst (R1/R0), with contour maps for the simultaneous variations of cocatalyst work function, coverage, and the nonstoichiometry of CeO2 in Fig. 5 using eqn (9) and (10). The areas enclosed by the dashed curves in Fig. 5 indicate the optimum cocatalyst deposition conditions for high catalytic activity of methane oxidation. For a high coverage of cocatalysts (lower γ value) with high work function for Nd = 1019 cm−3 a lower reaction rate was shown than that with a low coverage of cocatalysts (higher γ value). A number of previous experimental and theoretical studies have reported that the high coverage of a cocatalyst on CeO2 can lower the catalytic reaction.2,6,23,29 For example, Lustemberg et al. reported that an undoped CeO2 catalyst particle with low NiO coverage of 0.10–0.13 ML induces the highest reaction rate of methane oxidation, which is in good accordance with our theoretical observation in Fig. 5 for Nd = 1019 cm−3 (dashed circle at 0.87 < γ < 0.93).6 Considering the interface between the loaded catalyst and CeO2 as the only area where the reaction dominantly takes place, Ni and NiO on CeO2 were predicted to have a total energy barrier of 0.41 eV for the whole methane oxidation (Fig. 3c). However, with our analytical model, we can reason that the different interface band bending of the Ni/CeO2 and the NiO/CeO2 systems will result in different overall reaction activity over the CeO2 active site area.The effects of oxidation of metal cocatalysts on the activity of the methane oxidation reaction catalyzed by a CeO2 catalyst have not been actively discussed before. Pd0 and Ni0 species deposited on the CeO2 catalyst surface are commonly oxidized and behave as the main active species in experimental studies.1,12,21,59 The methane oxidation reaction activity on the CeO2 catalyst is rather improved when the Pd and Ni particles are oxidized to form PdO and NiO.12,59,60 The enhanced methane oxidation reaction activity of the CeO2 catalyst by cocatalyst oxidation in the literature12,59,60 agrees very well with our theoretical predictions in Fig. 5: the higher reaction rate ratio of PdO/CeO2 (work function 6.00 eV) than that of Pd/CeO2 (work function 5.60 eV) and Pt/CeO2 (work function 5.65 eV). Considering that the work function of bimetallic catalysts has a linear trend with different compositions of bimetallic alloys,61 bimetallic cocatalysts with CeO2 can also be used by manipulation of metal composition to change the work function and thus the depletion region width62–65 such as in the case of the CuNi/CeO2 catalyst reported by Hornes et al.14
Many research studies have already been devoted to studying the effect of oxygen vacancy formation in CeO2 on the oxidation reaction.4,5 Due to the unique properties of the Ce4+/Ce3+ redox pair of CeO2, the oxidation reaction on cocatalyst-decorated CeO2 has been explained by the MvK mechanism, in which lattice oxygen atoms of CeO2 are involved in the oxidation reaction.21,22,66,67 However, the underlying reaction mechanisms and active site are still controversial because the optimum cocatalyst coverage differs with the species of cocatalyst, especially when Ce3+ species have high concentrations.12,21
The first few cycles of methane oxidation on CeO2 can dominantly follow the MvK mechanism. However, as the methane oxidation takes place continuously, the oxygen vacancy formation energy increases.68,69 Accordingly, the contribution of the MvK mechanism to the methane oxidation, where oxygen vacancy formation is involved, is rapidly decreased as the Fermi level increases. Therefore, it is insufficient to explain the long-term oxidation reaction by the MvK mechanism alone. To precisely predict the reaction conditions of CeO2 for even long-term methane oxidation, the synergistic effect of the formation of oxygen vacancies and the change in band bending with increasing the surface Fermi level of CeO2 on the reaction rate should be considered.
As the oxygen vacancy formation shifts the Fermi level of CeO2 higher, the surface band bending is induced at the narrower area in the depletion region width (eqn (5) and Fig. S11†). Sm3+, Eu3+, or Zr4+ doping in Ni/CeO2 increases electron concentration (higher Nd value) by segregation at the grain boundary and oxygen vacancy formation. Ni NPs cluster more densely in a few nanometers than in the depletion region width, resulting in the high cocatalyst coverage (lower γ value).4,5,7 On the other hand, the distribution of dispersed Ni NPs of undoped Ni/CeO2 is wider (higher γ value) than that of heterovalent dopant doped CeO2,4 which is consistent with our calculations. Thus, our theoretical model can provide further elucidation on the oxidation reaction on CeO2, considering oxygen vacancy formation can change the Fermi level to heavy n-type CeO2, allowing us to understand the mechanism, including the long-term catalytic reaction.
Conclusions
As a new breakthrough method to solve the problem of inaccurate adsorption energy calculations and the model size limitation problem in the conventional DFT calculations for optimizing wide band gap semiconductor catalysts, we introduced a combination of Fermi level dependent adsorption energy theory and analytical models. In this work, methane oxidation on CeO2 (with a band gap of 3.2 eV) was used as the case model. Our DFT calculation results showed that the surface Fermi level position of the CeO2 catalyst can alter the reaction energy barrier and also the reaction pathways, which can clearly explain why only a few specific cocatalyst elements, such as Ni, Pt, Pd, and Au, are used in most of the literature. The combination of the DFT calculations and a new analytical model was used to consider the band bending effects at the cocatalyst–CeO2 interface to accurately predict the relation between the methane oxidation reactivity of CeO2 and the cocatalyst coverage. In addition, the synergistic effects of CeO2 doping concentration and cocatalyst deposition conditions in the methane oxidation reaction activity were successfully explained. The newly suggested method of this work is expected to be widely used for efficient optimization of doping concentration (bulk Fermi level position) and cocatalyst materials, without suffering from the typical cell size limitation problems in atomic-scale modeling for DFT calculations on modified wide band gap semiconductor catalysts.Data availability
The data supporting this article have been included as part of the ESI.†Author contributions
Conceptualization, methodology, software, writing – original draft: S. Ji, H. Ko, S. B. Cho, H. Choi. Supervision, writing – review & editing: D. Li, J. K. Kim, U. Sim, H. Ko, S. B. Cho, H. Choi. Formal analysis: H. Cho, C. Kim. Data curation, visualization: S. Ji, D. W. Jeon, H. Cho, C. Kim. Investigation: S. Ji, J. Choi, B.-I. Park, I. Roh, H. Choi.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National R&D Program through the National Research Foundation of Korea (NRF) funded by the Ministry of Science and ICT (RS-2023-00209910, RS-2023-00285390, RS-2024-00444182 and RS-2024-00407282) and Virtual Engineering Platform Project through the Ministry of Trade, Industry, and Energy of Korea (P0022336). We acknowledge the grant no. 2021-0-02076 and 2023-00262155 (IITP) funded by the Korea government (the Ministry of Science and ICT). D. Li is thankful for the support through the Research Development Fund by Xi'an Jiaotong-Liverpool University. H. Choi acknowledges the financial support received through an Enhancement Fund (AY23/24) from the School of Science at Xi'an Jiaotong-Liverpool University. We acknowledge and are thankful for the support received from the Suzhou Industrial Park High Quality Innovation Platform of Functional Molecular Materials and Devices (YZCXPT2023105) and the XJTLU Advanced Materials Research Center (AMRC).Notes and references
- J. Lee, T. H. Lim, E. Lee and D. H. Kim, ChemCatChem, 2021, 13, 3706–3712 CrossRef CAS.
- Y. Lykhach, S. M. Kozlov, T. Skála, A. Tovt, V. Stetsovych, N. Tsud, F. Dvořák, V. Johánek, A. Neitzel, J. Mysliveček, S. Fabris, V. Matolín, K. M. Neyman and J. Libuda, Nat. Mater., 2016, 15, 284–288 CrossRef CAS.
- J. Dou, Y. Tang, L. Nie, C. M. Andolina, X. Zhang, S. House, Y. Li, J. Yang and F. Feng Tao, Catal. Today, 2018, 311, 48–55 CrossRef CAS.
- J. Chen, B. D. Carlson, T. J. Toops, Z. Li, M. J. Lance, S. G. Karakalos, J.-S. Choi and E. A. Kyriakidou, ChemCatChem, 2020, 12, 5558–5568 CrossRef CAS.
- L. M. Toscani, M. S. Bellora, C. Huck-Iriart, A. L. Soldati, J. Sacanell, T. S. Martins, A. F. Craievich, M. C. A. Fantini, S. A. Larrondo and D. G. Lamas, Appl. Catal., A, 2021, 626, 118357 CrossRef CAS.
- P. G. Lustemberg, Z. Mao, A. Salcedo, B. Irigoyen, M. V. Ganduglia-Pirovano and C. T. Campbell, ACS Catal., 2021, 11, 10604–10613 CrossRef CAS PubMed.
- Z. Zhang, Z. Yu, K. Feng and B. Yan, Appl. Catal., B, 2022, 317, 121800 CrossRef CAS.
- A. Ruiz Puigdollers, P. Schlexer, S. Tosoni and G. Pacchioni, ACS Catal., 2017, 7, 6493–6513 CrossRef CAS.
- M. Sterrer, M. Yulikov, E. Fischbach, M. Heyde, H.-P. Rust, G. Pacchioni, T. Risse and H.-J. Freund, Angew. Chem., Int. Ed., 2006, 45, 2630–2632 CrossRef CAS.
- S. Abbet, A. Sanchez, U. Heiz, W.-D. Schneider, A. M. Ferrari, G. Pacchioni and N. Rösch, J. Am. Chem. Soc., 2000, 122, 3453–3457 CrossRef CAS.
- H. Wang, X.-K. Gu, X. Zheng, H. Pan, J. Zhu, S. Chen, L. Cao, W.-X. Li and J. Lu, Sci. Adv., 2019, 5, eaat6413 CrossRef PubMed.
- S. Chen, S. Li, R. You, Z. Guo, F. Wang, G. Li, W. Yuan, B. Zhu, Y. Gao, Z. Zhang, H. Yang and Y. Wang, ACS Catal., 2021, 11, 5666–5677 CrossRef CAS.
- Y. Mahara, J. Ohyama, T. Tojo, K. Murata, H. Ishikawa and A. Satsuma, Catal. Sci. Technol., 2016, 6, 4773–4776 RSC.
- A. Hornés, P. Bera, M. Fernández-García, A. Guerrero-Ruiz and A. Martínez-Arias, Appl. Catal., B, 2012, 111–112, 96–105 CrossRef.
- G. Righi, R. Magri and A. Selloni, J. Phys. Chem. C, 2020, 124, 17578–17585 CrossRef CAS.
- K. Polychronopoulou, A. A. AlKhoori, A. M. Efstathiou, M. A. Jaoude, C. M. Damaskinos, M. A. Baker, A. Almutawa, D. H. Anjum, M. A. Vasiliades, A. Belabbes, L. F. Vega, A. F. Zedan and S. J. Hinder, ACS Appl. Mater. Interfaces, 2021, 13, 22391–22415 CrossRef CAS.
- M. Arshad, A. Iqbal, T. Ahamad, J. Gupta, M. Arshad and A. S. Ahmed, J. Electron. Mater., 2023, 52, 5690–5706 CrossRef CAS.
- P. Knauth and H. L. Tuller, Solid State Ionics, 2000, 136–137, 1215–1224 CrossRef CAS.
- F. Khojasteh, M. R. Mersagh and H. Hashemipour, J. Alloys Compd., 2022, 890, 161709 CrossRef CAS.
- N. W. Kwak, S. J. Jeong, H. G. Seo, S. Lee, Y. Kim, J. K. Kim, P. Byeon, S.-Y. Chung and W. Jung, Nat. Commun., 2018, 9, 4829 CrossRef PubMed.
- J. Chen, T. Buchanan, E. A. Walker, T. J. Toops, Z. Li, P. Kunal and E. A. Kyriakidou, ACS Catal., 2021, 11, 9345–9354 CrossRef CAS.
- H. Ha, S. Yoon, K. An and H. Y. Kim, ACS Catal., 2018, 8, 11491–11501 CrossRef CAS.
- P. Pal, R. K. Singha, A. Saha, R. Bal and A. B. Panda, J. Phys. Chem. C, 2015, 119, 13610–13618 CrossRef CAS.
- G. B. Hoflund, Z. Li, T. J. Campbell, W. S. Epling and H. W. Hahn, MRS Online Proc. Libr., 1999, 581, 449 CrossRef.
- G. Spezzati, A. D. Benavidez, A. T. DeLaRiva, Y. Su, J. P. Hofmann, S. Asahina, E. J. Olivier, J. H. Neethling, J. T. Miller, A. K. Datye and E. J. M. Hensen, Appl. Catal., B, 2019, 243, 36–46 CrossRef CAS.
- J. Chen, H. N. Pham, T. Mon, T. J. Toops, A. K. Datye, Z. Li and E. A. Kyriakidou, ACS Appl. Nano Mater., 2023, 6, 4544–4553 CrossRef CAS.
- S. Damyanova, B. Pawelec, K. Arishtirova, M. V. M. Huerta and J. L. G. Fierro, Appl. Catal., B, 2009, 89, 149–159 CrossRef CAS.
- R. K. Singha, A. Shukla, A. Yadav, L. N. Sivakumar Konathala and R. Bal, Appl. Catal., B, 2017, 202, 473–488 CrossRef CAS.
- M. Li and A. C. van Veen, Appl. Catal., B, 2018, 237, 641–648 CrossRef CAS.
- Y. Zhang, L. Xu, B. Liu, X. Wang, T. Wang, X. Xiao, S. Wang and W. Huang, ACS Catal., 2023, 13, 5938–5948 CrossRef CAS.
- S. S. Kalanur and H. Seo, J. Energy Chem., 2022, 68, 612–623 CrossRef CAS.
- M. A. Gaikwad, U. P. Suryawanshi, U. V. Ghorpade, J. S. Jang, M. P. Suryawanshi and J. H. Kim, Small, 2022, 18, 2105084 CrossRef CAS.
- X. Ding, R. Jiang, J. Wu, M. Xing, Z. Qiao, X. Zeng, S. Wang and D. Cao, Adv. Funct. Mater., 2023, 2306786 CrossRef CAS.
- Y. Li, M. Je, J. Kim, C. Xia, S. H. Roh, W. So, H. Lee, D.-H. Kim, S. M. Cho, J. W. Bae, H. Choi and J. K. Kim, Chem. Eng. J., 2022, 438, 135532 CrossRef CAS.
- S. Kim, S. Ji, K. H. Kim, S. H. Roh, Y. Cho, C.-L. Lee, K.-S. Lee, D.-G. Choi, H. Choi, J. K. Kim and J. H. Park, Chem. Eng. J., 2021, 407, 126929 CrossRef CAS.
- Z. Zhang and J. T. Yates, Chem. Rev., 2012, 112, 5520–5551 CrossRef CAS PubMed.
- S. Krukowski, P. Kempisty and P. Strąk, J. Appl. Phys., 2013, 114, 063507 CrossRef.
- C. Jiang, S. J. A. Moniz, A. Wang, T. Zhang and J. Tang, Chem. Soc. Rev., 2017, 46, 4645–4660 RSC.
- Th. Wolkenstein, in Advances in Catalysis, Elsevier, 1960, vol. 12, pp. 189–264 Search PubMed.
- A. Rothschild, Y. Komem and N. Ashkenasy, J. Appl. Phys., 2002, 92, 7090–7097 CrossRef CAS.
- Y. Cherif, H. Azzi, K. Sridharan, S. Ji, H. Choi, M. G. Allan, S. Benaissa, K. Saidi-Bendahou, L. Damptey, C. S. Ribeiro, S. Krishnamurthy, S. Nagarajan, M. M. Maroto-Valer, M. F. Kuehnel and S. Pitchaimuthu, ACS Omega, 2023, 8, 1249–1261 CrossRef CAS PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- H. Ren, Y. H. Lee, E. A. Wu, H. Chung, Y. S. Meng, E. E. Fullerton and N. Q. Minh, ACS Appl. Energy Mater., 2020, 3, 8135–8142 CrossRef CAS.
- A. Yee, S. J. Morrison and H. Idriss, J. Catal., 1999, 186, 279–295 CrossRef CAS.
- M. M. Chirila, K. Sarkisian, M. E. Andrew, C.-W. Kwon, R. J. Rando and M. Harper, Ann. Occup. Hyg., 2015, 59, 336–346 CrossRef CAS PubMed.
- E. Celik, Y. Ma, T. Brezesinski and M. T. Elm, Phys. Chem. Chem. Phys., 2021, 23, 10706–10735 RSC.
- W. J. Albery and P. N. Bartlett, J. Electrochem. Soc., 1984, 131, 315 CrossRef CAS.
- T. Ioannides and X. E. Verykios, J. Catal., 1996, 161, 560–569 CrossRef CAS.
- P. Schlexer, D. Widmann, R. J. Behm and G. Pacchioni, ACS Catal., 2018, 8, 6513–6525 CrossRef CAS.
- P. Pantu and G. R. Gavalas, Appl. Catal., A, 2002, 223, 253–260 CrossRef CAS.
- R. Kumar Singha, A. Shukla, A. Yadav, S. Sain, C. Pendem, L. N. S. Kumar Konathala and R. Bal, Mol. Catal., 2017, 432, 131–143 CrossRef CAS.
- M. Danielis, S. Colussi, C. de Leitenburg, L. Soler, J. Llorca and A. Trovarelli, Catal. Sci. Technol., 2019, 9, 4232–4238 RSC.
- N. I. Santha, M. T. Sebastian, P. Mohanan, N. McN. Alford, K. Sarma, R. C. Pullar, S. Kamba, A. Pashkin, P. Samukhina and J. Petzelt, J. Am. Ceram. Soc., 2004, 87, 1233–1237 CrossRef CAS.
- D. Sharma and B. R. Mehta, J. Alloys Compd., 2018, 749, 329–335 CrossRef CAS.
- P. Atkins, J. De Paula and J. Keeler, Atkins' Physical Chemistry, Oxford University Press, 11th edn, 2017 Search PubMed.
- J. Resasco, L. DeRita, S. Dai, J. P. Chada, M. Xu, X. Yan, J. Finzel, S. Hanukovich, A. S. Hoffman, G. W. Graham, S. R. Bare, X. Pan and P. Christopher, J. Am. Chem. Soc., 2020, 142, 169–184 CrossRef CAS PubMed.
- S. Xie, L. Liu, Y. Lu, C. Wang, S. Cao, W. Diao, J. Deng, W. Tan, L. Ma, S. N. Ehrlich, Y. Li, Y. Zhang, K. Ye, H. Xin, M. Flytzani-Stephanopoulos and F. Liu, J. Am. Chem. Soc., 2022, 144, 21255–21266 CrossRef CAS PubMed.
- G. D. J. Smit, S. Rogge and T. M. Klapwijk, Appl. Phys. Lett., 2002, 81, 3852–3854 CrossRef CAS.
- N. J. Divins, A. Braga, X. Vendrell, I. Serrano, X. Garcia, L. Soler, I. Lucentini, M. Danielis, A. Mussio, S. Colussi, I. J. Villar-Garcia, C. Escudero, A. Trovarelli and J. Llorca, Nat. Commun., 2022, 13, 5080 CrossRef CAS.
- A. Mussio, M. Danielis, N. J. Divins, J. Llorca, S. Colussi and A. Trovarelli, ACS Appl. Mater. Interfaces, 2021, 13, 31614–31623 CrossRef CAS PubMed.
- A. M. Ismail, E. Csapó and C. Janáky, Electrochim. Acta, 2019, 313, 171–178 CrossRef CAS.
- D. G. Araiza, D. G. Arcos, A. Gómez-Cortés and G. Díaz, Catal. Today, 2021, 360, 46–54 CrossRef CAS.
- S. Roy, S. Hariharan and A. K. Tiwari, J. Phys. Chem. C, 2018, 122, 10857–10870 CrossRef CAS.
- L. Yang, L. Li, P. Xia, H. Li, J. Yang, X. Li, X. Zeng, X. Zhang, C. Xiao and Y. Xie, Chem. Commun., 2021, 57, 11629–11632 RSC.
- S. Lu, B. Weng, A. Chen, X. Li, H. Huang, X. Sun, W. Feng, Y. Lei, Q. Qian and M.-Q. Yang, ACS Appl. Mater. Interfaces, 2021, 13, 13044–13054 CrossRef CAS PubMed.
- S. Yoon, H. Ha, J. Kim, E. Nam, M. Yoo, B. Jeong, H. Y. Kim and K. An, J. Mater. Chem. A, 2021, 9, 26381–26390 RSC.
- J.-X. Liu, Y. Su, I. A. W. Filot and E. J. M. Hensen, J. Am. Chem. Soc., 2018, 140, 4580–4587 CrossRef CAS PubMed.
- X. Zhang, L. Zhu, Q. Hou, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Chem. Mater., 2023, 35, 207–227 CrossRef CAS PubMed.
- Y. Jiang, J. B. Adams, M. van Schilfgaarde, R. Sharma and P. A. Crozier, Appl. Phys. Lett., 2005, 87, 141917 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta03595j |
| This journal is © The Royal Society of Chemistry 2024 |