Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Formation of intrinsic point defects in AlN: a study of donor and acceptor characteristics using hybrid QM/MM techniques†
Lei
Zhu
 ab,
Xingfan
Zhang
ab,
Xingfan
Zhang
 a,
Qing
Hou
a,
Qing
Hou
 cd,
You
Lu
cd,
You
Lu
 e,
Thomas W.
Keal
e,
Thomas W.
Keal
 e,
John
Buckeridge
f,
C. Richard A.
Catlow
e,
John
Buckeridge
f,
C. Richard A.
Catlow
 *ag and
Alexey A.
Sokol
*ag and
Alexey A.
Sokol
 *a
*a
aDepartment of Chemistry, University College London, London, WC1H 0AJ, UK. E-mail: c.r.a.catlow@ucl.ac.uk; a.sokol@ucl.ac.uk
bDepartment of Materials, University of Oxford, Parks Road, Oxford OX1 3PH, UK
cSchool of Artificial Intelligence Science and Technology, University of Shanghai for Science and Technology, Shanghai, 200093, China
dInstitute of Photonic Chips, University of Shanghai for Science and Technology, Shanghai, China
eSTFC Scientific Computing, Daresbury Laboratory, Warrington, Cheshire WA4 4AD, UK
fSchool of Engineering, London South Bank University, 103 Borough Road, London, SE1 0AA, UK
gSchool of Chemistry, Cardiff University, Park Place, Cardiff CF10 1AT, UK
First published on 8th August 2024
Abstract
The wide-gap material aluminium nitride (AlN) is gaining increasing attention for its applications in optoelectronics, energy, and quantum computing, making the investigation of its defect properties crucial for effective use in these fields. This study employs a hybrid quantum mechanical/molecular mechanical (QM/MM) embedded cluster method and uses three different hybrid-level density functional theory (DFT) functionals (B97-2, PBE0, and BB1K) to investigate systematically the thermodynamic stability, electronic properties, and donor/acceptor nature of intrinsic charged point defects in AlN. Our approach allows for the examination of defects within a significantly larger simulation cell, enhancing the reliability of the calculations. Our findings highlight the stable structures of defects including the symmetry-breaking reconstruction of octahedral-centred nitrogen interstitial and nitrogen split-interstitial defects, as well as the potential of nitrogen vacancies and aluminium interstitial defects as sources of shallow donor species. Additionally, we compute equilibrium defect concentrations at different annealing temperatures up to 2800 K, elucidating the roles of nitrogen and aluminium vacancies and interstitials in the conductivity of undoped, n-type doped, and p-type doped AlN. This comprehensive study advances the understanding of defect stability and electronic properties in AlN, paving the way for its enhanced application in advanced technologies.
1 Introduction
Aluminium nitride (AlN) is an important material for energy,1 optoelectronic,2–4 and potentially quantum computing devices.5,6 The ultra-wide band gap of AlN enables efficient emission of ultraviolet light in UV light-emitting diodes (LEDs)2 for sterilisation and water purification, as well as excellent thermal and electrical insulating properties for high-power electronic applications.7 The investigation of defect properties of the material is crucial for understanding many of its fundamental characteristics and enhancing its performance in these applications.8 To control the electrical functionalities of the material, doping with various elements, including silicon for n-type9 and magnesium for p-type conductivity,10,11 has been applied, although the process requires careful control to achieve the desired defect concentrations and minimise compensating defects. Characteristic defect signatures of specific luminescence emissions have been reported,8 aiding in the identification and understanding of these defects.The many properties of AlN that relate to the defect structure remain unclear. It is widely considered that AlN tends to be n-type due to native defects such as nitrogen vacancies and oxygen impurities. In experiment, while the presence of N and Al vacancy defects has been identified by various techniques;12–19 other intrinsic point defects including interstitial and antisite defects have not been directly observed. These native vacancies,12,20–28 as well as related defect complexes with oxygen impurities,19,21,22,25,29–44 are proposed as possible sources of deep-state luminescence/absorption within the band gap. Other unintentionally contaminating or intentionally doped impurities include silicon,23,45,46 carbon,46–51 magnesium,10,52–54 and other species8,55 which are also found to be stable in the material. All these defects can act as either donors or acceptors, depending on their charge states, leading to different energy states within the band gap region. However, the imprecise control over eliminating unwanted impurities and introducing intended impurities leads to discrepancies and gaps in our knowledge, which persist regarding the nature and properties of these defects; and it is often difficult to identify whether a particular type of defect or a group of different defects is associated with a certain wavelength of photo-response. Consequently, a comprehensive understanding of these defects and their complex donor/acceptor behaviour is essential for the development and optimisation of AlN-based applications.
The stability and donor/acceptor properties of these intrinsic defects can be explored by computational techniques, such as the density functional theory (DFT) methods. Earlier DFT studies, using the local density approximation (LDA) and generalized gradient approximation (GGA) functionals, on defects in zinc blende and wurtzite phase AlN provided insights into structural and electronic configurations of intrinsic point defects, as well as many impurities.56–63 They were able to explore several defect types that had not been identified in experiment, including nitrogen split-interstitials and antisites. However, these LDA and GGA simulations suffer from the self-interaction error, which causes excessively delocalised charge densities and an underestimated band gap value, resulting in inaccurate representation of charged defect species for the Fermi level within the gap region. In recent years, the rapid growth in computer power has enabled the use of more chemically accurate methods with larger simulation cells. The Heyd–Scuseria–Ernzerhof (HSE) hybrid GGA functional has been widely used in defect studies of AlN,64–76 as the fraction of Hartree–Fock exchange is tuneable for better agreement with experimental physical properties including lattice constants, enthalpy of formation, and band gap.75 Experimental photo-absorption and photoluminescence energy bands have often been associated with the optical transitions involving the deep and shallow states of defects, as calculated in those studies using hybrid DFT functional methods.
Current DFT methods are mostly implemented for a system constructed with periodic boundary conditions (PBC) using plane-wave based software. For charged defects, such an implementation can give an ambiguous description of the reference potential level, and therefore an unreliable description of electron ionisation processes. Additionally, the supercell system, which is often constructed for these DFT calculations, suffers from the finite-size effect.77 For defect calculations, the defect is periodically repeated causing spurious interactions between defects in adjacent supercells, which requires the system either to be corrected78 for these interactions or to be scaled up so that the interactions are minimised due to distance. Because PBC-based methods become more expensive as the size of simulation cell increases, there is a substantial trade-off between choosing more accurate exchange–correlation functionals against scaling up the system.
In this work, we use a hybrid quantum mechanical/molecular mechanical (QM/MM) embedded cluster method for a systematic investigation of the electronic properties and thermodynamic stability of intrinsic point defects in AlN. This method allows us to study point defect properties at the hybrid DFT level in a simulation cell, which when including the MM region contains about 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms, 100 times larger than the 96-atom supercell used in the most recent AlN defect study using periodic boundary conditions.75 The defect is embedded in a central region which is treated quantum mechanically (QM) and an outer region where short-range and long-range interactions and polarization effects are modelled using an interatomic potential, or molecular mechanics (MM) approach. In this way, for defects at different charge states, the ionisation process has an unambiguous reference, or vacuum level, which improves the reliability of the calculations. There have been previous studies all using PBC-based techniques, but they either used a lower-level DFT theory or covered an incomplete set of defect types,61,64,73,75,79 making it difficult to draw conclusions about the stability of each defect species. Here, by accessing a wider range of hybrid functionals of different HF exchange fractions, we present a comprehensive survey based on QM/MM methods with a critical examination of the effect of different DFT functionals.
000 atoms, 100 times larger than the 96-atom supercell used in the most recent AlN defect study using periodic boundary conditions.75 The defect is embedded in a central region which is treated quantum mechanically (QM) and an outer region where short-range and long-range interactions and polarization effects are modelled using an interatomic potential, or molecular mechanics (MM) approach. In this way, for defects at different charge states, the ionisation process has an unambiguous reference, or vacuum level, which improves the reliability of the calculations. There have been previous studies all using PBC-based techniques, but they either used a lower-level DFT theory or covered an incomplete set of defect types,61,64,73,75,79 making it difficult to draw conclusions about the stability of each defect species. Here, by accessing a wider range of hybrid functionals of different HF exchange fractions, we present a comprehensive survey based on QM/MM methods with a critical examination of the effect of different DFT functionals.
While systematically investigating the geometries and electronic structures of all types of intrinsic defects in all their stable charge states, we are able to explore the novel structures and stability of the symmetry-breaking reconstruction of the octahedral-centred N interstitial and the N split-interstitial, both of which are found to be stable; the low formation energies of the Al interstitial, which were found to be comparable to the N vacancy; and the diffuse states of compact defect species, which indicate that the N vacancy and Al interstitial are a possible source of intrinsic shallow donor species. Our results using the B97-2, PBE0, and BB1K functionals show that, even at the hybrid level, different DFT theories can lead to different conclusions for the defect stability. In the final section, equilibrium defect concentrations are computed at different annealing temperatures up to 2800 K to study defect and charge species compensation in scenarios of undoped, n-type doped, and p-type doped materials at all relevant preparative conditions, highlighting the significant roles of the N vacancy, Al vacancy, and Al interstitial for the material's conductivity. Our previous study using the classical force field and the Mott–Littleton embedded cluster approach has already shown some important properties of defect stability, including the identification of the new lower-symmetric, lower-energy N interstitial configuration, and in-lattice migration mechanisms in their formal charges.80 In this study, we build on this earlier work by using the QM/MM approach. We focus on key properties of charged intrinsic point defect types in wide-gap AlN.
2 Computational approach
2.1 Hybrid QM/MM embedded cluster technique
The hybrid QM/MM embedded cluster method is applied to model point defect formation in AlN using ChemShell (Tcl version81,82 and Python version83). There are five concentric regions/layers in our QM/MM system (see the schematic illustration of regions 1–5 in Fig. S1, ESI†). In the inner-most central region (region 1), where the localised defect state is positioned, DFT calculations are performed using NWChem code.84 An 86-atom cluster (∼5 Å radius) is chosen to achieve computational efficiency and is sufficient to obtain accurate results (similar size QM clusters have been chosen in previous reports85–87). The QM cluster is modelled with three different DFT hybrid functionals, B97-2,88 PBE0,89,90 and BB1K91 (21%, 25%, and 42% exact Hartree–Fock (HF) exchange fractions, respectively). Table S1 (ESI)† shows all three functionals can reproduce structural parameters and optimized bond lengths from previous experiment measurements and calculations. Later in the study, we compare how the three different hybrid functionals could affect the local environment of defect species. The Def2-TZVP92 basis set is used for both Al and N. The outermost diffuse, as well as high angular momentum basis functions, are removed for both species (f for N, and d & f for Al), as deleting them results in a very small change in defect formation energies and saves a significant amount of computational time.Surrounding the central region, there is an “active” MM region (region 3), where all the atoms and shells are explicitly controlled by the classical force field model and the shell model for the polarization of the nitrogen ions.80,93 In the subsequent “frozen” MM region (region 4), the positions of atoms are fixed. The combined thickness of both active and frozen MM regions is ∼15 Å (containing approximately 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 atoms in total). The force field model used in both MM regions is the two-body interatomic potential fitted empirically to a broad range of structural and physical properties of bulk wurtzite AlN. We have successfully implemented the same potential model to predict ionisation potentials, defect formation energies, and defect migration mechanisms of AlN previously.80 All the MM calculations in our QM/MM system are performed with the GULP code.94,95 Lastly, at the surface of the whole QM/MM system, point charges are added to reproduce the Madelung potential of the infinite crystal around the defect site (region 5).
000 atoms in total). The force field model used in both MM regions is the two-body interatomic potential fitted empirically to a broad range of structural and physical properties of bulk wurtzite AlN. We have successfully implemented the same potential model to predict ionisation potentials, defect formation energies, and defect migration mechanisms of AlN previously.80 All the MM calculations in our QM/MM system are performed with the GULP code.94,95 Lastly, at the surface of the whole QM/MM system, point charges are added to reproduce the Madelung potential of the infinite crystal around the defect site (region 5).
At the interface (region 2) between the QM cluster and MM region, a thin layer of cations is associated with a local electron localising pseudopotential, which also compensates for force mismatches between the QM region and the MM region. The pseudopotential takes the form of a linear combination of three Gaussian functions with respect to the distance r between electrons and respective nuclei:
r2Up(r) = A1r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Z1r2) + A2r2 exp(−Z1r2) + A2r2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Z2r2) + A3r2 exp(−Z2r2) + A3r2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−Z3r2) exp(−Z3r2) | (1) |
The A and Z parameters are fitted separately using the fit_my_ecp96 software, where a global search is done by fulfilling two objectives: (i) minimising the gradient difference between the atoms in the QM, interface and active MM regions; (ii) minimising energy scatter of innermost localised states on anions. In general, the pseudopotentials need to be adjusted to work with the force field implemented in the technique. The resultant pseudopotential for the cations at the interface takes the form with coefficients given in atomic units:
r2Up(r) = −36r![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−25r2) + 42.6r2 exp(−25r2) + 42.6r2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−3.4r2) + 0.45r2 exp(−3.4r2) + 0.45r2![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) exp(−0.55r2) exp(−0.55r2) | (2) |
During a QM/MM calculation with a polarisable shell model potential, ChemShell alternates between QM and MM calculations iteratively to reach ultimate convergence of the whole system. A number of reports have been published using the same method for GaN85,97,98 and for other ionic materials.87,99–103 A more detailed discussion of our QM/MM implementation can be found in a previous publication.104
2.2 Calculations of defect formation energies
The processes of forming point defects in bulk AlN can be represented by the following reactions (using a slightly revised form of Kröger–Vink convention105) depending on two extremes of the chemical conditions, namely, the “N-rich/Al-poor” condition and “N-poor/Al-rich” condition (e− is an electron and h+ is a hole):Al vacancy (VAl)
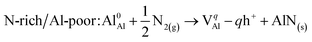 | (3) |
| N-poor/Al-rich: Al0Al → VqAl − qh+ + Al(s) | (4) |
N vacancy (VN)
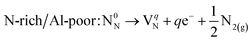 | (5) |
| N-poor/Al-rich: N0N + Al(s) → VqN + qe− + AlN(s) | (6) |
Al interstitial (Ali)
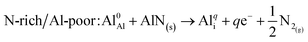 | (7) |
| N-poor/Al-rich: Al0Al + Al(s) → Alqi + qe− | (8) |
N interstitial (Ni)
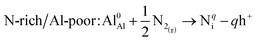 | (9) |
| N-poor/Al-rich: Al0Al + AlN(s) → Nqi − qh+ + Al(s) | (10) |
N antisite (NAl)
| N-rich/Al-poor: Al0Al + N2(g) → NqAl − qh+ + AlN(s) | (11) |
| N-poor/Al-rich: Al0Al + AlN(s) → NqAl − qh+ + 2Al(s) | (12) |
The formation energy (Ef) of a defect (X) at charge state q is defined as a function of Fermi energy level (EF) above the valence band maximum (VBM):
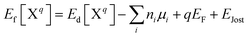 | (13) |
| μAl + μN = ΔHf(AlN) | (14) |
Since in the “frozen MM region” (region 4) the atomic positions of all the atoms (cores) do not respond to the presence of the defect centre and only shells react to the potential change from the defect, to account for the missing long-range polarisation effect in the frozen MM region and beyond to infinity, a correction term (EJost) is applied on any non-neutral charged defect states, where we use the correction formulated by Jost,108
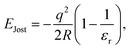 | (15) |
In the case of a vertical process (e.g., electron ionisation and optical excitation) where relaxation involves only electrons, an appropriate form of Jost's correction is applied involving the high-frequency dielectric constant ε∞. The description of Jost's correction in the case of vertical transition from q to q + Δq thus is:
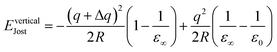 | (16) |
According to eqn (15) and eqn (16), the accuracy of the Jost correction can depend on the dielectric constants, as well as the size of the simulation cluster, which may vary according to the specific material system. Here we take ε0 = 10.98 and ε∞ = 4.68, obtained by averaging over dielectric tensor components calculated in GULP.80 As the QM cluster is a part of the infinite pre-optimized structure in the MM software environment (modelled using the GULP code), to keep all calculations consistent, it is reasonable to use the corresponding dielectric constants calculated by the same force field (which shows good agreement with experiments in previous study80).
3 Results and discussion
3.1 Ionisation potentials
The ionisation potential of a material is the minimum energy required to excite an electron to the vacuum state. In semiconductor materials, this energy corresponds to the electron transition from the top of valence band (valence band maximum, VBM) to the vacuum level.109 With the QM/MM embedded cluster method, we can compute the ‘bulk’ value, that is the ionisation potential neglecting any particular surface effects,110 by taking the energy difference between an ionized cluster (losing an electron and allowing electronic degrees of freedom to relax, Eionized) and a perfect cluster (Eperfect):| EIP = Eionized − Eperfect + EverticalJost | (17) |
E verticalJost (−0.38 eV) represents the polarisation correction of the transition from 0 to +1 charge state. As shown in Table 1, our calculated ionisation potentials (the negative of which is the VBM level relative to vacuum) are overall deeper than previous values obtained from surface/interface structures using PBC-based methods,112,113 which are limited by the ambiguity of their vacuum level and finite-size effects. The ionisation potential obtained from our force field model80 is slightly smaller (so that the VBM is closer to the vacuum level) than our QM/MM levels, but the discrepancy of at most 1 eV indicates that the force field model provides a useful initial estimate. In addition, the B97-2 VBM level is higher than that calculated using BB1K, which can be attributed to the different electronic localisation performance of the two hybrid functionals. A similar trend is also found in GaN98 using the same QM/MM method (c.f.Table 1). Importantly, we will see in later sections that the different electronic localization characteristics from different functionals and their different resultant VBM levels have a strong impact on defect formation energies and charge transition energies, as they are key terms determining these quantities.
| QM/MM | FF | Prev. DFT | |||
|---|---|---|---|---|---|
| B97-2 | PBE0 | BB1K | |||
| AlN | 7.63 | 7.98 | 8.38 | 7.35 | 5.8–7.5 |
| GaN | 6.63 | N/A | 7.34 | 5.7–6.7 | |
To the best of our knowledge, there is no experimental ionisation potential reported for AlN, but we can compare our calculated levels indirectly with measured electron affinities. We should note that electron affinities of AlN cannot be obtained directly using our QM/MM method, as high electron delocalisation of the conduction band states cannot be modelled using the embedded cluster method. Here, we obtain an estimation of the electron affinity of AlN by subtracting the experimental bandgap (6.2 eV) from the VBM levels. The electron affinities of AlN are: 1.23 eV (B97-2), 1.78 eV (PBE0), and 2.18 eV (BB1K). No negative electron affinity (NEA) is found for the pure AlN cluster from our calculations,114 which is in good agreement with experimental observations where electron affinities are measured to be between 0.3–2.6 eV.115–119 The large variation of the experimental CBM values is mainly due to the surface composition, orientation, and dipole moment of the measured samples, as proved by many theoretical studies.65,120,121 The experimentally measured CBM is affected by either upwards or downwards surface bending depending on the surface condition, so it is expected that their values differ from our “bulk ionisation potential”86 as discussed by Zhang et al.110
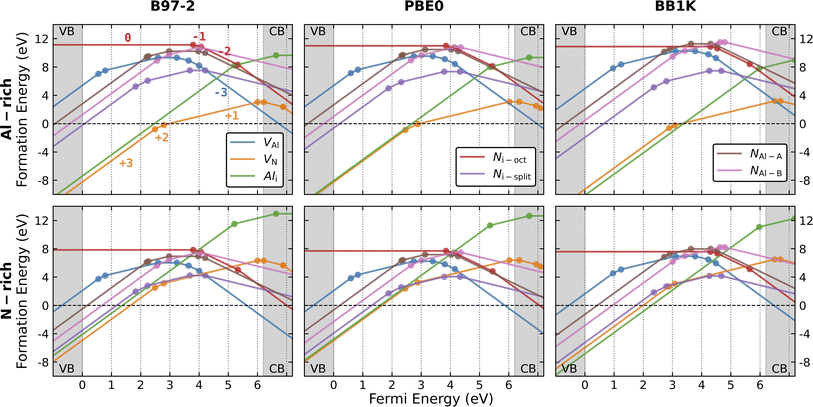
3.2 Formation of intrinsic point defects
Fig. 1 presents our calculated formation energies for the intrinsic defects, and their charge transition levels in the band gap region for N-rich and Al-rich conditions. We investigated the N and Al vacancies (VN and VAl), Al interstitial (Ali), N interstitial, and N antisite (NAl). For the N interstitial, two different configurations are investigated explicitly: the “split-interstitial” configuration (Ni-split) and the interstitial located close to the centre of the octahedral chamber of the wurtzite lattice (Ni-oct). The experimental band gap of 6.2 eV is used. The Al antisite defect is not considered for three reasons: first, the Al3+ ion is three times smaller than the N3− ion; second, Al is not likely to be stable in an anionic state; third, the B97-2 formation energy of the neutral Al antisite defect calculated in ChemShell is around 14.21 eV (Al-rich condition), much higher than all our considered defect species.From the results calculated using B97-2 and PBE0, the more energetically favourable intrinsic point defects are VN, Ni-split, and VAl in N-rich condition (Ni-split is excluded in Al-rich condition) for Fermi energies within the band gap region. These more stable defect species are in agreement with a previous study using the supercell approach and the HSE functional.75 However, we find Ali becomes more favourable than the most favourable VN as the proportion of HF exchange in the functional increases. For Fermi energies in the lower half of the band gap, the formation energy of Ali is only 0.20 eV higher than VN using the PBE0 functional, and lower by 0.87 eV using the BB1K functional. An early report found Ali had the lowest formation energy in zinc blende AlN in the band gap region closer to VBM using the LDA density functional,61 but the authors state its formation energy is over 2 eV higher in the wurtzite structure counterpart. Zhang et al. calculated the formation energy of Ali in the wurtzite structure, which they found to be significantly higher than that of VN using the GGA-level PBE functional.64 However, later calculation75 using the hybrid HSE functional with spin polarisation taken into account found the formation energy of Ali almost negligibly higher than that of VN. In our calculation, a higher fraction of HF exchange deepens the VBM level (Table 1), which in turn increases the energies needed for electrons to localize on (or ionise from) the charged defects and significantly changes their formation energies.
Alkauskas et al. have identified the problem of formation energies of charged defect species in relation to the shifts of band edge levels caused by different levels of theory.122 They proposed a band edge correction scheme, where inaccurate band edge energy levels from lower-level DFT theory simulations are shifted according to the more accurate band edge energies calculated with a hybrid functional. Inspired by the theory and the later implementation in GaN,123 another GGA-PBE simulation, with band edges corrected according to HSE energy levels, finds Ali formation energy lower than VN in the lower band gap region,79 similar to our BB1K results. Nevertheless, our calculations and the wide range of previous results show the predicted stability of Ali is closely dependent on the level of theory used and the band edge energy levels.
Although our results on the relative stability of each defect species are consistent with previous calculations, our formation energies of positively and negatively charged defect states are systematically lower. Taking V3+N as an example (summarised in Table S3, ESI†), our highest formation energy (from the B97-2 functional) is 3.81 eV lower than the lowest value from previous simulations at the VBM level. One reason could be the choice of DFT functional. There is a significant energy difference among all the formation energies of V3+N calculated at different DFT levels (Table S3†), with the lowest value obtained from simulations using a band-edge-corrected scheme at the GGA-PBE level.
Furthermore, our formation energies of charged defects may differ from values calculated using the PBC-based methods, as our method employs a different treatment of polarization and ionization processes. Nevertheless, both factors should not result in discrepancies in the energies of the neutral charge states. To illustrate this hypothesis, the formation energies of V0Al calculated in our QM/MM environment using different density functionals from the LDA level are compared with previous calculations (summarised in Table S4 (ESI)†). Our QM/MM method reproduces the results of previous reports at the LDA and the GGA level within reasonable accuracy. At the hybrid level, our BB1K formation energy of the V0Al shows the best agreement compared with previous HSE results, and our B97-2 and PBE0 counterparts are closer to previous GGA-PBE results (we have not directly compared with the HSE functional results, as the functional is not currently implemented in NWChem).
When comparing defect formation energies between our three functionals (taking vacancies and interstitials as examples, shown in Fig. S2, ESI†), BB1K results are generally lower than B97-2 and PBE0 results for positively charged defects, and higher for neutral and negatively charged defects, except for V1+Al, for which the BB1K formation energy is the higher. For neutral defects, the formation energies of most defect types are similar across the three functionals, with one exception in the case of V0Al. For the negative charge states, all formation energies calculated with BB1K surpass significantly those calculated with B97-2 and PBE0. Accurate electronic localization performance is crucial in the calculation of thermochemical formation energies, which can provide other important information such as ionisation potential energies. We have shown that our calculated different ionisation potential energies (Table 1) of electron/hole localisation from the vacuum level are key terms in the formation energies of all charged species. Among the three functionals, BB1K clearly simulates the most stable hole state as it calculates the largest ionization energy, but the B97-2 ionisation energy is also large in comparison to previous DFT simulations. These deeper VBM levels are the primary reason for our discrepancies to the results from previous studies.
A direct consequence of our lower formation energies of charged defects is the shift to higher energies relative to the VBM of all our charge transition levels.75 Table S5 (ESI)† summarises the charge transition energies of all the defect species discussed and the comparison with previous calculations. All our charge transition energy levels are closer to the CBM than previous calculated levels obtained using PBC-based methods. From previous calculations, such a shift to the CBM for the energy levels can also be seen when a “higher-rung” (more accurate) DFT functional is used (except for VN, as the direct transition of (+3|+1) is found in the lower-rung DFT calculations), which arises from the improved band edge levels. These transition levels are important for the optical transition processes, as they are often linked to experimental measurements. Previously deep acceptor VAl(−2|−3) was assigned to optical emission signals at 2.78 and 3.2 eV,20 and VAl(−1|−2) to the 2 eV signal.124 The statements from these two examples were drawn from previous DFT simulations ranging from LDA to hybrid levels of theories. From our calculations, the 2.78/3.2 eV signal can be related to a deep level of VAl(−1|0), and the 2 eV signal to acceptor levels of VAl(−2|−3). However, these transition levels represent charge transitions between fully relaxed defect structures and optical transition occurs much quicker than relaxation. Therefore, it is more suitable to associate experimental signals to calculated vertical transition energies between different charge states using configuration-coordination diagrams. Nevertheless, our simulations highlight the importance of ionization energy level for accurate defect energetics.
3.3 Defect structural and electronic properties
We now discuss the structural and electronic properties of each defect type in all their charge states and compare our results with available simulations and experiments. In particular, the localisation of electrons and holes at each charge state will be explicitly discussed, which, for AlN systems, have only been reported for very few intrinsic defect types56,61,69 without a systematic investigation. All our simulations start by creating defect species in their formal charges and adding/removing electrons. Most of our results reported below, including the defect structures and electronic information, are qualitatively consistent for all three functionals, unless otherwise stated.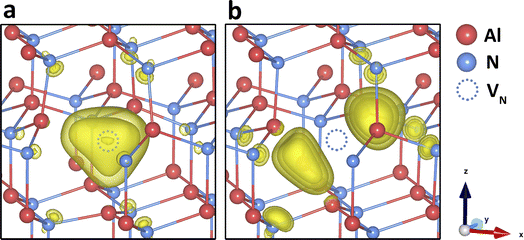 | ||
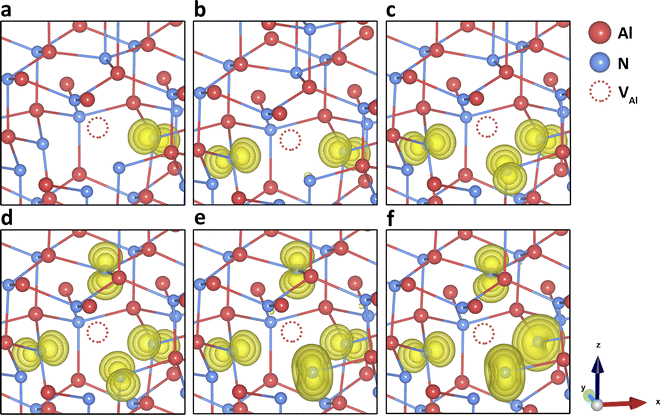
| Fig. 2 N vacancy in charge states (a) +2 and (b) 0 in AlN. Electron localisation is shown with spin density of (yellow isosurfaces of 0.01 a.u., 0.0075 a.u., and 0.005 a.u.). | ||
Although the local geometry of differently charged vacancies is in reasonable agreement with previous simulations, we did not find the stability of the negatively charged VN within the band gap, contrary to almost all previous simulations. As more electrons are added to the defect, the surrounding Al3+ ions gradually approach the defect centre, leading to a reduction in the bond lengths. When the charge state becomes more negative, the VN–Al bond lengths are shorter than those in the perfect lattice. At this point, the vacancy defect starts to attract the surrounding positively charged Al ions, due to the negative central Madelung potential. However, as shown in Fig. 1, the charge transition levels for the negatively charged VN are within the conduction band, indicating auto-ionization and instability for these species.
Fig. S3 (ESI)† summarises the stability of three types of N interstitials. Both Ni-oct(cen) and Ni-oct(recon) are structurally and energetically stable in four different charge states (−3 to 0) in the band gap. In the upper gap region, Ni-oct(recon) is more thermodynamically favourable than Ni-oct(cen) by 0.4 eV (for charge −3) and 0.74 eV (for charge −2) from B97-2 simulations (0.35 eV/0.64 eV from PBE0 and 0.39 eV/0.60 eV from BB1K). As the Fermi level shifts towards the mid-gap region, the energies of the two defects become closer in charge state −1 and Ni-oct(cen) becomes slightly more favourable than Ni-oct(recon) for the neutral charge state. On removing the first electron from charge state −3, the hole state localises on the introduced N species for Ni-oct(cen), whereas for Ni-oct(recon) the population of the spin is shared between the defect and the nudged-off N ion (Fig. 4d). The lower-symmetry configuration and delocalisation of the hole in the latter case can stabilise the local environment further around the defect. However, when ionising the second and the third electron local configuration, hole localisation can only occur on the introduced N ion (even if we forcefully ionise the nudged-off N ion), as shown in Fig. 4e and f. This factor could explain the largest energy difference found in the −2 charge state. The special case of the spin delocalization N2−i-oct(recon) indicates the electronically unstable nature of negative N ions in the wurtzite octahedral void. Thus, the two defect types are considered as interchangeable cases for the same Ni-oct defect and their combined lowest energies are presented in the single red line in Fig. 1.
Removing three electrons from the 2p orbitals of the N3− ion in turn forms corresponding high spin states (up to 3 lone spins) of the defect. On further ionisation, we cannot find any stable configuration of the Ni-oct in any of the positive charge states, and further relaxation forces the N defect to bind with another on-site N ion (the split-interstitial). Compared with all other types of defect states in the band gap, forming Ni-oct requires the highest formation energy. Therefore, Ni-oct is predicted to be a high energy species in AlN, so it is unlikely to be present in significant concentrations.
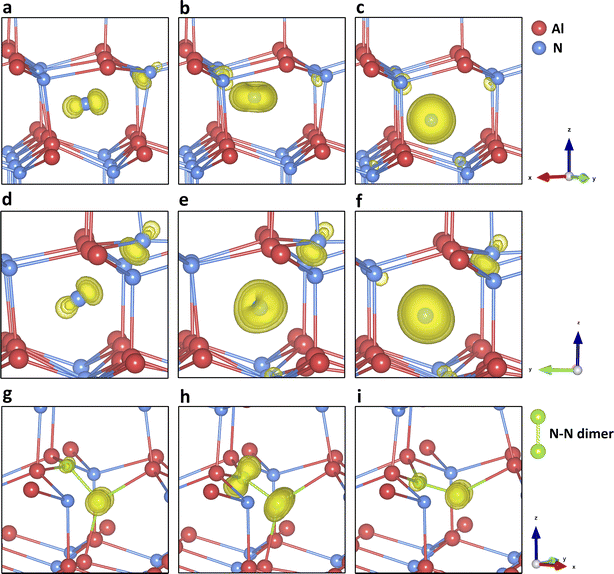
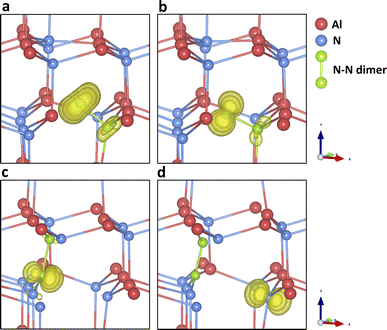
Fig. 4g–i present the configuration and spin densities for the N split-interstitial (Ni-split), where the interstitial N ion is bonded with another on-site N ion forming an N–N dimer structure, which is the most stable interstitial configuration across the whole gap region (see Fig. 1 and 4j–o). The species are stable in the charge states from +3 to −2 in the band gap. Some studies on this defect type did not find +3 charge states stable in cubic61 or wurtzite69,75 AlN, while others did73,79 (Chen et al. did not find the +2 and +1 states stable79). In the +3 charge state, the bond length of the N–N dimer is close to the bond length of the N2 gas molecule (1.09 Å). As more electrons are trapped by the defect, the N–N dimer is stretched by 6% (+2 charge state), 15% (+1), 24% (0), and 33% (−1). These geometries are found to be in good agreement with previous hybrid DFT studies.69,73 Meanwhile, the N–N dimer rotates around the same N atom site of the perfect AlN lattice along the (110) lattice plane, as the charge decreases. Going from the charge state of −1 to −2, no significant change is found in the bond length and N–N orientation. The added electron is delocalised across the whole QM cluster region, resulting in bond breakage between the two nitrogen atoms. The formation energy of N2−i-split is higher than N2−i-oct by 0.78 eV (from b97-2, 0.83 eV from PBE0, 1.18 eV from BB1K), indicating a possible structural transformation to the latter defect configuration in this charge state.
We find the most stable configuration of N1+i-split is a triplet (Fig. 4h). In the charge state of 0 or +2, a singlet is found in the most stable configuration (Fig. 4g and i). Furthermore, in the −1 and +3 charge states, the defect is most stable in the closed-shell electronic configuration. The spin densities of different charge states prove that the electronic configuration of the split interstitial is analogous to that of an N2 molecule. In the charge states of 0, +1, and +2, the spin density is as expected from the occupation of an anti-bonding π orbital. The N2−i-split does not form deep states under CBM, although a stable configuration can be found after geometry optimisation. The Ni-split defect is calculated to be amphoteric (Fig. 1). The optical transition energies are those of a deep donor in the lower half of the band gap region.
We found another structurally stable configuration for charge state −1 NAl, where the antisite defect can bond with the axial N atom. This configuration is less stable than the NAl-A in the same charge state, but it can transform into another antisite configuration (“config-B”, or NAl-B) as more electrons are removed from the point defect. We found NAl-B is stable in charge states from +3 to −1 in the band gap, and it is more stable than NAl-A in all positive charge states from +1 to +3. In the neutral charge state, the N axial dimer moves towards the two closest basal N atoms and reconstructs itself into a stable trigonal configuration (Fig. 5c and d). In charge state +1, the spin density shows a p-orbital-like characteristic (Fig. 5c) and localises at the central N of the trigonal structure. No localised hole is found in the system in charge state +2. In charge state +3, spin density shows a hole localises on the basal N atom outside the trigonal structure.
There have been several theoretical studies of NAl in AlN, but only a few of them discuss the two configurations of the defect. Most of the early work investigated the defect only in the cubic phase of AlN,57,59,61 and claimed that there is a small difference between the defect in the two structural phases.61 The EL2 geometry of the N antisite in cubic AlN in these reports is the closest configuration to our config-A and config-B types. More recent studies of the NAl are either unclear about the geometry,75 or only about the substitutional type,73 which is our proposed third configuration of NAl. However, the substitutional NAl is generally less stable than the other two configurations, so we do not present a detailed discussion. Experimentally, there is still no identification of the N antisite defect in AlN.
3.4 Diffuse states of intrinsic defects
There are limitations in our QM/MM method, with which it is difficult to calculate a highly diffuse defect state. The diffuse electronic part of the defect will be confined due to the nature of the embedded system, which might cause electron over-localisation and an incorrect electronic exchange–correlation energy. However, with a sufficiently large QM region, useful results can still be obtained on diffuse states, such as the stability of any shallow donor/acceptor states. To complement our results, we consider the possible cases where “compact” defect states can trap one or more electrons/holes in “diffuse” atom-like states of large effective radius, and compute the “attaching energies” of diffuse carriers attached to compact defects. The theory and the calculated attaching energies are summarised in Note S1 and Tables S6–S8 (ESI).†Table S9–S15 (ESI)† list the calculated formation energies of all the diffuse states of defects in different charge states with the corresponding compact states, where their formation energies can be compared directly, to determine which type is more favourable in each charge states. From these results, we found most defects have lower energies in their compact state. VAl, Ni-oct, Ni-split, NAl-A, and NAl-B show no preference for the diffuse states in any of their charge states, as their compact state energies are always lower than the diffuse variants. For Ali and VN, the energies of diffuse states are lower than the compact neutral charge state (Tables S9 and S10, ESI†). Calculations using B97-2 and PBE0 functionals show that Ali+ with a diffusely-bound electron has a lower energy than the compact Al0i (BB1K calculation shows the diffuse states of one, two, and three electrons are all more favourable than compact Al0i), which is a direct consequence of the higher formation energy of Al0i at the CBM (Fig. 1). The favourable diffuse states can also be seen in other charge states of Ali from the BB1K calculations, while the other functionals indicate otherwise. For VN, only the BB1K calculations predict the defect to be more favourable than its diffuse state of one electron compared with V0N. The BB1K calculation shows another lower energy diffuse electron state for V1−N, while PBE0 calculation shows the diffuse state is more favourable by only 0.02 eV and B97-2 calculation shows compact V1−N is more favourable. In conclusion, from these calculations, we found the diffuse states are more likely to appear in Al interstitials, where Al0i is a possible shallow donor source. The prediction as to the nature of V0N and V1−N varies depending on the choice of hybrid functional, which has a large impact on defect property prediction.
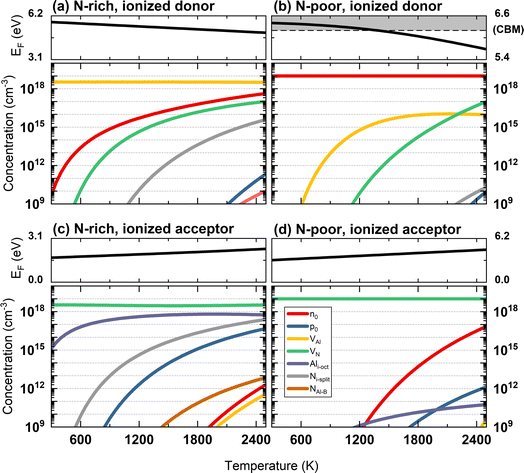
3.5 Defect and charge carrier concentrations
From our defect formation energies, we can calculate the equilibrium concentrations of defect species and charge carriers. At a given temperature, the equilibrium concentration of a defect can be determined by its defect formation energy employing a Boltzmann distribution. Meanwhile, the equilibrium concentrations of the charge carriers (i.e., [n0] for electrons and [p0] for holes) in a semiconductor material can be calculated by integrating the electronic density of states with the Fermi–Dirac distribution formula. The Fermi energy (EF), which is a common term in both concentrations, can be determined by a self-consistent method in the condition of charge neutrality in the system:| [n0] + [acceptors] = [p0] + [donors] | (18) |
As shown in Fig. 6 (left), in N-rich conditions, the Fermi level lies in the mid-gap region, slightly varying from 3.16 to 3.66 eV as the temperature increases. The highest equilibrium concentration among all the intrinsic defects is Ni-split and VN (the latter only about half an order of magnitude lower), indicating VN and Ni-split are the two dominant intrinsic defect species in AlN under N-rich chemical conditions. In the range of the self-consistent Fermi energy, V1+N and N1+i,split are the dominant charge states. In N-poor conditions (Fig. 6, right), due to the lower formation energy of VN, the equilibrium concentration of VN is significantly higher than all other defects. At 2500 K, the VN concentration is higher by 3 orders of magnitude than its counterpart in N-rich conditions. The concentrations of holes and other defect species are much lower due to the rise of the equilibrium Fermi energy. The Fermi energy ranges from 4.73 to 5.16 eV, closer to the CBM. In turn, the electron concentration (overlapped with the green curve in Fig. 6) increases. Close to the Fermi level, V1+N is still the dominant charge state in N-poor conditions. This indicates the negative charge carrier is compensated by the positive charge V1+N in N-poor chemical condition to maintain charge neutrality in the material.
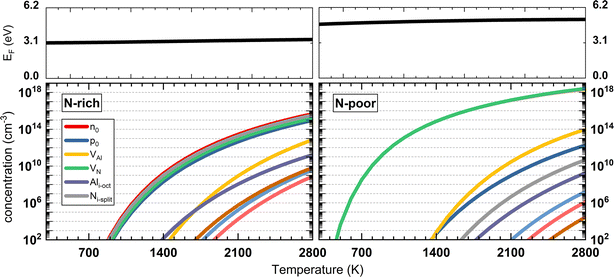 | ||
| Fig. 6 The calculated self-consistent Fermi energy and equilibrium concentrations of charge carriers and defect species as a function of temperature. | ||
As the defect formation energy is a function of chemical potential μ, which can be determined by the temperature and the partial pressure of the system, it is possible to compare our results directly to experiment. Here we follow the guidelines developed by Reuter and Scheffler:134 the N chemical potential (μN) as a function of temperature (T) and N partial pressure (P) can be expressed as:
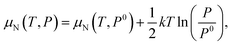 | (19) |
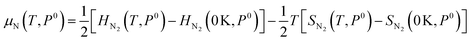 | (20) |
The zero state (μN(0 K, P0) = 1 eV) is defined when P0 = 1 atm. The enthalpy (HN2) and the entropy (SN2) of N2 at different temperatures are obtained from the thermochemical experiment database.135 The μN(T, P) with respect to temperature and N2 partial pressure is summarised in Table S16 and Fig. S4 (ESI).† Given the condition of −3.296 eV ≤ μN ≤ 0 eV for forming stable AlN, all the defect formation energies and, hence, the equilibrium concentrations of all the defect species can be determined by a specifying temperature and pressure. The equilibrium concentrations of defect species and charge carriers with respect to the N2 partial pressure (10−2 to 102 atm) at 2400 K are presented in Fig. 7 (only the four highest defect species are shown). Our results indicate that regardless of the N2 partial pressure (during crystal growth), VN remains the dominant defect species in pristine bulk AlN. As the concentration of electron carriers is several orders of magnitude higher than that of hole carriers, AlN exhibits n-type semiconductor characteristics. There appears to be no direct experimental evidence as to the intrinsic n-type nature of AlN (although it is nominally believed to be the case16), but n-type conductivity in undoped GaN has been observed and the carrier concentration is reported136 to be of the order of 1018 cm−3. In the same report, VN is identified as the primary native donor accounting for its n-type conductivity. Our result is qualitatively consistent with the conclusion of the GaN experiments and predicts the dominant concentration of VN results in intrinsic n-type conductivity in AlN.
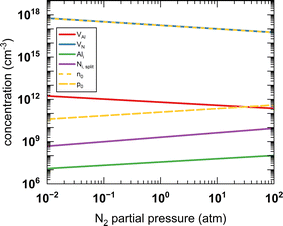 | ||
| Fig. 7 The calculated equilibrium concentrations of charge carriers and defect species as a function of N2 partial pressure at 2400 K. | ||
To investigate further the self-compensation characteristics in the material, a fully ionised donor or acceptor is introduced to determine how the equilibrium Fermi energy and species concentrations respond in the system. Our procedure allows us to add a fixed concentration of mass-less charged species to bias the charge neutrality of the equilibrium system without introducing any extrinsic defect species.127 In response to the bias, Fermi energies and concentrations of intrinsic defects and charge carriers are then readjusted self-consistently to meet the condition of charge neutrality. In the case of donors, we introduce a fix-concentration (1 × 1019 cm−3) of a fully-ionised donor (represented by a +1 charge species) to represent the n-type doping scenario. In both N-rich and N-poor conditions (see Fig. 8a and b), the negative charge carrier concentration increases significantly due to the presence of the ionised donor. In N-rich conditions, the ionised donor is primarily compensated by the negative charge VAl (3 × 1018 cm−3) due to its low formation energy (Fig. 1) in the range of the equilibrium Fermi level of 5.00–5.76 eV above the VBM. At higher temperatures, the positive charge VN starts to contribute more to the compensation, but it still leaves a significant number of uncompensated donors. Hence, n-type conductivity is restricted by the presence of negatively charged VAl. In N-poor conditions, our calculations show that the concentration of electrons remains at the level of 1019 cm−3 and most ionised donors are not compensated. The equilibrium Fermi level decreases from 6.41 eV (0.21 eV above CBM) to 6.12 eV (0.08 eV below CBM), which indicates significant quantities of free electrons. In a previous report of Tuomisto et al. using positron annihilation spectroscopy,18 the concentration of negative charge VAl was estimated analytically at about 1 × 1017 cm−3 in bulk AlN crystal (with O impurities concentration at the order of 1018 cm−3, one order of magnitude lower than our fixed donor concentration). Additionally, cation vacancies were identified as the major defect species in the Si-doped n-type AlxGa1−xN.9 Our results are in good agreement with these reports.
On introducing fixed-concentration (1 × 1019 cm−3) fully-ionised acceptors (represented by a −1 charge species), we found different behaviour. In N-rich conditions (Fig. 8c) the ionised acceptors are compensated primarily by positively charged VN and Ali. As the temperature rises, Ni-split starts to make an increasing contribution to the compensation because of the low formation energies of positively charged species. Although the Fermi levels are in the lower region of the band gap, between 1.74–2.36 eV above VBM, the concentration of hole charge carriers (p0) remains several orders of magnitudes smaller than the introduced acceptors and other defect species. Only at high temperatures, we see a significant concentration of hole carriers. In N-poor condition (Fig. 8d), only VN contributes significantly to the compensation compared to other defect species. As the Fermi levels are at the upper region of the band gap between 3.14–4.62 eV above VBM, the concentration of electron charge carriers is much higher than hole carriers, leading to weakly n-type semiconductor characteristics. Enhancing p-type conductivity has always been a challenge in Mg-doped p-type AlN, a characteristic that we can also see from our relatively low concentration of p0 in both chemical conditions. It is widely established that suppressing the formation of VN can effectively achieve higher p-type conduction in Mg-dope AlN by choosing N-rich growing condition10 or with a high V/III ratio.11 These experiment reports have not interpreted their findings in terms of Ali as another important self-compensating species, as it was ruled out by the high Ali formation energy calculated by early simulations.61
Since our investigation of fixed concentration charged species did not introduce any new defect species to the system, our discussion did not consider the formation of extrinsic defects, such as oxygen, carbon, etc., and their complex defect structures formed with the intrinsic defects. These impurity-incorporated defect complexes could have an impact on the defect formation energies, the charge transition levels, and, in turn, the equilibrium Fermi level positions. Among all, the Al-vacancy-O-substitution defect complex (VAl–n(ON)) is the most discussed defect complex, whose formation energy was calculated (using supercell approaches) to be over 2 eV lower than that of VAl at the HSE level.68,75 The lower formation energies could result in more defect species (VAl in Fig. 8a) compensating the ionised donors and possibly a higher n-type conductivity.
The identification of deep/shallow donor and acceptor states in most experiment reports commonly relies on photoluminescence (PL) signals, with assignments made based on previous theoretical results, specifically the charge transition levels and the configuration-coordinate diagrams. Using the QM/MM embedded cluster method, we have demonstrated a shift of the charge transfer levels towards CBM compared to the levels obtained using supercell methods (refer to the detailed discussion in Section 3.2). Future work will explore both the effects of dopants and optical transition energies.
4 Summary and conclusions
We have systematically investigated the stability and electronic structures of all intrinsic defect species at the dilute limit using our advanced embedded cluster QM/MM approach. While the relative stability of all defect species is consistent with previous DFT studies, our work provides significant new insights. Notably, the aluminium interstitial, Ali, emerged as the most favourable species in the lower region of the band gap from the hybrid BB1K calculation, indicating a significant presence of Ali in the material. Furthermore, we confirm the presence of the novel lower-symmetry nitrogen interstitial defect, calculated in our previous study using force field methods, and explore the electronically unstable nature of the defect species. We have found our formation energies of the charged defects to be generally lower than previous values calculated using supercell methods. As a result, shifts towards the CBM were observed in our charge transition energies compared to those from previous calculations. These differences may stem from either the choice of DFT functionals or the nature of our QM/MM method, which omits the finite-size effect from the supercell-based methods, enabling the simulation of accurate ionization potential levels against the true vacuum reference level. In addition to the structural properties of the defects, the electron localisation characteristics of all the defects have been systematically investigated for every charge state. The diffuse states of the defect species are compared with the compact counterparts, highlighting Al0i as a potential shallow donor source. The shallow nature of VN0 and VN1− varies depending on the exchange fraction of the hybrid functional.Concentration calculations indicate that AlN exhibits intrinsic n-type behaviour throughout the temperature range of 300 to 2800 K. With a concentration of 1 × 1019 cm−3 of fully-ionised donor species, a substantial amount of compensating negative charge VAl (on the order of 1018 cm−3 in N-rich condition) is evident. When the same concentration of ionised acceptors is introduced into the material, the p-type conductivity is hindered by compensation from the positive VN in both chemical potential limits and from Ali as a secondary contribution in N-rich condition. While these results reaffirm the dominant role of cation and anion vacancies in determining the defect properties of AlN, we emphasize that cation interstitials could also play a key role. Our implementation of the advanced QM/MM technique and the new insights into the nature of intrinsic defects in AlN will benefit not only the III–V nitride semiconductor science but also a broader spectrum of defect chemistry.
Data availability
The data supporting this article have been included as part of the ESI.† All open-source codes used in the study, including fit_my_ecp and SC-FERMI are referenced in the paper and available on GitHub.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the usage of several HPC services for the completion of this work. The usage of THOMAS/YOUNG is via the UK Materials and Molecular Modelling Hub for computational resources, MMM Hub, which is partially funded by EPSRC (EP/L000202, EP/T022213). The usage of ARCHER/ARCHER2 UK National Supercomputing Service (http://www.archer2.ac.uk/) is via our membership of the UK's HEC Materials Chemistry Consortium, which is funded by EPSRC (EP/L000202, EP/R029431, EP/T022213, EP/X035859). The co-author Qing Hou acknowledges funding from Shanghai Pujiang Program (grant 22PJ1411300).References
- R. Hahn, V. Glaw, A. Ginolas, M. Töpfer, K. Wittke and H. Reichl, Microelectron. Int., 1999, 16, 21–26 CrossRef CAS.
- T. Takano, T. Mino, J. Sakai, N. Noguchi, K. Tsubaki and H. Hirayama, Appl. Phys. Express, 2017, 10, 31002 CrossRef.
- M. Kneissl, T. Y. Seong, J. Han and H. Amano, Nat. Photonics, 2019, 13, 233–244 CrossRef CAS.
- Y. Taniyasu, M. Kasu and T. Makimoto, Nature, 2006, 441, 325–328 CrossRef CAS PubMed.
- Y. Xue, H. Wang, N. Xie, Q. Yang, F. Xu, B. Shen, J. Shi, D. Jiang, X. Dou, T. Yu and B. Sun, J. Phys. Chem. Lett., 2020, 11, 2689–2694 CrossRef CAS PubMed.
- J. R. Weber, W. F. Koehl, J. B. Varley, A. Janotti, B. B. Buckley, C. G. de Walle and D. D. Awschalom, Proc. Natl. Acad. Sci. U. S. A., 2010, 107, 8513–8518 CrossRef CAS PubMed.
- W. Werdecker and F. Aldinger, IEEE Trans. Compon., Hybrids, Manuf. Technol., 1984, 7, 399–404 CrossRef.
- T. Koppe, H. Hofsäss and U. Vetter, J. Lumin., 2016, 178, 267–281 CrossRef CAS.
- A. Uedono, K. Tenjinbayashi, T. Tsutsui, Y. Shimahara, H. Miyake, K. Hiramatsu, N. Oshima, R. Suzuki and S. Ishibashi, J. Appl. Phys., 2012, 111, 013512 CrossRef.
- Y. Wu, D. A. Laleyan, Z. Deng, C. Ahn, A. F. Aiello, A. Pandey, X. Liu, P. Wang, K. Sun, E. Ahmadi, Y. Sun, M. Kira, P. K. Bhattacharya, E. Kioupakis and Z. Mi, Adv. Electron. Mater., 2020, 6, 2000337 CrossRef CAS.
- T. Kinoshita, T. Obata, H. Yanagi and S. Inoue, Appl. Phys. Lett., 2013, 102, 012105 CrossRef.
- K. Atobe, M. Honda, N. Fukuoka, M. Okada and M. Nakagawa, Jpn. J. Appl. Phys., 1990, 29, 150–152 CrossRef CAS.
- S. M. Evans, N. C. Giles, L. E. Halliburton, G. A. Slack, S. B. Schujman and L. J. Schowalter, Appl. Phys. Lett., 2006, 88, 62112 CrossRef.
- S. Nakahata, K. Sogabe, T. Matsuura and A. Yamakawa, J. Am. Ceram. Soc., 1997, 80, 1612–1614 CrossRef CAS.
- P. M. Mason, H. Przybylinska, G. D. Watkins, W. J. Choyke and G. A. Slack, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1937–1947 CrossRef CAS.
- V. A. Soltamov, I. V. Ilyin, A. A. Soltamova, E. N. Mokhov and P. G. Baranov, J. Appl. Phys., 2010, 107, 113515 CrossRef.
- V. A. Soltamov, I. V. Ilyin, A. A. Soltamova, D. O. Tolmachev, N. G. Romanov, A. S. Gurin, V. A. Khramtsov, E. N. Mokhov, Y. N. Makarov, G. V. Mamin, S. B. Orlinskii and P. G. Baranov, Appl. Magn. Reson., 2013, 44, 1139–1165 CrossRef CAS.
- F. Tuomisto, J.-M. Mäki, T. Yu. Chemekova, Y. N. Makarov, O. V. Avdeev, E. N. Mokhov, A. S. Segal, M. G. Ramm, S. Davis, G. Huminic, H. Helava, M. Bickermann and B. M. Epelbaum, J. Cryst. Growth, 2008, 310, 3998–4001 CrossRef CAS.
- A. Uedono, S. Ishibashi, S. Keller, C. Moe, P. Cantu, T. M. Katona, D. S. Kamber, Y. Wu, E. Letts, S. A. Newman, S. Nakamura, J. S. Speck, U. K. Mishra, S. P. DenBaars, T. Onuma and S. F. Chichibu, J. Appl. Phys., 2009, 105, 54501 CrossRef.
- A. Sedhain, L. Du, J. H. Edgar, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2009, 95, 262104 CrossRef.
- T. Koyama, M. Sugawara, T. Hoshi, A. Uedono, J. F. Kaeding, R. Sharma, S. Nakamura and S. F. Chichibu, Appl. Phys. Lett., 2007, 90, 241914 CrossRef.
- T. Hoshi, T. Koyama, M. Sugawara, A. Uedono, J. F. Kaeding, R. Sharma, S. Nakamura and S. F. Chichibu, Phys. Status Solidi C, 2008, 5, 2129–2132 CrossRef CAS.
- B. Bastek, F. Bertram, J. Christen, T. Hempel, A. Dadgar and A. Krost, Appl. Phys. Lett., 2009, 95, 32106 CrossRef.
- S. F. Chichibu, K. Hazu, Y. Ishikawa, M. Tashiro, T. Ohtomo, K. Furusawa, A. Uedono, S. Mita, J. Xie, R. Collazo and Z. Sitar, Appl. Phys. Lett., 2013, 103, 142103 CrossRef.
- M. Bickermann, B. M. Epelbaum, O. Filip, P. Heimann, S. Nagata and A. Winnacker, Phys. Status Solidi B, 2009, 246, 1181–1183 CrossRef CAS.
- A. Sedhain, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2012, 100, 221107 CrossRef.
- Q. Hu, S. Tanaka, T. Yoneoka and T. Noda, Nucl. Instrum. Methods Phys. Res., Sect. B, 2000, 166–167, 70–74 CrossRef CAS.
- U. Vetter, S. Müller, M. Brötzmann, H. Hofsäss and J. B. Gruber, Diamond Relat. Mater., 2011, 20, 782–784 CrossRef CAS.
- J. A. Freitas, J. Cryst. Growth, 2005, 281, 168–182 CrossRef CAS.
- K. B. Nam, M. L. Nakarmi, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2005, 86, 222108 CrossRef.
- N. Nepal, M. L. Nakarmi, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2006, 89, 92107 CrossRef.
- S. Bellucci, A. I. Popov, C. Balasubramanian, G. Cinque, A. Marcelli, I. Karbovnyk, V. Savchyn and N. Krutyak, Radiat. Meas., 2007, 42, 708–711 CrossRef CAS.
- A. Sedhain, N. Nepal, M. L. Nakarmi, T. M. Al tahtamouni, J. Y. Lin, H. X. Jiang, Z. Gu and J. H. Edgar, Appl. Phys. Lett., 2008, 93, 41905 CrossRef.
- I. A. Weinstein, A. S. Vokhmintsev and D. M. Spiridonov, Diamond Relat. Mater., 2012, 25, 59–62 CrossRef CAS.
- L. Shen, N. Wang and X. Xiao, Mater. Lett., 2013, 94, 150–153 CrossRef CAS.
- Z. Wu, W. Zhang, H. Hu, S. Zuo, F. Wang, P. Yan, J. Wang, R. Zhuo and D. Yan, Mater. Lett., 2014, 136, 95–98 CrossRef CAS.
- W.-Y. Wang, P. Jin, G.-P. Liu, W. Li, B. Liu, X.-F. Liu and Z.-G. Wang, Chin. Phys. B, 2014, 23, 87810 CrossRef.
- J. Pastrňák, S. Pačesová and L. Roskovcová, Czech. J. Phys., B, 1974, 24, 1149–1161 CrossRef.
- R. A. Youngman and J. H. Harris, J. Am. Ceram. Soc., 1990, 73, 3238–3246 CrossRef CAS.
- M. Benabdesselam, P. Iacconi, D. Lapraz, P. Grosseau and B. Guilhot, J. Phys. Chem., 1995, 99, 10319–10323 CrossRef CAS.
- Q. Hu, S. Tanaka, T. Yoneoka and V. Grismanovs, Radiat. Eff. Defects Solids, 1999, 147, 283–292 CrossRef CAS.
- S. Schweizer, U. Rogulis, J.-M. Spaeth, L. Trinkler and B. Berzina, Phys. Status Solidi B, 2000, 219, 171–180 CrossRef CAS.
- Y. G. Cao, X. L. Chen, Y. C. Lan, J. Y. Li, Y. P. Xu, T. Xu, Q. L. Liu and J. K. Liang, J. Cryst. Growth, 2000, 213, 198–202 CrossRef CAS.
- B. Berzina, L. Trinkler, J. Sils and E. Palcevskis, Radiat. Eff. Defects Solids, 2001, 156, 241–247 CrossRef CAS.
- A. Dadgar, A. Krost, J. Christen, B. Bastek, F. Bertram, A. Krtschil, T. Hempel, J. Bläsing, U. Haboeck and A. Hoffmann, J. Cryst. Growth, 2006, 297, 306–310 CrossRef CAS.
- B. E. Gaddy, Z. Bryan, I. Bryan, J. Xie, R. Dalmau, B. Moody, Y. Kumagai, T. Nagashima, Y. Kubota, T. Kinoshita, A. Koukitu, R. Kirste, Z. Sitar, R. Collazo and D. L. Irving, Appl. Phys. Lett., 2014, 104, 202106 CrossRef.
- X. Tang, F. Hossain, K. Wongchotigul and M. G. Spencer, Appl. Phys. Lett., 1998, 72, 1501–1503 CrossRef CAS.
- K. Kornitzer, W. Limmer, K. Thonke, R. Sauer, D. G. Ebling, L. Steinke and K. W. Benz, J. Cryst. Growth, 1999, 201–202, 441–443 CrossRef.
- S. Tungasmita, P. O. Å. Persson, L. Hultman and J. Birch, J. Appl. Phys., 2002, 91, 3551–3555 CrossRef CAS.
- T. Nagashima, Y. Kubota, T. Kinoshita, Y. Kumagai, J. Xie, R. Collazo, H. Murakami, H. Okamoto, A. Koukitu and Z. Sitar, Appl. Phys. Express, 2012, 5, 125501 CrossRef.
- M. Bickermann, B. M. Epelbaum, O. Filip, B. Tautz, P. Heimann and A. Winnacker, Phys. Status Solidi C, 2012, 9, 449–452 CrossRef CAS.
- K. B. Nam, M. L. Nakarmi, J. Li, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2003, 83, 878–880 CrossRef CAS.
- M. L. Nakarmi, N. Nepal, J. Y. Lin and H. X. Jiang, Appl. Phys. Lett., 2009, 94, 091903 CrossRef.
- A. Pandey, X. Liu, Z. Deng, W. J. Shin, D. A. Laleyan, K. Mashooq, E. T. Reid, E. Kioupakis, P. Bhattacharya and Z. Mi, Phys. Rev. Mater., 2019, 3, 053401 CrossRef CAS.
- P. Wang, D. Wang, S. Mondal, M. Hu, J. Liu and Z. Mi, Semicond. Sci. Technol., 2023, 38, 043002 CrossRef.
- P. Boguslawski, E. Briggs, T. A. White, M. G. Wensell and J. Bernholc, MRS Online Proc. Libr., 1994, 339, 693–698 CrossRef CAS.
- T. Mattila and R. M. Nieminen, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 16676–16682 CrossRef CAS PubMed.
- I. Gorczyca, A. Svane and N. E. Christensen, Solid State Commun., 1997, 101, 747–752 CrossRef CAS.
- I. Gorczyca, A. Svane and N. E. Christensen, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 60, 8147–8157 CrossRef CAS.
- A. Fara, F. Bernardini and V. Fiorentini, J. Appl. Phys., 1999, 85, 2001–2003 CrossRef CAS.
- C. Stampfl and C. G. Van de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2002, 65, 155212 CrossRef.
- H. Seo, M. Govoni and G. Galli, Sci. Rep., 2016, 6, 20803 CrossRef CAS PubMed.
- Y. Osetsky, M.-H. Du, G. Samolyuk, S. J. Zinkle and E. Zarkadoula, Phys. Rev. Mater., 2022, 6, 094603 CrossRef CAS.
- Y. Zhang, W. Liu and H. Niu, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 35201 CrossRef.
- P. G. Moses, M. Miao, Q. Yan and C. G. Van de Walle, J. Chem. Phys., 2011, 134, 84703 CrossRef PubMed.
- L. Silvestri, K. Dunn, S. Prawer and F. Ladouceur, Appl. Phys. Lett., 2011, 99, 122109 CrossRef.
- L. Gordon, J. L. Lyons, A. Janotti and C. G. de Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 85204 CrossRef.
- Q. Yan, A. Janotti, M. Scheffler and C. G. Van de Walle, Appl. Phys. Lett., 2014, 105, 111104 CrossRef.
- A. Szállás, K. Szász, X. T. Trinh, N. T. Son, E. Janzén and A. Gali, J. Appl. Phys., 2014, 116, 113702 CrossRef.
- J. B. Varley, A. Janotti and C. G. Van de Walle, Phys. Rev. B, 2016, 93, 161201 CrossRef.
- J. S. Harris, J. N. Baker, B. E. Gaddy, I. Bryan, Z. Bryan, K. J. Mirrielees, P. Reddy, R. Collazo, Z. Sitar and D. L. Irving, Appl. Phys. Lett., 2018, 112, 152101 CrossRef.
- D. Alden, J. S. Harris, Z. Bryan, J. N. Baker, P. Reddy, S. Mita, G. Callsen, A. Hoffmann, D. L. Irving, R. Collazo and Z. Sitar, Phys. Rev. Appl., 2018, 9, 54036 CrossRef CAS.
- Y. Gao, D. Sun, X. Jiang and J. Zhao, J. Appl. Phys., 2019, 125, 215705 CrossRef.
- P. C. Bowes, Y. Wu, J. N. Baker, J. S. Harris and D. L. Irving, Appl. Phys. Lett., 2019, 115, 52101 CrossRef.
- I. A. Aleksandrov and K. S. Zhuravlev, J. Phys.: Condens. Matter, 2020, 32, 435501 CrossRef CAS PubMed.
- A. Kyrtsos, M. Matsubara and E. Bellotti, J. Phys.: Condens. Matter, 2020, 32, 365504 CrossRef CAS PubMed.
- S. Lany and A. Zunger, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 235104 CrossRef.
- A. Walsh, npj Comput. Mater., 2021, 7, 72 CrossRef CAS.
- Y. Chen, L. Wu, D. Liang, P. Lu, J. Wang, J. Chen, H. Cao and L. Han, Comput. Mater. Sci., 2021, 188, 110169 CrossRef CAS.
- L. Zhu, C. R. A. Catlow, Q. Hou, X. Zhang, J. Buckeridge and A. A. Sokol, J. Mater. Chem. A, 2023, 11, 15482–15498 RSC.
- P. Sherwood, A. H. de Vries, M. F. Guest, G. Schreckenbach, C. R. A. Catlow, S. A. French, A. A. Sokol, S. T. Bromley, W. Thiel, A. J. Turner, S. Billeter, F. Terstegen, S. Thiel, J. Kendrick, S. C. Rogers, J. Casci, M. Watson, F. King, E. Karlsen, M. Sjøvoll, A. Fahmi, A. Schäfer and C. Lennartz, J. Mol. Struct.: THEOCHEM, 2003, 632, 1–28 CrossRef CAS.
- J. Kästner, J. M. Carr, T. W. Keal, W. Thiel, A. Wander and P. Sherwood, J. Phys. Chem. A, 2009, 113, 11856–11865 CrossRef PubMed.
- Y. Lu, M. R. Farrow, P. Fayon, A. J. Logsdail, A. A. Sokol, C. R. A. Catlow, P. Sherwood and T. W. Keal, J. Chem. Theory Comput., 2019, 15, 1317–1328 CrossRef CAS PubMed.
- E. Aprà, E. J. Bylaska, W. A. de Jong, N. Govind, K. Kowalski, T. P. Straatsma, M. Valiev, H. J. J. van Dam, Y. Alexeev, J. Anchell, V. Anisimov, F. W. Aquino, R. Atta-Fynn, J. Autschbach, N. P. Bauman, J. C. Becca, D. E. Bernholdt, K. Bhaskaran-Nair, S. Bogatko, P. Borowski, J. Boschen, J. Brabec, A. Bruner, E. Cauët, Y. Chen, G. N. Chuev, C. J. Cramer, J. Daily, M. J. O. Deegan, T. H. Dunning, M. Dupuis, K. G. Dyall, G. I. Fann, S. A. Fischer, A. Fonari, H. Früchtl, L. Gagliardi, J. Garza, N. Gawande, S. Ghosh, K. Glaesemann, A. W. Götz, J. Hammond, V. Helms, E. D. Hermes, K. Hirao, S. Hirata, M. Jacquelin, L. Jensen, B. G. Johnson, H. Jónsson, R. A. Kendall, M. Klemm, R. Kobayashi, V. Konkov, S. Krishnamoorthy, M. Krishnan, Z. Lin, R. D. Lins, R. J. Littlefield, A. J. Logsdail, K. Lopata, W. Ma, A. V. Marenich, J. Martin del Campo, D. Mejia-Rodriguez, J. E. Moore, J. M. Mullin, T. Nakajima, D. R. Nascimento, J. A. Nichols, P. J. Nichols, J. Nieplocha, A. Otero-de-la-Roza, B. Palmer, A. Panyala, T. Pirojsirikul, B. Peng, R. Peverati, J. Pittner, L. Pollack, R. M. Richard, P. Sadayappan, G. C. Schatz, W. A. Shelton, D. W. Silverstein, D. M. A. Smith, T. A. Soares, D. Song, M. Swart, H. L. Taylor, G. S. Thomas, V. Tipparaju, D. G. Truhlar, K. Tsemekhman, T. Van Voorhis, Á. Vázquez-Mayagoitia, P. Verma, O. Villa, A. Vishnu, K. D. Vogiatzis, D. Wang, J. H. Weare, M. J. Williamson, T. L. Windus, K. Woliński, A. T. Wong, Q. Wu, C. Yang, Q. Yu, M. Zacharias, Z. Zhang, Y. Zhao and R. J. Harrison, J. Chem. Phys., 2020, 152, 184102 CrossRef PubMed.
- J. Buckeridge, C. R. A. Catlow, D. O. Scanlon, T. W. Keal, P. Sherwood, M. Miskufova, A. Walsh, S. M. Woodley and A. A. Sokol, Phys. Rev. Lett., 2015, 114, 16405 CrossRef CAS PubMed.
- J. Buckeridge, C. R. A. Catlow, M. R. Farrow, A. J. Logsdail, D. O. Scanlon, T. W. Keal, P. Sherwood, S. M. Woodley, A. A. Sokol and A. Walsh, Phys. Rev. Mater., 2018, 2, 54604 CrossRef CAS.
- Q. Hou, J. Buckeridge, A. Walsh, Z. Xie, Y. Lu, T. W. Keal, J. Guan, S. M. Woodley, C. R. A. Catlow and A. A. Sokol, Front. Chem., 2021, 9, 780935 CrossRef CAS PubMed.
- P. J. Wilson, T. J. Bradley and D. J. Tozer, J. Chem. Phys., 2001, 115, 9233–9242 CrossRef CAS.
- J. P. Perdew, M. Ernzerhof and K. Burke, J. Chem. Phys., 1996, 105, 9982–9985 CrossRef CAS.
- C. Adamo and V. Barone, J. Chem. Phys., 1999, 110, 6158–6170 CrossRef CAS.
- Y. Zhao, B. J. Lynch and D. G. Truhlar, J. Phys. Chem. A, 2004, 108, 2715–2719 CrossRef CAS.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305 RSC.
- B. G. Dick and A. W. Overhauser, Phys. Rev., 1958, 112, 90–103 CrossRef.
- J. D. Gale and A. L. Rohl, Mol. Simul., 2003, 29, 291–341 CrossRef CAS.
- J. D. Gale, J. Chem. Soc., Faraday Trans., 1997, 93, 629–637 RSC.
- A. Logsdail, Software to fit ECPs for the boundary on a QM/MM calculation with ChemShell, https://www.github.com/logsdail/fit_my_ecp, accessed February 22, 2022.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, D. O. Scanlon, S. M. Woodley and A. A. Sokol, Phys. Status Solidi A, 2017, 214, 1600445 CrossRef.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, M. R. Farrow, D. O. Scanlon, S. M. Woodley and A. A. Sokol, J. Phys. D: Appl. Phys., 2019, 52, 335104 CrossRef CAS.
- A. A. Sokol, S. A. French, S. T. Bromley, C. R. A. Catlow, H. J. J. van Dam and P. Sherwood, Faraday Discuss., 2007, 134, 267–282 RSC.
- D. J. Wilson, A. A. Sokol, S. A. French and C. R. A. Catlow, MRS Proc., 2004, 848, 371–376 Search PubMed.
- C. R. A. Catlow, A. A. Sokol and A. Walsh, Chem. Commun., 2011, 47, 3386–3388 RSC.
- A. J. Logsdail, C. A. Downing, T. W. Keal, P. Sherwood, A. A. Sokol and C. R. A. Catlow, Phys. Chem. Chem. Phys., 2016, 18, 28648–28660 RSC.
- X. Zhang, L. Zhu, Q. Hou, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, C. R. A. Catlow and A. A. Sokol, Chem. Mater., 2023, 35, 207–227 CrossRef CAS PubMed.
- A. A. Sokol, S. T. Bromley, S. A. French, C. R. A. Catlow and P. Sherwood, Int. J. Quantum Chem., 2004, 99, 695–712 CrossRef CAS.
- F. A. Kröger and H. J. Vink, in Solid State Physics, ed. F. Seitz and D. Turnbull, Academic Press, 1956, vol. 3, pp. 307–435 Search PubMed.
- J. R. Rumble, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, USA, 2020 Search PubMed.
- CRC Handbook, CRC Handbook of Chemistry and Physics, CRC Press/Taylor & Francis, Boca Raton, FL, USA, 2021 Search PubMed.
- W. Jost, J. Chem. Phys., 1933, 1, 466–475 CrossRef CAS.
- H. Jiang and Y.-C. Shen, J. Chem. Phys., 2013, 139, 164114 CrossRef PubMed.
- X. Zhang, T. Liu, L. Zhu, J. Guan, Y. Lu, T. W. Keal, J. Buckeridge, R. Catlow and A. A. Sokol, Angew. Chem., Int. Ed., 2023, 62, e202308411 CrossRef CAS PubMed.
- Z. Xie, Y. Sui, J. Buckeridge, C. R. A. Catlow, T. W. Keal, P. Sherwood, A. Walsh, M. R. Farrow, D. O. Scanlon, S. M. Woodley and A. A. Sokol, J. Phys. D: Appl. Phys., 2019, 52, 335104 CrossRef CAS.
- C. G. Van de Walle and J. Neugebauer, Nature, 2003, 423, 626–628 CrossRef CAS PubMed.
- P. G. Moses, M. Miao, Q. Yan and C. G. Van de Walle, J. Chem. Phys., 2011, 134, 84703 CrossRef PubMed.
- M. C. Benjamin, C. Wang, R. F. Davis and R. J. Nemanich, Appl. Phys. Lett., 1994, 64, 3288–3290 CrossRef CAS.
- C. I. Wu, A. Kahn, E. S. Hellman and D. N. E. Buchanan, Appl. Phys. Lett., 1998, 73, 1346–1348 CrossRef CAS.
- C. I. Wu and A. Kahn, Appl. Surf. Sci., 2000, 162–163, 250–255 CrossRef CAS.
- T. Kozawa, T. Mori, T. Ohwaki, Y. Taga and N. Sawaki, Jpn. J. Appl. Phys., 2000, 39, L772–L774 CrossRef CAS.
- S. P. Grabowski, M. Schneider, H. Nienhaus, W. Mönch, R. Dimitrov, O. Ambacher and M. Stutzmann, Appl. Phys. Lett., 2001, 78, 2503–2505 CrossRef CAS.
- P. Reddy, I. Bryan, Z. Bryan, J. Tweedie, S. Washiyama, R. Kirste, S. Mita, R. Collazo and Z. Sitar, Appl. Phys. Lett., 2015, 107, 91603 CrossRef.
- M. S. Miao, A. Janotti and C. G. Van De Walle, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 1–9 CrossRef.
- P. Strak, P. Kempisty, K. Sakowski and S. Krukowski, J. Vac. Sci. Technol., A, 2017, 35, 21406 CrossRef.
- A. Alkauskas, P. Broqvist and A. Pasquarello, Phys. Rev. Lett., 2008, 101, 046405 CrossRef PubMed.
- J. L. Lyons and C. G. Van de Walle, npj Comput. Mater., 2017, 3, 12 CrossRef.
- I. A. Aleksandrov, V. G. Mansurov, V. F. Plyusnin and K. S. Zhuravlev, Phys. Status Solidi C, 2015, 12, 353–356 CrossRef CAS.
- I. A. Aleksandrov, T. V. Malin, D. S. Milakhin, B. Y. Ber, D. Y. Kazantsev and K. S. Zhuravlev, Semicond. Sci. Technol., 2020, 35, 125006 CrossRef CAS.
- S. B. Orlinskii, P. G. Baranov, A. P. Bundakova, M. Bickermann and J. Schmidt, Phys. B, 2009, 404, 4873–4876 CrossRef CAS.
- J. Buckeridge, Comput. Phys. Commun., 2019, 244, 329–342 CrossRef CAS.
- G. A. Slack and T. F. McNelly, J. Cryst. Growth, 1977, 42, 560–563 CrossRef CAS.
- M. Bickermann, B. M. Epelbaum and A. Winnacker, J. Cryst. Growth, 2004, 269, 432–442 CrossRef CAS.
- R. Yu, G. Liu, G. Wang, C. Chen, M. Xu, H. Zhou, T. Wang, J. Yu, G. Zhao and L. Zhang, J. Mater. Chem. C, 2021, 9, 1852–1873 RSC.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS PubMed.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- K. Reuter and M. Scheffler, Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 65, 035406 CrossRef.
- M. Chase, NIST-JANAF Thermochemical Tables, American Institute of Physics-1, 4th edn, 1998 Search PubMed.
- M. Ilegems and H. C. Montgomery, J. Phys. Chem. Solids, 1973, 34, 885–895 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta04335a |
| This journal is © The Royal Society of Chemistry 2024 |