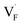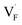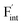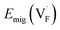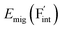Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Point-defect chemistry for ionic conduction in solid electrolytes with isovalent cation mixing†
Takafumi
Ogawa
 *a,
Kazuyuki
Sato
b,
Kazuhiro
Mori
c,
Shunsuke
Kobayashi
a,
Hiroki
Moriwake
*a,
Kazuyuki
Sato
b,
Kazuhiro
Mori
c,
Shunsuke
Kobayashi
a,
Hiroki
Moriwake
 a,
Yuichi
Ikuhara
ad and
Akihide
Kuwabara
a,
Yuichi
Ikuhara
ad and
Akihide
Kuwabara
 a
a
aNanostructures Research Laboratory, Japan Fine Ceramics Center, Nagoya 456-8587, Japan. E-mail: t_ogawa@jfcc.or.jp
bOffice of Institutional Advancement and Communications, Kyoto University,, Uji, Kyoto 611-0011, Japan
cInstitute of Materials Structure Science, High Energy Accelerator Research Organization (KEK), Ibaraki 319-1106, Japan
dInstitute of Engineering Innovation, The University of Tokyo, Tokyo 113-8656, Japan
First published on 17th October 2024
Abstract
Recent studies on solid electrolytes for electrochemical devices such as batteries and fuel cells have focused on investigating migration of mobile ions in ion-conducting crystalline solids, whereas the temperature dependence of the concentrations of charge carriers has received little attention. In this study, the role of point-defect concentrations on the conductivity of fluoride ions in BaF2–CaF2 solid solution was investigated using first-principles calculations. The BaF2–CaF2 solid solution exhibits ionic conductivity that is several orders of magnitude higher than that of the unmixed compounds, BaF2 and CaF2. The calculated equilibrium point-defect concentration of a mixed structure with a composition of Ba0.5Ca0.5F2 and unmixed structures shows that the cation mixing enhances anion Frenkel-pair concentrations by several orders of magnitudes. Although doped ions have the same valence state as that of an ion of a host material, a size mismatch between the doped and host ions could increase mobile defects. Activation, migration, and formation energies of mobile fluorine defects are compared among the examined structures by employing molecular dynamics simulations combined with machine-learning potentials and nudged elastic band calculations. The defect formation energy in the mixed phase is at least 0.75 eV lower than that in the unmixed cases, whereas the difference in migration energy is less than 0.15 eV. These results indicate that the increase in defect concentrations caused by cation mixing contributes to the enhancement of ionic conductivity. The formation energies of fluoride-ion vacancies and interstitial fluoride ions were also compared among fluorite-structured AF2 (A = Ca, Sr, Ba, Cd and Pb), which exhibits opposite trends between the two defects except for PbF2 when plotting as a function of ionic radius. The observed trends of the vacancy and interstitial defects correlate with the bonding strength parameter between neighboring F and A atoms and the space size of the interstitial site, respectively. The exceptional behavior of PbF2 is attributed to 6s2 lone-pair electrons of Pb2+. In Ba0.5Ca0.5F2, the formation energy of each defect is close to the lower energy between BaF2 and CaF2, resulting in enhanced defect concentrations. The results indicate that the complementary exploitation of point-defect chemistry can provide a comprehensive understanding of the ionic conduction mechanism, leading to the rational design of materials with higher ionic conductivity.
1 Introduction
Solid-state ionic conductors for energy conversion, energy storage and sensing have continuously attracted attention because of increasing demands for more efficient and safe power utilization with lower environmental loads, whose applications include lithium-ion and other cation batteries,1,2 proton and oxide-ion conducting solid oxide fuel cells3,4 and fluoride-ion batteries.5,6 Understanding the atomistic mechanism governing electrical conductivity in such solid electrolytes and achieving higher conductivity have been the focus of previous studies. Thus, considerable effort has been dedicated to elucidating the migration mechanism of mobile ions transferring charges,7,8 which includes exploring collective (or correlated) dynamics between ions and vicinal ions or polyhedra, as well as rotational dynamics or effects of the connectivity of constituent polyhedra.9–17 Theoretical studies of ionic conduction mechanisms assume that the concentration of mobile species is independent of temperature. Thus, in this study, the validity of this assumption was clarified.The well-established model for the electrical conductivity of charge carriers in ion-conducting crystalline solids is based on the random walk theory for diffusivity and the Nernst–Einstein relation connecting mobility and diffusivity.18 The total conductivity (σ) caused by contributions from charge carrier species (i) is expressed by 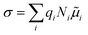 , where qi, Ni and
, where qi, Ni and ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) i denote the charge, concentration and mobility of species i, respectively. Charge carriers are predominant charged point defects that are thermodynamically created in an ionic conductor, for example, oxide-ion vacancies
i denote the charge, concentration and mobility of species i, respectively. Charge carriers are predominant charged point defects that are thermodynamically created in an ionic conductor, for example, oxide-ion vacancies 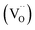 or interstitial oxide ions
or interstitial oxide ions 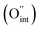 in oxide-ion conductors. These point defects diffuse through the hopping of ions from one site to the next sites; therefore, to identify defects that contribute to the ionic diffusivity is necessary. The mobility of defects is related to their diffusivity (Di), which is calculated as
in oxide-ion conductors. These point defects diffuse through the hopping of ions from one site to the next sites; therefore, to identify defects that contribute to the ionic diffusivity is necessary. The mobility of defects is related to their diffusivity (Di), which is calculated as ![[small mu, Greek, tilde]](https://www.rsc.org/images/entities/i_char_e0e0.gif) i = qiDi/kBT, leading to
i = qiDi/kBT, leading to 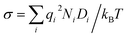 . When the diffusivity and concentration of defects are simply replaced by Arrhenius-type expressions, Di = D0,i exp(−Emig,i/kBT) and Ni = N0,i exp(−Edef,i/kBT), conductivity is rewritten as follows:
. When the diffusivity and concentration of defects are simply replaced by Arrhenius-type expressions, Di = D0,i exp(−Emig,i/kBT) and Ni = N0,i exp(−Edef,i/kBT), conductivity is rewritten as follows:
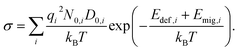 | (1) |
First-principles calculations based on the density functional theory (DFT) have become the major theoretical tool to investigate ionic conduction. In particular, first-principles MD (FPMD) simulations and nudged elastic band (NEB) methods are frequently employed. Although NEB calculations are used to determine the migration energy (Emig,i), FPMD simulations cause the diffusivity of atoms from the trajectories in association with the activation energy (Ea) without any apparent assumption on defect structures except for composition and initial atomic configuration. Despite short sampling times and limited cell size of typical FPMD simulations, these limitations have been recently addressed by exploiting machine-learning force fields (MLFFs).21 In contrast, point-defect concentrations under thermal equilibrium can be calculated,22,23 on a solid foundation of the methodology for calculating defect formation energy.24,25 Although the use of point-defect calculations for ion-conducting materials has been reported in the literature,26–30 it remains unclear how these calculations aid in elucidating the role of point-defect formation within the ionic conduction mechanism.
In this work, the largely enhanced F-ion conductivity in BaF2–CaF2 solid-solution systems with a fluorite crystal structure (Fm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m),31–35 was readdressed using DFT calculations. Although the BaF2 and CaF2 phase diagram indicates a phase-separation behavior below 1150 K,36 metastable nanoparticles with atomic-scale cation mixing have been prepared by high-energy ball milling31–34 and thermal plasma.35 The Ba1−xCaxF2 samples have exhibited a convex shape with the composition dependence of electrical conductivity (convex upward) and activation energies (convex downward) with extrema at x = 0.5.32,33
m),31–35 was readdressed using DFT calculations. Although the BaF2 and CaF2 phase diagram indicates a phase-separation behavior below 1150 K,36 metastable nanoparticles with atomic-scale cation mixing have been prepared by high-energy ball milling31–34 and thermal plasma.35 The Ba1−xCaxF2 samples have exhibited a convex shape with the composition dependence of electrical conductivity (convex upward) and activation energies (convex downward) with extrema at x = 0.5.32,33
The reported conductivity of Ba0.5Ca0.5F2 is higher by about five and two orders of magnitude than the values for the CaF2 and BaF2 nanoparticles, respectively.33 There are various known F-ion solid electrolytes with higher conductivity than Ba0.5Ca0.5F2, with β-PbSnF4 exhibiting the highest conductivity.37–39 Most of those contain elements with relatively high reduction potentials of the metal fluorides, such as Pb, Sn and Bi, compromising the electrochemical stability required for high-performance F-ion batteries.5,6 From the viewpoint of high electrochemical stability, fluorides with tysonite and fluorite structures, composed of elements with low reduction potential, such as rare-earth and alkaline-earth metals,37 have attracted attention as potential candidates for F-ion electrolytes. Among tysonite-type fluorides, Ba-doped LaF3 is known to exhibit the highest conductivity, exceeding 10−4 S cm−1 at around 300 K for single-crystalline samples,37,40,41 and disperse into a lower conductivity range compared to the single-crystalline values for polycrystalline samples.37,41,42 In this case, aliovalent cation doping effectively generates mobile F-ion vacancies  due to the charge balance,40 and the material is often employed as the solid electrolyte in electrochemical cells.5,6,42 Among the fluorite-type fluorides composed of relatively base metals, both Ba0.5Ca0.5F2 and La-doped BaF2 (Ba0.6La0.4F2.4) exhibit a relatively high ionic conductivity in the order of 10−5 S cm−1 at 400 K.38,43 Although these values are lower than those of tysonite-type Ba-doped LaF3, a recent study has shown that Ba0.5Ca0.5F2 can be used as an ion-conducting additive in the CuF2 composite electrode.44 While the concentration of interstitial F atoms
due to the charge balance,40 and the material is often employed as the solid electrolyte in electrochemical cells.5,6,42 Among the fluorite-type fluorides composed of relatively base metals, both Ba0.5Ca0.5F2 and La-doped BaF2 (Ba0.6La0.4F2.4) exhibit a relatively high ionic conductivity in the order of 10−5 S cm−1 at 400 K.38,43 Although these values are lower than those of tysonite-type Ba-doped LaF3, a recent study has shown that Ba0.5Ca0.5F2 can be used as an ion-conducting additive in the CuF2 composite electrode.44 While the concentration of interstitial F atoms  increases due to the aliovalent doping in La-doped BaF2, no additional charged defects are formed in Ba0.5Ca0.5F2 with respect to the charge balance. The latter isovalent cation mixing on the atomic scale has been harnessed not only in AF2 systems (A = Ca, Sr, Ba, Cd, Pb),31–34,38,45–48 but also in other various crystalline systems such as (La,Sc)F3,49 Li3In(Br,Cl)6,50 Na3(P,As)S451 and Gd2(Ti,Zr)2O7.9 Therefore, the interpretation of the conductivity enhancement in BaF2–CaF2 solid solutions would facilitate the rationalized design of ionic conductors following a similar strategy.
increases due to the aliovalent doping in La-doped BaF2, no additional charged defects are formed in Ba0.5Ca0.5F2 with respect to the charge balance. The latter isovalent cation mixing on the atomic scale has been harnessed not only in AF2 systems (A = Ca, Sr, Ba, Cd, Pb),31–34,38,45–48 but also in other various crystalline systems such as (La,Sc)F3,49 Li3In(Br,Cl)6,50 Na3(P,As)S451 and Gd2(Ti,Zr)2O7.9 Therefore, the interpretation of the conductivity enhancement in BaF2–CaF2 solid solutions would facilitate the rationalized design of ionic conductors following a similar strategy.
The impact of nanocrystallization on the ionic conductivity of CaF2 and BaF2 has been clearly demonstrated through comparison with single-crystal52 and microcrystalline samples,31,53 where introduction of grain boundaries is attributed to the enhancement of F-ion diffusivity in the nanocrystalline samples. As for (Ba,Ca)F2 mixed phases, although single-crystal or microcrystalline forms have not been synthesized, the enhanced conductivity is attributed to the diffusion of F ions in the bulk regions, involving atomic-scale mixing, as evidenced by X-ray diffraction (XRD), nuclear magnetic resonance (NMR)31–34,53 and neutron diffraction.35 This is further supported by the enhanced conductivity observed in single-crystal Ca1−xSrxF2 with the fluorite structure.45,54 The enhancement of the conductivity in (Ba,Ca)F2 mixed phases was attributed to the changes in migration energies,32 which was theoretically investigated by classical MD simulations of nanoparticle models containing grain boundaries.33 In contrast, NMR spin-lattice relaxation study has suggested that the prefactor part in the Arrhenius relation, which is determined by the number of mobile spins, the attempt frequency and entropy effects, contributes to the enhancement of conductivity.34 To the best of our knowledge, no studies have elucidated the conduction mechanism of the (Ba,Ca)F2 mixed phases based on DFT.
First, we examine the energetic stability and volumes of Ba1−xCaxF2 by performing exhaustive configuration search, and then point-defect concentrations for the mixed structure with a composition of x = 0.5 were investigated and compared with those of the unmixed phases, BaF2 and CaF2. MD simulations combined with MLFFs were used to obtain the activation energy of the mixed phase, and the migration energies of the defects in BaF2 and CaF2 were calculated by using the NEB method. The obtained activation and associated energies were analyzed and discussed. Then, the stability of F-related defects between AF2 crystals was compared to investigate the effect of cation mixing on the fluorite-structured system and examine the stability in Ba0.5Ca0.5F2.
2 Calculation methods
All electronic structure calculations were performed using the projector augmented wave (PAW) method within the DFT framework, as implemented in the VASP code.55,56 For the exchange-correlation functional, PBEsol was used.57 The cutoff energy was set to 550 eV when the lattice parameters and atomic coordinates were relaxed simultaneously and to 410 eV when only atomic coordinates were relaxed. The convergence criterion for the forces on atoms during a structural relaxation was set to less than 0.02 eV Å−1.In the exhaustive configuration search of Ba1−xCaxF2, all symmetrically inequivalent configurations for cells with up to 10 cations were produced using the CLUPAN tool,58 yielding 1622 configurations in total. In this case, a Γ-centered k-point grid with spacing smaller than 0.3 Å−1 was adopted for the Brillouin zone (BZ) integration. The formation energy and excess volume of the relaxed structures were analyzed.
Concentrations of isolated point defects were computed on the basis of the defect formation energies via point-defect equilibrium calculations, as described elsewhere in detail.23 A defect species with charge q(Dq) could correspond to a mobile species represented by i above when the migration energy is low enough to move. The defect formation energy (Edef(Dq)) is defined as follows:24
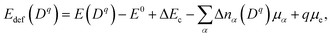 | (2) |
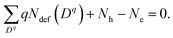 | (3) |
In this work, the chemical potential of the F atom, μF, is set to be the energy of an equilibrium reaction (activity) between metal (M) and metal fluorides (MFn), corresponding to the theoretical electrode potential of fluoride-ion batteries.37 The chemical potential for the Pb/PbF2 reaction was taken as the reference line.61 2 × 2 × 2 supercell structures of the fluorite cubic unit cell including a point defect were relaxed under fixed lattice parameters of the pristine cell without defects. In the case of Ba0.5Ca0.5F2, Ba and Ca atoms were arranged within the cell by using the special quasi-random structure (SQS) procedure,62 as implemented in the ATAT tool.63 The BZ integration for the supercells was performed using the 3 × 3 × 3 k-point grid. In this work, point-defect concentrations under thermal and charge equilibrium were calculated using the pydecs code.23
In measuring the difference in defect formation energy between an examined AF2 material and BaF2, potential offsets were calculated (see the ESI† for details on the calculation procedure). In obtaining the energy barriers of F-related defects in BaF2 and CaF2, the climbing-image NEB (cNEB) method64 with three intermediate images was used. The bonding characteristics of AF2 crystals were assessed via Crystal Orbital Overlap Populations (COOPs), Löwdin charges and Madelung energies by using LOBSTER.65
MD simulations of Ba0.5Ca0.5F2 were performed using the on-the-fly MLFF scheme, as implemented using the VASP (ver. 6.3.2) code.66 The time step was set to 2 fs. An on-the-fly MLFF was trained using the same 2 × 2 × 2 supercell as that used for the point-defect calculations, with NPT-ensemble MD combined with Langevin thermo-barostat.67 The training MD was performed by increasing the temperature from 300 K to 1500 K within 80 ps, followed by a short low-temperature MD run (for 0.2 ps at T = 10 K). The number of collected structures in the training dataset is 923 and the numbers of basis sets for Ba, Ca and F-atoms are 439, 839 and 4315, respectively. The root-mean squared errors in energies, forces and stress tensors of the generated MLFF are 1.02 meV per atom, 0.042 eV Å−1 and 0.45 kbar, respectively.
In obtaining diffusivity, MD calculations with the prepared MLFF were performed using a 4 × 4 × 4 supercell, including 768 atoms with cation configurations determined using the SQS scheme. The examined temperatures ranged from 600 K to 1000 K in increments of 100 K. First, NPT-ensemble MD simulations were performed to determine the lattice constants at each temperature (Fig. S1†). Using the obtained lattice constants, NVT-ensemble MD simulations were performed with Nosé-thermostat.68 After annealing for 100 ps, trajectories were gathered at every 20 fs for 500 ps. The accuracy of the adopted MLFF was rechecked for structures after annealing at each temperature, and it was found to meet the acceptable level (Fig. S2†). Mean square displacement (MSD) was calculated by averaging over atoms and different initial times with a maximum lag time of 300 ps to achieve sufficient statistical average convergence. The diffusivity of F atoms, DF, was obtained by fitting the time-dependent MSD, MSD(t), with the Einstein relation, that is, MSD(t) = 6DFt. In extracting event probability of interstitial F ions and co-generated F vacancies during MD sampling, the coordinates of each F-atom were mapped to the nearest lattice site using Voronoi tessellation.69 Atomic configurations and density maps were represented by the VESTA code.70
3 Results and discussion
3.1 BaF2–CaF2 solid solution
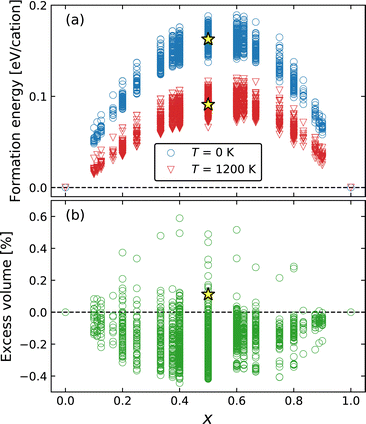
The thermodynamic stability of Ba1−xCaxF2 solid solutions was examined by the exhaustive configuration search which is used to evaluate the phase stability of the mixed phases and to discover possible ordered structures. Fig. 1a shows the formation energies measured from the composition-weighted average of the end-member energies. In the case of T = 1200 K, composition-dependent configuration entropy term (−TSconfig) was added, where Sconfig = −kB(x ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) x + (1 − x) ln(1 − x)). The results indicate a phase separation tendency, even though the tendency decreases at higher temperature. The metastability of the cation-mixed phases is consistent with the reported experimental behavior.31,33 The mechanochemically synthesized mixed phases were decomposed above 700 K, where cation diffusion is sufficiently activated. The calculated formation energy surpasses 0.15 eV per cation or 14.5 kJ mol−1, at around x = 0.5. Similar values have been observed in oxides; for example, the formation energy of fluorite-structured Ce1−xZrxO2 is approximately 15 kJ mol−1 at x = 0.5.71 In this oxide system, miscibility is observed at high temperatures, for example, above 1800 K at x = 0.5.72 Although our calculations show the phase separation behavior even at a high temperature of 1200 K, mixed phases were observed at temperatures above 1150 K over the entire composition range in the experimental phase diagram.36 Our calculations overestimate the transition temperature from a two-phase separation state to a single solid-solution state probably because our calculations do not include vibrational contributions. A similar overestimation was found in a previous calculation study on Ce1−xZrxO2.73
x + (1 − x) ln(1 − x)). The results indicate a phase separation tendency, even though the tendency decreases at higher temperature. The metastability of the cation-mixed phases is consistent with the reported experimental behavior.31,33 The mechanochemically synthesized mixed phases were decomposed above 700 K, where cation diffusion is sufficiently activated. The calculated formation energy surpasses 0.15 eV per cation or 14.5 kJ mol−1, at around x = 0.5. Similar values have been observed in oxides; for example, the formation energy of fluorite-structured Ce1−xZrxO2 is approximately 15 kJ mol−1 at x = 0.5.71 In this oxide system, miscibility is observed at high temperatures, for example, above 1800 K at x = 0.5.72 Although our calculations show the phase separation behavior even at a high temperature of 1200 K, mixed phases were observed at temperatures above 1150 K over the entire composition range in the experimental phase diagram.36 Our calculations overestimate the transition temperature from a two-phase separation state to a single solid-solution state probably because our calculations do not include vibrational contributions. A similar overestimation was found in a previous calculation study on Ce1−xZrxO2.73
The excess volume, which is a relative volume with respect to the composition-weighted average of the BaF2 and CaF2 volumes, is shown in Fig. 1b, exhibiting a small deviation to negative (contraction) and positive (expansion) directions with absolute values lower than 0.6%. Therefore, Vegard's law is almost satisfied in the mixed system. Determining the lattice constants of the mixed phase is experimentally difficult because of the broadening of the XRD peaks, although Düvel et al. reported the expansion tendency with an excess volume reaching 1.5–1.7% at around x = 0.3–0.5.33 In our exhaustive calculations, the examined cells include up to 10 cations, inevitably forming structures with a short-range order compared to a more realistic random structure available in a larger cell. However, the excess volume of a random structure would lie in the dispersion of the searched results because such a dispersed range may include two opposite extreme cases toward contraction and expansion.
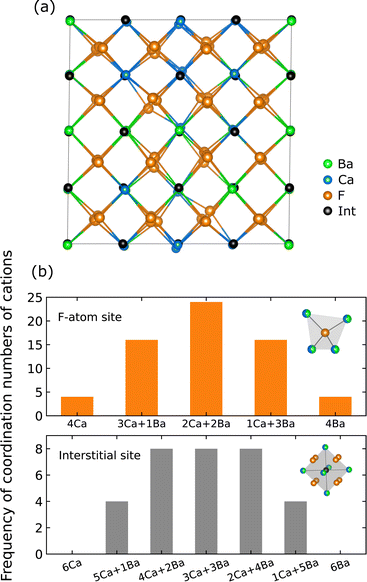
Fig. 2a shows the relaxed random structure prepared using the SQS scheme for Ba0.5Ca0.5F2, including 96 atoms (32 cations), where the interstitial positions are represented as the ideal fluorite crystal before relaxation. Fig. 2b shows the frequency of the combination of coordinating cations around 64 F-atom sites (8c) and 32 interstitial sites (4b) in the cell, where the 8c and 4b sites have tetrahedral and octahedral coordination, respectively, as represented in the insets of Fig. 2b. In the prepared model, the coordination environments around F-atom sites are almost fully random. The corresponding probability distribution around 19F-atoms determined by NMR for ball-milled samples has shown a slight deviation from the values of the ideal random distribution; thus, the frequencies of Ca3Ba and CaBa3 coordination patterns were larger and smaller than the ideal values, respectively.33 However, Breuer and Silkening reported that such differences in the local environment do not significantly affect the long-range conduction of F− ions through measurements of samples prepared at different ball-milling times.34 Therefore, the random structure model can capture the relationship between ionic conductivity and local structures.
The formation energy and excess volume of the SQS structure are shown in Fig. 1. Considering that the energy of the SQS structures is located in the middle of the energy dispersion obtained from the exhaustive search, the phase separation tendency is reconfirmed for the random structure in the larger cell. Structural relaxation induces local displacements from the ideal lattice sites (Fig. 2a). The observed excess volume expansion accounts for approximately 0.1%, which is relatively small compared with an experimental value of approximately 1.5%.33 In our calculations, the diffusivity of F ions can be affected by local structural distortion rather than the minute volume expansion.
3.2 Point-defect calculations of BaF2–CaF2 solid solution
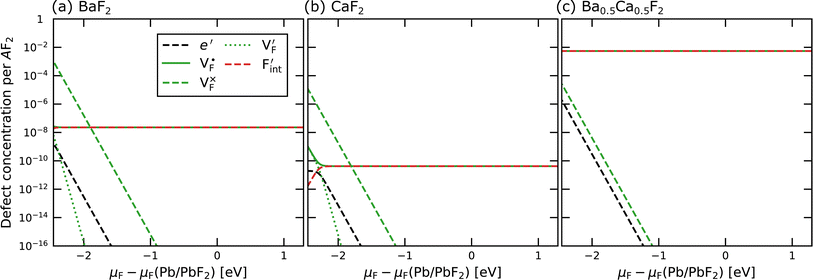
In determining the possible range of the chemical potential of the F atom (μF), μF values are calculated for various metal/metal-fluoride equilibrium reactions (M/MFn) as summarized in Fig. S4.† Cu/CuF2 has the highest potential among the examined cases in our calculations except for noble material series, and it has recently attracted considerable attention as a promising active cathode material for fluoride-ion batteries.44,74,75 Considering that fluorides with low equilibrium μF are more stable during electrochemical reactions, the fluorides of alkali and alkaline earth metals, including BaF2 and CaF2, are preferred as an electrolyte with a high electrochemical stability, which would allow the stable use of the (Ba,Ca)F2 phase in the composite electrode.44 In the following point-defect calculations, μF is swept between the values for Li/LiF and Cu/CuF2.The concentrations of point defects in BaF2, CaF2 and Ba0.5Ca0.5F2 were examined under thermal and charge equilibrium. For BaF2 and CaF2, the vacancies and interstitials of F and each cation (Ba or Ca) were evaluated, where the chemical potential of each cation is determined from the energy of the host material and μF. The resulting concentrations at T = 600 K are plotted in Fig. 3a and b, respectively. In this figure, the horizontal axes show variation of μF relative to the value at the equilibrium of Pb/PbF2. In both materials, the concentrations of cation-related defects are low; thus, they are not shown in the panels, and the predominant defects are the anion Frenkel pair, namely, positively charged F-vacancies 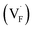 and negatively charged interstitial F-atoms
and negatively charged interstitial F-atoms 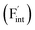 .
.
Based on the above examination for the unmixed compounds, for the Ba0.5Ca0.5F2 case, F vacancies (VFq, q = +, 0) and interstitial F atoms (Fintq, q = −, 0) were considered at each lattice site in the SQS cell shown in Fig. 2a. The obtained defect concentrations at each site are summed up within each defect type. The resulting concentrations at 600 K are plotted in Fig. 3c, indicating the higher concentrations of the predominant anion Frenkel pair by several orders of magnitude than those in CaF2 and BaF2.
The dependence of the  concentration (which is identical to that of
concentration (which is identical to that of  ) for the examined compounds is plotted as a function of inverse temperature (Fig. 4). Here, μF was set to the base value of Pb/PbF2, where the Frenkel pair is predominant in the examined temperature range. The defect concentrations in Ba0.5Ca0.5F2 are higher than those in unmixed compounds over the whole examined temperature range, and all lines exhibit constant gradients. Fitting the lines with the Arrhenius equation yields a nominal formation energy equivalent to half of the Frenkel-pair formation energy. For BaF2 and CaF2, the extracted values are 0.93 and 1.25 eV, which are almost identical to the defect formation energies evaluated from the point-defect equilibrium calculations. For the Ba0.5Ca0.5F2 case, the formation energy obtained from the fitting is 0.18 eV. The corresponding single value cannot be obtained from the point-defect equilibrium calculations because various defects at different lattice sites simultaneously contribute to the summed-up concentrations. Notably, not only an aliovalent dopant but also an isovalent dopant with a large difference in ionic size can remarkably increase charge carrier defects.
) for the examined compounds is plotted as a function of inverse temperature (Fig. 4). Here, μF was set to the base value of Pb/PbF2, where the Frenkel pair is predominant in the examined temperature range. The defect concentrations in Ba0.5Ca0.5F2 are higher than those in unmixed compounds over the whole examined temperature range, and all lines exhibit constant gradients. Fitting the lines with the Arrhenius equation yields a nominal formation energy equivalent to half of the Frenkel-pair formation energy. For BaF2 and CaF2, the extracted values are 0.93 and 1.25 eV, which are almost identical to the defect formation energies evaluated from the point-defect equilibrium calculations. For the Ba0.5Ca0.5F2 case, the formation energy obtained from the fitting is 0.18 eV. The corresponding single value cannot be obtained from the point-defect equilibrium calculations because various defects at different lattice sites simultaneously contribute to the summed-up concentrations. Notably, not only an aliovalent dopant but also an isovalent dopant with a large difference in ionic size can remarkably increase charge carrier defects.
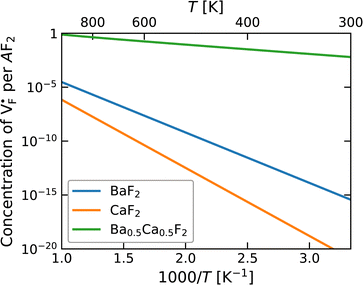 | ||
| Fig. 4 Point-defect concentrations as a function of temperature, where μF is fixed to be the value for Cu/CuF2. Under these conditions, anion Frenkel pairs are dominant. | ||
3.3 MD simulations of Ba0.5Ca0.5F2
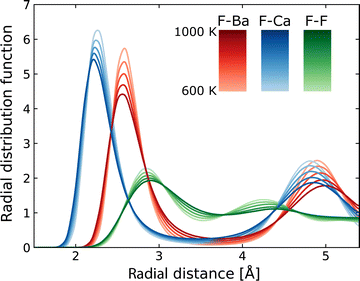
Using MLFF-MD simulations at 600 to 1000 K, radial distribution functions (RDFs) and diffusion properties of F ions in Ba0.5Ca0.5F2 are analyzed. The RDFs are plotted separately for pairs between the F atom and each constituent element, as shown in Fig. 5. The first peaks in the RDFs for the F–Ca pair appear at around 2.2 Å, which is shorter by about 0.3 Å than that of the F–Ba pair. These reflect the difference in the ionic radii (1.56 and 1.26 Å for Ba2+ and Ca2+ ions with eight coordination, respectively76) and coincide with the tendency of the lattice constants of BaF2–CaF2 solid solutions, which almost follows Vegard's law. The RDFs of the F–F pair have weaker and broader first peaks at a position farther than that of the first peaks of cations. All peaks in the RDFs weaken with the increase in temperature, reflecting the increased movement of atoms, but no significant changes in shape and no additional peaks are observed.The MSD of F atoms, which is plotted in Fig. 6a, shows usual ballistic and diffusive behaviors;77 The time evolution is proportional to t2 in the relatively short time range less than 0.1 ps and to t1 in the longer time range. During the simulations, no hopping diffusion of the cations was observed, indicating that the structural changes towards phase separation hardly occur without any cation defects in simulations, whereas the phase separation was observed at temperature above 700 K in experiments.33 Even in classical MD simulations of BaF2–CaF2 nanoparticles, including surfaces, grain boundaries and potential cation defects, apparent phase separation was not observed at 1200 K,33 which is consistent with our DFT-based MD simulations at temperatures below 1000 K.
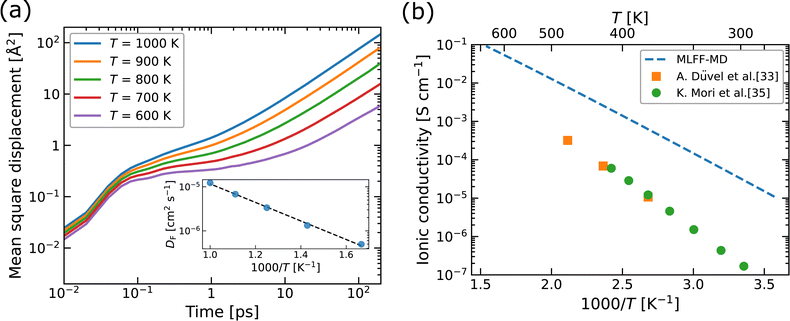 | ||
| Fig. 6 (a) Mean square displacement (MSD) as a function of time and (b) ionic conductivity as a function of 1000/T, for F atoms in Ba0.5Ca0.5F2. In the inset of (a), diffusion coefficients (DF) obtained by fitting the MSDs are plotted. In (b), the experimental values for Ba1−xCaxF2 with x ∼ 0.5 (ref. 33 and 35) are plotted for comparison. | ||
The diffusion coefficients (DF) extracted from the MSDs are plotted as a function of inverse temperature, as shown in the inset of Fig. 6a. We evaluated the standard deviations in the averaging of DF using the MD2D package,78 resulting in relative deviations of less than 6%, which is smaller than the size of the data points shown in the inset. The linear fit with the Arrhenius equation provides an activation energy (Ea) of 0.42 eV for F-atom diffusion. This value corresponds to the sum of the contributions from defect formation and migration as in the explicit formalism of the conductivity in eqn (1). The theoretical ionic conductivity (σ) below 500 K is obtained from extrapolated DF at higher temperatures than 600 K via the relation σ = e2NFDF/kBT, where NF denotes the concentration of F-atom lattice sites. The calculated σ values are compared with the experimental data extracted from the literature,33,35 as shown in Fig. 6b, which indicates that the theoretical results overestimate the experimental ones by about 1–2 orders of magnitude. We consider that two factors may contribute to the observed differences. The first factor is the possible existence of a superionic-like phase transition, associated with a change in mobile defect species and/or the formation of defect complexes, as reported for α-Li3N.79 Although we also calculated the MSDs at T = 300, 400 and 500 K, the linear dependence of the MSDs on simulation time could not be achieved within the MD sampling time. The elucidation of low-temperature diffusion properties would require longer simulation times and more careful examinations of the convergence, both of which are beyond the scope of this study. The second factor is the retarding effect at grain boundaries in nanoparticles on the conductivity in the experiments, as reported for Y-doped ZrO2 (ref. 80) and tysonite-type Ba-doped LaF3,41 though for the latter case, it has also been reported that the effect of grain boundaries could be suppressed by optimizing the microstructure.37
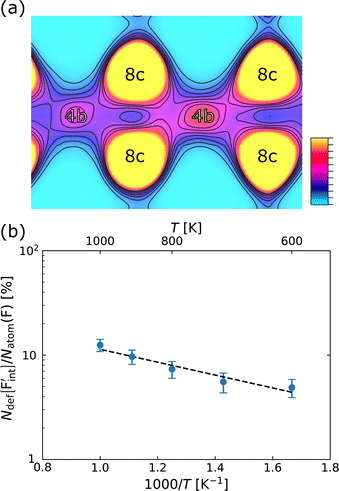
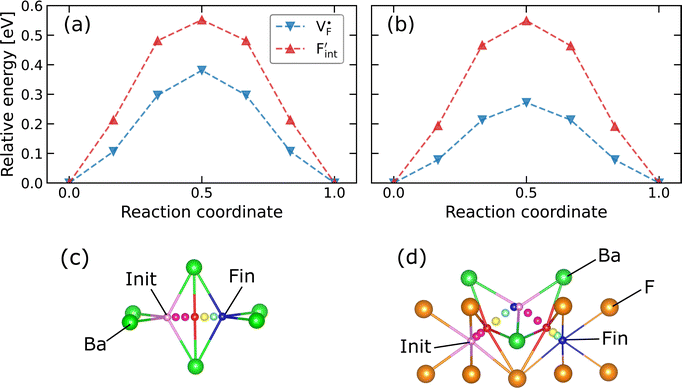
In confirming the temperature dependence of the concentrations of F-atom point defects contributing to ionic diffusion, the time evolution of spontaneously formed F-atom defects was extracted and analyzed from the MD trajectories. Fig. 7a shows the distribution of F atoms at T = 1000 K, which was generated by contracting the F-atom trajectories into the unit cell. As shown in the figure, although F-atoms reside predominantly at the 8c site, their distribution is also present at the interstitial 4b sites. In extracting the sojourn time of F atoms on the interstitial sites, the existing probability of F atoms at the site was calculated for each snapshot, and the time-series data were averaged, by using the Voronoi-tessellation mapping of F-atom coordinates onto the closest lattice site. The probability represents the concentrations of interstitial F-atoms, which are equivalent to those of F-vacancies. The obtained probabilities at each temperature are plotted in Fig. 7b as a function of inverse temperature. By fitting the data with the Arrhenius equation, the defect formation energy extracted from the MD simulations is 0.12 eV, which is close to that from the point-defect calculations (0.18 eV). The slight difference may be attributed to finite-temperature effects such as lattice vibration, thermal expansion and the clustering (association) of point defects, which are ignored in the above-mentioned point-defect calculations. The findings indicate that the approach of point-defect chemistry provides direct access to the defect formation energy that comprises the activation energy.
3.4 Comparison of activation energies
In comparing the activation energies, the migration energies of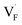 and
and 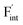 in CaF2 and BaF2 were calculated using the cNEB method, because the F-ion diffusivity of these compounds is too small to achieve statistical convergence during MD simulations without extrinsic dopants. In the case of
in CaF2 and BaF2 were calculated using the cNEB method, because the F-ion diffusivity of these compounds is too small to achieve statistical convergence during MD simulations without extrinsic dopants. In the case of 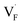 , an F-ion neighboring to a vacancy site migrates to the vacancy site (Fig. 8c). In the case of
, an F-ion neighboring to a vacancy site migrates to the vacancy site (Fig. 8c). In the case of 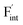 , the interstitialcy diffusion path involving the movement of the neighboring F-atom at the 8c site is examined because the direct migration pathway to the next interstitial site could not be defined (Fig. 8d). Fig. 8a and b show the calculated relative energies on the migration paths, and the obtained saddle-point energies (Emig) are summarized in Table 1. As shown in the table, the barriers for
, the interstitialcy diffusion path involving the movement of the neighboring F-atom at the 8c site is examined because the direct migration pathway to the next interstitial site could not be defined (Fig. 8d). Fig. 8a and b show the calculated relative energies on the migration paths, and the obtained saddle-point energies (Emig) are summarized in Table 1. As shown in the table, the barriers for 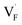 in BaF2 and CaF2 are lower by about 0.2 and 0.3 eV, respectively, than those for
in BaF2 and CaF2 are lower by about 0.2 and 0.3 eV, respectively, than those for 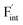 . These results indicate that
. These results indicate that 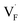 is more mobile than
is more mobile than 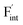 in BaF2 and CaF2.
in BaF2 and CaF2.
All the energies, associated with the activation energy of ionic conductivity, are summarized in Table 1. The activation energies for BaF2 and CaF2 were derived by summing the formation and migration energies for F-vacancies via the relation: Ea = Edef + Emig. Meanwhile, the migration energy for F-ion defects in Ba0.5Ca0.5F2 was calculated by subtracting the formation energy from the activation energy (Emig = Ea – Edef). As previously mentioned, the Ba0.5Ca0.5F2 model was constructed on the basis of the SQS scheme. In this model, various nonequivalent migration paths are observed; thus, comprehensive determination of the migration energy by NEB calculations is not feasible. The obtained Ea value shows a large difference between the mixed and unmixed phases, accounting for approximately 1 eV. As shown in Table 1, the Emig values of 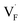 in the BaF2 and CaF2 are comparable to that of Ba0.5Ca0.5F2. The differences in the migration barrier among the fluorides are less than 0.15 eV. Therefore, the differences in the Ea value should be largely attributed to the difference in the defect formation energy.
in the BaF2 and CaF2 are comparable to that of Ba0.5Ca0.5F2. The differences in the migration barrier among the fluorides are less than 0.15 eV. Therefore, the differences in the Ea value should be largely attributed to the difference in the defect formation energy.
Table 1 also lists the experimental Ea values for BaF2 and CaF2 bulks81–84 and for Ba1−xCaxF2 nanoparticles at a composition near to x = 0.5.32,33 The experimental values of BaF2 and CaF2 are dispersed in the 1.3–2.1 eV range, containing the calculated values. In contrast, the Ea value of BaF2 and CaF2 nanoparticles exhibits relatively low values less than 0.8 and 1.0 eV, respectively,32,33 which would reflect particle-size effects. The experimental Ea values of the Ba0.5Ca0.5F2 nanoparticles are in the range of 0.5–0.6 eV, which are lower than those of BaF2 and CaF2 nanoparticles. Although distinguishing the nanoparticle and cation mixing effects in experiments is difficult because of the absence of experiments with larger grains as already mentioned, this work provides a theoretical clue on the effects of local structural disorders induced by the cation mixing on the Ea values and F-ion transport properties of the bulk region.
If MD simulation can be performed in a large cell for sufficiently long simulation time based on reliable energy and force calculations, then it would be a suitable tool to directly compute the activation energy of mobile atoms in an ionic conductor. However, a limited computational capability promotes the use of a searching method for the saddle point on a migration path, such as the cNEB method, to obtain the migration energy (Emig). Point-defect calculations can aid in the identification of dominant defect species and the estimation of defect formation energy (Edef). The essential role of point-defect concentrations in MD simulations is emphasized for ionic conductors such as AgI and β-PbF2 in the review by Hull.20 As demonstrated also in our MD simulations, when mobile ions in a crystal migrate through interstitial lattice sites or fractionally occupied sites such as vacancies, the temperature-dependent occupation probabilities can be a key factor to understand the migration behavior associated with the point-defect formation. Similar situations could arise in various solid electrolytes. For example, in sulfide-based compounds for Li-ion solid electrolytes, the Li-ion migration barrier is highly dependent on the type of anion sublattice (bcc or fcc/hcp), and the difference in the probability density of Li atoms between two sites on a Li-ion migration path is used to explain the trend of diffusivity.11 Considering that the latter probability density is related to point-defect concentrations, point-defect calculations may provide a comprehensive understanding of the underlying transport mechanism and suggest the way to tailoring crystals with higher ionic conduction.
3.5 Comparison of point-defect formation energy
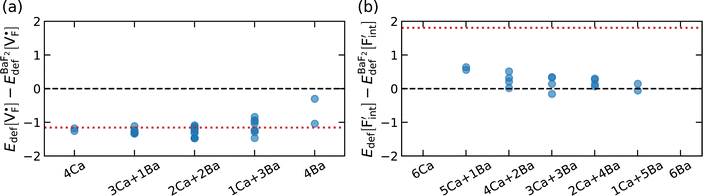
To investigate the mechanism responsible for the decrease in the defect formation energies (Edef) of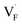 and
and 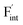 in Ba0.5Ca0.5F2, the difference in Edef between different materials was calculated. Here, we suppose that the subject material is adjacent to BaF2 and it shares the same Fermi level (see the ESI† for details). First, we compared the relative formation energies of AF2 series (A = Ca, Ba, Sr, Cd, Pb) with respect to the BaF2 values (Fig. 9a). The results indicate the opposite energy alignments between
in Ba0.5Ca0.5F2, the difference in Edef between different materials was calculated. Here, we suppose that the subject material is adjacent to BaF2 and it shares the same Fermi level (see the ESI† for details). First, we compared the relative formation energies of AF2 series (A = Ca, Ba, Sr, Cd, Pb) with respect to the BaF2 values (Fig. 9a). The results indicate the opposite energy alignments between 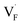 and
and  except for the PbF2 case. These trends are plotted as a function of the ionic radius (Fig. 9b), expressing systematic changes for each defect type except for PbF2, and relatively small changes in the anion Frenkel-pair energies.
except for the PbF2 case. These trends are plotted as a function of the ionic radius (Fig. 9b), expressing systematic changes for each defect type except for PbF2, and relatively small changes in the anion Frenkel-pair energies.
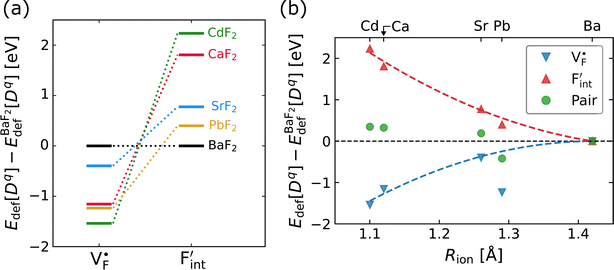 | ||
Fig. 9 (a) Comparison of the relative formation energies of  and and  of AF2 (A = Ca, Ba, Sr, Cd, Pb) with regard to BaF2 and (b) its dependence on the ionic radius of A2+ with eight coordination.76 In (b), points for half the formation energies of the anion Frenkel pair and fitted lines with a parabolic function except for PbF2 for guiding eyes are also shown. of AF2 (A = Ca, Ba, Sr, Cd, Pb) with regard to BaF2 and (b) its dependence on the ionic radius of A2+ with eight coordination.76 In (b), points for half the formation energies of the anion Frenkel pair and fitted lines with a parabolic function except for PbF2 for guiding eyes are also shown. | ||
In elucidating the origin of the stability trends, structural and electronic properties correlating with the relative formation energies were explored. The energetic trend for 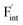 correlates with the lattice constants (Fig. 10a), including PbF2. Considering that the lattice constant in the fluorite structure is linearly proportional to the bond lengths between atoms in the crystal, the relationship can be interpreted as follows: the narrower the interstitial space, the greater the repulsion between the incorporated F and surrounding atoms. In contrast to the
correlates with the lattice constants (Fig. 10a), including PbF2. Considering that the lattice constant in the fluorite structure is linearly proportional to the bond lengths between atoms in the crystal, the relationship can be interpreted as follows: the narrower the interstitial space, the greater the repulsion between the incorporated F and surrounding atoms. In contrast to the 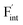 case, poor correlation was observed between the relative energies for
case, poor correlation was observed between the relative energies for 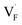 and bond lengths or lattice constants. The bonding characteristics calculated via the projection of electronic states onto local atomic orbitals were examined as described in the Method section. Electrostatic properties such as Löwdin charges and Madelung energy also exhibit poor correlation (Table S1†), but integrated COOP up to the Fermi level (ICOOP) between adjacent fluorine and the cation was found to have a linear relationship, as shown in Fig. 10b. Therefore, the bonding strength represented by the COOP analysis is a key factor to capture the trend of Edef
and bond lengths or lattice constants. The bonding characteristics calculated via the projection of electronic states onto local atomic orbitals were examined as described in the Method section. Electrostatic properties such as Löwdin charges and Madelung energy also exhibit poor correlation (Table S1†), but integrated COOP up to the Fermi level (ICOOP) between adjacent fluorine and the cation was found to have a linear relationship, as shown in Fig. 10b. Therefore, the bonding strength represented by the COOP analysis is a key factor to capture the trend of Edef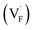 , including the PbF2 case.
, including the PbF2 case.
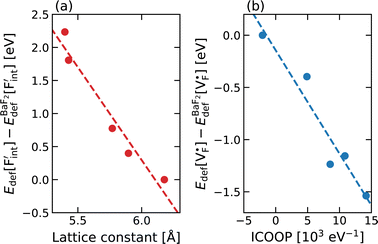 | ||
| Fig. 10 Correlation plots of relative defect formation energies for (a) interstitial F ions and (b) F-ion vacancies for AF2 (A = Ca, Ba, Sr, Cd, Pb). For the descriptors, see the main text. | ||
The curious exceptional behavior of the defects in PbF2 may be related to the 6s2 lone pair of Pb2+ ions. Such a lone pair strongly affects the crystal structures as well as local bonding characteristics,85,86 electric and optical properties87 and F-ion conductivity.87,88 The previous DFT calculations have shown that COOP analyses reveal the bonding characteristics between Pb and neighboring anions.85,86,89 Also in our case, the density of states and COOP of PbF2 exhibit similar hybridization to the case of other Pb-including compounds (Fig. S5†). Therefore, ICOOP can be a good indicator of the trend of 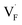 formation energy. Although such s2 lone pairs could enhance F-ion migrations,88,90 materials containing Sn and Pb would require more careful application with respect to electrochemical stability than compounds composed of Ba and Ca (Fig. S4†).
formation energy. Although such s2 lone pairs could enhance F-ion migrations,88,90 materials containing Sn and Pb would require more careful application with respect to electrochemical stability than compounds composed of Ba and Ca (Fig. S4†).
The relative formation energies with regard to the BaF2 values for 64 and 32 kinds of 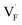 and
and 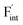 in the Ba0.5Ca0.5F2 cell are shown in Fig. 11. As shown in the figure, although the dependence of the energy on the local coordination environments is unclear, the energetic stability is different between the two defects. While the relative energies of
in the Ba0.5Ca0.5F2 cell are shown in Fig. 11. As shown in the figure, although the dependence of the energy on the local coordination environments is unclear, the energetic stability is different between the two defects. While the relative energies of 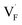 are low and comparable to those of CaF2, the relative energies of
are low and comparable to those of CaF2, the relative energies of 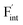 are near to those of BaF2. Therefore, the mixed phase exhibits a behavior inconsistent with the trend in the AF2 series. The lattice constant of the random structure scarcely expand from the average value (Fig. 1b). Thus, the decrease in the relative defect energy in the mixed phase could be attributed to the local structural disorder induced by the mixing of isovalent cations with a large ionic-radius difference. As an example, the local structures of
are near to those of BaF2. Therefore, the mixed phase exhibits a behavior inconsistent with the trend in the AF2 series. The lattice constant of the random structure scarcely expand from the average value (Fig. 1b). Thus, the decrease in the relative defect energy in the mixed phase could be attributed to the local structural disorder induced by the mixing of isovalent cations with a large ionic-radius difference. As an example, the local structures of 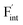 are depicted in Fig. S6,† representing that the large structural changes during relaxation occur in the mixed phase in contrast to the cases of BaF2 and CaF2. The large changes would be allowed by distortions contained not only in neighboring atoms, but also in more distant atoms. When additional aliovalent doping is applied into the disordered structure, as reported for (Ca,Sr)F2 doped with rare-earth metals,54 higher conductivity may be achieved as a result of the altered formation of F-ion defects.
are depicted in Fig. S6,† representing that the large structural changes during relaxation occur in the mixed phase in contrast to the cases of BaF2 and CaF2. The large changes would be allowed by distortions contained not only in neighboring atoms, but also in more distant atoms. When additional aliovalent doping is applied into the disordered structure, as reported for (Ca,Sr)F2 doped with rare-earth metals,54 higher conductivity may be achieved as a result of the altered formation of F-ion defects.
4 Conclusions
In this study, ionic conductivity enhancement in Ba1−xCaxF2 was investigated by evaluating the defect formation, migration and activation energies using point-defect calculations, migration-path searches and MLFF-MD simulations, under consistent DFT conditions. The comparison of the obtained energies for Ba0.5Ca0.5F2, BaF2 and CaF2 shows that the cation mixing of Ba2+ and Ca2+ induces the reduction of the formation energies of the F-ion Frenkel pair (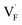 and
and 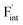 ), rather than the migration barriers. By arranging the relative defect formation energies for AF2 series,
), rather than the migration barriers. By arranging the relative defect formation energies for AF2 series, 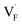 and
and 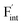 are found to exhibit opposite trends against ionic sizes of cations. Meanwhile, the energies of the F-ion vacancies and interstitials in Ba0.5Ca0.5F2 deviate from the trends, and each energy is close to the lower energy between CaF2 and BaF2. The latter anomalous behavior is due to the local structural distortions caused by the mixing of cations with a large difference in the ionic radius. In general, aliovalent dopants are used for the production of mobile charge carriers in the field of solid-state ionics. However, our findings indicate that isovalent dopants with a different size from the constituents of host materials may enhance the ionic conductivity in a wide range of materials other than the present system. Moreover, the present research indicates that enhancement of ionic conductivity not only results from the lowering of migration barriers but also from the increase in charge carrier or point-defect concentrations and thus suggests that the point-defect chemistry can provide insights into the underlying mechanism of ion conduction in crystalline solids.
are found to exhibit opposite trends against ionic sizes of cations. Meanwhile, the energies of the F-ion vacancies and interstitials in Ba0.5Ca0.5F2 deviate from the trends, and each energy is close to the lower energy between CaF2 and BaF2. The latter anomalous behavior is due to the local structural distortions caused by the mixing of cations with a large difference in the ionic radius. In general, aliovalent dopants are used for the production of mobile charge carriers in the field of solid-state ionics. However, our findings indicate that isovalent dopants with a different size from the constituents of host materials may enhance the ionic conductivity in a wide range of materials other than the present system. Moreover, the present research indicates that enhancement of ionic conductivity not only results from the lowering of migration barriers but also from the increase in charge carrier or point-defect concentrations and thus suggests that the point-defect chemistry can provide insights into the underlying mechanism of ion conduction in crystalline solids.
Data availability
Raw data were generated at Japan Fine Ceramics Center at Nagoya in Japan. Derived data supporting the findings of this study are available from the corresponding author T. O. on request.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the “Research and Development Initiative for Scientific Innovation of New Generation Batteries (RISING3),” JPNP 21006, commissioned by the New Energy and Industrial Technology Development Organization (NEDO) and by the Ministry of Education, Culture, Sports, Science and Technology as “Program for Promoting Research on the Supercomputer Fugaku” (Computational Research on Materials with Better Functions and Durability Toward Sustainable Development, JPMXP1020230325) and also partially supported by the Japan Society for the Promotion of Science (JSPS) KAKENHI (Grant no. JP24K01173, JP22H05142 and JP22H05146) and the Iketani Science and Technology Foundation (no. 0361237-A). The computational resources of supercomputer Fugaku provided by the RIKEN Center for Computational Science (Project ID: hp230205 and hp240224) were used.References
- D. Larcher and J.-M. Tarascon, Nat. Chem., 2015, 7, 19–29 CrossRef CAS PubMed.
- J. C. Bachman, S. Muy, A. Grimaud, H.-H. Chang, N. Pour, S. F. Lux, O. Paschos, F. Maglia, S. Lupart, P. Lamp, L. Giordano and Y. Shao-Horn, Chem. Rev., 2016, 116, 140–162 CrossRef CAS PubMed.
- Y. Zhang, R. Knibbe, J. Sunarso, Y. Zhong, W. Zhou, Z. Shao and Z. Zhu, Adv. Mater., 2017, 29, 1700132 CrossRef PubMed.
- W. Zhang and Y. H. Hu, Energy Sci. Eng., 2021, 9, 984–1011 CrossRef CAS.
- M. A. Nowroozi, I. Mohammad, P. Molaiyan, K. Wissel, A. R. Munnangi and O. Clemens, J. Mater. Chem. A, 2021, 9, 5980–6012 RSC.
- S. V. Gopinadh, P. V. R. L. Phanendra, B. John and T. D. Mercy, Sustainable Mater. Technol., 2022, 32, e00436 CrossRef CAS.
- B. C. Wood, J. B. Varley, K. E. Kweon, P. Shea, A. T. Hall, A. Grieder, M. Ward, V. P. Aguirre, D. Rigling, E. L. Ventura, C. Stancill and N. Adelstein, Philos. Trans. R. Soc., A, 2021, 379, 20190467 CrossRef CAS PubMed.
- Z. Zhang and L. F. Nazar, Nat. Rev. Mater., 2022, 7, 389–405 CrossRef.
- K. J. Moreno, G. Mendoza-Suárez, A. F. Fuentes, J. García-Barriocanal, C. León and J. Santamaria, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 132301 CrossRef.
- E. Kendrick, J. Kendrick, K. S. Knight, M. S. Islam and P. R. Slater, Nat. Mater., 2007, 6, 871–875 CrossRef CAS PubMed.
- Y. Wang, W. D. Richards, S. P. Ong, L. J. Miara, J. C. Kim, Y. Mo and G. Ceder, Nat. Mater., 2015, 14, 1026–1031 CrossRef CAS PubMed.
- N. Adelstein and B. C. Wood, Chem. Mater., 2016, 28, 7218–7231 CrossRef CAS.
- X. He, Y. Zhu and Y. Mo, Nat. Commun., 2017, 8, 15893 CrossRef CAS PubMed.
- X. Yang, A. J. Fernández-Carrión, J. Wang, F. Porcher, F. Fayon, M. Allix and X. Kuang, Nat. Commun., 2018, 9, 4484 CrossRef PubMed.
- D. Di Stefano, A. Miglio, K. Robeyns, Y. Filinchuk, M. Lechartier, A. Senyshyn, H. Ishida, S. Spannenberger, D. Prutsch, S. Lunghammer, D. Rettenwander, M. Wilkening, B. Roling, Y. Kato and G. Hautier, Chem, 2019, 5, 2450–2460 CAS.
- K. Jun, Y. Sun, Y. Xiao, Y. Zeng, R. Kim, H. Kim, L. J. Miara, D. Im, Y. Wang and G. Ceder, Nat. Mater., 2022, 21, 924–931 CrossRef CAS PubMed.
- H. Fang and P. Jena, Nat. Commun., 2022, 13, 2078 CrossRef CAS PubMed.
- P. Shewmon, Diffusion in Solids, Springer, 2nd edn, 2016 Search PubMed.
- R. C. Agrawal and R. K. Gupta, J. Mater. Sci., 1999, 34, 1131–1162 CrossRef CAS.
- S. Hull, Rep. Prog. Phys., 2004, 67, 1233–1314 CrossRef CAS.
- E. Kocer, T. W. Ko and J. Behler, Annu. Rev. Phys. Chem., 2022, 73, 163–186 CrossRef CAS PubMed.
- S. Anand, M. Y. Toriyama, C. Wolverton, S. M. Haile and G. J. Snyder, Acc. Mater. Res., 2022, 3, 685–696 CrossRef CAS.
- T. Ogawa, A. Taguchi and A. Kuwabara, npj Comput. Mater., 2022, 8, 79 CrossRef CAS.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- A. Zunger and O. I. Malyi, Chem. Rev., 2021, 121, 3031–3060 CrossRef CAS PubMed.
- H. Yildirim, A. Kinaci, M. K. Y. Chan and J. Greeley, ACS Appl. Mater. Interfaces, 2015, 7, 18985–18996 CrossRef CAS PubMed.
- J. Pan, Y.-T. Cheng and Y. Qi, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 134116 CrossRef.
- K. Oh, D. Chang, B. Lee, D.-H. Kim, G. Yoon, I. Park, B. Kim and K. Kang, Chem. Mater., 2018, 30, 4995–5004 CrossRef CAS.
- P. Gorai, H. Long, E. Jones, S. Santhanagopalan and V. Stevanović, J. Mater. Chem. A, 2020, 8, 3851–3858 RSC.
- P. Gorai, T. Famprikis, B. Singh, V. Stevanović and P. Canepa, Chem. Mater., 2021, 33, 7484–7498 CrossRef CAS.
- B. Ruprecht, M. Wilkening, A. Feldhoff, S. Steuernagel and P. Heitjans, Phys. Chem. Chem. Phys., 2009, 11, 3071–3081 RSC.
- A. Düvel, B. Ruprecht, P. Heitjans and M. Wilkening, J. Phys. Chem. C, 2011, 115, 23784–23789 CrossRef.
- A. Düvel, P. Heitjans, P. Fedorov, G. Scholz, G. Cibin, A. V. Chadwick, D. M. Pickup, S. Ramos, L. W. L. Sayle, E. K. L. Sayle, T. X. T. Sayle and D. C. Sayle, J. Am. Chem. Soc., 2017, 139, 5842–5848 CrossRef PubMed.
- S. Breuer and M. Wilkening, Dalton Trans., 2018, 47, 4105–4117 RSC.
- K. Mori, K. Sato, T. Ogawa, A. Kuwabara, S. Song, T. Saito, T. Fukunaga and T. Abe, ACS Appl. Energy Mater., 2024, 7, 7787–7797 CrossRef CAS.
- P. P. Fedorov, I. I. Buchinskaya, N. A. Ivanovskaya, V. V. Konovalova, S. V. Lavrishchev and B. P. Sobolev, Dokl. Phys. Chem., 2005, 401, 53–55 CrossRef CAS.
- K. Motohashi, T. Nakamura, Y. Kimura, Y. Uchimoto and K. Amezawa, Solid State Ionics, 2019, 338, 113–120 CrossRef CAS.
- A. Düvel, Dalton Trans., 2019, 48, 859–871 RSC.
- N. Matsui, T. Seki, K. Suzuki, M. Hirayama and R. Kanno, ACS Appl. Energy Mater., 2023, 6, 11663–11671 CrossRef CAS.
- A. Roos, F. van de Pol, R. Keim and J. Schoonman, Solid State Ionics, 1984, 13, 191–203 CrossRef CAS.
- C. Rongeat, M. A. Reddy, R. Witter and M. Fichtner, ACS Appl. Mater. Interfaces, 2014, 6, 2103–2110 CrossRef CAS PubMed.
- M. A. Reddy and M. Fichtner, J. Mater. Chem., 2011, 21, 17059 RSC.
- A. Düvel, J. Bednarcik, V. Šepelák and P. Heitjan, J. Phys. Chem. C, 2014, 118, 7117–7129 CrossRef.
- K. Shimoda, Y. Morita, K. Noi, T. Fukunaga, Z. Ogumi and T. Abe, ACS Energy Lett., 2023, 8, 2570–2575 CrossRef CAS.
- M. V. S. Sarma and S. V. Suryanarayana, Solid State Ionics, 1990, 42, 227–232 CrossRef CAS.
- M. Heise, G. Scholz, A. Düvel, P. Heitjans and E. Kemnitz, Solid State Sci., 2016, 60, 65–74 CrossRef CAS.
- M. Heise, G. Scholz, A. Düvel, P. Heitjans and E. Kemnitz, Solid State Sci., 2018, 77, 45–53 CrossRef CAS.
- S. Lunghammer, A. Düvel, P. Posch, B. Kunert, R. Resel and H. M. R. Wilkening, Solid State Ionics, 2019, 343, 115067 CrossRef CAS.
- L. B. Gulina, A. F. Privalov, M. Weigler, I. V. Murin, V. Tolstoy and M. Vogel, Appl. Magn. Reson., 2020, 51, 1691–1699 CrossRef CAS.
- A. Zevgolis, B. C. Wood, Z. Mehmedović, A. T. Hall, T. C. Alves and N. Adelstein, APL Mater., 2018, 6, 047903 CrossRef.
- Z. Yu, S.-L. Shang, J.-H. Seo, D. Wang, X. Luo, Q. Huang, S. Chen, J. Lu, X. Li, Z.-K. Liu and D. Wang, Adv. Mater., 2017, 29, 1605561 CrossRef PubMed.
- W. Puin and P. Heitjans, Nanostruct. Mater., 1995, 6, 885–888 CrossRef.
- B. Ruprecht, M. Wilkening, S. Steuernagel and P. Heitjans, J. Mater. Chem., 2008, 18, 5412–5416 RSC.
- N. I. Sorokin, D. N. Karimov, E. A. Krivandina, Z. I. Zhmurova and O. N. Komar’kova, Crystallogr. Rep., 2008, 53, 271–277 CrossRef CAS.
- G. Kresse and J. Furthmüller, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef PubMed.
- A. Seko, Y. Koyama and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 165122 CrossRef.
- C. Freysoldt, J. Neugebauer and C. G. Van de Walle, Phys. Rev. Lett., 2009, 102, 016402 CrossRef PubMed.
- Y. Kumagai and F. Oba, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 195205 CrossRef.
- D. Zhang, K. Yamamoto, A. Ochi, Y. Wang, T. Yoshinari, K. Nakanishi, H. Nakano, H. Miki, S. Nakanishi, H. Iba, T. Uchiyama, T. Watanabe, K. Amezawa and Y. Uchimoto, J. Mater. Chem. A, 2021, 9, 406–412 RSC.
- A. Zunger, S.-H. Wei, L. G. Ferreira and J. E. Bernard, Phys. Rev. Lett., 1990, 65, 353–356 CrossRef CAS PubMed.
- A. van de Walle, P. Tiwary, M. de Jong, D. Olmsted, M. Asta, A. Dick, D. Shin, Y. Wang, L.-Q. Chen and Z.-K. Liu, Calphad, 2013, 42, 13–18 CrossRef CAS.
- G. Henkelman, B. P. Uberuaga and H. Jónsson, J. Chem. Phys., 2000, 113, 9901–9904 CrossRef CAS.
- R. Nelson, C. Ertural, J. George, V. L. Deringer, G. Hautier and R. Dronskowski, J. Comput. Chem., 2020, 41, 1931–1940 CrossRef CAS PubMed.
- R. Jinnouchi, J. Lahnsteiner, F. Karsai, G. Kresse and M. Bokdam, Phys. Rev. Lett., 2019, 122, 225701 CrossRef CAS PubMed.
- M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press., 2nd edn, 2017 Search PubMed.
- S. Nosé, J. Phys. Soc. Jpn., 2001, 70, 75–77 CrossRef.
- U. Matsumoto, T. Ogawa, C. A. J. Fisher, S. Kitaoka and I. Tanaka, J. Phys. Chem. C, 2021, 125, 20460–20467 CrossRef CAS.
- K. Momma and F. Izumi, J. Appl. Crystallogr., 2011, 44, 1272–1276 CrossRef CAS.
- T. A. Lee, C. R. Stanek, K. J. McClellan, J. N. Mitchell and A. Navrotsky, J. Mater. Res., 2008, 23, 1105–1112 CrossRef CAS.
- M. Yoshimura, E. Tani and S. Sōmiya, Solid State Ionics, 1981, 3–4, 447–481 Search PubMed.
- L. C. Shuller-Nickles, R. C. Ewing and U. Becker, J. Solid State Chem., 2013, 197, 550–559 CrossRef CAS.
- D. T. Thieu, M. H. Fawey, H. Bhatia, T. Diemant, V. S. K. Chakravadhanula, R. J. Behm, C. Kübel and M. Fichtner, Adv. Funct. Mater., 2017, 27, 1701051 CrossRef.
- H. Nakano, T. Matsunaga, T. Mori, K. Nakanishi, Y. Morita, K. Ide, K. Okazaki, Y. Orikasa, T. Minato, K. Yamamoto, Z. Ogumi and Y. Uchimoto, Chem. Mater., 2021, 33, 459–466 CrossRef CAS.
- R. D. Shannon and C. T. Prewitt, Acta Crystallogr., 1970, B26, 1046–1048 CrossRef.
- W. Kob, J. Phys.: Condens. Matter, 1999, 11, R85 CrossRef CAS.
- Y. Li and H. Ni, Comput. Phys. Commun., 2023, 284, 108599 CrossRef CAS.
- G. Krenzer, J. Klarbring, K. Tolborg, H. Rossignol, A. R. McCluskey, B. J. Morgan and A. Walsh, Chem. Mater., 2023, 35, 6133–6140 CrossRef CAS.
- R. A. De Souza, M. J. Pietrowski, U. Anselmi-Tamburini, S. Kim, Z. A. Munir and M. Martin, Phys. Chem. Chem. Phys., 2008, 10, 2067–2072 RSC.
- B. M. Voronin and S. V. Volkov, J. Phys. Chem. Solids, 2001, 62, 1349–1358 CrossRef CAS.
- E. Barsis and A. Taylor, J. Chem. Phys., 1968, 48, 4362–4367 CrossRef CAS.
- W. Bollmann and H. Henniger, Phys. Status Solidi A, 1972, 11, 367–371 CrossRef CAS.
- E. Barsis and A. Taylor, J. Chem. Phys., 1966, 45, 1154–1162 CrossRef CAS.
- G. Trinquier and R. Hoffmann, J. Phys. Chem., 1984, 88, 6696–6711 CrossRef CAS.
- A. Walsh and G. W. Watson, J. Solid State Chem., 2005, 178, 1422–1428 CrossRef CAS.
- G. Laurita and R. Seshadri, Acc. Chem. Res., 2022, 55, 1004–1014 CrossRef CAS PubMed.
- N. Matsui, M. Murakami, K. Mori, T. Saito, K. Shimizu, K. Suzuki and R. Kanno, J. Mater. Chem. A, 2024, 12, 3989 RSC.
- M. G. Goesten and R. Hoffmann, J. Am. Chem. Soc., 2018, 140, 12996–13010 CrossRef CAS PubMed.
- B. Mercadier, S. W. Coles, M. Duttine, C. Legein, M. Body, O. J. Borkiewicz, O. Lebedev, B. J. Morgan, C. Masquelier and D. Dambournet, J. Am. Chem. Soc., 2023, 145, 23739–23754 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta05684a |
| This journal is © The Royal Society of Chemistry 2024 |