Alloying induced superionic β-phase formation in Mg₃Sb₂ based Zintl compounds

Abstract

The off-centering phenomenon manifests as locally distorted configurations with broken symmetry in a crystal structure due to the displacement of constituent atoms from their ideal coordination centers within the lattice. In contrast to the anticipated formation of anionic solid solutions of Mg₃(Sb_1−x−yBi_xGe_y)₂, herein we report β-Mg₃(Sb, Bi)₂ based superionic phase formation (space group – Ia3̄, 206) with off-centering of the dominant trigonal α-Mg₃(Sb, Bi)₂ phase and segregation of nanophase Mg₃Ge upon equiatomic (Bi, Ge) alloying. The discordant nature of Ge is unveiled within the layered α-Mg₃(Sb, Bi)₂ structure and is assessed employing (3 + 1) dimensional superspace to reveal an off-centering (dz) along the z direction for the constituent atoms in the range of ±0–0.02 Å. The (Bi, Ge) alloying results in favourable tuning of the desired p-type conduction for attaining higher power factors by band engineering and synergistic reduction of lattice thermal conductivity. The stable superionic polymorph co-existing in an anionic solid solution of Mg₃(Sb, Bi)₂ provides a renewed basis for understanding the crystal structure and its transformation in CaAl₂Si₂-type Zintl compounds.

---

1. Introduction

Zintl compounds constitute a fascinating class of thermoelectric (TE) materials that exhibit viable prospects in the applications of low-grade heat recovery and solid-state cooling.^1–5 One example is the exceptional n-type performance exhibited by Mg₃(Sb, Bi)₂ based anionic solid solutions in recent years with TE energy conversion efficiency (η) reaching ∼10% in the mid-temperature (500–700 K) range.^6–12 These compounds belong to the 1-2-2 Zintl family and are traditionally described as layered materials with a CaAl₂Si₂-type structure.^13–15 Being extensively reported, the trigonal α-Mg₃Sb₂ (P3̄m1, 164) phase constitutes an anionic framework of covalent [Mg₂Sb₂]²⁻ slabs, wherein Mg²⁺ cations are arranged as an ionically bonded interlayer. The Sb atoms in its anionic sites exhibit a trigonal pyramidal coordination, while Mg atoms located at interlayer Mg(I) and intralayer Mg(II) positions occupy octahedral and tetrahedral sites, respectively, displaying distinctive bonding configurations.

The evaluated Mg–Sb phase diagram (Fig. 1) based on thermal analysis suggests the occurrence of a phase transformation from α-Mg₃Sb₂ to β-Mg₃Sb₂ (Ia3̄, 206) at high temperature (∼1200 K), prior to melting congruently at ∼1500 K.^16–18 However, studies undertaken on the Mg–Sb binary system largely show the realisation of only α-Mg₃Sb₂ experimentally, thus suggesting its retention even at high temperature.¹⁴ Presumably the high-temperature β-phase exists only above ∼1200 K for Mg₃Sb₂, which poses a synthesis challenge due to the high reactivity and volatility of Mg atoms at elevated temperatures. Owing to the inherent difficulty in synthesizing high-quality β-phase Mg₃Sb₂ crystals, their structural description has thus remained unclear so far. Nonetheless, the high-temperature β-phase for the structural analogue Mg₃Bi₂ as evaluated by Barnes et al.¹⁹ is a disordered cubic structure (Im3̄m, 229), which demonstrates superionic properties.

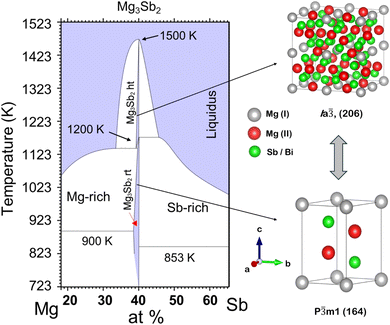Fig. 1 The Mg–Sb phase diagram near Mg₃Sb₂ indicating the phase transformation of α-Mg₃Sb₂ (P3̄m1, 164) ↔ β-Mg₃Sb₂ (Ia3̄, 206).^16–18

The structural flexibility and rich chemistry enabled by the Zintl–Klemm concept have allowed tuning of the coordination environment of Mg and Sb atoms (or their substitutes) by incorporating different dopants at the anionic and cationic sites.^14,20 In this work, we report the implication of co-substituting equiatomic (Bi, Ge) in Mg₃(Sb_1−x−yBi_xGe_y)₂ based anionic solid solutions, to achieve higher power factors by band engineering for p-type conduction and synergistic reduction of lattice thermal conductivity. As a discordant dopant, Ge atoms induce local distortions and broken symmetry within the lattice, effectively enhancing phonon scattering. This mechanism significantly reduces lattice thermal conductivity, contributing to an improved thermoelectric figure of merit (zT) of 0.3 (±0.1) at 673 K. Polycrystalline Mg₃(Sb_1−x−yBi_xGe_y)₂ materials with (0 < x < 0.1) were prepared by a high-energy milling process, followed by spark milling sintering. Upon equiatomic (Bi, Ge) alloying in the anionic framework [Mg₂Sb₂]²⁻ and high temperature (∼1023 K) sintering, the formation of a high-temperature β-phase of Mg₃(Sb, Bi)₂ was observed, with off-centering of constituent atoms within the dominant and co-existing α-Mg₃Sb₂ phase.

2 Results and discussion

2.1 Structural parameters, phase compositions and superionic phase formation

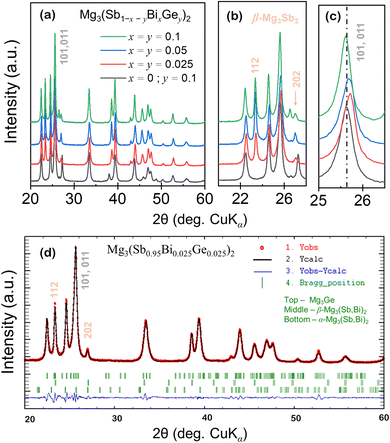
Anionic solid solutions of Mg₃(Sb_1−x−yBi_xGe_y)₂ were synthesized using a widely explored route of ball milling followed by spark plasma sintering as described in the Experimental details. The powder diffraction profiles of Mg₃(Sb_1−x−yBi_xGe_y)₂ polycrystals shown in Fig. 2(a) indicate major peaks corresponding to trigonal α-Mg₃Sb₂. Remarkably, for all the (Bi, Ge) alloyed compositions, additional peaks (at 2θ ∼23.3, 27.0) corresponding to the cubic β-Mg₃Sb₂ (space group – Ia3̄, 206), besides peaks from the trigonal Mg₃Ge (space group – P3̄, 147)²¹ phases were also indexed. The major peaks corresponding to the β-phase of Mg₃(Sb, Bi)₂ are indicated separately in Fig. 2(b) in the magnified 2θ range, while the structural information is presented in Table 1 along with residual factors (R-factors). With increasing Bi, Ge content (x, y), the PXRD peaks shift to higher angles (Fig. 1(c)) with respect to the synthesized Mg₃Sb_1.8Ge_0.2, suggesting the contraction of the α-Mg₃Sb₂ lattice upon (Bi, Ge) co-substitution. Also, the refined lattice parameter of the α-Mg₃Sb₂ phases as shown in Table 1 indicates a reduced lattice parameter c for alloyed compositions, which decreases marginally for higher alloying content i.e. x ∼ 0.1. This suggests the shift in the overlapping major (101) and (011) peaks to be an outcome of secondary phase formation, which alters the Sb/Bi ratio in the synthesized compounds. For comparison, the unit cell parameters of indexed phases in Mg₃(Sb_1−x−yBi_xGe_y)₂ nanocomposites are presented in detail in Table 1.

Fig. 2 (a) XRD diffraction of the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ polycrystals. Magnified view indicating (b) the major (112) and (202) peaks of β-Mg₃Sb₂ phase, and (c) the major 101 and 011 peaks of α-Mg₃Sb₂ phase. (d) Le Bail analysis of the XRD pattern of the pulverized sintered sample with a nominal composition of Mg₃(Sb_0.95Bi_0.025Ge_0.025)₂ revealing indexed phases, as indicated by the observed Bragg peaks.

Table 1 Constituting phases in the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ nanocomposites. Space group, lattice parameters, unit cell volume (Ų), and refinement parameters (weighted profile (R_wp); profile (R_p); and expected (R_exp) R-factor). Standard deviations are given in parentheses

Composition	Space group	Lattice parameters	Volume	R-factors^a
				GOF	Rp	Rwp
a
x = 0; y = 0.1	P3̄m1	a = b = 4.5797(3), c = 7.2758(6), α = β = 90°, γ = 120°	132.16(1)	2.95	6.06	8.55
	Ia3̄	a = b = c = 9.2634(7), α = β = γ = 90°	794.90(1)
	P1̄	a = b = 12.557(1), c = 4.252(1), α = β = 90°, γ = 120°	580.76(8)
x = y = 0.025	P3̄m1	a = b = 4.5840(2), c = 7.2531(4), α = β = 90°, γ = 120°	131.99(1)	1.84	4.13	5.72
	Ia3̄	a = b = c = 9.3502(4), α = β = γ = 90°	817.45(5)
	P1̄	a = b = 12.629(2), c = 4.166(1), α = β = 90°, γ = 120°	575.60(6)
x = y = 0.05	P3̄m1	a = b = 4.5785(2), c = 7.2494(4), α = β = 90°, γ = 120°	131.60(1)	2.38	5.06	7.25
	Ia3̄	a = b = c = 9.3504(4), α = β = γ = 90°	817.52(4)
	P1̄	a = b = 12.627(2), c = 4.162(1), α = β = 90°, γ = 120°	574.68(5)
x = y = 0.1	P3̄m1	a = b = 4.5798(2), c = 7.2542(4), α = β = 90°, γ = 120°	131.77(1)	2.20	4.65	6.45
	Ia3̄	a = b = c = 9.3317(3), α = β = γ = 90°	812.63(1)
	P1̄	a = b = 12.613(2), c = 4.268(1), α = β = 90°, γ = 120°	588.09(4)

---

Fig. 2(d) shows the observed, calculated, and difference profiles of the powder diffraction profiles of the representative synthesized Mg₃(Sb_0.95Bi_0.025Ge_0.025)₂ samples measured at 295 K. The short vertical lines below the patterns indicate the peak positions of possible Bragg reflections for α and β-phases of Mg₃(Sb, Bi)₂, implying their coexistence due to the locally distorted configurations with broken symmetry. The Mg–Sb phase diagram suggests that the β-phase melts above ∼1500 K and has a cubic structure, whose details beside the space group (i.e. Ia3̄, 206) are unknown.^16–18 The rapid transition to the superionic state, often occurring at elevated temperatures, presents challenges in determining intermediate states or precise structural details during the transition. This complexity is further aggravated by dynamic disorder, thermal expansion, and increased atomic vibrations, which obscure the characterization of these phases. In the superionic phase, a subset of ions, typically cations, becomes highly mobile, creating a “liquid-like” molten sublattice within the solid framework. Such ion redistribution can dramatically alter the scattering intensity of certain reflections. Moreover, the superionic state is typically characterized by the strongly anharmonic vibrations of the mobile ions, leading to unusual changes in peak intensities and positions. Such changes are often difficult to interpret using conventional crystallographic models, complicating the structural analysis. Thus, superspace formalism is well-suited for describing the complex structures in the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ samples using the superspace group (P3̄m1(00g)0s0), which effectively restores the translational symmetry that is lost in the superionic transition due to its incommensurate nature.^22–24

The superionic transitioning of a lower-symmetry (P3̄m1, 164) phase to a higher-symmetry (Ia3̄, 206) phase represents a notable increase in crystal symmetry. This phase transition is consistent with the Mg–Sb phase diagram reported in previous studies, further supporting the observed structural evolution.^16–18 Refinements of the powder X-ray diffraction evaluate the cubic β-Mg₃Sb₂ unit cell (Formula unit = 8) with a lattice parameter i.e. a = b = c ≈ 9.350 Å, having a volume per formula unit of ≈817.5 ų as also presented in Table 1. A more isotropic arrangement of atoms in the superionic β-Mg₃Sb₂ phase likely facilitates easier ion movement in multiple directions, compared to the trigonal structure, which has distinct atomic positions and potentially layered or anisotropic features. It is also noteworthy that the synthesized polycrystals exhibit an irreversible and co-existing β-phase, in contrast to the pressure-induced displacive and reversible (trigonal ↔ monoclinic) phase transition at above 7.8 and 4.0 GPa, respectively, for Mg₃Sb₂ and Mg₃Bi₂, as reported previously.²⁵ The constituting superionic phases exhibit a bigger, and highly disordered superionic cell, indicating their complex anionic structural motifs, while demonstrating the structural transition prevalent at elevated temperatures in similar Zintl compounds.

2.2 Domain separation, nanoprecipitation and transgranular fracture

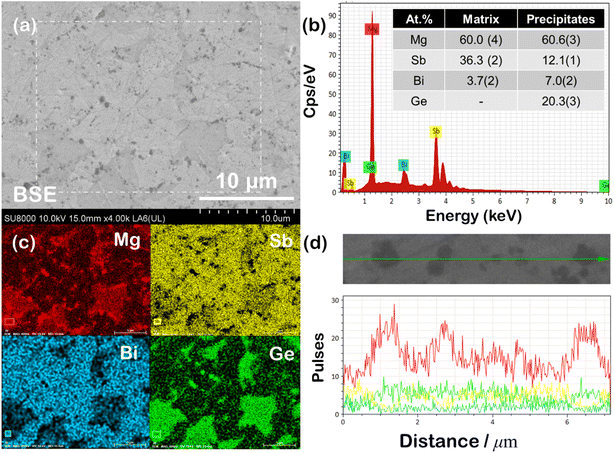
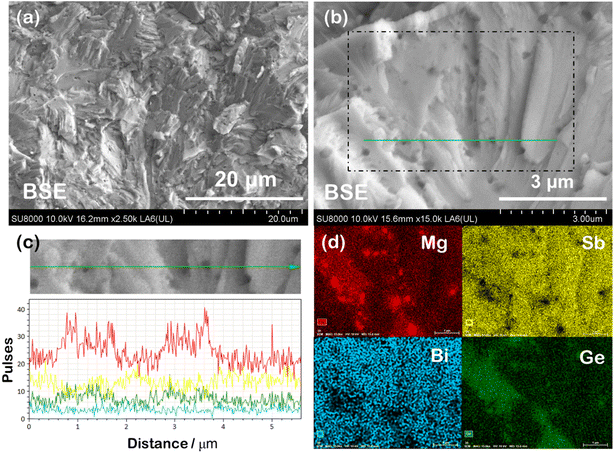
For a comprehensive understanding of the coexisting phases, polished and fractured samples were investigated using Scanning Electron Microscopy (SEM) in BSE (back scattered electron) and SE (secondary electron) modes. The BSE image of the representative polished Mg₃(Sb_1−x−yBi_xGe_y)₂ sample, shown in Fig. 3(a), reveals nanoprecipitation and compositional variations within the microstructure. The presence of secondary Mg₃Ge phases or impurities, identifiable by their darker contrast, suggests potential structural changes associated with the superionic transition. The back scattered electrons being sensitive to the atomic number and crystallographic orientation are scattered differently, resulting in contrast in the BSE micrographs. The EDS (energy dispersive X-ray) composition for nanoprecipitates corresponds to a Mg₃Ge based phase, while a higher Bi content is measured for the brighter domains within the matrix. The EDS spectrum for the mapped region, shown in Fig. 3(b), identifies the elemental constituents, with the average EDS composition of the primary phase or matrix (tabulated in the inset) closely aligning with the nominal composition. The average EDS composition of the dark appearing nanoprecipitates is measured to be Mg₃GeBi_0.4Sb_0.6, which corresponds to the trigonal Mg₃Ge phase (as designated previously and hereafter),²¹ as indexed in Fig. 2. Notably, compositional fluctuations within the domains, along with overlapping characteristic X-ray peaks of Mg (K_α peak is at 1.254 keV) and Ge (L_α ∼1.188 keV and L_β peaks ∼1.218 keV) in the EDS spectrum, make accurate identification and quantification of the exact compositions challenging. The elemental mapping shown in Fig. 3(c) indicates compositional variations more clearly, which are also identifiable on the grayscale contrast. Compositional contrast within grains points to localised variations in stoichiometry or the distribution of mobile ions, attributed to coexisting α and β-phases. Notably, the superionic transition is often accompanied by defect clusters or extensive Frenkel disorder,²⁶ which could also explain the observed contrast variations in BSE imaging and observation of high density Frenkel defects, as reported previously.^11,27 The line scan in Fig. 3(d) further confirms that the nanoprecipitates are composed of Mg- and Ge-rich regions, contrasting with the brighter, disordered primary phase.

Fig. 3 (a) BSE micrographs of the polished sintered surface, showing dark nanoprecipitates; (b) EDS spectrum accompanied by tabulated EDS compositions; (c) elemental mapping; and (d) line scan of a zoomed-in region, highlighting microstructural heterogeneity in a representative Mg₃(Sb_1−x−yBi_xGe_y)₂ sample with x = y ∼ 0.05.

The SE-SEM micrograph shown in Fig. 4(a) reveals a typical morphology of the fractured surface indicating a transgranular mode of fracture (i.e. crack propagation through the grains). The cleavage facets and aligned lamellae patterns were observed largely on the fracture surfaces, which are often associated with plastic deformation within the grains. The average grain size is evaluated to be larger than ∼1 μm, suggesting their contribution towards lowering of electrical resistivity due to reduced grain boundary scattering.²⁸ At higher magnification, the Mg₃Ge nanoinclusion segregation within the microstructure becomes distinctly visible. This can be attributed to local compositional fluctuations induced by discordant Ge atoms. The dark-appearing nanoprecipitates, observed embedded within the grains, further indicate the role of Ge in promoting phase separation at the nanoscale. We anticipate Mg₃Ge nucleation and segregation from the super-saturated Mg₃(Sb, Bi)₂ solid solution to be an outcome of limited solid solubility of Ge. The EDX line scan (Fig. 4(c)) for the zoomed-in region confirms the presence of Mg and Ge excess in the same regions corresponding to dark appearing nanoprecipitations embedded in the grains. Similar to the polished surface of the bulk samples, the elemental mapping (Fig. 4(d)) of the fractured surface also confirms the presence of Mg and Ge excess in dark appearing embedded nanoprecipitates. The EDS mapping revealing spatial distribution indicates that all the constituting elements, i.e. Mg, Sb, Bi and Ge, are well distributed uniformly throughout the sample.

Fig. 4 (a) Low magnification and (b) high magnification images of the fractured specimen, showing transgranular fracture and the presence of nanoprecipitates. (c) High-resolution line scan of the zoomed-in region, indicating embedded Mg and Ge-rich nanoprecipitates. (d) Elemental mapping of the region indicated in (b).

Interestingly, the incorporation of Ge in n-type Mg_3.2Sb_1.49−2xBi_0.5Te_0.01+xGe_x has led to the formation of Bi/Ge-rich Janus nanoprecipitates,²⁹ which may possess similarity to the observed secondary phase formation. As understood previously,²⁹ despite negligible mutual solid-state solubilities of Ge and Bi, during sintering (at a sintering temperature of ≈923 K) they become fully miscible through a co-melting process. During crystallization, the α-Mg₃(Sb, Bi)₂ and Bi–Ge liquid phases compete for formation, which we anticipate has induced Mg₃Ge phase formation and a partial displacive structural transition from the trigonal (P3̄m1) phase to the cubic (Ia3̄) phase during sintering. As the nominal composition of the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ nanocomposites lies well within the solid solubility range (i.e. x ∼ 0.4) of Bi in Mg₃Sb_2−xBi_x compounds,³⁰ the superionic phase formation and observation of Mg₃Ge are indicative of the discordant nature of Ge atoms, which exhibit limited solubility with Bi and undergo local co-melting of Bi and Ge during sintering.²⁹ These findings suggest that the synthesized nanocomposites possess a complex microstructure that necessitates high-resolution techniques to fully characterize and understand the origins of these compositional variations. The coexistence of these phases has a significant impact on the microstructure, deformation behaviour, and transport properties of the sintered material, as discussed in the subsequent sections.

2.3 Distorted coordination polyhedra, off centering and discordant Ge atoms

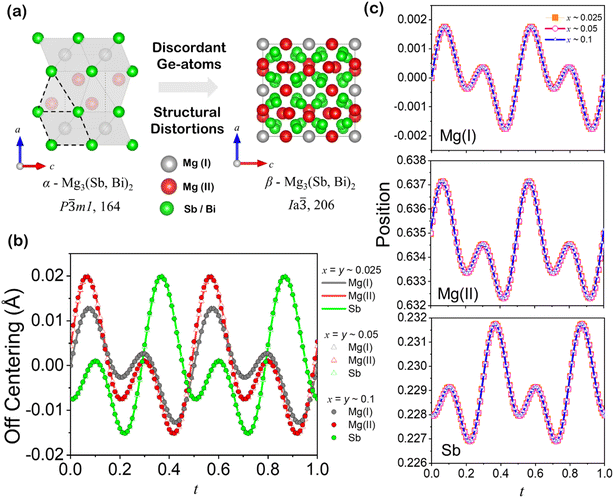
Superionic phases are characterized by the presence of highly mobile ions (usually cations) moving within a stable crystal framework formed by another set of ions (most likely the anionic framework). Their formation and stability of superionic phases are highly dependent on pressure and temperature conditions. The body-centered cubic structure (Ia3̄) of β-Mg₃(Sb, Bi)₂ is a distorted variant of the trigonal α-phase (P3̄m1) with high symmetry, complex coordination geometries and distorted coordination polyhedra, as shown in Fig. 5(a). The Mg atoms are tetrahedrally and octahedrally coordinated by Sb/Bi atoms in a trigonal α-phase and adapt a more complex coordination geometry having rapid diffusion of Mg ions at cationic crystallographic sites in the superionic phase. Similarly, trigonal pyramidal coordination of Sb/Bi atoms in the trigonal α-phase occupy a complex and presumably octahedral coordination within the larger superionic β-phase structure. We expect an inherent conflict to exist between the tetrahedral coordination preference of Ge atoms and the trigonal pyramidal coordination of its hosting Sb-site, which could lead to significant local deviations, such as off-centering, in the structure from the ideal state. Such local distortion resembles cluster behaviour and loss of nearest-neighbours, wherein the constituent Mg(I), Mg(II) and Sb atoms adopt a local coordination environment while providing charge balancing for the formation of Mg vacancy defects.³¹

Fig. 5 (a) Schematic depicting trigonal and superionic phase transitions. The tetrahedral and octahedral polyhedra are highlighted in the trigonal phase. (b) Evaluated off-centering for Mg(I), Mg(II) and Sb atoms for varying compositions. (c) Corresponding positional modulations of the atomic coordinates of Mg(I) ∼ (0, 0, 0), Mg(II) ∼ (1/3, 2/3, 0.634), and Sb ∼ (1/3, 2/3, 0.229) atoms plotted as a function of the fourth superspace coordinate (t).

As conventional 3-dimensional structural models overlook local and random distortions within the crystal structure, we employ a (3 + 1) dimensional superspace group (P3̄m1(00γ)0s0) to characterize inherent modulation in the synthesized samples.^22–24 Modulations can arise from displacive modulations (atomic positions modulated) or occupational modulations (site occupancies modulated). The superspace approach can model both types by introducing modulation functions for atomic coordinates and occupancies to capture the complex structural variations. Fig. 5(b) reveals the evaluated off-centering in angstroms of Mg(I), Mg(II) and Sb atoms along the z axis with varying alloying content, evaluated upon Rietveld refinement of the dominant α-Mg₃Sb₂ phase from their ideal lattice positions, i.e., 1a (0, 0, 0), 2d (1/3, 2/3, 0.664), and 2d (1/3, 2/3, 0.225), respectively, against the fourth superspace coordinate t. All the displacements (in angstroms) are periodic in the interval 0 ≤ t ≤ 1.0, considering up to the fourth order of cosine and sine components of the Fourier terms, with an isotropic displacement parameters of each atoms. The off-centering phenomenon in a crystal structure involves the displacement of atoms from their ideal coordination centers, leading to locally distorted configurations and broken symmetry, while maintaining the overall crystallographic symmetry of the material. Interestingly, the displacement occurs only along the z direction, which is likely triggered by the presence of Ge atoms in layered anionic solid solutions of Mg₃(Sb_1−x−yBi_xGe_y)₂. This counterintuitive site preference of Ge atoms arises from factors such as ionicity, covalency, and the flexibility of the host structure to accommodate the dopant atoms in energetically favourable sites. The off-centering of the constituting atoms is only allowed along the z direction in all the alloyed compositions, indicative of a low ideal shear strength of ∼1.95 GPa found for Mg₃Sb₂.³²

The overlapping periodicity of displacive modulations in the alloyed compositions, which corresponds to the atomic coordinates in the α-Mg₃(Sb, Bi)₂ phase, suggests off-centering as an inherent characteristic of the synthesized anionic solid solutions, which are independent of alloyed content as revealed in Fig. 5(b). The evaluated positional modulations of the atomic coordinates from their ideal, symmetric lattice position are shown in Fig. 5(c–e). Substituting Sb with Ge in Mg₃(Sb_1−x−yBi_xGe_y)₂ will lead to an uncommon and destabilizing coordination environment for Sb. Intuitively, Ge might tend to shift its lattice position from the anionic site to lower its energy, thereby disrupting local symmetry and enabling orbital hybridization that would otherwise be forbidden. Thus, even for the isostructural compounds, the local coordination and bond distances may vary, and detailed structural analysis is therefore required to draw any conclusions. The high symmetry superionic phase of Mg₃(Sb, Bi)₂ and Mg₃Ge rich nanoprecipitates accommodates alterations in the anionic structural motifs within their large unit cells, wherein the valence electron count per anionic atom determines the type of motif formed. Through electron transfer and the resulting electronic configurations, the trigonal α-Mg₃(Sb, Bi)₂ phase facilitates Bi-dopant solubility, as indicated by its relatively expanded unit cell. This highlights the versatility of Zintl phases in coexisting with diverse anionic substructures that can be explained well through the Zintl–Klemm concept.

2.4 Synergistic κ reduction and enhanced power factor

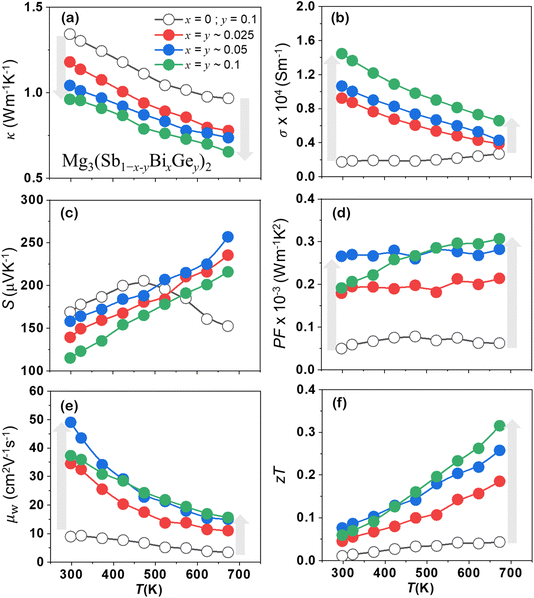
Recent investigations have unveiled off-centering behaviour in a diverse array of TE materials including GeTe compounds, PbSe, and I–V–VI₂ chalcogenides (such as AgSbTe₂ and AgSbSe₂), establishing it as the origin of their remarkably low thermal conductivity (κ).^33–36 Consequently, off-centering has emerged as an effective strategy to modulate thermal transport properties and enhance TE performance by exploiting the anharmonic lattice dynamics induced by the off-centre atomic displacements. Alloying and doping have become prevalent approaches for enhancing the electrical transport in Mg₃Sb₂ compounds as they exhibit inherently low κ_L. In the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ nanocomposites, the discordant Ge atoms induce displacive modulation in the dominant α-Mg₃Sb₂ phases, demonstrating off-centering behaviour for constituent atoms.

High temperature and pressure sintering leads to superionic phase formation, off-centering of constituting atoms in the trigonal α-Mg₃Sb₂, and Mg₃Ge phase nanoprecipitation. The lattice thermal conductivity (κ_L) being intimately related to the microstructure is significantly lowered (∼30%) in comparison to the Ge doped Mg₃Sb₂ as shown in Fig. 6(a). Nanoprecipitates and the superionic phase owing to their large and complex unit cell are anticipated to effectively scatter the phonons, contributing to κ_L reduction. The off-centering feature of the trigonal α-Mg₃Sb₂, wherein all the constituting atoms undergo displacive modulation, can be considered as a primary cause for κ_L reduction as it disrupts the overall periodic arrangement of atoms. The off-centering ranges from ∼0 to 0.02 Å at 300 K and occurs periodically in the structure, wherein locally off-centered atoms are expected to hinder the smooth propagation of phonons.

Fig. 6 Temperature dependence of the (a) total thermal conductivity, (b) power factor, (c) Seebeck coefficient, (d) electrical conductivity, (e) weighted mobility, and (f) thermoelectric figure of merit (zT) of nominal Mg₃(Sb_1−x−yBi_xGe_y)₂ polycrystals.

Pure and intrinsic p-type Mg₃Sb₂ exhibits poor electrical performance quantified as the power factor (S²σ), primarily due to its high electrical resistivity. However, the synthesized Mg₃(Sb_1−x−yBi_xGe_y)₂ (0 < x,y < 0.1) nanocomposites display a significant improvement in temperature dependent electrical conductivity σ(T), as shown in Fig. 6(b). For comparison, the TE properties of the synthesized Ge doped Mg₃Sb₂ are also shown alongside, wherein at 300 K the σ(T) of Mg₃Sb_1.8Ge_0.2 is ∼1.74 × 10³ S m⁻¹, and it improved significantly to ∼1.45 × 10⁴ S m⁻¹. All samples indicate degenerate semiconducting behaviour, wherein σ decreases with increasing temperature. The temperature-dependent S(T) shown in Fig. 6(c) displays p-type conduction, which gradually increases with rising temperature and decreases with increasing alloying content showcasing an inverse correlation with σ(T). A higher power factor as displayed in Fig. 6(d) was attained for all the alloyed compositions with the maximum value approaching 3 × 10⁻⁴ W m⁻¹ K⁻¹ for a higher alloy content (x > 0.05). The enhancement can be understood as an outcome of improved weighted mobility (μ_w)³⁷ derived S(T) and σ(T) measurements, as shown in Fig. 6(e). It provides a weighted average contribution of all energy levels to the overall mobility of the carrier in the crystal and provides good results at room temperature and above, and for mobilities as low as 10⁻³ cm² V⁻¹ s⁻¹. All the alloyed compositions exhibit higher μ_w and correspond well with the evaluated power factor enhancement. The temperature-dependent zT presented in Fig. 6(f) indicates comparatively higher values for alloyed off-centered compositions with a maximum zT ∼ 0.3(±0.05) at 673 K. Optimizing the Fermi level by cation site doping or band bending is anticipated to further enhance the zT of the synthesized alloyed compositions, which exhibits an inherently lowered κ_L. Thus, the high-symmetry superionic phase in Mg₃(Sb, Bi)₂-based compositions enhances electrical transport properties, providing a renewed basis for exploring structure–property relationships. This insight paves the way for designing Mg₃(Sb, Bi)₂ based Zintl phases as advanced functional materials with improved performance.

3. Conclusion

Complex crystal structures and mixed ionic-covalent bonding in Mg₃(Sb, Bi)₂ based Zintl compounds have remained critical for understanding their unique electronic structure and transport properties. In this study, we observed off-centering of constituting atoms in the dominant trigonal phase of α-Mg₃Sb₂, superionic β-phase formation and nano-segregation of the Mg₃Ge phase upon equiatomic (Bi, Ge) alloying in Mg₃(Sb_1−x−yBi_xGe_y)₂. The superionic phase formation significantly impacts the coordination environments of the cations (Mg) and anions (Sb/Bi), resulting in more complex structural motifs. The concentration of nanoprecipitates is determined by the alloying content, whereas the extent of off-centering and atomic disorder is independent of the alloying content. The off-centering enables the realization of a synergistic reduction in lattice thermal conductivity and power factor enhancement, resulting in zT enhancement. The strategic co-alloying of Ge and Bi and the formation of nano-precipitates offer promising avenues for optimizing the p-type TE performance of Mg₃Sb₂-based Zintl nanocomposites.

4 Experimental details

4.1 Material synthesis and processing

High-purity elemental constituents, i.e., magnesium turnings (Mg, 99.8%), antimony powder (Sb, 99.9999%), bismuth powder (Bi, 99.999%), and germanium powder (Ge, 99.999%), were stoichiometrically weighed in accordance with nominal compositions Mg₃(Sb_1−x−yBi_xGe_y)₂ wherein (0 < x < 0.2). Subsequently, they were loaded into a stainless-steel ball mill in a glovebox (MBRAUN UNILAB PLUS ECO.) under an argon atmosphere with the oxygen level (<0.1 ppm) for a high-energy milling (SPEX 8000D) process. The milling was carried out for 2 hours and the milled powder was collected and loaded into a high-density graphite die (Ø 10 mm) inside the glove box for sintering. To obtain dense samples, isothermal sintering through spark plasma sintering (SPS, SPS-1080 System, SPS SYNTEX INC) was carried out at 1023 K with a pressure of ∼60 MPa for 5 min. The volumetric densities of polycrystalline bulk samples were determined to be >97% of the theoretical density, using the Archimedes principle.

4.2 Structural characterization

X-ray diffraction (XRD) was performed at RT in the 2θ range of 20–60° using monochromatized CuK_α radiation (λ = 1.54 Å) on a MiniFlex 600/600-C (Rigaku) equipped with a high-speed 1D detector D/teX Ultra2. The microstructure and composition were characterized using a field emission scanning electron microscope (FESEM, Hitachi S 4800) equipped with an energy dispersive spectrometer (EDS, Horiba EMAX Evolution X-Max).

4.3 Thermoelectric characterization

Temperature-dependent thermoelectric transport measurements were conducted on bulk sintered samples within a temperature range of 300–673 K. For thermal diffusivity (D) and specific heat (C_P), circular disc specimens of approximately 10 mm diameter and 2 mm thickness were analysed using the flash diffusivity method (LFA467 HT HyperFlash, Netzsch, Germany) in an argon environment. Electronic thermal conductivity (κ_e) was assessed in accordance with the Wiedemann–Franz law κ_e = L × σ × T, where L is the Seebeck-dependent Lorenz number.³⁸ The L values estimated using the relationship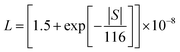 were found to be in the range of (1.6–1.9) × 10⁻⁸ W Ω K⁻². Simultaneously, temperature dependent measurements of electrical conductivity and Seebeck coefficients were performed using the four-probe DC method (ZEM-3, Ulvac-Riko, Japan) in a helium atmosphere on samples cut into rectangular bars with dimensions of approximately 9 mm × 2 mm × 2 mm. The accuracy in transport measurements is ±10% for thermal conductivity, ±7% for electrical conductivity, and ±7% for Seebeck coefficients.

Data availability

The data that support the findings of this study are available upon request from the authors.

Conflicts of interest

There is no conflict of interest to declare.

Acknowledgements

This research was supported by the JST Mirai Program, Japan (grant number – JPMJMI19A1).

References

1. S. M. Kauzlarich, Chem. Mater., 2023, 35, 7355–7362.
2. J. Shuai, J. Mao, S. Song, Q. Zhang, G. Chen and Z. Ren, Mater. Today Phys., 2017, 1, 74–95.
3. J. Wang, J. Mark, K. E. Woo, J. Voyles and K. Kovnir, Chem. Mater., 2019, 31, 8286–8300.
4. J. Mao, H. Zhu, Z. Ding, Z. Liu, G. A. Gamage, G. Chen and Z. Ren, Science, 2019, 365, 495–498.
5. S. Bano, R. Chetty, J. Babu and T. Mori, Device, 2024, 2, 100408.
6. H. Tamaki, H. K. Sato and T. Kanno, Adv. Mater., 2016, 28, 10182–10187.
7. J. Shuai, J. Mao, S. Song, Q. Zhu, J. Sun, Y. Wang, R. He, J. Zhou, G. Chen and D. J. Singh, Energy Environ. Sci., 2017, 10, 799–807.
8. J. Mao, Y. Wu, S. Song, Q. Zhu, J. Shuai, Z. Liu, Y. Pei and Z. Ren, ACS Energy Lett., 2017, 2, 2245–2250.
9. Z. Liu, N. Sato, W. Gao, K. Yubuta, N. Kawamoto, M. Mitome, K. Kurashima, Y. Owada, K. Nagase, C.-H. Lee, J. Yi, K. Tsuchiya and T. Mori, Joule, 2021, 5, 1196–1208.
10. L. Wang, N. Sato, Y. Peng, R. Chetty, N. Kawamoto, D. H. Nguyen and T. Mori, Adv. Energy Mater., 2023, 13, 2301667.
11. L. Wang, W. Zhang, S. Y. Back, N. Kawamoto, D. H. Nguyen and T. Mori, Nat. Commun., 2024, 15, 6800.
12. H. Cho, S. Y. Back, N. Sato, Z. Liu, W. Gao, L. Wang, H. D. Nguyen, N. Kawamoto and T. Mori, Adv. Funct. Mater., 2024, 34(44), 2407017.
13. C. Zheng, R. Hoffmann, R. Nesper and H. G. Von Schnering, J. Am. Chem. Soc., 1986, 108, 1876–1884.
14. A. Li, C. Fu, X. Zhao and T. Zhu, Research, 2020, 2020, 1934848.
15. M. Martinez-Ripoll, A. Haase and G. Brauer, Acta Crystallogr B Struct Sci, 1974, 30, 2006–2009.
16. A. A. Nayeb-Hashemi and J. B. Clark, Bull. Alloy Phase Diagrams, 1985, 6, 528–533.
17. H. Okamoto, J. Phase Equilib. Diffus., 2010, 31, 574.
18. M. Paliwal and I.-H. Jung, Calphad, 2009, 33, 744–754.
19. A. C. Barnes, C. Guo and W. S. Howells, J. Phys.: Condens. Matter, 1994, 6, L467–L471.
20. J. Zhang, L. Song, S. H. Pedersen, H. Yin, L. T. Hung and B. B. Iversen, Nat. Commun., 2017, 8, 13901.
21. N. Bolotina, T. Dyuzheva, N. Bendeliani, V. Petricek, A. Petrova and V. Simonov, J. Alloys Compd., 1998, 278, 29–33.
22. A. Yamamoto, Acta Crystallogr., Sect. A: Found. Crystallogr., 1993, 49, 831–846.
23. A. Yamamoto, Acta Crystallogr., Sect. A: Found. Crystallogr., 1992, 48, 476–483.
24. S. Van Smaalen, Incommensurate Crystallography, Oxford University Press Inc., New York, 2007, vol. 21.
25. M. Calderón-Cueva, W. Peng, S. M. Clarke, J. Ding, B. L. Brugman, G. Levental, A. Balodhi, M. Rylko, O. Delaire, J. P. S. Walsh, S. M. Dorfman and A. Zevalkink, Chem. Mater., 2021, 33, 567–573.
26. N. Hainovsky and J. Maier, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 15789.
27. T. Kanno, H. Tamaki, M. Yoshiya, H. Uchiyama, S. Maki, M. Takata and Y. Miyazaki, Adv. Funct. Mater., 2021, 31, 2008469.
28. K. Imasato, M. Wood, S. Anand, J. J. Kuo and G. J. Snyder, Adv. Energy Sustainability Res., 2022, 3, 2100208.
29. R. Shu, Z. Han, A. Elsukova, Y. Zhu, P. Qin, F. Jiang, J. Lu, P. O. Persson, J. Palisaitis and A. Le Febvrier, Adv. Sci., 2022, 9, 2202594.
30. A. Bhardwaj, N. S. Chauhan and D. K. Misra, J. Mater. Chem. A, 2015, 3, 10777–10786.
31. S. Ohno, K. Imasato, S. Anand, H. Tamaki, S. D. Kang, P. Gorai, H. K. Sato, E. S. Toberer, T. Kanno and G. J. Snyder, Joule, 2018, 2, 141–154.
32. G. Li, U. Aydemir, M. Wood, Q. An, W. A. Goddard III, P. Zhai, Q. Zhang and G. J. Snyder, J. Mater. Chem. A, 2017, 5, 9050–9059.
33. J. Dong, L. Hu, J. Liu, Y. Liu, Y. Jiang, Z. Yu, X. Y. Tan, A. Suwardi, Q. Zheng, Q. Li, J. Li, V. P. Dravid, Q. Yan and M. G. Kanatzidis, Adv. Funct. Mater., 2024, 34, 2314499.
34. C. Xie, X. Tang and G. Tan, Next Materials, 2023, 1, 100048.
35. Z. Ge, W. Li, J. Feng, F. Zheng, C. Jia, D. Wu and L. Jin, Adv. Energy Mater., 2022, 12, 2103770.
36. S. Cai, S. Hao, Z.-Z. Luo, X. Li, I. Hadar, T. P. Bailey, X. Hu, C. Uher, Y.-Y. Hu, C. Wolverton, V. P. Dravid and M. G. Kanatzidis, Energy Environ. Sci., 2020, 13, 200–211.
37. G. J. Snyder, A. H. Snyder, M. Wood, R. Gurunathan, B. H. Snyder and C. Niu, Adv. Mater., 2020, 32, 2001537.
38. H.-S. Kim, Z. M. Gibbs, Y. Tang, H. Wang and G. J. Snyder, APL Mater., 2015, 3, 041506.

---

Footnote

† Electronic supplementary information (ESI) available: Rietveld refined XRD patterns of Mg₃(Sb_1−x−yBi_xGe_y)₂; temperature dependent thermal properties; SEM micrographs; off-centering along x, y, and z directions. See DOI: https://doi.org/10.1039/d4ta06173j

---