Open Access Article
Open Access ArticleElectron transport kinetics for viologen-containing polypeptides with varying side group linker spacing†
Alexandra D.
Easley
a,
Cheng-Han
Li
 b,
Shih-Guo
Li
b,
Shih-Guo
Li
 b,
Tan P.
Nguyen
b,
Tan P.
Nguyen
 b,
Kai-Hua
Mick Kuo
b,
Karen L.
Wooley
b,
Kai-Hua
Mick Kuo
b,
Karen L.
Wooley
 *abc,
Daniel P.
Tabor
*abc,
Daniel P.
Tabor
 *b and
Jodie L.
Lutkenhaus
*b and
Jodie L.
Lutkenhaus
 *ac
*ac
aDepartment of Materials Science and Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: jodie.lutkenhaus@tamu.edu
bDepartment of Chemistry, Texas A&M University, College Station, TX 77843, USA. E-mail: daniel_tabor@tamu.edu
cArtie McFerrin Department of Chemical Engineering, Texas A&M University, College Station, TX 77843, USA. E-mail: wooley@chem.tamu.edu
First published on 6th November 2024
Abstract
Studies investigating the influence of the length of linkers between redox-active moieties and peptide-based polymer backbones were conducted to advance fundamental knowledge toward the design and development of sustainably-sourced, recyclable, and degradable materials for energy applications. In this work, precursor polypeptides were synthesized through the ring-opening polymerizations of N-carboxyanhydrides decorated with varying lengths of alkylchloride side chain groups, followed by post-polymerization installation of the viologen moieties. Electrochemical interrogation of the viologen-based polypeptides provided estimates of the electron transfer rate constants, both heterogeneous (k0) and electron self-exchange (kex), the apparent diffusion coefficient (Dap), and their device-based energy storage performance. For the first redox couple (viologen dication state to viologen radical-cation state), it was found that the rate of electron transfer among the pendant groups in all viologen-based polypeptides, kex, was not significantly impacted by linker length. In contrast, for the second redox couple (viologen radical-cation state to the neutral viologen), kex varied with linker length and was fastest during reduction from the viologen radical-cation state to the neutral viologen. Most interestingly, a linear relationship was identified between log(k0) and log(kex) with a slope of 1.85, indicating that electron transport in the viologen-based polypeptides followed most closely to Marcus–Hush theory with diffusion limitations or Laviron–Andrieux–Savéant (LAS) theory. Finally, the polypeptides were studied in lithium metal half cells to determine the relationship between kex and energy storage performance. The viologen-based polypeptide with the moderate length linker exhibited the highest capacity and lowest degree of swelling, but only moderate kex, demonstrating that the device performance was primarily influenced electrode swelling. Taken together, the viologen-polypeptide backbone dictated the mechanism of electron transfer, whereas the linker length could be used to alter the rate of electron transfer (kex). Balancing the rate of electron transfer (kex) and degree of swelling will be a major challenge to identify polymers for high performance energy storage devices.
Introduction
With the increase in demand for lithium-ion batteries and the strained supply of strategic elements, alternative active materials are needed for battery electrodes. One such material class of interest is redox-active polymers (RAPs), which include both conjugated polymers and non-conjugated polymers with redox-active pendant groups.1–5 Extensive work has been done to investigate structure–property relationships for conjugated polymers in the solid-state to reveal linkages among the conduction mechanism, regiochemistry, and crystallinity.6–9 However, there has been significantly less work done for non-conjugated RAPs, due to their amorphous nature for which “crystal-engineering” is precluded. For cathodic RAPs with pendant redox-active groups, such as 2,2,6,6-tetramethylpiperidin1oxyl (TEMPO) containing polymers, there have been several studies investigating the electron transport mechanism.10–12 However, there has been less work on anodic pendant RAPs,13,14 and most studies used flexible or semi-flexible backbones. Previously, our group reported redox-active polypeptides in degradable solid-state and redox flow batteries,15,16 for which the polypeptide backbones displayed solution-state α-helical chain conformations, but the electron transfer mechanism was not examined.Prior work shows that local ordering and mobility of redox-active groups influence electron transport. Akhoury et al. studied non-crosslinked and crosslinked ferrocene-based grafts on carbon particles.17 The authors found that bounded diffusion and electron hopping influenced the rate of electron transfer for the non-crosslinked grafts, whereas only electron hopping contributed in the crosslinked grafts, due to reduced mobility.17 Similarly, Whiting et al. studied poly(triphenylamine acrylate) brushes and spin-coated films and found that the ordered brushes led to increased rates of electron transfer as compared to the more disordered spin-coated films.18 In addition to the influence of the helical polypeptide backbone on electron transfer among redox-active pendant groups, electron tunneling through the helical backbone could also influence electron transport. Arikuma et al. demonstrated that for short ferrocene-terminated helical polypeptides (less than 16 repeat units), electron tunneling contributed to the overall rate of electron transfer.19 Deng et al. reported the synthesis of viologen-containing helical polyacetylenes; however, effects of the helical backbone and pendant group spacing on the electron transport mechanism were not studied.20
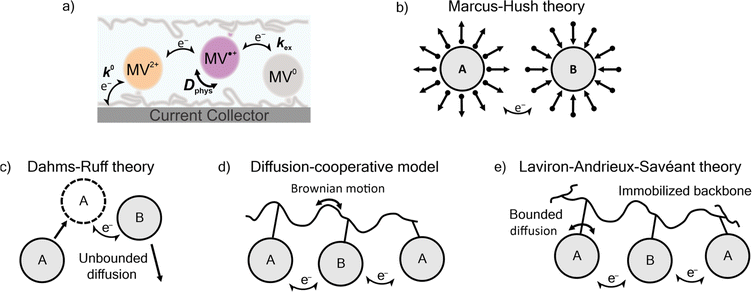
Three prominent theories consider the diffusion of polymer-bound redox active moieties: Dahms–Ruff (D–R) theory,21,22 Laviron–Andrieux–Savéant (LAS) theory,23,24 and the diffusion cooperative model (Fig. 1).10 D–R theory describes the electron transfer of freely-diffusive redox-active groups.21,22 In this model, charge transport is limited by the diffusion of the molecules, where electron transfer occurs only as rapidly as molecules contact each other. Explicitly stated, this model is applied in systems where the physical diffusion (Dphys) of the redox-active moieties is larger than the diffusion of electron transfer (De). Experimental studies have shown that D–R theory accurately describes electron transfer in metal complexes,25 viologen-polymer and dimer solutions,14,26 ferrocene polymer solutions,26 and viologen-based ionic liquids.27 As the physical diffusion (Dphys) of the redox-active moieties is further restricted and the redox-active moieties are immobilized (Dphys ≈ 0), De becomes larger than Dphys, and LAS theory is applicable.23,24 Previously, LAS theory has been used to describe electron transfer of TEMPO-containing polyether thin films,28 ferrocene-containing polyacrylamide gels,29 crosslinked TEMPO-containing polynorbornene,30 ferrocene-based metal–organic frameworks,31 and viologen and TEMPO nanoparticles.32
Recently, Burgess et al. and Sato et al. reported deviation from both D–R and LAS theory for viologen-based polymeric solutions and TEMPO-based polymer thin films, respectively.10,14 To account for this deviation, Sato et al. proposed the diffusion cooperative model, which considers the effects of Brownian motion of the polymer.10 In this model, the diffusion of electron transfer has contributions from both De and Dphys. The Dphys considered here is significantly reduced compared to the free diffusion of the D–R theory but greater than the lack of Dphys assumed in LAS theory. This intermediate Dphys model has also been applied to an immobilized TEMPO-containing polyamine,33 TEMPO-substituted poly(ethylene sulfide),34 and a variety of nitroxide-containing polymers with varying backbone and linker groups.10 However, much of the work described in those reports involved physically-restricted crosslinked polymers or polymers with a flexible backbone.
Here, we report the synthesis of viologen-based polypeptides with varying spacing between the backbone and viologen pendant group. The influence of backbone structure is also considered through comparison of the helical polypeptide backbone with a RAP having an aliphatic backbone. The polymers were processed to produce thin-film coatings, and the electron transfer rate constants were determined from chronoamperometry and cyclic voltammetry. The determined parameters included the apparent diffusion coefficient (Dap), the rate constant for electron self-exchange between pendant viologen groups (kex), and the rate constant for heterogenous charge transfer (k0). The physical diffusion coefficients (Dphys) for the polymers in solution and the viologen pendant group relative to the backbone were determined using dynamic light scattering (DLS) and computational methods, respectively. The relationship between De and Dphys was analyzed to determine the predominate mechanism of electron transport in the system. Finally, we evaluated the performance of the viologen-based polypeptides in half-cell batteries to relate the electron transfer kinetics to battery performance. Overall, these results present the dominant theory and redox couple for charge transport in viologen-functionalized polypeptides.
Experimental
Materials
Lithium chloride (LiCl, powder, ≥99.98% trace metals basis), and γ-butyrolactone (GBL, ≥99%) were used as received from Sigma-Aldrich. Dichloromethane (DCM, ≥99.5% stabilized) was used as received from VWR. Ultrapure water (MQ water) was collected from a Milli-Q® integral water purification system (18 MΩ cm). Methanol was used as received from VWR. Lithium metal was purchased from Alfa-Aesar. Indium tin oxide (ITO)-coated glass (CUV5B) was purchased from Delta and cleaned by subsequent sonication in soap water, water, acetone, and isopropyl alcohol, followed by drying with N2 and ozone plasma treatment for 10 min. Au-coated QSense quartz crystal microbalance sensors with a Ti adhesion layer (QSX 338) were purchased from Biolin Scientific and cleaned with 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1
1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 MQ H2O
1 MQ H2O![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) ammonium hydroxide
ammonium hydroxide![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) hydrogen peroxide at 75 °C for 5 min before use. Materials for synthesis can be found in the ESI.†
hydrogen peroxide at 75 °C for 5 min before use. Materials for synthesis can be found in the ESI.†
Chemical characterization
Attenuated total reflectance-Fourier transform infrared (ATR-FTIR) spectra were recorded for powder samples on an IR Prestige 21 system (Shimadzu Corp.). The data were analyzed using IRsolution v. 1.40 software. Circular dichroism (CD) spectra of the viologen polypeptide solutions in a quartz cell were recorded, between 180 and 280 nm, using a wavelength step of 1.0 nm, and had a path length of 1.0 cm, on a Chirascan CD spectrometer from Applied Photophysics, Ltd (Leatherhead, UK) equipped with a 150 watt xenon arc lamp. The viologen polypeptides and control viologen polymer were dissolved in H2O (HPLC grade) to generate solutions for analysis. The resulting CD spectra were analyzed using Pro-Data v. 5 software. 1H and 13C nuclear magnetic resonance (NMR) spectra were recorded on a Bruker AVANCE NEO 400 or Bruker AVANCE III 500 spectrometer. Thermogravimetric analysis (TGA) was conducted using a Mettler-Toledo TGA2/1100/464. The measurements were performed at a heating rate of 10 °C min−1 across a temperature range of 25 °C to 500 °C under a nitrogen atmosphere. Data were analyzed using Mettler-Toledo STARe v. 17.00 software to determine the onset degradation temperature (Td) for all the polymers. For the final viologen chloride polymers, the glass transition temperatures (Tg) were determined from the inflection point of the second heating cycle measured using modulated differential scanning calorimetry (MDSC) on a Q200 DSC (TA Instruments) with a heat–cool–heat cycle. The samples were ramped from −40 °C to 200 °C at a rate of 5 °C min−1 with an amplitude of 1.272 °C for a period of 60 s with nitrogen purge at 50 mL min−1. For all other polymers, the glass transition temperatures (Tg) were determined from the inflection point of the second heating cycle measured using DSC on a Mettler-Toledo DSC3/700/1190 (Mettler-Toledo, Inc., Columbus, OH) under a nitrogen atmosphere. The measurements were performed with heating and cooling rates of 10 °C min−1 over three heating and cooling cycles. Data analysis was conducted using Mettler-Toledo STARe v. 17.00 software. Finally, dynamic light scattering (DLS) data were collected, using the same aqueous solutions from the CD measurements, on a Malvern Zetasizer Nano ZS and analyzed with Zetasizer v7.13 to obtain the hydrodynamic radius values. Using the Stokes–Einstein equation, eqn (1), the solution state polymer diffusion coefficient (DDLS) can be calculated from the measured hydrodynamic radius (rh) in DLS.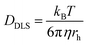 | (1) |
Synthesis of viologen polypeptides with varying alkyl spacer lengths
The viologen polypeptides were synthesized following the method of Nguyen et al.16 For the C3 and C9 viologen polypeptides, the first synthetic step was altered slightly by replacing 6-chloro-1-hexanol. Instead, 3-chloro-1-propanol and 9-chloro-1-nonanol were used to produce the C3 and C9 viologen polypeptides, respectively. Details of the synthetic steps can be found in the ESI.†Synthesis of the control viologen polymer
Poly(vinylbenzyl methyl viologen) was synthesized following a modified method as reported by Nagarjuna et al.35 First, methyl viologen chloride (MV-Cl) was synthesized following the procedure reported by Nguyen et al. followed by ion exchange using Dowex® A2 ion exchange resin.16 Poly(vinylbenzyl chloride) (PVBC) was synthesized via reversible addition-fragmentation chain-transfer (RAFT) polymerization following a modified method as reported by Moraes et al. and Nagarjuna et al.; however, 4-cyano-4-(((dodecylthio)carbonothioyl)thio)pentanoic acid was used as the RAFT chain transfer agent.35,36 Details of the synthetic steps can be found in the ESI.†Determination of thickness swelling ratio
Quartz crystal microbalance with dissipation (QCM-D) (QSense E1, Biolin Scientific) was used to determine the thickness swelling ratio of the viologen polymer films as a ratio of their dry film thickness (hdry) and swollen film thickness (hswollen). All QCM-D measurements were conducted in an Ar-filled glovebox. Baseline measurements were conducted on uncoated gold-coated AT-cut quartz crystal sensor in Ar and in 0.5 M LiCl in GBL. After measuring the baseline, the sensor was washed with MQ water and dried, followed by drop casting of a viologen polymer onto the sensor surface. The drop casting solution was 8 mM of repeat unit for each polypeptide in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) methanol
v) methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MQ water. 20 μL of the prepared solution was drop-cast on a gold-coated AT-cut quartz crystal sensor (coating area ≈ 1.13 cm2). The change in frequency and dissipation was determined for the polymer-coated sensor in Ar, followed by exposure to 0.5 M LiCl in GBL. The films were allowed to equilibrate for 16 h in 0.5 M LiCl in GBL and the swollen thickness was taken from the last two minutes of data. The change in frequency for each step was recorded and converted to thickness using the Sauerbrey equation.37 The thickness swelling ratio was calculated as hswollen/hdry. The above protocol was repeated for each viologen polymer on new QCM-D sensors.
MQ water. 20 μL of the prepared solution was drop-cast on a gold-coated AT-cut quartz crystal sensor (coating area ≈ 1.13 cm2). The change in frequency and dissipation was determined for the polymer-coated sensor in Ar, followed by exposure to 0.5 M LiCl in GBL. The films were allowed to equilibrate for 16 h in 0.5 M LiCl in GBL and the swollen thickness was taken from the last two minutes of data. The change in frequency for each step was recorded and converted to thickness using the Sauerbrey equation.37 The thickness swelling ratio was calculated as hswollen/hdry. The above protocol was repeated for each viologen polymer on new QCM-D sensors.
Experimental determination of rate constants
Thin films of each viologen polypeptide were prepared by dissolving 8 mM of repeat unit for each polypeptide in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (v
1 (v![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) v) methanol
v) methanol![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) MQ water, drop-casting 80 μL of the prepared solution onto ITO glass (coating area ≈ 1.3 cm2), and allowing to dry at ambient conditions for 24 h, followed by drying under vacuum at r.t. for 24 h. After drying, the mass of each film was measured to determine the mass loading and the thickness was determined using profilometry (KLA Alpha-Step D-500). Finally, the fabricated electrodes were utilized in a three-electrode cell (coated ITO glass working electrode with lithium metal reference and counter electrodes) with 10 mL of 0.5 M LiCl in GBL as the electrolyte. All electrochemical measurements were performed using a potentiostat (Solartron Electrochemical Interface 1287). Chronoamperometry (CA) was performed in two steps (1) from 3 V to 2.2 V vs. Li/Li+ and (2) from 2.2 V to 1.6 V vs. Li/Li+ to determine the properties for both redox couples separately and cyclic voltammetry (CV) was performed from 3.2 V to 1.5 V vs. Li/Li+ at 10, 25, 50, and 100 mV s−1.
MQ water, drop-casting 80 μL of the prepared solution onto ITO glass (coating area ≈ 1.3 cm2), and allowing to dry at ambient conditions for 24 h, followed by drying under vacuum at r.t. for 24 h. After drying, the mass of each film was measured to determine the mass loading and the thickness was determined using profilometry (KLA Alpha-Step D-500). Finally, the fabricated electrodes were utilized in a three-electrode cell (coated ITO glass working electrode with lithium metal reference and counter electrodes) with 10 mL of 0.5 M LiCl in GBL as the electrolyte. All electrochemical measurements were performed using a potentiostat (Solartron Electrochemical Interface 1287). Chronoamperometry (CA) was performed in two steps (1) from 3 V to 2.2 V vs. Li/Li+ and (2) from 2.2 V to 1.6 V vs. Li/Li+ to determine the properties for both redox couples separately and cyclic voltammetry (CV) was performed from 3.2 V to 1.5 V vs. Li/Li+ at 10, 25, 50, and 100 mV s−1.
The CA data were further analyzed to estimate the apparent diffusion coefficient (Dap) by fitting using the Cottrell equation (eqn (2)) assuming semi-infinite diffusion:10
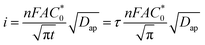 | (2) |
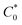 is the total concentration of redox sites (or repeat units in mol cm−3). Following the method of Paulse et al., the slope was determined from the line tangent to the CA data and the origin (0,0).38 If Dap ≥ Dphys, the rate constant for electron self-exchange, kex was found using the Dahms–Ruff equation (eqn (3)):
is the total concentration of redox sites (or repeat units in mol cm−3). Following the method of Paulse et al., the slope was determined from the line tangent to the CA data and the origin (0,0).38 If Dap ≥ Dphys, the rate constant for electron self-exchange, kex was found using the Dahms–Ruff equation (eqn (3)):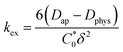 | (3) |
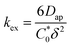 | (4) |
From the peak separation of the CV data at 10 mV s−1, the heterogeneous rate constant, k0, was calculated using the simplified method of Nicholson, eqn (5). The simplified form assumed the diffusion coefficient of the oxidized and reduced species are equal to Dap:
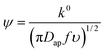 | (5) |
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 585C mol−1 e−1), R is the gas constant (or 8.3124 J mol−1 K−1) and T is the temperature (in K).
585C mol−1 e−1), R is the gas constant (or 8.3124 J mol−1 K−1) and T is the temperature (in K).
Evaluation of the capacity performance
The fabricated films were also used as working electrodes in a half cell with a lithium metal reference and filter paper soaked in 0.5 M LiCl in GBL as the separator and electrolyte, respectively. Galvanostatic charge–discharge (GCD) was performed on the half cells at different C-rates (1C is the current required to completely charge the battery in 1 h). GCD was performed for 5 cycles at 0.2, 0.4, 0.6, 0.8, 1.0, and 1.2C followed by 10 cycles at 0.2C.Molecular dynamics simulations
Atomistic MD simulations were performed using LAMMPS software package using OPLS-2005 force field extracted by the FFLD Server toolkit from Schrodinger utilities.39,40 A real space cutoff distance of 10 Å was used for non-bonded interactions including truncated Lennard-Jones potential and coulombic interactions. Long-range coulombic interactions were treated by using the particle–particle particle–mesh solver with 10−4 accuracy. Initial configurations of an oligomer (up to 26 monomers), 7600 GBL molecules as the solvent, and the corresponding number of chloride counterions for each state of charge within a 100 Å per side cubic box were packed using Packmol package.41 The LAMMPS input files were generated using Moltemplate tool.42 At the beginning of the simulation, energy minimization was performed to relax the system. The atomic velocities were initialized with Gaussian-distributed velocity associated with 300 K. After initialization, the system was maintained at 300 K for 50 ps under NVT ensemble followed by 50 ps simulation under NPT ensemble as pre-equilibration steps. Subsequently, the system was heated up linearly to 1000 K for 0.5 ns, maintained at 1000 K for 0.5 ns, and cooled down linearly from 1000 K to 300 K for 2 ns to search for a lower energy configuration under NVT ensemble throughout the process. The temperature was kept at 300 K and pressure at 1 bar under NPT ensemble for 2.5 ns as the production run. A Nosé–Hoover barostat or thermostat was applied to control the pressure or temperature of the system. The timestep was set to 0.5 fs initially using a standard velocity-Verlet integrator during the pre-equilibration steps and then set to 1.0 fs during the initial heating of the system. Each type of oligomer was simulated five times under randomized initial conditions. During the production run, the physical diffusion coefficient of viologen groups relative to the backbone (Dphys) were approximated by the regression slope of mean squared displacement of viologen groups relative to the center of mass of the whole oligomer divided by six. For the simulations in the solvated state (7600 GBL molecules and a single polypeptide oligomer) the repeat unit concentration (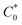 ) was ca. 44.9 mM, whereas the in the solvated state (with 1
) was ca. 44.9 mM, whereas the in the solvated state (with 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 atom ratio of GBL to six polypeptide oligomers),
1 atom ratio of GBL to six polypeptide oligomers), 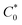 was ca. 3.85. M. The diffusion coefficients of the redox groups for the two different redox processes (MV2+/MV˙+ and MV˙+/MV0) were estimated by taking the average values of diffusion coefficients found at each state, Table S1.†
was ca. 3.85. M. The diffusion coefficients of the redox groups for the two different redox processes (MV2+/MV˙+ and MV˙+/MV0) were estimated by taking the average values of diffusion coefficients found at each state, Table S1.†
Electronic coupling and reorganization energy calculations
The geometry of methyl viologen was optimized at B3LYP/Def2-SV(P) level of theory with Gaussian 16 (revision B.01).43 To estimate the electronic coupling between these states of charge, the obtained geometry was further stacked as a dimer at a fixed plane-to-plane distance (height) at 3.5 Å then displaced from 0 to 7 Å along the long axis (displacement). The displacement was also fixed at 0 and 1 Å separately then shifted from 3 to 7 Å along the height. Dimer snapshots were extracted from MD trajectories after equilibration with the nitrogen atom linking with the carbon linker capped with a methyl group. Electronic coupling calculations were evaluated upon these dimer structures using ALMO (MSDFT2)44 implemented in Q-Chem 5.3 at PBE0/6-31+G(d) level of theory.45 This method was shown to be robust on electronic coupling calculations across different functional, and we conducted additional tests with the B3LYP and ωB97X-D functionals using same basis sets.Reorganization energy calculations were conducted using Gaussian 16 at the LC-ωHPBE/Def2-SV(P) level of theory. The calculation of the reorganization energy is one of the most sensitive parameters in modeling the kinetics of these systems, since the quantity is part of an exponential term for electron hopping rate calculation. Thus, we choose LC-ωHPBE which includes range-separated and dispersion-corrected method to capture the subtle changes that occur in the different charge states of the viologen molecules. A generic solvent was chosen with self-defined static and optical dielectric constants (41.78 and square of refractive index, 1.437 respectively) selected to correspond to the experimental results of GBL for the polarizable continuum model. The reorganization energy, λ can be expressed as the sum of inner and outer reorganization energy, λin and λout separately. With Nelsen's four-point method, λin can be estimated as following eqn (6):46
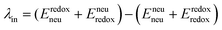 | (6) |
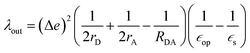 | (7) |
Results and discussion
Synthesis and chemical characterization of viologen polypeptides and control viologen polymer
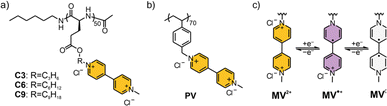
The three viologen polypeptides were synthesized through the post-polymerization modification of iodoalkyl-containing polypeptide precursors having C3, C6 or C9 alkyl chain lengths. The spacing between the polypeptide backbone and the viologen redox-active group was determined by this incorporation of alkyl chains of varying lengths within the precursors (Fig. 2a) to systematically study side chain effects. In addition to these polypeptides, poly(vinylbenzyl methyl viologen) (PV) was synthesized as a control (Fig. 2b) using post-polymerization modification of a chloro-containing poly(vinylbenzyl chloride) (PVBC) precursor. PV was selected as the control because it bears a hydrocarbon (non-peptide) backbone and because it has been extensively studied in the literature.35,49–51 By this design, the effect of having a peptide and non-peptide backbone can be compared.ATR-FTIR spectroscopy, NMR spectroscopy and elemental analysis were used to confirm the chemical structures during the synthetic steps for the studied polymers (Fig. S1–S14 and Table S1†). The secondary structure of the viologen polymers was confirmed by ATR-FTIR and CD spectroscopies. Absorbance values around 1650 cm−1 (amide I) and 1547 cm−1 (amide II) in the FTIR spectrum (Fig. S15†), along with bands at 208 nm and 222 nm in the CD spectrum (Fig. S16†), suggested α-helical conformations for C6 and C9 polypeptides. In contrast, PV and C3 did not exhibit helical structures, as evident by ATR-FTIR or CD spectroscopies in either organic or aqueous solutions.52,53 From 1H-NMR spectroscopy measurements and calculations, the molar mass for the precursor (prior to viologen installation) of C3 was 10.4 kDa, C6 was 12.4 kDa,16 C9 was 14.6 kDa, and PV was 9.8 kDa. From SEC, the number average molar mass (Mn) of the precursors were 10.6 kDa, 15.6 kDa,16 12.4 kDa, and 11.0 kDa for C3, C6, C9, and PV, respectively (Fig. S17†). The dispersities (Đ) for the three polypeptides were ca. 1.1, whereas Đ of PV was 1.25. All the viologen-functionalized polymers did not exhibit glass transitions or crystallization phenomena within the studied temperature range (Fig. S18†). From DLS, the hydrodynamic radii, rh, were determined to be 75 ± 3 nm, 51 ± 2 nm, 61 ± 3 nm, and 14 ± 1 nm for PV, C3, C6, and C9, respectively (Fig. S19†).
These relatively large rh values with low molar masses, suggest that each polymer sample formed aggregates in the aqueous solutions used for DLS measurements. Given that the peptides each have the same degree of polymerization, it can be inferred that both C3 and C6 formed multimolecular aggregates of greater numbers of chains than did the C9 analog. Finally, the swelling ratio of each polymer film in 0.5 M LiCl in γ-butyrolactone (GBL, the electrolyte used for electrochemical tests) was quantified using quartz crystal microbalance with dissipation monitoring (QCM-D), Fig. S20–S22.† The swelling ratios were 1.80, 1.22, 1.21, and 1.25 for PV, C3, C6, and C9, respectively (Table S2†). Additionally, no mass loss was observed for any of the polymers during the swelling period, suggesting that PV exhibited the greatest extent of swelling but no dissolution.
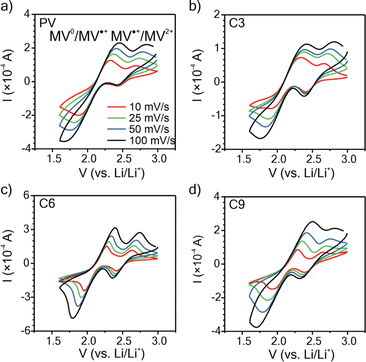
To understand how the side chain length affects the nature of the polypeptides' redox response, cyclic voltammetry (CV) was conducted using thin films on ITO glass (mass loadings: 0.25 to 0.40 mg cm−2 and thicknesses: 200 to 275 nm), Fig. 3. For the CVs obtained at 10 mV s−1, the three polypeptides exhibited two redox couples at similar potentials (E1/2 = 2.12 and 2.54 V vs. Li/Li+), consistent with that of PV and previous literature.35
For C3 and C6, the MV2+/MV˙+ redox couple was more reversible with a peak separation (ΔEp) of ca. 0.25 V as compared to 0.42 V ca. for the MV˙+/MV0 redox couple. C9 exhibited the same ΔEp of 0.32 V for both redox couples. PV exhibited a ΔEp consistent with C3 and C6. These results generally follow past literature for PV, for which MV˙+/MV0 is less reversible than MV2+/MV˙+.54 All polymers exhibited diffusion-limited redox reactions, as indicated by the linear fit of peak current vs. square-root of scan rate (Fig. S23†).
Experimental determination of diffusion within the viologen-based polymer thin films
To elucidate the apparent diffusion coefficient (Dap) for the polymer films, Cottrell plots from chronoamperometry (CA) were examined for oxidation and reduction and decoupled for MV2+/MV˙+ and MV˙+/MV0, Fig. 4, S24 and S25.† In general, PV and all three polypeptides exhibited linear CA responses with similar slopes for the reduction step of MV2+/MV˙+ and the oxidation step of MV0/MV˙+ (Fig. 4a–c and S25a†), which is consistent with previous literature13,14 and is indicative of similar rates of electron transfer. In contrast, the slopes for the reduction step of MV˙+/MV0 differed and followed the trend of C6 < C3 < C9 ≈ PV, which would suggest PV or C9 would exhibit the highest electron transfer rates.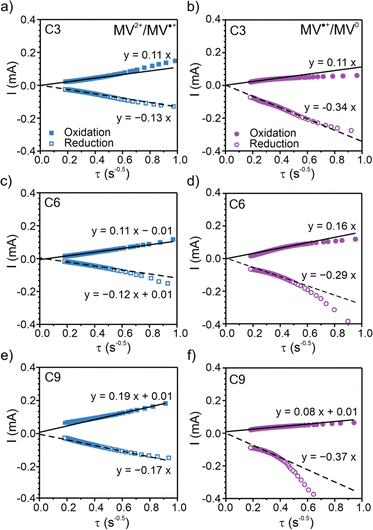 | ||
| Fig. 4 Chronoamperometry (CA) Cottrell plots for the two redox couples of the three polypeptides. (a), (c), and (e) CA response for the MV2+/MV˙+ redox couple. (b), (d), and (f) CA response for the MV˙+/MV0 redox couple. Viologen polypeptides coated on ITO glass were used as the working electrodes in a three-electrode beaker cell configuration. The supporting electrolyte was 0.5 M LiCl in GBL. Lithium metal was used as counter and reference electrodes. The Cottrell plots for PV are found in Fig. S25.† | ||
The slope of the tangent lines from the Cottrell plots were used to estimate the apparent diffusion coefficient (Dap) using eqn (2). The 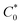 value of each polymer repeat unit was determined to be 2.03 M for PV, 2.92 M for C3, 2.65 M for C6, and 2.42 M for C9, assuming a polymer film density of 1.2 g cm−3. Despite changing the alkyl spacer length, the site-to-site distance (δ) of the pendant viologen groups in all three polypeptides remained similar at 4 Å (estimated using MD simulations), which is consistent with previous reports for PV.13,14 The Dap values were similar for all the polymers investigated and on the order of 10−13 cm2 s−1 (Fig. S26†), which is smaller by ca. 7 orders of magnitude than previous solution state reports (10−6–10−7 cm2 s−1).55–57 The low diffusion coefficients are hypothesized to be due to the polymer chains being more immobilized in the thin film state than in solution.
value of each polymer repeat unit was determined to be 2.03 M for PV, 2.92 M for C3, 2.65 M for C6, and 2.42 M for C9, assuming a polymer film density of 1.2 g cm−3. Despite changing the alkyl spacer length, the site-to-site distance (δ) of the pendant viologen groups in all three polypeptides remained similar at 4 Å (estimated using MD simulations), which is consistent with previous reports for PV.13,14 The Dap values were similar for all the polymers investigated and on the order of 10−13 cm2 s−1 (Fig. S26†), which is smaller by ca. 7 orders of magnitude than previous solution state reports (10−6–10−7 cm2 s−1).55–57 The low diffusion coefficients are hypothesized to be due to the polymer chains being more immobilized in the thin film state than in solution.
To evaluate the mechanism of electron transfer, the physical diffusion coefficient of the system must be compared to Dap. Dap is the sum of the physical and electron diffusion coefficients. Two different methods were used to approximate physical diffusion of the viologen-based polymers within the thin films. The first method determined the solution-state diffusion coefficient of the polymer using DLS (DDLS) and the second used MD simulations to obtain the physical diffusion of the viologen pendant groups (Dphys). DLS is one experimental method to measure the diffusion coefficient of a polymer chain, but it does not directly measure the diffusion of the redox-active pendant group, yet past literature assumes their equivalency.10 Therefore, MD trajectories were analyzed to provide a computational method to determine the redox-active group diffusion coefficient.
Initial MD simulations identified that the behavior of polypeptide oligomers converged at approximately 20 repeat units. Therefore, to minimize computational costs without sacrificing accuracy, oligomers with 26 repeat units were simulated (instead of the 50 repeat units studied experimentally). With these criteria, the diffusion coefficients of the redox-active methyl viologen groups (Dphys) were extracted from the trajectories of MD simulations of the oligomers in solvated states, taking GBL as the solvent. Table 1 shows the diffusion coefficients (Dphys) of the redox groups for the two different redox processes (MV2+/MV˙+ and MV˙+/MV0) calculated using MD simulations. For comparison, the DLS-measured rh of the polypeptides in the MV2+ form and eqn (1) were used to experimentally estimate the diffusion coefficient of the polymer in solution (DDLS).
| D DLS | D phys | |||
|---|---|---|---|---|
| MV2+ | MV˙+ | MV0 | ||
| PV | 0.83 ± 0.10 | N/A | N/A | N/A |
| C3 | 1.2 ± 0.25 | 2.2 ± 0.9 | 3.0 ± 0.9 | 11.9 ± 3.1 |
| C6 | 1.0 ± 0.12 | 1.3 ± 0.6 | 8.9 ± 3.0 | 11.1 ± 2.7 |
| C9 | 4.6 ± 0.74 | 4.0 ± 1.8 | 9.2 ± 3.3 | 11.9 ± 3.5 |
The obtained DDLS and Dphys values were on the order of 10−7 cm2 s−1 (Table 1), consistent with prior Dap values for solution state viologen molecules.55–57 Notably, both approximations are solution-state, but the electrochemical testing conditions are solid-state, which may result in overestimates of DDLS and Dphys. Previous studies on charged polymers and protein hydrogels suggest that the solution state diffusion coefficient is approximately 10 orders of magnitude larger than thin film diffusion (ca. 10−12 to 10−19 cm2 s−1).58,59 Using this approximation, the diffusion of the viologen polypeptides would be ca. 10−17 cm2 s−1. This value was smaller than the Dap (10−13 cm2 s−1) suggesting Laviron–Andrieux–Savéant (LAS) theory is the appropriate mechanism of electron transport in the viologen polypeptides.28
Experimental determination of rate constants kex and k0
To elucidate how the side chain lengths affect the rate constants of electron transfer of the polypeptides, thin films were investigated experimentally using CA and CV. Specifically, Dap from CA was used to calculate the rate constant for electron self-exchange (kex) and the peak separation from CV was used to calculate the heterogeneous rate constant (k0) using the method of Nicholson.Using eqn (4), the homogeneous electron transfer rate constant kex was determined and the values are summarized in Table S3† and Fig. 5. For all the polymers studied (independent of linker group), kex for the redox couple MV˙+/MV0 was greater than that for the redox couple of MV˙+/MV2+, except for C9 which exhibited a higher kex for oxidation of MV˙+/MV2+versus MV0/MV˙+. This trend was also observed by Dalton et al. and Hatozaki et al. for an electrolyte-swollen viologen film, where kex for MV˙+/MV0 was larger than MV2+/MV˙+.13,60,61 The greatest variability in kex for the polymers was for oxidation of MV0/MV˙+, where PV exhibited the largest value (1.9 × 103 M−1 s−1) and C9 the smallest (1.5 × 102 M−1 s−1). The larger kex value for PV could be due to the increased mobility of the polymer's random coil backbone (compared to the stiffer polypeptide backbones) leading to enhanced dimerization and a higher rate of electron transfer. Further discussion of trends found in the kex and k0 data can be found in the ESI (Fig. S27†).
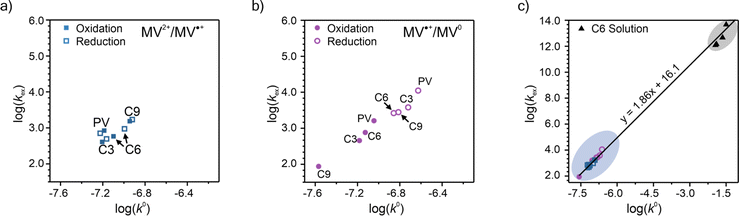 | ||
| Fig. 5 Summary of the log(kex) and log(k0) for PV, C3, C6, and C9. The results are presented as separate experimental values of oxidation and reduction for the (a) MV2+/MV˙+ and (b) MV˙+/MV0 redox couples. (c) Plot showing all the log(kex) vs. log(k0) for experimental data for both redox couples. Panels (a) and (b) show the enlarged region containing the CV/CA-determined rate constants for the viologen polypeptides studied in this work. In panel (c), the data points in the blue circle are from polymer thin-films and the data points in the black circle are from solution state values for a 0.2 mM solution of C6 dissolved in 0.5 M NaCl in H2O (raw CA and CV data can be found in Fig. S33†). | ||
One additional consideration for kex and the mechanism of electron transfer in the viologen polypeptides is the possibility of electron tunneling through the helical backbone of C6 or C9. According to LAS theory, kex should be equal to the activation-limited rate constant (kact) determined from Marcus–Hush theory (eqn (S2), Fig. S28 and 29).† However, if electron tunneling occurs it would manifest in an enhanced experimentally determined kex comparable to kact. Here, kact values were estimated using the electronic coupling (HAB) and reorganization energy (λ) determined from DFT calculations, which are described in detail in the ESI.†kact was ca. 109 M−1 s−1, which is significantly larger than the experimentally determined kex values for C6 and C9 (the helical polypeptides) and previously studied TEMPO-based monomer value (ca. 108 M−1 s−1).10 This finding suggests that there is no significant electron tunneling in the viologen polypeptide thin films, which is consistent with previous results for alanine and aminoisobutyric acid α-helical polypeptides with 48 repeat units (ca. 1.4 × 10−13 M−1 s−1).19
Finally, the previously discussed ΔEp values from CV at 10 mV s−1 were used to determine the heterogeneous rate constant (k0) following eqn (5). The calculated k0 values are summarized in Fig. 5a and b and are classified by redox couple, with the values for MV˙+/MV0 being slightly smaller than MV2+/MV˙+. The k0 values are plotted along with the kex values, for which combined values lying in the upper right quadrant indicate faster overall kinetics. For the MV2+/MV˙+ redox couple in Fig. 5a, no strong trend was observed among the polymers tested. For the MV˙+/MV0 redox couple in Fig. 5b, PV demonstrated faster kinetics. Further discussion of trends found in the kex and k0 data can be found in the ESI.†
Given the determined kex and k0 values, the electron transport mechanism was further confirmed through evaluation of the slope of the relationship between log(kex) and log(k0) in Fig. 5c. Remarkably, the plot resulted in a linear trend even for polymers of different linker lengths, including the control, which suggests that these viologens transfer charge by a similar mechanism. The slope was determined to be 1.85 and was compared to the slopes from Marcus–Hush theory and the diffusion cooperative model. First, the relationship from Marcus et al. is presented in eqn (8), similar to the relation found in LAS theory:47
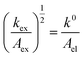 | (8) |
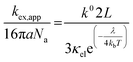 | (9) |
When reorganized, the linear relationship is log(kex,app) = log(k0) + log(b), where b = 2L16πaNa/3κelexp(−λ/4kbT). For the diffusion cooperative model, the expected slope from the log(kex) vs. log(k0) is 1. Given the slope analysis of 1.85, we conclude that the studied viologen polymers do not follow the diffusion cooperative model. Instead, the slope of 1.85 is closer to that of Marcus–Hush theory with diffusion limitations, which supports transport via LAS theory (Fig. 5).
Impact of transfer kinetics on electrode performance
An important consideration for the future design of RAPs is the relationship between electron transfer rates and the charge–discharge performance. To determine the capacity of the viologen polypeptides as thin films, galvanostatic charge–discharge (GCD) was utilized at a variety of C-rates in a half cell with lithium metal, where 1C is the current required to charge the battery in 1 hour. The theoretical capacities for the studied polymers were 149.2 mA h g−1 for PV, 130.3 mA h g−1 for C3, 118.3 mA h g−1 for C6, and 108.0 mA h g−1 for C9. For the half cells, all the polymers studied exhibited two peaks in the CV at 2.2–2.5 V and 1.7–2.1 V vs. Li/Li+ (Fig. S30†), which was similar to those observed in the three-electrode beaker cells (Fig. 3). In addition to CV, two characteristic plateaus at 2.15 and 2.55 V vs. Li/Li+ were observed in the GCD curves at 0.2C associated with the two redox couples (Fig. S31†).Fig. 6a summarizes the discharge capacity at varying C-rates for the viologen polypeptides and control viologen polymer. All the polymers exhibited capacities significantly lower than theoretical (e.g., C6 exhibited the maximum at ca. 40% of theoretical), due to the lack of conductive additives and insulating backbones. These additives were not added to the thin film electrodes so as to isolate the response of the polymer alone. Additionally, all the polymers exhibited capacity fade and low coulombic efficiencies, likely due to dissolution of the polymer into the electrolyte (Fig. S32†) during cycling. For all the polymers, as the C-rate increased there was a decrease in capacity and the two plateaus of the galvanostatic charge–discharge curves (Fig. S31†) became less pronounced.
At 0.2C, C6 exhibited the highest capacity of 1.28 × 10−2 mA h cm−2, and PV exhibited the lowest (0.45 × 10−2 mA h cm−2). At C-rates smaller than 1C, C6 showed the best performance followed by C9, C3, and PV. It is surprising that C6 should show the best capacity, especially because its kinetics were slower than that of PV. However, capacity can also be influenced by other factors, such as swelling and ion diffusion. For example, we have shown previously that some swelling of the electrode is needed, but too much swelling can cut off interchain electron transfer pathways.62,63 Here PV, which exhibited the worst capacity at 1C, swelled the most.
The respective contributions of the MV˙+/MV0 and MV2+/MV˙+ redox couples were considered by identifying the inflection point in the second derivative of the charge–discharge curves (Fig. 6b, c and S31†). In discharge (reduction), MV˙+/MV0+ contributes almost entirely to the observed discharge capacity for all the polymers. However, in charge (oxidation), MV˙+/MV0+ contributes to only about half of the observed charge capacity for C-rates less than 1C for all polymers; above 1C, C9 and PV exhibited decreased contributions from MV˙+/MV0+, whereas for C3 and C6 the contribution remains approximately 50% (Fig. 6c). These observed trends in capacity contribution for MV˙+/MV0+ mirror similar trends to those observed for kex. Specifically, kex for reduction of MV˙+/MV0 > reduction of MV2+/MV˙+, meaning in reduction the contribution of MV˙+/MV0 is much higher than MV2+/MV˙. However, upon charging kex for oxidation of MV˙+/MV2+ is only slightly larger than oxidation of MV0/MV˙+, so the two redox couples contributed equally to the charge capacity.
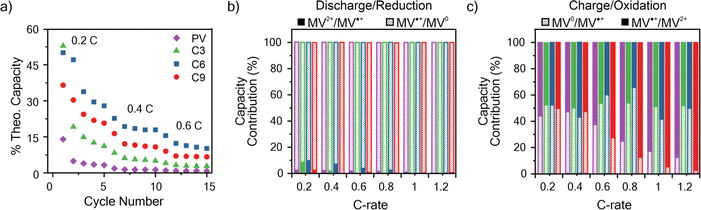 | ||
| Fig. 6 (a) Discharge capacity summary for the polymers studied at varying C-rates. (b) The percent of total discharge (reduction) capacity from the MV2+/MV˙+ and MV˙+/MV0 redox couples at varying C-rates. (c) The percent of total charge (oxidation) capacity from the MV0/MV˙+ and MV˙+/MV2+ redox couples at varying C-rates. The data is taken from the first galvanostatic charge–discharge cycle at each C-rate in Fig. S31.† The colors corresponding to each polymer in panel (a) are applicable to panels (b) and (c). The working electrodes were tested in a half cell against lithium metal. The working electrode was polymer thin film on ITO-coated glass and 0.5 M LiCl in GBL on filter paper as the supporting electrolyte and separator, respectively. | ||
Conclusions
The successful synthesis of viologen-containing polypeptides with varying linker lengths between the redox-active viologens and the polypeptide backbone was demonstrated and confirmed using a variety of characterization methods. Only the longer alkyl spacer lengths of C6 and C9 allowed for the polypeptide backbone to adopt an alpha-helical conformation. The polymers were cast into thin films to study the electron transfer kinetics using cyclic voltammetry (CV) and chronoamperometry (CA). From CV studies of C3, C6, and PV, it was found that MV˙+/MV0 was less reversible than MV2+/MV˙+, whereas for C9 the two redox couples exhibited the same reversibility. Additional investigation using Cottrell analysis of the CA data led to determination of Dap and kex. kex followed the pattern of reduction of MV˙+/MV0 > reduction of MV2+/MV˙+ and oxidation of MV0/MV˙+ > oxidation of MV˙+/MV2+, except of C9 which exhibited oxidation of MV˙+/MV2+ > oxidation of MV0/MV˙+. The largest difference in kex for the studied polymers was for oxidation of MV0/MV˙+, where PV exhibited the highest kex and C9 exhibited the smallest. Upon analysis of the linear relationship between log(kex) and log(k0), we conclude redox mechanism follows Marcus–Hush theory of electron transfer with diffusion limitations, supporting electron transport by LAS. Finally, galvanostatic-charge discharge of lithium metal half cells was used to evaluate the capacity performance. C6 showed highest capacity at C-rates less than 1C.However, additional studies are needed to confirm structure–property relationships for anodic RAPs. In varying the length of the linker group, we accessed both coil (PV, C3) and helix (C6, C9) conformations, but neither conformation appears to have strong trends in affecting the kinetics or capacities. It is possibly a product of using the viologen moiety, which can exhibit dimerization, stiffening the polymer through the redox units instead of the backbone. Further, swelling may influence capacity by influencing intermolecular electron transfer. Although swelling is needed for improving the access of ions into the electrode, too much swelling (as with PV) can lead to poor capacity. Future work should consider utilizing several different redox-active moieties on helical backbones to further resolve backbone effects. Also, swelling should be closely monitored. Last, composite electrodes with conductive additives will be needed to create practical organic battery electrodes with higher thicknesses. Besides these future works, the polypeptide RAPs remain interesting due to their on-command degradation and bio-inspired structure.16
Data availability
The data supporting this article have been included in the main text and as part of the ESI.†Author contributions
A. D. E., T. P. N., J. L. L., and K. L. W. developed the study. T. P. N. and S.-G. L. synthesized and structurally characterized the viologen polypeptides. A. D. E., S.-G. L., and K.-H. M. K. synthesized and structurally characterized the control viologen polymers. A. D. E. performed the electrochemical characterization of the materials. A. D. E. and S.-G. L. conducted thermal characterization. C.-H. L. and D. P. T. conducted all DFT calculations and MD simulations. The manuscript was written by A. D. E., with help from S.-G. L., C.-H. L., T. P. N., K.-H. M. K., D. P. T, J. L. L. and K. L. W.Conflicts of interest
There are no conflicts to declare.Acknowledgements
A. D. E., C.-H. L., J. L. L and D. P. T acknowledge support by the National Science Foundation under Grant No. 2119672. S.-G. L., T. N., K.-H. M. K. and K. L. W. acknowledge support by the National Science Foundation under Grant No. DMR-1905818 and the Welch Foundation through the W. T. Doherty-Welch Chair in Chemistry (A-0001). A. D. E. acknowledges support by the National Science Foundation Graduate Research Fellowship under Grant No. DGE:1746932. The molecular dynamics and electronic structure simulation work was supported by grant NSF-DMR-2119672 funded by the National Science Foundation (C.-H. L. and D. P. T.). J. L. L. acknowledges support from the Welch Foundation (A-2070). The software packages and initial simulation protocol developments were supported by the Robert A. Welch Foundation, Grant No. A-2049-20230405. Portions of this research were conducted with the advanced computing resources provided by Texas A&M High Performance Research Computing. Use of the Texas A&M University Laboratory for Synthetic-Biologic Interactions (RRID: SCR_022287) is acknowledged for characterization of polymer samples.References
- S. Muench, A. Wild, C. Friebe, B. Häupler, T. Janoschka and U. S. Schubert, Chem. Rev., 2016, 116, 9438–9484 CrossRef CAS PubMed.
- U. S. Schubert, C. Friebe and A. Lex-Balducci, ChemSusChem, 2019, 12(18), 4093–4115 CrossRef PubMed.
- C. N. Gannett, B. M. Peterson, L. Shen, J. Seok, B. P. Fors and H. D. Abruña, ChemSusChem, 2020, 13, 2428–2435 CrossRef CAS PubMed.
- J. Kim, J. H. Kim and K. Ariga, Joule, 2017, 1, 739–768 CrossRef CAS.
- N. Casado, G. Hernández, H. Sardon and D. Mecerreyes, Prog. Polym. Sci., 2016, 52, 107–135 CrossRef CAS.
- R. Noriega, J. Rivnay, K. Vandewal, F. P. V. Koch, N. Stingelin, P. Smith, M. F. Toney and A. Salleo, Nat. Mater., 2013, 12, 1038–1044 CrossRef CAS PubMed.
- A. Salleo, R. J. Kline, D. M. DeLongchamp and M. L. Chabinyc, Adv. Mater., 2010, 22, 3812–3838 CrossRef CAS PubMed.
- K. Hernández-Burgos, Z. J. Barton and J. Rodríguez-López, Chem. Mater., 2017, 29, 8918–8931 CrossRef.
- N. Casado and D. Mecerreyes, in Redox Polymers for Energy and Nanomedicine, The Royal Society of Chemistry, 2021, pp. 1–26 Search PubMed.
- K. Sato, R. Ichinoi, R. Mizukami, T. Serikawa, Y. Sasaki, J. Lutkenhaus, H. Nishide and K. Oyaizu, J. Am. Chem. Soc., 2018, 140, 1049–1056 CrossRef CAS PubMed.
- C. Karlsson, T. Suga and H. Nishide, ACS Appl. Mater. Interfaces, 2017, 9, 10692–10698 CrossRef CAS PubMed.
- P. Rohland, E. Schröter, O. Nolte, G. R. Newkome, M. D. Hager and U. S. Schubert, Prog. Polym. Sci., 2022, 125, 101474 CrossRef CAS.
- E. F. Dalton, N. A. Surridge, J. C. Jernigan, K. O. Wilbourn, J. S. Facci and R. W. Murray, Chem. Phys., 1990, 141, 143–157 CrossRef CAS.
- M. Burgess, E. Chénard, K. Hernández-Burgos, G. Nagarjuna, R. S. Assary, J. Hui, J. S. Moore and J. Rodríguez-López, Chem. Mater., 2016, 28, 7362–7374 CrossRef CAS.
- Z. Liang, T. P. Nguyen, N. Harsha Attanayake, A. D. Easley, J. L. Lutkenhaus, K. L. Wooley and S. A. Odom, Mater. Adv., 2022, 3, 6558–6565 RSC.
- T. P. Nguyen, A. D. Easley, N. Kang, S. Khan, S.-M. Lim, Y. H. Rezenom, S. Wang, D. K. Tran, J. Fan, R. A. Letteri, X. He, L. Su, C.-H. Yu, J. L. Lutkenhaus and K. L. Wooley, Nature, 2021, 593, 61–66 CrossRef CAS PubMed.
- A. Akhoury, L. Bromberg and T. A. Hatton, J. Phys. Chem. B, 2013, 117, 333–342 CrossRef CAS PubMed.
- G. L. Whiting, H. J. Snaith, S. Khodabakhsh, J. W. Andreasen, D. W. Breiby, M. M. Nielsen, N. C. Greenham, R. H. Friend and W. T. S. Huck, Nano Lett., 2006, 6, 573–578 CrossRef CAS PubMed.
- Y. Arikuma, H. Nakayama, T. Morita and S. Kimura, Angew. Chem., Int. Ed., 2010, 49, 1800–1804 CrossRef CAS PubMed.
- J. Deng, C. Zhou and N. Song, Macromolecules, 2009, 42, 6865–6872 CrossRef CAS.
- I. Ruff and V. J. Friedrich, J. Phys. Chem., 1971, 75, 3297–3302 CrossRef CAS.
- H. Dahms, J. Phys. Chem., 1968, 72, 362–364 CrossRef CAS.
- C. P. Andrieux and J. M. Savéant, J. Electroanal. Chem. Interfacial Electrochem., 1980, 111, 377–381 CrossRef CAS.
- E. Laviron, J. Electroanal. Chem. Interfacial Electrochem., 1980, 112, 1–9 CrossRef CAS.
- T.-Y. Kim, Y. Wang, A. L. Raithel and T. W. Hamann, ACS Energy Lett., 2020, 5, 583–588 CrossRef CAS.
- M. Burgess, K. Hernández-Burgos, J. K. Schuh, J. Davila, E. C. Montoto, R. H. Ewoldt and J. Rodríguez-López, J. Am. Chem. Soc., 2018, 140, 2093–2104 CrossRef CAS PubMed.
- N. Bodappa, Y.-C. Fu, P. Broekmann, J. Furrer, K. Zick, S. Vesztergom, H. Tahara and T. Sagara, Electrochim. Acta, 2019, 320, 134559 CrossRef CAS.
- K. Oyaizu, T. Kawamoto, T. Suga and H. Nishide, Macromolecules, 2010, 43, 10382–10389 CrossRef CAS.
- H. Bu, A. M. English and S. R. Mikkelsen, J. Phys. Chem. B, 1997, 101, 9593–9599 CrossRef CAS.
- K. Oyaizu, Y. Ando, H. Konishi and H. Nishide, J. Am. Chem. Soc., 2008, 130, 14459–14461 CrossRef CAS PubMed.
- G. S. Mohammad-Pour, K. O. Hatfield, D. C. Fairchild, K. Hernandez-Burgos, J. Rodríguez-López and F. J. Uribe-Romo, J. Am. Chem. Soc., 2019, 141, 19978–19982 CrossRef CAS PubMed.
- K. Hatakeyama-Sato, T. Nagano, S. Noguchi, Y. Sugai, J. Du, H. Nishide and K. Oyaizu, ACS Appl. Polym. Mater., 2019, 1, 188–196 CrossRef CAS.
- S. D. Place and P. Kavanagh, Electrochim. Acta, 2021, 392, 139044 CrossRef CAS.
- K. Hatakeyama-Sato, H. Wakamatsu, S. Matsumoto, K. Sadakuni, K. Matsuoka, T. Nagatsuka and K. Oyaizu, Macromol. Rapid Commun., 2021, 42, 2000607 CrossRef CAS PubMed.
- G. Nagarjuna, J. Hui, K. J. Cheng, T. Lichtenstein, M. Shen, J. S. Moore and J. Rodríguez-López, J. Am. Chem. Soc., 2014, 136, 16309–16316 CrossRef CAS PubMed.
- J. Moraes, K. Ohno, G. Gody, T. Maschmeyer and S. Perrier, Beilstein J. Org. Chem., 2013, 9, 1226–1234 CrossRef CAS PubMed.
- A. D. Easley, T. Ma, C. I. Eneh, J. Yun, R. M. Thakur and J. L. Lutkenhaus, J. Polym. Sci., 2022, 60, 1090–1107 CrossRef CAS.
- C. D. Paulse and P. G. Pickup, J. Phys. Chem., 1988, 92, 7002–7006 CrossRef CAS.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in ’t Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171 CrossRef CAS.
- J. L. Banks, H. S. Beard, Y. Cao, A. E. Cho, W. Damm, R. Farid, A. K. Felts, T. A. Halgren, D. T. Mainz, J. R. Maple, R. Murphy, D. M. Philipp, M. P. Repasky, L. Y. Zhang, B. J. Berne, R. A. Friesner, E. Gallicchio and R. M. Levy, J. Comput. Chem., 2005, 26, 1752–1780 CrossRef CAS PubMed.
- L. Martínez, R. Andrade, E. G. Birgin and J. M. Martínez, J. Comput. Chem., 2009, 30, 2157–2164 CrossRef PubMed.
- A. I. Jewett, D. Stelter, J. Lambert, S. M. Saladi, O. M. Roscioni, M. Ricci, L. Autin, M. Maritan, S. M. Bashusqeh, T. Keyes, R. T. Dame, J.-E. Shea, G. J. Jensen and D. S. Goodsell, J. Mol. Biol., 2021, 433, 166841 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery Jr, J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev. C.01, 2016 Search PubMed.
- Y. Mao, A. Montoya-Castillo and T. E. Markland, J. Chem. Phys., 2019, 151, 164114 CrossRef PubMed.
- Y. Shao, Z. Gan, E. Epifanovsky, A. T. B. Gilbert, M. Wormit, J. Kussmann, A. W. Lange, A. Behn, J. Deng, X. Feng, D. Ghosh, M. Goldey, P. R. Horn, L. D. Jacobson, I. Kaliman, R. Z. Khaliullin, T. Kuś, A. Landau, J. Liu, E. I. Proynov, Y. M. Rhee, R. M. Richard, M. A. Rohrdanz, R. P. Steele, E. J. Sundstrom, H. L. Woodcock III, P. M. Zimmerman, D. Zuev, B. Albrecht, E. Alguire, B. Austin, G. J. O. Beran, Y. A. Bernard, E. Berquist, K. Brandhorst, K. B. Bravaya, S. T. Brown, D. Casanova, C.-M. Chang, Y. Chen, S. H. Chien, K. D. Closser, D. L. Crittenden, M. Diedenhofen, R. A. DiStasio Jr, H. Do, A. D. Dutoi, R. G. Edgar, S. Fatehi, L. Fusti-Molnar, A. Ghysels, A. Golubeva-Zadorozhnaya, J. Gomes, M. W. D. Hanson-Heine, P. H. P. Harbach, A. W. Hauser, E. G. Hohenstein, Z. C. Holden, T.-C. Jagau, H. Ji, B. Kaduk, K. Khistyaev, J. Kim, J. Kim, R. A. King, P. Klunzinger, D. Kosenkov, T. Kowalczyk, C. M. Krauter, K. U. Lao, A. D. Laurent, K. V. Lawler, S. V. Levchenko, C. Y. Lin, F. Liu, E. Livshits, R. C. Lochan, A. Luenser, P. Manohar, S. F. Manzer, S.-P. Mao, N. Mardirossian, A. V. Marenich, S. A. Maurer, N. J. Mayhall, E. Neuscamman, C. M. Oana, R. Olivares-Amaya, D. P. O'Neill, J. A. Parkhill, T. M. Perrine, R. Peverati, A. Prociuk, D. R. Rehn, E. Rosta, N. J. Russ, S. M. Sharada, S. Sharma, D. W. Small, A. Sodt, T. Stein, D. Stück, Y.-C. Su, A. J. W. Thom, T. Tsuchimochi, V. Vanovschi, L. Vogt, O. Vydrov, T. Wang, M. A. Watson, J. Wenzel, A. White, C. F. Williams, J. Yang, S. Yeganeh, S. R. Yost, Z.-Q. You, I. Y. Zhang, X. Zhang, Y. Zhao, B. R. Brooks, G. K. L. Chan, D. M. Chipman, C. J. Cramer, W. A. Goddard III, M. S. Gordon, W. J. Hehre, A. Klamt, H. F. Schaefer III, M. W. Schmidt, C. D. Sherrill, D. G. Truhlar, A. Warshel, X. Xu, A. Aspuru-Guzik, R. Baer, A. T. Bell, N. A. Besley, J.-D. Chai, A. Dreuw, B. D. Dunietz, T. R. Furlani, S. R. Gwaltney, C.-P. Hsu, Y. Jung, J. Kong, D. S. Lambrecht, W. Liang, C. Ochsenfeld, V. A. Rassolov, L. V. Slipchenko, J. E. Subotnik, T. Van Voorhis, J. M. Herbert, A. I. Krylov, P. M. W. Gill and M. Head-Gordon, Mol. Phys., 2015, 113, 184–215 CrossRef CAS.
- S. F. Nelsen, S. C. Blackstock and Y. Kim, J. Am. Chem. Soc., 1987, 109, 677–682 CrossRef CAS.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus, Rev. Mod. Phys., 1993, 65, 599–610 CrossRef CAS.
- T. Janoschka, S. Morgenstern, H. Hiller, C. Friebe, K. Wolkersdörfer, B. Häupler, M. D. Hager and U. S. Schubert, Polym. Chem., 2015, 6, 7801–7811 RSC.
- N. Oyama, T. Ohsaka, H. Yamamoto and M. Kaneko, J. Phys. Chem., 1986, 90, 3850–3856 CrossRef CAS.
- T. Ohsaka, H. Yamamoto and N. Oyama, J. Phys. Chem., 1987, 91, 3775–3779 CrossRef CAS.
- H. Lu, J. Wang, Y. Bai, J. W. Lang, S. Liu, Y. Lin and J. Cheng, Nat. Commun., 2011, 2, 206 CrossRef PubMed.
- Y. Chen, T. Xue, C. Chen, S. Jang, P. V. Braun, J. Cheng and C. M. Evans, Nat. Mater., 2024, 1–8 Search PubMed.
- Y. Zhang, X. Jin, W. Zhang, C. Gu, X. Liu and Y.-M. Zhang, Dyes Pigm., 2023, 209, 110902 CrossRef CAS.
- B. Hu and T. L. Liu, J. Energy Chem., 2018, 27, 1326–1332 CrossRef.
- Y. Liu, Y. Li, P. Zuo, Q. Chen, G. Tang, P. Sun, Z. Yang and T. Xu, ChemSusChem, 2020, 13, 2245–2249 CrossRef CAS PubMed.
- X.-L. Lv, P. Sullivan, H.-C. Fu, X. Hu, H. Liu, S. Jin, W. Li and D. Feng, ACS Energy Lett., 2022, 7, 2428–2434 CrossRef CAS.
- S. Manoj Lalwani, C. I. Eneh and J. L. Lutkenhaus, Phys. Chem. Chem. Phys., 2020, 22, 24157–24177 RSC.
- S. Tang, M. Wang and B. D. Olsen, J. Am. Chem. Soc., 2015, 137, 3946–3957 CrossRef CAS PubMed.
- T. J. Lewis, H. S. White and M. S. Wrighton, J. Am. Chem. Soc., 1984, 106, 6947–6952 CrossRef CAS.
- O. Hatozaki, T. Ohsaka and N. Oyama, J. Phys. Chem., 1992, 96, 10492–10497 CrossRef CAS.
- T. Ma, A. D. Easley, S. Wang, P. Flouda and J. L. Lutkenhaus, Cell Rep. Phys. Sci., 2021, 2, 100414 CrossRef CAS.
- T. Ma, C.-H. Li, R. M. Thakur, D. P. Tabor and J. L. Lutkenhaus, Nat. Mater., 2023, 22, 495–502 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ta06766e |
| This journal is © The Royal Society of Chemistry 2024 |