High-strength fibrous sensors with an enhanced aggregate state for biomechanical monitoring of the Achilles tendon†
Ying
Guo
a,
Ting
Yan
a,
Han
Gao
b,
Luyi
Sun
b,
Shuanglei
Wei
a,
Jun
Chen
 b,
Yanhong
Wei
c,
Guoyin
Chen
a,
Kai
Hou
b,
Yanhong
Wei
c,
Guoyin
Chen
a,
Kai
Hou
 *ac and
Meifang
Zhu
*ac and
Meifang
Zhu
 a
a
aState Key Laboratory for Modification of Chemical Fibers and Polymer Materials, College of Materials Science and Engineering, Donghua University, 2999 North Renmin Road, Shanghai 201620, China. E-mail: houkai711@dhu.edu.cn
bDepartment of Sports Medicine, Huashan Hospital, Sports Medicine Institute of Fudan University, Fudan University, 12 Middle Wulumuqi Road, Shanghai 200040, China
cJiangsu Gem Advanced Fiber Materials Research Institute Co., Ltd, 12A, Zilang Sci&TechPark, 60 Chongzhou Avenue, Chongchuan District, Nantong 226000, China
First published on 23rd September 2024
Abstract
Continuous monitoring of biomechanical signals generated from the injured Achilles tendon is essential for the deep understanding of the recovery or rehabilitation process, thus decreasing the risk of secondary injuries. With tissue-like components and adjustable properties, hydrogel-based biomechanical sensors are considered promising materials for human motion detection. However, existing hydrogels are characterized by inferior mechanical properties with strength and modulus typically lower than 1 MPa, as well as poor stability under physiological conditions, which hampers their applications in implantable devices. Moreover, acquiring the stress signal from collected electrical signals remains challenging. Herein, based on the regulation of polymer aggregation, a high-strength fibrous sensor composed of polyvinyl alcohol (PVA) and reduced graphene oxide (rGO) for in vivo monitoring is prepared through a two-step procedure, including freeze–thaw and freeze–soak. Benefiting from the synergy of crystallization, Hofmeister effect and nanocomposite, the hydrogel fibers feature high tensile strength (8.34 ± 0.66 MPa) and elastic modulus (1.15 ± 0.10 MPa). Meanwhile, the removal of salt ions during fabrication improves the water content (69.18 ± 1.47%) and anti-swelling performance of such fibers and minimizes side effects after implantation. It is demonstrated that the fibrous sensor could record the relative resistance changes upon stretching with ideal sensitivity (GF = 1.57) and convert them into bearing stress through formula derivation and calculations. In vitro and in vivo assays further confirm its feasibility for real-time monitoring of joint motion, providing important references for medical diagnosis and treatment.
1. Introduction
The Achilles tendon links the triceps surae muscle to calcaneus, playing an important biological function in lower limb activities.1,2 When exposed to massive and repetitive stress, such tendons are prone to injury or even rupture. Owing to the hypocellular and hypovascular nature, mature tendons exhibit limited self-healing ability, so surgical treatment is often needed.3 Even after treatment, the recovery time is quite long, often accompanied by the risk of secondary injury. During the process, physical examination and imaging techniques are the most common methods for clinical evaluation. The former mainly relies on the subjective experience of medics while the latter requires complicated equipment and highly trained technicians, both failing in real-time monitoring.4,5 Moreover, these indirect measurement methods demonstrate controversial accuracy due to the interference of out-of-plane tissue motion.6 Therefore, sensors that can continuously monitor biomechanical signals in vivo are desirable. After implantation at the damaged site, the bearing load and deformation of the tendon under different circumstances can be obtained, helpful for medics to establish assessment models.To monitor the biomechanical signals more precisely, implantable sensors need to have similar compositions and properties to the Achilles tendon. The native tissue is assembled from highly aligned collagen fibrils, imparting it with superior tensile strength (54 ± 20 MPa) and modulus (212 ± 109 MPa) under small strains.7 Besides, the water content of the tendon is reported to be near 70%.8 Considering the operability and biosafety, water-containing fibers with comparable mechanical properties are ideal candidates for the fabrication of implantable sensors. Among various materials, hydrogels, cross-linked polymer networks with abundant water, have a tissue-like environment and adjustable properties. Benefiting from the development of formation technology, hydrogels have been processed into one-dimensional fibers in recent years,9,10 which makes them possible to be coupled with the tendon or artificial grafts. Additionally, conductive fillers can be incorporated directly into the precursor solution, obtaining hydrogels with enhanced conductivity and sensing performance after gelation.11–14 Such unique characteristics lay the foundation for in vivo mechanical sensing. Given the safety issue of ionic conductive hydrogels caused by ion diffusion, electronic conductive hydrogels are more suitable for practical applications.15 However, most research studies focus on exploring the correlation between generated electrical signals and strain. How to further obtain the bearing stress needs to be solved.
Furthermore, conventional hydrogels usually exhibit low strength (<1 MPa) and modulus (<0.1 MPa), resulting in a mechanical mismatch with the tendon and conductive fillers, which would affect the accuracy and sensitivity of the prepared sensors.16–19 In terms of long-term stability, the inevitable swelling of hydrogels under physiological conditions would cause a sharp decline in their mechanical and electrical properties. The above phenomena can be ascribed to the intrinsic hydrophilicity and low crosslink density, which facilitate the movement of polymer chains.13,20 In view of this situation, researchers have proposed various methods focusing on the design of chemical composition, such as the incorporation of nanofillers, synergy of multiple crosslinks and construction of double networks.21–23 In addition to these strategies, the free volume can also be tuned by the internal organization of hydrogels.24 Therefore, we anticipate that the introduction of an aggregate structure formed by the polymer network itself would restrain the chain motion and realize the coordinated optimization of anti-swelling and mechanical properties, thus ensuring the sensing performance under physiological conditions.
Herein, a high-strength fibrous sensor is developed for continuous monitoring of biomechanical signals in the Achilles tendon. In particular, electronic conductive PVA composite hydrogel fibers are fabricated through a facile two-step strategy, which is freeze–thawed and freeze–soaked. To deeply understand the interaction mechanism between ions and PVA chains, the microstructure and critical properties of hydrogel fibers treated with different types and concentrations of anions are investigated and compared. Because of the enhanced aggregate state of PVA by the salting-out phenomenon in the Hofmeister effect, the conflict between the mechanical properties and the water content of hydrogels is resolved in such materials. Then, graphene oxide (GO) nanofillers are introduced and in situ reduced by a green reducing agent to construct conductive channels. The resulting composite fibers present ideal sensitivity and repeatability in the range of 0–30% strain, together with environmental stability and biocompatibility. Particularly, the bearing stress can be derived from relative resistance changes of implantable sensors in real time. Such sensors are also successfully sutured on the artificial ankle joint and the Achilles tendon of the rabbit foot for in vitro and in vivo demonstrations, which would provide a novel evaluation method for tendon repair and rehabilitation.
2. Results and discussion
2.1. Preparation of high-strength fibrous sensors
Conventional hydrogel sensors mainly reveal the relationship between strain and relative resistance changes. However, excessive loading is a critical incentive for tendon injury.25,26 Hence, the real-time monitoring of stress conditions has profound implications for the assessment of injury recovery. As a common tendon for soleus and gastrocnemius muscles, the Achilles tendon possesses distinguished strength, while its strain is constrained within 20% by muscles and bones.27 To ensure monitoring accuracy during the postoperative rehabilitation process, the hydrogel fibers need to present excellent mechanical strength and high sensitivity at small strain. The fabrication process of PVA-based hydrogel fibers is described in Fig. 1. The viscous solution containing PVA and GO was first injected into the tube. After one freeze–thaw cycle, microcrystalline domains of PVA chains generated, serving as crosslinking points of the hydrogel network. Therefore, pre-gels with a relatively dense network were obtained, which could avoid stress concentrations under external loading. Besides, such pre-gels were free from chemical cross-linkers, providing them with high purity and biosafety. The next frozen pre-gels were soaked in the mixed solution of sodium citrate (Na3Cit) and L-ascorbic acid (VC). Considering the similar molecular weight of these two solutes, they would diffuse into the hydrogel network simultaneously. During this process, most oxygen-containing functional groups on GO sheets were in situ reduced by VC. The resulting rGO could provide electronic conductivity, allowing for in vivo strain sensing. Besides, Cit3− could alter the aggregation of PVA polymer chains, effectively improving the mechanical properties of hydrogel fibers. Finally, given that high concentration of salts would be detrimental to human tissues, the corresponding hydrogel fibers were soaked in DI water to remove the salt ions inside.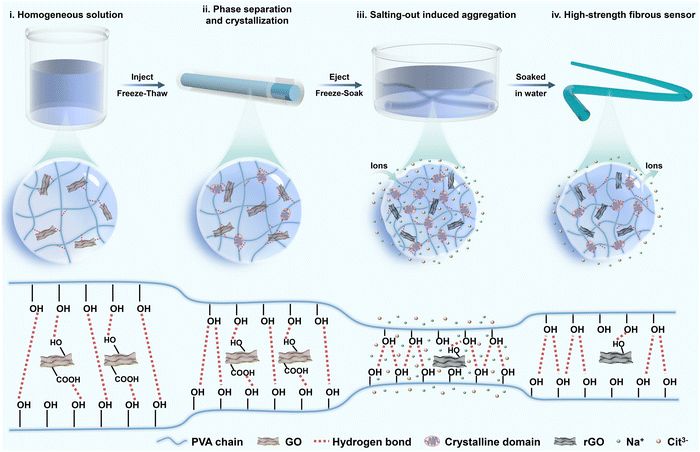 | ||
| Fig. 1 Design concept. A schematic illustration of the fabrication of the high-strength PVA-based fibrous sensor. | ||
2.2. Mechanical properties and structure of PVA hydrogel fibers
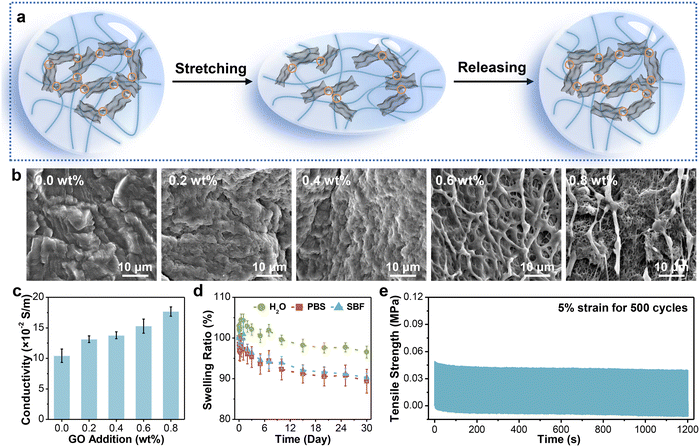
According to Hofmeister series, the effect of cations is less prominent than that of anions,28 so various sodium salts are selected to regulate the performance of hydrogel fibers. Fig. 2a (left column) shows the photographs of the corresponding hydrogel fibers. It can be seen that all samples showed a certain degree of decrease/increase in length after immersion in salt solution. Their diameter changed synchronously in accordance with SEM images in Fig. S1 (ESI†). Moreover, the transmittance of hydrogel fibers gradually turned from translucent to opaque. The difference in their appearance might be due to the changed aggregate state of polymer chains and crystalline structures. Subsequently, the tensile stress–strain curves of hydrogel fibers tuned by serious anions are illustrated in Fig. 2b. The tensile strength and Young’s modulus of such hydrogel fibers are further statistically obtained in Fig. 2c. Among them, the breaking strength and strain of the pure PVA hydrogel fiber were 0.83 ± 0.12 MPa and 232.29 ± 41.34%, respectively. The hydrogel fiber immersed in 1.0 M Na3Cit exhibited the highest breaking strength (3.70 ± 0.10 MPa) and elongation (385.58 ± 12.05%), which were 4.46 and 1.66 times of the pure PVA hydrogel fibers. However, hydrogel fibers of sodium chloride (NaCl) exhibited a tensile strength of 0.72 ± 0.04 MPa, even weaker than pure PVA hydrogel fibers. The Young’s modulus of hydrogel fibers with different sodium salts also followed the sequence: Cit3− > SO42− > CO32− > S2O32− > PVA > Cl−, consistent with the Hofmeister effect.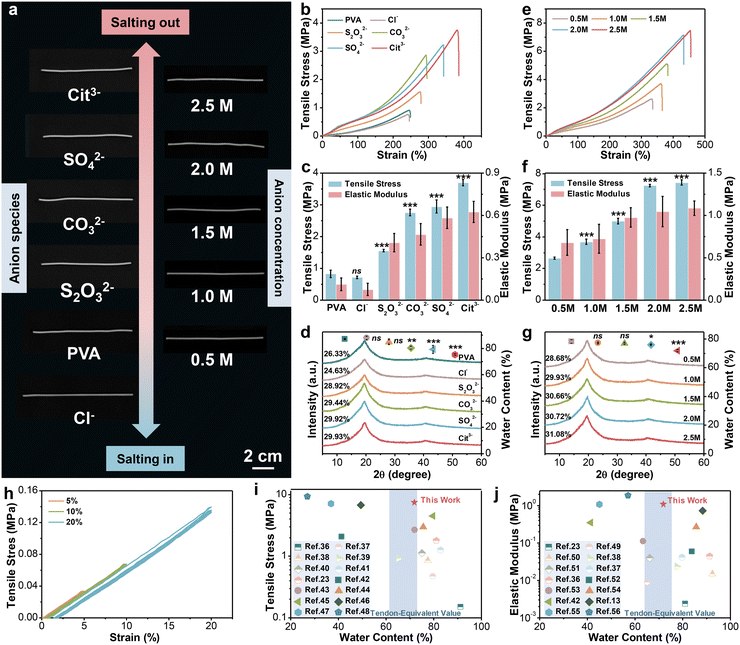 | ||
| Fig. 2 The mechanical properties and structure of PVA hydrogel fibers. (a) Digital images of hydrogel fibers tuned by 1.0 M sodium salts and Na3Cit with different concentrations. (b)–(d) Stress–strain curves, corresponding tensile strength and elastic modulus (n = 5), water content (n = 3) and XRD patterns of hydrogel fibers soaked with 1.0 M sodium salts. Student's t test was performed to compare the control group (PVA) to other groups. ns: not significant, **: p < 0.01, ***: p < 0.001. (e)–(g) Stress–strain curves, corresponding tensile strength and elastic modulus (n = 5), water content (n = 3) and XRD patterns of hydrogel fibers soaked in Na3Cit with different concentrations. Student’s t test was performed to compare the control group (0.5 M) to other groups. ns: not significant, *: p < 0.05, ***: p < 0.001. (h) Loading–unloading stress–strain curves of PVA-2.5 Na3Cit hydrogel fibers under small strains. (i) and (j) Ashby plots of the mechanical properties of PVA-2.5 Na3Cit and other hydrogel-based strain sensors reported in the references. Comparison of tensile strength versus water content (i). Comparison of the elastic modulus versus water content (j). The detailed data involved are summarized in Tables S3 and S4 (ESI†). | ||
In order to explore the underlying mechanism of changes in mechanical properties, the structures of series hydrogel fibers were analyzed by X-ray diffraction (XRD). From the XRD patterns in Fig. 2d, all the hydrogel fiber samples showed a sharp diffraction peak at 2θ = 19.7°, which corresponds to the (10![[1 with combining macron]](https://www.rsc.org/images/entities/char_0031_0304.gif) ) reflective plane of semi-crystalline PVA.29 At the same time, a small peak at 2θ = 40.8° belongs to the (102) reflective plane of the crystalline domains of PVA.30 The two characteristic peaks were still present after soaking into salt solution, but the intensity varied depending on the type of anions. The crystallinity was further calculated. The hydrogel fibers soaked in 1.0 M NaCl solution had the lowest crystallinity of 24.6%. The crystallinity of other hydrogel fibers made in sodium salts was higher than that of the pure PVA hydrogel fiber (28.7%) in the following order: Cit3− > SO42− > CO32− > S2O32−.
) reflective plane of semi-crystalline PVA.29 At the same time, a small peak at 2θ = 40.8° belongs to the (102) reflective plane of the crystalline domains of PVA.30 The two characteristic peaks were still present after soaking into salt solution, but the intensity varied depending on the type of anions. The crystallinity was further calculated. The hydrogel fibers soaked in 1.0 M NaCl solution had the lowest crystallinity of 24.6%. The crystallinity of other hydrogel fibers made in sodium salts was higher than that of the pure PVA hydrogel fiber (28.7%) in the following order: Cit3− > SO42− > CO32− > S2O32−.
The above results confirmed that the introduction of anions indeed affected the crystallization of hydrogels, which could be categorized into “kosmotropes” (e.g. S2O32−, CO32−, SO42−, and Cit3−) and “chaotropes” (e.g. Cl−). Kosmotropes with strong hydration ability can polarize water molecules that form hydrogen bonds with the hydroxyl groups on PVA chains, thus weakening the interaction between them, leading to the aggregation of PVA chains and the promotion of crystallization after phase separation.31,32 Such a phenomenon is also called “salting-out”. Nevertheless, the chaotropes prefer to bind with PVA chains directly and bring about extra charges on the molecular chains.33 The result is the dissociation of partial hydrogen bonds, as well as the decrease of the crystalline domain density, that is “salting-in” effect.34 The interaction between the PVA chains and anions also was reflected in the equilibrium water content of hydrogel fibers (Fig. 2d). The salting-out effect promoted the generation of crystalline domains and contributed to a densified crosslink network, endowing the resulting hydrogel fibers with high strength, ductility and modulus, while accompanied by a decrease in the water content. Conversely, the salting-in effect induced the partial dissolution of polymer chains. Hence, the hydrogel network became looser and provided more space for water molecules, which manifested as the deterioration of mechanical performance from a macroscopic perspective.
The morphology of hydrogel fibers is not only affected by the type of anion, but also affected by the concentration. From the photographs on the right column (Fig. 2a), few differences existed in the length of hydrogel fibers soaked in the Na3Cit solution with various concentrations. But the prepared fibers presented a skin-core structure as the Na3Cit concentration increased (Fig. S2, ESI†). This is because the strong salting-out effect induces the formation of a densified layer on the surface of fiber, hindering the diffusion of salt ions to the interior, which could also be observed in wet spinning.35 Moreover, the mechanical properties of hydrogel fibers were altered. As illustrated in Fig. 2e and f, with the increase of the Na3Cit concentration from 0.5 M to 2.5 M, the tensile strength of hydrogel fibers significantly improved from 2.65 ± 0.08 MPa to 7.44 ± 0.16 MPa. Meanwhile, the break elongation and elastic modulus also revealed an upward trend, up to 470.08 ± 9.78% and 1.09 ± 0.09 MPa for PVA-2.5 Na3Cit. Further calculations based on XRD patterns (Fig. 2g) demonstrated the positive relationship between the crystallinity and the Na3Cit concentration. With the increase of the salt concentration, the amount of water molecules polarized by Cit3− increases accordingly. Therefore, more hydrogen bonds form between the hydroxyl groups on PVA chains, which induce spontaneous aggregation and leads to higher crystallinity. This is also the reason for the outstanding mechanical properties of the PVA-2.5 Na3Cit hydrogel fiber. Additionally, the equilibrium water content of different hydrogel fibers decreased sequentially as the salt concentration increased (Fig. 2g). On the one hand, the stronger salting-out effect facilitates more intensive aggregation of polymer chains through phase separation. On the other hand, the elevated osmotic pressure expels more water molecules from the hydrogel network. The combination of these two factors results in an inverse correlation between the water content of hydrogel fibers and the Na3Cit concentration. Despite a slight decrease, the water content of PVA-2.5 Na3Cit still reached 71.93 ± 0.82%.
Since the daily activity of the tendon is in the range of 2–6% and the maximum strain is 15–20% when damaged, the consecutive loading–unloading test was conducted on PVA-2.5 Na3Cit in the same range without pause between each cycle (Fig. 2h). Such hydrogel fibers recovered to the original state after unloading without obvious hysteresis or residual strain, which confirmed its considerable elasticity at small strains. We further compared the properties of PVA-2.5 Na3Cit with other hydrogel-based strain sensors from the literature, including the water content, tensile strength and elastic modulus (Fig. 2i, j and Tables S3, S4, ESI†).13,23,36–56 The Hofmeister effect imparts such hydrogel fibers with the remarkable strength and elastic modulus, superior or comparable to most current hydrogel sensors. Especially, the water content of this material is close to that of human Achilles tendons (66.2 ± 5.5%), which would sustain internal osmotic pressure equilibrium after implantation and minimize the damage to tissues. The above-mentioned exceptional properties make PVA-2.5 Na3Cit suitable for the construction of sensors.
2.3. Performance characterization of composite hydrogel fibers
On this basis, GO sheets were incorporated into the hydrogel network and in situ reduced by VC. The working mechanism of the obtained fibrous sensor is revealed in Fig. 3a. In the initial state, the adjacent rGO layers are interconnected to each other, forming plentiful conductive pathways for electron transport. When applied to stretching at small strains, a small portion of rGO layers disconnects, resulting in partial disruption of the conductive network, which extends the electron transport distance. Therefore, the resistance of hydrogel fibers also increases. The disconnected pathways basically restore the original state after release due to the good elasticity of the hydrogel network. To determine the optimum addition of GO sheets, we characterized the internal structure and critical properties of hydrogel fibers with different GO additions.The microscopic morphology was first observed via SEM (Fig. 3b). It was worthy of note that there was no residual Na3Cit crystal on the surface of all samples, validating the removal of salt after soaking in deionized water. The surface of PVA-2.5 Na3Cit was smooth without obvious pores owing to the pore shrinkage and collapse during the freeze–drying process.57 Meanwhile, the hydrogel fibers became porous progressively with the increasing GO addition from 0.2 wt% to 0.8 wt%. During reduction, epoxy and alkoxy groups on the surface of GO are gradually removed by VC. But a small portion of oxygen-containing functional groups preserved, such as carbonyl and carboxyl groups, which would form hydrogen bonds with PVA chains.58 The strong interactions inhibit the pore collapse after lyophilization, so the hydrogel fibers with higher GO addition could maintain the original morphology.
The electrical conductivity is the premise of strain sensing, mainly depending on the GO addition here. The increase of GO addition means more overlap between rGO after in situ reduction, which would favor electron transport.59 The presence of rGO sheets in the hydrogel fiber was verified using Raman spectroscopy (Fig. S3, ESI†). Resulting from new defects and vacancies generated during the reduction process,60 the intensity ratio between D and G bands (ID/IG) increased from 0.88 for GO to 1.08 for the PVA-2.5 Na3Cit/0.8 GO fiber. Furthermore, the conductivity of hydrogel fibers was stepped up from 0.10 ± 0.01 to 0.18 ± 0.01 S/m (Fig. 3c). The introduction of nanofillers also resulted in the enhancement of mechanical properties (Fig. S4, ESI†). PVA-2.5 Na3Cit/0.8 GO presented a maximum tensile strength of 8.34 ± 0.66 MPa and a modulus of 1.15 ± 0.10 MPa. Although the water-binding ability of rGO composite hydrogel fibers decreased with the increase of crosslink density, their water contents were still around 70% (Fig. S5, ESI†).
Furthermore, owing to the hydrophilic nature of hydrogels, they tend to swell in an aqueous environment, which suffers from the dilution of polymer chains and a sharp decline in mechanical properties.61 When acted as implantable electronics, excessive swelling would also severely influence the electronic/ionic conductivity. More importantly, the volume expansion might even compress the surrounding nerves or tissues and bring about unexpected injuries.62 Consequently, the anti-swelling ability is desirable for composite hydrogel fibers developed here. The long-term swelling behavior of PVA-2.5 Na3Cit/0.8 GO was studied in three media (Fig. 3d). The weight of samples immersed in DI water increased first and then decreased, maintaining 96.54 ± 1.46% of the initial weight after 30 days. Meanwhile, the corresponding samples dehydrated more obviously in phosphate buffered solution (PBS) and simulated body fluid (SBF), obtaining equilibrium swelling ratios of 89.39 ± 2.92% and 90.31 ± 1.06%, respectively. Such a phenomenon might be caused by a high ion concentration in the solution, resulting in larger osmotic pressure and more water expelled from the hydrogel network.63 To sum up, this hydrogel fiber exhibited long-term stability in the aqueous environment, which arose from several factors. First, more crystalline domains of PVA chains formed during the freeze–soak process, making the hydrogel structure denser. Such a crystalline structure can remain stable below 75 °C.64 Besides, the hydrogel fibers have expanded in advance when immersed in DI water during preparation.
As the connective tissue between bones and muscles, the tendon possesses splendid anti-fatigue properties and can withstand deformation under thousands of cyclic loads. In this regard, a strain of 5%, close to the daily motion range of the tendon, was applied to PVA-2.5 Na3Cit/0.8 GO for multiple cycling tests. According to Fig. 3e, the maximum stress of the fiber dropped obviously in the first 50 cycles due to the dissociation of hydrogen bonds in the hydrogel network. However, the stress–time curve tended to be stable from the 51st to 500th cycle, during which the dissociation and reorganization of hydrogen bonds achieved equilibrium.65 Moreover, the maximum stress and elastic modulus retained ∼80% of the initial values after 500 cycles (Fig. S6, ESI†), demonstrating the considerable fatigue resistance of such hydrogel fibers.
2.4. Sensing performance of composite hydrogel fibers
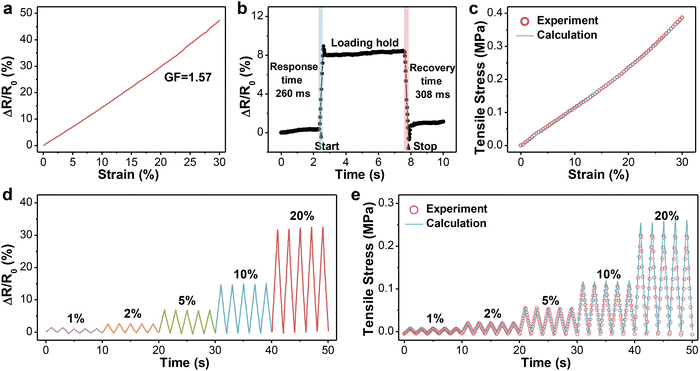
Considering the limited deformation of the human tendon, the relative resistance changes of PVA-2.5 Na3Cit/0.8 GO in the specific range were recorded and are presented in Fig. 4a. The resistance increased monotonically with the tensile strain, suggesting a strong linear relationship between them. The sensitivity of such hydrogels can be assessed quantitatively by GF, which is defined as the slope of the resistance–strain curve. The GF in the strain range of 0–30% was calculated to be 1.57 with a correlation coefficient (R2) of 0.99, which guaranteed the accuracy of signals. Then, PVA-2.5 Na3Cit/0.8 GO was subjected to cyclic stretching/releasing tests under different strains with a constant frequency. As can be seen from Fig. 4d, the maximum resistance varied regularly with the imposed strain and maintained at the same level in each five cycles, further proving the feasibility and reproducibility of hydrogel fibers for distinguishing small deformation. The response and recovery time of hydrogel fibers were determined as 260 ms and 308 ms, respectively (Fig. 4b). Combining high sensitivity, low detection limit and fast response, PVA-2.5 Na3Cit/0.8 GO has basically satisfied the prerequisites for monitoring tendon motion.According to the definition of the elastic modulus (E = σ/ε) and gauge factor (GF = (ΔR/R0)/ε) in the linear region, the relationship between the bearing stress and relative resistance changes could be derived, that is σ = (E/GF) × (ΔR/R0). Based on the equation, the monitoring accuracy of PVA-2.5 Na3Cit/0.8 GO was examined. As shown in Fig. 4c, the change in the calculated stress of the fibrous sensor upon strain overlapped the experimental values. In the cyclic testing under different strains, the calculated and experimental results also showed a high coincidence degree with a minor difference in peak values, whose ratios remained at 1.14 ± 0.15 (Fig. 4e). In this way, through the measurement of resistance in real time, the stress applied on the sensor could be conveniently obtained.
2.5. Biocompatibility and application demonstrations of the fibrous sensor
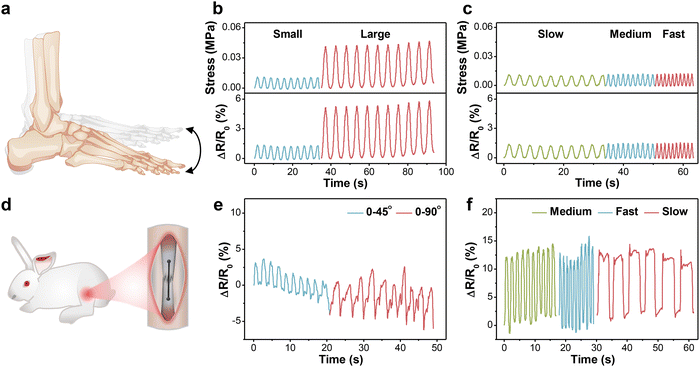
For the in vitro demonstration, a designed setup was first built using the human ankle joint model to mimic daily walking, in which the motion amplitude of the joint depended on the working stroke of reciprocating motor and the frequency was tuned by working speed (Fig. S8a, ESI†). The fibrous sensor was fixed on the joint, undergoing tension or compression with up and down motions (Fig. 5a). The generated signal was acquired and output through a multimeter. Fig. 5b and c present the relative resistance changes of the sensor under 10 cycles at different amplitudes and frequencies, respectively. As the motion amplitude enlarged, the maximum resistance rose accordingly and maintained good repeatability. Besides, the ΔR/R0 values were stable under different frequencies without an observable baseline shift, which proved that the values were independent of frequency. Based on the above method, the bearing stress of the fibrous sensor under different conditions could also be estimated.Prior to the animal experiments, the cytotoxicity of PVA-2.5 Na3Cit/0.8 GO was also estimated by phalloidin/DAPI staining and CCK-8 assay. According to the fluorescence images in Fig. S7a (ESI†), the number of MSCs increased gradually with the prolongation of incubation time. Most cells displayed a spindle-shaped morphology at first, which extended towards adjacent cells on day 3. MSCs continued to proliferate on day 5 and formed an interconnected cellular network. Therefore, the presence of such hydrogel fibers had no negative effect on cell spreading and proliferation. The CCK-8 results further corroborated the conclusion (Fig. S7b, ESI†). The OD values of two groups exhibited an upward trend during the culture period and there was no distinct difference between them.
Given the outstanding cytocompatibility, the PVA-2.5 Na3Cit/0.8 GO sensor was directly sutured onto the Achilles tendon of the New Zealand white rabbit for monitoring physiological strains (Fig. 5d and Fig. S8b, ESI†). When the rabbit foot is raised, the Achilles tendon and the fibrous sensor have no tension. the tendon and sensor are stretched as the foot remains straight, leading to an increase in resistance. Similar to the in vitro model, the output signals were stable under different angles and frequencies (Fig. 5e and f). The slight fluctuation might originate from muscular movements and artificial errors, which could be eliminated through the establishment of the quantitative model.
3. Conclusions
In summary, a high-strength hydrogel fibrous sensor is developed via a simple two-step strategy. The polymer aggregation and crystallization are regulated by the types and concentrations of anions, leading to a densified hydrogel network. The resulting hydrogel fibers present outstanding mechanical strength (8.34 ± 0.66 MPa), modulus (1.15 ± 0.10 MPa) and similar water content (69.18 ± 1.47%) with the Achilles tendon. The in situ reduction of GO after hydrogel formation improves the dispersion of nanofillers, endowing the fibers with ideal sensitivity (GF = 1.57) at small strains. Besides, the anti-swelling capacity in the aqueous environment and low cytotoxicity ensure their long-term use as an implantable sensor. The feasibility of the fibrous sensor for monitoring the biomechanical strain of the Achilles tendon is confirmed through in vitro and in vivo models. More importantly, the acquired resistance signal can be further converted into stress, approximatively reflecting the bearing load of the damaged site. Such sensors provide potential applications in real-time monitoring for Achilles tendon rehabilitation.4. Experimental section
4.1. Materials
PVA (20–99(L), 99% alcoholysis) was purchased from Anhui Wanwei Group Co., Ltd. Sodium salts (including NaCl, sodium carbonate (Na2CO3), sodium thiosulfate (Na2S2O3), sodium sulfate (Na2SO4) and Na3Cit), hydrochloric acid (HCl, 36–38%) and glutaraldehyde (GA, 25 v%) were supplied by Sinopharm Chemical Reagent Co., Ltd. GO sheets were synthesized through modified Hummers’ method reported previously.66 VC was received from Shanghai Aladdin Reagent Co., Ltd. PBS and SBF were provided by Shanghai Macklin Biochemical Co., Ltd and Beijing Solarbio Science & Technology Co., Ltd, respectively. Fetal bovine serum (FBS) and Dulbecco’s modified Eagle’s medium (DMEM) were obtained from Thermo Fisher Scientific (China) Co., Ltd. 4% Paraformaldehyde and cell counting kit-8 (CCK-8) were purchased from Yeasen Biotechnology (Shanghai) Co., Ltd. Triton X-100, 4’6-diamidino-2-phenylindole (DAPI) and TRITC-phalloidin were acquired from Wuhan Servicebio Technology Co., Ltd. All reagents were used as received without further purification. Deionized water (DI, 18.25 MΩ cm) was utilized throughout the experiment.4.2. Preparation of salting-out hydrogel fibers
A certain amount of PVA was added into DI water and stirred at 60 °C for 30 min, followed by heating at 90 °C for 2 h until completely dissolving to obtain 15.10 wt% PVA solution. The transparent solution was injected into the silicon tubes with an inner diameter of 2 mm using a syringe and placed in a refrigerator (−20 °C) for 18 h. After thawing at 25 °C for 6 h, the pre-gels with a certain shape and strength were prepared. Next, the frozen pre-gels were ejected by water pressure and soaked in the salt solution for another 6 h. The above freeze–soak step was repeated twice. The resulting hydrogel fibers were immersed in sufficient DI water at room temperature for 48 h to remove excessive salt ions. During this process, DI water was changed each day. The obtained hydrogel fibers are named PVA-X NaY, where X and Y denote the concentration and anion of the sodium salt. The composition of these samples is summarized in Table S1 (ESI†).4.3. Preparation of composite hydrogel fibers
GO and DI water with predetermined ratios were stirred for 10 min and sonicated under an ultrasonic cleaner (F-030ST, FUYANG, China) for 30 min, which were further treated with an ultrasonic homogenizer (JY92-IIN, Scientz, China) for 1 h in ice bath, forming homogeneous GO dispersion. PVA was then included and dissolved with a fixed concentration of 15.10 wt%. The preparation process of hydrogel fibers was the same as the above except that the pre-gels were soaked in the mixed solution of Na3Cit and VC to realize salting out and in situ reduction of GO. The molar concentration of Na3Cit was fixed at 2.5 M. The ratio of GO and VC was 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 5. Here, the composite hydrogel fibers are named PVA-2.5 Na3Cit/nGO, where n denotes the mass ratio of GO to PVA. The nomenclature and components of such fibers are listed in Table S2 (ESI†).
5. Here, the composite hydrogel fibers are named PVA-2.5 Na3Cit/nGO, where n denotes the mass ratio of GO to PVA. The nomenclature and components of such fibers are listed in Table S2 (ESI†).
4.4. Characterization
The morphology of hydrogel fibers was observed using an environmental scanning electron microscope (ESEM, Quanta 250, FEI, Czech Republic) with an accelerating voltage of 12.5 kV. Before the observation, the swollen samples were first quenched in liquid nitrogen, followed by freeze-drying in a lyophilizer (FD-1A-80, BiLon, China) for 36 h to completely remove the water. The fracture surfaces were sputtered with gold. XRD was performed using an X-ray diffractometer (D/max-2550VB+/PC, Rigaku, Japan) using Cu Kα radiation (λ = 1.54 Å, 40 kV, 200 mA). In particular, the obtained hydrogel fibers were immersed in a chemical crosslinking agent (including 50 mL of DI water, 0.5 mL of hydrochloric acid and 10 μL of glutaraldehyde) for 2 h to fix the amorphous phase, which could prevent crystallization in the following freeze-drying process. Afterwards, the excessive HCl and GA were washed out through sufficient DI water for another 2 h. The resulting samples were cut into pieces and transferred into the lyophilizer for 36 h. All patterns were collected with a scanning step of 0.02° in the range of 5°–60°. The crystallinity of full-dried hydrogel fibers (Xc) was calculated as follows:| Xc = Ac/(Ac + Aa) × 100% | (1) |
4.5. Mechanical testing
The stress–strain curves of hydrogel fibers were obtained through an electronic universal testing machine (UTM 2103, SUNS, China) equipped with a loading cell of 20 N at room temperature. The initial gauge distance and strain rate were set at 10 mm and 50 mm/min, respectively. The diameters of specimens were measured using a caliper before testing. The elastic modulus was defined as the slope of stress–strain curves in the initial linear range (ε = 0–30%).4.6. Water content measurement
The excess water was gently wiped from the surface of prepared hydrogel fibers and their weights were recorded. After freeze-drying for 36 h, the weights of corresponding samples under dried state were also determined. The water contents (WC) of hydrogel fibers were calculated through eqn (2):| WC = (W0 − Wdry)/W0 × 100% | (2) |
4.7. Environmental stability evaluation
The swelling behavior of hydrogel fibers was also determined by the gravimetric method. The whole experiment was performed in a low constant temperature water bath (BV200S, Yamato, Japan). The as-prepared samples were immersed in DI water, PBS and SBF at 37 °C, which were taken out and weighed at predetermined time points. The swelling ratio (SR) was calculated according to eqn (3):| SR = (Wt − W0)/W0 × 100% | (3) |
4.8. Electrical measurements
The hydrogel fibers were first cut into splines with a length of 20 mm. The resistance of such samples was measured using a multimeter (DMM6500, Keithley, USA). The corresponding conductivity (σ) was calculated from eqn (4):| σ = L/(R × S) | (4) |
The sensing performance of hydrogel fibers was investigated through the multimeter combining with a universal testing machine. The relative resistance change (ΔR/R0) was obtained from eqn (5):
| ΔR/R0 = (R − R0)/R0 × 100% | (5) |
The sensitivity of hydrogel fibers was evaluated through the gauge factor (GF), which was determined as follows:
| GF = (ΔR/R0)/ε | (6) |
4.9. In vitro demonstration of the fibrous sensor
To validate the possibility for motion monitoring, the fiber-based sensor was immobilized on the artificial ankle joint. A silicone tube was used to pull the joint model for simulating human walking, which was controlled by the reciprocating motor. In the meantime, the relative resistance changes in such a dynamic process were collected constantly through a multimeter. Besides, such a setup was equipped with a small humidifier to minimize water evaporation during the experiment.4.10. Biocompatibility of the fibrous sensor
The fiber samples were first cut into pieces and soaked in sterile water for 24 h, followed by transferring it into 75% ethanol for 2 h. After washing with PBS three times, these samples were sterilized by ultraviolet light for 30 min. Mesenchymal stem cells (MSCs) and samples were cocultured in 96-well plates. After this, DMEM was added into each well, and the group without samples was used as the control group. The plates were then incubated in a humidified atmosphere of 5% CO2 at 37 °C for 5 days. The culture medium was changed every two days. The quantitative analysis of cell proliferation was carried out using a CCK-8 regent. The culture medium of each well was replaced with 10 μL of CCK-8 solution on various durations (1, 3 and 5 days) and their absorbance at 450 nm was recorded using a microplate reader (Elx800, Bio Tek, USA).To visualize the cytoskeleton extension, the filamentous actins (F-actin) and the nucleus of MSCs were stained with TRITC-phalloidin (red) and DAPI (blue), respectively. The cells cultured for 1, 3 and 5 days were rinsed with PBS and fixed using 4% polyformaldehyde for 15 min. Afterwards, the cell membranes were ruptured by 0.1% Triton X-100 for 30 min and washed with PBS another 2 times. The cells were stained by TRITC-phalloidin and DAPI for 1 h and 10 min at 25 °C in the dark, and then observed using an inverted fluorescent microscope (DMi8, Leica, Germany).
4.11. Animal surgery and in vivo assessment
The included animal procedures in this study were approved by the Animal Care and Experiment Committee of Shanghai Fudan University (approval no. 2021JS Huashan Hospital-470). All animal housing and experiments were conducted in strict accordance with the standard of the Guide for the Care and Use of Laboratory Animal published by the Ministry of Science and Technology of the People’s Republic of China in 2006.New Zealand white rabbits (skeletally mature, weighing 2.5–3.5 kg) were chosen for in vivo assessment. After being anesthetized by pentobarbital (3 wt%, 30 mg/kg), their feet were shaved and sterilized with iodophor and 75% ethanol. During the surgery, the controlled injection of propofol through the ear vein was used for general anesthesia. The rabbit was fixed and an incision of 5 cm was made on its hind foot to expose the Achilles tendon. Then, the sterilized fibrous sensor was sutured directly along the tendon. The incision was closed in layers with both ends of the sensor placed outside, which could be connected with the multimeter. The resistance was monitored in real time and analyzed according to the protocol described above. Postoperatively, penicillin (50 KU/kg) was administered for 3 consecutive days to prevent infection.
4.12. Statistical analysis
Data with error bars were means ± standard deviation obtained by at least three replicates. The sample size was specified in the figure captions. Student’s t tests were performed using the SPSS Statistics software to examine the statistical difference between the control group and other groups. Significant differences were identified at p < 0.05. * denotes p < 0.05, ** p < 0.01, *** p < 0.001 and ns means not significant.Author contributions
Ying Guo: methodology, investigation, formal analysis, data curation, and writing – original draft. Ting Yan: investigation, data curation, and validation. Han Gao: methodology and investigation. Luyi Sun: validation. Shuanglei Wei: validation. Jun Chen: conceptualization and supervision. Yanhong Wei: funding acquisition. Guoyin Chen: writing – review and editing and visualization. Kai Hou: conceptualization, project administration, and writing – review and editing. Meifang Zhu: supervision and funding acquisition.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
The authors declare no conflicts of interest.Acknowledgements
This research is financially supported by the National Natural Science Foundation of China (No. 52173029 and 52303033), the National Key Research and Development Program of China (2021YFA1201300/2021YFA1201302), the Nantong Science and Technology Project (MS12022023 and JC22022103), and the Natural Science Foundation of Shanghai (21ZR1400500).References
- D. S. Heckman, G. S. Gluck and S. G. Parekh, Am. J. Sports Med., 2009, 37, 1223–1234 CrossRef.
- J. Zhang, W. Wang, X. Zhang, L. Yang and J. Zhang, Front. Mater., 2022, 9, 815930 CrossRef.
- T. Zhang, Y. Wu, X. Li, A. Zhang, H. Liu, M. Shi, Z. Zhang, W. Lu, Y. Guo, X. Tang, Q. Cui and Z. Li, Acta Biomater., 2023, 172, 280–296 CrossRef CAS PubMed.
- F. Niu, R. Ma, T. Zhao, H. Fan, J. Han, N. Zhu, Y. Hu, X. Meng and Z. Wang, J. Magn. Reson. Imaging, 2024, 60(4), 1243–1258 Search PubMed.
- M. Lee, Y. Lee, J. H. Choi, H. Kim, D. Jeong, K. Park, J. Kim, J. Park, W. Y. Jang, J. Seo and J. Lee, ACS Nano, 2024, 18, 12210–12224 CrossRef CAS PubMed.
- Q. Zhang, N. C. Adam, S. H. Hosseini Nasab, W. R. Taylor and C. R. Smith, Ann. Biomed. Eng., 2020, 49, 7–28 CrossRef.
- H. L. Birch, Int. J. Exp. Path., 2007, 88, 241–248 CrossRef PubMed.
- M. de Mos, B. van El, J. DeGroot, H. Jahr, H. T. M. van Schie, E. R. van Arkel, H. Tol, R. Heijboer, G. J. V. M. van Osch and J. A. N. Verhaar, Am. J. Sports Med., 2017, 35, 1549–1556 CrossRef PubMed.
- B. Zhu, D. Liu, J. Wu, C. Meng, X. Yang, Y. Wang, X. Jia, P. Jiang and X. Wang, Adv. Funct. Mater., 2024, 34, 2309795 CrossRef CAS.
- G. Chen, G. Wang, X. Tan, K. Hou, Q. Meng, P. Zhao, S. Wang, J. Zhang, Z. Zhou, T. Chen, Y. Cheng, B. S. Hsiao, E. Reichmanis and M. Zhu, Natl. Sci. Rev., 2021, 8, nwaa209 CrossRef CAS PubMed.
- Z. Li, C. Li, W. Sun, Y. Bai, Z. Li and Y. Deng, ACS Appl. Mater. Interfaces, 2023, 15, 12787–12796 CrossRef CAS.
- L. Zhao, H. Xu, L. Liu, Y. Zheng, W. Han and L. Wang, Adv. Sci., 2023, 10, 2303922 CrossRef CAS PubMed.
- Z. Sun, C. Dong, B. Chen, W. Li, H. Hu, J. Zhou, C. Li and Z. Huang, Small, 2023, 19, 2303612 CrossRef CAS.
- C. Wang, K. Hu, Y. Liu, M.-R. Zhang, Z. Wang and Z. Li, Materials, 2021, 14, 1955 CrossRef CAS.
- H. Yuk, B. Lu and X. Zhao, Chem. Soc. Rev., 2019, 48, 1642–1667 RSC.
- W. Li, L. Li, Z. Liu, S. Zheng, Q. Li and F. Yan, Adv. Mater., 2023, 35, 2301383 CrossRef CAS PubMed.
- T. Lei, J. Pan, N. Wang, Z. Xia, Q. Zhang, J. Fan, L. Tao, W. Shou and Y. Gao, Mater. Horiz., 2024, 11, 1234–1250 RSC.
- C. Wang, K. Hu, C. Zhao, Y. Zou, Y. Liu, X. Qu, D. Jiang, Z. Li, M.-R. Zhang and Z. Li, Small, 2020, 16, 1904758 CrossRef CAS PubMed.
- P. Liu, D. Yao, C. Lu, X. Gao and P. Dong, J. Mater. Sci.: Mater. Electron., 2024, 35, 97 CrossRef CAS.
- Y. Zhang, Y. Tan, J. Lao, H. Gao and J. Yu, ACS Nano, 2023, 17, 9681–9693 CrossRef CAS PubMed.
- Y. Li, D. Yang, Z. Wu, F.-L. Gao, X.-Z. Gao, H.-Y. Zhao, X. Li and Z.-Z. Yu, Nano Energy, 2023, 109, 108324 CrossRef CAS.
- Y. Xin, J. Liang, L. Ren, W. Gao, W. Qiu, Z. Li, B. Qu, A. Peng, Z. Ye, J. Fu, G. Zeng and X. He, Biomacromolecules, 2023, 24, 1287–1298 CrossRef CAS.
- D. Kong, Z. M. El-Bahy, H. Algadi, T. Li, S. M. El-Bahy, M. A. Nassan, J. Li, A. A. Faheim, A. Li, C. Xu, M. Huang, D. Cui and H. Wei, Adv. Compos. Hybrid Mater., 2022, 5, 1976–1987 CrossRef CAS.
- M. Dolmat, V. Kozlovskaya, J. F. Ankner and E. Kharlampieva, Macromolecules, 2023, 56, 8054–8068 CrossRef CAS.
- Y. Demangeot, R. Whiteley, V. Gremeaux and F. Degache, Scand. J. Med. Sci. Sports, 2023, 33, 110–126 CrossRef PubMed.
- K. G. Silbernagel, S. Hanlon and A. Sprague, J. Athl. Training, 2020, 55, 438–447 CrossRef PubMed.
- T. A. L. Wren, S. A. Yerby, G. S. Beaupré and D. R. Carter, Clin. Biomech., 2001, 16, 245–251 CrossRef CAS PubMed.
- W. Wei, Adv. Sci., 2023, 10, 2302057 CrossRef CAS.
- R. Ricciardi, F. Auriemma, C. De Rosa and F. Lauprêtre, Macromolecules, 2004, 37, 1921–1927 CrossRef CAS.
- M. Peng, G. Xiao, X. Tang and Y. Zhou, Macromolecules, 2014, 47, 8411–8419 CrossRef CAS.
- H. I. Okur, J. Hladílková, K. B. Rembert, Y. Cho, J. Heyda, J. Dzubiella, P. S. Cremer and P. Jungwirth, J. Phys. Chem. B, 2017, 121, 1997–2014 CrossRef CAS.
- W. Sun, J. Wang and M. He, Carbohydr. Polym., 2023, 303, 120446 CrossRef CAS.
- S. Wu, M. Hua, Y. Alsaid, Y. Du, Y. Ma, Y. Zhao, C.-Y. Lo, C. Wang, D. Wu, B. Yao, J. Strzalka, H. Zhou, X. Zhu and X. He, Adv. Mater., 2021, 33, 2007829 CrossRef CAS.
- R. Guo, Y. Bao, X. Zheng, W. Zhang, C. Liu, J. Chen, J. Xu, L. Wang and J. Ma, Adv. Funct. Mater., 2023, 33, 2213283 CrossRef CAS.
- C. Wang, Y. Liao, H.-Y. Yu, Y. Dong and J. Yao, Carbohydr. Polym., 2023, 319, 121175 CrossRef CAS.
- X. Zhang, B. Lang, W. Yu, L. Jia, F. Zhu, Y. Xue, X. Wu, Y. Qin, W. Chen, Y. Wang and Q. Zheng, Chem. Eng. J., 2023, 474, 145832 CrossRef CAS.
- X. Wu, Q. Yang, X. Zhang, C. Tsou, M. R. De Guzman, X. Li, L. Yuan, Y. Xia, Y. Sheng, Q. Li and C. Gao, Polymer, 2023, 273, 125887 CrossRef CAS.
- W. J. Yang, R. Zhang, X. Guo, R. Ma, Z. Liu, T. Wang and L. Wang, J. Mater. Chem. A, 2022, 10, 23649–23665 RSC.
- S. Yuan, J. Bai, S. Li, N. Ma, S. Deng, H. Zhu, T. Li and T. Zhang, Adv. Funct. Mater., 2023, 34, 2309626 CrossRef.
- Z. Zhou, C. Qian and W. Yuan, Compos. Sci. Technol., 2021, 203, 108608 CrossRef CAS.
- H. Zhang, L. Qin, Y. Chen, T. Long, R. Guan, X. Cheng, B. Chen and C. Zhou, Mater. Des., 2023, 229, 111911 CrossRef CAS.
- C. Qi, Z. Dong, Y. Huang, J. Xu and C. Lei, ACS Appl. Mater. Interfaces, 2022, 14, 30385–30397 CrossRef CAS.
- Y. Wang, L. Zhu, X. Kong, H. Lu, C. Wang, Y. Huang and M. Wu, Nanoscale, 2023, 15, 5938–5947 RSC.
- H. Cheng, W. Zhang, R. Pan, J. Yang, Y. Gong, Y. Zhuo, F. Wang, X. Yuan, Z. Gan, R. Hu, J. Ding, L. Chen, X. Zhang and X. Tian, ACS Appl. Polym. Mater., 2023, 5, 4146–4158 CrossRef CAS.
- S. Han, Q. Wu, J. Zhu, J. Zhang, A. Chen, S. Su, J. Liu, J. Huang, X. Yang and L. Guan, Mater. Horiz., 2023, 10, 1012–1019 RSC.
- A. Dutta, K. Ghosal, K. Sarkar, D. Pradhan and R. K. Das, Chem. Eng. J., 2021, 419, 129528 CrossRef CAS.
- Y. Gao, J. Peng, M. Zhou, Y. Yang, X. Wang, J. Wang, Y. Cao, W. Wang and D. Wu, J. Mater. Chem. B, 2020, 8, 11010–11020 RSC.
- H. Zhou, Z. Wang, W. Zhao, X. Tong, X. Jin, X. Zhang, Y. Yu, H. Liu, Y. Ma, S. Li and W. Chen, Chem. Eng. J., 2021, 403, 126307 CrossRef CAS.
- C. Zhu, L. Zhang, A. Zou, W. Wang, J. Zhang and A. Zhang, Chem. Eng. J., 2023, 475, 146161 CrossRef CAS.
- S. A. Kim, Y. Lee, K. Park, J. Park, S. An, J. Oh, M. Kang, Y. Lee, Y. Jo, S.-W. Cho and J. Seo, Int. J. Bioprint, 2023, 9, 765 CrossRef.
- H. Ding, X. Liang, Q. Wang, M. Wang, Z. Li and G. Sun, Carbohydr. Polym., 2020, 248, 116797 CrossRef CAS PubMed.
- Y. Wang, Y. Xie, X. Xie, D. Wu, H. Wu, X. Luo, Q. Wu, L. Zhao and J. Wu, Adv. Funct. Mater., 2023, 33, 2210224 CrossRef CAS.
- J. Cui, J. Chen, Z. Ni, W. Dong, M. Chen and D. Shi, ACS Appl. Mater. Interfaces, 2022, 14, 47148–47156 CrossRef CAS.
- L. Chen, X. Chang, J. Chen and Y. Zhu, ACS Appl. Mater. Interfaces, 2022, 14, 43833–43843 CrossRef CAS.
- C. Ma, Y. Wang, Z. Jiang, Z. Cao, H. Yu, G. Huang, Q. Wu, F. Ling, Z. Zhuang, H. Wang, J. Zheng and J. Wu, Chem. Eng. J., 2020, 399, 125697 CrossRef CAS.
- Q. Zhang, Q. Wang, G. Wang, Z. Zhang, S. Xia and G. Gao, ACS Appl. Mater. Interfaces, 2021, 13, 50411–50421 CrossRef CAS PubMed.
- Y. Zhang, L. Ye, M. Cui, B. Yang, J. Li, H. Sun and F. Yao, RSC Adv., 2015, 5, 78180–78191 RSC.
- Z. Sui, X. Zhang, Y. Lei and Y. Luo, Carbon, 2011, 49, 4314–4321 CrossRef CAS.
- R. Yin, C. Zhang, Y. Chen, Y. Wang, Q. Feng, Y. Liu, M. Yu, Y. Yuan, C.-Y. Xu, F. Liu and W. Zhao, Chem. Eng. J., 2023, 475, 145794 CrossRef CAS.
- R. Castaldo, R. Avolio, M. Cocca, M. E. Errico, M. Lavorgna, J. Šalplachta, C. Santillo and G. Gentile, Chem. Eng. J., 2022, 430, 133162 CrossRef CAS.
- M. Li, H. Lu, M. Pi, H. Zhou, Y. Wang, B. Yan, W. Cui and R. Ran, Adv. Sci., 2023, 10, 2304780 CrossRef CAS PubMed.
- X. Xia, Q. Liang, X. Sun, D. Yu, X. Huang, S. M. Mugo, W. Chen, D. Wang and Q. Zhang, Adv. Funct. Mater., 2022, 32, 2208024 CrossRef CAS.
- S. Wang, J. Li, Y. Pan, F. Liu, L. Zeng, Y. Gao and T. Lu, Soft Matter, 2022, 18, 6192–6199 RSC.
- C. Luo, A. Guo, J. Li, Z. Tang and F. Luo, ACS Appl. Mater. Interfaces, 2022, 14, 35434–35443 CrossRef CAS.
- L.-Y. Zeng, X.-C. Wang, Y. Wen, H.-M. Chen, H.-L. Ni, W.-H. Yu, Y.-F. Bai, K.-Q. Zhao and P. Hu, Carbohydr. Polym., 2023, 300, 120229 CrossRef CAS PubMed.
- S. Chen, W. Ma, Y. Cheng, Z. Weng, B. Sun, L. Wang, W. Chen, F. Li, M. Zhu and H.-M. Cheng, Nano Energy, 2015, 15, 642–653 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tb01255k |
| This journal is © The Royal Society of Chemistry 2024 |