The lattice symmetrization worked, but with a plot twist: effects of methylhydrazinium doping of MAPbI3 on phase transitions, cation dynamics and photoluminescence†
Mirosław
Mączka
 *a,
Maciej
Ptak
a,
Katarzyna
Fedoruk
*a,
Maciej
Ptak
a,
Katarzyna
Fedoruk
 b,
Dagmara
Stefańska
b,
Dagmara
Stefańska
 a,
Anna
Gągor
a,
Jan K.
Zaręba
a,
Anna
Gągor
a,
Jan K.
Zaręba
 c and
Adam
Sieradzki
c and
Adam
Sieradzki
 b
b
aW. Trzebiatowski Institute of Low Temperature and Structure Research of the Polish Academy of Sciences, Okólna 2, 50-422 Wroclaw, Poland. E-mail: M.Maczka@intibs.pl
bDepartment of Experimental Physics, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370 Wrocław, Poland
cAdvanced Materials Engineering and Modeling Group, Faculty of Chemistry, Wrocław University of Science and Technology, Wybrzeże Wyspiańskiego 27, 50-370, Wrocław, Poland
First published on 2nd January 2024
Abstract
Lattice symmetrization is a term coined for the intentional doping of methylammonium lead iodide (MAPbI3) with larger organic cations to lower the transition temperature to the cubic phase, whose stability is much preferred over the tetragonal one to avoid undesired lattice strain harmful for device operation, which could appear due to the cubic-tetragonal phase transition (PT) present near 330 K in undoped MAPbI3. The following case study of three-dimensional (3D) organic cation-alloyed perovskites of formula MA1−xMHyxPbI3 (MHy+ = methylhydrazinium; x < 0.25) unveils the complex impact of MHy+ doping on the stability of crystal phases. For low doping of x ≤ 0.115 the cubic-tetragonal PT temperature strongly decreases on doping, as expected. The MHy+-induced lattice symmetrization worked to the point that at room-temperature (RT) the cubic phase could be observed at a doping of x = 0.057, the lowest among so far used organic dopants. By contrast, the temperature of the tetragonal-orthorhombic PT increases on doping, opposite to what was observed for analogous doped MAPbI3 systems. Unexpectedly, however, beyond x > 0.2 the tendency reverses, as the temperatures of tetragonal-to-cubic PTs shift strongly to higher values. Significant changes in PT mechanism at high doping conditions are inferred from large thermal hystereses, Raman scattering data showing the presence of two unique MA+ cations in the orthorhombic phase, and dielectric spectroscopy demonstrating dipolar relaxation for low-doped systems, and its suppression for highly-doped ones. The substitution of MA+ with MHy+ leads to a weak widening of the band gap while retaining efficient emission and extended absorption, suitable for optoelectronic applications.
1. Introduction
3D lead halide perovskites with formula APbX3 (A = methylammonium (MA+), formamidinium (FA+), aziridinium (AZR+) and MHy+; X = Cl, Br, I) have become promising materials for various applications, including solar cells, light-emitting diodes, photodetectors, photodynamic therapy, nonlinear optics, and dielectric switching.1–11 In particular, MAPbI3 is the most promising material for low-cost solar cell applications with the certified power conversion efficiency reaching 25.7%.12 The excellent performance of MAPbI3 stems from its high absorption coefficient, defect tolerance, small exciton binding energy, and long-range charge transport.1–3,123D lead halide perovskite structure is composed of corner-shared PbX6 octahedra and A-site cations located in the cubo-octahedral cavities of the inorganic framework. The formation of 3D perovskite structure is usually rationalized using Goldschmidt's tolerance factor t = (rA + rX)/√2(rB + rX), where rA, rX and rB stand for the effective radii of the A+, X− and B2+ ions, respectively.13,14 Literature data show that the 3D perovskite structure is stable when 0.8 ≤ t ≤ 1.0,15 although some exceptions of 3D perovskites with t slightly higher than 1.0 are also known, e.g., MHyPbBr3 (t = 1.03) and MHyPbCl3 (t = 1.05).6,8 The tolerance factor of MAPbI3 is 0.912 (rMA = 217 pm,13) and this compound undergoes Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m (cubic phase I) → I4/mcm (tetragonal phase II) → Pnma (orthorhombic phase III) PTs at 327 and 162 K, respectively.16,17 Since the cubic to tetragonal PT may cause undesired strain, which is harmful to photoelectric device operation, the ‘lattice symmetrization’ strategy was proposed, which rests on extending the temperature stability range of the cubic phase by doping the organic part of MAPbI3 with large organic cations; in this way, the Goldschmidt factor t is brought closer to 1.0.18–20 Indeed, effectiveness of this strategy has been explored for a variety of cations, such as FA+ (rFA = 253 pm),21,22 dimethylammonium (DMA+, rDMA = 272 pm),20,23 ethylammonium (EA+, rEA = 274 pm),19,20,24 acetamidinium (ACE+, rACE = 277 pm),25 guanidinium (GA+, rGA = 278 pm),26,27 azetidinium (AZ+, rAZ = 250 pm)16 and imidazolium (IM+, rIM = 258 pm).28 In the case of MAPbBr3, the A-site was doped with FA+, DMA+ and EA+.29–32 The decrease of all PT temperatures was reported for MAPbI3 samples doped with DMA+, EA+, GA+ and FA+.19–24,27 In the case of AZ+, IM+ and ACE+, very small doping was possible (up to 5, 10 and 10%, respectively), which did not eventually lead to the stabilization of the cubic phase at RT.16,25,28 Interestingly, it was also shown that apart from the cubic phase stabilization, the doping with larger cations may also affect the key factors responsible for the excellent photovoltaic properties of MAPbI3, such as the charge carrier separation and lifetime, leading to the improved efficiency of solar cells.19,33 This effect can be associated with the large dipole moment of the dopant cations, local distortion and changes in the cation dynamics of the mixed systems.19,21,23,24,33 However, studies of the effect of doping with the large organic cations on the cation dynamics and structural PTs of MAPbX3 perovskites are still scarce. In general, two different behaviors were reported. Firstly, an investigation of MAPbBr3 doped with DMA+ cations revealed complete suppression of the PTs and glass phase signatures for doping larger than 10%.31 Similar suppression of the PTs was also reported for MAPbI3 doped with GA+ cations.27 Secondly, some dopant cations have led to weak suppression of the PTs up to 20% of doping level and signatures of the dipolar glass phase formation at doping levels higher than 30%. This behavior was observed for MAPbBr3 doped with FA+, and MAPbI3 doped with EA+ or FA+.21,24,29 It is worth adding that doping of MAPbI3 with 31 and 38% of EA+ led to a complete suppression of the tetragonal to orthorhombic PT and the formation of a new tetragonal phase with a different symmetry.24
m (cubic phase I) → I4/mcm (tetragonal phase II) → Pnma (orthorhombic phase III) PTs at 327 and 162 K, respectively.16,17 Since the cubic to tetragonal PT may cause undesired strain, which is harmful to photoelectric device operation, the ‘lattice symmetrization’ strategy was proposed, which rests on extending the temperature stability range of the cubic phase by doping the organic part of MAPbI3 with large organic cations; in this way, the Goldschmidt factor t is brought closer to 1.0.18–20 Indeed, effectiveness of this strategy has been explored for a variety of cations, such as FA+ (rFA = 253 pm),21,22 dimethylammonium (DMA+, rDMA = 272 pm),20,23 ethylammonium (EA+, rEA = 274 pm),19,20,24 acetamidinium (ACE+, rACE = 277 pm),25 guanidinium (GA+, rGA = 278 pm),26,27 azetidinium (AZ+, rAZ = 250 pm)16 and imidazolium (IM+, rIM = 258 pm).28 In the case of MAPbBr3, the A-site was doped with FA+, DMA+ and EA+.29–32 The decrease of all PT temperatures was reported for MAPbI3 samples doped with DMA+, EA+, GA+ and FA+.19–24,27 In the case of AZ+, IM+ and ACE+, very small doping was possible (up to 5, 10 and 10%, respectively), which did not eventually lead to the stabilization of the cubic phase at RT.16,25,28 Interestingly, it was also shown that apart from the cubic phase stabilization, the doping with larger cations may also affect the key factors responsible for the excellent photovoltaic properties of MAPbI3, such as the charge carrier separation and lifetime, leading to the improved efficiency of solar cells.19,33 This effect can be associated with the large dipole moment of the dopant cations, local distortion and changes in the cation dynamics of the mixed systems.19,21,23,24,33 However, studies of the effect of doping with the large organic cations on the cation dynamics and structural PTs of MAPbX3 perovskites are still scarce. In general, two different behaviors were reported. Firstly, an investigation of MAPbBr3 doped with DMA+ cations revealed complete suppression of the PTs and glass phase signatures for doping larger than 10%.31 Similar suppression of the PTs was also reported for MAPbI3 doped with GA+ cations.27 Secondly, some dopant cations have led to weak suppression of the PTs up to 20% of doping level and signatures of the dipolar glass phase formation at doping levels higher than 30%. This behavior was observed for MAPbBr3 doped with FA+, and MAPbI3 doped with EA+ or FA+.21,24,29 It is worth adding that doping of MAPbI3 with 31 and 38% of EA+ led to a complete suppression of the tetragonal to orthorhombic PT and the formation of a new tetragonal phase with a different symmetry.24
In this paper, we examine the effects of cation alloying of MAPbI3 with bulky MHy+ cations (rMHy = 264 pm,34), and their consequences for the stabilization of the cubic phase. MHy+ is significantly larger than MA+ and, therefore, MHy+ doping should increase t, leading to the stabilization of the cubic phase. Another equally important reason for choosing MHy+ is its documented ability to facilitate the formation of non-centrosymmetric perovskite phases.6–8,35–37 In particular, this cation plays a very unusual role in 3D MHyPbX3 (X = Cl, Br) perovskites, i.e., it leads to the strong deformation of the inorganic sublattice and appearance of spontaneous polarization at RT due to the formation of Pb–N coordination bonds and the presence of static stereo-active lone-pair electrons of the Pb2+ cation.6–8,38 Due to this unusual ability to form Pb–N coordination bonds, not observed for other previously used dopants, MHy+ is not just another organic cation that could fit the perovskite cage. We expected, therefore, that doping of MAPbI3 with MHy+ may lead to the significantly different behavior than reported for other dopants, including e.g. the emergence of polar phases. It is worth noting that the end member MHyPbI3 does not form 3D perovskite phase39 and, therefore, solubility limit and properties of MA1−xMHyxPbI3 system cannot be simply anticipated from properties of the end members, especially for the samples with large MHy+ content. Quite intriguingly, we found that the stabilization of the cubic phase is associated with the increase of the low-temperature (LT) tetragonal-to-orthorhombic PT temperature, the effect so far not reported for other organic dopants. Additionally, we observed that highly doped (x > 0.2) compositions reveal a set of unique features such as strong shifts of tetragonal-to-cubic PTs to higher values, presence of two unique MA+ cations, and modification of cation dynamics reflected in a dipolar relaxation for low-doped systems, and its suppression for highly-doped ones. We discuss origins of these unusual phenomena.
2. Experimental section
2.1. Synthesis
Single crystals of MA1−xMHyxPbI3 were grown in a similar way as recently reported for the MA1−xEAxPbI3 system.24 In this method, 4 mmol of PbI2, and stoichiometric amounts of methylamine (2 M solution in methanol, Sigma Aldrich) and methylhydrazine (98%, Sigma Aldrich) were dissolved in a mixture of propylene carbonate (PC, 99.7%, Sigma-Aldrich) and HI (57 wt% in H2O, stabilized with H3PO2, Sigma-Aldrich) under stirring on a hot plate (50 °C). The PC:HI volume ratio was 2.6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and the total amount of methylamine and methylhydrazine was 4 mmol. The clear solution was transferred into a glass vial, which was kept at 50 °C for 2–3 days. The black crystals with dimensions up to 5 mm, which grew on the bottom of the vial, were separated from the liquid and dried at RT. The methylamine to methylhydrazine ratios in the solutions were 1
1 and the total amount of methylamine and methylhydrazine was 4 mmol. The clear solution was transferred into a glass vial, which was kept at 50 °C for 2–3 days. The black crystals with dimensions up to 5 mm, which grew on the bottom of the vial, were separated from the liquid and dried at RT. The methylamine to methylhydrazine ratios in the solutions were 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 0, 9
0, 9![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 8
1, 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2, 7
2, 7![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 3, 6
3, 6![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 4, 4
4, 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 6 and 3
6 and 3![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 7.
7.
2.2. NMR spectroscopy
Quantitative determination of the organic amine composition of perovskite samples was performed with the use of 1H NMR spectroscopy. 1H NMR spectra were recorded in a liquid state on the Jeol JNM-ECZ 400S Research FT NMR spectrometer (JEOL Ltd, Tokyo, Japan) operating at 400 MHz. Samples were prepared by placing 3–5 mg of single crystals of a mixed-cation perovskites in ca. 0.7 mL of DMSO-d6, followed by warming to 50 °C and thorough sonication. Next, clear solutions were transferred to 5 mm Wilmad NMR tubes.2.3. Powder X-ray diffraction
Powder X-ray diffraction (PXRD) patterns of the ground crystals were measured in the reflection modes using an X’Pert PRO X-ray diffraction system equipped with a PIXcel ultrafast line detector and Soller slits for CuKα1 radiation (λ = 1.54056 Å).2.4. DSC measurements
Differential scanning calorimetry (DSC) was recorded on a Mettler Toledo DSC-3 calorimeter in the nitrogen at a heating/cooling rate of 5 K min−1 in the temperature range of 120–350 K. Nitrogen was used as a purging gas and the weight of the samples was 20–87 mg. Knowing the weight of the samples, the heat flow was converted to the heat capacity. The heat capacity changes associated with the PTs were calculated by subtracting from the data the baseline representing the system variation in the absence of the PTs. Entropy changes were estimated as the integral of the heat capacity changes with temperature.2.5. Single-crystal X-ray diffraction
The X-ray diffraction data from a single crystal were obtained using an Xcalibur diffractometer equipped with Mo Kα radiation source, a CCD Atlas camera, and an OxfordCryosystem cooling device. Data processing was performed using CrysAlisPro software version 1.171.38.43 (Rigaku OD, 2015).2.6. Raman spectroscopy
RT Raman spectra were measured for powdered crystals using a Bruker FT 100/S spectrometer with YAG:Nd laser excitation (λexc = 1064 nm) and 2 cm−1 spectral resolution. Temperature-dependent Raman spectra in the 1700–150 cm−1 range were measured using a Renishaw inVia Raman spectrometer equipped with a confocal DM2500 Leica optical microscope, a CCD detector, and a diode laser (λexc = 830 nm). The second experiment was performed in the 400–10 cm−1 range using an Eclipse filter. The sample was placed in a THMS600 temperature control stage and the spectral resolution was 2 cm−1.2.7. Broadband dielectric spectroscopy (BDS)
Dielectric measurements of the examined samples were conducted using a broadband dielectric Novocontrol Alpha analyzer. Measurements as a function of temperature and frequency were carried out on single crystals. A sinusoidal voltage with an amplitude of 1 V and frequency in the 1 Hz–1 MHz range was applied across the samples. The measurements were performed every 2 K in the temperature range of 130–350 K. Silver paste was applied on both parallel surfaces of all samples to ensure good electrical contact. The temperature was stabilized by means of nitrogen using the Novocontrol Quattro system.2.8. Optical absorption and photoluminescence (PL) studies
RT diffuse reflectance spectra of the powdered samples were measured using the Varian Cary 5E UV-VIS-NIR spectrophotometer. PL spectra as a function of temperature were measured with the Hamamatsu photonic multichannel analyzer PMA-12 equipped with a BT-CCD linear image sensor. A 450 nm laser diode was used as the excitation source. The temperature of the samples during emission measurements was controlled by applying Linkam THMS 600 heating/freezing stage. PL spectra were recorded with sample heating, except for the MA0.751MHy0.249PbI3 sample, for which PL was recorded in two cycles, one with the sample heating and the other on cooling. To record decay times, a femtosecond laser (Coherent Model Libra) (Coherent, Pennsylvania, USA) was used as an excitation source.3. Results and discussion
3.1. RT NMR and Raman spectroscopy
In order to determine the true content of MHy+ in the grown crystals, 1H NMR spectroscopy was employed. The spectra show that the methyl groups of MHy+ and MA+ cations give rise to the presence of a broad singlet at 2.56 ppm and a quartet at 2.33 ppm, respectively (Fig. S1, ESI†). The integration of these peaks and calculation of their ratios showed that the fraction x of the MHy+ cations in MA1−xMHyxPbI3 crystals is 0.005, 0.021, 0.057, 0.115, 0.207 and 0.249 for the samples with the nominal x in the solution of 0.1, 0.2, 0.3, 0.4, 0.6 and 0.7, i.e., the true x in the crystals is about three times lower than that in the solutions (Fig. S2, ESI†), probably due to much better solubility of MHyPbI3 compared to MAPbI3. Using the concept of tolerance factor,13,14 we calculated this factor as 0.912, 0.914, 0.917, 0.923, 0.932 and 0.936 for samples with x = 0.005, 0.021, 0.057, 0.115, 0.207 and 0.249, respectively.To further confirm the incorporation of the MHy+ cations, we measured Raman spectra. The spectra show many weak bands in the MA1−xMHyxPbI3 crystals, which become more prominent with increasing x (Fig. S3, ESI†). These bands, observed at 431, 849, 877, 1061, 1073, 1130, 1187, 1308, 1351, 1382, 1146, 1598, 2950 and 3251 cm−1, are typical for MHy+ cations, as evidenced by comparison with the Raman spectra of pure MHyPbI3 and MHyPbBr3 (Fig. S3, ESI†).
3.2. Powder X-ray diffraction
PXRD patterns of the studied samples are shown in Fig. S4 (ESI†). Former studies of MAPbI3 doped with various cations showed that the disappearance of the (211) diffraction peak near 2Θ 23.5° and the splitting of many other peaks can be used to differentiate the tetragonal and cubic phases.19,20,24,27 Fig. S4 (ESI†) shows that these features are observed for the x = 0.057 sample, indicating that less than 6% of MHy+ doping leads to the stabilization of the cubic phase I at RT. Note that this is a record-low value, which is smaller than those reported for the EA+ (8–9%),24 DMA+ (∼9%),23 FA+ (12.5%)21 or GA+ (more than 10%)27 dopants. The PXRD patterns showed no reflections of the secondary phase, indicating a stable, monophase 3D perovskite structure at least up to x = 0.249.3.3. DSC
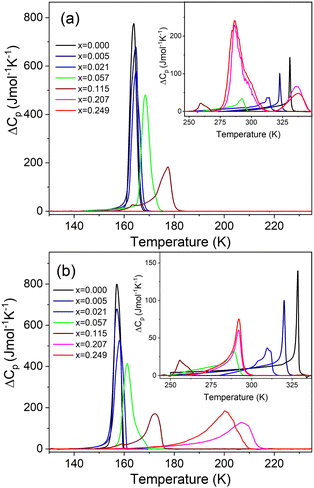
The DSC measurement of MAPbI3 shows the presence of two heat anomalies at T1 = 328.5 K (330.9 K) and T2 = 157.1 K (163.8 K) during cooling (heating), respectively (Fig. 1 and Fig. S5, Table S1, ESI†). These PT temperatures are in very good agreement with previous reports.24,40 Very sharp change of entropy at T2 (Fig. S6, ESI†) points to the first-order character of the LT PT. In the case of the high-temperature (HT) PT, the entropy shows a sudden drop at T1, followed by a further continuous change that extends down to ∼260 K (Fig. S6, ESI†). This behavior suggests a slightly first-order character of this PT. The associated changes in enthalpy ΔH and entropy ΔS were estimated to be of ∼0.50 kJ mol−1 and ∼1.57 J mol−1 K−1 for the PT at T1, and ∼2.43 kJ mol−1 and ∼15.31 J mol−1 K−1 for the PT at T2 (Table S1, ESI†). For an order–disorder PT, ΔS = R![[thin space (1/6-em)]](https://www.rsc.org/images/entities/i_char_2009.gif) ln(N), where R is the gas constant and N is the ratio of the number of configurations in the disordered and ordered phases. The estimated N is 1.21 and 6.31 for the PT at T1 and T2, respectively (Table S1, ESI†). The small (large) value of N at T1 (T2) is consistent with a small (large) change in the disorder of organic cations at these PTs.
ln(N), where R is the gas constant and N is the ratio of the number of configurations in the disordered and ordered phases. The estimated N is 1.21 and 6.31 for the PT at T1 and T2, respectively (Table S1, ESI†). The small (large) value of N at T1 (T2) is consistent with a small (large) change in the disorder of organic cations at these PTs.
Small doping of MAPbI3 with MHy+ leads to pronounced shift of T1 to lower values, i.e., T1 shifts to 320.1 K (322.8 K), 310.9 K (313.6 K), 289.2 K (292.5 K) and 255.6 K (259.3 K) for x = 0.005, 0.021, 0.057 and 0.115, respectively (Fig. 1 and Fig. S5, S6, Table S1, ESI†). Thus, the desirable cubic phase I is stabilized at RT already for x = 0.057, in agreement with the powder X-ray diffraction, whereas for literature precedents such as EA+, DMA+, FA+ and GA+ the minimal required content to induce that effect is in the range of 8–12.5%.19–24,27 Since the values of ΔH, ΔS and N change weakly up to x = 0.057, it is clear that doping of MHy+ to this level has a weak effect on the Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m → I4/mcm PT mechanism. For x = 0.115, ΔH, ΔS and N significantly decrease, indicating significant suppression of the PT (Table S1, ESI†).
m → I4/mcm PT mechanism. For x = 0.115, ΔH, ΔS and N significantly decrease, indicating significant suppression of the PT (Table S1, ESI†).
In contrast to T1, small doping with MHy+ leads to increase of T2 to 157.2 K (164.6 K), 158.2 K (164.8 K), 161.3 K (168.6 K) and 172.4 K (177.6 K) for x = 0.005, 0.02, 0.057 and 0.115, respectively (Fig. 1 and Fig. S5 and S6, Table S1, ESI†). This behavior is opposite to that observed for MAPbI3 doped with other cations larger than MA+ such as EA+ and GA+.24,27 For instance, for MA1−xEAxPbI3 (MA1−xFAxPbI3), T2 decreased to ∼127 K for x = 0.21,24 whereas for MA1−xGAxPbI3, T2 decreased to 150 K and both PTs were completely suppressed for x = 0.2.27 In a similar manner to T1, the doping of MAPbI3 with MHy+ up to x = 0.057 has a weak effect on the I4/mcm → Pnma PT mechanism but this PT is significantly suppressed for x = 0.115, as evidenced by about 2-fold decrease of ΔS.
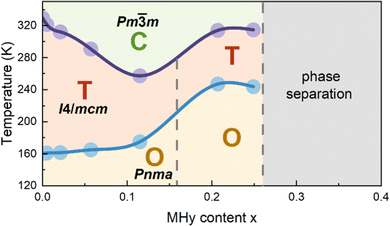
When x increases above 0.2, DSC shows fundamental changes in thermal behavior. First of all, T1 exhibits a pronounced shift to higher temperatures, i.e., to 292.0 K (336.4 K) and 292.1 K (337.6 K) for x = 0.207 and 0.249 during cooling (heating), respectively (Fig. 1 and Table S1, ESI†). Secondly, ΔH, ΔS and N significantly increase (Table S1, ESI†) and the DSC peaks strongly broaden (Fig. 1). Another characteristic feature is the appearance of a very large hysteresis, up to 46 K (Table S1, ESI†). A strong shift to higher temperatures and very large thermal hysteresis (up to 86 K) are also observed for the LT PT, i.e., T2 increases to 207.4 K (286.8 K) and 201.0 K (286.7 K) for x = 0.207 and 0.249, respectively (Table S1, ESI†). Furthermore, ΔS increases and for x = 0.249 it becomes comparable to the value observed for undoped MAPbI3. The observed changes in the thermal behavior suggest that high doping of MAPbI3 with MHy+ leads to significant changes in the PT mechanism. We summarized the obtained results in the temperature-composition phase diagram shown in Fig. 2. It is worth noting that the MA1−xEAxPbI3 system also showed new behavior for large doping (x = 0.31 and 0.38).24 However, in this case, the LT PT was completely suppressed and only one heat anomaly was observed near 215–217 K.24 Furthermore, this anomaly became sharper compared to the samples with x below 0.2. It is, therefore, clear that the high doping with MHy+ and EA+ leads to very different changes in the lattice dynamics and PT mechanism of MAPbI3.
3.4. Single-crystal X-ray diffraction
In order to obtain some insight into the structural changes occurring in the highly doped samples, we have performed a single-crystal X-ray diffraction study for MA1−xMHyxPbI3 with x = 0.249. At 300 K, the diffraction patterns are characteristic of Pm![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m symmetry, whereas at 235 K, additional patterns at hk0.5 layers impose enlargement of the unit cell to a + b, b − a, 2c and pseudo-merohedral twinning associated with tetragonal distortion (Fig. S7, ESI†). Finally, at 120 K, all diffraction patterns split, indicating symmetry reduction to orthorhombic with a primitive unit cell (Fig. S7, ESI†). The changes observed in diffraction patterns are consistent with symmetry breaking from cubic to tetragonal to orthorhombic in pure MAPbI3 crystals and in MA1−xEAxPbI3 solid solution, for x < 0.31.17,24 Thermal evolution of the cubic lattice parameter ac (Fig. S8, ESI†) reflects well the anomalies observed in calorimetric measurements at PTs, even though the changes in ac are slight and continuous.
m symmetry, whereas at 235 K, additional patterns at hk0.5 layers impose enlargement of the unit cell to a + b, b − a, 2c and pseudo-merohedral twinning associated with tetragonal distortion (Fig. S7, ESI†). Finally, at 120 K, all diffraction patterns split, indicating symmetry reduction to orthorhombic with a primitive unit cell (Fig. S7, ESI†). The changes observed in diffraction patterns are consistent with symmetry breaking from cubic to tetragonal to orthorhombic in pure MAPbI3 crystals and in MA1−xEAxPbI3 solid solution, for x < 0.31.17,24 Thermal evolution of the cubic lattice parameter ac (Fig. S8, ESI†) reflects well the anomalies observed in calorimetric measurements at PTs, even though the changes in ac are slight and continuous.
3.5. Temperature-dependent Raman study
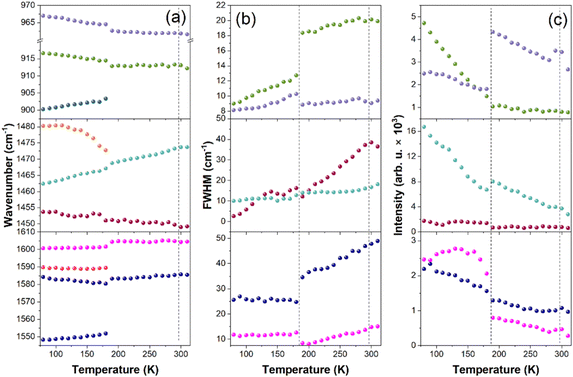
Since X-ray diffraction could not provide detailed structural information, especially on the behavior of organic cations, we performed a temperature-dependent Raman study to obtain further insight into lattice dynamics and mechanism of the PTs in the x = 0.249 sample (Fig. S9 and S10, ESI†). The internal modes of MA+ and MHy+ as well as the MA-cage mode are observed above 200 cm−1 and the assignment of these modes, based on previous reports,41–43 is shown in Fig. S9 (ESI†). The RT modes observed at 121 and 90 cm−1 (Fig. S10, ESI†) can be assigned to translations and librations of organic cations coupled with the Pb–I stretching modes. The shoulder at 50 cm−1 and the most intense Raman bands at 34 and 22 cm−1 correspond to octahedra distortion (Pb–I bend) and octahedra twist (PbI6 libration), respectively.41,43,44When the temperature decreases, bands related to internal vibrations of MA+ cations show weak changes down to 200 K, better visualized in plots of wavenumber, full width at half maximum (FWHM) and integral intensity presented in Fig. 3. Nevertheless, some bands show clear decrease in FWHM and increase in intensity, which points to a slowing down of MA+ rotational freedom (Fig. 3b and c). In the lattice modes region, the intensity of the 34 cm−1 mode significantly decreases and the shoulder at 50 cm−1 becomes a clearly resolved band (Fig. S10, ESI†). Thus, the structural PT near 290 K has a weak effect on the inorganic framework and MA+ cations exhibit pronounced disorder in phase II. A very similar behavior was reported at the cubic-tetragonal PTs in pure MAPbI3 and MAPbBr3.42,44 Thus, the Raman spectra of the MA0.751MHy0.249PbI3 sample are consistent with the X-ray diffraction data, which revealed tetragonal distortion of phase II. Although bands related to MHy+ are very weak, a closer inspection of the spectra shows that they exhibit significant narrowing already in phase II. For instance, the δ(NH2) band near 1603 cm−1 becomes narrow in phase II, i.e., its FWHM at 200 K is only 8.1 cm−1 (Fig. 3b) and very similar value was observed for MHyPbBr3 at 200 K, which at this temperature crystallizes in a polar structure with ordered MHy+ cations.6 We argue, therefore, that MHy+ cations are ordered in phase II.
On further cooling, pronounced changes are observed when temperature decreases from 190 K to 180 K. These changes correspond to the PT from phase II to phase III observed at 201 K in DSC. The slightly lower PT temperature in the Raman experiment is due to the laser heating of the sample. The PT leads to the splitting of many MA+ internal bands and changes in their relative intensities (Fig. 3a, c and Fig. S9, ESI†). The lowest wavenumber lattice mode also splits into three components at 44, 38 and 27 cm−1 (values at 80 K). Furthermore, many bands exhibit weak and sudden shifts (Fig. 3a). It is worth adding that visual observation under the Raman microscope revealed the appearance of some stripes in phase III, which disappeared when the crystal was heated back to RT (Fig. S11, ESI†). These features point to the discontinuous nature of the PT and the significant lowering of the crystal symmetry. The splitting and shifts are accompanied by a sudden drop of FWHM for δas(NH3) (by ∼10 cm−1) and ρas(NH3) + ρas(CH3) (by ∼6 cm−1) modes observed at 1583 and 913 cm−1 (Fig. 3b). This behavior proves that the PT from phase II to phase III is associated with the ordering of MA+ cations. Thus, similarly to the pure MAPbI3, the LT PT is triggered by ordering of MA+ cations, which results in significant distortion of the inorganic framework. However, there are also significant differences between the pure and the x = 0.249 sample. Firstly, the drop of FWHM at the PT temperature is much smaller for MA0.751MHy0.249PbI3 (about 30–35%) compared to pure MAPbI3 (65–75%).42 Furthermore, FWHM values of the δas(NH3) and ρas(NH3) + ρas(CH3) bands at 100 K are significantly larger for MA0.751MHy0.249PbI3 (25.8 and 9.7 cm−1, respectively) compared to MAPbI3 (∼8 and 5 cm−1).42 This behavior can be attributed to compositional disorder induced by presence of both MA+ and MHy+ cations. Secondly, no splitting was observed for the δas(NH3), δs(NH3) or ρas(NH3) + ρas(CH3) bands of pure MAPbI3 whereas these modes split for MA0.751MHy0.249PbI3 at 80 K into 1589.8 + 1584.2, 1480.3 + 1462.4 and 916.6 + 900.2 cm−1 doublets (Fig. 3a and Fig. S9, ESI†). Such a behavior suggests that phase III comprises two distinct MA+ cations. The closer inspection of weak Raman bands related to MHy+ cations shows that they also exhibit splitting into doublets. For instance, the 853.5, 1190.8 and 1603.7 cm−1 bands split into 853.2 + 839.1, 1210.0 + 1184.8 and 1603.9 + 1599.6 cm−1 doublets. Thus, although the X-ray diffraction data are consistent with cubic → tetragonal → orthorhombic symmetry lowering, as is the case in pure MAPbI3, the structure of phase III seems to be more complex since for pure MAPbI3 the orthorhombic phase contains only one unique MA+ cation.17 No splitting was observed also for MAPbI3 with large EA+ content, indicating that doping of MAPbI3 with EA+ and MHy+ has a very different effect on the LT crystal structure of the both systems. It is worth noting that doublets due to the presence of two unique MHy+ cations were observed for polar MHyPbBr3.6,43 For this compound and chloride analog, MHy+ embedded into the perovskite cavity formed Pb–N coordination bonds, which led to the strong distortion of the corresponding PbBr6 or PbCl6 octahedra, the disappearance of the tetragonal phase and shift of the orthorhombic-cubic PT to 418 K.6–8 It is, therefore, likely that similar effect is also present in MAPbI3 heavily doped with MHy+ and that ability of MHy+ to form Pb–N coordination bonds is responsible for the unusual behavior of the studied perovskite like the shift of the tetragonal-orthorhombic PT temperature to higher values on doping.
3.6. Dielectric properties
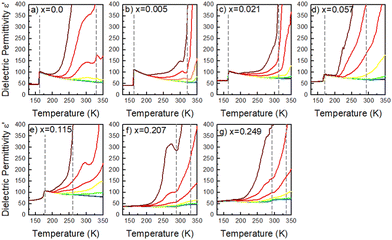
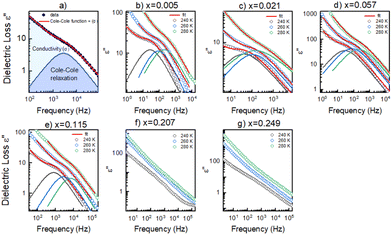
To get a more holistic view of the effect of MHy+ doping on molecular dynamics and the mechanism of PTs, the grown crystals were investigated using BDS measurements. Fig. 4a–g and Fig. S12 (ESI†) show the temperature dependence of the real part of dielectric permittivity ε′ for the MAPbI3 single crystals doped with various concentrations of the MHy+ cation. For the small mixing level (x ≤ 0.115), a step-like increase of ε′ up to 71 was observed at low temperatures (162–177 K range) due to the ordering of the MA+ electric dipoles (Fig. 4a–e). Temperatures of these anomalies are in good agreement with T2 established from the DSC data, i.e., the dielectric data confirm that doping with MHy+ leads to a shift of the tetragonal-orthorhombic PT temperature to higher values. When x increases to 0.207 and 0.249, the sharp anomaly in ε’ near 160–180 K vanishes but a broad anomaly becomes visible near 290 K (Fig. 4f–g and Fig. S12, ESI†). The temperature of this anomaly is in good agreement with the DSC data, which revealed the presence of the orthorhombic to tetragonal PT near 287 K on heating. Note that although the dielectric anomaly near 290 K is smeared, it also has a step-like character, in which ε’ increases by ∼9–10. This behavior is consistent with the ordering of MA+ in the orthorhombic phase III. In all investigated samples, the HT PT is obscured by a conductivity depicted as strong frequency dispersion, and only a trace of the PT is visible, observed as a slight change in slope of ε′(T).A more accurate description of the structural dynamics could be obtained from an analysis of dielectric spectra in the frequency domain (Fig. 5). A closer inspection of the complex dielectric permittivity as a function of frequency reveals that even a small amount of the MHy+ dopant in MAPbI3 induces a trace of a dipolar relaxation process at low temperatures (Fig. 5b). It is worth noting that for MAPbI3, no changes were observed that would indicate a relaxation process above 200 K. In order to estimate the characteristic dipolar relaxation time, the data were parameterized near the trace of the observed peak using a single Cole–Cole function and a conduction term. The analysis of the presented results shows that the maximum of the Cole–Cole function shifts towards higher frequencies with increasing concentration of MHy+ and disappears for x ≥ 0.207 (Fig. 5 and Fig. S13, ESI†). This behavior is related to the significant structural changes described in the Raman part. In the studied temperature range, the relaxation times (τ) exhibit linear tendencies as a function of the inverse temperature (1000/T) (Fig. S14, ESI†). Therefore, the relaxation times can be modeled using the Arrhenius relation:
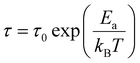 | (1) |
3.7. Optical properties
Since band gap engineering is a powerful tool for tuning optoelectronic properties of hybrid perovskites, we also studied the effect of MHy+ doping on the band gap and PL properties. Diffuse reflectance spectra show that the absorption edge exhibits a blue shift on MHy+ doping (Fig. S15, ESI†). Using the Kubelka–Munk relation:47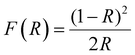 | (2) |
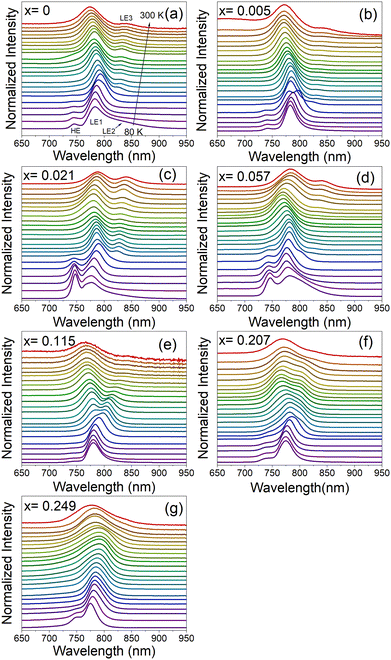
Fig. 6a–g and Fig. S17 (ESI†) show temperature-dependent normalized PL spectra of MA1−xMHyxPbI3 samples measured in the heating run and a comparison of the spectra for all samples recorded at 80 K, respectively. The spectrum of the pure MAPbI3 sample recorded at 80 K shows a weak band at 745.5 nm (1.663 eV), an intense band at 783.5 nm (1.582 eV) and a broad band at 840.5 nm (1.475 eV), see Fig. 6a and Fig. S17 (ESI†). For simplicity, we will denote these bands as HE (high energy), LE1 (low energy 1) and LE2 (low energy 2). The presence of HE and LE1 bands well below the PT temperature was reported by many researchers and they were often attributed to the ordered and disordered orthorhombic domains49 or the coexistence of the orthorhombic and tetragonal phases, respectively.50,51 Temperature-dependent PL spectra show that the HE band disappears at 140 K (Fig. 6a and Fig. S18, ESI†), in agreement with its assignment to the orthorhombic phase (note that the PT is observed at ∼20 K lower temperature compared to DSC due to laser heating of the sample). The presence of a broad LE2 band near 830–840 nm was reported previously,50,52 and this band could be related to recombination of bound exciton (BE).52 Our data show that this band is already quenched at 110 K. Plots of the bands’ positions as a function of temperature show that on heating to 135 K, the HE and LE1 bands exhibit blue and red shift, respectively. Temperature dependence of the LE1 band changes to a blue shift above the PT to the tetragonal phase (above 140 K). This behavior is in agreement with previous studies.49 It is worth noting that the orthorhombic-tetragonal PT at 140 K also leads to the appearance of a new weak LE3 band at 827.4 nm (1.498 eV), which exhibits red shift on heating (Fig. 6a and Fig. S18, ESI†). Former studies suggested that the LE1 band can be attributed to the emission from the substructures populated over the crystal surfaces, whereas LE3 arises from the interior crystal lattice.51
PL spectra of MAPbI3 doped with MHy+ measured at 80 K are very similar to the spectra of pure MAPbI3 (Fig. S17, ESI†). The intensity and position of the HE band do not show any clear correlation with the MHy+ doping level. The most intense LE1 band shows, however, a weak shift to higher energy with increasing MHy+ content, i.e., it shifts from 783.5 nm (1.582 eV) for x = 0 to 775.1 nm (1.600 eV) for x = 0.249. At 300 K, the LE1 band exhibits a shift to lower energy compared to pure MAPbI3, i.e., for x = 0.021 and 0.057 it appears at 787.1 nm (1.575 eV) and 784.4 nm (1.581 eV), respectively, compared to 774.2 nm (1.601 eV) for x = 0. On higher doping, the band shifts again to lower energy and it is observed at 774.7 nm (1.600 eV) for x = 0.249. RT temperature spectra also give information on the behavior of the LE3 band. This band is observed at very similar energies of 838.6–844.6 nm (1.468–1.478 eV) for x ≤ 0.115 but it becomes very weak and broad for the x = 0.207 and 0.249 samples, for which it appears near 830 nm (1.494 eV). In general, PL spectra provide evidence that the substitution of MHy+ for MA+ leads to weak widening of the band gap while retaining efficient PL and extended absorption similar to pure MAPbI3.
Temperature-dependent spectra show that doping with MHy+ affects temperature evolution of PL bands (Fig. 6a–g). First of all, the bulk-specific LE3 band manifests a more pronounced red shift on heating with increasing MHy+ content, i.e., in the 140–300 K range, the red shift is 13.0, 16.7, 35.7 and 43.0 nm for the x = 0, 0.021, 0.057 and 0.115 sample, respectively. In contrast to this behavior, the surface-specific LE1 band exhibits a weak blue shift on heating the x = 0.021 and x = 0.057 samples from 140 K to 250 K followed by a weak red shift on further heating. The corresponding LE1 bands of the x = 0.115 and x = 0.207 samples show red shift by about 13 nm in the 140–300 K range while for the x = 0.249 sample red shift up to 11 nm is observed up to 250 K followed by a weak blue shift on further heating. Theoretical studies of MAPbI3 revealed that the band gap and thus free exciton (FE) PL decrease with the decrease of the lattice constant, but they increase with a deviation of I atoms from the cubic symmetry sites.53 The observed changes in the temperature evolution of PL bands for the MHy+-doped sample can be therefore attributed, among others, to changes in the lattice expansion and distortion of the inorganic framework induced by the substitution of small MA+ by significantly larger MHy+ cations.
To further monitor if the PL response of the x = 0.249 sample is affected by the symmetry changes associated with structural PTs, the spectra of this sample were also recorded in the cooling run (Fig. S19, ESI†). The RT spectrum is dominated by the LE1 band near 775 nm but another very broad LE3 band is also visible near 831 nm. The position of the former band exhibits weak temperature dependence while the latter band exhibits pronounced blue shift and narrowing on cooling. Furthermore, the relative intensity LE1/LE3 strongly decreases with temperature. As a result, only one relatively narrow band is observed at 170 K near 793 nm. This change can be attributed to the tetragonal to orthorhombic PT, observed in DSC at 201 K. Significant narrowing of the PL is consistent with the ordering of MA+ cations, as revealed in the Raman experiment.
The activation energies of the investigated samples have been calculated based on the temperature-dependent PL spectra of the LE1 band, using the following equation:
We also monitored the luminescent decay profiles of the LE1 band at 80 K under the 450 nm excitation line generated by the femtosecond laser. It can be seen that the registered curves were non-exponential. The shortest lifetimes were determined for the pure MAPbI3 sample with the shorter component of 3.79 ns and the longer one of 28.66 ns. The latter component was considered as the contribution from the bulk.19 These components increase with increasing MHy+ doping level, especially for the high doping level (Table S2 and Fig. S21, ESI†). In particular, for x = 0.249 these components are 36 ns and 202 ns, respectively, indicating about 7-fold increase of the slow component compared to pure MAPbI3. Large increase in the carrier lifetime, which can be attributed to improved carrier dynamics due to the decreased number of defects and increased crystal symmetry, was previously noticed also for MAPbI3 doped with EA+ cations.19
4. Conclusions
In this work, we have explored cation-alloyed MA1−xMHyxPbI3 perovskite phases. We observe that the MHy+-induced lattice symmetrization of MAPbI3 takes place and this effect is the strongest among all known organic dopants. The tetragonal-orthorhombic PT temperature increases on MHy+ doping and this behavior is unprecedented in the mixed-cation MAPbI3 phases with other organic cations. This behavior is most likely related to the unusual property of MHy+, i.e., its ability to form Pb–N coordination bonds, which favors stronger distortion of the octahedral units.The doping level above x = 0.2 leads to significant changes in the thermal behavior, which indicate change in the PT mechanism. X-ray diffraction confirmed the presence of the cubic phase at RT as well as tetragonal and orthorhombic distortions of the inorganic lattice on cooling, similar to parent MAPbI3. Raman spectra revealed the disorder (order) of MA+ (MHy+) cations in the tetragonal phase and the ordering of MA+ cations in the orthorhombic phase. However, Raman data provided strong evidence that the orthorhombic phase of the x = 0.249 sample has more complex organic cation substructure since it comprises two unique MA+ cations, in contrast to only one unique MA+ in the parent MAPbI3. The dielectric spectroscopy confirmed significantly different dynamics of organic cations for the highly doped samples. It should be noted that the dielectric responses of all studied samples reveal rather high dielectric permittivity, which should effectively screen the charge carriers and defect states.
Finally, the absorption data revealed weak band gap widening on MHy+ doping, related to the slight expansion of the lattice. PL experiments revealed the presence of two emission bands at RT near 780 and 840 nm, which we attributed to the surface- and bulk-specific excitons, respectively. At low temperatures, another band appears near 750 nm, related to the emission of the orthorhombic phase. MHy+ doping clearly impacts PL properties, i.e., it leads to a weak blue shift of the ∼780 nm band and a large increase in the blue shift of the bulk-specific emission on cooling.
Overall, the results demonstrate that doping with MHy+ stabilizes the cubic phase and affects in a complex way structural, optical, phonon and dielectric properties, especially at a high doping level. The mixed-cation MA1−xMHyxPbI3 phases retain, however, efficient PL and extended absorption similar to the pure MAPbI3, suitable for optoelectronic applications.
Author contributions
Conceptualization: M. M. Data curation: M. P., K. F., A. G., D. S. and J. K. Z. Formal analysis: M. P., K. F., A. G., D. S., J. K. Z. and A. S. Funding acquisition: M. M. Investigation: M. P., K. F., A. G., D. S. and J. K. Z. Methodology: all authors. Project administration: M. M. Resources: M. M. Supervision: M. M. Validation: M. M., D. S. and A. S. Writing – original draft: all authors. Writing – review and editing: all authors. All the authors have given their approval to the final version of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported by the National Science Center (Narodowe Centrum Nauki) in Poland under project No. 2019/35/B/ST5/00043. J. K. Z. acknowledges support from Academia Iuvenum, Wroclaw University of Science and TechnologyNotes and references
- Y. Tu, J. Wu, G. Xu, X. Yang, R. Cai, Q. Gong, R. Zhu and W. Huang, Adv. Mater., 2021, 33, 2006545 CrossRef CAS PubMed.
- S. Kar, N. F. Jamaludin, N. Yantara, S. G. Mhaisalkar and W. L. Leong, Nanophotonics, 2021, 10, 2103–2143 CrossRef CAS.
- A. Mahapatra, D. Prochowicz, J. Kruszyńska, S. Satapathi, S. Akin, H. Kumari, P. Kumar, Z. Fazel, M. M. Tavakoli and P. Yadav, J. Mater. Chem. C, 2021, 9, 15189–15200 RSC.
- H. Liu, H. Zhang, H. Xu and L. Zhang, Appl. Sci., 2021, 11, 1453 CrossRef CAS.
- W. Chen, S. Bhaumik, S. A. Veldhuis, G. Xing, Q. Xu, M. Grätzel, S. Mhaisalkar, N. Mathews and T. C. Sum, Nat. Commun., 2017, 8, 15198 CrossRef CAS PubMed.
- M. Mączka, M. Ptak, A. Gągor, D. Stefańska, J. K. Zaręba and A. Sieradzki, Chem. Mater., 2020, 32, 1667–1673 CrossRef.
- M. Mączka, A. Gągor, J. K. Zaręba, D. Stefańska, M. Drozd, S. Balciunas, M. Simenas, J. Banys and A. Sieradzki, Chem. Mater., 2020, 32, 4072–4082 CrossRef.
- D. Drozdowski, A. Gągor, D. Stefańska, J. K. Zaręba, K. Fedoruk, M. Mączka and A. Sieradzki, J. Phys. Chem. C., 2022, 126, 1600–1610 CrossRef CAS.
- H. R. Petrosova, O. I. Kucheriv, S. Shova and I. A. Gural'skiy, Chem. Commun., 2022, 58, 5745–5748 RSC.
- D. Stefańska, M. Ptak and M. Mączka, Molecules, 2022, 27, 7949 CrossRef PubMed.
- O. A. Semenikhin, O. I. Kucheriv, L. Sacarescu, S. Shova and I. A. Gural'skiy, Chem. Commun., 2023, 59, 3566–3569 RSC.
- T. Yang, L. Gao, J. Lu, C. Ma, Y. Du, P. Wang, Z. Ding, S. Wang, P. Xu and D. Liu, et al. , Nat. Commun., 2023, 14, 839 CrossRef CAS PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- W. Travis, E. N. K. Glover, H. Bronstein, D. O. Scanlon and R. G. Palgrave, Chem. Sci., 2016, 7, 4548–4556 RSC.
- B. Saparov and D. B. Mitzi, Chem. Rev., 2016, 116, 4558–4596 CrossRef CAS PubMed.
- S. R. Pering, W. Deng, J. R. Troughton, P. S. Kubiak, D. Ghosh, R. G. Niemann, F. Brivio, F. E. Jeffrey, A. B. Walker and M. S. Islam, et al. , J. Mater. Chem. A, 2017, 5, 20658–20665 RSC.
- P. S. Whitfield, N. Herron, W. E. Guise, K. Page, Y. Q. Cheng, I. Milas and M. K. Crawford, Sci. Rep., 2016, 6, 35685 CrossRef CAS PubMed.
- C. C. Stoumpos, C. D. Malliakas and M. G. Kanatzidis, Inorg. Chem., 2013, 52, 9019–9038 CrossRef CAS PubMed.
- W. Peng, X. Miao, V. Adinolfi, E. Alarousu, O. El Tall, A. H. Emwas, C. Zhao, G. Walters and J. Liu, Angew. Chem. Int. Ed., 2016, 55, 10686–10690 CrossRef CAS PubMed.
- Z. Zhi, Y. Zhang, C. Cui, B. Li, W. Zhou, Z. Ning and Q. Mi, Adv. Mater., 2017, 29, 1701656 CrossRef PubMed.
- A. Mohanty, D. Swain, S. Govinda, T. N. G. Row and D. D. Sarma, ACS Energy Lett., 2019, 4, 2045–2051 CrossRef CAS.
- A. Francisco-López, B. Charles, M. I. Alonso, M. Garriga, M. Campoy-Quiles, M. T. Weller and A. R. Goni, J. Phys. Chem. C, 2020, 124, 3448–3458 CrossRef.
- F. Shao, P. Qin, D. Wang, G. Zhang, B. Wu, J. He, W. Peng, T. C. Sum, D. Wang and F. Huang, ACS Appl. Mater. Interfaces, 2019, 11, 740–746 CrossRef CAS PubMed.
- M. Simenas, S. Balciunas, A. Gągor, A. Pieniążek, K. Tolborg, M. Kinka, V. Klimavicius, S. Svirskas, V. Kalendra and M. Ptak, et al. , Chem. Mater., 2022, 34, 10104–10112 CrossRef CAS.
- P. Singh, R. Mukherjee and S. Avasthi, ACS Appl. Mater. Interfaces, 2020, 12, 13982–13987 CrossRef CAS PubMed.
- D. J. Kubicki, D. Prochowicz, A. Hofstetter, M. Saski, P. Yadav, D. Bi, N. Pellet, J. Lewiński, S. M. Zakeeruddin and M. Grätzel, et al. , J. Am. Chem. Soc., 2018, 140, 3345–3351 CrossRef CAS PubMed.
- F. B. Minussi, E. M. Bertoletti, S. P. Reis, J. F. Carvalho and E. B. Araujo, Chem. Commun., 2022, 58, 2212–2215 RSC.
- Q. Wang, F. Lin, C. C. Chueh, T. Zhao, M. Eslamian and A. K. Y. Jen, Mater. Today Energy, 2018, 7, 161–168 CrossRef.
- M. Simėnas, S. Balciunas, S. Svirskas, M. Kinka, M. Ptak, V. Kalendra, A. Gagor, D. Szewczyk, A. Sieradzki,R. Grigalaitis, et al., Chem. Mater., 2021, 33, 5926–5934 Search PubMed.
- C. Anelli, M. R. Chierotti, S. Bordignon, P. Quadrelli, D. Marongiu, G. Bongiovanni and L. Malavasi, Inorg. Chem., 2019, 58, 944–949 CrossRef CAS PubMed.
- M. Simenas, S. Balciunas, J. N. Wilson, S. Svirskas, M. Kinka, A. Garbaras, V. Kalendra, A. Gagor, D. Szewczyk and A. Sieradzki, et al. , Nat. Commun., 2020, 11, 5103 CrossRef CAS PubMed.
- S. Gholipour, A. M. Ali, J. P. Correa-Baena, S. H. Turren-Cruz, F. Tajabadi, W. Tress, N. Taghavinia, M. Grätzel, A. Abate and F. De Angelis, et al. , Adv. Mater., 2017, 29, 1702005 CrossRef PubMed.
- H. Park, A. Ali, R. Mall, H. Bensmail, S. Sanvito and F. El-Mellouhi, Mach. Learn.: Sci. Technol., 2021, 2, 025030 Search PubMed.
- M. Mączka, A. Gagor, M. Ptak, W. Paraguassu, T. A. Da Silva, A. Sieradzki and A. Pikul, Chem. Mater., 2017, 29, 2264–2275 CrossRef.
- M. Mączka, J. K. Zaręba, A. Gągor, D. Stefańska, M. Ptak, K. Rolder, D. Kajewski, A. Soszyński, K. Fedoruk and A. Sieradzki, Chem. Mater., 2021, 33, 2331–2342 CrossRef.
- M. Mączka, S. Sobczak, P. Ratajczyk, F. F. Leite, W. Paraguassu, F. Dybała, A. P. Herman, R. Kudrawiec and A. Katrusiak, Chem. Mater., 2022, 34, 7867–7877 CrossRef.
- K. Fedoruk, D. Drozdowski, M. Mączka, J. K. Zaręba, D. Stefańska, A. Gągor and A. Sieradzki, Inorg. Chem., 2022, 61, 15520–15531 CrossRef CAS PubMed.
- X. Huang, X. Li, Y. Tao, S. Guo, J. Gu, H. Hong, Y. Yao, Y. Guan, Y. Gao and C. Li, et al. , J. Am. Chem. Soc., 2022, 144, 12247–12260 CrossRef CAS PubMed.
- D. Drozdowski, A. Gągor and M. Mączka, J. Mol. Struct., 2022, 1249, 131660 CrossRef CAS.
- N. Onoda-Yamamuro, J. Phys. Chem. Solids, 1990, 51, 1383–1395 CrossRef CAS.
- A. M. A. Leguy, A. R. Goñi, J. M. Frost, J. Skelton, F. Brivio, X. Rodríguez-Martínez, O. J. Weber, A. Pallipurath, M. I. Alonso and M. Campoy-Quiles, et al. , Phys. Chem. Chem. Phys., 2016, 18, 27051–27066 RSC.
- K. Nakada, Y. Matsumoto, Y. Shimoi, K. Yamada and Y. Furukawa, Molecules, 2019, 24, 626 CrossRef PubMed.
- M. Mączka, J. Zienkiewicz and M. Ptak, J. Phys. Chem. C, 2022, 126, 4048–4056 CrossRef.
- M. Mączka and M. Ptak, Solids, 2022, 3, 111–121 CrossRef.
- I. Anusca, S. Balciunas, P. Gemeiner, S. Svirskas, M. Sanlialp, G. Lackner, C. Fettkenhauer, J. Belovickis, V. Samulionis and M. Ivanov, et al. , Adv. Energy Mater., 2017, 7, 1700600 CrossRef.
- D. Drozdowski, K. Fedoruk, A. Kabanski, M. Mączka, A. Sieradzki and A. Gagor, J. Mater. Chem. C, 2023, 11, 4907–4915 RSC.
- P. Kubelka and F. Munk, Z. Tech. Phys., 1931, 12, 593–601 Search PubMed.
- M. Ptak, A. Sieradzki, M. Simenas and M. Mączka, Coord. Chem. Rev., 2021, 448, 214180 CrossRef CAS.
- M. I. Dar, G. Jacopin, S. Meloni, A. Mattoni, N. Arora, A. Boziki, S. M. Zakeeruddin, U. Rothlisberger and M. Grätzel, Sci. Adv., 2016, 2, e1601156 CrossRef PubMed.
- A. D. Wright, C. Verdi, R. L. Milot, G. E. Eperon, M. A. Perez-Osorio, H. J. Snaith, F. Giustino, M. B. Johnston and L. M. Hertz, Nat. Commun., 2016, 7, 11755 CrossRef PubMed.
- C. X. Chen, J. Wang, M. Gao and D. Shi, Cryst. Growth Des., 2021, 21, 45–51 CrossRef CAS.
- H. H. Fang, R. Raissa, M. Abdu-Aguye, S. Adjokatse, G. R. Blake, J. Even and M. A. Loi, Adv. Funct. Mater., 2015, 25, 2378–2385 CrossRef CAS.
- J. Kim, S. C. Lee, S. H. Lee and K. H. Hong, J. Phys. Chem. C, 2015, 119, 4627–4634 CrossRef CAS.
- D. M. Niedzwiedzki, H. Zhou and P. Biswas, J. Phys. Chem. C, 2022, 126, 1046–1054 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available: Table S1: thermal parameters from the DSC measurements. Fig. S1–S19: NMR, Raman, absorption, dielectric and PL spectra, dependence of real MHy+ content in the grown crystals on content in the reaction mixture, PXRD patterns, DSC traces, temperature dependence of PT entropies, reciprocal space reconstructions, thermal evolution of lattice parameters, optical images of the crystal measured in the Raman experiment, inverse temperature evolution of the relaxation time, temperature dependence of MAPbI3 band positions. See DOI: https://doi.org/10.1039/d3tc02723f |
| This journal is © The Royal Society of Chemistry 2024 |