Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
A combined experimental and modelling approach for the evaluation of the thermoelectric properties of Ag-doped SnS†
Yu
Liu
a,
Jonathan M.
Skelton
 b,
Xiuqi
Xia
a,
Yibing
Zhu
a,
David J.
Lewis
b,
Xiuqi
Xia
a,
Yibing
Zhu
a,
David J.
Lewis
 *a and
Robert
Freer
*a and
Robert
Freer
 *a
*a
aDepartment of Materials, University of Manchester, Oxford Road, Manchester, M13 9PL, UK. E-mail: Robert.Freer@manchester.ac.uk; david.Lewis-4@manchester.ac.uk
bDepartment of Chemistry, University of Manchester, Oxford Road, Manchester, M13 9PL, UK
First published on 11th December 2023
Abstract
We report for the first time a systematic, combined computational and experimental study of the impact of Ag doping on the thermoelectric properties of SnS and introduce a fitting procedure to determine parameters that cannot easily be determined experimentally. Pristine and Ag-doped SnS ceramics were prepared by spark plasma sintering (SPS) at 853 K, serving as a reference for theoretical investigation. Ag doping was experimentally found to enhance the power factor and reduced thermal conductivity, improving the maximum thermoelectric figure of merit zT from 0.06 in pristine SnS to 0.22 in 2.78 at% Ag-doped SnS at 800 K. First-principles calculations were employed to establish the effects of Ag doping on the electronic structure, lattice dynamics and thermal conductivity. Electronic-structure calculations show that the holes created by Ag move the Fermi level into the valence band, resulting in a higher valley degeneracy, while lattice-dynamics modelling shows that disruption of the regular bonding network caused by Ag doping results in a substantial drop in the phonon group velocities and lattice thermal conductivity. A fitting procedure was used to determine the temperature-dependent carrier concentration and relaxation time by combining transport calculations with experimental measurements, providing insight into how the sample morphology and doping affect charge transport. This combined experimental and modelling approach provides unprecedented understanding of the effects of Ag doping on the thermoelectric performance of SnS, giving valuable insight into ongoing work on this and related chalcogenide thermoelectrics.
1. Introduction
In response to the growing need to reduce energy consumption and limit the environmental damage from fossil fuel extraction and global warming, thermoelectric materials are receiving increasing attention. Thermoelectric materials can convert heat into electrical energy, allowing substantial quantities of waste heat from e.g. industrial processes and combustion engines to generate power and thus reduce our dependence on fossil fuels.1,2 The thermoelectric performance of a material can be expressed in terms of the dimensionless thermoelectric figure of merit (zT), which is defined as:3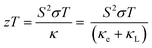 | (1) |
Tin sulfide (SnS) is one of several semiconducting IV–VI chalcogenides that have shown promise as high-performance thermoelectric materials. SnS is attractive because it is low-cost, non-toxic and earth-abundant.5 SnS crystalizes in a layered orthorhombic Pnma (or equivalent Pbnm and Pmcn) structure at room temperature and undergoes a reversible transformation to a more symmetric orthorhombic Cmcm phase at around 878 K.6,7 The high-temperature phase has been associated with strongly-anharmonic lattice dynamics and a low, intrinsic lattice thermal conductivity.8,9 However, while SnS possesses a high Seebeck coefficient, the electrical conductivity of pure SnS is very low due to its low intrinsic carrier concentration, resulting in a low power factor.10 Consequently, a variety of strategies have been used experimentally to maximise the zT of single-crystal and polycrystalline SnS.
He et al.11 prepared single-crystal SnS and obtained a maximum zT of ∼1.02 at 873 K along the layered b direction. Polycrystalline SnS has been prepared by a variety of techniques including melting, hot-pressing, rapid annealing and spark plasma sintering (SPS). Tan et al.12 synthesized SnS using SPS and reported a maximum zT of ∼0.16 at 823 K. In order to optimize electrical properties, Sn2+ is usually substituted by Ag+ or Na+ to generate holes. Tan et al.13 reported that 0.5% Ag doping increased the zT of SnS from ∼0.16 at 873 K to ∼0.6 at 923 K, and subsequently Zhou et al.14 achieved a peak zT of ∼0.65 at 850 K with Na-doped SnS.
There is now a growing body of work on the electronic and thermal transport properties of SnS, and these studies frequently make use of first-principles materials modelling employing density-functional theory (DFT).15–18 In particular, the electron transport coefficients can be obtained by solving the relevant Boltzmann transport equations using a DFT electronic structure. These calculations typically make use of the so-called constant relaxation-time approximation (CRTA), where the lifetimes of the electronic states are treated as a (single) unknown constant, τe, that can, for example, be fitted to experimental data.19 In the CRTA, the Seebeck coefficient is independent of τe, whereas the electrical conductivity and electronic thermal conductivity are determined with respect to it (i.e. as σ/τe and κe/τe). More recently, it has become possible to evaluate the (per electronic state) scattering rates from first principles, either using approximate models or from explicit electron–phonon coupling calculations.20 The lattice thermal conductivity is most commonly computed by performing structural-dynamics calculations to evaluate the phonon spectrum, and using a perturbative approach to evaluate the phonon lifetimes.21,22 It is also possible to evaluate the thermal conductivity using other approaches, for example molecular-dynamics simulations.23 Combining these two approaches allows the thermoelectric figure of merit to be estimated as a function of carrier concentration and temperature, providing an indication of what could be achievable in experiments and of the temperature and carrier concentration (i.e. doping levels) required to do so.24,25
Jiang et al.26 modelled the thermoelectric properties of p- and n-type doped Pnma SnS using this approach and estimated maximum zT values of 2.21 with a hole concentration of 1020 cm−3 and 3.13 with an electron concentration of 3 × 1019 cm−3, both at 750 K and along the layering a direction. Sun et al.27 investigated the electrical transport in Pnma and Cmcm SnS between 300 and 1080 K, and, using thermal conductivities obtained from experimental data, they estimated that the zT of SnS was increased from 0.03 to 1.61 ± 0.02 at 1080 K due to the high-temperature phase transition, with the optimum doping concentration predicted to be between 2.75 × 1019 and 8.01 × 1019 cm−3 for p-type doping, and between 6.68 × 1019 and 1.4 × 1020 cm−3 for n-type doping. These studies show that the thermoelectric performance of SnS can, in principle, be significantly enhanced by optimizing the carrier concentrations. However, whereas these calculations can estimate optimum carrier concentrations, they generally do not address how these should be achieved, and comparatively little is known about how the high doping levels needed to obtain large n impact the thermoelectric properties. Moreover, measurements and modelling are usually carried out in isolation, and predicted zT are typically based on approximations that can lead to significant deviations from experimental results, such as using constant or estimated electron relaxation times when calculating electrical transport properties, or not taking into account factors such as grain size in calculations. Despite widespread interest in SnS-based thermoelectrics, detailed comparison of the experiments and modelling for SnS-based materials is lacking in previous studies.
In this work, we examined Ag as a dopant due to its proven ability to substitute for Sn in the SnS lattice and introduce holes, thus enhancing the carrier concentration.13 We present here a combined experimental and theoretical study of the thermoelectric properties of Ag-doped SnS from 300–850 K, building on earlier reports on Ag-doped SnS that have focused predominantly on experimental work. Pristine and Ag-doped SnS ceramic samples were synthesized by a combination of mechanical alloying (MA) and spark plasma sintering (SPS). Based on earlier experiment work on Ag-doped SnS,13 and to enable comparison between experiments and calculations, Ag doping concentrations of 0.78, 1.56 and 2.78 at% were selected. We found that the thermoelectric performance of SnS improved with increasing Ag doping concentration, yielding a peak zT of 0.22 for 2.78 at% Ag-doped SnS at 800 K. We further employed first-principles calculations to study the electronic structure, lattice dynamics and transport properties of Ag-doped SnS. We also determine temperature-dependent carrier concentration and electron relaxation times by fitting the measured properties to electrical transport calculations, which provides important insight into how the material preparation influences the carrier concentration and electron scattering. We also investigated the impact of doping on the structural dynamics and lattice thermal conductivity. To the best of our knowledge, this is the first combined computational and experimental investigation of explicit hole doping in SnS, and our study highlights the utility of this approach for providing important insight to guide the optimization of high-performance thermoelectric materials in the future.
2. Methods
2.1. Preparation and characterization of Ag-doped SnS ceramic samples
Elemental Sn (Sigma-Aldrich, 99.5%), S (Sigma-Aldrich, 99.98%), and Ag powders (Sigma-Aldrich, 99.9%) were used as raw materials. SnS and Ag-doped SnS powders with doping concentrations of 0.78, 1.56 and 2.78 at% were prepared by mechanical alloying (MA) using a planetary ball mill at 450 rpm for 9 h under a nitrogen (N2) atmosphere. The powders were then consolidated by spark plasma sintering (SPS) at 853 K in vacuum for 5 min under an axial pressure of 50 MPa using an HPD25, FCT system GmbH SPS furnace. SnS and Ag-doped SnS ceramics with 20 mm diameter and 5 mm thickness were obtained. For convenience, the pristine SnS and Ag-doped samples with 0.78, 1.56, and 2.78 at% doping concentrations are hereafter referred as “SnS”, “0.78%”, “1.56%” and “2.78%” respectively.Powder X-ray diffraction (PXRD) measurements were performed on the SnS and Ag-doped SnS ceramic samples parallel and perpendicular to the SPS pressing direction using a PANaytical X’Pert Pro diffractometer with Cu Kα radiation (λ = 1.540598 Å). Fracture surfaces were investigated using scanning electron microscopy (SEM), and atomic compositions were characterized using energy-dispersive X-ray (EDX) spectroscopy, both using a Tescan MIRA3 FEG-SEM equipped with an EDX detector. The average grain sizes for the samples were estimated from SEM images of fracture surfaces using the line intercept method and ImageJ software. The in-plane Seebeck coefficient, electrical conductivity and power factor, i.e. those perpendicular to the pressing direction, were determined using an ULVAC ZEM-3 over a temperature range of 315–800 K under low helium (He) pressure.
The thermal conductivity of the samples over the same temperature range were obtained via the relation:28
| κ = ρDCp | (2) |
The sample densities ρ were calculated from measurements of the mass (m) and volume (V). Thermal diffusivity (D) was determined by laser-flash analysis with a Netzch LFA-427 under Argon (Ar) atmosphere. Based on the consistent grain structure (size and shape) in previous studies and the present experiments, the temperature-dependent heat capacity Cp of SnS and Ag-doped SnS were taken from the previous measurements on SnS and 1% Ag-doped SnS.13 Given the challenges inherent in reliably preparing high-quality thick samples, and the specific size requirements for LFA samples, only the out-of-plane thermal diffusivity and thermal conductivity κ(‖), i.e. parallel to SPS pressing direction, were measured in this work. The in-plane thermal conductivity κ(⊥), i.e. perpendicular to the SPS pressing direction, was evaluated from earlier work on the anisotropy of the lattice thermal conductivity of bulk SnS ceramics.29–31 Full details are provided in Section S2 of ESI.†
To determine the lattice thermal conductivity κL, the in-plane κe was estimated using a combination of electronic-transport calculations and the measured Seebeck coefficients and electrical-conductivities, and subtracted from the κe(⊥) deduced from thermal-diffusivity measurements. Finally, the in-plane zT was calculated using eqn (1).
2.2. Computational modelling
Calculations were performed using pseudopotential plane-wave density functional theory (DFT) as implemented in the Vienna Ab initio Simulation Package (VASP) code.32 Electron exchange and correlation were described using the revised Perdew–Burke–Ernzerhof generalized-gradient approximation (GGA) functional for solids (PBEsol).33 The interactions between the electrons and ions were described using projector augmented-wave (PAW) pseudopotentials34,35 with valence electron configurations of 4d105s25p2 for Sn, 3s23p4 for S and 4p64d105s1 for Ag. Based on explicit convergence tests a 500 eV plane-wave cutoff and a Γ-centered Monkhorst–Pack k-point mesh36 with 9 × 8 × 3 subdivisions were found to be sufficient to converge the total energy and external pressure of pristine SnS to within 1 meV per atom and 1 kbar respectively (Fig. S1, ESI†).An initial structure for SnS was fully optimised to tight tolerances of 10−8 eV and 10−2 eV Å−1, on the total energy and Hellmann–Feynman forces, respectively. The optimized structure of SnS is shown in Fig. S2 (ESI†), and the optimised lattice parameters (a = 3.96, b = 4.21 and c = 11.00 Å) are in good agreement with experimental results and previous calculations.8 As summarized in Table 1, this optimised structure was used to construct a series of supercells in which one of the Sn atoms was replaced by Ag to generate three models for (Sn1−xAgx)S with the same values of x as the experiments (0.78, 1.56 and 2.78 at%). Each doped model contains one Sn → Ag substitution, which, since all the Sn atoms are equivalent, avoids the need to consider different relative positions of the dopant atoms. These models were optimized as for bulk SnS, but with the k-point grids reduced according to the supercell expansion (Table 1).
| Supercell | # Atoms | k-points | Doping concentration (at%) | |||
|---|---|---|---|---|---|---|
| Sn | S | Ag | Total | |||
| 3 × 3 × 1 | 35 | 36 | 1 | 72 | 3 × 3 × 3 | 2.78 |
| 4 × 4 × 1 | 63 | 64 | 1 | 128 | 2 × 2 × 3 | 1.56% |
| 4 × 4 × 2 | 127 | 128 | 1 | 256 | 2 × 2 × 2 | 0.78% |
Electronic band structure and density of states (DoS) calculations were performed to analyse the electronic structure. For the doped SnS models, the band unfolding method implemented in the BandUP code was applied to reference the band structures to pristine SnS.37,38 This required that the doped structures were optimized with a fixed cell shape and volume (i.e. that only the atomic positions were relaxed). The fixed-cell and variable-cell optimisations were found to yield similar structures, with a maximum change in the cell volume of ∼1.1%. Single-point calculations were also performed on the optimised SnS and the 2.78% model, with the smallest number of atoms, using the HSE06 functional to compare the DoS to that obtained with PBEsol and to estimate the bandgaps more accurately.39
The electrical-transport properties, viz. the Seebeck coefficient S, electrical conductivity σ, power factor S2σ (PF) and electrical thermal conductivity κe, were determined from semi-classical Boltzmann transport theory within the constant relaxation-time approximation (CRTA) using the AMSET package.19 These calculations require a uniform band-structure calculation, i.e. a set of Kohn–Sham orbitals and band energies calculated on a regular grid of k-points. After careful testing (Fig. S4, ESI†), we used the HSE06 electronic structure of pristine SnS, calculated with a PAW pseudopotential excluding the Sn 4d states from the valence shell and with a 2× denser k-point sampling that was subsequently increased by a further 5× using band interpolation.
Within the CRTA, AMSET calculates each of the transport coefficients for a specified set of extrinsic hole or electron carrier concentrations (“doping levels”) n and temperatures for a given electronic relaxation time τe. We treated the n and τe as unknowns and implemented a fitting procedure to estimate these values for each of the measurements. An initial “sweep” was performed with hole concentrations n = 1015–1020 cm−3 at each of the experimental measurement temperatures. The calculated S as a function of n, at each temperature, were then compared to the experimental measurements to determine an effective carrier concentration, i.e. the n that allows the calculations to reproduce the measured S. The σ values at these n were then compared to the experimental conductivities to determine a scale for the initial τe and hence a fitted relaxation time at each measurement temperature. The fitted n and τe were then used to determine the PFs and κe from the transport calculations. Further details of the transport calculations, convergence testing and fitting procedure are provided in Section S3 of the ESI.†
The phonon spectra and lattice thermal conductivity of the pristine and Ag-doped SnS models were modelled using the Phonopy40,41 and Phono3py21 packages. The supercells and proportionally reduced k-point sampling listed in Table 2 were used to determine the second-order (harmonic) and third-order (anharmonic) force constants (FC2/FC3) using the supercell finite-displacement approach, with displacement steps of 10−2 and 3 × 10−2 Å respectively.
| SnS | (Sn1−xAgx)S | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2.78 at% | 1.56 at% | 0.78 at% | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| a The FC3 for the 2.78% Ag-doped SnS model were computed with a 5 Å cutoff radius. b The kL of the 0.78% and 1.56% models were estimated without an explicit FC3 calculation. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FC2 | Supercell | 4 × 4 × 2 | 1 × 1 × 2 | 1 × 1 × 2 | 1 × 1 × 1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. atoms | 256 | 144 | 256 | 256 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. config. | 8 | 240 | 416 | 832 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k-points | 2 × 2 × 2 | 3 × 3 × 2 | 2 × 2 × 2 | 2 × 2 × 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| FC3 | Supercell | 3 × 3 × 1 | 1 × 1 × 1 | — | — | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. atoms | 72 | 72s | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| No. config. | 2,794 | 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 880a 880a |
— | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k-points | 3 × 3 × 3 | 3 × 3 × 3 | — | — | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| q-points | Phonon | 24 × 24 × 12 | 8 × 8 × 12 | 6 × 6 × 12 | 6 × 6 × 6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| k L | 16 × 16 × 8 | 7 × 7 × 7 | —b | —b | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Atom-projected DoS curves were calculated by interpolating the frequencies onto regular Γ-centered q-point meshes with the subdivisions shown in Table 2. The phonon dispersion of SnS was computed by interpolating the frequencies along a path traversing the high-symmetry points in the Pmcn Brillouin zone. The phonon dispersions of the doped models were calculated by projecting the modes onto the parent SnS structure using the band-unfolding algorithm in the work of Allen et al.,42 which is implemented as part of the Phonopy Python API. We note that, in contrast to the electronic band unfolding, this does not require the doped unit cells to be relaxed at a fixed volume.
The lattice thermal conductivity was computed by solving the phonon Boltzmann transport equation (BTE) within the single-mode relaxation time approximation (SM-RTA) according to:43
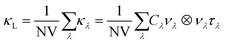 | (3) |
The macroscopic κL is computed as a sum of microscopic contributions κλ from individual phonon modes λ = qj with wavevector q, band index j, and heat capacities Cλ, group velocities νλ and lifetimes τλ. V is the unit cell volume and N is the number of wavevectors q included in the summation. The lattice thermal conductivities were calculated using the SM-RTA with modal properties calculated on the q-point meshes shown in Table 2. It was not practical to calculate FC3s for the larger 1.56 and 0.78% Ag-doped models, and we were only able to compute those for the 2.78% model within a 5 Å cutoff radius. The thermal conductivities of the 1.56 and 0.78% models were instead estimated by setting the three-phonon interaction strengths to appropriately-scaled average values determined for the bulk SnS or 2.78% models. Finally, we found that accounting only for the “particle-like” contribution to the κL by solving the BTE using eqn (3) led to unphysically low predicted thermal conductivities for the doped models, and it was necessary also to account for the contribution from “wave like” tunnelling of energy by solving the Wigner transport equation.44 Further details of the thermal-conductivity calculations on the doped models are provided in Section S4 of the ESI.†
3. Results and discussion
3.1. Sample composition and microstructure
Powder X-ray diffraction (PXRD) patterns for the SnS and Ag-doped SnS powders prepared using mechanical alloying are presented in Fig. 1(a). The patterns could be indexed against standard data for SnS (JCPDS: #01-075-0925), with no evidence of secondary phases, and the broad XRD peaks reflect the small particle sizes typically obtained using MA.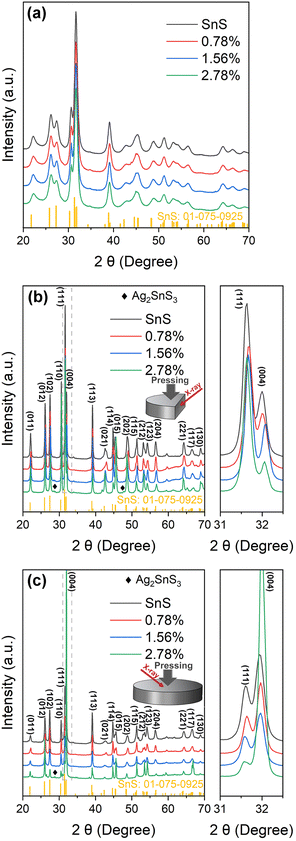 | ||
| Fig. 1 Powder X-ray diffraction (PXRD) patterns collected from SnS and Ag-doped SnS powders (a) and the surfaces of sintered samples parallel to (b) and perpendicular to (c) the pressing direction. | ||
The sintered samples are typically ≥89% of the theoretical density (Table S1, ESI†). XRD patterns collected from surfaces parallel (‖) and perpendicular (⊥) to the pressing direction are shown in Fig. 1(b) and (c). The patterns for the SnS, 0.78% and 1.56% samples indicate single-phase SnS, whereas the 2.78% samples contain Ag2SnS3 impurities. The region from 2θ = 31.0–32.5° shows that the peaks in the doped samples are displaced slightly to higher angles due to incorporation of the smaller Ag+ ions into the lattice in place of the larger Sn2+ ions (r = 1.15/1.18 Å).45
The differences in relative intensities of the XRD peaks from the parallel and perpendicular surfaces indicate texturing in the samples. The degree of orientation was determined from the Lotgering factor (LF),46 the calculation of which is described in Section S5 of the ESI.† The calculated LFs for the (11l) and (hk4) planes parallel and perpendicular to the pressing direction are shown in Table S4 (ESI†). All the samples exhibit a low degree of preferred orientation with respect to the (11l) diffraction planes parallel to the pressing direction, with LFs ranging from 0.075–0.124 for the 2.78% and SnS samples. The LFs for the (hk4) planes perpendicular to the pressing direction are larger, at 0.52 for the 2.78% sample and ∼0.28 for the SnS, 0.78% and 1.56% samples. The larger LF for the 2.78% sample suggests the Ag2SnS3 secondary phase in the 2.78% sample may contribute to increased alignment of the ab planes of the SnS grains perpendicular to the pressing direction. Overall, however, this analysis indicates only a modest degree of texturing.
SEM micrographs of fracture surfaces of the SnS and Ag-doped SnS samples parallel to the pressing direction show that the grain sizes increase with Ag concentration from 0.7 to 3.7 μm (Table S2, ESI†). There is evidence of porosity in the samples, mainly between the grains and occasionally inside the grains (Fig. 2 and Fig. S3, ESI†). The amount of porosity is marginally higher in samples with higher levels of Ag, consistent with their lower density (Table S1, ESI†). Sample compositions determined by EDX confirm that the actual Ag content in all three doped samples is close to the target values (Table S3, ESI†); the Ag-rich areas in the 2.78% sample are consistent with the Ag2SnS3 secondary phase identified by XRD (Fig. S3, ESI†).
 | ||
| Fig. 2 SEM images of fracture surfaces of the pristine SnS (a), 0.78% (b), 1.56% (c) and 2.78% (d) samples. | ||
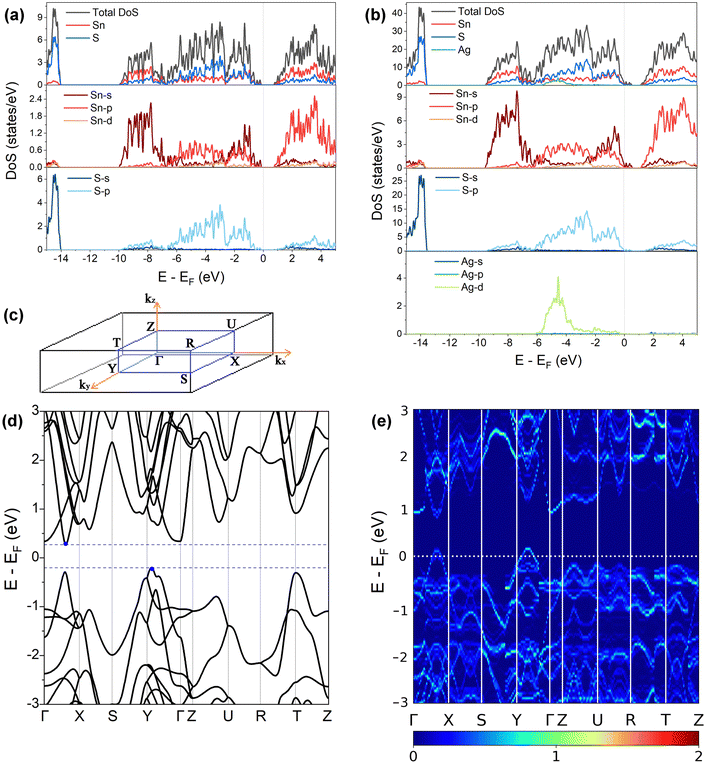
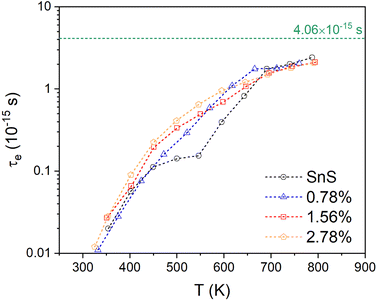
3.2. Electronic structure
Fig. 3(a) and (b) present the HSE06 DoS of the SnS and 2.78% models. The calculated bandgap of pristine SnS is ∼0.9 eV, which agrees well with the experimental value of 1.06 eV.47 The upper valence band and lower conduction band of SnS are mainly composed of Sn 5s/5p and S 3p states, and Sn 5p and S 3p states respectively. The S 3s states are separated from the other valence-band states by a gap of around 4 eV. The Fermi level EF is close to valence band edge, indicating that SnS is an intrinsic p-type semiconductor. In the DoS of the 2.78% Ag-doped model, Ag states contribute to the top of the valence band and the Fermi level is shifted into the band, indicating the creation of hole carriers.The Seebeck coefficient depends inversely on the carrier concentration according to:48
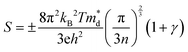 | (4) |
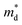 is the density of states (DoS) effective mass, and γ is a scattering factor. On the other hand, the electrical conductivity is proportional to n through the relation:4
is the density of states (DoS) effective mass, and γ is a scattering factor. On the other hand, the electrical conductivity is proportional to n through the relation:4| σ = neμ | (5) |
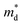 based on the free electron (parabolic band) approximation, and a larger DoS is equivalent a larger
based on the free electron (parabolic band) approximation, and a larger DoS is equivalent a larger 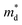 in eqn (4).49
in eqn (4).49
A comparison of the electronic density of states (DoS) curves of the pristine SnS and 2.78% Ag-doped models obtained at the PBEsol GGA and more accurate HSE06 hybrid levels of theory (Fig. S4, ESI†) shows that the two treatments predict a similar DoS but with a larger separation between the valence- and conduction bands in the hybrid calculation. This is due to the well-known tendency of GGA functionals to underestimate bandgaps.50 Electronic band structures were therefore computed with PBEsol, and DoS calculations were also performed on the larger 0.78% and 1.56% models with PBEsol for qualitative analysis.
Fig. 3(d) and (e) show the band structures of the pristine SnS and the 2.78% Ag-doped model along the Γ–X–S–Y–Γ–Z–U–R–T–Z band path through the Pmcn Brillouin zone shown in Fig. 3(c). This comparison again shows that Ag doping moves the Fermi level into the valence band and has the additional effect of slightly narrowing the gap between the host valence and conduction bands. As reported previously,51 SnS has multiple valence-band maxima (VBM) and conduction-band minima (CBM) at similar energies. The primary VBM of SnS is located along the Γ–Y path, with secondary maxima along Γ–X and at T. The primary CBM lies along Γ–X, resulting in an indirect bandgap, but there is a secondary minimum close to Γ.
The Seebeck coefficient and electrical conductivity are closely related to the form of the electronic bands near the VBM and CBM. The DoS effective mass 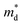 in eqn (4) is given by:52
in eqn (4) is given by:52
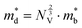 | (6) |
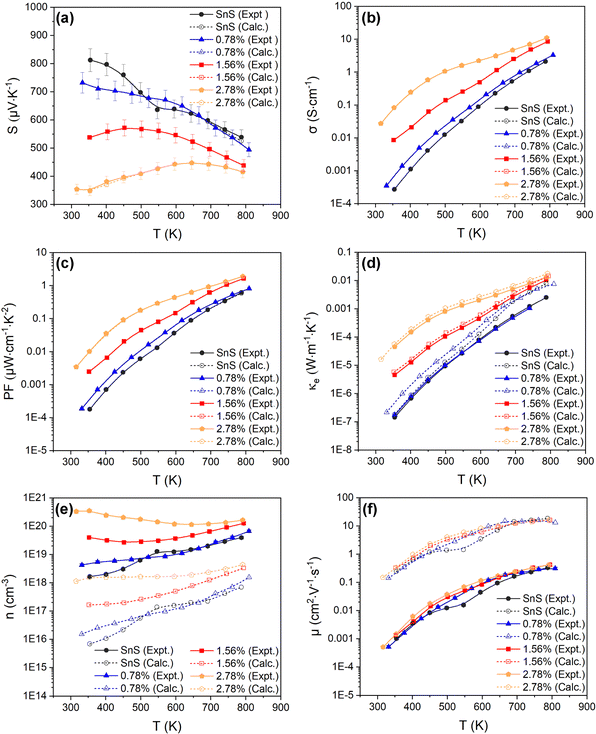
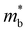 is the band effective mass. The mobility is however inversely proportional to
is the band effective mass. The mobility is however inversely proportional to 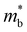 . An increase in NV therefore provides a means to enhance the Seebeck coefficient without degrading the conductivity. In SnS, the presence of multiple VBM at similar energies means displacement of the Fermi level into the valence band should increase the NV, as seen in Fig. 4(e).
. An increase in NV therefore provides a means to enhance the Seebeck coefficient without degrading the conductivity. In SnS, the presence of multiple VBM at similar energies means displacement of the Fermi level into the valence band should increase the NV, as seen in Fig. 4(e).
 | ||
| Fig. 4 Temperature-dependent Seebeck coefficient S (a), electrical conductivity σ (b), power factor S2σ (PF) (c), electronic thermal conductivity κe (d), carrier concentration n (e), and carrier mobility μ (f), of the SnS, 0.78%, 1.56% and 2.78% ceramic samples. Each plot compares the measured values (solid lines, filled symbols) to electronic-transport calculations with the doping levels and electron relaxation times fitted using the experimental measurements of S and σ (dashed lines, open symbols). The experimental n, μ and κe are determined from the measured S and σ using eqn (4) and (6)–(8). | ||
3.3. Electrical transport properties
Fig. 4(a)–(d) show the experimentally-determined in-plane Seebeck coefficient, electrical conductivity and power factor for the SnS and Ag-doped SnS ceramic samples from 315–800 K (solid lines, filled symbols). The polarity of the measured Seebeck coefficients (Fig. 4(a)) is consistent with p-type conductivity. For the pristine SnS and 0.78% Ag-doped samples the S values fall with temperature, whereas for the 1.56% and 2.78% samples the S values increase at low temperature to a maximum and then decrease at higher temperature. With increasing Ag content, the Seebeck coefficients generally fall while the electrical conductivity (σ) increases (c.f. Fig. 4(a) and (b)). The σ values of the pristine SnS and all three Ag-doped samples increase with temperature, which is indicative of non-degenerate semiconducting behaviour. The σ of the pristine and 0.78% doped samples are similar, suggesting the low level of doping provides only a modest enhancement, whereas the σ of the 1.56% and 2.78% samples are significantly larger, reaching 8.6 and 11 S cm−1 respectively. As a result, Ag doping improves the PF from 0.61 μW cm−1 K−2 for pristine SnS to 1.9 μW cm−1 K−2 for the 2.78% sample at 800 K (Fig. 4(c)). The increase in the PF with temperature and Ag content indicates that the improvements in the PF are dominated by the increases in σ.It was not possible to carry out Hall measurements to determine directly carrier concentrations and mobilities. However, assuming that one carrier is generated for each Ag for Sn substitution, and that the effects of other interactions, such as vacancy and interstitial defects are negligible, the carrier concentration n can be estimated from the Seebeck coefficients by:53,54
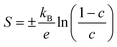 | (7) |
The estimated n and μ are shown in Fig. 4(e) and (f) (solid lines, filled symbols). As expected, the estimated carrier concentrations increase with Ag doping, (Fig. 4(e)). With reference to the behaviour of the Seebeck coefficients in Fig. 4(a) and the electronic-structure calculations discussed in Section 3.2, the results suggests that the impact of the increased n on the S outweighs the increase in NV expected from the calculated band structures. However, the range of estimated n values for pristine SnS (1.6 × 1018 to 4 × 1019 cm−3) is approximately three orders of magnitude larger than measured carrier concentrations determined from earlier work.13 Similarly, the estimated carrier mobility μ (Fig. 4(f)) is much lower than reported values from Hall measurements.13 Moreover, estimated carrier concentrations for the 2.78% model are on the order of 1020, well within the range expected for a degenerate semiconductor, which contradicts the nondegenerate behaviour evident from the measured electrical conductivity. The lack of agreement with previous Hall measurements on pristine SnS and the discrepancy between the estimated carrier concentrations and measured electrical conductivities suggest the relationship in eqn (7) may not be valid for these samples.
Finally, the electronic thermal conductivity κe is commonly calculated from the Wiedemann–Franz law:55
| κe = LσT | (8) |
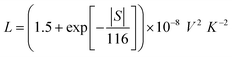 | (9) |
The calculated temperature-dependent L and κe for the samples are shown in Fig. S5 (ESI†) and Fig. 4(d) (solid lines, filled symbols) respectively. The electronic thermal conductivity κe increases significantly with Ag doping, in line with the conductivity (Fig. 5(b)). The pristine SnS and 0.78% Ag-doped samples have very similar κe, of the order of 10−7 and 10−3 W m−1 K−1 at 300 and 800 K, respectively, while the κe of the 1.56% and 2.78% samples rises by approximately 1–2 orders of magnitude at 300 K and an order of magnitude at 800 K. However, the maximum κe of ∼0.013 W m−1 K−1 at 800 K for the two more heavily-doped samples is still relatively small.
Given the apparent problems associated with using eqn (7) to estimate the n, and the fact that the semiconducting behaviour evident from the increase in σ with temperature suggests using eqn (7) to estimate the κe may be questionable, we instead attempted to obtain this data by fitting the measurements to first-principles transport calculations using semi-classical Boltzmann transport theory within the constant relation-time approximation (CRTA).
A high-quality HSE06 electronic-structure calculation on pristine SnS was performed to obtain an accurate uniform electronic band structure and bandgap. The Seebeck coefficients, electrical conductivity, power factors and electrical thermal conductivity as a function of n at each of the measurement temperatures were calculated, using an initial constant relaxation time τe = 4.06 × 10−15 s which was determined from experimental data through eqn (5).10,13,30 In the constant relaxation-time approximation, the S are independent of the τe, and we can therefore compare the experimental and calculated S to determine the (temperature-dependent) values of n that reproduce the measurements. The calculated σ are scaled by the τe, so the fitted n can then be used with the measured σ to determine the (again, temperature-dependent) τe that reproduce the measurements. The fitted S, σ and τe can then be used to calculate the mobility, PFs and electrical thermal conductivity. In this way, the transport calculations provide an alternative route to accessing n, μ and κe compared to the relationships in eqn (5), (7) and (8), and in addition provide insight into how the electron relaxation times vary with temperature.
This approach of course depends critically on the accuracy of the calculated electronic structure. HSE06 calculations of the electronic structure of SnS have previously been found to compare very well to X-ray photoelectron spectroscopy and inverse photoemission spectroscopy (XPS/IPES) measurements of the valence and conduction bands, in particular at the band edges where the transport occurs.47 We also note that the transport properties are all tensors, and are anisotropic in the orthorhombic Pmcn structure, but due to the low degree of preferred orientation in our ceramic materials we averaged the properties along the three crystal axes to compare to the experimental measurements.
Fig. 4(a)–(c) compare the calculated S, σ and PFs to the experimental measurements and confirm that this fitting procedure allows for quantitative reproduction of the measurements. The fitted n are shown alongside the values obtained from eqn (7) in Fig. 4(e). The fitted carrier concentrations for pristine SnS range from 6.9 × 1015 to 7 × 1017 cm−3 from 315–800 K, which is much lower than the estimated n (solid lines, filled symbols) but comparable to the measured values in earlier work.13 Similarly, the calculated μ are much larger than those derived from the measured σ and estimated n using eqn (5), but are again a better match to previous measurements.13 This indicates that the method of combining theoretical transport calculations and experimental is potentially a more reliable strategy for evaluating the n and μ than the relationships in eqn (5) and (7) when measurements are not possible or impractical, as would be the case, for example, for magnetic materials. The results for the three doped models show that, as noted above, the n of the pristine SnS and 0.78% samples are similar but considerably enhanced in the 1.56% and 2.78% samples, while the doping has a minimal effect on the μ. Increasing Ag doping concentration might be expected to enhance the carrier scattering,13 thereby suppressing the μ, but this could be offset by the significant grain growth.
Comparing the calculated κe of SnS and Ag-doped SnS to the values estimated using the Wiedemann–Franz law (eqn (8) and (9)) shows a ∼212% reduction for pristine SnS but a smaller ∼27% reduction for the 2.78% Ag-doped sample (Fig. 3(d)). This is consistent with the fact that the Wiedemann–Franz law was derived for metals and should become progressively more valid at heavier Ag doping levels and, consequently, for larger n.
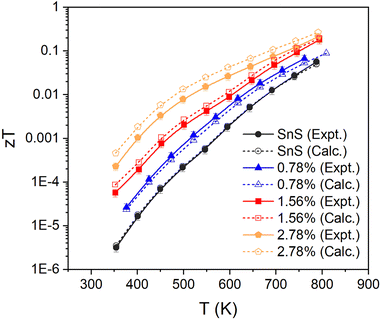
Finally, the fitted relaxation times (Fig. 5) show a strong temperature dependence, and vary by over two orders of magnitude from ∼10−17 s near room temperature to 2 × 10−15 s at 800 K. The latter is smaller, but comparable to, the τe = 4.06 × 10−15 s estimated from experiments.10,13,30 The temperature dependence of the τe also mirrors that of the mobility, as expected (c.f. Fig. 3(f)). This strong temperature dependence can be ascribed to the trapping of carriers at defects and grain boundaries and has been discussed previously,57 but it shows nevertheless that our fitting approach can potentially be used to quantify this.
3.4. Phonon density of states and dispersion
We now turn to the impact of the doping on the structural dynamics and thermal transport. Fig. 6(a)–(d) shows the calculated phonon DoS and dispersion of pristine SnS and the three doped models, computed along the same reciprocal-space path as the electronic band structures (c.f. Fig. 3(c)).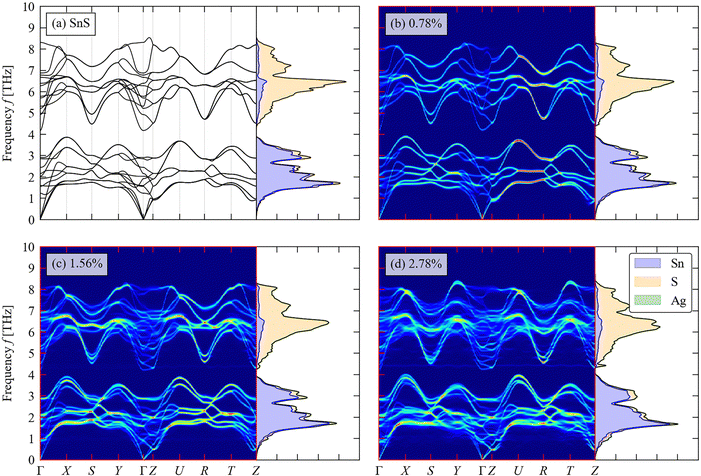 | ||
| Fig. 6 Total and atom-projected phonon density of states (DoS) curves and calculated phonon dispersion along a high-symmetry path through the Brillouin zone (c.f. Fig. 3(c)) of pristine SnS (a) and (b)–(d) Ag-doped SnS with doping concentrations of 0.78 at% (b), 1.56 at% (c) and 2.78 at% (d). | ||
For pristine SnS (Fig. 6(a)), the large mass difference between Sn and S results in two groups of modes separated by a so-called “phonon bandgap” between ∼3.8–4.4 THz, with the lower- and higher-frequency groups dominated by the motion of Sn and S atoms respectively. The phonon spectra are consistent with previous calculations.58 There are no imaginary frequencies in the dispersion, indicating that the Pmnc structure is dynamically stable as expected.59 The primitive cell of SnS contains na = 8 atoms, resulting in 3na = 24 branches at each wavevector q, comprising three acoustic branches and 21 optic modes. The dispersion is notably flatter along the Γ–Z direction, corresponding to the crystallographic c axis, than along the Γ–X and Γ–Y directions (a/b axes), which reflects the weaker interlayer interactions along the former. The low-frequency acoustic modes make the largest contribution to the thermal conductivity,60 and the flat dispersion of these modes along the Γ–Z implies low out-of-plane thermal transport as demonstrated in previous studies.61
As shown in Fig. 6(b)–(d), the phonon bandgap is generally reduced and the phonon DoS shifts to lower frequency with increasing Ag doping concentration. This could lead both to a decrease in the phonon group velocities and an increase in the number of energy-conserving phonon–phonon interactions, both of which would decrease the lattice thermal conductivity.58
3.5. Thermal transport
The thermal diffusivity as a function of temperature for the SnS and Ag-doped SnS ceramic samples was measured (Fig. S6, ESI†) and used to determine the total thermal conductivity κ according to eqn (2) (Fig. S7, ESI†). Due to the limitations imposed by sample thickness, only the out-of-plane thermal conductivity κ(‖), i.e. parallel to SPS pressing direction, could be measured. The in-plane lattice thermal conductivity κ(⊥), i.e. perpendicular to the SPS pressing direction, in which the electrical-transport measurements were performed, was estimated by dividing the κ(‖) by a factor of 0.73 obtained from previous work on SnS ceramics (see Section S2 of the ESI†).29–31 The in-plane lattice thermal conductivity κL was then obtained by subtracting the electronic thermal conductivity κe obtained from the transport calculations in Section 3.3 according to:| κL = κ − κe | (10) |
The measured κL are shown in Fig. 7 (solid lines, filled symbols). For pristine SnS, the measured κL decreases from ∼2 to ∼0.85 W m−1 K−1 from 350–800 K, which is consistent with previous studies.13,62 The κL of all Ag-doped samples are all lower than for pristine SnS. The 0.78% sample shows the largest reduction in κL to 0.6–1.0 W m−1 K−1, while the 1.56% and 2.78% samples show similar κL of 0.7–1.6 W m−1 K−1 (c.f. Fig. 2). One might intuitively expect the κL to converge towards that of pristine SnS as the doping concentration is reduced, but this is not seen in the measurement. Given that grain boundary scattering can have a significant impact on the κL, especially at lower temperature,29 this may be a result of the grain growth at higher Ag doping levels. In keeping with this, the reported room-temperature κL of the order of 1 W m−1 K−1 for polycrystalline SnS doped with 0.5 at% Na and Ag13,14 are comparable to the κL measured for our 0.78% Ag-doped sample. Since the κe is predicted to be very small, the total thermal conductivity κ and the κL show very similar values and trends.
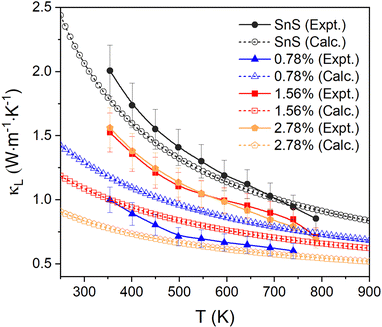 | ||
| Fig. 7 Comparison of the measured in-plane lattice thermal conductivity κL and the calculated κL of pristine and Ag-doped SnS. | ||
We also compared the experimental measurements to the calculated lattice thermal conductivity (see ESI† for details). As for the electrical-transport properties, the κL are tensors. Given the low degree of preferred orientation in the in-plane direction for all the samples, we calculated and compared the average over the three crystal axes to the experimental results. The lattice thermal conductivity of pristine SnS is comparable to and within the uncertainty of the experimental measurements over the full 350–800 K temperature range of the measurements.
The κL of the three Ag-doped models is predicted to decrease with doping concentration, leading to maximum differences between the calculated and experimental results of 18%, 33%, and 50% for the 0.78% for the 1.56% and 2.78% samples, respectively. The apparent underestimation of the κL in the 1.56% and 2.78% models could be due to the implicit assumption of complete dissolution of Ag in the lattice, leading to a higher concentration of point defects compared to experiments, to the grain growth in the ceramic samples, and/or to the presence of secondary phases in the 2.78% sample. The good agreement between the measurements and calculations on SnS is likely to be in part due to the calculations underestimating the bulk κL due to omission of a dispersion correction. However, the difference between the value obtained in the present work and comparable previous studies using a dispersion correction is ∼10%,58 suggesting the mean-free paths of (the majority of) the heat-carrying modes are smaller than the grain size, and thus that grain growth and porosity have a limited impact. We therefore tentatively attribute the larger-than-expected κL of the more heavily-doped samples to the presence of secondary phases. The underestimation could also be due to the approximations used to calculate the κL of the doped models, although given careful testing, and the fact that the calculations recover the (chemically-)intuitive result that the κL increases at lower doping concentrations, we think this is unlikely.
3.6. Thermoelectric figure of merit zT
Finally, we combine the in-plane electrical and thermal transport properties to obtain the thermoelectric figure of merit zT using eqn (1). Fig. 8 compares two sets of calculations: one using the measured κL and one using the calculated κL. Both sets of data show enhancement of zT with Ag doping concentration, with the largest measured zT increasing from 0.06 for pristine SnS to 0.22 for the 2.78% sample at 800 K. Our zT value is comparable to but slightly smaller than the previous reported zT of ∼0.3 for Ag-doped SnS.13 The calculated zT are higher than the measured values due to the smaller predicted κL, and the predicted zT is ∼0.27 for the 2.78% sample at 800 K. The results therefore suggest scope for improving the performance if the κL can be reduced.4. Conclusions
We have performed detailed characterisation of the thermoelectric properties of SnS and Ag-doped SnS ceramics using a combined experimental and computational approach. We find that Ag doping improves the electrical transport properties and reduces the lattice thermal conductivity, thereby enhancing the thermoelectric performance of SnS and yielding a maximum zT of 0.22 with 2.78 at% doping at 800 K.First-principles calculation were employed to analyse the electronic structure and transport properties. Electronic-structure calculations show that doping shifts the Fermi level down into the valence bands in the doped models, enhancing the hole carrier concentration and improving the valley degeneracy. We have developed a fitting procedure to use electronic-transport calculations to analyse experimental data, which yields more realistic estimates of the carrier concentrations, mobility and electrical thermal conductivity than the equations commonly employed in the absence of measurements. We find that Ag doping enhances the n with relatively little impact on the μ. The larger n compensates for the increased NV and results in a degraded Seebeck coefficient but larger electrical conductivity, with the result that enhancements to the power factor are dominated by the increase in σ. The fitting procedure also yields a temperature-dependent electronic relaxation time, which provides insight into the impact of phenomena such as carrier trapping on the transport. This method of combining experiments and calculations is novel and a potentially useful way to access difficult-to-measure properties, such as the n and μ when Hall measurements are unavailable or impractical, and the κe.
Structural-dynamics calculations indicate that Ag doping reduces the phonon group velocities, resulting in decreased lattice thermal conductivity. However, attempts to model the κL of the doped samples were unsuccessful and underestimated the κL considerably compared to measurements. Part of this may be ascribed to the lack of a dispersion correction in the calculations, but the errors in the predicted κL of the doped samples suggest that the approximations required to make the calculations tractable may need to be revisited.
Nonetheless, comparison of the zT obtained with the measured and (lower) calculated κL highlights the scope for improving the figure of merit through materials-engineering strategies to control the thermal conductivity.
Author contributions
Yu Liu: conceptualization, methodology, validation, formal analysis, investigation, data curation, visualization, writing – original draft. Jonathan M. Skelton: conceptualization, methodology, validation, formal analysis, investigation, writing – review & editing. Xiuqi Xia: investigation. Yibing Zhu: investigation. David J. Lewis and Robert Freer: conceptualization, resources, visualization, validation, formal analysis, supervision, project administration, writing – review & editing.Data-access statement
All research data supporting this work are directly available within this publication.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors are grateful to the EPSRC for funding this work (EP/H043462, EP/I036230/1, EP/L014068/1, EP/L017695/1, and EP/R022518/1). J. M. S. is currently supported by a UKRI Future Leaders Fellowship (MR/T043121/1) and previously held a University of Manchester Presidential Fellowship. The work was also supported by the Henry Royce Institute for Advanced Materials, funded through the EPSRC (EP/R00661X/1, EP/S019367/1, EP/P025021/1, and EP/P025498/1). We gratefully acknowledge the use of the facilities at the Department of Materials at the University of Manchester and support from the X-Ray staff. The calculations were performed on the ARCHER 2 UK National HPC facility, via J. M. S.'s membership to the UK Materials Consortium (MCC), which is funded by EPSRC (EP/R029431, EP/X035859). A subset of the calculations were performed on the University of Manchester Computational Shared Facility (CSF) HPC system, which is maintained by UoM Research IT. Y. L. thanks the China Scholarship Council for their financial support during her PhD program.References
- T. Hendricks, T. Caillat and T. Mori, Energies, 2022, 15, 7307 CrossRef CAS.
- R. Freer and A. V. Powell, J. Mater. Chem. C, 2020, 8, 441–463 RSC.
- G. J. Snyder and A. H. Snyder, Energy Environ. Sci., 2017, 10, 2280–2283 RSC.
- G. J. Snyder and E. S. Toberer, Nat. Mater., 2008, 7, 105–114 CrossRef CAS.
- J. Guan, Z. Zhang, M. Dou, J. Ji, Y. Song, J. Liu, Z. Li and F. Wang, J. Phys. Chem. Solids, 2020, 137, 109182 CrossRef CAS.
- A. J. Clayton, C. M. E. Charbonneau, W. C. Tsoi, P. J. Siderfin and S. J. C. Irvine, Sci. Technol. Adv. Mater., 2018, 19, 153–159 CrossRef PubMed.
- K. J. Norton, F. Alam and D. J. Lewis, Appl. Sci., 2021, 11, 2062 CrossRef CAS.
- R. Guo, X. Wang, Y. Kuang and B. Huang, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 115202 CrossRef.
- U. Aseginolaza, R. Bianco, L. Monacelli, L. Paulatto, M. Calandra, F. Mauri, A. Bergara and I. Errea, Phys. Rev. B, 2019, 100, 214307 CrossRef CAS.
- Asfandiyar, B. Cai, L. D. Zhao and J. F. Li, J. Materiomics, 2020, 6, 77–85 CrossRef.
- W. He, D. Wang, J. F. Dong, Y. Qiu, L. Fu, Y. Feng, Y. Hao, G. Wang, J. Wang, C. Liu, J. F. Li, J. He and L. D. Zhao, J. Mater. Chem. A, 2018, 6, 10048–10056 RSC.
- Q. Tan and J. F. Li, J. Electron. Mater., 2014, 43, 2435–2439 CrossRef CAS.
- Q. Tan, L. D. Zhao, J. F. Li, C. F. Wu, T. R. Wei, Z. B. Xing and M. G. Kanatzidis, J. Mater. Chem. A, 2014, 2, 17302–17306 RSC.
- B. Zhou, S. Li, W. Li, J. Li, X. Zhang, S. Lin, Z. Chen and Y. Pei, ACS Appl. Mater. Interfaces, 2017, 9, 34033–34041 CrossRef CAS.
- G. Kresse and J. Hafner, Phys. Rev. B: Condens. Matter Mater. Phys., 1993, 47, 558–561 CrossRef CAS.
- P. Giannozzi, S. Baroni, N. Bonini, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, G. L. Chiarotti, M. Cococcioni, I. Dabo, A. Dal Corso, S. de Gironcoli, S. Fabris, G. Fratesi, R. Gebauer, U. Gerstmann, C. Gougoussis, A. Kokalj, M. Lazzeri, L. Martin Samos, N. Marzari, F. Mauri, R. Mazzarello, S. Paolini, A. Pasquarello, L. Paulatto, C. Sbraccia, S. Scandolo, G. Sclauzero, A. P. Seitsonen, A. Smogunov, P. Umari and R. M. Wentzcovitch, J. Phys.: Condens. Matter, 2009, 21, 395502 CrossRef PubMed.
- P. Giannozzi, O. Andreussi, T. Brumme, O. Bunau, M. Buongiorno Nardelli, M. Calandra, R. Car, C. Cavazzoni, D. Ceresoli, M. Cococcioni, N. Colonna, I. Carnimeo, A. Dal Corso, S. de Gironcoli, P. Delugas, R. A. DiStasio, A. Ferretti, A. Floris, G. Fratesi, G. Fugallo, R. Gebauer, U. Gerstmann, F. Giustino, T. Gorni, J. Jia, M. Kawamura, H. Y. Ko, A. Kokalj, E. Kucukbenli, M. Lazzeri, M. Marsili, N. Marzari, F. Mauri, N. L. Nguyen, H. V. Nguyen, A. Oterodela Roza, L. Paulatto, S. Ponce, D. Rocca, R. Sabatini, B. Santra, M. Schlipf, A. P. Seitsonen, A. Smogunov, I. Timrov, T. Thonhauser, P. Umari, N. Vast, X. Wu and S. Baroni, J. Phys. Condens. Matter., 2017, 29, 465901 CrossRef CAS PubMed.
- P. Blaha, K. Schwarz, F. Tran, R. Laskowski, G. K. H. Madsen and L. D. Marks, J. Chem. Phys., 2020, 152, 074101 CrossRef CAS PubMed.
- G. K. H. Madsen, J. Carrete and M. J. Verstraete, Comput. Phys. Commun., 2018, 231, 140–145 CrossRef CAS.
- A. M. Ganose, J. Park, A. Faghaninia, R. Woods-Robinson, K. A. Persson and A. Jain, Nat. Commun., 2021, 12, 2222 CrossRef CAS PubMed.
- A. Togo, L. Chaput and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 094306 CrossRef.
- W. Li, J. Carrete, N. A. Katcho and N. Mingo, Comput. Phys. Commun., 2014, 185, 1747–1758 CrossRef CAS.
- B. L. Huang and M. Kaviany, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 77, 125209 CrossRef.
- J. M. Flitcroft, I. Pallikara and J. M. Skelton, Solids, 2022, 3, 155–176 CrossRef CAS.
- K. Brlec, K. B. Spooner, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2022, 10, 16813–16824 RSC.
- J. Jiang, Y. Pan, T. Zhou, Y. Niu, X. Kong, J. Song, C. Yang, Y. Yu and C. Wang, Mater. Today Commun., 2020, 24, 101167 CrossRef CAS.
- B. Z. Sun, Z. Ma, C. He and K. Wu, RSC Adv., 2015, 5, 56382–56390 RSC.
- H. Palneedi, D. R. Patil, S. Priya, K. Woo, J. W. Ye, Y. M. Woo, Y. S. Hwang, G. T. Hwang, J. H. Park and J. Ryu, Adv. Mater., 2023, 35, 2303553 CrossRef CAS.
- Y. M. Han, J. Zhao, M. Zhou, X.-X. Jiang, H.-Q. Leng and L. F. Li, J. Mater. Chem. A, 2015, 3, 4555–4559 RSC.
- H. Wu, K. Peng, B. Zhang, X. N. Gong, Z. Z. Feng, X. M. Zhang, M. Xi, X. M. Yan, Y. S. Zhang, G. Y. Wang, X. Lu and X. Y. Zhou, Mater. Today Phys., 2020, 14, 100221 CrossRef.
- Asfandiyar, T. R. Wei, Z. Li, F. H. Sun, Y. Pan, C. F. Wu, M. U. Farooq, H. Tang, F. Li, B. Li and J. F. Li, Sci. Rep., 2017, 7, 43262 CrossRef CAS PubMed.
- G. Kresse, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186 CrossRef CAS PubMed.
- J. P. Perdew, A. Ruzsinszky, G. I. Csonka, O. A. Vydrov, G. E. Scuseria, L. A. Constantin, X. Zhou and K. Burke, Phys. Rev. Lett., 2008, 100, 136406 CrossRef.
- P. E. Blochl, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef.
- G. Kresse and D. Joubert, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- H. J. Monkhorst and J. D. Pack, Phys. Rev. B: Condens. Matter Mater. Phys., 1976, 13, 5188–5192 CrossRef.
- P. V. C. Medeiros, S. S. Tsirkin, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 91, 041116 CrossRef.
- P. V. C. Medeiros, S. Stafström and J. Björk, Phys. Rev. B: Condens. Matter Mater. Phys., 2014, 89, 041407 CrossRef.
- A. V. Krukau, O. A. Vydrov, A. F. Izmaylov and G. E. Scuseria, J. Chem. Phys., 2006, 125, 224106 CrossRef.
- A. Togo, F. Oba and I. Tanaka, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134106 CrossRef.
- A. Togo and I. Tanaka, Scr. Mater., 2015, 108, 1–5 CrossRef CAS.
- P. B. Allen, T. Berlijn, D. A. Casavant and J. M. Soler, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 085322 CrossRef.
- J. M. Skelton, L. A. Burton, A. J. Jackson, F. Oba, S. C. Parker and A. Walsh, Phys. Chem. Chem. Phys., 2017, 19, 12452–12465 RSC.
- M. Simoncelli, N. Marzari and F. Mauri, Phys. Rev. X, 2022, 12, 041011 CAS.
- R. D. Shannon, Acta Cryst., 1976, A32, 751–767 CrossRef CAS.
- F. K. Lotgering, J. Inorg. Nucl. Chem., 1959, 9, 113–123 CrossRef CAS.
- T. J. Whittles, L. A. Burton, J. M. Skelton, A. Walsh, T. D. Veal and V. R. Dhanak, Chem. Mater., 2016, 28, 3718–3726 CrossRef CAS.
- H. Xie, Y. Liu, Y. Zhang, S. Hao, Z. Li, M. Cheng, S. Cai, G. J. Snyder, C. Wolverton, C. Uher, V. P. Dravid and M. G. Kanatzidis, J. Am. Chem. Soc., 2022, 144, 9113–9125 CrossRef CAS PubMed.
- J. Cui, C. Chen, W. He, J. Avila, L. D. Zhao, M. C. Asensio, J. He and Y. Chen, J. Mater. Chem. A, 2018, 6, 24588–24594 RSC.
- C. Freysoldt, B. Grabowski, T. Hickel, J. Neugebauer, G. Kresse, A. Janotti and C. G. Van de Walle, Rev. Mod. Phys., 2014, 86, 253–305 CrossRef.
- L. C. Gomes and A. Carvalho, Phys. Rev. B: Condens. Matter Mater. Phys., 2015, 92, 085406 CrossRef.
- A. Li, C. Hu, B. He, M. Yao, C. Fu, Y. Wang, X. Zhao, C. Felser and T. Zhu, Nat. Commun., 2021, 12, 5408 CrossRef CAS PubMed.
- H. L. Tuller and A. S. Nowick, J. Phys. Chem. Solids, 1977, 38, 859–867 CrossRef CAS.
- H. Taguchi, M. Sonoda and M. Nagao, J. Solid State Chem., 1998, 137, 82–86 CrossRef CAS.
- X. Zhang and L. D. Zhao, J. Materiomics, 2015, 1, 92–105 CrossRef.
- M. Wu, H. H. Cui, S. Cai, S. Hao, Y. Liu, T. P. Bailey, Y. Zhang, Z. Chen, Y. Luo, C. Uher, C. Wolverton, V. P. Dravid, Y. Yu, Z. Z. Luo, Z. Zou, Q. Yan and M. G. Kanatzidis, Adv. Energy Mater., 2022, 13, 2203325 CrossRef.
- S. Morikawa, T. Inamoto and M. Takashiri, Nanotechnology, 2018, 29, 075701 CrossRef.
- J. M. Skelton, J. Mater. Chem. C, 2021, 9, 11772–11787 RSC.
- I. Pallikara, P. Kayastha, J. M. Skelton and L. D. Whalley, Electron. Struct., 2022, 4, 033002 CrossRef.
- W. Rahim, J. M. Skelton and D. O. Scanlon, J. Mater. Chem. A, 2020, 8, 16405–16420 RSC.
- M. Einhorn, B. A. D. Williamson and D. O. Scanlon, J. Mate. Chem. A, 2020, 8, 7914–7924 RSC.
- Q. Tan, C. F. Wu, W. Sun and J. F. Li, RSC Adv., 2016, 6, 43985–43988 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03672c |
| This journal is © The Royal Society of Chemistry 2024 |