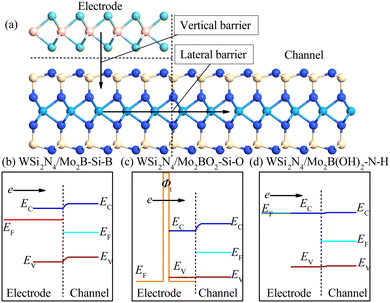
Designing CMOS compatible efficient ohmic contacts to WSi₂N₄via surface-engineered Mo₂B monolayer electrodes

Abstract

Forming ohmic contacts between metals and semiconductors is critical to achieving high-performance and energy-efficient electronics. Here we investigate the interface properties of WSi₂N₄ contacted by Mo₂B, O-modified Mo₂B (Mo₂BO₂) and OH-modified Mo₂B (Mo₂B(OH)₂) nanosheets using density functional theory simulations. We show that WSi₂N₄ and Mo₂B form n-type Schottky contacts with barrier heights that are robust against external electric fields. In contrast, functionalizing Mo₂B with O and OH causes the work function to energetically down- and up-shift significantly, thus forming both n-type and p-type ohmic contacts with WSi₂N₄, respectively. The possibility of achieving both p-type and n-type ohmic contacts immediately suggests the role of surface-engineered Mo₂B as a key enabler towards WSi₂N₄-based complementary metal–oxide–semiconductor (CMOS) device technology in which both n-type and p-type devices are needed. We further demonstrate the emergence of quasi-ohmic contact with ultralow lateral Schottky barrier and zero vertical interfacial tunneling barriers in Mo₂B(OH)₂-contacted WSi₂N₄ – a feature rarely found in other 2D/2D metal/semiconductor contacts, thus demonstrating surface-engineered Mo₂B as a promising electrode to WSi₂N₄ with high charge injection efficiency. These results offer design insights useful for the development of high-performance 2D semiconductor CMOS device technology.

---

1. Introduction

As silicon-based field effect transistors are approaching their physical scaling limits, the development of semiconductor technologies with advanced nanomaterials has become a topic of tremendous interest in both scientific and industry research.¹ Two-dimensional (2D) materials are considered a promising candidate to complement the silicon technology for extending Moore's Law, owing to their ultrathin body, excellent electronic properties, dangling bond free surface and unique atomically layered structure.^2–4 Since the successful preparation of graphene, a large variety of 2D materials have emerged, including transition metal dichalcogenides (TMDs),^5,6 MXenes,^7,8 black phosphorene^9–11 and MA₂Z₄,¹² many of which are promising for device applications, such as field effect transistors, spintronics, photovoltaic cells, photodetectors, and so on.^13–16 2D materials thus provide a platform for designing novel functional devices beyond conventional silicon technology.

Although 2D materials exhibit competitive performance, the contact resistance arising at the metal/2D-semiconductor interface remains a challenging issue to tame. Contact resistance governs the charge carrier injection efficiency from the metal electrode into the 2D channel,^17–20 and dictates the performance as well as energy efficiency of 2D semiconductor devices. Major research efforts have thus been devoted to reducing the contact resistance in 2D semiconductor devices. To achieve this, a suitable combination of metal and semiconductor materials to form an ohmic contact, in which the Fermi level of the metal lies within the bands rather than in the band gap,^21–23 is a critical first step. For most 3D metals, it is often difficult to achieve ideal ohmic contact with 2D semiconductors due to the strong interfacial interactions, such as orbital hybridization, metal-induced gap states (MIGS) and Fermi level pinning effect, which can compromise the functionality and tunability of a 3D-metal/2D-semiconductor contact. Semimetals, such as Bi and Sb,^24–27 have recently emerged as a promising metal contact candidate to 2D semiconductors due to the low MIGS and appropriate band alignment with archetypal 2D semiconductor species, such as MoS₂ and WS₂. Beyond 3D metals, metallic 2D layered materials, such as graphene, NbS₂²⁸ and transition metal borides,²⁹ provide an alternative strategy for achieving high-quality ohmic contacts. Due to the weak van der Waals (vdW) interactions and 2D/2D metal/semiconductor (MS) contact, MIGS is strongly suppressed, leading to nearly ideal contacts that approach the Schottky–Mott limit.³⁰ The atomic thickness of 2D metals is also beneficial in achieving MS contact with adjustable Schottky barriers^31–36 due to the weak screening effect.

WSi₂N₄ monolayer, an experimentally synthesized member of the MA₂Z₄ family, is a promising electronic material for semiconductor nanodevices due to its exceptional electrical properties.^37–39 As metal/semiconductor contact is nearly always present in semiconductor devices, the search for suitable electrode materials is a critical first step towards high-performance WSi₂N₄-based devices that have yet to be addressed thus far. In this work, the interfacial properties of monolayer WSi₂N₄ and MoB₂ contacts are systematically studied based on density functional theory (DFT) calculations. The results show that, although MoB₂ forms an n-type Schottky contact with WSi₂N₄, surface-engineered Mo₂B, namely the O-modified Mo₂BO₂ and OH-modified Mo₂B(OH)₂, forms p-type and n-type ohmic contact with WSi₂N₄, respectively. The possibility of achieving both p-and n-type ohmic contacts suggests that surface-engineered Mo₂B may pave a way towards WSi₂N₄-based complementary metal–oxide–semiconductor (CMOS) device technology.⁴⁰

2. Computational methods

All calculations are based on the DFT scheme implemented in the Vienna ab initio simulation package (VASP) code.^41,42 We employ the generalized gradient approximation (GGA) with the Perdew–Burke–Ernzerhof (PBE) functional to describe the exchange correlation interactions, together with the DFT-D3 method to correct the effect of weak vdW interaction.⁴³ The projector-augmented wave (PAW) method is used to describe the electron–ion interactions.⁴⁴ The k-mesh 15 × 15 × 1 and an energy cutoff of 500 eV are adopted. The convergence thresholds of force and energy are set to 0.01 eV Å⁻¹ and 10⁻⁶ eV, respectively. A vacuum space (>15 Å) between periodic images is used to suppress the interactions in the non-periodic directions. The dipole correction is taken into account in the calculation.

3 Results and discussion

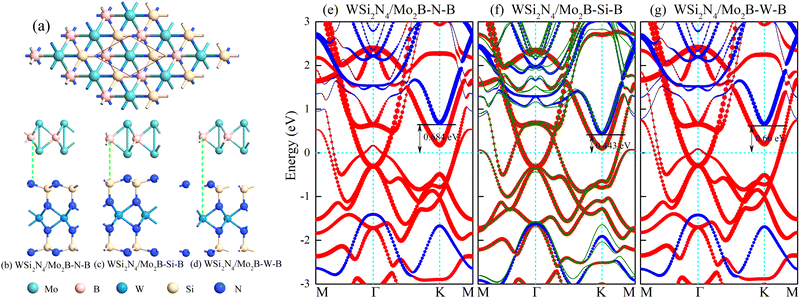
3.1. Structural and electronic properties of WSi₂N₄/Mo₂B contact: influence of stacking configurations

We examine the structural parameters of pristine WSi₂N₄ and Mo₂B before investigating the WSi₂N₄/Mo₂B heterostructures. The optimized lattice constants of WSi₂N₄ and Mo₂B are 2.91 Å and 2.87 Å, respectively, which are in agreement with previous studies.^45–47 A lattice mismatch of around 1.38% is obtained when WSi₂N₄ (1 × 1) and Mo₂B (1 × 1) are vertically stacked. Three possible vertical stacking patterns are investigated, which are denoted as WSi₂N₄/Mo₂B-N-B, WSi₂N₄/Mo₂B-Si-B and WSi₂N₄/Mo₂B-W-B [see Fig. 1(b)–(d)] in which the B atoms of Mo₂B are directly aligned with the N, Si and W atoms of WSi₂N₄, respectively. To further characterize the interfacial stability and to determine the most energetically stable stacking configurations, the binding energy is calculated as E_b = (E_h − E_m − E_w)/A, where the E_h, E_w and E_m are the total energies of the heterostructures, isolated WSi₂N₄ and isolated Mo₂B, respectively, and A is the surface area of the heterostructure supercell. The calculated binding energies are listed in Table 1. Here, the negative-valued E_b suggests that all three stacking configurations of WSi₂N₄/Mo₂B are energetically stable and may be realized experimentally. Among the three stacking patterns, WSi₂N₄/Mo₂B-Si-B stacking has the lowest E_sb, thus suggesting its energetic stability. The interlayer spacing of the WSi₂N₄/Mo₂B-Si-B stacking configuration is 2.32 Å, which is significantly lower than that of the other two stacking configurations.

Fig. 1 (a) and (b)–(d) Top view and side view of the structures of WSi₂N₄/Mo₂B heterostructures. (e)–(g) Projected band structures of WSi₂N₄/Mo₂B heterostructures in three different stacking models. The red and blue lines denote the contributions from Mo₂B and WSi₂N₄, respectively. The green lines represent the band structures with SOC.

Table 1 Calculated parameters of the WSi₂N₄ contact with MoB₂, MoB₂O₂ and MoB₂ (OH)₂. d, E_b and Φ_SB are the interlayer distance, binding energy and Schottky barrier height, respectively. Φ_t and ω_t are the height and the full width at half-maximum of the potential barrier, respectively. P_t is the electron transmission probability. ρ_t is the tunneling-specific resistivity in the unit of 10⁻⁹ Ω cm²

	WSi2N4/MoB2			WSi2N^4/MoB2O2			WSi2N4/MoB2 (OH)2
	N–B	Si–B	W–B	N–O	Si–O	W–O	N–H	Si–H	W–H
d (Å)	3.344	2.32	3.538	3.023	2.491	2.615	1.785	2.081	1.969
E b (eV Å^−2)	−0.407	−0.492	−0.406	−0.458	−0.472	−0.466	−0.526	−0.502	−0.505
Φ SB (eV)	0.684, n	0.443, n	0.660, n	Ohmic contact, p			Ohmic contact, n
Φ t (eV)	3.079	0.168	3.291	6.013	5.486	5.676	0	0.812	0.43
ω t (Å)	1.156	0.08	1.4	1.63	1.13	1.27	0	0.54	0.37
P t (%)	12.5	96.7	7.4	1.66	6.64	4.5	100	24.1	77.9
ρ t (10^−9 Ω cm^2)	4.42	4.26 × 10^−3	1.424	2.471	0.876	1.056	0	2.083 × 10^−2	1.527 × 10^−2

---

In Fig. 1(e)–(g), we show the projected band structure for the WSi₂N₄/Mo₂B heterostructures. As the monolayers are coupled via weak van der Waals force, the absence of strong interlayer interactions enables the band structures of WSi₂N₄ and Mo₂B to be well-preserved, with well-defined band edges of the semiconductor bands. The contact type and barrier height can usually be determined by the energy difference between the Fermi level and the semiconductor band edge in the heterostructure: Φ_n = E_CBM − E_F, Φ_p = E_F − E_VBM, where the E_CBM and E_VBM are the energy of the conduction band minimum and the valence band maximum of the semiconductor in the heterostructure, respectively. E_F is the Fermi energy. Here, for all three stacking configurations of WSi₂N₄/Mo₂B, the conduction bands are closer to the Fermi level, leading to an n-type Schottky contact with the Schottky barrier height (SBH) ranging from 0.443 eV to 0.684 eV (see Table 1). It is worth noting that the band structures of WSi₂N₄/Mo₂B-N-B and WSi₂N₄/Mo₂B-W-B are similar, giving rise to comparable SBH of 0.684 eV and 0.660 eV, respectively. However, the projected band structure of Mo₂B in WSi₂N₄/Mo₂B-Si-B near the Fermi level is obviously different from the other two stacking configurations, which arises from the closer interlayer distance and hence the slightly stronger interlayer interaction. Correspondingly, the SBH of the WSi₂N₄/MoB₂-SiB stacking configuration is about 0.2 eV lower than that of the other two. In addition, using WSi₂N₄/Mo₂B-Si-B as an example, we found that spin–orbit coupling (SOC) has little effect on the results [see Fig. 1(f)].

3.2. Interfacial properties of WSi₂N₄/Mo₂B contact: interfacial charge transfer and tunneling barrier

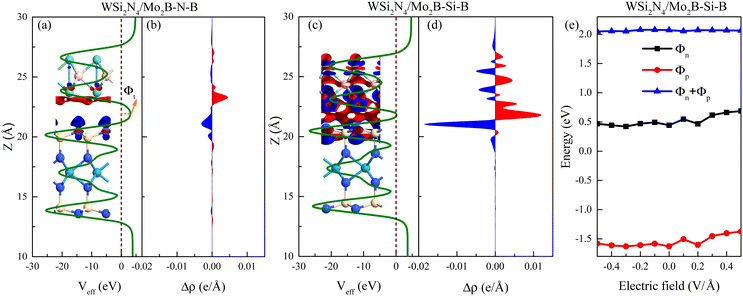
To confirm the stacking-dependent interlayer interaction observed above, we calculate the electrostatic potentials along the vertical direction of the heterostructures and the charge density differences according to Δρ = ρ_h − ρ_W − ρ_M, as displayed in Fig. 2(a)–(d). Here the ρ_h, ρ_W and ρ_M are the charge densities of the heterostructures, isolated WSi₂N₄ and Mo₂B, respectively. The blue and red regions represent the charge depletion and accumulation. The stacking of different materials to form heterostructures breaks the original symmetry of the material, which causes charge redistribution across the interface. It can be clearly seen from Fig. 2(a)–(d) that there are significant differences in the amount of electron transfer between the two stacking configurations. There is only a small amount of charge transfer between WSi₂N₄ and Mo₂B in WSi₂N₄/Mo₂B-N-B, while a significantly larger amount of charge transfer occurs between WSi₂N₄ and Mo₂B in the WSi₂N₄/Mo₂B-Si-B configuration. The transfer of a sizable amount of electrons from WSi₂N₄ to Mo₂B causes the Fermi level of Mo₂B to energetically upshift, resulting in a smaller n-type SBH of the WSi₂N₄/Mo₂B-Si-B configuration as compared to that of the WSi₂N₄/Mo₂B-N-B configuration. The work function of isolated Mo₂B is 4.897 eV, which changes to 4.624 eV in WSi₂N₄/Mo₂B-Si-B, and 4.784 eV in WSi₂N₄/Mo₂B-N-B, respectively, after forming a heterostructure with WSi₂N₄. It is worth noting that in addition to the Schottky barrier, the tunneling barrier at the interface of the semiconductor and metal also impedes the charge injection efficiency.^48,49 The tunneling barrier height Φ_t and width w_t of the heterostructures with different stacking configurations are summarized in Table 1, which are drastically different for the three configurations since the tunneling potential barrier is sensitively influenced by the spatial location and alignment of the atoms at the contacting interface. The tunneling barrier of WSi₂N₄/Mo₂B-Si-B is extremely low, which means that the electron tunneling probability will be high. The tunneling probability (P_t) across the interface can be estimated as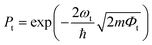 ,^48–50 where the ω_t is the full width at half-maximum of the potential barrier; ħ and m are the reduced Planck constant and the free electron mass, respectively; Φ_t represents the tunneling barrier height. The tunneling probability of WSi₂N₄/Mo₂B-Si-B is calculated to be 96.7%, which is close to 100% as the Fermi level nearly crosses the tunneling potential barrier top. Such a high transparency suggests that the charge injection across the WSi₂N₄/Mo₂B contact under the WSi₂N₄/Mo₂B-Si-B stacking configuration is predominantly limited by the SBH instead of the interfacial tunneling barrier. The tunneling-specific resistivity (ρ_t) can also be estimated based on Simmons tunneling injection model: 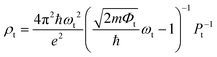under intermediate bias voltages and 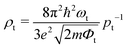when the ω_t is too small.^39,49 The calculated ρ_t is listed in Table 1.

Fig. 2 Electrostatic potential and plane-averaged differential charge density Δρ for WSi₂N₄/MoB₂-N-B (a) and (b) and WSi₂N₄/MoB₂-Si-B (c) and (d). The insets in panels (a) and (c) are the 3D isosurface of the electron charge density difference of WSi₂N₄/MoB₂-N-B and WSi₂N₄/MoB₂-Si-B, respectively. (e) The Schottky barrier height as a function of the external electric field for WSi₂N₄/MoB₂-Si-B.

We further find that the SBH under the WSi₂N₄/Mo₂B-Si-B stacking configuration is robust against an external electric field, as shown in Fig. 2(e), which is in stark contrast to many heterostructures studied previously.^{35,36,51–54} An external electric field is thus ineffective in driving a Schottky-to-ohmic transition in the WSi₂N₄/Mo₂B contact. Nevertheless, the robustness of the SBH of WSi₂N₄/Mo₂B may be beneficial for achieving a stable Schottky diode operation. We further note that reducing the distance between the semiconducting and the metallic monolayers can also reduce the SBH. However, as the distance between Mo and N atoms is only 2.32 Å in WSi₂N₄/Mo₂B-Si-B, which is close to the sum of their covalent radii, we do not expect further reducing the interlayer distance of WSi₂N₄/Mo₂B to be a feasible way of contact-type tuning.

3.3. n-Type and p-type ohmic contact design via Mo₂B surface engineering*

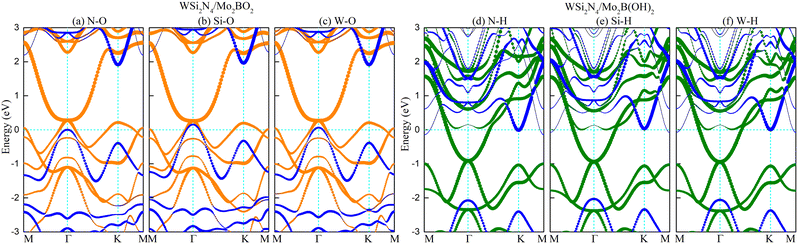
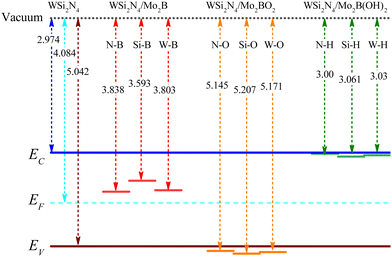
Modulating the metal work function provides an alternative way to tune the SBH. Since the outermost atoms of Mo₂B are the Mo atom, there is an abundance of free electrons on its surface, which can stably adsorb other atoms or small molecules. Previous studies have demonstrated that Mo₂B can be surface-engineered with O(Mo₂BO₂) or OH(Mo₂B(OH)₂) while still retaining its metallic nature, as well as its dynamic and thermal stability.⁴⁷ Importantly, the work functions of the surface-engineered Mo₂BO₂ and Mo₂B(OH)₂ are significantly modulated to the high value of 7.39 eV and the low value of 3.14 eV, respectively, which is in stark contrast to the work function of 4.89 eV in the pristine Mo₂B monolayer. Such significantly modulated work function immediately suggests surface engineering as a feasible approach to achieve n- and p-type ohmic contact to WSi₂N₄.

To verify whether surface-engineered Mo₂B can form ohmic contacts with WSi₂N₄, we reconstruct the WSi₂N₄ contact heterostructure using Mo₂BO₂ and Mo₂B(OH)₂ as the metal electrodes under the same set of stacking configurations (see Fig. 3 for the lattice structure and Table 1 for a summary of various contact parameters). Here we denote the stacking configurations as WSi₂N₄/Mo₂BO₂-(N, Si, W)-O and WSi₂N₄/Mo₂B(OH)₂-(N, Si, W)-H to denote the cases where (N, Si, W) is directly above the O or H atom. The E_b values of both WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂ contacts are negative, thus suggesting their energetic stability. The E_b of all stacking configurations of WSi₂N₄/Mo₂B(OH)₂ is generally lower than that of WSi₂N₄/Mo₂B. The electronic structure characteristics of WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂ contacts are shown in Fig. 4. Intriguingly, the valence band of WSi₂N₄ in WSi₂N₄/Mo₂BO₂ and the conduction band of WSi₂N₄ in WSi₂N₄/Mo₂B(OH)₂ cross the Fermi level, which means that WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂ form p-type and n-type ohmic contacts, respectively, under all three different stacking configurations. The surface engineering of Mo₂ with O or OH is thus an effective method to transform Mo₂B into an ohmic electrode for WSi₂N₄.

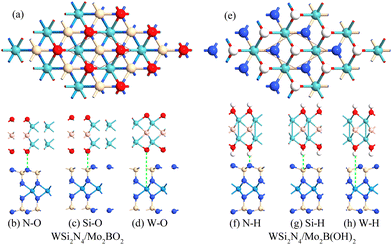Fig. 3 Top view and side view of the heterostructures of WSi₂N₄ contact with Mo₂BO₂ (a)–(d) and Mo₂B(OH)₂ (e)–(h), respectively.

Fig. 4 The projected electronic band structures of (a)–(c) WSi₂N₄/Mo₂BO₂ and (d)–(f) WSi₂N₄/Mo₂B(OH)₂ with different stack patterns. Blue, orange and olive symbols denote the contributions from WSi₂N₄, Mo₂BO₂ and Mo₂B(OH)₂, respectively.

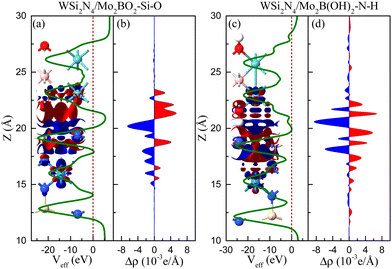
We now examine how the interfacial charge redistribution can shift the Fermi level upon forming a contact. To understand the role of Mo₂BO₂ and Mo₂B(OH)₂ in the charge transfer, using WSi₂N₄/Mo₂BO₂-Si-O and WSi₂N₄/Mo₂B(OH)₂-N-H as the respective examples, we calculate the plane-averaged electron density difference Δρ and the three dimensional isosurfaces, as depicted in Fig. 5. The electron accumulation region and depletion region are marked in red and blue, respectively. One can see that the charges are mainly accumulated in the Mo₂BO₂ layer, whereas they are depleted in the WSi₂N₄ layer for WSi₂N₄/Mo₂BO₂-Si-O (see Fig. 5(a) and (b)). However, the situation is reversed in WSi₂N₄/Mo₂B(OH)₂-N-H (see Fig. 5(c) and (d)). Thus, an opposite contact type is formed when WSi₂N₄ is in contact with Mo₂BO₂ and Mo₂B(OH)₂. Compared with WSi₂N₄/Mo₂B-Si-B (see Fig. 2), we find that although the charge is depleted around the WSi₂N₄ layer, the electron activity area is mainly in the metal layer in WSi₂N₄/Mo₂B-Si-B. However, the charge of the WSi₂N₄ layer is more affected. Surprisingly, the effective electrostatic potential of WSi₂N₄/Mo₂B(OH)₂-N-H exhibits zero interfacial tunneling barrier height, thus indicating that the WSi₂N₄/Mo₂B(OH)₂ ohmic contacts are compatible with high charge injection efficiency. This aspect is in contrast to WSi₂N₄/Mo₂BO₂ ohmic contact in which the interfacial tunneling barriers are significantly higher, with the best performing contact exhibiting a transmission probability of only P_t = 6.64% with the WSi₂N₄/Mo₂BO₂-Si-O stacking configuration, thus suggesting interfacial tunneling as a key factor that limits the charge injection across such a contact.

Fig. 5 Electrostatic potential and plane-averaged differential charge density Δρ for WSi₂N₄/Mo₂BO₂-Si-O (a) and (b) and WSi₂N₄/Mo₂B(OH)₂-N-H (c) and (d). The insets in panels (a) and (c) are the 3D isosurface of the electron charge density difference of WSi₂N₄/Mo₂BO₂-Si-O and WSi₂N₄/Mo₂B(OH)₂-N-H, respectively.

In addition to the Schottky barrier at the vertical contact interface between the semiconductor and the metal, the transport barrier between the lateral source/drain and the two-dimensional semiconductor channel interface is also another key factor that may influence the device performance. Fig. 6 shows a schematic drawing of the Mo₂B-WSi₂N₄ interface outlining the charge transport pathway across the interface. The lateral SBH is calculated as: Φ_n,L = E_CBM − E_F and Φ_p,L = E_F − E_VBM, where the E_CBM and E_VBM are the energies of the CBM and VBM of pure WSi₂N₄. E_F is the Fermi level of the heterostructure. The band edges of WSi₂N₄ and work functions of the heterostructures are summarized in Fig. 7. We present a schematic of the band alignments and electron injection mechanism in Fig. 6(b–d). For WSi₂N₄/Mo₂B-Si-B, there are high barriers in both the vertical (0.443 eV) and lateral (0.619 eV) directions [see Fig. 6(b)]. The Fermi level of WSi₂N₄/Mo₂BO₂-Si-O is slightly lower than the VBM of pure WSi₂N₄, suggesting that lateral p-type ohmic contact can be formed in WSi₂N₄/Mo₂BO₂-Si-O, as shown in Fig. 6(c). Unfortunately, it has a very high tunneling barrier (5.486 eV). Similarly, the Fermi level of the WSi₂N₄/Mo₂B(OH)₂-N-H contact aligns nearly with the CBM energy of the WSi₂N₄ channel, giving rise to n-type quasi-ohmic contact with ultra-low SBH (0.026 eV), as is demonstrated in Fig. 6(d). The WSi₂N₄/Mo₂B(OH)₂ thus represents an exceptional ohmic contact with simultaneous n-type ohmic or quasi-ohmic behaviors along both vertical and lateral transport directions. The zero interfacial tunneling WSi₂N₄/Mo₂B(OH)₂ represents another practically useful feature that rarely occurs in other 2D/2D metal/semiconductor contacts.

Fig. 6 (a) Schematic diagram of WSi₂N₄/Mo₂B contacts. The black arrow represents the carrier injection direction. (b)–(d) Schematic diagram of the band arrangement and carrier injection mechanism from electrode to channel for WSi₂N₄/Mo₂B, WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂.

Fig. 7 Work function alignment of WSi₂N₄, WSi₂N₄/Mo₂B, WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂. The blue, cyan and wine solid lines represent the CBM, Fermi level and VBM of pure WSi₂N₄. The red, orange and olive short horizontal lines represent the Fermi level positions of WSi₂N₄/Mo₂B, WSi₂N₄/Mo₂BO₂ and WSi₂N₄/Mo₂B(OH)₂ in different stacking patterns, respectively.

4. Conclusion

In conclusion, we study the contact properties of WSi₂N₄ with Mo₂B and Mo₂B whose surface is fully saturated by O and OH groups using DFT calculations. WSi₂N₄ and Mo₂B form n-type Schottky contacts in both the vertical and lateral directions, and the Schottky barrier in the vertical direction is robust to the electric field. p-Type ohmic contact is formed when WSi₂N₄ is in contact with Mo₂BO₂. Importantly, n-type ohmic contact with zero tunneling barrier in the vertical direction of the transistor and quasi-ohmic contact with ultra-low SBH in the lateral direction can be obtained in WSi₂N₄/Mo₂B(OH)₂, suggesting the potential role of WSi₂N₄/Mo₂B(OH)₂ in achieving an energy-efficient transistor device. Furthermore, the WSi₂N₄/Mo₂BO₂ contact, despite having a sizable interfacial tunneling barrier, similarly exhibits excellent p-type ohmic contact along the lateral direction. The simultaneous presence of n- and p-type contacts immediately suggests the potential of surface-engineered Mo₂B metallic monolayers as an electrode materials to achieve WSi₂N₄-based CMOS device technology. Our results reveal surface engineering of 2D metallic monolayers as a feasible route towards energy-efficient 2D semiconductor electronic devices.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

The authors acknowledge support from the National Natural Science Foundation of China (Grant No. 12104136), Scientific Research Found of Hunan Provincial Education Department (Grant No. 21B0622 and 21C0549), Hunan Provincial Natural Science Foundation of China (No. 2022JJ40008 and No. 2023JJ30094), and Science Foundation of Hengyang Normal University of China (Grant No. 2021QD12). Y. S. A. is supported by the Singapore Ministry of Education (MOE) Academic Research Fund (AcRF) Tier 2 Grant (MOE-T2EP502210019) and the SUTD-ZJU IDEA Thematic Research Grant (SUTD-ZJU (TR) 202203).

References

1. R. K. Ratnesh, A. Goel, G. Kaushik, H. Garg, Chandan, M. Singh and B. Prasad, Mater. Sci. Semicond. Process., 2021, 134, 106002.
2. F. Schwierz, J. Pezoldt and R. Granzner, Nanoscale, 2015, 7, 8261.
3. S. Das, A. Sebastian, E. Pop, C. J. McClellan, A. D. Franklin, T. Grasser, T. Knoblochm, Y. Illarionov, A. V. Penumatcha, J. Appenzeller, Z. Chen, W. Zhu, I. Asselberghs, L. Li, U. E. Avci, N. Bhat, T. D. Anthopoulos and R. Singh, Nat. Electron., 2021, 4, 786.
4. C. Liu, H. Chen, S. Wang, Q. Liu, Y. Jiang, D. W. Zhang, M. Liu and P. Zhou, Nat. Nanotechnol., 2020, 15, 545.
5. Q. H. Wang, K. Kalantar-Zadeh, A. Kis, J. N. Coleman and M. S. Strano, Nat. Nanotechnol., 2012, 7, 699.
6. S. Joseph, J. Mohan, S. Lakshmy, S. Thomas, B. Chakraborty, S. Thomas and N. Kalarikkal, Mater. Chem. Phys., 2023, 297, 127332.
7. M. Naguib, V. N. Mochalin, M. W. Barsoum and Y. Gogotsi, Adv. Mater., 2014, 26, 992.
8. A. Ahmed, S. Sharma, B. Adak, M. M. Hossain, A. M. LaChance, S. Mukhopadhyay and L. Sun, InfoMat, 2022, 4, e12295.
9. H. Liu, A. T. Neal, Z. Zhu, Z. Luo, X. Xu, D. Tomanek and P. D. Ye, ACS Nano, 2014, 8, 4033.
10. H. Liu, Y. Du, Y. Deng and P. D. Ye, Chem. Soc. Rev., 2015, 44, 2732.
11. V. Cheudhary, P. Neugebauer, O. Mounkachi, S. Lahbabi and A. E. Fatimy, 2D Mater., 2022, 9, 032001.
12. Y. Hong, Z. Liu, L. Wang, T. Zhou, W. Ma, C. Xu, S. Feng, L. Chen, M. Chen, D. Sun, X. Chen, H. Cheng and W. Ren, Science, 2020, 369, 670.
13. W. Fei, J. Trommer, M. C. Lemme, T. Mikolajick and A. Heinzig, InfoMat, 2022, 4, e12355.
14. S. B. Mitta, M. S. Choi, A. Nipane, F. Ali, C. Kim, J. T. Teherani, J. Hone and W. J. Yoo, 2D Mater., 2021, 8, 012002.
15. Y. S. Ang, L. Cao and L. K. Ang, InfoMat, 2021, 3, 502.
16. P. V. Pham, S. C. Bodepudi, K. Shehazad, Y. Liu, Y. Xu, B. Yu and X. Duan, Chem. Rev., 2022, 122, 6514.
17. D. S. Schulman, A. J. Amold and S. Das, Chem. Soc. Rev., 2018, 47, 3037.
18. Y. Wang, S. Liu, Q. Li, R. Quhe, C. Yang, Y. Guo, X. Zhang, Y. Pan, J. Li, H. Zhang, L. Xu, B. Shi, H. Tang, Y. Li, J. Yang, Z. Zhang, L. Xiao, F. Pan and J. Lu, Rep. Prog. Phys., 2021, 84, 056501.
19. Y. Zheng, J. Gao, C. Han and W. Chen, Cell Rep. Phys. Sci., 2021, 2, 100298.
20. X. Liu, M. S. Choi, E. Hwang, W. J. Yoo and J. Sun, Adv. Mater., 2022, 34, 2108425.
21. L. Cao, G. Zhou, Q. Wu, S. Yang, H. Y. Yang, Y. S. Ang and L. K. Ang, Phys. Rev. Appl., 2020, 13, 054030.
22. C. S. Lau, J. Y. Chee, Y. S. Ang, S. W. Tong, L. Cao, Z. Ooi, T. Wang, L. K. Ang, Y. Wang, M. Chhowalla and K. E. J. Goh, ACS Nano, 2020, 14, 13700.
23. L. Cao, X. Deng, Z. Tang, G. Zhou and Y. S. Ang, Appl. Phys. Lett., 2022, 121, 113104.
24. P.-C. Shen, et al. , Nature, 2021, 593, 211.
25. T. Wu and J. Guo, Appl. Phys. Lett., 2022, 121, 023507.
26. W. Li, et al. , Nature, 2023, 613, 274.
27. T. Su, Y. Li, Q. Wang, W. Zhao, L. Cao and Y. S. Ang, J. Phys. D: Appl. Phys., 2023, 56, 234001.
28. X. Ding, S. Zhang, M. Zhao, Y. Xiang, K. H. L. Zhang, X. T. Zu, S. Li and L. Qiao, Phys. Rev. Appl., 2019, 12, 064061.
29. B. Zhang, J. Zhou and Z. Sun, J. Mater. Chem. A, 2022, 10, 15965.
30. Y. Liu, P. Stradins and S. H. Wei, Sci. Adv., 2016, 2, e1600069.
31. M. K. Mohanata and A. D. Sarkat, Appl. Surf. Sci., 2021, 540, 148389.
32. Z. Xu, M. Chen and S. F. Liu, J. Phys. Chem. Lett., 2021, 12, 1718.
33. X. Zhang, L. Feng, S. Zhong, Y. Ye, H. Pan, P. Liu, X. Zheng, H. Li, M. Qu and X. Wang, Sci. China Mater., 2023, 66, 811.
34. Z. Li, Y. Zheng, G. Li, H. Wang, W. Zhu, H. Wang, Z. Chen, Y. Yuan, X. C. Zeng and Y. Wu, J. Phys. Chem. Lett., 2023, 14, 2941.
35. S. Nguyen, C. Q. Nguyen, Y. S. Ang, N. V. Hiang, N. M. Hung and C. V. Nguyen, Langmuir, 2023, 39, 6637.
36. C. V. Nguyen, Phys. Rev. B, 2021, 103, 115429.
37. C. C. Tho, C. Yu, Q. Tang, Q. Wang, T. Su, Z. Feng, Q. Wu, C. V. Nguyen, W. Ong, S. Liang, S. Guo, L. Cao, S. Zhang, S. A. Yang, L. K. Ang, G. Wang and Y. S. Ang, Adv. Mater. Interfaces, 2023, 10, 2201856.
38. Y. Yin, Q. Gong, M. Yi and W. Guo, Adv. Funct. Mater., 2023, 2214050.
39. C. C. Tho, S. Guo, S. Liang, W. L. Ong, C. S. Lau, L. Cao, G. Zhao and Y. S. Ang, Appl. Phys. Rev., 2023, 10, 041307.
40. L. Kong, Y. Chen and Y. Liu, Nano Res., 2021, 14, 1768.
41. G. Kresse and J. Furthmüller, Phys. Rev. B, 1996, 54, 11169.
42. G. Kresse and J. Furthmüller, Comput. Mater. Sci., 1996, 6, 15.
43. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, J. Chem. Phys., 2010, 132, 154104.
44. G. Kresse and D. Joubert, Phys. Rev. B, 1999, 59, 1758.
45. L. Wang, Y. Shi, M. Liu, A. Zhang, Y. Hong, R. Li, Q. Gao, M. Chen, W. Ren, H. Cheng, Y. Li and X. Chen, Nat. Commun., 2021, 12, 2361.
46. Z. Wang, S. W. Fan, H. G. Piao and Z. S. Lu, Appl. Surf. Sci., 2021, 538, 148026.
47. A. Shukla, G. Sharma and S. Krishnamurty, Appl. Surf. Sci., 2023, 615, 156299.
48. A. Allain, J. Kang, K. Banerjee and A. Kis, Nat. Mater., 2015, 14, 1195.
49. Q. Wang, L. Cao, S. Liang, W. Wu, G. Wang, C. H. Lee, W. L. Ong, H. Y. Yang, L. K. Ang, S. A. Yang and Y. S. Ang, npj 2D Mater. Appl., 2021, 5, 71.
50. Y. Wang, H. Yuan, Z. Li, J. Yang and A. C. S. Appl, Electron. Mater., 2022, 4, 1082.
51. L. Cao, G. Zhou, Q. Wang, L. K. Ang and Y. S. Ang, Appl. Phys. Lett., 2021, 118, 013106.
52. J. E. Padilha, A. Fazzio and A. J. R. Silva, Phys. Rev. Lett., 2015, 114, 066803.
53. L. Cao, Y. S. Ang, Q. Wu and L. K. Ang, Appl. Phys. Lett., 2019, 115, 241601.
54. N. T. T. Binh, C. Q. Nguyen, T. V. Vu and C. V. Nguyen, J. Phys. Chem. Lett., 2021, 12, 3934.

---