High-performance molecular spin filters based on a square-planar four-coordinate Fe complex and covalent pyrazine anchoring groups†
Yudi
Wang
 a,
Haoyang
Pan
ab,
Yuxuan
Jiang
ac,
Jie
Li
a,
Dongying
Lin
a,
Shi
Li
a,
Yongfeng
Wang
a,
Haoyang
Pan
ab,
Yuxuan
Jiang
ac,
Jie
Li
a,
Dongying
Lin
a,
Shi
Li
a,
Yongfeng
Wang
 a,
Stefano
Sanvito
d and
Shimin
Hou
a,
Stefano
Sanvito
d and
Shimin
Hou
 *ac
*ac
aKey Laboratory for the Physics and Chemistry of Nanodevices, School of Electronics, Peking University, Beijing 100871, China. E-mail: smhou@pku.edu.cn
bInstitute of Spin Science and Technology, South China University of Technology, Guangzhou 511442, China
cCentre for Nanoscale Science and Technology, Academy for Advanced Interdisciplinary Studies, Peking University, Beijing 100871, China
dSchool of Physics, AMBER and CRANN Institute, Trinity College, Dublin 2, Ireland
First published on 11th December 2023
Abstract
Achieving a high degree of spin polarization at the nanoscale is essential in the field of molecular spintronics. In order to design an efficient molecular spin filter generating highly spin-polarized currents, three requirements need to be met: (1) a large spin polarization (SP), implying a substantial difference between the transmission coefficients for the two spin channels at the Fermi energy, EF; (2) a sufficiently high transmission for the favored spin channel, and (3) an appreciable difference in transmission between the two spin channels over a broad energy range around EF. Considering that for single-molecule devices, frontier molecular orbitals, especially the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the central molecule, generally play a dominant role in the device performance, here we propose a promising method for meeting all the three requirements. Our concept is based on a magnetic molecule, whose HOMO and LUMO of one spin type are entirely localized, making little contribution to the transport around EF, in stark contrast to the delocalized HOMO and LUMO of the other spin type. A high electric current for the favored spin channel can then be obtained, thanks to the small energy gap between the delocalized HOMO and LUMO, as well as an appropriate interfacial charge transfer that moves the delocalized HOMO or LUMO close to the electrodes’ EF. High-performance molecular spin filters are thus effectively realized by a square-planar four-coordinate Fe complex (FeN4) sandwiched between two armchair single-walled carbon nanotube (SWCNT) electrodes with covalent pyrazine anchors. This demonstrates the validity of our proposed concept and offers a new and tantalizing route towards the design of future high-performance molecular spintronic devices.
Introduction
Spintronics, whose main goal is to use the electron spin for information processing, has many potential advantages over conventional electronics, such as low-power consumption and high data processing speed.1–5 With the concomitant trend towards miniaturization, driving electronic devices to their ultimate molecular-scale limit, organic molecules have been considered promising for integration into spintronic devices due to their weak spin–orbit and hyperfine interactions.2,6–9 This results in the possibility of preserving spin coherence over times and distances much longer than in conventional inorganic metals or semiconductors.2,4,6,8–11 In addition, organic materials provide a tantalizing opportunity for creating a variety of high-performance devices due to their rich diversity and functionality.3,12,13 Therefore, a new field, namely molecular spintronics, has emerged, with the goal of developing a new generation of spintronic devices based on molecular materials or, in the longer term, on individual or a few molecules.4 In this field, the successful implementation of key spin-dependent transport phenomena, including magnetoresistance and spin transfer torque, primarily requires the efficient generation of highly spin-polarized currents.6,11,14–18 Ideally, one spin channel should be dominant, showing metallic transport in contrast to the insulating behavior of the other.6,14,17–19 An important criterion for assessing the spin-filtering performance of a junction is spin polarization, defined as SP = [T↑(EF) − T↓(EF)]/[T↑(EF) + T↓(EF)], where T↑(EF) and T↓(EF) represent the transmission coefficients for the spin-up (majority) and spin-down (minority) channels at the Fermi energy (EF), respectively.6 In addition, to further quantify the spin-filtering effect at finite bias voltages, that is, the degree of spin polarization of an electric current, an efficiency parameter, namely the spin-filtering efficiency (SFE), is calculated by evaluating the spin-up and spin-down currents (respectively I↑ and I↓) at different applied bias, namely the SFE = (I↑ − I↓)/(I↑ + I↓).20 Generally, large SP at zero bias is an essential prerequisite for a perfect molecular spin filter. Furthermore, to be experimentally observable, a sufficiently high conductance for the favored spin type is also of fundamental importance. For practical applications, the transmission for the two spin channels must differ appreciably over a broad energy range around EF, so that a highly spin-polarized electric current can be efficiently generated.19 Nowadays, designing novel spin filters whose performances meet all the above three requirements is highly desirable, since it may pave the way for the development of high-performance molecular spintronic devices. Note also that the time of operation of such devices will be comparable with the blocking time set by magneto-crystalline anisotropy.The strategy for constructing such half-metallic molecular spintronic devices can involve two options. One option is to use a nonmagnetic molecular bridge with magnetism introduced to the system through two magnetic electrodes.11,19,21,22 For example, zigzag-edged graphene nanoribbons (zGNRs) are possible magnetic electrodes. Spin filtering is achievable in single-molecule spintronic devices constructed with zGNR electrodes due to the parity matching principle of the wave functions of tunnelling electrons in all parts of the device (i.e., the left and right zGNR electrodes and the central molecule).20,23 In addition, ferromagnetic electrodes such as nickel-based ones were also proposed to produce strongly spin-polarized currents, mainly due to an s-blocking mechanism.6,24,25 The second option is to use a magnetic molecule as the scattering center in combination with two nonmagnetic electrodes.11,21,26–29 It is well-known that for electronic devices based on single molecules, the interaction of frontier molecular orbitals (FMOs) with the continuum states of the electrodes dictates the energy level alignment and the electronic coupling, which are two fundamental factors determining the device performance.30–32 Generally speaking, the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO) of the central molecule are energetically closer to the electrodes’ EF than other orbitals and therefore they play a dominant role in the transport properties of a single-molecule junction.33,34 As a result, electron transport in the second type of molecular spintronic devices is intricately linked to the spin-dependent electronic structure of the central magnetic molecule, especially the difference in the HOMOs and LUMOs between the two spin types. When the HOMO–LUMO energy gap for one spin type is much smaller than that for the other, the magnetic molecule may hold great potential as a functional unit in molecular spin filters.35,36
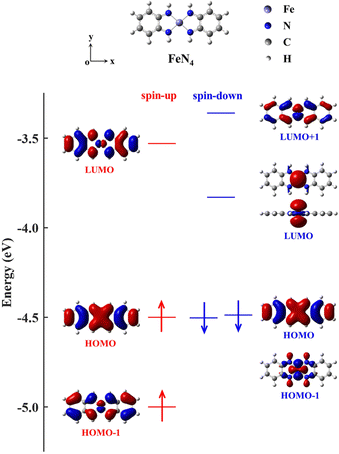
To achieve this goal, coordination chemistry plays a key role by providing a variety of transition metal complexes.3,37 They consist of an inner transition metal core surrounded by diverse organic ligands, offering appealing possibilities since their atomic, electronic, and magnetic properties can be effectively tuned by varying the central cores and/or ligands.4,8,27,38,39 As potential candidates, the transition metal complexes in which the transition metal atom such as Ni, palladium (Pd), platinum (Pt), iron (Fe), cobalt (Co) or copper (Cu) adopts a square-planar four-coordinate motif with various noninnocent ligands have received wide interest from both experimental and theoretical points of view.40–44 Taking the square-planar four-coordinate Fe complex containing o-phenylenediamines (denoted as FeN4 in Fig. 1) as an example, whose transport properties have been theoretically investigated in previous research,38,45 we observe that the HOMO–LUMO gap of the spin-up electrons (0.97 eV) is 0.31 eV larger than that (0.66 eV) of the spin-down ones (see the energy-level diagram of Fig. 1). However, when FeN4 is covalently connected to two armchair (5,5) single-walled carbon nanotube (SWCNT) electrodes,38 the low-bias electrical conductance of the resultant molecular junction is observed to be mainly determined by the spin-up channel, which displays a prominent spin-up LUMO peak in the transmission spectrum around EF. In contrast, despite the smaller HOMO–LUMO gap of the spin-down channel, the spin-down LUMO contributes little to the transmission, owing to its localization nature and the ensuing weak coupling to the SWCNT electrodes. However, the completely delocalized spin-down HOMO perfectly couples to the electronic states of the SWCNT electrodes, also offering a transmission channel. This results in T↑(EF) and T↓(EF) to be 5.1 × 10−2 and 8.6 × 10−3, respectively, that is, the junction exhibits moderate spin-polarization,38 not suitable for practical applications.
Based on the above results, in order to design high-performance molecular spin filters, we propose a new strategy based on a special type of magnetic molecules. In particular, we aim to explore molecules where, for one spin type, both the HOMO and LUMO are completely localized. This results in a weak electronic coupling with the continuum states of the electrodes, providing a broad low transmission region around EF. At the same time, the HOMO and LUMO for the other spin type must be fully delocalized, implying their strong coupling to the electrodes. A relatively small energy gap between these two delocalized orbitals is desired to ensure better transmission for this spin channel. Furthermore, appropriate charge transfer between the central molecule and the electrodes may be used to tune the position of the Fermi level with respect to the delocalized HOMO or LUMO.33 With this configuration, both high spin polarization and high transmission for the favored spin channel are expected over a broad energy range.
The design of magnetic molecules with these characteristics can be pursued by considering alternative metal complexes containing the o-phenylenediamine ligand, a class of compounds that have received much attention due to their applications in catalytic and biological processes.46–52 Notably, previous investigations on the spin-polarized transport properties of such complexes have been scarce so far.38,45,53 Hence, here, we focus on complexes made of Fe with o-phenylenediamines, based on a square-planar four-coordinate motif, and investigate their potential as high-performance spin filters when sandwiched between two armchair SWCNT electrodes, or two N-doped graphene electrodes. In both cases, it is expected that the interaction between the π-type continuum of states of the carbon electrodes and the π-type FMOs of the central molecule can result in efficient electron transport. Since both fused benzene and pyrazine groups promote planarity and enhance conjugation, thus shrinking the energy gap between the delocalized HOMO and LUMO,32,54 we employ both benzene and pyrazine as end groups to functionalize FeN4. We find that both the resulting molecules have the desired feature, namely the delocalized HOMO and LUMO for the spin-up electrons together with the completely localized HOMO and LUMO for the spin-down ones. Combining the non-equilibrium Green's function formalism with density functional theory (that is, the NEGF+DFT approach),9,55–62 we show that large spin polarization together with high transmission of the spin-up channel can be achieved for both benzene- and pyrazine-terminated FeN4 attached to two armchair SWCNT electrodes. In these, the localized spin-down HOMO and LUMO do not contribute to the junction transmission. Notably, since pyrazine anchors can induce partial electron transfer from the electrodes to the central molecule due to their electronegative N atoms,32 the spin-up LUMO-dominated transmission peak lies exactly at EF, making spin-filtering efficient and effective. Further calculations show that this remarkable spin-filtering performance is robust against different SWCNT edges, SWCNT's curvature, and even with N-doped graphene electrodes. Our findings demonstrate a potential route to realize high-performance and robust advanced molecular spintronic devices.
Computational methods
Geometry optimization and spin-resolved electronic structure calculations of the molecular junctions and the isolated molecules have been performed with the SIESTA code, which is an efficient numerical implementation of DFT.63,64 The atomic cores are described using improved Troullier–Martins norm-conserving pseudopotentials and the valence states are expanded over a finite-range numerical basis set.65 A user-defined double-zeta plus polarization (DZP) basis set is constructed for H, C, N, O, F and Fe atoms. The generalized gradient approximation (GGA) within the Perdew–Burke–Ernzerhof (PBE) formulation is employed for the exchange–correlation energy.66 The real space grid is defined using an equivalent cutoff of 250 Ry. Geometry optimization is performed using a standard conjugate gradient until all the atomic forces are smaller than 0.03 eV Å−1 for molecular junctions and 0.01 eV Å−1 for isolated molecules. For these isolated molecules, DFT calculations are also performed using the Gaussian 16 package at the PBE/6-311+G(d,p) level.67 All the results involving optimized atomic structures, spin density, and frontier molecular orbital energy level diagrams obtained using the SIESTA code are well consistent with those obtained via the Gaussian 16 package (see Fig. S1–S3, ESI†). This further confirms the reliability of the pseudopotentials and basis sets built for this work.The spin-resolved transport calculations have been performed using the SMEAGOL code, which is a practical implementation of the NEGF+DFT method employing SIESTA as the DFT engine.9,60,61 Herein, the same pseudopotentials, basis sets, and GGA functional are used. It should be noted that standard GGA functionals often have difficulties in describing correctly the electronic structure of transition metal complexes. By comparing with the results obtained by treating the strong correlation of the Fe 3d electrons using a GGA+U method,68,69 we can infer that the PBE GGA functional is rather accurate for the low-bias spin-polarized transport calculations of these FeN4-based molecular junctions (see Fig. S4 of the ESI† for a comparison between the GGA and GGA+U results). The unit cell of the extended molecule consists of the central FeN4 molecule, benzene or pyrazine anchors, and two SWCNT electrodes with the armchair edges (see Fig. S5 of the ESI† for further calculations, indicating the reliability of our junction models). The transport is, by definition, along the z-axis. The matching between the Hartree potential of the electrodes and that at the edges of the extended molecule is guaranteed by a constant shift of the Hartree potential of the extended molecule relative to that of the electrodes.9,60,61 In order to model isolated one-dimensional armchair SWCNT electrodes, the k-point grid of 1 × 1 × 1 is adopted using a large vacuum region surrounding the junctions. The spin-resolved current–voltage, I–V, curves of the junctions are calculated using the Landauer–Büttiker formula as70
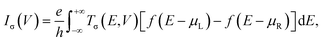 | (1) |
| Tσ(E,V) = Tr[ΓL,σGRσΓR,σGR+σ](E,V), | (2) |
Results and discussion
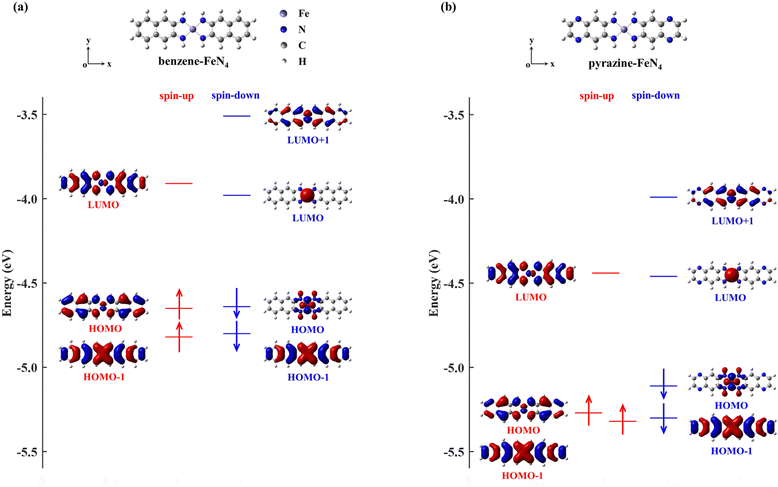
In order to narrow the FeN4 HOMO–LUMO gap of the spin-up electrons for a better transmission of this spin channel, we consider the isolated FeN4 being functionalized with two typical aromatic end groups, namely fused benzene and pyrazine. We begin our study by looking at their electronic properties before considering the junction transport. The resultant benzene- and pyrazine-ended FeN4 molecules are shown in Fig. 2(a) and (b), and they are denoted as benzene–FeN4 and pyrazine–FeN4, respectively. In Fig. 2, we also show the energy-level diagram together with the spatial distribution of the FMOs, finding that the two molecules have similar orbital spatial distributions for all the FMOs listed. Clearly, when comparing with the FMOs of the isolated FeN4 (see Fig. 1), we can conclude that the fused benzene and pyrazine end groups have significant effects on the electronic structure. This is mainly evident in two aspects. First, a change in the order of the HOMO and HOMO−1 with respect to FeN4 can be found for both spin species in benzene–FeN4 and pyrazine–FeN4, while the other FMOs retain a similar orbital distribution. For example, for both benzene–FeN4 and pyrazine–FeN4, the spin-up HOMO is primarily derived from the Fe 3dyz orbital (consider that all molecules are placed in the x–y plane), whereas for FeN4, the Fe 3dyz orbital character is for the spin-up HOMO−1, which is 0.50 eV lower in energy than the spin-up HOMO. In turn, the spin-up HOMO of FeN4 has no contribution from Fe 3d atomic orbitals (see Fig. 1). As for the spin-down electrons, although the FeN4 HOMO and HOMO−1 are almost degenerate, the HOMOs for benzene–FeN4 and pyrazine–FeN4, mainly attributed to the Fe 3dx2−y2 orbital and completely localized, are respectively 0.16 and 0.19 eV higher in energy than the HOMO−1. This, in turn, looks like the FeN4 HOMO and is also π-type. Such an energy level arrangement of the spin-down electrons in both benzene–FeN4 and pyrazine–FeN4, namely a localized HOMO combined with a delocalized HOMO−1, is precisely what we envision. Note that since the orbital rearrangement only concerns occupied states, it has no effects on the molecular magnetic moment. Thus, in analogy to FeN4, the magnetic moment of benzene–FeN4 and pyrazine–FeN4 is computed at 2.0μB (bohr magneton), implying that their ground state is a spin triplet. As expected and shown in Fig. S1b–S3b of the ESI,† the spin density is mostly distributed around the central Fe ion, which is responsible for the molecular magnetic moment.As a second feature, we observe a significant reduction in the spin-up HOMO–LUMO gap of both benzene–FeN4 and pyrazine–FeN4, when compared to that of the isolated FeN4 (0.97 eV). The spin-up HOMO–LUMO gaps for benzene–FeN4 and pyrazine–FeN4 are 0.74 and 0.83 eV, corresponding to a decrease of 0.23 and 0.14 eV, respectively. In contrast, it is worth noting that improvement in conjugation has no effect on the energy separation of the spin-down states between the localized LUMO and the localized occupied orbitals, namely the HOMO of benzene–FeN4 and pyrazine–FeN4 as well as the HOMO−1 of FeN4. Thus, the two main changes in the electronic structure described above due to the benzene and pyrazine end groups result, not only in a smaller spin-up HOMO–LUMO gap, but also in the delocalization (localization) of the spin-up (spin-down) HOMO and LUMO states. Such features perfectly meet the target magnetic-molecule properties needed for our proposed strategy to make high-performance molecular spin filters. Therefore, benzene–FeN4 and pyrazine–FeN4 both serve as potential candidates for the spin-down filtering together with efficient electron transport governed by the spin-up channel.
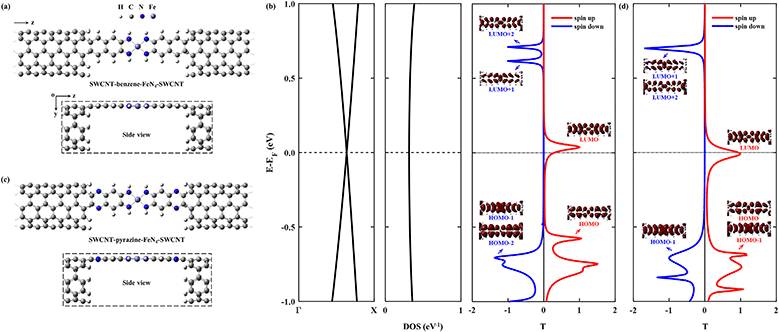
Then we construct two molecular junctions, namely SWCNT–benzene–FeN4–SWCNT and SWCNT–pyrazine–FeN4–SWCNT, where benzene and pyrazine are employed as anchors to connect FeN4 to two semi-infinite open-ended armchair (5,5) SWCNTs. These appear as ideal electrodes due to the long spin-relaxation length and weak spin decoherence of graphitic nanostructures.71–73 In addition, two bands cross EF in the band structure of an infinite armchair (5,5) SWCNT, demonstrating that it is a typical quasi-one-dimensional metal with a constant density of states (DOS) around EF.74,75 In order to find the equilibrium geometry, we systematically vary the separation between the two SWCNTs and optimize the positions of the central benzene–FeN4 or pyrazine–FeN4 and the adjacent several layers of the left and right electrodes until the total energy reaches a local minimum. Fig. 3(a) and (c) show both the top and side views of the optimized atomic structures of the two junctions. The central square-planar four-coordinate motif is placed in the x–z plane by definition. It is worth noting that both benzene–FeN4 and pyrazine–FeN4 well retain their planar conformation in the presence of two SWCNT electrodes and the optimized bond lengths in the central molecular region do not notably change, compared to those of the isolated molecules. For example, the Fe–N bond lengths are both optimized to be 1.88 Å in the two junctions, while they are 1.87 Å in the isolated molecules (see Fig. S2a and S3a, ESI†). Similarly, the adjacent C–N bond lengths are calculated to be 1.37 and 1.36 Å in the SWCNT–benzene–FeN4–SWCNT and SWCNT–pyrazine–FeN4–SWCNT junctions, respectively, identical to those in their corresponding isolated molecules. In addition to the marginal change in the atomic structure, we also find that both benzene–FeN4 and pyrazine–FeN4 well preserve their unique magnetic properties in the two-probe systems. Since the spin density is mostly distributed around the central Fe ion (see Fig. S6, ESI†), the magnetism of these molecular junctions mainly originates from the Fe ion.
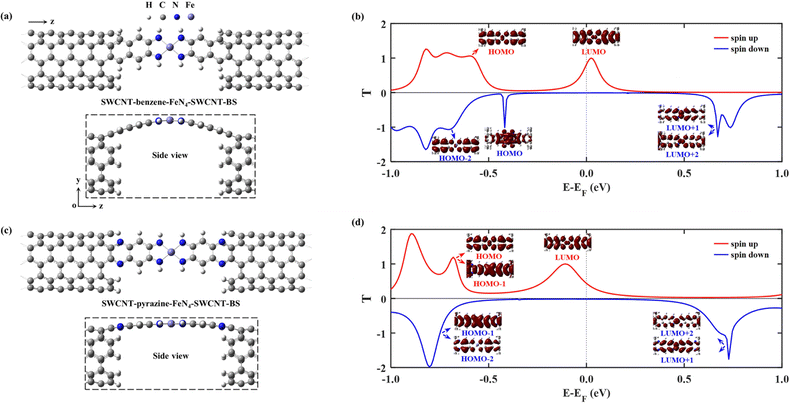
We first study the spin transport properties of the SWCNT–benzene–FeN4–SWCNT junction. Its equilibrium transmission curves are displayed in Fig. 3(b), with red and blue lines corresponding to the spin-up and spin-down transmission spectra, respectively. As we can see, the transmission spectra show remarkably spin-polarized features. Clearly, one appreciable spin-up transmission peak appears close to EF, centered at around 0.04 eV, with its tail extending below EF and thus providing a high zero-bias transmission. In stark contrast, all prominent transmission peaks for the spin-down channel lie far away from EF and decay rapidly towards it, resulting in a considerably broad region of tiny transmission going roughly from −0.60 eV to 0.55 eV. In order to fully quantify the marked difference in transmission between the two spin channels at the Fermi level, T↑(EF) and T↓(EF) are calculated to be 0.25 and 1.8 × 10−3, respectively, resulting in a spin polarization of 98.6%. Hence, the SWCNT–benzene–FeN4–SWCNT junction is predicted to exhibit remarkable spin-filtering together with a large equilibrium transmission around EF.
In order to provide an intuitive understanding of the electronic coupling between the FMOs and the electrode states, the conducting eigenchannels76,77 corresponding to the selected transmission peaks around EF are also calculated and displayed in Fig. 3(b). From the eigenchannel analysis, we can visually display the dominating FMO of each transmission peak. By comparing the spatial distribution of the eigenchannels with the FMOs of the isolated benzene–FeN4 molecule, we can conclude that the spin-up transmission peak close to EF originates from the spin-up LUMO, whereas the one below EF, centered at −0.58 eV, is ascribed to the spin-up HOMO. This reveals an energy separation of 0.62 eV between these two states, which is further lowered by 0.12 eV when compared with the spin-up HOMO–LUMO gap of the isolated benzene–FeN4 (0.74 eV), an effect due to the strong electronic coupling with the SWCNT electrodes. As for the spin-down electrons, clearly the transmission peaks located at 0.71, 0.62, and −0.71 eV are dominated by the spin-down LUMO+2, LUMO+1, and the HOMO−1 and HOMO−2, respectively. No evident transmission peaks present a distinct spin-down HOMO or LUMO character due to their localization nature and their extremely weak coupling to the continuum states of the SWCNT electrodes. In addition, their localized features are also manifested by two narrow peaks located at −0.48 and 0.17 eV in the spin-down projected density of states (PDOS) spectra for the Fe 3dx2−y2 and 3dz2 atomic orbitals (see Fig. S7, ESI†).77 Taken all together, we confirm that the junction conductance is primarily determined by the spin-up channel, especially the spin-up LUMO-dominated transmission peak. Compared to the single-molecule junction in which FeN4 is covalently connected to two armchair (5,5) SWCNT electrodes as we mentioned before38 (see Section S6 of the ESI† for our calculations of the spin-resolved transport properties of this molecular junction), the introduction of the benzene anchors not only narrows the energy separation between the HOMO- and LUMO-dominated transmission peaks for the spin-up channel, since the benzene anchors retain the conjugation of the entire junction, but also causes low transmission of the spin-down channel over a significantly broader energy range around EF due to the negligible contribution of the localized spin-down benzene–FeN4 HOMO and LUMO to the junction transport. Thus, the spin-up LUMO-dominated transmission peak is located much closer to EF with a substantial increase in T↑(EF), as well as a decrease in T↓(EF). This dramatically improves the spin-filtering performance.
Next we move to investigate the spin-transport properties through SWCNT–pyrazine–FeN4–SWCNT and examine the effect of the pyrazine anchoring group on the junction's spin-filtering behavior. Considering the similarity between benzene and pyrazine, the pyrazine anchors are also found to be efficient and effective in extending the conjugation of FeN4 and in coupling with the SWCNT electrodes. This is manifested as a further reduction in the energy separation between the spin-up HOMO- and LUMO-dominated transmission peaks in the SWCNT–pyrazine–FeN4–SWCNT junction (0.69 eV in Fig. 3(d)), when compared to the spin-up HOMO–LUMO gap of pyrazine–FeN4 in the gas phase (0.83 eV). In addition, the more electronegative N atoms in the pyrazine anchors result in partial electron transfer (∼0.34 e obtained from the Bader charge analysis or ∼0.49 e according to the Mulliken population analysis) from the two SWCNT electrodes to the central pyrazine–FeN4 region.78–82 By symmetry, the π-type continuum states of the SWCNT electrodes primarily interact with the π-type spin-up LUMO orbital, but they are orthogonal to the localized spin-down LUMO. Thus, the substantial increase in the number of electrons in the central pyrazine–FeN4 region leads to a partial occupation of the spin-up LUMO state, whose associated transmission peak ends up to lie exactly at EF (see Fig. 3(d)). Therefore, in the SWCNT–pyrazine–FeN4–SWCNT junction, T↑(EF) reaches up to 0.99. Since the localized spin-down HOMO and LUMO also contribute negligibly to the junction transmission, no prominent transmission peaks are observed between that at −0.71 eV, dominated by the spin-down HOMO−1, and the one located at 0.70 eV, originating from both the spin-down LUMO+1 and LUMO+2. As a result, T↓(EF) is calculated to be 3.3 × 10−3 and the corresponding spin polarization is as high as 99.3%, a value even larger than that found for the SWCNT–benzene–FeN4–SWCNT junction.
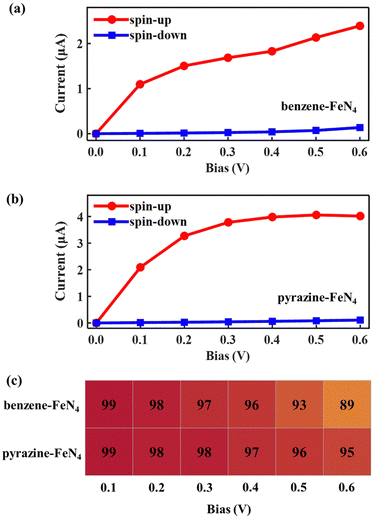
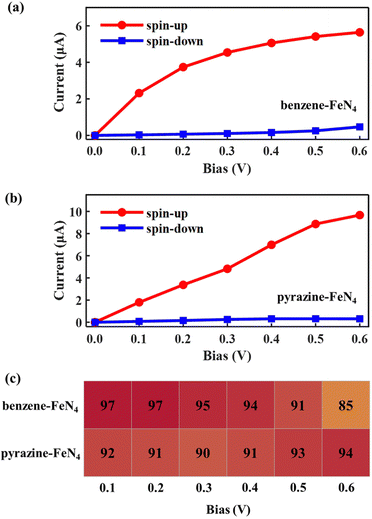
Considering the nearly perfect tunnelling suppression of the spin-down channel at zero bias, we now investigate the spin-filtering performance of SWCNT–benzene–FeN4–SWCNT and SWCNT–pyrazine–FeN4–SWCNT at finite bias by calculating their spin-resolved current–voltage, I–V, curves up to 0.6 V with 0.1 V resolution. As demonstrated in Fig. 4(a) and (b), the spin-up currents are significantly higher than the spin-down ones across the entire bias window, indicating that both junctions sustain high spin-polarization and that the spin-up channel dominates the output currents. However, the anchors do have an effect on the bias-dependent spin-filtering efficiency as well as the ratio of the spin-up current to the spin-down one,6,38 defined as R = I↑/I↓ (see Fig. 4(c) and Fig. S12, ESI†). For SWCNT–benzene–FeN4–SWCNT, since the spin-up LUMO-dominated transmission peak gradually enters the bias window (see Fig. S13 of the ESI† for the bias-dependent transmission spectra of SWCNT–benzene–FeN4–SWCNT), the spin-up current increases monotonically within our calculated bias range and it is 2.39 μA at 0.6 V. It is worth noting that for all the applied voltages, the transmission spectra around EF show no significant deformations and only the spin-up conductance path, more specifically, the spin-up LUMO-dominated transmission peak can enter the bias window. In contrast, the spin-down transmission peaks are always positioned outside the bias window so that the spin-down current remains low for all the applied voltages. This slightly rises only beyond 0.5 V, since the tails of some spin-down transmission peaks approach the bias window below EF. The resultant spin-down electric current at 0.6 V, obtained to be 0.14 μA, reduces the spin filtering, resulting in an SFE of 89% as well as an R of 18.
When compared to SWCNT–benzene–FeN4–SWCNT, the total electric current is significantly enhanced in SWCNT–pyrazine–FeN4–SWCNT, which displays much more efficient electronic transport (see Fig. 4(b)). By inspecting the corresponding bias-dependent transmission spectra shown in Fig. S14 of the ESI,† we observe that the central region of the spin-up LUMO-dominated transmission peak is always inside the bias window for all the applied bias voltages. Therefore, the spin-up current rapidly increases between 0.1 and 0.4 V. Although it starts to saturate beyond 0.4 V, since there are no additional states contributing to the transmission within the bias range, the spin-up current remains as high as 4.02 μA at 0.6 V. In addition to the high spin-up current, the SWCNT–pyrazine–FeN4–SWCNT junction also benefits from a better spin-down filtering at finite bias, since the spin-down transmission peaks are positioned further away from the bias window than those of the SWCNT–benzene–FeN4–SWCNT junction. Therefore, the calculated R varies between 37 and 159 in the 0.1–0.6 V interval (see Fig. S12, ESI†), and the SFE is within 95–99%. Taken all together, we conclude that molecular junctions based on benzene–FeN4 and pyrazine–FeN4 can both retain efficient spin filtering at finite bias. When comparing the two, the junction constructed with pyrazine anchors presents better spin-filtering performance, due to its higher electric current and a more efficient tunnelling suppression in the spin-down channel.
In practice, it is very hard to control the precise atomic structure of the nanogap between the SWCNT electrodes, a feature that remains largely unknown in experiments. In fact, both benzene–FeN4 and pyrazine–FeN4 can also bind to the outermost second layer of the SWCNT electrodes instead of the outermost one. The effect of such different binding geometry is investigated next, and such new junctions are denoted as SWCNT–benzene–FeN4–SWCNT–BS and SWCNT–pyrazine–FeN4–SWCNT–BS (see atomic structures in Fig. 5(a) and (c)). The change in the binding sites of the central molecule results in two significant effects. First, the equilibrium atomic structures of these two molecular junctions can be affected by the increasing steric hindrance. In particular, as demonstrated in the side view of Fig. 5(a), the central benzene–FeN4 of SWCNT–benzene–FeN4–SWCNT–BS is heavily distorted from planarity. Such a large structural distortion leads to an enhanced σ–π orbital overlap, that is, an overlap between the σ-type spin-down HOMO of the isolated benzene–FeN4, with dominant weight on the central square-planar four-coordinate motif, and the π-type orbitals distributed on the C atoms of four adjacent benzene rings. This σ–π interaction gives rise to a transmitting channel associated with the benzene–FeN4 spin-down HOMO. Therefore, a transmission peak approaching unity appears at −0.42 eV in the spin-down transmission spectrum of SWCNT–benzene–FeN4–SWCNT–BS. Further eigenchannel analysis of this transmission peak (see Fig. 5(b) and Fig. S15a of the ESI†) and PDOS spectra (see Fig. S15, ESI†) provide a visual illustration of the contributions of both σ-type and π-type orbitals, especially the Fe 3dx2−y2/3dz2 and C 2p ones, to the spin-down transmission peak at −0.42 eV. It is worth mentioning that this spin-down HOMO-induced peak significantly narrows the low transmission region around EF, a feature that may reduce the spin-down filtering capability at finite bias. In contrast to the benzene–FeN4–SWCNT–BS junction, the geometrical distortion of the central pyrazine–FeN4 is significantly attenuated in SWCNT–pyrazine–FeN4–SWCNT–BS. This markedly reduces the contribution of the σ–π interaction to the transmission, confirmed by the narrow peaks at −0.34 eV in the spin-down PDOS spectra for the Fe 3dx2−y2 and 3dz2 orbitals together with no appreciable contribution of the π-type orbitals, distributed on the aromatic pyrazine and benzene rings of the central pyrazine–FeN4 (see Fig. S16, ESI†). Therefore, no prominent transmission peaks present a distinct spin-down HOMO character (see the blue line in Fig. 5(d)).
Secondly, as shown in previous theoretical studies, this change in the molecular binding sites at the electrode edges can result in an increase in the coupling strength, which is determined by the local density of states (LDOS) at the C atoms connecting the electrodes to the central molecule due to the interference patterns at the electrode edges (see a comparison of the LDOS of C atoms at the connecting sites in Fig. S17 of the ESI† for further elaboration of the increasing electronic coupling).32,83 The transmission peaks are therefore significantly broadened as shown in Fig. 5(b) and (d), compared to those in Fig. 3(b) and (d), a feature that changes the zero-bias transmission. In the case of benzene–FeN4, the broadening of the spin-up LUMO-dominated peak enhances T↑(EF) to 0.76 (Fig. 5(b)) from 0.25 (Fig. 3(b)). In contrast, for SWCNT–pyrazine–FeN4–SWCNT–BS, the same peak is much broader (see Fig. 5(d)), due to the nearly planar molecular geometry, but it is also shifted downward in energy, leading to a decrease of T↑(EF) to 0.46. In addition, for both benzene- and pyrazine-linked junctions, T↓(EF) increases via the change in the molecular binding sites. In particular, T↓(EF) is calculated to be 8.2 × 10−3 as shown in Fig. 5(b) and it is 1.9 × 10−2 as shown in Fig. 5(d), resulting in a spin polarization of 97.9% for the SWCNT–benzene–FeN4–SWCNT–BS junction and a reduced spin polarization of 92.1% for SWCNT–pyrazine–FeN4–SWCNT–BS.
Next, we examine the finite-bias properties of the two junctions, as shown in Fig. 6. Clearly, the electric currents considerably increase when compared to those in Fig. 4(a) and (b), mainly due to the enhanced coupling to the electrodes. For example, at 0.6 V, the spin-up currents are computed at 5.65 and 9.67 μA, that is, they are more than twice as high as those shown in Fig. 4(a) (2.39 μA) and Fig. 4(b) (4.02 μA). The resulting spin-filtering efficiency for different voltages is also reported in Fig. 6(c). As we can see, despite the change in the molecular binding sites, highly spin-polarized currents can also be obtained for molecular junctions based on benzene–FeN4 and pyrazine–FeN4. However, for SWCNT–benzene–FeN4–SWCNT–BS, although the spin-up LUMO-dominated transmission peak enters almost entirely into the bias window at 0.6 V, the spin-down HOMO-induced peak also contributes at such bias (see Fig. S18, ESI†). This results in an increase of the spin-down current from 0.25 (at 0.5 V) to 0.47 μA (at 0.6 V) and the calculated SFE, therefore, deteriorates rapidly to a relatively low value (85%). As for the SWCNT–pyrazine–FeN4–SWCNT–BS junction, due to the remarkable broadening of the spin-up LUMO-dominated transmission peak and its slight shift relative to EF, the spin-up current rapidly increases from 0.1 to 0.6 V. In addition, since the spin-down transmission peaks are always located far away from EF for all the applied bias voltages (see Fig. S19, ESI†), the spin-down current is always low and is calculated to be 0.31 μA at 0.6 V. The corresponding SFE is then 94%, that is, the junction provides a much better spin-down filtering at this specific bias voltage compared to the SWCNT–benzene–FeN4–SWCNT–BS one. Consequently, we can conclude that although benzene–FeN4 and pyrazine–FeN4 both display delocalized spin-up HOMO and LUMO, together with localized spin-down HOMO and LUMO, the molecular junctions based on pyrazine–FeN4 are always more efficient and effective in generating highly spin-polarized electric currents, compared to those based on benzene–FeN4. This is because they present higher currents for the spin-up electrons and more pronounced spin-down filtering at finite bias voltages. Such pyrazine-linked molecular devices have the potential to be constructed through direct quinone-amino condensation reactions in experiments.84–88 In what follows we focus our attention on molecular junctions based on pyrazine–FeN4 and further investigate the sensitivity of their device performance to various alterations of the electrodes.
Usually, hydrogen atoms are employed to saturate the dangling bonds appearing at the edges of carbon-based electrodes (this is the assumption we have used so far). However, since distinct edge structures can affect the electronic properties of the electrodes,89,90 we further replace H atoms by F or representative oxidic functional groups, such as hydroxyl groups (OH), and investigate their effects on the spin transport properties of the SWCNT–pyrazine–FeN4–SWCNT junction. Fig. S20 of the ESI† shows the spin-resolved transmission spectra for the molecular junctions constructed with F- and OH-terminated electrode edges. Compared to hydrogen passivation, F and OH only have a minor effect on the overall shape of the spin-resolved transmission spectra, especially around EF. However, the much more electronegative F or O atoms result in surface dipoles pointing from F or OH to the inside of the SWCNT electrodes. These inhibit the occupation of the spin-up LUMO, leading to an upshift of the spin-up LUMO-dominated transmission peak. At the same time, the electronic coupling strength also changes: the F-termination slightly increases the LDOS at the C atoms connecting the SWCNT electrode edges to the central pyrazine–FeN4 compared to that of the H-termination. However, the OH-termination results in a substantial increase in the LDOS of the C atoms at the connecting sites (see Fig. S21, ESI†). As a result, the spin-up LUMO-dominated transmission peak is significantly broadened in the molecular junction undergoing OH termination together with an increase in T↓(EF), resulting in a spin polarization of 91.1%. For the F passivation, a spin polarization value as high as 97.4% is obtained, demonstrating that spin polarization can be retained with different edge passivation patterns.
In the above calculations, we focus our attention on the spin transport through molecular junctions constructed with two semi-infinite armchair (5,5) SWCNT electrodes. In order to investigate the feasibility of these molecular junctions based on pyrazine–FeN4 and other carbon-based electrode materials, finally we change the SWCNT curvature and also use two-dimensional N-doped graphene as the electrodes instead. Due to the similar electronic structure of all armchair SWCNTs comprising two energy bands in the vicinity of EF, the molecular junctions constructed with different armchair SWCNTs all exhibit perfect spin-filtering behavior (see Fig. S22, ESI†). N-doped graphene electrodes with a doping concentration of 2.5% significantly improve the DOS of the electrodes around the Fermi energy and thus may lead to an enhanced injected current (see Fig. S23, ESI†). Fig. S24 of the ESI† shows the optimized atomic structure of the molecular junction constructed with two N-doped graphene electrodes and its corresponding spin-resolved equilibrium transmission spectra. A significant broadened transmission peak, also dominated by the spin-up LUMO, is observed, together with a low transmission region going roughly from −0.7 to 0.5 eV for the spin-down channel. This gives rise to nearly perfect spin-down filtering. In this case, T↑(EF) and T↓(EF) are respectively calculated to be 0.43 and 5.3 × 10−3, resulting in a spin polarization as high as 97.6%. These results further demonstrate the robustness of the remarkable spin-filtering behavior associated with the junctions based on pyrazine–FeN4, which is less sensitive to the interface configurations and the electrode material. Therefore, these FeN4-based and pyrazine-linked molecular junctions provide a promising platform for applications in high-performance and reliable molecular spin filters.
Conclusion
In summary, we have proposed a promising strategy to design single-molecule spintronic devices, where highly spin-polarized currents can be efficiently generated using magnetic molecules whose HOMO and LUMO of one spin type are completely localized, while they are delocalized for the opposite spin. This can be achieved when FeN4 is functionalized with two pyrazine end groups, showing delocalized spin-up HOMO and LUMO together with localized HOMO and LUMO in the spin-down channel. In order to obtain high transmission for the spin-up channel, appropriate interfacial charge transfer is required so that either the delocalized HOMO or LUMO approaches the electrodes’ EF. Pyrazine anchors can meet this requirement, since they have electronegative N atoms, which are expected to induce partial electron transfer from electrodes to the central molecule. Therefore, when FeN4 is sandwiched between two SWCNT electrodes with pyrazine anchors, it is intriguing to show that the spin-up LUMO-dominated transmission peak lies exactly at EF. At the same time, no appreciable transmission peaks are observed around EF for spin-down electrons, a fact that ensures little spin-down current at finite bias also. The remarkable spin filtering is well retained against different molecular binding sites and different edge passivation patterns. In addition, excellent spin polarization is very robust regardless of the curvature of armchair SWCNT electrodes and when nitrogen-doped graphene electrodes are employed. Our findings highlight the great potential of FeN4-based pyrazine-linked molecular junctions for future high-performance molecular spin filters and open up a new door for the design of advanced molecular spintronic devices with highly spin-polarized currents.Author contributions
Yudi Wang and Shimin Hou conceived the idea. Yudi Wang carried out the theoretical calculations, data analysis and wrote the initial draft. Haoyang Pan, Yuxuan Jiang, Jie Li, and Shi Li helped to discuss and analyze the theoretical results. Dongying Lin and Haoyang Pan helped in the implementation of the computer code and supporting algorithms. Yongfeng Wang, Stefano Sanvito, and Shimin Hou critically reviewed and helped to revise and polish the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This project was supported by the National Natural Science Foundation of China (grant no. 21933002) and the High-performance Computing Platform of Peking University. SS acknowledges the Science Foundation, Ireland (AMBER Center grant 12/RC/2278_P2) for the financial support.Notes and references
- I. Žutić, J. Fabian and S. D. Sarma, Rev. Mod. Phys., 2004, 76, 323–410 CrossRef.
- S. Sanvito, Chem. Soc. Rev., 2011, 40, 3336–3355 RSC.
- E. Coronado and M. Yamashita, Dalton Trans., 2016, 45, 16553–16555 RSC.
- E. Coronado, Nat. Rev. Mater., 2020, 5, 87–104 CrossRef.
- S. Zhang, S. A. Dayeh, Y. Li, S. A. Crooker, D. L. Smith and S. T. Picraux, Nano Lett., 2013, 13, 430–435 CrossRef CAS.
- S. Li, Y. Wang, Y. Wang, S. Sanvito and S. Hou, J. Phys. Chem. C, 2021, 125, 6945–6953 CrossRef CAS.
- S. Sanvito, J. Mater. Chem., 2007, 17, 4455–4459 RSC.
- L. Bogani and W. Wernsdorfer, Nat. Mater., 2008, 7, 179–186 CrossRef CAS.
- A. R. Rocha, V. M. García-suárez, S. W. Bailey, C. J. Lambert, J. Ferrer and S. Sanvito, Nat. Mater., 2005, 4, 335–339 CrossRef CAS.
- D. Li and G. Yu, Adv. Funct. Mater., 2021, 31, 2100550 CrossRef CAS.
- S. A. Tawfik, L. Weston, X. Y. Cui, S. P. Ringer and C. Stampfl, J. Phys. Chem. Lett., 2017, 8, 2189–2194 CrossRef CAS PubMed.
- S. Fahrendorf, N. Atodiresei, C. Besson, V. Caciuc, F. Matthes, S. Blügel, P. Kögerler, D. E. Bürgler and C. M. Schneider, Nat. Commun., 2013, 4, 2425 CrossRef PubMed.
- W. Zhang, G.-P. Zhang, Z.-L. Li, X.-X. Fu, C.-K. Wang and M. Wang, Phys. Chem. Chem. Phys., 2022, 24, 1849–1859 RSC.
- S. Sen and S. Chakrabarti, J. Am. Chem. Soc., 2010, 132, 15334–15339 CrossRef CAS.
- A. N. Pal, D. Li, S. Sarkar, S. Chakrabarti, A. Vilan, L. Kronik, A. Smogunov and O. Tal, Nat. Commun., 2019, 10, 5565 CrossRef CAS PubMed.
- G.-P. Zhang, Y.-Q. Mu, M.-Z. Wei, S. Wang, H. Huang, G.-C. Hu, Z.-L. Li and C.-K. Wang, J. Mater. Chem. C, 2018, 6, 2105–2112 RSC.
- X. Liu, J. Yang, X. Zhai, H. Yan, Y. Zhang, L. Zhou, J.-G. Wan, G. Ge and G. Wang, Phys. Chem. Chem. Phys., 2020, 22, 6755–6762 RSC.
- P. Zhao and G. Chen, J. Magn. Magn. Mater., 2020, 493, 165712 CrossRef CAS.
- C. Herrmann, G. C. Solomon and M. A. Ratner, J. Am. Chem. Soc., 2010, 132, 3682–3684 CrossRef CAS PubMed.
- Y. Song, C.-K. Wang, G. Chen and G.-P. Zhang, Phys. Chem. Chem. Phys., 2021, 23, 18760–18769 RSC.
- X. Shen, L. Sun, Z. Yi, E. Benassi, R. Zhang, Z. Shen, S. Sanvito and S. Hou, Phys. Chem. Chem. Phys., 2010, 12, 10805–10811 RSC.
- C. Yu, Q. Feng, X. Li and J. Yang, Nanoscale, 2022, 14, 15799–15803 RSC.
- P. Zhao, Q. H. Wu, H. Y. Liu, D. S. Liu and G. Chen, J. Mater. Chem. C, 2014, 2, 6648–6654 RSC.
- A. Smogunov and Y. J. Dappe, Nano Lett., 2015, 15, 3552–3556 CrossRef CAS.
- D. Li, Phys. Rev. B, 2019, 99, 174438 CrossRef CAS.
- X. Shen, L. Sun, E. Benassi, Z. Shen, X. Zhao, S. Sanvito and S. Hou, J. Chem. Phys., 2010, 132, 054703 CrossRef PubMed.
- A. Ostovan, N. Papior and S. S. Naghavi, Phys. Rev. B, 2021, 104, 235435 CrossRef CAS.
- Z. Yi, X. Shen, L. Sun, Z. Shen, S. Hou and S. Sanvito, ACS Nano, 2010, 4, 2274–2282 CrossRef CAS PubMed.
- X. Shen, Z. Yi, Z. Shen, X. Zhao, J. Wu, S. Hou and S. Sanvito, Nanotechnology, 2009, 20, 385401 CrossRef.
- O. Adak, E. Rosenthal, J. Meisner, E. F. Andrade, A. N. Pasupathy, C. Nuckolls, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2015, 15, 4143–4149 CrossRef CAS PubMed.
- Z. Jiang, H. Wang, Y. Wang, S. Sanvito and S. Hou, J. Phys. Chem. C, 2017, 121, 27344–27350 CrossRef CAS.
- Y. Wang, H. Pan, D. Lin, S. Li, Y. Wang, S. Sanvito and S. Hou, Phys. Chem. Chem. Phys., 2022, 24, 21337–21347 RSC.
- S. Li, Y. Jiang, Y. Wang, S. Sanvito and S. Hou, J. Phys. Chem. Lett., 2021, 12, 7596–7604 CrossRef CAS.
- Y. Hu, X. Li, Q. Li and J. Yang, Angew. Chem., Int. Ed., 2022, 61, e202205036 CrossRef CAS.
- F. Li, J. Huang, J. Wang and Q. Li, Molecules, 2019, 24, 1747 CrossRef CAS.
- J. Huang, Q. Li, K. Xu, H. Su and J. Yang, J. Phys. Chem. C, 2010, 114, 11946–11950 CrossRef CAS.
- A. Lunghi and S. Sanvito, Nat. Rev. Chem., 2022, 6, 761–781 CrossRef CAS PubMed.
- J. Huang, W. Wang, S. Yang, H. Su, Q. Li and J. Yang, Chem. Phys. Lett., 2012, 539–540, 102–106 CrossRef CAS.
- P. Zhao, Q. H. Wu, D. S. Liu and G. Chen, J. Chem. Phys., 2014, 140, 044311 CrossRef CAS.
- D. Herebian, E. Bothe, F. Neese, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2003, 125, 9116–9128 CrossRef CAS PubMed.
- P. Chaudhuri, C. N. Verani, E. Bill, E. Bothe, T. Weyhermüller and K. Wieghardt, J. Am. Chem. Soc., 2001, 123, 2213–2223 CrossRef CAS.
- F. L. Benedito, T. Petrenko, E. Bill, T. Weyhermüller and K. Wieghardt, Inorg. Chem., 2009, 48, 10913–10925 CrossRef CAS PubMed.
- D. Sellmann, U. Kleine-Kleffmann, L. Zapf, G. Huttner and L. Zsolnai, J. Organomet. Chem., 1984, 263, 321–331 CrossRef CAS.
- K. Ray, A. Begum, T. Weyhermüller, S. Piligkos, J. van Slageren, F. Neese and K. Wieghardt, J. Am. Chem. Soc., 2005, 127, 4403–4415 CrossRef CAS.
- J. Huang, W. Wang, Q. Li and J. Yang, J. Chem. Phys., 2014, 140, 164703 CrossRef.
- S. Pascal and O. Siri, Coord. Chem. Rev., 2017, 350, 178–195 CrossRef CAS.
- O. R. Luca and R. H. Crabtree, Chem. Soc. Rev., 2013, 42, 1440–1459 RSC.
- V. Lyaskovskyy and B. de Bruin, ACS Catal., 2012, 2, 270–279 CrossRef CAS.
- J. L. Boyer, J. Rochford, M.-K. Tsai, J. T. Muckerman and E. Fujita, Coord. Chem. Rev., 2010, 254, 309–330 CrossRef CAS.
- A. Mederos, S. Domínguez, R. Hernández-Molina, J. Sanchiz and F. Brito, Coord. Chem. Rev., 1999, 193–195, 913–939 CrossRef CAS.
- H.-L. Chan, H.-Q. Liu, B.-C. Tzeng, Y.-S. You, S.-M. Peng, M. Yang and C.-M. Che, Inorg. Chem., 2002, 41, 3161–3171 CrossRef CAS PubMed.
- T. Bugarcic, A. Habtemariam, R. J. Deeth, F. P. A. Fabbiani, S. Parsons and P. J. Sadler, Inorg. Chem., 2009, 48, 9444–9453 CrossRef CAS.
- J. Huang, W. Wang, S. Yang, Q. Li and J. Yang, Nanotechnology, 2012, 23, 255202 CrossRef PubMed.
- V. T. T. Huong, T. B. Tai and M. T. Nguyen, Phys. Chem. Chem. Phys., 2016, 18, 6259–6267 RSC.
- P. Hohenberg and W. Kohn, Phys. Rev., 1964, 136, B864–B871 CrossRef.
- W. Kohn and L. J. Sham, Phys. Rev., 1965, 140, A1133–A1138 CrossRef.
- Y. Meir and N. S. Wingreen, Phys. Rev. Lett., 1992, 68, 2512–2515 CrossRef PubMed.
- Y. Xue, S. Datta and M. A. Ratner, Chem. Phys., 2002, 281, 151–170 CrossRef CAS.
- M. Brandbyge, J.-L. Mozos, P. Ordejón, J. Taylor and K. Stokbro, Phys. Rev. B, 2002, 65, 165401 CrossRef.
- A. R. Rocha, V. M. García-Suárez, S. Bailey, C. Lambert, J. Ferrer and S. Sanvito, Phys. Rev. B, 2006, 73, 085414 CrossRef.
- I. Rungger and S. Sanvito, Phys. Rev. B, 2008, 78, 035407 CrossRef.
- S. Wang, N. T. Hung, H. Tian, M. S. Islam and R. Saito, Phys. Rev. Appl., 2021, 16, 024030 CrossRef CAS.
- J. M. Soler, E. Artacho, J. D. Gale, A. García, J. Junquera, P. Ordejón and D. Sánchez-Portal, J. Phys.: Condens. Matter, 2002, 14, 2745–2779 CrossRef CAS.
- A. García, N. Papior, A. Akhtar, E. Artacho, V. Blum, E. Bosoni, P. Brandimarte, M. Brandbyge, J. I. Cerdá, F. Corsetti, R. Cuadrado, V. Dikan, J. Ferrer, J. Gale, P. García-Fernández, V. M. García-Suárez, S. García, G. Huhs, S. Illera, R. Korytár, P. Koval, I. Lebedeva, L. Lin, P. López-Tarifa, S. G. Mayo, S. Mohr, P. Ordejón, A. Postnikov, Y. Pouillon, M. Pruneda, R. Robles, D. Sánchez-Portal, J. M. Soler, R. Ullah, V. W.-Z. Yu and J. Junquera, J. Chem. Phys., 2020, 152, 204108 CrossRef.
- N. Troullier and J. L. Martins, Phys. Rev. B, 1991, 43, 1993–2006 CrossRef CAS.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865–3868 CrossRef CAS PubMed.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16, Revision A.03, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- A. I. Liechtenstein, V. I. Anisimov and J. Zaanen, Phys. Rev. B, 1995, 52, R5467–R5470 CrossRef CAS PubMed.
- S. L. Dudarev, G. A. Botton, S. Y. Savrasov, C. J. Humphreys and A. P. Sutton, Phys. Rev. B, 1998, 57, 1505–1509 CrossRef CAS.
- M. Büttiker, Y. Imry, R. Landauer and S. Pinhas, Phys. Rev. B, 1985, 31, 6207–6215 CrossRef.
- H. Yang, M. E. Itkis, R. Moriya, C. Rettner, J.-S. Jeong, D. S. Pickard, R. C. Haddon and S. S. P. Parkin, Phys. Rev. B, 2012, 85, 052401 CrossRef.
- M. Koleini, M. Paulsson and M. Brandbyge, Phys. Rev. Lett., 2007, 98, 197202 CrossRef PubMed.
- B. Trauzettel, D. V. Bulaev, D. Loss and G. Burkard, Nat. Phys., 2007, 3, 192–196 Search PubMed.
- R. Saito, G. Dresselhaus and M. S. Dresselhaus, Physical Properties of Carbon Nanotubes, Imperial College Press, London, 1998 Search PubMed.
- H. S. P. Wong and D. Akinwande, Carbon Nanotube and Graphene Device Physics, Cambridge University Press, Cambridge, 2010 Search PubMed.
- M. Paulsson and M. Brandbyge, Phys. Rev. B, 2007, 76, 115117 CrossRef.
- R. Li, S. Hou, J. Zhang, Z. Qian, Z. Shen and X. Zhao, J. Chem. Phys., 2006, 125, 194113 CrossRef PubMed.
- R. Bader, Atoms in Molecules: A Quantum Theory, Oxford University Press, New York, 1990 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- M. Yu and D. R. Trinkle, J. Chem. Phys., 2011, 134, 064111 CrossRef PubMed.
- H. Sadeghi, S. Sangtarash and C. Lambert, Nano Lett., 2017, 17, 4611–4618 CrossRef CAS PubMed.
- Z. Chen, J. Wang, T. Cai, Z. Hu, J. Chu, F. Wang, X. Gan and Z. Song, ACS Appl. Mater. Interfaces, 2022, 14, 27994–28003 CrossRef CAS PubMed.
- C. Wang, X. Li, B. Yu, Y. Wang, Z. Yang, H. Wang, H. Lin, J. Ma, G. Li and Z. Jin, ACS Energy Lett., 2020, 5, 411–417 CrossRef CAS.
- Y. Zhao, M. Wu, H. Chen, J. Zhu, J. Liu, Z. Ye, Y. Zhang, H. Zhang, Y. Ma, C. Li and Y. Chen, Nano Energy, 2021, 86, 106055 CrossRef CAS.
- S. Oh, J. R. Gallagher, J. T. Miller and Y. Surendranath, J. Am. Chem. Soc., 2016, 138, 1820–1823 CrossRef CAS.
- M. N. Jackson, S. Oh, C. J. Kaminsky, S. B. Chu, G. Zhang, J. T. Miller and Y. Surendranath, J. Am. Chem. Soc., 2018, 140, 1004–1010 CrossRef CAS.
- V. Kaushik, S. Pathak, H. Sharma, S. Sachdev, S. Anwer and C. Prakash, Phys. B, 2022, 625, 413491 CrossRef CAS.
- D.-b Lu, Y.-l Song, Z.-x Yang and G.-q Li, Appl. Surf. Sci., 2011, 257, 6440–6444 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3tc03719c |
| This journal is © The Royal Society of Chemistry 2024 |