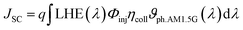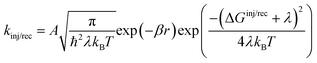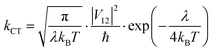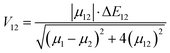Charge transfer properties of novel linear carbon chain-based dyes†
Received
13th October 2023
, Accepted 7th December 2023
First published on 8th December 2023
Abstract
In this study, we designed a series of dyes based on the D–π–A scheme, featuring the novel 2-amino pyrrole group, D1, as the donor unit, combined with three different acceptor groups: benzothiadiazole (A2), cyanoacrilic acid, (A3), and a unique pyrimidin-pyridinium salt derivative, A1, not previously employed in DSSC applications. A linear carbon chain (LCC) of varying lengths was used as the π-bridge. We compared the performance of D1 dyes with the well-established electron donor phenothiazine, D2. Spectroscopic, electronic and photochemical properties of these designed compounds were investigated through density functional theory (DFT) and time-dependent density functional theory (TDDFT) simulations. The calculated light-harvesting efficiency (LHE) values showed that A1 yielded the best results, and generally, D1 donors outperformed the reference D2. Additionally, longer LCCs contributed positively to LHE. The study of electron density difference (EDD) maps showed clear charge transfer from the donor unit to the acceptor unit in all cases. Dyes with D1 exhibited lower intramolecular reorganization energy (λi) values, indicating faster charge transfer compared to those with D2. Negative free energy injection values (ΔGinj) were calculated for all sensitizers, signifying efficient electron injection, especially in D2-containing dyes. However, these compounds exhibited positive free energy regeneration values (ΔGreg), implying thermodynamically unfavorable regeneration processes. Conversely, D1-containing compounds demonstrated favorable values for regeneration. Increasing the length of the LCC positively affected ΔGreg but had a less favorable impact on ΔGinj. The calculated charge transfer (qCT) values revealed that the most favorable results occurred when pairing the donor with A1, indicating that this acceptor group promoted charge separation. Simulations of dye@(TiO2)14 anatase complexes indicated that the binding of the designed dyes to the semiconductor improved their transport properties. In summary, all the calculated parameters indicated that D1 possesses superior properties for use in DSSC applications when coupled to A1 and, generally, dyes featuring D1 were predicted to perform well in photovoltaic applications. It is worth noting that ΔGreg values may hinder regeneration in D2-containing dyes, despite their excellent values in other calculated parameters. Our study offers valuable insights for refining dye design in order to boost the performance of dye-sensitized solar cells (DSSCs).
1. Introduction
Solar energy stands out as one of the most accessible and cost-effective renewable energy sources. Consequently, a wide range of photovoltaic technologies have emerged to efficiently convert sunlight into electrical current. While the majority of photovoltaic cells in current use rely on silicon,1 efficient alternatives, such as perovskite solar cells and dye-sensitized solar cells (DSSCs), have come into prominence.2 Since their introduction by Grätzel and O’Regan,3 DSSCs have emerged as a promising technology for efficiently harnessing solar energy to generate electrical power. They have attracted growing interest due to their cost-effective manufacturing, distinctive optical and mechanical properties, and high device efficiency.4,5 An essential component of DSSCs is the photosensitizer, which plays a crucial role in absorbing photons and initiating the charge separation process.6 Over time, extensive research efforts have been devoted to optimizing dye design with the goal of improving DSSC performance. These investigations have explored a wide range of photosensitizers, primarily grouped into three main classes: ruthenium(II) complexes,7–11 zinc(II) porphyrin derivatives12–18 and metal-free organic dyes. Among these classes, free-metal organic dyes have garnered particular attention due to their low-cost fabrication processes and favorable environmental impact. This category typically comprises three distinct regions, each serving a different purpose. First, an electron acceptor moiety (A) anchors the dye to the semiconducting electrode, ensuring an efficient electronic coupling between the sensitizers and the substrate. Second, a linker section (π), consisting of a conjugated system, facilitates electron transfer. Finally, an electron donor moiety (D), which is located at the free end of the molecule. As a result, these dyes typically adopt a push–pull structure, denoted as D–π–A. Various strategies have been explored to optimize both the electron acceptor and electron donor moieties in order to achieve higher efficiency and improved performance in photovoltaic applications. In order to enhance the efficiency of charge transfer, the careful selection of appropriate donor–acceptor pairs is essential. Within this context, the role of the π-linker holds significant importance. A multitude of innovative metal-free DSSCs have been developed, utilizing a range of compounds including triphenylamine, dialkylaniline, coumarin, oligoene, indoline, perylene, phenothiazine, tetrahydroquinoline, and carbazole.19–28 Among the assortment of novel metal-free DSSCs, dyes based on phenothiazine (PTZ) have demonstrated remarkable performance in DSSC applications. This group of sensitizers exhibiting strong electron-donating properties, superior to triphenylamine, is arranged in a non-planar butterfly conformation in the ground state, thus obstructing the molecular aggregation.29 In particular, some reports indicate that DSSCs based on PTZ dyes display power conversion efficiency (PCE) superior to the commercial N719 sensitizer under the same fabricating and testing conditions.30,31 In combination with the cyanoacrilic group as an electron-attracting component, the PTZ-based dye has shown significantly increased photocurrent and PCE when co-deposited with deoxycholic acid.32 Xie and coworkers synthesized two innovative organic sensitizers utilizing PTZ and oligothiophene vinylene as conjugation spacers, which yielded a PCE value of 5.4%.33 Additionally, co-sensitizing a PTZ-containing porphyrin sensitizer with a metal-free dye resulted in a co-sensitized device, achieving an efficiency of 11.5%.34 Buene et al. synthesized several PTZ-based dyes to investigate the impact of auxiliary donors, the role of the π-spacer, and anchoring units. They found that the π-spacer is most effective when linked to the 3-position of PTZ, and thiophene outperformed the phenyl spacer.35 In another study, the same group explored various sensitizers, featuring different auxiliary donor groups and determined that pyrene was the most effective, achieving the highest cell efficiency at 5.36%.36 Han et al. introduced auxiliary acceptors (quinoxaline, benzothiadiazole, and BTZ) into PTZ-based dyes to enhance LHE.37 Hua and coworkers developed two novel PTZ-based dyes with the encapsulated insulated molecular wire as an auxiliary donor, effectively reducing dye aggregation and improving photovoltaic cell performance.38 Two new sensitizers with a D/A–π–D–π–A framework were introduced by Slodek and coworkers. The D–π–D–π–A structure exhibited higher PCE, and both dyes achieved higher PCE compared to the N719-based device.39 A comprehensive review of recent articles concerning the use of PTZ derivatives in single, double and multi anchoring configurations for DSSC applications is offered by Devadiga and coworkers.40 The acceptor-anchoring groups are mainly represented by cyanoacrylic moieties which are present in the vast majority of DSSCs with best performance (see all references reported above). Several research groups have explored the employment of a benzothiadiazole group (BTD) with promising outcomes. Yella et al. introduced a novel porphyrin sensitizer employing a push–pull system that incorporated this strong electron-withdrawing group. The resulting device achieved an impressive efficiency of approximately 13% when employing a cobalt-based electrolyte.41 Wang and coworkers linked the BTZ-benzoic acid moiety to a rigidified N-annulated benzoindenopentaphene through an ethynyl group. This led to an exceptional efficiency of 12.6% for the DSSC using this dye, representing one of the highest efficiencies observed for a DSSC sensitized with a single metal-free dye.42 Recently, Ding et al. synthesized two new PTZ-based dyes that incorporated the BTD-benzoic acid unit with a distinguishing ethynyl linkage between BTD and benzoic acid. The results indicated that the insertion of an ethynyl group resulted in a more planar structure, leading to increased dye loading and redshifted intramolecular charge transfer (ICT) absorption with a higher molar extinction coefficient obtaining improved photovoltaic performance.43 To investigate the impact of various acceptors with varying amounts of electron withdrawing groups on free-metal dyes, a series of organic analogues with alternative acceptors were computationally examined. The authors observed that introducing the BTD unit into dyes enhanced π-conjugacy, resulting in a redshift in the UV-VIS spectra and longer excited-state lifetimes. Further investigations demonstrated that the increased presence of BTD groups in the dyes had an adverse effect on properties such as ICT, interface electronic transfer, regeneration driving force and electron-injection efficiency.44 The solvent also plays a critical role in influencing the DSSC properties.45,46 Its primary function is to dissolve the dye and establish contact with the semiconductor surface, thereby initiating the adsorption process. Both aprotic and protic solvents, including acetonitrile, methoxypropionitrile, dimethylformamide, dimethylsulfoxide, ethanol and water, have been thoroughly investigated in numerous experimental and theoretical studies.45–50 Several research studies have shown that aprotic solvents with high polarity, such as acetonitrile, are the preferred choice for DSSCs. This preference stems from their ability to facilitate both dye adsorption and electron injection.45,46,50 Our research group recently investigated the role of linear carbon chains (LCCs) in free metal dyes utilizing the donor–acceptor pair formed by the 2-amine pyrrole as the electron-donating group and the cyanoacrylic group as the electron-acceptor. We thoroughly assessed the optoelectronic characteristics of these dyes and evaluated their potential performance in DSSC applications.51,52 In this study, we investigate the charge transfer efficiency of 2-amine pyrrole, hereafter referred as D1, in combination with three different electron-acceptor groups, as illustrated in Scheme 1. As discussed above, two of these electron-acceptor groups are widely employed in DSSCs, the BTD derivative, referred to as A2, and the cyanoacrilic group, referred to as A3. The third group, labeled as A1, is based on a pyrimidin-pyridinium salt derivative, and, to the best of our knowledge, has not been employed in DSSC applications before. The π-linker between the donor and the acceptor groups is represented by a LCC of varying lengths (C4, C8). It is worth noting that LCCs exhibit electrical conduction and possess unusual optoelectronic properties due
to their extensive π-conjugated system.53–59 Additionally, they can be easily synthesized and exhibit long-term stability.60 In this study, the LCC is flanked by thiophene groups at both ends, as recent literature suggests that good efficiency has been achieved using dithiophene derivatives in the π-bridge.61,62 Furthermore, an ethylenic bridge is introduced to link the thiophene ring with the acceptor group, thereby increasing the planarity of the structure. We assess the charge transfer efficiency of the D1 group in comparison to that of the PTZ derivative, hereafter referred to as D2 (see Scheme 1). This choice is based on the demonstrated excellent results of this electron-donating group in DSSC applications. Finally, simulations of dye@(TiO2)14 anatase nanocluster systems were carried out to elucidate the electronic structure at the interface and to analyze the impact of bonding with semiconductors on electronic transition and injection. The insight gained from this study can serve as a valuable reference for the synthesis and optimization of a novel and more efficient class of metal free dyes for DSSC applications.
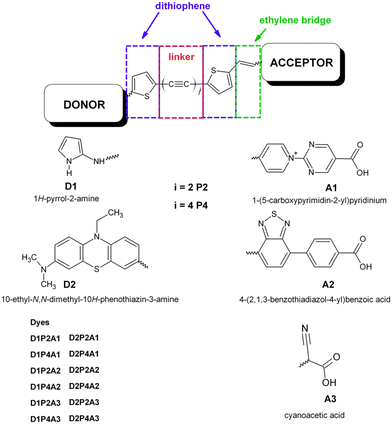 |
| | Scheme 1 Molecular structure of the designed dyes. | |
2. Methods
Molecular simulations of the investigated dyes were carried out using the Gaussian 16 program package.63 The geometries of all compounds were fully optimized using the B3LYP functional employing the 6-311+G(2d,p) basis set. For the computation of UV/VIS spectra, we employed the TD-DFT approach, along with the same basis set, considering the lowest 10 singlet–singlet transitions. It is worth highlighting that as demonstrated previously, the long range corrected functional, CAM-B3LYP, has consistently yielded results that align closely with experimental data for compounds with a similar structural framework.64,65 However, it should be noted that the molecules under investigation are not currently available for experimental analysis, consequently, there is a lack of experimental data available for comparative assessment. In our earlier investigations, we employed the solvated model based on density (SMD) to account the solvation effects. When comparing this approach with the conductor-like polarizable continuum model (CPCM) and IEFPCM methods, we observed minimal variations in both UV-Vis absorption values and absorption intensities.51 As a result, we have consistently adopted this methodology. In order to model the semiconductor, we selected a (TiO2)14 cluster, which was carved out from the crystallographic structure of TiO2 anatase by cleaving the (1 0 1) surface. The dyes were anchored to the TiO2 surface through bonding between the two oxygen atoms of the cyanoacrylate group and two titanium atoms. This choice is based on previous studies that consistently demonstrate the bidentate mode as the most stable binding geometry.66–68 It's worth mentioning that the (TiO2)9 cluster has been proven to be the smallest acceptable model capable of accurately reproducing the physical parameters of a real TiO2 semiconductor. As such, the size of the cluster proposed here can be considered a representative model of TiO2.69–71 The optimization of dye@(TiO2)14 geometries was carried out employing the effective core potential LANL2DZ and its accompanying basis set for the Ti atom, whereas the double-ξ basis set 6-31G(d) together with the B3LYP-D3 functional was selected for the other atoms. To consider the solvation effect, we utilized the solvated SMD model. The natural transition orbitals (NTOs) were visualized using Chimera software, and the Multiwfn 3.8 program72 was chosen to evaluate the transferred charge, qCT, and the charge-transfer distance, DCT.
The light-harvesting efficiency (LHE) helps in calculating the dye's efficiency and is determined using the equation:
where
ε(
λ) is the molar absorption coefficient whose value depends on wavelength and
Γ is the dye loading amount corresponding to the product of the dye concentration
c with TiO
2 film thickness
b, (
Γ = c ×
b). The short circuit photocurrent,
Jsc, a crucial performance indicator for DSSC devices, is directly proportional to the light harvesting efficiency value and can be determined by the following equation:
73| | 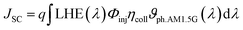 | (2) |
where
q is the elementary charge of an electron,
ϑph.AM1.5G stands the photon flux corresponding to the AM 1.5G solar radiation spectrum.
Φinj denotes the electron injection efficiency which depends on the injection time and is defined as follows:
74| | 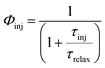 | (3) |
τinj is the injection time and
τrelax is the relaxation lifetime of the dye's excited states. On the other hand,
ηcoll represents the electron collection efficiency and its value can be calculated as:
| | 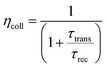 | (4) |
where
τrec denotes the recombination time, whereas
τtrans is the electron-transport time from the CB of the semiconductor to the electrode. Both
Φinj and
ηcoll are related to free energy injection and free energy recombination because of the fact that
τinj and
τrec are the inverses of
krec and
kinj, which, according to Marcus theory,
75 are defined as:
| | 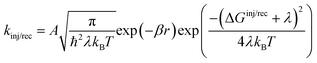 | (5) |
where
A is a constant,
β is the attenuation factor,
r is the electron transfer distance and denotes the reorganization energy comprising both intramolecular (
λi) and intermolecular (
λo) reorganization energies. The intramolecular reorganization energy quantifies the change in energy associated with the molecule's structural reorganization during the charge transfer process, while the intermolecular reorganization energy characterizes the relaxation of the surrounding medium in which the charge transfer occurs.
76 Due to its significantly smaller values compared to
λi,
λo is usually neglected.
77λi can be further divided in hole and electron reorganization energy (
λh +
λe) which can be calculated using the following formulas:
76| | | λe = [E−(M) − E−(M−)] + [E(M−) − E(M)] | (6) |
| | | λh = [E+(M) − E+(M+)] + [E(M+) − E(M)] | (7) |
where
E(M
+)/
E(M
−) represents the neutral energy levels of the optimized cationic/anionic geometries, while
E+(M)/
E−(M) denotes the cationic/anionic energies of the optimized neutral structures.
Finally, kCT is a critical parameter that is related to λ and, in the absence of any barrier, can be calculated as:
| | 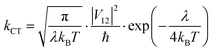 | (9) |
where
V12 represents the coupling constant between the potential curves of the reagent and the product, and it can be determined using the generalized Mulliken–Hush formalism as
78| | 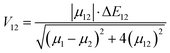 | (10) |
where
μ12 represents the transition dipole moment, Δ
E12 is the energy difference,
μ1 and
μ12 are the adiabatic electronic dipoles.
3. Results and discussion
3.1 Frontiers molecular orbital analysis and absorption spectra
An essential prerequisite for the potential utilization of dye sensitizers in DSSCs is the appropriate energy level of the LUMO, enabling efficient electron injection into the TiO2 conduction band (CB). Moreover, an optimal HOMO energy level plays a significant role in facilitating efficient electron collection. Fig. 1 displays the energy diagram of the selected molecular orbitals for the investigated dyes. This diagram clearly illustrates that the compounds featuring the amino-pyrrolic donor group, D1, have HOMO energy levels positioned below −4.8 eV, which correspond to the redox potential of the electrolyte I−/I3− with respect to the vacuum level,79 thus ensuring efficient electron recovery. Conversely, dyes featuring the PTZ group as the electron-donor, D2, show the HOMO energy level slightly above −4.8 eV, suggesting that, in these instances, the recombination process may be hindered. On the other hand, in all considered cases, the LUMO energy levels are significantly higher than the TiO2 CB, which is at −4.0 eV,80 enabling the rapid injection of excited dyes’ electrons into the semiconductor.
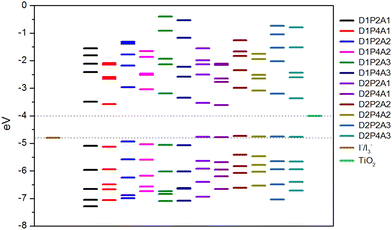 |
| | Fig. 1 Selected MOs energy levels for the designed dyes at the B3LYP/6-311+G(2d,p)/SMD level together with TiO2 CB and I−/I3− redox potential. | |
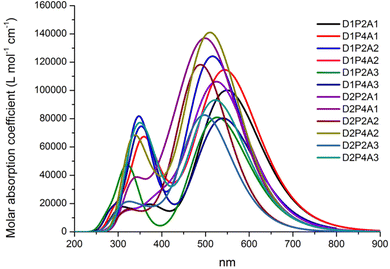
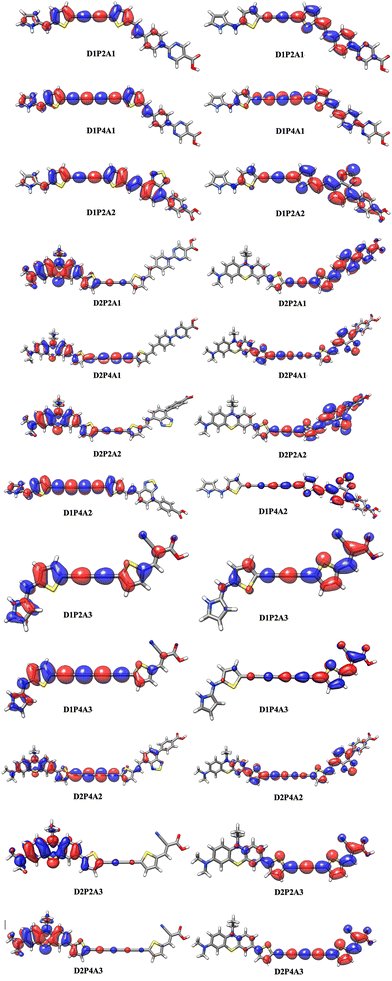
The absorption properties have been calculated for ten excited states and the dominant electronic transitions are summarized in Table 1, which include information on vertical electronic absorption energies, oscillator strengths, and maximum short circuit photocurrent, Jsc-max. Fig. 2 displays the UV/VIS absorption spectra of the investigated molecules, revealing a prominent absorption peak in the visible region with considerable intensity. The main contribution to this peak is due to the HOMO → LUMO transition and is indicative of intermolecular charge transfer. Additionally, a secondary, albeit less intense, absorption band is observed in the UV region across nearly all cases. Fig. 3 depicts the natural transition orbitals (NTOs) of the lowest energy excited state for the dyes in question. This illustration, which indicates rearrangement after the excitation, demonstrates the favorable inductive and electron-drawing characteristics of both the donor and acceptor groups.
Table 1 Absorption wavelengths, oscillator strength, Jsc-max (mA cm−2) under ideal conditions where Φinj = ηcoll = 1, Γ = 30 nmol cm−2 is considered for all dyes, and main contributions (f > 0.2) to the transitions of dyes in acetonitrile at the CAM-B3LYP/6-311+G(2d,p)/SMD level
| Compound |
λ
|
f
|
J
sc-max |
Main contribution to the transition |
| nm |
eV |
| D1P2A1 |
549.30 |
2.26 |
2.47 |
21.08 |
H → L (64%) |
|
|
389.14 |
3.19 |
0.24 |
|
H−1 → L (42%) |
|
|
363.28 |
3.41 |
0.25 |
|
H → L+1 (34%) |
|
|
309.52 |
4.01 |
0.32 |
|
H−2 → L (21%) |
| D1P4A1 |
547.36 |
2.27 |
2.40 |
23.02 |
H → L (58%) |
|
|
536.54 |
2.31 |
0.40 |
|
H → L+2 (60%) |
|
|
426.43 |
2.91 |
0.39 |
|
H−1 → L (30%) |
|
|
358.53 |
3.46 |
1.18 |
|
H−1 → L+2 (15%) |
|
|
355.61 |
3.49 |
0.38 |
|
H−1 → L+2 (33%) |
|
|
297.46 |
4.17 |
0.34 |
|
H−2 → L (31%) |
| D1P2A2 |
497.49 |
2.49 |
2.44 |
16.07 |
H → L (51%) |
|
|
404.05 |
3.07 |
0.31 |
|
H → L+1 (47%) |
|
|
299.51 |
4.14 |
0.30 |
|
H−2 → L (21%) |
| D1P4A2 |
517.24 |
2.40 |
3.03 |
20.16 |
H → L (40%) |
|
|
345.93 |
3.58 |
1.71 |
|
H−3 → L+2 (30%) |
| D1P2A3 |
519.24 |
2.39 |
1.85 |
17.63 |
H → L (76%) |
|
|
294.64 |
4.21 |
0.30 |
|
H−2 → L (25%) |
|
|
281.58 |
4.40 |
0.24 |
|
H−6 → L (68%) |
| D1P4A3 |
538.99 |
2.30 |
1.75 |
21.06 |
H → L (50%) |
|
|
366.70 |
3.38 |
0.86 |
|
H−2 → L+1 (37%) |
|
|
343.14 |
3.61 |
1.09 |
|
H → L+2 (30%) |
|
|
287.05 |
4.32 |
0.33 |
|
H−3 → L (38%) |
| D2P2A1 |
528.35 |
2.35 |
2.55 |
20.01 |
H → L (39%) |
|
|
431.47 |
2.87 |
0.31 |
|
H−1 → L (40%) |
|
|
395.92 |
3.13 |
0.39 |
|
H → L+1 (30%) |
| D2P4A1 |
521.95 |
2.38 |
2.30 |
20.18 |
H → L (49%) |
|
|
482.11 |
2.57 |
0.74 |
|
H−1 → L+2 (30%) |
|
|
453.11 |
2.74 |
0.60 |
|
H−2 → L (28%) |
|
|
411.30 |
3.01 |
0.48 |
|
H → L+1 (39%) |
|
|
337.22 |
3.68 |
0.55 |
|
H → L+2 (27%) |
| D2P2A2 |
485.52 |
2.55 |
2.58 |
16.07 |
H → L (56%) |
|
|
444.18 |
2.79 |
0.28 |
|
H−1 → L (22%) |
|
|
410.19 |
3.02 |
0.29 |
|
H−1 → L+1 (27%) |
|
|
364.59 |
3.40 |
0.52 |
|
H → L (23%) |
|
|
329.57 |
3.76 |
1.06 |
|
H → L+8 (20%) |
| D2P4A2 |
512.65 |
2.42 |
2.95 |
19.87 |
H → L (50%) |
|
|
444.18 |
2.79 |
0.28 |
|
H−1 → L (22%) |
|
|
410.19 |
3.02 |
0.29 |
|
H−1 → L+1 (27%) |
|
|
364.59 |
3.40 |
0.52 |
|
H → L (23%) |
|
|
329.57 |
3.76 |
1.06 |
|
H → L+8 (20%) |
| D2P2A3 |
498.75 |
2.49 |
2.02 |
13.62 |
H → L (45%) |
|
|
328.25 |
3.78 |
0.24 |
|
H−1 → L+1 (24%) |
| D2P4A3 |
523.42 |
2.37 |
2.28 |
19.69 |
H → L (34%) |
|
|
336.76 |
3.68 |
1.03 |
|
H−4 → L+1 (21%) |
|
|
333.77 |
3.71 |
1.14 |
|
H−4 → L+1 (21%) |
 |
| | Fig. 2 Absorption spectra of dyes in acetonitrile at the TD-CAM-B3LYP/6-311+G(2d,d)/SMD level. The spectra are Gaussian-broadened with a half width half maximum of 0.35 eV. | |
 |
| | Fig. 3 Diagram of natural transition orbitals (NTOs, S0 → S1) of the dyes in acetonitrile at the TD-CAM-B3LYP/6-311+G(2d,p)/SMD level. The surfaces are generated with an isovalue at 0.02. | |
To assess the impact on photovoltaic properties, it is essential to consider both absorption intensity and the optical absorption range. These combined data can be summarized by the light harvesting efficiency value, LHE (λ), whose curves along with the AM 1.5G solar spectrum are reported in the ESI,† Fig. S1. Table 1 reports the summation of the products of the LHE (λ) with the AM 1.5G (λ) solar spectrum within the wavelength range of 280 to 830 nm. Here we made the assumption that under optimal conditions, where Φinj = ηcoll = 1, this sum corresponds to Jsc-max. This information highlights that the most favorable LHE (λ) performance is achieved when employing the acceptor group A1; furthermore, D1 yields the most promising results as an electron donor. Although the PTZ donor group results in a high absorption intensity (see Fig. 2), it exhibits a narrower optical absorption range, and best outcomes are observed when it is paired with the electron acceptor A1, whereas results are more modest when combined with A3 and A2 acceptor groups. In all studied cases, increasing the length of LCC leads to a higher LHE (λ).
To visualize the electron density during the S0 → S1 transition, an analysis of the dyes’ electronic structure was conducted. The resulting electron density difference (EDD) maps are presented in Fig. 4 for D1P2A1 and D1P4A1, while those for the remaining dyes can be found in the ESI,† Fig. S2. In these maps, the blue region indicates an increase in electron density, while the red region signifies a decrease in electron density due to the excitation of electrons during the transition. Both figures clearly show that the acceptor unit exhibits the highest electron density, whereas the donor unit displays the lowest electron density. As a consequence, we can conclude that during the transition, there is a charge transfer from the donor unit to the acceptor unit in all investigated dyes.
 |
| | Fig. 4 Electron density difference (EDD) maps of D1P2A1 and D1P4A1 dyes simulated by Gaussview (the red and blue colors indicate a decrease and increase of charge densities, respectively). The density differences are 0.0001 a.u. | |
3.2 Ionization potential, electron affinity and reorganization energy
The ionization potential (IP) refers to the energy required to extract an electron from a molecule's neutral state. Conversely, electron affinity (EA) is the energy gap between the neutral molecule and its anionic form, both in their lowest energy charge-transfer states. The values of IP and EA play a crucial role in determining the suitability of a dye as a photosensitizer for DSSCs. These parameters were computed using the following equations:where E(M), E+(M+) and E−(M−) are the energies of the dyes related to the neutral, cationic and anionic optimized structures. The computed values of ionization potentials, electron affinities and intramolecular reorganization energies, for the investigated dyes are presented in Table 2. A lower value of λi is indicative of slower recombination processes.
Table 2 Calculated values of charge transfer rate (kCT in s−1), reorganization energies λi, λe, λh (eV), ionization potential (IP in eV), electron affinity (EA in eV) and V12 (eV) for all the dyes
| Compound |
k
CT × 1013 |
λ
h
|
λ
e
|
λ
i
|
IP |
EA |
V
12
|
| D1P2A1 |
4.99 |
0.249 |
0.200 |
0.449 |
5.07 |
3.71 |
0.392 |
| D1P4A1 |
2.54 |
0.255 |
0.261 |
0.515 |
5.11 |
3.78 |
0.399 |
| D1P2A2 |
5.73 |
0.176 |
0.240 |
0.416 |
4.96 |
3.14 |
0.352 |
| D1P4A2 |
3.49 |
0.214 |
0.263 |
0.478 |
5.08 |
3.22 |
0.382 |
| D1P2A3 |
4.51 |
0.258 |
0.200 |
0.458 |
5.03 |
3.26 |
0.391 |
| D1P4A3 |
2.41 |
0.244 |
0.278 |
0.522 |
5.06 |
3.33 |
0.402 |
| D2P2A1 |
0.99 |
0.381 |
0.233 |
0.614 |
4.75 |
3.73 |
0.420 |
| D2P4A1 |
1.14 |
0.367 |
0.235 |
0.601 |
4.75 |
3.81 |
0.422 |
| D2P2A2 |
0.84 |
0.373 |
0.242 |
0.615 |
4.63 |
3.16 |
0.387 |
| D2P4A2 |
1.58 |
0.321 |
0.235 |
0.556 |
4.65 |
3.25 |
0.392 |
| D2P2A3 |
0.61 |
0.369 |
0.260 |
0.629 |
4.70 |
3.38 |
0.355 |
| D2P4A3 |
0.32 |
0.371 |
0.312 |
0.683 |
4.72 |
3.53 |
0.343 |
The IP values vary within a range of 4.63 to 5.11 eV. Notably, D1P4A1 stands out with the highest IP value, suggesting reduced ability for electron injection into the TiO2 semiconductor. Consistently, it displays one of the higher EA values, specifically 3.78 eV, signifying a more favorable regeneration process. In general, dyes featuring D1 exhibit the higher IP values, whereas the A1 acceptor, characterized by a positive charge on the pyridine nitrogen atom, induces higher EA values to the dyes. Both λh and λe values are positive, signifying favorable hole and electron transfer characteristics for the designed sensitizers. However, those with the D2 donor group exhibit smaller λe values compared to λh. This implies that for these dyes, electron mobility exceeds hole mobility due to the inverse relationship between the charge transfer rate, kCT, and the reorganization energy.81–84
In the case of the D1 donor group, λe values are lower than λh only when the LCC length is shorter (n = 2). As the chain length increases, the mobility of negative charges decreases relative to that of holes. The discrepancy between λh and λe suggests a more balanced transport in dyes employing D1. From the data presented in Table 2, it results that λi is lower for compounds featuring D1, thus indicating that D1-containing dyes exhibit superior charge transfer abilities, a trait that is advantageous for efficient photocurrent generation and, as a result, indicates improved performance in solar devices.
3.3 Electron injection and electron regeneration driving forces (ΔGinj, ΔGreg)
The fundamental importance of aligning the frontier orbitals of both the dye and the semiconductor in order to achieve efficient electron injection and dye regeneration is widely recognized.85–88 To delve deeper into the charge transfer process, driving force for electron injection, ΔGinj, and regeneration, ΔGreg, were determined. ΔGinj quantifies the free energy associated with the electron injection process, represents the difference between the excited electron of the sensitizer and the injected electron onto the TiO2 surface and is given by:| | | ΔGinj = Eox-dye* − ECB | (13) |
where ECB is the reduction potential of the TiO2 CB (ECB = 4.0 eV), Eox-dye* is the oxidation potential of the dye in its excited state and can be computed as:| | | Eox-dye* = Eox-dye − E0–0 | (14) |
where Eox-dye refers to the oxidation potential of the ground state, while E0–0 is the vertical electronic transition energy corresponding to λmax. Dye regeneration is the process wherein the oxidized dye is restored by the redox electrolyte after electron injection. Several studies have shown that this parameter significantly impacts the photovoltaic performance of DSSCs. The driving force for the regeneration can be determined from Eox-dye as follows:| | | ΔGreg = Eredox-electrolyte − Eox-dye | (15) |
where the redox Eredox-electrolyte redox potential is −4.8 eV. The values of ΔGinj and ΔGreg are presented in Table 3.
Table 3 Calculated Eox-dye, Eox-dye*, ΔGinj, ΔGreg (eV), qCT (a.u.) and DCT in Å for all the dyes
| Compound |
E
ox-dye
|
E
ox-dye* |
ΔGinj |
ΔGreg |
q
CT
|
D
CT
|
| D1P2A1 |
5.09 |
2.83 |
−1.17 |
−0.29 |
0.880 |
10.450 |
| D1P4A1 |
5.12 |
2.86 |
−1.14 |
−0.32 |
0.940 |
13.137 |
| D1P2A2 |
4.93 |
2.44 |
−1.16 |
−0.13 |
0.842 |
10.840 |
| D1P4A2 |
5.03 |
2.64 |
−1.14 |
−0.23 |
0.852 |
12.564 |
| D1P2A3 |
5.05 |
2.66 |
−1.34 |
−0.25 |
0.752 |
8.932 |
| D1P4A3 |
5.07 |
2.77 |
−1.23 |
−0.27 |
0.772 |
10.131 |
| D2P2A1 |
4.76 |
2.42 |
−1.58 |
0.04 |
0.934 |
13.707 |
| D2P4A1 |
4.78 |
2.40 |
−1.60 |
0.03 |
0.987 |
16.671 |
| D2P2A2 |
4.73 |
2.18 |
−1.82 |
0.07 |
0.864 |
11.240 |
| D2P4A2 |
4.75 |
2.33 |
−1.67 |
0.05 |
0.878 |
13.786 |
| D2P2A3 |
4.75 |
2.27 |
−1.73 |
0.05 |
0.875 |
14.173 |
| D2P4A3 |
4.76 |
2.39 |
−1.61 |
0.04 |
0.893 |
15.334 |
The Eox-dye* values reveal that dyes featuring D2 undergo oxidation more easily than those with the D1 donor group. Additionally, the ΔGinj values consistently show a negative trend, highlighting that electron injection is a thermodynamically favored process. Notably, these values decrease as we move from the series characterized by D1 to the one featuring D2. In general, lower ΔGinj values correspond to enhanced efficiency in electron injection, consequently, the data from Table 2 suggest that electron injection is most effective in D2-containing compounds. However, it should be noted that kinj, which represents the inverse of injection time, also depends on the reorganization energy, as mentioned earlier, therefore a more detailed investigation into the adsorption of the sensitizer on TiO2 is necessary for more accurate predictions.
Efficient dye regeneration necessitates ΔGreg values to be negative and within the range of 0.2–0.3 eV.73 Our calculations reveal that dyes with D2 exhibit positive ΔGreg values, indicating that the regeneration process is thermodynamically unfavorable for these sensitizers. In contrast, compounds featuring D1 yield conducive values toward regeneration. To evaluate how charge transfer occurs within the dyes during electron transition, we employed Multiwfn 3.8 software to assess parameters such as transferred charge (qCT) and transferred charge distance (DCT).72 Upon examining the numerical values of qCT shown in Table 2, it becomes evident that sensitizers featuring D2 tend to show slightly higher qCT values in comparison to those with D1. In general, the most favorable results are observed when the donor is paired with A1, indicating that this acceptor group facilitates the formation of a charge-separated state. Simulated charge transfer distance corroborates this notion, as a longer distance is conducive to charge separated state of dyes. Considering all the parameters outlined in Tables 2 and 3, it can be inferred that D1 generally confers superior properties for use in DSSC applications when coupled to A1. In a broader context, sensitizers featuring D1 are predicted to perform well in photovoltaic applications. On the other hand, it is worth noting that in the specific configuration we studied, ΔGreg values may hinder regeneration in dyes featuring D2, despite they show excellent values for the other calculated parameters.
3.4 TiO2-dye adsorption
To effectively predict the performance of a solar cell device, it is essential to carry out prediction studies focused on the interface between the dye and the semiconductor. In pursuit of this objective, we have employed a (TiO2)14 cluster as a representative model for the TiO2 semiconductor surface. As mentioned earlier, bidentate carboxylate groups have been utilized as anchoring agents due to the stability they offer, as supported by several studies.66–68 In Table 4 are reported the dipole moment, μ of dye@TiO2, in comparison with that of free dyes, and the interaction energies, Eint, calculated as:
| Eint = Edye@TiO2 − (Edye + ETiO2) |
Calculated Ti–O distances fall within the range of 1.96–2.10 Å, aligning closely with the theoretically reported Ti–O bond lengths (ranging from 2.03 to 2.24 Å) for different dye–TiO2 clusters.73 These results are indicative of the favorable interaction between the dyes and the semiconductor surface, as supported by the calculated Eint values for dye@(TiO2)14. Additionally, Table 4 reveals that the calculated dipole moments of the dye@TiO2 clusters are larger than those of the free dyes. These findings imply that the binding to the semiconductor enhances the transport properties. From Fig. 5 and Fig. S3 in the ESI,† it become evident that the HOMO levels of dyes@(TiO2)14 are localized to the sensitizers, preserving the HOMO characteristics found in isolated dyes. These HOMO values show an increase when compared to the free dyes. On the other hand, the LUMO levels, along with most of the LUMO+n levels, are primarily centered on the substrate, displaying characteristics similar to TiO2.
Table 4
E
int (kcal mol−1) and dipole moment μ (Debye) for the dye@TiO2 complexes at the B3LYP-D3/6-31G(d)/LANL2DZ/SMD level. In parenthesis, the dipole moment of the corresponding isolated dyes
| Complexes |
E
int
|
μ
|
| D1P2A1@(TiO2)14 |
−15.49 |
13.11 (10.97) |
| D1P4A1@(TiO2)14 |
−16.10 |
19.94 (15.34) |
| D1P2A2@(TiO2)14 |
−13.27 |
15.59 (11.24) |
| D1P4A2@(TiO2)14 |
−14.43 |
17.66 (12.46) |
| D1P2A3@(TiO2)14 |
−14.91 |
11.40 (9.53) |
| D1P4A3@(TiO2)14 |
−15.89 |
13.13 (11.55) |
| D2P2A1@(TiO2)14 |
−14.59 |
24.28 (19.56) |
| D2P4A1@(TiO2)14 |
−15.01 |
26.44 (23.94) |
| D2P2A2@(TiO2)14 |
−13.14 |
17.32 (14.79) |
| D2P4A2@(TiO2)14 |
−14.53 |
20.86 (18.22) |
| D2P2A3@(TiO2)14 |
−15.07 |
19.18 (15.51) |
| D2P4A3@(TiO2)14 |
−15.81 |
20.05 (16.74) |
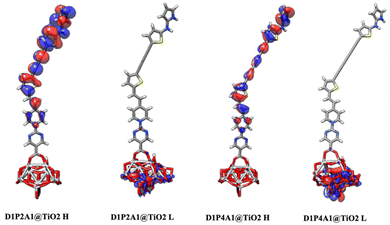 |
| | Fig. 5 Optimized geometries of the bidentate binding mode of D1P2A1 and D1P4A1 dyes on (TiO2)14. HOMOs (H) and LUMOs (L) are also depicted. | |
4. Conclusions
We conducted a theoretical investigation into the spectroscopic, electronic and photochemical properties of newly designed dyes which featured 2-amino pyrrole, D1, as the donor moiety, and were paired with three distinct withdrawing groups. Two of them, benzothiadiazole, A2, and cyanoacrylic acid, A3, are commonly used in DSSC applications, while a novel electron-attractor group, a derivative of pyridinium salt, was introduced for the first time. Additionally, a linear carbon chain (LCC) of varying lengths was used as the π-bridge. Analogs of these sensitizers were modeled using phenothiazine, D2, as the electron donor group, in place of D1, to compare the effectiveness of the 2-amino-pyrrole donor group. LHE (λ), as determined from the calculated absorption spectra, reveals that dyes containing D1 are expected to exhibit superior performance compared to their D2-containing counterparts. Furthermore, the introduction of the innovative electron-attracting group A1 yields the most promising results. The EDD maps demonstrated charge transfer from the donor unit to the acceptor unit in all studied cases. D1-containing sensitizers exhibit lower reorganization energy (λi) values, resulting in faster charge transfer when compared to those with D2. Efficient electron injection is predicted for all sensitizers, particularly those featuring D2; however dyes with this donor group show positive ΔGreg values, implying an unfavorable regeneration process. Increasing the length of the LCC has a positive effect on the LHE (λ) and ΔGreg but has a less favorable impact on ΔGinj. The acceptor group A1 facilitates charge separation, as indicated by the calculated charge transfer values, qCT. Simulation of dye@(TiO2)14 complexes suggests that the binding with the semiconductor enhanced the transport properties. In short, all calculated parameters indicate that the novel D1 and A1 groups are poised to deliver superior properties for DSSC applications. Consequently, we can conclude that most of the designed dyes may have the potential to serve as candidates for the fabrication of DSSCs.
Author contributions
Giuseppe Consiglio: conceptualization, investigation, writing, revision and editing. Adam Gorcyński: investigation, writing, revision and editing. Salvatore Petralia: investigation, writing, revision and editing. Giuseppe Forte: conceptualization, supervision, methodology, and writing original draft.
Conflicts of interest
The authors declare no conflicts of interest.
Acknowledgements
This work has been partially funded by the European Union (NextGeneration EU), through the MUR-PNRR project SAMOTHRACE (ECS00000022).
References
- C. Battaglia, A. Cuevas and S. De Wolf, Energy Environ. Sci., 2016, 9, 1552–1576 RSC.
- P. Y. Chen, J. Qi, M. T. Klug, X. Dang, P. T. Hammond and A. M. Belcher, Energy Environ. Sci., 2014, 7, 3659–3665 RSC.
- B. O’Regan and M. Grätzel, Nature, 1991, 353, 737–740 CrossRef.
- M. L. Parisi, S. Maranghi and R. Basosi, Renewable Sustable Energy Rev., 2014, 39, 124–138 CrossRef CAS.
- X. Zhou, Y. Zhang, A. L. Porter, Y. Guo and D. Zhu, Scientometrics, 2014, 100, 705–721 CrossRef.
- S. Shalini, R. Balasundaraprabhu, T. Satish Kumar, N. Prabavathy, S. Senthilarasu and S. Prasanna, Int. J. Energy Res., 2016, 40, 1303–1320 CrossRef CAS.
- M. K. Nazeeruddin, P. Péchy and M. Grätzel, Chem. Commun., 1997, 1705–1706 RSC.
- M. K. Nazeeruddin, P. Péchy, T. Renouard, S. M. Zakeeruddin, R. Humphry-Baker, P. Comte, P. Liska, L. Cevey, E. Costa, V. Shklover, L. Spiccia, G. D. Deacon, C. A. Bignozzi and M. Grätzel, J. Am. Chem. Soc., 2001, 123, 1613–1624 CrossRef CAS PubMed.
- R. Buscaino, C. Baiocchi, C. Barolo, C. Medana, M. Grätzel, M. K. Nazeeruddin and G. Viscardi, Inorg. Chim. Acta, 2008, 361, 798–805 CrossRef CAS.
- Z. Z. Lu, J. Peng, W. De, C. H. Lin, C. G. Wu, K. C. Ho, Y. C. Lin and K. L. Lu, Eur. J. Inorg. Chem., 2016, 1214–1224 CrossRef CAS.
- J. F. Huang, J. M. Liu, P. Y. Su, Y. F. Chen, Y. Shen, L. M. Xiao, D. B. Kuang and C. Y. Su, Electrochim. Acta, 2015, 174, 494–501 CrossRef CAS.
- A. Yella, H. W. Lee, H. N. Tsao, C. Yi, A. K. Chandiran, M. K. Nazeeruddin, E. W. G. Diau, C. Y. Yeh, S. M. Zakeeruddin and M. Grätzel, Science, 2011, 334, 629–634 CrossRef CAS PubMed.
- S. Mathew, A. Yella, P. Gao, R. Humphry-Baker, B. F. Curchod, N. Ashari-Astani, I. Tavernelli, U. Rothlisberger, M. K. Nazeeruddin and M. Grätzel, Nat. Chem., 2014, 6, 242–247 CrossRef CAS PubMed.
- G. Consiglio, S. Failla, C. G. Fortuna, L. D’Urso and G. Forte, Comput. Theor. Chem., 2015, 1067, 1–6 CrossRef CAS.
- I. P. Oliveri, G. Forte, G. Consiglio, S. Failla and S. Di Bella, Inorg. Chem., 2017, 56, 14206–14213 CrossRef CAS PubMed.
- S. Aghazada, P. Gao, A. Yella, G. Marotta, T. Moehl, J. Teuscher, J. E. Moser, F. De Angelis, M. Grätzel and M. K. Nazeeruddin, Inorg. Chem., 2016, 55, 6653–6659 CrossRef CAS PubMed.
- N. V. Krishna, J. V. S. Krishna, M. Mrinalini, S. Prasanthkumar and L. Giribabu, ChemSusChem, 2017, 10, 4668–4689 CrossRef CAS PubMed.
- C. C. Chen, J. S. Chen, V. S. Nguyen, T. C. Wei and C. Y. Yeh, Angew. Chem., 2021, 60(9), 4886–4893 CrossRef CAS PubMed.
- M. Xu, S. Wenger, H. Bala, D. Shi, R. Li, Y. Zhou, S. M. Zakeeruddin, M. Grätzel and P. Wang, J. Phys. Chem. C, 2009, 113, 2966–2973 CrossRef CAS.
- S. Ahmad, E. Guillén, L. Kavan, M. Grätzel and M. K. Nazeeruddin, Energy Environ. Sci., 2013, 6, 3439–3466 RSC.
- C. Zhong, J. Gao, Y. Cui, T. Li and L. Han, J. Power Sources, 2015, 273, 831–838 CrossRef CAS.
- A. Venkateswararao, P. Tyagi, K. R. J. Thomas, P. W. Chen and K. C. Ho, Tetrahedron, 2014, 70, 6318–6327 CrossRef CAS.
- S. S. K. Raavi, P. Docampo, C. Wehrenfennig, M. J. P. Alcocer, G. Sadoughi, L. M. Herz, H. J. Snaith and A. Petrozza, J. Phys. Chem. C, 2014, 118, 16825–16830 CrossRef CAS.
- M. Mao, X. L. Zhang, X. Q. Fang, G. H. Wu, S. Y. Dai, Q. H. Song and X. X. Zhang, J. Power Sources, 2014, 268, 965–976 CrossRef CAS.
- J. Liu, X. Sun, Z. Li, B. Jin, G. Lai, H. Li, C. Wang, Y. Shen and J. Hua, J. Photochem. Photobiol., A, 2014, 294, 54–61 CrossRef CAS.
- T. Kitamura, M. Ikeda, K. Shigaki, T. Inoue, N. A. Anderson, X. Ai, T. Lian and S. Yanagida, Chem. Mater., 2004, 16, 1806–1812 CrossRef CAS.
- S. L. Li, K. J. Jiang, K. F. Shao and L. M. Yang, Chem. Commun., 2006, 2792–2794 RSC.
- R. Chen, X. Yang, H. Tian, X. Wang, A. Hagfeldt and L. Sun, Chem. Mater., 2007, 19, 4007–4015 CrossRef CAS.
- X. Q. Zhu, Z. Dai, A. Yu, S. Wu and J. P. Cheng, J. Phys. Chem. B, 2008, 112, 11694–11707 CrossRef CAS PubMed.
- R. Y. Y. Lin, F. L. Wu, C. T. Li, P. Y. Chen, K. C. Ho and J. T. Lin, ChemSusChem, 2015, 8, 2503–2513 CrossRef CAS PubMed.
- Y. Hua, S. Chang and D. Huang, Chem. Mater., 2013, 25, 2146–2153 CrossRef CAS.
- M. Ling Jang, J. J. Wen, Z. M. Chen, W. H. Tsai, T. C. Lin, T. J. Chow and Y. J. Chang, ChemSusChem, 2019, 8, 3654–3665 CrossRef PubMed.
- Z. B. Xie, A. Midya, K. P. Loh, S. Adams, D. J. Blackwood, J. Wang, X. J. Zhang and Z. K. Chen, Prog. Photovoltaics, 2010, 18, 573–581 CAS.
- Y. Xie, Y. Tang, W. Wu, Y. Wang, J. Liu and X. Li, J. Am. Chem. Soc., 2015, 137, 14055–14058 CrossRef CAS PubMed.
- A. F. Buene, A. Hagfeldt and B. H. Hoff, Dyes Pigments., 2019, 169, 66–72 CrossRef CAS.
- A. F. Buene, E. E. Ose, A. G. Zakariassen, A. Hagfeldt and B. H. Hoff, J. Mater. Chem. A, 2019, 7, 7581–7590 RSC.
- M. L. Han, Y. Z. Zhu and S. Liu, J. Power Sources, 2018, 387, 117–125 CrossRef CAS.
- T. Hua, Z. S. Huang, K. Cai, L. Wang, H. Tang, H. Meier and D. Cao, Electrochim. Acta, 2019, 302, 225–233 CrossRef CAS.
- A. Slodek, D. Zych, S. Golba, S. Zimosz and E. Schab-Balcerzak, J. Mater. Chem. C, 2019, 7, 5830–5840 RSC.
- D. Devadiga, M. Selvakumar, P. Shetty, M. S. Santosh, R. S. Chandrabose and S. Karazhanov, Int. J. Energy Res., 2021, 45, 6584–6643 CrossRef CAS.
- A. Yella, C. L. Mai, S. M. Zakeeruddin, S. N. Chang, C. H. Hsieh, C. Y. Yeh and M. Grätzel, Angew. Chem., 2014, 53(11), 2973–2977 CrossRef CAS PubMed.
- J. Wang, H. Wu, L. Jin, J. Zhang, Y. Yuan and P. Wang, ChemSusChem, 2017, 10, 2962–2967 CrossRef CAS PubMed.
- Y. Ding, J. Li, S. Liu, Y. Tan, K. Shi, Y. Jiao, B. Mi, W. Xu and Z. Gao, Dyes Pigm., 2021, 194, 109664 CrossRef CAS.
- Z. Z. Sun, S. Feng and W. L. Ding, Sol. Energy, 2020, 195, 491–498 CrossRef CAS.
- K. M. Lee, V. Suryanarayanan and K. C. Ho, J. Power Sources, 2009, 188, 635–641 CrossRef CAS.
- J. Wu, Z. Lan, J. Lin, M. Huang and P. Li, J. Power Sources, 2007, 173, 585–591 CrossRef CAS.
- E. Mosconi, A. Selloni and F. De Angelis, J. Phys. Chem. C, 2012, 116, 5932–5940 CrossRef CAS.
- H. Tian, X. Yang, R. Chen, R. Zhang, A. Hagfeldt and L. Sun, J. Phys. Chem. C, 2008, 112, 11023–11033 CrossRef CAS.
- T. Le Bahers, F. Labat, T. Pauportè and I. Ciofini, Phys. Chem. Chem. Phys., 2010, 12, 14710–14719 RSC.
- H. Fang, J. Ma, M. J. Wilhelm, B. G. DeLacy and H. L. Dai, Part. Part. Syst. Charact., 2021, 38, 2000220 CrossRef CAS.
- G. Consiglio, A. Gorcynski, S. Petralia and G. Forte, RSC Adv., 2023, 13, 1019–1030 RSC.
- G. Consiglio, A. Gorcynski, S. Petralia and G. Forte, Dalton Trans., 2023, 52, 15995–16004 RSC.
- G. Forte, L. D’Urso, E. Fazio, S. Patanè, F. Neri, O. Puglisi and G. Compagnini, Appl. Surf. Sci., 2013, 272, 76–81 CrossRef CAS.
- E. Fazio, L. D’Urso, G. Consiglio, A. Giuffrida, G. Compagnini, O. Puglisi, S. Patanè, F. Neri and G. Forte, J. Phys. Chem. C, 2014, 118, 28812–28819 CrossRef CAS.
- N. R. Agarwai, A. Lucotti, M. Tommasini, W. A. Chalifoux and R. R. Tykwinski, J. Phys. Chem. C, 2016, 120(20), 11131–11139 CrossRef.
- P. Marabotti, A. Milani, A. Lucotti, L. Brambilla, M. Tommasini, C. Castiglioni, P. Mecik, B. Pigulski, S. Szafert and C. S. Casari, Carbon Trends, 2021, 5, 100115 CrossRef CAS.
- S. Eisler, A. D. Slepkov, E. Elliott, T. Luu, R. McDonald, F. A. Hegmann and R. Tykwinski, J. Am. Chem. Soc., 2005, 127, 2666–2676 CrossRef CAS PubMed.
- L. K. Zaitriand and S. M. Mekelleche, Mol. Phys., 2020, 118, 1–10 Search PubMed.
- C. S. Casari, M. Tommasini, R. R. Tykwinski and A. Milani, Nanoscale, 2016, 8, 4414–4435 RSC.
-
F. Cataldo, Polyynes: Synthesis, Properties, and Applications, 2005 Search PubMed.
- W. H. Liu, I. C. Wu, C. H. Lai, C.-H. Lai, P. T. Chou, Y. T. Li, C. L. Chen, Y. Y. Hsu and Y. Chi, Chem. Commun., 2008, 5152–5154 RSC.
- C. Bonaccorso, F. De Rossi, M. Panigati, C. G. Fortuna, G. Forte, T. M. Brown, G. M. Farinola and G. Musumarra, Tetrahedron, 2015, 71, 7260–7266 CrossRef CAS.
-
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Rev C.01, Gaussian, Inc., Wallingford CT, 2016 Search PubMed.
- J. Preat, C. Michaux, D. Jacquemin and E. A. Perpete, J. Phys. Chem. C, 2009, 113, 16821–16833 CrossRef CAS.
- M. Pastore, E. Mosconi, F. De Angelis and M. Gratzel, J. Phys. Chem. C, 2010, 114, 7205–7212 CrossRef CAS.
- D. Fadili, Z. M. E. Fahim, S. M. Bouzzine, O. T. Alaoui and M. Hamidi, Comput. Theor. Chem., 2022, 1210, 113645 CrossRef CAS.
- C. O’Rourke and D. Bowler, J. Phys.: Condens. Matter, 2014, 26, 195302 CrossRef PubMed.
- M. Wagstaffe, A. G. Thomson, M. J. Jackman, M. Torres-Molina, K. L. Syres and K. Handrup, J. Phys. Chem. C, 2016, 120(3), 1693–1700 CrossRef CAS.
- R. Sánchez-de-Armas, M. A. San Miguel, J. Oviedo and J. F. Sanz, Phys. Chem. Chem. Phys., 2012, 14(1), 225–233 RSC.
- R. Sánchez-de-Armas, M. A. San-Miguel, J. Oviedo, A. Márquez and J. F. Sanz, Phys. Chem. Chem. Phys., 2011, 13(4), 1506–1514 RSC.
- R. Sánchez-de-Armas, J. OviedoLópez, M. A. San-Miguel, J. F. Sanz, P. Ordejón and M. Pruneda, J. Chem. Theory Comput., 2010, 6(9), 2856–2865 CrossRef PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- L. L. Estrella, M. P. Balanay and D. H. Kim, J. Phys. Chem. A, 2016, 120, 5917–5927 CrossRef CAS PubMed.
- R. A. Marcus, J. Chem. Phys., 1956, 24, 966–978 CrossRef CAS.
- R. A. Marcus and N. Sutin, Rev. Bioenerget., 1985, 811, 265–322 CAS.
- M. P. Balany and D. H. Kim, THEOCHEM, 2009, 910, 20–26 CrossRef.
- T. P. Nguyen, J. H. Shim and J. Y. Lee, J. Phys. Chem. C, 2015, 119, 11301–11310 CrossRef CAS.
- J. C. Cave and M. D. Newton, Chem. Phys. Lett., 1996, 249, 15–19 CrossRef.
- J. Preat, A. Hagfeldt and E. A. Perpete, Energy Environ. Sci., 2011, 4, 4537–4549 RSC.
- J. B. Asbury, Y. Q. Wang, E. C. Hao, H. N. Ghosh and T. Q. Lian, Res. Chem. Intermed., 2001, 27, 393–406 CrossRef CAS.
- G. R. Hutchison, M. A. Ratner and T. J. Marks, J. Am. Chem. Soc., 2005, 127, 2339–2350 CrossRef CAS PubMed.
- H. Geng, Y. Niu, Q. Peng, Z. Shuai, V. Coropceanu and J. L. Bredas, J. Chem. Phys., 2011, 135, 104703 CrossRef PubMed.
- A. Amini and A. Harriman, J. Photochem. Photobiol., C, 2003, 4, 155–177 CrossRef CAS.
- Y. K. Lan and C. I. Huang, J. Phys. Chem. B, 2008, 112, 14857–14862 CrossRef CAS PubMed.
- A. Hagfeldt, G. Boschloo, L. Sun and H. Pettersson, Chem. Rev., 2010, 110, 6595–6663 CrossRef CAS PubMed.
- M. Pastore, S. Fantacci and F. De Angelis, J. Phys. Chem. C, 2013, 117(8), 3685–3700 CrossRef CAS.
- T. Manzoor, S. Asmi, S. Niaz and A. H. Pandith, Int. J. Quantum Chem., 2017, 117, 1–14 CrossRef.
- D. Unny, G. R. Kandregula and K. Ramanujam, New J. Chem., 2021, 45, 16989–17001 RSC.
|
| This journal is © The Royal Society of Chemistry 2024 |
Click here to see how this site uses Cookies. View our privacy policy here.  Open Access Article
Open Access Article a,
Adam
Gorcyński
a,
Adam
Gorcyński
 b,
Salvatore
Petralia
b,
Salvatore
Petralia
 c and
Giuseppe
Forte
c and
Giuseppe
Forte
 *c
*c