Resolving charge transfer mechanisms in molecular tunnel junctions using dynamic charge transfer and static current–voltage measurements

Abstract

Understanding charge transfer (CT) dynamics is important for controlling the tunneling mechanism in molecular junctions. Synchrotron-based core-hole clock (CHC) spectroscopy can quantify the femtosecond-scale CT time τ_CT across the metal–molecule interface, which affects the current density (J) produced with applied bias (V) in the junctions. However, directly determining the tunneling behavior from a comparison of the CHC τ_CT and the J(V) measurement of a junction requires prior knowledge of the molecular orbitals involved. To solve this problem, we examined CT dynamics across self-assembled monolayers (SAMs) based on oligophenylene ethynylene (OPE) wires with ferrocene (Fc) terminal groups with Au, Ag and Pt bottom electrodes. Density functional theory (DFT) helped identify the donor and acceptor levels, which are typically the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO). The measured J(V) response of the SAM junctions with gallium-indium (EGaIn) alloy as the top electrode demonstrates that the tunneling decay coefficient β provides an intensive parameter to assess CT efficiency. We find that more delocalized molecular wavefunctions (in this case, LUMO+2, with contributions from Fc and OPE) facilitate faster and more efficient CT than more localized acceptor levels (here, the more iron-centered LUMO+1). These orbital-specific effects explain why we measure comparable β values for CT via LUMO+1 and J via HOMO and LUMO at −1 V bias. Our study highlights the utility of τ_CT measured by CHC in experimentally confirming the orbitals participating in charge transport measurements and shows that higher-lying delocalized orbitals can in some instances dominate over frontier orbitals despite larger energy offset (or increase in tunneling barrier height).

---

Introduction

Synchrotron-based core-hole clock (CHC) spectroscopy has been applied to probe the charge transfer (CT) dynamics across metal–molecule interfaces.¹ The results provide essential knowledge on the fundamental physics of charge transport.^2,3 Specifically, understanding ultrafast interfacial CT dynamics and the interfacial energetic losses is crucial for determining the photoelectronic conversion efficiency devices, including of organic solar cells.^4,5 The unique capability of CHC to quantify the femtosecond CT time scale from different orbitals within a single molecule makes it particularly valuable to study systems with multiple orbitals close to the Fermi level (E_F) of the metal substrate.^6–8 However, it is important to clarify that the orbitals involved with CT during CHC spectroscopy are not necessarily the same as those orbitals involved with charge transport in molecular junctions under static direct-current conditions, as observed in J(V) measurements of current density (J) vs. voltage (V). For instance, CHC exclusively explores dynamic CT from unoccupied molecular orbitals to the continuum states of the metal substrates, while occupied molecular orbitals are accessible in the J(V) measurements depending on the polarity of the applied bias voltage. Moreover, although both CHC CT time τ_CT and J(V) current evaluate how fast the electrons tunnel through a molecule, the underlying mechanisms provided by the two methods diverge significantly. The ability to distinguish charge transport related to specific orbitals in J(V) experiments remains speculative. Therefore, it is still an open question whether trends in CT rates from CHC spectroscopy studies can be related to trends in tunneling rates measured by J(V) measurements and whether, by comparing these two methods, it is possible to determine which orbitals are involved in measurements of tunneling rates across molecular junctions.

J(V) measurements of molecular junctions can be performed using a variety of techniques.^9–11 These techniques differ in terms of their junction formation methods, yielding varying contact resistances and, consequently, different currents for a given molecule. In large-area junctions, the effective contact area could be 10⁻⁴ to 10⁻⁶ times smaller than the geometrical contact area,^12–14 and the presence of defects may further affect the measured currents.^15–18 However, the observed length-dependent behavior of the current or conductance for a molecular series remains consistent across various platforms. The tunneling decay coefficient (β) can be obtained from the general tunneling equation

where J is the current density, J₀ is the pre-exponential factor, d is the tunneling distance, m is effective mass of the charge carrier, φ denotes the tunneling barrier height, ℏ stands for the reduced Planck constant (h/2π), and α is a parameter used to modify the rectangular barrier model. J and J₀ are extensive parameters that depend on the junction area, and β is an intensive parameter that is consistent for a molecule or a series of molecules with similar structure. Therefore, β is often used as an indication of how efficiently molecular wires conduct currents. For instance, oligophenylene ethynylene (OPE) wires, with β = 0.2–0.4 Å⁻¹,^19,20 are regarded as better conductors than free and cyano-capped alkanethiolates with β = 0.7–1.0 Å⁻¹.^21,22

In CHC studies, CT time τ_CT also follows an exponential decay with tunneling distance⁶

τ_CT = τ₀e^βd (2)

where τ₀ is the pre-exponential factor for CT time. CHC studies on oligophenyl, acene and alkyl backbones give β values of 0.55 Å⁻¹, 0.25 Å⁻¹ and 0.72 Å⁻¹,^2,7,23 respectively, close to the β of 0.44 Å⁻¹, 0.20 Å⁻¹ and 0.76 Å⁻¹ observed in J(V) measurements for their corresponding molecular junctions.^24,25 These findings suggest that there are common physical principles underlying both the static and dynamic aspects of the charge transport, despite the contrasting methodologies employed in CHC and J(V) to assess tunneling. However, the above CHC studies employed only two molecular lengths to determine β,^7,23 potentially introducing substantial statistical uncertainty. For example, the β values for the acene wires⁷ are derived from only two molecular lengths because the τ_CT for longer wires are beyond the upper detection limit (150 fs) of the resonant Auger electron spectroscopy (RAES) at N K-edge.²⁶ Therefore, more comprehensive studies encompassing a broader range of tunneling distances and diverse electrode substrates are required to precisely determine β values from CT times in CHC studies.

Here, we report the tunneling decay behavior for conjugated molecular wires using both the CHC technique and J(V) measurements. We designed a series of OPE wires functionalized with a ferrocene (Fc) head group, denoted as S-CH₂-OPE_nFc where OPE is Ph–C≡C and n = 1–3. The self-assembled monolayers (SAMs) of these molecules were formed on template-stripped Au, Ag and Pt surfaces following earlier reported methods.²⁷ In the CHC scheme as illustrated in Fig. 1a, CT from molecular orbitals to the metal can in principle be explored via the promotion of excited electrons into low-lying unoccupied molecular orbitals (LUMOs) above the E_F of the metal electrodes, in this case specifically the LUMO+1 level with strong Fc contribution and the more delocalized LUMO+2.²⁸ In J(V) measurements (cf.Fig. 1b), the Fc-centered highest occupied molecular orbital (HOMO) located just below E_F participates in the charge transport in the molecular junctions under negative bias, yielding well-performing molecular diodes.²⁹ Charging of the Fc unit leads to molecular orbital gating and lowering of the LUMO level (dashed arrow Fig. 1b; this level is more delocalized over the molecule, as shown below in density functional theory, DFT, calculations, Fig. 2), which allows it to participate in the mechanism of charge transport.²⁷ The shared elements of the charge transfer/transport mechanism in the CHC experiment and at negative bias in the J(V) measurements both involving the LUMO(s) are illustrated in Fig. 1. Both processes involve electron injection into a molecular orbital close to the E_F of the bottom electrode, followed by tunneling along the molecular backbone involving the LUMO.

Fig. 1 Schematic illustration of charge transport in SAMs of M/S-CH₂-OPE_nFc (M = Ag, Au, Pt, n = 1–3) in (a) CHC spectroscopy and (b) J(V) measurement at negative bias using EGaIn as the top electrode. In panel (a), the photon hν excites C 1s core electrons into low-lying empty levels (dashed red arrow) within the molecules. The excited electrons can transfer to the metal electrode (solid red arrow). In panel (b), upon the application of a negative bias to the junctions, the HOMO level moves into the bias window, facilitating charge transport between the electrodes (red arrows). The intramolecular gating effect can shift the LUMO into the bias window (blue arrow in panel b²⁷). The horizontal positions of the molecular orbitals are drawn based on their locations along the molecular wires. EGaIn stands for eutectic gallium–indium alloy.³⁰

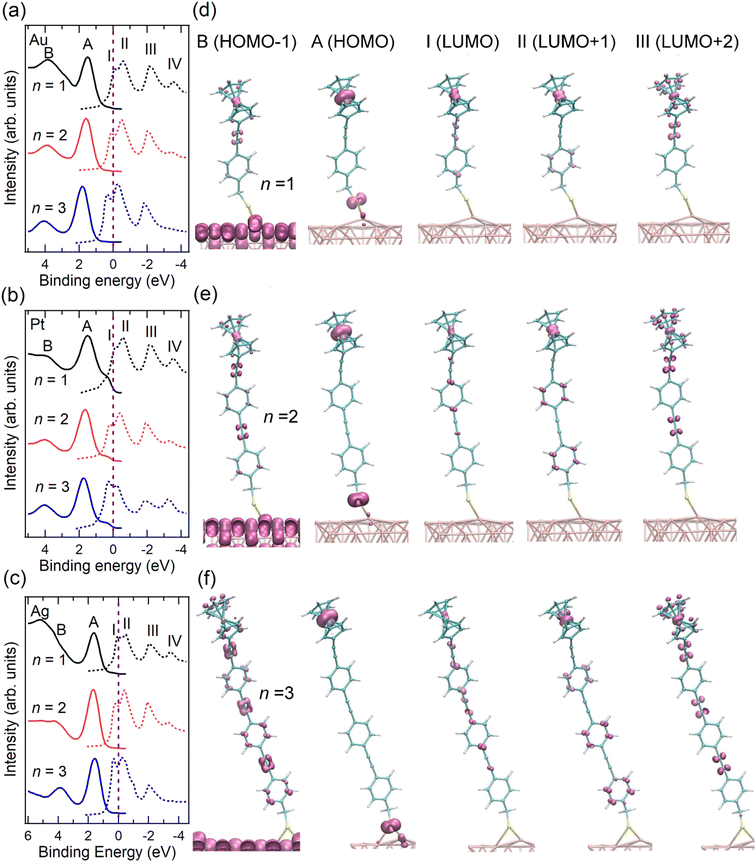Fig. 2 VB (solid lines) and re-scaled NEXAFS spectra (dashed lines) of SAMs (a) Au/S-CH₂-OPE_nFc, (b) Pt/S-CH₂-OPE_nFc, and (c) Ag/S-CH₂-OPE_nFc (n = 1–3). The NEXAFS spectra were aligned to Fermi level (set at 0 eV, above the top of the valence band), as marked by vertical dashed lines, through subtracting their photon energy from the binding energy of the C 1s peak corresponding to the Cp rings in the PES spectra (Fig. S2, ESI†), following previously reported procedures.^3,6,28 Computed region B (HOMO−1), A (HOMO), I (LUMO), II (LUMO+1), and III (LUMO+2) electron density surfaces for S-CH₂-OPE_nFc on Au(111) with (d) n = 1, (e) n = 2, and (f) n = 3. All surfaces are visualized at the common isovalue of 0.1 atomic units and colored mauve. The HOMO is dominated by Fc iron-centered Fe 3d_z² density with minor contribution from S, while the LUMO is delocalized over the OPE chain with contributions from Fe 3d_xz/3d_yz.

In this work, we quantified τ_CT from LUMO+1 and LUMO+2 across a series of S-CH₂-OPE_nFc monolayers with various molecular lengths (n = 1–3), which allows us to extract their β values on Au, Ag and Pt metal substrates. In addition, we fabricated junctions using EGaIn (Fig. 1b) as the top electrode and obtained β values for J at +1 V and −1 V, respectively. We draw the following conclusions from the results: (1) in the CHC study, CT from the LUMO+2 level, which is strongly delocalized over the molecule results in shorter CT times and smaller β values than CT from the more Fc-localized LUMO+1 orbital. (2) In the J(V) measurements, β values consistently exhibit higher values at +1 V than those at −1 V. We attribute this difference to the distinct tunneling mechanisms: coherent tunneling at +1 V (lacking molecular orbital involvement) and incoherent tunneling at −1 V (where charge injection in the LUMO is mediated by the HOMO dominated charge transport²⁷). (3) The β values associated with CT time derived from LUMO+1 closely mirror the β values corresponding to J at −1 V. We believe this correspondence arises from the similarity in the spatial distribution revealed by DFT calculations of the LUMO+1 (regulating CHC CT) and HOMO and LUMO (regulating J(V) at −1 V). Both the LUMO and LUMO+1 show some delocalization over the molecular backbone, which reaffirms the intramolecular orbital gating effect induced by the HOMO which is localized on the Fe 3d orbitals. Our results indicate the potential to relate behaviors in J(V) measurements to insights gained from CHC studies, and vice versa, despite the distinct experimental conditions governing CHC and J(V) measurements. This holds particularly true when the CT centers in the molecule are well defined.

Results and discussion

Energy level alignment at the metal–SAM interfaces

We fabricated SAMs of M/S-CH₂-OPE_nFc (M = Au, Pt, Ag; n = 1–3) and characterized their structure by photoemission spectroscopy (PES) (ESI† Fig. S1–S4) using protocols reported before.^27,31 For M = Pt, the S 2p signals are dominated by the S₁ doublet (dominant peak at ∼162.2 eV) associated with chemisorbed sulfur, with minor contributions from S₂ doublet (∼163.4 eV) associated with physisorbed S. For M = Ag and Au, an additional signal S₀ doublet (∼161.1 eV) is present. This S₀ feature has been assigned to chemisorbed sulfur for disordered phases or to atomic sulfur (or other impurities) resulting from decomposition of the precursor.^32–35 We attribute the S₀ feature to the disordered phase of the alkanethiolate SAMs because we have not found evidence for decomposition of the precursors. In prior work we could link the disordered phase to the S₀ feature through a detailed monolayer characterization study.³⁶ The significant disordered phase in the Ag/S-CH₂-OPE_nFc SAMs is likely responsible for a reduced tunneling distance d (thin-area defects^15,37) in the J(V) measurements, resulting in high leakage current and thus low rectification ratio (RR) values³⁸ (Fig. S9, ESI†). The CHC results are, in principle, not affected by disorder in the same way because d is defined by the molecular length for the through-bond CT from the molecule to the substrate.³⁹

To examine the energy level alignment at the metal–molecule interfaces, we recorded the valence band (VB) and near edge X-ray absorption fine structure (NEXAFS) spectra of each SAM. Fig. 2(a–c) maps the relative energy level positions at the measured interfaces, aligned with respect to E_F of the metals. The NEXAFS spectra here were aligned by subtracting their photon energy from the binding energy (BE) of the C 1s peak corresponding to the Cp rings in the PES spectra (Fig. S2, ESI†) following previously reported procedure.⁶ In the VB spectra, peak A marks the HOMO of the molecule, centered on the Fe 3d level of the Fc terminal group. This is supported by the calculated projected density of states (PDOS) distributions for the frontier orbitals of Au/S-CH₂-OPE₁Fc shown in Fig. S5 (ESI†) and electron density surfaces shown in Fig. 2(d-f) (calculated with DFT methods given in ESI† S3). Peak A shifts by ∼0.1 eV towards higher BE from n = 1 to n = 3 on all substrates, reflecting the weaker photo-hole screening effects when Fc is located further away from the substrate.^40–42 Peak B represents the HOMO−1 level of the molecules which involves the π orbitals of OPE backbones and the Cp rings, along with minor contributions from the Fe 3d orbitals (Fig. S5 and Fig. 2d–f, ESI†).

In the NEXAFS spectra, peak I corresponds to the transition from C 1s to the LUMO orbitals on the OPE backbones. The PDOS calculations in Fig. S6 (ESI†) shows also some contribution to the LUMO from the Fe, as opposed to none in the previously studied S-CH₂-DPA-C_n-Fc series (further details of PDOS are in ESI† Section S3).^6,27 Peak II (LUMO+1) represents a mix of transitions to the Fe 3d_xz/3d_yz orbitals and the π* of the phenyl rings. In contrast to our earlier studies on S-CH₂-DPA-C_n-Fc,⁶ the Cp rings and the OPE backbone in the S-CH₂-OPE_nFc series are conjugated, and the LUMO+1 orbitals have more contributions from OPE units. Peak III corresponds to the transition to the delocalized LUMO+2 orbitals extending along the OPE wires and Cp rings, with minor contributions from the Fe 3d_xy orbitals. Peak IV marks the transition to the σ* of the C–H/C–S bonds, as discussed in our earlier study of Au/S(CH₂)₁₁Fc SAMs.⁴² All the unoccupied orbitals (peaks I–IV) shift by ∼0.4 eV to lower BE from n = 1 to n = 3. This shift arises from the decreasing HOMO–LUMO gap with the increasing number of OPE units with a reduction of 0.3 ± 0.1 eV per OPE unit calculated from the calculated DFT band structures, averaged over the Au/S-CH₂-OPE_nFc (n = 1–3) series. As shown in Fig. 2(a–c), both LUMO+1 and LUMO+2 orbitals are located above E_F, which facilitates their participation in the transfer of excited electrons to the metal substrates. The weak peak feature IV is not always visible in the NEXAFS spectra, therefore we do not discuss its CT behavior in this study. In addition, the LUMO of molecules lies below the E_F when n = 2 and n = 3 due to core-hole excitonic effect. Consequently, the CT from LUMO is not always applicable and not considered further in this work.³

The resonant PES (RPES) contour plots of M/S-CH₂-OPE_nFc (M = Au, Pt, Ag; n = 1–3) in the photon energy range of 284 eV to 289 eV are summarized in Fig. 3. For clarity, we omitted the features at >8 eV BE consisting of normal Auger decay signals from lower-lying levels. In RPES, resonance occurs when the energy of the incident photon aligns with the energy gap between the core level and the low-lying empty acceptor levels.⁴³ The associated VB features are resonantly enhanced, leading to the high-intensity regions in the contour plots. The strength of enhancement is determined by the degree of spatial overlap between the corresponding occupied and unoccupied orbitals. This phenomenon is related to the photon energy dependent enhancement of valence states. Specifically, resonant enhancement of a feature derived from a valence-orbital becomes most pronounced when the photon energies correspond to electrons excitations to the unoccupied orbitals that spatially overlap with specific valence orbitals.⁴³ For instance, the resonant enhancement for peak A (HOMO at ∼2 eV) predominantly associated with Fe is dependent on the contribution of Fe 3d character in the unoccupied orbitals. As a result, peak A is strongly enhanced in the energy range of LUMO+1 (285.2–286.0 eV guided by II) with a significant contribution form Fe 3d_xz/3d_yz and weakly enhanced in the energy range of LUMO (284.8–285.1 eV guided by I), which is localized over the OPE chains. On the contrary, peak B (HOMO−1 at ∼4 eV, more delocalized across the molecule), exhibits more uniform enhancement across all the absorption features (guided by I, II and III).

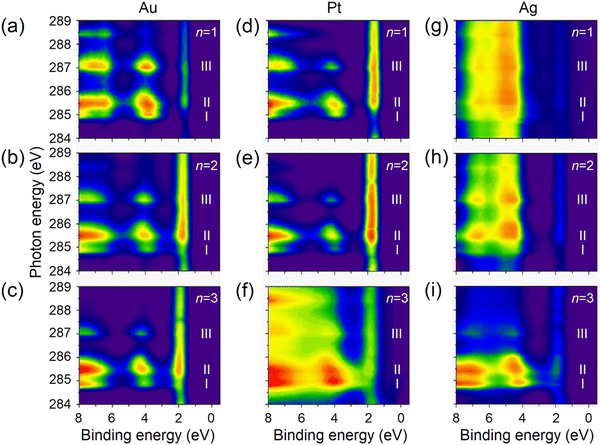Fig. 3 The RPES contour plots for SAMs of M/S-CH₂-OPE_nFc with (a)–(c) M = Au, (d)–(f) M = Pt, (g)–(i) M = Ag. Subpanels are arranged from top to bottom showing n = 1 to n = 3.

On the Ag substrate, the resonance enhancement of HOMO and HOMO−1 is overlapped with emission originating from the Ag 4d orbitals within the 4–8 eV.⁴⁴ The resonance enhancement becomes dominant for n = 3. This phenomenon is due to the taller monolayer height of S-CH₂-OPE₃Fc (∼23 Å in Table S1, ESI†), attenuating the signals from Ag and facilitating the visibility of the molecular VB features.⁴⁵ A similar effect is seen on Pt but around BE range of 1.5–2 eV, where Pt 5d levels have the maximal signals.⁴⁶

Core-hole clock spectroscopy.

We integrated the resonant photoemission signals from each SAM in the BE range of 0–7 eV and plotted them as a function of photon energy. The integrated RPES spectra and corresponding least-squares fitting are shown in Fig. 4 (the detailed procedure for the fitting is described in ESI† S4). The intensity of each resonance represents the population of electrons undergoing participator decay. Integrating the signals in a broader binding energy range of 0–20 eV includes all the decay pathways of excited electrons (Fig. S7, ESI†). The ratio of the RPES and the NEXAFS signals was used to calculate the τ_CT for resonances II and III (details in ESI† S4). It is noted that Au/S-OPE₃Fc, exhibiting the longest, most extensive CT time (Fig. S8, ESI†), serves as a reference higher bound estimate of CT time in a truly isolated system in which no CT from Fc can occur. While this calibration, which has been adopted previously,⁶ might give τ_CT values slightly higher than the actual values, the conclusions drawn from the comparisons of τ_CT values with a consistent reference remain valid. The results are summarized in Table 1. We plotted the τ_CT in logarithmic scale as a function of molecular length d_mol in Fig. 5 and determined the β values for the CT using eqn (2).

Fig. 4 Integrated RPES spectra for SAMs of (a) Au/S-CH₂-OPE_nFc, (b) Pt/S-CH₂-OPE_nFc and (c) Ag/S-CH₂-OPE_nFc. The intensity at each photon energy is a result of the integration of VB spectra in the binding energy range of 0–7 eV. The fitted peak denotes resonance I (purple), II (green), III (navy blue) and IV (cyan). The signals were all normalized by the NEXAFS spectra of the corresponding clean non-functionalized metal surfaces to resolve the molecular signals.

Table 1 Charge transfer times τ_CT from the resonance II (LUMO+1) and resonance III (LUMO+2) to the metal surfaces^a

Metal	Resonance	τ CT (fs)
		S-CH2-OPEnFc
		n = 1	n = 2	n = 3
a The error represents the standard deviation of the fitting residual for each resonance.
Ag	II	11 ± 3	24 ± 4	151 ± 60
	III	10 ± 5	11 ± 6	10 ± 5
Au	II	29 ± 11	28 ± 10	27 ± 8
	III	17 ± 12	17 ± 11	17 ± 11
Pt	II	21 ± 8	34 ± 16	74 ± 67
	III	17 ± 15	17 ± 14	19 ± 17

---

Fig. 5 The τ_CT from resonance II (red) and III (blue) to the metal surfaces, along with current densities at −1 V (purple) and +1 V (green) for (a) Au, (b) Pt and (c) Ag as a function of d_mol, which is the distance between the metal surface and the furthest Cp carbon atom in the molecule. The lines represent the best linear fits for τ_CT (in log-scale) and log|J|. The β values are calculated from the slopes of the fitted lines.

It is found that τ_CT associated with resonance III is effectively length-independent on all three metal substrates. We attribute this characteristic and consequently ultra-low β values to two factors: (1) the orbital responsible for resonance III (LUMO+2) is highly delocalized over the Cp rings in Fc and the OPE backbone (cf.Fig. 2d–f). (2) The reduction in tunneling barrier height φ is evident by the reduction of the energy gap between LUMO+2 and the E_F by ∼0.5 eV from n = 1 to n = 3. Conversely, resonance II does show length dependency with SAMs on Pt (Fig. 5b) and Ag (Fig. 5c). This can be attributed to the stronger localization of the LUMO+1 on Fc, specifically Fe 3d (see also DFT data in Fig. S6, ESI†).

When n = 1, the short tunneling distance does not differentiate the two orbitals of resonance II and III, leading to similar τ_CT values. However, for n = 2 and 3, resonance III gives lower values of τ_CT, subsequently yielding reduced β values, despite having a larger energy gap (larger φ). This observation underscores the significant impact of orbital delocalization on the overall mechanism.

J(V) response in molecular junctions.

To investigate the implications of the CHC results in the static current measurements, we fabricated molecular junctions with the structure of M/S-CH₂-OPE_nFc//GaO_x/EGaIn (M = Au, Ag, Pt) following previously reported methods.²⁷ The data for junctions on Au have been reported before in ref. 27, the J(V) responses obtained from junctions with Ag and Pt electrodes are summarized in Fig. S9 (ESI†). The corresponding β values at +1 V and −1 V are given in Fig. 5.

As shown in Fig. 2a–c, the energy level alignment of the molecule on Au, Ag and Pt surfaces does not differ significantly, because of Fermi-level pining.^25,47 As shown in Fig. 5, the rectification ratios (RR = |J(−1 V)|/|J(+1 V)|) for junctions with Pt bottom electrodes are comparable with the junctions with Au as the bottom electrode (see also Fig. S9 and Table S2, ESI†). However, this diode behavior is absent for junctions with Ag bottom electrodes (Fig. 5c and Fig. S9c, ESI†). It has been reported before that the disordered regions in the SAM increases the leakage current of a diode,³⁶ which is the current at positive bias (“off” state) in this study. The lack of rectification for Ag is attributed to the presence of the disordered phase (with a percentage of 25–50%) in the SAM structure, as indicated by the S₀ peak in the S 2p spectra (Fig. S1, ESI†) as discussed above. At +1 V bias, no molecular orbitals are inside the conduction window and so the charge transport is dominated by coherent tunneling. Similar values for β (+1 V, Au) = 0.285 ± 0.077 Å⁻¹ and β (+1 V, Pt) = 0.314 ± 0.104 Å⁻¹ are identified, which agree well with the β values for OPE wires reported by others.^20,48,49 On the other hand, β (+1 V, Ag) = 0.121 ± 0.008 Å⁻¹ is markedly lower than those for Au and Pt electrodes, which can be explained by the earlier mentioned disordered phase leading to high leakage current offsetting the effect of increasing d_mol. The β (−1 V) values on Pt (0.075 ± 0.004 Å⁻¹) and Au (0.043 ± 0.013 Å⁻¹) surfaces are lower than the β (+1 V) values, suggesting that incoherent tunneling is the primary mechanism by which one or more molecular orbitals participate in the charge transport. Among the three metal surfaces with different work function (WF_Ag ∼ 4.3 eV, WF_Au ∼ 5.2 eV, WF_Pt ∼ 5.7 eV),⁵⁰J at a certain bias follows the trend J(Ag) > J(Au) > J(Pt), indicating that a lower electrode work function leads to higher currents in the junctions.⁵¹ This result agrees with measurements on perylene diimide molecular junctions.⁵² The opposite trend, however, has also been documented in other systems,^53,54 and the underlying reason for this difference remains unclear, likely depending on the positioning of the MOs relative to the electrode Fermi level.

Fig. 5 reveals a notable agreement between the β (−1 V) values in the J(V) measurements and the β_II of CT for resonance II in the CHC study for all three metals. As illustrated in Fig. 1b, at negative bias in the J(V) measurements, the charge transport is predominantly mediated by the HOMO, which has strong Fe 3d character, and involves charge injection into the LUMO, which is delocalized over the molecular backbone. This process engages both frontier orbitals.²⁷ In the CHC scheme as illustrated in Fig. 1a, resonance II represents the CT from LUMO+1 which is also delocalized over the backbone but with substantial Fe 3d character (for DFT MO surface, see Fig. 2d–f). As a result, the CT process from LUMO+1 in the CHC technique mirrors the charge transport mechanism at the negative bias of the J (−1 V) measurement, in particular for Ag and Pt electrodes. In comparison, at positive bias in the J(V) measurements, no molecular orbitals participate in the charge transport. The resulting off resonant coherent tunneling gives high β (+1 V) values.

Turning our attention to resonance III in CHC, the CT occurs from delocalized LUMO+2 that has major contributions from C≡C π* orbitals of the OPE backbone. This characteristic accounts for the near-zero values of β_III values, indicating electron transfer from OPE to metal electrode with near-constant tunneling distance. Given the similarity in spatial distribution between LUMO, LUMO+1 and LUMO+2, a length-independent charge transfer from LUMO is thus expected. This behavior mirrors the near-zero β (−1 V) associated with incoherent transport at negative bias for the Au electrode, which supports our earlier finding that intramolecular orbital gating lowers the LUMO level into the bias window to participate in charge transport (Fig. 1b). Given the localized nature of the HOMO, length dependent charge transport would otherwise been expected.²⁷

Experimental

A detailed description of the synthesis of the monolayer precursors is given in ref. 27. All other experimental procedures follow previously reported methods and are described in the ESI†: fabrication of the metal surfaces and formation of SAMs (Section S1, ESI†), photoemission spectroscopy (Section S2, ESI†), all details regarding DFT calculation (Section S3, ESI†), core-hole clock analysis (Section S4, ESI†), and Junction fabrication and statistics (Section S5, ESI†).

Conclusions

In this work, we studied the dynamics of CT across molecular wires with OPE backbones and investigated the electrical characteristics of their electrode-contacted molecular junctions. Our data shows that CHC spectroscopy can give valuable insights into the tunneling mechanism in the molecular junctions despite the difference in the working conditions of CHC and junction J(V) measurements, namely, excited vs. ground state orbitals, unbiased vs. biased SAMs, one vs. two electrodes, measured time vs. current density, and dynamic vs. static. By comparing the tunneling decay coefficient β value derived from orbital selective core-hole-clock charge transfer time τ_CT with the β value derived from charge transport measurements in molecular tunneling junctions, we were able to identify from DFT electron density surfaces the most likely orbital involved in charge transport measurements. Although usually only the HOMO and LUMO levels are considered, our findings give new insights into how neighboring non-frontier MOs further from the Fermi level may play an important role, with CT occurring preferentially via more delocalized orbitals.^55–57 The findings of this work can expand the scope of applications for the CHC technique, making it an important tool to resolve the fine details of CT mechanisms and aid the design of molecular electronic devices.

Author contributions

The manuscript was written through contributions of all authors. All authors have given approval to the final version of the manuscript.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

We acknowledge the National Research Foundation (NRF) for supporting this research under its Medium Sized Centre Programme and the Competitive Research Programme (CRP; NRF-CRP17-2017-08). D.Q. acknowledges the support of the Australian Research Council (grant no. DP230101904). D.T. thanks Science Foundation Ireland (SFI) for support (award no. 12/RC/2275_P2, SSPC), and for computing resources at the SFI/Higher Education Authority Irish Center for High-End Computing (ICHEC). L.C. acknowledges the support of the National Natural Science Foundation of China (Grant No. 12074385). Part of this research was undertaken on the Soft X-ray Spectroscopy beamline at the Australian Synchrotron, part of ANSTO. We also express our thanks to the beamline scientists Dr Bruce Cowie and Dr Anton Tadich for their help in conducting the SAM characterization.

References

1. P. A. Brühwiler, O. Karis and N. Mårtensson, Rev. Mod. Phys., 2002, 74, 703–740.
2. M. Zharnikov, Acc. Chem. Res., 2020, 53, 2975–2984.
3. L. Cao, X. Y. Gao, A. T. S. Wee and D. C. Qi, Adv. Mater., 2014, 26, 7880–7888.
4. K. Nakano, Y. Chen, B. Xiao, W. Han, J. Huang, H. Yoshida, E. Zhou and K. Tajima, Nat. Commun., 2019, 10, 2520.
5. Y. Zhong, M. Causa, G. J. Moore, P. Krauspe, B. Xiao, F. Günther, J. Kublitski, R. Shivhare, J. Benduhn, E. BarOr, S. Mukherjee, K. M. Yallum, J. Réhault, S. C. B. Mannsfeld, D. Neher, L. J. Richter, D. M. DeLongchamp, F. Ortmann, K. Vandewal, E. Zhou and N. Banerji, Nat. Commun., 2020, 11, 833.
6. Z. Y. Zhang, L. Cao, X. Chen, D. Thompson, D. C. Qi and C. A. Nijhuis, J. Phys. Chem. C, 2021, 125, 18474–18482.
7. T. Wachter, A. Troster, S. Hock, A. Terfort and M. Zharnikov, J. Phys. Chem. C, 2018, 122, 4105–4115.
8. F. E. Oropeza, M. Barawi, E. Alfonso-Gonzalez, V. A. D. O’Shea, J. F. Trigo, C. Guillen, F. Saiz and I. J. Villar-Garcia, J. Mater. Chem. C, 2021, 9, 11859–11872.
9. P. Gehring, J. M. Thijssen and H. S. J. van der Zant, Nat. Rev. Phys., 2019, 1, 381–396.
10. H. N. Si, S. C. Zhang, S. F. Ma, Z. H. Xiong, A. Kausar, Q. L. Liao, Z. Zhang, A. Sattar, Z. Kang and Y. Zhang, Adv. Energy Mater., 2020, 10, 1903922.
11. A. Vilan, D. Aswal and D. Cahen, Chem. Rev., 2017, 117, 4248–4286.
12. X. P. Chen, H. T. Hu, J. Trasobares and C. A. Nijhuis, ACS Appl. Mater. Interfaces, 2019, 11, 21018–21029.
13. F. C. Simeone, H. J. Yoon, M. M. Thuo, J. R. Barber, B. Smith and G. M. Whitesides, J. Am. Chem. Soc., 2013, 135, 18131–18144.
14. P. Rothemund, C. M. Bowers, Z. G. Suo and G. M. Whitesides, Chem. Mater., 2018, 30, 129–137.
15. E. A. Weiss, R. C. Chiechi, G. K. Kaufman, J. K. Kriebel, Z. F. Li, M. Duati, M. A. Rampi and G. M. Whitesides, J. Am. Chem. Soc., 2007, 129, 4336–4349.
16. L. Jiang, C. S. S. Sangeeth, A. Wan, A. Vilan and C. A. Nijhuis, J. Phys. Chem. C, 2015, 119, 960–969.
17. C. S. S. Sangeeth, L. Jiang and C. A. Nijhuis, RSC Adv., 2018, 8, 19939–19949.
18. G. D. Kong, J. Jin, M. Thuo, H. Song, J. F. Joung, S. Park and H. J. Yoon, J. Am. Chem. Soc., 2018, 140, 12303–12307.
19. L. J. O'Driscoll, X. T. Wang, M. Jay, A. S. Batsanov, H. Sadeghi, C. J. Lambert, B. J. Robinson and M. R. Bryce, Angew. Chem., Int. Ed., 2020, 59, 882–889.
20. M. Carlotti, M. Degen, Y. X. Zhang and R. C. Chiechi, J. Phys. Chem. C, 2016, 120, 20437–20445.
21. H. B. Akkerman and B. de Boer, J. Phys.: Condens. Matter, 2008, 20, 013001.
22. P. Kao, S. Neppl, P. Feulner, D. L. Allara and M. Zharnikov, J. Phys. Chem. C, 2010, 114, 13766–13773.
23. M. Zharnikov, J. Electron Spectrosc. Relat. Phenom., 2015, 200, 160–173.
24. S. Karthauser, J. Phys.: Condens. Matter, 2011, 23, 013001.
25. B. Kim, S. H. Choi, X. Y. Zhu and C. D. Frisbie, J. Am. Chem. Soc., 2011, 133, 19864–19877.
26. H. Hamoudi, S. Neppl, P. Kao, B. Schupbach, P. Feulner, A. Terfort, D. Allara and M. Zharnikov, Phys. Rev. Lett., 2011, 107, 027801.
27. C. A. Nijhuis, Z. Zhang, F. Adoah, C. Nickle, S. K. Karuppannan, L. Wang, L. Jiang, A. Tadich, B. Cowie, T. Salim, D.-C. Qi, D. Thompson and E. D. Barco, Adv. Electron. Mater., 2023, 9, 2200637.
28. L. Cao, M. Yang, L. Yuan, N. Nerngchamnong, Y. P. Feng, A. T. S. Wee, D. C. Qi and C. A. Nijhuis, J. Phys.: Condens. Matter, 2016, 28, 094006.
29. D. Thompson and C. A. Nijhuis, Acc. Chem. Res., 2016, 49, 2061–2069.
30. R. C. Chiechi, E. A. Weiss, M. D. Dickey and G. M. Whitesides, Angew. Chem., Int. Ed., 2008, 47, 142–144.
31. Y. M. Han, C. Nickle, Z. Y. Zhang, H. Astier, T. J. Duffin, D. C. Qi, Z. Wang, E. del Barco, D. Thompson and C. A. Nijhuis, Nat. Mater., 2020, 19, 843–848.
32. Y. W. Yang and L. J. Fan, Langmuir, 2002, 18, 1157–1164.
33. J. A. Rodriguez, J. Dvorak, T. Jirsak, G. Liu, J. Hrbek, Y. Aray and C. González, J. Am. Chem. Soc., 2003, 125, 276–285.
34. F. P. Cometto, V. A. Macagno, P. Paredes-Olivera, E. M. Patrito, H. Ascolani and G. Zampieri, J. Phys. Chem. C, 2010, 114, 10183–10194.
35. A. Asyuda, S. Das and M. Zharnikov, J. Phys. Chem. C, 2021, 125, 21754–21763.
36. L. Jiang, L. Yuan, L. Cao and C. A. Nijhuis, J. Am. Chem. Soc., 2014, 136, 1982–1991.
37. L. Jiang, C. S. S. Sangeeth, L. Yuan, D. Thompson and C. A. Nijhuis, Nano Lett., 2015, 15, 6643–6649.
38. L. J. Wang, L. Yuan, L. Jiang, X. J. Yu, L. Cao and C. A. Nijhuis, J. Phys. Chem. C, 2019, 123, 19759–19767.
39. K. Senthil Kumar, L. Jiang and C. A. Nijhuis, RSC Adv., 2017, 7, 14544–14551.
40. M. G. Helander, M. T. Greiner, Z. B. Wang and Z. H. Lu, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 81, 153308.
41. N. Koch, G. Heimel, J. S. Wu, E. Zojer, R. L. Johnson, J. L. Bredas, K. Mullen and J. P. Rabe, Chem. Phys. Lett., 2005, 413, 390–395.
42. L. Cao, L. Yuan, M. Yang, N. Nerngchamnong, D. Thompson, X. Yu, D.-C. Qi and C. A. Nijhuis, Nanoscale Adv., 2019, 1, 1991–2002.
43. J. Kikuma and B. P. Tonner, J. Electron Spectrosc. Relat. Phenom., 1996, 82, 41–52.
44. G. Panaccione, G. Cautero, M. Cautero, A. Fondacaro, M. Grioni, P. Lacovig, G. Monaco, F. Offi, G. Paolicelli, M. Sacchi, N. Stojic, G. Stefani, R. Tommasini and P. Torelli, J. Phys.: Condens. Matter, 2005, 17, 2671–2679.
45. P. E. Laibinis, C. D. Bain and G. M. Whitesides, J. Chem. Phys., 1991, 95, 7017–7021.
46. C. S. Fadley and D. A. Shirley, J. Res. Nat. Bur. Stand. A Phys. Chem., 1970, 74A, 543–558.
47. C. Van Dyck, V. Geskin and J. Cornil, Adv. Funct. Mater., 2014, 24, 6154–6165.
48. W. J. Hong, H. Li, S. X. Liu, Y. C. Fu, J. F. Li, V. Kaliginedi, S. Decurtins and T. Wandlowski, J. Am. Chem. Soc., 2012, 134, 19425–19431.
49. L. J. O'Driscoll and M. R. Bryce, Nanoscale, 2021, 13, 10668–10711.
50. C. Jia and X. Guo, Chem. Soc. Rev., 2013, 42, 5642–5660.
51. L. Yuan, D. Thompson, L. Cao, N. Nerngchangnong and C. A. Nijhuis, J. Phys. Chem. C, 2015, 119, 17910–17919.
52. C. E. Smith, Z. T. Xie, I. Baldea and C. D. Frisbie, Nanoscale, 2018, 10, 964–975.
53. Z. T. Xie, I. Baldea and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 3670–3681.
54. Z. T. Xie, I. Baldea and C. D. Frisbie, J. Am. Chem. Soc., 2019, 141, 18182–18192.
55. N. Cao, W. Bro-Jørgensen, X. Zheng and G. C. Solomon, J. Chem. Phys., 2023, 158, 124305.
56. J. Chen, S. Gathiaka, Z. Wang and M. Thuo, J. Phys. Chem. C, 2017, 121, 23931–23938.
57. Y. Zang, E. D. Fung, T. Fu, S. Ray, M. H. Garner, A. Borges, M. L. Steigerwald, S. Patil, G. Solomon and L. Venkataraman, Nano Lett., 2021, 21, 673–679.

---

Footnotes

† Electronic supplementary information (ESI) available: Fabrication of the metal surfaces and formation of SAMs, photoemission spectroscopy, all details regarding DFT calculation, core-hole clock analysis, and Junction fabrication and statistics. See DOI: https://doi.org/10.1039/d3tc04184k

‡ These authors contributed equally.

---