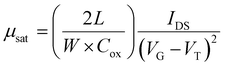Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
The Hansen solubility approach towards green solvent processing: n-channel organic field-effect transistors under ambient conditions†
Ibrahim
Deneme
,
Tevhide Ayça
Yıldız
,
Nilgun
Kayaci
and
Hakan
Usta
 *
*
Department of Nanotechnology Engineering, Abdullah Gül University, 38080 Kayseri, Turkey. E-mail: hakan.usta@agu.edu.tr
First published on 22nd February 2024
Abstract
The adoption of green solvents is of utmost importance for the solution-based fabrication of semiconductor thin films and for the commercialization of (opto)electronic devices, especially in response to evolving regulatory mandates for handling organic materials. Despite the increasing interest in this area, the scarcity of green solvent-processed n-channel OFETs, especially functioning under ambient conditions, highlights the need for further research. In this study, we demonstrated the Hansen solubility approach to study the solubility behavior of an ambient-stable n-type semiconductor, 2,2′-(2,8-bis(3-dodecylthiophen-2-yl)indeno[1,2-b]fluorene-6,12-diylidene)dimalononitrile (β,β′-C12-TIFDMT), and to analyze potential green solvents for thin-film processing. The Hansen solubility parameters were determined to be δD = 20.8 MPa1/2, δP = 5.8 MPa1/2, and δH = 5.5 MPa1/2 with a radius (R0) of 8.3 MPa1/2. A green solvent screening analysis based on the minimal distance constraint and quantitative sustainability score identified ethoxybenzene, anisole, 2-methylanisole, and 2-methyltetrahydrofuran as suitable green solvents (Ra′s = 5.17–7.93 MPa1/2 < R0). A strong thermodynamic correlation was identified between the solubility and the semiconductor–solvent distance in the 3D Hansen solubility space, in which the maximum solubility limit could be estimated with the enthalpy of fusion (ΔHfus) and melting temperature (Tmp) of the semiconductor. To the best of our knowledge, this relationship between the maximum solubility limit and thermal properties has been established for the first time for organic semiconductors. Bottom-gate/top-contact OFETs fabricated by spin-coating the semiconductor green solutions exhibited μes reaching ∼0.2 cm2 V−1 s−1 (Ion/Ioff ∼106–107 and Von ∼0–5 V) under ambient conditions. This device performance, to our knowledge, is the highest reported for an ambient-stable green solvent-processed n-channel OFET. Our HSP-based rational approach and unique findings presented in this study can shed critical light on how green solvents can be efficiently incorporated in solution processing in organic (opto)electronics, and whether ambient-stable n-type semiconductors can continue to play an important role in green OFETs.
Introduction
Electron-deficient π-conjugated small molecules represent a captivating class of organic materials that have shown tremendous potential as semiconductors in n-channel organic field-effect transistors (OFETs), as well as electron transport layers in a wide range of optoelectronic devices, including photovoltaics and light-emitting diodes/transistors.1–4 Although a π-system functionalized with an electron-withdrawing group (e.g., fluoro, imide, carbonyl, cyano, and dicyanovinylene) becomes technically π-electron-deficient,5–7 the famous examples with high electron mobilities include naphthalene diimide,8–10 perylene diimide,11,12 quinoidal,13–15 and indenofluorene16,17 π-architectures. Small molecules offer a remarkable fine-tuning ability over frontier orbital energetics, optical transitions, physicochemical properties, and solubilities compared to polymers and macromolecules.18–20 Furthermore, conventional synthesis and purification processes for small molecules enable the reproducible achievement of high purity levels with monodispersity and minimal batch-to-batch variations.21–23 Over the past three decades, n-type semiconducting molecules have played an essential role in advancing the functions and performances of organic (opto)electronic devices, which has enabled a plethora of structural, physicochemical, mechanical, and optoelectronic properties that are mostly unattainable with conventional elemental or compound semiconductors.5,24–26 Among these properties, solubility in organic solvents stands out as a unique tunable feature of molecular semiconductors that holds significant potential for large-scale roll-to-roll manufacturing.25,27,28 Molecular semiconductors generally exhibit greater solubility in organic solvents compared to polymers, primarily due to the increased entropy of the mixing effect as dictated by statistical thermodynamics.29,30 Despite these advantages, incorporating solubility into n-type semiconducting π-architectures, particularly in conjunction with ambient processing and ambient characterization of their corresponding semiconducting thin films, continues to present challenges from both molecular design and semiconductor device standpoints.12,31,32 As a result, only a limited number of π-structures exhibiting these properties have been reported to date in OFETs.8,9,14,15,33Solution-processable and ambient stable n-type semiconducting molecules have been mostly studied by processing their solutions in environmentally dangerous and toxic halogenated/aromatic hydrocarbon solvents such as chloroform, dichloromethane, chlorobenzene, and toluene.5,8 These solvents not only pose significant risks to human health and diverse ecosystems but are also predominantly derived from fossil fuels, making them non-sustainable in nature.29,34,35 In recent years, the utilization of green solvents in the solution processing of molecular semiconductors has emerged as a crucial research direction for advancing the future development of organic optoelectronics, yet with very limited examples for n-channel OFETs (Table S1, ESI†).29,34,36,37 In one of these studies, Ho et al.35 demonstrated green solvent-processed OFETs (μe = 0.07–0.13 cm2 V−1 s−1 measured under vacuum) by shearing the solutions of n-type molecules N,N′-dioctyl-3,4,9,10-perylenedicarboximide and N,N′-bis(n-alkyl)-(1,7 and 1,6)-dicyanoperylene-3,4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 9,10-bis(dicarboximide) (PTCDI-C8 and PDIF-CN2, respectively, in Table S1, ESI†) in anisole and Purasolv EHL (2-ethylhexyl ester of natural L-lactic acid). In another study, Harris et al.38 reported the synthesis of a bay-functionalized PDI-based molecular semiconductor (X1 in Table S1, ESI†), which exhibited μes of ∼5 × 10−5 cm2 V−1 s−1 (measured under vacuum) in their green solvent (alcohol/amine binary mixture) processed thin films in n-channel OFETs. In a very recent study by Corzo et al.,39 an electron-deficient molecule (O-IDTBR in Table S1, ESI†), which is typically used as an acceptor in bulk-heterojunction solar cells, was processed from a terpene biosolvent into an n-type semiconducting film in bottom-contact/top-gate OFETs (μe ∼0.37–0.91 cm2 V−1 s−1 as measured under vacuum). Alternatively, the utilization of green solvents as non-solvent additives to modify the morphology and crystallinity of the semiconductor has also been demonstrated, rather than relying solely on the dissolving capabilities of pure green solvents.40,41 In another recent study by Wang et al.,42 a versatile high-resolution patterning strategy was developed for the fabrication of ultraflexible transistor circuitry, which demonstrated a semiconducting channel (μe ∼0.1 cm2 V−1 s−1) based on the n-semiconducting polymer, N2200, processed from an environmentally benign solvent, THF, under ambient conditions. In a recent study by Lee et al.,43 binary semiconductor solution systems were prepared by introducing 2-methyltetrahydrofuran (2-MeTHF) into the chloroform solution of an n-type polymer (P(NDI2OD-T2) in Table S1, ESI†), and diethyl succinate into the chlorobenzene solution of an n-type small molecule (TU-3 in Table S1, ESI†). This approach led to n-channel OFETs with μes ranging from 0.13 to 0.33 cm2 V−1 s−1, as measured under vacuum conditions.
9,10-bis(dicarboximide) (PTCDI-C8 and PDIF-CN2, respectively, in Table S1, ESI†) in anisole and Purasolv EHL (2-ethylhexyl ester of natural L-lactic acid). In another study, Harris et al.38 reported the synthesis of a bay-functionalized PDI-based molecular semiconductor (X1 in Table S1, ESI†), which exhibited μes of ∼5 × 10−5 cm2 V−1 s−1 (measured under vacuum) in their green solvent (alcohol/amine binary mixture) processed thin films in n-channel OFETs. In a very recent study by Corzo et al.,39 an electron-deficient molecule (O-IDTBR in Table S1, ESI†), which is typically used as an acceptor in bulk-heterojunction solar cells, was processed from a terpene biosolvent into an n-type semiconducting film in bottom-contact/top-gate OFETs (μe ∼0.37–0.91 cm2 V−1 s−1 as measured under vacuum). Alternatively, the utilization of green solvents as non-solvent additives to modify the morphology and crystallinity of the semiconductor has also been demonstrated, rather than relying solely on the dissolving capabilities of pure green solvents.40,41 In another recent study by Wang et al.,42 a versatile high-resolution patterning strategy was developed for the fabrication of ultraflexible transistor circuitry, which demonstrated a semiconducting channel (μe ∼0.1 cm2 V−1 s−1) based on the n-semiconducting polymer, N2200, processed from an environmentally benign solvent, THF, under ambient conditions. In a recent study by Lee et al.,43 binary semiconductor solution systems were prepared by introducing 2-methyltetrahydrofuran (2-MeTHF) into the chloroform solution of an n-type polymer (P(NDI2OD-T2) in Table S1, ESI†), and diethyl succinate into the chlorobenzene solution of an n-type small molecule (TU-3 in Table S1, ESI†). This approach led to n-channel OFETs with μes ranging from 0.13 to 0.33 cm2 V−1 s−1, as measured under vacuum conditions.
Despite the recent efforts, the obtainment of green solvent processed n-channel OFETs with favorable electron mobilities (μe > 0.1 cm2 V−1 s−1) and transistor characteristics (Ion/Ioff ≥ 105 and Von ∼0 V) measured under ambient conditions remains highly challenging, emphasizing the need for further studies. At this point, it is important to highlight that during solution processing, specific solute–solvent interactions, along with solvent properties such as evaporation rate, viscosity/surface wettability, and film-forming capacity, critically influence the molecular self-assembly process.2,8,45,46 Altering the solvent used for the semiconductor can result in notable changes in the microstructural and morphological characteristics of thin films, subsequently impacting the efficiency of electron transport. Hence, replacing toxic and non-sustainable solvents with environmentally friendly and sustainable alternatives is not a straightforward effort, and it requires a rational approach. Due to the intricate nature of solubility involving a wide range of interaction types, it is essential to conduct rational studies, rather than a trial-and-error approach, in order to determine which green solvents are compatible with a specific semiconductor. For this purpose, utilizing solubility parameters (δs) proves to be a practical approach. This concept was first introduced by Hildebrand and Scott in the 1950s,47,48 which is defined as the square root of the total cohesive energy density (δ = (Ecohesive/Vmolar)1/2), and was later extended by Hansen47,49 in 1967 to include three distinct interaction contributions of dispersive (δD), polar (δP), and hydrogen-bonding (δH) origins, which are defined as Hansen solubility parameters (HSPs). A fundamental understanding of this theory posits that the total cohesive energy of a molecule comprises three primary intermolecular forces: dispersion, polarity, and hydrogen bonding, and molecules can only dissolve each other if they possess similar specific interaction strengths. In a similar manner, this principle can be extended to organic semiconductors, with each semiconductor anticipated to show a specific δD, δP, and δH coordinate point in the 3D Hansen solubility space. Additionally, a solubility sphere, determined by an interaction radius (R0), can be defined based on the specific solubility criteria relevant to a given application.22,50,51
In this study, by employing a HSP analysis-aided rational solubility approach, we explore potential green solvents for the ambient-stable, high-performance n-type semiconducting molecule, β,β′-C12-TIFDMT (Fig. 1). This semiconductor, synthesized in-house at a half-gram scale, was chosen for this study due to its excellent n-channel behavior (μe ∼0.9 cm2 V−1 s−1, Ion/Ioff ∼107–108, and Von ∼0 V under ambient conditions) in bottom-gate/top-contact OFETs, when processed from chlorinated solvents.52 The solubility of the semiconductor across a set of 30 organic solvents with diverse chemical structures and HSPs were determined by UV-Vis absorption spectroscopy and gravimetric methods. The solubilities ranged from 7.3 g L−1 (8.3 × 10−3 M) to 0.03 g L−1 (3.0 × 10−5 M) and insolubility, and the HSPs were determined to be δD = 20.8 MPa1/2, δP = 5.8 MPa1/2, and δH = 5.5 MPa1/2 with a radius (R0) of 8.3 MPa1/2 based on the solubility sphere method using classic Hansen algorithm in HSPiP software.53 A green solvent screening analysis was then performed by using the minimal distance constraint (Ra < R0) and the solvent sustainability credits. Accordingly, ethoxybenzene (Ra = 5.19 MPa1/2), anisole (Ra = 6.32 MPa1/2), 2-methylanisole (Ra = 5.17 MPa1/2), and 2-methyltetrahydrofuran (Ra = 7.93 MPa1/2) were identified as suitable green solvents for solution processing, all of which yield sufficient solubilities (≥4 g L−1) for thin-film processing. In addition, a strong thermodynamic correlation was identified between the solubility and the semiconductor–solvent distance in the 3D Hansen solubility space, from which the maximum solubility limit could be estimated with the semiconductor's thermal properties of melting enthalpy (ΔHfusion) and temperature (Tm). Bottom-gate/top-contact OFETs were fabricated under ambient conditions by spin-coating the semiconductor green solutions onto p++-Si/SiO2/PS-brush (Mn = 5 kDa) substrates. Clear n-channel transistor behaviors were observed under ambient conditions with μes reaching ∼0.2 cm2 V−1 s−1, Ion/Ioff ∼106–107, and Von ∼0–5 V.
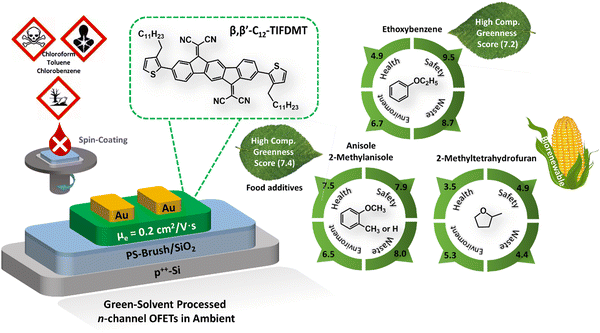 | ||
| Fig. 1 A bottom-gate/top-contact OFET device structure (p++-Si/SiO2/PS-brush/semiconductor/Au) was employed in this study to study green solvents, and the chemical structure of the ambient-stable n-type semiconductor, 2,2′-(2,8-bis(3-dodecylthiophen-2-yl)indeno[1,2-b]fluorene-6,12-diylidene)dimalononitrile (β,β′-C12-TIFDMT). The chemical structures of the green solvents, anisole, 2-methylanisole, ethoxybenzene, and 2-methyltetrahydrofuran, are shown with the corresponding GlaxoSmithKline (GSK)'s44 four category scores of health, safety, environment, and waste (disposal). Representative hazard pictograms based on the “globally harmonized system of classification and labelling of chemicals” (GHS) are also shown for some toxic and environmentally hazardous solvents (e.g., chloroform, toluene, and chlorobenzene). | ||
Experimental section
Materials and methods
All reagents and solvents were obtained from commercial vendors and used as received, unless otherwise noted. β,β′-C12-TIFDMT was synthesized in accordance with the synthesis and purification methods outlined in our previous report.52 Differential scanning calorimetry (DSC) was performed under nitrogen at a heating rate of 10 C min−1 on a Mettler Toledo DSC822e instrument. Indium and zinc standards (Mettler Toledo, Schwerzenbach, Switzerland) were used for calibration in DSC. UV-Vis absorption spectra were recorded on a Shimadzu UV-1800 UV-Vis spectrophotometer. Hansen solubility sphere, parameters, and fitting accuracy were determined by using the classic Hansen algorithm in the HSPiP Program (5thEdition Version 5.4.08) with a solubility limit of 2 g L−1.53 Solubility scores of “1” and “0” are assigned for good and bad solvents, respectively. The group contribution methodology was employed using neural network techniques in the HSPiP program.Solubility measurements
The semiconductor solubility in various solvents was measured by UV-Vis absorption spectroscopy. First, a linear calibration curve was generated at the semiconductor's absorption maximum (λmax = 338 nm) in chloroform by collecting the UV-Vis absorption spectra of standard solutions (4.55 × 10−7–4.55 × 10−5 M). Then, saturated semiconductor solutions were prepared by weighing a small amount (∼5.0 mg) of the organic semiconductor solid into a vial and adding 500 μL of a particular solvent via a micropipette. Next, the mixture was stirred/sonicated for 30 min at room temperature, filtered through a PTFE syringe filter (VWR, part of Avantor, 0.20 μm pore size), and diluted (200×) with chloroform in order to reach an optical absorption region in the range of the calibration curve. For each solvent, the absorbance at the absorption maximum was measured, and the corresponding solubility value was calculated by substituting this absorbance value into the calibration curve equation based on the Beer–Lambert law (A = ε·b·c). When the solubility exceeds 1.0 g L−1 in a particular solvent, an additional gravimetric method is also used for confirmation. In the gravimetric method, a small amount (∼5.0 mg) of the semiconductor solid was precisely weighed into a vial, and incremental volumes (in 50–100 μL portions) of a particular solvent were added via a micropipette. After each addition, the solution was stirred/sonicated for 10 min at room temperature. Solvent addition was continued until complete dissolution was visually observed. Once complete dissolution was confirmed, the semiconductor solution was filtered through a PTFE syringe filter (VWR, part of Avantor, 0.20 μm pore size) and then evaporated to dryness with a rotary evaporator. The gravimetric solubility was calculated based on the recovered semiconductor solid weight (mosc) and the total amount of solvent (Vsolvent) using the following equation: solubility = mosc/Vsolvent.OFET device fabrication and characterization
β,β′-C12-TIFDMT thin films (∼40–45 nm) were deposited onto the PS-brush-treated substrates, p++-Si/SiO2/PS-brush (Mn = 5 kDa), by spin-coating the corresponding semiconductor solutions in anisole, 2-methylanisole, ethoxybenzene, and 2-methyltetrahydrofuran (4.0 mg mL−1) at 1500, 1700, and 2000 rpm under ambient conditions. The thin films were thermally annealed at 170, 190 and 200 °C (for 30 min) in a vacuum oven. The bottom-gate/top-contact OFET devices were finished by thermal evaporation of Au source–drain electrodes (50 nm thick, growth rate of 0.2 Å s−1). Semiconducting channels with lengths (L) and widths (W) of 30/40/50/60/80 μm and 1000 μm, respectively, were obtained. The transistor characteristics were measured using a Keithley 2614B source-measure unit in an Everbeing BD-6 probe station under ambient conditions (without excluding natural or fluorescent lighting). Electron mobilities (μe), threshold voltages (VT), and Ion/Ioff ratios were calculated in the saturation regime by the following formula:where IDS is the source–drain current, L is the channel length, W is the channel width, Cox is the areal capacitance of the gate dielectric with the PS-brush interlayer per unit area (taken as 10.5 nF cm−2),54VG is the gate voltage, and VT is the threshold voltage. The reported values are the averages of at least ten different devices. The surface morphologies and microstructures of the semiconductor thin films were investigated by atomic force microscopy on a NanoSurf FlexAFM C3000 instrument and grazing incidence X-ray diffraction (GIXRD) on a Malvern Panalytical Empyrean diffractometer.
Results and discussion
Study of solubility and determination of Hansen solubility parameters
The n-type semiconductor, β,β′-C12-TIFDMT, was synthesized in-house at a half-gram scale, following the synthesis and purification methods outlined in our previous report.52 In order to determine the semiconductor HSP sphere and the corresponding parameters, we employed a set of 30 organic solvents (Table 1) encompassing diverse structures, including aromatics, alcohols, polar aprotic solvents, non-polar solvents, chlorinated alkanes/aromatics, terpenes, and esters. These solvents exhibited a wide range of δD (14.5–20.0), δP (0–18.0), and δH (0–26.0) values in the Hansen space to improve the fitting of the semiconductor solubility sphere. The maximum solubility of these solvents was measured by using UV-Vis absorption spectroscopy. The initial step involved generating a linear calibration curve at maximum molecular absorption (Fig. S1, ESI†). A molar absorptivity value (ε) of 5.85 × 104 M−1 cm−1 was obtained by fitting the calibration curve (Fig. 2(a)) using the Beer–Lambert law. The saturated semiconductor solutions were prepared in 30 different solvents and were diluted with chloroform in order to reach an optical absorption region in the range of the calibration curve shown in Fig. 2(a). Here, it is important to note that the diluted semiconductor solutions showed the same spectra in the 325–450 nm region as the original spectrum recorded in pure chloroform (Fig. 2(b)). This is a result of the presence of a residual test solvent in the diluted solutions (0.5% (v/v)), which highlights the method's ability to give accurate maximum absorbance values. For each solvent, absorbance at λmax = 338 nm was measured and translated into the corresponding solubility value by using a calibration curve equation. On the other hand, for the solvents with a solubility ≥ 1.0 g L−1, an additional gravimetric method was also employed for confirmation, which yielded solubility results within ∼3–4% of the spectroscopic method.| Solvent | Hansen parameters (MPa1/2) | Solubility (g L−1) | Molarity (×10−3 M) | Interaction distance (Ra) (MPa1/2) | Solubility score | ||
|---|---|---|---|---|---|---|---|
| δ D | δ P | δ H | |||||
| Aromatics | |||||||
| Benzene | 18.4 | 0 | 2.0 | 2.01 | 2.29 | 8.3 | 1 |
| Toluene | 18.0 | 1.4 | 2.0 | 6.70 | 7.60 | 7.9 | 1 |
| o-Xylene | 17.8 | 1.0 | 3.1 | 5.02 | 5.71 | 8.0 | 1 |
| Alcohols | |||||||
| 1-Butanol | 16.0 | 5.7 | 15.8 | 0.10 | 0.11 | 14.1 | 0 |
| tert-Butanol | 15.2 | 5.1 | 14.7 | 0.03 | 0.03 | 14.5 | 0 |
| Ethanol | 15.8 | 8.8 | 19.4 | Insoluble | — | — | 0 |
| Ethylene glycol | 17.0 | 11.0 | 26.0 | Insoluble | — | — | 0 |
| Methanol | 14.7 | 12.3 | 22.3 | 0.03 | 0.03 | 21.8 | 0 |
| 2-Propanol | 15.8 | 6.1 | 16.4 | Insoluble | — | — | 0 |
| Polar aprotic | |||||||
| Acetone | 15.5 | 10.4 | 7.0 | 0.05 | 0.06 | 11.7 | 0 |
| Acetonitrile | 15.3 | 18.0 | 6.1 | Insoluble | — | — | 0 |
| Cyclopentanone | 17.9 | 11.9 | 5.2 | 0.79 | 0.90 | 8.4 | 0 |
| Diethyl ether | 14.5 | 2.9 | 4.6 | 0.04 | 0.05 | 13.0 | 0 |
| Dimethyl sulfoxide | 18.4 | 16.4 | 10.2 | Insoluble | — | — | 0 |
| N,N-Dimethylformamide | 17.4 | 13.7 | 11.3 | 0.13 | 0.15 | 11.9 | 0 |
| 1,4-Dioxane | 17.5 | 1.8 | 9 | 1.11 | 1.26 | 8.5 | 0 |
| Ethylene carbonate | 18.0 | 21.7 | 5.1 | Insoluble | — | — | 0 |
| Methyl iso-butyl ketone | 15.3 | 6.1 | 4.1 | 0.14 | 0.16 | 11.1 | 0 |
| N-Methyl-2-pyrrolidone | 18.0 | 12.3 | 7.2 | 0.50 | 0.57 | 8.7 | 0 |
| Propylene carbonate | 20.0 | 18.0 | 4.1 | 0.05 | 0.06 | 12.4 | 0 |
| Tetrahydrofuran | 16.8 | 5.7 | 8.0 | 5.30 | 6.00 | 8.4 | 1 |
| Chlorinated alkanes/aromatics | |||||||
| Chloroform | 17.8 | 3.1 | 5.7 | 6.92 | 7.81 | 6.6 | 1 |
| Methylene dichloride | 17.0 | 7.3 | 7.1 | 4.93 | 5.62 | 7.9 | 1 |
| Chlorobenzene | 19.0 | 4.3 | 2.0 | 7.30 | 8.30 | 5.2 | 1 |
| Esters | |||||||
| n-Amyl acetate | 15.8 | 3.3 | 6.1 | 0.16 | 0.18 | 10.3 | 0 |
| Ethyl acetate | 15.8 | 5.3 | 7.2 | 0.13 | 0.15 | 10.2 | 0 |
| Propylene glycol monoethyl ether acetate | 15.6 | 6.3 | 7.7 | 0.08 | 0.09 | 10.6 | 0 |
| Terpenes | |||||||
| d-Limonene | 17.2 | 1.8 | 4.3 | 0.30 | 0.34 | 8.3 | 0 |
| Non-polar | |||||||
| Cyclohexane | 16.8 | 0 | 0.2 | 0.08 | 0.09 | 11.2 | 0 |
| Hexane | 14.9 | 0 | 0 | 0.05 | 0.06 | 14.3 | 0 |
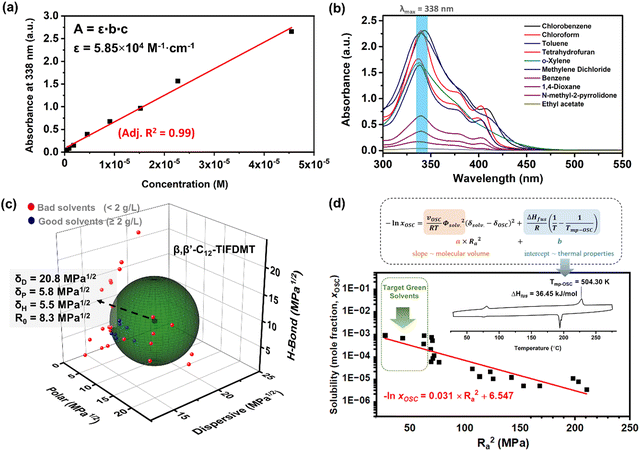 | ||
| Fig. 2 (a) The calibration curve based on the absorbance of β,β′-C12-TIFDMT in chloroform at varied standard solution concentrations (4.55 × 10−7 M–4.55 × 10−5 M) recorded at absorption maximum (λmax = 338 nm); the linear fitting was performed according to Beer–Lambert law (adjusted R2 is 0.99). (b) Optical absorption spectra of β,β′-C12-TIFDMT in saturated solutions in selected organic solvents after 200× dilution with chloroform. (c) Hansen solubility sphere and parameters of β,β′-C12-TIFDMT were determined by using the classic Hansen algorithm (HSPiP Program) with a solubility limit of 2 g L−1. The Hansen solubility parameters (δD, δP, δH, and R0) are in MPa1/2, and the bad (23) and the good (7) solvents are shown in the 3D Hansen solubility space with red and blue spheres, respectively. (d) The linear correlation between the semiconductor solubility in the mole fraction unit (xOSC) and the squared solute−solvent distance (Ra2) in the HSP space (correlation coefficient ∼ −0.9), and the logarithmic equation derived based on the Scatchard−Hildebrand regular solution theory.50 Inset shows the differential scanning calorimetry (10 °C min−1 heating ramp under N2) scan of β,β′-C12-TIFDMT with the corresponding enthalpy of fusion (ΔHfus) and the melting temperature (Tmp-OSC) values. | ||
As shown in Table 1, β,β′-C12-TIFDMT exhibited a broad spectrum of solubilities in 30 different organic solvents, ranging from complete insolubility to as high as 7.3 g L−1 (8.3 × 10−3 M), with variation dependent on the specific solute–solvent interactions. In particular, chlorinated alkanes/aromatics (4.9–7.3 g L−1 (5.6–8.3 × 10−3 M): chloroform, methylene dichloride, and chlorobenzene) and aromatics (2.0–6.7 g L−1 (2.3–7.6 × 10−3 M): benzene, toluene, o-xylene) were found to be the best solvents for β,β′-C12-TIFDMT. Also, a good solubility value of 5.3 g L−1 (6.0 × 10−3 M) was recorded in tetrahydrofuran. 1-Butanol, cyclopentanone, 1,4-dioxane, methyl iso-butyl ketone, N-methyl-2-pyrrolidone, N,N-dimethylformamide n-amyl acetate, ethyl acetate, and d-limonene showed solubilities in the range of 0.13–1.11 g L−1 (0.15–1.26 × 10−3 M). Solubility in the remaining solvents was ≤0.10 g L−1. The solubility scores of “1” (indicating a good solvent) and “0” (indicating a non-solvent) were assigned based on a threshold concentration value of 2.0 g L−1 at room temperature. Under the assumption of a spherical solubility sphere, the best fitting accuracy (0.999) was attained using the classic Hansen algorithm in the HSPiP program (Fig. S2, ESI†).53 As shown in Fig. 2(c), the HSPs for β,β′-C12-TIFDMT were determined to be δD = 20.8 MPa1/2, δP = 5.8 MPa1/2, and δH = 5.5 MPa1/2 with an interaction radius (R0) of 8.3 MPa1/2. Given that δD ≫ δP and δH, the major source of cohesive energy in the solid state (Ecohesive) for β,β′-C12-TIFDMT arises from dispersion interactions, with polar and hydrogen-bonding contributions playing comparatively lesser roles. While Hansen's original solubility theory does not explicitly address π-interactions, the dispersion term (δD) obtained herein indeed comprises π-interactions (i.e., π⋯π, C–H⋯π, and N/S⋯π) between the relatively large, rod-shaped and polarizable TIFDMT donor–acceptor–donor π-backbones, as well as dispersion interactions between aliphatic dodecyl substituents.55,56 Note that while the strength of the latter interactions is important for thin-film crystallization and microstructure, the former interactions are essential in establishing an electronic structure for efficient charge transport.52,57 The major contribution of the dispersion interactions in the β,β′-C12-TIFDMT's HSP parameters was also evident with the group contribution methodology (Fig. S3, ESI†). This approach was employed in the HSPiP using neural network techniques,58,59 in which the β,β′-C12-TIFDMT molecular structure is divided into various aromatic-aliphatics-functional group components and the HSPs are estimated as the sum of the contributions from these components. On the basis of the solubility parameters, the best solvents, chlorobenzene (7.3 g L−1) and chloroform (6.9 g L−1), are calculated to give the closest interaction distances to β,β′-C12-TIFDMT (Ra = 5.2 MPa1/2 and 6.6 MPa1/2, respectively) compared to all other solvents. This serves as an additional validation of the precision and reliability of our HSP analysis for the present semiconductor. Given that the δD value of our semiconductor is 20.8 MPa1/2, solvents with greater solubilities generally have δD values exceeding ∼17–18 MPa1/2. This is primarily because the difference in the dispersion parameters (ΔδDs) has a fourfold effect on the Ra calculation, in contrast to the effects of polar (ΔδP) or hydrogen bonding (ΔδH) parameters.47,50 Conversely, when considering the moderate δP and δH values of β,β′-C12-TIFDMT (5.5–5.8 MPa1/2), solvents with extremely high or low δP and δH values (i.e., very polar and non-polar solvents) tend to result in very low solubility. These observations lay the groundwork for a fundamental understanding of the upcoming green solvent analysis.
Quantitative correlation of the semiconductor solubility and HSP parameters
A key advantage of HSP analysis is the ability to establish a quantitative thermodynamic correlation between solubility values and the interaction distances (Ras) in the 3D Hansen space for semiconductors. Surprisingly, this still largely remains unexplored in the field of (opto)electronics. Despite several studies exploring the HSPs of semiconductors,22,39,44 to the best of our knowledge, such a correlation has been examined in only a few previous reports, and a direct relationship with thermal characteristics has not been established.50,60,61 As the solubilities of our semiconductor ranged over almost three orders of magnitude among 24 solvents, and these solvents gave widely ranged semiconductor–solvent interaction distances (Ra) of 5.2–21.8 MPa1/2 (Table 1) in the 3D Hansen space, we were able to study such thermodynamic correlations for β,β′-C12-TIFDMT. Note that these six solvents are omitted from this analysis since the semiconductor is practically insoluble in these solvents. This correlation was based on a Hansen-adapted Scatchard–Hildebrand regular solution theory,50,62 in which the squared difference in the Hildebrand solubility parameters (δ1 − δ2)2 is replaced by the squared interaction distance (Ra2) in the HSP space. As shown in eqn (1),R is the gas constant and T is the solubility measurement temperature (absolute). A logarithmic relationship between the Ra2 value and the solubility mole fraction (xOSC) would be expected if the Hansen solubility parameters for the semiconductor were accurately determined.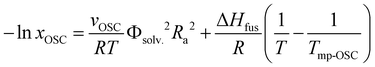 | (1) |
In this equation, the slope depends on the molar volume (vOSC) of the subcooled liquid of the pure semiconductor solid and the solvent volume fraction (Φsolv. ≈ 1 for dilute solutions), the intercept is a function of the thermal properties of the semiconductor solid, which are the semiconductor's enthalpy of fusion (ΔHfus) and the melting temperature (Tmp-OSC). The slope indicates the sensitivity of the semiconductor solubility to changes in the Ra value, while the intercept represents the maximum solubility limit of the semiconductor in an ideal solvent as Ra approaches 0. The second part of eqn (1) indeed shows the solubility equation described for ideal solutions.63 Additionally, it is important to note that in eqn (1), the Flory–Huggins correction term for the entropy of mixing is considered to be significantly smaller than the HSP term, and as a result, it is not included in the calculation.61 As shown in Fig. 2(d), when xOSC is plotted against Ra2 on a logarithmic scale (see Table S2 for data details, ESI†), a strong negative correlation (correlation coefficient ≈ −0.9) was calculated between these two parameters and the relationship can be regressed to the equation given in Fig. 2(d). Most importantly, the intercept is calculated to be 6.547, and it matches very well with the enthalpy of fusion (ΔHfus = 36.45 kJ mol−1) and the melting temperature (Tmp-OSC = 504.30 K) of the semiconductor solid obtained via differential scanning calorimetry (DSC) (Fig. S4, see the ESI† for details). This correspondence between the Scatchard–Hildebrand regular solution theory and DSC characteristics is highly promising and has the potential to pave the way for a new approach in semiconductors, enabling the prediction of their maximum solubility limits solely based on thermal characteristics.
Exploring suitable green solvents for semiconductor processing
In light of the recent regulatory demands concerning chemical substances, the adoption of green solvent processing is undeniably important for solution-based fabrication of organic (opto)electronic devices.39,44,64 The qualification of an organic liquid as a green solvent is a multifaceted concept that reflects diverse and sometimes controversial aspects of health, safety, environmental impact, and overall sustainability. More specifically, the solvents could be evaluated and classified into ten distinct subcategories: health hazard, exposure potential, flammability and explosion, reactivity and stability, air impact, aqueous impact, incineration, recycling, biotreatment, and volatile organic compounds, according to the regularly updated GlaxoSmithKline (GSK) solvent sustainability guide.65,66 As demonstrated by Larsen et al. in a quantitative methodology,44 these subcategories could be converted into four category scores and then combined to generate a composite score value (G). The G value ranges between 1 and 10, and a high score (>7) is desirable for a solvent suggesting a favorable greenness. On the other hand, the green solvent of choice should be able to dissolve the semiconductor at the required concentrations, which is at least 4.0 mg mL−1 at room temperature or moderately elevated temperatures (∼50–60 °C) in our case for spin-coating. According to the Hansen solubility approach,22,47,49 the selection of a green solvent to dissolve a semiconducting molecule strictly depends on the similarities between the dispersive, polar, and hydrogen-bonding interactions (i.e., δD, δP, and δH values, respectively) of the pure green solvent and the semiconductor structure. In other words, the similarities between these interactions lead to a reduction in the interaction distance (Ra), thereby increasing molecular solubility.On the basis of the HSPs determined for β,β′-C12-TIFDMT (δD = 20.8 MPa1/2, δP = 5.8 MPa1/2, and δH = 5.5 MPa1/2), a set of potential green solvents (21 green solvents shown in Table S3, ESI†) were screened by using the minimal distance constraint (Ra < R0 = 8.3 MPa1/2) in the 3D Hansen solubility space and sustainability credits. Consequently, we identified four solvents with reasonably small interaction distances: ethoxybenzene (Ra = 5.19 MPa1/2), anisole (Ra = 6.32 MPa1/2), 2-methylanisole (Ra = 5.17 MPa1/2), and 2-methyltetrahydrofuran (Ra = 7.93 MPa1/2). Here, it is noteworthy that these Ra values are expected to align with the high solubility region of the Scatchard–Hildebrand fitting curve in Fig. 2(d), aiming to achieve solubilities exceeding 10−3 M, which is sufficient for thin-film fabrication. These solvents exhibit relatively larger δD values (16.9–18.4 MPa1/2) compared to other environmentally friendly solvents, which, as previously mentioned, highlights the significant role of dispersion interactions in determining the overall solubility. Moreover, the boiling points of these solvents are in a reasonable temperature range (boiling points ≈ 78–170 °C), which is crucial for an effective spin-coating process to achieve favorable semiconducting morphologies and microstructures.29,67,68 With regard to the greenness of these solvents, anisole and 2-methylanisole are well-known food additives,29,37,69 while ethoxybenzene and anisole exhibit excellent sustainability with high G values of 7.2 and 7.4, respectively.44 In this context, it is worth highlighting that the GSK composite score for ethoxybenzene might potentially be even higher, as a relatively conservative health score (4.9) was assigned to ethoxybenzene due to limited information available in this particular category.44 In today's industry, although anisole production predominantly relies on petrochemicals, we note that it is also possible to obtain anisole from renewable sources such as lignin and guaiacol.70 On the other hand, despite its relatively lower greenness compared to our other three green solvents, 2-methyltetrahydrofuran is a biorenewable green solvent and it could be manufactured with a carbon footprint of ∼40× reduced CO2 emission as compared to conventional tetrahydrofuran.71
Thin-film microstructure/morphology and field-effect transistor characterization
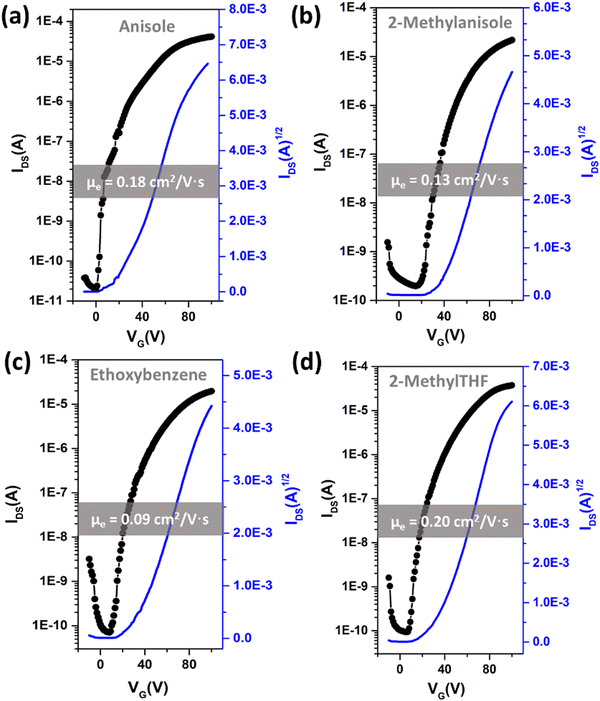
After determining four potential green solvents for our n-type semiconductor processing, bottom-gate/top-contact OFETs were fabricated by spin coating β,β′-C12-TIFDMT green solutions (4.0 g L−1) in anisole, 2-methylanisole, ethoxybenzene, and 2-methyltetrahydrofuran onto p++-Si/SiO2/PS-brush (Mn = 5 kDa) substrates. An ultrathin (∼3.6 nm) polystyrene brush (PS-brush) layer was employed since its densely packed (grafting density ≈ 0.45 chains nm−2) hydrophobic surface facilitates the formation of a proper microstructure for efficient electron transport.52,54 When selecting these green solvents, the similarity of the dispersive, polar, and hydrogen-bonding interactions between the semiconductor and the solvents serves not only to enhance molecular solubility but also to promote uninterrupted molecular arrangement during solution processing. This is because it reduces the likelihood of abrupt and drastic changes in the short-range intermolecular cohesive forces when transitioning from a solution state, where semiconducting molecules are surrounded by solvent molecules, to a thin-film state, where semiconducting molecules interact only with each other. This phenomenon has indeed been evident in the literature, where a majority of the high-performing semiconducting thin films were fabricated from solvents with favorable solubility parameters (e.g., chloroform, toluene, and chlorobenzene), despite the absence of Hansen solubility parameter (HSP) analyses in most of these studies.5,46,72In order to completely realize the potential of these green solvents to yield favorable microstructures with efficient electron transport, spin-coating rates of 1500, 1700, and 2000 rpm were used and the semiconductor thin films were thermally annealed at temperatures of 170 °C, 190 °C, and 200 °C. Typical transfer and output plots are shown in Fig. 4 and Fig. S5 (ESI†), and the transistor results for all these conditions are listed in Table S4 (ESI†). The OFETs from all four solvents exhibited clear n-channel characteristics under ambient conditions. In their best working conditions, the OFETs processed from anisole and 2-methyltetrahydrofuran gave μmax = 0.18–0.20 cm2 V−1 s−1 (μavg = 0.07–0.13 ± 0.04) with Ion/Ioff ratios of ∼106–107 and threshold voltages (VTs) of 2.1–9.4 V, while the OFETs from 2-methylanisole and ethoxybenzene yielded μmax = 0.09–0.13 cm2 V−1 s−1 (μavg = 0.05 ± 0.03) with Ion/Ioff ratios of ∼105–106 and slightly increased VTs of 18.4–27.1 V. In particular, in the transfer curve of the thin film fabricated from anisole (Fig. 4(a)), a clear near-zero turn-on voltage is evident. The hysteresis of the IDS–VG transfer characteristics was also analyzed for all the green solvents, and a lower back-sweep current hysteresis behavior was observed for all OFETs with ΔVG magnitudes (ΔVG = VGR – VGF at IDS of ∼10−7–10−8 A) of 8–19 V (Fig. S6, ESI†). A similar behavior with relatively larger hysteresis magnitudes was observed in recently reported green-solvent-processed OFETs.35 This could potentially be attributed to charge carrier trapping in deep states and electronic effects at the dielectric–semiconductor interface.73,74 As shown in Fig. 5, thin films processed from anisole, 2-methylanisole, and ethoxybenzene exhibited two-dimensional micron-sized (∼1–3 μm) grains that are grown in the substrate plane. However, their microstructures did not reveal a large crystallinity in the out-of-plane direction, showing weak (100) peaks in the low-angle region (2θ = 3.35–3.46°) and broad (010) peaks in the higher-angle (2θ = 21.20–21.40°) region. On the other hand, thin films processed from 2-methyltetrahydrofuran exhibit a different morphology with smaller grains (∼400–600 nm). In the 2-methyltetrahydrofuran-processed thin films, long-range ordering in the out-of-plane direction was evident with a strong (100) peak at 2θ = 3.43° along with the presence of (200) and (300) diffraction peaks. Based on the observed broad (010) peaks, we note that short-range π-interactions (∼4.1 Å) were present for all thin films. Among the four green solvents employed in thin-film fabrication, thin films processed from 2-methyltetrahydrofuran yields the highest crystallinity with a strong out-of-plane long-range ordering. Considering that the solution concentration and the dielectric surface are the same for all four green solvents, the observed greater crystallization performance of β,β′-C12-TIFDMT from 2-methyltetrahydrofuran suggests a different solvent–solute interaction behavior in 2-methyltetrahydrofuran, compared with the other green solvents. We analyzed the Ra2 values for all the green solvents (Ra1–4 in Fig. 3) in order to explore the solvent–semiconductor interaction differences. The larger the value of Ra2, the larger the differences in the cohesive energetics of the semiconductor and solvent, and the lower the semiconductor solubility in that particular solvent based on the Hansen-adapted Scatchard–Hildebrand regular solution theory, as discussed earlier. Amazingly, 2-methyltetrahydrofuran exhibits the largest Ra2 value (62.41) compared to those of the other green solvents (Ra2 = 27–39.69 for anisole, 2-methylanisole, and ethoxybenzene) (Fig. 3). Based on our HSP analysis, the large Ra2 value likely contributes to the strong molecular self-assembly behavior observed in 2-methyltetrahydrofuran during spin coating as the solvent evaporates, leading to thin-film crystallization.
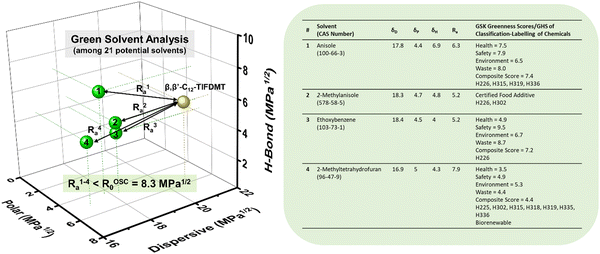 | ||
| Fig. 3 Hansen solubility parameters (δD, δP, δH in MPa1/2) of four potential green solvents, anisole (1), 2-methylanisole (2), ethoxybenzene (3), and 2-methyltetrahydrofuran (4), and their corresponding semiconductor–solvent interaction distances with respect to β,β′-C12-TIFDMT (Ra1–4 = (4ΔδD2 + ΔδP2 + ΔδH2)1/2 in MPa1/2, in which Δδ for a specific Hansen parameter is “δOSC − δsolvent”). The GlaxoSmithKline (GSK)'s four category scores of health, safety, environment, and waste (disposal) are shown in the table for the green solvents, along with the composite scores and the representative hazard statements based on the “globally harmonized system of classification and labelling of chemicals” (GHS),44 in which H225: highly flammable liquid and vapor, H226: flammable liquid and vapor, H302: harmful if swallowed, H315: causes skin irritation, H318: serious eye damage, H319: serious eye irritation, H335: may cause respiratory irritation, H336: may cause drowsiness or dizziness. | ||
Conclusions
In summary, the solubility behavior of an ambient-stable n-type semiconductor, 2,2′-(2,8-bis(3-dodecylthiophen-2-yl)indeno[1,2-b]fluorene-6,12-diylidene)dimalononitrile (β,β′-C12-TIFDMT), was studied using the solubility sphere method and classic Hansen algorithm. As the solubility in 30 different solvents ranged from 7.3 g L−1 (8.3 × 10−3 M) to 0.03 g L−1 (3.0 × 10−5 M) and insolubility, the HSPs were determined to be δD = 20.8 MPa1/2, δP = 5.8 MPa1/2, and δH = 5.5 MPa1/2 with an interaction radius (R0) of 8.3 MPa1/2. A strong thermodynamic correlation based on the Scatchard–Hildebrand regular solution theory was identified between the molecular solubility and the semiconductor–solvent interaction distance Ra. From the fitting curve, it is evident that the maximum solubility limit could be estimated from the semiconductor's thermal properties of the enthalpy of fusion (ΔHfus) and melting temperature (Tmp). To the best of our knowledge, this relationship has been established for the first time for organic semiconductors. Using the minimal distance constraint in the HSP space and quantitative sustainability score, four suitable green solvents (i.e., ethoxybenzene, anisole, 2-methylanisole, and 2-methyltetrahydrofuran) were identified for β,β′-C12-TIFDMT with Ras of 5.17–7.93 MPa1/2 (<R0). These solvents yielded sufficient solubility (≥ 4 g L−1) for thin-film processing. Bottom-gate/top-contact OFETs were fabricated by spin-coating the semiconductor green solutions, and the μe values reached ∼0.2 cm2 V−1 s−1 (Ion/Ioff ∼106–107 and Von ∼0–5 V) under ambient conditions. To our knowledge, this n-channel device performance is the highest reported for ambient-stable green solvent-processed OFET. Our HSP-based rational approach, an emerging yet underexplored methodology in the field, along with the unique findings presented herein, has the potential to significantly contribute to the integration of green solvents into the solution processing of n-channel semiconductors and to the broader development of charge-transport materials for green optoelectronics.Author contributions
H. U. conceived and designed the experiments. I. D. synthesized and purified the small molecular semiconductor. T. A. Y. and I. D. fabricated and characterized the organic field-effect transistors. N. K. performed the solubility measurements. H. U. wrote the paper. All authors discussed the results and commented on the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
H. U., I. D., T. A. Y., and N. K. acknowledge support from the Scientific and Technological Research Council of Turkey (TUBITAK) (grant no. 121C261). We thank Prof. Gokhan Demirel and Prof. Fahri Alkan for fruitful discussions.References
- C. Lee, S. Lee, G.-U. Kim, W. Lee and B. J. Kim, Chem. Rev., 2019, 119, 8028–8086 CrossRef CAS PubMed.
- O. Ostroverkhova, Chem. Rev., 2016, 116, 13279–13412 CrossRef CAS PubMed.
- X. Gao and Y. Hu, J. Mater. Chem. C, 2014, 2, 3099–3117 RSC.
- S. Moschetto, E. Benvenuti, H. Usta, R. Ozdemir, A. Facchetti, M. Muccini, M. Prosa and S. Toffanin, Adv. Mater. Interfaces, 2022, 9, 2101926 CrossRef CAS.
- H. Usta, A. Facchetti and T. J. Marks, Acc. Chem. Res., 2011, 44, 501–510 CrossRef CAS PubMed.
- A. Riaño, P. Mayorga Burrezo, M. J. Mancheño, A. Timalsina, J. Smith, A. Facchetti, T. J. Marks, J. T. López Navarrete, J. L. Segura, J. Casado and R. Ponce Ortiz, J. Mater. Chem. C, 2014, 2, 6376 RSC.
- Y. Wang, H. Guo, S. Ling, I. Arrechea-Marcos, Y. Wang, J. T. López Navarrete, R. P. Ortiz and X. Guo, Angew. Chem., Int. Ed., 2017, 56, 9924–9929 CrossRef CAS PubMed.
- F. Zhang, Y. Hu, T. Schuettfort, C. Di, X. Gao, C. R. McNeill, L. Thomsen, S. C. B. Mannsfeld, W. Yuan, H. Sirringhaus and D. Zhu, J. Am. Chem. Soc., 2013, 135, 2338–2349 CrossRef CAS PubMed.
- Y. Hu, Y. Qin, X. Gao, F. Zhang, C. A. Di, Z. Zhao, H. Li and D. Zhu, Org. Lett., 2012, 14, 292–295 CrossRef CAS PubMed.
- B. A. Jones, A. Facchetti, T. J. Marks and M. R. Wasielewski, Chem. Mater., 2007, 19, 2703–2705 CrossRef CAS.
- J. Zhang, L. Tan, W. Jiang, W. Hu and Z. Wang, J. Mater. Chem. C, 2013, 1, 3200–3206 RSC.
- B. A. Jones, M. J. Ahrens, M.-H. Yoon, A. Facchetti, T. J. Marks and M. R. Wasielewski, Angew. Chem., 2004, 116, 6523–6526 CrossRef.
- C. Zhang, Y. Zang, E. Gann, C. R. McNeill, X. Zhu, C. A. Di and D. Zhu, J. Am. Chem. Soc., 2014, 136, 16176–16184 CrossRef CAS PubMed.
- Q. Wu, R. Li, W. Hong, H. Li, X. Gao and D. Zhu, Chem. Mater., 2011, 23, 3138–3140 CrossRef CAS.
- A. Velusamy, C. Yu, S. N. Afraj, C. Lin, W. Lo, C. Yeh, Y. Wu, H. Hsieh, J. Chen, G. Lee, S. Tung, C. Liu, M. Chen and A. Facchetti, Adv. Sci., 2021, 8, 2002930 CrossRef CAS PubMed.
- H. Usta, C. Risko, Z. Wang, H. Huang, M. K. Deliomeroglu, A. Zhukhovitskiy, A. Facchetti and T. J. Marks, J. Am. Chem. Soc., 2009, 131, 5586–5608 CrossRef CAS PubMed.
- A. Can, A. Facchetti and H. Usta, J. Mater. Chem. C, 2022, 10, 8496–8535 RSC.
- K. Takimiya, S. Shinamura, I. Osaka and E. Miyazaki, Adv. Mater., 2011, 23, 4347–4370 CrossRef CAS PubMed.
- M. M. Torrent and C. Rovira, Chem. Soc. Rev., 2008, 37, 827–838 RSC.
- S. Ma, J. Wang, K. Feng, H. Zhang, Z. Wu, Y. Wang, B. Liu, Y. Li, M. An, R. Gonzalez-Nuñez, R. Ponce Ortiz, H. Y. Woo and X. Guo, ACS Appl. Mater. Interfaces, 2023, 15, 1639–1651 CrossRef CAS PubMed.
- H. Usta and A. Facchetti, Large Area and Flexible Electronics, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2015, pp. 1–100 Search PubMed.
- I. Burgués-Ceballos, F. Machui, J. Min, T. Ameri, M. M. Voigt, Y. N. Luponosov, S. A. Ponomarenko, P. D. Lacharmoise, M. Campoy-Quiles and C. J. Brabec, Adv. Funct. Mater., 2014, 24, 1449–1457 CrossRef.
- G.-S. Ryu, Z. Chen, H. Usta, Y.-Y. Noh and A. Facchetti, MRS Commun., 2016, 6, 47–60 CrossRef CAS.
- B. J. Jung, N. J. Tremblay, M.-L. Yeh and H. E. Katz, Chem. Mater., 2011, 23, 568–582 CrossRef CAS.
- S. E. Root, S. Savagatrup, A. D. Printz, D. Rodriquez and D. J. Lipomi, Chem. Rev., 2017, 117, 6467–6499 CrossRef CAS PubMed.
- M. N. Le, K. Baeg, K. Kim, S. Kang, B. D. Choi, C. Park, S. Jeon, S. Lee, J. Jo, S. Kim, J. Park, D. Ho, J. Hong, M. Kim, H. Kim, C. Kim, K. Kim, Y. Kim, S. K. Park and M. Kim, Adv. Funct. Mater., 2021, 31, 2103285 CrossRef CAS.
- T. Kim, J.-H. Kim, T. E. Kang, C. Lee, H. Kang, M. Shin, C. Wang, B. Ma, U. Jeong, T.-S. Kim and B. J. Kim, Nat. Commun., 2015, 6, 8547 CrossRef CAS PubMed.
- H. Zhu, E. Shin, A. Liu, D. Ji, Y. Xu and Y. Noh, Adv. Funct. Mater., 2020, 30, 1904588 CrossRef CAS.
- J. Lee, S. A. Park, S. U. Ryu, D. Chung, T. Park and S. Y. Son, J. Mater. Chem. A, 2020, 8, 21455–21473 RSC.
- J. Lee, C. Sun, B. S. Ma, H. J. Kim, C. Wang, J. M. Ryu, C. Lim, T. Kim, Y. Kim, S. Kwon and B. J. Kim, Adv. Energy Mater., 2021, 11, 2003367 CrossRef CAS.
- H. Usta, A. Facchetti and T. J. Marks, J. Am. Chem. Soc., 2008, 130, 8580–8581 CrossRef CAS PubMed.
- R. Ozdemir, D. Choi, M. Ozdemir, H. Kim, S. T. Kostakoğlu, M. Erkartal, H. Kim, C. Kim and H. Usta, ChemPhysChem, 2017, 18, 850–861 CrossRef CAS PubMed.
- L. Wang, J. S. Park, H. G. Lee, G.-U. Kim, D. Kim, C. Kim, S. Lee, F. S. Kim and B. J. Kim, ACS Appl. Mater. Interfaces, 2020, 12, 56240–56250 CrossRef CAS PubMed.
- F. Campana, C. Kim, A. Marrocchi and L. Vaccaro, J. Mater. Chem. C, 2020, 8, 15027–15047 RSC.
- D. Ho, J. Lee, S. Park, Y. Park, K. Cho, F. Campana, D. Lanari, A. Facchetti, S. Seo, C. Kim, A. Marrocchi and L. Vaccaro, J. Mater. Chem. C, 2020, 8, 5786–5794 RSC.
- T. L. Nguyen, C. Lee, H. Kim, Y. Kim, W. Lee, J. H. Oh, B. J. Kim and H. Y. Woo, Macromolecules, 2017, 50, 4415–4424 CrossRef CAS.
- S. Pang, Z. Chen, J. Li, Y. Chen, Z. Liu, H. Wu, C. Duan, F. Huang and Y. Cao, Mater. Horiz., 2023, 10, 473–482 RSC.
- D. H. Harris, S. Brixi, B. S. Gelfand, B. H. Lessard and G. C. Welch, J. Mater. Chem. C, 2020, 8, 9811–9815 RSC.
- D. Corzo, D. Rosas-Villalva, A. C, G. Tostado-Blázquez, E. B. Alexandre, L. H. Hernandez, J. Han, H. Xu, M. Babics, S. De Wolf and D. Baran, Nat. Energy, 2023, 8, 62–73 CrossRef.
- H. Opoku, B. Nketia-Yawson, E. S. Shin and Y.-Y. Noh, Org. Electron., 2017, 41, 198–204 CrossRef CAS.
- H. Opoku, B. Nketia-Yawson, E.-S. Shin and Y.-Y. Noh, J. Mater. Chem. C, 2018, 6, 661–667 RSC.
- B. Wang, W. Huang, S. Lee, L. Huang, Z. Wang, Y. Chen, Z. Chen, L.-W. Feng, G. Wang, T. Yokota, T. Someya, T. J. Marks and A. Facchetti, Nat. Commun., 2021, 12, 4937 CrossRef CAS PubMed.
- Y. Lee, D. Ho, F. Valentini, T. Earmme, A. Marrocchi, L. Vaccaro and C. Kim, J. Mater. Chem. C, 2021, 9, 16506–16515 RSC.
- C. Larsen, P. Lundberg, S. Tang, J. Ràfols-Ribé, A. Sandström, E. Mattias Lindh, J. Wang and L. Edman, Nat. Commun., 2021, 12, 4510 CrossRef CAS PubMed.
- J. Rivnay, S. C. B. Mannsfeld, C. E. Miller, A. Salleo and M. F. Toney, Chem. Rev., 2012, 112, 5488–5519 CrossRef CAS PubMed.
- C. Wang, H. Dong, W. Hu, Y. Liu and D. Zhu, Chem. Rev., 2012, 112, 2208–2267 CrossRef CAS PubMed.
- A. F. M. Barton, Chem. Rev., 1975, 75, 731–753 CrossRef CAS.
- J. H. Hildebrand, Chem. Rev., 1949, 44, 37–45 CrossRef CAS PubMed.
- C. M. Hansen, Hansen solubility parameters: A user's handbook, 2nd edn, 2007 Search PubMed.
- Y. Takebayashi, N. Morii, K. Sue, T. Furuya, S. Yoda, D. Ikemizu and H. Taka, Ind. Eng. Chem. Res., 2015, 54, 8801–8808 CrossRef CAS.
- F. Machui, S. Langner, X. Zhu, S. Abbott and C. J. Brabec, Sol. Energy Mater. Sol. Cells, 2012, 100, 138–146 CrossRef CAS.
- A. Can, I. Deneme, G. Demirel and H. Usta, ACS Appl. Mater. Interfaces, 2023, 15, 41666–41679 CrossRef CAS PubMed.
- S. Abbott and Y. Hiroshi, Hansen Solubility Parameters Pract. Version 5.4.08, Copyr. © 2008/23 Prof. Steven Abbott Dr Yamamoto Hiroshi (accessed August 2023) Search PubMed.
- S. H. Park, H. S. Lee, J.-D. Kim, D. W. Breiby, E. Kim, Y. D. Park, D. Y. Ryu, D. R. Lee and J. H. Cho, J. Mater. Chem., 2011, 21, 15580–15586 RSC.
- E. M. Pérez and N. Martín, Chem. Soc. Rev., 2015, 44, 6425–6433 RSC.
- J. P. Wagner and P. R. Schreiner, Angew. Chem., Int. Ed., 2015, 54, 12274–12296 CrossRef CAS PubMed.
- R. Ozdemir, S. Park, İ. Deneme, Y. Park, Y. Zorlu, H. A. Alidagi, K. Harmandar, C. Kim and H. Usta, Org. Chem. Front., 2018, 5, 2912–2924 RSC.
- A. Randová and L. Bartovská, Fluid Phase Equilib., 2016, 429, 166–176 CrossRef.
- E. Stefanis and C. Panayiotou, Int. J. Thermophys., 2008, 29, 568–585 CrossRef CAS.
- X.-Z. Shao, L.-S. Wang and M.-Y. Li, Ind. Eng. Chem. Res., 2012, 51, 5082–5089 CrossRef CAS.
- Y. Takebayashi, K. Sue, T. Furuya and S. Yoda, J. Chem. Eng. Data, 2018, 63, 3889–3901 CrossRef CAS.
- G. Scatchard, Chem. Rev., 1931, 8, 321–333 CrossRef CAS.
- P. W. Atkins and J. De Paula, Atkins’ Physical Chemistry, 8th edn, Oxford University Press, London, England, 2006 Search PubMed.
- F. P. Byrne, S. Jin, G. Paggiola, T. H. M. Petchey, J. H. Clark, T. J. Farmer, A. J. Hunt, C. Robert McElroy and J. Sherwood, Sustainable Chem. Processes, 2016, 4, 7 CrossRef.
- R. K. Henderson, C. Jiménez-González, D. J. C. Constable, S. R. Alston, G. G. A. Inglis, G. Fisher, J. Sherwood, S. P. Binks and A. D. Curzons, Green Chem., 2011, 13, 854 RSC.
- C. M. Alder, J. D. Hayler, R. K. Henderson, A. M. Redman, L. Shukla, L. E. Shuster and H. F. Sneddon, Green Chem., 2016, 18, 3879–3890 RSC.
- D. Chen, A. Nakahara, D. Wei, D. Nordlund and T. P. Russell, Nano Lett., 2011, 11, 561–567 CrossRef CAS PubMed.
- H. Lee, C. Park, D. H. Sin, J. H. Park and K. Cho, Adv. Mater., 2018, 30, 1–39 Search PubMed.
- J. Lee, M. Malekshahi Byranvand, G. Kang, S. Y. Son, S. Song, G.-W. Kim and T. Park, J. Am. Chem. Soc., 2017, 139, 12175–12181 CrossRef CAS PubMed.
- F. G. Delolo, E. N. dos Santos and E. V. Gusevskaya, Green Chem., 2019, 21, 1091–1098 RSC.
- C. S. Slater, M. J. Savelski, D. Hitchcock and E. J. Cavanagh, J. Environ. Sci. Health, Part A: Toxic/Hazard. Subst. Environ. Eng., 2016, 51, 487–494 CrossRef CAS PubMed.
- H. Dong, X. Fu, J. Liu, Z. Wang and W. Hu, Adv. Mater., 2013, 25, 6158–6183 CrossRef CAS PubMed.
- M.-H. Yoon, C. Kim, A. Facchetti and T. J. Marks, J. Am. Chem. Soc., 2006, 128, 12851–12869 CrossRef CAS PubMed.
- M. Egginger, S. Bauer, R. Schwödiauer, H. Neugebauer and N. S. Sariciftci, Monatsh. Chem., 2009, 140, 735–750 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4tc00324a |
| This journal is © The Royal Society of Chemistry 2024 |