Open Access Article
Open Access ArticleWhat can Blyholder teach us about PFAS degradation on metal surfaces?†
Glen R.
Jenness
 * and
Manoj K.
Shukla
*
* and
Manoj K.
Shukla
*
Environmental Laboratory, US Army Engineer Research and Development Center, 3909 Halls Ferry Road, Vicksburg, Mississippi 39180, USA. E-mail: Glen.R.Jenness@usace.army.mil; Manoj.K.Shukla@usace.army.mil
First published on 3rd January 2024
Abstract
Per- and poly-fluoroalkyl substances (PFAS) molecules have long been used in a variety of applications as they are chemically robust and resistant to chemical transformations. However, it has recently come to light that these compounds are toxic, and remediation efforts are required to remove them from our society. In a recent study (Jenness et al., Env. Sci. Proc. Impacts, 2022, 24, 2085) we explored the use of silylium-carborane for the degradation of perfluorobutanoic acid (PFBA) and three derivatives. In the course of our study, we found the degradation of the C–F bond was facilitated by a low-lying unoccupied anti-bonding orbital. Based on this finding, we propose the usage of metal catalysts for the degradation of the C–F bond as metals have been shown to take advantage of such low-lying anti-bonding orbitals. Utilizing density functional theory (DFT) calculations, we explored how the C–F bond in PFBA can be split by the entirety of the d-block metals. Deriving a series of linear scaling relationships, we demonstrate that metals conforming to the bcc point-group perform the best for this chemistry. In particular, iron (Fe) has a good balance of fluorine and PFBA binding and reaction energies and would be a worthy candidate for further studies.
Environmental significancePer- and polyfluoroalkyl substances (PFAS) are fluorochemicals that are extremely persistent and widely distributed, and capable of bioaccumulation. Found in a variety of locations these compounds cause a variety of health issues in humans and our feedstocks. PFAS feature a robust C–F bond that is extremely difficult to cleave; however, for the remediation of contaminated sites and the destruction of our existing stocks as a preventative measure it is necessary to develop methods to do preferentially cleave the C–F bond. In the current study, we have investigated the degradation of PFAS on a theoretical level using density functional theory. Examination of how a representative PFAS molecule interacts with 27 metal surfaces allows us to determine the electronic factors responsible for the degradation of PFAS molecules and assess how various metals perform for the destruction of these forever compounds. |
1 Introduction
In recent years per- and poly-fluoroalkyl substances (PFAS) have emerged as an environmental health threat.1–3 The United States Environmental Protection Agency (EPA) has recommended a life-time advisory level for several PFAS molecules, including perfluorooctanoic acid (PFOA) and perfluorooctanesulfonic acid (PFOS), with levels being 0.004 parts-per-trillion (ppt) and 0.02 ppt, respectively.1 These compounds feature numerous C–F bonds, which is one of the strongest single carbon bonds with a bond dissociation energy of ∼115–127 kcal mol−1.4–8 In comparison, the carbon–hydrogen bond is 90–105 kcal mol−1,5,7 the carbon–carbon bond is 85–104 kcal mol−1,5,9 and the carbon–oxygen bond is 80–110 kcal mol−1.5 As a consequence, care needs to be taken with degradation as it is easy to favor bonds other than the C–F bond. The moniker of “forever chemicals” for these fluorocarbons is well deserved.However it is not just their chemical robustness that makes them a public health threat; that is due to their ubiquitous nature as they are used at all levels of our society2,10–12 and are found in cosmetics, firefighting foam, protective coatings, and consumer packaging2,3,13,14 (for a comprehensive listing of PFAS uses in our society see the reviews by Glüge et al.2 and Panieri et al.3). PFAS molecules have been linked to low mammalian birth weights, compromised immune systems, and cancer.11,12,15 In addition to consumer products PFAS contamination can occur through soil and groundwater sources,10,16–24 which leads to accumulation in our local food chains,25–27 oceans,28 and prenatally in humans.29 These effects are compounded in areas rich in salt and organic matter as they lead to an increase in the environmental transport and retention.30,31
This has led to a large research effort in finding new chemistries and techniques for the chemical degradation of PFAS molecules. These studies have included conventional techniques such as using solvated electrons,6,32–36 electrochemical methods,37–40 photochemical reduction,41,42 thermal degradation,43 oxidation via activated persulfate,44,45 microbial degradation,46 chemically assisted degradations,47–51 microbial treatment,52,53 and low-temperature hydroxide-mediated decarboxylation and defluorination.54 More exotic methods such as plasma treatment55–57 and degradation through the application of soundwaves58 have also been used. However, care needs to be taken with chemical degradation techniques in the environment as they can result in a variety of chemical byproducts that are hazardous.59,60
In a recent study51 we investigated the usage of halogenated carborane anions ([HCB11H5Y6]−, Y = {F, Cl, Br, I}) interacting with silylium catalysts (Et3SiH/Et3Si+) for the chemical degradation of perfluorobutanoic acid (PFBA) and its reduced analogues through the use of density functional theory (DFT). We found that the silylium acts in tandem with its cationic counterpart to remove a –F from PFBA whilst a hydride is inserted from the other side of the carbocation in a concerted mechanism. Adding a carborane anion into the complex resulted in some of the barriers becoming nearly zero; however there was a slight decrease in the strength of the reaction energies. Examination of the electronic structure of the components of the catalytic system reveals that PFBA has an anti-bonding σ* orbital for its lowest unoccupied molecular orbital (LUMO), which becomes partially occupied as it interacts with the silylium. The addition of carborane results in a “charge lensing” type effect where-in the electrostatic repulsion between the donated electrons and the negative charge on the carborane results in this anti-bonding orbital having a higher occupation, which weakens the C–F bond further. Finally, we noted that changing the halogenation of the carborane can mediate this effect, with iodine having the strongest effect.
The notion of PFAS molecules having a low-lying anti-bonding orbital is not a new one, and has been mentioned in prior literature. For example, Hughes et al. mentions that the low-lying σ* anti-bonding orbital is an “Achilles' heel” for fluorocarbons.61 Additionally, in the review by Kuehnel et al. it is further noted that C–F bonds have a low-lying σ* anti-bonding orbital which can be exploited by activation of the C–F bond, leading to cross-linking reactions.62 Moreover, in a recent study by Michalczyk et al. they note that increased charge transfer to the C–F bond results in an elongation of the bond length, which in turns facilitates C–F cleavage.63
The nature of this anti-bonding LUMO for PFBA was rather intriguing to us, and naturally calls to mind the Blyholder back-bonding mechanism. In the first half of the 20th century, there were a set of experiments measuring the infrared (IR) C–O stretch frequency (νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O) of carbon monoxide (CO) adsorbed on various metal surfaces. It was observed that instead of the gas-phase value of ∼2100 cm−1, the νC
O) of carbon monoxide (CO) adsorbed on various metal surfaces. It was observed that instead of the gas-phase value of ∼2100 cm−1, the νC![[triple bond, length as m-dash]](https://www.rsc.org/images/entities/char_e002.gif) O would go as low as ∼1800 cm−1.64 Several hypothesis had been offered, including the possibility of CO binding to bridge sites instead of a more linear M–CO configuration. In 1964 it was Blyholder, with the use of a Hückel Hamiltonian, who presented the first molecular orbital description that qualitatively described these trends.65 CO features a set of lone-pair electrons on both ends of the molecule that are available to bind with the d-electrons of a metal surface; the most favorable bonding configuration features a σ-bond between the metal center and the carbon atom. Blyholder found that the formation of the σ-bond puts a large negative charge on the carbon atom, which migrates into the anti-bonding 2π* orbitals of the CO. This in turns destabilizes the CO triple bond, resulting in the observed experimental IR frequency shifts.64–70 This phenomena has been termed back-bonding and has been found to be a robust conceptual picture of CO bonding on metal surfaces from both a theoretical66,70–80 and experimental perspective.66,76,79,81–87 The back-bonding phenomena has been leveraged in the catalysis field for a variety of different molecules with low-lying σ* and π* anti-bonding orbitals,88–94 and has even been found to explain how micro-organisms utilize CO naturally.95
O would go as low as ∼1800 cm−1.64 Several hypothesis had been offered, including the possibility of CO binding to bridge sites instead of a more linear M–CO configuration. In 1964 it was Blyholder, with the use of a Hückel Hamiltonian, who presented the first molecular orbital description that qualitatively described these trends.65 CO features a set of lone-pair electrons on both ends of the molecule that are available to bind with the d-electrons of a metal surface; the most favorable bonding configuration features a σ-bond between the metal center and the carbon atom. Blyholder found that the formation of the σ-bond puts a large negative charge on the carbon atom, which migrates into the anti-bonding 2π* orbitals of the CO. This in turns destabilizes the CO triple bond, resulting in the observed experimental IR frequency shifts.64–70 This phenomena has been termed back-bonding and has been found to be a robust conceptual picture of CO bonding on metal surfaces from both a theoretical66,70–80 and experimental perspective.66,76,79,81–87 The back-bonding phenomena has been leveraged in the catalysis field for a variety of different molecules with low-lying σ* and π* anti-bonding orbitals,88–94 and has even been found to explain how micro-organisms utilize CO naturally.95
Our question is now can we leverage prior work on metal catalysts and our understanding of back-bonding to choose catalysts for PFAS degradation? While prior work has been done on the degradation of fluorocarbons using metals (both heterogeneous4,96–99 and homogeneous62,100–103), to the best of our knowledge a systematic study of transition metal catalysts for PFAS degradation has not been performed. Therefore, we hypothesize that metal surfaces are capable of cleaving C–F bonds in an energetically favorable fashion, and do so via a back-bonding type mechanism. To demonstrate our hypothesis, we utilized density functional theory to study the adsorption of a model PFAS molecule (perfluorobutanoic acid or PFBA) on 27 single crystal surfaces that span the entirety of the d-block (with the addition of lead). We find that PFAS molecules follow the same linear scaling relationship behavior that has been noted in AHx (where A = {N, C, O}) chemistry on these surfaces. Moreover, we also find that certain metals are capable of transforming the LUMO of PFAS into an orbital that has more of a singularly occupied molecular orbital (SOMO) nature. This indicates that metal catalysts can, in fact, not only degrade PFAS molecules but does so through a back-bonding mechanism.
2 Results and discussion
2.1 Electronic structure of PFAS
Recently, perfluoroctonoic acid (PFOA) had its lifetime exposure limits changed by several orders of magnitude as it has been determined to be more toxic than originally predicted.1 However the size of PFOA makes it impractical for atomistic surface simulations as grid-based periodic DFT codes scale as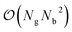 (where Ng is number of grid points and Nb is number of bands/orbitals).104,105 In our previous study51 we utilized perfluorobutanoic acid (PFBA) as our representative PFAS as its short chain allows for more rigorous computational methods to be used and as several studies have demonstrated that at least 4 carbons are required to reproduce one of the key structural properties of PFAS: the helicity;106–113 however since publishing that work one question we routinely receive is how well would our results transfer to longer chain PFAS molecules. Therefore in this section we examine several key electronic and molecular features of PFBA and compare them to PFOA and the simplest fluorinated carboxylic acid (fluoroformic acid or FFA). While FFA was chosen on pedagogical grounds, it should be noted that it has been detected and characterized in the gas-phase.114 These molecules are shown in Fig. 1. For purposes of this study, we focus on the Cα–F bond as it has been shown that –CβF2– and –CωF3 groups are harder to defluorinate.4,6
(where Ng is number of grid points and Nb is number of bands/orbitals).104,105 In our previous study51 we utilized perfluorobutanoic acid (PFBA) as our representative PFAS as its short chain allows for more rigorous computational methods to be used and as several studies have demonstrated that at least 4 carbons are required to reproduce one of the key structural properties of PFAS: the helicity;106–113 however since publishing that work one question we routinely receive is how well would our results transfer to longer chain PFAS molecules. Therefore in this section we examine several key electronic and molecular features of PFBA and compare them to PFOA and the simplest fluorinated carboxylic acid (fluoroformic acid or FFA). While FFA was chosen on pedagogical grounds, it should be noted that it has been detected and characterized in the gas-phase.114 These molecules are shown in Fig. 1. For purposes of this study, we focus on the Cα–F bond as it has been shown that –CβF2– and –CωF3 groups are harder to defluorinate.4,6
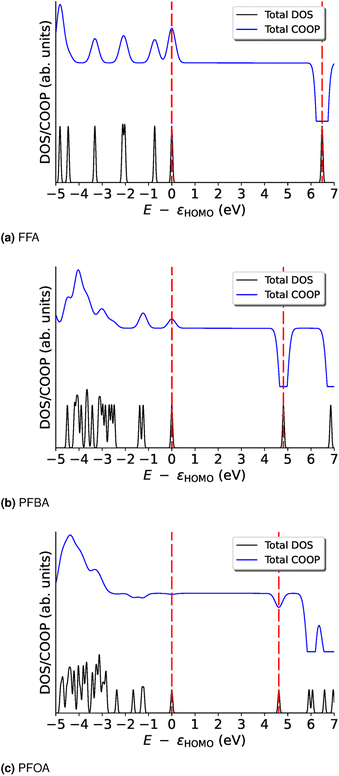 | ||
| Fig. 2 Total density of states (DOS) and crystal orbital overlap population (COOP) curves for (a) FFA, (b) PFBA, and (c) PFOA. The energies are shifted by εHOMO. Red dashed lines denote the location of the HOMO and LUMO energies. For the bond-specific COOP, see Fig. S1–S3.† | ||
In order to further probe these trends, we examine the COOP curves on a bond basis; these results are shown in Fig. S1–S3.† For FFA (Fig. S1†), we can see that the HOMO and LUMO carry the same overall trend for all the bonds, i.e., they are all either bonding (HOMO) or anti-bonding (LUMO). We will note that the majority of the bonding nature of the HOMO arises from the Cacid–OH and Cacid![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bonds. In Fig. S1,† we see that the majority of the bonding nature of the HOMO arises from the carbon backbone as the bonding peak from the –C
O bonds. In Fig. S1,† we see that the majority of the bonding nature of the HOMO arises from the carbon backbone as the bonding peak from the –C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O moiety is nearly canceled by the anti-bonding nature of the –OH and –C–O bonds of the alcohol group. For the C–F bonds, we find that the –Cω– and –Cβ–F bonds are very weakly bonding (almost non-bonding) and that the Cα–F bonds are largely bonding in nature. With the exception of the –O–H bond, all the LUMO peaks are anti-bonding. In Fig. S3† we see that the non-bonding nature of the HOMO for PFOA is not due to a “cancellation” of bonding/anti-bonding terms, but rather we find that this orbital is nearly non-bonding across all the bonds. For the LUMO, the anti-bonding nature of this orbital arises from the various –C–F and –C–C– bonds found in PFOA. The biggest contributers to the anti-bonding nature of the LUMO are found for the carboxylic acid group and the –Cα–F2 group.
O moiety is nearly canceled by the anti-bonding nature of the –OH and –C–O bonds of the alcohol group. For the C–F bonds, we find that the –Cω– and –Cβ–F bonds are very weakly bonding (almost non-bonding) and that the Cα–F bonds are largely bonding in nature. With the exception of the –O–H bond, all the LUMO peaks are anti-bonding. In Fig. S3† we see that the non-bonding nature of the HOMO for PFOA is not due to a “cancellation” of bonding/anti-bonding terms, but rather we find that this orbital is nearly non-bonding across all the bonds. For the LUMO, the anti-bonding nature of this orbital arises from the various –C–F and –C–C– bonds found in PFOA. The biggest contributers to the anti-bonding nature of the LUMO are found for the carboxylic acid group and the –Cα–F2 group.
These observations can be verified by visual inspection of the HOMO and LUMO of FFA, PFBA, and PFOA as shown in Fig. S4–S6.† For all three molecules we observe an accumulation of the wavefunction on the carboxylic acid groups, with the –Cacid![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond carrying the majority of the molecular orbital. As we move along the sequence FFA → PFBA → PFOA we find that the LUMO begins to accumulate on the Cα–F bonds. Visual inspection of the LUMO for PFBA and PFOA (as well as the quantitative analysis from COOP) demonstrates that the nature of the HOMO and LUMO are relatively unchanged with the addition of more –CF2– groups. Utilizing the frontier electron theory of Fukui,115,116 we can hypothesize that the positive parts of the LUMO wavefunction (denoted by yellow regions Fig. S4–S6†) are available for donation of electrons from a catalyst. In particular, if we examine the molecular geometry we find a plane that encompasses the –Cα–COOH end of the PFAS; such a plane could conceivably bind parallel to a flat metal surface, and thus expose the positive regions of the LUMO to the (nearly) free electrons of the surface.
O bond carrying the majority of the molecular orbital. As we move along the sequence FFA → PFBA → PFOA we find that the LUMO begins to accumulate on the Cα–F bonds. Visual inspection of the LUMO for PFBA and PFOA (as well as the quantitative analysis from COOP) demonstrates that the nature of the HOMO and LUMO are relatively unchanged with the addition of more –CF2– groups. Utilizing the frontier electron theory of Fukui,115,116 we can hypothesize that the positive parts of the LUMO wavefunction (denoted by yellow regions Fig. S4–S6†) are available for donation of electrons from a catalyst. In particular, if we examine the molecular geometry we find a plane that encompasses the –Cα–COOH end of the PFAS; such a plane could conceivably bind parallel to a flat metal surface, and thus expose the positive regions of the LUMO to the (nearly) free electrons of the surface.
To further quantify these results, we calculated atomic Fukui functions for FFA, PFBA, and PFOA according to Section 4.2. We present our results using Hirshfeld charges in Tables S1–S3† and for Bader charges in Tables S4–S6.† For FFA, we find that f+ is highest for the acidic hydrogen and the carbonyl oxygen has the highest f−; these results are in line with the HOMO/LUMO orbital pictures shown in Fig. S4† and discussed above (recall from Parr and Wang117 that f− ≈ ρHOMO and f+ ≈ ρLUMO). Comparison of Tables S1 and S4† reveals that these trends hold regardless of choice of charge distribution scheme. In regards to PFBA, we find f− is highest for the carbonyl oxygen using Hirshfeld charges, and both the carbonyl and Cβ carbons when employing Bader charges. While both schemes are in agreement with respect to the carbonyl, they differ in regards to the Cβ with Bader charges indicating it would behave more as an electrophile. The f+ results show a shift from the acidic hydrogen atom to a Fα atom using Hirshfeld and Cα using Bader. Taken together, these results indicate that the –CαF2– group would act as a nucleophile. The numerical values of the Fukui functions line up with what is expected from the molecular orbitals shown in Fig. S5;† the HOMO is distributed along the Cacid![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) O bond and the –CαF2– group (in accordance with the f− values), and the LUMO is distributed amongst the –COOH group and the Cβ atom. Finally we consider the Fukui functions of PFOA (Tables S3 and S6†). We find that using a Hirshfeld charge distribution the f+ is highest for the Cacid and carbonyl oxygen atoms, and f− is highest for the carbonyl oxygen. For the Bader charge distribution it is Cacid and Cα for f+, and for f− it is the carbonyl oxygen. The Hirshfeld charges are rather puzzling in that it predicts a carbonyl oxygen (which carries an excess negative charge) should act more as a nucleophile; however the Fukui functions predict that it acts as both a nucleophile and an electrophile. The HOMO and LUMO shown in Fig. S6† are in agreement with the numerical Fukui functions. Thus while the molecular orbitals in Fig. S5 and S6† are visually similar, the Fukui functions indicate that for PFBA the –CαF2– group would be more chemically active whilst for PFOA it would be the –COOH group.
O bond and the –CαF2– group (in accordance with the f− values), and the LUMO is distributed amongst the –COOH group and the Cβ atom. Finally we consider the Fukui functions of PFOA (Tables S3 and S6†). We find that using a Hirshfeld charge distribution the f+ is highest for the Cacid and carbonyl oxygen atoms, and f− is highest for the carbonyl oxygen. For the Bader charge distribution it is Cacid and Cα for f+, and for f− it is the carbonyl oxygen. The Hirshfeld charges are rather puzzling in that it predicts a carbonyl oxygen (which carries an excess negative charge) should act more as a nucleophile; however the Fukui functions predict that it acts as both a nucleophile and an electrophile. The HOMO and LUMO shown in Fig. S6† are in agreement with the numerical Fukui functions. Thus while the molecular orbitals in Fig. S5 and S6† are visually similar, the Fukui functions indicate that for PFBA the –CαF2– group would be more chemically active whilst for PFOA it would be the –COOH group.
Before turning towards the examination of the molecular vibrations, we wish to touch upon the changes in the Cα–F bond with respect to the removal or addition of an electron. These bond lengths can be found in Table 1. In the neutral form, the C–F bond changes on the 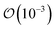 Å as we move from FFA → PFBA → PFOA sequence; however, addition of an electron results in this distance increasing for PFBA and PFOA, with FFA having only a minor change in length. We found that the addition of an electron (N + 1 column in Table 1) results in a partial dissociation of the Cα–F bond for PFBA with a ∼41% increase in bond distance. The change for PFOA is more modest, being ∼3%. With the removal of an electron (the N − 1 column in Table 1), we find that FFA contracts its C–F bond by ∼6.5%, and PFBA/PFOA contracting their Cα–F bond by ∼4%. Taking the above discussions and combining it with the observed topological changes in our PFAS molecules indicates that back-bonding mechanism wherein a catalyst gives up electron charge density to the PFAS would result in a weaker C–F bond by virtue of filling the unoccupied σ* LUMO. In contrast, our results also indicate that removal of an electron from the PFAS will result in a contraction and a subsequent strengthening of the C–F bond owing to the anti-bonding nature of the HOMO around this bond (as shown in Fig. 2 and S1–S3†).
Å as we move from FFA → PFBA → PFOA sequence; however, addition of an electron results in this distance increasing for PFBA and PFOA, with FFA having only a minor change in length. We found that the addition of an electron (N + 1 column in Table 1) results in a partial dissociation of the Cα–F bond for PFBA with a ∼41% increase in bond distance. The change for PFOA is more modest, being ∼3%. With the removal of an electron (the N − 1 column in Table 1), we find that FFA contracts its C–F bond by ∼6.5%, and PFBA/PFOA contracting their Cα–F bond by ∼4%. Taking the above discussions and combining it with the observed topological changes in our PFAS molecules indicates that back-bonding mechanism wherein a catalyst gives up electron charge density to the PFAS would result in a weaker C–F bond by virtue of filling the unoccupied σ* LUMO. In contrast, our results also indicate that removal of an electron from the PFAS will result in a contraction and a subsequent strengthening of the C–F bond owing to the anti-bonding nature of the HOMO around this bond (as shown in Fig. 2 and S1–S3†).
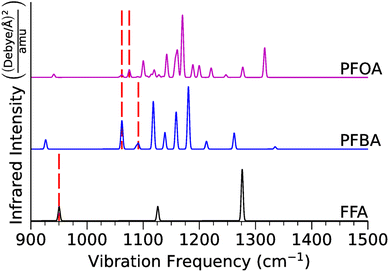 | ||
| Fig. 3 Calculated infrared vibrational spectra for FFA, PFBA, and PFOA in the gas-phase. The red dashed vertical lines denote locations of the C–F stretch (FFA) and the location of the –CαF2– stretches (PFBA and PFOA). Numerical data and mode assignments are in Tables S8–S10.† | ||
For FFA, we found that the C–F stretching mode is located at 950 cm−1. As we add –CF2– groups to form PFBA, this frequency shifts to ∼1062 cm−1 for a Cβ–F stretch, and ∼1062 cm−1 and ∼1091 cm−1 for a Cα–I stretch. The CωF3 vibrations can be found at ∼726 cm−1, ∼808 cm−1, and ∼1158 cm−1. Moving to PFOA, we found that the major Cα–F stretches were located at ∼1062 cm−1 and ∼1075 cm−1, and the Cβ–F stretches at ∼1075 cm−1, ∼1090 cm−1, ∼1100 cm−1, ∼1114 cm−1, ∼1127 cm−1, ∼1135 cm−1, ∼1141 cm−1. Finally, for CωF3 the major stretches are at ∼1119 cm−1, ∼1135 cm−1, and ∼1157 cm−1. Our results indicate that while FFA is too small of a molecule to accurately represent a PFAS molecule, PFBA is capturing the salient vibrational features of PFOA (albeit with some minor shifts in the frequencies).
Visually these differences can be seen in Fig. 3 where we plot the predicted infrared spectra of FFA, PFBA, and PFOA; here, we highlight the vibrational frequencies of the –CαF2– moiety as that is the major group we are looking to catalyze. As one would expect, the predicted spectra gets more dense as the molecular complexity increases. However, examination of Fig. 3 using the mode assignments in Tables S9 and S10† highlights a problem with using infrared spectra as an means for identification; namely, the C–F frequencies are located in the regions typically assigned to C–C backbone vibrational modes with the predicted intensities for the C–F modes being much less than the carbon backbone intensities. While we can conclude that the addition of –CF2– groups does not affect the fundamental C–F vibrations, adding onto the carbon backbone would result in the C–F modes being overtaken by the backbone vibrational modes.
Our conclusions can be backed up by prior experiments. For example, in studying PFAS complexing with an iron-based organometallic Fulong et al.120 noted that the C–F modes are buried within the regular bands. This is supported by the FT-IR experiments by Yu et al.121 who noted that while they studied PFAS complexes, they could not locate the C–F bands. Tatsuno and Ando,122 in contrast, found for linear CnF2n+2 molecules a –CF2– and F3C mode at ∼1153 cm−1 and ∼1240 cm−1, in good agreement with our results (taking into consideration limitations of DFT). Recently, there have been attempts to establish databases of infrared spectra for PFAS molecules, and while currently limited to a few PFAS, they have shown that as one increases the size of the PFAS molecule, the salient features of the spectra remain largely unchanged.123–125 However, these databases do not report mode assignments, so a comparison of our vibrational modes to these studies is not possible. Conversely, there has been a historical interest in fluorinated amorphous carbon films, and while these materials are more heterogeneous than PFAS the modes reported in these studies line up with what we and others have reported.126–133
In this section, we have compared several techniques to evaluate the electronic structure of FFA, PFBA, and PFOA. Examination of the bonding/anti-bonding nature of the molecular orbitals, the location of the HOMO and LUMO, calculation of Fukui functions, and by scrutinizing the molecular vibrations we conclude that PFBA is indeed a good computational model for PFOA and predictions made for PFBA can be also be broadly applied to PFOA.
2.2 PFAS on metal surfaces
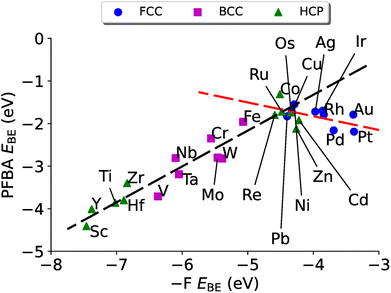
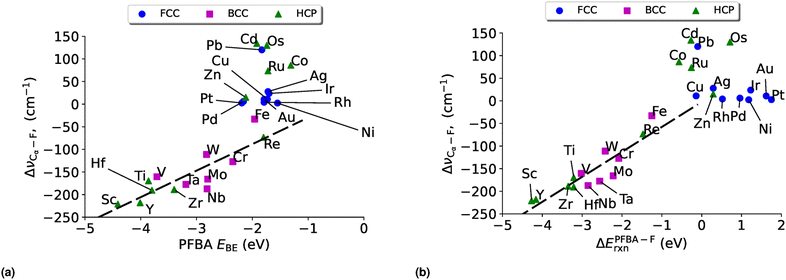
Having discussed the electronic structure of FFA, PFBA, and PFOA, we turn our attention to how PFBA interacts with transition metal surfaces. We explore several descriptors for characterizing this interaction as outlined in Section 4.3. In the following discussion, we only consider the protonated form of PFBA. This is due to two key reasons; for the first we are interested in PFAS degradation in the limit of bulk PFAS and as such the carboxylic acid groups would remain protonated. This also means that we do not consider any solvent, either explicitly or implicitly, as PFAS molecules typically have a low dielectric constant,2 which is unlikely to impact reaction energies and trends.134 Secondly as the electrostatic potential with a charged two-dimensional surface diverges,135 it would be necessary to include a surface bound hydrogen atom to counter the charge; however this would introduce an additional perturbation in our study that potentially could obfuscate our results via a three-body effect. Thus, PFBA remains in its neutral molecular state in the following discussion. Finally, we wish to note on the choice of metal surfaces. Currently there exists no consensus on which catalytic material is appropriate for C–F bond breaking in PFAS degradation. Thus, one of the goals of this study is to fill this gap and through the application of DFT identify possible candidates and provide a rationale based on quantum chemical principals. As such, we have chosen to study the entirety of the d-block transition metals in order to achieve this goal.The resulting plot in Fig. 4 is a volcano plot that is commonly encountered in heterogeneous catalysis.138–142 The individual arms of the volcano plot in Fig. 4 are related to the underlying crystal structure of the metal surface. The right side of the plot is the fcc metals where the flat binding mode is preferred, and the left side of the volcano plot is bcc metals where the carbo binding mode is preferred. Curiously we find that the hcp metals are split, with hcp metals to the left of Re preferring the carbo mode and metals to the right of Re preferring the flat mode; Re has a near identical EPFBABE for both the flat and carbo modes. For purposes of Fig. 4 the carbo mode of Re is plotted with the caveat that neither binding mode for this metal will affect our results and conclusions.
In fitting both sides of the volcano plot, we find for the right side a poor linear relationship (R2 = 0.27); however, for the left side we find an excellent linear relationship (R2 = 0.91) with a slope of 0.84 and a y-intercept of 2.04 eV. From the work of Nørskov and coworkers136,137 we know that the slope of such a linear scaling relationship is related to the valency of the adatom used to generate it. Halogens have five p-electrons and given that p-states can hold six electrons, this results in the fluorine p-states having a filling of 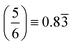 which is in remarkable agreement with our slope of 0.84.
which is in remarkable agreement with our slope of 0.84.
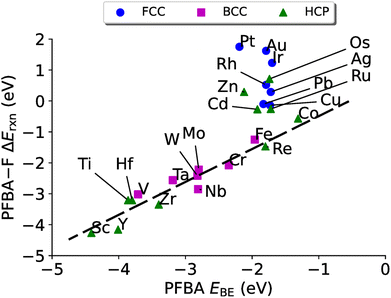
Another common descriptor of reactivity is the binding energy of the reactant, and has been shown to be an effective descriptor for ethanol dehydration on γ-Al2O3,143 conversion of furan on metal catalysts,144 the hydrogen oxidation reaction,145 and for electrocatalysts.146 In Fig. 5 we plot the binding energy of PFBA on transition metal surfaces versus the reaction energy to remove a fluorine from the Cα position. Before discussing the data, we wish to point out that while the strength of our reaction energies may seem large, they are not unprecedentedly so; moreover, prior studies report enthalpies, which include zero-point energy (ZPE) corrections which will lower the overall magnitude of the reaction energies147–155 while in the current paper we report the raw DFT values.
While we do not observe the same volcano plot behavior that we saw in Fig. 4 (although one could make the argument that it is a volcano plot, just rotated), we do see a good linear correlation for the metals that have a preference to bind PFBA in the carbo mode (all the bcc metals and hcp metals to the left of Re, plus Co). After a linear regression we arrive at a slop of 0.54, a y-intercept of 1.06 eV with a R2 of 0.90. The metals that prefer to bind PFBA in the flat configuration (all fcc metals and hcp metals to the right of Re, minus Co), on the other hand, do not show a linear scaling relationship. If we examine Table S11,† we can see that all the metals that prefer the flat configuration have a PFBA binding energy that is grouped strongly around ∼−1.8 eV. This type of behavior is fairly typical of van der Waals complexes on metal surfaces.
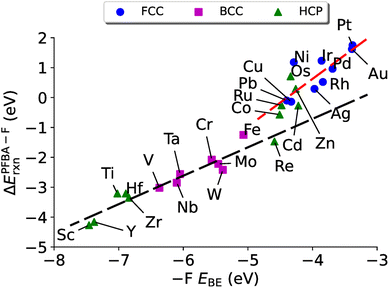
A natural question at this point is if ΔEPFBA–Frxn is related linearly to EPFBABE, which in turn is related to E–FBE, can we relate ΔEPFBA–Frxn to E–FBE? In Fig. 6 we plot E–FBEversus ΔEPFBA–Frxn and find two linear regimes: one corresponding to the carbo mode of PFBA being preferred (R2 = 0.92) and one for the flat mode being preferred (R2 = 0.67). Therefore, we can conclude this section by stating the evidence allows us to demonstrate that descriptor based approaches can be applied to the problem of PFAS degradation in a similar fashion to the prior studies on heterogeneous catalysts discussed in Section 4.3. In particular, the fluorophilicity of a particular metal surface can be utilized to provide an estimate of how favorable it would be to remove a fluorine from PFBA; however, caution needs to emphasized here as it has been shown that choosing catalysts with too strong of a binding towards a particular chemical species can lead to poisoning of the catalyst.139 Taking this effect into consideration with the results of Fig. 4–6, we suggest that iron might be a worthwhile catalyst for PFAS degradation. This is agreement with recent research that utilizes iron complexes as a catalyst.40,156–162
From Fig. 7a we can see that as we increase the PFBA binding strength (i.e. the more negative EPFBABE is) we see a greater increase in the red shift of the Cα–F stretching frequency (i.e., a more negative ΔνCα–F). This indicates that as we adsorb PFBA onto our metal surfaces, the Cα–F bond increases in length and therefore becomes weaker. In a similar fashion, we can see a similar trend when we consider ΔEPFBA–Frxn in Fig. 7b; as our reaction becomes more exothermic we observe an increasing red shift in the Cα–F stretch frequency. The link between the observed red-shifts and the bond lengths are demonstrated by comparing Tables S11 and S13;† from here we can see that a more negative ΔνCα–F does in fact relate to an increase in the bond length. This lends further support that we are weakening the Cα–F bond.
Further support of our hypothesis can be achieved by examination of the density-of-states of PFBA and the PFBA/metal complex. In addition to the standard partial density-of-states (where we localize the wavefunction onto atom centers and weight the total density-of-states by the resulting atomistic wavefunction coefficients), we also consider a method whereby we use the projectors available to us from the PAW method163 to project molecular orbitals of PFBA onto the total density-of-states.164 This allows us to determine exactly how the surface band structure influences the bonding environment of the PFBA. We present the results of such a projection in Fig. S7–S33† alongside the sp- and d-PDOS of the metal surface. A final note before discussing our results, while this method allows for all the molecular orbitals of an adsorbate to be available to do the projection, we only consider the two orbitals that comprise the HOMO and LUMO of the gas-phase PFBA.
The first thing of note is the change in the PFBA HOMO–LUMO gap for the various metals. For example, for the fcc metals we find that the average HOMO–LUMO gap is 4.73 eV, with a standard deviation of 0.42 eV. For gas-phase PFBA the HOMO–LUMO gap is 4.88 eV, which lines up with the values reported for the fcc metals and is in good agreement with the weak binding energies these metals display. For the bcc metals, we find an average HOMO–LUMO gap of 1.53 eV with a standard deviation of 0.27 eV. Finally for hcp metals, we again see a bifurcation of the results; for those metals to the left of Re we get an average gap of 1.34 with a standard deviation of 0.21 eV and for the metals to the right of Re the gap is 5.15 eV with a standard deviation of 0.25 eV. Re itself has a gap of 1.49 eV.
If we take PFBA and add an electron, then we get a singly occupied molecular orbital (SOMO) with two energies for the SOMO−1 (i.e., our old HOMO) leading to two gap energies of 2.44 eV for the α-spin and 2.24 eV for the β-spin. These gaps are in line with the HOMO–LUMO gaps given by the molecular orbital PDOS method for the bcc and half of the hcp metals, indicating that PFBA's LUMO is transformed into a SOMO. Further evidence for this can be given by examination of the charge density differences shown in Fig. S88–S114.† It is clear from these figures that for metals that lower the energy of the PFBA LUMO there is a large concentration of negative charge on the Cα–F bond, which lends further credence to the notion that the PFBA LUMO is transformed into a SOMO. We believe that this is evidence that the C–F bonds in PFAS molecules can be degraded via a back-donation mechanism.
3 Conclusions
In the current study, we built upon our earlier work on PFAS degradation that revealed a low-lying σ* anti-bonding orbital associated with PFAS molecules. Our work utilizes a four-carbon chain PFAS (perfluorobutanoic acid, PFBA) as a representative PFAS molecule; in order to ensure this is an appropriate model, a comparison between fluoroformic acid (FFA) and perfluoroctanoic acid (PFOA) was carried out to examine how the electronic structure of perfluoro-carbons is affected by the inclusion of additional –CF2– and –CH3 groups. Examination of the molecular orbitals, Fukui functions, and vibrational spectra reveal that while there are differences between the three molecules PFBA is indeed a good model for longer chain perfluoro-carbons, such as PFOA.Having established this, we next examined the binding and reaction energies for PFBA interacting on a set of transition metal catalysts. The primary goal was to see if metal catalysts can partake in the Blyholder back-bonding mechanism, wherein electrons from the metal back-fill an anti-bonding orbital of an adsorbate. We first established that linear scaling relationships, a key tool in understanding catalytic behavior and the prediction of its behavior, exist for PFBA on metal surfaces. Using the binding energy, reaction energy, and vibration shifts as descriptors we are able to demonstrate that there is a clear correlation between these three indicating that PFBA follows a similar chemistry that has been previously established for hydrocarbons.
As for evidence of the Blyholder back-bonding mechanism, we employed a molecular orbital PDOS technique that allows us to see how the molecular orbitals of an adsorbate behave upon adsorption. We find that for metals that feature a strong binding energy (and consequently a more exothermic reaction energy and large red-shifts in the vibrational modes) the PFBA LUMO takes on a character that is similar to a SOMO. Moreover, the HOMO–LUMO gaps for PFBA on the metal surfaces are in-line with a negatively charged gas-phase PFBA. Finally, charge density differences show for these metals a large accumulation of negative charge around the Cα–F bond which lends further credence to our back-bonding hypothesis.
Thus, we conclude that PFBA does participate in a back-bonding mechanism which can be leveraged to design better PFAS degradation catalysts from a more rational, ab initio standpoint. As a final note, comparison of our linear scaling relationships indicates that iron would be an ideal candidate for the further study of PFAS degradation.
4 Computational methodology
Periodic density functional theory (DFT) calculations were carried out with GPAW165 and the Atomic Simulation Environment (ASE).166 The optPBE-vdW exchange-correlation functional was used for the valence electrons167,168 with the core electrons being treated with the projector augmented wavefunction (PAW) method.163,169,170 The optPBE-vdW functional is a generalized gradient approximation (GGA)-based functional, with the electron correlation being represented via a nonlocal kernal that accounts for interactions between two electron density points. In treating the electron correlation in such a fashion, weak interactions are picked up and thus optPBE-vdW is desireable for studying surface interactions.167,168 Fermi level discontinuities were with the Fermi–Dirac smearing method with a smearing parameter of 0.15 eV. Total energies were self-consistently minimized to 10−6 eV with the Davidson method.171Surface calculations employed a three-step optimization process in order to best utilize our computational resources. In the first step, the initial degrees of freedom were optimized with a linear-combination of atomic orbital (LCAO) double-ζ basis set.172 Once the forces were converged to 0.05 eV Å−1, we did two optimization calculations utilizing a finite-difference basis set169,173 with a grid spacing of 0.2 Å (which corresponds to a kinetic energy cutoff of ∼900 eV (ref. 173)). In the first finite-difference optimization, we only considered the Γ-point; the subsequent optimization used a (3 × 3 × 1) Monkhorst–Pack k-point mesh.174 As both basis set types allow for the arbitrary setting of periodic boundary conditions, we only applied the periodic boundary in the x- and y-directions (which allows us to utilize only a single k-point in the z-direction). Both finite-difference optimizations were done to a force-threshold of 0.05 eV Å−1. The majority of the optimizations were done with the ASE implementation of the limited memory Broyden–Fletcher–Goldfarb–Shanno (LBFGS) method175 (a comparison between BFGS and LBFGS reveals no difference in geometry and energy for PFBA/V(110), and therefore we determine LBFGS to be sufficient). However, a few calculations revealed instabilities with the LBFGS optimizer; for these cases the fast inertial relaxation engine (FIRE)176 was used. The reason for utilizing such a successive optimization scheme is thus: the LCAO method, while capable of producing accurate geometries, suffers from basis set superposition errors (BSSE). While correction schemes exist for overcoming BSSE,177 the finite-difference method does not suffer from that limitation and is ideal for the calculation of final energies. However, it should be noted that the LCAO method is, in our experience, ∼6× faster than finite-difference, which reduces computational overhead. Similarly, finite-difference at the Γ-point is roughly 5× faster than performing it with the 3 × 3 × 1 k-point grid (once one accounts for the symmetry of the irreducible Brillouin zone). Thus the successive optimization method outlined above allows us to conserve computational resources and enables the performance of the high-throughput calculations required by the current study efficiently.
We considered the full d-block of metals (with the exception of mercury as it does not exist as a solid at room temperature), and took the lowest energy surfaces for each crystal structure. For the face-centered cubic (FCC) metals this is the (111) surface, for the body-centered cubic (BCC) metals this is the (110), and for the hexagonal-closed pack (HCP) metals it is the (0001) surface. Bulk unit cell parameters were generated using the above procedure with the exception of the k-point mesh and choice of basis set. Unit cells were optimized using a plane-wave basis set of 600 eV and a k-point mesh of (9 × 9 × 9). Surfaces were constructed using 4 layers and a p(5 × 5) repetition.
Vibrations were calculated via the construction of a numerical Hessian as implemented in ASE. As the finite-difference calculations with a (3 × 3 × 1) Monkhorst–Pack k-point mesh are quite demanding, we opted to calculate the vibrations at the Γ-point only using the geometry at the (3 × 3 × 1) k-point mesh. In order to ascertain the errors associated with this approximation, we calculated the C–F stretch frequency of FFA adsorbed onto the V(111) surface for a variety of methods and geometries in Table S7.† Overall, we found that our method works quite well with an error of 0.01 cm−1 in the stretching frequency. Infrared intensities were calculated using the method of Porezag and Pederson.178
4.1 Molecular orbitals
For the analysis of our molecular orbitals we utilized the crystal orbital overlap population (COOP)179 method as it has proven invaluable in our previous research.51,180–182 Here, we take the density of states (DOS) and weigh it with a Mullikan factor,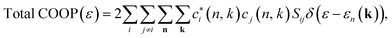 | (1) |
4.2 Fukui functions
Frontier molecular orbital theory115,116 was additionally utilized using Parr and Wang's DFT formulation,117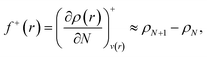 | (2a) |
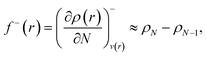 | (2b) |
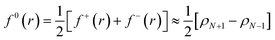 | (2c) |
| f+A(r) = nA(N+1) − nA(N), | (3a) |
| f−A(r) = nA(N) − nA(N − 1), | (3b) |
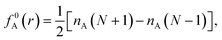 | (3c) |
| f+A(r) = qA(N) − qA(N + 1), | (4a) |
| f−A(r) = qA(N − 1) − qA(N). | (4b) |
As f0A is simply the mean between f+A and f−A it is unchanged with the adoption of condensed atomic charges. While a variety of charge partitioning schemes can be used for the calculation of eqn (2) and (3), we chose to utilize the Hirshfeld partitioning scheme188 as implemented in GPAW and the Bader atoms-in-molecules approach189,190 as implemented by Henkelman and coworkers.191–193 The required electronic densities were calculated using the optPBE-vdW functional and a grid-based basis set with a grid spacing of 0.2 Å. However, we found that the default initial guess used in GPAW resulted in non-converging self-consistent fields (SCF); to circumvent this we generated a triple-ζ plus polarization (tzp) basis set using GPAW's basis set generation tools. Initial orbitals and virtual space were then generated from this tzp basis set. The molecular geometries of the charged FFA, PFBA, and PFOA were then fully relaxed, Hirshfeld/Bader charges calculated, and numerical derivatives for the atomic Fukui functions were then taken.
4.3 Reactivity descriptors
Researchers in heterogeneous catalysis use a variety of descriptors to describe reactions at surfaces. These studies have been successful in relating reaction energies to activation and reaction energies,139,141,146,148,154,194–204 utilization of density-of-states properties,137,143,194,205–216 coordination number between the catalyst and reactants,145,214,217–219 the binding energy of the adsorbates with the catalyst surface,24,136–138,140,142–145,182,220–225 and molecular vibrations.223,226–230 Intrinsic to these descriptors is the chemical phenomena of charge transfer230–236—either from the catalyst (in the case of metals) or from the adsorbate (in the case of oxides). For example, Dunnington and Schmidt have shown using a periodic formulation of the natural bond orbital analysis that contact with a metal surface results in the partial occupancy of adsorbate anti-bonding orbitals.231 A recent study by Jia et al.230 have demonstrated a correlation between charge transfer, binding energies, and activation energies on metal surfaces. These descriptor based techniques has even been applied to machine learning approaches for the prediction of catalytic activity.237–240In the current study we consider three descriptors: the binding energy of PFBA to a metal surface (EBE), the reaction energy (ΔErxn) of removing a –F from the Cα of PFBA, and the vibrational shift of the Cα–F bond as compared to the gas-phase (ΔνCα–F). We define EBE as,
| EBE = EDFTPFBA+M − EDFTM − EDFTPFBA, | (5) |
| ΔErxn = EDFTfinal state − EDFTinitial state, | (6) |
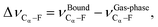 | (7) |
Author contributions
Dr Glen R. Jenness: conceptualization, methodology, software, investigation, formal analysis, writing-original draft, writing-review & editing; Dr Manoj K. Shukla: conceptualization, methodology, writing-review & editing, supervision, projection administration, funding acquisition.Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.Acknowledgements
G. R. J. would like to acknowledge Drs Ashyln M. Koval, Timothy C. Schutt, William A. Pisani, Timothy C. Ricard, and Robert W. Lamb for their input on the manuscript and useful discussions. The use of trade, product, or firm names in this report is for descriptive purposes only and does not imply endorsement by the U.S. Government. The tests described and the resulting data presented herein, unless otherwise noted, were obtained from research conducted under the Installation and Operational Environments (IOE) Program of the United States Army Corps of Engineers and the Environmental Security Technology Certification Program of the Department of Defense by the USAERDC. Permission was granted by the Chief of Engineers to publish this information. The findings of this report are not to be construed as an official Department of the Army position unless so designated by other authorized documents. This work was supported by a grant of computer time from the DOD High Performance Computing Modernization Program at ERDC, Vicksburg. This document has been approved for public release (Distribution Statement A).References
- C. Hogue, EPA Sets Health Advisory Levels for 6 PFAS, Chem. Eng. News, 2022, 100, 13 Search PubMed.
- J. Glüge, M. Scheringer, I. T. Cousins, J. C. Dewitt, G. Goldenman, D. Herzke, R. Lohmann, C. A. Ng, X. Trier and Z. Wang, An Overview of the Uses of Per- and Polyfluoroalkyl Substances (PFAS), Environ. Sci.: Processes Impacts, 2020, 22, 2345–2373 RSC.
- E. Panieri, K. Baralic, D. Djukic-Cosic, A. B. Djordjevic and L. Saso, PFAS Molecules: A Major Concern for the Human Health and the Environment, Toxics, 2022, 10, 44 CrossRef CAS PubMed.
- F. J. Urbano and J. M. Marinas, Hydrogenolysis of Organohalogen Compounds over Palladium Supported Catalysts, J. Mol. Catal. A: Chem., 2001, 173, 329–345 CrossRef CAS.
- S. J. Blanksby and G. B. Ellison, Bond Dissociation Energies of Organic Molecules, Acc. Chem. Res., 2003, 36, 255–263 CrossRef CAS PubMed.
- M. J. Bentel, Y. Yu, L. Xu, Z. Li, B. M. Wong, Y. Men and J. Liu, Defluorination of Per- and Polyfluoroalkyl Substances (PFASs) with Hydrated Electrons: Structural Dependence and Implications to PFAS Remediation and Management, Environ. Sci. Technol., 2019, 53, 3718–3728 CrossRef CAS PubMed.
- O. Eisenstein, J. Milani and R. N. Perutz, Selectivity of C–H Activation and Competition between C–H and C–F Bond Activation at Fluorocarbons, Chem. Rev., 2017, 117, 8710–8753 CrossRef CAS PubMed.
- Z. Liu, M. J. Bentel, Y. Yu, C. Ren, J. Gao, V. F. Pulikkal, M. Sun, Y. Men and J. Liu, Near-Quantitative Defluorination of Perfluorinated and Fluorotelomer Carboxylates and Sulfonates with Integrated Oxidation and Reduction, Environ. Sci. Technol., 2021, 55, 7052–7062 CrossRef CAS PubMed.
- A. A. Zavitsas, The Relation between Bond Lengths and Dissociation Energies of Carbon-Carbon Bonds, J. Phys. Chem. A, 2003, 107, 897–898 CrossRef CAS.
- K. Prevedouros, I. T. Cousins, R. C. Buck and S. H. Korzeniowski, Sources, Fate and Transport of Perfluorocarboxylates, Environ. Sci. Technol., 2006, 40, 32–44 CrossRef CAS PubMed.
- EPA, Basic Information on PFAS, 2021, https://www.epa.gov/pfas/basic-information-pfas Search PubMed.
- T. Pancras, G. Schrauwen, T. Held, K. Baker, I. Ross and H. Slenders, Environmental Fate and Effects of Poly- and Perfluoroalkyl Substances (PFAS), 2016 Search PubMed.
- X. C. Hu, D. Q. Andrews, A. B. Lindstrom, T. A. Bruton, L. A. Schaider, P. Grandjean, R. Lohmann, C. C. Carignan, A. Blum, S. A. Balan, C. P. Higgins and E. M. Sunderland, Detection of Poly- and Perfluoroalkyl Substances (PFASs) in U.S. Drinking Water Linked to Industrial Sites, Military Fire Training Areas, and Wastewater Treatment Plants, Environ. Sci. Technol. Lett., 2016, 3, 344–350 CrossRef CAS PubMed.
- Z. Wang, J. C. Dewitt, C. P. Higgins and I. T. Cousins, A Never-Ending Story of Per- and Polyfluoroalkyl Substances (PFASs)?, Environ. Sci. Technol., 2017, 51, 2508–2518 CrossRef CAS PubMed.
- M.-A. Verner, A. E. Loccisano, N.-H. Morken, M. Yoon, H. Wu, R. McDougall, M. Maisonet, M. Marcus, R. Kishi, C. Miyashita, M.-H. Chen, W.-S. Hsieh, M. E. Andersen, H. J. Clewell and M. P. Longnecker, Associations of Perfluoroalkyl Substances (PFAS) with Lower Birth Weight: An Evaluation of Potential Confounding by Glomerular Filtration Rate Using a Physiologically Based Pharmacokinetic Model (PBPK), Environ. Health Perspect., 2015, 123, 1317–1324 CrossRef CAS PubMed.
- M. L. Brusseau, Assessing the Potential Contributions of Additional Retention Processes to PFAS Retardation in the Subsurface, Sci. Total Environ., 2018, 613–614, 176–185 CrossRef CAS PubMed.
- R. Darlington, E. Barth and J. McKernan, The Challenges of PFAS Remediation, Mil. Eng., 2018, 110, 58–60 Search PubMed.
- B. M. Sharma, G. K. Bharat, S. Tayal, T. Larssen, J. Bečanová, P. Karásková, P. G. Whitehead, M. N. Futter, D. Butterfield and L. Nizzetto, Perfluoroalkyl Substances (PFAS) in River and Ground/Drinking Water of the Ganges River Basin: Emissions and Implications for Human Exposure, Environ. Pollut., 2016, 208, 704–713 CrossRef CAS PubMed.
- S. Bergström, PhD thesis, Sveriges Lantbruksuniversitet (Swedish University of Agricultural Sciences), Uppsala, Sweden, 2014.
- A. Möller, L. Ahrens, R. Surm, J. Westerveld, F. V. D. Wielen, R. Ebinghaus and P. D. Voogt, Distribution and Sources of Poly-Fluoroalkyl Substances (PFAS) in the River Rhine Watershed, Environ. Pollut., 2010, 158, 3243–3250 CrossRef PubMed.
- F. Li, C. Zhang, Y. Qu, J. Chen, L. Chen, Y. Liu and Q. Zhou, Quantitative Characterization of Short- and Long-Chain Perfluorinated Acids in Solid Matrices in Shanghai, China, Sci. Total Environ., 2010, 408, 617–623 CrossRef CAS PubMed.
- K. Y. Kwok, E. Yamazaki, N. Yamashita, S. Taniyasu, M. B. Murphy, Y. Horii, G. Petrick, R. Kallerborn, K. Kannan, K. Murano and P. K. S. Lam, Transport of Perfluoroalkyl Substances (PFAS) from an Arctic Glacier to Downstream Locations: Implications for Sources, Sci. Total Environ., 2013, 447, 46–55 CrossRef CAS PubMed.
- H. N. P. Vo, H. H. Ngo, W. Guo, T. M. H. Nguyen, J. Li, H. Liang, L. Deng, Z. Chen and T. A. H. Nguyen, Poly- and Perfluoroalkyl Substances in Water and Wastewater: A Comprehensive Review from Sources to Remediation, Journal of Water Process Engineering, 2020, 36, 101393 CrossRef.
- B. Xu, S. Liu, J. L. Zhou, C. Zheng, J. Weifeng, B. Chen, T. Zhang and W. Qiu, PFAS and Their Substitutes in Groundwater: Occurrence, Transformation and Remediation, J. Hazard. Mater., 2021, 412, 125159 CrossRef CAS PubMed.
- M. Haukås, U. Berger, H. Hop, B. Gulliksen and G. W. Gabrielsen, Bioaccumulation of Per- and Polyfluorinated Alkyl Substances (PFAS) in Selected Species from the Barents Sea Food Web, Environ. Pollut., 2007, 148, 360–371 CrossRef PubMed.
- B. C. Kelly, M. G. Ikonomou, J. D. Blair, D. Hoover, R. Grace, F. a P. C. Gobas and B. Surridge, Perfluoroalkyl Contaminants in an Arctic Marine Food Web: Trophic Magnification and Wildlife Exposure, Environ. Sci. Technol., 2009, 4037–4043 CrossRef CAS PubMed.
- S. Dasgupta, A. Reddam, Z. Liu, J. Liu and D. C. Volz, High-Content Screening in Zebrafish Identifies Perfluorooctanesulfonamide as a Potent Developmental Toxicant, Environ. Pollut., 2020, 256, 113550 CrossRef CAS PubMed.
- B. González-Gaya, J. Dachs, J. L. Roscales, G. Caballero and B. Jiménez, Perfluoroalkylated Substances in the Global Tropical and Subtropical Surface Oceans, Environ. Sci. Technol., 2014, 48, 13076–13084 CrossRef PubMed.
- S. K. Sagiv, S. L. Rifas-Shiman, T. F. Webster, A. M. Mora, M. H. Harris, A. M. Calafat, X. Ye, M. W. Gillman and E. Oken, Sociodemographic and Perinatal Predictors of Early Pregnancy Per- and Polyfluoroalkyl Substance (PFAS) Concentrations, Environ. Sci. Technol., 2015, 49, 11849–11858 CrossRef CAS PubMed.
- E. R. McKenzie, R. L. Siegrist, J. E. McCray and C. P. Higgins, Effects of Chemical Oxidants on Perfluoroalkyl Acid Transport in One-Dimensional Porous Media Columns, Environ. Sci. Technol., 2015, 49, 1681–1689 CrossRef CAS PubMed.
- J. Jeon, K. Kannan, B. J. Lim, K. G. An and S. D. Kim, Effects of Salinity and Organic Matter on the Partitioning of Perfluoroalkyl Acid (PFAS) to Clay Particles, J. Environ. Monit., 2011, 13, 1803–1810 RSC.
- D. J. V. Hoomissen and S. Vyas, Early Events in the Reductive Dehalogenation of Linear Perfluoroalkyl Substances, Environ. Sci. Technol. Lett., 2019, 6, 365–371 CrossRef.
- J. Gao, Z. Liu, M. J. Bentel, Y. Yu, Y. Men and J. Liu, Defluorination of Omega-Hydroperfluorocarboxylates (omega-HPFCAs): Distinct Reactivities from Perfluoro and Fluorotelomeric Carboxylates, Environ. Sci. Technol., 2021, 55, 14146–14155 CrossRef CAS PubMed.
- Z. Liu, Z. Chen, J. Gao, Y. Yu, Y. Men, C. Gu and J. Liu, Accelerated Degradation of Perfluorosulfonates and Perfluorocarboxylates by UV/Sulfite + Iodide: Reaction Mechanisms and System Efficiencies, Environ. Sci. Technol., 2022, 56, 3699–3709 CrossRef CAS PubMed.
- A. M. Michalak, J. Xia, D. Brdjanovic, A.-N. Mbiyozo, D. Sedlak, T. Pradeep, U. Lall, N. Rao and J. Gupta, The Frontiers of Water and Sanitation, Nature Water, 2023, 1, 10–18 CrossRef.
- S. Yang, S. Fernando, T. M. Holsen and Y. Yang, Inhibition of Perchlorate Formation during the Electrochemical Oxidation of Perfluoroalkyl Acid in Groundwater, Environ. Sci. Technol. Lett., 2019, 6, 775–780 CrossRef CAS.
- C. E. Schaefer, C. Andaya, A. Urtiaga, E. R. McKenzie and C. P. Higgins, Electrochemical Treatment of Perfluorooctanoic Acid (PFOA) and Perfluorooctane Sulfonic Acid (PFOS) in Groundwater Impacted by Aqueous Film Forming Foams (AFFFs), J. Hazard. Mater., 2015, 295, 170–175 CrossRef CAS PubMed.
- U. Rao, Y. Su, C. M. Khor, B. Jung, S. Ma, D. M. Cwiertny, B. M. Wong and D. Jassby, Structural Dependence of Reductive Defluorination of Linear PFAS Compounds in a UV/Electrochemical System, Environ. Sci. Technol., 2020, 54, 10668–10677 CrossRef CAS PubMed.
- J. Stonebridge, R. Baldwin, N. R. Thomson and C. Ptacek, Fluoride-Selective Electrode as a Tool to Evaluate the Degradation of PFAS in Groundwater: A Bench-Scale Investigation, Groundwater Monit. Rem., 2020, 40, 73–80 CrossRef CAS.
- P. B. Medina, V. A. Contreras, F. Hartmann, D. Schmitt, A. Klimek, J. Elbert, M. Gallei and X. Su, Investigating the Electrochemically Driven Capture and Release of Long-Chain PFAS by Redox Metallopolymer Sorbents, ACS Appl. Mater. Interfaces, 2023, 15, 22112–22122 CrossRef PubMed.
- L. Duan, B. Wang, K. Heck, S. Guo, C. A. Clark, J. Arredondo, M. Wang, T. P. Senftle, P. Westerhoff, X. Wen, Y. Song and M. S. Wong, Efficient Photocatalytic PFOA Degradation over Boron Nitride, Environ. Sci. Technol. Lett., 2020, 7, 613–619 CrossRef CAS.
- F. Li, Z. Wei, K. He, L. Blaney, X. Cheng, T. Xu, W. Liu and D. Zhao, A Concentrate-and-Destroy Technique for Degradation of Perfluorooctanoic Acid in Water Using a New Adsorptive Photocatalyst, Water Res., 2020, 185, 1–14 Search PubMed.
- W. Zhang, H. Cao and Y. Liang, Degradation by Hydrothermal Liquefaction of Fluoroalkylether Compounds Accumulated in Cattails (Typha latifolia), J. Environ. Chem. Eng., 2021, 9, 105363 CrossRef CAS.
- Y.-J. Lei, Y. Tian, Z. Sobhani, R. Naidu and C. Fang, Synergistic Degradation of PFAS in Water and Soil by Dual-Frequency Ultrasonic Activated Persulfate, Chem. Eng. J., 2020, 388, 124215 CrossRef CAS.
- A. H. da S Filho and G. L. C. de Souza, Examining the Degradation of Environmentally-Daunting Per- and Polyfluoroalkyl Substances from a Fundamental Chemical Perspective, Phys. Chem. Chem. Phys., 2020, 22, 17659–17667 RSC.
- B. Liu, H. M. Chen, C. Liu, S. C. Andrews, C. Hahn and P. Yang, Large-Scale Synthesis of Transition-Metal-Doped TiO2 Nanowires with Controllable Overpotential, J. Am. Chem. Soc., 2013, 135, 9995–9998 CrossRef CAS PubMed.
- V. J. Scott, R. Çelenligil Çetin and O. V. Ozerov, Room-Temperature Catalytic Hydrodefluorination of C(sp3)–F Bonds, J. Am. Chem. Soc., 2005, 127, 2852–2853 CrossRef CAS PubMed.
- C. Douvris and O. V. Ozerov, Hydrodefluorination of Perfluoroalkyl Groups Using Silylium-Carborane Catalysts, Science, 2008, 321, 1188–1190 CrossRef CAS PubMed.
- C. Douvris, C. M. Nagaraja, C. H. Chen, B. M. Foxman and O. V. Ozerov, Hydrodefluorination and Other Hydrodehalogenation of Aliphatic Carbon-Halogen Bonds Using Silylium Catalysis, J. Am. Chem. Soc., 2010, 132, 4946–4953 CrossRef CAS PubMed.
- J. Liu, D. J. V. Hoomissen, T. Liu, A. Maizel, X. Huo, S. R. Ferna, C. Ren, X. Xiao, Y. Fang and C. E. Schaefer, Reductive Defluorination of Branched Per- and Polyfluoroalkyl Substances with Cobalt Complex Catalysts, Environ. Sci. Technol. Lett., 2018, 5, 289–294 CrossRef CAS.
- G. R. Jenness, A. M. Koval, B. D. Etz and M. K. Shukla, Atomistic Insights Into the Hydrodefluorination of PFAS Using Silylium Catalysts, Environ. Sci.: Processes Impacts, 2022, 24, 2085–2099 RSC.
- S. Che, B. Jin, Z. Liu, Y. Yu, J. Liu and Y. Men, Structure-Specific Aerobic Defluorination of Short-Chain Fluorinated Carboxylic Acids by Activated Sludge Communities, Environ. Sci. Technol. Lett., 2021, 8, 668–674 CrossRef CAS PubMed.
- B. Jin, Y. Zhu, W. Zhao, Z. Liu, S. Che, K. Chen, Y. H. Lin, J. Liu and Y. Men, Aerobic Biotransformation and Defluorination of Fluoroalkylether Substances (Ether PFAS): Substrate Specificity, Pathways, and Applications, Environ. Sci. Technol. Lett., 2023, 10, 755–761 CrossRef CAS PubMed.
- B. Trang, Y. Li, X.-S. Xue, M. Ateia, K. N. Houk and W. R. Dichtel, Low-Temperature Mineralization of Perfluorocarboxylic Acids, Science, 2022, 377, 839 CrossRef CAS PubMed.
- R. K. Singh, S. Fernando, S. F. Baygi, N. Multari, S. M. Thagard and T. M. Holsen, Breakdown Products from Perfluorinated Alkyl Substances (PFAS) Degradation in a Plasma-Based Water Treatment Process, Environ. Sci. Technol., 2019, 53, 2731–2738 CrossRef CAS PubMed.
- A. J. Lewis, T. Joyce, M. Hadaya, F. Ebrahimi, I. Dragiev, N. Giardetti, J. Yang, G. Fridman, A. Rabinovich, A. A. Fridman, E. R. McKenzie and C. M. Sales, Rapid Degradation of PFAS in Aqueous Solutions by Reverse Vortex Flow Gliding Arc Plasma, Environ. Sci.: Water Res. Technol., 2020, 6, 1044–1057 RSC.
- D. Palma, D. Papagiannaki, M. Lai, R. Binetti, M. Sleiman, M. Minella and C. Richard, PFAS Degradation in Ultrapure and Groundwater Using Non-Thermal Plasma, Molecules, 2021, 26, 1–13 CrossRef PubMed.
- H. Cao, W. Zhang, C. Wang and Y. Liang, Sonochemical Degradation of Poly- and Perfluoroalkyl Substances–A Review, Ultrason. Sonochem., 2020, 69, 105245 CrossRef CAS PubMed.
- M. E. McGuire, C. Schaefer, T. Richards, W. J. Backe, J. A. Field, E. Houtz, D. L. Sedlak, J. L. Guelfo, A. Wunsch and C. P. Higgins, Evidence of Remediation-Induced Alteration of Subsurface Poly- and Perfluoroalkyl Substance Distribution at a Former Firefighter Training Area, Environ. Sci. Technol., 2014, 48, 6644–6652 CrossRef CAS PubMed.
- J. Horst, J. McDonough, I. Ross and E. Houtz, Understanding and Managing the Potential By-Products of PFAS Destruction, Groundwater Monit. Rem., 2020, 40, 17–27 CrossRef.
- R. P. Hughes, R. B. Laritchev, L. N. Zakharov and A. L. Rheingold, Reductive Activation of Carbon-Fluorine Bonds in Perfluoroalkyl Ligands: An Unexpected Route to the Only Known Tetrafluorobutatriene Transition Metal Complex: Ir(η5-C5Me5)(PMe3)(2,3-η2-CF2
![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) C
C![[double bond, length as m-dash]](https://www.rsc.org/images/entities/char_e001.gif) CF2), J. Am. Chem. Soc., 2004, 126, 2308–2309 CrossRef CAS PubMed.
CF2), J. Am. Chem. Soc., 2004, 126, 2308–2309 CrossRef CAS PubMed. - M. F. Kuehnel, D. Lentz and T. Braun, Synthesis of Fluorinated Building Blocks by Transition-Metal-Mediated Hydrodefluorination Reactions, Angew. Chem., 2013, 52, 3328–3348 CrossRef PubMed.
- M. Michalczyk, B. Kizior, W. Zierkiewicz and S. Scheiner, Factors Contributing to Halogen Bond Strength and Stretch or Contraction of Internal Covalent Bond, Phys. Chem. Chem. Phys., 2023, 2907 RSC.
- S. Royer and D. Duprez, Catalytic Oxidation of Carbon Monoxide over Transition Metal Oxides, ChemCatChem, 2011, 3, 24–65 CrossRef CAS.
- G. Blyholder, Molecular Orbital View of Chemisorbed Carbon Monoxide, J. Phys. Chem., 1964, 68, 2772–2777 CrossRef CAS.
- G. Blyholder and M. C. Allen, Infrared Spectra and Molecular Orbital Model for Carbon Monoxide Adsorbed on Metals, J. Am. Chem. Soc., 1969, 91, 3158 CrossRef CAS.
- G. Pacchioni, G. Cogliandro and P. S. Bagus, Characterization of Oxide Surfaces by Infrared Spectroscopy of Adsorbed Carbon Monoxide: A Theoretical Investigation of the Frequency Shift of CO on MgO and NiO, Surf. Sci., 1991, 255, 344354 CrossRef.
- F. Aubke and C. Wang, Carbon Monoxide as a A-Donor Ligand in Coordination Chemistry, 1994 Search PubMed.
- K. W. Kolasinski, Surface Science, John Wiley & Sons, 2002 Search PubMed.
- C. D. Zeinalipour-Yazdi, A. L. Cooksy and A. M. Efstathiou, CO Adsorption on Transition Metal Clusters: Trends from Density Functional Theory, Surf. Sci., 2008, 602, 1858–1862 CrossRef CAS.
- G. Blyholder, CNDO Model of Carbon Monoxide Chemisorbed on Nickel, J. Phys. Chem., 1975, 79, 756 CrossRef CAS.
- F. Illas, S. Zurita, J. Rubio and A. M. Marquez, Origin of the Vibrational Shift of CO Chemisorbed on Pt(111), Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 52, 12372 CrossRef CAS PubMed.
- H. Aizawa and S. Tsuneyuki, First-Principles Study of CO Bonding to Pt(111): Validity of the Blyholder Model, Surf. Sci., 1998, 399, L364–L370 CrossRef CAS.
- M. T. M. Koper and R. A. V. Santen, Electric Field Effects on CO and NO Adsorption at the Pt(111) Surface, J. Electroanal. Chem., 1999, 476, 64–70 CrossRef CAS.
- W. V. Glassey, G. A. Papoian and R. Hoffmann, Total Energy Partitioning within a One-Electron Formalism: A Hamilton Population Study of Surface-Co Interaction in the C(2×2)-Co/Ni(100) Chemisorption System, J. Chem. Phys., 1999, 111, 893–910 CrossRef CAS.
- P. J. Feibelman, B. Hammer, J. K. Nørskov, F. Wagner, M. Scheffler, R. Stumpf, R. Watwe and J. Dumesic, The Co/Pt(111) Puzzle, J. Phys. Chem. B, 2001, 105, 4018–4025 CrossRef CAS.
- Y. D. Kim, A. P. Seitsonen and H. Over, Adsorption Characteristics of CO and N2 on RuO2(110), Phys. Rev. B: Condens. Matter Mater. Phys., 2001, 63, 115419 CrossRef.
- E. J. Walter, S. P. Lewis and A. M. Rappe, First Principles Study of Carbon Monoxide Adsorption on Zirconia-Supported Copper, Surf. Sci., 2001, 495, 44–50 CrossRef CAS.
- A. Nilsson and L. G. M. Pettersson, Chemical Bonding on Surfaces Probed by X-Ray Emission Spectroscopy and Density Functional Theory, Surf. Sci. Rep., 2004, 55, 49–167 CrossRef CAS.
- L. G. M. Pettersson and A. Nilsson, A Molecular Perspective on the d-Band Model: Synergy between Experiment and Theory, Top. Catal., 2014, 57, 2–13 CrossRef CAS.
- R. J. Smith, J. Anderson and G. J. Lapeyre, Further Studies of Ni (001)c(2×2)CO: Evidence for Back Donation in the Chemisorption Bond, Phys. Rev. B: Condens. Matter Mater. Phys., 1980, 22, 632 CrossRef CAS.
- Y.-T. Wong and R. Hoffmann, Chemisorption of Carbon Monoxide on Three Metal Surfaces: Ni(111), Pd(111), and Pt(111): A Comparative Study, J. Phys. Chem., 1991, 95, 859–867 CrossRef CAS.
- M. J. Kappers and J. H. V. D. Maas, Correlation between CO Frequency and Pt Coordination Number. A DRIFT Study on Supported Pt Catalysts, Catal. Lett., 1991, 10, 365–374 CrossRef CAS.
- G. S. Icking-Konert, H. Handschuh, G. Ganteför and W. Eberhardt, Bonding of CO to Metal Particles: Photoelectron Spectra of Nin(CO)m− and Ptn(CO)m− Clusters, Phys. Rev. Lett., 1996, 76, 1047–1050 CrossRef CAS PubMed.
- G. Gantefor, G. S. Icking-Konert, H. Handschuh and W. Eberhardt, CO Chemisorption on Nin, Pdn, and Ptn Clusters, Int. J. Mass Spectrom. Ion Processes, 1996, 159, 81–109 CrossRef.
- A. Nilsson, N. Wassdahl, M. Weinelt, O. Karis, T. Wiell, P. Bennich, J. Hasselström, A. Föhlisch, J. Stöhr and M. Samant, Local Probing of the Surface Chemical Bond Using X-Ray Emission Spectroscopy, Appl. Phys. A, 1997, 65, 147–154 CrossRef CAS.
- A. Föhlisch, M. Nyberg, J. Hasselström, O. Karis, L. G. M. Pettersson and A. Nilsson, How Carbon Monoxide Adsorbs in Different Sites, Phys. Rev. Lett., 2000, 85, 3309 CrossRef PubMed.
- D. M. Khramov, V. M. Lynch and C. W. Bielawski, N-Heterocyclic Carbene - Transition Metal Complexes: Spectroscopic and Crystallographic Analyses of π-Back-bonding Interactions, Organometallics, 2007, 26, 6042–6049 CrossRef CAS.
- R. Bonetto, F. Crisanti and A. Sartorel, Carbon Dioxide Reduction Mediated by Iron Catalysts: Mechanism and Intermediates That Guide Selectivity, ACS Omega, 2020, 5, 21309–21319 CrossRef CAS PubMed.
- A. Tortajada, F. Juliá-Hernández, M. Börjesson, T. Moragas and R. Martin, Transition-Metal-Catalyzed Carboxylation Reactions with Carbon Dioxide, Angew. Chem., 2018, 130, 16178–16214 CrossRef.
- Z. D. Brown and P. P. Power, Mechanisms of Reactions of Open-Shell, Heavier Group 14 Derivatives with Small Molecules: n−π* Back-Bonding in Isocyanide Complexes, C–H Activation Under Ambient Conditions, CO Coupling, and Ancillary Molecular Interactions, Inorg. Chem., 2013, 52, 6248–6259 CrossRef CAS PubMed.
- A. Mansikkamäki, P. P. Power and H. M. Tuononen, Computational Analysis of n → π* Back-Bonding in Metallylene-Isocyanide Complexes R2MCNR′ (M = Si, Ge, Sn; R = tBu, Ph; R′ = Me, tBu, Ph), Organometallics, 2013, 32, 6690–6700 CrossRef.
- H. Li, H. Feng, W. Sun, R. B. King and H. F. Schaefer, Extreme Metal Carbonyl Back Bonding in Cyclopentadienylthorium Carbonyls Generates Bridging C2O2 Ligands by Carbonyl Coupling, Inorg. Chem., 2013, 52, 6893–6904 CrossRef CAS PubMed.
- L. Foppa, C. Copéret and A. Comas-Vives, Increased Back-Bonding Explains Step-Edge Reactivity and Particle Size Effect for CO Activation on Ru Nanoparticles, J. Am. Chem. Soc., 2016, 138, 16655–16668 CrossRef CAS PubMed.
- S. W. Ragsdale, Life with Carbon Monoxide, Crit. Rev. Biochem. Mol. Biol., 2004, 39, 165–195 CrossRef CAS PubMed.
- J. D. Citron, J. E. Lyons and L. H. Sommer, Palladium-Catalyzed Reactions of Triorganosilicon Hydrides with Halocarbons, J. Org. Chem., 1968, 34, 638 CrossRef.
- M. Hudlicky, Catalytic Hydrogenolysis of Carbon-Fluorine Bonds: π Bond Participation Mechanism, J. Fluorine Chem., 1989, 44, 345–359 CrossRef CAS.
- A. S. Nair and T. Pradeep, Halocarbon Mineralization and Catalytic Destruction by Metal Nanoparticles, Curr. Sci., 2003, 84, 1560 CAS.
- K. J. Stanger and R. J. Angelici, Hydrodefluorination of Fluorobenzene Catalyzed by Rhodium Metal Prepared from [Rh(COD)2]+BF4− and Supported on SiO2 and Pd-SiO2, J. Mol. Catal. A: Chem., 2004, 207, 59–68 CrossRef CAS.
- H. R. Clark and M. M. Jones, Metal Ion Promoted Hydrolysis of Fluorocarbons, J. Am. Chem. Soc., 1969, 91, 4302 CrossRef CAS.
- E. Adisson, A. Deffieux, M. Fontanille and K. Bujadoux, Polymerization of Ethylene at High Temperature by Vanadium-Based Heterogeneous Ziegler—Natta Catalysts. II. Study of the Activation by Halocarbons, J. Polym. Sci., Part A: Polym. Chem., 1994, 32, 1033–1041 CrossRef CAS.
- J. L. Kiplinger and T. G. Richmond, Group IV Metallocene-Mediated Synthesis of Fluoroaromatics via Selective Defluorination of Saturated Perfluorocarbons, J. Am. Chem. Soc., 1996, 118, 1805 CrossRef CAS.
- R. Gupta and R. D. Young, A Review on the Halodefluorination of Aliphatic Fluorides, Synthesis, 2022, 54, 1671–1683 CrossRef CAS.
- J. Lehtomäki, I. Makkonen, M. A. Caro, A. Harju and O. Lopez-Acevedo, Orbital-Free Density Functional Theory Implementation with the Projector Augmented-Wave Method, J. Chem. Phys., 2014, 141, 234102 CrossRef PubMed.
- N. Romero, C. Glinsvad, A. Larsen, J. Enkovaara, S. Shende, V. Morozov and J. Mortensen, Design and Performance Characterization of Electronic Structure Calculations on Massively Parallel Supercomputers: A Case Study of GPAW on the Blue Gene/P Architecture, Concurrency and Computation: Practice and Experience, 2015, 27, 69–93 CrossRef.
- C. W. Bunn and E. R. Howells, Structures of Molecules and Crystals of Fluoro-Carbons, Nature, 1954, 549–551 CrossRef CAS.
- D. A. Dixon, Torsional Potential About the Central C–C Bond in Perfluoro-n-butane, J. Phys. Chem., 1992, 96, 3698–3701 CrossRef CAS.
- G. D. Smith, R. L. Jaffe and D. Y. Yoon, Conformational Characteristics of Poly(Oxymethylene) Based Upon Ab Initio Electronic Structure Calculations on Model Molecules, Macromolecules, 1994, 27, 3166–3173 CrossRef CAS.
- B. Albinsson and J. Michl, The Gauche, Ortho, and Anti Conformers of Perfluoro-N-Butane: Matrix-Isolation IR Spectra, J. Am. Chem. Soc., 1995, 117, 6378–6379 CrossRef CAS.
- U. Röthlisberger, K. Laasonen, M. L. Klein and M. Sprik, The Torsional Potential of Perfluoro n-Alkanes: A Density Functional Study, J. Chem. Phys., 1996, 104, 3692–3700 CrossRef.
- S. S. Jang, M. Blanco, W. A. G. Goddard III, G. Caldwell, R. B. Ross and F. Field, The Source of Helicity in Perfluorinated N-Alkanes, Macromolecules, 2003, 36, 5331–5341 CrossRef CAS.
- R. A. Cormanich, D. O'Hagan and M. Bühl, Hyperconjugation Is the Source of Helicity in Perfluorinated N-Alkanes, Angew. Chem., Int. Ed., 2017, 56, 7867–7870 CrossRef CAS PubMed.
- N. Díaz, F. Jiménez-Grávalos, D. Suárez, E. Francisco and Á. Martín-Pendás, Fluorine Conformational Effects Characterized by Energy Decomposition Analysis, Phys. Chem. Chem. Phys., 2019, 21, 25258–25275 RSC.
- F. A. Wiedmann and C. Wesdemiotis, Experimental Evidence for the Existence of Fluoroformic Acid and Its Ionized and Protonated Forms in the Gas Phase, J. Am. Chem. Soc., 1994, 116, 2481–2485 CrossRef CAS.
- K. Fukui, T. Yonezawa and H. Shingu, A Molecular Orbital Theory of Reactivity in Aromatic Hydrocarbons, J. Chem. Phys., 1952, 20, 722–725 CrossRef CAS.
- K. Fukui, Role of Frontier Orbitals in Chemical Reactions, Science, 1982, 218, 747 CrossRef CAS PubMed.
- R. G. Parr and W. Yang, Density Functional Approach to the Frontier-Electron Theory of Chemical Reactivity, J. Am. Chem. Soc., 1984, 106, 4049–4050 CrossRef CAS.
- D. A. McQuarrie, Statistical Mechanics, Harper & Row, 1975 Search PubMed.
- D. A. McQuarrie and J. D. Simon, Physcial Chemistry: A Molecular Approach, 1997 Search PubMed.
- C. R. P. Fulong, M. G. E. Guardian, D. S. Aga and T. R. Cook, A Self-Assembled Iron(II) Metallacage as a Trap for Per- and Polyfluoroalkyl Substances in Water, Inorg. Chem., 2020, 59, 6697–6708 CrossRef CAS PubMed.
- Q. Yu and J. Xu, Structure and Surface Properties of Fluorinated Organic-Inorganic Hybrid Films, J. Sol-Gel Sci. Technol., 2012, 61, 243–248 CrossRef CAS.
- H. Tatsuno and S. Ando, Structure and Dynamics of Perfluoroalkane/β-cyclodextrin Inclusion Compounds as Studied by Solid-State 19F MAS and 1H →19F CP/MAS NMR Spectroscopy, J. Phys. Chem. B, 2006, 110, 25751–25760 CrossRef CAS PubMed.
- S. Wallace, S. Lambrakos, A. Shabaev and L. Massa, Calculated IR Absorption Spectra for Perfluoroalkyl and Polyfluoroalkyl (PFAS) Molecules, Struct. Chem., 2021, 32, 899 CrossRef CAS.
- S. Wallace, S. G. Lambrakos, A. Shabaev and L. Massa, On Using DFT to Construct an IR Spectrum Database for PFAS Molecules, Struct. Chem., 2022, 33, 247–256 CrossRef CAS.
- T. J. Baker, R. G. Tonkyn, C. J. Thompson, M. K. Dunlap, P. G. K. van Groos, N. A. Thakur, M. J. Wilhelm, T. L. Myers and T. J. Johnson, An Infrared Spectral Database for Gas-Phase Quantitation of Volatile Per- and Polyfluoroalkyl Substances (PFAS), J. Quant. Spectrosc. Radiat. Transfer, 2023, 295, 108420 CrossRef CAS.
- E. C. Tuazon, W. G. Fateley and F. F. Bentley, Carbon-Fluorine Bond Stretchings in Some Acyclic Organic Molecules, Appl. Spectrosc., 1968, 42, 319 Search PubMed.
- H. Giegengack and D. Hinze, Investigations of the Structure of Thin Fluorocarbon Films by X-Ray Diffraction and Infrared Spectroscopy, Phys. Status Solidi A, 1971, 8, 513 CrossRef CAS.
- S. Liu, S. Gangopadhyay, G. Sreenivas, S. S. Ang and H. A. Naseem, Infrared Studies of Hydrogenated Amorphous Carbon (a-C:H) and Its Alloys (a-C:H,N,F), Phys. Rev. B: Condens. Matter Mater. Phys., 1997, 55, 13020 CrossRef CAS.
- H. Yokomichi and A. Masuda, Effect of Sputtering with Hydrogen Dilution on Fluorine Concentration of Low Hydrogen Content Fluorinated Amorphous Carbon Thin Films with Low Dielectric Constant, J. Appl. Phys., 1999, 86, 2468 CrossRef CAS.
- X. Wang, H. R. Harris, K. Bouldin, H. Temkin, S. Gangopadhyay, M. D. Strathman and M. West, Structural Properties of Fluorinated Amorphous Carbon Films, J. Appl. Phys., 2000, 87, 621–623 CrossRef CAS.
- I. T. Suydam and S. G. Boxer, Vibrational Stark Effects Calibrate the Sensitivity of Vibrational Probes for Electric Fields in Proteins, Biochemistry, 2003, 42, 12050–12055 CrossRef CAS PubMed.
- W. Zhang, M. Dubois, K. Guérin, P. Bonnet, H. Kharbache, F. Masin, A. P. Kharitonov and A. Hamwi, Effect of Curvature on C–F Bonding in Fluorinated Carbons: From Fullerene and Derivatives to Graphite, Phys. Chem. Chem. Phys., 2010, 12, 1388–1398 RSC.
- V. Y. Osipov, N. M. Romanov, K. Kogane, H. Touhara, Y. Hattori and K. Takai, Intrinsic Infrared Absorption for Carbon–Fluorine Bonding in Fluorinated Nanodiamond, Mendeleev Commun., 2020, 30, 84–87 CrossRef CAS.
- G. A. Picayo, B. D. Etz, S. Vyas and M. P. Jensen, Characterization of the ALSEP Process at Equilibrium: Speciation and Stoichiometry of the Extracted Complex, ACS Omega, 2020, 5, 8076–8089 CrossRef CAS PubMed.
- H.-P. Komsa and A. Pasquarello, Finite-Size Supercell Correction for Charged Defects at Surfaces and Interfaces, Phys. Rev. Lett., 2013, 110, 095505 CrossRef PubMed.
- F. Abild-Pedersen, J. Greeley, F. Studt, J. Rossmeisl, T. Munter, P. Moses, E. Skúlason, T. Bligaard and J. Nørskov, Scaling Properties of Adsorption Energies for Hydrogen-Containing Molecules on Transition-Metal Surfaces, Phys. Rev. Lett., 2007, 99, 16105 CrossRef CAS PubMed.
- J. K. Nørskov, F. Abild-Pedersen, F. Studt and T. Bligaard, Density Functional Theory in Surface Chemistry and Catalysis, Proc. Natl. Acad. Sci. U. S. A., 2011, 108, 937–943 CrossRef PubMed.
- J. K. Nørskov, J. Rossmeisl, A. Logadottir, L. Lindqvist, J. R. Kitchin, T. Bligaard and H. Jónsson, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892 CrossRef.
- T. Bligaard, J. Nørskov, S. Dahl, J. Matthiesen, C. Christensen and J. Sehested, The Brønsted–Evans–Polanyi Relation and the Volcano Curve in Heterogeneous Catalysis, J. Catal., 2004, 224, 206–217 CrossRef CAS.
- J. Cheng and P. Hu, Utilization of the Three-Dimensional Volcano Surface to Understand the Chemistry of Multiphase Systems in Heterogeneous Catalysis, J. Am. Chem. Soc., 2008, 130, 10868–10869 CrossRef CAS PubMed.
- J. K. Nørskov, T. Bligaard, J. Rossmeisl and C. H. Christensen, Towards the Computational Design of Solid Catalysts, Nat. Chem., 2009, 1, 37–46 CrossRef PubMed.
- A. B. Laursen, A. S. Varela, F. Dionigi, H. Fanchiu, C. Miller, O. L. Trinhammer, J. Rossmeisl and S. Dahl, Electrochemical Hydrogen Evolution: Sabatiers Principle and the Volcano Plot, J. Chem. Educ., 2012, 89, 1595–1599 CrossRef CAS.
- G. R. Jenness, M. A. Christiansen, S. Caratzoulas, D. G. Vlachos and R. J. Gorte, Site-Dependent Lewis Acidity of γ-Al2O3 and Its Impact on Ethanol Dehydration and Etherification, J. Phys. Chem. C, 2014, 118, 12899–12907 CrossRef CAS.
- S. Wang, V. Vorotnikov and D. G. Vlachos, A DFT Study of Furan Hydrogenation and Ring Opening on Pd(111), Green Chem., 2014, 16, 736–747 RSC.
- Z. Zhuang, S. A. Giles, J. Zheng, G. R. Jenness, S. Caratzoulas, D. G. Vlachos and Y. Yan, Nickel Supported on Nitrogen-Doped Carbon Nanotubes as Hydrogen Oxidation Reaction Catalyst in Alkaline Electrolyte, Nat. Commun., 2016, 7, 10141 CrossRef CAS PubMed.
- L. Rebollar, S. Intikhab, N. J. Oliveira, Y. Yan, B. Xu, I. T. McCrum, J. D. Snyder and M. H. Tang, “Beyond Adsorption” Descriptors in Hydrogen Electrocatalysis, ACS Catal., 2020, 10, 14747–14762 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, Error Estimates in Semi-Empirical Estimation Methods of Surface Reactions, J. Catal., 2013, 297, 202–216 CrossRef CAS.
- J. E. Sutton and D. G. Vlachos, A Theoretical and Computational Analysis of Linear Free Energy Relations for the Estimation of Activation Energies, ACS Catal., 2012, 2, 1624–1634 CrossRef CAS.
- C.-H. Lin, C.-L. Chen and J. Wang, Mechanistic Studies of Water–Gas-Shift Reaction on Transition Metals, J. Phys. Chem. C, 2011, 115, 18582–18588 CrossRef CAS.
- N. R. Peela, J. E. Sutton, I. C. Lee and D. G. Vlachos, Microkinetic Modeling of Ethane Total Oxidation on Pt, Ind. Eng. Chem. Res., 2014, 53, 10051–10058 CrossRef CAS.
- N. Kapur, J. Hyun, B. Shan, J. B. Nicholas and K. Cho, Ab Initio Study of CO Hydrogenation to Oxygenates on Reduced Rh Terraces and Stepped Surfaces, J. Phys. Chem. C, 2010, 114, 10171–10182 CrossRef CAS.
- H. A. Dabbagh, M. Zamani and B. H. Davis, Nanoscale Surface Study and Reactions Mechanism of 2-Butanol over the γ-Alumina (100) Surface and Nanochannel: A DFT Study, J. Mol. Catal. A: Chem., 2010, 333, 54–68 CrossRef CAS.
- S. V. Churakov, M. Iannuzzi and M. Parrinello, Ab Initio Study of Dehydroxylation–Carbonation Reaction on Brucite Surface, J. Phys. Chem. B, 2004, 108, 11567–11574 CrossRef CAS.
- K. A. Goulas, A. V. Mironenko, G. R. Jenness, T. Mazal and D. G. Vlachos, Fundamentals of C–O Bond Activation on Metal Oxide Catalysts, Nat. Catal., 2019, 2, 269–276 CrossRef CAS.
- S. Li, X. Lu, W. Guo, H. Zhu, M. Li, L. Zhao, Y. Li and H. Shan, Formaldehyde Oxidation on the Pt/TiO2(101) Surface: A DFT Investigation, J. Organomet. Chem., 2012, 704, 38–48 CrossRef CAS.
- S. M. Mitchell, M. Ahmad, A. L. Teel and R. J. Watts, Degradation of Perfluorooctanoic Acid by Reactive Species Generated Through Catalyzed H2O2 Propagation Reactions, Environ. Sci. Technol. Lett., 2013, 1, 117–121 CrossRef.
- K. H. Kucharzyk, R. Darlington, M. Benotti, R. Deeb and E. Hawley, Novel Treatment Technologies for PFAS Compounds: A Critical Review, J. Environ. Manage., 2017, 204, 757–764 CrossRef CAS PubMed.
- A. C. Parenky, N. G. de Souza, P. Asgari, J. Jeon, M. N. Nadagouda and H. Choi, Removal of Perfluorooctanesulfonic Acid in Water by Combining Zerovalent Iron Particles with Common Oxidants, Environ. Eng. Sci., 2020, 37, 472–481 CrossRef CAS.
- J. Zhang, H. Pang, S. Gray, S. Ma, Z. Xie and L. Gao, PFAS Removal from Wastewater by In-Situ Formed Ferric Nanoparticles: Solid Phase Loading and Removal Efficiency, J. Environ. Chem. Eng., 2021, 9, 105452 CrossRef CAS.
- Y. Qi, H. Cao, W. Pan, C. Wang and Y. Liang, The Role of Dissolved Organic Matter during Per- and Polyfluorinated Substance (PFAS) Adsorption, Degradation, and Plant Uptake: A Review, J. Hazard. Mater., 2022, 436, 129139 CrossRef CAS PubMed.
- M. Hvizdak, S. E. Kandel, H. M. Work, E. G. Gracey, R. L. McCullough and J. N. Lampe, Per- and Polyfluoroalkyl Substances (PFAS) Inhibit Cytochrome P450 CYP3A7 Through Direct Coordination to the Heme Iron and Water Displacement, J. Inorg. Biochem., 2023, 240, 112120 CrossRef CAS PubMed.
- Y. Kang, Z. Guo, H. Ma, H. Wu and J. Zhang, Enhanced Removal of Perfluorooctanoic Acid (PFOA) and Perfluorooctane Sulfonate (PFOS) in Constructed Wetlands: Iron Cycling and Microbial Mechanisms, ACS ES&T Water, 2023, 3, 287–297 Search PubMed.
- P. E. Blöchl, Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1994, 50, 17953–17979 CrossRef PubMed.
- GPAW PDOS Projection, https://wiki.fysik.dtu.dk/gpaw/tutorialsexercises/electronic/pdos/pdos.html.
- J. Enkovaara, C. Rostgaard, J. J. Mortensen, J. Chen, M. Dułak, L. Ferrighi, J. Gavnholt, C. Glinsvad, V. Haikola, H. a. Hansen, H. H. Kristoffersen, M. Kuisma, a. H. Larsen, L. Lehtovaara, M. Ljungberg, O. Lopez-Acevedo, P. G. Moses, J. Ojanen, T. Olsen, V. Petzold, N. a. Romero, J. Stausholm-Møller, M. Strange, G. a. Tritsaris, M. Vanin, M. Walter, B. Hammer, H. Häkkinen, G. K. H. Madsen, R. M. Nieminen, J. K. Nørskov, M. Puska, T. T. Rantala, J. Schiøtz, K. S. Thygesen and K. W. Jacobsen, Electronic Structure Calculations with GPAW: A Real-Space Implementation of the Projector Augmented-Wave Method, J. Phys.: Condens. Matter, 2010, 22, 253202–253226 CrossRef CAS PubMed.
- A. H. Larsen, J. J. Mortensen, J. Blomqvist, I. E. Castelli, R. Christensen, M. Dułak, J. Friis, M. N. Groves, B. Hammer, C. Hargus, E. D. Hermes, P. C. Jennings, P. B. Jensen, J. Kermode, J. R. Kitchin, E. L. Kolsbjerg, J. Kubal, K. Kaasbjerg, S. Lysgaard, J. B. Maronsson, T. Maxson, T. Olsen, L. Pastewka, A. Peterson, C. Rostgaard, J. Schiøtz, O. Schütt, M. Strange, K. S. Thygesen, T. Vegge, L. Vilhelmsen, M. Walter, Z. Zeng and K. W. Jacobsen, The Atomic Simulation Environment—A Python Library for Working with Atoms, J. Phys.: Condens. Matter, 2017, 29, 273002 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Chemical Accuracy for the Van Der Waals Density Functional, J. Phys.: Condens. Matter, 2010, 22, 022201 CrossRef PubMed.
- J. Klimeš, D. R. Bowler and A. Michaelides, Van Der Waals Density Functionals Applied to Solids, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 83, 1–13 CrossRef.
- J. Mortensen, L. Hansen and K. Jacobsen, Real-Space Grid Implementation of the Projector Augmented Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 035109 CrossRef.
- G. Kresse, From Ultrasoft Pseudopotentials to the Projector Augmented-Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 1999, 59, 1758–1775 CrossRef CAS.
- E. R. Davidson, in Matrix Eigenvector Methods, ed. G. H. F. Diercksen and S. Wilson, Springer, Netherlands, 1983, vol. 113, pp. 95–113 Search PubMed.
- A. H. Larsen, M. Vanin, J. J. Mortensen, K. S. Thygesen and K. W. Jacobsen, Localized Atomic Basis Set in the Projector Augmented Wave Method, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 195112 CrossRef.
- E. Briggs, D. Sullivan and J. Bernholc, Real-Space Multigrid-Based Approach to Large-Scale Electronic Structure Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 14362–14375 CrossRef CAS PubMed.
- H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B: Solid State, 1976, 13, 5188–5192 CrossRef.
- D. C. Liu and J. Nocedal, On the Limited Memory BFGS Method for Large Scale Optimization, Mathematical Programming, 1989, 45, 503–528 CrossRef.
- E. Bitzek, P. Koskinen, F. Gähler, M. Moseler and P. Gumbsch, Structural Relaxation Made Simple, Phys. Rev. Lett., 2006, 97, 1–4 CrossRef PubMed.
- S. F. Boys and F. Bernardi, The Calculation of Small Molecular Interactions by the Differences of Separate Total Energies. Some Procedures with Reduced Errors, Mol. Phys., 1970, 19, 553–566 CrossRef CAS.
- D. Porezag and M. R. Pederson, Infrared Intensities and Raman-Scattering Activities within Density-Functional Theory, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 7830–7836 CrossRef CAS PubMed.
- T. Hughbanks and R. Hoffmann, Chains of Trans-Edge-Sharing Molybdenum Octahedra: Metal-Metal Bonding in Extended Systems, J. Am. Chem. Soc., 1983, 105, 3528–3537 CrossRef CAS.
- G. R. Jenness and J. R. Schmidt, Unraveling the Role of Metal–Support Interactions in Heterogeneous Catalysis: Oxygenate Selectivity in Fischer–Tropsch Synthesis, ACS Catal., 2013, 3, 2881–2890 CrossRef CAS.
- G. R. Jenness, W. Wan, J. G. Chen and D. G. Vlachos, Reaction Pathways and Intermediates in Selective Ring Opening of Biomass-Derived Heterocyclic Compounds by Iridium, ACS Catal., 2016, 6, 7002–7009 CrossRef CAS.
- G. R. Jenness, J. Seiter and M. K. Shukla, DFT Investigation on the Adsorption of Munition Compounds on α-Fe2O3: Similarity and Differences with α-Al2O3, Phys. Chem. Chem. Phys., 2018, 20, 18850–18861 RSC.
- J. Korchowiec, H. Gerwens and K. Jug, Relaxed Fukui Function Indices and Their Application to Chemical Reactivity Problems, Chem. Phys. Lett., 1994, 222, 58–64 CrossRef CAS.
- R. Balawender and L. Komorowski, Atomic Fukui Function Indices and Local Softness Ab Initio, J. Chem. Phys., 1998, 109, 5203–5211 CrossRef CAS.
- H. Chermette, Chemical Reactivity Indexes in Density Functional Theory, J. Comput. Chem., 1999, 20, 129–154 CrossRef CAS.
- P. W. Ayers, R. C. Morrison and R. K. Roy, Variational Principles for Describing Chemical Reactions: Condensed Reactivity Indices, J. Chem. Phys., 2002, 116, 8731–8744 CrossRef CAS.
- G. Fitzgerald, On the Use of Fractional Charges for Computing Fukui Functions, Mol. Simul., 2008, 34, 931–936 CrossRef CAS.
- F. L. Hirshfeld, Bonded-Atom Fragments for Describing Molecular Charge Densities, Theor. Chim. Acta, 1977, 44, 129–138 CrossRef CAS.
- R. F. W. Bader, A Quantum Theory of Molecular Structure and Its Applications, Chem. Rev., 1991, 91, 893–928 CrossRef CAS.
- R. Bader, Atoms in Molecules: A Quantum Theory, Clarendon, 1994 Search PubMed.
- G. Henkelman, A. Arnaldsson and H. Jónsson, A Fast and Robust Algorithm for Bader Decomposition of Charge Density, Comput. Mater. Sci., 2006, 36, 354–360 CrossRef.
- E. Sanville, S. D. Kenny, R. Smith and G. Henkelman, Improved Grid-Based Algorithm for Bader Charge Allocation, J. Comput. Chem., 2007, 28, 899–908 CrossRef CAS PubMed.
- W. Tang, E. Sanville and G. Henkelman, A Grid-Based Bader Analysis Algorithm without Lattice Bias, J. Phys.: Condens. Matter, 2009, 21, 084204 CrossRef CAS PubMed.
- B. Hammer, Bond Activation at Monatomic Steps: NO Dissociation at Corrugated Ru(0001), Phys. Rev. Lett., 1999, 83, 3681–3684 CrossRef CAS.
- J. Nørskov, T. Bligaard, A. Logadottir, S. R. Bahn, L. B. Hansen, M. Bollinger, H. Bengaard, B. Hammer, Z. Sljivancanin, M. Mavrikakis, Y. Xu, S. Dahl and C. J. H. Jacobsen, Universality in Heterogeneous Catalysis, J. Catal., 2002, 209, 275–278 CrossRef.
- J. K. Nørskov, T. Bligaard, B. Hvolbaek, F. Abild-Pedersen, I. Chorkendorff and C. H. Christensen, The Nature of the Active Site in Heterogeneous Metal Catalysis, Chem. Soc. Rev., 2008, 37, 2163–2171 RSC.
- M. Salciccioli, Y. Chen and D. G. Vlachos, Density Functional Theory-Derived Group Additivity and Linear Scaling Methods for Prediction of Oxygenate Stability on Metal Catalysts: Adsorption of Open-Ring Alcohol and Polyol Dehydrogenation Intermediates on Pt-Based Metals, J. Phys. Chem. C, 2010, 114, 20155–20166 CrossRef CAS.
- J. L. C. Fajín, M. N. D. S. Cordeiro, F. Illas and J. R. B. Gomes, Descriptors Controlling the Catalytic Activity of Metallic Surfaces Toward Water Splitting, J. Catal., 2010, 276, 92–100 CrossRef.
- A. Vojvodic, F. Calle-Vallejo, W. Guo, S. Wang, A. Toftelund, F. Studt, J. I. Martínez, J. Shen, I. C. Man, J. Rossmeisl, T. Bligaard, J. K. Noørskov, F. Abild-Pedersen, J. K. Nørskov and F. Abild-Pedersen, On the Behavior of Brønsted-Evans-Polanyi Relations for Transition Metal Oxides, J. Chem. Phys., 2011, 134, 244509 CrossRef CAS PubMed.
- I. C. Man, H.-Y. Su, F. Calle-Vallejo, H. a. Hansen, J. I. Martinez, N. G. Inoglu, J. Kitchin, T. F. Jaramillo, J. K. Norskov and J. Rossmeisl, Universality in Oxygen Evolution Electrocatalysis on Oxide Surfaces, ChemCatChem, 2011, 3, 1159–1165 CrossRef CAS.
- S. Wang, V. Vorotnikov, J. E. Sutton and D. G. Vlachos, Brønsted–Evans–Polanyi and Transition State Scaling Relations of Furan Derivatives on Pd (111) and Their Relation to Those of Small Molecules, ACS Catal., 2014, 4, 604–612 CrossRef CAS.
- V. Vorotnikov and D. G. Vlachos, Group Additivity and Modified Linear Scaling Relations for Estimating Surface Thermochemistry on Transition Metal Surfaces: Application to Furanics, J. Phys. Chem. C, 2015, 119, 10417 CrossRef CAS.
- G. H. Gu and D. G. Vlachos, Group Additivity for Thermochemical Property Estimation of Lignin Monomers on Pt(111), J. Phys. Chem. C, 2016, 120, 19234–19241 CrossRef CAS.
- P. Deshlahra and E. Iglesia, Reactivity and Selectivity Descriptors for the Activation of C–H Bonds in Hydrocarbons and Oxygenates on Metal Oxides, J. Phys. Chem. C, 2016, 120, 16744 CrossRef.
- W. A. Harrison, Electronic Structure and the Properties of Solids, Dover Publications Inc., 1989 Search PubMed.
- J. Nørskov, Chemisorption on Metal Surfaces, Rep. Prog. Phys., 1990, 53, 1253 CrossRef.
- B. Hammer and J. K. Norskov, Electronic Factors Determining the Reactivity of Metal Surfaces, Surf. Sci., 1995, 343, 211–220 CrossRef CAS.
- A. Ruban, B. Hammer, P. Stoltze, H. L. Skriver and J. K. Nørskov, Surface Electronic Structure and Reactivity of Transition and Noble, J. Mol. Catal. A: Chem., 1997, 421–429 CrossRef CAS.
- N. Ínoglu and J. Kitchin, Simple Model Explaining and Predicting Coverage-Dependent Atomic Adsorption Energies on Transition Metal Surfaces, Phys. Rev. B: Condens. Matter Mater. Phys., 2010, 82, 1–5 CrossRef.
- D. a Hansgen, L. M. Thomanek, J. G. Chen and D. G. Vlachos, Experimental and Theoretical Studies of Ammonia Decomposition Activity on Fe-Pt, Co-Pt, and Cu-Pt Bimetallic Surfaces, J. Chem. Phys., 2011, 134, 184701 CrossRef PubMed.
- Y.-L. Lee, J. Kleis, J. Rossmeisl, Y. Shao-Horn and D. Morgan, Prediction of Solid Oxide Fuel Cell Cathode Activity with First-Principles Descriptors, Energy Environ. Sci., 2011, 4, 3966 RSC.
- Z. Xu and J. R. Kitchin, Relating the Electronic Structure and Reactivity of the 3D Transition Metal Monoxide Surfaces, Catal. Commun., 2014, 52, 60–64 CrossRef CAS.
- A. M. Deml, V. Stevanovic, C. L. Muhich, C. B. Musgrave and R. O'Hayre, Oxide Enthalpy of Formation and Band Gap Energy as Accurate Descriptors of Oxygen Vacancy Formation Energetics, Energy Environ. Sci., 2014, 7, 1996 RSC.
- F. Calle-Vallejo, J. I. Martínez, J. M. García-Lastra, P. Sautet and D. Loffreda, Fast Prediction of Adsorption Properties for Platinum Nanocatalysts with Generalized Coordination Numbers, Angew. Chem., Int. Ed., 2014, 53, 8316–8319 CrossRef CAS PubMed.
- F. Calle-Vallejo, O. Diaz-Morales, M. Kolb and M. T. Koper, Why Is Bulk Thermochemistry a Good Descriptor for the Electrocatalytic Activity of Transition Metal Oxides?, ACS Catal., 2014, 2014, 869 Search PubMed.
- Z. Xu and J. R. Kitchin, Relationships between the Surface Electronic and Chemical Properties of Doped 4D and 5D Late Transition Metal Dioxides, J. Chem. Phys., 2015, 142, 104703 CrossRef PubMed.
- F. Calle-Vallejo, J. Tymoczko, V. Colic, Q. H. Vu, M. D. Pohl, K. Morgenstern, D. Loffreda, P. Sautet, W. Schuhmann and A. S. Bandarenka, Finding Optimal Surface Sites on Heterogeneous Catalysts by Counting Nearest Neighbors, Science, 2015, 350, 185 CrossRef CAS PubMed.
- S. Dutta, A. Bohre, W. Zheng, G. R. Jenness, M. Núñez, B. Saha and D. G. Vlachos, Solventless C–C Coupling of Low Carbon Furanics to High Carbon Fuel Precursors Using an Improved Graphene Oxide Carbocatalyst, ACS Catal., 2017, 7, 3905–3915 CrossRef CAS.
- Z. Zhuang, S. A. Giles, G. R. Jenness, R. Abbasi, X. Chen, B. Wang, D. G. Vlachos and Y. Yan, Oxygen Evolution on Iron Oxide Nanoparticles: The Impact of Crystallinity and Size on the Overpotential, J. Electrochem. Soc., 2021, 168, 034518 CrossRef CAS.
- W. P. Krekelberg, J. Greeley and M. Mavrikakis, Atomic and Molecular Adsorption on Ir(111), J. Phys. Chem. B, 2003, 108, 987–994 CrossRef.
- A. a. Gokhale, S. Kandoi, J. P. Greeley, M. Mavrikakis and J. a. Dumesic, Molecular-Level Descriptions of Surface Chemistry in Kinetic Models Using Density Functional Theory, Chem. Eng. Sci., 2004, 59, 4679–4691 CrossRef CAS.
- Y. Wang, J. H. Montoya, C. Tsai, M. S. Ahlquist, J. K. Nørskov and F. Studt, Scaling Relationships for Binding Energies of Transition Metal Complexes, Catal. Lett., 2016, 146, 304–308 CrossRef CAS.
- P. V. Kumar and D. J. Norris, Tailoring Energy Transfer from Hot Electrons to Adsorbate Vibrations for Plasmon-Enhanced Catalysis, ACS Catal., 2017, 7, 8343–8350 CrossRef CAS.
- R. Réocreux, E. C. H. Sykes, A. Michaelides and M. Stamatakis, Stick or Spill? Scaling Relationships for the Binding Energies of Adsorbates on Single-Atom Alloy Catalysts, J. Phys. Chem. Lett., 2022, 13, 7314–7319 CrossRef PubMed.
- X. Liao, R. Lu, L. Xia, Q. Liu, H. Wang, K. Zhao, Z. Wang and Y. Zhao, Density Functional Theory for Electrocatalysis, Energy Environ. Mater., 2022, 5, 157–185 CrossRef CAS.
- J. Greeley, A. A. Gokhale, J. Kreuser, J. A. Dumesic, H. Topsøe, N.-Y. Topsøe and M. Mavrikakis, CO Vibrational Frequencies on Methanol Synthesis Catalysts: A DFT Study, J. Catal., 2003, 213, 63–72 CrossRef CAS.
- C. Popa, M. V. Ganduglia-Pirovano and J. Sauer, Periodic Density Functional Theory Study of VOn Species Supported on the CeO2(111) Surface, J. Phys. Chem. C, 2011, 115, 7399–7410 CrossRef CAS.
- A. Milo, E. N. Bess and M. S. Sigman, Interrogating Selectivity in Catalysis Using Molecular Vibrations, Nature, 2014, 507, 210–214 CrossRef CAS PubMed.
- C. Qian, Y. Wang and Z. Wang, A DFT Study of Enhancement of H2O Activation in Vibrational Excitation, Inorg. Chim. Acta, 2021, 514, 119980 CrossRef CAS.
- C. Jia, Q. Wang, J. Yang, K. Ye, X. Li, W. Zhong, H. Shen, E. Sharman, Y. Luo and J. Jiang, Toward Rational Design of Dual-Metal-Site Catalysts: Catalytic Descriptor Exploration, ACS Catal., 2022, 12, 3420–3429 CrossRef CAS.
- B. D. Dunnington and J. R. Schmidt, Molecular Bonding-Based Descriptors for Surface Adsorption and Reactivity, J. Catal., 2015, 324, 50–58 CrossRef CAS.
- W. T. Hong, K. A. Stoerzinger, Y. L. Lee, L. Giordano, A. Grimaud, A. M. Johnson, J. Hwang, E. J. Crumlin, W. Yang and Y. Shao-Horn, Charge-Transfer-Energy-Dependent Oxygen Evolution Reaction Mechanisms for Perovskite Oxides, Energy Environ. Sci., 2017, 10, 2190–2200 RSC.
- W. Zhong, Y. Qiu, H. Shen, X. Wang, J. Yuan, C. Jia, S. Bi and J. Jiang, Electronic Spin Moment as a Catalytic Descriptor for Fe Single-Atom Catalysts Supported on C2N, J. Am. Chem. Soc., 2021, 143, 4405–4413 CrossRef CAS PubMed.
- P. Hutchison, R. E. Warburton, Y. Surendranath and S. Hammes-Schiffer, Correlation between Electronic Descriptor and Proton-Coupled Electron Transfer Thermodynamics in Doped Graphite-Conjugated Catalysts, J. Phys. Chem. Lett., 2022, 13, 11216–11222 CrossRef CAS PubMed.
- M. Zafari, M. Umer, A. S. Nissimagoudar, R. Anand, M. Ha, S. Umer, G. Lee and K. S. Kim, Unveiling the Role of Charge Transfer in Enhanced Electrochemical Nitrogen Fixation at Single-Atom Catalysts on BX Sheets (X = As, P, Sb), J. Phys. Chem. Lett., 2022, 13, 4530–4537 CrossRef CAS PubMed.
- Z. Qu, F. Sun, X. Pi, H. Wang, X. Li, J. Gao and G. Zhao, Revealing the Activity Origin of Oxygen-Doped Amorphous Carbon Material for SO2 Catalytic Oxidation: A Descriptor Considering Dynamic Electron Transfer during O2 Activation, Carbon, 2023, 201, 37–48 CrossRef CAS.
- R. Jinnouchi and R. Asahi, Predicting Catalytic Activity of Nanoparticles by a DFT-Aided Machine-Learning Algorithm, J. Phys. Chem. Lett., 2017, 8, 4279–4283 CrossRef CAS PubMed.
- G. H. Gu, P. Plechac and D. G. Vlachos, Thermochemistry of Gas-Phase and Surface Species via Lasso-Assisted Subgraph Selection, React. Chem. Eng., 2018, 3, 454–466 RSC.
- S. Back, J. Yoon, N. Tian, W. Zhong, K. Tran and Z. W. Ulissi, Convolutional Neural Network of Atomic Surface Structures to Predict Binding Energies for High-Throughput Screening of Catalysts, J. Phys. Chem. Lett., 2019, 10, 4401–4408 CrossRef CAS PubMed.
- S. Pablo-García, R. García-Muelas, A. Sabadell-Rendón and N. López, Dimensionality Reduction of Complex Reaction Networks in Heterogeneous Catalysis: From Linear-Scaling Relationships to Statistical Learning Techniques, Comput. Mol. Sci., 2021, 11, e1540 CrossRef.
Footnote |
| † Electronic supplementary information (ESI) available: Numerical data for all figures in the current study, figures showing initial and final states, figures showing charge density differences. See DOI: https://doi.org/10.1039/d3va00281k |
| This journal is © The Royal Society of Chemistry 2024 |