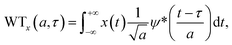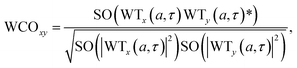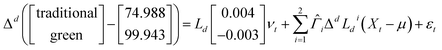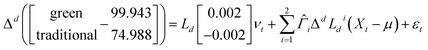Open Access Article
Open Access ArticleThe financial market wants to believe in European sustainability. Time trends and persistence analysis of green vs. brown bond yields
Manuel
Monge
 *
*
Faculty of Law, Business and Government, Universidad Francisco de Vitoria, Madrid, 28223, Spain. E-mail: manuel.monge@ufv.es
First published on 23rd August 2024
Abstract
Green bonds are becoming a popular investment option as a result of growing investor awareness of social and environmental issues. Green bonds are financial securities used to fund initiatives aimed at mitigating the effects of global industrialization on the environment and climate change, as well as initiatives that make use of cutting-edge technology. For the SDGs to be achieved, this kind of financial product must be successfully promoted. Therefore, the objective of this research work is to statistically analyze the characteristics of green and brown bond yields. In addition, to ascertain how the two yields relate to one another and how they change over time.
Environmental significanceGreen bonds are becoming a popular investment option as a result of growing investor awareness of social and environmental issues. Green bonds are financial securities used to fund initiatives aimed at mitigating the effects of global industrialization on the environment and climate change, as well as initiatives that make use of cutting-edge technology. For the SDGs to be achieved, this kind of financial product must be successfully promoted. Therefore, the objective of this research work is to statistically analyze the characteristics of green and brown bond yields. In addition, to ascertain how the two yields relate to one another and how they change over time. |
1. Introduction
Research on ESG has been conducted for a long time, though not always with the term ESG in mind. Over 60 years have been dedicated to researching themes like corporate environmental responsibility (CER) and corporate social responsibility (CSR).Since the 1990s, a large number of studies have been published, the majority of which (perhaps as a result of increased data availability) have focused on the empirical links between corporate social/environmental responsibility and corporate financial performance (CFP).1 Most studies conclude that there is a beneficial correlation between CFP and ESG. Among other things, market stock prices and accounting metrics like return on assets are used to quantify the relationship.2
Green and conventional bonds represent two distinct approaches to financing within the broader financial market, each aligned with different environmental and economic objectives.
A green bond is any fixed income instrument whose sole purpose is to finance or refinance, in whole or in part, new and/or existing green projects. Green bonds are securities whose proceeds are used to finance projects that address the environment or climate change, as well as projects that use cutting-edge technology to reduce the negative consequences of global industrialization.
These securities began to be used by governmental or supranational development banks to finance and promote initiatives related to the environment or climate change. In recent years, governments are using this asset class, and an increasing number of corporations have begun to issue green bonds as well.
This type of financial products tries to mobilize capital from the financial market with the objective of meeting the challenge of climate change.3
There are many reasons for the existence of this type of financial product:
(1) Financing sustainable projects (e.g. water management, clean transportation, sustainable agriculture, energy efficiency, renewable energy, among others). This aids in raising money from the public and commercial sectors to combat environmental degradation and climate change.4
(2) Growth in investor interest in sustainability, driven by factors such as climate-related risks, regulatory pressures and a shift in consumer and corporate values toward environmental responsibility.
(3) Investors align their portfolios with a low-carbon economy, potentially reducing exposure to assets that might lose value as the world transitions away from fossil fuels.
(4) Issuers of green bonds are frequently bound by rules like the Climate Bonds Standard or the Green Bond Principles, which guarantee responsibility, transparency, and the use of proceeds for projects that improve the environment. For investors, this offers a level of legitimacy and trust.
Thus, green bonds have a similar structure to conventional bonds, with the exception that the “use of proceeds” will be used only to finance or refinance green projects.4
In contrast, conventional (or brown) bonds are debt instruments used to finance projects and industries that do not take into account the green deal and climate change. Industries related to fossil fuels or other environmentally damaging activities.
Understanding the broader financial market's involvement in addressing environmental sustainability and climate change requires an understanding of both green and brown bonds. They mirror the changing dynamics of the market as it strikes a balance between environmental stewardship and economic prosperity. The burgeoning issuance of green bonds and the mounting mistrust of brown bonds signify a paradigm shift in the way capital markets are addressing environmental concerns on a worldwide scale.
This change is a part of a wider trend that is impacting capital flows more and more by incorporating ESG factors into investment decisions. As green bonds become more popular, they not only help finance the shift to a sustainable economy but also indicate that the way financial markets evaluate risk, value, and long-term growth prospects is changing.
Hacıömeroğlu et al.5 states that by 2025, the worldwide market for ESG (environmental, social, and governance) assets will be valued at over $53 trillion, or over one-third of all assets under management. Zhang et al.6 suggest that the growing market demand for ethical investments indicates the existence of investors who hope to influence societal change via their financial decisions.
Even though this segment has seen a lot of great advances compared to conventional ones,7–9 not all of them have been viewed favorably.
Successful promotion of this type of financial product is very important for the achievement of the SDGs. According to Bhutta et al.,10 their issuance carries associated costs and investors consider their profitability due to their risky nature.
In addition, the “true greenness” of green bonds is frequently disputed, and accusations of greenwashing are common.11–13 Immel et al.13 argue that one factor contributing to this uncertainty is the fact that green bonds often come with a credit rating, but they only optionally offer additional environmental, social, and governance (ESG) ratings.
Following Maul and Schiereck,14 we explicitly evaluate the bond pricing literature since bond pricing is more complex and technical due to the wide diversity of bonds (various coupon type, maturity, payment rank, callability, etc.). There are differences between green and conventional bonds with similar characteristics and different performance outcomes.15–24
Numerous research works examining the performance of green bonds have been released, exhibiting varying findings and methods of study. Based on a range of bond indices25 and primary market yields13,24,26 the majority of research indicate a negative green premium. Studies on the yield differentials between conventional and green bonds in the secondary market23,24 show conflicting results, indicating that a premium is only observed in certain circumstances (e.g., institutional and certified green issuers). According to some, the reason why green bonds have lower yields than conventional bonds is because investors have a pro-environmental mentality26 and because certain issuers have stronger ESG credibility, which influences demand preferences.24
On the other hand, Pham and Nguyen27 investigate how well green bonds perform in uncertain circumstances. By examining the impact of stock, oil, and economic policy uncertainty (EPU) on green bond returns, their research illuminates the diversification potential of green bond markets. Between October 2014 and November 2020, they employed three uncertainty indices in addition to four significant green bond indices. The authors discover that at uncertain times, there is a state-dependent and time-varying relationship between green bonds. That similar thesis is asserted by Abakah et al.28 It is suggested that investors should diversify their portfolios to reduce risk and participate in environmentally friendly projects thanks to the nascent and expanding green bond market.
A sizable body of research has now been written analyzing the behavior of green versus brown (conventional) assets. The majority of research looks at these two asset classes' ex post returns or co-movement and price spillover.29–44
One significant question that the studies mentioned above did not address is how persistent green stock prices are in comparison to brown stock prices.
To the best of our knowledge, the quantitative analysis and the fractional techniques that we present to analyze the yields of green and conventional bonds in this study provides several contributions not found in the existing literature.
First it applies long memory techniques to provide evidence on the statistical properties (more specifically, mean reversion and persistence) of the conventional bond yields and green bond yields. This analysis is important for many reasons: (1) it helps us to understand whether the series has a short or long memory behavior. This is related to the persistence in the data and how reliable it is for future prediction. (2) We can also determine more precisely whether the data are stationary or non-stationary and how much we need to differ the data from a fractional point of view to get the main characteristics of the data behavior to be constant over time in the period we are analyzing. (3) Finally, we will be able to understand how the time series behaves in the face of an exogenous shock and know if it tends to revert to the mean, or on the contrary needs additional measures to return to its original trend.
From a multivariate analysis, we started by performing causality tests. We use causality tests to be able to determine whether one variable can be useful and be used to predict another. If the relationship between the variables we analyze is not useful, we would say that the relationship is spurious.
In this work we calculate two types of tests: the first is the VAR-based Granger-causality test based on the time domain. With this technique we will be able to determine whether the relationship between the two variables is causal, and in a second step, with the Breitung and Candelon45 test based on the frequency domain we will be able to say whether the relationship is statistically significant in the short, medium or long term.
Additionally, we use the fractional cointegration test in the analysis of two time series because it allows us to identify long-run equilibrium relationships between series that have long memory or persistence, better capturing complex dynamics and slow adjustments that might not be detected by traditional methods. This is crucial when series exhibit fractional integration behavior, offering a more accurate and flexible analysis.
Finally, we carried out a wavelet analysis, using the Continuous Wavelet Transform (CWT). This allows us to decompose and analyze the series at different time scales simultaneously, capturing both local (short term) and global (long term) relationships. This is particularly useful for identifying patterns, trends, and complex dynamic relationships that vary over time and frequency, which is not possible with traditional methods.
The structure of this paper is as follows. Section 2 describes the data used for our study. Section 3 explains the methodologies used to carry out the research. The results are discussed in Section 4. Finally, the conclusions are found in Section 5.
2. Data
The database analyzed in this research paper was obtained from Thomson Reuters Eikon, a widely recognized financial data platform. To analyze the green bonds returns in Europe we have selected the iBoxx Global Green Bonds Select Index, to represent the performance of green bonds in Europe. The bonds included in this index are classified as green bonds according to the Climate Bonds Initiative (CBI) Green Bonds Standard. This standard ensures that the proceeds of these bonds are used for projects that have positive environmental benefits, such as renewable energy, energy efficiency, and pollution reduction. The index includes investment grade and high yield government, sub-sovereign and corporate debt. The bonds are denominated in Euros, reflecting the European focus of the study.To represent the performance of conventional (brown) bonds in Europe, we use the SPDR Bloomberg Euro Aggregate Bond index. This index tracks the performance of the Bloomberg Euro Aggregate Bond Index, which includes a broad range of fixed-rate, investment grade bonds. The bonds in this index are issued by governments and corporations, providing a comprehensive view of the conventional bond market. Like the green bonds, these bonds are also denominated in Euros, ensuring consistency in the comparison between green and conventional bonds.
The selection criteria, emphasizing investment grade and high yield bonds, provide a comprehensive view of how different types of bonds behave in response to market developments, offering valuable insights for both financial markets and sustainable efforts.
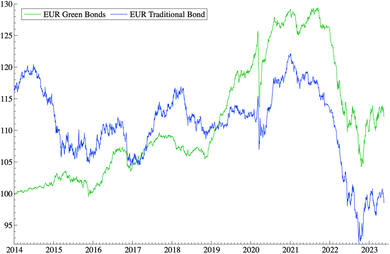
The time series analyzed in this manuscript are represented in Fig. 1.
This extended time frame allows for a thorough examination of the behavior of both green and brown bonds over various economic cycles, including periods of significant market stress such as the COVID-19 pandemic and the Russia–Ukraine conflict.
The dataset used is of daily frequency, which provides detailed insights into the day-to-day movements of bond yields, allowing for more precise statistical analysis.
3. Methodology
3.1. Unit roots
Statistics and econometrics use single or multi-equation regression models of time series with the objective to model variables and to understand the interrelations.46But before to use these types of models, it is important to understand the behavior of these time series. To be able to work with the series, the fundamental assumption is to conclude if the process follows a non-stationary I(1) behavior when it contains a unit root or if it is stationary I(0) when it does not.47
So, to determine the integration order of each time series we use standard unit root test. The best known and most widely used unit root test is the Dickey–Fuller test.48 If a non-systematic component in Dickey–Fuller models is autocorrelated, the Augmented Dickey–Fuller test is constructed.49 Many other tests have been considered due to the greater power, such as Phillips50 and Phillips and Perron51 in which a non-parametric estimate of spectral density ut of at the zero frequency has been used. The methodology based on Kwiatkowski et al.52 has been used to analyze the deterministic trend.
3.2. ARFIMA (p, d, q) model
Once we have tested the integration order of each time series by using standard unit root tests, we employ a more advanced methodology. Following the idea that was introduced by Adenstedt,53 Granger and Joyeux,54 Granger55,56 and Hosking,57 to achieve stationarity I(0), the number of differences does not necessarily have to be an integer value, since it can be any point on the real line and therefore fractional I(d).So, in order to make the time series stationary I(0), we differentiate the time series with a fractional number. This is an advanced procedure over unit root tests due to the lower power under fractional alternatives.58–60
Another feature of the I(d) models is to determine and capture the persistence of the observations. This is when observations are far apart in time but highly correlated.
The fractional integrated method that we use in this research paper is the ARFIMA (p, d, q) model where the mathematical notation is:
| (1 − L)dxt = ut, t = 1, 2, | (1) |
From eqn (1), the polynomial (1 − L)d is expressed in terms of binomial expansion where for all real d, xt depends not only on a finite number of past observations but also on the whole of its history. So a higher value of d implies a higher level of association between the observations of the series.
Depending on the value of the parameter d, we can differentiate between various cases.
Table 1 summarizes the different results of d: Although there are several procedures for estimating the degree of long-memory and fractional integration,61–67 we follow Sowell64 maximum likelihood approach and use the Akaike information criterion (AIC)68 and the Bayesian information criterion (BIC)69 to select the most appropriate ARFIMA model.
| d = 0 | x t process is short memory |
| d > 0 | x t process is long memory |
| d < 0.5 | x t is covariance stationary |
| d ≥ 0.5 | x t is nonstationary |
| d < 1 | x t is mean reverting |
| d ≥ 1 | x t is not mean reverting |
3.3. Breitung–Candelon causality test
The causality test proposed by Breitung and Candelon45 contribute to provide an idea about whether the relationship between both time series is temporary or permanent.70–72 This test has an advantage over other commonly used causality tests in that it can interpret Granger-causality across different frequency domains. This is accomplished by categorizing the spectral association that exists between two time series, one of which is based on the bivariate spectral-density matrix and the other on coherence. The categorization then yields a total of immediate forward and backward causality mechanisms.For specification, the interdependence between two variables x and y can be captured by the following VAR(p) model:45
| xt = α1xt−1 + αpxt−p + β1yt−1 + … + βpyt−p + β1t | (2) |
The null hypothesis, H0: My→x(w) = 0, as tested by Geweke,73 matches the null hypothesis of linear restriction given as:
| R(w)β = 0 | (3) |
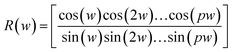 | (4) |
The F-statistics for the null hypothesis in eqn (3) has an approximated distribution of F(2, T − 2P) for Fw ∈ (0, π). Furthermore, the frequency-based Granger causality test is often examined within the framework of cointegration. Therefore, Breitung and Candelon45 substitute xt in eqn (2) for Δxt. Thus, the presence of cointegration between the series implies that the zero-frequency causality has similar notion with the main long-term causality. On the other hand, if in the stationary no long-run relationship holds, the evidence of causal relationship at a low frequency suggests that the frequency element of the variable under consideration can be predicted by an additional variable.
3.4. FCVAR model
Following Johansen and Nielsen,74 we use their multivariate Fractional Cointegrated VAR (FCVAR) model to check the relationship of the variables in the long term. The FCVAR model is notated in the next equation: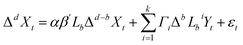 | (5) |
3.5. Wavelet analysis
Wavelet methodology allows time series to be analysed in the time-frequency domain. Thus, for this research article we use two tools named wavelet coherency and wavelet phase difference, because the requirement of stationarity is not necessary and studying the interaction in time and frequency domain of the time series reveals evidence of potential changes (structural changes).Furthermore, the most important information is hidden in the frequency content of the signal. So, as we know, we can define the time series as an aggregation of components operating on different frequencies.
Finally, if we follow the research carried out by Zhou,75 Podobnik and Stanley,76 Gu and Zhou77 and Jiang and Zhou78 we can conclude that misleading results will be found if we apply a typical cross-correlation to study statistical relationships between two multifractal time series.
The wavelet coherency plot represents the correlation of time series and helps us to identify hidden patterns and/or information in the time-frequency domain. The wavelet transform, represented by WTx(a,τ), of a time series x(t) obtained by projecting a mother wavelet ψ, is defined as:
Wavelet coherence helps us understand how one time series interacts with another. We can define this term as:
4. Empirical results
The first analysis that we carry out in this research paper is the unit root/stationarity test to analyze the conventional and green bonds prices in Europe from January 2, 2014 to May 18, 2023 in daily frequency. In data analysis this is very important as it allows a more consistent interpretation of the model parameters. A trend or seasonal variation can distort the results and lead to erroneous conclusions about the underlying relationships in the data. To do this analysis we perform the Augmented Dickey–Fuller (ADF) test, the Phillips Perron (PP) test and the Kwiatkowski–Phillips–Schmidt–Shin (KPSS) test. The results are displayed in Table 2.| ADF | PP | KPSS | |||||
|---|---|---|---|---|---|---|---|
| (i) | (ii) | (iii) | (ii) | (iii) | (ii) | (iii) | |
| Original data | |||||||
| EUR green bonds | 0.6839 | −1.2887 | −0.6909 | −1.328 | −0.8709 | 17.4615 | 1.8561 |
| EUR traditional bonds | −1.0548 | −0.9569 | −1.1784 | −1.0045 | −1.2162 | 2.5522 | 1.9069 |
The results suggest that both variables present a nonstationary I(1) behaviour. Therefore, the original series and the sub-samples present a trend that is not deterministic but stochastic. This means that deviations from the mean are not automatically corrected over time. Each future value depends on the previous value plus an error term, thus accumulating the impact of all past errors.
If we perform the analysis on the first differences for both time series we observe an I(0) behaviour. This is something to be expected noting that the above methods only consider integer degrees of differentiation, i.e., 0 for stationary series and 1 for nonstationary ones. Thus, in what follows, we permit more flexibility in the dynamic specification of the model by allowing fractional differentiation throughout the previously described ARFIMA approach.
Due to the lower power of the unit root methods under fractional alternatives, we also employ fractionally integrated methods, and use ARFIMA (p, d, q) models to study the persistence of both securities.
The advantages of using the ARFIMA (p, d, q) model over any Unit Root tests are several: (1) they allow fractional values for d providing greater flexibility in how the series is modeled; (2) they capture long-term dependence; (3) they offer a complete framework for modeling and predicting time series.
The Akaike information criterion (AIC)69 and the Bayesian information criterion (BIC)68 are used to select the appropriate AR and MA orders in the models.
Table 3 displays the estimates of the fractional differencing parameter d and the AR and MA terms, using Sowell's maximum likelihood estimator64 of various ARFIMA (p, d, q) specifications with all combinations of p, q ≤ 2, for each time series.
| Data analyzed | Sample size (days) | Model selected | d | Std. Error | Interval | I(d) |
|---|---|---|---|---|---|---|
| Original time series | ||||||
| EUR green bonds | 2265 | ARFIMA (0, d, 0) | 1.17 | 0.017 | [1.14, 1.20] | I(1) |
| EUR traditional bonds | 2265 | ARFIMA (0, d, 0) | 1.02 | 0.016 | [0.99, 1.05] | I(1) |
From Table 3, we observe that the fractional results that we get focusing on the original time series of green bonds and traditional bonds is higher than 1 in both cases (d ≥ 1).
So, the results suggest that the unit root null I(1) hypothesis cannot be rejected and the parameter d is statistically significantly above 1, in both cases. The results suggest that yields on both securities are non-stationary with permanent effects of shocks, implying that there is no reversion to the mean. Therefore, once a shock occurs (e.g., a significant change in market conditions or policy), bond yields do not revert to a previous level or trend. Instead, they establish a new trend or level, which could result in a continued upward or downward movement. So, for investors and policymakers, this finding suggests that the yields on green and traditional bonds are highly sensitive to market conditions, policy changes, or economic shocks, and these effects are long-lasting.
Once we have conducted the univariate analysis, we want to know if both time series have relationship or cause any effect over the other. So, in Table 4 we display the results that we get using Granger causality using VAR model test to examine the interactions between property prices and rental housing prices. The Granger causality test consist of a vector autoregressive representation (VAR) consisting of the two series:
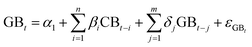 | (6) |
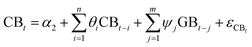 | (7) |
| Direction of causality | Lagsa | Prob. | Decision | Outcome |
|---|---|---|---|---|
| a We have used Akaike Information Criterion to detect the number of lags. | ||||
| d_EUR green bonds → d_EUR traditional bonds | 3 | 0.0002 | Reject null | Green bond total returns cause performance behaviors in the traditional bond |
| d_EUR traditional bonds → d_EUR green bonds | 3 | 0.0000 | Reject null | Traditional bond yields cause total return behaviors in green bonds |
The application of the VAR methodology is based on the following validations. First, VAR can only be applied when all the variables are either integrated of order zero or one. In this case, we have proved that both variables have the same behavior I(d). Second, one can estimate the level and the first difference relationship between variables using the ordinary least squares method. Third, variables are not expected to have long run relationships since they are integrated of order zero.
The two Granger causality hypotheses that are tested in this study are as follows. The first hypothesis is 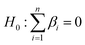 (green bond prices do not influence conventional bond prices) and
(green bond prices do not influence conventional bond prices) and 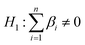 (green bond prices influences conventional bond prices) and the second hypothesis is
(green bond prices influences conventional bond prices) and the second hypothesis is 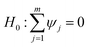 (conventional bond prices do not influence green bond prices) and
(conventional bond prices do not influence green bond prices) and 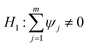 (conventional bond prices influence green bond prices).81
(conventional bond prices influence green bond prices).81
Performing a bivariate causality analysis allows us to identify the influences that one variable or time series exerts on the other. Also, past values of the causal variable provide useful information that can be exploited to predict future values of the dependent variable.
Table 4 represents the Granger causality results when causality runs from green bond total returns to conventional bond yields and vice versa. We observe from the results that green bond total returns cause performance behaviors in the traditional bond. Also, we find that traditional bond yields cause total return behaviors in green bonds. This indicates a feedback relationship where both variables influence each other. In other words, each of the two variables provides useful information to predict the other.
Once we have measured the causal relationship between both variables in time domain, we use a methodology based on Breitung and Candelon45 based on frequency domain to measure the causal effects of both variables in the long, medium and short term.
The results are displayed in Table 5.
| Hypothesis | Long term (ω = 0.05) | Medium term (ω = 1.5) | Short term (ω = 2.5) |
|---|---|---|---|
| a It shows that there is a significant causality relationship at the 5% significance level. The values in the brackets are the probability value of the F statistics calculated for the relevant ω values. | |||
| Original time series | |||
| Green bond returns → conventional bond returns | 8.525a (0.014) | 14.47a (0.0007) | 28.48a (0.000) |
| Conventional bond returns→ green bond returns | 15.80a (0.0003) | 17.64a (0.0001) | 1.18 (0.5534) |
Using the frequency domain causality test for the time series that we are analyzing, we find same results as Granger causality test, where the results suggest that both time series have causal relationship in both directions. Using the frequency domain test, we see that conventional bond yields do not cause total return behaviors in short-term green bonds. With the exception of the other assumption considered, this is only the case in the medium and long term.
These results are in line with the findings presented by Umar et al.82 and the connectedness of the most significant global equity indices that comprise companies with the highest environmental, social, and governance (ESG) performance.
After the results obtained in the causality test, we want to understand the relationship that exists in the long term between both variables. To do this, we follow the model introduced by Johansen83 which was further expanded by Johansen and Nielsen.74 The model is called the Fractional Cointegrated Vector AutoRegressive (FCVAR) model, and it is a step ahead of the Cointegrated Vector AutoRegressive (CVAR) model proposed by Johansen.84
The results of the FCVAR model have been summarized in Table 6.
We are going to focus on two terms. In the integrating and cointegrating part (d ≠ b) and the beta term to analyze the behavior of the time series.
From Panel I, where we analyze the long-term relationship between brown bonds and green bonds, we observe that the order of integration of individual series into a cointegrating system is d = 0.980. The reduction in the degree of integration in the cointegrating regression is b = 0.655. Thus, imply that the order of integration is about d − b = 0.325 for the cointegrating relationship. This result means that there is a stationary process and the effect of an exogenous shock is going to be long-lived. In the cointegration part, as it could not be otherwise, we obtain the same result if we invert the variables (see Panel II). So, the results indicate a long-term relationship between green and traditional bonds that is persistent but not perfect, with prolonged memory implying a gradual reversion to equilibrium after shocks. Additionally, this could indicate that the series are influenced by long-term factors that generate prolonged memory in the system.
This result is interesting for two reasons. Investors should consider their investment strategies since this might influence decisions regarding the duration and time horizon of investments. The policymakers need to consider that market interventions may have prolonged effects on the relationships between green and traditional bonds, and these effects may not fully revert in the short-term.
One the other hand, if we observe the cointegrating equation beta, from Panel I, the results suggest that an increase in the traditional bond yields produces a decrease (−0.457) in the green bond total returns. Conversely, if green bond yields are increased by one point, the drop in conventional bond yields is larger (−2.187).
This result makes sense given that some investors in the market think they can influence social change through their financial decisions6 and that individuals are more dedicated to changing their behavior to support sustainability and environmental issues.85
Finally, we use wavelet analysis that is a multivariate analysis based on the time-frequency domain to understand the correlation that exists between both variables. Also, with this methodology we are able to detect structural changes in the whole sample.
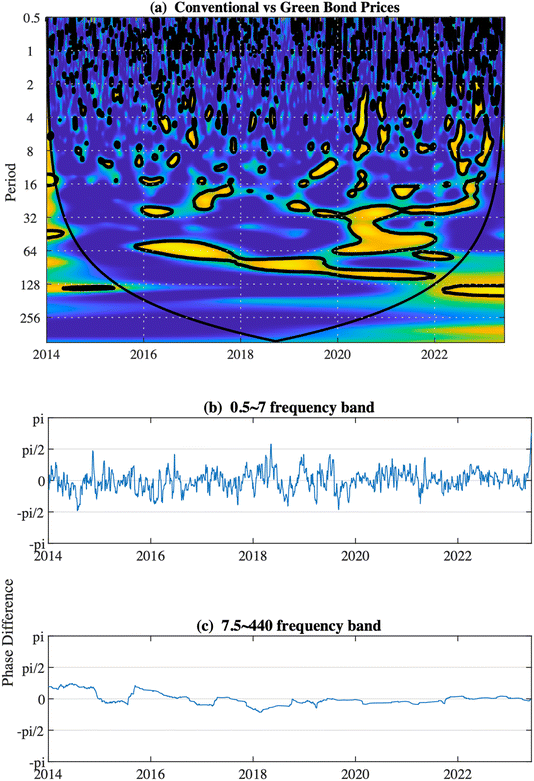
From Fig. 2, we can get several results. Wavelet coherency is represented in Section (a) of Fig. 2 and tell us when and at which frequencies the interrelations between time series occur and when they are the strongest, identifying the main regions with statistically significant coherency. Although we find relationship in (a) between both variables in the very short-term corresponding to 0.5 to 7 days during the period analyzed, the regions of high coherence are the medium and low frequencies (in the frequency band from 7.5 to 440 business days) that correspond to the medium and long-term, respectively. Putting the focus on low coherency, we observe high correlation (high coherency) in the period from end 2015 to early 2023. Once we have identified the regions that corresponds to the high coherency, we note that the phase difference in Section (b) shows that the profitability of conventional bonds ceased to be attractive and the weight of reversing climate change through the financing of sustainable and green projects through financial products such as bonds was imposed from the end of 2015 until the beginning of 2022, where this trend has been reversed again and where the results show that the correlation is above  again.
again.
5. Conclusions
Over the last ten years, a growing market for social impact investments has emerged as a result of increased investor awareness of environmental and social challenges. Green bonds stand out among the many options available as one of the direct tools offered by financial markets to mitigate the negative consequences of climate change.86,87Since the European Investment Bank introduced green bonds in 2007 to finance energy efficiency and renewable energy projects, the concept has attracted increasing attention. Most companies, municipalities, public sector organizations and supranational institutions now issue green bonds, which have similar characteristics to traditional fixed income bonds. The proceeds of these bonds are earmarked for environmental projects, such as waste and pollution projects, green buildings and renewable energy projects.
By diversifying traditional asset portfolios, green bonds, as a more advanced and environmentally conscious financial product, present substantial investment opportunities for individual and institutional investors, particularly those who care about the environment. Green bonds' financial success is questionable, nevertheless, particularly in light of changes in traditional financial products and the financial markets.
Thus, this research paper explores how the green and brown bond market in Europe and their profitability interact. To do so, we employed advanced methodological tools to perform the thorough statistical and econometric analysis of the data. In order to determine the level of dependence in the data and to investigate the time series' stationarity and response to an external shock, we first conducted a univariate analysis of the data using fractional integration models. The results that we get using fractional integration suggests that the unit root null I(1) hypothesis cannot be rejected in both variables analysed and d is statistically significantly above 1. This result reveals that both green and brown bond yields exhibit non-mean-reverting behavior, indicating that shocks to these yields have permanent effects. This suggests that once an external shock impacts the bond yields, the effects are long-lasting and do not revert to the original trend. This fact implies that financial institutions and investors need to adopt long-term risk management strategies. So, understanding the factors that influence these shocks is crucial for developing resilient investment portfolios.
To rule out possible spurious relationships, we have calculated the VAR-based Granger-causality test based on time domain. The results suggest a bidirectional causal relationship between green bond returns and traditional bond yields. This means that changes in green bond returns influence traditional bond yields and vice versa. According to Breitung and Candelon45 causality test based on frequency domain, this relationship is evident across different time horizons (medium and long-term). This result are crucial because the investors cannot treat green bonds as isolated from traditional bonds; instead, they need to consider how shifts is sustainability efforts and market conditions impact the entire bond market.
Then, the fractional cointegration analysis indicates that there is a long-term equilibrium relationship between both securities, with the effect of exogenous shocks being persistent. The order of cointegration is fractional, meaning that the bonds are linked over the long term, but not in the traditional sense of cointegration.
Finally, the wavelet analysis shows that there are periods of high correlation between green and brown bonds, particularly from the end of 2015 to early 2023. During this period, green bonds became more attractive as investments, especially during phases where sustainability efforts intensified. However, this trend begins to reverse in favor of traditional bonds from 2022 onward.
Thus, it is noted that the reversal of trends in favor of green bonds in recent years suggests that investor sentiment and market dynamics are fluid. Financial markets must remain adaptable, as the attractiveness of green versus brown bonds can change based on economic conditions, regulatory changes and societal shifts toward sustainability.
The findings underscore the critical role of green bonds in financing the transition to a low-carbon economy. The permanent impact of shocks on green bond yields suggests that sustained investment in these instruments is necessary to maintain momentum towards sustainability goals. The persistence of shocks in bond yields means that policy changes, such as the introduction of green bond standards or carbon taxes, can have long-term effects on the bond market. Policymakers need to carefully design and implement these policies, considering their enduring impact on financial markets.
Given the concerns about greenwashing and the variability in the “greenness” of bonds, there is a need for more robust verification and transparency standards. Ensuring that green bonds genuinely contribute to sustainability efforts is crucial for maintaining investor confidence and the overall effectiveness of these financial instruments.
The results of the study imply that policy and regulatory frameworks significantly influence the performance of green bonds. As governments and institutions drive for greater sustainability, their policies will have a lasting impact on the financial instruments that support these goals. Regulators may need to take these findings into account when designing policies that encourage green investments while managing the risks associated with brown bonds, avoid market destabilization, and remain attentive to market dynamics and prepared to intervene if necessary to ensure financial stability.
In order for investors and policymakers to make fully informed decisions, there are other methodological approaches that could be considered in future research, such as structural break tests, alternative model specifications, cross-validation with other data sources, non-linear causality tests, out-of-sample validation, among others are other potential avenues.
Data availability
The data that support the findings of this study are available from the corresponding author, upon reasonable request.Conflicts of interest
There are no conflicts to declare.References
- G. Capelle-Blancard and S. Monjon, Trends in the literature on socially responsible investment: Looking for the keys under the lamppost, Bus. Ethics Eur. Rev., 2012, 21(3), 239–250 CrossRef.
- D. Schiereck, G. Friede, and A. Bassen, Financial performances of green securities, in The Rise of Green Finance in Europe, ed. M Migliorelli and P Dessertine, Palgrave Macmillan, Cham, 2019 Search PubMed.
- R. Ferrer, S. J. H. Shahzad and P. Soriano, Are green bonds a different asset class? Evidence from time-frequency connectedness analysis, J. Cleaner Prod., 2021, 292, 125988 CrossRef.
- A. Maltais and B. Nykvist, Understanding the role of green bonds in advancing sustainability, J. Sustain. Finance Invest., 2020, 1–20 Search PubMed.
- H. A. Hacıömeroğlu, S. Danışoğlu and Z. N. Güner, For the love of the environment: An analysis of Green versus Brown bonds during the COVID-19 pandemic, Finance Res. Lett., 2022, 47, 102576 CrossRef.
- D. Zhang, Z. Zhang and S. Managi, A bibliometric analysis on green finance: Current status, development, and future directions, Finance Res. Lett., 2019, 29, 425–430 CrossRef.
- S. Bhojraj and P. Sengupta, Effect of corporate governance on bond ratings and yields: The role of institutional investors and outside directors, J. Bus., 2003, 76(3), 455–475 CrossRef.
- G. Friede, T. Busch and A. Bassen, ESG and financial performance: Aggregated evidence from more than 2000 empirical studies, J. Sustain. Finance Invest., 2015, 5(4), 210–233 CrossRef.
- S. Polbennikov, A. Desclée, L. Dynkin and A. Maitra, ESG ratings and performance of corporate bonds, J. Fixed Income, 2016, 26(1), 21–41 CrossRef.
- U. S. Bhutta, A. Tariq, M. Farrukh, A. Raza and M. K. Iqbal, Green bonds for sustainable development: Review of literature on development and impact of green bonds, Technol. Forecast. Soc. Change, 2022, 175, 121378 CrossRef.
- W. S. Laufer, Social accountability and corporate greenwashing, J. Bus. Ethics, 2003, 43, 253–261 CrossRef.
- Y. Wu, K. Zhang and J. Xie, Bad greenwashing, good greenwashing: Corporate social responsibility and information transparency, Manag. Sci., 2020, 66(7), 3095–3112 CrossRef.
- M. Immel, B. Hachenberg, F. Kiesel, and D. Schiereck, Green bonds: Shades of green and brown, in Risks Related to Environmental, Social and Governmental Issues (ESG), Springer Nature Switzerland, Cham, 2022, pp. 21–34 Search PubMed.
- D. Maul and D. Schiereck, The bond event study methodology since 1974, Rev. Quant. Finance Account., 2017, 48, 749–787 CrossRef.
- W. Ge and M. Liu, Corporate social responsibility and the cost of corporate bonds, J. Account. Public Policy, 2015, 34(6), 597–624 CrossRef.
- R. Preclaw, and A. Bakshi, The Cost of Being Green, Barclays Research, 2015, available from, https://www.environmental-finance.com/assets/files/US_Credit_Focus_The_Cost_of_Being_Green.pdf, accessed 20 Feb 2020 Search PubMed.
- A. Karpf and A. Mandel, Does it pay to be green?, SSRN Electron. J., 2017 DOI:10.2139/ssrn.2923484.
- M. Baker, D. Bergstresser, G. Serafeim and J. Wurgler, The pricing and ownership of US green bonds, Annu. Rev. Fin. Econ., 2022, 14, 415–437 CrossRef.
- B. Hachenberg and D. Schiereck, Are green bonds priced differently from conventional bonds?, J. Asset Manag., 2018, 19, 371–383 CrossRef.
- C. Partridge and F. Medda, Green premium in the primary and secondary US municipal bond markets, SSRN Electron. J., 2018 DOI:10.2139/ssrn.3237032.
- G. Gianfrate and M. Peri, The green advantage: Exploring the convenience of issuing green bonds, J. Cleaner Prod., 2019, 219, 127–135 CrossRef.
- O. D. Zerbib, The effect of pro-environmental preferences on bond prices: Evidence from green bonds, J. Bank. Finance, 2019, 98, 39–60 CrossRef.
- M. J. Bachelet, L. Becchetti and S. Manfredonia, The green bonds premium puzzle: The role of issuer characteristics and third-party verification, Sustainability, 2019, 11(4), 1098 CrossRef.
- J. Kapraun and C. Scheins, (In)-Credibly green: Which bonds trade at a green bond premium?, SSRN Electron. J., 2019 DOI:10.2139/ssrn.3347337.
- T. Ehlers, and F. Packer, Green Bond Finance and Certification, BIS Q. Rev., 2017, pp. 89–104 Search PubMed.
- K. U. Löffler, A. Petreski and A. Stephan, Drivers of green bond issuance and new evidence on the “greenium”, Eur. Econ. Rev., 2021, 11(1), 1–24 Search PubMed.
- L. Pham and C. P. Nguyen, How do stock, oil, and economic policy uncertainty influence the green bond market?, Finance Res. Lett., 2022, 45, 102128 CrossRef.
- E. J. A. Abakah, Jr E. Addo, L. A. Gil-Alana and A. K. Tiwari, Re-examination of international bond market dependence: Evidence from a pair copula approach, Int. Rev. Financ. Anal., 2021, 74, 101678 CrossRef.
- C. E. Chang, W. A. Nelson and H. D. Witte, Do green mutual funds perform well?, Manag. Res. Rev., 2012, 35(8), 693–708 CrossRef.
- B. R. Auer and F. Schuhmacher, Do socially (ir)responsible investments pay? New evidence from international ESG data, Q. Rev. Econ. Finance, 2016, 59, 51–62 CrossRef.
- J. C. Reboredo, Green bond and financial markets: Co-movement, diversification and price spillover effects, Energy Econ., 2018, 74, 38–50 CrossRef.
- S. Hammoudeh, A. N. Ajmi and K. Mokni, Relationship between green bonds and financial and environmental variables: A novel time-varying causality, Energy Econ., 2020, 92, 104941 CrossRef.
- J. C. Reboredo and A. Ugolini, Price connectedness between green bonds and financial markets, Econ. Model., 2020, 88, 25–38 CrossRef.
- J. Aswani and S. Rajgopal, Rethinking the value and emission implications of green bonds, SSRN Electron. J., 2022 DOI:10.2139/ssrn.4215882 . available from: https://ssrn.com/abstract=4215882.
- D. Luo, ESG, liquidity, and stock returns, J. Int. Financ. Mark. Inst. Money, 2022, 78, 101526 CrossRef.
- M. Shackleton, J. Yan and Y. Tao, What drives a firm's ES performance? Evidence from stock returns, J. Bank. Finance, 2022, 136, 106304 CrossRef.
- O. S. Yaya, A. E. Ogbonna and X. V. Vo, Oil shocks and volatility of green investments: GARCH-MIDAS analyses, Resour. Pol., 2022, 78, 102789 CrossRef.
- P. Bolton and M. Kacperczyk, Do investors care about carbon risk?, J. Financ. Econ., 2021, 142, 517–542 CrossRef.
- P. Bolton and M. Kacperczyk, Global pricing of carbon-transition risk, J. Finance, 2023, 78(6), 3677–3754 CrossRef.
- W. Mensi, X. V. Vo, H.-U. Ko and S. H. Kang, Frequency spillovers between green bonds, global factors and stock market before and during COVID-19 crisis, Econ. Anal. Pol., 2023, 77, 558–580 Search PubMed.
- D. Abu-Ghunmi, L. Abu-Ghunmi, B. A. Khamees, K. Anderson and M. A. Gunmi, Green economy and stock market returns: evidence from European stock markets, J. Open Innov. Technol. Mark. Complex, 2023, 9, 100146 CrossRef.
- K. Agoraki, N. Aslanidis and G. P. Kouretas, How has COVID-19 affected the performance of green investment funds?, J. Int. Money Finance, 2023, 131, 102792 CrossRef PubMed.
- A. K. Tiwari, E. J. A. Abakah, O. S. Yaya and K. O. Appiah, Tail risk dependence, co-movement and predictability between green bond and green stocks, Appl. Econ., 2023, 55(2), 201–222 CrossRef.
- W. Yiming, L. Xun, M. Umair and A. Aizhan, COVID-19 and the transformation of emerging economies: Financialization, green bonds, and stock market volatility, Resour. Pol., 2024, 92, 104963 CrossRef.
- J. Breitung and B. Candelon, Testing for short and long-run causality: A frequency domain approach, J. Econom., 2006, 132(2), 363–378 CrossRef.
- G. E. P. Box, and G. M. Jenkins, Time Series Analysis, Forecasting and Control, Holden-Day, San Francisco, 1970 Search PubMed.
- C. R. Nelson and C. R. Plosser, Trends and random walks in macroeconomic time series: Some evidence and implications, J. Monet. Econ., 1982, 10(2), 139–162 CrossRef.
- D. A. Dickey and W. A. Fuller, Distributions of the estimators for autoregressive time series with a unit root, J. Am. Stat. Assoc., 1979, 74(366), 427–481 CrossRef.
- D. A. Dickey and W. A. Fuller, Likelihood ratio statistics for autoregressive time series with a unit root, Econometrica, 1981, 49, 1057–1072 CrossRef.
- P. C. B. Phillips, Time series regression with a unit root, Econometrica, 1987, 277–301 CrossRef.
- P. C. B. Phillips and P. Perron, Testing for a unit root in time series regression, Biometrika, 1988, 75, 335–346 CrossRef.
- D. Kwiatkowski, P. C. B. Phillips, P. Schmidt and Y. Shin, Testing the null hypothesis of stationarity against the alternative of a unit root, J. Econom., 1992, 54(1–3), 159–178 CrossRef.
- R. K. Adenstedt, On large-sample estimation for the mean of a stationary random sequence, Ann. Stat., 1974, 1095–1107 Search PubMed.
- C. W. Granger and R. Joyeux, An introduction to long-memory time series models and fractional differencing, J. Time Ser. Anal., 1980, 1(1), 15–29 CrossRef.
- C. W. Granger, Long memory relationships and the aggregation of dynamic models, J. Econom., 1980, 14(2), 227–238 CrossRef.
- C. W. Granger, Some properties of time series data and their use in econometric model specification, J. Econom., 1981, 16(1), 121–130 CrossRef.
- J. R. Hosking, Modeling persistence in hydrological time series using fractional differencing, Water Resour. Res., 1981, 20(12), 1898–1908 CrossRef.
- F. X. Diebold and G. D. Rudebush, On the power of Dickey-Fuller tests against fractional alternatives, Econ. Lett., 1991, 35, 155–160 CrossRef.
- U. Hassler and J. Wolters, On the power of unit root tests against fractional alternatives, Econ. Lett., 1994, 45(1), 1–5 CrossRef.
- D. Lee and P. Schmidt, On the power of the KPSS test of stationarity against fractionally-integrated alternatives, J. Econom., 1996, 73(1), 285–302 CrossRef.
- J. Geweke and S. Porter-Hudak, The estimation and application of long memory time series models, J. Time Ser. Anal., 1983, 4(4), 221–238 CrossRef.
- P. C. B. Phillips, Discrete Fourier Transforms of Fractional Processes. Department of Economics, University of Auckland, 1999 Search PubMed.
- P. C. B. Phillips, Unit root log periodogram regression, J. Econom., 2007, 138(1), 104–124 CrossRef.
- F. Sowell, Maximum likelihood estimation of stationary univariate fractionally integrated time series models, J. Econom., 1992, 53(1–3), 165–188 CrossRef.
- P. M. Robinson, Efficient tests of nonstationary hypotheses, J. Am. Stat. Assoc., 1994, 89, 1420–1437 CrossRef.
- P. M. Robinson, Gaussian semi-parametric estimation of long range dependence, Ann. Stat., 1995, 23, 1630–1661 Search PubMed.
- P. M. Robinson, Log periodogram regression of time series with long range dependence, Ann. Stat., 1995, 23(3), 1048–1072 Search PubMed.
- H. Akaike, Maximum likelihood identification of Gaussian autoregressive moving average models, Biometrika, 1973, 60(2), 255–265 CrossRef.
- H. Akaike, A Bayesian extension of the minimum AIC procedure of autoregressive model fitting, Biometrika, 1979, 66(2), 237–242 CrossRef.
- H. Tastan, Testing for spectral Granger causality, STATA J., 2015, 15(4), 1157–1166 CrossRef.
- Ç. Ciner, Eurocurrency interest rate linkages: A frequency domain analysis, Int. Rev. Econ. Finance, 2011, 20, 498–505 CrossRef.
- M. Kırca, Ş. Canbay and K. Pirali, Is the relationship between oil-gas prices index and economic growth in Turkey permanent?, Resour. Pol., 2020, 69, 101838 CrossRef PubMed.
- J. Geweke, Measurement of linear dependence and feedback between multiple time series, J. Am. Stat. Assoc., 1982, 304–313 CrossRef.
- S. Johansen and M. O. Nielsen, Likelihood inference for a fractionally cointegrated vector autoregressive model, Econometrica, 2012, 80, 2667–2732 CrossRef.
- W. X. Zhou, Multifractal detrended cross-correlation analysis for two nonstationary signals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2008, 77(6), 066211 CrossRef PubMed.
- B. Podobnik and H. E. Stanley, Detrended cross-correlation analysis: A new method for analyzing two nonstationary time series, Phys. Rev. Lett., 2008, 100(8), 084102 CrossRef PubMed.
- G. F. Gu and W. X. Zhou, Detrending moving average algorithm for multifractals, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2010, 82(1), 011136 CrossRef PubMed.
- Z. Q. Jiang and W. X. Zhou, Multifractal detrending moving-average cross-correlation analysis, Phys. Rev. E: Stat., Nonlinear, Soft Matter Phys., 2011, 84(1), 016106 CrossRef PubMed.
- L. Aguiar-Conraria and M. J. Soares, The continuous wavelet transform: Moving beyond uni- and bivariate analysis, J. Econ. Surv., 2014, 28, 344–375 CrossRef.
- L. Aguiar-Conraria, N. Azevedo and M. J. Soares, Using wavelets to decompose the time-frequency effects of monetary policy, Physica A, 2008, 387, 2863–2878 CrossRef.
- D. Asteriou, and S. G. Hall, Applied Econometrics, Palgrave Macmillan, London, 2015 Search PubMed.
- Z. Umar, D. Kenourgios and S. Papathanasiou, The static and dynamic connectedness of environmental, social, and governance investments: International evidence, Econ. Model., 2020, 93, 112–124 CrossRef PubMed.
- S. Johansen, A representation theory for a class of vector autoregressive models for fractional processes, Econom. Theor., 2008, 24, 651–676 CrossRef.
- S. Johansen, Likelihood-based Inference in Cointegrated Vector Autoregressive Models, Oxford University Press, New York, NY, 1996 Search PubMed.
- N. Kachaner, J. Nielsen, A. Portafaix, and F. Rodzko, The Pandemic Is Heightening Environmental Awareness, Boston Consulting Group, 2020 Search PubMed.
- M. Flaherty, A. Gevorkyan, S. Radpour and W. Semmler, Financing climate policies through climate bonds–A three stage model and empirics, Res. Int. Bus. Finance, 2017, 42, 468–479 CrossRef.
- I. Monasterolo and M. Raberto, The EIRIN flow-of-funds behavioural model of green fiscal policies and green sovereign bonds, Ecol. Econ., 2018, 144, 228–243 CrossRef.
Footnote |
| † https://sites.google.com/site/aguiarconraria/joanasoares-wavelets |
| This journal is © The Royal Society of Chemistry 2024 |