Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Effectiveness and limitation of the performance prediction of perovskite solar cells by process informatics†
Ryo
Fukasawa
 a,
Toru
Asahi
a and
Takuya
Taniguchi
a,
Toru
Asahi
a and
Takuya
Taniguchi
 *b
*b
aDepartment of Advanced Science and Engineering, Graduate School of Advanced Science and Engineering, Waseda University, 3-4-1 Okubo, Shinjuku-Ku, Tokyo, 169-8555, Japan
bCenter for Data Science, Waseda University, 1-6-1 Nishiwaseda, Shinjuku-ku, Tokyo 169-8050, Japan. E-mail: takuya.taniguchi@aoni.waseda.jp
First published on 8th March 2024
Abstract
Perovskite solar cells have garnered significant interest owing to their low fabrication costs and comparatively high power conversion efficiency (PCE). The performance of these cells is influenced not solely by material composition but also by experimental processes, rendering PCE prediction a challenging endeavor. It is also crucial to quantitatively assess the impact of process conditions on performance. In this work, we developed machine learning regression incorporating process information derived from an open-access perovskite database. Our analysis showed that the split of process information influenced the prediction accuracy and clarified the relative contribution of each process condition. The limitation of performance prediction was also prone to data degeneracy. The insights gained from this work may facilitate the data-driven design of innovative perovskite solar cells.
Introduction
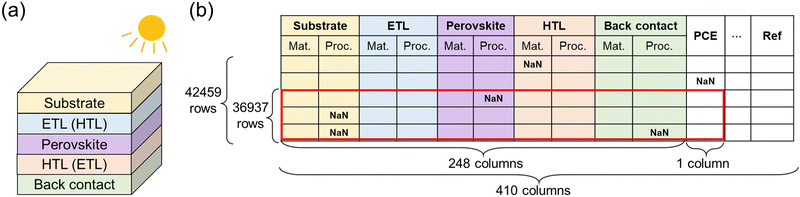
The inception of perovskite solar cells can be traced back to the pioneering work by Miyasaka's group,1 which has subsequently elicited considerable interest in recent years.2–4 While perovskite solar cells exhibit stability challenges compared to traditional silicon-based cells,5,6 they are acknowledged for their superior power conversion efficiency (PCE) under suboptimal or diffused light conditions.7–9 Further advantages of perovskite solar cells include their economical production costs, lightweight nature, and minimal energy consumption during manufacturing.10–12Addressing the crucial societal need for enhancing the PCE of perovskite solar cells is paramount, as it would facilitate electricity generation from renewable energy. Various architectures of perovskite solar cells have been developed,13 predominantly falling into nip and pin types (Fig. 1a). Both types encompass five distinct functional layers: the substrate, electron transport layer (ETL), perovskite layer, hole transport layer (HTL), and back contact. The critical distinction between these two types resides in the sequence of the ETL and HTL, and this differentiation results in the opposite direction of the current generation.
The PCE of perovskite solar cells is significantly influenced by the material composition and the fabrication process of each layer.14–16 For instance, literature has shown that utilizing spin-coating with an anti-solvent to form the perovskite layer leads to an enhanced PCE compared to the absence of an anti-solvent, even with identical material composition.17 The effect is attributed to crystallization speed, improving the quality of the perovskite crystal. Furthermore, it is also reported that the PCE increases when ETL materials are deposited by radio frequency magnetron sputtering compared to the conventional sol–gel method.18 The different fabrication conditions of perovskite solar cells have substantial influences on the microscopic structure and physicochemical properties of the cells and, ultimately, the PCE of the device.
Such experimental findings have spurred the advancement of process informatics for perovskite solar cells. Odabaşı et al. analyzed what process conditions influenced PCE using their curated dataset.19 They also conducted a machine learning analysis on the stability of perovskite solar cells using a manually curated dataset.20 These studies were the notable applications of process informatics for perovskite solar cells, but the variety and amount of data were limited compared with the number of available publications. Later on, Jacobsson et al. established an open-access perovskite database, named the Perovskite Database, to collect and share material and process data of perovskite solar cells in a standardized format.21 This database has the most extensive data size, consisting of material and process information of 410 columns (Fig. 1b). The database promoted large-scale analyses of the stability and open-circuit voltage of perovskite solar cells.22,23 Such an open database enables process informatics to find the relationship between process conditions and the performance of perovskite solar cells.
Process data contains diverse information, such as solvents and the order of additives, which are primarily qualitative variables, thus requiring careful consideration for the mathematical representation. However, such representation comparison of process data has never been tackled, making the effectiveness and limitation of process informatics unclear. In this work, we analyzed the effectiveness and limitations of PCE prediction considering all material and process variables within the Perovskite Database. We compared several treatments of process data with delimiters, and identified a suitable data representation in machine learning. The interpretation of the machine learning model allowed us to find the relative influence of materials and processes on the PCE. We also analyzed the origin of regression error, and clarified the limits of machine learning due to data degeneracy. This work should contribute to the data-driven development of perovskite solar cells.
Experimental
Data curation
We downloaded the dataset from the Perovskite Database,21 which contained 42![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 459 records as of 31 March 2022. The database contains 410 columns of information, and we excluded columns irrelevant to PCE, such as literature information. Due to the exclusion, 248 columns related to the material and experimental process conditions were used for the explanatory variables. All used columns are shown in Table S1 (ESI†).
459 records as of 31 March 2022. The database contains 410 columns of information, and we excluded columns irrelevant to PCE, such as literature information. Due to the exclusion, 248 columns related to the material and experimental process conditions were used for the explanatory variables. All used columns are shown in Table S1 (ESI†).
Then, we excluded rows that contained missing data in the columns of PCE and material compositions. Missing information in process columns was allowed. We also excluded rows with the following conditions: non-ASCII characters, the existence of commas in the string, and the wrong ratio of perovskite compositions due to a typo when depositing data. After the data extraction, we obtained 36![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 937 records for analysis in this study.
937 records for analysis in this study.
Vectorization of data
The abbreviations of perovskite materials were converted into the correct chemical formula for the perovskite composition based on the manually prepared correspondence table (Table S2, ESI†). Once chemical formulae were obtained, perovskite materials were vectorized by a composition-based feature vector (CBFV) library.24 Three representations, Oliynyk,25 Magpie,26 and mat2vec,27 were examined as feature vectors. Magpie uses statistics of the physical properties of compositional elements such as atomic weight and radius, resulting in a 132-dimensional vector. Oliynyk provides more information (a 264-dimensional vector) than Magpie, including thermoelectric properties. Mat2vec employs a latent vector from unsupervised word embeddings for each element, yielding a 1200-dimensional vector.The dataset contains three types of delimiters: vertical bar (|), double chevron (>>), and semicolon (;). The vertical bar represents the boundaries of the thin film, the double chevron represents the process of pre- and post-relationships, and the semicolon is a separator that connects several substances or reaction conditions given in a thin film or reaction process.
For the delimiters, three order splits were performed. The 1st order split was delimited by a vertical bar, the 2nd by a double chevron, and the 3rd by a semicolon (Fig. 2a). After splitting data by delimiters, unique information was encoded into dummy variables, and the number of dimensions depended on the number of unique information in a column.
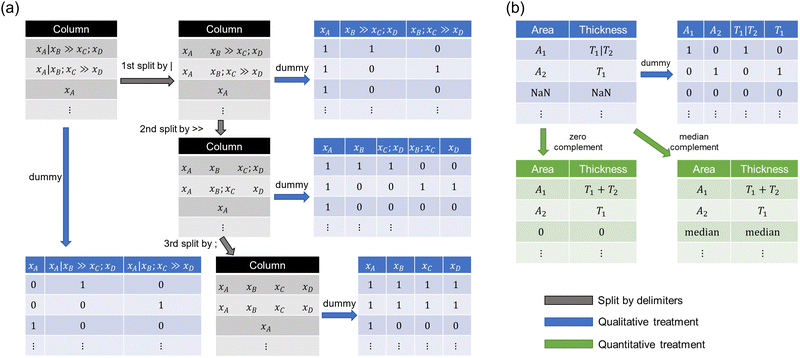 | ||
| Fig. 2 Scheme of data split and vectorization. (a) Treatment of delimiters and how to vectorize them into dummy variables. (b) Treatment for cell area and thicknesses. | ||
Three treatments were performed for a cell area and five thicknesses of layers (Fig. 2b). Dummy vectorization treats area and thicknesses as qualitative variables and encodes them into binary vectors. When treating area and thicknesses as quantitative, values delimited by the vertical bar were summed up, and the missing values were complemented by zero or median (Fig. 2b). The other columns were vectorized into dummy variables because they are difficult to treat as numerical values. This is because the process conditions sometimes include stepwise information (such as “100|200”) for time and temperature, which was unable to be converted in a numeric value. Note that such dummy vectorization has the advantage in the data distinction while having the disadvantage in measuring the closeness between data.
Machine learning implementation
We examined three regression models, random forest (RF), neural network (NN), and gradient-boost decision tree (GBDT). The dataset was split into 8![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 for training and test, respectively. When performing hyperparameter optimization, 25% of the training dataset was used for validation. The same test dataset was used in all regressions, and the prediction performance was evaluated by the typical coefficient of determination (R2), the mean absolute error (MAE), and the root mean squared error (RMSE). Machine learning and hyperparameter optimization were implemented using scikit-learn, pandas, numpy, and optuna libraries. The machine learning model was interpreted using feature importance and Shapley additive explanations (SHAP).28
2 for training and test, respectively. When performing hyperparameter optimization, 25% of the training dataset was used for validation. The same test dataset was used in all regressions, and the prediction performance was evaluated by the typical coefficient of determination (R2), the mean absolute error (MAE), and the root mean squared error (RMSE). Machine learning and hyperparameter optimization were implemented using scikit-learn, pandas, numpy, and optuna libraries. The machine learning model was interpreted using feature importance and Shapley additive explanations (SHAP).28
Results and discussion
Comparison of predictive performance
The distribution of PCE in our curated dataset is similar to the original database (Fig. 3). The relationships between some quantitative variables and PCE were also visualized (Fig. S1, ESI†), while there was no clear tendency of higher or lower PCE.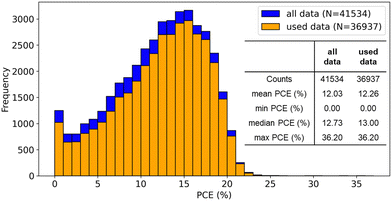 | ||
| Fig. 3 Comparison of PCE distribution between all data in the original database and used data in our analysis. | ||
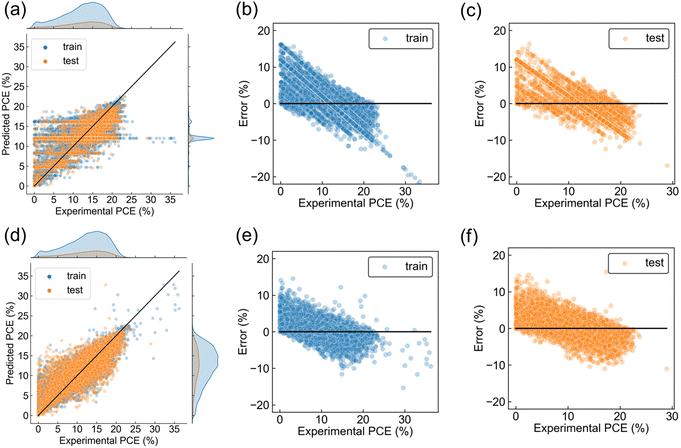
First, regressions of PCE using only perovskite composition were performed to determine which representation was better. Three chemical representations (Oliynyk, Magpie, and mat2vec) and dummy vectorization were compared using RF model as a prediction function. Oliynyk was the best representation based on higher R2 and smaller RMSE and MAE on the test dataset (Table 1), and we decided to use Oliynyk in the following analysis. This result does not mean that the perovskite composition is enough to predict PCE because the R2 was low for sufficient prediction (Table 1). The scatter plot of experimental and predicted PCE displayed most predictions distributed around the mean of the dataset (Fig. 4a), which is often observed when the learning is not sufficient due to the deficiency of data representations. Training and test errors were also quite large, with a negative tendency (Fig. 4b and c). Here, error was defined as prediction minus experimental PCE. The other representations showed similar experimental-predicted plots to that of Oliynyk (Fig. S2, ESI†). Since dummy vectorization just distinguished the data without chemical information, it can be said that three chemical vectors worked to capture some chemical information. Even though, the deficiency of data representation should be solved by considering process information as explanatory variables.
| Dummy | Oliynyk | Magpie | mat2vec | |
|---|---|---|---|---|
| Train | ||||
| R 2 | 0.3105 | 0.3159 | 0.3156 | 0.3160 |
| RMSE | 4.2807 | 4.2636 | 4.2647 | 4.2634 |
| MAE | 3.3410 | 3.3121 | 3.3144 | 3.3109 |
| Test | ||||
| R 2 | 0.2262 | 0.2929 | 0.2901 | 0.2922 |
| RMSE | 4.4888 | 4.2910 | 4.2994 | 4.2932 |
| MAE | 3.5042 | 3.3897 | 3.3955 | 3.3925 |
The other representation such as the tolerance factor, which is used to predict whether a crystal structure is perovskite, may be available. Although there are some studies that have calculated the value for organic–inorganic hybrid perovskites for screening,29 the calculation is not as simple as for inorganic perovskites. In addition, our study does not intend the screening, but focuses on data representation of perovskite materials for machine learning.
PCE regressions were then performed using all columns of materials and processes (248 columns). Perovskite composition was treated with the Oliynyk representation. Different splits were performed for columns, including process delimiters (Fig. 2a). The columns of a cell area and layer thicknesses were manipulated in three ways (Fig. 2b). The other columns were encoded as dummy variables. Twelve representations were compared based on the R2 metric of the test dataset after hyperparameter optimization of RF model (Fig. S3 and Table S3, ESI†). The combination of 1st split and zero complements yielded the highest metric (Table 2 and Fig. S4, ESI†). Other metrics, RMSE and MAE, were also minimum by the data representation (Table S4, ESI†). We have confirmed that the data representation was the best when the different train-test divisions were used (Table S5, ESI†).
| w/o Split | 1st Spit | 2nd Split | 3rd Split | |
|---|---|---|---|---|
| Dummy | 0.7019 | 0.7020 | 0.7035 | 0.7059 |
| Zero complement | 0.7061 | 0.7177 | 0.6986 | 0.7126 |
| Median complement | 0.7153 | 0.7125 | 0.7099 | 0.7060 |
The experimental-predicted plot was improved by including all materials and processes, compared to perovskite composition alone (Fig. 4a and d). The prediction distribution became similar shape to that of experimental PCE, and scatter plots were distributed roughly along the reference line, suggesting a successful regression (Fig. 4d). Even though, note that many plots are still far from the reference line. The distributions of prediction errors showed that the data in the region of lower PCE tended to be overestimated, and the data in the region of higher PCE tended to be underestimated, resulting in a negative slope in both the training and test dataset (Fig. 4e and f). Steeper slopes were observed in error plots of perovskite composition alone due to a more significant bias (Fig. 4b and c), and the inclusion of process information suppressed the steepness due to a smaller bias. This phenomenon, negative slope in error plot, was also observed in the regression of organic photovoltaics.30,31 The literature reported that fewer data in the range of lower PCE caused such error distribution, and the regression of perovskite solar cells may have fallen into the same situation.
As we observed differences in the regression results depending on the data representation, we discuss the effectiveness of split and complement methods. Dummy vectorization is a method for separating different data using binary values in varying dimensions, while it does not assess the similarity between data points. On the other hand, data splitting with a delimiter allows the evaluation of data similarity because common elements are represented in the same dimension, although the split may compromise data separation. The optimal balance between data similarity and data separation is 1st split based on the regression results. For example, a data of “DMF ≫ DMSO” and another data of “DMSO ≫ DMF” are converted to the same vector (i.e. data degeneracy) by 2nd and 3rd splits, increasing the regression error. The detail of data degeneracy is discussed in the following section.
Furthermore, as to the data completion for area and thicknesses, it was found that the completion of missing values with zero yielded better results than using the median. It is known that the completion of missing values with the mean is not ideal due to the induction of bias,32 and using the median probably produced similar outcomes. Hence, it is suggested that zero completion is preferable to median completion. Other predictive functions of GBDT and NN afforded lower prediction performance than RF, identifying RF was the best (Fig. S5–S7, ESI†).
We then evaluated the generalization ability of the trained model. Newly registered data (n = 294) as of 24 August 2023, were used for test data. The trained model resulted in test metrics, R2 of 0.45 and MAE of 3.20% (Fig. S8, ESI†). The metrics became worse the previous test (Fig. 4d), while still better than the mean model (R2: −0.33, MAE: 5.40%). This may reflect that recent studies use new materials and/or fabrication methods, and the data distribution changes depending on time. The new process information appeared max. 48 conditions per data (Fig. S8e, ESI†). The new information from both important and unimportant columns based on feature importance influenced the increase in prediction error (Fig. S8f, ESI†). The influence of new information from unimportant columns on prediction error is detrimental for regression, but it has significance in terms of chemical insights. This is because it suggests that process variables, which were not previously recognized as important, may in fact be variables that affect PCE.
The origin of the regression error
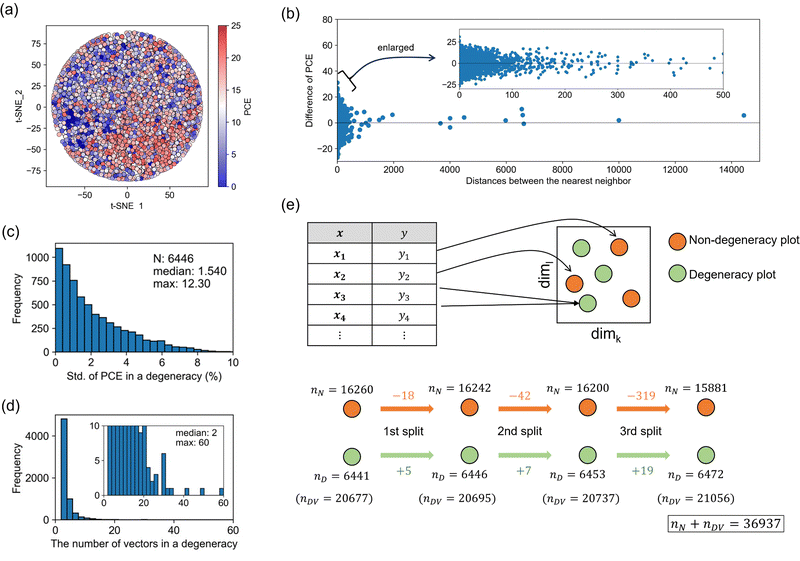
As shown in Fig. 4, a bias remains in the predictions considering all materials and processes, and in this section, we analyze the reason in detail. First, the data vectorized by the best representation (1st split and zero complements) were embedded in two dimensions by t-distributed stochastic neighbor embedding, t-SNE (Fig. 5a). Each plot was colored depending on experimental PCE. Ideally, if close vectors have similar PCE, the color gradation would be observed. Plots with higher PCE (shown in red) were relatively assembled in the lower right area, and plots with smaller PCE (shown in blue) were in the left area. However, color gradation was unclear because many areas have a mixed distribution of red and blue plots. It means that close vectors have largely different PCE, leading to reduce the accuracy of prediction.Next, we compared the difference in PCE between the closest vectors (Fig. 5b). When we calculated the nearest neighbor distance using the best representation, 90% of the data were within the distance 5. It was also found that the difference in PCE was distributed more widely for the closer vectors, ranging from −20% to 30%. In many cases, the distance was zero, i.e., identical vectors were created by degenerating from different data corresponding to different PCEs. This data degeneracy negatively affects the regression performance.
We further investigated the occurrence of data degeneracy. The standard deviation of PCE in a degeneracy distributed as shown in Fig. 5c. The median was 1.54%, and the maximum difference was 12.30% (Fig. 5c). The total degenerated unique points were 6446, consisting of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 695 vectors. The number of vectors in a degeneracy mainly was 2, and the maximum was 60 (Fig. 5d). While these distributions did not change largely by different splitting methods (Fig. S9, ESI†), the number of data degeneracies increased as the splitting order increased (Fig. 5e). There are 6441 degenerated unique points consisting of 20
695 vectors. The number of vectors in a degeneracy mainly was 2, and the maximum was 60 (Fig. 5d). While these distributions did not change largely by different splitting methods (Fig. S9, ESI†), the number of data degeneracies increased as the splitting order increased (Fig. 5e). There are 6441 degenerated unique points consisting of 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 677 vectors at the beginning. This means that the original database contains the same information at different records, probably due to not fully capturing process variables in the database. Such data degeneracy causes the limitation of predictive performance. The number of degeneracies increases depending on the split order because the data may become the same vector, as illustrated in Fig. 2. If the degeneracy occurs in data with a large difference in PCE, it will harm the regression. The split method also has a positive effect on measuring the closeness between data, and thus there is a suitable balance between positive and negative effects.
677 vectors at the beginning. This means that the original database contains the same information at different records, probably due to not fully capturing process variables in the database. Such data degeneracy causes the limitation of predictive performance. The number of degeneracies increases depending on the split order because the data may become the same vector, as illustrated in Fig. 2. If the degeneracy occurs in data with a large difference in PCE, it will harm the regression. The split method also has a positive effect on measuring the closeness between data, and thus there is a suitable balance between positive and negative effects.
We have also investigated how many degeneracy occurred in common material and deposition. The most common combination in the database is spincoated MAPbI3 on TiO2 with Spiro as an HTL (n = 2383). The PCEs of the same combination widely distrubuted, with a minimum of 0% and a maximum of 25.4% (Fig. S10, ESI†). The variation results from the variation of fabrication processes, and this result also suggest the importance of considering process information. Even though, vectorization resulted in many degeneracies, preventing the accurate prediction of PCE by machine learning.
Model interpretability
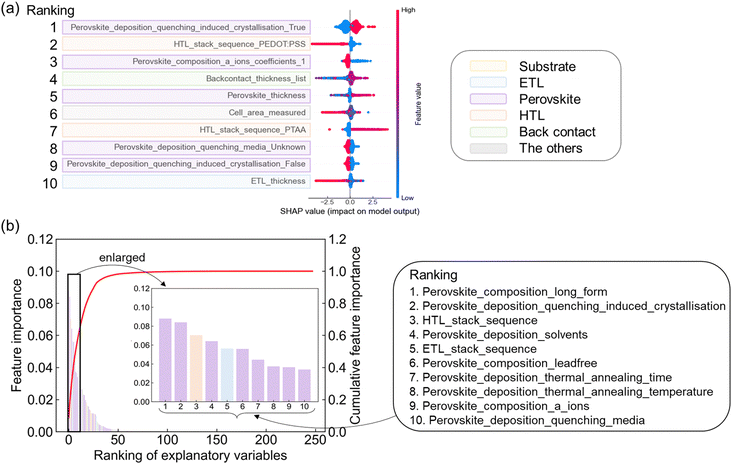
Although prediction accuracy is limited due to data degeneracy, an interpretation of the machine learning model is important for obtaining chemical insight. We performed SHAP analysis, which is beneficial for identifying the positive or negative effect of each variable.28,33,34 Here, the top 10 dimensions after sorting by the averaged SHAP value are highlighted in different colors depending on the layer (Fig. 6a). The 1st ranked dimension, the quenching condition assigned as perovskite process, showed low feature values (shown as blue points) distributing in the negative region of SHAP values and high feature values (red points) distributing in the positive region. This result suggests that the use of anti-solvent as quenching media enhances PCE. This is consistent with the experimental finding,17 as explained in the introduction. The features related to HTL layer, 2nd and 7th in the ranking, showed a relationship that PCE tended to increase using PTAA rather than PEDOT:PSS. This result has also been experimentally found.35 The 3rd feature related to perovskite material indicates that single-cationic perovskites are inferior to mixed ones, consistent with experimental result.36 The ranking of SHAP value identified the most influential process for each functional layer (Table S6, ESI†). The spin-coating had the positive effect as the deposition of ETL, perovskite, and HTL layers. Evaporation had a positive effect for back contact.The detailed fabrication conditions were identified for perovskite layer. The most positive effect on PCE by solvent was the case of DMF![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) DMSO = 4
DMSO = 4![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. The most positive effect by quenching media was diethyl ether. These SHAP interpretations afforded known chemical insights and confirmed the validity of the trained RF model consistent with experimental findings.
1. The most positive effect by quenching media was diethyl ether. These SHAP interpretations afforded known chemical insights and confirmed the validity of the trained RF model consistent with experimental findings.
We also quantified the relative impact of each parameter on PCE predictions using feature importance calculated from RF. The feature importance of 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 305 dimension was calculated (Table S7, ESI†) and then aggregated in the raw 248 columns in the dataset (Table S8, ESI†). The results show that, as in the case of SHAP, perovskite materials and processes were the top-ranked features (Fig. 6c). Furthermore, the feature importance of the material and process condition of each functional layer was summarized (Table 3). The information on the perovskite layer contributed about 63% to the prediction of PCE, especially the process conditions contributed 41%. Information on the ETL and HTL layers also contributed about 12% each to the prediction. The substrate and back contact were rated as less critical because these layers contribute neither to carrier generation nor transport.
305 dimension was calculated (Table S7, ESI†) and then aggregated in the raw 248 columns in the dataset (Table S8, ESI†). The results show that, as in the case of SHAP, perovskite materials and processes were the top-ranked features (Fig. 6c). Furthermore, the feature importance of the material and process condition of each functional layer was summarized (Table 3). The information on the perovskite layer contributed about 63% to the prediction of PCE, especially the process conditions contributed 41%. Information on the ETL and HTL layers also contributed about 12% each to the prediction. The substrate and back contact were rated as less critical because these layers contribute neither to carrier generation nor transport.
| Material | Process | |
|---|---|---|
| Substrate | 0.0115 | 0.0005 |
| ETL | 0.0563 | 0.0758 |
| Perovskite | 0.2251 | 0.4107 |
| HTL | 0.0705 | 0.0476 |
| Back contact | 0.0161 | 0.0336 |
| Other | 0.0058 | 0.0463 |
| Total | 0.3854 | 0.6146 |
Feature importance quantitatively evaluated the relative importance of material and process information, showing the significance of considering process conditions for experimental material development and machine-learning prediction. Although these findings are qualitatively known, we think that the novelty of this work should lie in the quantitative evaluation of relative importance of process parameters. We also checked the validity of SHAP and feature importance. If data distribution is largely different between layers, the importance of less distributed layer will be underestimated. However, we did not see large difference of data distribution between layers (Fig. S11, ESI†). This supports the result of quantitative evaluation.
We further examined how variable selection affected the regression. When 27 variables were selected based on the aggregated feature importance, there was only a slight decrease in prediction ability, and the difference between the training and test metrics was suppressed (Fig. S12, ESI†). When 8 variables were selected, the prediction error became worse. Thus, suitable variable selection worked on the slight suppression of overfitting.
Finally, we address the advantage and limitation of machine learning interpretation. The advantage of model interpretation is to evaluate the influence factors on PCE quantitatively, and hopefully to unveil the unknown important factors based on known data. However, even when the influential factors are found, it does not guarantee that it is the optimal condition. If we find the truly optimal conditions, we need generative AI and/or virtual material (device) simulation. Incorporating hundreds of process information into them is impossible with current technology. In addition, we recognize the importance of cell stability as well as PCE. The data analysis on cell stability is more challenging than PCE because the stability measured by various standards are stored in the database. A literature proposed the standardization of stability (called TS80m index),22 and the index will be available for machine learning of our workflow. Since it is beyond the scope of this work, we would like to tackle in the stability prediction incorporating process information in future work.
Conclusions
We developed the machine learning model incorporating process information curated from the Perovskite Database. The predictive accuracy improved by considering process information, and the interpretation of the trained RF model confirmed the model's validity, consistent with experimental findings. We clarified the relative importance of the material and process information of each layer, suggesting the significance of considering process conditions for experimental material development and machine-learning prediction. Despite the effectiveness of machine learning, we found that there is a limitation due to data degeneracy. Data degeneracies exist in the original database, affecting machine learning negatively. The balance between data degeneracy and measuring closeness was regulated by split and complement method, identifying that the best representation was 1st split and zero complements. The findings of this work will contribute to the data-driven development of perovskite solar cells.Data availability
The original dataset used in this work is available at https://www.perovskitedatabase.com.Code availability
Codes reproducing all analyses in this work are available in the GitHub repository of https://github.com/Fukapy/Perovskite_PI.Author contributions
Ryo Fukasawa: conceptualization, data curation, formal analysis, methodology, visualization, writing – original draft. Toru Asahi: supervision. Takuya Taniguchi: conceptualization, visualization, funding acquisition, project administration, resources, validation, writing – review & editing, supervision.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This study was financially supported by JSPS Grant-in-Aid (22K14747), Waseda University Grant for Special Research Projects (2022C-313), JST ACT-X (JPMJAX23DD), JST START (JPMJST2053), and a research grant from Yashima Environment Technology Foundation.References
- A. Kojima, K. Teshima, Y. Shirai and T. Miyasaka, J. Am. Chem. Soc., 2009, 131, 6050–6051 CrossRef CAS PubMed.
- N. G. Park, Mater. Today, 2015, 18, 65–72 CrossRef CAS.
- I. Hussain, H. P. Tran, J. Jaksik, J. Moore, N. Islam and M. J. Uddin, Emergent Mater., 2018, 1, 133–154 CrossRef CAS.
- H. Tang, S. He and C. Peng, Nanoscale Res. Lett., 2017, 12, 1–8 CrossRef CAS PubMed.
- L. Meng, J. You and Y. Yang, Nat. Commun., 2018, 9, 5265 CrossRef CAS PubMed.
- J. P. Correa-Baena, M. Saliba, T. Buonassisi, M. Grätzel, A. Abate, W. Tress and A. Hagfeldt, Science, 2017, 358, 739–744 CrossRef CAS PubMed.
- J. Y. Kim, J. W. Lee, H. S. Jung, H. Shin and N. G. Park, Chem. Rev., 2020, 120, 7867–7918 CrossRef CAS PubMed.
- D. Marongiu, S. Lai, V. Sarritzu, E. Pinna, G. Mula, M. L. Mercuri, M. Saba, F. Quochi, A. Mura and G. Bongiovanni, ACS Appl. Mater. Interfaces, 2019, 11, 10021–10027 CrossRef CAS PubMed.
- A. B. Nikolskaia, M. F. Vildanova, S. S. Kozlov and O. I. Shevaleevskiy, Russ. Chem. Bull., 2020, 69, 1245–1252 CrossRef CAS.
- C. D. Bailie and M. D. McGehee, MRS Bull., 2015, 40, 681–686 CrossRef CAS.
- S. Kang, J. Jeong, S. Cho, Y. J. Yoon, S. Park, S. Lim, J. Y. Kim and H. Ko, J. Mater. Chem. A, 2019, 7, 1107–1114 RSC.
- Z. Song, C. L. McElvany, A. B. Phillips, I. Celik, P. W. Krantz, S. C. Watthage, G. K. Liyanage, D. Apul and M. J. Heben, Energy Environ. Sci., 2017, 10, 1297–1305 RSC.
- C. Momblona, L. Gil-Escrig, E. Bandiello, E. M. Hutter, M. Sessolo, K. Lederer, J. Blochwitz-Nimoth and H. J. Bolink, Energy Environ. Sci., 2016, 9, 3456–3463 RSC.
- F. Azri, A. Meftah, N. Sengouga and A. Meftah, Sol. Energy, 2019, 181, 372–378 CrossRef CAS.
- K. D. Jayan and V. Sebastian, Sol. Energy, 2021, 217, 40–48 CrossRef.
- S. Gholipour, J. P. Correa-Baena, K. Domanski, T. Matsui, L. Steier, F. Giordano, F. Tajabadi, W. Tress, M. Saliba, A. Abate and A. A. Morteza, Adv. Energy Mater., 2016, 6, 1601116 CrossRef.
- M. Xiao, F. Huang, W. Huang, Y. Dkhissi, Y. Zhu, J. Etheridge, A. Gray-Weale, U. Bach, Y. B. Cheng and L. Spiccia, Angew. Chem., Int. Ed., 2014, 53, 9898–9903 CrossRef CAS PubMed.
- S. S. Mali, C. K. Hong, A. I. Inamdar, H. Im and S. E. Shim, Nanoscale, 2017, 9, 3095–3104 RSC.
- Ç. Odabaşı and R. Yıldırım, Nano Energy, 2019, 56, 770–791 CrossRef.
- Ç. Odabaşı and R. Yıldırım, Sol. Energy Mater. Sol. Cells, 2020, 205, 110284 CrossRef.
- J. Jacobsson, A. Hultqvist, A. G. Fernández, A. Anand, A. A. Ashouri, A. Hagfeldt, A. Crovetto, A. Abate, A. G. Ricciardulli, A. Vijayan, A. Kulkarni, A. Y. Anderson, B. P. Darwich, B. Yang, B. L. Coles, C. A. R. Perini, C. Rehermann, D. Ramirez, D. F. Jimenez, D. D. Girolamo, D. Jia, E. Avila, E. J. J. Perez, F. Baumann, F. Mathies, G. S. A. González, G. Boschloo, G. Nasti, G. Paramasivam, G. M. Denegri, H. Näsström, H. Michaels, H. Köbler, H. Wu, I. Benesperi, M. I. Dar, I. B. Pehlivan, I. E. Gould, J. N. Vagott, J. Dagar, J. K. J. Yang, J. Li, J. A. Smith, J. Pascual, J. J. J. Rendón, J. F. Montoya, J. P. C. Baena, J. Qiu, J. Wang, K. Sveinbjörnsson, K. Hirselandt, K. Dey, K. Frohna, L. Mathies, L. A. Castriotta, M. H. Aldamasy, M. V. Montoya, M. A. R. Preciado, M. A. Flatken, M. V. Khenkin, M. Grischek, M. Kedia, M. Saliba, M. Anaya, M. Veldhoen, N. Arora, O. Shargaieva, O. Maus, O. S. Game, O. Yudilevich, P. Fassl, Q. Zhou, R. Betancur, R. Munir, R. Patidar, S. D. Stranks, S. Alam, S. Kar, T. Unold, T. Abzieher, T. Edvinsson, T. W. David, U. W. Paetzold, W. Zia, W. Fu, W. Zuo, V. R. F. Schröder, W. Tress, X. Zhang, Y. H. Chiang, Z. Iqbal, Z. Xie and E. Unger, Nat. Energy, 2022, 7, 107–115 CrossRef.
- Z. Zhang, H. Wang, T. J. Jacobsson and J. Luo, Nat. Commun., 2022, 13, 7639 CrossRef CAS PubMed.
- J. Thiesbrummel, F. Peña-Camargo, K. O. Brinkmann, E. Gutierrez-Partida, F. Yang, J. Warby, S. Albrecht, D. Neher, T. Riedl, H. J. Snaith and M. Stolterfoht, Adv. Energy Mater., 2023, 13, 2202674 CrossRef CAS.
- A. Y. T. Wang, R. J. Murdock, S. K. Kauwe, A. O. Oliynyk, A. Gurlo, J. Brgoch, K. A. Persson and T. D. Sparks, Chem. Mater., 2020, 32, 4954–4965 CrossRef CAS.
- A. O. Oliynyk, E. Antono, T. D. Sparks, L. Ghadbeigi, M. W. Gaultois, B. Meredig and A. Mar, Chem. Mater., 2016, 28, 7324–7331 CrossRef CAS.
- L. Ward, A. Agrawal, A. Choudhary and C. Wolverton, npj. Comput. Mater., 2016, 2, 1–7 CrossRef.
- V. Tshitoyan, J. Dagdelen, L. Weston, A. Dunn, Z. Rong, O. Kononova, K. A. Persson, G. Ceder and A. Jain, Nature, 2019, 571, 95–98 CrossRef CAS PubMed.
- S. M. Lundberg and S. I. Lee, Adv. NIPS, 2017, 30 Search PubMed.
- G. Kieslich, S. Sun and A. K. Cheetham, Chem. Sci., 2015, 6, 3430–3433 RSC.
- Y. Miyake and A. Saeki, J. Phys. Chem. Lett., 2021, 12, 12391–12401 CrossRef CAS PubMed.
- Y. Miyake, K. Kranthiraja, F. Ishiwari and A. Saeki, Chem. Mater., 2022, 34, 6912–6920 CrossRef CAS.
- S. van Buuren, Flexible Imputation of Missing Data, Chapman and Hall/CRC, 2018, 2nd edn Search PubMed.
- K. Hatakeyama-Sato, M. Umeki, H. Adachi, N. Kuwata, G. Hasegawa and K. Oyaizu, npj. Comput. Mater., 2022, 8, 170 CrossRef.
- D. Takagi, K. Ishizaki, T. Asahi and T. Taniguchi, Digital Discovery, 2023, 2, 1126–1133 RSC.
- C. Gao, H. Dong, X. Bao, Y. Zhang, A. Saparbaev, L. Yu, S. Wen, R. Yang and L. Dong, J. Mater. Chem. C, 2018, 6, 8234–8241 RSC.
- S. Wang, J. Hu, A. Wang, Y. Cui, B. Chen, X. Niu and F. Hao, J. Energy Chem., 2022, 66, 422–428 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d3ya00617d |
| This journal is © The Royal Society of Chemistry 2024 |