Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Teaching an old dog new tricks: Ti-doped ZnFe2O4 as active material in zinc ion batteries – a proof of concept†
S.
Krämer‡
 a,
J.
Hopster‡
a,
J.
Hopster‡
 ab,
A.
Windmüller
ab,
A.
Windmüller
 c,
R.-A.
Eichel
c,
R.-A.
Eichel
 ce,
M.
Grünebaum
ce,
M.
Grünebaum
 a,
T.
Jüstel
a,
T.
Jüstel
 b,
M.
Winter
b,
M.
Winter
 ad and
K.
Neuhaus
ad and
K.
Neuhaus
 *a
*a
aForschungszentrum Jülich GmbH, Institute of Energy and Climate Research IEK-12: Helmholtz Institute Münster (HI MS), Corrensstr. 46, 48149 Münster, Germany. E-mail: k.neuhaus@fz-juelich.de
bFachhochschule Münster, Department of Chemical Engineering, Stegerwaldstraße 39, 48565 Steinfurt, Germany
cForschungszentrum Jülich GmbH, Institute of Energy and Climate Research IEK-9: Fundamental Electrochemistry, 52425 Jülich, Germany
dUniversity of Münster, MEET Battery Research Center, Institute of Physical Chemistry, Corrensstr. 46, 48149 Münster, Germany
eInstitute of Physical Chemistry, RWTH Aachen University, Landoltweg 2, 52074 Aachen, Germany
First published on 10th June 2024
Abstract
In this work, the suitability of the spinel material ZnFe2O4, which has already been widely investigated in the context of its magnetic and photocatalytic properties, for use as active material for the cathode side in zinc ion batteries is presented. In addition to pure ZnFe2O4, part of the Fe3+ was doped with Ti4+ to achieve stabilization of Zn vacancies in the material and increase ionic conductivity as indicated by previous modelling results. Ceramic samples with the composition ZnFe2−xTixO4 (x = 0 to 0.25) were prepared via a Pechini synthesis route and investigated regarding their optical, structural and electrochemical characteristics. It has been successfully demonstrated that both pure and Ti doped ZnFe2O4 can be used as active material in the positive electrodes of zinc metal batteries or in an “anode-free” setup with Sn metal. Cells with calcined ZnFe2xTixO4 (x = 0.09)|0.5 M zinc triflate in acetonitrile|Zn showed a stable cycling behavior over 1000 cycles and an average initial specific capacity of 55 mA h g−1.
1 Introduction
ZnFe2O4 is a well-investigated, versatile material with a spinel structure, which reportedly shows electrical conductivity in the range of 5 to 10 mS cm−1, a relatively small electronic bandgap of about 1.9 eV and values of 2.02 eV and 2.33 eV for the indirect and direct optical band gap.1 Apart from the low production price, the high and globally uniform availability of the constituents, high chemical stability against air or moisture and the harmlessness with regard to health and the environment, these characteristics make it an ideal candidate for photocatalytic or energy harvesting applications. In addition, nanostructured ZnFe2O4 has gained interest because depending on the size of the nanostructure and the synthesis method, Zn and Fe can partially exchange sites in the crystal structure. The degree of cation exchange allows tuning of the electronic and spin structure of the material making it interesting for various uses ranging from spintronic and microwave applications to sensor materials.1In the field of energy storage, ZnFe2O4 has previously been discussed as possible material for the negative electrode in lithium ion batteries (LIB). Even though its high theoretical capacity of 1072 A h kg−1 as well as its low toxicity compared to conventional Co- and Ni-containing compounds and the low production costs make it highly attractive, further investigations showed that the cycle stability is less than ideal, because the ZnFe2O4 breaks down to ZnO and Fe2O3 during repeated charging and discharging in a cell and metal ion dissolution takes place.2 In addition, the energy efficiency is very low.3 Still, various studies have been conducted that either condone decomposition since even the decay products still work well as negative electrode or do not charge and discharge over the full voltage window (shallow cycling) to prevent decomposition.4
Recently, theoretical studies by Morkhova et al.5 and Liu et al.6 indicated that, like ZnMn2O4, ZnFe2O4 could be very promising as active material for the positive electrode of zinc ion batteries (ZIB). Interestingly, the term zinc ion battery is also used for cell configurations contain Zn–metal anodes, which would be better called Zn metal batteries (ZMB). This logical differentiation is similar to that for lithium ion batteries (LIB) and lithium metal batteries (LMB).
The prerequisite for use as reversible cathode are zinc vacancies that have to be introduced in the structure. To this end, Morkhova et al.5 substituted part of the Fe3+ with Fe4+ to introduce zinc vacancies and their DFT modelling results showed a low zinc vacancy formation energy of 0.46 eV and a small migration energy barrier of 0.54 eV. The volumetric capacity of a ZnFe2O4 positive electrode was calculated to be 1142 mA h cm−3.5,6 Liu et al. calculate a voltage of 2.5 V for the hypothetical reaction Fe2O4 + Zn2+ → ZnFe2O4 + 2e−, a theoretical specific energy of 600 W h kg−1 and a theoretical specific capacity of 225 mA h g−1.6 This would also make the material competitive with regards to other cathode materials already in use and it would also be feasible for use with other anode materials with a higher standard potential than zinc metal like e.g. 9,10-anthraquinone.7
In literature, the closely related spinel-structured material ZnMn2O4 has already been successfully applied as positive electrode material in aqueous zinc metal batteries (AZMB).8–11 When applied with zinc metal as negative electrode, potentials in the range of 1.2 V vs. Zn|Zn2+ and specific capacities in the range of up to 220 mA h g−1 were reached8,10,12 in combination with good cycling stability and capacity retention. To promote performance, strategies so far were addressing an increase in defect concentration: manganese vacancies or oxygen vacancies were found to promote Zn ion conductivity,8,13 additional conductive coating e.g. with carbon or combination with carbon nanotubes, graphene etc. to promote electronic conductivity,9–11 and optimization of the microstructure to enhance the surface area.8 For pristine, sintered ZnMn2O4, the measured specific capacities were rather low in contrast: 25 or 7 mA h g−1 for 0.5 and 8 A g−1 in a cell setup with ZnMn2O4|1 M ZnSO4|Zn, respectively.13 Hence, very low capacities can also be expected for undoped, sintered ZnFe2O4 without further optimization for application.
Although various approaches on doping strategies for ZnFe2O4 have been shown in order to optimize electron conductivity, band gap and magnetic properties, no reports on experimental results for the use of (doped) ZnFe2O4 in context of promoting Zn ion conductivity or application in zinc batteries have been published so far to our knowledge. Of course, it is reasonable to expect that – similar to ZnMn2O4 – pure ZnFe2O4 without A-site vacancies will show a suboptimal cell performance when comparing calculations to reality and that the calculated standard redox potential is somewhat overestimated. But even if only a fraction of the theoretical energy density could be achieved under real conditions such an active material would still be competitive compared to the variety of manganese oxide or vanadium-based active materials already under investigation.12
Since under lab conditions, substitution of Fe3+ with Fe4+ to booster zinc vacancy formation as proposed by Morkhova et al.5 is not feasible, in the present study, ZnFe2O4 was doped with Ti4+. We expect that the Ti4+ aliovalent substitution of either Zn2+ or Fe3+ has to be compensated by a valence change of Fe3+ to Fe2+ or defect formation according to
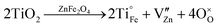 | (1) |
Increasing the intrinsic zinc vacancy concentration would enable the development of interconnected transport pathways or, ideally, the formation of a percolation network for zinc ion transport within the particles, which would ensure the utilization of the capacity for zinc ion uptake and release of an entire particle and not just the outer layers when (dis)charging the cell. Ideally, an easier access to the particle cores would counterbalance or even outweigh the lowered zinc ion uptake capacity.
Previous studies for photocatalytic applications found Ti4+ to work as an n-type dopant in ZnFe2O4, leading to increased electronic conductivity14 with an optimum around 6 cat% Ti doping referring to the B site cations (Zn0.94Fe1.88Ti0.12O4)15 and that Ti addition has no effect on the band structure of the material. Others find ZnFe2O4 to have the best electronic conductivity which decreases with increasing substitution with Ti.16 Indeed, ref. 16 and 17 postulate a small polaron hopping process for electronic conduction in ZnFe2O4via Fe3+/2+ cations, which means interruption of electron percolation pathways by high Ti4+ concentrations on the B place.
Apart from the effect on conductivity, Ti4+ could have another beneficial effect: it is likely that pure ZnFe2O4 in contact with liquid electrolyte could decompose by charging and discharging processes to Fe2O3 and ZnO in the same way as has been observed in lithium ion batteries. Therefore, stabilization of the material in the discharged state by the addition of a tetravalent cation on the B site seems a reasonable pathway to increase cycling stability.
In the present study, samples with the compositions ZnFe2−xTixO4 (with x = 0 to 0.25) were produced by a Pechini synthesis route. The crystal structure, microstructure, optical and electrochemical characteristics of the material were analyzed and compared to literature results.
2 Results and discussion
2.1 Structural analysis
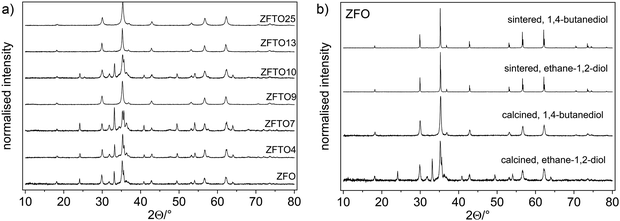
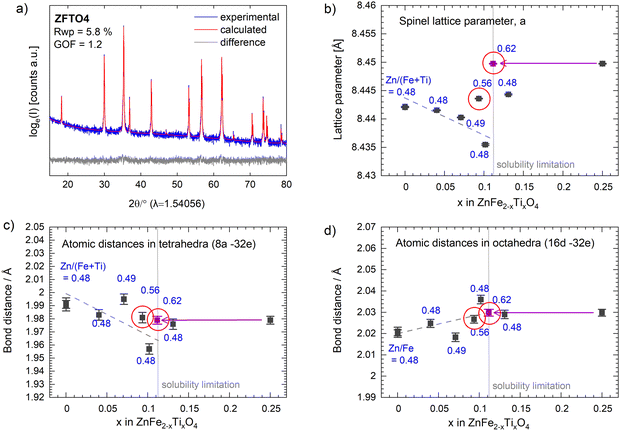
PPXRD measurements of the powders after calcination showed a small content of additional oxides for samples produced using ethane-1,2-diol (ZFO, ZFTO4, ZFTO7 and ZFTO10). The additional reflexes were attributed mainly to Fe2O3 (PDF 01-073-3825) and ZnO (PDF 01-081-8838). In contrast, the samples produced using 1,2-butanediol (ZFTO9, ZFTO13 and ZFTO25 as shown in Fig. 1a) showed a much smaller content of secondary phases. This can also be observed by comparing the PPXRD spectra of ZFO either prepared with ethane-1,2-diol or 1,2-butanediol (Fig. 1b).Further analysis of the PPXRD data was performed to gather information on the position of Ti in the structure and to determine a limit of Ti solubility. Fig. 2a shows an exemplary fit for ZFTO4 sample. The Supporting Information contains an overview of all fits and results of the refined parameters (Fig. S1 and Table S1, ESI†) according to the Rietveld analysis of the spinel structure based on Cu-Kα PPXRD data.
The model structure was based on a “normal” spinel structure with [Zn]8a[Fe2]16dO432e. The refinement considered the fractional coordinate of the x = y = z position of the oxygen atom at the 32e site, while 8a and 16d are special positions with no degree of freedom. For Ti doped samples, Ti occupancies were allowed to refine, but constrained to yield full occupancies at the specific sites. That is Ti + Zn in the tetrahedral 8a site equals 1 and Ti + Fe in the octahedral 16d site equals 1. However, due to the very similar structure factors of Ti, Fe and Zn and the very low doping concentrations, there was no least squares minimization achieved considering the Ti occupancies and thus Ti occupancies were not considered throughout the whole analysis. Based on the described model the fits converged with weighted pattern residuals (Rwp) below 7% and goodness-of-fit (GOF) below 1.3 for all samples (individual Rwp and GOF values are provided with Fig. S1, ESI†).
The refined lattice parameters lay in the range of 8.4354 to 8.4498 Å (Fig. 2b), which is a total deviation of only 0.17%. This small change in lattice parameter is understandable from the very low doping concentrations, even though Ti4+ (if tetrahedrally coordinated) has a considerable smaller ionic radius (0.42 Å) than the other involved cations (Zn2+ IV: 0.6 Å; Fe3+ VI HS: 0.645 Å, Ti4+ VI: 0.605 Å).18 The cationic distribution of ZnFe2O4 spinels is well known to be “normal”, meaning Zn2+ occupies the tetrahedral site, whereas Fe3+ occupies the octahedral sites. Ti4+ can enter the tetrahedral or octahedral site, because its electronic configuration does not lead to an energetic preference for either side.19
As suspected, we observe significant secondary phase formation for the ZFTO25 sample, with the highest Ti concentration. Here, Fe2TiO5 is identified in spacegroup C2/m and quantified to a relative weight fraction of 9.7 ± 0.1 wt%. The formation of the Fe rich secondary phase depletes the remaining spinel in Ti and Fe, leading to a calculated stoichiometry of Zn1.15Fe1.74Ti0.11O4. Accordingly, Ti4+ in a concentration of 0.11 mol per formula unit demonstrates the solubility limit of Ti4+ in spinel ZnFe2O4 in this experimental series. The lattice parameter evolution below that solubility limit now displays a decreasing trend (dashed line in Fig. 2b). The red circled data points have a Zn/(Fe + Ti) molar ratio higher than 0.55, meaning a significant part of Zn is forced to occupy the octahedral site in spinel in these samples. Therefore, these values are not considered for the lattice parameter trends upon Ti doping with a Zn/(Fi + Ti) molar ratio of around 0.5. It can be noted that the Zn/(Fe + Ti) ratios and also the Zn/Fe molar ratios (Table S2, ESI†) vary from sample to sample, explaining the scattering of the data points along the trend line. However, the decreasing trend of the lattice parameter evolution upon Ti4+ doping can be very well understood from the doping of the smaller Ti4+ onto either the tetrahedral site or the octahedral site. The results confirm the successful Ti4+ insertion into ZnFe2O4 for Ti4+ concentrations below 0.11 mol per formula unit.
Furthermore, the comparably larger lattice parameters of the spinel compounds above the Ti4+ solubility limit in ZnFe2O4 can be understood from the Zn2+ enrichment at the octahedral site. This happens, when the spinel main phase depletes in Fe upon formation of Fe rich Ti containing secondary phases, as the observed Fe2TiO5. The depletion will cause a site mixing of the larger Zn2+ and new Fe2+ cations at octahedral and tetrahedral sites and thus an overall lattice expansion. From this result, we also have to assume that the ZFTO13 sample, which lies sharply behind the solubility limit contains secondary phases (probably Fe2TiO5). Most likely it was failed to be detected in PPXRD due to its very low weight fraction and the high Fe-fluorescence caused background in the given diffractograms. However, the rather large lattice parameter of ZFTO13 strongly suggests Zn enrichment (and thus Fe depletion) in the spinel main phase. Furthermore, even the deviation of the lattice parameter of the sample ZFTO9 can be well explained by the higher Zn(Fe + Ti) molar ratio (0.56) and the occupation of the excess Zn2+ at octahedral sites.
Upon the Rietveld refinement, the x = y = z fractional coordinate of oxygen in the unit cell was refined. In an ideal case, this fractional coordinate is 0.25 and resembles an ideal cubic close packed oxygen sublattice within the spinel lattice. However, x changes with the sizes of the tetrahedrally and octahedrally coordinated cations.20 The refined oxygen position was thus used to calculate the atomic distances in the tetrahedral and octahedral coordination (Fig. 2c and d). Below the solubility limit, a decreasing trend (1.2% decrease) in the bond distances in the tetrahedral configuration can be observed, while a slightly increasing trend for the octahedral coordination (0.4%) can be observed. The counterbalancing of the polyhedral volumes, meaning the octahedral volume increases while the tetrahedral volumes decreases and vice versa, is typical for the corner shared tetrahedra and octahedra in spinels.20 Our observation, however, strongly suggests that the insertion of Ti4+ majorly happens at the tetrahedral site, with the much smaller IV Ti4+ (0.42 Å) causing the tetrahedral polyhedra to shrink and leading to the overall decrease in unit cell volume – as also observed from the lattice parameter trends below 0.11 mol Ti per formula unit.
2.2 Microstructure characterization and magnetic characteristics
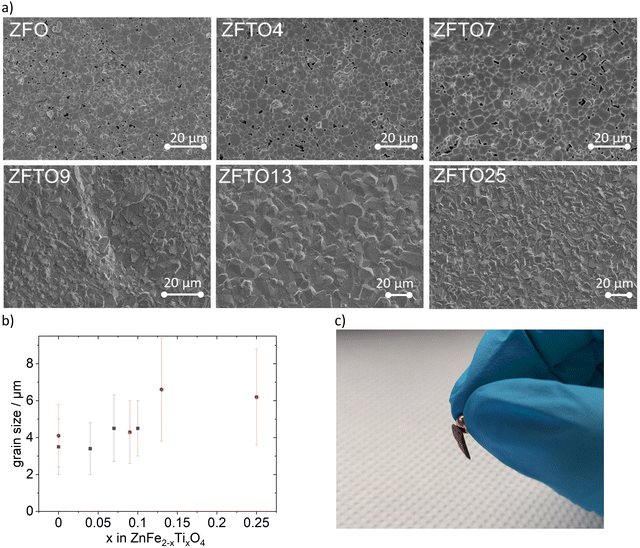
SEM measurements (cf.Fig. 3a) showed slightly increased grain sizes for Ti doped samples compared to the pristine ZFO, but the standard deviation for all samples was relatively high (cf.Fig. 3b). The grain size distribution of ZnFe2O4 when prepared using ethylene glycol or 1,2-butanediol (red dot in Fig. 3b) did not differ notably.All obtained samples could be picked up with a standard magnet (cf.Fig. 3c). This is an advantage for later material recovery for recycling if used in composite materials.
2.3 Electrochemical and optical analysis
Fig. 4a–d shows the electronic conductivity for all samples as measured by impedance spectroscopy. For impedance spectra analysis, an equivalent circuit consisting of a resistor (R_GI and R_GB) and a constant phase element (CPE_GI and CPE_GB) in parallel for the grain interior (GI) and the grain boundary (GB) resistance were used, as depicted in Fig. 4d.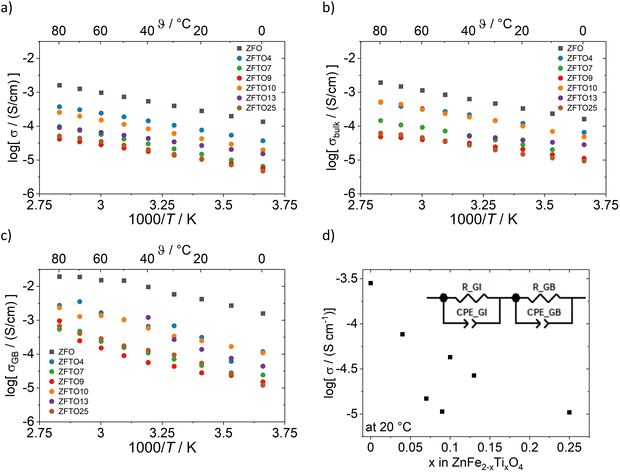 | ||
| Fig. 4 Conductivity values for sintered pellets from impedance spectroscopy measurements with ion blocking contacts: (a) total conductivity, (b) bulk conductivity, (c) grain boundary conductivity. For ZFTO13, bulk and grain boundary contribution were not distinguishable at temperatures above 40 °C in all measurements. (d) Total conductivity at 20 °C and the equivalent circuit used for impedance spectroscopy analysis (GI stands for grain interior and GB for grain boundary). For the total electronic conductivity shown in (a) and (d), the sample density was taken into account for the cell constant, as it was below 95% for all samples (see Table S3, ESI†). | ||
Impedance spectroscopy measurements showed that all samples have a comparably high electronic conductivity which decreases with Ti addition (cf.Fig. 4), which is in accordance to findings by ref. 16. The decrease is not linear but there is a drop in conductivity and then a local maximum around x = 0.1, as depicted in Fig. 4d. The especially low conductivity of ZTFO9 could possibly at least partly be explained by the comparably high Zn concentration of this sample (cf.Table 3). The conductivity of the ZFO samples prepared using ethane-1,2-diol and 1,2-butanediol did not differ within the margin of measurement error.
The grain boundaries show a higher electronic conductivity than the bulk in impedance spectroscopy measurements, but also a higher activation energy compared to the bulk transport, while the activation energy for electron transport at the grain boundaries is strongly increased (cf.Table 1). Total activation energies were in the range between 0.31 to 0.21 eV with a minimum for ZFTO13. The low activation energies, which are in good agreement with ref. 17, suggest that the dominant process for electronic conduction in the samples is small polaron hopping via the Fe3+ cations.
| Sample | E A,total/eV | E A,bulk/eV | E A,GB/eV |
|---|---|---|---|
| ZFO | 0.29 ± 0.01 | 0.28 ± 0.01 | 0.30 ± 0.01 |
| ZFTO4 | 0.27 ± 0.01 | 0.21 ± 0.01 | 0.42 ± 0.03 |
| ZFTO7 | 0.31 ± 0.01 | 0.29 ± 0.01 | 0.36 ± 0.02 |
| ZFTO9 | 0.23 ± 0.01 | 0.18 ± 0.01 | 0.38 ± 0.03 |
| ZFTO10 | 0.29 ± 0.01 | 0.27 ± 0.01 | 0.25 ± 0.01 |
| ZFTO13 | 0.21 ± 0.01 | 0.14 ± 0.01 | 0.58 ± 0.01 |
| ZFTO25 | 0.28 ± 0.01 | 0.24 ± 0.01 | 0.42 ± 0.01 |
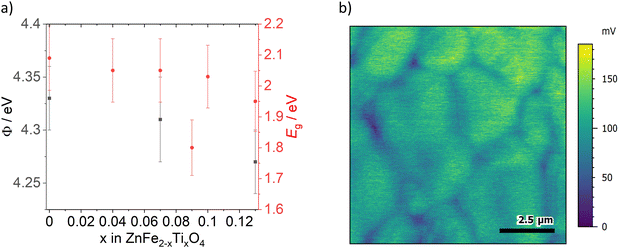
Kelvin probe force microscopy measurements of ZFO, ZFTO7 and ZFTO13 showed a slight decrease in work function with increasing Ti content (Fig. 5a). In addition, it was observed that for all measured samples, the grain boundaries showed a lower surface potential compared to the grain interiors (Fig. 5b). The difference was evaluated for 25 different grain boundary position in the three samples, but the potential difference for the samples did not depend on the Ti concentration and was roughly in the range of 25 mV, but with a large variation between individual grain boundaries (cf. Fig. S2, ESI†). It can therefore be assumed that this difference is merely due to band bending, which can typically be found at grain boundaries due to the different crystallographic orientation of adjacent grains.21
The optical band gap energy for all materials (cf.Fig. 5a) was calculated from reflection measurements. It is in the range between 2.1 and 1.9 eV. The value of 2.09 ± 0.10 eV for pure ZnFe2O4 is in good accordance to the literature value of 2.02 eV,1 and agrees roughly with the modelling results of Morkhova et al., who predict an electronic band gap energy of 1.694 eV (optical band gap energy is always ∼200–400 meV higher than electronic band gap energy as it includes the exciton binding energy).
Please note that, in correspondence to the electronic conductivity measurements, ZFTO9 shows a distinctly other reflection behavior and band gap energy then the other samples (see Tauc plot in Fig. S3, ESI†) and also a slightly darker color. This is probably due to the comparably high Zn concentration in the material compared to the other samples (cf.Table 3). In accordance to the findings of Guo et al.,15 no pronounced effect of Ti addition on the band gap is apparent.
2.4 Application in a cell
Three samples were chosen for final battery testing: (i) sintered, undoped ZFO prepared with 1,4-butanediol (ii) sintered ZFTO13 (which already shows onset of secondary phase formation but probably has the highest Ti-concentration in the ZFTO phase), and (iii) calcined ZFTO9, since this material showed slightly higher Zn concentrations than the other samples and is deemed well below onset of secondary phase formation.To prevent this, in analogy to cells with ZnMn2O4 active material, Fe3+ ions in form of salt additives were added to the electrolyte to stop Fe3+ leaching.12 Iron salts are often poorly soluble in water. Addition of the highly soluble Fe(NO3)3 to the 3 M zinc triflate solution leads to an unfavorably low pH (around 1) and addition of FeSO4 leads to instantaneous formation and precipitation of Fe(OH)3, which was only re-solvable by addition of HNO3. Due to this, iron gluconate dihydrate (C12H22FeO14·2H2O) was tested as environmentally benign iron source for the electrolyte, but the pH of the electrolyte was lowered to pH 2 and the cyclisation was only marginally improved in comparison with pure zinc triflate solution. For all tested additive salts, the gas formation due to low pH led to abortion of the CV measurements in the first cycle.
Galvanostatic cycling in symmetric cells with two ZFO or ZFTO9 shows that a shuttle of Zn2+ ions between to two electrodes is possible for around 800 cycles (cf. Fig. S5, ESI†). Nevertheless, for ZFTO9 the overvoltage of 1.8 V is quite high. In full cell this leads to the aggravated de-/insertion of Zn2+ ions and thus to a low specific capacity upon galvanostatic cycling (cf.Fig. 7).
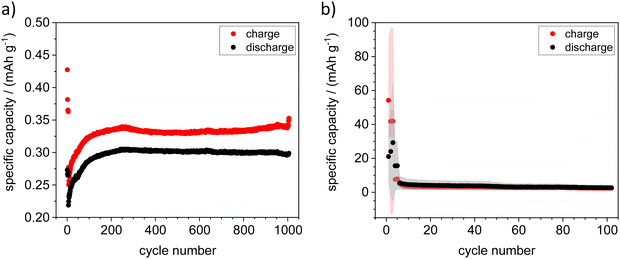
Cyclization with Zn metal sheet as the negative electrode was possible in some cases, but the results were not reproducible. The cycling behavior and reproducibility of the cells improved dramatically when a sputtered Zn thin film on Ti sheet was used as the negative electrode. As the sputtered electrodes were transferred to a glovebox directly after the sputtering process, no passivation layer could build up here, which greatly improved the performance of the cells and lead to an average initial specific capacity of 55 mA h g−1 (cf.Fig. 7). Although the specific capacity decreased after ten cycles, it remained ten times higher over 100 cycles than the initial capacity for cycling against Zn metal sheet. In addition, we were also able to obtain easily reproducible results in an “anode-free” setup with Sn metal sheet as a negative electrode.
For ZFTO13, no galvanostatic cycling in symmetric and full cells was possible at all. Impedance measurements, performed on uncycled full cells, reveal that for ZFTO13 in comparison to ZFTO9 the charge transfer resistance for Zn2+ ions at the electrode–electrolyte interface is even higher with about 500 Ω (cf.Fig. 8), which can potentially already be attributed to secondary phases in the material.
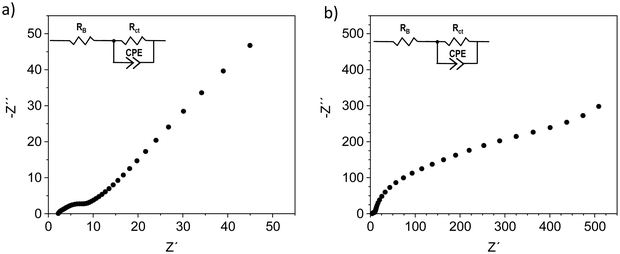 | ||
| Fig. 8 Impedance measurement with (a) ZFTO9‖Sn and (b) ZFTO13‖Sn. The error of fitting was below 3% using the given equivalent circuit. | ||
Apart from this, the cell tests show that material is not yet optimized for the use as cathode active material, but has potential for reversible Zn2+ de-/insertion.
SEM measurements of the electrode sheets showed that the active material particles were comparatively large in size (between 10–80 μm, cf. Fig. S6, ESI†) and also had a broad size distribution, which is not optimal for cell performance. Smaller particle sizes can enhance the electrochemical performance of cathode materials in zinc batteries. For instance, in a study by ref. 23 reducing the particle size of manganese sesquioxide nearly tripled the initial capacity of aqueous zinc ion batteries (from d50 = 8.51 μm with 50 mA h g−1 to d50 = 3.21 with 140 mA h g−1), although smaller particles were also associated with accelerated aging processes and increased internal resistance during cycling. Basically, the improvement can be attributed to reduced diffusion limitations when there are many small particles instead of one large particle,24 although in the case of manganese sesquioxide smaller particles were also associated with accelerated aging processes and increased internal resistance during cycling.
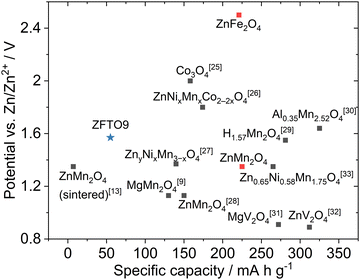
Even though the specific capacities for ZFTO and pure ZFO achieved in this study were low, the material could still be competitive with other oxidic spinels in ZMB/ZIB in the future with appropriate optimization of particle size and morphology. The performance of various spinels as active materials in the positive electrode in ZMB is plotted in the overview shown in Fig. 9. The specific capacity of the material presented here (blue star) is better than that of unoptimized ZnMn2O4 (ZnMn2O4 sintered in Fig. 9), while the potential obtained is clearly above what is theoretically possible for ZnMn2O4 (red square). However, the theoretically determined, very high potential of ZnFe2O4 from ref. 5 and 6 (also indicated in red) was definitely not reached.
3 Conclusions and outlook
It has been demonstrated that pure and Ti-doped ZnFe2O4 can be applied as active material at the positive electrode in ZIBs and ZMBs. As was to be expected, however, the measured specific capacities are very low, as the powder morphology has not yet been optimized for use as an active material. However, the capacities are higher than those of sintered, unoptimized ZnMn2O4.13With regard to material analytics, we can conclude that Ti4+ does not work as a typical n-type dopant in ZnFe2O4 because the work function slightly decreases with increasing Ti4+ addition, and also the activation energies for electron transport are in good accordance to the theory that electronic conductivity in ZnFe2O4 is governed by small polaron hopping via Fe cations. Accordingly, the electronic conductivity is reduced by Ti addition, although in total, the electronic conductivity of the Ti-doped materials is still on a high level with a range of roughly 0.01 to 0.1 mS cm−1 at 20 °C. However, we cannot ultimately explain the effect: most likely option is the interruption of small polaron hopping pathways by Ti4+ introduction.
It was shown that the concentration of titanium is limited to a maximum of x = 0.11. In our study, pure zinc ferrite and material with low Ti concentrations (specifically x = 0.09) was found to work as active material in ZIBs. Samples above the solubility limit of Ti (in our case x = 0.13) did not show a stable cycling behavior. Addition of higher amounts of Ti is hence not deemed favorable to improve application of ZnFe2O4 as active material in zinc batteries.
From studies on the use of ZnFe2O4 and ZnMn2O4 in various electrochemical applications, a variety of synthesis methods are already known for micro-structuring the material in order to increase the surface area and enable more effective use, ideally in combination with an electron conductive coating. This is a future target to considerably improve performance, especially the capacity, of ZnFe2O4-based materials for use in zinc metal and zinc ion batteries.
4 Methods
4.1 Materials synthesis
| Compound | Formula | Purity | Manufacturer |
|---|---|---|---|
| Zinc nitrate hexahydrate | Zn(NO3)2·6H2O | ≥99% | Sigma-Aldrich |
| Iron nitrate nonahydrate | Fe(NO3)3·9H2O | ≥98% | Sigma-Aldrich |
| Titanium isopropoxide | TiC12H28O4 | 97% | Sigma-Aldrich |
| Citric acid monohydrate | C6H8O7·H2O | p.a. | Sigma-Aldrich |
| Ethane-1,2-diol | C2H6O2 | ≥99% | Sigma-Aldrich |
| Nitric acid | HNO3 | 65% | Fisher Scientific |
| 1,4-Butanediol | C4H10O2 | ≥99% | Merck |
The Pechini synthesis was adapted from ref. 34 and 35: as titanium nitrate is not readily solvable in water, a soluble titanyl nitrate solution (TiO(NO3)2) was produced using titanium isopropoxide and nitric acid as educts:34 titanium isopropoxide was mixed with water and the resulting fine titanium hydrate was thoroughly washed with water and then re-dissolved with HNO3 to form a TiO(NO3)2 solution, which was stabilized with citric acid. The titanium content of the solution was controlled using TGA (Discovery TGA 5500, Waters, USA) before using it for further synthesis steps.
For sol–gel synthesis, the nitrates and the TiO(NO3)2 solution in the desired molar ratio were combined with deionized water in a flask and stirred until completely dissolved. The solution was then heated to 50 °C and citric acid monohydrate (ncitric![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) acid = 2·ncations) and 30 minutes later ethane-1,2-diol (ndiol = 4·ncations) were added as chelating agents. The solution was then gelled at 100 °C for ∼24 h and subsequently calcined at 400 °C for 2 h and then 600 °C for 1 h with a heating/cooling rate of 5 K min−1.
acid = 2·ncations) and 30 minutes later ethane-1,2-diol (ndiol = 4·ncations) were added as chelating agents. The solution was then gelled at 100 °C for ∼24 h and subsequently calcined at 400 °C for 2 h and then 600 °C for 1 h with a heating/cooling rate of 5 K min−1.
For selected experiments, the ethane-1,2-diol in the Pechini synthesis was replaced by 1,4-butanediol. Here, a notably better calcination behavior was observed, yielding a single phase material before sintering as discussed in Section 3.1. In addition, the dried material before the calcination step was much less sticky and therefore easier to handle.
All calcined materials were thoroughly ground in an agate mortar and subsequently pressed into pellets. The pellets were fired at 1200 °C for 6 h with a heating/cooling rate of 5 K min−1 using Al2O3 sintering caskets.
Previous sintering tests were performed at temperatures between 1000–1400 °C with the same heating/cooling rate and holding time. Here, at temperatures above 1200 °C, distinct reflexes of a secondary phase (Fe2O3) were observed. Below 1200 °C, additional reflexes appear which could not be assigned exactly. Probably, they originate from an orthorhombic phase with a reasonable candidate being pseudobrookite (Fe2TiO5, PDF 00-041-1432).
The chemical composition of all sintered samples was controlled using micro-X-ray fluorescence (μXRF, M4 Tornado, Bruker, USA). Measurements were performed on the as-received samples in air. Detailed cation ratios and respective abbreviations can be found in Table 3.
| Composition | Abbreviation |
|---|---|
| Zn0.95Fe2.00O4 | ZFO |
| Zn0.97Fe1.98Ti0.04O4 | ZFTO4 |
| Zn0.97Fe1.93Ti0.07O4 | ZFTO7 |
| Zn1.04Fe1.76Ti0.09O4 | ZFTO9 |
| Zn0.96Fe1.89Ti0.1O4 | ZFTO10 |
| Zn0.97Fe1.88Ti0.13O4 | ZFTO13 |
| Zn1.06Fe1.44Ti0.25O4 | ZFTO25* |
Instead, for examination as active material in battery test cells, sintered pellets were crushed again in an agate mortar and mixed with PVDF and carbon black in a ratio of 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10
10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 10 to prepare electrode sheet. The electrode paste was stirred in NMP overnight and coated on titanium foil as current collector by using the doctor blade method. After drying at 80 °C for 6 h, the electrodes were calendared to 70% of their previous thickness and dried and annealed at 110 °C for 12 h under vacuum. The mass loading of the prepared electrodes with sintered ZFO and ZFTO13 as active material was around 3.5 mg cm−2. In parallel, the calcined powders with the composition ZFO and ZFTO9 were also used for electrode sheet production, since for ZnMn2O4, the capacity obtained for materials sintered at high temperatures was very low.
10 to prepare electrode sheet. The electrode paste was stirred in NMP overnight and coated on titanium foil as current collector by using the doctor blade method. After drying at 80 °C for 6 h, the electrodes were calendared to 70% of their previous thickness and dried and annealed at 110 °C for 12 h under vacuum. The mass loading of the prepared electrodes with sintered ZFO and ZFTO13 as active material was around 3.5 mg cm−2. In parallel, the calcined powders with the composition ZFO and ZFTO9 were also used for electrode sheet production, since for ZnMn2O4, the capacity obtained for materials sintered at high temperatures was very low.
4.2 Structural analysis and microstructure characterization
Powder X-ray diffraction (PPXRD) was measured using a D8 Advance instrument (Bruker Corporation, USA) with CuKα radiation and a 2Θ range of 10–80°. The samples were thoroughly ground in an agate mortar before measurements.Structural analysis through Pawley36 and Rietveld37 refinements based on fittings against the collected Cu-Kα PPXRD data was carried out within the software package Diffrac. Topas Version 7 (Bruker). All samples were analyzed according to the Pawley method first, to determine the lattice parameters. Spinel in spacegroup Fd![[3 with combining macron]](https://www.rsc.org/images/entities/char_0033_0304.gif) m with a lattice parameter of a = 8.44 Å was used as the starting model. Fe2TiO5 (C2/m, a = 22.28 Å, b = 3.73 Å, c = 9.80 Å, β = 116.03°) was included as secondary phase into the fitting procedure of the ZFTO25 sample. The derived lattice parameters from the Pawley method were used as starting parameters in the subsequent Rietveld analysis of the spinel structure.
m with a lattice parameter of a = 8.44 Å was used as the starting model. Fe2TiO5 (C2/m, a = 22.28 Å, b = 3.73 Å, c = 9.80 Å, β = 116.03°) was included as secondary phase into the fitting procedure of the ZFTO25 sample. The derived lattice parameters from the Pawley method were used as starting parameters in the subsequent Rietveld analysis of the spinel structure.
SEM measurements to observe grain sizes were performed using a JEOL JSM 6510, (Jeol, Japan). To ensure good sample conductivity, the samples were previously sputtered with a thin Au layer. Grain size analysis was performed using Mountains SPIP Starter 8.0 (DigitalSurf, France). To obtain the grain sizes, the largest diameter of the grains was measured for 100 grains for each sample.
4.3 Electrochemical analysis
For temperature-dependent impedance spectroscopy, ceramic pellets were sputtered with an (ion blocking) Au layer on both sides to ensure good electrode-sample contact. Measurements were performed with a Autolab M204 potentiostat/galvanostat with FRA32M module (Metrohm AG, Switzerland) at temperatures between 0 to 80 °C (temperature control: drying cabinet, Binder, Germany). All compositions were measured two to six times over the whole temperature range to ensure reproducibility of the results.Kelvin Probe Force Microscopy (KPFM) measurements were performed in an Ar atmosphere using a Cypher ES (Asylum Research/Oxford Instruments, UK) with PPP-NCSTPt tips (Nanosensors, Switzerland). The samples were used as received without further surface modification and were dried in an Ar stream in the instrument before starting the measurements. KPFM measurements yield data about the local surface potential of a sample, which under ideal conditions is directly related to the Volta potential. If Ti4+ works as an n-type dopant in ZnFe2O414 an increasing work function (which means an decreasing surface potential) with increasing Ti4+ content can be expected. Surface potential analysis was performed using Gwyddion 2.55 (GNU General Public License): the average surface potential for each sample was determined from several images. Before and after the measurements, the tip was calibrated on a freshly cleaved highly ordered pyrolytic graphite reference surface to minimize influence of tip wear on the results. KPFM Analysis for grain–grain boundary potential difference was performed with the software Mountains SPIP Starter 8.0 (DigitalSurf, France).
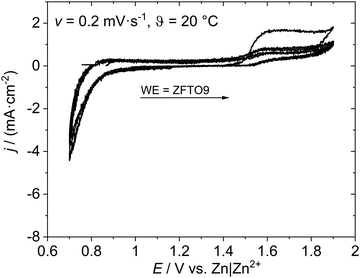
Cyclic voltammetry (CV) was performed on an Autolab M204 potentiostat (Metrohm AG, Switzerland) to determine the oxidation and reduction peaks of the synthesized materials. The measurements were done in a three-electrode arrangement in Swagelok® cells, where the positive electrode as working electrode has a circular area of 1.13 mm2. Zinc metal was used as counter (area 1.13 mm2) and reference electrode (area ∼1 mm2). As electrolyte 0.5 M zinc triflate in acetonitrile was used, which was soaked into Whatman GF-D separator. The CV measurements were performed with a scan rate of 0.2 mV s−1 for three cycles starting from the OCP value in a range between 0.7 and 1.9 V vs. Zn|Zn2+.
Measurements for electrolyte stability were conducted in a setup with platinum as working electrode (area 0.785 mm2), stainless steel as counter (area 8.635 mm2) and Ag|AgCl reference electrode (area ∼1 mm2).38 The CV measurements were performed with a scan rate of 1 mV s−1 from open circuit potential to 4 V vs. Ag|AgCl. The amount of electrolyte used in the CV cell was 250 μL.
Galvanostatic cycling experiments were performed at a Maccor® Series 4000 battery tester (Maccor Inc., Oklahoma, USA). Symmetric cell-setups were in build in coin cell (CR2032) using the two positive or negative electrodes (∅ = 12 mm) and Whatman GF-A separator (∅ = 13 mm, 1-layer) soaked with 0.5 M zinc triflate in acetonitrile. For the ones with positive electrodes, one of the electrodes was depleted of Zn2+ prior to usage in positive electrode‖Zn cell configuration, disassembled, washed with diethyl ether and then rebuild in symmetric setup. Either a current density of 0.1 mA cm−2 or a current density changing from 0.1, 0.15 to 0.2 mA cm−2 was applied. For full cell tests with Zn metal sheet and Sn metal sheet, Swagelok® cells with sintered ZFO‖metal and calcined ZFTO9‖metal were built using a Whatman GF-D separator, where 0.5 M zinc triflate in acetonitrile was used as electrolyte. Additionally, cells with the same configuration but with a negative electrode made of Ti sheet sputtered with a Zn metal thin film of about 50 nm thickness were prepared. Sputtering was performed with a Q150 S sputter (Quantum Design, USA) and a Zn target with 99.99% purity. To clean the target, a cleaning step with a sputtering current of 150 mA for 1 min was executed before sputtering the Ti sheet with 90 mA for 30 s.
The cells were galvanostatically cycled in the voltage range between 0.7 and 1.9 V with 0.1C. All different electrochemical setup working with organic electrolytes were assembled in an argon-filled glovebox (M. Braun, Germany). All measurements were performed at 20 °C.
4.4 Optical measurements
Diffuse reflectance spectra were recorded on powders produced by crushing ceramic pellets in a mortar by using an Edinburgh Instruments FS920 spectrometer combined with a PTFE-coated Ulbricht sphere. The samples were irradiated in a range from 250 to 800 nm with a 450 W xenon arc lamp. Excitation and emission wavelength were adjusted using two TMS300 monochromators with 1800 grooves per mm gratings. A Peltier cooled (−20 °C) R928 detector from Hamamatsu was used for detection. Furthermore, BaSO4 (99.99%, Sigma-Aldrich) was used as a white reflectance standard material.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors thank Marvin Oude Lansink for help with preparation equipment and oven usage and Michael Holtkamp for μXRF measurements. A patent application for Ti-doped zinc ferrite as an active material for the positive electrode has been filed with the German Patent and Trademark Office under the number 102024103447.5.References
- M. Bohra, V. Alman and R. Arras, Nanomaterials, 2021, 11(5), 1286 CrossRef CAS PubMed.
- H. Jia, R. Kloepsch, X. He, M. Evertz, S. Nowak, J. Li, M. Winter and T. Placke, Acta Chim. Slov., 2016, 63(3), 470 CrossRef CAS PubMed.
- P. Meister, H. Jia, J. Li, R. Kloepsch, M. Winter and T. Placke, Chem. Mater., 2016, 28(20), 7203 CrossRef CAS.
- M. Bini, M. Ambrosetti and D. Spada, Appl. Sci., 2021, 11(24), 11713 CrossRef CAS.
- Y. A. Morkhova, M. Rothenberger, T. Leisegang, S. Adams, V. A. Blatov and A. A. Kabanov, J. Phys. Chem. C, 2021, 125(32), 17590 CrossRef CAS.
- M. Liu, Z. Rong, R. Malik, P. Canepa, A. Jain, G. Ceder and K. A. Persson, Energy Environ. Sci., 2015, 8(3), 964 RSC.
- L. Yan, X. Zeng, Z. Li, X. Meng, D. Wei, T. Liu, M. Ling, Z. Lin and C. Liang, Mater. Today Energy, 2019, 13, 323 CrossRef.
- K. Cai, S. Luo, J. Feng, J. Wang, Y. Zhan, Q. Wang, Y. Zhang and X. Liu, Chem. Rec., 2022, 22(1), e202100169 CrossRef CAS PubMed.
- N. Zhang, F. Cheng, Y. Liu, Q. Zhao, K. Lei, C. Chen, X. Liu and J. Chen, J. Am. Ceram. Soc., 2016, 138(39), 12894 CrossRef CAS PubMed.
- L. Chen, Z. Yang, H. Qin, X. Zeng and J. Meng, J. Power Sources, 2019, 425, 162 CrossRef CAS.
- F. Gao, B. Mei, X. Xu, J. Ren, D. Zhao, Z. Zhang, Z. Wang, Y. Wu, X. Liu and Y. Zhang, Chem. Eng. J., 2022, 448, 137742 CrossRef CAS.
- G. Fang, J. Zhou, A. Pan and S. Liang, ACS Energy Lett., 2018, 3(10), 2480 CrossRef CAS.
- T.-H. Wu and W.-Y. Liang, ACS Appl. Mater. Interfaces, 2021, 13(20), 23822 CrossRef CAS PubMed.
- J. H. Kim, J. H. Kim, J. H. Kim, Y. K. Kim and J. S. Lee, Sol. RRL, 2020, 4(8), 1900328 CrossRef CAS.
- Y. Guo, N. Zhang, X. Wang, Q. Qian, S. Zhang, Z. Li and Z. Zou, J. Mater. Chem. A, 2017, 5(16), 7571 RSC.
- R. A. Grigoryan and L. A. Grigoryan, Inorg. Mater., 2004, 40(3), 295 CrossRef CAS.
- R. C. Kambale, N. R. Adhate, B. K. Chougule and Y. D. Kolekar, J. Alloys Compd., 2010, 491(1–2), 372 CrossRef CAS.
- R. D. Shannon, Acta Crystallogr., Sect. A: Cryst. Phys., Diffr., Theor. Gen. Crystallogr., 1976, 32(5), 751 CrossRef.
- R. G. Burns, Mineralogical applications of crystal field theory, Cambridge University Press, 1993 Search PubMed.
- K. E. Sickafus, J. M. Wills and N. W. Grimes, J. Am. Ceram. Soc., 1999, 82(12), 3279 CrossRef CAS.
- Z. Zhang and J. T. Yates Jr, Chem. Rev., 2012, 112(10), 5520 CrossRef CAS PubMed.
- Y. Lv, Y. Xiao, L. Ma, C. Zhi and S. Chen, Adv. Mater., 2022, 34(4), 2106409 CrossRef CAS PubMed.
- C. Bischoff, O. Fitz, C. Schiller, H. Gentischer, D. Biro and H.-M. Henning, Batteries, 2018, 4(3), 44 CrossRef.
- P. Minnmann, F. Strauss, A. Bielefeld, R. Ruess, P. Adelhelm, S. Burkhardt, S. L. Dreyer, E. Trevisanello, H. Ehrenberg and T. Brezesinski, Adv. Energy Mater., 2022, 12(35), 2201425 CrossRef CAS.
- L. Ma, S. Chen, H. Li, Z. Ruan, Z. Tang, Z. Liu, Z. Wang, Y. Huang, Z. Pei and J. A. Zapien, Energy Environ. Sci., 2018, 11(9), 2521 RSC.
- C. Pan, R. Zhang, R. G. Nuzzo and A. A. Gewirth, Adv. Energy Mater., 2018, 8(22), 1800589 CrossRef.
- J. Long, J. Gu, Z. Yang, J. Mao, J. Hao, Z. Chen and Z. Guo, J. Mater. Chem. A, 2019, 7(30), 17854 RSC.
- V. Soundharrajan, B. Sambandam, S. Kim, V. Mathew, J. Jo, S. Kim, J. Lee, S. Islam, K. Kim and Y.-K. Sun, ACS Energy Lett., 2018, 3(8), 1998 CrossRef CAS.
- Y. Wu, K. Zhang, S. Chen, Y. Liu, Y. Tao, X. Zhang, Y. Ding and S. Dai, ACS Appl. Energy Mater., 2019, 3(1), 319 CrossRef.
- D. Wang, S. Zhang, C. Li, X. Chen, W. Zhang, X. Ge, H. Lin, Z. Shi and S. Feng, Small, 2022, 18(7), 2105970 CrossRef CAS PubMed.
- W. Tang, B. Lan, C. Tang, Q. An, L. Chen, W. Zhang, C. Zuo, S. Dong and P. Luo, ACS Sustainable Chem. Eng., 2020, 8(9), 3681 CrossRef CAS.
- Y. Liu, C. Li, J. Xu, M. Ou, C. Fang, S. Sun, Y. Qiu, J. Peng, G. Lu and Q. Li, Nano Energy, 2020, 67, 104211 CrossRef CAS.
- S. Mallick, V. S. K. Choutipalli, S. Bag, V. Subramanian and C. R. Raj, ACS Appl. Mater. Interfaces, 2022, 14(33), 37577 CrossRef CAS PubMed.
- F. Schulze-Küppers, S. F. P. Ten Donkelaar, S. Baumann, P. Prigorodov, Y. J. Sohn, H. J. M. Bouwmeester, W. A. Meulenberg and O. Guillon, Sep. Purif. Technol., 2015, 147, 414 CrossRef.
- M. Gharagozlou and S. Naghibi, Prog. Color, Color. Coat., 2021, 14(2), 139 CAS.
- G. S. Pawley, J. Appl. Crystallogr., 1981, 14(6), 357 CrossRef CAS.
- H. M. Rietveld, J. Appl. Crystallogr., 1969, 2(2), 65 CrossRef CAS.
- H.-D. Wiemhöfer, M. Grünebaum and M. M. Hiller, WIPO Utility Pat., WO2014139494A1, 2014.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00134f |
| ‡ Both authors contributed equally to the manuscript. |
| This journal is © The Royal Society of Chemistry 2024 |