Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Temperature dependence of hydrogen diffusion in reservoir rocks: implications for hydrogen geologic storage†
Yun
Yang
 *a,
Amber
Zandanel
a,
Shimin
Liu
*a,
Amber
Zandanel
a,
Shimin
Liu
 b,
Chelsea W.
Neil
b,
Chelsea W.
Neil
 a,
Timothy C.
Germann
a and
Michael R.
Gross
a
a,
Timothy C.
Germann
a and
Michael R.
Gross
a
aEnergy and Natural Resources Security Group, Los Alamos National Laboratory, P.O. Box 1663, Los Alamos, New Mexico 87545, USA. E-mail: yun-yang@lanl.gov
bDepartment of Energy and Mineral Engineering, Pennsylvania State University, USA
First published on 9th July 2024
Abstract
Hydrogen (H2) has recently gained momentum as a promising clean energy alternative to fossil fuels. The intermittent nature of renewable energy, as the source of green H2, necessitates temporary H2 storage in subsurface geologic formations. To quantify storage potential and leakage risk, it is crucial to fully characterize subsurface H2 transport behavior. This work aims to measure the diffusion of H2 through relevant reservoir rocks, including two sandstones (Amherst Grey and Birmingham) and a limestone (Indiana). Breakthrough as a function of temperature is measured and used to calculate the effective diffusion coefficients and activation energy for diffusion at three different temperatures between 20 and 75 °C. Calculated diffusion coefficients are then used to estimate the subsurface plume size during storage in sandstone and limestone reservoirs. We observe that diffusive flow slightly expands plume size by up to 7%, and this effect is most pronounced in formations with low water saturation. While the use of cushion gas can maintain reservoir pressure and enhance injection efficiency, it can also enlarge H2 plume and hinder the recovery process due to molecular diffusion if the cushion gas differs from H2.
1. Introduction
Underground hydrogen storage (UHS) provides an affordable and viable option for large-scale energy storage.1–3 In light of the rapid depletion of fossil fuels and progressively worsening environmental concerns caused by the extensive use of traditional energy, there is an imperative need to develop alternative clean energy sources for sustainable economic and societal development.4 Clean energy sources generally include nuclear power and renewable energy sources. In either case, the strongly fluctuating nature of energy production has been noted as the primary barrier to widespread deployment.5–8 Specifically, due to the surplus in energy demand, nuclear stations have evolved from being base load plants to providing power during short periods of peak demand.9 Considering the high capital cost of nuclear power plants, it is not optimal to leave some of them idle during off-peak demand periods and have them only operate during peak demand periods. If energy is stored via economic means at times of excess energy supply, then the required number of nuclear stations can be reduced. Similarly, renewable sources such as wind and solar energy also exhibit variability in energy supply as they are heavily dependent upon weather conditions.10,11 To overcome the variability of both energy source and market demand, hydrogen (H2), generated by electrolysis (power-to-gas), is projected to be the most favorable energy carrier by 2030 and associatively, large-scale economical and reliable hydrogen storage is at the heart of the clean hydrogen economy.2,12–14Geologic storage of H2 in subsurface porous formation, due to its immense capacity and relatively low cost (compared with surface storage), has gained momentum in academia and the energy industry to facilitate the fossil fuel to renewable energy revolution.15,16 Based on decades of cumulative research efforts, we have gained extensive knowledge of underground natural gas storage (UGS) in naturally occurring formations (hydrocarbon reservoirs, aquifers) and artificial cavities (salt caverns).17,18 UGS generally comprises permeable rock layers which serve as reservoirs, overlain by strata with ultra-low permeability, serving as cap rocks for trapping reservoir fluid.14,19 In theory, if H2 molecules behave the same as natural gas under geologic conditions, UGS should satisfy the requirements for storing H2 (e.g., engineering, operation, safety and capacity). However, there are limited field demonstrations of UHS due to the high cost to produce H2 (at least $900 per ton vs. average oil cost of $385 per ton) and uncertainty surrounding the injection and production of H2 from the subsurface formations.2,3 Two projects associated with UHS in subsurface porous media include the German Hydrogen to Store (H2STORE) project20 and the Austrian Sun Storage project (Underground Sun Storage Project final report, 2017).21 The H2STORE project20 explored the feasibility of utilizing UHS in siliciclastic depleted gas reservoirs. It specifically focused on the potential impacts of hydrogen on the petrophysical, geochemical, and mineralogical properties of siliciclastic reservoir rocks and caprocks within large, depleted gas storage sites. The results showed that, despite interactions between hydrogen and reservoir, these interactions do not significantly degrade the purity of the recovered hydrogen,22,23 thereby demonstrating the feasibility of utilizing UHS in depleted gas reservoirs. However, this project is restricted to synthetic reservoir simulation, and more extensive field studies are needed for long-term monitoring. On the other hand, the Underground Sun Storage Project21 injected and recovered a mixture of hydrogen (∼10 vol%) and natural gas from a litharenitic sandstone reservoir and revealed a recovery factor of 82% for H2 injected. However, only a small volume of H2 was involved in this field trial, significantly reducing the scale of H2 storage capacity and efficiency, and the feasibility of large-scale UHS remains unclear. To upscale UHS applications, safe and economic injection and production of H2 needs to be guaranteed, which necessitates a solid understanding of the hydro-, bio-, fluid-dynamics of UHS. Subsurface transport of H2 is controlled by the hydrodynamic behavior of H2, which includes rock properties, fluid properties (density, viscosity, molecular diffusion coefficient, fluid–fluid interfacial tension, solubility), and rock–fluid interactions (wettability, solid–fluid interfacial tension, relative permeability). This behavior can be mathematically represented using a compositional two-phase flow model that includes water and gas as phases, with all pertinent chemical species as components.22 Advective flow is dominant during active injection and withdrawal periods, affecting the displacement of formation fluids and hydrogen.24,25 Feldmann et al., 201622 conducted a numerical simulation research to investigate subsurface H2 transport and storage in a depleted gas reservoir for five years of seasonal cyclic operation, focusing on hydrodynamic and gas mixing processes. They found that mechanical dispersion, due to the movement of fluids in the porous medium, combined with molecular diffusion, can amplify the gas mixing process, which is crucial for understanding H2 behavior in the subsurface. Lysyy et al., 202126 developed a site-specific numerical simulation study to investigate the feasibility of UHS in depleted gas reservoir of Norne field, offshore Norway. After several injection and withdrawal cycles, the final recovery factor obtained from a prolonged withdrawal period was 87%. During idle periods with no flow, molecular diffusion played a significant role in mixing and spreading of H2 in the reservoir, leading to a 30% H2 gas mixture. Similar conclusions were drawn by Hagemann et al. 2016,27 who found molecular diffusion of H2 strongly controls gas mixing process. A thorough understanding of H2 molecular diffusion is essential for accurately estimating plume migration dynamics and optimizing the overall storage and recovery process.
In the present work, H2 permeation (diffusion) behaviors in various reservoir rocks (sandstone and limestone) were measured using a modified two-bulb diffusion cell. Based on the observed diffusion rate, we calculate H2 diffusion coefficients at various temperatures. By examining the temperature dependence of H2 diffusion behavior, we investigated the diffusion mechanism of H2 in reservoir rocks from the pore scale, which is rarely discussed in the literature. Additionally, the impact of diffusion on H2 plume size during H2 injection is analyzed. This work provides fundamental data for H2 permeation in subsurface reservoir rocks at geologic conditions.
2. Background
To date, the Sun project21 is the only completed field trial that has resulted in a full field dataset to demonstrate UHS feasibility in depleted hydrocarbon reservoirs. One primary objective of this project was to investigate fundamental mechanisms controlling H2 loss in subsurface reservoirs subjected to repeated injections and extraction cycles. Because of the concentration contrast between the injection stream and reservoir fluid and high H2 diffusion coefficients, the field trial21 shows that about 4 to 5% of H2 was diffused and dissipated into the reservoir and could not be recovered. It should be noted that the injected fluid only contained 10 vol% of H2 and underwent a relatively short storage period (∼4 months). H2 diffusive loss is expected to be considerably larger for longer-duration, pure H2 storage. There have been limited experimental studies28–32 to measure H2 diffusion in minerals and some reservoir rocks, as complied in Table 1. Except for diffusion measurements on coal, other existing works28–30,33–35 were conducted at low-temperature and low-pressure conditions. Even for coal, the diffusion coefficients were quantified through gas adsorption kinetics that inherently assumed a strong adsorbent-adsorbate system.31,32 This may be true for the H2 – coal system (as coal is a microporous media) but is unlikely to be valid for other non-sorptive reservoir rock types. For this reason, the present work aims to provide a benchmark dataset on H2 diffusion in natural rock samples at elevated temperatures using an improved diffusion cell design. Additionally, by systematically exploring the temperature effects on diffusion, we can determine activation energies that can be used to extrapolate diffusion behavior for a wide range of reservoir temperature conditions.| Rock type | D (m2 s−1) | T (°C) | P (MPa) | Sample type | Porosity | Source |
|---|---|---|---|---|---|---|
| Sandstone | 6.5 × 10−6–1.9 × 10−5 | 25 | 0.1 | Core | 0.2–0.4 | Currie 196034 |
| Sandstone (Berea, Bandera, etc.) | 4 × 10−6–1 × 10−5 | 25 | 0.1 | Core | 0.18–0.19 | Donaldson et al., 197636 |
| Berea sandstone | 2.1 × 10−7–1.5 × 10−6 | 28 | Up to 4 | Core | 0.19–0.25 | Arekhov et al., 202333 |
| Sandstone (Bentheimer, Chattian, etc.) | 5 × 10−9–2 × 10−7 | Up to 100 | Up to 30 | Core | 0.17–0.32 | Michelson et al., 202337 |
| Gypsum | 1.5 × 10−5 | 22 | 0.1 | Sheet | Not measured | Yang et al., 201335 |
| Opalinus claystone | (1.2–1.8) × 10−9 (water saturated) | 20 | 0.1 | Core | 0.237 | Strauch et al., 202330 |
| Anthracite coal | (1–6.8) × 10−9 | Up to 60 | 1.3 | Powder | Not measured | Keshavarz et al., 202231 |
| Coal in different ranks | (0.5–1.8) × 10−10 | 30 | Up to 10 | Powder | Not measured | Liu and Liu 202332 |
3. Methods
3.1 Experimental diffusion apparatus and procedure
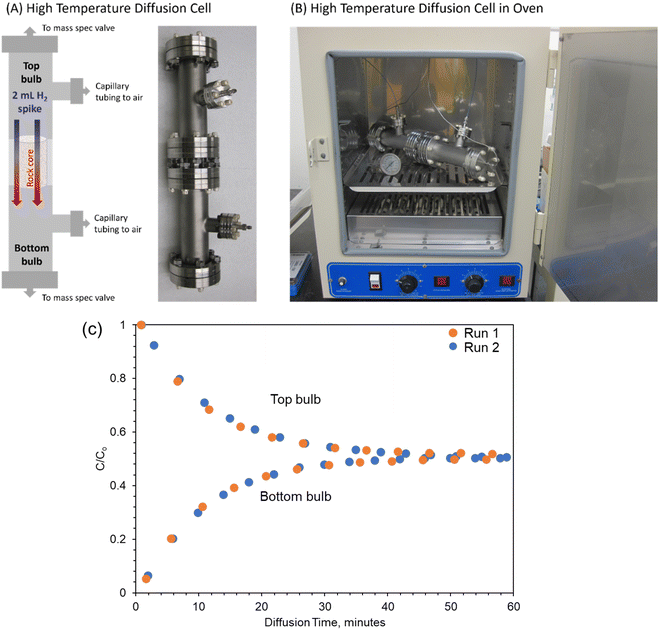
This work adopts the two-bulb method to measure the self-diffusion coefficient of H2 through the reservoir rocks at dry conditions (samples are filled with air). Fig. 1 shows the experimental apparatus that includes two bulb volumes and a connecting bridge of 316 stainless steel for holding the rock sample. The cell was constructed using ConFlat® parts with copper gaskets. The rock cores used for experiments were 1′′ long by 1′′ in diameter. The cores were sealed on the outside using a UV-curing resin (UV15X-6NONMED-2, Master Bond, Inc., Hackensack, NJ, USA). The cores were then placed in the center of the bridging pieces, which were 1.5′′ in diameter. The axial space around the core was filled with Room Temperature Vulcanization (RTV) silicone (SILPAK, Inc. Pomona, CA, USA) to prevent diffusion around the outside of the rock core. This silicone was previously shown to be impermeable to gases.38 The void volume of the system's components (including connecting pipe, bulb, bridge, ball valve) is measured through water displacement. The system dimensions are provided in Table 2.| Length of bridge | 2.54 cm |
| Cross-sectional area of bridge | 5.067 cm2 |
| Volume of top bulb (including connecting pipe, valve) | 126.305 cm3 |
| Volume of bottom bulb (including connecting pipe, valve) | 126.305 cm3 |
To begin a diffusion experiment, the bottom bulb as depicted in Fig. 1 was spiked with a 5% H2 mixture to reach an injected H2 volume of 2 mL (approximately 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 800 ppmv). Each bulb was connected to a mass spectrometer (Pfeiffer Vacuum OmniStar GSD 320 mass spectrometer, Pfeiffer Vacuum, Aßlar, Germany) through one outlet port, which was connected to a dead-ended multiposition selector valve (VICI Valco Instruments, Houston, TX). The second port was connected to a length of capillary tubing open to the atmosphere. This tubing prevents the formation of a vacuum during gas sampling, which would affect diffusion rates, while also preventing extensive back diffusion of air. This port allows for the replacement of sampled gas with air, which will result in some dilution of the spiked and diffusion chambers with air. The multiposition valve was used to sample from both bulbs for one minute every four minutes, and measured air the rest of the time to prevent oversampling. The sampling rate of gas from the mass spec is 0.2 mL minute−1. Therefore, the total gas sampled from the system over the course of the diffusion experiment is approximately 4 to 5 mL for an 80-to-100-minute experiment. The volume of the spiked and diffusion chambers is 126.3 cm3, so this volume is equivalent to 3.2–4.0% of the chamber volume being removed and replaced by air. Diffusion experiments were run until the two bulb concentrations equilibrated. Experiments were conducted at ambient temperatures up to 60–75 °C. Between diffusion runs, samples were placed in a vacuum oven to remove residual hydrogen gas. The impact of dilution due to sampling can be found in Fig. S1 in the ESI.† Dilution did have a slight impact on the c/c0 values. However, this impact was very small (0.2–3.7% standard deviation in c/c0 values) over the considered diffusion timescale. Additionally, because sampling rates are equivalent between spiked/breakthrough chambers, rock types, and temperatures, we do not anticipate a significant change in the concentration gradient, which is the driving force for diffusion. Since the diffusion is normalized to c∞ (see Section 3.3), changes in the equilibrium concentration are accounted for in diffusion coefficient calculation.
800 ppmv). Each bulb was connected to a mass spectrometer (Pfeiffer Vacuum OmniStar GSD 320 mass spectrometer, Pfeiffer Vacuum, Aßlar, Germany) through one outlet port, which was connected to a dead-ended multiposition selector valve (VICI Valco Instruments, Houston, TX). The second port was connected to a length of capillary tubing open to the atmosphere. This tubing prevents the formation of a vacuum during gas sampling, which would affect diffusion rates, while also preventing extensive back diffusion of air. This port allows for the replacement of sampled gas with air, which will result in some dilution of the spiked and diffusion chambers with air. The multiposition valve was used to sample from both bulbs for one minute every four minutes, and measured air the rest of the time to prevent oversampling. The sampling rate of gas from the mass spec is 0.2 mL minute−1. Therefore, the total gas sampled from the system over the course of the diffusion experiment is approximately 4 to 5 mL for an 80-to-100-minute experiment. The volume of the spiked and diffusion chambers is 126.3 cm3, so this volume is equivalent to 3.2–4.0% of the chamber volume being removed and replaced by air. Diffusion experiments were run until the two bulb concentrations equilibrated. Experiments were conducted at ambient temperatures up to 60–75 °C. Between diffusion runs, samples were placed in a vacuum oven to remove residual hydrogen gas. The impact of dilution due to sampling can be found in Fig. S1 in the ESI.† Dilution did have a slight impact on the c/c0 values. However, this impact was very small (0.2–3.7% standard deviation in c/c0 values) over the considered diffusion timescale. Additionally, because sampling rates are equivalent between spiked/breakthrough chambers, rock types, and temperatures, we do not anticipate a significant change in the concentration gradient, which is the driving force for diffusion. Since the diffusion is normalized to c∞ (see Section 3.3), changes in the equilibrium concentration are accounted for in diffusion coefficient calculation.
3.2 X-ray diffraction (XRD) analysis
For mineral analysis, quantitative X-ray diffraction (QXRD) analysis was carried out to identify the mineralogy of the studied rock samples.39 Powdered samples were used, and the generated diffraction patterns were utilized to visualize diffraction measurements and identify the proportion of different minerals contained in each rock sample.39 Samples were measured using a Siemens D-500 X-ray diffractometer using CuKα radiation (Bruker AXS, Madison, WI, USA) and quantification was accomplished using alumina powder (Al2O3) as an internal standard. Peak identification used JADE software's search-match function (Materials Data, Inc., Livermore, CA, USA). The measured patterns were compared to a library of XRD patterns of known minerals, and the relative abundance of individual minerals was estimated based on peak intensities, providing quantitative mineralogy information.The two sandstones are rich in quartz, ranging in abundance from 85.4 wt% to 91.5 wt% (Table 3). K-feldspar (Microcline) and Clay (Kaolinite) are also identified in varying proportions. The limestone predominantly consists of calcite with a value around 99 wt% and a minor constituent of quartz of 1 wt%.
| Sample | Calcite | Quartz | Microcline | Kaolinite |
|---|---|---|---|---|
| Amherst Gray Sandstone | — | 85.4% | 10.8% | 3.7% |
| Birmingham Sandstone | — | 91.5% | 5.6% | 2.8% |
| Indiana Limestone | 98.8% | 1.2% | — | — |
3.3 Diffusion theory
The two-bulb method has been extensively used to measure gaseous diffusion over wide temperature ranges from 65 to 400 K. Due to the relative compactness and convenient opening mechanisms (without moving parts), the two-bulb method facilitates thermal equilibrium, which makes it easier to measure diffusion at different temperatures.40 Because the bulb volume is substantially larger than the bridge volume, the following assumptions are made:40–42• Diffusion through the rock sample is in quasi-steady-state – constant flow flux along the connecting tube.
• A linear variation in concentration is established in the tube bounded by the concentration in the bulbs.
• Concentration gradients occur only in the connecting tube, and uniform concentration is surmised in the bulbs.
The first two assumptions are derived from the quasi-steady state that neglects the transient period required to establish a constant gradient across the entire length of the tube. Departure from a quasi-steady state often arises due to design artifacts of the apparatus when the bulbs are not sufficiently large enough compared to the connecting tube. Because our system has bulb volume exceeding the connecting tube volume by more than tenfold, the tube and the rock sample inside it are surmised to be in a quasi-steady state. The last assumption is made on the basis of much smaller diffusivity in the connecting tube than in the bulbs. This occurs because the rock samples inside the connecting tube occupy the available void space for diffusion, which leads to a significant decrease in the diffusion rate.
To determine the effective diffusion coefficient, the time-series concentration of the bulb is given by40–42
 | (1) |
In the above formula, c(t) → c∞ for sufficiently large diffusion time (i.e., time to reach equilibrium conditions). A linear relationship can be found by log-transformation of the concentration solution, i.e.,
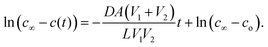 | (2) |
The effective diffusion coefficient of the rock samples can be determined from the slope of the semi-log plot of (c∞ − c) against diffusion time. (c∞ − c) is the concentration change in the spiked or breakthrough bulb, monitored through continuous sampling and mass spectrometry analysis. The detailed derivation can be found in ESI.†
4. Results and discussion
4.1 Experimental quantification of diffusion coefficients for different rock samples
Fig. 2 shows the measurements of H2 concentration in the top and bottom bulbs as the system approaches equilibrium, which is found to follow an exponential series. All experimental trials have the same initial C/C0 of H2 of 1. The equilibrium C/C0 varies slightly among rock samples, ranging from 0.43 to 0.47. Since the top and bottom bulbs have the same volume, the concentration, in theory, should approach 0.5 mol cm−3 at equilibrium. The difference between measured and theoretical equilibrium concentration implies the existence of gas retention within the rock samples, likely caused by bulk phase gas trapped in dead-end pores and/or gas condensed at the pore surface (adsorption).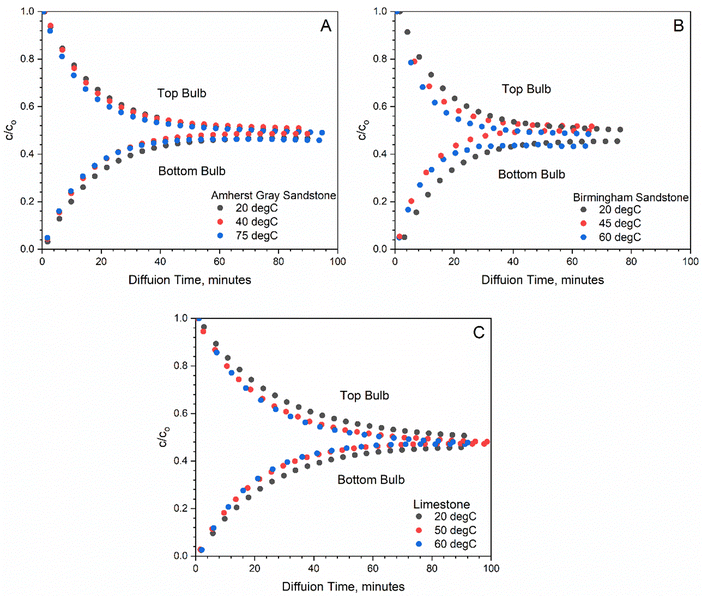 | ||
| Fig. 2 Changes in concentration of hydrogen in the top and bottom bulb for two sandstone (A, B) and one limestone (C) samples at different temperatures. | ||
Because the bulbs have substantially larger volumes than the volume of the connecting tube, initial the transient period can be neglected, and a quasi-steady state is surmised. As a result, a linear relationship is found in the semi-log plot of H2 concentration versus diffusion time for all rock samples studied during the initial H2 breakthrough period (first 20–60 minutes) (see Fig. 3). The slope of these linear lines is used to determine the effective diffusion coefficient for the studied rock samples following eqn (2). Table 4 summarizes the measured diffusion coefficient for Birmingham Sandstone, Amherst Gray Sandstone and Indiana Limestone at investigated temperatures, where Birmingham Sandstone has the highest H2 diffusion coefficient (0.045–0.07 cm2 s−1) and limestone possesses the lowest H2 diffusion coefficient (0.026–0.033 cm2 s−1). With reference to H2 diffusion coefficients in air at comparable temperatures, the measured diffusion coefficients for all tested rocks are approximately two orders of magnitudes smaller. This is caused by solid grains present in the diffusive pathway, which reduces the available void volume for flow and elongates the streamlines. Thus, sandstones with higher porosity have higher diffusion coefficients than limestone with lower porosity.
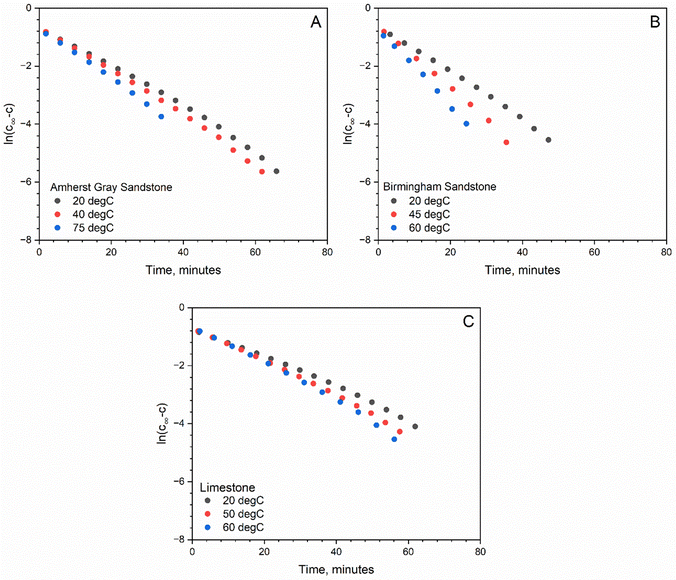 | ||
| Fig. 3 log transformation of time series concentration to calculate diffusion coefficient according to eqn (2) for two sandstone samples (A, B) and one lime stone sample (C). | ||
| Sample | D ambient | D middle | D high | E A | ϕ | K |
|---|---|---|---|---|---|---|
| Amherst Gray Sandstone | 3.6 | 4 | 4.7 | 4174 | 0.185 | 15–150 |
| Birmingham Sandstone | 4.5 | 5.9 | 7 | 9108 | 0.228 | 250–500 |
| Indiana Limestone | 2.6 | 3.1 | 3.3 | 4650 | 0.053 | 2–20 |
| In ordinary air | 71 | 87 | 95 | 1 |
Previous work43 indicates that the methane diffusion coefficient in sandstone with porosity of 10–20% typically falls within the range of 0.002 to 0.01 cm2 s−1 at ambient temperature. In this work, we expect the methane diffusion coefficients of our sandstone samples, which have similar porosities (see Table 4), to be relatively close in value. Because of the relatively small molecular size and lower viscosity of H2 molecules, the obtained H2 diffusion coefficient is notably greater than that of methane, reaching values up to 20 times higher. Most reservoir engineering tools used in conventional hydrocarbon gas production are often limited to passive transport (advective flow equations) due to the comparatively small flux transported through Brownian motion (molecular diffusion), which is no longer a valid assumption for subsurface H2 flow in reservoir rocks. Although Fick's diffusion law is considered in some unconventional reservoir engineering tools, simplifications are made in diffusion modeling to reduce computational cost.44,45 For example, diffusion coefficient is often treated as a constant throughout reservoir and over time,46,47 which conflicts with the reality that diffusion varies with fluid composition and reservoir conditions. Therefore, an advection–diffusion system must be coupled with the governing equations for incompressible flow within porous media to develop hydrodynamic modeling tools for the geologic storage of H2.
4.2 Relationship between temperature and effective diffusion coefficients of H2
The temperature dependence of the diffusion coefficient is useful to correlate diffusion behaviors of reservoirs at different depths. For all rocks studied, the H2 diffusion coefficient has a monotonically increasing trend with increasing temperatures (see Fig. 4). This is because higher temperatures lead to increased gas molecular kinetic energy, facilitating faster breakthrough of gas molecules into the receiving bulb. In particular, Birmingham Sandstone has diffusion behavior that is most sensitive to temperature: its diffusion coefficient increases by 57% as temperature increases from 20 °C to 60 °C. When subjected to a similar temperature increase, the measured diffusion coefficients of the other two rocks only increase by less than 30%. Overall, H2 diffusion in reservoir rocks is strongly dependent on temperature. Storage reservoirs at higher temperatures are thus expected to have more diffusive flow. On average, the growth rate of H2 diffusion coefficient per 1 °C increase in temperature is estimated to range from 0.5% to 1.4%. Because the rate of diffusion is temperature-dependent, the Arrhenius equation is applied to describe how H2 diffusion through rock samples varies with temperature. The linear relationship between the natural log of the effective diffusion coefficient and the inverse temperature was also used to calculate activation energy, EA, according to the Arrhenius equation (Table 4). Knowing the value for EA is critical to quantify how sensitive the diffusion rate is to temperature changes and for predicting diffusion rate at temperatures where experimental measurements are not available.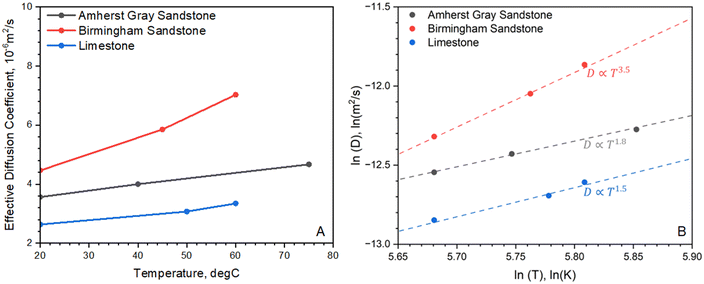 | ||
| Fig. 4 Temperature dependence of diffusion coefficient in (A) normal scale and (B) log–log scale for Amherst Gray Sandstone, Birmingham Sandstone and Indiana Limestone. | ||
Despite the inherent heterogeneity present in reservoir rocks, a single value of diffusion coefficient is often used to represent the transport capacity for the entire rock sample. This is valid as long as effective medium approximation is applicable, where the average domain size (microscopic length scale) is substantially larger than the molecular dimension but much smaller than the characteristic length of the macroscopic sample.48,49 To evaluate this assumption, mercury intrusion porosimetry (MIP) was conducted to characterize pore volume and its distribution for the studied rock samples. MIP operates on the basis of using high injection pressure to force mercury into pore space in a porous medium. Since smaller pores have higher resistance to mercury penetration, the externally applied pressure builds up as mercury accesses smaller pores. Based on the correlation between capillary (entrance) pressure and pore size, pore size distribution can be determined from the recorded mercury intrusion volume at specific pressures.50
Assuming a cylindrical pore model, the pore size distribution is determined using the Washburn law:51P = (−4γ![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) cos
cos![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) θ)/d, where P is the mercury injection pressure, γ is the surface tension of mercury (∼484 mN m−1), θ is the solid/mercury contact angle (∼130°), d is the penetrating pore throat size. The obtained porosity values for the three rocks studied are listed in Table 4 with Birmingham Sandstone being the most porous rock (hence having the largest diffusion coefficient) and the corresponding pore size distributions (PSDs) are shown in Fig. 5. The two sandstone samples have similar bimodal pore size distributions between 20 nm and 300 μm with two clearly separated maxima above 1 μm. In comparison, a lower proportion of large pores is found in the Limestone sample, but with comparable pore sizes ranging between 30 nm and 300 μm. The microscopic length scale is approximated as the average pore size, ranging from 0.66 μm (Limestone) to 1.2 μm (Birmingham Sandstone), which is substantially smaller than the macroscopic length scale involved in the testing system (∼2.54 cm). As the average domain size is significantly smaller than the characteristic length of the sample, it fulfills one of the requirements for using the effective medium approximation.
θ)/d, where P is the mercury injection pressure, γ is the surface tension of mercury (∼484 mN m−1), θ is the solid/mercury contact angle (∼130°), d is the penetrating pore throat size. The obtained porosity values for the three rocks studied are listed in Table 4 with Birmingham Sandstone being the most porous rock (hence having the largest diffusion coefficient) and the corresponding pore size distributions (PSDs) are shown in Fig. 5. The two sandstone samples have similar bimodal pore size distributions between 20 nm and 300 μm with two clearly separated maxima above 1 μm. In comparison, a lower proportion of large pores is found in the Limestone sample, but with comparable pore sizes ranging between 30 nm and 300 μm. The microscopic length scale is approximated as the average pore size, ranging from 0.66 μm (Limestone) to 1.2 μm (Birmingham Sandstone), which is substantially smaller than the macroscopic length scale involved in the testing system (∼2.54 cm). As the average domain size is significantly smaller than the characteristic length of the sample, it fulfills one of the requirements for using the effective medium approximation.
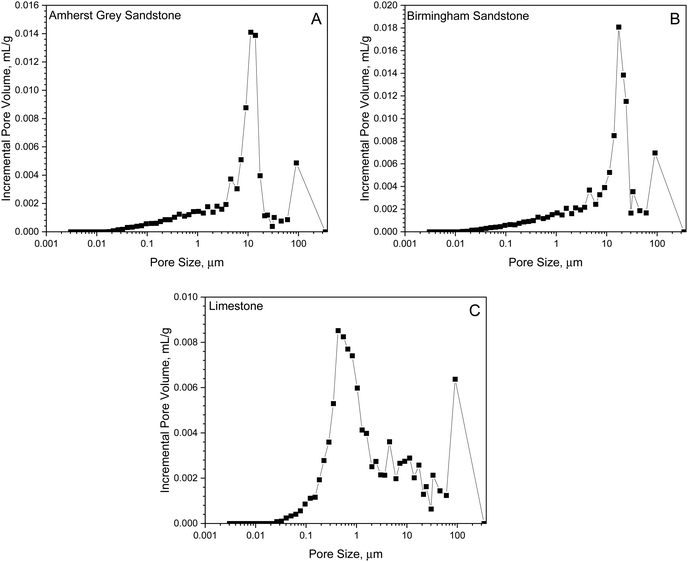 | ||
| Fig. 5 Pore size distribution on (A) Amherst Gray Sandstone, (B) Birmingham Sandstone, and (C) Indiana Limestone obtained from MIP with θ = 130°. | ||
In order to apply the effective medium approximation, the other requirement is that the pore scale involved in diffusion is much greater than the molecular dimension of diffusing species. To satisfy this requirement, bulk diffusion must be the dominant diffusion regime. The mean free path of H2 under normal conditions (1 atm and 25 °C) is 130 nm52 and is expected to be larger as kinetic energy increases with increasing temperature. Since the lower limit of the MIP-derived PSDs is less than 130 nm, it is possible for gas molecules to collide with the pore wall in addition to intermolecular collisions. In other words, both Knudsen and bulk diffusion are likely to occur in bulk-phase H2 diffusion for the studied reservoir rocks when a concentration gradient exists. Theoretically, Knudsen diffusion is driven by collisions between gas molecules and the pore wall, whereas intermolecular diffusion causes bulk diffusion.53,54 The contribution of individual diffusion regimes to overall diffusive flow flux depends on the relative magnitude of the mean free path to pore size (Knudsen number).55,56 In general, if Knudsen number is greater than 0.1, then Knudsen diffusion should be considered. At the investigated temperatures, the mean free path of H2 molecules range from 111 nm to 118 nm and therefore, Knudsen diffusion manifests at pores with pore size less than 1 μm, which contributes to ∼10% of the total pore volume of studied sandstone samples. As the mean free path increases with temperature, the frequency of H2 molecules colliding with the pore wall also increases at higher temperatures, adding additional momentum to diffusive flow. The contribution of Knudsen diffusion to overall diffusive flux, therefore, varies with temperature and the microscopic length scale involved.
If molecular collisions are of cardinal importance in the overall diffusive transport, the resulting derivative of diffusion coefficient with temperature 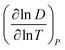 lies between 3/2 and 2 for binary molecular diffusion.40 The temperature dependence of the binary gaseous diffusion coefficient, D under bulk diffusion is inferred from the Chapman–Enskog kinetic theory of gas,57
lies between 3/2 and 2 for binary molecular diffusion.40 The temperature dependence of the binary gaseous diffusion coefficient, D under bulk diffusion is inferred from the Chapman–Enskog kinetic theory of gas,57
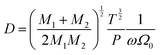 | (3) |
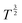 to T2.
to T2.
Fig. 4B shows the log transformation of temperature-diffusion coefficient data. The resulting derivative 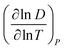 for Amherst Sandstone is 1.8, and for limestone is 1.5, within the range of theoretical prediction between
for Amherst Sandstone is 1.8, and for limestone is 1.5, within the range of theoretical prediction between 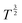 and T2. However, the derivative
and T2. However, the derivative 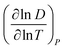 for Birmingham Sandstone exceeds the limit of bulk diffusion. It is likely to be caused by Knudsen diffusion processes, which provides additional momentum through pore wall collisions, resulting in a higher temperature dependence of the diffusion coefficient.
for Birmingham Sandstone exceeds the limit of bulk diffusion. It is likely to be caused by Knudsen diffusion processes, which provides additional momentum through pore wall collisions, resulting in a higher temperature dependence of the diffusion coefficient.
Although most pore volume in the studied reservoir rocks is provided by large pores (>1 μm) and nanopores only contribute less than 20% of the total porosity, the outcome of this work suggests that the confinement effect on H2 diffusion flow in Birmingham Sandstone due to collisions with pore walls manifests as reservoir temperature increases. Based on Fig. 5, the limestone sample appears to have a more uniform pore size distribution than the two sandstone samples. Therefore, less temperature dependence is found in H2 diffusion through limestone compared to sandstone.
4.3 Geometric factor of natural rocks
Compared with the molecular diffusivity of H2 in ordinary air, the measured diffusion coefficients in the studied rock samples are one order of magnitude smaller than the diffusivity in the absence of porous media. This is caused by H2 interaction with the surrounding pore network, which increases diffusional resistance and reduces diffusion rate. In any porous system, the presence of solid grains decreases the void volume for transport and simultaneously, causes the diffusive path of gas molecules to deviate from straight lines. Consequently, the diffusion coefficients must be scaled with tortuosity and porosity. As noted earlier, the effective medium approximation is reasonable for the system studied herein, because the microscopic length scale is much smaller than the macroscopic length scale. Based on effective medium approximation, the relationship between the effective diffusion coefficient of porous media, D and the self-diffusion coefficient (i.e., gaseous diffusion coefficient in ordinary air), Dp is given by58 (Milllington 1959),| D = Dpϕ/τ. | (4) |
The above formula only considers transport through available pore spaces and neglects mass flux through the solid grain. The values for Dp can be obtained from Table 4, which lists H2 diffusion coefficient in ordinary air at various temperatures. From a geometrical point of view, ϕ accounts for the reduced area for diffusion, and τ accounts for the elongated diffusion path between two points in a porous medium relative to the direct distance between points. There are no consistent observations between ϕ and τ, but in general, a decrease in ϕ causes an increase in τ as more solid grains are present in the diffusion path.59 Unlike ϕ, τ is not directly measurable for natural rocks. The magnitude of τ depends on various factors, including grain geometry and dimension, pore size distribution and connectivity, and diffusing species.60 Thus, the effective diffusion coefficient of any given system is unique to that system and requires experimental quantification.
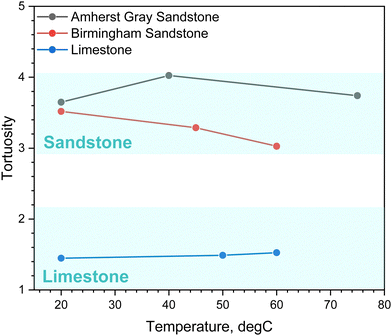
In this work, molecular diffusion measurements are applied to determine the tortuosity of pore channels. The porosity and tortuosity of reservoir rock samples are directly related to the ratio of the effective diffusion coefficient to the molecular diffusion coefficient in the absence of a porous medium. Using eqn (4), the tortuosity values for the studied rock samples was estimated from the measured effective diffusion coefficients and the results are shown in Fig. 6. The estimated tortuosity from diffusion measurements varies between 3 and 4 for the two sandstones. These values resemble results from Donaldson et al. (1976),36 with reported tortuosity ranging from 3 to 10 for H2-air diffusion in sandstone. The limestone has a slightly lower tortuosity that ranges from 1 to 2. Because the limestone has a more homogenous pore size distribution with lesser variations in pore volume than the two sandstones (see Fig. 5), the elongation of the diffusive path caused by constrictions of changing pore size is less severe in limestone, resulting in a lower tortuosity. Limestone is generally fine-grained and tightly packed; thereby, its tortuosity value closely aligns with the literature-reported tortuosity value for a system consisting of closely packed uniform spheres (∼1.34).61
The tortuosity exhibits slight temperature dependence for Indiana Limestone and Amherst Gray Sandstone, whereas Birmingham Sandstone appears to have less sinuous diffusive path at higher temperatures. Despite the remarkable similarity in the pore size distributions of the two sandstones, hydraulic tortuosity derived from diffusion measurements reacts differently in response to temperature changes. The two sandstones also share a similar mineral composition, mainly made up of quartz, which comprises over 85% of their mineralogy. Considering that the H2 diffusion coefficient in pure quartz is on the order of magnitude of 10−6 cm2 s−1,62 H2 molecules should be primarily transported through available pore space, rather than within the solid grains. It is evident that there exist additional mechanisms that influence the flow of H2 through the porous network of Birmingham Sandstone. One limitation with MIP characterization technique is that it provides information on pore size distribution but fails to characterize pore connectivity and tortuosity. Even though the two sandstones have comparable pore size distribution, the actual arrangement of pores may differ. The current characterization technique therefore may not provide direct information into these properties.
Nevertheless, it is worth noting that a noticeable gas retention effect is observed in Birmingham Sandstone when examining the stabilized concentration of spiked and breakthrough chambers (see Fig. 2). Additionally, the extent of gas retention in Birmingham Sandstone diminishes as temperature increases, as evidenced by the reduced difference in concentration between the two chambers at high temperatures. It is highly likely that Birmingham Sandstone contains some dead-end pores, which could contribute to the observed gas retention effect. As temperature increases, the intensified Brownian motion of H2 molecules is likely to release the gas trapped in these dead-end pores, explaining the reduction in gas retention. The decreased gas retention effect at higher temperatures results in an overall decrease in the distance that diffusing molecules need to travel, leading to the observed reduced tortuosity with temperature. Birmingham sandstone is also distinguishable from other Berea sandstones because it contains iron cement spots,63 though not in quantities sufficient to be measured using our QXRD. Spots in Birmingham samples were visible as reddish pots, which were revealed using scanning electron microscopy (SEM) and energy dispersive X-ray spectroscopy (EDS) to be iron oxides, while iron present in Amherst samples was primarily pyrite and iron carbonates (Fig. 7). These iron oxide inclusions may interact differently with H2 gas. The dominant reaction between iron oxide and H2 is a redox reaction, as described by Yekta et al., (2018):64
| 3Fe2O3 + H2 → 2Fe3O4 + H2O |
However, under geological conditions, pyrite reduction reactions with hydrogen have not been observed in previous study.65 Consequently, Birmingham Sandstone has the potential to react with H2 at higher temperatures. Due to the consumption of H2, a higher concentration gradient occurs at elevated temperatures, which facilitates the diffusion process and leads to stronger temperature-dependent behavior. Thus, in our diffusion experiments, we observed that the H2 diffusion coefficient in Birmingham Sandstone is more sensitive to temperature changes compared to Amherst Sandstone (see Fig. 4).
In light of findings from this and previous work,36 most reservoir rocks tend to have relatively low tortuosity (less than 5) in H2 diffusion. In practical scenarios where experimental diffusion measurements is unavailable, the effective diffusion coefficient, D for the reservoir rock can be estimated as the product of porosity and the self-diffusion coefficient, serving as a reasonable first-order approximation. Nevertheless, achieving an accurate estimation of D necessitates a comprehensive analysis of the underlying diffusion mechanisms involved. As noted earlier, molecular diffusion occurs by bulk diffusion and/or Knudsen diffusion. Bulk diffusion dominates in pores with radii greater than 1 μm and Knudsen diffusion dominates in pores with radii less than 0.01 μm. The pore size distributions measured for the two sandstones and one limestone studied in this work reveal that most pores possess radii exceeding 0.01 μm, with a noticeable portion of pores lying between 0.01 μm and 1 μm. Herein, Knudsen and bulk diffusion occur simultaneously for H2 diffusion in the two sandstones and one limestone studied.
5. Implementation in geologic hydrogen storage
For large-scale and long-term hydrogen storage, depleted hydrocarbon fields are of major interest as a cost-effective option because of their known reservoir characteristics and well-developed infrastructure.66 A simulation modeling study26 that investigated seasonal hydrogen storage in a depleted gas field of Europe reported increasing hydrogen purity with increasing withdrawal cycles. They also highlighted that viscous fingering and gravity override only slightly impacted seasonal hydrogen storage. It is unambiguous that hydrogen recovery efficiency can be enhanced by repeating injection-withdrawal cycles,67–70 but the recovery efficiency is also affected by injection rate and time, as well as reservoir rock properties, which are rarely discussed. To date, despite the tremendous storage potential in depleted hydrocarbon fields, commercial storage of pure hydrogen is only achieved in salt caverns, partially due to an insufficient understanding of the underlying hydrodynamic processes involved in UHS in porous rock.71Similar to natural gas storage, cushion gas is utilized and injected into a storage formation in precedent to H2 to maintain sufficient reservoir pressure during the withdrawal period.2,68,72 As a result, hydrogen injection imposes a highly saturated and homogenous hydrogen plume near the wellbore. Advection in association with pressure gradient and diffusion due to concentration gradient are two primary flow mechanisms leading to the subsurface transport of hydrogen.3 Because diffusion controlled by molecular kinetics is a much slower process than advection, the optimal hydrogen storage zone is deemed to be a highly permeable zone where the advective flux far exceeds the diffusive flux.73
In gas production from conventional reservoirs, advective flow driven by pressure gradients is typically considered, while diffusive flow driven by concentration gradients is often neglected. The depleted gas reservoir typically has low pressure and high water saturation, resulting in low effective gas permeability. Especially for the first few injection cycles, a strong concentration gradient is exposed between the hydrogen-rich or pure hydrogen injection stream and reservoir fluids, so gas-phase diffusion through the rock matrix becomes significant. Given that predicting plume evolution is critical for any injection strategy, estimating the spread of the plume during injection operations becomes essential for field development planning. To evaluate the relative importance of diffusive and advective fluxes, we integrate measured hydrogen diffusion coefficients into the calculations of plume extent for both sandstone and limestone reservoirs.
In this section, we aimed to investigate the effect of H2 diffusion in reservoir rocks on plume migration using compositional reservoir simulations for UHS in depleted gas reservoirs (sandstone and carbonates). A schematic of simulation model is given in Fig. S2 (ESI†). These simulations are performed using CMG GEM,74 where the diffusion of H2 molecules through pores is modeled using Fick's law75,76
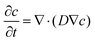 | (5) |
Two H2 diffusion coefficients must be entered into the simulation code: one for gaseous phase, the other for aqueous phase. The diffusion coefficient in gaseous phase is set to be the experimentally measured diffusion coefficient, where the values for sandstone and limestone are 0.04 cm2 s−1 and 0.031 cm2 s−1. The diffusion coefficient in aqueous phase is set to be the molecular diffusion coefficient of H2 in pure water (∼5.11 × 10−5 cm2 s−1),52 scaled by porosity.
In both depleted sandstone and carbonate reservoirs, we assumed homogenous models. The purpose of this simple geometry is to emphasize the general behavior of H2 plume migration in reservoir rock under advective and diffusive flow, rather than particular behavior that may arise in specific reservoirs with different geometry, hydrology, and heterogeneity. The model simulates a reservoir covering an area of 2290 m by 2290 m with a thickness of 10 m. It assumes good caprock integrity and thus, only includes the reservoir rocks. Table 5 lists the input reservoir properties used to determine the plume extent, where rock permeability ranges from 10 mD (limestone)77,78 to 65 mD (sandstone).79 Other parameters used are taken from typical sandstone and limestone reservoir properties.77,78,80,81 The relative permeability of hydrogen is obtained from drainage displacement tests on sandstone and carbonates at comparable pressure and temperature conditions.82,83 H2 is injected for one month at constant rate of 33.3 ton per day and stored for one month, representing a short-term gas storage trial. To assess the impact of H2 diffusion on plume migration, the plume radius is extrapolated following one month of storage in reservoirs with varying levels of water saturation. These varying saturations represent different volumes of cushion gas (CH4) used prior to H2 injection and degrees of reservoir depletion.
| Properties | Sandstone | Limestone | Units |
|---|---|---|---|
| Rock porosity | 0.3 | 0.05 | Dimensionless |
| Absolute permeability | 65 | 10 | mD |
| D H2 in gaseous phase | 0.04 | 0.031 | cm2 s−1 |
| D H2 in water phase | 1 × 10−5 | 2.6 × 10−6 | cm2 s−1 |
| Reservoir thickness | 10 | 10 | m |
| Reservoir temperature | 300 | 348 | K |
| Initial reservoir pressure | 10 | 6.9 | MPa |
| Cumulative injection amount | 1000 | 1000 | Ton |
| Initial water saturation | 0 to 1 | 0 to 1 | Dimensionless |
| PVT model for H2 | Soave–Redlich–Kwong84 | Soave–Redlich–Kwong84 |
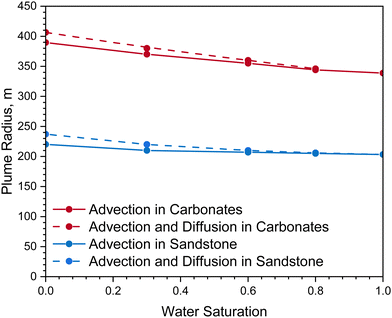
Fig. 8 demonstrates the impact of H2 diffusion on hydrogen plume size and its dependence on water saturation after a storage period of one month. For a sandstone reservoir, the simulated plume size due to pure advective flow ranges from 200 m to 220 m across various initial water content levels; for a limestone reservoir, the resulted plume size due to pure advective flow ranges from 340 m to 390 m at investigated water saturations. Higher water saturation results in reduced effective gas permeability and decreases the available pore volume for gas storage, which in turn limits plume migration. In all scenarios, advection is always the dominant flow regime for H2 transport in reservoir layers.
In both sandstone and limestone reservoirs, plume sizes slightly expand when diffusion is considered; however, as water saturation increases, this expansion diminished as a result of reduced diffusive flow. If cushion gas is injected into the storage reservoir during the site initialization stage, the simulated plume size due to diffusion sees an increase of up to 7% at the lowest water saturation investigated; at higher water levels, the impact of H2 diffusion on plume size becomes negligible. In water-saturated reservoirs, the effective H2 diffusion coefficient is determined by the diffusion coefficients in both the aqueous and gaseous phases. Since the H2 diffusion rate in water is significantly lower than in gas, reservoirs with higher water saturations result in smaller plume areas. This smaller plume area aids in more efficient H2 recovery during withdrawal periods. Overall, with a gaseous H2 diffusion coefficient in reservoir rocks on the order of 1 × 10−6 m2 s−1, diffusion flow has a minimal impact on plume migration. Advection predominantly governs H2 transport in these layers.3,13
6. Conclusions
6.1 Measured H2 diffusion coefficient in reservoir rocks
This work provides a benchmark dataset for temperature-dependent H2 diffusion in various reservoir rock types (including sandstone and limestone). The measured H2 diffusion coefficients fall within the range of 0.036 cm2 s−1 to 0.07 cm2 s−1 for Birmingham and Amherst Gray Sandstone and 0.026 cm2 s−1 to 0.03 cm2 s−1 for limestone at investigated temperatures (20 to 75 °C). These measured H2 diffusion values are more than 10-fold smaller than the binary diffusion coefficient in the H2-air system (devoid of porous media). The extents of reduction in diffusion coefficients offers valuable quantitative insights into the microstructure of reservoir rocks. By deploying effective medium approximation, the estimated diffusive tortuosity for H2 diffusion, characterizing the complexity of pore network, ranges from 1 to 2 for limestone and 3 to 4 for sandstone.As methane diffusion coefficients typically ranging from 0.002 to 0.01 cm2 s−1, we surmise that concentration-driven diffusion will be more predominant during H2 storage compared to methane. Therefore, hydrodynamic modeling of the subsurface flow of H2 during UHS requires an accurate H2 diffusion coefficient.
6.2 Temperature dependence of H2 diffusion coefficient
For all reservoir rocks studied, H2 diffusion rate shows a noticeably increasing trend with increasing temperature, where the growth rate of H2 diffusion coefficient per 1 °C of temperature ranges between 0.5% and 1.4%. Furthermore, the measured H2 diffusion coefficients are found to be directly proportional to temperature in logarithmic scale, consistent with Chapman–Enskog gas kinetic theory. Consequently, the dominant diffusion regime for H2 diffusion in reservoir rocks is bulk diffusion due to intermolecular collisions. The presence of Knudsen diffusion, though it only contributes minorly to total mass flux, amplifies the temperature dependence of H2 diffusion.6.3 Effect of H2 diffusion on forming plume size
When storing H2 in depleted hydrocarbon reservoirs, H2 diffusion results in an up to 7% increase in H2 plume size for storage reservoirs, and this expansion effect diminishes as initial water saturation of the reservoir rocks increases. While this work only provides a preliminary analysis of the diffusion effect on geologic H2 storage, it is suggested that conventional reservoir simulation tools built upon pressure-driven advection (Darcy) flow can be improved for diffusion flow to predict the fate of injected H2, which is the key to design and optimize field operations.Data availability
The data supporting this article have been included as part of the ESI† and the Results and discussion section of the manuscript.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This work was supported by the U.S. Department of Energy through the Los Alamos National Laboratory. Los Alamos National Laboratory is operated by Triad National Security, LLC, for the National Nuclear Security Administration of U.S. Department of Energy (Contract No. 89233218CNA000001). Research presented in this article was supported by the Laboratory Directed Research and Development program of Los Alamos National Laboratory under project number 20230022DR. The authors acknowledge the Materials Research Institute (MRI) at Pennsylvania State University for access to Mercury Porosimetry. We also would like to acknowledge CMG, Ltd for providing academic licenses of the software suite.References
- R. Tarkowski, Underground hydrogen storage: Characteristics and prospects, Renewable Sustainable Energy Rev., 2019, 105, 86–94 CrossRef CAS.
- N. Heinemann, J. Alcalde, J. M. Miocic, S. J. T. Hangx, J. Kallmeyer, C. Ostertag-Henning, A. Hassanpouryouzband, E. M. Thaysen, G. J. Strobel and C. Schmidt-Hattenberger, et al., Enabling large-scale hydrogen storage in porous media – the scientific challenges, Energy Environ. Sci., 2021, 14(2), 853–864, 10.1039/D0EE03536J.
- D. Zivar, S. Kumar and J. Foroozesh, Underground hydrogen storage: A comprehensive review, Int. J. Hydrogen Energy, 2021, 46(45), 23436–23462 CrossRef CAS.
- Y. Yang, S. Liu and H. Ma, Impact of unrecovered shale gas reserve on methane emissions from abandoned shale gas wells, Sci. Total Environ., 2024, 913, 169750, DOI:10.1016/j.scitotenv.2023.169750.
- C. Karakosta, C. Pappas, V. Marinakis and J. Psarras, Renewable energy and nuclear power towards sustainable development: Characteristics and prospects, Renewable Sustainable Energy Rev., 2013, 22, 187–197 CrossRef.
- G. R. Timilsina, L. Kurdgelashvili and P. A. Narbel, Solar energy: Markets, economics and policies, Renewable Sustainable Energy Rev., 2012, 16(1), 449–465 CrossRef.
- M. F. Orhan, I. Dincer, M. A. Rosen and M. Kanoglu, Integrated hydrogen production options based on renewable and nuclear energy sources, Renewable Sustainable Energy Rev., 2012, 16(8), 6059–6082 CrossRef CAS.
- H. Ma, Z. Sun, Z. Xue, C. Zhang and Z. Chen, A systemic review of hydrogen supply chain in energy transition, Front. Energy, 2023, 17(2), 102–122, DOI:10.1007/s11708-023-0861-0.
- Technical Report: Flexible Nuclear Energy for Clean Energy Systems; NREL/TP-6A50-77088; National Renewable Energy Laboratory, Golden, CO, 2020.
- S. Weitemeyer, D. Kleinhans, T. Vogt and C. Agert, Integration of Renewable Energy Sources in future power systems: The role of storage, Renewable Energy, 2015, 75, 14–20 CrossRef.
- S. O. Amrouche, D. Rekioua, T. Rekioua and S. Bacha, Overview of energy storage in renewable energy systems, Int. J. Hydrogen Energy, 2016, 41(45), 20914–20927 CrossRef.
- IEA, The Future of Hydrogen, The International Energy Agency, Paris, 2019, https://www.iea.org/reports/the-future-of-hydrogen Search PubMed.
- S. Krevor, H. de Coninck, S. E. Gasda, N. S. Ghaleigh, V. de Gooyert, H. Hajibeygi, R. Juanes, J. Neufeld, J. J. Roberts and F. Swennenhuis, Subsurface carbon dioxide and hydrogen storage for a sustainable energy future, Nat. Rev. Earth Environ., 2023, 4(2), 102–118, DOI:10.1038/s43017-022-00376-8.
- M. Arbabzadeh, R. Sioshansi, J. X. Johnson and G. A. Keoleian, The role of energy storage in deep decarbonization of electricity production, Nat. Commun., 2019, 10(1), 3413, DOI:10.1038/s41467-019-11161-5.
- R. Moradi and K. M. Groth, Hydrogen storage and delivery: Review of the state of the art technologies and risk and reliability analysis, Int. J. Hydrogen Energy, 2019, 44(23), 12254–12269 CrossRef CAS.
- R. Gholami, Hydrogen storage in geological porous media: Solubility, mineral trapping, H2S generation and salt precipitation, J. Energy Storage, 2023, 59, 106576 CrossRef.
- V. Reitenbach, L. Ganzer, D. Albrecht and B. Hagemann, Influence of added hydrogen on underground gas storage: a review of key issues, Environ. Earth Sci., 2015, 73, 6927–6937 CrossRef CAS.
- D. L. Katz and M. R. Tek, Overview on underground storage of natural gas, J. Pet. Technol., 1981, 33(06), 943–951 CrossRef.
- C. Yang, T. Wang, Y. Li, H. Yang, J. Li, B. Xu, Y. Yang and J. J. K. Daemen, Feasibility analysis of using abandoned salt caverns for large-scale underground energy storage in China, Appl. Energy, 2015, 137, 467–481, DOI:10.1016/j.apenergy.2014.07.048.
- D. Pudlo, L. Ganzer, S. Henkel, M. Kühn, A. Liebscher, M. De Lucia, M. Panfilov, P. Pilz, V. Reitenbach and D. Albrecht, The H2STORE project: hydrogen underground storage–A feasible way in storing electrical power in geological media? in Clean Energy Systems in the Subsurface: Production, Storage and Conversion: Proceedings of the 3rd Sino-German Conference “Underground Storage of CO2 and Energy”, Goslar, Germany, 21–23 May 2013, Springer, 2013, pp. 395–412.
- R. Tichler, A. Zauner, M. Baresch, K. De Bruyn, C. Friedl, M. Furtlehner, S. Goers, J. Lindorfer, J. Mayerhofer, G. Reiter and M. Schwarz, Underground Sun Storage: Final Report Public, 2017, 840705.
- F. Feldmann, B. Hagemann, L. Ganzer and M. Panfilov, Numerical simulation of hydrodynamic and gas mixing processes in underground hydrogen storages, Environ. Earth Sci., 2016, 75(16), 1165, DOI:10.1007/s12665-016-5948-z.
- E. Sarı and E. Çiftçi, Underground hydrogen storage in a depleted gas field for seasonal storage: A numerical case study of the Tekirdağ gas field, Fuel, 2024, 358, 130310, DOI:10.1016/j.fuel.2023.130310.
- P. Purswani, E. J. Guiltinan, Y. Chen, Q. Kang, M. Mehana, C. W. Neil, T. C. Germann and M. R. Gross, Pore-scale modeling of carbon dioxide and hydrogen transport during geologic gas storage, Geophys. Res. Lett., 2024, 51(12), e2024GL109216 CrossRef CAS.
- K. C. Bijay, L. P. Frash, N. M. Creasy, C. W. Neil, P. Purswani, W. Li, U. Iyare and M. R. Gross, Laboratory study of cyclic underground hydrogen storage in porous media with evidence of a dry near-well zone and evaporation induced salt precipitation, Int. J. Hydrogen Energy, 2024, 71, 515–527 CrossRef.
- M. Lysyy, M. Fernø and G. Ersland, Seasonal hydrogen storage in a depleted oil and gas field, Int. J. Hydrogen Energy, 2021, 46(49), 25160–25174, DOI:10.1016/j.ijhydene.2021.05.030.
- B. Hagemann, M. Rasoulzadeh, M. Panfilov, L. Ganzer and V. Reitenbach, Hydrogenization of underground storage of natural gas, Comput. Geosci., 2016, 20(3), 595–606, DOI:10.1007/s10596-015-9515-6.
- J. Michelsen, E. M. Thaysen, S. Hogeweg, B. Hagemann, A. Hassanpouryouzband, N. Langanke, K. Edlmann and L. Ganzer, Hydrogen reservoir flow behaviour: Measurements of molecular diffusion, mechanical dispersion and relative permeability, H2020 HyUSPRe project report, 2023, p. 67.
- E. Jacops, M. Aertsens, N. Maes, C. Bruggeman, B. Krooss, A. Amann-Hildenbrand, R. Swennen and R. Littke, Interplay of molecular size and pore network geometry on the diffusion of dissolved gases and HTO in Boom Clay, Appl. Geochem., 2017, 76, 182–195 CrossRef CAS.
- B. Strauch, P. Pilz, J. Hierold and M. Zimmer, Experimental simulations of hydrogen migration through potential storage rocks, Int. J. Hydrogen Energy, 2023, 48(66), 25808–25820 CrossRef CAS.
- A. Keshavarz, H. Abid, M. Ali and S. Iglauer, Hydrogen diffusion in coal: Implications for hydrogen geo-storage, J. Colloid Interface Sci., 2022, 608, 1457–1462 CAS.
- A. Liu and S. Liu, Hydrogen sorption and diffusion in coals: Implications for hydrogen geo-storage, Appl. Energy, 2023, 334, 120746, DOI:10.1016/j.apenergy.2023.120746.
- V. Arekhov, T. Zhainakov, T. Clemens and J. Wegner, Measurement of Effective Hydrogen-Methane Gas Diffusion Coefficients in Reservoir Rocks, SPE Reservoir Eval. Eng., 2023, 1–16, DOI:10.2118/214451-pa (acccessed 9/28/2023).
- J. A. Currie, Gaseous diffusion in porous media. Part 2. - Dry granular materials, Br. J. Appl. Phys., 1960, 11(8), 318, DOI:10.1088/0508-3443/11/8/303.
- J. C. Yang, W. M. Pitts, M. Fernandez and K. Prasad, Measurements of effective diffusion coefficients of helium and hydrogen through gypsum, Int. J. Hydrogen Energy, 2013, 38(19), 8125–8131, DOI:10.1016/j.ijhydene.2012.09.030.
- E. C. Donaldson, R. F. Kendall and F. S. Manning, Dispersion and tortuosity in sandstones, in SPE Annual Technical Conference and Exhibition, 1976.
- J. Michelsen, E. M. Thaysen, S. Hogeweg, B. Hagemann, A. Hassanpouryouzband, N. Langanke, K. Edlmann and L. Ganzer, Hydrogen reservoir flow behaviour: Measurements of molecular diffusion, mechanical dispersion and relative permeability, 2023 Search PubMed.
- C. W. Neil, H. Boukhalfa, H. Xu, S. D. Ware, J. Ortiz, S. Avendaño, D. Harp, S. Broome, R. P. Hjelm and Y. Mao, Gas diffusion through variably-water-saturated zeolitic tuff: Implications for transport following a subsurface nuclear event, J. Environ. Radioact., 2022, 250, 106905 CrossRef CAS PubMed.
- A. A. Bunaciu, E. G. Udristioiu and H. Y. Aboul-Enein, X-ray diffraction: instrumentation and applications, Crit. Rev. Anal. Chem., 2015, 45(4), 289–299 CrossRef CAS PubMed.
- T. R. Marrero and E. A. Mason, Gaseous Diffusion Coefficients, J. Phys. Chem. Ref. Data, 2009, 1(1), 3–118, DOI:10.1063/1.3253094.
- M. J. Paul, S. R. Biegalski, D. A. Haas and J. D. Lowrey, Adsorptive transport of noble gas tracers in porous media, International Journal of Modern Physics: Conference Series, World Scientific, 2018, vol. 48, p. 1860124 Search PubMed.
- E. P. Ney and F. C. Armistead, The self-diffusion coefficient of uranium hexafluoride, Phys. Rev., 1947, 71(1), 14 CrossRef CAS.
- L. L. y Chen, D. L. Katz and M. R. Tek, Binary gas diffusion of methane-nitrogen through porous solids, AIChE J., 1977, 23(3), 336–341 CrossRef CAS.
- Y. Yang and S. Liu, Integrated modeling of multi-scale transport in coal and its application for coalbed methane recovery, Fuel, 2021, 300, 120971, DOI:10.1016/j.fuel.2021.120971.
- Y. Yang and S. Liu, Estimation and modeling of pressure-dependent gas diffusion coefficient for coal: A fractal theory-based approach, Fuel, 2019, 253, 588–606, DOI:10.1016/j.fuel.2019.05.009.
- H. Ma, Y. Yang, Y. Zhang, Z. Li, K. Zhang, Z. Xue, J. Zhang and Z. Chen, Optimized schemes of enhanced shale gas recovery by CO2-N2 mixtures associated with CO2 sequestration, Energy Convers. Manage., 2022, 268, 116062, DOI:10.1016/j.enconman.2022.116062.
- Z. Xue, Y. Zhang, H. Ma, Y. Lu, K. Zhang, Y. Wei, S. Yang, M. Chai, Z. Sun, P. Deng and Z. Chen, A Combined Neural Network Forecasting Approach for CO2-Enhanced Shale Gas Recovery, SPE J., 2024, 1–12, DOI:10.2118/219774-pa.
- D. Stroud, The effective medium approximations: Some recent developments, Superlattices Microstruct., 1998, 23(3–4), 567–573 CrossRef.
- S. Torquato and S. Torquato, Effective-medium approximations, Random Heterogeneous Materials: Microstructure and Macroscopic Properties, 2002, pp. 459–484 Search PubMed.
- V. S. Velan, G. Velayutham, N. Rajalakshmi and K. Dhathathreyan, Influence of compressive stress on the pore structure of carbon cloth based gas diffusion layer investigated by capillary flow porometry, Int. J. Hydrogen Energy, 2014, 39(4), 1752–1759 CrossRef.
- E. W. Washburn, The dynamics of capillary flow, Phys. Rev., 1921, 17(3), 273 CrossRef.
- NIST Chemistry WebBook, NIST Standard Reference Database Number 69 .
- E. A. Mason and A. P. Malinauskas, Gas Transport in Porous Media: The Dusty-gas Model, Elsevier, 1983 Search PubMed.
- J. Welty, G. L. Rorrer and D. G. Foster, Fundamentals of momentum, heat, and mass transfer, John Wiley & Sons, 2020 Search PubMed.
- M. Knudsen, Die Gesetze der Molekularströmung und der inneren Reibungsströmung der Gase durch Röhren, Ann. Phys., 1909, 333(1), 75–130 CrossRef.
- W. Steckelmacher, Knudsen flow 75 years on: the current state of the art for flow of rarefied gases in tubes and systems, Rep. Prog. Phys., 1986, 49(10), 1083 CrossRef CAS.
- T. Marrero and E. Mason, Correlation and prediction of gaseous diffusion coefficients, AIChE J., 1973, 19(3), 498–503 CrossRef CAS.
- R. Millington, Gas diffusion in porous media, Science, 1959, 130(3367), 100–102 CrossRef CAS.
- L. Shen and Z. Chen, Critical review of the impact of tortuosity on diffusion, Chem. Eng. Sci., 2007, 62(14), 3748–3755 CAS.
- P. Guo, Dependency of tortuosity and permeability of porous media on directional distribution of pore voids, Transp. Porous Media, 2012, 95, 285–303 CrossRef CAS.
- J. M. Dallavalle, Micromeritics: the technology of fine particles, Pitman Publishing Limited, 1948 Search PubMed.
- J. R. Farver, Oxygen and hydrogen diffusion in minerals, Rev. Mineral. Geochem., 2010, 72(1), 447–507 CrossRef CAS.
- J. T. Hannibal, Berea sandstone: A heritage stone of international significance from Ohio, USA, Geol. Soc., Spec. Publ., 2020, 486(1), 177–204 CrossRef.
- A. E. Yekta, M. Pichavant and P. Audigane, Evaluation of geochemical reactivity of hydrogen in sandstone: Application to geological storage, Appl. Geochem., 2018, 95, 182–194, DOI:10.1016/j.apgeochem.2018.05.021.
- A. Al-Yaseri, A. Amao and A. Fatah, Experimental investigation of shale/hydrogen geochemical interactions, Fuel, 2023, 346, 128272, DOI:10.1016/j.fuel.2023.128272.
- A. S. Lord, P. H. Kobos and D. J. Borns, Geologic storage of hydrogen: Scaling up to meet city transportation demands, Int. J. Hydrogen Energy, 2014, 39(28), 15570–15582 CrossRef CAS.
- S. Harati, S. R. Gomari, F. Gasanzade, S. Bauer, T. Pak and C. Orr, Underground hydrogen storage to balance seasonal variations in energy demand: Impact of well configuration on storage performance in deep saline aquifers, Int. J. Hydrogen Energy, 2023, 48(69), 26894–26910 CrossRef CAS.
- S. R. Thiyagarajan, H. Emadi, A. Hussain, P. Patange and M. Watson, A comprehensive review of the mechanisms and efficiency of underground hydrogen storage, J. Energy Storage, 2022, 51, 104490 CrossRef.
- H. Zhang, Y. Zhang, M. Al Kobaisi, S. Iglauer and M. Arif, Effect of cyclic hysteretic multiphase flow on underground hydrogen storage: A numerical investigation, Int. J. Hydrogen Energy, 2024, 49, 336–350 CrossRef CAS.
- S. Mao, M. Mehana, T. Huang, G. Moridis, T. Miller, E. Guiltinan and M. R. Gross, Strategies for hydrogen storage in a depleted sandstone reservoir from the San Joaquin Basin, California (USA) based on high-fidelity numerical simulations, J. Energy Storage, 2024, 94, 112508 CrossRef.
- A. Ozarslan, Large-scale hydrogen energy storage in salt caverns, Int. J. Hydrogen Energy, 2012, 37(19), 14265–14277 CrossRef CAS.
- P. Deng, Z. Chen, X. Peng, J. Wang, S. Zhu, H. Ma and Z. Wu, Optimized lower pressure limit for condensate underground gas storage using a dynamic pseudo-component model, Energy, 2023, 285, 129505, DOI:10.1016/j.energy.2023.129505.
- K. Luboń and R. Tarkowski, Numerical simulation of hydrogen injection and withdrawal to and from a deep aquifer in NW Poland, Int. J. Hydrogen Energy, 2020, 45(3), 2068–2083 CrossRef.
- CMG-GEM, GEM User's Guide, Advanced compositional and GHG reservoir simulator, 2022.
- A. Fick, About diffusion, Ann. Phys., 1855, 170(1), 59–86, DOI:10.1002/andp.18551700105.
- J. Crank, The mathematics of diffusion, Oxford University Press, 1979 Search PubMed.
- M. A. Kargarpour, Carbonate reservoir characterization: an integrated approach, J. Pet. Explor. Prod. Technol., 2020, 10(7), 2655–2667 CrossRef.
- X. Xie, W. W. Weiss, Z. Tong and N. R. Morrow, Improved Oil Recovery from Carbonate Reservoirs by Chemical Stimulation, SPE J., 2005, 10(03), 276–285 CrossRef CAS.
- R. M. Abraham-A, F. Taioli and A. I. Nzekwu, Physical properties of sandstone reservoirs: Implication for fluid mobility, Energy Geosci., 2022, 3(4), 349–359 CrossRef.
- D. L. Gautier and D. D. Rice, Conventional and low-permeability reservoirs of shallow gas in the northern Great Plains, J. Pet. Technol., 1982, 34(07), 1600–1608 CrossRef.
- A. S. Lord, Overview of geologic storage of natural gas with an emphasis on assessing the feasibility of storing hydrogen, SAND2009-5878, Sandia National Laboratories Albuquerque, New Mexico, 2009 Search PubMed.
- A. Rezaei, A. Hassanpouryouzband, I. Molnar, Z. Derikvand, R. S. Haszeldine and K. Edlmann, Relative Permeability of Hydrogen and Aqueous Brines in Sandstones and Carbonates at Reservoir Conditions, Geophys. Res. Lett., 2022, 49(12), e2022GL099433, DOI:10.1029/2022GL099433.
- M. Lysyy, T. Føyen, E. B. Johannesen, M. Fernø and G. Ersland, Hydrogen Relative Permeability Hysteresis in Underground Storage, Geophys. Res. Lett., 2022, 49(17), e2022GL100364, DOI:10.1029/2022GL100364.
- O. Redlich and J. N. Kwong, On the thermodynamics of solutions; an equation of state; fugacities of gaseous solutions, Chem. Rev., 1949, 44(1), 233–244, DOI:10.1021/cr60137a013 From NLM.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00233d |
| This journal is © The Royal Society of Chemistry 2024 |