Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Influence of crossover on capacity fade of symmetric redox flow cells†
Thomas Y.
George‡
 ,
Eric M.
Fell‡
,
Eric M.
Fell‡
 ,
Kyumin
Lee
,
Kyumin
Lee
 ,
Michael S.
Emanuel
,
Michael S.
Emanuel
 and
Michael J.
Aziz
and
Michael J.
Aziz
 *
*
Harvard John A. Paulson School of Engineering and Applied Sciences, Cambridge, Massachusetts 02138, USA. E-mail: maziz@harvard.edu
First published on 3rd October 2024
Abstract
Volumetrically unbalanced compositionally symmetric cell cycling with potentiostatic (CV) or galvanostatic-with-potential-hold (CCCV) protocols is a rigorous technique for evaluating the calendar lifetime of reactants for redox flow batteries. Here, we evaluate the influence of reactant crossover through the membrane on symmetric cell cycling behavior. We tested symmetric cells of anthraquinone disulfonic acid (AQDS) with Nafion membranes of varied thickness and manufacture (NR211, NR212, N115, and N117, ranging 25–183 μm). Membranes were tested both as-received and pretreated with a common procedure of soaking in water at elevated temperature and then in dilute hydrogen peroxide. We found no significant difference in capacity fade rates of symmetric cells with any of the membranes as-received, indicating a negligible influence of crossover. However, we observed increased capacity fade with increased permeability through pretreated membranes. Supported by zero-dimensional modeling and operando UV-vis spectrophotometry, we propose a mechanism for net crossover in AQDS symmetric cells based on a higher time-averaged concentration of quinhydrone dimers in the non-capacity limiting side (NCLS) compared to the capacity limiting side (CLS), driving net crossover of AQDS reactants out of the CLS. Further, we illustrate other hypothetical scenarios of net crossover using the zero-dimensional model. Overall, many membrane–electrolyte systems used in symmetric cell studies have sufficiently low crossover flux as to avoid the influence of crossover on capacity fade, but under conditions of higher crossover flux, complex interactions of crossover and chemical reactions may result in diverse capacity fade trajectories, the mechanisms of which may be untangled with operando characterization and modeling.
1 Introduction
Redox flow batteries (RFBs) constitute a promising platform for stationary energy storage, which may contribute significantly to the decarbonization of electricity if paired with intermittent renewable energy generation (i.e. from solar and wind).1,2 The large scale deployment of RFBs depends greatly on their ability to demonstrate stable charge–discharge cycling for decadal operating lifetimes without impractically high maintenance or material replacement costs.3 Understanding, quantifying, and minimizing the various mechanisms of capacity fade are therefore of paramount importance to RFB research and development.RFBs comprise a positive and negative electrolyte (posolyte and negolyte respectively) containing dissolved redox reactants, which are stored in external reservoirs and pumped through an electrochemical flow reactor. The reactor includes electrodes (typically porous carbon) sandwiching a separator (typically an ion exchange membrane) that is devised to inhibit mixing between posolyte and negolyte while maintaining ionic conductivity. Many RFB designs employ redox-active metal ions as reactants.4,5 In this case, capacity fade may be caused by crossover of reactants through the membrane, parasitic side reactions that unbalance battery state of charge (SOC), and precipitation.6 For example, each of these mechanisms may operate in the incumbent all-vanadium RFB,7–9 although crossover is the ubiquitous mechanism and has received the most research attention.10–13 Crossover rates of vanadium ions through commercial ion exchange membranes are typically high, so long-term operation of vanadium-based flow batteries requires periodic interruption to rebalance and restore the initial composition of posolyte and negolyte.14–16
More recently, synthetic organic redox reactants have emerged for RFBs. Organic redox reactants have tunable structures through chemical synthesis, unlocking a vast space of physical and chemical properties.17 Composed of some of the most abundant atoms on Earth, organic redox reactants may avoid the material availability issues surrounding many metals18 and may avoid the ecological hazards of mining and extraction,19 provided the synthesis uses sustainable feedstocks. However, organic redox reactants are subject to myriad SOC-dependent chemical reactions that can result in structural changes and the loss of redox activity under cycling conditions. This chemical degradation may occur at rates spanning orders of magnitude, with complex mechanisms dependent on specific chemistry.20 Further, these reactions may be superimposed on top of mechanisms such as crossover, complicating the matter of understanding the cause of capacity fade in organic-based RFBs.
The volumetrically unbalanced compositionally symmetric cell method was devised to isolate the contribution of chemical decomposition to capacity fade.21 We define a volumetrically unbalanced compositionally symmetric cell (hereafter referred to as symmetric cell) as a cell with initially zero volts theoretical open circuit potential, with both electrolytes containing the same redox couple at the same concentration at 50% SOC, and with one electrolyte (the capacity limiting side, hereafter CLS) having smaller volume than the other (the non-capacity limiting side, hereafter NCLS). In principle the symmetric cell minimizes concentration gradients across the membrane, which would otherwise drive crossover.
When a symmetric cell is cycled while accessing the full capacity of the CLS (0% to 100% SOC), the measured capacity fade reveals the loss of redox active material in the CLS. Full-capacity cycling of the CLS is achieved by potentiostatic or galvanostatic-with-potential-hold cycling methods (also known as CV or CCCV, respectively) with sufficient applied overpotentials.21 Galvanostatic (CC) cycling alone has been shown to mask capacity fade by leaving unaccessed capacity and by introducing artifacts from temperature fluctuations and other sources of change to the internal resistance.22,23 We have previously benchmarked the reproducibility of the symmetric cell method with potentiostatic cycling of published anthraquinone reactants in a high-throughput setup controlling eight cells simultaneously.24 However, the permeability of negatively charged anthraquinone ions through Nafion in alkaline conditions—the membrane–electrolyte system relevant to our previous work—has been shown to be undetectably low.25–28 The real influence of crossover in symmetric cell cycling of organics under higher-permeability conditions has remained unexamined.29 Addressing this critical gap in understanding is the purpose of the present research.
Recently, it has been hypothesized that crossover could still influence symmetric cell cycling.3,29–31 It has been proposed that net crossover could affect capacity if the oxidized and reduced forms of a reactant have different membrane permeabilities.3 If the cell is cycled in such a way that different SOCs are maintained for different amounts of time or if the electrolytes do not start at exactly 50% SOC, i.e. the time-averaged SOC in both electrolytes is not 50%, this could allow either net loss of the faster permeable species from the CLS to the NCLS (increasing capacity fade) or net gain of the faster permeable species from the NCLS to the CLS (decreasing capacity fade).30 It has also been proposed that unequal ionic strength across the membrane or large excursions in viscosity and density during cycling could bring about pressure-driven crossover.30
In the present work, we use symmetric cells cycling anthraquinone disulfonic acid (AQDS) in 1 M H2SO4 supporting electrolyte with Nafion cation exchange membranes—the first aqueous organic RFB membrane–electrolyte system published32—as a model system to probe crossover effects. In previous work, AQDS has exhibited both moderate capacity fade20,21 and moderate permeability through as-received Nafion.33 The mechanism of chemical decomposition is a reaction of the reduced state (anthrahydroquinone) forming anthrone, a mechanism that is common to anthraquinones.34,35 AQDS has also been reported to dimerize both with itself and with its charged state based on concentration- and pH-dependent equilibria.36–38 Quinhydrone dimers have been observed with in situ spectroscopy in flow cells under acidic conditions.39,40
By testing symmetric cells with identical electrolytes but varied membrane thicknesses and pretreatments, we are able to control crossover without otherwise affecting the AQDS (electro)chemistry. Nafion membranes are available in a variety of thicknesses, and membranes with the same nominal chemical makeup exhibit properties strongly dependent on the physical manufacturing process and the thermal and environmental history.41,42 Pretreatment before use in batteries has been shown to change Nafion permeability of redox reactants by orders of magnitude.43
We applied a zero-dimensional, open-source flow battery model (RFBzero) to simulate a proposed scheme for crossover effects on AQDS symmetric cell cycling,44 using experimental results as model inputs. Zero-dimensional modeling has previously proven useful for describing crossover behavior of vanadium ions in all-vanadium flow batteries,45–47 and more recent zero-dimensional models have included chemical degradation or self-discharge of reactants as well as crossover.48–50 In this work, the zero-dimensional model describes the mechanism of net crossover in AQDS symmetric cells, and we further apply the model to test other scenarios for the influence of different symmetric cell conditions on crossover.
2 Experimental
2.1 Chemicals and materials
18 M sulfuric acid (95.0–98.0%) was purchased from VWR Chemicals BDH and diluted to 1 M with deionized water (18.2 MΩ cm) for use in experiments. Sodium anthraquinone 2,7-disulfonate, hereafter referred to as AQDS throughout the manuscript, was purchased from AFG Scientific. Sodium sulfate was purchased from Sigma-Aldrich. Vanadyl sulfate hydrate was purchased from Spectrum Chemical Mfg. Corp and vanadium(V) oxide was purchased from Sigma-Aldrich. Nafion N117, NR212, and NR211 were purchased from Ion Power, and Nafion N115 was purchased from VWR (supplied by BeanTown Chemical).2.2 Membrane pretreatment
All “pretreated” membranes in this study were soaked for 20 minutes in deionized water at 80 °C followed by 35 minutes soaked in 5% hydrogen peroxide in water at room temperature.43,51 Membranes were otherwise used as-received. All membranes were soaked in 1 M H2SO4 at least overnight prior to experiments.2.3 Permeability
Permeability measurements were made using custom glass H-cells from Adams and Chittenden. Membranes were clamped between two chambers containing 10 mL of donating and receiving electrolyte, respectively. The donating electrolyte comprised 0.1 M AQDS and 1 M H2SO4 and the receiving electrolyte comprised 0.1 M Na2SO4 and 1 M H2SO4 to balance the total concentration of ions in the donating electrolyte. The H-cells were placed on a multi-channel magnetic stir plate (Scilogex) for continuous stirring of electrolytes during permeation experiments. Perodically, aliquots were taken from the receiving electrolytes, diluted in a cuvette as needed, and the concentration of AQDS was measured with UV-vis spectrophotometry (Agilent). The AQDS calibration curve used for concentration determination is provided as Fig. S1 (ESI†). The volume of the aliquot removed from the H-cell receiving electrolyte was replaced with pristine receiving solution, and the resulting dilution of the receiving side was accounted for in the calculation of permeability by a procedure reported previously.33 Triplicate H-cells were studied for each unique combination of Nafion membrane and pretreatment in this work.2.4 Flow cell assembly
Flow cell hardware (Fuel Cell Technologies, Inc.), including interdigitated flow plates (MWI, Inc.), electrodes (Sigracet GDL 39AA baked in air at 400 °C for 24 h), gaskets (Viton), fluorinated ethylene propylene tubing, and KNF diaphragm pumps (FF 12 DCB-4) were selected and assembled identically to our previous report,24 with the exception of membranes which were handled as per the foregoing sections. The geometric active area of the cells is 5 cm2.2.5 Symmetric cell protocols
All flow cells in this work were studied in an N2-filled glovebox (Vacuum Atmospheres Company). A Novonix battery cycler with a DC-offset unit providing a voltage range of −1 to +4 V was used for all cell cycling, whereas a Gamry Interface 1010B potentiostat located inside the glovebox was used for electrochemical impedance spectroscopy. Four point connections to the cycler/potentiostat for each cell were used for all experiments. Eight symmetric cells were cycled simultaneously in the high-throughput setup described previously.24All electrolytes for electrochemical testing were prepared in the glovebox using deoxygenated deionized water. Electrolytes for a set of eight symmetric cells were prepared in one batch: a large volume of 0.1 M AQDS in 1 M H2SO4 was charged to its maximum accessible capacity (charged to a 1.3 V cutoff and held at that cell voltage until current dropped to 1 mA cm−2) against an excess of 0.3 M VOSO4 in 1 M H2SO4 posolyte, and then this completely charged AQDS electrolyte was mixed with an equal volume of 0.1 M AQDS in 1 M H2SO4 at 0% SOC. The resulting 50% SOC mixed electrolyte was then divided to make a 5 mL CLS and 10 mL NCLS for each symmetric cell.
Electrochemical impedance spectroscopy on cells at 50% SOC was carried out at open circuit voltage with a 10 mV amplitude AC voltage at a frequency range from 20 kHz to 10 Hz. We report ohmic resistance as the high-frequency intercept of the real axis of the resulting Nyquist plot.
Symmetric cells were cycled in a CCCV protocol with ±10 mA cm−2 constant current density followed by potential holds at 0.2 V (charging, reducing the CLS reactant) or −0.2 V (discharging, oxidizing the CLS reactant), starting with charging on the first half-cycle. Each charge/discharge potential was held until the current dropped to ±1 mA cm−2 to achieve cycling of the entire accessible capacity. Electrolytes were circulated at a constant rate of approximately 60 mL min−1.
2.6 Operando UV-vis spectrophotometry
A full cell (posolyte and negolyte compositionally different) was constructed with 5 mL 0.1 M AQDS in 1 M H2SO4 as the negolyte CLS (initially 0% SOC) and 50 mL 0.3 M VOSO4 0.05 M V2O5 1 M H2SO4 as the posolyte NCLS. The cell hardware and cell assembly were the same as for the symmetric cells, and as-received Nafion N117 soaked overnight in 1 M H2SO4 was used as the membrane. Electrolytes were flowed at approximately 10 mL min−1 (slower flow rate needed due to the in-line cuvette) and the AQDS flow path included an in-line flow cuvette (100 μm path length, sufficiently thin to avoid the need to dilute) connected to a UV-vis spectrophotometer (OceanOptics) within the glovebox. The cell was cycled with a CCCV method: ±10 mA cm−2 constant current density until a potential limit of 1.3 V (charge) or 0.4 V (discharge) with a constant potential hold until the current dropped to ±1 mA cm−2. As the cell cycled, UV-vis spectra of the AQDS solution were continuously recorded.3 The model
We refer the reader to the open-source Python code and complete documentation of the RFBzero model44 for detail beyond what is summarized in the following section.The model we have implemented is adopted from published work,48 with modification to describe the particularities of the AQDS electrolyte system. In general, the model solves for variables of a flow battery system at incremental time steps. As the model is zero-dimensional, these variables are assumed to be spatially invariant. The concentrations of oxidized and reduced species in the CLS and NCLS are updated based on the faradaic current during each increment. The open circuit voltage is then determined by the concentrations in the CLS and NCLS through the Nernst equation. Cell voltage is evaluated as the sum of the open circuit voltage and the overpotentials associated with activation, ohmic resistance, and mass transport.
For the AQDS electrolyte system, concentrations of the redox reactant in its oxidized and reduced states are further modified by chemical degradation, crossover, and the formation of quinhydrone dimers. This section provides rate equations for the contributions of each of these processes. At each time step in the model, concentrations of oxidized and reduced states are updated by the faradaic current and then adjusted by each of these rate equations.
The rate of chemical degradation is given as the time derivative of the concentration of reduced species 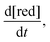 with a first-order rate law with the chemical degradation rate constant kchemdeg (units of s−1), as shown in eqn (1):
with a first-order rate law with the chemical degradation rate constant kchemdeg (units of s−1), as shown in eqn (1):
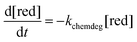 | (1) |
The contribution of the crossover rate is described by eqn (2) (crossover of the oxidized state) and 3 (crossover of the reduced state):
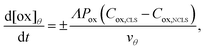 | (2) |
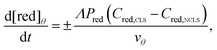 | (3) |
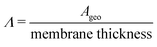 (cm) where Ageo = geometric area (cm2). This formulation allows for tracking concentration changes of oxidized and reduced states of the redox reactant in the CLS and the NCLS as the two reservoirs exchange material through the membrane by diffusion-driven crossover (concentration gradient driving force assuming dilute solutions). The sign written as ± in eqn (2) and (3) is set as positive or negative at each time step depending on the direction of the concentration gradient such that, when one reservoir (CLS or NCLS) loses material, that material is gained by the other reservoir. This means that within the model, the signs of eqn (2) and (3) for CLS and NCLS respectively will change over the course of a given cycle.
(cm) where Ageo = geometric area (cm2). This formulation allows for tracking concentration changes of oxidized and reduced states of the redox reactant in the CLS and the NCLS as the two reservoirs exchange material through the membrane by diffusion-driven crossover (concentration gradient driving force assuming dilute solutions). The sign written as ± in eqn (2) and (3) is set as positive or negative at each time step depending on the direction of the concentration gradient such that, when one reservoir (CLS or NCLS) loses material, that material is gained by the other reservoir. This means that within the model, the signs of eqn (2) and (3) for CLS and NCLS respectively will change over the course of a given cycle.
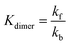
Finally, the contribution of AQDS dimerization is described by eqn (4) and (5):
 | (4) |
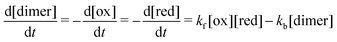 | (5) |
4 Results and discussion
4.1 Symmetric cell cycling and permeability
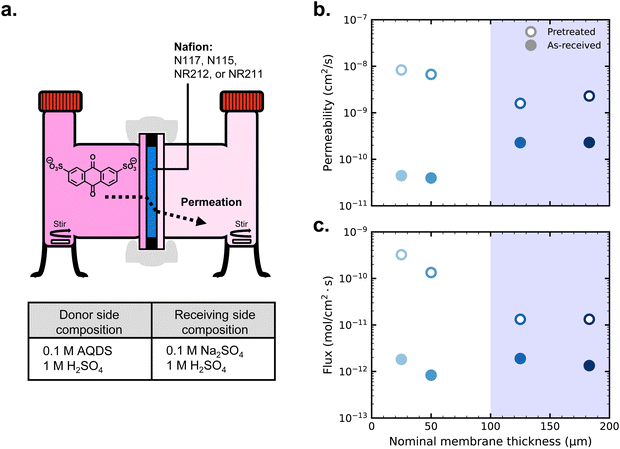
First, we cycled AQDS symmetric cells with each of four thicknesses of Nafion but otherwise identical cell parameters. All Nafion membranes were soaked overnight in 1 M H2SO4 but otherwise used as-received. Fig. 1a depicts a schematic of the symmetric cell setup. Fig. 1c shows the nominal thickness of each Nafion membrane used in this work. From Nafion NR211 at approximately 25 μm to Nafion N117 at 183 μm, the membrane thicknesses tested in this work range over almost an order of magnitude. The blue shading in the figure demarcates Nafion in the “N” family, which are thicker and manufactured by extrusion, from the “NR” family which are thinner and manufactured by casting from a polymer dispersion solution and then drying at elevated temperature. In addition to the differences in thickness, somewhat different intensive properties are expected between the extruded and the dispersion-cast membranes because extrusion is expected to result in a relatively higher degree of amorphous structure.41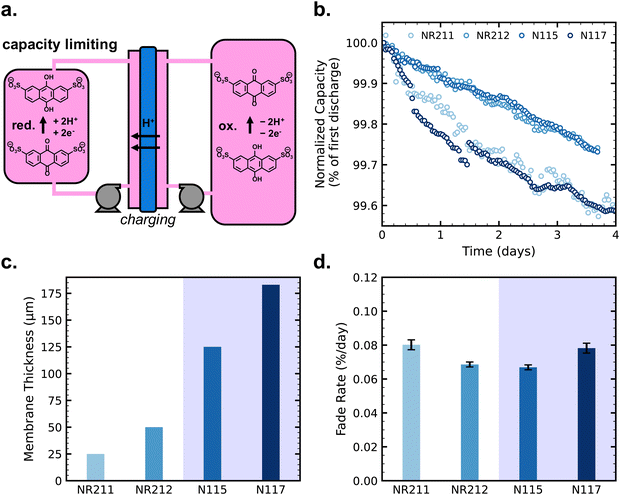 | ||
| Fig. 1 (a) Schematic of the AQDS symmetric cell depicted in charging mode; (b) discharge capacity over time for symmetric cells with as-received membranes, normalized by the capacity of the first discharge; (c) nominal membrane thicknesses; and (d) capacity fade rates for cells with each Nafion membrane (as-received), with error bars denoting uncertainty in a given single-cell fade rate measurement as per ref. 24. | ||
Capacity (normalized to first discharge capacity for comparison between cells) vs. time and resulting capacity fade rate (% day−1) for each of four cells with different membranes are shown in Fig. 1b and d respectively (non-normalized capacity in Fig. S2, ESI†). Despite differences in the membrane, capacity fade rates did not differ between cells by greater than 0.02% day−1. This degree of cell-to-cell variation is within expected error for this magnitude of fade rate.24 Therefore, we conclude that differences in the magnitude of net crossover across these four cells are negligible.
To evaluate the effect of crossover in these symmetric cells, we had to exacerbate the magnitude of crossover flux by decreasing the selectivity of the membranes. To this end, we employed a pretreatment that has become common in the flow battery literature: soaking for 20 minutes in deionized water at 80 °C followed by 35 minutes soaking in 5% hydrogen peroxide in water at room temperature.43,51 This pretreatment has been shown to increase the ionic conductivity of Nafion while more drastically increasing permeability of redox reactants,43 an unfavorable tradeoff that is not recommended for stable battery cycling. The hydrated morphology of Nafion is sensitive to its thermal history. Elevated-temperature pretreatment has the effect of increasing the subsequent water content of the membrane,42 enabling greater crossover.
Fig. 2a depicts the schematic H-cell setup for permeability measurements, including the compositions of donating and receiving chambers to balance ion concentration. Fig. 2b displays the AQDS permeabilities of both pretreated and as-received samples of each thickness of Nafion (permeabilities also tabulated in Table S1, ESI†). Permeability experiments were triplicated, but the error bars from the standard deviations of permeability from the average of each set of three values are smaller than the points on the figure. UV-vis calibration of AQDS is provided in Fig. S1 (ESI†), and supporting data for permeability measurements are shown in Fig. S3 and S4 (ESI†) for as-received and pretreated membranes, respectively.
At each thickness, pretreated membranes have greater permeabilities than as-received membranes. This difference is about one order of magnitude for the thicker, extruded membranes and about two orders of magnitude for the thinner, dispersion-cast membranes. Previous work on Nafion pretreatment has shown that boiling the membranes in 0.5 M H2SO4 and then deionized water for two hours gives subsequently similar vanadyl permeability and proton conductivity for both extruded and dispersion-cast Nafion.41 In our work, using the common Nafion pretreatment among the aqueous organic flow battery community, it may be the case that the thicker membranes did not reach structural equilibrium. Regardless, the properties for each membrane following pre-treatment are reproducible, enabling us to make connections between ex situ permeability studies and symmetric cell cycling results.
Among the as-received membranes, extruded Nafion exhibits greater permeability than dispersion-cast Nafion, arising from structural differences between the polymer films following manufacturing.41 Otherwise permeability does not depend on membrane thickness; permeability is an effective diffusion coefficient influenced by the intensive transport properties of the membrane phase and the equilibrium concentration ratio of crossing species in the membrane to that in the electrolyte. Crossover flux (Fig. 2c), however, depends on both the permeability of the membrane and its thickness, and is relevant for determining the amount of crossover that will occur in a battery. Between two membranes with equal permeability, a membrane twice as thick will exhibit half the crossover flux, e.g. NR212 vs. NR211.
Next, we carried out AQDS symmetric cell cycling with pretreated Nafion membranes for comparison with the results from as-received membranes. Fig. 3a shows capacity (normalized to first discharge capacity for comparison between cells) vs. time for eight simultaneously cycled symmetric cells with pretreated membranes, with duplicate cells for each membrane thickness (non-normalized data in Fig. S5, ESI†). Capacity fade rates for cells with different pretreated Nafion membranes follow this trend: NR211 > NR212 > N115 ≈ N117. This is the same trend as AQDS crossover flux as shown in Fig. 2c. Flux from ex situ permeability measurements vs. symmetric cell fade rate for the pretreated membranes is shown in Fig. 3c. As-received N115 and N117 exhibit equivalent AQDS permeability as expected because they are both extruded membranes, but pretreated N115 exhibits slightly lower permeability sufficient to offset the difference in thickness, giving pretreated N115 and N117 equivalent crossover flux.
 | ||
| Fig. 3 (a) Discharge capacity over time for symmetric cells with pretreated membranes (duplicate cells shown for each of four membranes), normalized by the capacity of the first discharge; (b) capacity fade rates for cells with each Nafion membrane (as-received and pretreated compared, duplicates shown for pretreated cell tests), with error bars denoting uncertainty in a given single-cell fade rate measurement as per ref. 24; (c) crossover flux from ex situ permeability measurements vs. capacity fade rates of duplicate symmetric cells with pretreated membranes; and (d) average coulombic efficiency (CE) of symmetric cells with each membrane condition (error bars denote standard deviation within a single cell run). | ||
Further, Fig. 3d shows that average coulombic efficiency (CE) over cycling correlates with the trend of crossover flux and capacity fade rate, with lower coulombic efficiency associated with higher fade rate and higher crossover flux. Coulombic inefficiency is indicative of crossover because crossover during the course of a charging half-cycle may result in fewer coulombs accessible on the subsequent discharging half-cycle. We conclude that the differences in capacity fade rates of the symmetric cells arise from the differences in net crossover between the membranes.
When we compare the results from pretreated membranes with results from as-received membranes, we observe that capacity fade rates of cells with pretreated N115 and N117 approach those of cells with as-received membranes (Fig. 3b and Fig. S6, ESI†). From the ex situ crossover measurements, pretreated N115 and N117 exhibit a flux of 10−11 mol cm−2 s−1 whereas the as-received membranes exhibit a flux of approximately 10−12 mol cm−2 s−1. Our results suggest that, in general, there is a threshold of crossover flux below which crossover effects on fade rate are no longer apparent. This threshold depends on the relative rates of reactant concentration change by chemical degradation (eqn (1)) and crossover (eqn (2) and (3)), and the rates related to reactant crossover depend on the reservoir volume and membrane area. For this specific system, the threshold of ex situ crossover flux below which crossover effects are no longer apparent in symmetric cell cycling lies between 10−11 and 10−12 mol cm−2 s−1.
The foregoing discussion uses crossover flux based on ex situ measurements of permeability, in which diffusion is the only operative crossover mechanism, to estimate crossover flux in a battery, where current-dependent mechanisms of crossover also operate in principle. The low operating current (10 mA cm−2 or lower) for the cycling we report combined with the expected low uptake of the negatively charged AQDS into the membrane phase provide conditions under which diffusion-dominated crossover is assumed.27,52 Further, over 97% of the accessed capacity (Fig. S7, ESI†) and 93–95% of the time (Fig. S8, ESI†) for discharge half-cycles in the CCCV protocol was spent in the constant current regime despite differences in membrane thickness or pretreatment (30–90 mΩ range of cell resistances shown in Fig. S6b, ESI†). This suggests a similar driving force for AQDS migration in all of the cycling experiments. For these reasons, the analysis in this work considers only diffusion-driven crossover, although other conditions in the literature may require considerations of current-dependent crossover as well.53
4.2 Zero-dimensional model of the AQDS crossover mechanism
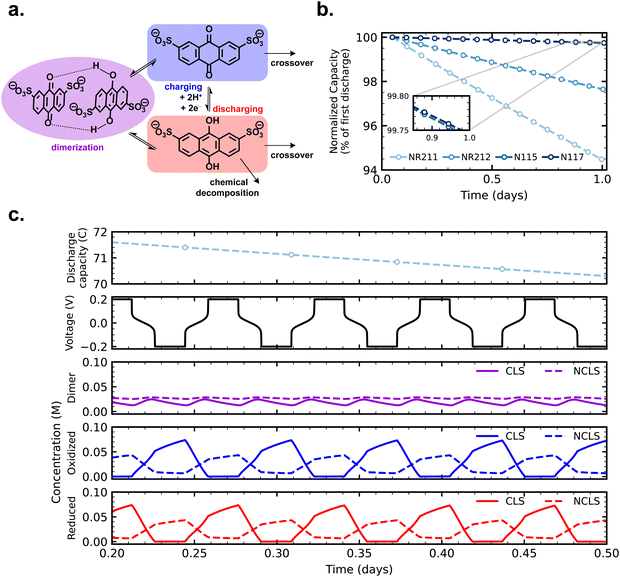
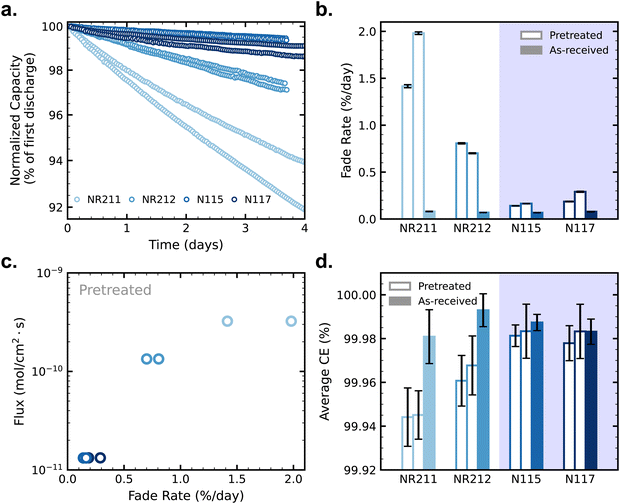
With crossover effects in symmetric cell cycling now established, we turn to zero-dimensional modeling to elucidate the mechanism of net crossover in AQDS symmetric cells. Fig. 4a depicts the reactions and fluxes of AQDS species treated in the model. The vertical reaction arrows show the normal electrochemical cycling of AQDS in which AQDS is charged to its anthrahydroquinone and reversibly discharged in a coupled two-proton two-electron pathway at pH 0 (approximately 0.2 V vs. SHE). Both the oxidized and reduced states are subject to crossover through the membrane (eqn (2) and (3)) and we assume, given their equivalent charge number and similar structure and size,27 that the permeabilities of both through a given membrane are equal (i.e. Pox = Pred). The reduced (charged) state is also subject to chemical degradation, which we describe as first order in anthrahydroquinone concentration in accordance with previous work (eqn (1)).21 Experimentally determined permeabilities and cell area-specific resistances used as model inputs are listed in Table S1 (ESI†). A kchemdeg value of 1 × 10−8 s−1 was chosen for modeled fade rates of cells with as-received membranes (modeled cycling shown in Fig. S9, ESI†) to match experimental values within 0.02% day−1. For comparison, Fig. S10 (ESI†) displays simulated cycling with the kchemdeg value of 1 × 10−8 s−1 but zero membrane permeability and no dimerization.The combined mechanisms of crossover of both oxidized and reduced states and degradation of the reduced state, when Pox = Pred ≠ 0, are not sufficient to explain the observed experimental trend of increasing symmetric cell capacity fade with increasing crossover flux, as we shall see. When both CLS and NCLS have the same time-averaged SOC of 50% throughout cycling, both sides have the same net loss of AQDS through the SOC-dependent first-order chemical degradation reaction, and any AQDS crossover will be balanced by equal flux in the opposite direction, even if the magnitude of that flux is greater for a more permeable membrane.
An additional mechanism, one that could effect a time-averaged net imbalance of AQDS concentration between CLS and NCLS, is needed to account for the observed experimental trend. In addition to crossover and chemical degradation, Fig. 4 and eqn (4) and (5) illustrate the bimolecular reaction of an anthraquinone and an anthrahydroquinone forming a quinhydrone dimer, which has been observed spectroscopically in acidic AQDS electrolytes. Previous work has shown the concentration and SOC dependence of AQDS dimerization over one charging half-cycle (i.e. 0–100% SOC).39 In this work, we assembled a full cell in which 5 mL 0.1 M AQDS in 1 M H2SO4 as the negolyte CLS (initially 0% SOC but otherwise chosen to match the CLS of symmetric cells in this work) was cycled against an excess vanadium posolyte, and AQDS dimerization was monitored over four cycles with an in-line, operando UV-vis measurement (Fig. S11, ESI†). The published molar attenuation coefficients of the quinhydrone dimer in ref. 39 were used to track dimer concentration over the course of cycling and this value, combined with the coulometry, was used to determine the concentration of oxidized and reduced states of AQDS and thus the reaction quotient of the dimerization reaction (Qdimer).
The periodic fluctuation of Qdimer in Fig. S11 (ESI†) indicates the dimerization reaction is out of equilibrium during cycling (at equilibrium, Qdimer = Kdimer) but may approach equilibrium around 50% SOC, when both the dimer concentration and Qdimer are close to their local maxima for a given cycle. Adjusting the model parameters of the dimerization equilibrium constant Kdimer and the respective forward and backward rate constants kf and kb, we found that the accessed capacity of an AQDS electrolyte under CCCV cycling depends on the dimerization kinetics (Fig. S12, ESI†). This mechanism has been proposed to explain missing capacity in AQDS cells in the literature,36–38 but is now supported by microkinetic modeling for the first time. At a Kdimer of 75 M−1 (close to both the previously published value of 80 M−1 and the average measured local maxima of Qdimer in Fig. S11, ESI†) and kf = 0.03 M−1 s−1, the modeled capacity of an AQDS symmetric cell from this work with as-received N117 matched the experimental result within approximately 1% error (Fig. S12, ESI†).
Along with the parameterization described in Fig. S12 (ESI†), we also directly fit the operando UV-vis spectra to extract kf = 0.142 M−1 s−1 at Kdimer of 80 M−1 (Note S1, Fig. S13 and S14, ESI†). Although these values are similar to the parameters chosen for the model to match our symmetric cell experiments, we attribute the discrepancy to differences between the full cell experiment, the symmetric cell experiments, and the zero-dimensional model which can only approximate the overpotentials in an operating flow battery. A thorough quantitative understanding of the effect of dimerization on accessed capacity must explain differences between experiments done across the wide range of current densities and reactant concentrations that have been previously reported.36,54 We hypothesize that faradaic and dimerization reactions may compete such that both the homogeneous chemical reaction kinetics and the electrochemical cycling conditions contribute to observed behavior. Future work to measure the dimerization kinetics should first study the reaction rate between pure samples of oxidized and reduced states of AQDS, but this is a challenging experiment, because the reduced state cannot be formed by electrochemically reducing the oxidized state without forming the dimer along the way. Meanwhile, the constants chosen here sufficiently match our experimental observations to enable a qualitative description of the experimental trends.
Crossover of oxidized and reduced AQDS states, chemical degradation of the reduced state, and dimerization operate in concert in cycling AQDS symmetric cells to give the capacity fade rates observed in our experiments. We assumed the permeability of the dimer through all membranes is zero in the model; importantly the real permeability must be far lower than that of the oxidized and reduced states given the comparative size and charge of the dimer.27Fig. 4b shows simulated cycling of AQDS symmetric cells with pretreated membranes, with increasing fade rate with increasing crossover flux (thinner membranes), matching the experimental trend. Model parameters and a comparison of experimental and modeled fade rates are given in Table S2 (ESI†).
Fig. 4c provides concentration time-series data for reduced, oxidized, and dimerized states over 12 hours of simulated cycling of an AQDS symmetric cell with pretreated Nafion NR211. The concentrations of dimer in the CLS and NCLS over time are the key to explaining the mechanism of net crossover. The concentration of dimer is SOC-dependent and is greatest at intermediate SOC. Although in principle in a perfect symmetric cell, both CLS and NCLS should have the same time-averaged SOC of 50%, dimerization means that the NCLS, which always cycles in a narrower and more intermediate SOC range than the CLS, will have a higher time-averaged dimer concentration than the CLS. A higher time-averaged dimer concentration in the NCLS means that the NCLS has a lower time-averaged concentration of monomeric species than the CLS because more of the species in the NCLS are instead dimerized. This provides the concentration difference for net crossover of AQDS species from CLS to NCLS. The net crossover from CLS to NCLS in AQDS symmetric cells means that increasing the crossover flux through the membrane results in increasing capacity fade, as observed in our experimental data and explained by the zero-dimensional model.
The formation of quinhydrone dimers in AQDS electrolytes creates a special scenario for the influence of net crossover on symmetric cell capacity fade, though we hypothesize that the same net crossover scheme could occur with other chemistries. We propose that any quinone redox couple able to form quinhydrone dimers could exhibit the same behavior. More generally, other SOC-dependent intermolecular interactions, or even SOC-dependent precipitation and re-dissolution, could similarly unbalance crossover fluxes between CLS and NCLS in a symmetric cell due to time-averaged SOC differences.
4.3 Zero-dimensional models of other possible crossover scenarios
With the zero-dimensional model validated for AQDS symmetric cells, we extend its application to a series of hypothetical cases that may be relevant to other flow battery chemistries as illustrative examples. Fig. 5a and c consider cases where the oxidized and reduced state form a dimer in a bimolecular reaction similar to AQDS (eqn (4) and (5)). For Fig. 5a, Kdimer is varied while all other parameters are kept the same as for the AQDS model (pretreated membranes). For Fig. 5c, Kdimer is fixed at 75 M−1 and kchemdeg is varied instead. In Fig. 5b and d, Kdimer is set to zero (no dimerization). Fig. 5b shows how capacity fade is influenced by adjusting the ratio of Pox to Pred for fixed reduced state decomposition rate constant kchemdeg. Fig. 5d shows the influence of kchemdeg when the chemically decomposing species has the lower permeability by a factor of five. The model parameters and simulated fade rates for Fig. 5 are reported in Table S3 (ESI†), and the equivalent model results with non-normalized capacity are shown in Fig. S15 (ESI†) (which also shows the influence of dimerization on accessed capacity, obscured in the normalized data).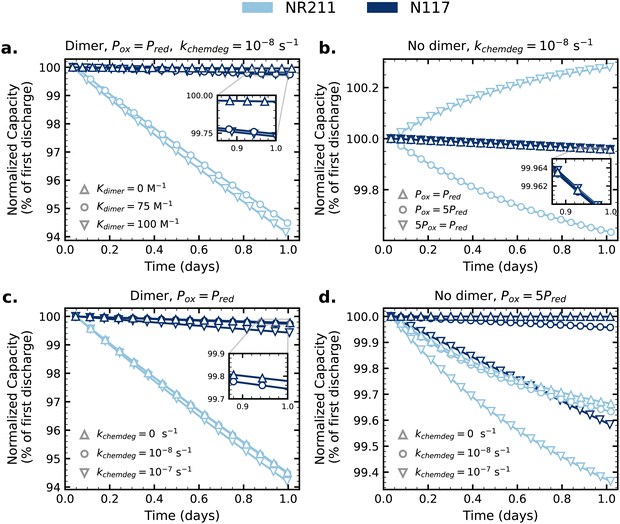 | ||
| Fig. 5 Simulated cycling of symmetric cells with parameters varied to explore other possible modes of net crossover (parameters and resulting capacity fade rates listed in Table S3, non-normalized capacity in Fig. S12, ESI†). In (a) and (b), “NR211” and “N117” traces with Kdimer = 0 overlap completely. Model parameters are tabulated in Table S3 (ESI†), with membrane permeabilities based on experimental values for pretreated membranes. | ||
In Fig. 5a, the traces for NR211 and N117 overlap perfectly when Kdimer = 0: without dimerization the imbalance of AQDS concentration between CLS and NCLS to allow for net crossover does not occur and thus net crossover is zero and the fade rate depends only on chemical decomposition. Increasing the dimerization equilibrium constant from 75 to 100 M−1 increases capacity fade by increasing the driving force for net crossover; the effect is stronger when crossover flux is higher (higher for NR211 than N117). Fig. S15a (ESI†) shows that increasing Kdimer decreases the accessible capacity. With fixed Kdimer = 75 M−1 in Fig. 5c, with crossover fluxes from the AQDS model, increasing the kchemdeg increases capacity fade as expected, but it is notable that for NR211 the effect on capacity fade of increasing kchemdeg by an order of magnitude is small compared to the effect of crossover.
Fig. 5b illustrates that when crossover flux is sufficiently large relative to chemical degradation, and the oxidized and reduced states have unequal permeabilities, concentration imbalances between CLS and NCLS drive crossover-dependent capacity behavior. The case where Pox = Pred in this panel is equivalent to the case where Kdimer = 0 in Fig. 5a, in which equal Pox and Pred without dimerization result in no net crossover. For the crossover flux through pretreated N117 used in the AQDS model, the magnitude is low enough that multiplying either Pox or Pred by a factor of five does not have a significant effect, but an effect is evident when crossover flux is higher as for NR211. When the faster-crossing redox state is formed in the CLS in the first half-cycle, there is a concentration driving force for the crossover of that species from CLS to NCLS during the first half-cycle and in the first half of the second half-cycle, and a mirrored concentration driving force for the crossover of the slower-crossing redox state from NCLS to CLS. As a result, the CLS loses capacity by net crossover on the first cycle, and the ensuing concentration imbalance causes crossover-driven capacity gain of the CLS for following cycles (“NR211” downward triangles in Fig. 5b). In the opposite way, when the slower-crossing redox state is formed in the CLS in the first half-cycle, the CLS gains capacity above theoretical capacity on the first half-cycle, and the ensuing concentration imbalance causes crossover-driven capacity loss of the CLS in the following cycles (“NR211” circles in Fig. 5b). Fig. S15b (ESI†) shows that the initial discharge capacity is greater than the theoretical value of 96.5C when Pox > Pred, and lower than the theoretical capacity when Pox < Pred, in support of this proposed mechanism. One significant implication of this result is that when Pox and Pred are unequal, the choice of oxidizing or reducing the CLS reactant in the first half-cycle may affect the trajectory of capacity fade or capacity gain (Fig. S16, ESI†).
Fig. 5d illustrates how the relative magnitudes of crossover flux and chemical degradation rate affect capacity fade, in this case when Pox = 5Pred. From the values in the AQDS model input, crossover flux through pretreated NR211 is approximately 25× greater than through pretreated N117. Without chemical degradation but with Pox = 5Pred, the effect of crossover is negligible in the “N117” case but the “NR211” case exhibits capacity fade (and capacity above the theoretical capacity in the first cycle, Fig. S15d, ESI†). For both thinner and thicker membrane scenarios, increasing kchemdeg increases capacity fade rate as expected and, for a given kchemdeg, capacity fade over one day is greater in the thinner membrane scenario due to crossover.
For scenarios where crossover influences capacity fade, most obvious in the thinner membrane examples in Fig. 5, the slopes of capacity vs. time plots (rate of capacity fade or capacity gain) become shallower with time. During each cycle, net crossover is driven by time-averaged concentration imbalances between CLS and NCLS. Over the course of cycling, crossover acts to diminish these imbalances. Fig. S17 (ESI†) shows the scenario in Fig. 5b playing out over four days, rather than just one day, of cycling. The rate of capacity loss due to net crossover when Pox > Pred slows with time, and the capacity gain effect when Pox < Pred weakens until capacity begins to fade by day two of cycling.
The cases shown in Fig. 5b and d are relevant for reactants with non-proton-coupled electrochemistry, when electrochemical reactions change the charge number, and thereby change the permeability through a charged membrane, of the reactants. This is the case for many anthraquinones in alkaline conditions and for the commonly used ferro-/ferricyanide redox couple, for example. The diverse time-dependent capacity trajectories simulated in these scenarios compose a cautionary tale against over-interpreting short-duration cycling behavior, especially when the mechanisms governing the cycling species are unknown.55 However, we underscore that using a membrane-electrolyte system with sufficiently low crossover flux can avoid the complicated interaction of chemical reactions and net crossover. The combination of ex situ permeability and chemical stability tests with zero-dimensional modeling may be useful as a preliminary screening protocol for choosing materials and conditions for experiments in redox flow cells.
5 Conclusions
We found a negligible effect of membrane crossover on AQDS symmetric cells with as-received membranes, indicating that the crossover fluxes present in many symmetric cell studies of aqueous organic flow batteries are not sufficiently high as to affect measured capacity fade rates. However, the higher crossover fluxes through pretreated NR211 and NR212 caused increased symmetric cell capacity fade with increased crossover.We used the open-source zero-dimensional model RFBzero to illustrate how the dimerization of AQDS leads to concentration differences between the capacity limiting side (CLS) and non-capacity limiting side (NCLS) that drive net crossover from the CLS to the NCLS to explain this trend. Furthermore, we demonstrated how various symmetric cell scenarios can be simulated in 0D, beyond the conditions we studied experimentally. We underscore that zero-dimensional modeling is a relatively simple but powerful tool for untangling the multiple reactions and fluxes in redox flow batteries to understand the mechanisms behind observed cycling behavior.
Data availability
Data and source code for this article, including results of crossover experiments, cycling data, UV-vis data, cell cycling simulations, and estimation of the AQDS dimerization rate are available at https://github.com/AzizGordonEchem/2024-06-Xover-Fade.Conflicts of interest
There are no conflicts to declare.Acknowledgements
This research was supported in part by U.S. DOE award DE-AC05-76RL01830 through PNNL subcontract 654799. We are very grateful for stimulating discussions and feedback from Prof. David Kwabi, Jeremy Fell, and Jordan Sosa.References
- Z. Yang, J. Zhang, M. C. Kintner-Meyer, X. Lu, D. Choi, J. P. Lemmon and J. Liu, Chem. Rev., 2011, 111, 3577–3613 CrossRef PubMed.
- J. Rugolo and M. J. Aziz, Energy Environ. Sci., 2012, 5, 7151–7160 RSC.
- F. R. Brushett, M. J. Aziz and K. E. Rodby, ACS Energy Lett., 2020, 5, 879–884 CrossRef.
- A. Z. Weber, M. M. Mench, J. P. Meyers, P. N. Ross, J. T. Gostick and Q. Liu, J. Appl. Electrochem., 2011, 41, 1137–1164 CrossRef.
- G. L. Soloveichik, Chem. Rev., 2015, 115, 11533–11558 CrossRef PubMed.
- Y. Yao, J. Lei, Y. Shi, F. Ai and Y. C. Lu, Nat. Energy, 2021, 6, 582–588 CrossRef.
- C. N. Sun, F. M. Delnick, L. Baggetto, G. M. Veith and T. A. Zawodzinski, J. Power Sources, 2014, 248, 560–564 CrossRef.
- M. Skyllaskazacos, C. Menictas and M. Kazacos, J. Electrochem. Soc., 1996, 143, L86 CrossRef.
- A. Bourke, D. Oboroceanu, N. Quill, C. Lenihan, M. A. Safi, M. A. Miller, R. F. Savinell, J. S. Wainright, V. SasikumarSP, M. Rybalchenko, P. Amini, N. Dalton, R. P. Lynch and D. N. Buckley, J. Electrochem. Soc., 2023, 170, 030504 CrossRef.
- K. W. Knehr, E. Agar, C. R. Dennison, A. R. Kalidindi and E. C. Kumbur, J. Electrochem. Soc., 2012, 159, A1446–A1459 CrossRef.
- J. S. Lawton, A. Jones and T. Zawodzinski, J. Electrochem. Soc., 2013, 160, A697–A702 CrossRef.
- R. A. Elgammal, Z. Tang, C. N. Sun, J. Lawton and T. A. Zawodzinski, Electrochim. Acta, 2017, 237, 1–11 CrossRef.
- R. M. Darling, J. D. Saraidaridis, C. Shovlin, M. Fortin, L. A. Murdock and B. C. Benicewicz, J. Electrochem. Soc., 2021, 168, 040516 CrossRef.
- Q. Luo, L. Li, W. Wang, Z. Nie, X. Wei, B. Li, B. Chen, Z. Yang and V. Sprenkle, ChemSusChem, 2013, 6, 268–274 CrossRef PubMed.
- L. Wei, X. Z. Fan, H. R. Jiang, K. Liu, M. C. Wu and T. S. Zhao, J. Power Sources, 2020, 478, 228725 CrossRef.
- M. L. Perry, J. D. Saraidaridis and R. M. Darling, Cur. Opin. Electrochem., 2020, 21, 311–318 CrossRef.
- X. Wei, W. Pan, W. Duan, A. Hollas, Z. Yang, B. Li, Z. Nie, J. Liu, D. Reed, W. Wang and V. Sprenkle, ACS Energy Lett., 2017, 2, 2187–2204 CrossRef.
- K. E. Rodby, R. L. Jaffe, E. A. Olivetti and F. R. Brushett, J. Power Sources, 2023, 560, 232605 CrossRef.
- S. Weber, J. F. Peters, M. Baumann and M. Weil, Environ. Sci. Technol., 2018, 52, 10864–10873 CrossRef.
- D. G. Kwabi, Y. Ji and M. J. Aziz, Chem. Rev., 2020, 120, 6467–6489 CrossRef PubMed.
- M.-A. Goulet and M. J. Aziz, J. Electrochem. Soc., 2018, 165, A1466–A1477 CrossRef.
- J. Xu, S. Pang, X. Wang, P. Wang and Y. Ji, Joule, 2021, 5, 2437–2449 CrossRef.
- A. Wang, R. Tan, D. Liu, J. Lu, X. Wei, A. Alvarez-Fernandez, C. Ye, C. Breakwell, S. Guldin, A. R. Kucernak, K. E. Jelfs, N. P. Brandon, N. B. McKeown and Q. Song, Adv. Mater., 2023, 35, 2210098 CrossRef.
- E. M. Fell and M. J. Aziz, J. Electrochem. Soc., 2023, 170, 100507 CrossRef.
- M. Wu, M. Bahari, Y. Jing, K. Amini, E. M. Fell, T. Y. George, R. G. Gordon and M. J. Aziz, Batteries Supercaps, 2022, 5, e202200009 CrossRef.
- K. Amini, E. F. Kerr, T. Y. George, A. M. Alfaraidi, Y. Jing, T. Tsukamoto, R. G. Gordon and M. J. Aziz, Adv. Funct. Mater., 2023, 33, 2211338 CrossRef.
- T. Y. George, E. F. Kerr, N. O. Haya, A. M. Alfaraidi, R. G. Gordon and M. J. Aziz, J. Electrochem. Soc., 2023, 170, 040509 CrossRef.
- A. M. Alfaraidi, D. Xi, N. Ni, T. Y. George, T. Tsukamoto, R. G. Gordon, M. J. Aziz and R. Y. Liu, ACS Appl. Energy Mater., 2023, 6, 12259–12266 CrossRef.
- I. A. Volodin, C. Stolze, C. C. Mesa, U. Haagen, C. Terechin, M. D. Hager and U. S. Schubert, Sens. Actuators, B, 2024, 403, 135101 CrossRef.
- O. Nolte, I. A. Volodin, C. Stolze, M. D. Hager and U. S. Schubert, Mater. Horiz., 2021, 8, 1866–1925 RSC.
- I. A. Volodin, C. Stolze, O. Nolte, P. Rohland, M. D. Hager and U. S. Schubert, ACS Appl. Energy Mater., 2023, 6, 302–316 CrossRef CAS.
- B. Huskinson, M. P. Marshak, C. Suh, S. Er, M. R. Gerhardt, C. J. Galvin, X. Chen, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Nature, 2014, 505, 195–198 CrossRef PubMed.
- T. Y. George, E. F. Kerr, N. O. Haya, A. M. Alfaraidi, R. G. Gordon and M. J. Aziz, J. Electrochem. Soc., 2023, 170, 040509 CrossRef.
- F. Wang, H. Sheng, W. Li, J. B. Gerken, S. Jin and S. S. Stahl, ACS Energy Lett., 2021, 6, 1533–1539 CrossRef PubMed.
- Y. Jing, E. W. Zhao, M. A. Goulet, M. Bahari, E. M. Fell, S. Jin, A. Davoodi, E. Jónsson, M. Wu, C. P. Grey, R. G. Gordon and M. J. Aziz, Nat. Chem., 2022, 14, 1103–1109 CrossRef PubMed.
- T. J. Carney, S. J. Collins, J. S. Moore and F. R. Brushett, Chem. Mater., 2017, 29, 4801–4810 CrossRef.
- C. Wiberg, T. J. Carney, F. Brushett, E. Ahlberg and E. Wang, Electrochim. Acta, 2019, 317, 478–785 CrossRef.
- A. Pasadakis-Kavounis, V. Baj and J. Hjelm, J. Electrochem. Soc., 2024, 171, 020501 CrossRef.
- L. Tong, Q. Chen, A. A. Wong, R. Gómez-Bombarelli, A. Aspuru-Guzik, R. G. Gordon and M. J. Aziz, Phys. Chem. Chem. Phys., 2017, 19, 31684–31691 RSC.
- B. Caja-Munoz, K. Chighine, J. P. Dognon, L. Dubois and P. Berthault, Anal. Chem., 2023, 95, 6020–6028 CrossRef.
- W. Xie, R. M. Darling and M. L. Perry, J. Electrochem. Soc., 2016, 163, A5084–A5089 CrossRef.
- A. Kusoglu and A. Z. Weber, Chem. Rev., 2017, 117, 987–1104 CrossRef PubMed.
- T. Y. George, I. C. Thomas, N. O. Haya, J. P. Deneen, C. Wang and M. J. Aziz, ACS Appl. Mater. Interfaces, 2023, 15, 57252–57264 Search PubMed.
- E. M. Fell, J. A. Fell and M. J. Aziz, J. Open Source Software, 2024, 9, 6537 CrossRef.
- P. A. Boettcher, E. Agar, C. R. Dennison and E. C. Kumbur, J. Electrochem. Soc., 2016, 163, A5244–A5252 CrossRef.
- M. Pugach, M. Kondratenko, S. Briola and A. Bischi, Appl. Energy, 2018, 226, 560–569 CrossRef CAS.
- S. B. Lee, K. Mitra, H. D. Pratt, T. M. Anderson, V. Ramadesigan, B. R. Chalamala and V. R. Subramanian, J. Electrochem. Energy Convers. Storage, 2019, 17, 011008 CrossRef.
- S. Modak and D. G. Kwabi, J. Electrochem. Soc., 2021, 168, 080528 CrossRef.
- B. J. Neyhouse, J. Lee and F. R. Brushett, J. Electrochem. Soc., 2022, 169, 090503 CrossRef.
- E. M. Fell, D. De Porcellinis, Y. Jing, V. Gutierrez-Venegas, T. Y. George, R. G. Gordon, S. Granados-Focil and M. J. Aziz, J. Electrochem. Soc., 2023, 170, 070525 CrossRef.
- K. Lin, Q. Chen, M. R. Gerhardt, L. Tong, S. B. Kim, L. Eisenach, A. W. Valle, D. Hardee, R. G. Gordon, M. J. Aziz and M. P. Marshak, Science, 2015, 349, 1529–1532 CrossRef PubMed.
- R. M. Darling, A. Z. Weber, M. C. Tucker and M. L. Perry, J. Electrochem. Soc., 2016, 163, A5014–A5022 CrossRef.
- B. J. Neyhouse, R. M. Darling, J. D. Saraidaridis and F. R. Brushett, J. Electrochem. Soc., 2023, 170, 080514 CrossRef.
- Q. Chen, L. Eisenach and M. J. Aziz, J. Electrochem. Soc., 2016, 163, A5057–A5063 CrossRef.
- E. Fell, High-Throughput Electrochemical Characterization of Aqueous Organic Redox Flow Batteries. PhD thesis, Harvard University, 2024.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ya00407h |
| ‡ Equal contribution. |
| This journal is © The Royal Society of Chemistry 2024 |