Machine learning-assisted surface-enhanced raman spectroscopy for the rapid determination of the glutathione redox ratio†
Wilson A.
Garuba
 a,
Brian A.
Barth
b,
Adam E.
Imel
a,
Brian A.
Barth
b,
Adam E.
Imel
 c and
Bhavya
Sharma
c and
Bhavya
Sharma
 *a
*a
aDepartment of Chemistry, University of Tennessee, Knoxville, TN 37996, USA. E-mail: bhavya.sharma@utk.edu
bDepartment of Chemical and Biomolecular Engineering, University of Tennessee, Knoxville, TN 37996, USA
cUniversity of Tennessee – Oak Ridge Innovation Institute, Knoxville, TN 37996, USA
First published on 2nd April 2025
Abstract
Rapid and accurate detection of glutathione in its reduced (GSH) and oxidized (GSSG) forms is essential for monitoring oxidative stress in biological systems. Oxidative stress is a key indicator of various diseases, and glutathione plays a vital role in maintaining the balance between oxidative and anti-oxidative processes. Surface-enhanced Raman spectroscopy (SERS) offers a highly sensitive and selective analytical approach for detecting biomolecules. However, complex biological matrices and molecules with similar chemical structure (such as GSH and GSSG) often result in overlapping vibrational signatures, making it challenging to quantify the GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratio. To address this challenge, we integrated machine learning (ML) algorithms with SERS to accurately quantify the GSH
GSSG ratio. To address this challenge, we integrated machine learning (ML) algorithms with SERS to accurately quantify the GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratio in aqueous solutions. Three machine learning algorithms – support vector regression (SVR), extreme gradient boosting (XGBoost), and multilayer perceptron (MLP) were trained and evaluated using preprocessed SERS spectra of mixtures of various GSH
GSSG ratio in aqueous solutions. Three machine learning algorithms – support vector regression (SVR), extreme gradient boosting (XGBoost), and multilayer perceptron (MLP) were trained and evaluated using preprocessed SERS spectra of mixtures of various GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratios. Among these models, MLP exhibits the highest accuracy and robustness with correlation coefficient for the test set (Q2) value of 0.966. This study highlights a practical protocol for leveraging machine learning and SERS to achieve rapid, and accurate determination of glutathione redox ratios.
GSSG ratios. Among these models, MLP exhibits the highest accuracy and robustness with correlation coefficient for the test set (Q2) value of 0.966. This study highlights a practical protocol for leveraging machine learning and SERS to achieve rapid, and accurate determination of glutathione redox ratios.
Introduction
A key biomarker of neurological health is oxidative stress. Oxidative stress is caused by the exposure of cells to reactive oxygen species (ROS).1 ROS are free radicals produced during intense biochemical and physiological processes. These processes increase internally generated oxidants, which can lead to oxidative damage.2 To protect against this oxidative damage, the body utilizes reduced glutathione (GSH) as an antioxidant to scavenge the free radicals and protect the body from oxidative stress. GSH is the most abundant non-protein thiol in cells. It is used in many biochemical functions in the body, including protein and DNA synthesis, detoxification, regulation of cellular proliferation and apoptosis, and antioxidant defense.3–5 The chemical structure of GSH consists of three amino acids: cysteine, glutamic acid, and glycine. The linkage of the γ-carboxyl group of glutamate to the amino group of cysteine distinguishes this bond from peptide bonds in proteins.The synthesis and degradation of GSH are important biochemical processes regulated by oxidative stress responses. During this process, GSH is oxidized to the disulfide form, GSSG, with the aid of an enzyme, glutathione peroxidase. The GSH to GSSG (GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG) ratio has been investigated as a biomarker for diagnosing various diseases, including diabetes, Parkinson's disease, Alzheimer's disease, and a host of neurodegenerative diseases.6–9 Under normal conditions, this ratio is greater than 100; in cases of oxidative stress, it can fall below 10.10–12
GSSG) ratio has been investigated as a biomarker for diagnosing various diseases, including diabetes, Parkinson's disease, Alzheimer's disease, and a host of neurodegenerative diseases.6–9 Under normal conditions, this ratio is greater than 100; in cases of oxidative stress, it can fall below 10.10–12
Traditional analytical techniques such as high-performance liquid chromatography (HPLC),13 liquid chromatography-tandem mass spectrometry,14 capillary electrophoresis,15 and UV/vis spectrometry16 are generally used to determine the GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratio. While these methods have provided accurate results, they are limited by multi-step sample preparation and derivatization. For example, a general protocol for determining this ratio requires masking agents such as N-ethylmaleimide and 2-vinyl pyridine to mask GSH from a sample of total glutathione before calculating the ratio. Alternatively, flow cytometry has been used to quantify GSH in blood cells.17 This method involves the incorporation of fluorescence dyes that strongly bind to the –SH group in GSH. Several fluorescence dyes were assessed for glutathione staining, with monobromobimane demonstrating the most significant potential for human cell staining. However, monobromobimane can bind to other molecules besides GSH, thereby complicating the ratio of GSH
GSSG ratio. While these methods have provided accurate results, they are limited by multi-step sample preparation and derivatization. For example, a general protocol for determining this ratio requires masking agents such as N-ethylmaleimide and 2-vinyl pyridine to mask GSH from a sample of total glutathione before calculating the ratio. Alternatively, flow cytometry has been used to quantify GSH in blood cells.17 This method involves the incorporation of fluorescence dyes that strongly bind to the –SH group in GSH. Several fluorescence dyes were assessed for glutathione staining, with monobromobimane demonstrating the most significant potential for human cell staining. However, monobromobimane can bind to other molecules besides GSH, thereby complicating the ratio of GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG measured. Here, we discuss the combination of machine learning (ML) and surface-enhanced Raman spectroscopy (SERS) to address the need for a rapid, highly specific and sensitive method for measuring the glutathione redox ratio.
GSSG measured. Here, we discuss the combination of machine learning (ML) and surface-enhanced Raman spectroscopy (SERS) to address the need for a rapid, highly specific and sensitive method for measuring the glutathione redox ratio.
GSH has previously been detected with SERS.18–22 Here, we introduce the use of gold core silver shell nanoparticles (Au@AgNPs) as the SERS substrate for the SERS spectra of various GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratios in aqueous solutions. The enhancement in the analytical signal due to the metal nanostructures can be quantified using the analytical enhancement factor (AEF), defined by the ratio of SERS intensity to the normal Raman intensity, normalized by the respective concentrations.23 EF is used to characterize the enhancement capabilities of plasmonic materials and largely depends on the material's shape, size, and composition. While single metal nanoparticles provide high EFs, bimetallic core–shell plasmonic nanoparticles have been reported to demonstrate significantly improved optical, electrical, and magnetic properties.24–26 The SERS spectra were pre-processed prior to training the machine learning models. The pre-processed SERS spectra were then tested with three ML algorithms, SVR, XGBoost, and MLP. To the best of our knowledge, this work reports, for the first time, the application of machine learning and SERS for determining the glutathione redox ratio.
GSSG ratios in aqueous solutions. The enhancement in the analytical signal due to the metal nanostructures can be quantified using the analytical enhancement factor (AEF), defined by the ratio of SERS intensity to the normal Raman intensity, normalized by the respective concentrations.23 EF is used to characterize the enhancement capabilities of plasmonic materials and largely depends on the material's shape, size, and composition. While single metal nanoparticles provide high EFs, bimetallic core–shell plasmonic nanoparticles have been reported to demonstrate significantly improved optical, electrical, and magnetic properties.24–26 The SERS spectra were pre-processed prior to training the machine learning models. The pre-processed SERS spectra were then tested with three ML algorithms, SVR, XGBoost, and MLP. To the best of our knowledge, this work reports, for the first time, the application of machine learning and SERS for determining the glutathione redox ratio.
Experimental methods
Materials
Tetrachloroauric(III) acid trihydrate (AuCl4), trisodium citrate dihydrate (99%), L(+)-ascorbic acid (99%), L-glutathione, and glutathione disulfide were all purchased from Fischer Scientific. All glassware was cleaned with aqua regia and deionized (DI) water (18.2 MΩ cm) before use. DI water was also used in all syntheses and sample preparation.Synthesis of SERS substrates
Previous work in our group established the suitability of 60 nm AuNPs for SERS enhancements of neurochemicals.27–30 In this work, we compared the enhancement ability of two SERS substrates: 60 nm gold nanoparticles (AuNPs) and gold core-silver shell nanoparticles (Au@AgNPs). AuNPs and Au@AgNPs were synthesized using a citrate reduction method. For the AuNPs, 5 mg of HAuCl4 was dissolved in 50 mL of deionized water (DI water), and the solution was brought to a boil. Subsequently, 350 μL of a 1% (w/v) sodium citrate solution was added while stirring continuously for approximately 5 minutes. This led to a reddish color, indicating the successful synthesis of AuNPs with an average diameter of 60 nm. To synthesize the Au@AgNPs, 30 nm gold core nanoparticles were prepared using the same citrate reduction method, with 615 μL of 1% (w/v) citrate solution as the reducing agent. To form a silver shell around the gold cores, 3 mL of 0.1 M ascorbic acid (AA) was added to 20 mL of the gold core nanoparticle solution, followed by the gradual addition of 16 mL of 1 mM AgNO3. The solution was centrifuged at 5000 rpm for 15 minutes to obtain the core–shell nanoparticles.Nanoparticle characterization
To test for their SERS activity, 2 mL aliquots of both the AuNP and Au@AgNP solutions were centrifuged (AuNPs at 4200 rpm and Au@AgNPs at 5000 rpm), and the collected pellets were each tested using 200 μL of 2 mM GSH and GSSG solutions. The Au@AgNPs demonstrated enhanced SERS activity compared to the 60 nm AuNPs, making them more suitable for subsequent mixture experiments. The synthesized colloidal solutions were characterized using UV-visible extinction spectroscopy (Cary 5000, Agilent) to confirm their optical properties, and transmission electron microscopy (TEM, JEOL JEM-1400 Flash, 0.2 nm lateral resolution) was employed to analyze the morphology, core nanoparticle diameter, and silver shell thickness of the Au@AgNPs.To further characterize the size distributions of the as-prepared nanoparticles, we employed dynamic light scattering (DLS) and small-angle X-ray scattering (SAXS). DLS measurements were performed on a Litesizer DLS 500 system (Anton Paar) equipped with a 40 mW, 658 nm semiconductor laser diode. SAXS experiments were performed using the Xenocs Xeuss 3.0 instrument at the University of Tennessee–Knoxville Polymer Characterization Laboratory. Suspensions of AuNPs and Au@AgNPs were analysed at a detector distance of 900 mm from the sample, providing access to a scattering vector range of q ≈ 0.01–0.1 Å−1 using 1.54 Å X-rays. Data were acquired with a collection time of 600 s for each sample. Borosilicate glass capillaries (1.5 mm outer diameter) were used for all measurements. Scattering curve model fitting was conducted using SasView 6.0.0 (https://www.sasview.org/), an open-source scattering analysis software. Sphere models were applied to Au nanoparticles, while core–shell sphere models were used for Au core–Ag shell particles. The sphere model assumes a single scattering length density (SLD) for the nanoparticle core, while the core–shell sphere model includes a core surrounded by a shell with a different SLD. Both core and shell SLDs, as was the shell thickness, were allowed to vary during fitting. Size polydispersity was also incorporated to estimate nanoparticle size distributions. Detailed fitting parameters and theoretical descriptions are provided in the SasView 6.0.0 documentation.
Sample preparation
Under normal physiological conditions, the ratio of GSH to GSSG is typically above 100, whereas, under oxidative stress, this ratio drops to less than 10. Based on these conditions, we prepared duplicate samples with glutathione ratios ranging from normal to oxidative stress levels, specifically at 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 5
1, 5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 10
1, 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 15
1, 15![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 20
1, 20![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 25
1, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 30
1, 30![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 35
1, 35![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 40
1, 40![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 45
1, 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 50
1, 50![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 55
1, 55![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 60
1, 60![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 65
1, 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 70
1, 70![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 75
1, 75![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 80
1, 80![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 85
1, 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 90
1, 90![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 95
1, 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 100
1 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1. We prepared 2 mM solutions of GSH and GSSG. Au@AgNPs (2 mL) were centrifuged at 5000 rpm, the excess solution was removed, and the pellet combined with 200 μL the prepared solutions for each ratio. SERS spectra of these prepared samples were collected immediately.
1. We prepared 2 mM solutions of GSH and GSSG. Au@AgNPs (2 mL) were centrifuged at 5000 rpm, the excess solution was removed, and the pellet combined with 200 μL the prepared solutions for each ratio. SERS spectra of these prepared samples were collected immediately.
Data collection
SERS spectra were collected using a homebuilt confocal Raman microscope. A 785 nm diode laser produced the excitation wavelength (IPS lasers). This light was directed into an inverted Nikon Ti-U microscope with a 40× objective (Nikon, NA 0.60). The 180° backscattered Raman light was collected through the same objective and then directed through a dichroic mirror (Chroma Technology Corporation). The Raman scattered light is directed through a Razor Edge long-pass filter (Semrock) to the 100 μm slit of an IsoPlane SCT-320 spectrometer (Princeton Instruments), where the light is dispersed and detected with a PIXIS 400 CCD camera (Princeton Instruments). Spectra were collected using 10 seconds acquisition times.Pre-processing SERS spectra
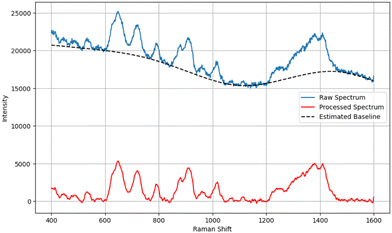
SERS spectra were pre-processed utilizing functions available in Python open-source libraries. Baseline correction was performed using the penalized spline version of the asymmetrically reweighted penalized least squares (arPLS) algorithm, improving the visibility of the Raman spectral features of interest. A Savitzky–Golay filter was implemented for spectral smoothing, as shown in Fig. 1. SERS spectra were truncated from 400–1600 cm−1 to 400–800 cm−1 to focus on the wavenumber region of the spectra relevant to GSH and GSSG. We also implemented and compared the effect of standardizing and normalizing algorithms on the performance of our models. Standard normal variate (SNV) scales the spectra with a mean of 0 and a standard deviation of 1, and max–min scaling works by scaling the data to 0 and 1.Machine learning models
Machine learning (ML) algorithms analyse and identify patterns in complex datasets. ML algorithms such as support vector machines (SVM), tree-based algorithms such as Random Forest (RF), extreme gradient boosting (XGBoost), unsupervised ML algorithms like principal component analysis (PCA), t-distributed stochastic neighbour embedding (t-SNE) and neural networks, such as multilayer perceptron (MLP) or convolutional neural networks (CNN), can be adapted for analysis of Raman spectra. These models can also be combined to improve model accuracy and reduces overfitting of data. For example, PCA-SVM was implemented to classify breast cancer31 and in artificial cerebrospinal fluid, the SERS spectra of dopamine was differentiated from DOPAC, one of its metabolites, in mixtures.30Here, we incorporated three regression models capable of analysing Raman spectra and predicting the ratio of GSH to GSSG in aqueous solutions. These models are support vector regression (SVR),32 extreme gradient boosting (XGBoost),33 and a feedforward artificial neural network called multilayer perceptron (MLP).34 While MLP is often considered a generic neural network, it can be optimized for specialized tasks particularly when data, such as SERS spectra, are continuous. Here, the MLP was chosen over more complex neural networks because while it is simpler, it is more suitable for regression analysis. These models will be used to estimate quantitative outcomes based on the spectral features observed in Raman spectral data. The models were carefully selected based on the size of our dataset and the available computational resources. Unlike deep learning models that require large datasets (for example, 10 s of thousands of spectra) and are computationally expensive, these selected models are computationally efficient and learn complex relationships from smaller datasets.
To ensure robust generalization capabilities of the SVR model for unseen data, we carefully selected the appropriate kernel, tolerance levels (ε), and the regularization parameter C. The kernel was manually selected after evaluating several options, including linear, polynomial, and radial basis function (RBF) kernels, to identify the one that provided the best performance. Then, cross-validation was employed with GridSearchCV to fine-tune the tolerance level (ε) and the regularization parameter C, optimizing the trade-off between the model's sensitivity, error margin, and ability to avoid overfitting. This comprehensive approach ensured the model performed well during the training and inference phases, enabling effective generalization to new, unseen data.35
XGBoost, a powerful ensemble machine learning and specialized decision tree method, was also implemented in this study. It operates within the gradient boosting framework, sequentially optimizing multiple weak models into a robust predictive model. We developed the XGBoost regression algorithm in a Jupyter Notebook alongside the SVR model. We systematically searched key hyperparameters to optimize the XGBoost model's performance, including the maximum depth of decision trees, the number of trees in the ensemble, and the learning rate. GridSearchCV was also employed to identify the optimal combination of parameters, ensuring the best possible predictive performance.
For the Multilayer Perceptron (MLP), a feedforward artificial neural network used for a wide range of machine learning tasks, we utilized the scikit-learn library (Python 3.12.0) to build the model within the same Jupyter Notebook as the SVR. The hyperbolic tangent (tanh) function was chosen as the activation function because it converged more rapidly and with better accuracy than other functions such as the rectified linear unit function (ReLU) for this application. We employed GridSearchCV to iterate over various values for each hyperparameter, as detailed in Table 1, to select the optimal configuration for the MLP model.
| SVR | XGB | MLP |
|---|---|---|
| Regularization parameter, C: 1000 | Number of trees: 500 | Number of hidden layers :3 |
| Epsilon, ε: 0.1 | Max. depth: 6 | Hidden layer sizes: 50, 50, 30 |
| Gamma, γ: 0.1 | Learning rate: 0.1 | Activation function: tanh |
| Kernel: RBF | Optimizer: Adam | |
| Learning rate: adaptive |
Performance evaluations
The SERS spectral dataset includes over 2000 SERS spectra, with approximately 100 SERS spectra collected for each mixture ratio. The SERS spectra of selected mixture ratios (5![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 25
1, 25![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 45
1, 45![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 65
1, 65![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, 85
1, 85![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1, and 95
1, and 95![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were separated out for testing, while the models were trained with the remaining data. SERS spectra of the first and last ratio (1
1) were separated out for testing, while the models were trained with the remaining data. SERS spectra of the first and last ratio (1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 100
1 and 100![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1) were strategically included in the training data to avoid extrapolation during evaluation. The training set was used to train the models employing K-fold cross-validation (K = 5) to optimize the performance. The trained models were then evaluated using the independent test set. We evaluated the performance of the optimized model using the coefficient of determination (R2) and root mean square error (RMSE) metrics. R2 measures the proportion of the variance in the dependent variable that is predictable from the independent variable. The RMSE measures the mean error between the actual and predicted values. The equations for both metrics are shown below.
1) were strategically included in the training data to avoid extrapolation during evaluation. The training set was used to train the models employing K-fold cross-validation (K = 5) to optimize the performance. The trained models were then evaluated using the independent test set. We evaluated the performance of the optimized model using the coefficient of determination (R2) and root mean square error (RMSE) metrics. R2 measures the proportion of the variance in the dependent variable that is predictable from the independent variable. The RMSE measures the mean error between the actual and predicted values. The equations for both metrics are shown below.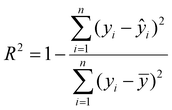 | (1) |
 | (2) |
 is the predicted value,(
is the predicted value,(![[y with combining overline]](https://www.rsc.org/images/entities/i_char_0079_0305.gif) ) is the mean of the actual value, and n is the number of observations.
) is the mean of the actual value, and n is the number of observations.
Results and discussion
Model generalization, reduced overfitting, and high accuracy are the primary benchmarks for evaluating the performance of ML models. The model needs to be trained with high-quality data to achieve this. To this end, we synthesized two SERS substrates, 60 nm gold nanoparticles (AuNPs) and a 30 nm AuNP coated with Ag shell (Au@AgNPs). AuNPs are widely used for SERS because of their relative stability and tunability; however, they provide a lower enhancement than Ag, which provides a stronger localized surface plasmon resonance (LSPR) effect in the visible region of electromagnetic fields. With the Au@AgNPs, we utilized the combined advantages of both plasmonic metals, the stability of the AuNPs with the higher enhancement of silver. ESI Fig. 1A† shows the LSPR spectra of three SERS substrates, AuNPs (30 nm diameter), AuNPs (60 nm diameter) and Au@AgNPs. The maximum LSPR peak of the Au@AgNPs is at λmax = 409 nm with a shoulder at approximately 500 nm, which arises from the gold core. The gold core LSPR λmax blue-shifts in the core–shell system from the LSPR λmax = 531 nm of the 30 nm Au core. In ESI Fig. 1B,† the TEM image of the as-prepared Au@AgNPs is shown, with a higher resolution TEM image (ESI Fig. 1C†), that shows the silver shell (∼10 nm) surrounding the Au core. We compared the SERS activity of the Au@AgNPs with 60 nm AuNPs to determine which substrate provides Raman spectra with a higher signal-to-noise ratio (SNR).DLS and SAXS results align closely with the expected sizes of the Au core and bimetallic nanoparticles, as shown in Table 2. Using a spherical model, SAXS analysis estimated the Au nanoparticle diameter (dNP) at 29.8 nm with a polydispersity of 20%. Adopting a core–shell model for the bimetallic nanoparticles yielded a core–shell diameter (dNP) of 37.4 nm with a shell thickness of 8.0 nm, with polydispersities of 22% for the core and 56% for the core–shell. DLS measurements further corroborated these findings, indicating diameters of 27.3 nm for the Au core and 36.1 nm for the Au@Ag nanoparticles, accompanied by polydispersities of 27.8% and 26.1%, respectively. The zeta potential shifted from −24.8 mV for the Au core to −31.7 mV after Ag deposition, suggesting improved colloidal stability in the bimetallic nanoparticles. Representative DLS and SAXS data plots are provided in ESI Fig. 2.†
| Nanoparticle Type | Methods | |||
|---|---|---|---|---|
| LSPR (λmax,nm) | DLS dNP (nm) | SAXS dNP (nm) | Zeta potential (mV) | |
| AuNPs | 535 | 27.3 | 29.8 | −24.8 |
| Au@AgNPs | 409 (shell) | 36.1 | 37.4 | −31.7 |
| 500 (core) | ||||
For the measurements of GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG, we first collected individual SERS spectra of GSH and GSSG to identify their distinctive spectral features (Fig. 2). We compared the SERS spectra of GSH and GSSG collected with the 60 nm AuNPs (green and red) to those collected with the Au@AgNPs (purple and blue). The core–shell nanoparticles resulted in higher signal-to-noise SERS spectra. In the SERS spectrum of GSSG, the 503 cm−1 Raman band arises from the S–S stretching vibration, which is the primary characteristic peak of the disulfide bond. The SERS spectrum of GSH shows two prominent Raman bands at 647 cm−1 and 720 cm−1. The band at 647 cm−1 is attributed to the vibrational modes of the sulphur atom in the cysteine (Cys) residue, specifically the C–S stretching mode. The 720 cm−1 band in GSH is associated with the deformation of the –COO− group. In GSSG, the disulfide bond formation significantly alters the molecular geometry. This disulphide linkage restricts the conformational freedom of the molecule, which can affect the vibrations of the –COO− groups, preventing them from undergoing changes in structure in the same manner as in GSH. This alteration can reduce the intensity of the –COO− deformation mode or shift its frequency, making it less prominent.36,37 Other prominent peak assignments are shown in Table 3. The spectral differences between GSH and GSSG provide the basis for distinguishing varying ratios of their mixtures. Before model training, the spectra were truncated to the 400–800 cm−1 range to focus on the informative regions of the spectral range.
GSSG, we first collected individual SERS spectra of GSH and GSSG to identify their distinctive spectral features (Fig. 2). We compared the SERS spectra of GSH and GSSG collected with the 60 nm AuNPs (green and red) to those collected with the Au@AgNPs (purple and blue). The core–shell nanoparticles resulted in higher signal-to-noise SERS spectra. In the SERS spectrum of GSSG, the 503 cm−1 Raman band arises from the S–S stretching vibration, which is the primary characteristic peak of the disulfide bond. The SERS spectrum of GSH shows two prominent Raman bands at 647 cm−1 and 720 cm−1. The band at 647 cm−1 is attributed to the vibrational modes of the sulphur atom in the cysteine (Cys) residue, specifically the C–S stretching mode. The 720 cm−1 band in GSH is associated with the deformation of the –COO− group. In GSSG, the disulfide bond formation significantly alters the molecular geometry. This disulphide linkage restricts the conformational freedom of the molecule, which can affect the vibrations of the –COO− groups, preventing them from undergoing changes in structure in the same manner as in GSH. This alteration can reduce the intensity of the –COO− deformation mode or shift its frequency, making it less prominent.36,37 Other prominent peak assignments are shown in Table 3. The spectral differences between GSH and GSSG provide the basis for distinguishing varying ratios of their mixtures. Before model training, the spectra were truncated to the 400–800 cm−1 range to focus on the informative regions of the spectral range.
 | ||
| Fig. 2 SERS spectra of pure GSH and GSSG with the 60 nm AuNP and the Au@AgNPs. The dominant peaks for GSH and GSSG are 503 cm−1 and 720 cm−1, respectively. | ||
| GSH | GSSG | Peak assignments |
|---|---|---|
| 503 | –S–S– stretch | |
| 527 | N–C–C deformation | |
| 625, 644 | 647 | –C–S– stretch |
| 720 | –COO– deformation | |
| 790 | 786 | –COO– bend |
| 909 | 910 | –C–COO– stretch |
| 1010 | 1008 | –C–C– stretch |
| 1242 | 1251 | Amide III |
| 1378, 1413 | 1392 | –COO– stretch |
To validate this approach, we performed Principal Component Analysis (PCA) on the entire dataset to identify the major contributors to the variation (ESI3†). The results show that the first principal component (PC1), which arises from the 647 cm−1 and 720 cm−1 bands, strongly correlates with the GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratio.
GSSG ratio.
Machine learning models for predicting GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) GSSG ratios
GSSG ratios
Selecting an appropriate pre-processing strategy can significantly improve model performance. These datasets were subjected to a pre-processing strategy, which included background subtraction, smoothing, and removing cosmic rays. The baseline removal and smoothing steps used were essential in removing the background and increasing the signal-to-noise ratio of the datasets. Normalizing Raman spectra reduces data variability arising from fluctuations in experimental conditions and instrumental differences. Max–min scaling (normalization) effectively reduces intensity variations, allowing for a direct comparison of spectral features between the glutathione redox couple molecules, substantially improving model performance. Contrarily, our findings suggest that SNV (standardization) may degrade the ML performance of Raman spectra of glutathione, potentially leading to information loss and reduced model accuracy (ESI4†). This is because SNV which works by subtracting the data by their mean (0) and dividing with a standard deviation of one (1) may alter the proportional difference between peak intensities. Peaks with higher intensities may become lower and vice versa. This consequently mask features that can contribute to model predictions.38
We trained and tested the models with the normalized datasets. The max–min normalization was applied to scale the intensities to a range of 0 and 1. Table 4 presents the correlation coefficient for the test sets (Q2) and the RMSE values. While all the models perform relatively well, the MLP performs better with a Q2 value of 0.966 and RMSE of 5.22.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratios before applying dimensionality reduction. MLP achieved the highest accuracy (Q2 = 0.966, RMSE = 5.220)
GSSG ratios before applying dimensionality reduction. MLP achieved the highest accuracy (Q2 = 0.966, RMSE = 5.220)
| Model | Q2 | RMSE |
|---|---|---|
| SVR | 0.939 | 6.970 |
| XGB | 0.951 | 6.230 |
| MLP | 0.966 | 5.220 |
Hyperparameters tuning and model optimization
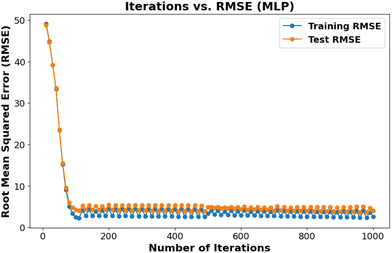
Hyperparameter optimization is important in ensuring generalizability and preventing overfitting machine learning models. We employed the GridSearchCV algorithm to systematically search a predefined range of hyperparameter values and identify the optimal combination that yields maximum accuracy. This approach enables the development of robust and high-performing models. For example, Table 1 presents the optimal regularization parameter (C = 1000) for the SVR model, selected from a range of values to achieve optimal performance. Fig. 3 displays the iteration versus RMSE plot for the MLP model.Determining GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/h3_char_2009.gif) GSSG ratios
GSSG ratios
The three models demonstrated robust generalization when tested on the unseen test data. The MLP model shows an improved performance with an Q2 of 0.966. This can be attributed to MLP's ability to more effectively capture complex non-linear relationships with the datasets. The linear regression plot (Fig. 4) provides a visual representation of the predictive performance of the models, confirming the reliability of the application of ML for determining the GSH![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) GSSG ratio.
GSSG ratio.
Conclusions
We successfully developed and validated novel methods by combining SERS and ML for determining the glutathione redox ratio, an important biomarker for assessing oxidative stress. Our results demonstrated bimetallic SERS substrates, with the gold core silver shell (Au@AgNPs), produce Raman scattering signals with significantly higher signal-to-noise ratios (SNR) compared to gold nanoparticles (AuNPs). Also, we highlighted the importance of appropriate pre-processing strategies to improve the performance of ML models. By harnessing the strengths of three ML algorithms – SVR, XGBoost, and MLP – we established a rapid and accurate approach for quantifying reduced (GSH) and oxidized (GSSG) glutathione. Notably, MLP demonstrated superior performance in terms of generalization and accuracy. This methodology offers a promising tool for assessing oxidative stress and holds potential for applications in various fields, including molecular diagnostics.Author contributions
W. A. G. contributed towards experimental design, investigation, machine learning model development, data analysis, data interpretation and writing the original draft. Contributions from B. A. B. include DLS and zeta potential measurements and data analysis. Contributions from A. E. I. include SAXS measurements, modelling SAXS data, data analysis, and writing. B. S. contributed towards conceptualisation, experimental design, data interpretation, supervision, and reviewing and editing the writing.Data availability
Data for this article, including Raman spectra as .csv files, and Python code are available at: https://doi.org/10.5281/zenodo.12689402.Conflicts of interest
There are no conflicts to declare.Acknowledgements
The authors would like to acknowledge the University of Tennessee Advanced Microscopy and Imaging Centre for instrument use, scientific and technical assistance. This work benefited from the use of the SasView application, originally developed under NSF award DMR-0520547. SasView contains code developed with funding from the European Union's Horizon 2020 research and innovation programme under the SINE2020 project, grant agreement no. 654000. SAXS measurements were enabled by the Major Research Instrumentation program of the National Science Foundation under Award No. DMR-1827474.References
- K. Jomova, R. Raptova, S. Y. Alomar, S. H. Alwasel, E. Nepovimova, K. Kuca and M. Valko, Arch. Toxicol., 2023, 97, 2499–2574 CrossRef CAS PubMed.
- H. Bayr, Crit. Care Med., 2005, 33, S498–S501 CrossRef PubMed.
- T. P. Akerboom and H. Sies, Methods in enzymology, Elsevier, 1981, vol. 77, pp. 373–382 Search PubMed.
- D. M. Townsend, K. D. Tew and H. Tapiero, Biomed. Pharmacother., 2003, 57, 145–155 CrossRef CAS PubMed.
- M. Prakash, M. S. Shetty, P. Tilak and N. Anwar, Online J. Health Allied Sci., 2009, 8, 2 Search PubMed.
- P. Rani, S. Krishnan and C. Rani Cathrine, Frontiers in neurology, 2017, 8, 263010 CrossRef PubMed.
- Y.-T. Chang, W.-N. Chang, N.-W. Tsai, C.-C. Huang, C.-T. Kung, Y.-J. Su, W.-C. Lin, B.-C. Cheng, C.-M. Su and Y.-F. Chiang, BioMed Res. Int., 2014, 182303–182317 Search PubMed.
- L. K. Mischley, L. J. Standish, N. S. Weiss, J. M. Padowski, T. J. Kavanagh, C. C. White and M. E. Rosenfeld, Oxid. Med. Cell. Longevity, 2016, 9409363–9409369 CrossRef PubMed.
- N. Braidy, M. Zarka, B.-E. Jugder, J. Welch, T. Jayasena, D. K. Chan, P. Sachdev and W. Bridge, Front. Aging Neurosci., 2019, 11, 177 CrossRef PubMed.
- O. Zitka, S. Skalickova, J. Gumulec, M. Masarik, V. Adam, J. Hubalek, L. Trnkova, J. Kruseova, T. Eckschlager and R. Kizek, Oncol. Lett., 2012, 4, 1247–1253 CrossRef CAS PubMed.
- Y.-C. Chai, S. S. Ashraf, K. Rokutan, R. B. Johnston and J. A. Thomas, Arch. Biochem. Biophys., 1994, 310, 273–281 CrossRef CAS PubMed.
- R. Rossi, I. Dalle-Donne, A. Milzani and D. Giustarini, Clin. Chem., 2006, 52, 1406–1414 CrossRef CAS PubMed.
- R. Rossi, D. Giustarini, S. Fineschi, G. De Cunto, G. Lungarella and E. Cavarra, Free Radical Res., 2009, 43, 538–545 CrossRef CAS PubMed.
- T. Moore, A. Le, A.-K. Niemi, T. Kwan, K. Cusmano-Ozog, G. M. Enns and T. M. Cowan, J. Chromatogr. B:Anal. Technol. Biomed. Life Sci., 2013, 929, 51–55 CrossRef CAS PubMed.
- A. V. Ivanov, M. A. Popov, V. V. e. Aleksandrin, L. M. Kozhevnikova, A. A. Moskovtsev, M. P. Kruglova, S. E. Vladimirovna, S. V. Aleksandrovich and A. A. Kubatiev, Electrophoresis, 2022, 43, 1859–1870 CrossRef CAS PubMed.
- D. Giustarini, I. Dalle-Donne, R. Colombo, A. Milzani and R. Rossi, Free Radicals Biol. Med., 2003, 35, 1365–1372 CrossRef CAS PubMed.
- D. W. Hedley and S. Chow, Cytometry A, 1994, 15, 349–358 CrossRef CAS PubMed.
- Z. Ke, Z. Yu and Q. Huang, Plasma Processes Polym., 2013, 10, 181–188 CrossRef CAS.
- A. Saha and N. R. Jana, Anal. Chem., 2013, 85, 9221–9228 CrossRef CAS PubMed.
- A. n. Sánchez-Illana, F. Mayr, D. Cuesta-García, J. D. Piñeiro-Ramos, A. s. Cantarero, M. d. l. Guardia, M. x. Vento, B. Lendl, G. Quintás and J. Kuligowski, Anal. Chem., 2018, 90, 9093–9100 CrossRef PubMed.
- Y. Zhu, J. Wu, K. Wang, H. Xu, M. Qu, Z. Gao, L. Guo and J. Xie, Talanta, 2021, 224, 121852 CrossRef CAS PubMed.
- S. Ma and Q. Huang, RSC Adv., 2015, 5, 57847–57852 RSC.
- E. C. Le Ru, E. Blackie, M. Meyer and P. G. Etchegoin, J. Phys. Chem. C, 2007, 111, 13794–13803 CrossRef CAS.
- R. Güzel, Z. Üstündağ, H. Ekşi, S. Keskin, B. Taner, Z. G. Durgun, A. A. İ. Turan and A. O. Solak, J. Colloid Interface Sci., 2010, 351, 35–42 CrossRef PubMed.
- Y. Cui, B. Ren, J.-L. Yao, R.-A. Gu and Z.-Q. Tian, J. Phys. Chem. B, 2006, 110, 4002–4006 CrossRef CAS PubMed.
- S. Tian, W. You, Y. Shen, X. Gu, M. Ge, S. Ahmadi, S. Ahmad and H.-B. Kraatz, New J. Chem., 2019, 43, 14772–14780 RSC.
- A. S. Moody, P. C. Baghernejad, K. R. Webb and B. Sharma, Anal. Chem., 2017, 89, 5688–5692 CrossRef CAS PubMed.
- A. S. Moody, T. D. Payne, B. A. Barth and B. Sharma, Analyst, 2020, 145, 1885–1893 RSC.
- A. S. Moody and B. Sharma, ACS Chem. Neurosci., 2018, 9, 1380–1387 CrossRef CAS PubMed.
- P. A. Pimiento, N. E. Dunn and B. Sharma, J. Raman Spectrosc., 2023, 54, 917–928 CrossRef CAS.
- L. Zhang, C. Li, D. Peng, X. Yi, S. He, F. Liu, X. Zheng, W. E. Huang, L. Zhao and X. Huang, Spectrochim. Acta, Part A, 2022, 264, 120300 CrossRef CAS PubMed.
- P. Li, J. Ma and N. Zhong, Optik, 2021, 247, 167879 CrossRef CAS.
- Z. Guleken, P. Jakubczyk, W. Paja, K. Pancerz, A. Wosiak, İ. Yaylım, G.İ Gültekin, N. Tarhan, M. T. Hakan and D. Sönmez, Comput. Methods Programs Biomed., 2023, 234, 107523 CrossRef PubMed.
- R. Ullah, S. Khan, Z. Ali, H. Ali, A. Ahmad and I. Ahmed, Photodiagn. Photodyn. Ther., 2022, 39, 102924 CrossRef CAS PubMed.
- W. Gao, L. Zhou, S. Liu, Y. Guan, H. Gao and B. Hui, Bioresour. Technol., 2022, 348, 126812 CrossRef CAS PubMed.
- E. Podstawka, Y. Ozaki and L. M. Proniewicz, Appl. Spectrosc., 2004, 58, 570–580 CrossRef CAS PubMed.
- H. E. Van Wart and H. A. Scheraga, Proc. Natl. Acad. Sci. U. S. A., 1986, 83, 3064–3067 CrossRef CAS PubMed.
- N. K. Afseth, V. H. Segtnan and J. P. Wold, Appl. Spectrosc., 2006, 60, 1358–1367 CrossRef CAS PubMed.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4an00978a |
| This journal is © The Royal Society of Chemistry 2025 |