PyFasma: an open-source, modular Python package for preprocessing and multivariate analysis of Raman spectroscopy data

Abstract

Raman spectroscopy is a versatile, label-free technique for probing molecular composition in biological samples. However, the detection of subtle biochemical traits in high-throughput spectral datasets requires careful preprocessing, dimensionality reduction, and statistically sound analytical strategies. We present PyFasma, an open-source Python package for Raman spectroscopy, integrating essential preprocessing tools (e.g., spike removal, smoothing, baseline correction, normalization), multivariate techniques (PCA, PLS-DA), and spectral deconvolution within a modular, Jupyter Notebook-friendly framework. In addition to describing the software, we demonstrate PyFasma's capabilities through a practical biomedical case study comparing Raman spectra from healthy and osteoporotic cortical bone samples. The results revealed statistically significant differences in mineral-to-matrix ratio and crystallinity between assigned groups, with PCA and PLS-DA successfully distinguishing pathological from normal bone spectra. PyFasma encourages best practices in model validation, including the powerful but often overlooked, repeated stratified cross-validation, enhancing the generalizability of multivariate analyses. It also offers an easy-to-use, extensible solution for Raman data analysis, enabling the reproducible and robust interpretation of complex spectra of biological samples.

---

1 Introduction

Raman spectroscopy has emerged as an efficient tool in biomedical research, offering label-free, non-destructive molecular characterization of biological samples.^1–3 Recent advances in instrumentation, computational algorithms, and chemometric pipelines have significantly boosted the throughput of Raman-based analyses. These developments enable the acquisition of massive spectral datasets, which require robust preprocessing and statistical analysis to extract meaningful biological insights and identify subtle spectral variations.

The typical preprocessing steps involve removal of cosmic rays artifacts, signal smoothing, baseline correction, and intensities normalization.⁴ Cosmic rays are intense, spurious peaks caused by high-energy particles interacting with the detector.⁵ Signal smoothing reduces random noise, enhancing the clarity of Raman peaks while preserving essential spectral features.⁶ Baseline correction mitigates the influence of background fluorescence, allowing the spectral features that correspond to molecular vibrations to be more clearly discerned.⁷ Normalization techniques, such as area or intensity normalization, adjust for in-sample heterogeneity and variations in experimental conditions and enable consistent comparison between spectra collected under different experimental conditions or from different samples. Preprocessing enhances the signal-to-noise ratio and improves the reproducibility of results, leading to more accurate multivariate analyses and reliable qualitative and quantitative assessments. Without proper preprocessing, subtle spectral features critical for distinguishing sample types or detecting specific biomolecular changes may be obscured, ultimately reducing the sensitivity and specificity of the analysis.

Furthermore, Raman spectroscopy is increasingly applied in high-throughput experimental setups, where large numbers of spectra are acquired under varying conditions. As noted, effective data analysis requires rigorous preprocessing. However, when working with large datasets, manual processing becomes impractical and introduces variability due to user-dependent choices. Moreover, while graphical user interface (GUI) software may seem more accessible, it often falls short when handling large datasets typical of Raman experiments. Repetitive actions, such as clicking through menus, can quickly become tedious or inefficient. Although scripts and custom workflows are frequently developed within research groups, they are rarely shared or maintained in open formats, restricting their broader utility.

Lately, the application of Raman spectroscopy has progressed from a focus on purely qualitative spectral interpretation to a data-intensive analysis that emphasizes comparative and semi-quantitative approaches.^8,9 Raman analysis heavily relies on dimensionality reduction techniques, with Principal Component Analysis (PCA) playing a central role. Integrating PCA and other multivariate analysis techniques directly into a software package enables a coherent and efficient data analysis workflow.

Additionally, spectral bands often overlap due to closely spaced vibrational modes from Raman active molecular groups, broadened peaks, and variations in the local chemical environment. Deconvolution techniques mathematically resolve overlapping peaks, giving the position and the intensity of each resolved sub-band in addition to its shape (FWHM) and area, which are critical parameters for semi-quantitative analysis. For instance, deconvoluted band intensities can correlate with relative concentrations of specific molecular species, while peak shifts and widths are indicative of the sample's physical condition, bonding environment, and physiological state. Moreover, the method enhances reproducibility and consistency in analyses, as it provides a standardized approach to handling overlapping bands.

To meet all the above challenges, a variety of software tools have been developed for the analysis of spectroscopic data,^10–14 including Raman spectroscopy.^15–18 Although several open-source or freely available software packages are available, many are not specifically designed for Raman spectroscopy, which presents unique challenges such as fluorescence backgrounds, overlapping vibrational bands, and subtle signal variations that require specialized preprocessing and analysis workflows. In other cases, software is distributed as open-source but depends on commercial frameworks that restrict accessibility and long-term adoption despite the code itself being freely available. Some packages focus solely on preprocessing steps, without including multivariate statistical analysis modules. Others are designed either for experienced users, requiring programming or domain knowledge, or focus only on beginners, sacrificing flexibility and extensibility.

In this study, we present a Python-based framework specifically designed to perform preprocessing of Raman spectroscopy data, with built-in support for dimensionality reduction and spectral deconvolution algorithms. PyFasma is designed with a Jupyter Notebook-centric approach and features a high-level programming interface that is accessible to both novice and advanced users. It also promotes adaptability, reproducibility, and transparency in analytical workflows. To demonstrate its utility, we applied an end-to-end workflow to a representative case study investigating compositional changes in osteoporotic bone.

2 Materials and methods

2.1. PyFasma package overview

PyFasma is a free and open-source Python package, licensed under the GNU General Public License (GPL), that offers a high-level programming interface (API), providing the necessary tools to preprocess Raman spectra and deconvolute complex Raman bands, apply Principal Components Analysis (PCA) and Partial Least Squares Discriminant Analysis (PLS-DA) to Raman data, and create publication-ready plots. PyFasma can be easily installed by following the instructions provided online (https://pyfasma-def3fa.gitlab.io/).

PyFasma is a modular Python package built around the pandas DataFrame,¹⁹ chosen for its powerful data manipulation capabilities and seamless integration within Jupyter-based workflows. While example workflows are provided as Jupyter Notebooks for convenience, PyFasma itself is a standard Python package that can be used independently into standalone scripts, batch processes, or automated pipelines. The pandas DataFrame design enables vectorized, column-wise processing of large Raman datasets. The package comprises seven modules: helpers, fileio, numpyfuncs, dffuncs, plotting, modeling, and deconvolution, each designed to support distinct stages of a typical Raman spectroscopy workflow (Fig. 1).

Fig. 1 PyFasma modules.

Spectral data are imported and merged using the fileio module, which enables batch processing of CSV and SPC files with flexible file selection and optional directory structure preservation during format conversion. Preprocessing operations are implemented in numpyfuncs and dffuncs. The former provides array-based spectral methods, while the latter extends these operations to DataFrame columns via the .pyfasma accessor. Supported methods include cropping, interpolation, spike removal, smoothing (Savitzky–Golay, moving average, Gaussian), differentiation of arbitrary order, background removal using tested baseline correction algorithms (I-ModPoly,²⁰ SNIP,²¹ airPLS²²), and normalization (e.g., peak height, area, vector).

Multivariate statistical analysis is handled by the modelling module, which includes PCA and PLS-DA classes built on scikit-learn.²³ These accept DataFrames with Raman shift values as columns and samples as rows. Class labels for supervised learning are passed via a flexible hue parameter. Both models support scores/loadings plots and return results in standardized DataFrame formats, with visualizations generated through the plotting module and customizable via Matplotlib's object-oriented API (https://matplotlib.org/stable/api/).

The deconvolution module provides tools for fitting Gaussian, Lorentzian, or Voigt band shapes using the LMFIT library.²⁴ Unlike traditional implementations, PyFasma uses peak heights (intensities) and Full Widths at Half Maxima (FWHM) as fitting parameters instead of amplitudes (areas under curves) and sigmas/gammas (peak widths). Using these more intuitive parameters allows for clearer interpretation of spectral features, aligning closely with standard spectroscopic analysis practices. Results are returned as structured objects, along with goodness-of-fit statistics and publication-quality plots.

2.2. Samples

The performance of the PyFasma workflow was evaluated using cortical bone samples collected from ten female New Zealand rabbits. All animal procedures were approved by the Ioannina University Institutional Animal Care and Use Committee, in accordance with national legislation and the EU Directive 2010/63/EU. The rabbits were divided into two groups: one consisting of healthy individuals and the other with osteoporosis that was induced using a protocol for inflammation-mediated osteoporosis (IMO), as previously described.^25,26 From each bone, six slices approximately 2 mm thick were obtained from the central diaphysis (which is mainly composed of cortical bone), extending symmetrically towards the proximal and distal epiphyses. Raman spectra were acquired from three different points on the transverse surface of each slice, spaced approximately 120° apart. In a few cases, spectra were obtained from only two points, and one bone yielded four slices instead of six. Spectral acquisition was performed using a BWTEK i-Raman Plus spectrometer operating at 785 nm, with a power output of 100 mW at the probe and a signal collection time of 6 s. In total, 134 healthy and 69 osteoporotic Raman spectra were collected.

3 Results and discussion

We will demonstrate the basic usage of PyFasma through a complete workflow, starting with the conversion of SPC files (raw spectra) to CSV (Comma-Separated Values format), followed by preprocessing of the obtained Raman spectra, PCA and PLS modeling, and deconvolution to calculate the mineral-to-matrix ratio and crystallinity in healthy and osteoporotic bone samples.

3.1 Batch conversion and merge

The collected spectra are saved as SPC files inside the spc_files directory with a hierarchical tree structure similar to the one shown in Fig. 2a. The files use unique identifiers as their filenames that indicate the animal's identifying number, body part, bone slice, and collection site, as well its health condition (“Rbhf” for healthy animals and “Rbof” for animals with osteoporosis). While this naming convention is not mandatory, it serves the purpose of defining the two classes of normal and osteoporotic bones. Our target is to convert all SPC spectra to CSV and save them in the csv_files directory without altering the tree structure of the data using the fileio.spc2csv function as shown in Fig. 2b. By default, this function displays a text preview of the conversions and apply = True is used to apply them immediately.

Fig. 2 (a) Tree structure of SPC files. (b) PyFasma code to convert SPC files to CSV while preserving the tree structure. (c) PyFasma code to merge CSV files into a single DataFrame.

After conversion, the fileio.merge_csvs function is used to recursively find and merge the CSV files in the specified path (csv_files directory) to a DataFrame df (Fig. 2c). Merging takes place on the first column of each file (which contains the Raman shift) and the filenames of the CSV files are used for naming the columns of the DataFrame. To avoid potential merging issues caused by uneven spacing in the Raman shift axes (originating from multiple acquisitions or instrument software) the data are interpolated to a common, evenly spaced Raman shift vector specified in the xnew parameter.

3.2 Preprocessing

A typical preprocessing pipeline involves interpolating the data to use a common, constant step, removing noise from the data (e.g. shot noise, cosmic rays, detector artifacts), removing the fluorescence background, normalization, and cropping to a region of interest. While effort towards objective selection of preprocessing parameters using sophisticated algorithms is being made,²⁷ human intervention and trial-and-error is still required up to a point. Although fully automated optimization is still an open challenge in the field, PyFasma promotes transparency by enabling users to preserve each preprocessing step in separate DataFrame, ensuring that all transformations are traceable and reproducible.

In our case, we will apply the preprocessing steps to the df DataFrame created in the previous section. First, the DataFrame containing the spectra is cropped to a narrower range (100–2400 cm⁻¹) (Fig. 3a) to remove unwanted peaks. Then, the spectra are denoised by removing spikes and applying a Savitzky–Golay filter with a 17-points window and a 3rd degree polynomial (Fig. 3b). The spectra are then baseline-corrected using the SNIP algorithm using 20 iterations (set by the max_half_window parameter) in a decreasing manner. The result of denoising and the estimated background for a typical bone spectrum is presented in Fig. 3c. Finally, the spectra are intensity-normalized to the peak with the maximum intensity in the range 950–970 cm⁻¹ (phosphate v₁ peak) and cropped to the fingerprint region (Fig. 3d). Fig. 3e shows the mean preprocessed spectra for healthy and osteoporotic samples, with the characteristic Raman bands of bone annotated.

Fig. 3 PyFasma preprocesses Raman spectra within a single DataFrame that is iteratively updated, preserving a reproducible and traceable transformation history: (a) spectra crop (100–2400 cm⁻¹). (b) Spike removal and smooth with a Savitzky–Golay filter. (c) Background removal using the SNIP algorithm. (d) Normalization to the phosphate peak intensity (max between 950–970 cm⁻¹) and crop to the fingerprint region (400–1800 cm⁻¹). (e) Processed mean healthy and osteoporotic spectra. Raman bands that are associated with bone structure and quality are also denoted.

3.3. Multivariate analysis

3.3.1 Principal components analysis. Raman spectra are typically analysed using multivariate statistical methods, with Principal Components Analysis (PCA) being the most common. PCA is an unsupervised method that does not require labelled data. It computes the covariance matrix of the dataset and projects the data onto a new set of orthogonal axes, chosen to maximize the variance captured in the data. The new axes are called Principal Components (PCs) and are linear combinations of the original variables, with their coefficients (loadings) indicating each variable's contribution. The coordinates of the original data projected onto the PCs are known as scores, and the PCs are ranked in descending order of explained variance.

With PyFasma, PCA is applied by using the modeling.PCA class and the code shown in Fig. 4a. After importing the modeling module, we create a sample_class list that contains the classes of the samples (“Healthy”, “Osteoporotic”) in the DataFrame containing the preprocessed data. The classes are assigned by list comprehension with a conditional based on the name of the samples (column names of the DataFrame). The list data structure is used as the value of the hue parameter, which encodes the classes with different colors and symbols and allows them to be visually differentiated and compared, upon initializing the PCA class. We also set the n_components parameter to 10, which determines the number of principal components to be kept, or, in other words the dimensionality of the data transformed by PCA. The choice of 10 components was exploratory and intended to capture the majority of variance while preserving subtle group differences. By default, when running the code of Fig. 4a, a plot that summarizes the PCA results is displayed (Fig. 4b).

Fig. 4 (a) PyFasma code used for applying PCA to the data. (b) PCA summary plot containing a scree plot, the loadings plots for the first three PCs, and the scores plots for the first three PCs. The diagonal plots of the scores plots are the univariate KDEs for each PC, the plots below the diagonal are scatter plots of PC pairs, and the plots above the diagonal are bivariate KDEs for PC pairs. The 95% covariance ellipses for each class are also drawn in the scatter plots.

This plot contains a scree plot (a plot of the cumulative explained variance ratio for each component) that helps determine the number of components that should be retained in the PCA model. The optimal number depends on the data and application, but often the presence of a bending, or so-called “knee”, in the cumulative explained variance ratio in the scree plot is a good indication of it. The summarizing plot also includes plots of the first three loadings, as well as a scores plots grid of the first three components that include scatter plots and bivariate Kernel Density Estimates (KDE) plots of PC pairs, below and above the diagonal, respectively, and univariate KDE plots for each component on the diagonal. The scatter plots also contain the 95% covariance ellipses for each class. All visualizations in the summary plot along with all PCA data since DataFrames are accessible through the methods of the pca object.

3.3.2 Partial least squares discriminant analysis. Partial Least Squares Discriminant Analysis (PLS-DA) is an adaptation of Partial Least Squares Regression (PLSR), a supervised statistical analysis method widely used in chemometrics and specifically in Raman spectroscopy for dimensionality reduction and prediction. While PLSR is typically used for predicting continuous outcomes, PLS-DA modifies the approach to work with categorical data, making it suitable for classification tasks. In PLS-DA, a linear model is constructed to maximize the covariance between an X matrix of independent variables (in this case, Raman intensities) and a Y matrix of dependent variables (the assigned class of each sample). This process identifies latent variables (LV), which are the underlying factors that capture the most significant variation in the data and facilitate the differentiation between classes.

Before applying PLS-DA to the preprocessed data using PyFasma, the data must be split into train and test datasets. We used scikit-learn's model_selection.train_test_split method for splitting the data to a 70/30 train/test ratio by also using stratification to overcome the imbalance of the classes. A 70/30 train/test split was chosen as a balanced compromise between stable model fitting and unbiased evaluation. Stratification was applied to maintain the original class distribution in both subsets, which is essential given the moderate class imbalance and the relatively small dataset size. The next step is the determination of the optimal number of components that the predictive model should use, to avoid overfitting or underfitting the training data.^28,29 This is typically achieved using cross-validation on the training data for a varying number of model components.

Cross-validation is a resampling technique used to evaluate the predictive performance of a model by partitioning the training data into complementary subsets. In k-fold cross-validation, the dataset is divided into k equally sized folds. The model is trained on k − 1 of these folds and evaluated on the remaining fold, which serves as the validation set. The process is repeated k times, each time using a different fold for validation. To improve the reliability and stability of the performance estimate, repeated k-fold cross-validation can be employed.^30,31 In this approach, the k-fold procedure is repeated multiple times with different random partitions of the data, and the results are averaged across all repetitions.³² This helps reduce the variance of the performance estimate and mitigates the influence of any particular data split, leading to a more reliable selection of the optimal number of components.³³ To mitigate class imbalance in classification tasks, cross-validation can be conducted using a stratified approach, ensuring that each fold maintains the same class distribution as the entire dataset. When this stratified method is combined with repeated cross-validation, it provides more consistent and representative estimates of model performance, particularly in scenarios involving imbalanced datasets.³⁴ The code for performing repeated stratified k-fold cross-validation within PyFasma, along with the corresponding evaluation metrics plot, is shown in Fig. 5. Notably, all of the above steps are managed through a unified group of optional function arguments within the package.

Fig. 5 (a) PyFasma code for performing repeated stratified k-fold cross-validation on the training data. (b) Evaluation metrics plot showing the accuracy, Q², MSE, and R² of the cross-validated data for models with up to 10 components. The error bars represent the standard deviation of the evaluation metrics.

A commonly used metric for determining the optimal number of PLS components is the Mean Squared Error (MSE), or its square root, the Root Mean Squared Error (RMSE).^35,36 The MSE is calculated as the average of the squared differences between predicted and actual values, while the RMSE expresses this error in the same units as the response variable by taking the square root of the MSE. In addition to MSE, the evaluation plot in Fig. 5 includes three other metrics: accuracy, Q², and R², which provide complementary insights and support a more robust selection of the optimal number of components.³⁷ Accuracy is defined as the ratio of correctly predicted samples to the total number of samples in the test set (or validation set in cross-validation). Q² and R² are coefficients of determination that quantify the proportion of variance explained by the model. R² is calculated on the training data and indicates how well the model fits the data, whereas Q² is computed from cross-validated predictions and reflects the model's predictive ability on unseen data. In practice, R² reflects in-sample fit, and Q² reflects how reliably the model generalizes under cross-validation. A robust model is expected to show both a high R² and a high Q² while a large gap between them may indicate an overfitted (R² ≫ Q²) or underfitted model (when both indices are low).

Fig. 5 suggests that a PLS-DA model with two components performs well, as it yields high accuracy, low mean squared error (MSE), and closely aligned Q² and R² values, indicating consistent predictive performance across the training and validation subsets of the k-folds.

After selecting the optimal number of components, PLS-DA is performed using the code shown in Fig. 6a. The X- and Y-scores plots of the training data, as well as the confusion matrix for the test data can be generated using the corresponding methods of the pls object (Fig. 6b–d).

Fig. 6 (a) PyFasma code pipeline used to create: a PLS-DA model with two components, X- and Y-scores plot for the training data, and a confusion matrix on the test data. (b) X-scores plot for the training data. (c) Y-Scores plot for the training data. (d) Confusion matrix for the test data of the predictive model.

3.3. Deconvolution

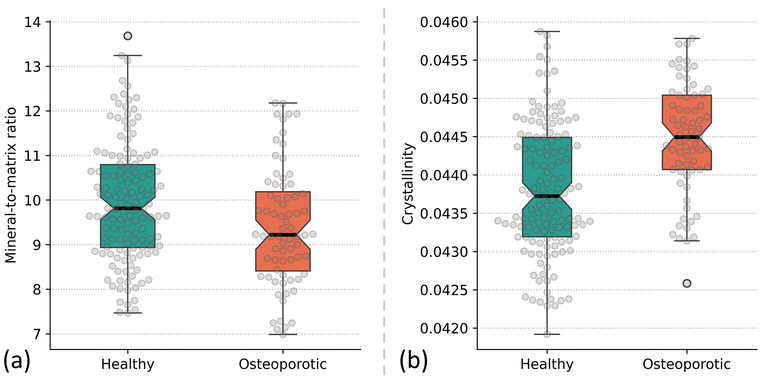
To demonstrate the use of PyFasma's deconvolution module, we will compare the mineral-to-matrix ratio of the healthy and osteoporotic rabbit tibia spectra, as well as their crystallinity. Deconvolution enables the extraction of the relevant spectral parameters by resolving overlapping Raman bands associated with mineral and matrix components. In this case, this process effectively enhances spectral resolution, allowing for a more precise assessment of hydroxyapatite content and crystallite properties than intensity-based methods. By applying deconvolution, differences in mineralization and crystallinity between healthy and osteoporotic bone can be quantified, providing insights into spectral alterations associated with disease-induced changes.

For calculating the mineral-to-matrix ratio, the first spectral region we will use is the 900–990 cm⁻¹ region, which is the most prominent feature of bone Raman spectra. In this region we find the symmetric stretching vibration (ν₁) of the phosphate group (PO₄³⁻) at 960 cm⁻¹, which is strongly related to the mineral content of the bone.^9,38 This region also contains other sub-bands which are revealed by second derivative analysis: a band at ∼921 cm⁻¹, which is attributed to the v(C–C) vibrations of proline in collagen's backbone, and a band at ∼947 cm⁻¹, associated with Type B carbonate substitutions in hydroxyapatite.³⁹ The second region, related to the organic bone matrix, is the Amide I region at 1580–1720 cm⁻¹, mostly composed of collagen-related sub-bands at ∼1602 cm⁻¹, ∼1640 cm⁻¹, ∼1664 cm⁻¹, ∼1681 cm⁻¹ and ∼1690 cm⁻¹, as can be confirmed by second order derivative spectra and goodness-of-fit analysis. The above positions of the sub-bands, with minor adjustments to our spectra along with estimates for their heights and FWHM, are used as the initial guesses for the FitGaussian class of the deconvolution module which is used to deconvolve the bands using Gaussian curves (Fig. 7a). The class is initialized using the DataFrame of the preprocessed data cropped to the respective region and the params_list parameter, which contains a list of dictionaries. Each dictionary contains the initial estimates (height, center, FWHM) and their respective boundaries (min, max), where required, for each Gaussian curve. Initial estimates were chosen by second-derivative analysis of representative spectra and/or by previously reported band assignments in the literature. The mineral-to-matrix ratio is then calculated as the intensity (height) ratio of the phosphate sub-band at 960 cm⁻¹ to the intensity of the Amide I sub-band at 1664 cm⁻¹, which is the most intense band in this region and corresponds to the stretching vibration of C=O. To calculate crystallinity, which reflects the size and structural order of hydroxyapatite crystals in bone, we will again use the 900–990 cm⁻¹ region, this time fitted with a single Gaussian curve.⁴⁰ Crystallinity can be assessed by calculating the inverse of the FWHM of the fitted curve, with broader peaks indicating lower crystallinity, and more disordered crystal structures. Typical deconvolution results for the phosphate and Amide I regions are shown in Fig. 7(b–d). After deconvolution, the heights of the Gaussian curves used for the calculation of the mineral-to-matrix ratio as well as the FWHMs for the calculation of crystallinity are obtained by using the values_df method of the respective fit object.

Fig. 7 (a) PyFasma code used for fitting the DataFrame of the phosphate region with three Gaussian curves and code to plot the fit result for a typical sample. The code is similar for the Amide I region deconvolution. (b) Deconvolution of the phosphate region with three Gaussian curves. The intensity (height) of the curve at 960 cm⁻¹ is used for the calculation of the mineral-to-matrix ratio. (c) Deconvolution of the Amide I region with five Gaussian curves. The intensity (height) of the curve at 1664 cm⁻¹ is used for the calculation of the mineral-to-matrix ratio. (d) Typical fit of the phosphate region with a single Gaussian curve for the determination of FWHM and calculation of crystallinity. Since the fit consists of a single Gaussian component, the blue curve (representing the component) entirely overlaps with the red curve (representing the overall fit), rendering the latter invisible in the plot.

3.4 Discussion

Fig. 3 depicts the preprocessing procedure that leads to spectra with no artifacts, improved signal-to-noise ratio, and with minimal background. Fig. 3e shows the typical Raman bands of bone tissue. Eye-inspection of the mean preprocessed spectra shows subtle but existing differences between the healthy and osteoporotic tibia spectra, especially in the v₂ and v₄ phosphate vibrations at 430 cm⁻¹ and 585 cm⁻¹, respectively, and in the Amide III band at 1246 cm⁻¹,⁴¹ suggesting alterations on both the inorganic and organic content of osteoporotic bone compared to healthy. How the differences between the two classes of spectra reflect underlying biochemical variations is further assessed using multivariate statistical analysis with PCA and PLS-DA.

The scree plot of PCA, presented in Fig. 4b, indicates that most of the observed variance in the data is explained by the first three PCs (76.10%). The PC1–PC2 and PC2–PC3 scores plots (off-diagonal plots) show clear discrimination between the healthy and osteoporotic samples along the PC2 axis. This is also evident in the univariate KDE plots (diagonal), where the PC2 KDE distributions for healthy and osteoporotic samples are clearly discriminated, while the KDE distributions for PC1 and PC3 overlap. In the loadings plot for PC1, which accounts for 62.15% of the total variance, all bands exhibit similar contributions to the variance, as expected, because the molecular structure of bone remains largely similar between healthy and osteoporotic samples. However, alterations due to osteoporosis become more apparent in higher-order principal components, indicating subtle variations in spectral features that distinguish the two groups. More specifically, in the PC2 loading, which is responsible for 10.73% of the observed variance, the most prominent features are located at 430 cm⁻¹ and 590 cm⁻¹ and are attributed to v₂ and v₄ phosphate vibrations, respectively. Thus, the main discriminatory factor between healthy and osteoporotic bones are variations in the mineral content.⁴² Another prominent narrow peak in PC2 is observed at 968 cm⁻¹, which results from the broader contour of the main phosphate band at 960 cm⁻¹ in healthy bone compared to osteoporotic bone due to the increased crystallinity of the hydroxyapatite crystals.⁴³ These results are consistent with previous findings that osteoporotic bone exhibits increased mineral crystal size and reduced lattice disorder,⁴² which manifest as narrower phosphate bands in Raman spectra. Such changes reflect altered mineral remodelling dynamics and support the notion that osteoporosis affects not only bone density but also mineral organization at the molecular scale.⁴⁴

For the PLS-DA procedure, repeated stratified k-fold cross-validation was used to estimate the number of components needed to construct the predictive PLS-DA model. The cross-validation metrics (accuracy, Q², MSE, R²) indicated that the optimal number of components for the predictive vector is 2 (Fig. 5b), thus the PLS-DA model was constructed with that number of components. The X- and Y-scores for LV1 and LV2 (Fig. 6(b and c)), which explain most of the data variance, reveal two well-separated clusters that correspond to the healthy and osteoporotic classes. These clusters are clearly distinguishable, as in the case of PCA, highlighting the capability of the PLS-DA model in effectively capturing the underlying spectral differences between the two conditions. The excellent discrimination is further demonstrated in the confusion matrix, which was used to evaluate the predictive model using the test data (Fig. 6d). The matrix demonstrates that the model correctly classified all samples, yielding perfect sensitivity, specificity, F-score, and accuracy values. Although the model achieved perfect classification on the test set, this result should be read with caution. Overfitting is a known risk when working with moderately sized and imbalanced datasets. That said, PyFasma implements repeated stratified k-fold cross-validation, which is a robust, yet often neglected, validation strategy in spectroscopic analysis. Unlike a single train-test split, this method systematically resamples the data while preserving class proportions, leading to more consistent performance metrics. In our view, such repeated stratified validation should be considered essential for unbiased modelling, especially in biomedical applications.

To quantify differences between the healthy and osteoporotic spectra, Gaussian deconvolution was performed on the phosphate region at 960 cm⁻¹ and the Amide I region at 1580–1720 cm⁻¹. The mineral-to-matrix ratio and crystallinity were then determined for each class. The mineral-to-matrix ratio was calculated as the intensity of the 960 cm⁻¹ band of the phosphate region, deconvoluted into three Gaussian curves, to the intensity of the 1664 cm⁻¹ band of the Amide I region, deconvoluted into five Gaussian curves. The mean mineral-to-matrix ratios were 9.95 for the healthy group and 9.49 for the osteoporotic group, suggesting a relative reduction in mineral content in osteoporotic bone. A Shapiro–Wilk test confirmed that the ratios for both classes followed a normal distribution, making them suitable for a subsequent Welch's t-test. The results confirmed a statistically significant difference between the mean mineral-to-matrix ratios of the two groups (p < 0.01). Boxplots illustrating the distribution of mineral-to-matrix ratios for both classes are presented in Fig. 8a. Crystallinity was assessed by analysing the FWHM of the 960 cm⁻¹ phosphate band, obtained through a single Gaussian fit. A lower FWHM corresponds to a more ordered mineral structure, indicative of increased crystallinity. Normality was verified using the Shapiro–Wilk test, confirming the suitability of parametric statistical analysis. A one-sided Welch's t-test was conducted to evaluate whether crystallinity was significantly higher in the osteoporotic samples compared to the healthy ones. The analysis revealed a statistically significant difference (p < 0.001). The finding aligns with earlier observations that osteoporosis is characterized by increased mineral crystal size and reduced lattice disorder.⁴² Boxplots (not currently part of PyFasma) depicting the crystallinity distributions for both groups are shown in Fig. 8b.

Fig. 8 Boxplots of (a) mineral-to-matrix ratio and (b) crystallinity for healthy and osteoporotic tibia samples. The boxplots are overlayed by swarm plots, showing the distribution of the relevant values. Outliers are highlighted with a solid outline.

4 Conclusion

PyFasma simplifies Raman spectral analysis by offering a user-friendly robust workflow. Using bone as a test case, a complex biological tissue with overlapping spectral features, the software efficiently handled raw Raman data, yielding artifact-free spectra. These preprocessed spectra enabled the clear differentiation between healthy and osteoporotic samples and supported the quantitative evaluation of key biochemical markers, such as the mineral-to-matrix ratio and crystallinity. In addition to its ease of use, PyFasma is fully modular and programmatically accessible, making it an attractive platform for scientists with programming experience who wish to customize workflows or expand the package's capabilities. In an era where Python has become the lingua franca of computing, PyFasma's open architecture and pythonic design ensures seamless integration into Raman spectroscopy research workflows.

Author contributions

EP, NK: methodology, formal analysis, and writing – original draft, writing – review & editing. EP: code. NK: conceptualization, resources, and funding acquisition.

Data availability

PyFasma is open-source software (https://pyfasma-def3fa.gitlab.io/). A subset of the spectra used in this study is included as examples. The full spectral dataset is available upon reasonable request.

Conflicts of interest

The authors declare no competing interests.

Acknowledgements

This research is co-financed by Greece and the European Union (European Social Fund – ESF) through the Operational Programme “Human Resources Development, Education and Lifelong Learning” in the context of the project “Strengthening Human Resources Research Potential via Doctorate Research” (MIS-5000432), implemented by the State Scholarships Foundation (IKY).

The publication of this article in OA mode was financially supported by HEAL-Link.

References

1. Y. Tang, X. Wang, G. Zhou, S. Guo, Z. Li, Y. Hu and W. Li, J. Anal. Test., 2025, 9, 136–152.
2. A. Chandra, V. Kumar, U. C. Garnaik, R. Dada, I. Qamar, V. K. Goel and S. Agarwal, ACS Omega, 2024, 9, 50049–50063.
3. Y. Wang, L. Fang, Y. Wang and Z. Xiong, Adv. Sci., 2024, 11, 2300668.
4. R. teja Vulchi, V. Morgunov, R. Junjuri and T. Bocklitz, Molecules, 2024, 29, 4748.
5. N. Coca-Lopez, Anal. Chim. Acta, 2024, 1295, 342312.
6. S. Fang, S. Wu, Z. Chen, C. He, L. L. Lin and J. Ye, TrAC, Trends Anal. Chem., 2024, 172, 117578.
7. N. Kourkoumelis, A. Polymeros and M. Tzaphlidou, J. Spectrosc., 2012, 27, 441–447.
8. M. Kashif and H. J. Byrne, Appl. Sci., 2025, 15, 2606.
9. E. Pavlou and N. Kourkoumelis, Chemom. Intell. Lab. Syst., 2022, 228, 104634.
10. J. Popp and T. Biskup, Chem.:Methods, 2022, 2, e202100097.
11. J. Ezenarro, D. Schorn-García, O. Busto and R. Boqué, Chemom. Intell. Lab. Syst., 2024, 247, 105096.
12. M. Grant-Peters, C. Rich-Griffin, J. E. Grant-Peters, G. Cinque and C. A. Dendrou, Bioinformatics, 2022, 38, 3490–3492.
13. M. Toplak, G. Birarda, S. Read, C. Sandt, S. M. Rosendahl, L. Vaccari, J. Demšar and F. Borondics, Synchrotron Radiat. News, 2017, 30, 40–45.
14. E. Flores, N. Mozhzhukhina, X. Li, P. Norby, A. Matic and T. Vegge, Chem.:Methods, 2022, 2, e202100094.
15. G. Sheehy, F. Picot, F. Dallaire, K. Ember, T. Nguyen, K. Petrecca, D. Trudel and F. Leblond, J. Biomed. Opt., 2023, 28(2), 025002.
16. D. Storozhuk, O. Ryabchykov, J. Popp and T. Bocklitz, arXiv, 2022, preprint,  DOI:10.48550/arXiv.2201.07586.
17. D. Georgiev, S. V. Pedersen, R. Xie, Á. Fernández-Galiana, M. M. Stevens and M. Barahona, Anal. Chem., 2024, 96, 8492–8500.
18. G. Georgiev, N. Coca-Lopez, D. Lellinger, L. Iliev, E. Marinov, S. Tsoneva, N. Kochev, M. A. Bañares, R. Portela and N. Jeliazkova, J. Raman Spectrosc., 2025 DOI:10.1002/jrs.6789.
19. W. McKinney and Scipy,  DOI:10.25080/Majora-92bf1922-00a.
20. J. Zhao, H. Lui, D. I. McLean and H. Zeng, Appl. Spectrosc., 2007, 61, 1225–1232.
21. C. G. Ryan, E. Clayton, W. L. Griffin, S. H. Sie and D. R. Cousens, Nucl. Instrum. Methods Phys. Res., Sect. B, 1988, 34, 396–402.
22. Z.-M. Zhang, S. Chen and Y.-Z. Liang, Analyst, 2010, 135, 1138–1146.
23. F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and É. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830.
24. M. Newville, T. Stensitzki, D. B. Allen and A. Ingargiola, LMFIT (version 0.8.0) Zenodo 2014,  DOI:10.5281/zenodo.598352.
25. A. Hadjipanteli, N. Kourkoumelis, P. Fromme, J. Huang and R. D. Speller, Phys. Med., 2016, 32, 162–168.
26. A. Hadjipanteli, N. Kourkoumelis, P. Fromme, A. Olivo, J. Huang and R. Speller, Physiol. Meas., 2013, 34, 1399.
27. J. Ma, M. Zuo, B. Wu and W. Wang, J. Raman Spectrosc., 2025, 56, 337–344.
28. I. A. Bratchenko and L. A. Bratchenko, mSystems, 2025, 10, e00063–e00025.
29. L. A. Bratchenko and I. A. Bratchenko, J. Raman Spectrosc., 2025, 56, 353–364.
30. E. Gurian, A. Di Silvestre, E. Mitri, D. Pascut, C. Tiribelli, M. Giuffrè, L. S. Crocè, V. Sergo and A. Bonifacio, Anal. Bioanal. Chem., 2021, 413, 1303–1312.
31. C. Chrimatopoulos, E. Pavlou, N. Kourkoumelis and V. Sakkas, Chemom. Intell. Lab. Syst., 2022, 230, 104660.
32. L. A. Yates, Z. Aandahl, S. A. Richards and B. W. Brook, Ecol. Monogr., 2023, 93, e1557.
33. Y. Jung, J. Nonparametric Stat., 2018, 30, 197–215.
34. P. Thölke, Y.-J. Mantilla-Ramos, H. Abdelhedi, C. Maschke, A. Dehgan, Y. Harel, A. Kemtur, L. Mekki Berrada, M. Sahraoui, T. Young, A. Bellemare Pépin, C. El Khantour, M. Landry, A. Pascarella, V. Hadid, E. Combrisson, J. O'Byrne and K. Jerbi, NeuroImage, 2023, 277, 120253.
35. L. A. Bratchenko, Y. A. Khristoforova, I. A. Pimenova, E. N. Tupikova, M. A. Skuratova, G. A. Dvoynikov-Sechnoy, S. Wang, P. A. Lebedev and I. A. Bratchenko, Light: Adv. Manuf., 2025, 6, 35.
36. S. Z. Al-Sammarraie, L. A. Bratchenko, E. N. Tupikova, M. A. Skuratova, S. Wang, P. A. Lebedev and I. A. Bratchenko, J. Biomed. Photonics Eng., 2024, 10, 1.
37. E. Szymańska, E. Saccenti, A. K. Smilde and J. A. Westerhuis, Metabolomics, 2012, 8, 3–16.
38. M. D. Morris and G. S. Mandair, Clin. Orthop. Relat. Res., 2011, 469, 2160–2169.
39. G. S. Mandair and M. D. Morris, BoneKEy Rep., 2015, 4, 620.
40. M. Unal, R. Ahmed, A. Mahadevan-Jansen and J. S. Nyman, Analyst, 2021, 146, 7464–7490.
41. K. N. Eckstein, S. M. Thomas, A. K. Scott, C. P. Neu, N. A. Hadley-Miller, K. A. Payne and V. L. Ferguson, J. Mech. Behav. Biomed. Mater., 2022, 128, 105102.
42. N. Kourkoumelis, X. Zhang, Z. Lin and J. Wang, Clin. Rev. Bone Miner. Metab., 2019, 17, 24–39.
43. R. Gautam, R. Ahmed, E. Haugen, M. Unal, S. Fitzgerald, S. Uppuganti, A. Mahadevan-Jansen and J. S. Nyman, Spectrochim. Acta, Part A, 2023, 303, 123240.
44. M. Unal, S. Uppuganti, S. Timur, A. Mahadevan-Jansen, O. Akkus and J. S. Nyman, Sci. Rep., 2019, 9, 7195.

---