Structurally and electronically driven uniaxial negative thermal expansion in BaIrO₃

Abstract

Negative thermal expansion is known to exist in a range of structure types but is extremely rare in hexagonal perovskites. Here we demonstrate that BaIrO₃ displays negative linear thermal expansion in the direction of its face-shared IrO₆ trimers, and apparent zero volume thermal expansion below 100 K. We present evidence that this anomalous thermal expansion is driven by an unusual form of rigid body phonon behaviour governed by the effective trimer valence state and therefore has structural and electronic components to the underlying mechanism.

---

Negative thermal expansion (NTE) is a fascinating – and highly functional – property.¹ But as only a small minority of materials are known to exhibit NTE, discovering new examples, and revealing the mechanisms behind this unusual behaviour, is of great value.^1–3 The underlying mechanisms are generally either of structural or electronic origin. The most well-known example for the first type is that of vibrations transverse to the bond direction in flexible framework structures constructed of rigid units as in ReO₃.⁴ Complementary to this are electronically mediated cases driven by thermal changes in the interatomic bonding potential or by magnetostriction.² Such behaviour generally occurs at phase transitions,⁵ or gradually evolves in a low-temperature phase as a function of the (magnetic) order parameter.⁶ NTE can be considered to be strong if the linear thermal expansion coefficient, α, is of order |α| > 10⁻⁵ K⁻¹i.e. larger than the α of positive thermal expansion in many everyday materials.⁷

In hexagonal perovskites (HP), which contain units of face-shared octahedra, very few examples of NTE are known. Ba₃BiRu₂O₉, Ba₃BiIr₂O₉ and Ba₄BiIr₃O₁₂ all fall in the class of electronically driven NTE coinciding with their magnetic ordering transitions.^8–10 [(CH₃)₂NH₂]PbBr₃ exhibits uniaxial NTE, as a result of a bonding-related order–disorder phase transition.¹¹ To the best of our knowledge, there are no examples of HPs that exhibit structurally-driven NTE. Simplistically that might be expected – face-sharing octahedra cannot be tilted by transverse phonons in the way vertex-sharing octahedra can. But that does not rule out the face-sharing units themselves being the rigid units that experience vibrational motion. Here, we present evidence for such NTE in a HP, BaIrO₃, for the first time. Intriguingly our data indicate that it is closely linked to the electronic structure of the trimer building blocks, hinting at a mixed structural-electronic origin.

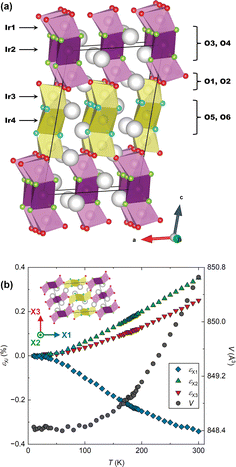
The structure of BaIrO₃, which is a monoclinically-distorted (space group C2/m) variant of the 9R HP structure is illustrated in Fig. 1a.¹² There are four Ir crystallographic sites, each octahedrally coordinated and arranged through face-sharing into linear Ir₃O₁₂ trimers oriented approximately parallel to the c axis of the unit cell. In the undistorted 9R structure these trimers are crystallographically equivalent, but the monoclinic distortion present in BaIrO₃ breaks this degeneracy. Half the trimers comprise Ir1–Ir2–Ir1 iridium sites, whilst the other half comprise Ir3–Ir4–Ir3 sites. The trimers of one type share vertices exclusively with trimers of the other type (i.e. Ir1–O–Ir3 linkages). This results in a structure comprising alternating ‘layers’ of each trimer type stacking along the c axis. As will become apparent, the inequivalence of the two types of trimer is essential to the occurrence of NTE in BaIrO₃.

Fig. 1 (a) The crystal structure of BaIrO₃, with the Ir and O sites labelled. (b) The lattice strains ε_Xi along the principal axes Xi as a percentage of the 10 K values, and the unit cell volume. The inset shows the orientation of the unit cell relative to the three principal axes.

BaIrO₃ is metallic, with magnetic transition at T_C = 184 K.¹³ Transport and optical conductivity studies indicate that this is accompanied by a charge density wave,¹⁴ with μSR suggesting a small moment consistent with very weak ferromagnetism.¹⁵ The details of the transition remain contentious,^16–22 and no structural changes have been resolved crystallographically. While additional transitions at 26 K and 80 K have been reported, they were absent in high quality powder samples.²³

NTE at low temperatures was first reported based on laboratory X-ray measurements by Cheng et al.¹⁸ A recent synchrotron X-ray diffraction study was able to connect this to the distortions of the trimer units, revealing inequivalency of the temperature dependencies of the two symmetry-inequivalent trimers.²¹ While at the same time being only weakly affected by the 184 K transition. The potentially unusual NTE mechanism in this compound motivated our high-resolution neutron diffraction study reported here.

We collected high-resolution powder neutron diffraction data for a ¹⁹³Ir-enriched²⁴ sample of BaIrO₃ between 10 K and 300 K. Subsequent Rietveld refinement allowed us to determine the lattice parameters, all atomic positions and atomic displacement parameters B_iso over the whole temperature range. Using PASCal²⁵ we calculate the principal axes Xi and the infinitesimal Lagrangian strains ε_Xi along them (Fig. 1b). X1 is effectively parallel to the c axis (it has components 0.9996c and −0.0287a, equating to a 5° offset); X2 is exactly parallel to b; and X3 is orthogonal to X1 and X2 (its components are 0.9869a and 0.1612c). From ε_Xi we extract the principal linear thermal expansion coefficients α_Xi (see ESI†) as shown in Table 1. Linear temperature dependence is found for all three α_Xi for T ≥ 80 K.

Table 1 Linear thermal expansion coefficients α_Xi along the principal axes Xi, either side of T_C = 184 K

α Xi /×10^−6 K^−1	80–182 K	186–270 K
α X1	−16.0(2)	−10.6(2)
α X2	13.2(1)	15.1(1)
α X3	8.7(1)	11.9(1)

---

The phenomenology of this linear NTE is notable. Not only is the magnitude very large (|α_X1| > 10⁻⁵ K⁻¹),⁷ but below 100 K ε_X1 effectively cancels with ε_X2,3 resulting in an average volumetric thermal expansion coefficient [small alpha, Greek, macron]_V in the range of 10 to 100 K of [small alpha, Greek, macron]_V = 1.9 × 10⁻⁷ (ESI†), comparable to the best examples in the literature and of potential interest for cryogenic applications.²⁶

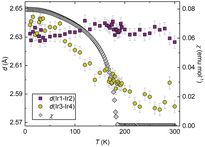
Surprisingly we found only a small, albeit significant, change in the linear thermal expansion on crossing the magnetic ordering temperature T_C = 184 K. This contrasts with the NTE found in the other HPs as introduced previously, which all contract abruptly within the narrow temperature range of a first-order phase transition. Ba₃BiRu₂O₉, Ba₃BiIr₂O₉ and Ba₄BiIr₃O₁₂ all contract uniaxially along the direction in which their constituent dimers/trimers are oriented – and the contractions are driven by a shortening of the Ir–Ir (or Ru–Ru) distances within those face-sharing units. Thanks to the face-sharing geometry, the metal centres within neighbouring octahedra have both the orientation and proximity for direct d–d overlap to be possible. We do not find such a simple correlation in BaIrO₃, not only are the distances within the Ir1–Ir2–Ir1 and Ir3–Ir4–Ir3 trimers different to one another (a consequence of the monoclinic distortion present), but their variation with temperature is different too (see Fig. 2). Above T_C = 184 K both the Ir1–Ir2 and Ir3–Ir4 distances lengthen on cooling, though the latter do so at a rate approximately three times greater than the former. But below T_C, the Ir1–Ir2 distance switches to a slight contraction on cooling, whilst the Ir3–Ir4 bond not only retains its abnormal behaviour but its rate of extension increases further. In short, the NTE is completely due to the Ir3–Ir4–Ir3 trimer with the Ir1–Ir2–Ir1 trimer effectively invariant.

Fig. 2 Variation of the two face-sharing Ir–Ir distances in BaIrO₃, both show a change in slope in crossing T_C = 184 K, and the magnetic ordering transition evident in the susceptibility χ = M/H (μ₀H = 0.1 T).

To further investigate the mechanism we now turn to the temperature evolution of the remaining atomic parameters, which were inaccessible to previous studies. Most significant is the displacement of the constituent Ir and O atoms, determined via refinement of B_iso. Anomalously large atomic displacements are a signature of phonon-driven NTE, as they capture, in the static picture of a diffraction pattern, dynamic displacements of atoms away from their equilibrium sites. Large (and anisotropic) atomic displacements are seen in a number of such materials,⁷ well known examples including ZrW₂O₈ and ScF₃.^27,28 Neutron diffraction is particularly powerful for studying this as it allows the oxygen positions to be captured in the presence of heavy elements and the flat form-factor improves the precision and accuracy of displacement parameter determination. We used a single B_iso for the iridium sites (Ir1,2 and Ir3,4) and oxygen sites (O3,4 and O5,6) within each symmetry-inequivalent trimer, as well as an independent B_iso for the bridging oxygen sites (O1,2). A comparison of the refined values (Fig. 3) clearly shows that the atoms in the Ir3–Ir4–Ir3 trimer (those Ir sites and the O5,6 pair) have far larger displacement parameters than their analogues in the Ir1–Ir2–Ir1 trimer. And the B_iso of the O1,2 pair is the largest of all. The behaviour of the Ir3,4 trimer over the whole temperature regime we studied would suggest that the NTE in BaIrO₃ is of structural origin and the result of vibrations in which the Ir₃O₁₂ trimers, rather than individual IrO₆ octahedra, are the rigid units. Within the unit cell there are 30 atoms and thus 90 possible phonon modes, making it very challenging to determine which specific mode(s) are responsible. However, from a crude analysis one can readily visualise cooperative displacements of the Ir and O sites that would result in NTE. A transverse displacement of the O1 and O2 sites causing a rotation of the trimers in the ac plane, for example, analogous to the tilting of vertex-sharing octahedra in ReO₃-type NTE materials, would contract the lattice along c. This is the first time such behaviour has been found in a HP.

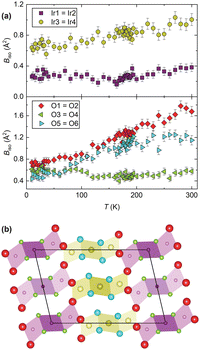Fig. 3 (a) Refined B_iso values for the Ir and O sites. (b) Projection of the structure along b with the atomic radii proportional to the 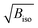values at 300 K (Ba sites omitted for clarity).

An essential comparison can be made to BaRuO₃, with an undistorted R3̄m 9R HP structure, and an entirely conventional positive thermal expansion (and no anomalies in its atomic displacement parameters).²⁹ All of its Ru₃O₁₂ trimers are equivalent – in other words, whichever effect is responsible for the NTE in BaIrO₃ is not available in its Ru-analogue. Comparison also rules out the electronic effect of strengthening metal–metal bonding being in itself responsible for the NTE, because it is similarly present in both of them. At 300 K, the Ir1–Ir2 distance in BaIrO₃ is 2.63 Å whilst the Ir3–Ir4 distance is 2.58 Å. Both of these are shorter than the 2.69 Å nearest-neighbour separation in elemental Ir at the same temperature. Comparably, the 300 K Ru–Ru distance in BaRuO₃ is 2.55 Å,²⁹ compared to 2.65 Å in elemental Ru.

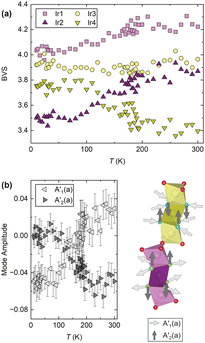
However, if the NTE were of purely structural origin, one would naively expect both trimers to show similar behaviour given their superficially small structural differences. But, as shown in Fig. 2, they are fundamentally different. Hence a purely structural mechanism cannot be sufficient and electronic effects have to be important in BaIrO₃: like many iridates, it hosts finely-balanced states.³⁰ Through being able to accurately refine the oxygen site positions we are able to calculate the bond valence sum (BVS)³¹ for each Ir centre (Fig. 4a). We find that at all temperatures they are significantly different between the two trimers, indicating fundamentally different electronic characteristics. For example, Ir2 and Ir4 differ in their BVS/oxidation state by 0.5 at room temperature. This difference of electron density distribution must be one of the drivers of the different trimer expansivities. Furthermore, whilst all four BVS are temperature-independent above T_C, three of them vary significantly below it (Fig. 4a). Ir1 (Ir^4.2+ to Ir^4.0+) and Ir2 (Ir^3.9+ to Ir^3.5+) both lose valence, whilst Ir4 (Ir^3.4+ to Ir^3.8+) gains it, and the Ir3 site is stable Ir^3.9+. In other words, at T_C there is a transfer of charge from the Ir3–Ir4–Ir3 trimers to the Ir1–Ir2–Ir1 ones. Between 300 K and 10 K this equates to a transfer of 1.0(1) charge. This change in the BVS at T_C is a likely source for the evolution of the NTE across the transition, and is further evidence of an electronic component to its mechanism. We cannot say precisely how without more diverse experimental input – spectroscopy, for example, may show a corresponding change in phonon frequencies if the charge transfer stiffens the Ir3–Ir4 interaction and weakens the Ir1–Ir2 one – but there is clearly a change in the electronic structure associated with the magnetic ordering which affects the NTE. The very small ordered moment makes a magnetostrictive origin of the evolution of the NTE below the transition rather improbable. A magnetostrictive scenario would furthermore require significantly different magnetic moments on the two trimers – something not seen by μSR.

Fig. 4 (a) The calculated bond valence sums for the four Ir sites, which show that inter-trimer charge transfer occurs below T_C. (b) Symmetry mode analysis reveals a simultaneous structural distortion, by which the Ir₂O₆ octahedron gains volume on cooling and the Ir₄O₆ octahedron shrinks by an equivalent amount. Arrows on the crystal structure section indicate the corresponding atomic displacements.

We cannot currently explain the charge transfer occurring at T_C = 184 K. The electronic structure of BaIrO₃ remains under discussion, though it is reassuring that a recent reflectivity study is consistent with the inter-trimer charge transfer observed by us.²² Further insight is provided by symmetry-mode analysis (Fig. 4b), which reveals an anti-correlation in two modes of the T1+ irrep (which is activated by the monoclinic lattice distortion) that corresponds to a gain in volume by the central Ir₂O₆ octahedron of one of the trimers and an equivalent loss in volume by the Ir₄O₆ octahedron of the other trimer (Fig. 4b). These subtle but detectable structural features, which have never been reported before, may help to reconcile the different mechanisms that have been put forward to describe the ordering transition in BaIrO₃.

In conclusion, we have quantified the uniaxial NTE in BaIrO₃ for the first time, and unveiled an effective volume ZTE below 100 K. While the evolution of B_iso in the Ir3,4 trimer suggests a structural origin for the NTE it seems irreconcilable with the more conventional behaviour of the structurally similar Ir1,2 trimer. Irrespective of this, it is clear that the origin of the NTE is fundamentally different from that of the other HP NTE materials. Intriguingly, we uncovered significant differences in the oxidation states of the two trimers of up to 0.5, indicating an electronic origin of the disparities in their thermal behaviour. Furthermore, the NTE response changes upon crossing T_C = 184 K, and we have found concurrent changes in the trimer bond valences, which appear to be related to inter-trimer charge transfer at this phase transition. These observations clearly mark the NTE as not easily classifiable into purely structural or purely electronic origin, an unprecedented scenario clearly motivating further studies.

We acknowledge funding from the Engineering and Physical Sciences Research Council [grant numbers EP/T011130/1 and EP/P024564/1]. Experiments at the ISIS Neutron and Muon Source were supported by a beamtime allocation RB1910632 from the Science and Technology Facilities Council: https://doi.org/10.5286/ISIS.E.RB1910632-1.

Data availability

Data for this article have been included as part of the ESI.† Neutron diffraction data are available from: https://doi.org/10.5286/ISIS.E.RB1910632-1.

Conflicts of interest

There are no conflicts to declare.

References

1. K. Takenaka, Sci. Technol. Adv. Mater., 2012, 13, 013001.
2. J. P. Attfield, Front. Chem., 2018, 6, 371.
3. Q. Li, K. Lin, Z. Liu, L. Hu, Y. Cao, J. Chen and X. Xing, Chem. Rev., 2022, 122, 8438–8486.
4. T. Chatterji, P. F. Henry, R. Mittal and S. L. Chaplot, Phys. Rev. B: Condens. Matter Mater. Phys., 2008, 78, 134105.
5. Y. W. Long, N. Hayashi, T. Saito, M. Azuma, S. Muranaka and Y. Shimakawa, Nature, 2009, 458, 60–63.
6. B. Dabrowski, M. Avdeev, O. Chmaissem, S. Kolesnik, P. W. Klamut, M. Maxwell and J. D. Jorgensen, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 104411.
7. N. Shi, Y. Song, X. Xing and J. Chen, Coord. Chem. Rev., 2021, 449, 214204.
8. W. Miiller, M. Avdeev, Q. Zhou, A. J. Studer, B. J. Kennedy, G. J. Kearley and C. D. Ling, Phys. Rev. B: Condens. Matter Mater. Phys., 2011, 84, 220406(R).
9. W. Miiller, M. Avdeev, Q. Zhou, B. J. Kennedy, N. Sharma, R. Kutteh, G. J. Kearley, S. Schmid, K. S. Knight, P. E. R. Blanchard and C. D. Ling, J. Am. Chem. Soc., 2012, 134, 3265–3270.
10. W. Miiller, M. T. Dunstan, Z. Huang, Z. Mohamed, B. J. Kennedy, M. Avdeev and C. D. Ling, Inorg. Chem., 2013, 52, 12461–12467.
11. J. S. Rodríguez-Hernández, M. A. P. Gómez, D. S. Abreu, A. Nonato, R. X. da Silva, A. García-Fernández, M. A. Señarís-Rodríguez, M. Sánchez-Andújar, A. P. Ayala and C. W. A. Paschoal, J. Mater. Chem. C, 2022, 10, 17567–17576.
12. T. Siegrist and B. L. Chamberland, J. Less-Common Met., 1991, 170, 93–99.
13. A. V. Powell and P. D. Battle, J. Alloys Compd., 1993, 191, 313–318.
14. G. Cao, J. Crow, R. Guertin, P. Henning, C. Homes, M. Strongin, D. Basov and E. Lochnere, Solid State Commun., 2000, 113, 657–662.
15. M. L. Brooks, S. J. Blundell, T. Lancaster, W. Hayes, F. L. Pratt, P. P. C. Frampton and P. D. Battle, Phys. Rev. B: Condens. Matter Mater. Phys., 2005, 71, 220411(R).
16. M.-H. Whangbo and H.-J. Koo, Solid State Commun., 2001, 118, 491–495.
17. K. Maiti, R. S. Singh, V. R. R. Medicherla, S. Rayaprol and E. V. Sampathkumaran, Phys. Rev. Lett., 2005, 95, 016404.
18. J.-G. Cheng, J.-S. Zhou, J. A. Alonso, J. B. Goodenough, Y. Sui, K. Matsubayashi and Y. Uwatoko, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 104430.
19. M. A. Laguna-Marco, D. Haskel, N. Souza-Neto, J. C. Lang, V. V. Krishnamurthy, S. Chikara, G. Cao and M. van Veenendaal, Phys. Rev. Lett., 2010, 105, 216407.
20. W. Ju, G.-Q. Liu and Z. Yang, Phys. Rev. B: Condens. Matter Mater. Phys., 2013, 87, 075112.
21. I. Terasaki, S. Ito, T. Igarashi, S. Asai, H. Taniguchi, R. Okazaki, Y. Yasui, K. Kobayashi, R. Kumai, H. Nakao and Y. Murakami, Crystals, 2016, 6, 27.
22. R. Okazaki, S. Ito, K. Tanabe, H. Taniguchi, Y. Ikemoto, T. Moriwaki and I. Terasaki, Phys. Rev. B, 2018, 98, 205131.
23. N. Kini, A. Bentien, S. Ramakrishnan and C. Geibel, Phys. B, 2005, 359–361, 1264–1266.
24. A. C. Hannon, A. S. Gibbs and H. Takagi, J. Appl. Crystallogr., 2018, 51, 854–866.
25. M. Lertkiattrakul, M. L. Evans and M. J. Cliffe, J. Open Source Softw., 2023, 8, 5556.
26. T. H. K. Barron, J. G. Collins and G. K. White, Adv. Phys., 1980, 29, 609–730.
27. J. S. O. Evans, T. A. Mary, T. Vogt, M. A. Subramanian and A. W. Sleight, Chem. Mater., 1996, 8, 2809–2823.
28. M. T. Dove, J. Du, Z. Wei, D. A. Keen, M. G. Tucker and A. E. Phillips, Phys. Rev. B, 2020, 102, 094105.
29. P. Kayser, S. Injac, B. J. Kennedy, A. L. M. de Oliveira, Y. Shirako and M. Hasegawa, Dalton Trans., 2017, 46, 2974–2980.
30. A. J. Browne, A. Krajewska and A. S. Gibbs, J. Mater. Chem. C, 2021, 9, 11640–11654.
31. O. C. Gagné and F. C. Hawthorne, Acta Crystallogr., Sect. B: Struct. Sci., Cryst. Eng. Mater., 2015, 71, 562–578.

---

Footnote

† Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cc06174h

---