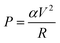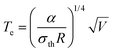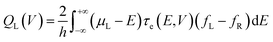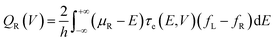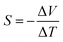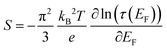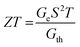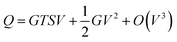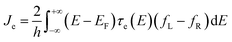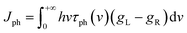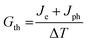Thermoelectric and thermal properties of molecular junctions: mechanisms, characterization methods and applications

Abstract

The rapid development of artificial intelligence requires tremendous energy consumption. Due to the limitations of cooling and energy recovery systems, effectively lowering power dissipation and utilizing the waste heat of electronic devices remain challenges. Molecular electronics, with its potential for low energy consumption and high-efficiency thermoelectric conversion, offers a feasible solution for future computational devices. Over the past two decades, researchers have made significant progress in the study of thermal and thermoelectric properties of molecular junctions. In this feature article, we first introduced four mechanisms of thermal and thermoelectric transport in molecular junctions guided by quantum theory. We then reviewed the evolution of characterization techniques for assessing the local temperature, thermopower, and thermal conductance of molecular junctions. Subsequently, we introduced the practical applications that have been implemented so far. This review concludes by addressing the principal challenges currently faced in the field and identifying crucial directions for future research.

---

Chao Fang

Chao Fang is currently pursuing his PhD at Xiamen University under the supervision of Associate Professor Junyang Liu and Professor Wenjing Hong. His research focuses on scientific instrument setup and chip nanofabrication for studying thermal and thermoelectric transport in single molecules.

Yuting Li

Yuting Li is currently pursuing her master's degree at Xiamen University under the supervision of Associate Professor Junyang Liu. Her research focuses on the development and application of micro–nanodevices, with an emphasis on exploring the potential of novel materials in this field.

Siwen Wang

Siwen Wang is currently pursuing her master's degree at Xiamen University under the guidance of Associate Professor Junyang Liu. Her research focuses on the integration of molecular layer memory resistors.

Mingchen Liang

Mingchen Liang is currently pursuing his PhD at Xiamen University under the supervision of Associate Professor Junyang Liu. His research focuses on molecular devices and the tuning of thermal conductance in single-molecule junctions.

Junyang Liu

Junyang Liu received his PhD from Xiamen University in 2016 under the supervision of Professor Zhong-Qun Tian. Since 2020, he has been an Associate Professor of Chemical Engineering at Xiamen University. His research interests include single-molecule electronics, microchip nanofabrication for single-molecule reaction dynamics and single-molecule device integration.

Wenjing Hong

Wenjing Hong received his PhD in molecular electronics (summa cum laude) from the University of Bern in 2013. Since 2015, he has been a Full Professor at the College of Chemistry and Chemical Engineering, College of Materials and Institute of Artificial Intelligence, Xiamen University. His research mainly focuses on single-molecule electronics and artificial intelligence for science. More details can be found at https://Pilab.xmu.edu.cn.

---

1. Introduction

In recent years, the rapid development of artificial intelligence (AI) has brought transformative changes across numerous fields, promoting unprecedented progress and efficiency enhancements.¹ However, the steadily increasing energy demands for AI training and inference are becoming a significant constraint on the development of more advanced AI technologies,² highlighting the critical requirements for innovative solutions to reduce energy consumption and reuse waste heat. Molecular electronics,^3–6 which involves creating logic circuits from single molecules, stands out as one of the most promising approaches to tackle this issue, particularly because of its potential to significantly reduce energy usage.⁷

Understanding the thermoelectric and thermal properties of molecular junctions is crucial for investigating low-energy molecular devices, as these properties reflect energy conversion efficiency and are essential for studying energy transfer at nanoscale interfaces.^8–13 Unlike traditional macroscopic thermal properties, the nanoscale dimensions of molecular junctions necessitate considering quantum effects^14–16 and pose considerable measurement challenges. With the continuous advancement and refinement of single-molecule characterization techniques,^17,18 many thermal phenomena have been detected at the single-molecule level.^7,11 These theories and advanced characterization methods provide new insights into molecular properties^18–21 and lay the groundwork for low-energy consumption and effective thermal management in future molecular integrated circuits.

In this feature article, we reviewed the thermoelectric and thermal properties of molecular junctions from three perspectives: phenomena, characterization methods, and applications. Initially, we identified four primary mechanisms of thermoelectric and thermal transport between source and drain electrodes with a temperature difference: local heating and dissipation, Seebeck effect, Peltier cooling, and thermal transport across molecular junctions, as derived from quantum theory. Next, we outlined the characterization methods for three key properties: local temperature, thermopower, and thermal conductance. Then, we reviewed the applications in three areas: probing the electronic structure, sensing the chemical and physical properties within molecular junctions, and developing thermal devices for efficient heat management. Finally, we concluded by discussing the future prospects of the field, highlighting potential advancements and the ongoing needs for innovation.

2. Mechanisms of thermoelectric and thermal transport in molecular junctions

2.1 Local heating and dissipation

In classical resistors, when current flows through, energy is transferred to the surrounding lattice due to the inelastic relaxation of electrons, resulting in local heating—a phenomenon commonly referred to as Joule heating.⁸ However, as the scale downwards to the nanoscale, such as metal atomic wires and molecular junctions, the extremely small cross-sectional area results in very high current densities, significantly increasing the occurrence of inelastic scattering of electron–electron and electron–phonon, leading to significant local heating.^22–24 Due to the limited electron–phonon coupling within the molecule, the heat transferred to the molecule constitutes a very small portion (α),⁸ with most of it dissipating back to the electrodes through thermal dissipation (Fig. 1(a)). The power dissipated into the ionic degrees of freedom in the molecules can be written as follows:
where α needs to be determined from a microscopic theory, V and R are the bias voltage and junction resistance. At the steady state, the effective temperature of the bridged molecule can be written as follows:⁸
where σ_th is the lattice thermal conductance.

Fig. 1 Four mechanisms of thermoelectric and thermal transport in molecular junctions: (a) Local heating and dissipation, (b) Seebeck coefficient, (c) Peltier cooling and (d) thermal transport across junctions.

Many theories have been utilized to describe local heating and thermal dissipation in molecular junctions, including models based on classical Fourier heat conduction,²⁵ nonequilibrium Green's function formalism,²⁶ hydrodynamic models,²⁷ and the Landauer quantum transport model calculated via transmission probabilities.²⁸ Among these, the Landauer theory is the most commonly used theory for explaining particles’ transport in molecular junctions.¹⁴ When employing this model to analyze local heating and thermal dissipation in molecular junctions, it is necessary to neglect the dissipation effects acting on the molecule (α = 0). The heat dissipated by the left and right electrodes can be described using the Landauer formalism:²⁸

where h is the Planck constant, μ_L/R is the chemical potentials of electrodes, τ_e(E,V) is the energy (E) and bias (V) dependent electron transmission function, and f_L/R is the Fermi–Dirac distribution of electrodes. This model reveals that thermal dissipation in molecular junctions exhibits significant asymmetry across the two electrodes and is strongly dependent on the electronic structure and bias polarity.

2.2 Seebeck effect

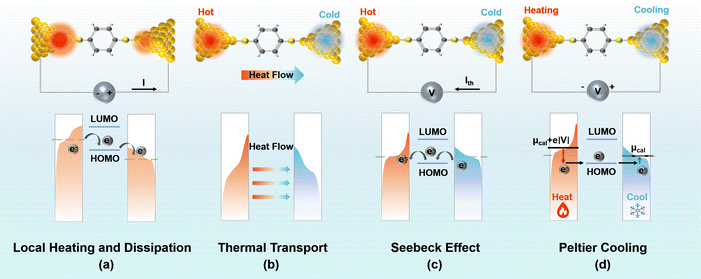
Similar to macroscopic thermoelectric materials, when a temperature difference was applied to a molecular junction, a thermoelectric voltage induced by the Seebeck effect will be generated. This occurs because the temperature influences the Fermi–Dirac distribution of electrons within the electrodes²⁹ (Fig. 1(b)). The presence of a temperature gradient (ΔT) results in a non-equilibrium state of the chemical potentials at the electrode terminals, thereby producing a thermoelectric voltage (ΔV). The Seebeck coefficient can be determined via experimental measurement as follows:

This phenomenon, originally predicted by Landauer theory, identifies the Seebeck coefficient of a molecular junction as an intrinsic property,^9,30 and it can be expressed as follows:

where k_B is the Boltzmann constant and τ(E_F) is the electron transmission at the electrode Fermi level (E_F).

From the formula, it can be seen that the sign of the Seebeck coefficient of a molecular junction depends on the slope of the electron transmission at the Fermi level of the electrodes. This also indicates that the sign of the Seebeck coefficient is related to the nature of the charge carriers, where the positive Seebeck coefficient represents hole-dominated transport and the negative Seebeck coefficient represents electron-dominated transport.³⁰ Therefore, the Seebeck coefficient of a molecular junction can be used to determine whether the electrical transport is dominated by the HOMO (when the Seebeck coefficient is positive) or the LUMO (when the Seebeck coefficient is negative), which was also the initial intention for researchers to study the Seebeck effect in molecular junctions.²⁹

The Seebeck coefficient, also commonly referred to as thermopower, is a crucial parameter for assessing the thermoelectric conversion efficiency of thermoelectric materials. Similar to bulk materials, the efficiency of molecular junctions also increases monotonically as a function of the dimensionless figure of merit, ZT. This relationship can be expressed as follows:

where G_e, S, T, and G_th are the electrical conductance, Seebeck coefficient (thermopower), temperature and thermal conductance. The thermal conductance, governed by thermal transport across junctions, will be discussed in Section 2.4. To date, thermoelectric materials exhibiting high ZT values, nearly reaching 3, have primarily been inorganic.³¹ However, single-molecule devices hold the potential to achieve ZT values as high as 6, thanks to quantum effects.³²

In addition, a power factor (PF) is another parameter to describe thermoelectric performance, which can be expressed as follows:

PF = G_eS²

Unlike ZT, which considers both the electrical and thermal transport properties, the PF focuses solely on electrical performance. The PF is particularly useful for optimizing materials in thermoelectric cooling and wearable electronics, where electrical transport is prioritized. In contrast, ZT is crucial for assessing energy conversion efficiency in power generation, where minimizing thermal conductivity is also essential. Due to technical challenges in measuring thermal conductance at the single-molecule level, the PF is typically used to evaluate the thermoelectric performance of single-molecule junctions.

2.3 Peltier cooling

Utilizing the Peltier effect for targeted cooling in molecular junctions has been recognized by scientists as a potential solution for mitigating localized overheating issues within molecular electronic circuits. Researchers have proposed a variety of theoretical models to facilitate this phenomenon, encompassing strategies such as depletion of high-energy electrons and inelastic electron tunnelling,³³ current-induced vibrational cooling,³⁴ and the enhancement of inelastic absorption processes.³⁵

Similarly, the Peltier cooling process can also be explained by the Landauer theory. According to the principle of thermal dissipation, the heat dissipation at one electrode can be expressed as follows:³⁶

where G and S are the conductance and Seebeck coefficient at a bias of V, and O(V³) represents the higher-order terms. It can be noted that when the bias voltage is sufficiently small and has a sign opposite to the Seebeck coefficient of molecular junctions, thermal dissipation can become negative. This means that the electrode will dissipate out heat, leading to a reduction in its temperature and effectively enabling localized cooling.

2.4 Thermal transport across junctions

When a temperature gradient (ΔT) exists between electrodes, heat is also transferred through the molecule, like the heat conduction at the macroscopic scale, both electrons and phonons contribute to the thermal conductance of the molecular junction. Given that the elastic mean free path of phonons in the electrodes, like that of electrons, far exceeds the size of a single molecule, the transport of phonons between the two electrodes can also be explained using Landauer theory. The heat current carried by electrons and phonons can be expressed respectively as follows:³⁷

where v represents the frequency of phonons, τ_ph(v) is the phonon transmission function, and g_L/R is the Bose–Einstein distributions for the left and right thermal reservoirs, respectively, which varies according to the temperatures of the electrodes. The thermal conductance can be expressed as follows:

Unlike the electric current, which can be measured directly, the measurement of heat flow typically requires the use of calorimetric devices. Based on this theory, the phonon transmission spectrum could be calculated, and the integrated transmission at all energy levels within the Debye energy of the electrodes collectively contributes to the molecular thermal conductance. Computational studies^38–40 have indicated that the thermal conductance of different molecular junctions exhibits varying length dependencies, and the anchoring groups significantly influence thermal conductance as well. However, temperature dependence remains nearly identical across these studies.

For some π-conjugated molecular systems, anti-resonance dips similar to those observed in electron transmission spectra are also seen in the phonon transmission spectra,⁴¹ suggesting the existence of single-molecule phonon interference. Furthermore, by substituting side chains with halogens, the energy levels of these anti-resonances can be lowered to within the Debye energy of gold electrodes,⁴² resulting in lower thermal conductance for molecules with destructive phonon interference. This implies that molecular thermal conductance measurement can be used to verify the presence of phonon interference.

3. Characterization methods for the thermoelectric and thermal properties of molecular junctions

3.1. Characterization methods for local temperature in molecular junctions

In electric transport of molecular junctions, the Joule heating effect leads to an increase in the temperature of the molecule. The inherent heat capacity of the molecule facilitates the transfer of energy from the molecule to the electrodes, thus enabling the thermal dissipation.⁸ Consequently, characterizing the local temperature of the molecular junction is essential for investigating its internal thermal transport mechanisms.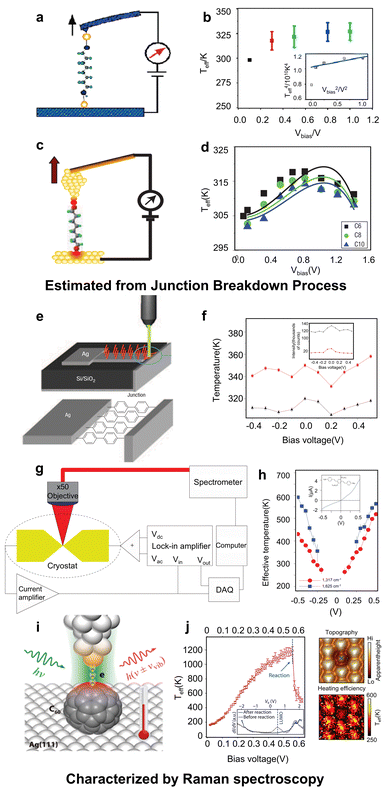

3.1.1 Estimated from the molecular junction breakdown process. Due to size limitations, early characterization of local temperature in molecular junctions was achieved through indirect measurement techniques. Tao's group at the Arizona State University pioneered experimental explorations in this area utilizing their self-developed single-molecule characterization techniques. They indirectly characterized the local temperature of molecular junctions by measuring the junction breakdown process. For instance, in 2006, Huang et al.⁴³ used the atomic force microscopy break-junction (AFM-BJ) technique⁴⁴ (Fig. 2(a)) to measure the force needed to break the octanedithiol junctions at different biases. Since the breaking of molecular junctions is a thermally activated process,⁴⁵ they were able to derive the local effective temperature (Fig. 2(b)) through formula fitting. In 2007, Huang et al.⁴⁶ further employed the scanning tunnelling microscopy break-junction (STM-BJ) technique⁴⁷ (Fig. 2(c)) to measure the stretching distances before the junctions broke under different stretching speeds, again using the principle of thermal activation to determine the local effective temperatures of n-alkanedithiol molecules. This study also found that the local temperatures in the molecular junctions strongly depended on the bias and length (Fig. 2(d)). Later on, the same method was employed by Tsutsui et al.⁴⁸ in the longer lasting mechanically controllable break-junction (MCBJ) technique,⁴⁹ allowing them to measure the threshold bias voltage required for local heating in the molecular junctions.

Fig. 2 Indirect measurement of local temperature in molecular junctions. (a) and (b) Estimation of the local temperature of octanedithiol junctions from the breaking force by AFM-BJ. (c) and (d) Estimation of the local temperature of n-alkanedithiol junctions from the stretching distances before the junctions broke by STM-BJ. (e) and (f) Measurement of the local temperature of biphenyldithiol in ‘on-edge’ junctions by Raman spectroscopy. (g) and (h) Measurement of the local temperature of three-ring oligophenylene vinylene in electromigration-fabricated static junctions by Raman spectroscopy. (i)–(k) Characterization of the local temperature in fullerene junctions by TERS. Reproduced with permissions from ref. 43 (a) and (b), ref. 46 (c) and (d), ref. 50 (e) and (f), ref. 51 (g) and (h) and ref. 52 (i)–(k). Copyrights: (2006) American Chemical Society (a) and (b); (2007, 2008, and 2011) Springer Nature (c), (d), (e), (f) (g), and (h); (2024) The American Association for the Advancement of Science (i) and (k).

3.1.2 Raman spectroscopy. Another indirect method to characterize the local temperature of a molecular junction is the Raman spectroscopy. In Raman spectra, the anti-Stokes/Stokes ratio for each vibrational mode represents the steady-state non-equilibrium population in the presence of inelastic tunnelling current,⁵³ and this ratio can be used to obtain the effective temperature of a specific mode. In 2008, Ioffe et al.⁵⁰ utilized this principle with the ‘on-edge’ molecular junction construction method⁵⁴ (Fig. 2(e)), and also leveraged the surface-enhanced Raman scattering (SERS) phenomenon^55,56 produced by the metal nano-gap, to measure the effective temperature in the Ag–biphenyldithiol–Ag molecular junction (Fig. 2(f)). In 2010, Ward et al.⁵¹ combined this method with electromigration techniques⁵⁷ (Fig. 2(g)) to characterize the local temperature of the single three-ring oligophenylene vinylene molecular junction, discovering that just a few hundred millivolts of bias could cause a temperature increase of about 300 K (Fig. 2(h)).

The aforementioned studies indicated that the local heating effects in molecular junctions pose significant challenges to the stability, particularly when large biases are required to induce the operation of single-molecule switches. In a recent study reported by Meng et al.,⁵² they utilized tip-enhanced Raman spectroscopy (TERS)^56,58 to measure fullerene molecules (Fig. 2(i)) and found that the local effective temperature of the molecule could be heated up to 1150 K only under a bias of 0.4 V (Fig. 2(j)). Higher biases would directly lead to the complete decomposition of the molecule. Furthermore, they found that the conformation of fullerene significantly affects the threshold bias for decomposition. This study further underscores the importance of thermal property investigation in molecular electronics.

3.1.3 Nanoscale thermometers. With the advancement of micro–nano fabrication techniques, it has become possible to directly measure the local temperature of molecular junctions by constructing a nanoscale thermometer nearby. For example, in 2013, Lee et al.⁵⁹ fabricated a chromium–gold thermocouple on a tip electrode (Fig. 3(a)) to directly measure the temperature of the tip electrode by capturing the thermoelectric potential when current is passed through a single-e-molecule junction. Using this method, they measured the thermal dissipation processes in two types of molecular junctions: 1,4-benzenediisonitrile (LUMO dominated transport) and 1,4-benzenediamine (HOMO dominated transport). They found that the heat dissipation from the molecular junction to the electrodes was highly asymmetric, and this asymmetry was strongly dependent on the electronic energy levels and applied bias polarity (Fig. 3(b) and (c)).

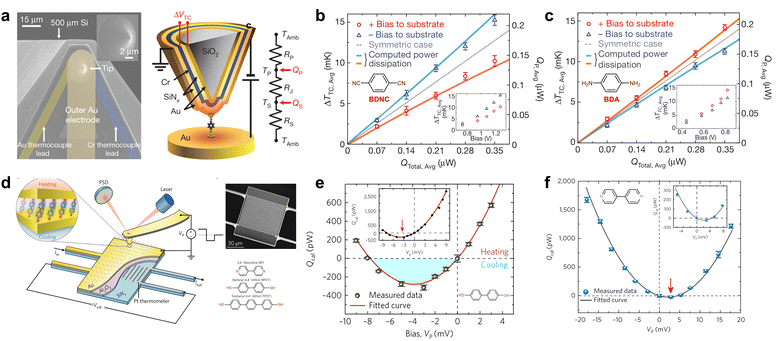Fig. 3 Direct measurements of local temperature in molecular junctions using a nanoscale thermometer. (a) Tip electrode with the chromium–gold thermocouple. (b) Thermal dissipation to electrodes in 1,4-benzenediisonitrile junctions with LUMO dominated transport. (c) Thermal dissipation to electrodes in 1,4-benzenediamine junctions with HOMO dominated transport. (d) Platinum-based picowatt-resolution calorimetric microdevices. (e) Peltier cooling in biphenyl-4,4′-dithiol with HOMO dominated transport. (f) Peltier cooling in 4,4-bipyridine junctions with LUMO dominated transport. Reproduced with permissions from ref. 59 (a)–(c) and ref. 36 (d)–(f). Copyrights: (2013, 2018) Springer Nature (a)–(c) and (d)–(f).

Subsequently, nanoscale calorimetric devices based on the thermosensitive material platinum^36,60–64 have also been employed for measuring the local temperature of molecular junctions. For instance, in 2018, Cui et al.³⁶ developed an experimental platform with platinum-based picowatt-resolution calorimetric microdevices (Fig. 3(d)). This setup facilitated the comprehensive analysis of the electrical, thermoelectric, and energy dissipation properties of molecular junctions. Utilizing this technique, they explored the Peltier effect in gold junctions containing molecules such as biphenyl-4,4′-dithiol and 4,4-bipyridine. Their research illuminated the connection between thermal effects—both heating and cooling—and the characteristics of charge transmission (Fig. 3(e) and (f)).

3.2. Characterization for thermopower in molecular junctions

The ability to convert a temperature difference directly into electrical voltage, and vice versa, hinges significantly on a parameter known as the thermopower. This parameter is primarily determined by the intrinsic Seebeck coefficient, which fundamentally describes how effectively a material can convert thermal energy into electrical energy.³⁰ With the diversification of single-molecule characterization methodologies in recent years,^17,18 the methods for characterizing the thermopower of molecular junctions have also expanded.⁹ This development provides more strategies for the creation of high ZT molecular thermoelectric materials.

3.2.1 STM-BJ capturing. The challenge in measuring single-molecule thermopower mainly lies in capturing single molecules, detecting weak signals on the microvolt scale, and controlling temperature differences accurately. Modifying the STM-BJ technique to measure the thermopower of molecular junctions is the most common method. The different modifications depend on factors such as the control strategy, the signal acquisition approach, the type of current amplifier used, and so on. Broadly, these modifications can be categorized into four distinct types.
Thermovoltage measurement. Measuring the thermovoltage induced by single molecules is the most direct and simplest way to obtain thermopower. This was first reported by Reddy et al.³⁰ in 2007. In their approach, they maintained the substrate temperature above that of the tip. The process involved using the STM-BJ technique to initially capture the molecules, followed by switching from an electrical conductance measurement circuit to a thermovoltage measurement setup, thereby enabling the direct acquisition of the thermopower in a single-molecule junction (Fig. 4(a)). Through this approach, they were able to measure the thermopower of 1,4-benzenedithiol across varying electrode temperature differences, ultimately quantifying the Seebeck coefficient based on the linear relationship between the thermopower and temperature difference (Fig. 4(b)). This method is straightforward and effective and has been adopted by other research groups⁶⁵ for molecular thermoelectric measurements. Nonetheless, a significant limitation of this approach is the challenge in accurately capturing signals at the microvolt level, where noise can easily mask the signal, and thermal radiation complicates the precise control of temperature differentials between the tip and the substrate.

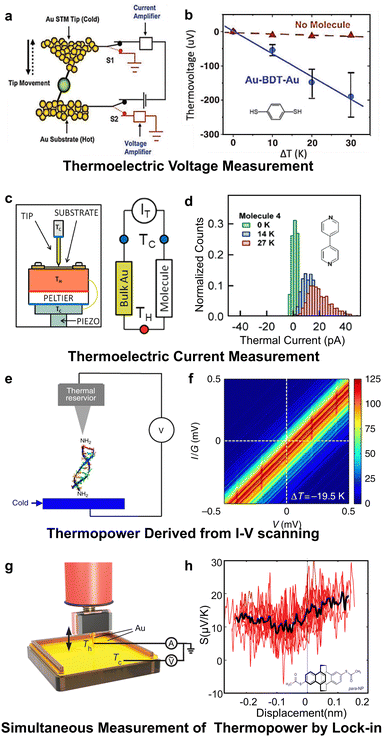Fig. 4 Thermopower measurements by modified STM-BJ techniques. (a) and (b) Thermoelectric voltage measurement of 1,4-benzenedithiol. (c) and (d) Thermoelectric current measurement of 4,4′-bipyridine. (e) and (f) Thermopower derived from I–V scanning for DNA molecules. (g) and (h) Simultaneous thermopower measurement of para-connected naphthalenophane by lock-in. Reproduced with permissions from ref. 30 (a) and (b), ref. 66 (c) and (d), ref. 67 (e) and (f) and ref. 68 (g) and (h). Copyrights: (2007) Science (a) and (b), (2012) American Chemical Society (c) and (d) and (2016, 2024) Springer Nature (e), (f), (g), and (h).

Thermocurrent measurement. An alternative modification technique involves the measurement of thermopower by capturing the associated thermocurrent (Fig. 4(c)), which was first reported by Widawsky et al.⁶⁶ in 2012. This method does not involve switching circuits. Upon trapping single molecules, the same current amplifier that measures the current induced by the bias was also used to measure the current generated by the molecular thermopower. Subsequently, the thermopower is derived from the ratio of thermocurrent to the molecular conductance. Using this method, they measured the Seebeck coefficients of molecules such as 4,4′-bipyridine (Fig. 4(d)). This approach simplified the measurement circuitry design; however, it imposes stringent requirements on the current amplifier, necessitating both a broad dynamic range and a high resolution.
I–V scanning technique. Current–voltage scanning (I–V) is also employed to assess the thermopower of molecular junctions.^67,69 In the presence of a temperature difference across the junction, a current offset induced by the molecular thermopower would occurs at zero bias (Fig. 4(f)). By extracting this current offset, the molecular thermopower can be determined. In 2016, Li et al.⁶⁷ utilized this method to measure the thermopower of DNA molecules (Fig. 4(e)). The advantage of this technique is that it allows for the simultaneous measurement of molecular conductance and thermopower, although it faces the same challenges for amplifiers as the last method described.
Simultaneous measurement through a lock-in technique. In addition to the previously described molecule-hovering techniques, Poel et al.,⁶⁸ in 2024, implemented a novel method that involves applying an alternating current (AC) bias and employing a lock-in amplifier to extract signals at specific frequencies (Fig. 4(g)). This approach facilitates the real-time extraction of thermopower during the molecular junction-breaking process and allows some in situ experiments (Fig. 4(h)). It effectively allows for the simultaneous measurement of conductance and thermopower, even during the extreme short molecule stretching process, thus resolving the problems of short lifetimes of molecular junctions associated with the STM-BJ thermopower measurement.

3.2.2 AFM and STM imaging techniques. Due to enhanced precision and spatial resolution, conductive AFM and STM imaging techniques have also been applied for the measurement of thermopower in molecular junctions. In 2010, Tan et al.⁷⁰ first achieved simultaneous measurements of force, electrical conductance, and thermopower in molecular junctions using conductive AFM (Fig. 5(a)). By maintaining the force between the AFM tip and a triphenylene-assembled molecular layer at approximately 1 nN, they measured the thermopower of the monolayer consisting of about 100 molecules (Fig. 5(b)). Compared to the STM-BJ technique, this approach demonstrates better linearity between thermopower and temperature differences. Thus, this approach was widely used to study the effects of physical and chemical factors such as molecular length,⁷¹ interfacial coupling,⁷¹ and quantum interference⁷² on thermoelectric properties.

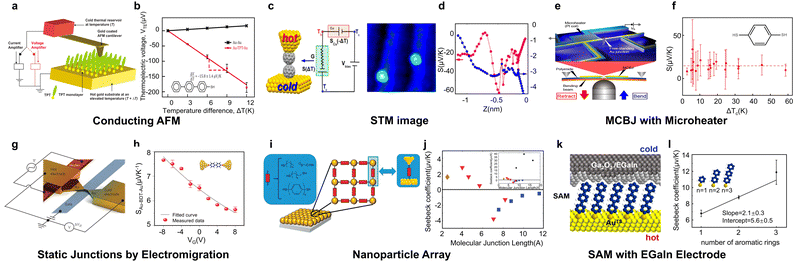Fig. 5 Thermopower measurement by conducting (a) and (b) AFM for terphenyl-4-thiol junctions, (c) and (d) STM-image for fullerene, (e) and (f) MCBJ with a microheater for 1,4-benzenedithiol, (g) and (h) static junctions with electromigration for biphenyl-4,4′-dithiol, (i) and (j) nanoparticle array for thiol-anchored alkyl chains and benzene, and (k) and (l) SAM with an EGaIn electrode for benzene with different lengths. Reproduced with permissions from ref. 70 (a) and (b), ref. 69 (c) and (d), ref. 73 (e) and (f), ref. 74 (g) and (h), ref. 75 (i) and (j) and ref. 76 (k) and (l). Copyrights: (2010) AIP Publishing (a) and (b), (2013 and 2018) American Chemical Society (c), (d), (k), and (l), (2015 and 2014) Springer Nature (e), (f), (g), and (h), and (2015) Royal Society of Chemistry (i) and (j).

The STM imaging technique has been primarily used in the study of the thermopower of fullerene molecules.^69,77 This method was first reported by Evangeli et al.⁶⁹ in 2013. Using this approach, it is able to precisely capture individual fullerene molecules and manipulate them to form dimers (Fig. 5(c)). The Seebeck coefficient of these dimers was found to be approximately double than that of the monomers (Fig. 5(d)), demonstrating that intermolecular interactions can serve as a potential strategy to enhance the thermoelectric performance of molecular junctions. These advancements highlight how conductive AFM and STM imaging techniques have not only refined our ability to measure thermopower in molecular junctions but also provided deeper insights into the influence of molecular structures and interactions on thermoelectric properties.

3.2.3 MCBJ with microheaters. Compared to STM-BJ, the mechanically controllable break junction (MCBJ) technique can maintain molecular junctions with higher stability^49,78 and has also been adapted for the measurement of single-molecule thermopower,^73,79,80 although it does not facilitate the construction of electrode temperature differences as conveniently as the STM-BJ. Therefore, in 2015, Tsutsui, et al.⁷³ employed micro–nano fabrication techniques to construct micrometer-scale platinum heaters near the MCBJ electrodes to establish a temperature gradient across the electrode pairs (Fig. 5(e)). Through this approach, they were also able to measure the Seebeck coefficient of 1,4-benzenedithiol (Fig. 5(f)). This micrometer heating design effectively reduces thermal radiation between electrodes, allowing for more precise control of temperature differences.

3.2.4 Static junctions by micro–nano fabrication. Static single-molecule junctions, with their advantages of more stable configurations and convenience in gate control for in situ property studies, have also been adapted for thermopower measurements. In 2014, Kim et al.⁷⁴ first accomplished the measurement of thermopower in static single-molecule junctions. They constructed gold nanogaps using electromigration techniques and patterned microheaters and gate electrodes near the electrode pairs through micro–nano fabrication techniques, also achieving the first instance of tuning the thermopower of molecular junctions with an electrostatic field (Fig. 5(g)). Through this method, they were able to perform in situ control of the thermopower of biphenyl-4,4′-dithiol (Fig. 5(h)) and fullerene. Furthermore, in 2017, Gehring et al.⁸¹ also achieved the measurement and control of thermopower in static molecular junctions with graphene as electrodes by using electrical burning to create a nano-gap. These studies collectively demonstrate the significant progress in the precision and controllability of thermopower measurements within static single-molecule junctions, underscoring the potential for finely tuned molecular electronics through advanced fabrication and control techniques.

3.2.5 Nanoparticle arrays. Another novel method for constructing molecular junctions—nanoparticle arrays—has also been adapted for measuring the thermopower. In such arrays, all the molecular junctions between nanoparticles are considered identical, and thus their molecular conductance and thermopower are the same (Fig. 5(i)). By maintaining a temperature difference between two probes within the array and synchronously measuring the thermovoltage, the Seebeck coefficient can be obtained. Based on this method, in 2015, Chang et al.⁷⁵ synthesized gold nanoparticles with a diameter of 7 nm and spaced these nanoparticles using thiol-anchored alkyl chains and benzene ring molecules of varying lengths to form arrays, ultimately enabling the measurement of the Seebeck coefficient (Fig. 5(j)). This approach, leveraging nanoparticle arrays for uniform thermopower measurements, exemplifies the innovative use of nanoscale engineering to enhance the reproducibility and scalability of molecular junction-based thermoelectric studies.

3.2.6 SAM with EGaIn electrodes. The characterization of thermopower in large-area self-assembled molecular layers (SAMs) is primarily achieved through devices constructed with eutectic gallium–indium (EGaIn) electrodes.^82,83 These electrodes can exist in a liquid state at room temperature and possess excellent self-healing properties and chemical compatibility with molecules, effectively preventing short out in molecular devices. In 2018, Park et al.⁷⁶ first accomplished the characterization of thermopower in large-area molecular junctions using this method (Fig. 5(k)). They also found that, similar to single-molecule junctions, the Seebeck coefficient of large-area benzene ring molecular junctions exhibited a better linear relationship with molecular lengths (Fig. 5(l)). Later on, in 2019, they experimentally determined the power factor of SAM (conjugated HS(PH)_n, non-conjugated HS(Cy)_k and HSC_m) with varying lengths for the first time.⁸⁴ They found that the power factor of the alkyl SAMs ranged from 2.0 × 10⁻⁸ to 8.0 × 10⁻¹² μW m⁻¹ K⁻² and exhibited strong negative length dependence. In contrast, for conjugated SAMs, the opposing effects of conductivity and thermopower balanced the power factor as the molecular length increased, resulting in a maximum power factor of 3.6 × 10⁻⁸ μW m⁻¹ K⁻².

The trade-off between the thermopower and electrical conductivity varies across different molecular systems,^82–87 posing a significant challenge in thermoelectric material design. Achieving an optimal balance requires tailored strategies to enhance power factor while mitigating the adverse effects of charge transport limitations. At the current stage, compared to single-molecule thermoelectricity, SAM-based thermoelectric devices are more promising for practical applications, such as wearable thermoelectric devices.⁸⁸ Consequently, various strategies have been developed to enhance the Seebeck coefficient of SAM-based thermoelectric devices, including surface flattening of electrodes,⁸⁶ Fermi-level tuning using semimetal electrodes,⁸⁹ and orbital gating with analogous bimetallic electrodes via underpotential deposition (UPD).⁸⁷ Surprisingly, replacing the gold bottom electrode with bismuth (Bi) can enhance the Seebeck coefficient by more than two orders of magnitude.⁸⁹

Compared to single-molecule junctions, large-area junction systems provide a well-organized and uniform platform, making them easier to fabricate and characterize at a larger scale, which is ideal for practical applications and ensemble studies. However, SAMs often lack the precision and tunability at the molecular level that single-molecule systems offer. Single-molecule studies, on the other hand, allow for the investigation of intrinsic molecular properties and behaviors without ensemble averaging, enabling deeper insights into molecular-scale phenomena. Nevertheless, single-molecule systems can be challenging to manipulate and are typically limited by lower stability and reproducibility compared to SAM.

3.3. Characterization for thermal conductance in molecular junctions

As another crucial parameter that directly determines the ZT of thermoelectric materials, thermal conductance also affects the efficiency of heat-to-electricity conversion. Unlike the measurement of the Seebeck coefficient and electrical conductance, thermal conductance cannot be directly measured and typically requires indirect methods through the measurement of other physical properties such as temperature^90–93 or reflectance,⁹⁴ posing a high technical barrier. For individual molecules, their thermal conductance is on the order of pW K⁻¹, and such small magnitudes have limited the progress in this area of research.

3.3.1 SAM thermal conductivity. Compared to single molecules, self-assembled monolayers (SAMs) exhibit greater heat flow due to their larger heat transfer area when subjected to the same temperature difference across electrodes, making their thermal conductance easier to be measured. Thus, early studies on the thermal conductance of molecular junctions began with SAMs. In addition, as two-dimensional materials, the thermal conductance of SAMs depends on the electrode–molecule contacting area, it is more common to use the term ‘thermal conductivity’ rather than ‘thermal conductance’ to describe this property.
3-ω method. The classical 3-ω technique, which usually requires a metal heating wire serving both as a heater and a resistive temperature sensor, was initially used. This method involves applying an alternating current and then detecting a voltage signal at three times the frequency to measure thermal conductivity⁹⁵ (Fig. 6(a)). It was initially applied to measure the thermal conductivity of bulk amorphous solids, crystals, and amorphous thin films with thicknesses of microns thick.⁹⁶ In 2006, Wang et al.⁹⁷ first employed the 3-ω method to study the thermal conductivity of Au-alkanedithiol-GaAs molecular layers prepared by nanotransfer printing (Fig. 6(b)), and they found that the thermal conductivity of these molecular layers did not show significant dependence on the length (Fig. 6(c)).

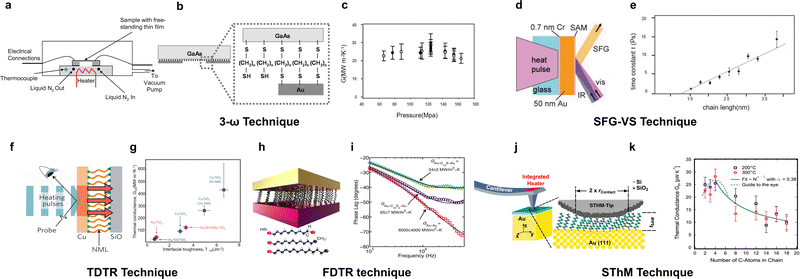Fig. 6 SAM thermal conductivity measured by the (a)–(c) 3-ω technique for alkanedithiol, (d) and (e) sum frequency generation vibrational spectroscopy (SFG-VS) technique for n-alkanethiol, (f) and (g) time-domain thermal reflectance (TDTR) technique for nanomolecular monolayers with different interfacial bondings, (h) and (i) frequency-domain thermal reflectance (FDTR) technique for alkanedithiol with different electrodes, and (j) and (k) scanning thermal microscopy (SThM) technique for alkane thiols with different lengths. Reproduced with permissions from ref. 95 (a), ref. 97 (b) and (c), ref. 98 (d) and (e), ref. 99 (f) and (g), ref. 100 (h) and (i) and ref. 101 (i)–(k). Copyrights: (2008) ASME International (a), (2006) AIP Publishing (b) and (c), (2007) Science (d) and (e), (2013) Springer Nature (f) and (g), (2015) American Chemical Society (h) and (i), and (2014) American Physical Society (j) and (k).

Sum frequency generation vibrational spectroscopy. Using femtosecond pulsed laser heating combined with sum frequency generation spectroscopy for SAM thermal conductivity is also developed.⁹⁸ In this research, a nonlinear coherent vibrational spectroscopy method (Fig. 6(d)) was utilized to observe ultrafast thermal-induced disorder that occurred when heat propagated to the methyl groups at the terminal ends of the chains. It was discovered that the initial surge of thermal energy ballistically propagated down to the chains with a velocity of approximately 1000 meters per second (Fig. 6(e)), and the molecular thermal conductance per chain was estimated to be around 50 picowatts per Kelvin. And they found the flow of heat into the chains was limited by the interfacial conductance.
Pump–probe technique. Molecular thermal conductivity measurements using pump–probe techniques can be classified into two types: time-domain thermal reflectance (TDTR) and frequency-domain thermal reflectance (FDTR). Both TDTR and FDTR work in a similar mechanism: a pump laser pulse rapidly excites electrons within the transducer film over picoseconds, resulting in a temperature increase and subsequent heat transfer into the SAM. For TDTR, after the initial heating by the pump laser pulse, a subsequent probe laser pulse measures the decay of thermoreflectance over time. By this way, Losego et al.¹⁰² and O’Brien et al.⁹⁹ found that the interfacial bond strength significantly effects the thermal conductivity of SAMs, and junctions with thiol (–SH) terminal groups have a higher thermal conductance over those with methyl (–CH₃) groups (Fig. 6(f) and (g)). For FDTR, a series of pulsed or continuous-wave laser pulses are used to determine the phase shift of the thermoreflectance signals by frequency. By this way, Majumdar et al.¹⁰⁰ in 2015 found that vibrational modes of the electrodes play a significant role in SAM's thermal conductivity, even though the thermal carriers of the metal electrodes are electrons (Fig. 6(h) and (i)). Laser spectroscopy methods present a notable drawback in that the theoretical model used to derive thermal conductivity is grounded in classical physics, which inherently neglects any quantum size effects. However, its advantages lie in its high spatial resolution, non-contact measurement capability, and suitability for studying a wide range of materials under various conditions.
Scanning thermal microscopy. A vacuum-operated scanning thermal microscope (SThM) has also been employed to study the thermal conductivity of monolayers. In 2014, Meier et al.¹⁰¹ examined the thermal conductance of Au–alkanedithiol–SiO₂ junctions using a scanning thermal probe. During the interaction with the sample, the heat transfer from the heated tip through the cantilever and into the sample is recorded. By examining the thermal conductance versus displacement curves in both non-contact and contact regimes, as well as the geometry of the tip–sample interaction, the thermal conductivity of the SAMs can be spatially resolved and quantified. Using this method, they found that the thermal conductance of alkanedithiol initially increases with increasing molecular length, subsequently decreases, and ultimately stabilizes once the molecular length attains a certain critical threshold. This report is consistent with previous theoretical predictions on single molecule junctions by Segal et al.³⁸

3.3.2 Atomic and single-molecule thermal conductance. Compared to the measurement of thermal conductivity in SAM molecular layers, measuring the thermal conductance of a single molecule is more challenging. In addition to extracting pico-watt level heat flow signals as previously mentioned, it requires an ultra-high vacuum environment to suppress air-mediated heat transfer that could drown out the signals. Moreover, circuit design must be optimized to minimize noise as much as possible, allowing for a temperature resolution around milli-Kelvin to facilitate the extraction of thermal conductance from single molecules.

With the advancement of high-resolution calorimetry and thermometry techniques, the measurement of thermal conductance at atomic and single-molecule scales has only been achieved in recent years by the Pramod Ready's and Bernd Gotsmann's group. Both groups have achieved this by utilizing electrode chips fitted with platinum resistance thermometers (PRTs), employing micro-electro-mechanical system (MEMS) fabrication techniques. This is further enhanced by the comprehensive data collection capabilities provided by STM-BJ technique. However, there is a difference in their approaches: the Ready group conducted measurements using a tip-based chip, while Gotsmann employed a substrate-based chip.

Tip with integrated PRT. The design of the tip-based chip was reported by Cui et al.⁶⁰ in 2017. It resembles a scanning thermal microscope probe, featuring a T-shaped cantilever beam structure by low-stress silicon nitride that maximizes thermal resolution while ensuring sufficient rigidity to accommodate the normal stretching processes of STM-BJ (Fig. 7(a)). The experiment involves maintaining a temperature difference between the tip and the substrate and performing slow atomic-scale stretching, while continuously measuring the real-time temperature of the PRT using electrical modulation and lock-in techniques. This setup allows for the determination of thermal conductance at different conductance plateaus. The experimental results demonstrate that the thermal conductance of gold atomic wires, like their electrical conductance, exhibits quantized characteristics (Fig. 7(b)), and the classical Wiedemann–Franz law still applies even at the scale of metallic atomic junctions.

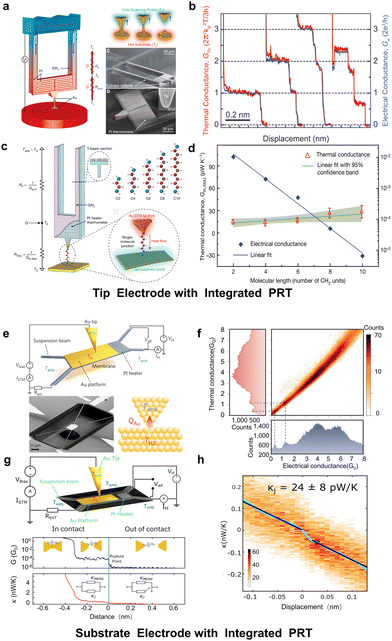Fig. 7 Thermal conductance measurements for atomic and single-molecule junctions by calorimetric electrodes with an integrated platinum resistance thermometer (PRT). (a) and (b) Quantized thermal transport in atomic junctions and (c) and (d) thermal conductance of alkanedithiol with different lengths measured using a tip electrode with the integrated PRT. (e) and (f) Heat transport through atomic contacts and (g) and (h) thermal conductance of dihydrobenzo[b]-dithiophene measured using a substrate electrode with an integrated PRT. Reproduced with permissions from ref. 60 (a) and (b), ref. 62 (c) and (d), ref. 61 (e) and (f) and ref. 63 (i)–(k). Copyrights: (2017) Science (a) and (b) and (2019, 2017, and 2023) Springer Nature (c), (d), (e), (f), (g), and (h).

Utilizing the same device, Cui et al.⁶² in 2019 reported their measurements of thermal conductance in n-alkanedithiol molecules (Fig. 7(c)). The thermal conductance of molecular junctions (10–100 pW K⁻¹) is usually smaller compared to that of metallic atomic junctions (around 500 pW K⁻¹), indicating a greater challenge in measurements. Changes in the thermal conductance pathway before and after the rupture of the molecular junction, involving the entire heat transfer between the heated tip and the environment, causing temperature variations in the PRT. By measuring the signal change in the PRT and using an averaging scheme with multiple traces to improving the signal-to-noise ratio, the thermal conductance of a single molecule can be determined (Fig. 7(d)). Additionally, the authors observed that the thermal conductance of alkane chain molecules does not strongly depend on their length, which contrasts with predictions from theoretical studies.³⁸

Substrates with the integrated PRT. In the same year of 2017, Mosso et al.⁶¹ first reported the use of a substrate chip containing a PRT to measure the thermal conductance of atomic wires. They also used silicon nitride to construct a suspended structure to ensure high calorimetric resolution of the chip (Fig. 7(e)). They observed a clear correlation between the measured thermal conductance and electrical conductance of atomic wires (Fig. 7(f)), although some of the conductance values did not align perfectly with the quantum conductance. They supposed that it is possible due to the presence of absorbed contaminant molecules (such as CO and H₂O) on the gold membranes, which can shift the conductance peak.

Using the substrate-based PRT calorimetric chip, Mosso et al.⁶³ reported in 2019 their measurements of thermal conductance for single molecules as well and found that thermal transport within molecular junctions is determined by the degree of phonon mismatch between the molecules and the metal electrodes. In 2023, employing the same methodology, Gemma et al.⁶⁴ achieved simultaneous characterization of electrical conductance, thermal conductance, and Seebeck coefficient for the dihydrobenzo[b]-dithiophene molecule (Fig. 7(g)) and obtained its thermoelectric figure of merit (1.3 × 10⁻⁵), achieving the first full characterization of the thermoelectric properties of a single molecule (Fig. 7(h)).

Such nanoscale thermal imaging is a powerful technique for studying heat transport at the molecular and atomic scales, offering high spatial resolution and the ability to directly visualize temperature distributions. It is versatile and applicable to a wide range of materials, from nanostructures to molecular systems. However, it also has limitations, including the need for meticulous calibration and potential artifacts introduced by probe–sample interactions in contact-based methods. Non-contact approaches, while less invasive, often suffer from reduced spatial resolution. Additionally, many techniques require a controlled environment, such as a vacuum, to minimize external interference. Despite these challenges, nanoscale thermal imaging provides unique insights into localized thermal behaviors, making it an essential tool for advanced thermal studies.

4. Applications of thermoelectric and thermal properties of molecular junctions

In this section, we will introduce three main applications of the thermoelectric and thermal properties of molecular junctions, including addressing the electronic structure of molecular junctions, sensing chemical and physical properties within molecular junctions and fabricating molecular devices for heat management.

4.1. Addressing the electronic structure of molecular junctions

The primary purpose of studying single-molecule thermoelectricity is to determine the electronic structure of molecular junctions. This stems from the uncertainty in the Fermi level position caused by the unpredictable nature of the interface contact between the molecule and the electrodes, making it unknown which Frontier molecular orbital dominates the electronic transport within the junction. In contrast, the thermoelectric potential generated by a temperature difference is an easily interpretable linear response, which is not highly sensitive to the quality of the interface contact.²⁹ By precisely measuring the Seebeck coefficient of a molecule, one can infer the internal energy level structure, particularly the positions of the highest occupied molecular orbital (HOMO) and the lowest unoccupied molecular orbital (LUMO). For instance, by measuring the thermopower of a DPP molecule, Liu et al.¹⁰³ were able to identify the LUMO as the dominant transport pathway in its molecular junction, thereby discovering the mechanism of its photo-induced tunnelling phenomenon.

4.2. Sensing chemical and physical properties within molecular junctions

4.2.1 Molecular length. The relationship between the electrical transport and length in molecular junctions exhibits regular molecular dependence, characterized by a logarithmic correlation induced by quantum tunnelling mechanisms at short distances and a linear correlation induced by hopping mechanisms at longer distances.¹⁰⁴ In addition, a recent work¹⁰⁵ found that systems with extended conjugation show length-independent conductance due to the coherent delocalization of the wavefunction through the whole molecule.¹⁰⁶ However, although the thermoelectric properties of molecular junctions also show length dependence,³⁰ there is currently no unified model to describe them, due to the completely different behaviors exhibited by different target molecules. The Seebeck coefficient of the alkane chain was found to decrease¹⁰⁷ or remain nearly unchanged⁸⁵ as the molecular length increases, depending on the anchoring groups; however, the Seebeck coefficient of phenyl shows a trend of increase with length.^{30,71,85,107,108} The different phenomenon is due to the electronic conjugated structure of the benzene ring molecules.

In addition, changes in transport mechanisms caused by variations in the molecular length can also influence the control of thermopower. In DNA molecules⁶⁷ and large-area self-assembled molecular layers,^83,109 it was observed that the Seebeck coefficient's dependence on length is weaker under transport dominated by the long-distance hopping mechanism than that by the tunnelling mechanism. In addition, a recent study also found that the length-dependent thermopower of self-assembled monolayers of alkanethiolates may vary with the direction of the temperature gradient.¹¹⁰ The changes described above do not result in a change in the sign of the Seebeck coefficient. However, a study reported by Dell et al.¹¹¹ in 2015 found that variations in the length of thiophene-1,1-dioxide type molecules can even lead to a transition of the Seebeck coefficient from positive to negative (Fig. 8(a) and (b)). This clearly indicates that, with an increase in molecular length, the dominant charge carriers in the transport shift from holes to electrons. The aforementioned studies indicated that the thermopower can serve as an effective means to investigate the properties of molecular junctions related to length.

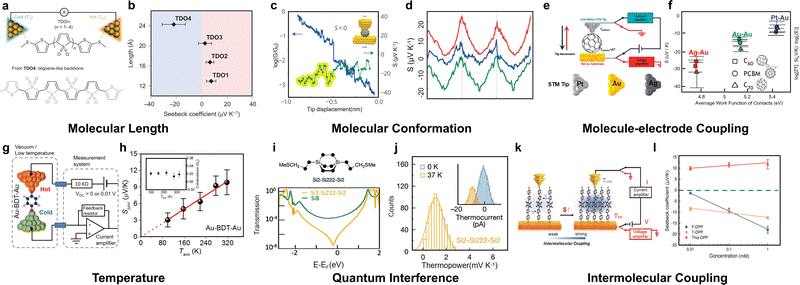Fig. 8 Measured thermopower as a function of the (a) and (b) molecular length for Au-oligothiophene-1,1-dioxide (TDO)n–Au junctions, (b) and (c) molecular conformation for endohedral fullerene Sc₃N@C80, (e) and (f) molecule–electrode coupling for C60 with different metal leads, (g) and (h) temperature for benzene-1,4-dithiol, (i) and (j) quantum interference for silicon-based molecules and (k) and (l) intermolecular coupling for diketopyrrolopyrrole junctions. Reproduced with permissions from ref. 111 (a) and (b), ref. 77 (c) and (d), ref. 112 (e) and (f), ref. 113 (g) and (h), ref. 114 (i) and (j) and ref. 115 (k) and (l). Copyrights: (2015, 2016, and 2018) Springer Nature (a), (b), (c), (d), (i), and (j), (2011) American Chemical Society (e) and (f), (2016) AIP Publishing (g) and (h), and (2023) SciEngine (k) and (l).

4.2.2 Molecular conformation. Changes in the molecular configuration, which lead to alterations in the electronic structure, significantly affect the thermopower as well. The most extensively studied molecules in this regard are fullerenes and their derivatives^77,116,117 due to their easily manipulated cage-like structures by mechanical forces during molecular junction breaking processes and can induce configurational changes. For example, in 2016, Rincón-García et al.⁷⁷ reported that applying mechanical pressure to the Sc₃N@C₈₀ fullerene derivative with a tip could freely switch its Seebeck coefficient between positive and negative (Fig. 8(c) and (d)). This bi-thermoelectric property is due to the proximity of the fullerene molecule's resonance peaks to the electrode's Fermi level, which can be easily shifted by external pressure.

In addition to fullerenes, the thermoelectric properties of molecules such as benzene rings,⁷³ helicenes,¹¹⁸ and magnetic molecules¹¹⁹ have also been found to exhibit significant dependence on their conformation induced by mechanical forces. Moreover, modifications of side-chain groups around backbones such as 2,7-dipyridylfluorene,¹²⁰ oligo(phenylene-ethynylene),⁶⁵ and anthracene¹²¹ can also lead to changes in the overall conformation, thereby affecting molecular thermoelectric properties. These studies demonstrate the great potential of thermopower in sensing molecular mechanical forces and configuration-related properties.

These findings highlight the critical role of the molecular configuration in determining thermoelectric properties, showcasing the interplay between mechanical forces, electronic structure, and thermopower. By leveraging this sensitivity to the conformation, researchers can not only gain deeper insights into molecular-scale heat and charge transport but also design innovative molecular devices for applications such as nanoscale sensors, energy conversion, and force detection.

4.2.3 Molecule–electrode coupling. Another application of molecular thermopower is to explore the coupling strength at the molecule–electrode interface, which is a key factor affecting the electrical transport properties of molecular junctions.¹²² The interface coupling is mainly influenced by two factors: the anchoring groups of the molecular junction and the choice of an electrode material. For conjugated molecules anchored to gold electrodes, the most commonly used anchoring groups such as thiol (–SH),^{30,71,107,123} amino (–NH₂),^66,107 and thioacetate (–SAc)^124,125 show positive Seebeck coefficients, while isocynide (–CN),^71,123 pyridine (–Py),^66,124 and methylthio (–SMe)^65,124 exhibit negative Seebeck coefficients. The choice of different electrode materials directly affects the energy level alignment to the molecules, leading to different thermoelectric transport.^112,126 These have been experimentally explored by many researchers. For example, in 2011, Yee et al.¹¹² measured the thermopower of fullerene molecules using three different electrode materials: gold, silver, and platinum. They found that although fullerenes show high variability in electrical conductance due to different bonding geometries with the electrodes (Fig. 8(e) and (f)), the thermopower exhibited predictable trends based on the alignment of the LUMO with the work function of the electrodes.

4.2.4 Nanoscale calorimetry. As the smallest known operable devices and thermoelectric conversion units, single-molecule junctions also have significant potential in the field of nanoscale calorimetry. For example, under known temperature conditions, the local heat flow can be determined by measuring the Seebeck coefficient of molecules.^36,59 Additionally, the Seebeck coefficient of molecular junctions is theoretically highly temperature-dependent,⁹ which was confirmed experimentally by Kim et al.¹¹³ in 2016. They found a strong linear correlation between the Seebeck coefficients of benzene-1,4-dithiol molecules in a vacuum and low-temperature environments (Fig. 8(g) and (h)), providing a potential approach for nanoscale calorimetry under extreme conditions in the future.

4.2.5 Quantum interference. Quantum interference (QI) has long been considered an effective strategy to enhance the thermoelectric performance of single molecules because destructive quantum interference (DQI) can create a sharp anti-resonance dip near the Fermi level of the electrodes, directly enhancing the Seebeck coefficient. Researchers have confirmed this by experimentally measuring the thermopower of molecular systems with DQI effects, including oligophenylene ethynylenes,⁷² anthracene,¹²⁷ thiophene,¹²⁸ radicals¹²⁹ and so on. On the other hand, thermoelectric properties can also be used as a means to corroborate the presence of QI effects. For example, in 2018, Garner et al.¹¹⁴ utilized the measurement of the Seebeck coefficient to validate the presence of DQI between Sigma orbitals in silicon-based molecules. Such DQI results in a substantial enhancement of the single-molecule Seebeck coefficient, reaching values as high as 1 mV K⁻¹ (Fig. 8(i) and (j)), with a power factor of approximately 2.4 × 10⁻⁴k_B² h⁻¹. However, although DQI can significantly enhance the Seebeck coefficient, its suppression of conductance may counteract this improvement, preventing the power factor from reaching a high value.

4.2.6 Intermolecular interactions. Molecular electronics, with its nanoscale operational size, has been proven to be an effective means for sensing weak interaction forces,¹³⁰ especially π–π interactions between molecules. Intermolecular forces have also been shown to regulate the thermoelectric properties of molecules.⁶⁹ For example, in 2023, Fang et al.¹¹⁵ controlled the packing density between diketopyrrolopyrrole molecules by changing the concentration of solutions during molecular assembly to study the impact of intermolecular interactions on thermoelectric properties. They found that intermolecular interactions could enhance the thermopower by nearly an order of magnitude (Fig. 8(k) and (l)). This research demonstrates that, in addition to sensing intermolecular interactions through electrical conductance measurements, thermopower measurement is also an effective alternative.

4.3. Fabricating molecular devices for heat management

Another important application of thermal and thermoelectric properties in molecular junctions is to fabricate devices for nanoscale thermal management. Due to the high technical barriers associated with thermal transport characterization, there are not many reported research results so far. However, existing studies can generally be divided into two categories: one involves constructing three-terminal thermoelectric devices for in situ control of thermoelectric conversion, and the other involves building thermal devices to manage the direction of local heat flow. The former has been achieved at the single-molecule level, while the latter currently remains at the level of two-dimensional molecular layers.

4.3.1 Thermoelectric transistors. There are currently two construction methods for molecular thermoelectric transistors, both of which involve static junctions. One method uses the electromigration technique⁵⁷ to create gold electrode devices, while the other employs electric burning¹³¹ to create graphene devices.^132,133 These are the two mainstream methods currently used to construct single-molecule transistors.

Molecular thermoelectric transistors based on gold electrodes have been more extensively studied.⁷⁴ For example, in 2021, Gehring et al.¹³⁴ constructed a thermoelectric transistor using a single metal-coordination compound molecule. They obtained thermoelectric Coulomb blockade diagrams similar to electrical conductance Coulomb blockade diagrams by controlling the gate voltage and bias voltage and observed evidence of molecular excited states through thermoelectric properties (Fig. 9(a) and (b)). And they found that these features could only be reproduced by considering both vibrational coupling and electronic degeneracies in a rate equation model, thus providing direct insights into the interactions between electronic and vibrational degrees of freedom as well as the role of spin entropy in single molecules. Moreover, through this type of thermoelectric transistor, the thermopower and power factor of a single molecule could be tuned up to 414 μV K⁻¹ and 3.6 × 10⁻⁴ k_B² h⁻¹, respectively, resulting in a theoretical ZT value close to 0.7. Although the enhancement of the Seebeck coefficient with this tuning method does not reach the level achieved via DQI, it simultaneously enhances both conductance and thermopower, resulting in the highest power factor for single-molecule junctions reported to date.

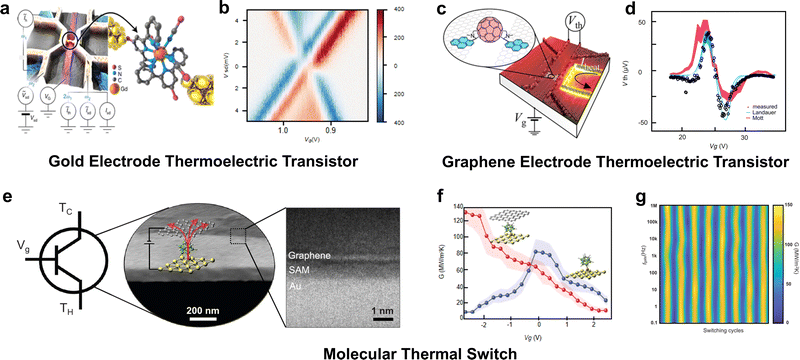Fig. 9 (a) and (b) Gold electrode based thermoelectric transistors constructed from metal-coordination molecules. (c) and (d) Graphene electrode based thermoelectric transistors constructed from fullerene derivatives. (e)–(g) Electric field modulated thermal switch constructed from the monolayer of carborane-thiol cage molecules. Reproduced with permissions from ref. 134 (a) and (b), ref. 81 (c) and (d) and ref. 135 (e)–(g). Copyrights: (2017) American Chemical Society (a) and (b), (2021) Springer Nature (c) and (d), and (2023) Science (e)–(g).

Graphene electrodes, compared to gold electrodes, exhibit more stable properties and higher gate control efficiency.¹⁸ The first graphene-based thermoelectric transistor was reported by Gehring et al.⁸¹ as well in 2017. They constructed a single-molecule thermoelectric transistor by modifying fullerene molecules to facilitate Pi–Pi interactions with graphene electrodes. They found that the power factor of the graphene–fullerene junction could be adjusted to several orders of magnitude close to the theoretical limit of an isolated Breit–Wigner resonance (Fig. 9(c) and (d)). Additionally, the experimental results showed that the power factor of an isolated level is determined solely by tunnel coupling to the leads and temperature. These findings pave new pathways for exploring thermoelectricity and charge transport in individual molecules, highlighting the importance of level alignment and coupling with the electrodes for optimal energy conversion in organic thermoelectric materials. This further underscores that constructing thermoelectric transistors is an effective means to harness and utilize thermal energy in future molecular integrated circuits.

4.3.2 Thermal switch. Compared to thermoelectric conversion, developing thermal devices such as thermal diodes,¹³⁶ thermal rectifiers,¹³⁷ thermal transistors,¹³⁸ and thermal memory¹³⁹ for logic computation and heat management based on heat currents represents a cutting-edge method to repurpose heat energy. However, controlling and measuring heat flow in thermal circuits presents significantly greater challenges than managing electrical currents in electronic circuits. Consequently, devices that leverage thermal effects are predominantly theoretical, with limited experimental achievements documented.

The first thermal devices constructed using molecular junctions, specifically a thermal switch, were reported by Li et al.¹³⁵ in 2023. They developed a method to modulate thermal transport in a monolayer of carborane-thiol cage molecules using an electric field. Researchers demonstrated that this modulation, both continuous and reversible, depends on precisely controlled chemical bonding and charge distributions at the molecular interface. The thermal switch they constructed is capable of achieving ultrahigh switching speeds over 1 megahertz, with thermal conductance on/off ratios exceeding 1300%, and durability for more than 1 million switching cycles (Fig. 9(e)–(g)). This work opens new avenues in molecular engineering for the development of thermal management systems and the design of thermal circuits, particularly within the context of molecular integrated circuits.

5. Conclusions and outlook

Over the past two decades, research studies on the thermal and thermoelectric properties of molecular junctions have achieved significant breakthroughs. These advancements range from validating theoretical mechanisms to enhancing characterization methodologies, and extending to practical applications, all of which have played a pivotal role in advancing molecular electronics. This progress not only bridges the gap between theory and practical implementation but also highlights the transformative potential of molecular systems in energy management and conversion technologies. However, due to the technical barriers of characterization methods, many fields have not yet achieved experimental breakthroughs. From the perspective of molecular electronics development, we have identified five main challenges for the future advancement of research in molecular thermal and thermoelectric properties.

The first challenge is to develop molecular thermoelectric materials that exhibit high ZT values. This involves synthesizing materials with favorable electronic and thermal properties that can maximize the Seebeck coefficient while minimizing thermal conductivity, through the improvement of DQI,^72,114,129 thermoelectric gating,^74,81,134 and other recently reported strategies.⁷ The second challenge is to achieve in situ tuning of thermal transport in molecular junctions, which is significant for dynamic heat management for future molecular integration circuits. This typically requires the fabrication of three-terminal devices with electric¹³⁵ or thermal gating,¹⁴⁰ involving significant technical challenges. The third challenge is to develop scalable fabrication methods while ensuring device stability and reproducibility, addressing issues like variability and integration with existing techniques. This necessitates the development of robust molecule–electrode contacts that can maintain structural integrity and functional integrity even under harsh environmental conditions.^12,141,142 The fourth challenge is to construct multifunctional molecular thermal devices^136–139 that can manage heat, leading to innovative applications in nanoscale cooling, heating, and energy management systems. The fifth challenge involves developing time-resolved spectroscopic techniques to capture phonon dynamics¹⁴³ within molecular junctions, which would enhance our understanding of thermal transport mechanisms and aid in creating more efficient thermal management strategies.

These challenges underscore the convergence of materials science, chemistry, and physics in pushing the boundaries of molecular thermoelectric techniques and highlighting the potential for significant advancements in energy efficiency and device miniaturization.

Author contributions

C. F. wrote the manuscript; Y. L., S. W., M. L. and C. Y. prepared the figures; J. L. and W. H. helped to revise and polish the manuscript. All authors gave approval to the final version of the manuscript.

Data availability

No primary research results, software or code have been included and no new data were generated or analyzed as part of this review.

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This work was supported by the National Key R&D Program of China (2024YFA1208103), the National Natural Science Foundation of China (no. 22173075, 21933012, 22325303, 22250003, and 22303071), the Fujian Provincial Department of Science and Technology (2023H6002), and the Fundamental Research Funds for the Central Universities (no. 20720220020 and 20720200068).

Notes and references

1. Y. Xu, X. Liu, X. Cao, C. Huang, E. Liu, S. Qian, X. Liu, Y. Wu, F. Dong, C.-W. Qiu, J. Qiu, K. Hua, W. Su, J. Wu, H. Xu, Y. Han, C. Fu, Z. Yin, M. Liu, R. Roepman, S. Dietmann, M. Virta, F. Kengara, Z. Zhang, L. Zhang, T. Zhao, J. Dai, J. Yang, L. Lan, M. Luo, Z. Liu, T. An, B. Zhang, X. He, S. Cong, X. Liu, W. Zhang, J. P. Lewis, J. M. Tiedje, Q. Wang, Z. An, F. Wang, L. Zhang, T. Huang, C. Lu, Z. Cai, F. Wang and J. Zhang, Innovation, 2021, 2, 100179.
2. N. Wei, C. Li, X. Peng, F. Zeng and X. Lu, J. Petrol. Sci. Eng., 2019, 181, 106187.
3. A. Aviram and M. A. Ratner, Chem. Phys. Lett., 1974, 29, 277–283.
4. M. L. Perrin, E. Burzurí and H. S. J. van der Zant, Chem. Soc. Rev., 2015, 44, 902–919.
5. D. Xiang, X. Wang, C. Jia, T. Lee and X. Guo, Chem. Rev., 2016, 116, 4318–4440.
6. N. Xin, J. Guan, C. Zhou, X. Chen, C. Gu, Y. Li, M. A. Ratner, A. Nitzan, J. F. Stoddart and X. Guo, Nat. Rev. Phys., 2019, 1, 211–230.
7. H. Zhang, Y. Zhu, P. Duan, M. Shiri, S. C. Yelishala, S. Shen, Z. Song, C. Jia, X. Guo, L. Cui and K. Wang, Appl. Phys. Rev., 2024, 11, 041312.
8. Y. Dubi and M. Di Ventra, Rev. Mod. Phys., 2011, 83, 131–155.
9. L. Rincón-García, C. Evangeli, G. Rubio-Bollinger and N. Agraït, Chem. Soc. Rev., 2016, 45, 4285–4306.
10. S. Park, H. Kang and H. J. Yoon, J. Mater. Chem. A, 2019, 7, 14419–14446.
11. K. Wang, E. Meyhofer and P. Reddy, Adv. Funct. Mater., 2020, 30, 29.
12. A. Gemma and B. Gotsmann, Nat. Nanotechnol., 2021, 16, 1299–1301.
13. Y. Tanaka, Chem. – Eur. J., 2023, 29, e202300472.
14. C. J. Lambert, Chem. Soc. Rev., 2015, 44, 875–888.
15. J. Liu, X. Huang, F. Wang and W. Hong, Acc. Chem. Res., 2019, 52, 151–160.
16. P. Gehring, J. M. Thijssen and H. S. J. van der Zant, Nat. Rev. Phys., 2019, 1, 381–396.
17. Y. Zhao, W. Liu, J. Zhao, Y. Wang, J. Zheng, J. Liu, W. Hong and Z.-Q. Tian, Int. J. Extreme Manuf., 2022, 4, 022003.
18. C. Yan, C. Fang, J. Gan, J. Wang, X. Zhao, X. Wang, J. Li, Y. Zhang, H. Liu, X. Li, J. Bai, J. Liu and W. Hong, ACS Nano, 2024, 18, 28531–28556.
19. R. J. Nichols and S. J. Higgins, Acc. Chem. Res., 2016, 49, 2640–2648.
20. T. A. Su, M. Neupane, M. L. Steigerwald, L. Venkataraman and C. Nuckolls, Nat. Rev. Mater., 2016, 1, 16002.
21. H. Chen, C. Jia, X. Zhu, C. Yang, X. Guo and J. F. Stoddart, Nat. Rev. Mater., 2023, 8, 165–185.
22. T. N. Todorov, Philos. Mag. B, 1998, 77, 965–973.
23. Y.-C. Chen, M. Zwolak and M. Di Ventra, Nano Lett., 2003, 3, 1691–1694.
24. Y.-C. Chen, M. Zwolak and M. Di Ventra, Nano Lett., 2005, 5, 621–624.
25. D. Segal and A. Nitzan, J. Chem. Phys., 2002, 117, 3915–3927.
26. M. Galperin, A. Nitzan and M. A. Ratner, Phys. Rev. B: Condens. Matter Mater. Phys., 2007, 75, 155312.
27. R. D’Agosta, N. Sai and M. Di Ventra, Nano Lett., 2006, 6, 2935–2938.
28. L. A. Zotti, M. Bürkle, F. Pauly, W. Lee, K. Kim, W. Jeong, Y. Asai, P. Reddy and J. C. Cuevas, New J. Phys., 2014, 16, 015004.
29. M. Paulsson and S. Datta, Phys. Rev. B: Condens. Matter Mater. Phys., 2003, 67, 241403.
30. P. Reddy, S. Y. Jang, R. A. Segalman and A. Majumdar, Science, 2007, 315, 1568–1571.
31. J. Wei, L. Yang, Z. Ma, P. Song, M. Zhang, J. Ma, F. Yang and X. Wang, J. Mater. Sci., 2020, 55, 12642–12704.
32. X.-H. Cao, W.-X. Zhou, C.-Y. Chen, L.-M. Tang, M. Long and K.-Q. Chen, Sci. Rep., 2017, 7, 10842.
33. M. Galperin, K. Saito, A. V. Balatsky and A. Nitzan, Phys. Rev. B: Condens. Matter Mater. Phys., 2009, 80, 115427.
34. L. Simine and D. Segal, Phys. Chem. Chem. Phys., 2012, 14, 13820–13834.
35. J. Lykkebo, G. Romano, A. Gagliardi, A. Pecchia and G. C. Solomon, J. Chem. Phys., 2016, 144, 114310.
36. L. J. Cui, R. J. Miao, K. Wang, D. Thompson, L. A. Zotti, J. C. Cuevas, E. Meyhofer and P. Reddy, Nat. Nanotechnol., 2018, 13, 122–127.
37. K. Esfarjani, M. Zebarjadi and Y. Kawazoe, Phys. Rev. B: Condens. Matter Mater. Phys., 2006, 73, 085406.
38. D. Segal, A. Nitzan and P. Hänggi, J. Chem. Phys., 2003, 119, 6840–6855.
39. H. Sadeghi, S. Sangtarash and C. J. Lambert, Nano Lett., 2015, 15, 7467–7472.
40. J. C. Klöckner, M. Bürkle, J. C. Cuevas and F. Pauly, Phys. Rev. B, 2016, 94, 205425.
41. T. Markussen, J. Chem. Phys., 2013, 139, 244101.
42. J. C. Klöckner, J. C. Cuevas and F. Pauly, Phys. Rev. B, 2017, 96, 245419.
43. Z. Huang, B. Xu, Y. Chen, M. Di Ventra and N. Tao, Nano Lett., 2006, 6, 1240–1244.
44. B. Xu, X. Xiao and N. J. Tao, J. Am. Chem. Soc., 2003, 125, 16164–16165.
45. E. Evans, Annu. Rev. Biophys., 2001, 30, 105–128.
46. Z. Huang, F. Chen, R. D’Agosta, P. A. Bennett, M. Di Ventra and N. Tao, Nat. Nanotechnol., 2007, 2, 698–703.
47. B. Q. Xu and N. J. J. Tao, Science, 2003, 301, 1221–1223.
48. M. Tsutsui, M. Taniguchi and T. Kawai, Nano Lett., 2008, 8, 3293–3297.
49. M. A. Reed, C. Zhou, C. J. Muller, T. P. Burgin and J. M. Tour, Science, 1997, 278, 252–254.
50. Z. Ioffe, T. Shamai, A. Ophir, G. Noy, I. Yutsis, K. Kfir, O. Cheshnovsky and Y. Selzer, Nat. Nanotechnol., 2008, 3, 727–732.
51. D. R. Ward, D. A. Corley, J. M. Tour and D. Natelson, Nat. Nanotechnol., 2011, 6, 33–38.
52. Q. Meng, J. Zhang, Y. Zhang, W. Chu, W. Mao, Y. Zhang, J. Yang, Y. Luo, Z. Dong and J. G. Hou, Sci. Adv., 2024, 10, eadl1015.
53. M. Oron-Carl and R. Krupke, Phys. Rev. Lett., 2008, 100, 127401.
54. T. Shamai, A. Ophir and Y. Selzer, Appl. Phys. Lett., 2007, 91, 102108.
55. M. Moskovits, J. Raman Spectrosc., 2005, 36, 485–496.
56. S. Hu, B.-J. Liu, J.-M. Feng, C. Zong, K.-Q. Lin, X. Wang, D.-Y. Wu and B. Ren, J. Am. Chem. Soc., 2018, 140, 13680–13686.
57. H. Park, A. K. L. Lim, A. P. Alivisatos, J. Park and P. L. McEuen, Appl. Phys. Lett., 1999, 75, 301–303.
58. R. Zhang, Y. Zhang, Z. C. Dong, S. Jiang, C. Zhang, L. G. Chen, L. Zhang, Y. Liao, J. Aizpurua, Y. Luo, J. L. Yang and J. G. Hou, Nature, 2013, 498, 82–86.
59. W. Lee, K. Kim, W. Jeong, L. A. Zotti, F. Pauly, J. C. Cuevas and P. Reddy, Nature, 2013, 498, 209–212.
60. L. J. Cui, W. Jeong, S. Hur, M. Matt, J. C. Klockner, F. Pauly, P. Nielaba, J. C. Cuevas, E. Meyhofer and P. Reddy, Science, 2017, 355, 1192–1195.
61. N. Mosso, U. Drechsler, F. Menges, P. Nirmalraj, S. Karg, H. Riel and B. Gotsmann, Nat. Nanotechnol., 2017, 12, 430–433.
62. L. Cui, S. Hur, Z. A. Akbar, J. C. Klöckner, W. Jeong, F. Pauly, S.-Y. Jang, P. Reddy and E. Meyhofer, Nature, 2019, 572, 628–633.
63. N. Mosso, H. Sadeghi, A. Gemma, S. Sangtarash, U. Drechsler, C. Lambert and B. Gotsmann, Nano Lett., 2019, 19, 7614–7622.
64. A. Gemma, F. Tabatabaei, U. Drechsler, A. Zulji, H. Dekkiche, N. Mosso, T. Niehaus, M. R. Bryce, S. Merabia and B. Gotsmann, Nat. Commun., 2023, 14, 3868.
65. H. Chen, S. Sangtarash, G. Li, M. Gantenbein, W. Cao, A. Alqorashi, J. Liu, C. Zhang, Y. Zhang, L. Chen, Y. Chen, G. Olsen, H. Sadeghi, M. R. Bryce, C. J. Lambert and W. Hong, Nanoscale, 2020, 12, 15150–15156.
66. J. R. Widawsky, P. Darancet, J. B. Neaton and L. Venkataraman, Nano Lett., 2012, 12, 354–358.
67. Y. Li, L. Xiang, J. L. Palma, Y. Asai and N. Tao, Nat. Commun., 2016, 7, 11294.
68. S. van der Poel, J. Hurtado-Gallego, M. Blaschke, R. López-Nebreda, A. Gallego, M. Mayor, F. Pauly, H. S. J. van der Zant and N. Agraït, Nat. Commun., 2024, 15, 10097.
69. C. Evangeli, K. Gillemot, E. Leary, M. T. González, G. Rubio-Bollinger, C. J. Lambert and N. Agraït, Nano Lett., 2013, 13, 2141–2145.
70. A. Tan, S. Sadat and P. Reddy, Appl. Phys. Lett., 2010, 96, 013110.
71. A. Tan, J. Balachandran, S. Sadat, V. Gavini, B. D. Dunietz, S.-Y. Jang and P. Reddy, J. Am. Chem. Soc., 2011, 133, 8838–8841.
72. R. Miao, H. Xu, M. Skripnik, L. Cui, K. Wang, K. G. L. Pedersen, M. Leijnse, F. Pauly, K. Wärnmark, E. Meyhofer, P. Reddy and H. Linke, Nano Lett., 2018, 18, 5666–5672.
73. M. Tsutsui, T. Morikawa, Y. He, A. Arima and M. Taniguchi, Sci. Rep., 2015, 5, 11519.
74. Y. Kim, W. Jeong, K. Kim, W. Lee and P. Reddy, Nat. Nanotechnol., 2014, 9, 881–885.
75. W. B. Chang, B. Russ, V. Ho, J. J. Urban and R. A. Segalman, Phys. Chem. Chem. Phys., 2015, 17, 6207–6211.
76. S. Park and H. J. Yoon, Nano Lett., 2018, 18, 7715–7718.
77. L. Rincon-Garcia, A. K. Ismael, C. Evangeli, I. Grace, G. Rubio-Bollinger, K. Porfyrakis, N. Agrait and C. J. Lambert, Nat. Mater., 2016, 15, 289–293.
78. C. Tang, T. Stuyver, T. Lu, J. Liu, Y. Ye, T. Gao, L. Lin, J. Zheng, W. Liu, J. Shi, S. Shaik, H. Xia and W. Hong, Nat. Commun., 2023, 14, 3657.
79. T. Morikawa, A. Arima, M. Tsutsui and M. Taniguchi, Nanoscale, 2014, 6, 8235–8241.
80. S. Kaneko, Y. Nakamura, R. Matsushita, S. Marqués-González and M. Kiguchi, Appl. Phys. Express, 2015, 8, 065201.
81. P. Gehring, A. Harzheim, J. Spièce, Y. Sheng, G. Rogers, C. Evangeli, A. Mishra, B. J. Robinson, K. Porfyrakis, J. H. Warner, O. V. Kolosov, G. A. D. Briggs and J. A. Mol, Nano Lett., 2017, 17, 7055–7061.
82. J. Jang, P. He and H. J. Yoon, Acc. Chem. Res., 2023, 56, 1613–1622.
83. J. Jang, J. W. Jo, T. Ohto and H. J. Yoon, J. Am. Chem. Soc., 2024, 146, 4922–4929.
84. S. Park, S. Kang and H. J. Yoon, ACS Cent. Sci., 2019, 5, 1975–1982.
85. J. R. Widawsky, W. Chen, H. Vázquez, T. Kim, R. Breslow, M. S. Hybertsen and L. Venkataraman, Nano Lett., 2013, 13, 2889–2894.
86. W. Peng, Z. Cao, N. Chen, Y. Xie and Y. Li, J. Mater. Chem. A, 2022, 10, 23304–23313.
87. P. He, A. H. S. Daaoub, S. Sangtarash, H. Sadeghi and H. J. Yoon, Nano Lett., 2024, 24, 1988–1995.
88. X. Hao, J. Wang and H. Wang, Chem. Soc. Rev., 2025, 54, 1957–1985.
89. T. Frank, S. Shmueli, M. Cohen Jungerman, P. Shekhter and Y. Selzer, Nano Lett., 2023, 23, 10473–10479.
90. S. Sadat, Y. J. Chua, W. Lee, Y. Ganjeh, K. Kurabayashi, E. Meyhofer and P. Reddy, Appl. Phys. Lett., 2011, 99, 043106.
91. S. Sadat, E. Meyhofer and P. Reddy, Rev. Sci. Instrum., 2012, 83, 084902.
92. S. Sadat, E. Meyhofer and P. Reddy, Appl. Phys. Lett., 2013, 102, 163110.
93. S. F. Karg, V. Troncale, U. Drechsler, P. Mensch, P. Das Kanungo, H. Schmid, V. Schmidt, L. Gignac, H. Riel and B. Gotsmann, Nanotechnology, 2014, 25, 305702.
94. D. G. Cahill, Rev. Sci. Instrum., 2004, 75, 5119–5122.
95. A. Jain and K. E. Goodson, J. Heat Transfer, 2008, 130, 102402.
96. D. G. Cahill, Rev. Sci. Instrum., 1990, 61, 802–808.
97. R. Y. Wang, R. A. Segalman and A. Majumdar, Appl. Phys. Lett., 2006, 89, 173113.
98. Z. Wang, J. A. Carter, A. Lagutchev, Y. K. Koh, N.-H. Seong, D. G. Cahill and D. D. Dlott, Science, 2007, 317, 787–790.
99. P. J. O’Brien, S. Shenogin, J. Liu, P. K. Chow, D. Laurencin, P. H. Mutin, M. Yamaguchi, P. Keblinski and G. Ramanath, Nat. Mater., 2013, 12, 118–122.
100. S. Majumdar, J. A. Sierra-Suarez, S. N. Schiffres, W.-L. Ong, C. F. Higgs, III, A. J. H. McGaughey and J. A. Malen, Nano Lett., 2015, 15, 2985–2991.
101. T. Meier, F. Menges, P. Nirmalraj, H. Hölscher, H. Riel and B. Gotsmann, Phys. Rev. Lett., 2014, 113, 060801.
102. M. D. Losego, M. E. Grady, N. R. Sottos, D. G. Cahill and P. V. Braun, Nat. Mater., 2012, 11, 502–506.
103. H. Liu, L. Chen, H. Zhang, Z. Yang, J. Ye, P. Zhou, C. Fang, W. Xu, J. Shi, J. Liu, Y. Yang and W. Hong, Nat. Mater., 2023, 22, 1007–1012.
104. S. Ho Choi, B. Kim and C. D. Frisbie, Science, 2008, 320, 1482–1486.
105. J.-R. Deng, M. T. González, H. Zhu, H. L. Anderson and E. Leary, J. Am. Chem. Soc., 2024, 146, 3651–3659.
106. M. Vitek, J.-R. Deng, H. L. Anderson and I. Rončević, ACS Nano, 2025, 19, 1405–1411.
107. J. A. Malen, P. Doak, K. Baheti, T. D. Tilley, R. A. Segalman and A. Majumdar, Nano Lett., 2009, 9, 1164–1169.
108. A. Tan, J. Balachandran, B. D. Dunietz, S.-Y. Jang, V. Gavini and P. Reddy, Appl. Phys. Lett., 2012, 101, 243107.
109. S. Park, J. W. Jo, J. Jang, T. Ohto, H. Tada and H. J. Yoon, Nano Lett., 2022, 22, 7682–7689.
110. C. L. Mthembu and R. C. Chiechi, J. Mater. Chem. C, 2025, 13, 1272–1280.
111. E. J. Dell, B. Capozzi, J. L. Xia, L. Venkataraman and L. M. Campos, Nat. Chem., 2015, 7, 209–214.
112. S. K. Yee, J. A. Malen, A. Majumdar and R. A. Segalman, Nano Lett., 2011, 11, 4089–4094.
113. Y. Kim, A. Lenert, E. Meyhofer and P. Reddy, Appl. Phys. Lett., 2016, 109, 033102.
114. M. H. Garner, H. X. Li, Y. Chen, T. A. Su, Z. Shangguan, D. W. Paley, T. F. Liu, F. Ng, H. X. Li, S. X. Xiao, C. Nuckolls, L. Venkataraman and G. C. Solomon, Nature, 2018, 558, 415–419.
115. C. Fang, R. Almughathawi, Q. Wu, W. Cao, H. Chen, S. Hou, Y. Gu, H. Zhang, Y. Zhao, J. Zheng, G. Li, J. Shi, J. Liu, B.-W. Mao, Z. Liu, C. J. Lambert and W. Hong, Natl. Sci. Open, 2023, 2, 20220039.
116. S. K. Lee, M. Buerkle, R. Yamada, Y. Asai and H. Tada, Nanoscale, 2015, 7, 20497–20502.
117. S. Fujii, E. Montes, H. Cho, Y. Yue, M. Koike, T. Nishino, H. Vázquez and M. Kiguchi, Adv. Electron. Mater., 2022, 8, 2200700.
118. J. Vacek, J. V. Chocholoušová, I. G. Stará, I. Starý and Y. Dubi, Nanoscale, 2015, 7, 8793–8802.
119. M. Alsaqer, A. H. S. Daaoub, S. Sangtarash and H. Sadeghi, Nano Lett., 2023, 23, 10719–10724.
120. G. Yzambart, L. Rincón-García, A. A. Al-Jobory, A. K. Ismael, G. Rubio-Bollinger, C. J. Lambert, N. Agraït and M. R. Bryce, J. Phys. Chem. C, 2018, 122, 27198–27204.
121. S. Ramezani Akbarabadi, H. Rahimpour Soleimani and M. Bagheri Tagani, Sci. Rep., 2021, 11, 8958.
122. F. Chen, X. Li, J. Hihath, Z. Huang and N. Tao, J. Am. Chem. Soc., 2006, 128, 15874–15881.
123. K. Baheti, J. A. Malen, P. Doak, P. Reddy, S.-Y. Jang, T. D. Tilley, A. Majumdar and R. A. Segalman, Nano Lett., 2008, 8, 715–719.
124. A. Ismael, X. Wang, T. L. R. Bennett, L. A. Wilkinson, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, Chem. Sci., 2020, 11, 6836–6841.
125. J. M. Hamill, A. Ismael, A. Al-Jobory, T. L. R. Bennett, M. Alshahrani, X. Wang, M. Akers-Douglas, L. A. Wilkinson, B. J. Robinson, N. J. Long, C. Lambert and T. Albrecht, J. Phys. Chem. C, 2023, 127, 7484–7491.
126. S. K. Lee, T. Ohto, R. Yamada and H. Tada, Nano Lett., 2014, 14, 5276–5280.
127. X. Wang, T. L. R. Bennett, A. Ismael, L. A. Wilkinson, J. Hamill, A. J. P. White, I. M. Grace, O. V. Kolosov, T. Albrecht, B. J. Robinson, N. J. Long, L. F. Cohen and C. J. Lambert, J. Am. Chem. Soc., 2020, 142, 8555–8560.
128. H. Chen, Y. Chen, H. Zhang, W. Cao, C. Fang, Y. Zhou, Z. Xiao, J. Shi, W. Chen, J. Liu and W. Hong, Chin. Chem. Lett., 2022, 33, 523–526.
129. J. Hurtado-Gallego, S. Sangtarash, R. Davidson, L. Rincón-García, A. Daaoub, G. Rubio-Bollinger, C. J. Lambert, V. S. Oganesyan, M. R. Bryce, N. Agraït and H. Sadeghi, Nano Lett., 2022, 22, 948–953.
130. X. Li, W. Ge, S. Guo, J. Bai and W. Hong, Angew. Chem., Int. Ed., 2023, 62, e202216819.
131. F. Prins, A. Barreiro, J. W. Ruitenberg, J. S. Seldenthuis, N. Aliaga-Alcalde, L. M. K. Vandersypen and H. S. J. van der Zant, Nano Lett., 2011, 11, 4607–4611.
132. C. Jia, A. Migliore, N. Xin, S. Huang, J. Wang, Q. Yang, S. Wang, H. Chen, D. Wang, B. Feng, Z. Liu, G. Zhang, D.-H. Qu, H. Tian, M. A. Ratner, H. Q. Xu, A. Nitzan and X. Guo, Science, 2016, 352, 1443–1445.
133. Z. Chen, I. M. Grace, S. L. Woltering, L. Chen, A. Gee, J. Baugh, G. A. D. Briggs, L. Bogani, J. A. Mol, C. J. Lambert, H. L. Anderson and J. O. Thomas, Nat. Nanotechnol., 2024, 19, 986–992.
134. P. Gehring, J. K. Sowa, C. Hsu, J. de Bruijckere, M. van der Star, J. J. Le Roy, L. Bogani, E. M. Gauger and H. S. J. van der Zant, Nat. Nanotechnol., 2021, 16, 426–430.
135. M. Li, H. Wu, E. M. Avery, Z. Qin, D. P. Goronzy, H. D. Nguyen, T. Liu, P. S. Weiss and Y. Hu, Science, 2023, 382, 585–589.
136. B. Li, L. Wang and G. Casati, Phys. Rev. Lett., 2004, 93, 184301.
137. M. Terraneo, M. Peyrard and G. Casati, Phys. Rev. Lett., 2002, 88, 094302.
138. B. Li, L. Wang and G. Casati, Appl. Phys. Lett., 2006, 88, 143501.
139. L. Wang and B. Li, Phys. Rev. Lett., 2008, 101, 267203.
140. J. W. Lim, A. Majumder, R. Mittapally, A.-R. Gutierrez, Y. Luan, E. Meyhofer and P. Reddy, Nat. Commun., 2024, 15, 5584.
141. A. Krzykawska, M. Wróbel, K. Kozieł and P. Cyganik, ACS Nano, 2020, 14, 6043–6057.
142. S. Park, S. Kang and H. J. Yoon, Nano Lett., 2022, 22, 3953–3960.
143. Y. Yoon, Z. Lu, C. Uzundal, R. Qi, W. Zhao, S. Chen, Q. Feng, W. Kim, M. H. Naik, K. Watanabe, T. Taniguchi, S. G. Louie, M. F. Crommie and F. Wang, Nature, 2024, 631, 771–776.

---