Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Predicting the solid–liquid phase diagram of a ternary system with cocrystal formation†
Sahar
Nasrallah
,
Ahmad
Alhadid‡
 * and
Mirjana
Minceva
* and
Mirjana
Minceva
 *
*
Biothermodynamics, TUM School of Life Sciences, Technical University of Munich, Maximus-von Imhof-Forum 2, Freising 85354, Germany. E-mail: ahmad.alhadid@tum.de; mirjana.minceva@tum.de
First published on 12th February 2025
Abstract
Cocrystals are commonly synthesized to improve a target solute's physicochemical properties. Solvent-based cocrystallization is the most widely used process to obtain cocrystals. Developing and scaling up the production of cocrystals by solvent-based methods require the knowledge of the solid–liquid equilibrium (SLE) phase diagram of the target solute/coformer/solvent system. However, the experimental determination of the complete SLE phase diagram of a ternary system at different temperatures over the entire composition range is tedious. In this work, we propose a thermodynamic approach to predict the SLE phase diagram of a ternary system with cocrystal formation. First, the solubility of the coformer and cocrystals in the solvent is measured at different temperatures. Second, these data are fitted to obtain the binary interaction parameters of the non-random two-liquid (NRTL) model. Finally, the SLE phase diagram of the target solute/coformer/solvent system at different temperatures is predicted, utilizing the activity coefficients of the components and the melting properties of the cocrystal. Two systems were used to validate the approach: choline chloride (ChCl)/catechol/acetonitrile with ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol 1
catechol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cocrystals and tetramethyl ammonium chloride (TMACl)/catechol/acetonitrile with TMACl
2 cocrystals and tetramethyl ammonium chloride (TMACl)/catechol/acetonitrile with TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol 1
catechol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 cocrystals. The proposed approach predicted the SLE phase diagram of the two systems, unraveling the solubility of catechol and the cocrystals of the two systems in acetonitrile as well as the dissolution behavior of the cocrystals, i.e., congruent or incongruent dissolution. The proposed methodology highlights the benefit of using thermodynamic modeling for cocrystal engineering and design.
2 cocrystals. The proposed approach predicted the SLE phase diagram of the two systems, unraveling the solubility of catechol and the cocrystals of the two systems in acetonitrile as well as the dissolution behavior of the cocrystals, i.e., congruent or incongruent dissolution. The proposed methodology highlights the benefit of using thermodynamic modeling for cocrystal engineering and design.
1. Introduction
Cocrystallization has been used in many fields, such as pharmaceutical formulation, energetic materials, and optoelectronic applications, to tune the physicochemical properties of target solutes.1–3 Because most pharmaceutical formulations are in a solid form, most of the cocrystals reported in the literature include active pharmaceutical ingredients (APIs).4 API-based cocrystals have been formulated to improve the API physicochemical properties such as solubility, stability, and dissolution kinetics.5 Although the main challenge remains in designing and searching for new cocrystals,6,7 predicting the solubility of the formed cocrystals and optimizing their production process should be considered essential steps in their development.8,9Solvent-based cocrystallization is the most widely used cocrystal preparation method.10 With this method, cocrystals are isolated from the target solute/coformer/solvent ternary system by crystallization. However, only congruently melting cocrystals can be prepared by solvent-based cocrystallization methods, while incongruently melting cocrystals cannot be isolated from the liquid solution at the same stoichiometric ratio of the cocrystals.11,12 Thus, efficient design and scale-up of the solvent-based cocrystallization method require a knowledge of the solubility of the cocrystals and their dissolution behavior. The solid–liquid equilibrium (SLE) phase diagram of the ternary target solute/coformer/solvent system unravels the solubility of the cocrystals, the type of the crystallized solid, and the dissolution behavior of the cocrystal.8,13
Nevertheless, the experimental determination of the SLE phase diagram of a ternary system at different temperatures over the entire composition range is a tedious task. On the other hand, thermodynamic models can be used to predict the SLE phase diagram of a ternary system at any temperature.14 Thermodynamic modeling of SLE requires the melting properties of pure components, the stoichiometry and melting properties of existing cocrystals, and the activity coefficients of the target solute, coformer, and solvent in the liquid solution. Rapeenun et al.15 and Perlovich16 proposed shortcut thermodynamic-based methods to predict the solubility of cocrystals in solvents. However, the activity coefficients of components in the liquid solution were assumed to be independent of temperature and composition, limiting the applicability of their proposed approaches to predict the SLE phase diagram over the entire composition range at different temperatures. Thus, to predict the complete SLE phase diagram of the target solute/coformer/solvent ternary system at different temperatures, the temperature and composition dependency of the activity coefficients should be considered.
The activity coefficients of components in the liquid solution at any temperature and composition can be calculated using thermodynamic models.17–19 However, system-specific binary interaction parameters are needed for systems with a substantial deviation from ideality. The binary interaction parameters are usually obtained from experimental solubility data of the binary system. However, target solutes can be practically insoluble in the solvent, and accordingly, the solubility data of the target solute in the selected solvent are experimentally inaccessible. Instead, ternary SLE data of the target solute/coformer/solvent system are fitted to obtain target solute–solvent binary interaction parameters.14,18 However, the nonideality of the ternary liquid solution might not be correctly described using the binary interaction parameters obtained only from the binary systems. Thus, ternary SLE data are needed to ensure that the model can capture the nonideality of the ternary system. Ternary SLE data are commonly obtained using the shake-flask method, which is time-consuming, particularly at different temperatures and for systems with the formation of several cocrystals. In contrast, solubility data of pure congruently melting cocrystals can be measured similarly to that of a pure substance. In this case, the target solute/conformer cocrystal is a pure solid phase while the liquid solution is a ternary mixture of target solute/coformer/solvent. Thus, determining the solubility of congruently melting cocrystals in the solvent at different temperatures can be considered a shortcut method for measuring the SLE data of the ternary systems, which are needed to estimate thermodynamic model parameters efficiently.
This work proposes an approach to predict the SLE phase diagram of a ternary system with cocrystal formation at different temperatures. Two systems were used to validate the approach: choline chloride (ChCl)/catechol/acetonitrile with ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol 1
catechol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (C11) and 1
1 (C11) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (C12) cocrystals and tetramethyl ammonium chloride (TMACl)/catechol/acetonitrile with TMACl
2 (C12) cocrystals and tetramethyl ammonium chloride (TMACl)/catechol/acetonitrile with TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol 1
catechol 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 (C11) and 1
1 (C11) and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 (C12) cocrystals. The solubilities of the coformer and cocrystals were measured in acetonitrile at different temperatures using a high-throughput experimental technique. The SLE data of the respective binary system and the cocrystal solubility data were used to obtain the binary interaction parameters of the NRTL model. After that, the SLE phase diagram of the ternary system was calculated over the entire composition range, utilizing the thermodynamic model and the melting properties of pure components and cocrystals. The predicted SLE phase diagram was used to determine the solubility lines of the cocrystals and coformer, the form of the crystallized solid phase, and the dissolution behavior of the cocrystals.
2 (C12) cocrystals. The solubilities of the coformer and cocrystals were measured in acetonitrile at different temperatures using a high-throughput experimental technique. The SLE data of the respective binary system and the cocrystal solubility data were used to obtain the binary interaction parameters of the NRTL model. After that, the SLE phase diagram of the ternary system was calculated over the entire composition range, utilizing the thermodynamic model and the melting properties of pure components and cocrystals. The predicted SLE phase diagram was used to determine the solubility lines of the cocrystals and coformer, the form of the crystallized solid phase, and the dissolution behavior of the cocrystals.
2. Materials and methods
2.1 Methodology to predict the SLE phase diagram of ternary systems
Fig. 1 shows a schematic representation of the proposed approach. The methodology of the proposed approach relies on having the prerequisites needed to model the SLE phase diagram of a ternary system with cocrystal formation at different temperatures: the melting properties of constituents, the melting properties and stoichiometry of cocrystals, and the activity coefficients of components in the liquid solution. A ternary system consists of a target solute, coformer, and solvent. First, cocrystal formation in the binary target solute/coformer should be studied. Cocrystal formation studies usually report the complete SLE phase diagram and the melting properties and stoichiometry of the cocrystals. Second, the melting properties of the target solute, coformer, and cocrystals should be known. The melting properties of the target solute, coformer, and cocrystals can be obtained by thermal analysis techniques such as differential scanning calorimetry (DSC). Third, the activity coefficients of components in the liquid solution are needed. The activity coefficients of components in the ternary liquid solution can be calculated using thermodynamic models. Correlative thermodynamic models utilize binary interaction parameters to calculate the activity coefficients of components. The binary interaction parameters are obtained by fitting the experimental SLE data of the three sub-binary systems: target solute/coformer, target solute/solvent, and coformer/solvent. However, for systems with strong intermolecular interactions, the nonideality of the ternary liquid solution might not be correctly described using the binary interaction parameters obtained only from the binary systems. Thus, ternary SLE data are needed to ensure that the model can capture the nonideality of the ternary system. The cocrystal solubility in the solvent can be measured similarly to that of pure components, making these ternary SLE data easily accessible when using high-throughput experimental techniques.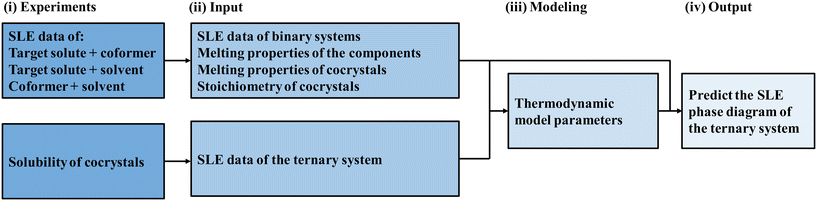 | ||
| Fig. 1 Schematic representation of the proposed approach for predicting the solid–liquid phase diagram of the target solute/coformer/solvent ternary system. | ||
Cocrystal solubility in the solvent at different temperatures is used along with the SLE data of the binary target solute/coformer, target solute/solvent, and coformer/solvent systems to obtain the binary interaction parameters of the thermodynamic model. Eventually, the SLE phase diagram of the ternary target solute/coformer/solvent system is predicted. The SLE phase diagram provides the solubility of the target solute, coformer, and cocrystal (i.e., which component crystallizes at each solution composition) and the dissolution behavior of the cocrystals. This valuable information aids in designing solvent-based cocrystallization methods (Fig. 1).
2.2 Selected systems
Two model systems were selected to validate the proposed approach: ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile. We assumed ChCl and TMACl as target solutes, catechol as the coformer, and acetonitrile as the solvent. Two cocrystals are formed in the two systems with ChCl/TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals.20–22 The SLE data of the binary ChCl/catechol and TMACl/catechol systems are available in the literature.20,21 Nevertheless, it is worth mentioning that the SLE data of the binary ChCl/acetonitrile and TMACl/acetonitrile were not considered in this work, because ChCl and TMACl are thermally unstable and their reported melting properties could be uncertain.23–25 Therefore, the model parameters were obtained by fitting the experimental liquidus data of catechol and cocrystals in the binary ChCl/catechol and TMACl/catechol systems as well as the solubility data of the ChCl
catechol C11 and C12 cocrystals.20–22 The SLE data of the binary ChCl/catechol and TMACl/catechol systems are available in the literature.20,21 Nevertheless, it is worth mentioning that the SLE data of the binary ChCl/acetonitrile and TMACl/acetonitrile were not considered in this work, because ChCl and TMACl are thermally unstable and their reported melting properties could be uncertain.23–25 Therefore, the model parameters were obtained by fitting the experimental liquidus data of catechol and cocrystals in the binary ChCl/catechol and TMACl/catechol systems as well as the solubility data of the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals and TMACl
catechol C11 and C12 cocrystals and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal in acetonitrile.
catechol C11 cocrystal in acetonitrile.
2.3 Sample preparation
Table 1 shows the chemicals used to prepare the cocrystals and the samples for the solubility measurements. ChCl and TMACl are very hygroscopic and were dried under vacuum at 360 K before use. All other chemicals were used as received without further purification. The studied cocrystals were prepared by mixing salts with catechol in 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 molar ratios (salt to catechol). The weighing was conducted on a Sartorius analytical balance (Germany) with an uncertainty of ±0.01 mg. The mixtures were introduced into glass vials, sealed immediately, and gently heated with continuous stirring until a clear liquid was formed. The fully melted binary mixtures were then quenched at 193 K and annealed at 253 K for one day to ensure complete crystallization. The final cocrystal powders were ground to a uniform consistency.
2 molar ratios (salt to catechol). The weighing was conducted on a Sartorius analytical balance (Germany) with an uncertainty of ±0.01 mg. The mixtures were introduced into glass vials, sealed immediately, and gently heated with continuous stirring until a clear liquid was formed. The fully melted binary mixtures were then quenched at 193 K and annealed at 253 K for one day to ensure complete crystallization. The final cocrystal powders were ground to a uniform consistency.
2.4 Differential scanning calorimetry
DSC measurements were conducted to measure the melting properties of pure catechol and the cocrystals. The DSC device (NETZSCH DSC 200 F3, Germany) was calibrated using six calibration standards as described elsewhere.20 Measurements were performed under a nitrogen flow of 150 mL min−1. The samples were placed in triplicate into hermetically sealed DSC crucibles. The samples underwent a heating run at a rate of 5 K min−1 until 10 K above the melting temperature of the sample, followed by a cooling run at the same rate until 253 K. A second heating run was then conducted at 5 K min−1 until 10 K above the melting temperature of the sample. The solidus and melting temperatures of pure catechol and cocrystals were determined from the onset temperature of the respective peak, and the liquidus temperatures were determined from the peak maximum temperature. Table 2 shows the melting properties of catechol and cocrystals compared to those reported in the literature.| Solid phase | T m/K | Δhm/kJ mol−1 | ΔcL→Sp/J mol−1 K−1 | ||
|---|---|---|---|---|---|
| This work | Literature | This work | Literature | ||
| Catechol | 377.4 ± 0.3 | 377.1 (ref. 17) | 22.21 ± 0.6 | 21.99 (ref. 17) | 68.0 (ref. 26) |
ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 catechol C11 |
327.9 ± 0.4 | 327.4 (ref. 17) | 34.96 ± 0.4 | 34.15 (ref. 17) | — |
ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 catechol C12 |
325.9 ± 0.1 | 325.7 (ref. 17) | 39.57 ± 0.7 | 39.54 (ref. 17) | — |
TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 catechol C11 |
398.9 ± 0.1 | 397.9 (ref. 18) | 21.9 ± 0.2 | 21.13 (ref. 18) | — |
TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 catechol C12 |
368.9 ± 0.2 | 369.6 (ref. 18) | 38.7 ± 0.6 | 38.27 (ref. 18) | — |
2.5 Solubility measurements
The solubility of pure catechol and cocrystals in acetonitrile was measured using a Crystal 16 multi-reactor crystallizer (Technobis, Netherlands). The instrument determines the melting temperature of a solution by measuring the light transmissivity through the sample, identifying the ‘clear point’—the temperature at which the solution becomes fully transparent at a known composition. Known amounts of the solid phase were weighed and added to 1 mL of solvent in glass vials. Then, the vials were subjected to a thermal program under continuous stirring. The temperature was raised from 273.15 to 10 K below the boiling point of acetonitrile at a 0.5 K min−1 rate. The clear point temperature was considered as the liquidus temperature of the mixture at the prepared sample composition. The measurements were performed in triplicate. The TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal melts incongruently in acetonitrile,21,22 and accordingly, its solubility was not measured. It should be noted that the solid phase was not characterized, assuming that the precipitate consists of stable cocrystals in the same stoichiometric ratios as in the liquid phase. The crystallization of the ChCl
catechol C12 cocrystal melts incongruently in acetonitrile,21,22 and accordingly, its solubility was not measured. It should be noted that the solid phase was not characterized, assuming that the precipitate consists of stable cocrystals in the same stoichiometric ratios as in the liquid phase. The crystallization of the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals from the acetonitrile solution was confirmed in our previous study.20
catechol C11 and C12 cocrystals from the acetonitrile solution was confirmed in our previous study.20
The shake-flask method was employed to determine the solubility of pure ChCl and TMACl as well as selected mixed solid samples consisting of the cocrystals and catechol in acetonitrile at 298.1 K and 1 bar. The solid sample was added to a specific amount of acetonitrile in 2 mL microcentrifuge tubes. The samples were then shaken in a vortex mixer for 15 minutes. If a homogeneous solution was achieved, an additional solid sample was added. Heterogeneous solutions were placed in a thermomixer and stirred at 800 rpm for 48 hours at 298.1 K. Then, the tubes were centrifuged for 20 minutes at 1300 rpm using a Mini-Spin Centrifuge (Eppendorf, Germany). Aliquots of the supernatant were collected and diluted with acetonitrile to determine the catechol concentration with a UV-vis spectrophotometer (Analytik Jena, Germany) at the wavelength of λmax = 277.5 nm (ref. 27) using the catechol–acetonitrile calibration curve shown in Fig. S1 in the ESI.† Then, the ChCl and TMACl concentrations in the sample were determined gravimetrically by evaporating the acetonitrile. Additionally, the solid residue obtained in the shake-flask experiments was analyzed using DSC to verify the crystalized form of the solid phase; the DSC curves are reported in Fig. S2 and S3 in the ESI.†
2.6 Thermodynamic modeling
The solubility of pure catechol was calculated by the following equation: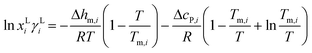 | (1) |
The cocrystal solubility line was calculated as follows:
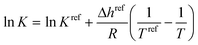 | (2) |
| K = (xLAγLA)vA(xLBγLB)vB | (3) |
| Kref = (xLref,AγLA(xLref,A, Tref))vA(xLref,BγLB(xLref,B, Tref))vB | (4) |
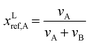 | (5) |
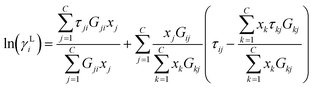 | (6) |
| Gij = exp(−0.3τij) Gji = exp(−0.3τji) | (7) |
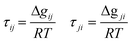 | (8) |
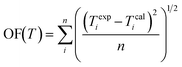 | (9) |
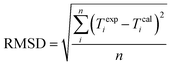 | (10) |
3. Results & discussion
3.1 Determining the binary interaction parameters
The NRTL model was used to calculate the activity coefficients of components in the binary and ternary liquid solutions. The binary interaction parameters of the model were obtained by fitting the experimental SLE data of the binary ChCl/catechol and TMACl/catechol systems as well as the solubility of catechol, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals, and TMACl
catechol C11 and C12 cocrystals, and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal. The experimental SLE data of the binary ChCl/catechol and TMACl/catechol were taken from the literature;20,21 the solubility data of catechol, ChCl
catechol C11 cocrystal. The experimental SLE data of the binary ChCl/catechol and TMACl/catechol were taken from the literature;20,21 the solubility data of catechol, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals, and TMACl
catechol C11 and C12 cocrystals, and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal measured in this work are reported in Table S1 in the ESI.† The obtained binary interaction parameters of the NRTL model and the infinite dilution activity coefficients (γ∞) of components in the binary systems at 298.1 K calculated using the NRTL model are shown in Table 3. The obtained binary interaction parameters of the ChCl/catechol and TMACl/catechol systems are similar to those calculated in our previous research using only the binary SLE data of the two systems.20,21 A strong negative deviation from ideality is observed in the catechol/acetonitrile, ChCl/catechol, and TMACl/catechol systems, as indicated by the γ∞ values. The negative deviation from ideality is more significant in the ChCl/catechol and TMACl/catechol systems than in the catechol/acetonitrile system. The γ∞ value of ChCl in acetonitrile indicates a negative deviation from the ideal behavior. However, based on the observed low solubility of pure ChCl in acetonitrile, the system is not expected to show a negative deviation from the ideal behavior. The solubility of ChCl in the liquid solution when dissolving the cocrystals is significantly higher than that when dissolving pure ChCl in acetonitrile (see Tables S1 and S2 in the ESI†). This improvement in ChCl solubility could be attributed to the complex interactions between ChCl and catechol in acetonitrile, which a simple model like NRTL cannot fully capture. Therefore, the NRTL model likely overestimated the negative deviation from the ideality of the ChCl/acetonitrile system. On the other hand, the TMACl/acetonitrile system shows a positive deviation from ideality, aligning with the very low solubility of pure TMACl in acetonitrile (see Table S2 in the ESI†).
catechol C11 cocrystal measured in this work are reported in Table S1 in the ESI.† The obtained binary interaction parameters of the NRTL model and the infinite dilution activity coefficients (γ∞) of components in the binary systems at 298.1 K calculated using the NRTL model are shown in Table 3. The obtained binary interaction parameters of the ChCl/catechol and TMACl/catechol systems are similar to those calculated in our previous research using only the binary SLE data of the two systems.20,21 A strong negative deviation from ideality is observed in the catechol/acetonitrile, ChCl/catechol, and TMACl/catechol systems, as indicated by the γ∞ values. The negative deviation from ideality is more significant in the ChCl/catechol and TMACl/catechol systems than in the catechol/acetonitrile system. The γ∞ value of ChCl in acetonitrile indicates a negative deviation from the ideal behavior. However, based on the observed low solubility of pure ChCl in acetonitrile, the system is not expected to show a negative deviation from the ideal behavior. The solubility of ChCl in the liquid solution when dissolving the cocrystals is significantly higher than that when dissolving pure ChCl in acetonitrile (see Tables S1 and S2 in the ESI†). This improvement in ChCl solubility could be attributed to the complex interactions between ChCl and catechol in acetonitrile, which a simple model like NRTL cannot fully capture. Therefore, the NRTL model likely overestimated the negative deviation from the ideality of the ChCl/acetonitrile system. On the other hand, the TMACl/acetonitrile system shows a positive deviation from ideality, aligning with the very low solubility of pure TMACl in acetonitrile (see Table S2 in the ESI†).
| System | Δgij/kJ mol−1 | Δgji/kJ mol−1 | ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞1 γ∞1 |
ln![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) γ∞2 γ∞2 |
||
|---|---|---|---|---|---|---|
| Lit. | Lit. | |||||
| ChCl/catechol | −9.6066 | −9.6230 (ref. 21) | −9.0398 | −8.1797 (ref. 21) | −16.0471 | −14.7705 |
| Catechol/acetonitrile | 5.6810 | — | −5.4251 | — | −1.0365 | −1.9289 |
| ChCl/acetonitrile | 214.6133 | — | −1.8160 | — | −0.7327 | 85.6805 |
| TMACl/catechol | −9.6969 | −9.9180 (ref. 21) | −4.5254 | −3.9180 (ref. 21) | −14.4798 | −7.0703 |
| TMACl/acetonitrile | 1.0522 | — | 6.9754 | — | 3.1883 | 1.6343 |
3.2 SLE phase diagram of binary systems and cocrystal solubility
The SLE phase diagram of the binary ChCl/catechol and TMACl/catechol systems and catechol solubility in acetonitrile was calculated using the activity coefficients of components determined by the NRTL model and the melting properties of catechol and cocrystals (see Table 2). Fig. 2 shows the binary SLE phase diagrams for the catechol/acetonitrile (Fig. 2a), ChCl/catechol (Fig. 2b), and TMACl/catechol (Fig. 2c) systems calculated using the NRTL model and assuming the ideal solution model, i.e., γ = 1. As seen in Fig. 2, the NRTL model allows the good description of the binary SLE phase diagram of ChCl/catechol and TMACl/catechol systems as well as the solubility of catechol in acetonitrile. Thus, the obtained binary interaction parameters provide reliable estimates for the activity coefficients of components in the liquid phase of the binary catechol/acetonitrile, ChCl/catechol, and TMACl/catechol systems.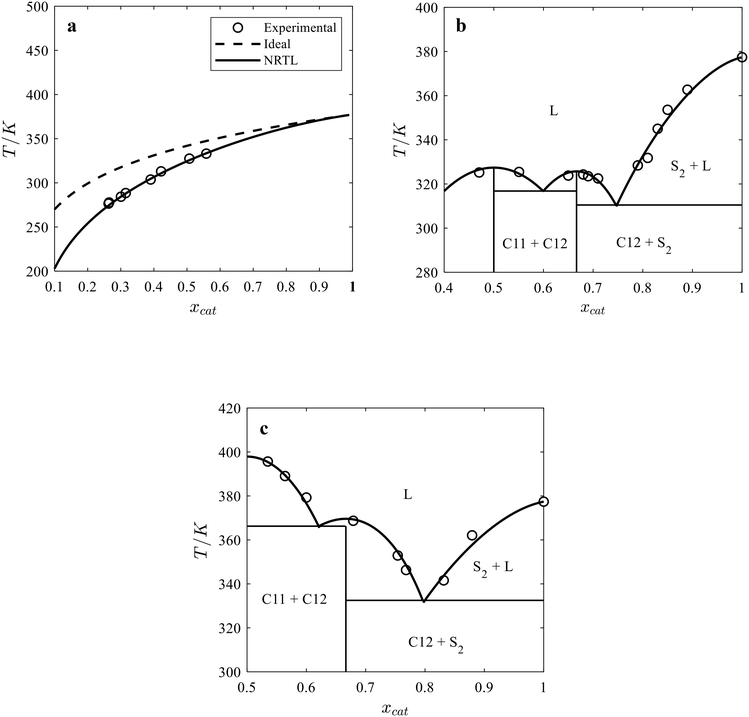 | ||
| Fig. 2 Solid–liquid phase diagrams of (a) catechol/acetonitrile, (b) choline chloride/catechol, and (c) tetramethylammonium chloride/catechol. | ||
Next, the solubilities of ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals and TMACl
catechol C11 and C12 cocrystals and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
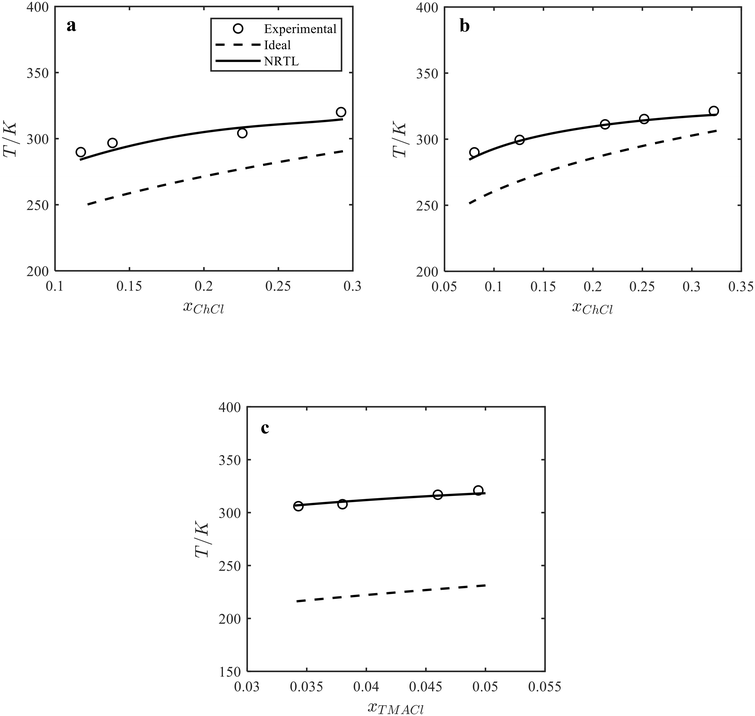
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal in acetonitrile at different temperatures were calculated using the activity coefficients of components determined by the NRTL model and the melting properties and stoichiometry of cocrystals. Fig. 3 shows the liquidus temperature of the cocrystal and acetonitrile mixture of the ChCl
catechol C11 cocrystal in acetonitrile at different temperatures were calculated using the activity coefficients of components determined by the NRTL model and the melting properties and stoichiometry of cocrystals. Fig. 3 shows the liquidus temperature of the cocrystal and acetonitrile mixture of the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal (Fig. 3a), ChCl
catechol C12 cocrystal (Fig. 3a), ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal (Fig. 3b), and TMACl
catechol C11 cocrystal (Fig. 3b), and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal (Fig. 3c) calculated by the NRTL model and assuming the ideal solution model. As seen in Fig. 3, the predicted liquidus temperatures of the cocrystal and acetonitrile mixtures by the NRTL model (solid lines) agree with the experimental data. In contrast to the binary systems (see Fig. 2), the experimental liquidus temperatures of the cocrystal and acetonitrile mixtures are higher than those predicted using the ideal solution model (dashed line), indicating a positive deviation from the ideal behavior in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems.
catechol C11 cocrystal (Fig. 3c) calculated by the NRTL model and assuming the ideal solution model. As seen in Fig. 3, the predicted liquidus temperatures of the cocrystal and acetonitrile mixtures by the NRTL model (solid lines) agree with the experimental data. In contrast to the binary systems (see Fig. 2), the experimental liquidus temperatures of the cocrystal and acetonitrile mixtures are higher than those predicted using the ideal solution model (dashed line), indicating a positive deviation from the ideal behavior in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems.
Table 4 shows the mole fraction of components when dissolving ChCl, TMACl, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal, ChCl
catechol C12 cocrystal, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal, and TMACl
catechol C11 cocrystal, and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal in acetonitrile at 298.1 K using the shake-flask method. As seen in Table 4, the mole fraction of ChCl when dissolving pure ChCl in acetonitrile is 0.0013, while its mole fraction in the ternary solution when dissolving the ChCl
catechol C11 cocrystal in acetonitrile at 298.1 K using the shake-flask method. As seen in Table 4, the mole fraction of ChCl when dissolving pure ChCl in acetonitrile is 0.0013, while its mole fraction in the ternary solution when dissolving the ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 and C11 cocrystals in acetonitrile is 0.1549 and 0.1393, respectively. Furthermore, the mole fraction of TMACl when dissolving pure TMACl in acetonitrile is 0.0019, while the mole fraction of TMACl in the ternary solution when dissolving the C11 cocrystal is 0.0513. Hence, despite the positive deviation from ideality, dissolving the cocrystals results in liquid solutions that are significantly richer in ChCl and TMACl than when dissolving pure ChCl and TMACl in acetonitrile. The higher solubility enhancement of ChCl than TMACl is attributed to the stronger interactions between ChCl and catechol, as depicted by the more significant negative deviation from ideality in the binary ChCl/catechol system compared to the TMACl/catechol system (see Table 3).30 In conclusion, using ternary SLE data is required to capture the complex interactions in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems.
catechol C12 and C11 cocrystals in acetonitrile is 0.1549 and 0.1393, respectively. Furthermore, the mole fraction of TMACl when dissolving pure TMACl in acetonitrile is 0.0019, while the mole fraction of TMACl in the ternary solution when dissolving the C11 cocrystal is 0.0513. Hence, despite the positive deviation from ideality, dissolving the cocrystals results in liquid solutions that are significantly richer in ChCl and TMACl than when dissolving pure ChCl and TMACl in acetonitrile. The higher solubility enhancement of ChCl than TMACl is attributed to the stronger interactions between ChCl and catechol, as depicted by the more significant negative deviation from ideality in the binary ChCl/catechol system compared to the TMACl/catechol system (see Table 3).30 In conclusion, using ternary SLE data is required to capture the complex interactions in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems.
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal, ChCl
catechol C12 cocrystal, ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal, and TMACl
catechol C11 cocrystal, and TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal in acetonitrile at 298.1 K using the shake-flask method
catechol C11 cocrystal in acetonitrile at 298.1 K using the shake-flask method
| System | x 1 | x 2 | x 3 |
|---|---|---|---|
| ChCl (1) + catechol (2) + acetonitrile (3) | |||
| ChCl/acetonitrile | 0.0013 ± 0.0001 | — | 0.9987 |
ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11/acetonitrile catechol C11/acetonitrile |
0.1393 ± 0.0036 | 0.1348 ± 0.0020 | 0.7259 |
ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12/acetonitrile catechol C12/acetonitrile |
0.1549 ± 0.0043 | 0.2787 ± 0.0009 | 0.5664 |
| TMACl (1) + catechol (2) + acetonitrile (3) | |||
|---|---|---|---|
| TMACl/acetonitrile | 0.0019 ± 0.0001 | — | 0.9981 |
TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) : :![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11/acetonitrile catechol C11/acetonitrile |
0.0513 ± 0.0012 | 0.0533 ± 0.0011 | 0.8954 |
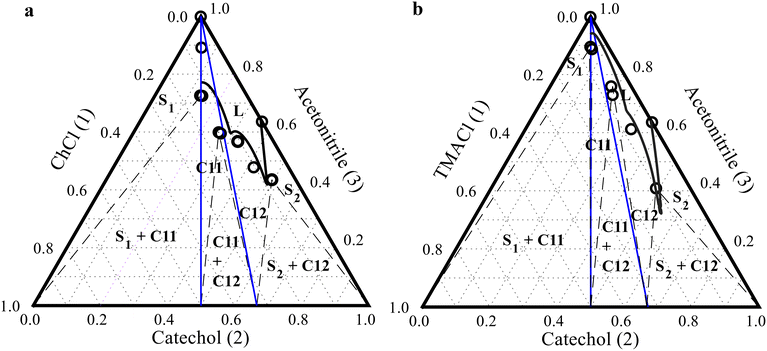
3.3 Predicting the ternary SLE phase diagram
The SLE data of the binary ChCl/catechol and TMACl/catechol and the solubility of catechol and cocrystals in acetonitrile at different temperatures were fitted to obtain the binary interaction parameters of the NRTL model. The obtained binary interaction parameters of the NRTL model allow the calculation of the activity coefficients of components in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems. The melting properties of the components and cocrystals (Table 2) and the calculated activity coefficients of the components were used to predict the SLE phase diagram of the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems. Fig. 4 shows the SLE phase diagrams of the ChCl/catechol/acetonitrile (Fig. 4a) and TMACl/catechol/acetonitrile (Fig. 4b) systems at 298.1 K calculated using the NRTL model in comparison with experimental data measured in this work (see Table S2 in the ESI†). The experimental SLE data of the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile cocrystal systems shown in Fig. 4 were not used to obtain the binary interaction parameters of the NRTL model. It is worth mentioning that our approach allows the prediction of the complete SLE phase diagram of the ternary system. However, the liquidus lines of ChCl and TMACl cannot be modeled because they are thermally unstable, and their reported melting properties could be uncertain.23–25 The regions in the SLE phase diagram indicating the solid phase crystallizing from the liquid mixture are specified by the experimental equilibrium solubility measurements using the shake-flask method. The solid phases in equilibrium at the invariant (eutectic) points were characterized by DSC measurements (see Fig. S3 in the ESI†).As seen in Fig. 4a, the NRTL model successfully predicts the solubility lines of the cocrystals and catechol in the ternary ChCl/catechol/acetonitrile system, although the NRTL model binary interaction parameters were obtained solely from the solubility data of pure catechol and cocrystals in acetonitrile at different temperatures and the SLE data of the binary ChCl/catechol system. Nevertheless, a slight deviation is observed between the invariant point predicted by the NRTL model and the experimentally measured one. This deviation is expected due to the complex interactions in the ternary ChCl/catechol/acetonitrile system. Due to the significant difference in the solubility of ChCl and catechol in acetonitrile, the diagram is shifted towards the catechol axis (right side), resulting in an asymmetric shape of the phase diagram. The 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 1 and 1
1 and 1![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 2 stoichiometric lines (blue lines in Fig. 4a) intersect with the solubility curves of both ChCl
2 stoichiometric lines (blue lines in Fig. 4a) intersect with the solubility curves of both ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals, confirming a congruent dissolution behavior. Both ChCl
catechol C11 and C12 cocrystals, confirming a congruent dissolution behavior. Both ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals dissolve in acetonitrile, yielding solutions with the corresponding stoichiometric ratios between ChCl and catechol in the cocrystal in equilibrium with the pure cocrystal solid phase. Single crystals of ChCl
catechol C11 and C12 cocrystals dissolve in acetonitrile, yielding solutions with the corresponding stoichiometric ratios between ChCl and catechol in the cocrystal in equilibrium with the pure cocrystal solid phase. Single crystals of ChCl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals were isolated from their solution in acetonitrile by cooling, confirming their congruent dissolution.20
catechol C11 and C12 cocrystals were isolated from their solution in acetonitrile by cooling, confirming their congruent dissolution.20
As seen in Fig. 4b, the calculated solubility lines in the ternary TMACl/catechol/acetonitrile system deviate from the experimental data, especially for the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal. The two invariant points in the TMACl/catechol/acetonitrile system were not predicted correctly by the NRTL model. Furthermore, the TMACl
catechol C11 cocrystal. The two invariant points in the TMACl/catechol/acetonitrile system were not predicted correctly by the NRTL model. Furthermore, the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal shows congruent dissolution behavior. In contrast, the TMACl
catechol C11 cocrystal shows congruent dissolution behavior. In contrast, the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal exhibits incongruent dissolution behavior, as shown by the misalignment between the stoichiometric lines (blue lines in Fig. 4b) and the TMACl
catechol C12 cocrystal exhibits incongruent dissolution behavior, as shown by the misalignment between the stoichiometric lines (blue lines in Fig. 4b) and the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal crystallization region. As the TMACl
catechol C12 cocrystal crystallization region. As the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal dissolves in acetonitrile, a heterogeneous mixture of the solid TMACl
catechol C12 cocrystal dissolves in acetonitrile, a heterogeneous mixture of the solid TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 and C12 cocrystals is initially formed. As dissolution continues with the addition of more acetonitrile, the pure TMACl
catechol C11 and C12 cocrystals is initially formed. As dissolution continues with the addition of more acetonitrile, the pure TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C11 cocrystal solid phase crystallizes from the solution with the stoichiometric ratio of the TMACl
catechol C11 cocrystal solid phase crystallizes from the solution with the stoichiometric ratio of the TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 cocrystal. The incongruent dissolution behavior of TMACl
catechol C12 cocrystal. The incongruent dissolution behavior of TMACl![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) :
:![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) catechol C12 was confirmed in our previous study.21
catechol C12 was confirmed in our previous study.21
In conclusion, the NRTL model provides fair predictions of the solid phase formed at each mixture composition and the dissolution behavior of the cocrystals, enabling an efficient design of cocrystal production and purification processes.
4. Conclusion
In this work, we present a thermodynamic-based approach to predict the SLE phase diagram of a ternary target solute/coformer/solvent system with cocrystal formation. The SLE phase diagram of the ternary target solute/coformer/solvent system is predicted using the melting properties of the target solute and coformer, the melting properties and stoichiometry of the cocrystal, and the activity coefficient of components in the ternary liquid solution. The activity coefficients are calculated using the NRTL model. The binary interaction parameters of the NRTL model are obtained from the SLE data of the target solute/coformer and the solubility of the target solute, coformer, and cocrystals in the solvent at different temperatures. The solubility data of the target solute, coformer, and cocrystals in the solvent at different temperatures can be readily measured using high-throughput methods. The approach was applied to two ternary systems: ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile.It is found that the binary interaction parameters obtained by fitting the SLE data of the binary ChCl/catechol and TMACl/catechol and the solubility of the cocrystals and pure catechol in acetonitrile at different temperatures capture the nonideality of the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems. Accordingly, the SLE phase diagram of the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems is predicted. Although the calculated solubility lines of the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems by the NRTL model slightly deviate from the experimental data, fair predictions of the type of the solid phase crystallized at each composition of the mixture are obtained. Furthermore, the model predicts the dissolution behavior of the cocrystals in the ternary ChCl/catechol/acetonitrile and TMACl/catechol/acetonitrile systems.
This work provides a general approach to predicting the SLE phase diagram of ternary systems with cocrystal formation. Our proposed approach presents an efficient strategy for designing solvent-based cocrystallization processes. Furthermore, its applicability extends to pharmaceutical formulations, enabling the prediction of solubility enhancement in API-based cocrystals in various solvents.
Data availability
The data supporting this article have been included in the main manuscript and the ESI† file.Conflicts of interest
There are no conflicts to declare.Acknowledgements
Sahar Nasrallah would like to thank the German Academic Exchange Service (DAAD) for financial support.References
- N. V. Muravyev, L. Fershtat and Q. Zhang, Chem. Eng. J., 2024, 486, 150410 CrossRef CAS.
- H. Y. Liu, Y. C. Li and X. D. Wang, CrystEngComm, 2023, 25, 3126–3141 RSC.
- S. N. Wong, Y. C. S. Chen, B. Xuan, C. C. Sun and S. F. Chow, CrystEngComm, 2021, 23, 7005–7038 RSC.
- B. M. Couillaud, P. Espeau, N. Mignet and Y. Corvis, ChemMedChem, 2019, 14, 8–23 CrossRef CAS PubMed.
- L. Liu, J.-R. Wang and X. Mei, CrystEngComm, 2022, 24, 2002–2022 RSC.
- S. N. Wong, M. Fu, S. Li, W. T. C. Kwok, S. Chow, K. H. Low and S. F. Chow, CrystEngComm, 2024, 26, 1505–1526 RSC.
- J. Roshni and T. Karthick, J. Mol. Struct., 2025, 1321, 139868 CrossRef CAS.
- A. Saha, A. A. Ahangar, A. A. Dar, S. Thirunahari and J. V. Parambil, Cryst. Growth Des., 2023, 23, 7558–7581 CrossRef CAS.
- J. T. J. Freitas, L. F. Diniz, D. S. Gomes, P. M. A. F. de Paula, S. H. A. de Castro, L. S. Martins, D. F. Silva, A. L. M. Horta, F. A. S. Guimarães, V. F. M. Calisto and R. Diniz, CrystEngComm, 2022, 24, 7803–7812 RSC.
- S. Sarangi, P. N. Remya and N. Damodharan, J. Drug Delivery Sci. Technol., 2024, 95, 105619 CrossRef CAS.
- R. A. Chiarella, R. J. Davey and M. L. Peterson, Cryst. Growth Des., 2007, 7, 1223–1226 CrossRef CAS.
- S. Pal, Cryst. Growth Des., 2021, 21, 249–259 CrossRef CAS.
- L. Codan, L. Daza and E. Sirota, Org. Process Res. Dev., 2023, 27, 513–522 CrossRef CAS.
- L. Lange and G. Sadowski, Cryst. Growth Des., 2016, 16, 4439–4449 CrossRef CAS.
- P. Rapeenun, J. Rarey and A. E. Flood, Cryst. Growth Des., 2021, 21, 5534–5543 CrossRef CAS.
- G. L. Perlovich, CrystEngComm, 2022, 24, 2217–2220 RSC.
- F. Wolbert, C. Brandenbusch and G. Sadowski, Mol. Pharmaceutics, 2019, 16, 3091–3099 CrossRef CAS PubMed.
- L. Lange and G. Sadowski, Cryst. Growth Des., 2015, 15, 4406–4416 CrossRef CAS.
- C. Loschen and A. Klamt, Cryst. Growth Des., 2018, 18, 5600–5608 CrossRef CAS.
- A. Alhadid, C. Jandl, L. Mokrushina and M. Minceva, Cryst. Growth Des., 2022, 22, 1933–1942 CrossRef CAS.
- A. Alhadid, C. Jandl, S. Nasrallah, S. M. Kronawitter, L. Mokrushina, G. Kieslich and M. Minceva, J. Chem. Phys., 2023, 159, 094503 CrossRef CAS PubMed.
- M. A. Khan, J. Mol. Struct., 1986, 145, 203–218 CrossRef CAS.
- M. A. R. Martins, D. O. Abranches, L. P. Silva, S. P. Pinho and J. A. P. Coutinho, Ind. Eng. Chem. Res., 2022, 61, 11988–11995 CrossRef CAS.
- A. van den Bruinhorst, J. Avila, M. Rosenthal, A. Pellegrino, M. Burghammer and M. Costa Gomes, Nat. Commun., 2023, 14, 6684 CrossRef CAS PubMed.
- G. B. Correa, D. O. Abranches, E. Marin-Rimoldi, Y. Zhang, E. J. Maginn and F. W. Tavares, J. Phys. Chem. Lett., 2024, 15, 11801–11805 CrossRef CAS PubMed.
- P. Bret-Dibat and A. Lichanot, Thermochim. Acta, 1989, 147, 261–271 CrossRef CAS.
- M. Dewar, V. P. Kubba and R. Pettit, J. Chem. Soc., 1958, 3076–3079 RSC.
- H. Renon and J. M. Prausnitz, AIChE J., 1968, 14, 135–144 CrossRef CAS.
- J. M. Prausnitz, R. N. Lichtenthaler and E. G. d. Azevedo, Molecular Thermodynamics of Fluid-Phase Equilibria, Prentice Hall PTR, Upper Saddle River, NJ, 1999 Search PubMed.
- S. Nasrallah, A. Alhadid and M. Minceva, Cryst. Growth Des., 2024, 24, 6364–6372 CrossRef CAS.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ce01256a |
| ‡ Present address: College of Engineering and Technology, American University of the Middle East, Kuwait. (E-mail: ahmad.al-hadid@aum.edu.kw). |
| This journal is © The Royal Society of Chemistry 2025 |