Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
On the pK of crystal surfaces: molecular modeling of crystallite protonation, local reorganization, and solute dissociation†
Patrick
Duchstein‡
 ,
Moritz
Macht‡
and
Dirk
Zahn
,
Moritz
Macht‡
and
Dirk
Zahn
 *
*
Lehrstuhl für Theoretische Chemie/Computer Chemie Centrum, Friedrich-Alexander Universität Erlangen-Nürnberg, Nägelsbachstraße 25, 91052 Erlangen, Germany. E-mail: dirk.zahn@fau.de; Web: https://www.chemistry.nat.fau.eu/ccc/groups/zahn-group/
First published on 19th February 2025
Abstract
We demonstrate the application of the ‘instantaneous pK’ approach to the molecular dynamics simulation of crystallite models exposed to an acidic solvent environment. For this, the bulk solution properties pH and pK are scrutinized into local aspects and effectively characterized for individual molecules of crystal faces, edges and steps, respectively. To illustrate this concept, we introduce two prototype cases: the acid-induced dissociation of i) calcite and ii) carbamazepine (CBZ, form III) drugs. We find acid-induced calcite dissociation follows a rather intuitive mechanism, namely the protonation of crystal edges/steps leading to ion-by-ion dissociation of HCO3− and Ca2+ species into water. In contrast, our simulations of CBZ solvation at pH = 3 and pH = 2, respectively, reveal a more complex dissolution behavior. The molecular crystals were found to accommodate a substantial degree of CBZ protonation without drug release to the solvent. Instead, the crystallite edges and corners are re-arranged in favor of a surprisingly stable core–shell structure featuring a CBZ core and a mixed CBZ/CBZH shell of +0.005 and +0.03 C m−2 surface charge at pH = 3 and pH = 2, respectively. The resulting crystallite models are persistent and even more drastic acidity is needed to enable actual dissociation of CBZH into water.
Introduction
The acid-induced dissociation of solids is a common route to dissolving crystals with abundant applications ranging from pharmaceutical formulation to household cleaning. While the overall reaction equations are rather simple, the mechanisms of crystal surface rearrangement and solute dissociation into the solution may be quite complex. Indeed, on the molecular scale, our understanding of the involved processes is quite limited. A simple picture of crystal dissociation could be solute-by-solute dissociation – e.g. following the reverse process of what might have been observed for crystal growth. However, this does not necessarily apply to dissociation routes involving strong edge/surface reconstruction or the release of fragments.The need for molecular scale insights becomes particularly evident for contrasting systems that were precipitated at high pH, while dissociation is then encountered at low pH. This scenario is far from hypothetical, as for example the precipitation of calcium carbonate is a notorious problem in both technical processes and household cleaning. Effective removal of such precipitates commonly relies on acidic solutions, provoking chemical damage of the involved installations and environmental issues. In turn, molecular scale understanding of the involved processes facilitates the development of additives that might enable calcite dissociation at mildly acidic pH – much in analogy to the design of antiscalants for stabilizing CaCO3 solutions at neutral to basic pH, respectively.1–3
On the other hand, drug formulation for oral administration is often based on molecular crystals precipitated in an aprotic solvent while featuring constituents that can be protonated once the tablet reaches the intestinal system. Quantification and control of acid-induced dissociation is then of critical importance to provide well-defined kinetics of drug release to the patient.4–6 To this end, the beforehand mentioned simple picture of solute-by-solute dissociation must be discriminated from stepwise routes such as crystal protonation while releasing solutes only at low rates, followed by (e.g. charge-induced) fragmentation and possibly quite fast dissociation of the resulting pieces.
In what follows, we depicted two model systems as case studies to demonstrate the analysis of pH-dependent crystal–water interfaces from molecular simulations. Based on our recently developed approach to assessing protonation states via ‘instantaneous pK’ calculations, we elucidate models of i) a calcite (nano)crystal and ii) a crystallite of CBZ drug molecules. Benefitting from molecular scale resolution, our simulation protocol appears particularly suited for identifying preferential etching of corners and edges, or the selective dissociation of different crystal faces.
Methods
The common picture of pK (and pKa) is that of a global property of a solution as given by the thermodynamic balance of the concentration c of an acid (HA) and its conjugated base, which reflects averages over spatial and temporal fluctuations.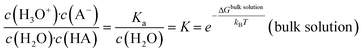 | (1) |
To this end, the HA and A− species are considered as dispersed solutes in the bulk solution, respectively. However, when looking into HA/A− species that are incorporated in solute aggregates or within a crystal surface, we must account for the local environment of the specific acid/base entity. This is reflected by the concept of a ‘local pK’ as a consequence of the change in free energy levels ΔG when contrasting the bulk solution and specific local environments.7,8
 | (2) |
| ΔGlocal − ΔGbulk solution ≈ 〈ΔElocal〉s − 〈ΔEbulk solution〉s | (3) |
While global averages taken for all interactions in a crystal–solvent system call for ns-scale sampling times, we recently demonstrated that focusing on the most relevant interaction terms helps to reduce fluctuations drastically such that the sampling runs reduce to the 10 ps scale.11 Indeed, in the example of calcium carbonate aggregates, the ‘instantaneous pK’ method was shown to provide the pK of local protonation sites at margins of ±0.4 to ±0.1 pH units, for 10 to 75 ps sampling runs, respectively. In the following, this spatially and temporally resolved interpretation of the pK is referred to as pKinst.
In what follows, we will depict analogous selections s of the most relevant interaction terms as in ref. 11, namely sampling only contributions involving the molecule to be protonated. In turn, solvent–solvent terms are ignored and also interactions within the crystal are ignored if the cut-off distance (chosen identical to the general cut-off delimiter applied to the intermolecular potentials) from the inspected protonation site is exceeded.
Simulation details
Calcite/calcium hydrogencarbonate ion solutions
Our molecular mechanics models of calcium, carbonate and bicarbonate ions in both calcite and in aqueous solution were adopted from the literature.12–14 The use of these well-established force field parameters is in full analogy to our earlier study reported in ref. 11, thus providing full comparability. Likewise, we also use analogous setups for the constant-temperature, constant-pressure molecular dynamics simulations and treatment of the electrostatic interactions.11 To model the calcite particle in an aqueous environment, a 3D-periodic solvent box of 16 × 18 × 18 nm3 (124![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 451 water molecules) was created.
451 water molecules) was created.
Carbamazepine/protonated counterparts
The molecular mechanics model of CBZ was taken from our recent work related to the subtle polymorphism of CBZ crystals.15,16 Therein, we outlined modifications of the general-purpose force field GAFF 1.4, including adjustments to partial charges and the tailoring of selected intramolecular interaction terms.For the protonated CBZ species, i.e. CBZH, we followed the same workflow to generate a GAFF-based molecular mechanics model. The underlying partial charges and interaction parameters for both CBZ and CBZH are provided in the ESI† (Table S1–S3). The solvent was described by the TIP3P water model (3D-periodic box of 14.5 × 12.5 × 11.5 nm3 dimensions featuring 211![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 674 water molecules), and the Lorentz–Berthelot mixing rules were applied.16
674 water molecules), and the Lorentz–Berthelot mixing rules were applied.16
Molecular dynamics settings
All molecular dynamics simulations were carried out using the LAMMPS suite with an integration time step of 1 fs.17 The built-in Nosé–Hoover thermostat–barostat combination was applied for temperature and pressure control at 300 K and 1 atm, respectively. To ensure decoupling of thermostat and barostat fluctuations, the underlying damping factors were chosen as 0.1 ps and 1.0 ps, respectively.To ensure reasonable relaxation of our simulation systems mimicking crystallite solvation, we follow a two-step strategy. First, the water box is relaxed whilst the crystallite is kept fixed. Relaxation of the simulation cell volume V and total energy E is benchmarked by comparing subsequent sketches of 1 ns runs, using <10−5 deviation of the relative changes ΔV/〈V〉 and ΔE/〈E〉, respectively, as convergence criteria. After such pre-equilibration of the solvent, the relaxation of all degrees of freedom is investigated using system-specific, more sensitive criteria as described in the results section.
Sampling of pK data
To identify possible protonation sites on the crystallite surfaces/edges, we used a simple geometric criterion based on nearest neighbor distance delimiters. The latter should be sufficiently large to avoid biasing the pKinst analysis – albeit reasonably small to save computational costs. Based on our inspection of the radial distance distribution functions sampled for the proton acceptor sites of carbonate/CBZ and the hydrogen atoms of the embedding water phase, we suggest a minimum distance of 2.2 Å as a reasonably generous delimiter for O⋯H contacts that might qualify for proton transfer. In the case of CO32− ions featuring more than one oxygen atom as possible protonation sites, we focused on the shortest O⋯H contact only.The pKinst values were calculated according to the minimized local energy scheme “ΔElocal,min” reported in ref. 11, namely monitoring only the locally relevant interactions of the carbonate/CBZ molecule under investigation. Statistics were collected from 10 ps MD runs under ambient conditions – from which snapshots were taken every 0.1 ps. The depicted configurations were then subjected to steepest descent energy minimization with convergence criteria of 10−8 eV and 10−8 eV Å−1 for energy and force, respectively, and an iteration limit of 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 steps. This effectively damps molecular vibrations such that 10 ps runs indeed suffice to collect pKinst values at <0.4 accuracy.
000 steps. This effectively damps molecular vibrations such that 10 ps runs indeed suffice to collect pKinst values at <0.4 accuracy.
Upon crystallite protonation, the overall charge of the model systems was balanced by introducing a corresponding amount of chloride ions – which were also described by the GAFF 1.4 force field.15 In both of the two systems investigated, we found Cl− to act as counter-ions dispersed in the solution without immediate interactions with the surfaces or dissociated solutes. For the identification of ionic species that were considered as dissociated from the crystallite models, we used a simple distance criterion – which threshold was set to twice the nearest-neighbor distance in the crystal lattice.
Results
Calcite crystallite
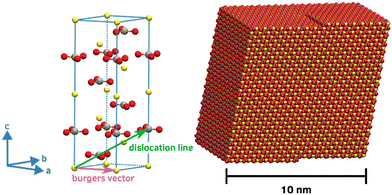
Our calcite crystallite models is based on a rhombohedral nanoparticle cut from the crystal structure along the crystallographically equivalent {104} planes. Comprising 17![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 416 CaCO3 formula units, the overall shape of this structure features edge lengths of about 10 nm in all directions. To account for screw-driven steps within the calcite faces – typically encountered in calcite crystallite structures, we modified the single-crystalline nanoparticle model accordingly. For this, a mixed dislocation anchored at the core of the particle was introduced to create a realistic screw-like structure without overlapping atoms or excessive gaps. This was achieved from extending a ‘pure’ screw dislocation, by a Burgers vector that is neither orthogonal nor parallel to the dislocation line. Instead, our choice of the dislocation line was oriented along the <441> direction, parallel to the particle's edge, while the Burgers vector was set to <100>, effectively mapping a carbonate molecule onto its in-plane neighbor. This configuration results in a smooth, screw-like structure whilst largely avoiding overlaps, gaps or excessive protrusions or kinks (Fig. 1). To confirm the stability of our modification, we performed energy minimization of both the single-crystalline block and the derived screw-like structure. From this, we found our model to be disfavored by only 0.0045 eV per formula unit as compared to the single crystal.
416 CaCO3 formula units, the overall shape of this structure features edge lengths of about 10 nm in all directions. To account for screw-driven steps within the calcite faces – typically encountered in calcite crystallite structures, we modified the single-crystalline nanoparticle model accordingly. For this, a mixed dislocation anchored at the core of the particle was introduced to create a realistic screw-like structure without overlapping atoms or excessive gaps. This was achieved from extending a ‘pure’ screw dislocation, by a Burgers vector that is neither orthogonal nor parallel to the dislocation line. Instead, our choice of the dislocation line was oriented along the <441> direction, parallel to the particle's edge, while the Burgers vector was set to <100>, effectively mapping a carbonate molecule onto its in-plane neighbor. This configuration results in a smooth, screw-like structure whilst largely avoiding overlaps, gaps or excessive protrusions or kinks (Fig. 1). To confirm the stability of our modification, we performed energy minimization of both the single-crystalline block and the derived screw-like structure. From this, we found our model to be disfavored by only 0.0045 eV per formula unit as compared to the single crystal.
To model the calcite particle in aqueous environment, a 3D-periodic solvent box of 16 × 18 × 18 nm3 was created. After first quenching to 0 K, the system was heated to 300 K and allowed to relax under ambient conditions over a duration of 1 ns. Throughout this equilibration run, the dislocation remained stable, while individual carbonate ions located at the corners, edges, on the steps, and also on the flat surface displayed slight (rotational) mobility. However, all ions maintained their respective lattice positions within the crystallite model. In addition, the overall volume and energy of the simulation system was found to converge within the first 100 ps of the relaxation run.
After equilibration, we scanned the H(water)⋯O(crystallite) distances to create a candidate list of potential protonation sites. This list features all surface-exposed carbonate ions in contact with water, totaling 3058 possible protonation states to be investigate. The evaluation of the individual pKinst of each surface-exposed carbonate ion can be implemented in a massively parallel setup of simulation runs, as each protonation state refers to a separate molecular simulation system. For the sake of comparability with common experiments, we transfer our pKinst data into pKa values of the corresponding acid (see also eqn (1)). The computed (local) pKa values range from −10 to 7, with the most abundant value of pKa = −3 being observed for protonation of carbonate ions located at flat surfaces (see also Fig. S1†). In contrast, ions at edges and corners exhibited different pKa characteristics, including the pKa range of interest for protonation by mildly acidic solutions as discussed in the following.
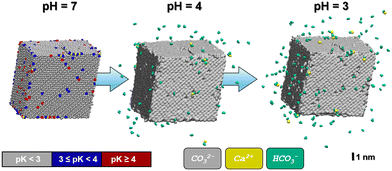
As one would intuitively expect, the calcite crystallite model is particularly prone to protonation at its most exposed surface sites, namely corners and edges. In Fig. 2, the particle is depicted using a color code to visualize the pKa values of the corresponding (hydrogen) carbonate ions. In line with typical limescale removers such as citric acid (pKa = 3.1), we focus on moderate acid conditions, namely pH = 3, 4 or higher. At pH = 4, only a comparably small number of 93 carbonate ions are protonated (with ∼68% of those being located at the edges/steps of the crystallite model) are protonated.
To illustrate the evolution of the calcite crystallite in the acidic environment, we prepared two independent relaxation runs based on the models referring to the protonation states predicted at pH = 4 and pH = 3. To this end, the simulation run referring to pH = 4 is initiated from the crystallite–water system discussed above, however implementing protonation of all 93 carbonate ions with pKa ≥ 4, whilst introducing the same amount of Cl− ions into the water phase to balance total charge. Upon relaxation from the MD simulation under ambient conditions, we found 66 of the formed HCO3− ions to dissociate from the crystallite within 1 ns whereas only 9 Ca2+ ions were released into solution. Our models thus suggest a notched crystal with a positive excess charge of 141, which implies a charge density of 0.013 C m−2, respectively.
In turn, at pH = 3 we find a substantial number (158) of protonation events with 75% of these leading to bicarbonate dissociation within a 1 ns relaxation run. Upon the release of this multitude of HCO3− ions, we also observe the dissociation of 17 Ca2+ ions. The amount of released calcium ions however only compensates only about 1/4 of the +158 charge induced from protonation and dissociation of HCO3− ions. Indeed, the dissociated calcium ions exclusively stem from local sites that experienced the protonation of several carbonate species at the nearest neighbor contact. We thus argue that the release of the calcium ion is provoked by the loss of salt-bridges from at least two protonation and HCO3− dissociation steps. Namely,
 | (i) |
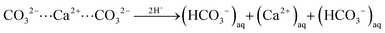 | (ii) |
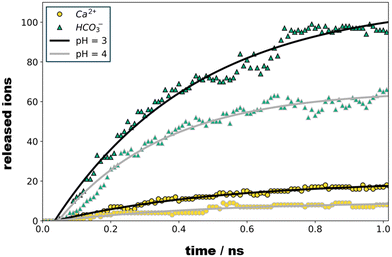
Upon 1 ns propagation, we find the crystallite charge to converge to +225, which reflects a surface charge density of 0.018 C m−2. The number of Ca2+ and HCO3− species released from our crystallite model is shown as functions of time in Fig. 3. Note that the dissociation kinetics are boosted from the protonation of all sites suggested suitable for pH = 4 and pH = 3 – without re-evaluating the local pK after each protonation step. While one-by-one protonation and relaxation simulation runs would provoke enormous computational costs, we suggest our simulation models as comparably simple estimates that provide at least qualitative assessment of the ratio of Ca2+ and HCO3− ions released.
Carbamazepine
As a starting point, we depicted a nanoparticle model of CBZ form III (8 × 5 × 4 supercell, 640 molecules) from our earlier study reported in ref. 16. Form III reflects the thermodynamically most stable polymorph of CBZ and also the shape of the chosen crystallite was observed to be quite stable in vacuum.16 Our model thus mimics a CBZ crystallite grown in an apolar solvent as commonly used in pharmaceutical formulation. Upon immersion into water, it is however quite intuitive to expect substantial reorganization. Indeed, our initial crystallite model features CBZ–CBZ hydrogen bonding whilst predominantly exposing the apolar moieties of CBZ towards the outer faces.Careful system relaxation was performed after embedding the CBZ crystallite into water. For this, we initially kept the CBZ atoms fixed whilst quenching the embedding water molecules. After heating to 300 K, the system was then propagated under ambient conditions for 5 ns to allow relaxation of the overall volume and energy. Next, full relaxation of all degrees of freedom, thus including the CBZ molecules, was studied. During this relaxation run, significant rearrangements were observed during the initial 0.1–1 ns, in particular at the edges of the crystallite. While the inner structure of CBZ form III is preserved, the evolution of the crystal surface upon solvation in water is illustrated in Fig. 4. The system was propagated for a total of 10 ns whereas relaxation of (H)CBZ molecules at the CBZ–water interface is observed after 2 ns, respectively. We point out that the observed CBZ–water interface converged to a locally stable arrangement without exhibiting dehydrate formation, which arguably would call for much longer termed relaxation at pH = 7.
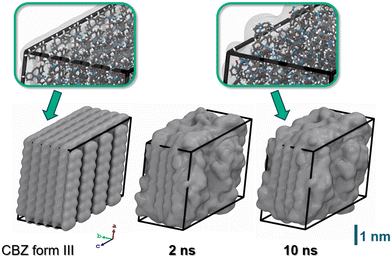 | ||
| Fig. 4 Snapshots of the CBZ crystallite. Left: Starting configuration featuring hydrophobic crystal faces as observed for interfaces to apolar solvents or vacuum. Center and right: Same model, but after 2 and 10 ns propagation in water (solvent not shown). In line with the low solubility of CBZ in water, the structure of CBZ polymorph III is basically retained.18 However, molecules at the crystallite corners and edges substantially rearrange to provide hydrogen bonding with the polar solvent. The atom colors of the insets are chosen as H (white), C (grey), N (blue) and O (red), respectively. | ||
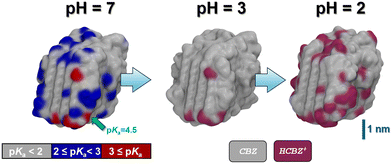
Following relaxation of the unprotonated CBZ crystallite in water, we then scanned potential sites for the uptake of protons. For this, we created a pre-selection list based on geometric considerations in analogy to the calcite system. This leads to a total of 189 possible sites for CBZ protonation, of which the corresponding CBZH showed pKa values ranging from 5 to −5. To this end, the unprotonated CBZ form III crystallite relaxed in water readily reflects neutral pH, and even mildly acid conditions. However, at the crystallite corners and edges protonation of the particularly exposed CBZ molecules implies a local pKa of 2 to 5, whereas local pKa values from −5 to 2 are observed for protonation of the less exposed CBZ molecules at the crystallite faces, respectively (Fig. 5).
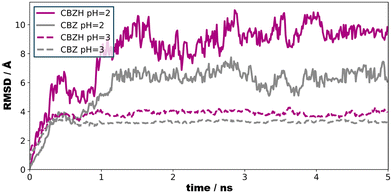
To illustrate the effect of acidic solutions on the molecular crystal model, we implemented the protonation of surface CBZ species according to the estimated pKa (of the corresponding CBZH acid) as sampled for the crystallite model shown in Fig. 5(left) . This was performed for two scenarios, namely pH = 3 and pH = 2. This choice was motivated by the acidity of the gastric system – with the pH of human stomach fluid typically ranging from 3.5 to 1.5, respectively. In both simulation runs, we find that the CBZ/CBZH nanoparticles undergo substantial surface reorganization – as indicated by the root-mean-square deviation profiles shown in Fig. 6. Strikingly, the inner CBZ core not only maintains its crystal lattice positions but also retains the rather amorphous CBZH shell. Along this line, the molecular surface of the crystallite increases quite significantly. While the solvent accessible surface was calculated as 318 nm2 for pH = 7, the roughening of crystallite edges at pH = 3 and pH = 2 increases the surface to and 321 and 387 nm2, respectively.
Our simulation models thus suggest that CBZ may accommodate substantial charging by proton uptake before dissociation. Indeed, upon relaxation of the crystallite model at pH = 2, we find that surface rearrangements lead to numerous solvent-exposed CBZ molecules that are candidates for even further protonation of the crystallite. To this end, the illustrated structure in Fig. 5 may serve as a starting point for investigating the uptake of further protons – possibly using even lower pH – to impose acid-induced dissociation. While a rigorous study of step-by-step protonation and relaxation iterations exceeds the scope of the present work, here we already demonstrate a ‘non-classical’ aspect of CBZ dissociation characteristics. Indeed, the observed protrusions of the amorphous CBZH/CBZ shell suggests the fragmentation of charged agglomerates as a speculative mechanism of crystal dissociation.
Conclusions
The approximate assessment of protonation states in molecular models is of central importance for enabling pH-dependent formulation of simulation systems. Given a large number of possible protonation sites, quantum chemical approaches often imply prohibitively large computational costs. In turn, the assignment of protonation states by the help of experimental pKa data is well-established in molecular mechanics simulations, including the modelling of proteins that feature numerous proton donor/acceptor moieties at the nm scale distance. To account for the local environment, it is intuitive to sample local interactions to estimate correction terms to provide a ‘local pKa’.7,8For the modelling of crystal surfaces, such assessment of protonation states is complicated by the large number of possible protonation sites and by the structural instability that might result from protonation. To account for the proton affinity of a candidate site – as it is ‘seen’ by an aqueous H+ nearby – we need to sample the underlying energy terms at the 10 ps scale, i.e. accounting for momentous configurations. In turn, structural evolution of crystal surfaces at time scales beyond that of proton diffusion in water leads to time-dependent fluctuations of the local pKa of our models.
By depicting snapshots from relaxed calcite and CBZ drug crystals in water (at pH = 7, no protonation), we demonstrated the calculation of instantaneous, local pKa as a molecular property that helps to visualize proton affinity of the solvent-assessable surface of crystallites. While the preferred protonation of exposed carbonate or CBZ species at the corners and edges of the nanoparticle models is quite intuitive, predicting structural relaxation upon assigning the protonation state of the overall crystal is less straight-forward. The acid-induced dissociation of calcite is suggested as a one-by-one mechanism in which the formed bicarbonate species are dispelled to the solvent and calcium ions would follow upon losing a sufficient number of carbonate neighbors. In turn, the molecular crystal of CBZ displays a ‘non-classical’ behavior, namely surface roughening upon protonation before inevitable decomposition at sufficiently low pH. The observed core–shell structures suggest that a substantial degree of protonation may be accommodated before acid-induced dissociation. Considering the amphiphilic nature of CBZ (as prototypic for class II drugs of the biopharmaceutical classification system) we suggest that dissociation likely involves fragmentation of agglomerates rather than expelling single solutes – much in analogy to the solute aggregates recently observed in under-saturated bulk solutions.18,19
We point out that the present study focused on the assessment of local, instantaneous pKa values of crystallite models depicted from non-acidic solution. The assignment of protonation states was implemented on the basis of a single reference system, whereas relaxation of protonated crystallites in principle calls for subsequent re-evaluation of the instantaneous pKa values as a function of time. While surely indispensable to the evaluation of kinetic properties, we suggest the more approximate approach of the present study as a computationally favorable route to exploring crystal dissociation mechanisms from molecular dynamics simulations.
Data availability
See DOI: https://doi.org/10.1039/D4CE01292E. It is our pleasure to submit the manuscript “On the pK of crystal surfaces: molecular modeling of crystallite protonation, local reorganization, and solute dissociation” to Cryst. Eng. Comm. All data is presented in the manuscript. Our simulation models can be made accessible upon request to the corresponding author.Conflicts of interest
There are no conflicts to declare.Acknowledgements
PD and DZ acknowledge funding from Procter & Gamble Inc. whereas MM and DZ received financial support from the Deutsche Forschungsgemeinschaft (DFG, German Research Foundation, grant number ZA 420/14-1). High-performance computing was provided by the Erlangen National High Performance Computing Center (NHR@FAU).References
- P. Raiteri, R. Demichelis, J. D. Gale, M. Kellermeier, D. Gebauer, D. Quigley, L. B. Wright and T. R. Walsh, Faraday Discuss., 2012, 159, 61–85, 10.1039/c2fd20052j.
- D. Gebauer, H. Cölfen, A. Verch and M. Antonietti, Adv. Mater., 2009, 21, 435–439, DOI:10.1002/adma.200801614.
- D. Gebauer, Minerals, 2018, 8, 179, DOI:10.3390/min8050179.
- D. R. Cowsar, Controlled Release of Biologically Active Agents, Springer US, Boston, MA, 1974, vol. 47 Search PubMed.
- L. D. Simon, L. Ruiz-Cardona, E. M. Topp and V. J. Stella, Drug Dev. Ind. Pharm., 1994, 20, 2341–2351, DOI:10.3109/03639049409042641.
- S. H. Yuk, S. H. Cho and H. B. Lee, J. Controlled Release, 1995, 37, 69–74, DOI:10.1016/0168–3659(95)00065-G.
- D. Zahn, Chem. Phys. Lett., 2017, 682, 55–59, DOI:10.1016/j.cplett.2017.06.002.
- D. Zahn, RSC Adv., 2017, 7, 54063–54067, 10.1039/c7ra11462a.
- G. Li and Q. Cui, J. Phys. Chem. B, 2003, 107, 14521, DOI:10.1021/jp0356158.
- J. R. Pliego, Chem. Phys. Lett., 2003, 367, 145–149, DOI:10.1016/S0009-2614(02)01686-X.
- P. Duchstein, F. Löffler and D. Zahn, ChemPhysChem, 2024, 25, e202300489, DOI:10.1002/cphc.202300489.
- R. Demichelis, P. Raiteri, J. D. Gale, D. Quigley and D. Gebauer, Nat. Commun., 2011, 2, 590, DOI:10.1038/ncomms1604.
- P. Raiteri and J. D. Gale, J. Am. Chem. Soc., 2010, 132, 17623–17634, DOI:10.1021/ja108508k.
- Y. Wu, H. L. Tepper and G. A. Voth, J. Chem. Phys., 2006, 124, 024503, DOI:10.1063/1.2136877.
- J. Wang, R. M. Wolf, J. W. Caldwell, P. A. Kollman and D. A. Case, J. Comput. Chem., 2004, 25, 1157–1174, DOI:10.1002/jcc.20035.
- A. Gadelmeier, M. Macht and D. Zahn, J. Pharm. Sci., 2022, 111, 2898–2906, DOI:10.1016/j.xphs.2022.06.001.
- A. P. Thompson, H. M. Aktulga, R. Berger, D. S. Bolintineanu, W. M. Brown, P. S. Crozier, P. J. in't Veld, A. Kohlmeyer, S. G. Moore, T. D. Nguyen, R. Shan, M. J. Stevens, J. Tranchida, C. Trott and S. J. Plimpton, Comput. Phys. Commun., 2022, 271, 108171, DOI:10.1016/j.cpc.2021.108171.
- A. Shayanfar, S. Velaga and A. Jouyban, Fluid Phase Equilib., 2014, 363, 97–105, DOI:10.1016/j.fluid.2013.11.024.
- H. Lu, M. Macht, R. Rosenberg, E. Wiedenbeck, M. Lukas, D. Qi, D. Maltseva, D. Zahn, H. Cölfen and M. Bonn, Small, 2024, 20, 2307858, DOI:10.1002/smll.202307858.
Footnotes |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4ce01292e |
| ‡ P. D. and M. M. contributed equally to this work. |
| This journal is © The Royal Society of Chemistry 2025 |