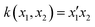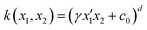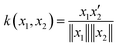Deciphering nonlinear optical properties in functionalized hexaphyrins via explainable machine learning†
Eline
Desmedt
 ,
Michiel
Jacobs
,
Michiel
Jacobs
 ,
Mercedes
Alonso
,
Mercedes
Alonso
 * and
Freija
De Vleeschouwer
* and
Freija
De Vleeschouwer
 *
*
Department of General Chemistry: Algemene Chemie (ALGC), Vrije Universiteit Brussel, Pleinlaan 2, 1050 Brussel, Belgium. E-mail: Mercedes.Alonso.Giner@vub.be; Freija.De.Vleeschouwer@vub.be
First published on 7th November 2024
Abstract
Over the years, several studies have aimed to elucidate why certain molecules show more enhanced nonlinear optical (NLO) properties than others. This knowledge is particularly valuable in the design of new NLO switches, where the ON and OFF states of the switch display markedly different NLO behaviors. In the literature, orbital contributions, aromaticity, planarity, and intramolecular charge transfer have been put forward as key factors in this regard. Based on our previous work on functionalized hexaphyrin-based redox switches, we aim at identifying through explainable machine learning the driving forces of the first hyperpolarizability related to the hyper-Rayleigh scattering (βHRS) of meso-substituted and/or core-modified [26]- and [30]hexaphyrins. The significant correlation between βHRS and the HOMO–LUMO energy gap can be further improved by including other orbitals as well as charge-transfer features in a 6-fold cross-validated kernel-ridge-regression model. Our Shapley additive explanations (SHAP) analysis shows that the charge transfer excitation length is more important for 30R systems, whereas the transition dipole moment between the ground and first excited state is one of the main contributors for 26R systems. We also demonstrate that, besides various hexaphyrin-based redox states, the ML model can describe to a large degree the βHRS response of other hexaphyrins, differing in substitution pattern and topology (26D and 28M).
Introduction
Ever since the discovery of second harmonic generation (SHG) in a ruby crystal in the 1960s, the interest in discovering new materials with nonlinear optical (NLO) properties has spiked.1 Owing to their tailorability and processability, organic materials with enhanced NLO properties are sometimes even preferred over the standard inorganic materials or crystals for potential applications in optical computing, optoelectronics and photonics.2–5 With the increasing demand to reduce the size of our current electronic devices, these organic NLO materials are especially promising for the creation of novel molecular devices with switchable NLO properties to combine with or replace our current silicon-based electronics.6,7 Molecular switches are only one example of these molecular devices, which can act as key components in photonic and optoelectronic applications such as logic gates and memory devices.8 After applying an external stimulus, these single molecules can be reversibly converted to other stable states. The contrast associated to the significant difference in NLO response between the different molecular states of the switch is frequently used as a figure-of-merit to assess the switch's performance.9 It can be assessed by several NLO quantities such as the first and second hyperpolarizability, denoted as β and γ, respectively. Various optical phenomena such as the SHG, two-photon absorption (TPA), third-harmonic generation (THG), and the hyper-Rayleigh scattering (HRS) are connected to these hyperpolarizabilities.Efforts have been made to acquire an in-depth understanding of the structure–property relationships for molecules involving NLO properties. For polyenes and polymethine dyes, several studies found that β and γ are highly connected to the molecular structure through the bond-length alternation (BLA) and bond-order alternation (BOA).10–12 More recently, the NLO anisotropies of different X-shaped pyrazine isomers were elucidated by scrutinizing the low-lying excited states’ symmetry.13 Multiple studies have also established structure–property relationships for various NLO molecular switches to understand their change in NLO properties.9,14,15 Tuning the intramolecular charge transfer in push–pull molecules changes the NLO properties immensely.16 In RuII/III redox-switches, the β mainly stems from excited states characterized by metal-to-ligand charge transfer.17 When the RuII/III centers are oxidized, the donor character of the Ru is diminished by reducing the push–pull π-conjugation in these systems. Consequently, the first hyperpolarizability related to the hyper-Rayleigh scattering, βHRS, decreases in value. In addition, this study revealed symmetry-NLO relationships for these systems.17 Another example is the pH-controlled dimethyldihydropyrene/cyclophanediene photoswitch, where protonation of the acceptor yields a higher NLO response as a result of a larger π-conjugation and more apparent charge transfer transitions.18 The opposite behaviour is observed by protonating the donor of the push–pull system. Regarding one of the most studied systems, the azobenzene, orbital contribution decomposition analysis showed that the main orbital contributions to the β response come from the azo bond.19 However, the response can be augmented by including additional substituents on the neighbouring phenyl rings. In 1977, Oudar and Chemla presented the simple two-state approximation (TSA) to rationalize the β response considering only one electronic excited state, usually S1 (eqn (1)).20
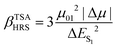 | (1) |
In this model, μ01, |Δμ|, and ΔES1 are the transition dipole moment between S0 and S1, the absolute difference between the excited state dipole moment and the ground state dipole moment, and the associated excitation energy, respectively. This model had varying success in describing the β response in experimental and theoretical studies.20–28
Another well-studied family of molecular switches, and the main focus of this paper, is a specific class of porphyrin-based molecules known as expanded porphyrins. Compared to the porphyrin molecule, expanded porphyrins consist of a larger extended π-conjugated system, which red-shifts the absorption bands and increases the TPA cross-sections (σ(2)).29 Thanks to this expansion and their conformational flexibility, these systems have been proposed as interesting candidates for various applications such as near-infrared dyes, biosensors, nonlinear optical materials, and molecular electronics.30–33 Recently these macrocycles have been put forward as potential nonlinear optical molecular switches, because of their ability to reversibly switch between different redox states and/or distinct π-conjugation topologies causing drastic changes in NLO properties.34–36 Harnessing the expanded porphyrin's switching abilities allows to turn their NLO properties “ON” or “OFF” and to use them as a test bed to study the relationship between NLO properties and aromaticity.
Kim and co-workers substantially investigated the σ(2) of various expanded porphyrins and connected these enhanced values to the intramolecular charge transfer or the rigid planarity of molecules with a large π-conjugated system fulfilling the [4n + 2] Hückel rule for aromaticity.37–41 Hence, the authors proposed this molecular property as a quantitative measure to estimate experimentally the aromaticity of the macrocyclic π-system. For example, the σ(2) of the rectangular aromatic [26]hexaphyrin is found to be four times higher than the antiaromatic [28]hexaphyrin.40 On top of that, a strong linear correlation between the σ(2), nucleus-independent chemical shift (NICS(0)) value, and the molecular planarity was retrieved.37–40 However, this correlation diminishes for core-modified expanded porphyrins.37 Furthermore, Chandrasheka and coworkers also traced back the enhanced σ(2) intensities of core-modified expanded porphyrins to aromatic, planar expanded porphyrin structures.42
Nevertheless, determining the relationship between the topology, aromaticity, and nonlinear optical properties for expanded porphyrins remains complex as noted by the computational work of Alonso and co-workers.34,35,43 For porphyrinoid systems with a high ring strain and reduced symmetry, they observed significantly enhanced first hyperpolarizabilities (βHRS and β) but retrieved no clear connection with aromaticity. On the other hand, the value of the second hyperpolarizability is higher for aromatic twisted-Hückel topologies, than for their antiaromatic counterparts. This observation also applies to meso-aryl-substituted porphyrinoids. In summary, they concluded that factors such as symmetry, planarity and the size of the macrocycle contribute to further understanding of the NLO properties.
The aforementioned studies provide a broad overview of structure–property relationships and correlations to understand and compare the NLO property trends of different types of molecules, including molecular switches within different families of expanded porphyrins with varying conformations, topologies and oxidation states. In this work, we will primarily focus on elucidating the NLO response of different chemically functionalized hexaphyrin-based redox states. In previous works, we searched for new functionalized 26R → 28R and 30R → 28R switches with high nonlinear optical contrasts using inverse molecular design algorithms.44–46 These functionalizations included combinations of core-modifications and meso-substitutions on the hexaphyrin's framework. Analysis of the inverse design dataset allowed us to derive structure–property relationships for the best-performing [26]- and [30]-hexaphyrin-based switches.45,46 Even though the 26R → 28R and 30R → 28R switches are structurally very similar, the optimal functionalization pattern yielding high NLO contrasts are strikingly different for both. Push–pull meso-substitution patterns were found to increase the NLO response for both 26R and 30R systems, but there is a difference in preference for strong electron-donating groups (EDGs) and strong electron-withdrawing groups (EWGs). With respect to core-modifications, we observed that they can synergistically enhance the NLO response of the 30R.45 However, the best-performing 26R → 28R switches do not favor the inclusion of core-modifications.
The balance between different types of functionalization, their position and the potentially synergistic effect between them, makes the prediction and understanding of the resulting NLO response intricate. In this follow-up study, we aim to identify the driving forces that govern the NLO response of the 26R and 30R by developing an explainable machine-learning model. First, the correlation between our target property, βHRS, and a broad range of property features is analyzed, of which most have been previously connected to NLO properties of alternative organic molecules. Based on the best correlating features, we build kernel-ridge-regression (KRR) based machine-learning models to predict our target property. However, our ultimate goal is not to predict the NLO response, but to understand the influence of the features on the target property by applying interpretable machine-learning techniques on our KRR models, such as an analysis based on Shapley values.
Computational details
Calculation of the quantum-chemical features
Unless stated otherwise, all features were extracted from quantum-chemical calculations performed with the Gaussian16 software package.47 All hexaphyrin geometries were obtained by performing geometry optimizations at the CAM-B3LYP/6-311G(d,p) level of theory and are characterized as minima on the potential energy surface through harmonic vibrational frequency analyses.48,49 The choice for this level of theory is based on several benchmark studies, which compared the relative energies of expanded porphyrins with different DFT functionals to the golden standard canonical CCSD(T) at the extrapolated basis set limit.50–52Our target property is the first hyperpolarizability associated to the HRS phenomenon, abbreviated as βHRS.53–55 This quantity is related to the intensity of the incoherent light scattered at twice the frequency of the incident laser pulse. Under the condition that the incoherently scattered light is perpendicular to the laser's propagation plane, the HRS equation can be simplified to eqn (2):
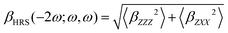 | (2) |
In addition, the depolarization ratio (DR) is computed in eqn (3). Where 〈βZZZ2〉 and 〈βZXX2〉 represent in both equations the orientational averages of β.
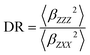 | (3) |
To compute the HRS hyperpolarizability tensors in the static regime, the coupled-perturbed Kohn–Sham equations were employed. Based on several studies on the importance of large amounts of exact HF exchange at larger interelectronic distances to semi-quantitatively describe the βHRS of expanded porphyrins, we employed the long-range corrected CAM-B3LYP functional.21,56–58 Regarding the basis set, it is recommended to use split valence double- or even triple-ζ basis sets with one set of diffuse and polarization functions for sufficiently describing the dominant β tensor components and depolarization ratios.9,59,60 Hence, for carrying out the NLO response calculations, we chose CAM-B3LYP/6-311+G(d,p).
At the same level of theory as our NLO calculations, we computed the different frontier molecular orbital (FMO) energies: HOMO−1 (H−1), HOMO (H), LUMO (L), and LUMO+1 (L+1). In addition to the FMO energies, we also evaluated several orbital energy differences, including, the HOMO–LUMO gap (ΔHL) and the differences between (I) H and H−1 (ΔH), (II) L and L+1 (ΔL), (III) H−1 and L (ΔL_H−1), (IV) H and L+1 (ΔL+1_H), and (V) the criterion |ΔH − ΔL|2.61–64 The selection of the orbital transitions is based on previous works, which highlighted the importance of these transitions to rationalize optical properties such as absorbance spectroscopy and magnetic circular dichroism for porphyrinoid systems.61–64 Moreover, the trace of the quadrupole moments (Qtrace) and the dipole moment (μ) were also extracted from these calculations.
Next, several electronic descriptors such as the vertical ionization energy (IE) and the vertical electron affinity (EA) were computed with B3LYP/6-311+G(d,p),49,65,66 in line with previous studies within our research group.67–69 Using the IE and EA, three additional descriptors were calculated: the electronic chemical potential (μe), the chemical hardness (η) and the electrophilicity index (ω). The electronic chemical potential70 or the negative electronegativity (χ) for an N-electron system is defined in eqn (4):
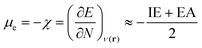 | (4) |
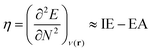 | (5) |
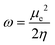 | (6) |
To estimate the amount of charge transfer within the hexaphyrin macrocycles, we relied on orbital- and density-based indices such as Δr, the transferred charge (qCT) and the charge transfer excitation length (DCT).73,74 The Δr index is based on the electron–hole distance or the distance between the charge centroids of the orbitals involved in the excitations.73 Regarding the density-based indices, we computed the difference in electronic densities of the ground (ρGS(r)) and the first excited state (ρES(r)), respectively (eqn (7)).74 The electronic densities associated to their vertical electronic excitations at the TD-DFT CAM-B3LYP/6-311G+(d,p) and charge transfer indices were computed with the Gaussian16 and Multiwfn software packages, respectively.47,75
| Δρ(r) = ρES(r) − ρGS(r) | (7) |
Two different co-domains of Δρ(r) are identified based on the sign of the density describing either a charge accumulation (ρ+(r)) or a charge depletion (ρ−(r)) upon absorption. At the center of charge, the distribution of the depletion and accumulation can be characterized by eqn (8).
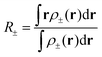 | (8) |
The final charge transfer excitation length is then defined in eqn (9) as the spatial distance between these two barycenters (R+ and R−). In addition, qCT is defined by integrating over all space of the two co-domains (ρ+ and ρ−).
| DCT = |R+ − R−| | (9) |
In addition, the electronic dipole moments related to S1, the transition dipole moment μ01 and the excitation energy ΔES1 between the ground state and its first excited state, respectively, are extracted from the TD-DFT calculations to compute Oudar and Chemla's TSA to the β response. Note that qCT and DCT are computed based on the unrelaxed densities, while the dipole moments are computed with the relaxed density.
Widely used structural descriptors to describe porphyrinoid macrocycles such as the torsional ring strain (Φp) and π-conjugation index (Π) were included in our feature set.76,77 The average dihedral angle between neighboring pyrrole rings is described by the torsional ring strain. On the other hand, the effective overlap of the adjacent p-orbitals is expressed by the Π descriptor. Negative Π values are associated with Möbius conformations, while the Hückel conformations exhibit a positive Π value. Porphyrinoids with macrocyclic aromaticity are characterized with a Π value above 0.30.76
Because nonlinear optical properties have been previously linked to aromaticity, we computed a diverse set of aromaticity descriptors rooted in different criteria to evaluate the multidimensional character of aromaticity.78–80 Two aromaticity indices were selected based on the structural criteria: bond-length alternation (BLA)81 and the harmonic oscillator model of aromaticity (HOMA).82 Four electronic indices, i.e., AV1245 index,83,84 AVmin index,84 bond-order alternation (BOA),81 and aromatic fluctuation index (FLU),85,86 were considered. In line with our previous research on porphyrinoid systems, the six aforementioned indices were computed along the most conjugated pathway, which corresponds to the annulene pathway in neutral macrocycles.84,87 For the calculation of these structural and electronic indices, the ESI-3D code88 in conjunction with the AIMAll software89 was used. The latter software was employed to compute the atomic overlap matrices and relies on the quantum theory of atoms in molecules (QTAIM) partition scheme. Based on the magnetic criteria, both the isotropic and out-of-plane tensor components of nucleus independent chemical shifts (NICS)90–92 are computed using the gauge-independent atomic orbital method (GIAO).93,94 Three different positions were considered for the NICS calculation: (I) at the the geometric center of the macrocyclic ring defined by its heavy atoms, (II) 1 Å above, and (III) 1 Å below the molecular plane. The molecular plane for nonplanar structures is defined by a least-square fitting considering all coordinates of the heavy atoms of the macrocycle.95 All aromaticity indices were computed with the long-range corrected CAM-B3LYP48 and the 6-311+G(d,p) basis set49 to reduce the impact of the delocalization error.84,96
Machine-learning models
All input features for the machine-learning models were standardized by subtracting the mean and scaling to the unit variance (eqn (10)).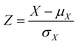 | (10) |
Next, we constructed different kernel ridge regression (KRR) models with the scikit-learn python package.97 Ridge regression models (11) build further on linear regression models (OLS) by introducing an additional penalty term, also known as the regularisation term L2, to the ordinary least squares function. The incorporation of this penalty term aids in the generalization of the model and prevents overfitting.
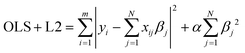 | (11) |
Ridge regression is particularly useful when correlated features are considered.
KRR models add a kernel trick, which alters the input data by a mathematical function known as a kernel. Examples of such kernels are listed in Table 1.
Since only a few hyperparameters are needed to be tuned, KRR are robust models and even suitable for small datasets. We resorted to KRR models, because the size of our dataset is rather small and we still wanted to introduce nonlinearity to our model.
Our dataset was split in a training and test set, containing 75% and 25% of the data, respectively. For the hyperparametrization, we performed 1000 trials on the training set with the Optuna package98 to tune five different hyperparameters as listed in Table 2. The objective of these hyperparametrization runs was to minimize our selected validation metric, the mean absolute error (MAE), with the six-fold cross-validation scheme.
| Hyperparameter | Boundaries |
|---|---|
| α | 0.01 < α < 1000 |
| Kernel | Linear, polynomial, radial basis function laplacian, sigmoid, cosine |
| Degree | 1, 2, 3, 4, 5 |
| γ | 0.1 < γ < 10 |
| Coefficient0 | 0.1 < coefficient0 < 2 |
After acquiring our best set of tuned hyperparameters (see Table S1 in the ESI†), we fitted our KRR model on the full training set and predicted the NLO response of the test set. The model's performance was evaluated through the MAE and R2, whereas the contribution of each feature on the model's performance was assessed via the feature permutation importance technique as implemented in scikit-learn python package.97
Finally, we applied a SHapley Additive exPlanations (SHAP) analysis99,100 to our selected KRR model to understand the contribution of the different input features to the ML model prediction value, relative to a given baseline (here, the average of the predictions). Shapley values are derived from concepts of cooperative game theory to find a fair contribution of profits and costs (i.e., the ML predictions) by different players (i.e., the input features) forming a coalition. The advantage of SHAP is that both global feature importances as well as their importance on the local predictions can be determined. For this analysis, we used R package shapr to calculate the SHAP values with the Kernel SHAP method as this package takes feature dependence into account for the computation.101 The SHAP python package was employed for the visualization of the SHAP values.99,100
Results and discussion
Correlations between features and βHRS response
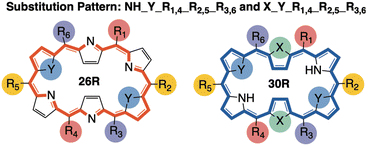
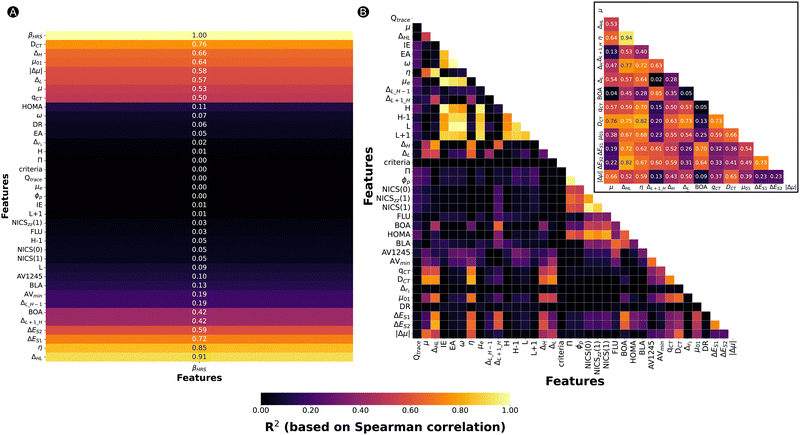
Based on our previous work, we collected a dataset consisting of 562 functionalized hexaphyrins with the X2Y2A2B2C2 pattern biased towards high hyperpolarizabilities related to the hyper-Rayleigh scattering βHRS (Fig. 1).45,46 More specifically, this dataset contains 242 and 320 meso-substituted and core-modified [26]- and [30]hexaphyrin structures with a Hückel topology (26R and 30R), respectively. All structures contain combinations of the following meso-substituents on the positions R1–R6: NO2, CN, F, H, CH3, OH and NH2. Depending on the oxidation state of the hexaphyrin, up to two core-modification sets (X, Y) are present, where NH is replaced by O, S or Se. Only Y modifications were allowed for 26R to avoid charged molecules. The labelling of the 26R and 30R following their substitution pattern is presented in Fig. 1.As already mentioned, this dataset is composed of structures which are skewed towards high nonlinear optical responses since they were generated during NLO contrast optimization runs using an inverse design algorithm. For a detailed comparison between the [26]- and [30]hexaphyrins, we refer to our previous work, in which we extensively described the different design rules for the molecular switches based on these two redox states.46 Aside from the target property, the βHRS response, we computed 35 additional properties. These features can be categorized based on their intrinsic character as indicated in Table 3. By investigating the intercorrelation between the individual 35 features as well as the correlation with our target property, βHRS, we aim to identify the driving forces responsible for increasing the nonlinear optical response of hexaphyrin macrocycles.
| Category | Features |
|---|---|
| Aromaticity (structural) | BLA & HOMA |
| Aromaticity (electronic) | AV1245, AVmin BOA & FLU |
| Aromaticity (magnetic) | NICS(0), NICSzz(1) & NICS(1) |
| Orbital | H−1, H, L, L+1, ΔH, ΔL, ΔHL, ΔL_H−1, ΔL+1_H & criteria |
| Charge transfer | q CT, DCT, Δr & μ01 |
| Electronic | Q trace, μ, IE, EA, ω, η, μe, ΔES1, ΔES2, |Δμ| & DR |
| Geometrical | Π & ϕp |
Fig. 2A summarizes the coefficients of determination (R2) based on the Spearman correlation between the 35 features and the βHRS. Each feature is ranked according to its Spearmann correlation value from a positive to negative correlation. Only 13 of the 35 features have an R2 greater than 0.42, namely, ΔHL, η, ΔES1, ΔES2, ΔL+1_H, BOA, qCT, μ, ΔL, |Δμ|, μ01, ΔH, and DCT. These 13 features belong to different categories as defined in Table 3, being either aromaticity-, electronic-, orbital- or charge transfer-based descriptors. Note that even though DR and aromaticity descriptors are commonly used to rationalize the NLO properties, they do not correlate with our target property, with the exception of BOA. A scatterplot of βHRSversus DR is provided in Fig. S1 (ESI†), which shows that our dataset of hexaphyrins is described by a broad range of DR values ranging from 1.5 until 6.7. Our best-performing structures are distinguished by a DR value close to 5, which is characteristic for a 1D push–pull chromophore. Nevertheless, a large number of structures have a DR around 5, yet a βHRS below 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. Hence, DR is not able to sufficiently explain the variations in βHRS. Next, we checked the correlation between the individual 35 features in Fig. 2B. The electronic-based descriptors (IE, EA, ω and μe) and the orbital energies of H−1, H, L and L+1 show R2 values larger than 0.80, both within their category and between the two categories. Additionally, the geometrical-based descriptors Π and ϕp show a high correlation. The last set of features with high R2 values are the aromaticity indices based on magnetic criteria, NICS(0), NICSzz (1) and NICS(1). Intermediate R2 values between 0.60 and 0.80 are observed between NICS indices, HOMA and the geometrical descriptors. Overall, the aromaticity indices based on different criteria seem to correlate among each other, where the R2 ranges between 0.40 and 0.80.
000 a.u. Hence, DR is not able to sufficiently explain the variations in βHRS. Next, we checked the correlation between the individual 35 features in Fig. 2B. The electronic-based descriptors (IE, EA, ω and μe) and the orbital energies of H−1, H, L and L+1 show R2 values larger than 0.80, both within their category and between the two categories. Additionally, the geometrical-based descriptors Π and ϕp show a high correlation. The last set of features with high R2 values are the aromaticity indices based on magnetic criteria, NICS(0), NICSzz (1) and NICS(1). Intermediate R2 values between 0.60 and 0.80 are observed between NICS indices, HOMA and the geometrical descriptors. Overall, the aromaticity indices based on different criteria seem to correlate among each other, where the R2 ranges between 0.40 and 0.80.
The additional subplot of Fig. 2B concentrates on the intercorrelation between the 13 features highly correlating with βHRS. BOA and ΔL+1_H show only low to moderate correlation with respect to the other features. Therefore, these two features may bring unique information into the ML model. Most other properties are characterized by higher R2 values. To reduce the number of input features, we opted to remove features that correlate highly with the ΔHL, since this feature correlates best with the βHRS response (R2 = 0.91). Consequently, the chemical hardness (η) (R2 = 0.94), the excitation energy associated to S2 (ΔES2) (R2 = 0.82), and ΔH (R2 = 0.77) were not retained. An additional reason for the exclusion of ΔH is that DCT and ΔL+1_H also correlate reasonably well with this feature, so the model input of ΔH may be compensated by these other input features. Despite its significant correlation with four of the remaining input features, we decided to keep DCT in our input set because of its correlation with βHRS. In summary, the following properties will be used as input features for the ML model: ΔHL, ΔL+1_H, BOA, qCT, μ, ΔL, μ01, |Δμ|, ΔES1, and DCT.
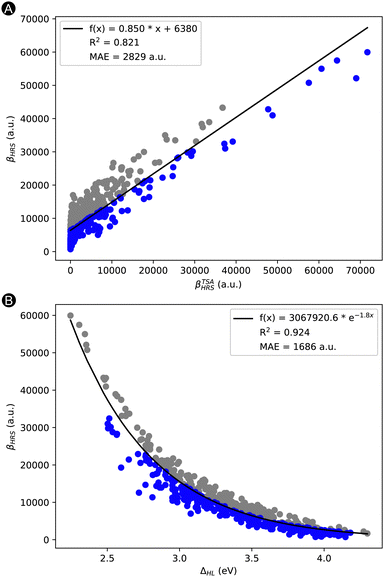
Remark that this list of features still contains the three properties building up the TSA of Oudar and Chemla: |Δμ|, μ01, and ΔES1. In Fig. 3A, we plotted our target property βHRSversus the βTSAHRS obtained through Oudar en Chemla's TSA. Despite its frequent successes in other molecular switches, the TSA describes only to a certain degree the target property with an MAE of 2829 a.u. and an R2 of 0.821. Interestingly, our best performing feature (ΔHL) explains already quite well the trend in βHRS response. We performed an exponential regression on the βHRSvs. ΔHL, which resulted in an R2 of 0.924 and mean absolute error (MAE) of 1686 a.u. (Fig. 3B). The question arises whether we can better explain the variance of the NLO response, by creating a machine learning (ML) model with additional features that can improve the performance of the TSA and exponential model.
Training, testing and understanding of machine learning models
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u. and include a similar number of the best-performing hexaphyrins with a large βHRS response.
000 a.u. and include a similar number of the best-performing hexaphyrins with a large βHRS response.
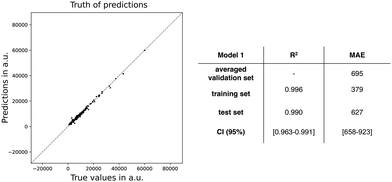
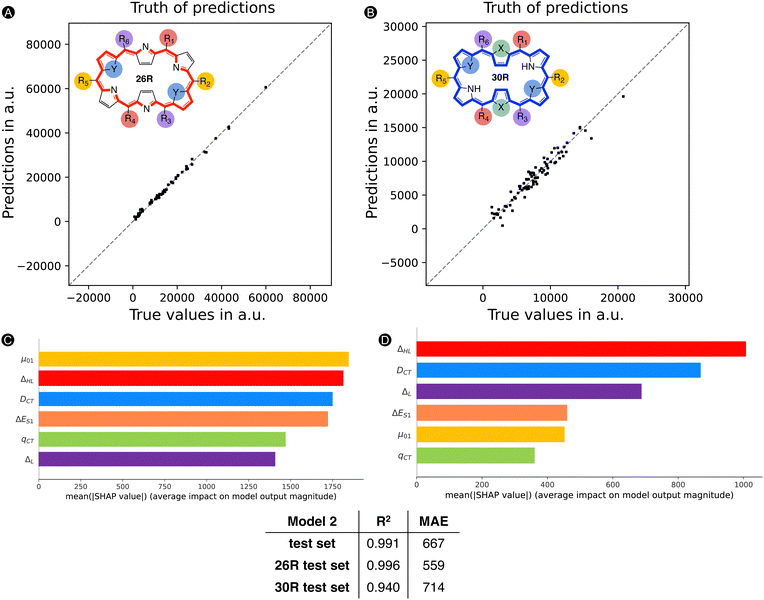
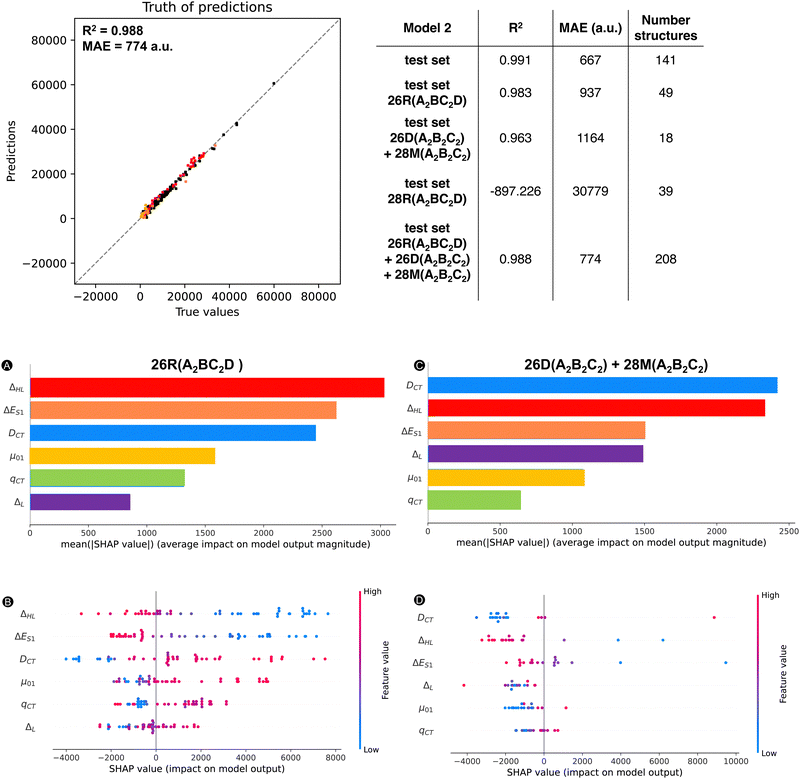
Next, we trained a kernel ridge regression model (KRR) with our selected ten features: ΔHL, ΔL+1_H, BOA, qCT, μ, ΔL, μ01, |Δμ|, ΔES1, and DCT. The objective during the training and hyperparametrization tuning of our ML model was to minimize the MAE. For the hyperparametrization optimization, we used 6-fold cross-validation to prevent overfitting. Using the most optimal hyperparameters, the KRR model was fitted to the full training dataset. Both the averaged cross-validation statistics (MAE and R2), calculated over the six validation sets, and the full training set statistics are reported in Fig. 4, in addition to the external test set statistics along with the 95%-confidence interval (CI). Fig. 4 also includes the truth of predictions plot for the test set data. A markedly lower MAE and higher R2 are found for the full training set, which may indicate overfitting during the model training. Regarding the test set, similar values for MAE and R2 are obtained as the cross-validation sets (MAE: 695 vs. 627 a.u.) with only a difference of 68 a.u. Compared to the cross-validation, the test set performs a bit better as reflected by the MAE falling out of the 95% confidence interval. In summary, the model generalizes quite well similar unseen data. Remark that the performance of model 1 is significantly better than our exponential model as the model 1's MAE is far below half of the exponential and TSA models.
Since some features were found to be somewhat correlated, we performed a feature permutation importance analysis, as implemented into scikit-learn,97 to understand how each feature contributes to the performance of our ML model. Here, the feature importances are calculated as the difference between the statistics of the entire dataset and that of the dataset with one feature column permuted. Because the feature permutation has a different interpretation for the test set and training set, we performed this analysis on both sets. All feature permutations are collected in Table 4 for the MAE statistics.
| ΔMAE (train) | ΔMAE (test) | |
|---|---|---|
| Δ HL | 1653 ± 73 | 1559 ± 113 |
| D CT | 3789 ± 139 | 3650 ± 193 |
| Δ L+1_H | 1430 ± 58 | 1123 ± 86 |
| Δ L | 1429 ± 69 | 1347 ± 129 |
| μ 01 | 2321 ± 99 | 2021 ± 182 |
| q CT | 2439 ± 102 | 1874 ± 184 |
| ΔES1 | 2496 ± 186 | 2130 ± 251 |
| |Δμ| | 1141 ± 79 | 854 ± 118 |
| BOA | 1260 ± 71 | 1007 ± 122 |
| μ | 983 ± 97 | 1179 ± 57 |
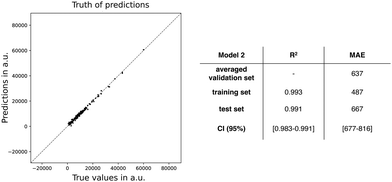
By inspecting the importances of the test set, we can derive which features will contribute to the generalization power of our model. Additionally, the feature importances related to the training set can identify which features are possibly overfitting our trained model. At first glance, both test and training set of model 1 present similar trends for their feature importances and generally within the same order of magnitude. Consequently, the interpretation of this analysis for both datasets is the same. The DCT is the most influential feature in the model, both for the training and test set of model 1 with a potential increase in MAE value of around 3700 a.u. Other important features are: ΔES1, qCT, and μ01. Unexpectedly, ΔHL comes in fourth place despite its high correlation with the target property. A slight discrepancy in feature importances between the train and test set is observed for ΔES1, μ01, and especially qCT. Since this divergence might indicate that model 1 is overfit, a reduction of input features is advisable. Our strategy is to continue reducing the feature set based on the balance between model performance and feature importances. The analysis of this strategy is described in ESI† (cf. Fig. S3). By consecutively removing the feature with the lowest feature importance, new models are generated until the resulting model has a (too) negative effect on the model performance, here through the MAE statistic. In the end, we obtain our final model, denoted as model 2, with only six features: ΔHL, qCT, ΔL, μ01, ΔES1, and DCT. Note that this final model still contains the features of the TSA and the exponential models, except for |Δμ|.
Next, we applied the feature permutation importance analysis on model 2 (Table 5). In contrast to the model 1, ΔHL becomes equally important as DCT for both the training and test sets, whereas μ01 and ΔL increase substantially in feature importance. Note the slight discrepancy between training and test set for qCT in terms of MAE. In conclusion, all features significantly contribute to the model performance, both for the training and test data.
| Model 6 features | ΔMAE (train) | ΔMAE (test) |
|---|---|---|
| Δ HL | 4735 ± 186 | 4347 ± 295 |
| D CT | 4730 ± 214 | 4498 ± 360 |
| Δ L | 1247 ± 72 | 1043 ± 106 |
| μ 01 | 2982 ± 154 | 2898 ± 267 |
| q CT | 2152 ± 133 | 1776 ± 243 |
| ΔES1 | 2028 ± 90 | 1960 ± 195 |
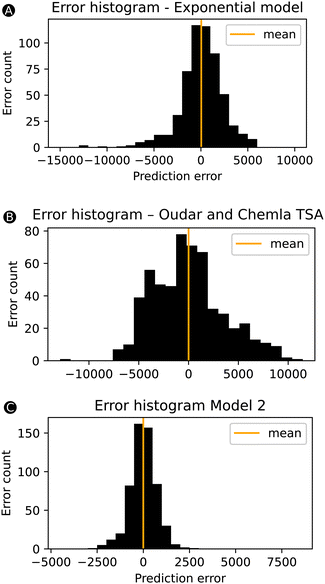
Despite the slight drop in performance going from model 1 to model 2, the performance of model 2 remains significantly better than our initial exponential model based on only one feature ΔHL. Fig. 6 compares three error-bar histograms showing the prediction error distributions for the exponential model, the two-state model of Oudar and Chemla, and model 2. For the construction of the error-bar plots, all datapoints were considered. Besides a much narrower distribution for model 2, we also note that the exponential model and the two-state model description of this total dataset results in a significant number of datapoints having errors above 2000 or below −2000 a.u., being 166 or 30% for the exponential model and and 314 or 56% for the TSA, while model 2 has as few as 9 datapoints within this range. In short, the addition of other features besides the ΔHL allows model 2 to drastically reduce the number of outliers. To confirm this observation, we computed the MAE of these 166 systems based on the model 2 predictions, and, indeed, the initial MAE of 3580 a.u. using the exponential model is significantly reduced to 587 a.u. by using model 2.
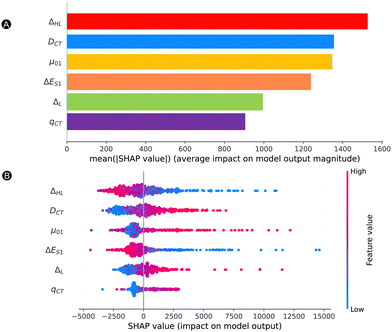
![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 a.u. The trends of Fig. 7 are the same regardless of the dataset type. All features have a nonnegligible impact on the magnitude of the model output, with a minimal average contribution of 900 a.u. Our most impactful features are the ΔHL, DCT and μ01, with mean SHAP values over 1200 a.u., which are well above the MAE.
500 a.u. The trends of Fig. 7 are the same regardless of the dataset type. All features have a nonnegligible impact on the magnitude of the model output, with a minimal average contribution of 900 a.u. Our most impactful features are the ΔHL, DCT and μ01, with mean SHAP values over 1200 a.u., which are well above the MAE.
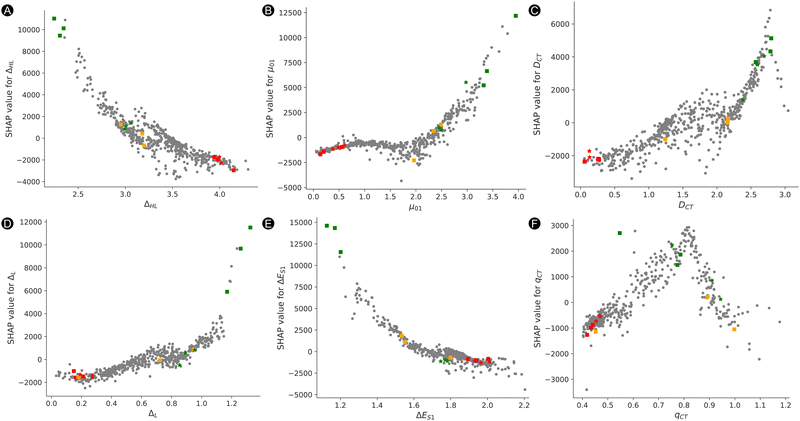
To gain insight on how each feature impacts the model predictions (SHAP value) depending on the feature value, we provide a beeswarm plot in Fig. 7B. Both ΔHL and ΔES1 show the same trend where lower feature values have a positive impact on the NLO response, while high feature values have a negative impact on the output. That means that the lower is the HOMO and LUMO energy gap or the excitation energy, the higher is the βHRS response. On the other hand, DCT, μ01, and ΔL behave in the opposite manner, where higher and lower values have a positive and negative impact on the βHRS response, respectively. With respect to the baseline (SHAP values of 0), most structures have lower SHAP values, but they do not extend that much when compared to the higher SHAP values (SHAP ranges are between −4000 and 16![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 000 a.u.). There is no clear trend for qCT, for which we see an overlap between high and low qCT to the left and the right of the baseline. Additional information on the exact relationship between the feature value and SHAP value is provided in Fig. S5A–F in the ESI.† Here, we observe a reversed and sharp v-curve relationship between qCT and its SHAP value. This v-curve peaks around a feature value of 0.8. Values lower and higher than 0.8 almost linearly decrease in SHAP contribution. The SHAP values associated with qCT generally contribute less but quite evenly with respect to the baseline. Hence, our main features contributing most to the prediction of high NLO responses by model 2 are primarily orbital and charge transfer-based features, ΔHL and DCT as well as μ01. Note that the relationship between the HOMO–LUMO energy difference and its SHAP contribution to βHRS seems close to exponential (Fig. S5A in ESI†), as we observed before for the exponential regression model.
000 a.u.). There is no clear trend for qCT, for which we see an overlap between high and low qCT to the left and the right of the baseline. Additional information on the exact relationship between the feature value and SHAP value is provided in Fig. S5A–F in the ESI.† Here, we observe a reversed and sharp v-curve relationship between qCT and its SHAP value. This v-curve peaks around a feature value of 0.8. Values lower and higher than 0.8 almost linearly decrease in SHAP contribution. The SHAP values associated with qCT generally contribute less but quite evenly with respect to the baseline. Hence, our main features contributing most to the prediction of high NLO responses by model 2 are primarily orbital and charge transfer-based features, ΔHL and DCT as well as μ01. Note that the relationship between the HOMO–LUMO energy difference and its SHAP contribution to βHRS seems close to exponential (Fig. S5A in ESI†), as we observed before for the exponential regression model.
First, we reassessed the MAE for the [26]- and [30]hexaphyrin systems separately by focusing only on those present in the test set. Fig. 8 summarizes the scatterplots of the true values versus the predictions by ML model 2 for the subsets of [26]- and [30]hexaphyrins. The MAEs of the test sets containing either 26R or 30R systems remain around the same value as for the total test set. In addition, both subsets show an R2 of 0.94 and more, with the model performance being a bit better for the 26R systems.
Next, we reapplied the SHAP analysis to the 26R and 30R hexaphyrin subsets (both training and test sets) to verify if the features contribute differently to the prediction of their NLO response. In Fig. 8, two barplots are displayed highlighting the average impact on the model output for all [26]- (left) and [30]hexaphyrins (right), relative to their respective baseline, 14![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 163 a.u. for the former and 7731 a.u. for the latter. Despite the base value being adjusted for each subset, we clearly observe that the average SHAP values are lower for 30R systems than 26R macrocycles for the different features. Importantly, the top three features influencing the average impact on the model output differ for the two hexaphyrin redox states. The [26]hexaphyrins are mostly impacted by the μ01, ΔHL, and DCT, in nearly equal amounts. In fact, all features still significantly contribute to the prediction with a SHAP value of minimally 1400 a.u. Regarding the 30R systems, ΔHL becomes more important and μ01 drops significantly in βHRS contribution. DCT remains in the top 3 of dominant features. Interestingly, ΔL now becomes a vital feature in terms of the average contribution to the output prediction. The S1 excitation energy remains on the fourth place but seems less influential than for the 26R. For both hexaphyrins, qCT is one of the least impactful features on the model output. Note that for the [30]-hexaphyrins ΔES1, μ01 and qCT contribute, on average, a relatively small amount.
163 a.u. for the former and 7731 a.u. for the latter. Despite the base value being adjusted for each subset, we clearly observe that the average SHAP values are lower for 30R systems than 26R macrocycles for the different features. Importantly, the top three features influencing the average impact on the model output differ for the two hexaphyrin redox states. The [26]hexaphyrins are mostly impacted by the μ01, ΔHL, and DCT, in nearly equal amounts. In fact, all features still significantly contribute to the prediction with a SHAP value of minimally 1400 a.u. Regarding the 30R systems, ΔHL becomes more important and μ01 drops significantly in βHRS contribution. DCT remains in the top 3 of dominant features. Interestingly, ΔL now becomes a vital feature in terms of the average contribution to the output prediction. The S1 excitation energy remains on the fourth place but seems less influential than for the 26R. For both hexaphyrins, qCT is one of the least impactful features on the model output. Note that for the [30]-hexaphyrins ΔES1, μ01 and qCT contribute, on average, a relatively small amount.
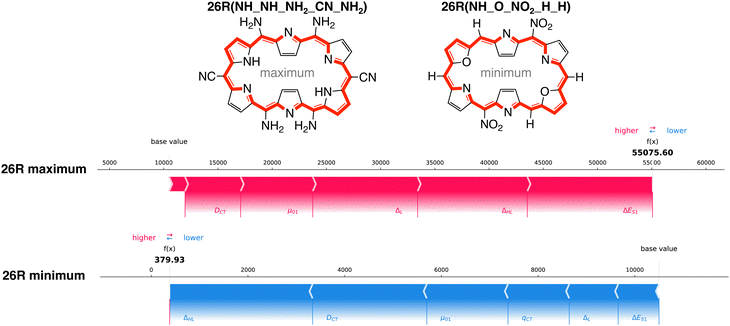
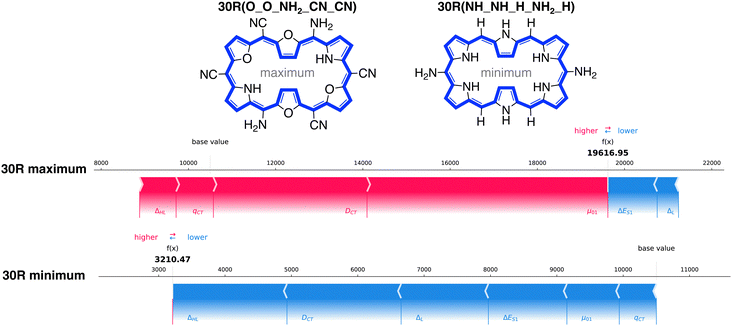
How do the features influence our best- and worst-performing 26R and 30R in terms of NLO response? Our best-performing 26R are denoted as 26R(NH_NH_NH2_CN_NH2), 26R(NH_Se_NH2_CN_NH2) and 26R(NH_S_NH2_CN_NH2) and all contain the same meso-substitution pattern with 2 sets of strongly electron-donating groups (EDGs) and 1 set of strongly electron-withdrawing groups (EWGs). The three 26R macrocycles with the lowest NLO response (26R(NH_O_NO2_H_H), 26R(NH_S_CN_CN_CN) and 26R(NH_S_NO2_CN_CN)) consist of combinations of core-modifications and meso-substitutions with 1 or 3 pairs of EWGs. In Fig. 9, we present the force plots100 of the 26R systems with minimal and maximal βHRS response, with the baseline at 10![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 500 a.u. taken as the prediction average of the full dataset (including both [26]- and [30]hexaphyrins). These force plots depict for each instance the influence of each feature on the model's prediction. Starting from the base value, each feature increases (red) or decreases (blue) the base value to obtain the function value (f(x)). The other force plots of the second and third structures with either minimal and maximal βHRS responses can be found in the ESI† (Fig. S6–S9).
500 a.u. taken as the prediction average of the full dataset (including both [26]- and [30]hexaphyrins). These force plots depict for each instance the influence of each feature on the model's prediction. Starting from the base value, each feature increases (red) or decreases (blue) the base value to obtain the function value (f(x)). The other force plots of the second and third structures with either minimal and maximal βHRS responses can be found in the ESI† (Fig. S6–S9).
All force plots of best performing 26R structures show that all six features have a positive impact on the model's prediction. Hence, all features aid in increasing the base value towards the predicted value. ΔES1 has the most influence for the three maxima. Depending on the optimum, either μ01, ΔHL, and ΔL play an important role. Interestingly, DCT plays a minor role, despite being in the top three of average feature impact on model output magnitude (Fig. 8A). The opposite trend is observed for the 26R systems with a low βHRS response, where all features lower the base value. Here, DCT and ΔHL are the most important features. Therefore, DCT has a larger impact in reducing the NLO response than enhancing it, relative to the other features.
The best-performing 30R systems contain two sets of core-modifications and EWGs and one set of EDGs, 30R(O_O_NH2_CN_CN), 30R(O_S_NH2_CN_CN) and 30R(O_O_NH2_NO2_CN). Our worst-performing are 30R(NH_NH_H_NH2_H), 30R(NH_NH_H_OH_H) and 30R(NH_NH_H_F_H) and only consist of one set of strong EDGs or weak EWGs as meso-substituents on the macrocycle and no core-modifications. Similarly to the 26R systems, we only display the systems with the lowest and highest βHRS response in Fig. 10.
In contrast to the best 26R, the force plots of the best 30R structures show that not all features necessarily increase the baseline prediction. In all three structures, ΔES1 has the highest negative impact on the predicted average. Surprisingly, even though μ01 is ranked second to lowest for the [30]hexaphyrins, it shows the highest positive impact for the 30R maximum followed by DCT. In the two remaining structures, other features such as qCT, DCT, and ΔHL play a varying positive role on the NLO response. In contrast, the worst performing 30R structures behave similarly to the worst performing 26R with DCT, ΔHL, and to a lesser degree ΔL as the main important features. This explains the gain in importance of DCT for 30R compared to 26R, as this feature greatly impacts both high and low responses for the former but only low responses for the latter.
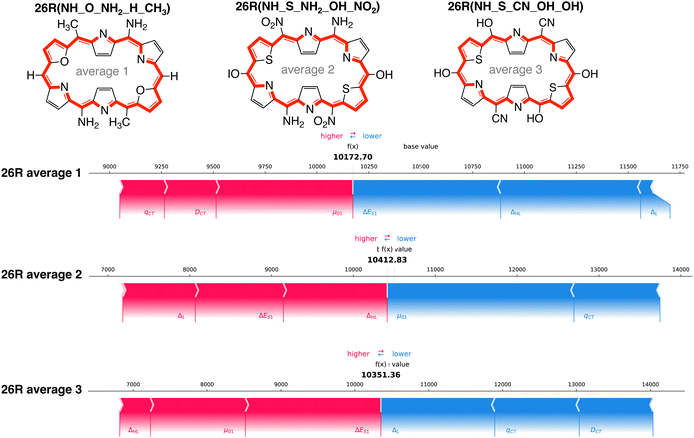
Aside from the structures with the highest and lowest βHRS response, we selected three additional systems with predicted βHRS values close to the average of the entire dataset, the baseline of our SHAP analysis. We focused on 26R structures, as we found for both high and low response structures similar dominant features. These [26]hexaphyrins incorporate at least one set of core-modifications and different combinations of meso-substitutions on their macrocycle: 26R(NH_O_NH2_H_CH3), 26R(NH_S_NH2_OH_NO2) and 26R(NH_S_CN_CN_OH). The force plots of these systems are provided in Fig. 11.
For all three systems, we observe that nearly all individual features distinctly contribute to the predicted NLO response, some positively and some negatively. A clear trend on how each feature influences the final prediction of the model is difficult to establish. Despite the similar total prediction output, a different combination of features is responsible for the predicted βHRS value. For example, for 26R average 2, the two orbital and one electronic-based features increase the response prediction, whereas the charge-transfer-based features diminish the prediction by the same amount. The similarly substituted 26R average 3, having the same core-modification set and also two sets of EDGs and one set of EWGs (though on different positions), differs with the previous structure in that μ0,1 now positively contributes and ΔL negatively.
Lastly, to estimate where these 15 selected systems are positioned within the SHAP versus feature value space, we plotted dependency plots for each feature. The dependency plots in Fig. 12 show the SHAP value of a feature versus the feature value. The 26R and 30R systems are represented by a square and star marker, respectively. The systems are colored in red, orange and green corresponding to lowest, medium and highest responses accordingly. The scatter plot for ΔHL as presented in Fig. 12A shows that the best-performing 26R have high SHAP values for low ΔHL feature values. The βHRS response of the orange markers and the best-performing 30R, represented by green stars, are only slightly positively influenced by the ΔHL except for one system 26R(NH_O_NH2_H_CH3) with an average βHRS response. For example, the SHAP value for ΔHL of 26R(NH_NH_NH2_CN_NH2) is much higher and positive, 11![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) 019 a.u., than the best-performing 30R with a SHAP value of 836 a.u. For the worst performing structures depicted in red, the ΔHL has always a negative influence on the model output. Fig. 12B–D show the opposite of Fig. 12A, where high feature values have a positive impact on the model's output and low values the opposite. Nonetheless, a few outliers should be noted which deviate from the expected trend. Regarding the μ01 feature (Fig. 12B), the best-performing [30]hexaphyrin-based structures are close to the [26]hexaphyrins with an average βHRS response, except for one system, 30R(O_O_NH2_CN_CN), which has a higher μ01 than the other [30]hexaphyrins. In addition, one 26R system, 26R(NH_S_NH2_OH_NO2), is negatively impacted by μ01 as reflected by its negative SHAP value and lower feature value. The opposite is observed for DCT (Fig. 12C), where the best-performing [30]hexaphyrin-based structures lie closely to the best-performing [26]hexaphyrin-based structures, with the exception of 30R(O_S_NH2_CN_CN), which resides near the average performing structures. For those two charge-transfer-based descriptors, the worst-performing 26R and 30R are all at the end of the curves. The average-response structures are more spread for DCT. In Fig. 12D, one of the average 26R structures, 26R(NH_S_CN_OH_OH), is positioned closer to those with a low βHRS response highlighted in red, because lower differences between L and L+1 (ΔL) result in more negative SHAP values. Fig. 12E shows similar trends as Fig. 12A, where the best-performing 26R structures show positive SHAP values for low feature values and the opposite is true for the worst 26R and 30R structures. Except for 26R(NH_O_NH2_H_CH3), all average-structures are characterized by a postive SHAP value with an excitation energy ΔES1 around 1.6 eV. In contrast to ΔHL, the best-performing 30R structures are much closer to the overall worst performing structures and are characterized by negative SHAP and low ΔES1 values. The outlying 26R(NH_O_NH2_H_CH3) is also positioned closer to the best-performing 30R structures. Finally, a general trend remains difficult to distinguish for the qCT feature in Fig. 12F. As mentioned before, the peak of the structures with the highest positive impact on the model is perceived at a feature value of 0.8. Remarkably, our best-performing structure 26R(NH_NH_NH2_CN_NH2) has a very high positive impact on the final prediction for a low feature value of 0.57 but lies well outside the v-curve.
019 a.u., than the best-performing 30R with a SHAP value of 836 a.u. For the worst performing structures depicted in red, the ΔHL has always a negative influence on the model output. Fig. 12B–D show the opposite of Fig. 12A, where high feature values have a positive impact on the model's output and low values the opposite. Nonetheless, a few outliers should be noted which deviate from the expected trend. Regarding the μ01 feature (Fig. 12B), the best-performing [30]hexaphyrin-based structures are close to the [26]hexaphyrins with an average βHRS response, except for one system, 30R(O_O_NH2_CN_CN), which has a higher μ01 than the other [30]hexaphyrins. In addition, one 26R system, 26R(NH_S_NH2_OH_NO2), is negatively impacted by μ01 as reflected by its negative SHAP value and lower feature value. The opposite is observed for DCT (Fig. 12C), where the best-performing [30]hexaphyrin-based structures lie closely to the best-performing [26]hexaphyrin-based structures, with the exception of 30R(O_S_NH2_CN_CN), which resides near the average performing structures. For those two charge-transfer-based descriptors, the worst-performing 26R and 30R are all at the end of the curves. The average-response structures are more spread for DCT. In Fig. 12D, one of the average 26R structures, 26R(NH_S_CN_OH_OH), is positioned closer to those with a low βHRS response highlighted in red, because lower differences between L and L+1 (ΔL) result in more negative SHAP values. Fig. 12E shows similar trends as Fig. 12A, where the best-performing 26R structures show positive SHAP values for low feature values and the opposite is true for the worst 26R and 30R structures. Except for 26R(NH_O_NH2_H_CH3), all average-structures are characterized by a postive SHAP value with an excitation energy ΔES1 around 1.6 eV. In contrast to ΔHL, the best-performing 30R structures are much closer to the overall worst performing structures and are characterized by negative SHAP and low ΔES1 values. The outlying 26R(NH_O_NH2_H_CH3) is also positioned closer to the best-performing 30R structures. Finally, a general trend remains difficult to distinguish for the qCT feature in Fig. 12F. As mentioned before, the peak of the structures with the highest positive impact on the model is perceived at a feature value of 0.8. Remarkably, our best-performing structure 26R(NH_NH_NH2_CN_NH2) has a very high positive impact on the final prediction for a low feature value of 0.57 but lies well outside the v-curve.
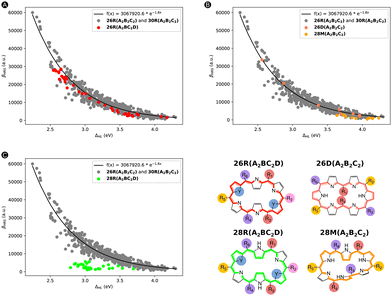
To start off, we replotted in Fig. 13 the relationship between the βHRSversus ΔHL for our initial dataset, in which we additionally highlighted one of the extra test sets in a different color. The two test sets (26R(A2BC2D) and 26D + 28M(A2B2C2)) presented in Fig. 13A and B, respectively, follow the trend, thus associating high βHRS responses with low ΔHL values. However, the test set containing 28R(A2BC2D) structures does not follow this exponential relationship. In essence, systems with either a different substitution pattern or different hexaphyrin conformations can behave similarly to the 26R(A2B2C2) and 30R(A2B2C2) dataset. In the ESI,† we also provided the scatterplots regarding TSA (i.e., βHRSversus βTSAHRS) for our external test sets. The 26R(A2BC2D) dataset but also 28R(A2BC2D) (reasonably) follow the previous TSA trend, while 26D + 28M(A2B2C2) is not well described by this model.
Subsequently, we predicted the βHRS response of the three test sets with our ML model 2. For the individual scatter plots for each new test set, we refer to the ESI† (Fig. S11). If we combine our initial test set with the two test sets 26R(A2BC2D) and 26D + 28M(A2B2C2), for which the exponential model provided a good description, and recalculate the MAE and R2, Fig. 14 is obtained. Here, 26R(A2BC2D) and 26D(A2B2C2) + 28M(A2B2C2) are colored in red and salmon and orange, respectively. Even after the addition of the new data points, our R2 of 0.988 stays similar to that of the initial test set (R2: 0.991). Since our ML model has not yet encountered these types of structures, the MAE increases but not substantially (774 a.u. vs. 667 a.u.). This observation also applies to the R2 of the first and second extra test set individually in comparison to the initial test set (Fig. 14). However, the MAEs of the individual (26R(A2BC2D) and 26D + 28M(A2B2C2)) sets increase by 40% and 75%, respectively, so a different substitution pattern is generalized better than a change of topology and/or oxidation state. Nonetheless, these predictions are still better than the initial exponential model (MAE of 1686 a.u.) and the revised exponential model, including these first two external test sets (MAE of 1736 a.u. and R2 of 0.913). As expected, the 28R(A2BC2D) test set performs the worst of all new sets with an MAE almost 20 times higher than our exponential model. This bad performance stems from the negative βHRS response predictions by model 2 for the 28R(A2BC2D) test sets. In summary, our ML model is able to reasonably describe hexaphyrins of the same oxidation state and topology with a different substitution pattern and hexaphyrins of different oxidation state and topology, with the exception of the 28R structures.
To gain insight into which features contribute to the prediction for the first two external test sets, we applied our SHAP analysis tools (using the average prediction of the original total dataset as base value) to understand our model's decisions (Fig. 14). For the 26R(A2BC2D) set, which contains [26]hexaphyrins with a different substitution pattern, the ΔHL is the most significant feature (Fig. 14A). This feature rises from second to first place in importance compared to the 26R conformers having A2B2C2 pattern in Fig. 8A. The second most influential feature of this external dataset is ΔES1, which has also increased in importance. Surprisingly, our top feature for the initial 26R dataset, μ01, drops significantly in averaged SHAP value. DCT remains in the third position and qCT and ΔL are still the least influential features. Apart from the feature importance, the trends in Fig. 14B are overall quite similar as in Fig. 7B, which deals with the entire dataset and does not distinguish between the different hexaphyrin types. Higher values for DCT, μ01 and ΔL correspond with positive impacts on the model output. The opposite is still true for ΔHL and ΔES1. For our second test set, 26D + 28M(A2B2C2), DCT and ΔHL are our most important features (Fig. 14C), which is more or less in line with the [30]hexaphyrins in Fig. 8B. ΔL and ΔES1 become equally important and the latter jumps to the third place in the ranking compared to the trends observed for the 30R hexaphyrins. Again, qCT is among the worst-performing of all features. Since only 18 data points are present in this external test set, the beeswarm plot in Fig. 14D becomes less interpretable but it shows similar trends as Fig. 7B for the entire dataset. Except for some small deviations in the ΔL feature vs. SHAP scatter plot in Fig. S12D in the ESI,† the other scatter plots (Fig. S12, ESI†) confirm that the two external datasets follow indeed the general trend.
Conclusion
In this work, we employed explainable machine learning to further understand the underlying factors influencing the NLO response of chemically functionalizated [26]- and [30]hexaphyrins. To this end, we investigated various quantum-chemical descriptors and their relationship with our target property, βHRS. Only 13 features correlated sufficiently with R2 values above 0.4. They can be categorized as, primarily, orbital-based (4) and charge-transfer (3) features but also electronic (5) and aromaticity (1) descriptors. The intercorrelation between each of these thirteen features was also established. Before applying any machine-learning model to our dataset, we checked two additional models to predict the βHRS response based on either the two-state approximation of Oudar and Chemla and only the HOMO–LUMO energy gap. Overall, the HOMO–LUMO gap is the best-performing feature in predicting the βHRS response of the hexaphyrin macrocycles for which exponential regression yielded an MAE of 1686 a.u. After removing highly intercorrelating features, we constructed a ML model using 6-fold cross-validated kernel ridge regression with 10 input features and the MAE as the validation metric (model 1). As model 1 shows signs of overfitting, we further reduced the number of features to 6 by keeping the balance between the model performance and high feature importances for the model. Our final ML model contained 6 features only including orbital, electronic and charge-transfer based descriptors and resulted in an MAE value far below half of that of the exponential model. We applied explainable ML model techniques such as a SHAP analysis to obtain the average impact of each feature on the model output. From the SHAP analysis, we concluded that all of the features have an impact on the model output, but ΔHL, DCT, and μ01 influence the model output the most. We would like to emphasize that even though nearly all features of the TSA and the exponential model are included in the ML input feature set, other descriptors such as DCT still have a big importance on both the performance of the model as the interpretation of the final predictions. Next, we re-evaluated the performance of our model for the two subgroups in our dataset, the 26R and 30R structures. By reapplying the SHAP analysis on the 26R and 30R structures separately, we could scrutinize whether the most influential features are different for each group. We found that, besides μ01, the NLO response of the 26R structures are mostly affected by ΔHL and DCT. For the 30R, DCT gains importance whereas that of μ01 significantly drops. Analysis of the three best- and worst-performing 26R and 30R structures indicated that, even though the DCT is in the top three of important features, the best-performing 26R structures are less influenced by this property in contrast to 30R. Lastly, we assessed the generalization of our ML model by predicting the NLO response of other types of hexaphyrins, which were not present in the training dataset. Three external datasets were constructed with either 26R or 28R with another meso-substitution pattern, and a collection of hexaphyrins sharing the original meso-substitution pattern but with another topology (26D and 28M). With the exception of the 28R set, our model could reasonably describe our additional external test sets. Our SHAP analysis concluded that 26R(A2BC2D) resembles the 26R(A2B2C2) set, except for μ01, and that the 26D + 28M(A2B2C2) set follows the trends of the 30R.Author contributions
E. D., F. D. V., and M. A. conceptualized the project. E. D. performed all quantum chemical calculations, coded and constructed the ML models based on the code provided by M. J. In addition, M. J. supported E. D. in case of technical difficulties with the code. F. D. V. supervised the project. E. D. analyzed the data. The first draft of the manuscript was written by E. D. and F. D. V. All authors were involved in future editing and reviewing process. All authors have read and agreed to the published version of the manuscript.Data availability
The data supporting this article have been included as part of the ESI.†Conflicts of interest
There are no conflicts of interest to report.Acknowledgements
F. D. V. and M. A. wish to thank the VUB for the Strategic Research Program awarded to the ALGC research group. E. D. thanks the Fund for Scientific Research-Flanders (FWO-11E0321N) for financial support. The resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation – Flanders (FWO) and the Flemish Government. E. D. and F. D. V. would like to thank Prof. Dr Marc Elskens at the Vrije Universiteit Brussel and MSc Mark Heezen for the fruitful discussions on the topic of machine-learning models and statistics.Notes and references
- P. A. Franken, A. E. Hill, C. W. Peters and G. Weinreich, Phys. Rev. Lett., 1961, 7, 118–119 CrossRef.
- T. Kaino and S. Tomaru, Adv. Mater., 1993, 5, 172–178 CrossRef CAS.
- B. J. Coe, Chem. – Eur. J., 1999, 5, 2464–2471 CrossRef CAS.
- S. R. Marder, Chem. Commun., 2006, 131–134 RSC.
- J. A. Delaire and K. Nakatani, Chem. Rev., 2000, 100, 1817–1846 CrossRef CAS.
- J. L. Zhang, J. Q. Zhong, J. D. Lin, W. P. Hu, K. Wu, G. Q. Xu, A. T. S. Wee and W. Chen, Chem. Soc. Rev., 2015, 44, 2998–3022 RSC.
- L. Sun, Y. A. Diaz-Fernandez, T. A. Gschneidtner, F. Westerlund, S. Lara-Avila and K. Moth-Poulsen, Chem. Soc. Rev., 2014, 43, 7378–7411 RSC.
- S. Gao, X. Yi, J. Shang, G. Liu and R.-W. Li, Chem. Soc. Rev., 2019, 48, 1531–1565 RSC.
- F. Castet, V. Rodriguez, J.-L. Pozzo, L. Ducasse, A. Plaquet and B. Champagne, Acc. Chem. Res., 2013, 46, 2656–2665 CrossRef CAS PubMed.
- F. Meyers, S. R. Marder, B. M. Pierce and J. L. Bredas, J. Am. Chem. Soc., 1994, 116, 10703–10714 CrossRef CAS.
- S. R. Marder, C. B. Gorman, F. Meyers, J. W. Perry, G. Bourhill, J.-L. Bredas and B. M. Pierce, Science, 1994, 265, 632–635 CrossRef CAS PubMed.
- J. M. Hales, S. Barlow, H. Kim, S. Mukhopadhyay, J.-L. Brédas, J. W. Perry and S. R. Marder, Chem. Mater., 2014, 26, 549–560 CrossRef CAS.
- V. Postils, Z. Burešová, D. Casanova, B. Champagne, F. Bureš, V. Rodriguez and F. Castet, Phys. Chem. Chem. Phys., 2024, 26, 1709–1721 RSC.
- P. Beaujean, L. Sanguinet, V. Rodriguez, F. Castet and B. Champagne, Molecules, 2022, 27, 2770 CrossRef CAS PubMed.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- P. K. Samanta and R. Misra, J. Appl. Phys., 2023, 133, 020901 CrossRef CAS.
- P. Beaujean and B. Champagne, Inorg. Chem., 2022, 61, 1928–1940 CrossRef CAS PubMed.
- Y. Yao, H.-L. Xu and Z.-M. Su, J. Mater. Chem. C, 2022, 10, 12338–12349 RSC.
- C. Naim, F. Castet and E. Matito, Phys. Chem. Chem. Phys., 2021, 23, 21227–21239 RSC.
- J. L. Oudar and D. S. Chemla, J. Phys. Chem., 1977, 66, 2664–2668 CrossRef CAS.
- L. Lescos, S. P. Sitkiewicz, P. Beaujean, M. Blanchard-Desce, B. Champagne, E. Matito and F. Castet, Phys. Chem. Chem. Phys., 2020, 22, 16579–16594 RSC.
- C. Tonnelé and F. Castet, Photochem. Photobiol. Sci., 2019, 18, 2759–2765 CrossRef.
- C. Tonnelé, B. Champagne, L. Muccioli and F. Castet, Phys. Chem. Chem. Phys., 2018, 20, 27658–27667 RSC.
- Y. Zhang and B. Champagne, J. Phys. Chem. C, 2013, 117, 1833–1848 CrossRef CAS.
- F. Bondu, J. Quertinmont, V. Rodriguez, J.-L. Pozzo, A. Plaquet, B. Champagne and F. Castet, Chem. – Eur. J., 2015, 21, 18749–18757 CrossRef CAS PubMed.
- M. Pauley and C. Wang, Rev. Sci. Instrum., 1999, 70, 1277–1284 CrossRef CAS.
- A. E. Stiegman, E. Graham, K. J. Perry, L. R. Khundkar, L. T. Cheng and J. W. Perry, J. Am. Chem. Soc., 1991, 113, 7658–7666 CrossRef CAS.
- C. Dehu, F. Meyers and J. L. Bredas, J. Am. Chem. Soc., 1993, 115, 6198–6206 CrossRef CAS.
- T. Tanaka and A. Osuka, Chem. Rev., 2017, 117, 2584–2640 CrossRef CAS.
- H. Mori, T. Tanaka and A. Osuka, J. Mater. Chem. C, 2013, 1, 2500–2519 RSC.
- S. Pascal, S. David, C. Andraud and O. Maury, Chem. Soc. Rev., 2021, 50, 6613–6658 RSC.
- K. Shimomura, H. Kai, Y. Nakamura, Y. Hong, S. Mori, K. Miki, K. Ohe, Y. Notsuka, Y. Yamaoka and M. Ishida, et al. , J. Am. Chem. Soc., 2020, 142, 4429–4437 CrossRef CAS PubMed.
- Y. Ding, W.-H. Zhu and Y. Xie, Chem. Rev., 2017, 117, 2203–2256 CrossRef CAS PubMed.
- T. Woller, P. Geerlings, F. De Proft, B. Champagne and M. Alonso, Molecules, 2018, 23, 1333 CrossRef.
- T. Woller, P. Geerlings, F. De Proft, B. Champagne and M. Alonso, J. Phys. Chem. C, 2019, 123, 7318–7335 CrossRef CAS.
- M. Torrent-Sucarrat, S. Navarro, E. Marcos, J. M. Anglada and J. M. Luis, J. Phys. Chem. C, 2017, 121, 19348–19357 CrossRef CAS.
- J. M. Lim, Z. S. Yoon, J.-Y. Shin, K. S. Kim, M.-C. Yoon and D. Kim, Chem. Commun., 2008, 261–273 RSC.
- Z. S. Yoon, J. H. Kwon, M.-C. Yoon, M. K. Koh, S. B. Noh, J. L. Sessler, J. T. Lee, D. Seidel, A. Aguilar, S. Shimizu, M. Suzuki, A. Osuka and D. Kim, J. Am. Chem. Soc., 2006, 128, 14128–14134 CrossRef CAS PubMed.
- Z. S. Yoon, D.-G. Cho, K. S. Kim, J. L. Sessler and D. Kim, J. Am. Chem. Soc., 2008, 130, 6930–6931 CrossRef CAS PubMed.
- T. K. Ahn, J. H. Kwon, D. Y. Kim, D. W. Cho, D. H. Jeong, S. K. Kim, M. Suzuki, S. Shimizu, A. Osuka and D. Kim, J. Am. Chem. Soc., 2005, 127, 12856–12861 CrossRef CAS PubMed.
- K. S. Kim, S. B. Noh, T. Katsuda, S. Ito, A. Osuka and D. Kim, Chem. Commun., 2007, 2479–2481 RSC.
- H. Rath, J. Sankar, V. PrabhuRaja, T. K. Chandrashekar, A. Nag and D. Goswami, J. Am. Chem. Soc., 2005, 127, 11608–11609 CrossRef CAS.
- T. Woller, J. Contreras-García, P. Geerlings, F. De Proft and M. Alonso, Phys. Chem. Chem. Phys., 2016, 18, 11885–11900 RSC.
- E. Desmedt, T. Woller, J. L. Teunissen, F. De Vleeschouwer and M. Alonso, Front. Chem., 2021, 9, 786036 CrossRef CAS.
- E. Desmedt, D. Smets, T. Woller, M. Alonso and F. De Vleeschouwer, Phys. Chem. Chem. Phys., 2023, 25, 17128–17142 RSC.
- E. Desmedt, L. Serrano Gimenez, F. De Vleeschouwer and M. Alonso, Molecules, 2023, 28, 7371 CrossRef CAS.
- M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, G. Scalmani, V. Barone, G. A. Petersson, H. Nakatsuji, X. Li, M. Caricato, A. V. Marenich, J. Bloino, B. G. Janesko, R. Gomperts, B. Mennucci, H. P. Hratchian, J. V. Ortiz, A. F. Izmaylov, J. L. Sonnenberg, D. Williams-Young, F. Ding, F. Lipparini, F. Egidi, J. Goings, B. Peng, A. Petrone, T. Henderson, D. Ranasinghe, V. G. Zakrzewski, J. Gao, N. Rega, G. Zheng, W. Liang, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, T. Vreven, K. Throssell, J. A. Montgomery, Jr., J. E. Peralta, F. Ogliaro, M. J. Bearpark, J. J. Heyd, E. N. Brothers, K. N. Kudin, V. N. Staroverov, T. A. Keith, R. Kobayashi, J. Normand, K. Raghavachari, A. P. Rendell, J. C. Burant, S. S. Iyengar, J. Tomasi, M. Cossi, J. M. Millam, M. Klene, C. Adamo, R. Cammi, J. W. Ochterski, R. L. Martin, K. Morokuma, O. Farkas, J. B. Foresman and D. J. Fox, Gaussian 16 Revision A.01, Gaussian Inc., Wallingford, CT, 2016 Search PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51–57 CrossRef CAS.
- W. J. Hehre, L. Radom, P. V. R. Schleyer and J. A. Pople, Ab initio molecular orbital theory, Wiley, 1986 Search PubMed.
- N. Sylvetsky, A. Banerjee, M. Alonso and J. M. L. Martin, J. Chem. Theory Comput., 2020, 16, 3641–3653 CrossRef CAS PubMed.
- T. Woller, A. Banerjee, N. Sylvetsky, G. Santra, X. Deraet, F. De Proft, J. M. L. Martin and M. Alonso, J. Phys. Chem. A, 2020, 124, 2380–2397 CrossRef CAS PubMed.
- M. Torrent-Sucarrat, S. Navarro, F. P. Cossío, J. M. Anglada and J. M. Luis, J. Comput. Chem., 2017, 38, 2819–2828 CrossRef CAS.
- T. Verbiest, K. Clays and V. Rodriguez, Second-order nonlinear optical characterization techniques: an introduction, CRC Press, 2009 Search PubMed.
- K. Clays and A. Persoons, Phys. Rev. Lett., 1991, 66, 2980–2983 CrossRef CAS.
- E. Hendrickx, K. Clays and A. Persoons, Acc. Chem. Res., 1998, 31, 675–683 CrossRef CAS.
- M. Torrent-Sucarrat, J. M. Anglada and J. M. Luis, J. Chem. Theory Comput., 2011, 7, 3935–3943 CrossRef CAS.
- M. Torrent-Sucarrat, J. M. Anglada and J. M. Luis, J. Chem. Phys., 2012, 137, 184306 CrossRef PubMed.
- M. Torrent-Sucarrat, S. Navarro, E. Marcos, J. M. Anglada and J. M. Luis, J. Phys. Chem. C, 2017, 121, 19348–19357 CrossRef CAS.
- M. de Wergifosse and B. Champagne, J. Chem. Phys., 2011, 134, 074113 CrossRef PubMed.
- A. Plaquet, M. Guillaume, B. Champagne, F. Castet, L. Ducasse, J.-L. Pozzo and V. Rodriguez, Phys. Chem. Chem. Phys., 2008, 10, 6223–6232 RSC.
- J. Waluk and J. Michl, J. Org. Chem., 1991, 56, 2729–2735 CrossRef CAS.
- J. Michl, J. Am. Chem. Soc., 1978, 100, 6801–6811 CrossRef CAS.
- J. Michl, J. Am. Chem. Soc., 1978, 100, 6812–6818 CrossRef CAS.
- A. Zhang, L. Kwan and M. J. Stillman, Org. Biomol. Chem., 2017, 15, 9081–9094 RSC.
- A. D. Becke, J. Chem. Phys., 1993, 98, 5648–5652 CrossRef CAS.
- C. Lee, W. Yang and R. G. Parr, Phys. Rev. B: Condens. Matter Mater. Phys., 1988, 37, 785–789 CrossRef CAS PubMed.
- F. De Vleeschouwer, V. Van Speybroeck, M. Waroquier, P. Geerlings and F. De Proft, Org. Lett., 2007, 9, 2721–2724 CrossRef CAS PubMed.
- F. De Vleeschouwer, A. Chankisjijev, P. Geerlings and F. De Proft, Eur. J. Org. Chem., 2015, 506–513 CrossRef CAS.
- F. De Vleeschouwer, P. Geerlings and F. De Proft, ChemPhysChem, 2016, 17, 1414–1424 CrossRef CAS.
- R. G. Parr, R. A. Donnelly, M. Levy and W. E. Palke, J. Chem. Phys., 1978, 68, 3801–3807 CrossRef CAS.
- R. G. Parr and R. G. Pearson, J. Am. Chem. Soc., 1983, 105, 7512–7516 CrossRef CAS.
- R. G. Parr, L. v Szentpály and S. Liu, J. Am. Chem. Soc., 1999, 121, 1922–1924 CrossRef CAS.
- C. A. Guido, P. Cortona, B. Mennucci and C. Adamo, J. Chem. Theory Comput., 2013, 9, 3118–3126 CrossRef CAS PubMed.
- T. Le Bahers, C. Adamo and I. Ciofini, J. Chem. Theory Comput., 2011, 7, 2498–2506 CrossRef CAS PubMed.
- T. Lu and F. Chen, J. Comput. Chem., 2012, 33, 580–592 CrossRef CAS PubMed.
- M. Stepień, N. Sprutta and L. Latos-Grażyński, Angew. Chem., Int. Ed., 2011, 50, 4288–4340 CrossRef.
- M. Alonso, P. Geerlings and F. De Proft, Chem. – Eur. J., 2012, 18, 10916–10928 CrossRef CAS PubMed.
- J. I. Wu, I. Fernández and P. V. R. Schleyer, J. Am. Chem. Soc., 2013, 135, 315–321 CrossRef CAS PubMed.
- M. Solà, Front. Chem., 2017, 5, 22 Search PubMed.
- J. Yan, T. Slanina, J. Bergman and H. Ottosson, Chem. – Eur. J., 2023, 29, e202203748 CrossRef CAS PubMed.
- I. Casademont-Reig, E. Ramos-Cordoba, M. Torrent-Sucarrat and E. Matito, Molecules, 2020, 25, 711 CrossRef CAS PubMed.
- J. Kruszewski and T. Krygowski, Tetrahedron Lett., 1972, 13, 3839–3842 CrossRef.
- E. Matito, Phys. Chem. Chem. Phys., 2016, 18, 11839–11846 RSC.
- I. Casademont-Reig, T. Woller, J. Contreras-García, M. Alonso, M. Torrent-Sucarrat and E. Matito, Phys. Chem. Chem. Phys., 2018, 20, 2787–2796 RSC.
- E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2005, 122, 014109 CrossRef.
- E. Matito, M. Duran and M. Solà, J. Chem. Phys., 2006, 125, 059901 CrossRef.
- I. Casademont-Reig, T. Woller, V. García, J. Contreras-García, W. Tiznado, M. Torrent-Sucarrat, E. Matito and M. Alonso, Chem. – Eur. J., 2023, 29, e202202264 CrossRef CAS PubMed.
- E. Matito, ESI-3D: electron sharing indexes program for 3D molecular space partitioning, 2006, https://iqc.udg.es/eduard/ESI, Institut de Qumica Computacional i Catàlisi (IQCC), Universitat de Girona, Girona.
- T. A. Keith, TK Gristmill Software, AIMAll, 2017, https://aim.tkgristmill.com, TK Gristmill Software, Overland Park KS, USA.
- P. Lazzeretti, Phys. Chem. Chem. Phys., 2004, 6, 217–223 RSC.
- Z. Chen, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Chem. Rev., 2005, 105, 3842–3888 CrossRef CAS PubMed.
- H. Fallah-Bagher-Shaidaei, C. S. Wannere, C. Corminboeuf, R. Puchta and P. V. R. Schleyer, Org. Lett., 2006, 8, 863–866 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251 CrossRef CAS.
- K. Wolinski, J. F. Hinton and P. Pulay, J. Am. Chem. Soc., 1990, 112, 8251–8260 CrossRef CAS.
- J. C. Dobrowolski and P. F. J. Lipiński, RSC Adv., 2016, 6, 23900–23904 RSC.
- D. W. Szczepanik, M. Solà, M. Andrzejak, B. Pawełek, J. Dominikowska, M. Kukułka, K. Dyduch, T. M. Krygowski and H. Szatylowicz, J. Comput. Chem., 2017, 38, 1640–1654 CrossRef CAS.
- F. Pedregosa, G. Varoquaux, A. Gramfort, V. Michel, B. Thirion, O. Grisel, M. Blondel, P. Prettenhofer, R. Weiss, V. Dubourg, J. Vanderplas, A. Passos, D. Cournapeau, M. Brucher, M. Perrot and E. Duchesnay, J. Mach. Learn. Res., 2011, 12, 2825–2830 Search PubMed.
- T. Akiba, S. Sano, T. Yanase, T. Ohta and M. Koyama, Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 2019.
- S. M. Lundberg and S.-I. Lee, in Advances in Neural Information Processing Systems 30, ed. I. Guyon, U. V. Luxburg, S. Bengio, H. Wallach, R. Fergus, S. Vishwanathan and R. Garnett, Curran Associates, Inc., 2017, pp. 4765–4774 Search PubMed.
- S. M. Lundberg, B. Nair, M. S. Vavilala, M. Horibe, M. J. Eisses, T. Adams, D. E. Liston, D. K.-W. Low, S.-F. Newman and J. Kim, et al. , Nat. Biomed. Eng., 2018, 2, 749 CrossRef.
- K. Aas, M. Jullum and A. Løland, Artif. Intell., 2021, 298, 103502 CrossRef.
- E. Desmedt, I. Casademont-Reig, R. Monreal-Corona, F. De Vleeschouwer and M. Alonso, Chem. – Eur. J., 2024, e202401933 CrossRef CAS.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp03303e |
| This journal is © the Owner Societies 2025 |