Solid state NMR and DFT studies of azo–hydrazone tautomerism in azo dyes and chitosan-dye films

Abstract

The properties of materials containing azobenzene depend strongly on the dynamics of cis and trans isomerization which in turn are influenced by the presence of different possible tautomers. Two commonly used food azo dyes, Allura Red (ALR) and Amaranth (AMA), were studied by NMR spectroscopy to experimentally determine their tautomeric forms and then theoretically rationalized. Variable temperature 2D ¹H–¹⁵N HMBC NMR provided a direct measure of the hydrazone percentage of the dyes in solution which was complimented by ¹H ultrafast magic-angle spinning (MAS) and ¹³C CPMAS solid state NMR to characterize the structures of the solid dyes alone and incorporated into chitosan films designed to disassemble upon exposure to light and water. Density functional theory (DFT) calculations were carried out to predict tautomeric equilibria in comparison to NMR measurements and rationalize the observed equilibrium in terms of electronic structure effects computed in the natural bond orbital analysis framework. In agreement with NMR results, the hydrazone form was strongly favored in a polar solvent, driven primarily by stabilizing resonance delocalization and favourable electrostatic interactions with solvent. Our observations show that the ALR and AMA dyes exist predominantly in the hydrazone form of their tautomeric equilibrium in solution, in the solid-state, and in a chitosan-dye film. These results indicate that since disassembly of the chitosan-dye films, potential substitutes for petrol-based polymer films, is based on the cis–trans isomerization of the azo form, other water soluble food dyes with higher azo contents should be explored.

---

1. Introduction

Tautomerism, one of the most important forms of structural isomerism, plays a significant role in many areas of the chemical industry, including dye manufacturing. Azo dyes constitute more than 60% of total dyes used in the textile and food industries, representing the largest production volume of dyes today.¹ Azo dyes with functional groups containing OH, NH, or SH hydrogens are classified as tautomeric, having both azo and hydrazo forms.^2,3 As early as 1884, Zincke and Bindewald conclusively demonstrated this tautomerism by performing two distinct experiments that resulted in the same product, relating to the fast equilibrium between the azo and hydrazo forms.⁴ Analyzing whether a dye is in its azo (enol) and/or hydrazone (keto) form is both of fundamental interest and vital for potential applications.^5,6 This structural property is of relevance to our ongoing effort to develop sustainable, low-toxicity, and biocompatible photo-reversible materials by combining azo-based food dyes with bio-sourced polymers.^7,8 The incorporation of azo groups is the most common approach to create photo-reversible materials through cis–trans isomerization via irradiation with visible light.^9–11 The rate and efficiency of the disassembly of azo dye-polymer complexes depend on this photoswitching which in turn is strongly influenced by the presence of tautomerism for azo dyes with hydrogen bonding functional groups. Control of the disassembly rate through molecular design, based on the characterization of the enol/keto populations, is desirable for practical biodegradable and recyclable packaging materials.

In previous work, water soluble anionic food dyes were complexed with bio-sourced chitosan, a polycation, to create water insoluble polymer films. The films can then be disassembled through exposure to water and sunlight via photoisomerization which disrupts the polymer–dye ionic bonds. Allura Red (ALR) and Amaranth (AMA) were chosen as low toxicity, water soluble food dyes, suitable for producing environmentally friendly materials from readily recyclable components. These azo-dye polymer films, produced by a simple solvent casting method, could potentially replace certain petrol-based polymer films as they have mechanical properties and water resistance comparable to current plastic packaging materials.^7,8

The presence of the hydroxyl group in the ortho ring position with respect to the azo group in ALR and AMA azo dyes complicates the trans to cis isomerization due to the presence of hydrazone character. Distinct isomerization mechanisms are possible for the azo and hydrazone forms, which can potentially impact the efficiency of light-triggered disassembly of azobenzene-based recyclable plastics. Tautomerism has been shown to accelerate the thermal cis–trans back isomerization of azobenzenes,^12,13 which can make efficient bulk photoisomerization difficult without intense irradiation. In addition, in one study, Thongchai et al. found that bulk photoisomerization of an arylazo photoswitch acid violet 3 was lost when the hydrazone tautomeric form was acquired under neutral pH conditions.¹⁴ Indeed, determining tautomeric equilibria and elucidating the mechanistic effects driving the preference for one tautomeric form are important for designing novel plastic materials whose disassembly is predicated on azobenzene photoisomerization.

Nuclear magnetic resonance (NMR) spectroscopy, particularly ¹⁵N NMR, is a useful approach to quantifying this tautomeric equilibrium. ¹⁵N NMR is particularly advantageous since both nitrogen atoms are directly involved in the azo–hydrazone equilibrium.^5,6 Here we apply variable temperature 2D ¹H–¹⁵N HMBC NMR to determine the azo and hydrazone populations of the solvated dyes and ultra-fast magic angle spinning (MAS) ¹H and ¹H–¹³C cross polarization (CPMAS) NMR to determine the structures of the solid dyes and azo-dye chitosan films. In addition, density functional theory (DFT) is used to predict tautomeric equilibria of ALR and AMA under solvent-free and implicit solvation conditions. Presently, there are few detailed computational reports which evaluate the electronic structure and environmental effects driving tautomeric equilibrium.¹⁵ Here, we employ the natural bond orbital (NBO) population analysis formalism to identify trends in hybridization, charge localization, and σ and π donor–acceptor interactions correlating with the relative stability of both tautomeric forms.

2. Materials and methods

2.1 Azo dyes and chitosan-dye film preparation

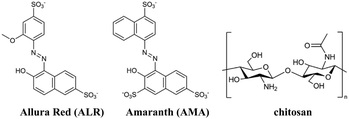
The structures of azo dyes ALR and AMA, and chitosan (CS) polymer are presented in Fig. 1. The solvent-casting method was selected to prepare thick free-standing films. 100.0 mL of a 0.01 M solution of azo dye (ALR or AMA) in distilled water was added dropwise into a 100.0 mL solution of chitosan polymer (0.01 M solution in 1% acetic acid in distilled water). Given the charge difference of ALR having one more charge than chitosan, the amount of ALR added was halved and AMR was reduced to one-third for a 3 : 1 charge ratio to balance the charges. The solutions were mixed at room temperature with stirring and poured into Teflon dishes for slow solvent evaporation until a film formed. The films were then removed by gently peeling them off.

Fig. 1 Structures of ALR, AMA and chitosan.

2.2 NMR spectroscopy

Variable temperature heteronuclear multiple-bond correlation (HMBC) experiments were carried out on a Bruker AVIIIHD 800 MHz spectrometer equipped with a TCI cryoprobe using the gradient-selected HMBC pulse sequence (HMBCgpndqf). Ammonia was the ¹⁵N internal standard, and the dye solutions were prepared with approximately 5% (w/w) dye concentration in DMF.

For the solution ¹H NMR spectra at 800 MHz, 1 scan was acquired with an acquisition time of 2 s.

For the ¹H–¹⁵N HMBC parameters, 1 s relaxation delays and 63.89 and 12.64 ms acquisition times were used with spectral widths of 16 025 Hz and 20 242 Hz for ¹H and ¹⁵N, respectively. The data acquisition size was set to 2048 and 512 points for the ¹H versus ¹⁵N dimensions for sufficient resolution of the heteronuclear couplings. The 2D spectra were collected at temperatures of −30, −15, 0, 15, 30, 40, 50 and 60 °C with 32 scans per time increment.

For the ¹H–¹³C HSQC NMR experiments, 1 s relaxation delays and 63.89 and 3.53 ms acquisition times were used with spectral widths of 16 025 Hz and 36 224 Hz for ¹H and ¹³C, respectively. The data acquisition size was set to 2048 and 256 points for the ¹H versus ¹³C dimensions with 1 scan per increment.

The ¹H MAS SSNMR spectra of the solid dyes and dye-chitosan films were recorded on a 600 MHz wide bore Avance I Bruker NMR spectrometer equipped with a 1.3 mm ultrafast MAS SSNMR probe. Sample spinning frequencies of 55 kHz were used to achieve high resolution ¹H solid-state NMR spectra. A 90° pulse length of 1.7 μs and 4 scans were used to acquire the ¹H MAS NMR spectra.

The ¹H–³C CPMAS spectra of the dyes and dye-chitosan films were obtained on a 400 MHz Varian NMR using a linear ramp cross polarization time of 3.5 ms, SPINAL decoupling, a recycle delay of 3 s and 512 scans.

2.3 Computational chemistry

DFT calculations were performed with the Orca 5.0.3 software.^16–18 AMA and ALR geometries were optimized under solvent-free conditions using the M06-2X functional¹⁹ and def2-TZVP basis set²⁰ on all atoms, except for sulfonate oxygens where the minimally diffuse basis set ma-def2-TZVP^20,21 was instead applied for an appropriate treatment of anionic SO₃⁻ groups. Calculations were sped up by evaluating Coulomb repulsion integrals in the resolution of identity (RI) approximation²² with a def2/J auxiliary basis set.²³ Vibrational analysis was performed to verify local minimum geometries by the absence of imaginary frequencies and to obtain solvent-free thermodynamic corrections.²⁴ To obtain solvent-corrected electronic energies, single points on all calculated structures were evaluated in a DMF continuum solvent model using the solvent model by density (SMD)²⁵ at the M06-2X//def2-TZVP/ma-def2-TZVP level. Tautomeric forms were characterized in the natural bond orbital (NBO) formalism with the NBO 7.0 software.²⁶ NBO deletion analysis was performed on DFT-optimized geometries using the Hartree Fock (HF) method with an identical basis set as DFT calculations due to the ill-suited nature of density functionals for calculating NBO deletions. Structures, NBOs, and frequencies were visualized with Chemcraft.²⁷

3. Results and discussion

3.1 2D ¹H–¹⁵N HMBC NMR

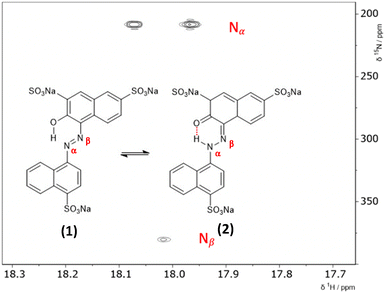
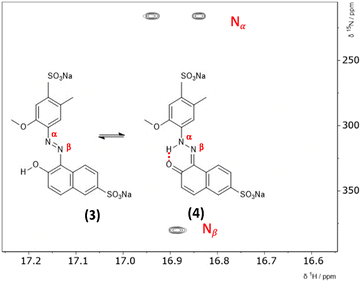
The hydrazone content can be calculated from the one bond ¹H–¹⁵N coupling constants, ¹J_NH of the N_α nitrogen.^28,29 Dimethylformamide (DMF) was selected as the solvent due to its wide temperature range, ensuring stability during the NMR measurements. Both ALR and AMA dyes exhibited good solubility in DMF across the entire temperature range examined. Lyčka recently showed that the inverse detection ¹H–¹⁵N HMBC NMR experiment, in combination with a cryoprobe and a high magnetic field, is sensitive enough to quantify azo–hydrazo tautomerism in azo dyes at natural abundance of ¹⁵N.^5,6 Representative ¹H–¹⁵N HMBC spectra with the hydrazone (keto) and azo forms of the two dyes are shown in Fig. 2 and 3 and all of the ¹H–¹⁵N HMBC spectra are provided in the ESI† (Fig. S4–S17). Not all correlations are observed, especially for AMA at higher temperatures. This is likely due to the very low natural abundance of ¹⁵N (0.365%). The signal intensities are still low even with indirect detection via the protons combined with a high field NMR equipped with a cryoprobe. Since the population of the hydrazone tautomer decreases with increasing temperature, correlations to both nitrogens will be weaker, and the intensity of the cross peaks will decrease. Temperature related changes of the relaxation times may also be contributing to the loss of signal intensity. The assignment of the N_α and N_β nitrogens is based on previous studies^5,6 and the hydrazone proton will be visibly split into a doublet in the indirect ¹⁵N dimension at the N_α chemical shift due to a one bond ¹H–¹⁵N coupling. Since the tautomeric equilibrium is very fast on the NMR timescale, only one peak is observed at 16.6 ppm for the N_α–H/OH proton. The hydrazone content was calculated using eqn (1) and ¹J(¹⁵N_α, ¹H)_H = 96.5 Hz from a model compound with 100% hydrazone form and an intramolecular hydrogen bond as proposed by Bekárek et al.^28,29 The ¹⁵N shifts can also be used with model azo and hydrazone forms according to eqn (2).⁶

%H = [¹J(¹⁵N_α, ¹H)_ex/¹J(¹⁵N_α, ¹H)_H] × 100 (1)

%H = {1 − [δ(¹⁵N_α,β)_ex − δ(¹⁵N_α,β)_H]/[δ(¹⁵N_α,β)_A − δ(¹⁵N_α,β)_H]}100 (2)

Fig. 2 ¹H–¹⁵N HMBC spectrum of AMA at −30.00 °C, measured in DMF with the azo (1) and hydrazone (2) forms showing the intramolecular hydrogen bond. The two cross peaks at the N_α chemical shift in the ¹⁵N indirect dimension are due to a one-bond ¹H–¹⁵N coupling of the hydrazone proton with the N_α nitrogen.

Fig. 3 ¹H–¹⁵N HMBC spectrum of ALR at −30.00 °C, measured in DMF with the azo (3) and hydrazone (4) forms showing the intramolecular hydrogen bond. The two cross peaks at the N_α chemical shift in the ¹⁵N indirect dimension are due to the splitting of the hydrazone proton by the N_α nitrogen.

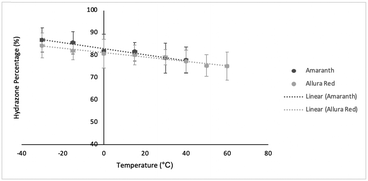
The coupling constants, ¹⁵N chemical shifts and the calculated hydrazone content are listed in Table 1 as a function of temperature and are also plotted in Fig. 4. As can be seen from these data, there is relatively little variation, but the azo content increases slightly with temperature. The hydrazone content calculated from the ¹⁵N_α shifts is consistently higher than values calculated from the coupling constants but shows the same trend with temperature. Very similar temperature dependence has been reported for other azo dyes that are primarily in the hydrazone form.^5,6

Table 1 ¹J(¹⁵N, ¹H) coupling constants and hydrazone content versus temperature

T (°C)	ALR			ALR %(H)		AMA			AMA %(H)
	^1JNH (Hz)	δNα (ppm)	δNβ (ppm)	Based on ^1JNH	Based on δNα	^1JNH (Hz)	δNα (ppm)	δNβ (ppm)	Based on ^1JNH	Based on δNα
60.0	72.5	234.7	389.7	75.1	78.7	—			—
50.0	72.7	232.7	388.7	75.4	79.5	—			—
40.0	74.6	230.8	387.8	77.3	80.0	75.0	229.1	—	77.8	80.8
30.0	76.4	228.8	—	79.2	80.0	76.0	225.2	—	78.8	82.3
15.0	77.3	225.9	385.3	80.0	82.0	78.7	220.8	387.0	81.6	83.9
0.0	77.9	222.7	383.4	80.7	83.2	79.0	215.4	384.2	81.9	85.8
−15.0	79.1	219.5	381.9	82.0	84.5	82.6	212.0	382.2	85.6	87.0
−30.0	81.4	216.1	379.9	84.3	85.6	83.7	208.1	380.2	86.8	88.5

---

Fig. 4 Temperature dependence of hydrazone content for ALR and AMA.

3.2 1H ultrafast MAS and 13C CPMAS NMR

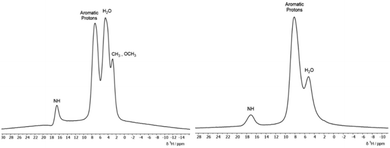
To detect the presence of the hydrazone form in the solid dyes via ¹H MAS SSNMR, high spinning frequencies are required to resolve the signals due to the strong homonuclear proton–proton dipolar couplings which can result in static linewidths as large as 50 kHz. The ¹H ultrafast MAS SSNMR spectra for the two solid dyes are presented in Fig. 5. Due to the sulfonate groups, these materials are hygroscopic and a peak for bound water is seen in both solid dyes at ∼4 ppm. Both dyes have a broad aromatic peak centred at ∼8 ppm and the methyl and methoxy protons of ALR are resolved. Most notable is the relatively strong peak at ∼17 ppm for the N_αH resonance that matches the ¹H chemical shift from solution NMR experiments done here and in other studies^5,6 where the dyes are predominately in the hydrazone form. An early study determined that the ¹H chemical shift of the NH/OH peak is more sensitive to solvent effects and should not be used to calculate the tautomer ratios, unlike the ¹⁵N chemical shifts. However, the ¹³C chemical shift of the C=O/C–OH carbon is found to reliably increase with the hydrazone content.³⁰ The ¹³C solution chemical shifts of the C=O/C–OH carbons of 175 ppm and 173 ppm for ALR and AMA, respectively, match similar naphthol based dyes with high hydrazone content where the shifts range from 169 to 174 ppm as compared to the azo form, which range from 150 to 165 ppm.³⁰ Given that the shifts of the C=O/C–OH carbon remain unchanged for solid ALR and AMA, (ESI,† Fig. S18 and S20), we conclude that the solid dyes are also predominantly in the hydrazone form.

Fig. 5 600 MHz ¹H MAS NMR spectra of ALR (left) and AMA (right).

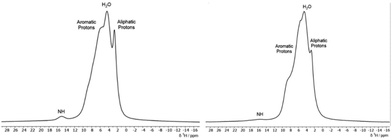
In Fig. 6, the ¹H MAS SSNMR spectra of the dye-chitosan films are presented. As the films were prepared at low pH, both the amine groups on the chitosan and the sulfonate groups of the dyes are fully charged. The chitosan aliphatic protons are partially resolved, but the other protons overlap with the bound water and aromatic peak of the dyes. For both films, the N_α–H proton peak of the hydrazone form of the dye is present but is broadened and shifted to a lower chemical shift of ∼15 ppm. Broadening the NMR signals of the polymer complexed dyes is to be expected due to the disordered local environment as compared to a crystalline solid. In regard to the lower shift of the N_α–H proton in the chitosan films, its chemical shift reflects the fast intramolecular exchange with the hydroxyl proton in the ortho position. The hydroxyl chemical shift in turn reflects intermolecular exchange with the bound water and among the amine and hydroxyl protons of the hydrated chitosan which could account for the lower shift. As stated above, the C=O/C–OH chemical shift is a better measure of the tautomer form. For the ALR/chitosan film, the C=O/C–OH carbon shift remains at 175 ppm which supports the hydrazone form for ALR incorporated into the chitosan film. The AMA/chitosan film differs because in addition to the 173 ppm C=O/C–OH peak of solid AMA, a second broader peak appears at 180 ppm. The complexation with chitosan is different for the two dyes: for charge neutrality, there are 3 chitosan monomers per AMA molecule which has three sulfonate groups, whereas for ALR, there are 2 chitosan monomers per AMA molecule. While AMA is still predominantly in the hydrazone form in the film, the complexation to chitosan may alter the stabilizing intra- and intermolecular interactions, as discussed in the next section. Calculations of the ¹³C chemical shifts of the solid dyes would be useful but require knowledge of the crystal structure as discussed by Bártová et al.³¹ Various attempts to grow large enough crystals for X-ray diffraction were unsuccessful. The ¹⁵N chemical shifts of the N_α and N_β nitrogens can alternatively be used to calculate the hydrazone content. Unfortunately, in the case of ¹⁵N SSNMR, this would require ¹⁵N enrichment or acquisition times on the order of days due to the low natural abundance of this isotope combined with long relaxation times.³¹ Dynamic nuclear polarization (DNP) NMR spectroscopy would likely provide sufficient sensitivity to detect natural abundance ¹⁵N signals, even for the azo-dye-chitosan samples.³²

Fig. 6 600 MHz ¹H MAS NMR spectra of chitosan/ALR (left) and chitosan/AMA (right) films.

3.3 DFT modelling of tautomeric equilibria

To estimate the ratio of the azo and hydrazone forms in solution in comparison to NMR data and rationalize the tautomeric equilibria observed, we mounted a DFT investigation of both dyes. We investigated the structures of the most stable isomer for both tautomeric forms (Fig. 2 and 3). For the azo form, the planar trans isomer is known to be more stable than the bent cis isomer. For the hydrazone form, the most stable isomeric form is the cis isomer, where the tautomeric hydrogen and ketone oxygen are on the same side of the imine C=N double bond and form an intramolecular hydrogen bond. The azo forms of AMA and ALR are denoted 1 and 3, respectively, while the hydrazone forms are denoted 2 and 4 (Fig. 2 and 3). We calculated the tautomeric equilibria in a solvent continuum model of polar DMF as well as in a solvent-free environment as a generic model for nonpolar solvents. Although more simplified computational treatments of sulfonated azo dyes may omit sulfonate groups, as they are less electronically active than other substituents of interest (i.e. hydroxyl, methoxy, etc.), their inclusion has been found to dramatically shift the predicted tautomeric equilibrium in previous reports,³³ as well as findings presented herein.

In previous studies of the azo–hydrazone equilibrium of arylazo dyes, the M06-2X meta hybrid exchange–correlation functional was found to accurately predict the dominant tautomeric form at equilibrium.^34–38 The M06-2X functional is known in the quantum chemistry community to be highly sensitive to the size of the integration grid in DFT calculations. We found, in addition, that the default resolution of identity (RI) approximation with ‘chain-of-spheres’ (RIJCOSX) implemented for hybrid DFT in Orca,³⁹ our quantum chemistry program of choice, contributed further numerical noise to the energy gradient that created instability and convergence problems in geometry optimizations. To rectify these convergence problems, the RI approximation was applied to coulomb integrals only, while exchange integrals were treated analytically.

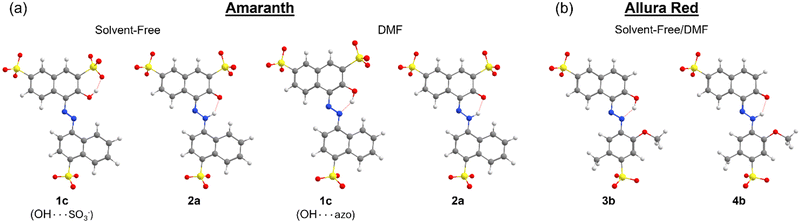
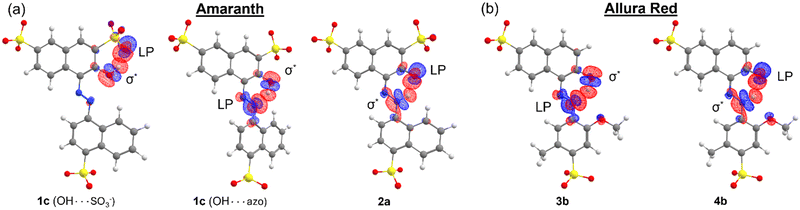
All possible rotations of the naphthyl and phenyl rings about the N=N or N–N bond were explored for the azo and hydrazone tautomeric forms of AMA and ALR, corresponding to distinct conformations a, b, c, and d (ESI,† Fig. S23 and S24). Absolute and relative electronic energies and Gibbs free energies are reported in the ESI,† Tables S1–S6. In DMF, the minimum-energy conformers for AMA were 1c and 2a for the azo form and hydrazone form, respectively, while for ALR, the corresponding minimum-energy conformers were 3b and 4b. These minimum-energy conformers, shown in Fig. 7, are marked by the formation of an intramolecular hydrogen bond involving the hydroxyl group and azo lone pair in the azo form, or the ketone oxygen and tautomeric hydrogen in the hydrazone form. This hydrogen bond forms a six-membered pseudo-ring, tending to lock in this pseudo-ring and the conjoined naphthyl ring in one plane. In addition, minimum-energy conformers acquired geometries which minimize steric hindrance as much as possible. For AMA, conformations 1c and 2a are such that the naphthyl rings are maximally separated; however, completely planar geometries were not possible for the azo form. By contrast, conformations 3b and 4b of ALR are both planar owing to less steric hindrance from the phenyl ring compared to the bulkier naphthyl ring in AMA. To our knowledge, crystal structures have not been determined for AMA or ALR; however, the identified minimum-energy conformations for both dyes show good agreement with previous computational treatments of similar dyes⁴⁰ and our previous work.^7,8

Fig. 7 Minimum-energy conformations of the azo and hydrazone forms of (a) AMA and (b) ALR calculated at the M06-2X//def2-TZVP/ma-def2-TZVP level under solvent-free conditions or in a solvent continuum model (SMD) of DMF. The red dotted lines signify hydrogen bonding.

Under solvent-free conditions, the minimum-energy azo conformer of AMA is such that the hydroxyl group prefers to interact with the nearby sulfonate group on the naphthol ring as opposed to the azo group, likely to reduce coulombic separation. We also consider that, in principle, solvent-free conformations of ALR where the hydroxyl group twists away from the azo group are possible. However, for all conformers a, b, c, and d, of the azo form (ESI,† Fig. S23 and S24), the calculated energy relative to the same structures possessing the stabilizing OH⋯azo hydrogen bond was on the order of 50 kJ mol⁻¹ or greater. Therefore, we excluded these conformations from further analysis.

Assuming a Boltzmann distribution of all possible conformations for both dyes, the Gibbs free energy of tautomerization was taken as the difference in Boltzmann-averaged Gibbs free energy, 〈G_hyd〉 and 〈G_azo〉, of the hydrazone and azo forms. The equilibrium ratio of azo and hydrazone tautomers, K, is related to the standard Gibbs free energy of tautomerization according to eqn (3).

Although thermodynamic corrections were calculated under solvent-free conditions at a pressure of 1 atm, given that the tautomerization process is unimolecular, the addition of a correction term for standard state of 1 bar in gas or 1 M in solvent was redundant. Predicted tautomerization free energies at 298.15 K, equilibrium constants K, and percentage of the hydrazone form are reported in Table 2. For both dyes, tautomeric equilibrium is shifted towards the hydrazone form in polar DMF, whereas the azo form is more strongly favoured when solvent is excluded. Calculated percentages of the hydrazone form in DMF agree satisfactorily with NMR measurements within experimental errors (Table 1). Considering anticipated error bounds for our choice of theory level, as discussed next, there is no significant difference in predicted tautomeric equilibria between AMA and ALR in DMF solvent. In general, a recent benchmarking study has shown that many commonly used functionals do not fit experimental results closely, unless a specialized functional whose parameters are fitted to tautomeric equilibrium data is specially designed.³⁴ Indeed, in our previous work, the B3LYP functional overestimated the stability of the hydrazone form of AMA under solvent-free conditions starkly in contrast to calculations presented here.^7,8 On the other hand, the M06-2X functional was identified as one of the top performers, with a modest mean average error of 0.46 kcal mol⁻¹ compared to experimental measurements.³⁴ Full geometry optimizations in SMD solvent would likely improve the accuracy of predicted tautomeric equilibria and delineate more clearly changes across a spectrum of solvent polarities. However, the numerical treatment of vibrational frequencies required for the SMD model in Orca were computationally restrictive in this work, and thus optimizations were carried out only in a solvent-free environment. In one study on an arylhydrazone rotary switch, Deneva et al. found that a combined implicit and explicit treatment of solvation significantly affected tautomeric equilibrium and proton transfer processes through solvent–solute interactions and disruption of intra- and intermolecular hydrogen bonding.³⁸ These results suggest explicit solvation as the gold-standard for predicting tautomeric equilibria accurately, yet implicit treatments nevertheless provide utility in rationalizing experimental observations, as discussed next.

Table 2 Predicted tautomerization Gibbs free energy at 298.15 K, equilibrium constant K, and hydrazone percentage for dyes AMA and ALR in solvent-free conditions and a solvent continuum model (SMD) of DMF, calculated at the M06-2X//def2-TZVP/ma-def2-TZVP level

Condition	ΔGazo–hyd (kJ mol^−1)	K	% hydrazone
AMA
Gas	9.8	2.0 × 10^−2	2
DMF	−4.2	5.4	84
ALR
Gas	0.8	0.7	42
DMF	−1.6	1.9	66

---

3.4 Natural bond orbital analysis

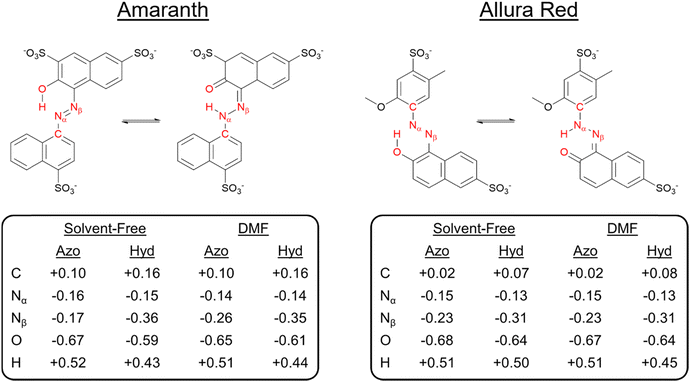
To identify the underlying causes for the observed tautomeric equilibria for both dyes under DMF and solvent-free conditions, we performed a natural bond orbital (NBO) population analysis⁴¹ (ESI,† Fig. S25). Analyzing first one-center lone pair (LP) NBOs, in both solvent-free and DMF solvent models, the LP on the tautomeric nitrogen N_α is in an unhybridized p orbital in the hydrazone form, compared to an approximately sp²-hybridized orbital in the azo form, which is consistent with ketone resonance. In addition, the occupancy of the N_α LP NBO drops significantly in the hydrazone form. For AMA, the occupancy drops from 1.95 to 1.58 and from 1.88 to 1.55 in the solvent-free and DMF phases, respectively, whereas for ALR, the occupancy drops from 1.88 to 1.52 in both phases similarly. Departures from two-fold NBO occupancy are indicative of resonance delocalization effects, demonstrating that the LP on the tautomeric nitrogen in the hydrazone form is strongly delocalized into the π system of the molecule. Next, we investigated the N_α–N_β σ bond as a second important site subject to significant rearrangement of electron density upon tautomerization. For AMA, the hybridization of N_β increases from sp^2.1 in the azo form to sp^2.6 in the hydrazone form in both solvent-free and solvated phases. Similarly, for ALR, the hybridization of N_β increases from sp^2.2 to sp^2.5. In the hydrazone form, the N_α–N_β σ bond NBO becomes more strongly polarized towards the tautomeric nitrogen, whereas in the azo form, there is no significant polarization towards either nitrogen. The increased p character of N_α and stronger polarization towards N_α in the N_α–N_β σ bond, as well as the less efficient screening afforded by the N_α LP present in an unhybridized p orbital rather than an sp² hybrid suggest that the tautomeric nitrogen N_α becomes more electronegative in the hydrazone form.

A stronger localization of charge in either tautomeric form would enable more stabilizing electrostatic interactions with polar solvent, such as DMF employed experimentally in this work. To address this possibility, we calculated natural atomic charges for both tautomeric forms of AMA and ALR in the solvent-free and DMF phases, which are summarized in Fig. 8. For AMA, the hydrazone form is marked by significant localization of negative charge to the tautomeric nitrogen N_α with natural atomic charges of −0.36 and −0.35 in solvent-free and DMF phases, respectively, compared to a smaller negative charge on N_β. By contrast, the charge difference between N_α and N_β is minimized in the azo form, where the charges on N_α and N_β in DMF are −0.26 and −0.14, respectively. Compared to the azo form, positive charge tends to accumulate on carbon atoms in proximity to the azo bond in the hydrazone form, further localizing charge throughout the structure. The N_α and N_β charge difference is completely neutralized under solvent-free conditions with the absence of the six-membered pseudo-ring, where the charges on N_α and N_β are −0.16 and −0.17, respectively. Similar trends are observed for ALR; however, given that twisting the hydroxyl group out of the pseudo-six-membered ring configuration was highly unfavourable under solvent-free conditions, complete neutralization of the charge difference between N_α and N_β did not occur for this dye.

Fig. 8 Natural atomic charges for the azo and hydrazone forms of AMA and ALR calculated at the M06-2X//def2-TZVP/ma-def2-TZVP level under solvent-free conditions and or a solvent continuum model (SMD) of DMF.

Focusing first on AMA, in DMF, steric hindrance and electrostatic interactions tend to favour the hydrazone form, as evidenced by a negative change in the localized contribution, ΔE(L), while resonance delocalization effects more strongly stabilize the azo form. (Table 3) Comparing the minimum-energy geometries 1c and 2a in DMF solvent (Fig. 7), the hydrazone form is nearly planar. The naphthyl ring twists out of the plane of the six-membered pseudo-ring by 3.4 degrees, whereas in the azo form, this twist is significantly larger at 20.4 degrees due to steric hindrance between the hydroxyl hydrogen and the nearby hydrogen on the naphthyl ring. The competing effects ΔE(L) and ΔE(NL) change under solvent-free conditions, where the hydrazone form is instead more strongly stabilized by resonance delocalization. Compared to the minimum-energy azo structure in DMF solvent, the counterpart structure under solvent-free conditions recovers a geometry which is significantly more planar. However, the hydroxyl group is twisted out of the plane formed by the six-membered pseudo-ring, weakening the resonance delocalization of the oxygen lone pairs into the neighbouring π system. We additionally observed this effect reflected in the hybridization of the hydroxyl oxygen in the O–H σ bond NBO, which increased from sp^2.8 in DMF to sp³ in solvent-free phases, a tetrahedral hybrid configuration which couples more poorly into the π system.

Table 3 Difference in the localized contribution ΔE(L) and delocalized contribution ΔE(NL) between the azo and hydrazone forms of AMA and ALR calculated with NBO energetic deletion analysis at the HF//def2-TZVP/ma-def2-TZVP level

Condition	Ehyd(L) − Eazo(L) (kcal mol^−1)	Ehyd(NL) − Eazo(NL) (kcal mol^−1)
AMA
Solvent-free	21.5	−19.3
DMF	−12.0	9.4
ALR
Solvent-free	14.3	−15.1
DMF	6.7	−8.5

---

We considered lastly tautomeric stability in the framework of NBO energetic deletions. For the ALR dye, under solvent-free conditions and in DMF, steric hindrance and electrostatic interactions favour the azo form, while resonance delocalization effects stabilize the hydrazone form. Unlike AMA, the phenyl ring of ALR is substituted with additional electronically active functional groups, namely the methoxy group in the ortho position with respect to the tautomeric nitrogen. The π-donating effect of this ring substituent can further enhance the delocalization of the tautomeric nitrogen LP, increasing the resonance stability of the hydrazone form. This effect suggests a strategy to select for the stability of the hydrazone form through ring substitution with π-donors and π-acceptors in proximity to the tautomeric nitrogen. At the same time however, repulsion between the tautomeric nitrogen LP and the LPs on the methoxy oxygen lowers the stability of the localized Lewis structure overall, while this repulsive interaction is less pronounced in the azo form.

Finally, we investigated the donor–acceptor interaction involving the delocalization of LPs into the six-membered pseudo-ring of both dyes. In the azo form, this interaction involves the delocalization of the azo LP into the H–O σ* antibonding NBO, while for the hydrazone form, this interaction involves the delocalization of the ketone oxygen LPs into the N–H σ* antibonding NBO. The Fock matrix elements corresponding to these donor–acceptor interactions were deleted, and the energetic contribution E(NL) of such deletions is reported in Table 4. In all cases, this interaction was stronger in the azo form than that in the hydrazone form. As shown in Fig. 9, the overlap of the =N: LP NBO and H–O σ* antibonding NBO orbitals is larger and more direct, whereas for the =O:⋯H–N interaction, there is less orbital overlap between the NBOs. These results suggest that the resonance stability of the hydrazone form, where applicable, is driven principally by donor–acceptor interactions involving the π system of the molecule. Indeed, for both tautomeric forms, resonance-assisted hydrogen bonding (RAHB) comes into play in the six-membered pseudo-ring,⁴² which is reflected preliminarily in the tendency towards the equalization of bond lengths and natural bond orders in this pseudo-ring. In particular, the natural bond orders of O–H and N–H bonds are on the order of 0.40 and 0.48 in the azo and hydrazone forms, respectively (ESI,† Fig. S25). Additionally, a recent study has identified that the strength of RAHBs is driven by the π system acting as an effective conduit for charge localization,⁴³ which we observed for the hydrazone form of AMA and ALR. The analysis of RAHBs and their contribution to the preferred tautomeric equilibrium in AMA and ALR is the subject of future work.

Table 4 Delocalized contribution E(NL) from the deletion of the =N:⋯H–O and =O:⋯H–N donor–acceptor interaction in the azo and hydrazone forms, respectively, of AMA and ALR calculated with NBO energetic deletion analysis at the HF//def2-TZVP/ma-def2-TZVP level

Condition	Ehyd(NL) (kcal mol^−1)	Eazo(NL) (kcal mol^−1)
AMA
Solvent-free	19.8	26.7
DMF	30.8	44.3
ALR
Solvent-free	14.7	32.7
DMF	22.8	40.1

---

Fig. 9 Orbital overlap of the azo LP and H–O σ* antibonding NBOs and of the ketone oxygen LPs and N–H σ* antibonding NBOs in the azo and hydrazone forms, respectively, of (a) AMA and (b) ALR. NBOs were calculated at the M06-2X//def2-TZVP/ma-def2-TZVP level. Due to the similarity between the NBOs calculated from solvent-free and implicitly solvated densities, only NBOs calculated in a solvent-continuum model (SMD) of DMF are shown, with the exception of 1c (OH⋯SO₃⁻), where solvent-free calculated NBOs are shown.

4. Conclusions

Azo–hydrazone tautomerism in two water-soluble food dyes was studied experimentally by NMR spectroscopy and theoretically by DFT calculations to understand the molecular origin of the observed structures. The NMR study shows that for both ALR and AMA, the hydrazone structure dominates in a polar solvent, in the solid-state and when complexed to chitosan. Solution NMR shows that the hydrazone content for both dyes is ∼80% with only a very weak temperature dependence. The Gibbs free energy of tautomerization calculated by DFT reasonably predicted hydrazone populations of 84% and 66% for AMA and ALR, respectively, in DMF. The M06-2X functional and electronic energies evaluated in an SMD model of DMF were found to predict tautomeric equilibria more accurately than previous studies. To understand the underlying cause for the stability of the hydrazone structure in polar solvents, natural bond orbital analysis (NBO) was carried out, revealing that resonance delocalization effects involving the π system and charge localization to the tautomeric nitrogen stabilize the hydrazone form in polar solvent.

Recent literature has shown that the protonation of the azo group, whether by the addition of acid to solutions of azo dye or the existence of a hydrazone tautomer, can shut down bulk photoisomerization by rendering the formation of the cis isomer along excited state potential energy surfaces unfavourable.^14,44,45 Thus, it is important to identify and rationalize the existence of azo–hydrazone tautomeric equilibrium in the azo food dyes because the proposed application of recyclable bioplastics relies on robust photoswitching characteristic of the azo form, which is possibly lost in the hydrazone form. Based on these results, other water-soluble food dyes with larger azo form content, such as acid orange 12,⁶ should be first tested to see whether they complex with chitosan to form robust casted films like ALR and AMA^7,8 and then determine whether these films disassemble more efficiently.

Future work will be to determine the dyes’ crystal structures and to prepare ¹⁵N labeled samples to characterize the tautomer populations via the ¹⁵N chemical shifts of the solid dyes and the chitosan-dye films. On the theoretical side, the role of resonance-assisted hydrogen bonding in the tautomeric equilibrium remains to be explored.

Author contributions

Coral Hillel: conceptualization, data curation, formal analysis, methodology, validation, investigation, writing – original draft, writing – review & editing, and visualization. Sarah Collins: data curation, formal analysis, methodology, validation, and investigation. Amanpreet Parihar: data curation, formal analysis, methodology, validation. Ozzy Mermut: conceptualization, methodology, validation, project administration, funding acquisition, resources, supervision, and writing – review & editing. Christopher Barrett: conceptualization, methodology, validation, project administration, funding acquisition, resources, supervision, and writing – review & editing. William Pietro: conceptualization, methodology, validation, project administration, funding acquisition, resources, supervision, and writing – review & editing. Linda Reven: conceptualization, methodology, validation, project administration, funding acquisition, resources, supervision, and writing – review & editing.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

There are no conflicts to declare.

Acknowledgements

This study was financially supported by the Natural Sciences and Engineering Research Council of Canada (NSERC). We also acknowledge the Canada First Research Excellence Fund, for grants to York University through both VISTA (CFREF-2015-00013) and Connected Minds (CFREF-2022-00010) programs. The J. P. Bickell Foundation is thanked for their support.

References

1. S. Benkhaya, S. M'rabet and A. El Harfi, Heliyon, 2022, 6, e03271.
2. R. Christie, Colour Chemistry, Royal Society of Chemistry, Cambridge, 2nd edn, 2015.
3. K. Bártová, I. Císařová, A. Lyčka and M. Dračínský, Dyes Pigm., 2020, 178, 108342.
4. T. Zincke and H. Bindewald, Ber. Dtsch. Chem. Ges., 1884, 17, 3026.
5. A. Lyčka, Dyes Pigm., 2023, 209, 110896.
6. A. Lyčka, Dyes Pigm., 2024, 222, 111748.
7. M. Kim, C. Hillel, K. Edwards., T. H. Borchers, O. Mermut, W. J. Pietro and C. J. Barrett, Front. Mater., 2024, 11, 1334863.
8. M. Kim, C. Hillel, K. Edwards, W. Pietro, O. Mermut and C. J. Barrett, RSC Adv., 2024, 14, 25771–25784.
9. V. Y. Chang, C. Fedele, A. Priimagi, A. Shishido and C. J. Barrett, Adv. Opt. Mater., 2019, 7, 1900091.
10. H. B. Cheng, S. Zhang, J. Qi, X. J. Liang and J. Yoon, Adv. Mater., 2021, 33, 2007290.
11. S. Crespi, N. A. Simeth and B. König, Nat. Rev. Chem., 2019, 133–146.
12. M. Poutanen, X. Ahmed, L. Rautkari, O. Ikkala and A. Priimagi, ACS Macro Lett., 2018, 7, 381–386.
13. J. Garcia-Amorós, A. Sánchez-Ferrer, W. A. Massad, S. Nonell and D. Velasco, Phys. Chem. Chem. Phys., 2010, 12, 13238–13242.
14. I.-A. Thongchai, Z. J. Knepp, D. R. Fertal, H. Flynn, E. R. Young and L. A. Fredin, J. Phys. Chem. A, 2024, 128, 785–791.
15. A. S. Özen, P. Doruker and V. Aviyente, J. Phys. Chem. A, 2007, 111, 13506–13514.
16. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 73–78.
17. F. Neese, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2017, 8, e1327.
18. F. Neese, F. Wennmohs, U. Becker and C. Riplinger, J. Chem. Phys., 2020, 152, 224108.
19. Y. Zhao and D. G. Truhlar, Theor. Chem. Acc., 2008, 120, 215–241.
20. F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297–3305.
21. J. Zheng, X. Xu and D. G. Truhlar, Theor. Chem. Acc., 2011, 128, 295–305.
22. F. Weigend, Phys. Chem. Chem. Phys., 2002, 4, 4285–4291.
23. F. Weigend, Phys. Chem. Chem. Phys., 2006, 8, 1057–1065.
24. D. Bykov, T. Petrenko, R. Izsák, S. Kossmann, U. Becker, E. Valeev and F. Neese, Mol. Phys., 2015, 113, 1961–1977.
25. A. V. Marenich, C. J. Cramer and D. G. Truhlar, J. Phys. Chem. B, 2009, 113, 6378–6396.
26. E. D. Glendening, J. K. Badenhoop, A. E. Reed, J. E. Carpenter, J. A. Bohmann, C. M. Morales, P. Karafiloglou, C. R. Landis and F. Weinhold, NBO 7.0, Theoretical Chemistry Institute, University of Wisconsin, Madison, WI, 2018.
27. Chemcraft – graphical software for visualization of quantum chemistry computations, Version 1.8, build 682, https://www.chemcraftprog.com.
28. V. Bekárek, K. Rothschein, P. Vetešnik and M. Večera, Tetrahedron Lett., 1968, 9, 3711–3713.
29. V. Bekarek, I. Dobáš, J. Socha, P. Vetešnik and M. Večera, Collect. Czech. Chem. Commun., 1970, 35, 1406–1414.
30. A. Lyčka, J. Jirman and M. Nečas, Dyes Pigm., 1991, 15, 23–29.
31. K. Bártová, I. Císařová, A. Lyčka and M. Dračínský, Dyes Pigm., 2020, 178, 108342.
32. A. N. Smith, K. Märker, S. Hediger and G. De Paëpe, J. Phys. Chem. Lett., 2019, 10, 4652–4662.
33. J. P. Graham, M. A. Rauf, S. Hisaindee and M. Nawaz, J. Mol. Struct., 2013, 1040, 1–8.
34. L. Antonov, Molecules, 2019, 24, 2252.
35. J. Dostanić, D. Mijin, G. Ušćumlić, D. M. Jovanović, M. Zlatar and D. Lončarević, Spectrochim. Acta, Part A, 2014, 23, 37–45,  DOI:10.1016/j.saa.2013.12.064.
36. L. Racané, Z. Mihalić, H. Cerić, J. Popović and V. Tralić-Kulenović, Dyes Pigm., 2013, 96, 672–678.
37. S. Angelova, V. Paskaleva, N. Lochev and L. Antonov, Mol. Phys., 2019, 117, 1604–1612.
38. V. Deneva, N. G. Vassilev, S. Hristova, D. Yordanov, Y. Hayashi, S. Kawauchi, F. Fennel, T. Völzer, S. Lochbrunner and L. Antonov, Comput. Mater. Sci., 2020, 177, 109570.
39. B. Helmich-Paris, B. de Souza, F. Neese and R. Izsák, J. Chem. Phys., 2021, 155, 104109.
40. K. Bevziuk, A. Chebotarev, D. Snigur, Y. Bazel, M. Fizer and V. Sidey, J. Mol. Struct., 2017, 1144, 216–224.
41. A. E. Reed, L. A. Curtiss and F. Weinhold, Chem. Rev., 1988, 88, 899–926.
42. P. Gilli, V. Bertolasi, V. Ferretti and G. Gilli, J. Am. Chem. Soc., 2000, 122, 10405–10417.
43. J. M. Guevara-Vela, E. Romero-Montalvo, A. Costales, A. M. Pendás and T. Rocha-Rinza, Phys. Chem. Chem. Phys., 2016, 18, 26383–26390.
44. S. M. Martin, Z. J. Knepp, I.-A. Thongchai, K. Englehart, K. Sorto, A. Jaffer, L. A. Fredin and E. R. Young, New J. Chem., 2023, 47, 11882–11889.
45. S. M. Martin, R. C. Hamburger, T. Huang, L. A. Fredin and E. R. Young, Phys. Chem. Chem. Phys., 2024, 26, 10804–10813.

---

Footnote

† Electronic supplementary information (ESI) available: Additional NMR spectra and computational parameters. See DOI: https://doi.org/10.1039/d4cp04159c

---