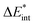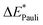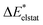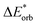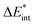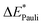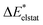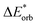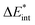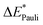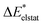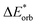Open Access Article
Open Access ArticleCreative Commons Attribution 3.0 Unported Licence
Energy decomposition analysis for excited states: an extension based on TDDFT†
Florian Kreuter and
Ralf Tonner-Zech *
*
Wilhelm-Ostwald-Institut für Physikalische und Theoretisch Chemie, Universität Leipzig, Linnéstr. 2, 04103 Leipzig, Germany. E-mail: ralf.tonner@uni-leipzig.de
First published on 10th February 2025
Abstract
To enhance the understanding of photochemical reactivity and its mechanisms, it is essential to analyze bonding interactions in excited-state reactions. Such insights can aid in optimizing these reactions. This paper presents an energy decomposition analysis method for excited states (exc-EDA), integrating the ground state EDA approach by Morokuma, Ziegler and Rauk with time-dependent density functional theory (TDDFT). The methodology focuses on calculating excitation energies, particularly for the intermediate states of the EDA. We introduce two variants: the first uses non-relaxed excitation coefficients (exc-u-EDA), where the excitation coefficients of the excited fragment are used directly; the second optimizes these coefficients for the intermediate states (exc-r-EDA). Exc-EDA can be applied with various density functionals, but the accuracy depends on the functional's ability to describe the excited state properly. Smaller basis sets result in lower energy values due to fewer virtual orbitals, while larger basis sets produce consistent relative results but may involve different excited states in intermediate steps leading to artificial increase of energy terms in the EDA. The method's convergence behavior resembles that of TDDFT, with a computational cost approximately three times that of the underlying TDDFT calculation. At the current stage, the method requires that the excitation is localized on one of the fragments, but it also enables an analysis of the subsequent charge-transfer effects. Application of exc-EDA to singlet fission in pentacene clusters demonstrates its practical value, offering quantitative insights into excited-state bonding and revealing clear, intuitive trends.
1. Introduction
The excited state of molecules is highly relevant in various research fields like photochemistry, solar to chemical energy conversion, and photocatalysis.1 Here, molecules not only exhibit an electronic but also an atomic structure distinct from the ground state, enabling reactions that are not possible in the ground state.2 Often, chemical interactions in the excited state are decisive for conversion efficiency or selectivity.3 It would be highly beneficial to quantify these interactions with an electronic structure analysis method and be able to derive trends and predict new avenues for experiment. Such a bonding analysis method would allow for a more comprehensive understanding of the reactivity, including the mechanisms underlying photochemical reactions. There are several theoretical approaches4 for the description of excited states, including multi-reference methods5 such as complete active space SCF (CASSCF),6 complete active space perturbation theory of second order (CASPT2),7 n-electron valence state perturbation theory (NEVPT2),8 multireference CI (MRCI)9 and restricted active space SCF (RASSCF).10 Single-reference calculations2,4 can be performed using coupled cluster (CC) approaches11 like equation-of-motion CC (EOM-CC)12 or approximate second-order CC (CC2),13 but also the algebraic diagrammatic construction (ADC),14 full configuration interaction (FCI) and time-dependent density functional theory (TDDFT).2,15,16 TDDFT is the most efficient method for calculating excitation energies and experimental spectra.2 It also has the advantage of being a ‘black-box’ method, making it more user-friendly compared to other methods, particularly the multi-reference methods.4 Therefore, TDDFT is the most used method for calculating excited states in molecular chemistry. Conversely, TDDFT encounters difficulties with long-range charge transfer (CT) excitations, double excitations, and Rydberg excitations.2,4,16 The challenges of TDDFT with CT and Rydberg excitations are primarily attributed to the semilocality of the underlying density functionals. In the derivation of linear response (LR-)TDDFT, only single excitations are considered, which explains the issues with double excitations.The character of chemical bonds is often analyzed to understand chemical reactions and trends. One major approach is energy decomposition analysis (EDA).17 In this method, the system is divided into two fragments, with the bond being analyzed between them (Fig. 1). EDA then divides the bonding energy into distinct contributions, which can be chemically interpreted. For the EDA based on developments by Morokuma and the related extended transition state method by Ziegler and Rauk (jointly called EDA in the following) these are electrostatic interactions between charge densities of fragments, Pauli repulsion, and orbital interaction.18–21 We will use this method as a starting point for our development.
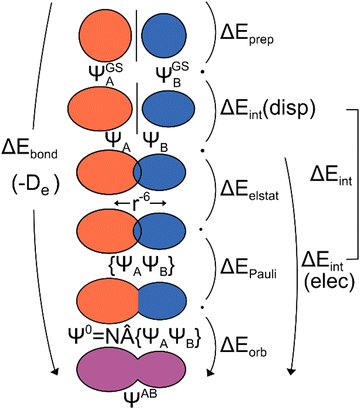 | ||
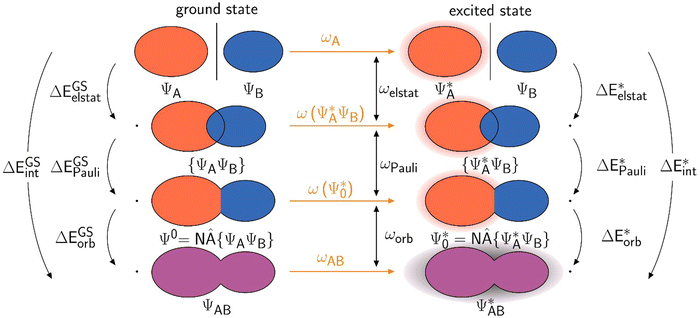
| Fig. 1 Schematic representation of the ground state EDA (adapted from ref. 22). | ||
Further EDA and EDA-type methods comprise generalized Kohn–Sham-EDA (GKS-EDA),23 interacting quantum atoms (IQA),24 block-localized wave function (BLW) EDA25 and its variant the absolutely localized molecular orbital EDA (ALMO-EDA),26 generalized product function (GPF) EDA,27 natural EDA (NEDA)28 and localized molecular orbital (LMO) EDA.29 These methods are either based on the determination of the electron density or orbital space. Additionally, there are EDA methods based on perturbation theory, such as symmetry-adapted perturbation theory (SAPT).30 The use of EDA methods allows for the investigation of a multitude of inter- and intramolecular bond types, including those of a covalent nature observed in organic molecules20 and ligand–metal interactions observed in transition metal complexes.20 Additionally, hydrogen bonds, donor–acceptor bonding, and other interactions can be analyzed. To obtain a more precise picture of the orbitals involved in the respective bond, the natural orbital for chemical valence (NOCV) extension21 for the EDA was developed by Mitoraj and Ziegler. The orbital contribution in deformation densities formed by the NOCVs, which visualizes the charge flow during bond formation, can thus be decomposed further. In addition to molecular systems, energy decomposition analysis for extended systems (pEDA)22 can be used to understand bonding questions in surface and material science.31 The activation strain model (ASM)32 employs the EDA for the precise investigation of reactivity. This model splits the energies along the reaction path into the reaction stress (deformation of the reactants) and an interaction contribution.33
However, most of these methods are applicable to the electronic ground state only. So far, only ALMO-EDA,34 GKS-EDA,35 and density functional-based tight binding EDA (DFTB-EDA),36 have been extended to treat excited states. ALMO-EDA splits the bonding energy into frozen, polarization, and charge transfer terms. The frozen contribution can be approximately matched to the sum of Pauli repulsion and electrostatic interaction in EDA. The ALMO-EDA for the excited state obtains the contributions by calculating the changes caused by the electronic excitation and adding them to the contributions in the ground state. For the calculation of the excitation, configuration interaction single (CIS)2 or the similar TDDFT method with Tamm–Dancoff approximation (TDA) can be used. DFTB-EDA is a semiempirical method that is efficient but less accurate. GKS-EDA splits the bonding energy into electrostatic, exchange-repulsion, polarization, and correlation contributions. The extension to excited states is based on the fact that each intermediate wave function is constructed as a linear combination of simply excited determinants. A further method is the multistate energy decomposition analysis (MS-EDA) method.37 It breaks down the formation reaction of an excimer into different thermodynamic intermediate steps.
What is common to all methods for excited state bonding analysis is that they can be used for exciplex or excimer systems only, where the bonding results from the electronic excitation of one fragment.38 The reason is that choosing the excited fragment is (mostly) straightforward in these systems while the second fragment stays in the ground state. Our development will follow the same approach. A different angle is taken by Kimber and Plasser:39 their approach splits the excitation energy into orbital energy differences, coulomb attraction between hole and electron, repulsive exchange interaction, and exchange correlation (XC)-contributions.
In addition to the EDA methods, natural transition orbitals (NTO)40 are used to understand excited states. Similar to the natural bond orbital (NBO) approach41 for the ground state, NTO is a reduction of the orbital space. This reduces the excitation to mostly one or a few transitions between localized orbitals, as opposed to the mixed character resulting from the canonical orbital picture. Furthermore, the orbitals involved in the excitation can be visualized using the adaptive natural density partitioning method.42 Additionally, various qualitative descriptors for charge CT43 and double excitation44 are in use.
For the ground state, many studies have successfully applied the EDA method to better understand chemical bonding. These studies range from chemical bonding in small main group compounds18,20 to the analysis of donor–acceptor bonds in Lewis acid–base adducts45 and the study of ligand–metal interactions in transition complexes.46 This method has also been used, for example, to study the influence of aromaticity47 on the bonds in benzene. More exotic bonds were also analyzed like halogen,48,49 chalcogen,48,50 and pnictogen48,51 bonding, the interactions between alkali metal cations with hydrides52 and host–guest interactions in heterocalixarenes.53
What is lacking is an extension of this powerful analysis method to the excited state. Here, we show how the EDA scheme can be combined with TDDFT to achieve this goal. This excited state EDA (exc-EDA) is based on the calculation of the excitation energy for the intermediate states. Aside from the theoretical foundation, test systems are presented to identify the computational approach for using the method efficiently. As an application-oriented example, pentacene clusters, a relevant system for singlet fission, is analyzed with the exc-EDA method.
2. Theory
2.1. Ground state EDA
The use of EDA allows for the determination of the character of a chemical bond by breaking down the bonding energy ΔEbond into chemically interpretable contributions. This is achieved by dividing the system AB into two fragments, A and B. We use the generic term ‘system’ for AB which can be two molecular fragments, a molecule and a surface, etc. The bonding energy ΔEbond is equivalent to the negative dissociation energy De and represents the energy difference between the system EAB and the relaxed fragments A (EGSA) and B (EGSB) (eqn (1)).| ΔEbond = EAB − EGSA − EGSB = −De | (1) |
To break down the bond energy into its various components, the EDA introduces intermediate stages of bond formation (Fig. 1). The initial step involves deforming the fragments from their optimized structure (ΨGSA + ΨGSB) to the structure in the system (ΨA + Ψb). This process also considers the change in electronic state if applicable. The preparation energy ΔEprep summarizes all these effects, representing the energy difference between the fragments in the system structure and the ground state structure (eqn (2)).
| ΔEprep = EA + EB − EGSA − EGSB | (2) |
The ‘prepared’ fragments are then bonded with the attractive interaction energy ΔEint. It is the central quantity in the EDA and summarizes all interactions between the fragments. In a first step, it can be split into an electronic ΔEint(elec) and a dispersion term ΔEint(disp) (eqn (3)).
| ΔEbond = ΔEprep + ΔEint = ΔEprep + ΔEint(disp) + ΔEint(elec) | (3) |
The dispersion contribution ΔEint(disp) simply reflects the difference in dispersion interaction between the system and the ground state fragments. The calculation of the respective interactions uses dispersion correction methods (mostly DFT-D354). As the dispersion energy of such semiempirical methods depends only on the atomic arrangement, it is not considered in the next section for the extension of EDA to excited states since we are only interested in vertical excitations where atomic structure does not change.
To further decompose the electronic part of the interaction energy ΔEint(elec), we start by setting the separately calculated charge densities of the fragments to the equilibrium distance. That leads to the Coulomb interaction between the charge densities: the quasiclassical electrostatic contribution ΔEelstat (eqn (4)). For most bonds, the attractive interaction of the electron density of one fragment with the positive nuclei of the other fragment (2nd and 3rd term in eqn (4)) outweighs the nuclei–nuclei (1st term) and electron–electron repulsion (4th term), making this contribution attractive.
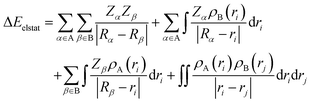 | (4) |
This step results in the product wave function {ΨAΨB}. However, this wave function violates the Pauli principle and must be antisymmetrized and normalized to the intermediate wave function Ψ0 = NÂΨAΨB in the next step. This leads to a constraint on the wave function and a repulsive contribution known as Pauli repulsion ΔEPauli (eqn (5)).
| ΔEPauli = E(Ψ0) − E({ΨAΨB}) | (5) |
The final step involves relaxing the orbitals from the antisymmetrized intermediate state Ψ0 to the orbitals in the system (eqn (6)). This term is called orbital contribution ΔEorb. It is always attractive for ground state EDA and contains charge transfer and polarization contributions.
| ΔEorb = EAB − E(Ψ0) | (6) |
The electronic interaction energy ΔEint(elec) is then the sum of the quasi-electrostatic ΔEelstat, Pauli repulsion ΔEPauli, and orbital contribution ΔEorb (eqn (7)).
| ΔEint(elec) = ΔEelstat + ΔEPauli + ΔEorb | (7) |
2.2. Extension to use one excited state fragment
The exc-EDA similarly divides the system into two fragments to investigate their bonding interactions quantitatively. Currently, exciplexes can be analyzed where one fragment is excited (A*) while the other remains in the ground state (B). The excitation of fragment A* results in a bond between the two fragments. This approach has the advantage of unambiguous fragment assignment and has been used in all other excited state EDA approaches up to now. The exc-EDA uses the interaction energy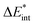 as the central term, which is decomposed.
as the central term, which is decomposed. 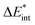 can be determined by calculating the energy difference between the excited system (AB)* and the sum of excited fragment A* and ground state fragment B (eqn (8)).
can be determined by calculating the energy difference between the excited system (AB)* and the sum of excited fragment A* and ground state fragment B (eqn (8)).
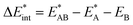 | (8) |
The asterisk (*) indicates that the excited state is considered for these energies. It should be noted that only vertical excitations are used when calculating the interaction energy, as structural effects are not considered. This means that the fragments have the same structure as the ground state structure of the system. With this choice we focus on the electronic changes upon excitation without obscuring geometrical relaxations that follow. Additionally, the interaction energy 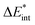 for the excited states can be separated into a ground state component ΔEGSint and an excitation component ωint.
for the excited states can be separated into a ground state component ΔEGSint and an excitation component ωint.
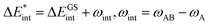 | (9) |
For the remainder of the paper, the energy terms for the excited states are denoted by 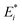 , while the ground state contributions are denoted by EGSi. The changes in energy terms due to excitation are denoted by ωi. Additionally, eqn (9) shows that
, while the ground state contributions are denoted by EGSi. The changes in energy terms due to excitation are denoted by ωi. Additionally, eqn (9) shows that 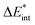 describes the change in excitation of fragment A* resulting from interactions with fragment B.
describes the change in excitation of fragment A* resulting from interactions with fragment B.
As described in the previous section, we only use dispersion interaction for the ground state (eqn (10)), as the method used (DFT-D3) is only dependent on structure and we consider vertical excitations, only. Conversely, the density and polarizability change during excitation, which then naturally causes changes in dispersion interactions. However, it should be noted that none of the dispersion correction methods that take the electron density explicitly into account is available for excited states up to now. In the future, our method could be extended if a suitable density-dependent dispersion correction approach is available.
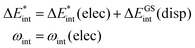 | (10) |
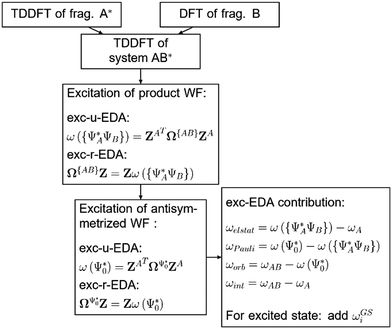
A scheme visualizing exc-EDA is shown in Fig. 2.
As can be seen in Fig. 2, the new method is based on calculating the excitation energy for the two intermediate states (product state 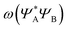 and antisymmetrized state
and antisymmetrized state 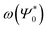 ). Moreover, Fig. 2 illustrates the product and antisymmetrized wave function for the excited states in a manner analogous to that employed for the ground state. Then, the excitation energy ω (orange in Fig. 2) is calculated based on these ground state wave functions, where we use the respective ground state orbitals. Analogous to calculating the contributions for the ground state, the excited state contribution ΔE* and excitation contribution ω are calculated by the difference of excited state energy resp. excitation energy of the corresponding states. Eqn (11) shows the LR-TDDFT approach in matrix representation.2
). Moreover, Fig. 2 illustrates the product and antisymmetrized wave function for the excited states in a manner analogous to that employed for the ground state. Then, the excitation energy ω (orange in Fig. 2) is calculated based on these ground state wave functions, where we use the respective ground state orbitals. Analogous to calculating the contributions for the ground state, the excited state contribution ΔE* and excitation contribution ω are calculated by the difference of excited state energy resp. excitation energy of the corresponding states. Eqn (11) shows the LR-TDDFT approach in matrix representation.2
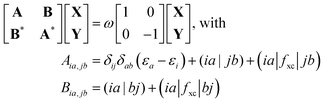 | (11) |
Here, matrix A describes the excitation effects, matrix B the de-excitation effects, and higher-order correlation effects. X is the excitation vector corresponding to A, and Y is the de-excitation vector corresponding to B. The ω values are the eigenvalues of the TDDFT eigenvalue problem (eqn (11)), which correspond to the excitation energy. To calculate matrices A and B, it is necessary to know the orbital energies εi and εa, the two-electron integrals (ia|jb) and the exchange–correlation contribution (ia|fxc|jb). If all orbitals are real, this allows us to transform eqn (11) into a normal eigenvalue problem (eqn (12)).2
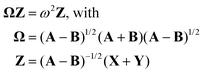 | (12) |
In this context, Ω represents the summarized excitation matrix, while Z represents the corresponding excitation vector. Another way to convert eqn (11) into a normal eigenvalue problem is to use TDA.55 This approximation neglects the B-matrix, which describes de-excitation. As the values of B and Y are usually very small,55 this is a good approximation. The eigenvalue problem to be solved in the TDA is shown in eqn (13).
| AX = ωX | (13) |
Exc-EDA can be used with or without TDA. Eqn (11)–(13) show that the orbital energies εi and orbitals ϕi are required to calculate the excitation energy ω. The orbitals ϕi are used to determine both the exchange–correlation contribution and the two-electron integrals. To this end, we use the respective orbitals ϕi from ground state EDA intermediate steps. Since the orbital energies εi of the intermediate steps are not calculated in the currently available implementation of ground state EDA, we determine them within the newly developed method. To do this, we construct the Fock matrix from the respective orbitals for the intermediate states and then transfer it to the MO basis. The Fock matrix is approximately diagonalized using the overlap matrix. If the Fock matrix is completely diagonalized, the new coefficients result in states that go beyond those considered in the EDA. Furthermore, the exc-EDA method does not require an exact calculation of the excitation energy as it works on the basis of a model state. For its purposes, an approximate excitation energy is sufficient, which can be calculated efficiently with this method. We then use the diagonal elements as an approximation for the orbital energies εi.
There are two different approaches for calculating the excitation energy ω for the intermediate states. The first is in the spirit of the original EDA that all orbital interactions are summarized in the orbital contribution ΔEorb. Thus, the excitation vector Z resp. X must not contain any contributions for excitation between the fragments. To achieve this, we construct the excitation vector Z (X) from the excitation vectors ZA (XA) of the fragments. This approach does not change the excitation coefficients for the two intermediate states. This is why the method is referred to as “unrelaxed coefficients” (exc-u-EDA). We then determine the respective excitation energy ωi for the intermediate states by calculating the matrix-vector product between the excitation vector Z (X) and the excitation matrix Ω (A) (eqn (14)).
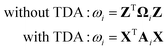 | (14) |
The intermediate states determined with this variant are more similar to the fragments, which means that all excitations between the fragments are summarized in the orbital contribution. This makes the orbital contribution quite large, especially when there is charge transfer between the fragments.
The other variant we implemented is based on a standard way of calculating excitation energies. Here, the intermediate states are constructed for the ground state, and then the excitation energy ωi is calculated based on these intermediate states. In this variant, the orbitals ϕi and orbital energies εi for the respective intermediate state are used to build up the excitation matrix Ω resp. A. The eigenvalues of this matrix, or excitation energy ωi, are then determined using the Davidson approach.56 This changes the excitation coefficients, which is why this variant is referred to as “relaxed coefficients” (exc-r-EDA). This means that excitations between the fragments are already accounted for in the product wave function, which makes the intermediate states more similar to the relaxed full system (AB)*. Charge transfer effects are thus distributed over the different EDA terms. For this reason, this variant is more suitable for systems with considerable charge transfer. Fig. 3 shows the implementation of the method schematically.
Initially, exc-EDA performs the calculations for the fragments, utilizing TDDFT for fragment A and (ground state) DFT for fragment B (Fig. 3). Subsequently, a TDDFT calculation is done for the system (AB)*. Thereafter, the excitations for the two intermediate steps are calculated with both variants (Fig. 3). Finally, the actual EDA excitation contributions ωi are calculated from the differences between the excitation energies of the intermediate states (Fig. 3). The EDA term for the excited state 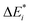 is obtained by adding the ground state values ΔEGSi (eqn (15)).
is obtained by adding the ground state values ΔEGSi (eqn (15)).
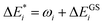 | (15) |
Therefore, the quasi-electrostatic excitation contribution ωelstat is equal to the difference between the excitation energy of the product wave function (ω({ΨAΨB})) and the excited fragment A (ωA) (eqn (16)).
| ωelstat = ω({ΨAΨB}) − ωA | (16) |
This contribution ωelstat describes the changes in Coulomb interaction due to the excitation of fragment A. In particular, the relaxed variant can lead to larger contributions due to charge transfer between the fragments. This can result in partial charge differences, which leads to an increase of electrostatic interaction. If an initial charge difference is equilibrated by charge transfer, it can also lead to a decrease in electrostatic interaction due to the excitation.
Next, the Pauli excitation contribution ωPauli corresponds to the change in excitation energy between the antisymmetrized ω(Ψ0) and product wave functions ω({ΨAΨB}) (eqn (17)).
| ωPauli = ω(Ψ0) − ω({ΨAΨB}) | (17) |
The magnitude of this contribution is primarily determined by the shift in electron density during excitation. An increase in electron density in the bonding region leads to an enhancement of Pauli repulsion, while a decrease in electron density in the overlapping region of the fragments results in a weaker Pauli repulsion.
Finally, the orbital excitation contribution ωorb is the excitation energy difference between the system and the antisymmetrized wave function ω(Ψ0) (eqn (18)).
| ωorb = ωAB − ω(Ψ0) | (18) |
As previously stated, the orbital contribution for the unrelaxed variant can become quite large. Note that the usual trends for ground state EDA interaction terms (electrostatic and orbital interaction are attractive, Pauli repulsion is repulsive) are not necessarily true for the change upon excitation as outlined above.
3. Computational details
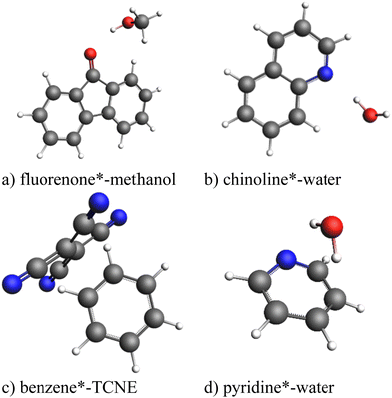
All calculations were performed using a developer's version of the ADF module in the Amsterdam modeling suite (AMS) program package.57 To test the exc-EDA method, the bonding in the complexes fluorenone*–methanol, quinoline*–H2O, pyridine*–H2O, and benzene*–tetracyanoethylene (TCNE) (Fig. 4) was analyzed. These complexes were previously proposed as a suitable test set for excited-state EDA approaches.35 The asterisk (*) indicates the excited fragment, chosen based on the significantly lower excitation energy, except in the benzene–TCNE system, where the excitation affects both fragments (see Table 1).| System | Fragment A* | Fragment B |
|---|---|---|
| a Energies in kJ mol−1 with B3LYP/TZ2P without TDA. The asterisk marks the excited fragment A* in exc-EDA. | ||
| Fluorenone*–methanol | 306 | 624 |
| Quinoline*–water | 428 | 678 |
| Benzene*–TCNE | 526 | 423 |
| Pyridine*–water | 461 | 678 |
In most cases, the excited fragment has excitation energies more than 200 kJ mol−1 lower than the other fragment, except for benzene*–TCNE, where benzene's excitation energy is 103 kJ mol−1 higher. Despite this, benzene is used as the excited fragment because excitation results in charge transfer from benzene to TCNE (Fig. 8). Thus, only charge transfer systems in which the excited fragment donates electrons to the other fragment are considered. Other types of charge transfer excitations, where the excited fragment acts as an electron acceptor or where ion pairs exist in the ground state and are rebalanced upon excitation, will be examined in future studies. The initial focus here is to establish the fundamental principles of exc-EDA.
All calculations used the TZ2P basis set,58 numerical quality “VeryGood” and no symmetry. The integration grid was the Becke Grid59 with quality “VeryGood”. No relativistic correction methods were applied, while the exc-EDA is also implemented to be used together with the zeroth order regular approximation (ZORA). As outlined above, no dispersion correction was used. The structures taken from previous work35 were reoptimized with B3LYP/TZ2P with the settings outlined above.
Next, exc-EDA was applied to this system, whereby the first singlet excited state was used for both the fragments and the complete systems because it is the most relevant for photochemical processes. These tests were run with and without TDA. For all excitation calculations, the adiabatic local density approximation (ALDA) was applied. Different hybrid functionals (B3LYP,60 PBE061) and range-separated (hybrid) functionals (CAMY-B3LYP,62 LC-BLYP,63 LC-PBE63) were used. Previously, it has been shown that the results for the test set for these density functionals are comparable to more accurate EOM-CC data.35
Ground state EDA-NOCV and NTO were performed with B3LYP/TZ2P, and settings shown above. The results of these calculations enabled the formulation of expectations regarding the chemical bonding in the excited state. These expectations were then used to rationalize and check the results of the exc-EDA. Thereby, the same setting as the EDA was used.
Furthermore, calculations were conducted using the QCHEM 6.0.0 program package64 to derive ALMO-EDA results for excited states for the test set. B3LYP was employed as the functional, as it yielded satisfactory outcomes for all functionals with the exc-EDA (see Tables 3, 4, 6 and 7). The def2-QZVPP65 basis set and the structures from exc-EDA were used for ALMO-EDA. In addition, TDA was employed because the ALMO-EDA is only implemented with TDA. First singlet excitation was calculated for all systems. The SCF convergence criteria were set to 10−8 Hartree. Otherwise, the QCHEM default settings were used, and the SG-1 integration grid was applied. No symmetry and no relativistic correction were considered.
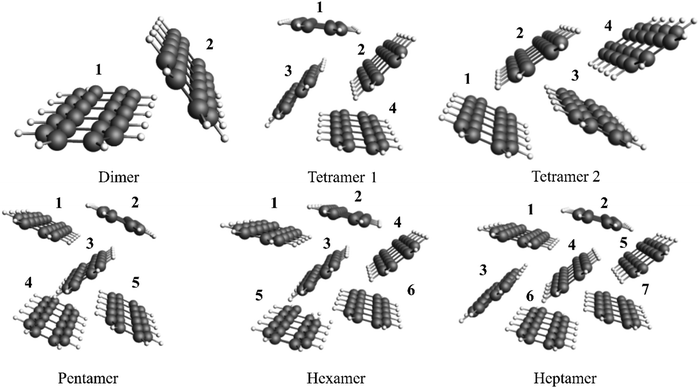
Finally, bonding between monomers were analyzed with exc-EDA in pentacene clusters. This system was selected for application of the novel method since it is of interest for singlet fission.66,67 This will be further discussed below. Engels et al.68 demonstrated that the absorption spectra of pentacene crystals can be replicated with the aid of cluster models using TDDFT. The bonding in different clusters (Fig. 5) was analyzed. Structures were taken from previous work68 together with the suggested density functional ωB97X-D369 and DZP58 as the basis set, with numerical accuracy set to “normal” for efficiency. The first singlet excitation for the system and the excited fragment were then examined, whereby each monomer is individually considered as an excited fragment in separate exc-EDA calculations.
The tetramer 1 and tetramer 2 reflect different symmetry motives from the solid. In tetramer 1, monomers 1 and 4, as well as monomers 2 and 3, are symmetrically equivalent. In contrast, tetramer 2 has no symmetrically equivalent monomers.
4. Application of exc-EDA
For the systems studied as test set, only the decomposition of the electronic interaction energy is considered. Furthermore, the dispersion contribution in the ground state is also included for pentacene clusters. Consequently, preparation energy (ΔEprep) and bonding energy (ΔEbond) are neither calculated nor discussed, as vertical excitations are considered in this context.Prior to the analysis of the exc-EDA results, the expected trends based on “chemical intuition” are discussed in the context of each test system. The primary focus is on the EDA contributions of the excitation ωi (Fig. 2), as these are calculated by exc-EDA. Furthermore, the results obtained with different XC functionals are compared to demonstrate the robustness of the method and to identify potential outliers. A comparison of the results with and without TDA shows that the new method is applicable in both variants.
4.1. Fluorenone–methanol
Fluorenone forms a hydrogen-bond with methanol in the ground state, which is found in ground state EDA (Table 2 for B3LYP and Table S1 (ESI†) for the other density functionals). Here, as for the other systems, we do not see significant changes in the EDA results by using different functionals as was also previously found for a broader test set.70| Fluorenone–methanol | Quinoline–water | Benzene–TCNE | Pyridine–water | |||||
|---|---|---|---|---|---|---|---|---|
| a Percentage values give the relative contributions to the attractive EDA terms ΔEelstat and ΔEorb. Energies in kJ mol−1. Computed with B3LYP/TZ2P. | ||||||||
| ΔEGSint | −26 | −28 | −10 | −4 | ||||
| ΔEGSPauli | 41 | 56 | 15 | 21 | ||||
ΔEGSelstat![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−45 | 67% | −56 | 67% | −17 | 68% | −15 | 63% |
ΔEGSorb![[thin space (1/6-em)]](https://www.rsc.org/images/entities/char_2009.gif) a a |
−22 | 33% | −27 | 33% | −8 | 32% | −9 | 37% |
The result for the ground state EDA (Table 2) align with typical hydrogen-bonding interactions, showing an interaction energy between fluorenone and methanol of −26 kJ mol−1. Here, the attractive interactions are primarily governed by ΔEGSelstat, which accounts for 2/3 of the total interaction energy, while ΔEGSorb contributes only 1/3. Additionally, the absolute values of Pauli repulsion and electrostatic interaction are comparable.
The first singlet excitation is characterized by a HOMO–LUMO transition,23,35 with both orbitals localized exclusively on the fluorenone moiety. This makes it an optimal test system. Fig. 6 illustrates the NTO for this excitation, revealing a shift in electron density from the π-system of fluorenone towards the oxygen atom. This shift strengthens the hydrogen bond, consistent with the findings of Han et al.71 The increased electron density at the oxygen atom leads to a more pronounced negative charge, suggesting a larger quasi-electrostatic contribution in the excited state. Additionally, the Pauli repulsion is expected to become stronger, as the excitation increases the electron density in the bonding region. Furthermore, the enhanced electron density at the oxygen atom should also result in a greater orbital contribution, given that the orbitals at the oxygen atom play a key role in bonding with methanol.
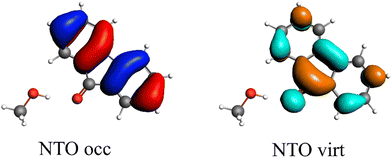 | ||
| Fig. 6 Calculated NTO of B3LYP/TZ2P/TDA-level for fluorenone–methanol, where the occupied (left) and virtual NTO (right) represent 98% of the density-change for the excitation. | ||
The results for the excitation contributions ωi and for the excited state contributions 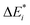 of exc-EDA are shown in Table 3.
of exc-EDA are shown in Table 3.
| Exc-u-EDA | Without TDA | TDA | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE | |
| a Energies in kJ mol−1 with TZ2P. | ||||||||||
| ωint | −12 | −12 | −12 | −13 | −13 | −12 | −12 | −13 | −13 | −13 |
| ωPauli | 12 | 13 | 13 | 13 | 13 | 13 | 13 | 13 | 12 | 12 |
| ωelstat | −15 | −15 | −15 | −14 | −14 | −16 | −16 | −16 | −15 | −15 |
| ωorb | −9 | −9 | −10 | −11 | −11 | −9 | −9 | −10 | −11 | −10 |
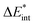 |
−41 | −38 | −44 | −51 | −46 | −41 | −38 | −44 | −51 | −46 |
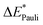 |
49 | 54 | 48 | 42 | 45 | 49 | 54 | 48 | 41 | 44 |
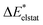 |
−59 | −60 | −61 | −62 | −60 | −60 | −61 | −61 | −62 | −60 |
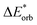 |
−30 | −31 | −31 | −31 | −31 | −30 | −31 | −31 | −30 | −30 |
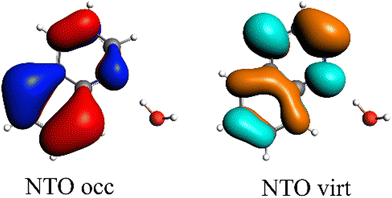
All results from Table 3 indicate a strengthening of the hydrogen bond, as reflected by the negative value of the interaction contribution ωint. This enhancement is primarily driven by an increase in both ωelstat and ωorb, with ωelstat showing a particularly pronounced effect. Although ωPauli also increases upon excitation, it remains smaller than the attractive contributions. The EDA contributions ωi due to the excitation (approximately 25–30%) to the excited state values 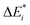 is lower than the contributions of the ground state ΔEGSi. The only exceptions are some results from range-separated functionals discussed next.
is lower than the contributions of the ground state ΔEGSi. The only exceptions are some results from range-separated functionals discussed next.
The results indicate only minor functional dependence, with variations smaller than 2 kJ mol−1 for all contributions, except for the exc-r-EDA with range-separated functionals. This suggests that the exc-r-EDA variant significantly overestimates ωelstat, which is counterbalanced by the large values for ωPauli. This discrepancy arises because the intermediate states involve different excited states, corresponding to excitations from lower occupied MOs (HOMO−10 and HOMO−9) to LUMO and LUMO+1. As a result, these findings can be considered outliers.
The outcomes of the fluorenone–methanol system demonstrate minimal difference (less than 1 kJ mol−1) between the calculations with and without TDA except for the discussed outliers. For the exc-r-EDA the change of using TDA is 7 kJ mol−1 (7%) for CAM-B3LYP and 9 kJ mol−1 (3%) for both others, while this does not change the character of the bond. Therefore, TDA provides a satisfactory approximation for the system as it was found for TDDFT in general.55
The results from exc-EDA can be rationalized by the increase in electron density at the oxygen atom of fluorenone upon excitation, as hypothesized in the beginning of the section. The strength of exc-EDA lies in its ability to quantitatively compare such effects across different systems.
4.2. Quinoline–water
As in the previous system, a hydrogen bond forms between the heteroatom in the aromatic ring of quinoline and water in the ground state. The ground state EDA results for this interaction are presented in Table 2 for B3LYP and in Table S2 (ESI†) for the other density functionals. The attractive interaction is again dominated by electrostatic interactions (63%) and also here, the Pauli repulsion has similar value than the electrostatic contribution.The NTOs for the first singlet state of the system (Fig. 7) show that the excitation occurs exclusively within the π-system of quinoline. Unlike the previous system, this excitation includes contributions from both the HOMO → LUMO and HOMO−1 → LUMO+1 transitions.23,35 Since all these orbitals are part of the π-system of quinoline, only quinoline needs to be considered as excited fragment A*. Additionally, Fig. 7 shows a slight increase in electron density at the nitrogen atom. Unlike the previous system, nitrogen orbitals are involved in both the occupied and virtual NTOs, with a slightly higher proportion for the virtual NTOs. Given the smaller increase in electron density on nitrogen compared to the previous system, we expect similar effects (stronger electrostatic interactions, Pauli repulsion, and orbital interactions) but to a lesser degree.
 | ||
| Fig. 7 Calculated NTO (B3LYP/TZ2P/TDA) for quinoline–water, where the occupied (left) and virtual NTO (right) represent 90% of the excitation. | ||
The results of the EDA analysis for the quinoline–water system are presented in Table 4.
| Without TDA | TDA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Exc-u-EDA | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE |
| a Energies in kJ mol−1 with TZ2P. | ||||||||||
| ωint | −9 | −9 | −8 | −5 | −5 | 27 | 26 | 19 | −1 | 8 |
| ωPauli | 12 | 11 | 12 | 13 | 13 | −17 | −17 | −21 | 6 | −23 |
| ωelstat | −5 | −5 | −5 | −5 | −5 | 82 | 81 | 88 | −2 | 92 |
| ωorb | −15 | −16 | −15 | −14 | −14 | −38 | −39 | −48 | −5 | −61 |
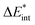 |
−41 | −37 | −41 | −45 | −42 | −4 | −2 | −14 | −41 | −29 |
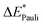 |
62 | 67 | 62 | 58 | 59 | 33 | 39 | 29 | 51 | 23 |
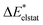 |
−60 | −61 | −62 | −64 | −62 | 27 | 25 | 31 | −61 | 35 |
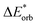 |
−42 | −44 | −42 | −39 | −39 | −65 | −66 | −74 | −31 | −86 |
For this system, the results differ significantly between calculations with and without TDA, except for LC-BLYP. As anticipated, the calculation without TDA shows a slight strengthening of ωint (less pronounced than in the fluorenone–methanol system). Conversely, when TDA is applied, the bond is weakened, except for LC-BLYP. This discrepancy can be attributed to the different excited states computed with and without TDA, as illustrated in Table 5.
| Without TDA | With TDA | |||
|---|---|---|---|---|
| Quinoline | Quinoline–H2O | Quinoline | Quinoline–H2O | |
| B3LYP | 93% HOMO → LUMO | 93% HOMO → LUMO | 98% HOMO1 → LUMO1 | 83% HOMO → LUMO |
| 5% HOMO1 → LUMO1 | ||||
| PBE0 | 93% HOMO → LUMO | 94% HOMO → LUMO | 98% HOMO2 → LUMO | 88% HOMO2 → LUMO |
| 7% HOMO3 → LUMO | ||||
| CAM-B3LYP | 93% HOMO → LUMO | 94% HOMO → LUMO | 95% HOMO2 → LUMO | 56% HOMO1 → LUMO |
| 5% HOMO1 → LUMO1 | 38% HOMO → LUMO1 | |||
| LC-BLYP | 87% HOMO → LUMO | 89% HOMO → LUMO | 58% HOMO1 → LUMO | 60% HOMO1 → LUMO |
| 11% HOMO1 → LUMO1 | 9% HOMO1 → LUMO1 | 37% HOMO → LUMO1 | 36% HOMO → LUMO1 | |
| LC-PBE | 87% HOMO → LUMO | 89% HOMO → LUMO | 87% HOMO2 → LUMO | 59% HOMO1 → LUMO |
| 10% HOMO1 → LUMO1 | 10% HOMO1 → LUMO1 | 7% HOMO2 → LUMO3 | 37% HOMO → LUMO1 | |
The data in Table 5 show that the excitation without TDA for the fragment and the full system are similar, with discrepancies of less than 2% in the orbital contributions, leading to comparable bond stabilization. For both the system and the fragment, the excitation is predominantly a HOMO → LUMO transition, accounting for approximately 90% of the total excitation. Additionally, HOMO−1 → LUMO+1 excitations contribute with values of 5% and 3% for the fragment and system, respectively, as calculated with CAM-B3LYP, and about 10% for the LC functionals. In calculations with TDA, except for LC-BLYP, there is a marked divergence between the excitation character of the fragment and the system, with contribution changes exceeding 10%. For LC-BLYP, the excitation is comprised of 60% HOMO−1 → LUMO and 35% HOMO → LUMO+1 transitions. This divergence highlights significant differences between functionals, and the lack of similar excitations across functionals complicates the reconciliation of exc-EDA results with TDA. Consequently, we focus on results obtained without TDA for this system. To avoid such issues, it is advisable to benchmark the appropriateness of TDA for the system and fragment under investigation.
In addition to strengthening the bond, all contributions increase upon excitation (without TDA). The results for different variants of exc-EDA show relatively large differences, reflecting their inherent properties. The exc-r-EDA results reveal that the values for ωelstat and ωPauli are overestimated. Specifically, these values exceed 130 kJ mol−1 for hybrid functionals and are over 220 kJ mol−1 and more than 330 kJ mol−1 for CAM-B3LYP and LC functionals, respectively. This is due to the different excited states involved in the intermediate steps, as indicated by the results with TDA, which show multiple close-lying excitations.
For exc-u-EDA, the deviations of all contributions between functionals are less than 4 kJ mol−1, with all contributions being approximately 10 kJ mol−1. The bond strengthening primarily arises from ωbond, which increases three times more than ωorb. The increase in ωPauli is 1 kJ mol−1 less for LC compared to ωorb and 3 kJ mol−1 less for the other functionals. The largest contribution to the bonding comes from the ground state interactions. Specifically, the excitation contribution to the electrostatic interaction is minimal, at approximately 8% of the total, whereas the excitation contributions are 35% for the orbital term and between 16% and 22% for Pauli repulsion.
In general, the outcomes of exc-u-EDA without TDA support the hypothesis that the bond is more readily strengthened compared to the fluorenone system, owing to a more pronounced increase in electron density at the heteroatom. However, the remaining results are complicated by the presence of multiple close-lying excited states.
4.3. Benzene–TCNE
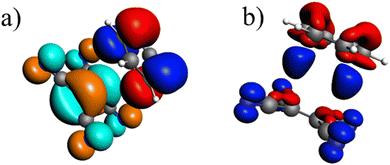
In the ground state the bond between benzene and TCNE is weaker as in the previous systems and the ground state EDA results are represented in Table 2 for B3LYP and the other functional in Table S3 (ESI†). It shows a similar relative contribution of electrostatic (68%) to orbital (32%) terms to the attractive interaction. Additionally, the Pauli repulsion is observed to be of slightly smaller value than the electrostatic contribution.To gain a deeper understanding of the orbital interactions and the processes occurring during excitation, NOCVs were also calculated. The inclusion of NOCVs was necessary because NTOs alone (Fig. 8a) are insufficient for estimating the EDA contributions in the excited state due to a significant charge transfer (CT) character of the excitation. The most significant NOCV-based deformation density is depicted in Fig. 8b (further NOCV data are found in the ESI,† Fig. S1) which shows the charge transfer from the π-system of benzene to the antibonding π-orbitals of TCNE. Fig. 8a displays the first singlet excitation for the system via NTO, which confirms it as a charge transfer excitation.35,72 As with the NOCVs, the electron density shifts from the π-system of benzene to the antibonding π-orbitals of TCNE. Unlike the previous system, both fragments are involved in the excitation. Since only electrons from benzene orbitals are excited, fragmentation of the excitation is possible and thus the exc-EDA can be used. Therefore, the bonding analysis can be conducted by focusing only on the excitation of benzene as the fragment. Thus, the excitation of this compound is considered in such a way that first the benzene moiety is excited and then in a second step interacts with TCNE leading to CT.
The Pauli repulsion is not expected to change significantly due to excitation, as the charge density in the bonding regions remains relatively constant. The excitation results in charge transfer, which leads to the formation of differently charged fragments within the system, likely increasing the electrostatic contribution. However, since this charge transfer is the primary contributor to the orbital interaction, it is anticipated that the orbital contribution will be reduced, as the charge transfer has already occurred. This picture is only expected for the exc-r-EDA variant since the exc-u-EDA variant considers all charge transfer in the orbital contribution. Thus, for this variant, the stabilization should be mainly due to an increase in the orbital contribution. The results of the bonding analysis are shown in Table 6.
| Without TDA | TDA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Exc-u-EDA | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE |
| a Energies in kJ mol−1 with TZ2P. | ||||||||||
| ωint | −329 | −339 | −281 | −223 | −226 | −331 | −341 | −284 | −173 | −175 |
| ωPauli | 182 | 179 | 199 | 213 | 204 | 174 | 173 | 184 | 206 | 198 |
| ωelstat | 2 | 2 | 2 | 0 | 0 | 1 | 2 | 1 | 0 | 0 |
| ωorb | −512 | −519 | −481 | −436 | −430 | −506 | −516 | −469 | −379 | −373 |
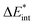 |
−345 | −348 | −297 | −247 | −247 | −347 | −350 | −300 | −197 | −196 |
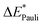 |
190 | 194 | 207 | 215 | 209 | 182 | 188 | 193 | 208 | 203 |
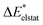 |
−15 | −15 | −16 | −19 | −18 | −15 | −15 | −16 | −19 | −18 |
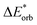 |
−520 | −527 | −488 | −443 | −438 | −514 | −523 | −476 | −386 | −380 |
Overall, the benzene–TCNE system exhibits the greatest strengthening of the bonding due to excitation, with values ranging from −180 to −340 kJ mol−1 for ωint. Hybrid functionals show the largest increase, around −330 kJ mol−1, followed by CAM-B3LYP at approximately −280 kJ mol−1. Long-range corrected functionals display the smallest values of about −220 kJ mol−1 and −180 kJ mol−1. This significant increase can primarily be attributed to charge transfer from benzene to TCNE.
As expected, the results of the two variants of exc-EDA differ substantially for this system. The results with and without TDA are relatively similar for both variants, with discrepancies of less than 8% for exc-u-EDA and less than 1% for exc-r-EDA. Importantly, these variations do not alter the character of the bond. However, there are two notable exceptions. First, for long-range corrected functionals, the difference is approximately 20% for ωint and 12% for ωorb with exc-u-EDA, and 20% for ωelstat with exc-r-EDA. This discrepancy in ωint is also observed with exc-r-EDA, as both variants yield comparable interaction energies. Overall, the differences fall within the expected range for using TDA. Second, ωelstat is near zero for exc-u-EDA while it is substantial for exc-r-EDA. This was anticipated since the exc-u-EDA variant encounters difficulties in describing this system because all effects of the charge transfer are encapsulated in ωorb. This also explains the relatively large value for ωorb, exceeding 400 kJ mol−1. Additionally, ωPauli increases by approximately 200 kJ mol−1. For hybrid functionals, the increase of ωPauli due to excitation is about 30 kJ mol−1 smaller than for long-range corrected functionals, while the gain in ωorb is 80 kJ mol−1 larger, leading to differences in ωint. The results for CAM-B3LYP fall between these two extremes. Conversely, the results from the exc-r-EDA variant indicate that the significant strengthening of the bond is primarily attributed to the enhancement of ωelstat, which is 2–3 times larger than the increase in ωorb, consistent with expectations. However, contrary to expectations, there is also a notable increase in ωPauli. This suggests that the electron density in the bonding plane is slightly augmented by the excitation. The strengthening of both ωPauli and ωorb is 40 kJ mol−1 greater for LC functionals compared to hybrid functionals. Conversely, the gain in electrostatic attraction is approximately 100 kJ mol−1 smaller for LC functionals. This discrepancy can be attributed to the superior description of the exchange contributions, which more comprehensively accounts for long-range interactions between orbitals. As a result, the proportion of the attractive interaction from the orbital contribution increases from 23% (in hybrids) to 35% (in LC functionals). As with the other variant, the results for CAM-B3LYP fall between these extremes.
Notably, both exc-EDA variants exhibit greater functional dependence here compared to previous test systems. This is not a result of the method itself but rather stems from the TDDFT calculation of the excited state. The behavior of the EDA contributions mirrors that of the interaction energy, which is calculated independently of the EDA method. Notably, all EDA contributions in the excited state are primarily influenced by the changes induced by the excitation (over 90%), given the relatively small values in the ground state.
Moreover, this system highlights the usefulness of the exc-r-EDA variant, as it is the only variant capable of producing results for CT excitations that align with bonding considerations. Therefore, a difference between the two variants is an indicator for a CT excitation.
4.4. Pyridine–water
The bond between the π-system of pyridine and water is analogous to the bond in the preceding system, though it exhibits a slightly weaker interaction, with a bonding energy of 5 kJ mol−1. This similarity is reflected in the EDA results, which are presented in Table 2 for B3LYP and in Table S4 (ESI†) for the other functionals.The attractive interaction is predominantly driven by electrostatic interactions, which accounts for approximately 63% of the total interaction energy. This stems from the electron density of the π-system in the aromatic ring interacting with the positively charged hydrogen atom of the water molecule, a contribution slightly smaller than that observed in the benzene–TCNE system. The Pauli repulsion (21 kJ mol−1) is the largest contribution, exceeding the electrostatic component by 6 kJ mol−1. This higher Pauli repulsion accounts for the relatively low overall interaction energy.
As with the previous system, NOCVs were calculated to gain deeper insights into the orbital interactions. The two most significant deformation densities for the ground state, along with the NTO, are shown in Fig. 9 (additional data in Fig. S4, ESI†). The most significant NOCVs primarily reveal a charge transfer from the π-system of pyridine to the bonding plane, specifically into the antibonding orbitals of water. Examination of the NTO reveals that the electron density originating from the π-system is transferred into an NTO that closely resembles NOCV 2. The virtual NTO also includes portions of the water orbitals. However, since the occupied NTO is localized on pyridine, the fragmentation can be effectively modeled by exciting only the pyridine in the fragment calculations.
The orbital contribution is significantly enhanced by the excitation, as the interaction described by NOCV 2 (Fig. 9b, right) is strengthened due to the increased electron density. This increased electron density in the bonding plane leads to an increase in Pauli repulsion. Additionally, the excitation slightly reduces the electron density in the π-system, weakening the interaction with the positively charged hydrogen atom. Simultaneously, the excitation enhances the electrostatic interaction through a minor charge transfer from pyridine to water. Overall, the electrostatic interaction is expected to be slightly increased by the excitation. The exc-EDA results of the final test system, pyridine–water, are presented in Table 7.
| Without TDA | TDA | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Unrelaxed | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE | PBE0 | B3LYP | CAMY-B3LYP | LC-BLYP | LC-PBE |
| a Energies in kJ mol−1 with TZ2P. | ||||||||||
| ωint | −5 | −5 | −5 | −5 | −5 | −5 | −5 | −5 | −5 | −5 |
| ωPauli | 145 | 148 | 162 | 205 | 172 | 162 | 164 | 181 | 228 | 192 |
| ωelstat | −9 | −9 | −11 | −14 | −13 | −10 | −10 | −12 | −16 | −14 |
| ωorb | −141 | −144 | −157 | −195 | −164 | −156 | −160 | −174 | −217 | −182 |
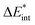 |
−14 | −9 | −14 | −20 | −18 | −14 | −9 | −14 | −20 | −17 |
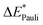 |
161 | 168 | 177 | 214 | 183 | 177 | 185 | 196 | 238 | 203 |
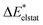 |
−24 | −24 | −26 | −31 | −29 | −25 | −25 | −28 | −32 | −30 |
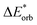 |
−150 | −153 | −165 | −203 | −172 | −165 | −169 | −183 | −225 | −191 |
The results presented in Table 7 show an increase in all EDA contributions. Notably, the enhancement of ωorb exceeds that of ωelstat, except in the case of exc-r-EDA with range-separated functionals. However, the more substantial increase in the attractive contributions is offset by an even greater increase in ωPauli, leading to a modest overall bond enhancement of 5 kJ mol−1 across all calculations.
When applying the TDA, the exc-u-EDA contributions become 10% more negative. Except for ωelstat and ωPauli with LC-functionals, the deviation due to TDA remains under 5%. However, the difference between these contributions and others is significantly larger (exceeding 30%) suggesting an artificial alteration in the excitation for the intermediate states. Despite these deviations, the overall character of the bond remains unchanged. The two exc-EDA variants lead to different results due to the partial CT nature of the excitation. Particularly noticeable are deviations in the ωPauli and the ωelstat contributions, with differences of over 100 kJ mol−1. The ωelstat term of exc-u-EDA is about 10 kJ mol−1, which is significantly higher than in previous systems. ωPauli and ωorb contributions are similar, but significantly larger than ωelstat, with ωPauli increasing by 5–10 kJ mol−1 more than ωorb. For the hybrid functionals, ωPauli and ωorb are smaller about 15–20 kJ mol−1 compared to CAMY-B3LYP and LC-PBE0, while LC-BLYP shows an increase of about 30 kJ mol−1. Nevertheless, the character of the bond remains unchanged.
For exc-r-EDA, the increase in the electrostatic contribution is larger than 100 kJ mol−1. For the hybrid functionals, ωelstat accounts for about 55% of the attractive interactions. For CAMY-B3LYP the electrostatic contribution is 57%, for the long-range corrected functionals even 65–85%. ωorb is similar for exc-r-EDA as for exc-u-EDA, but the ωPauli are significantly larger for exc-r-EDA to compensate for the larger increase in attractive interactions. For hybrid functionals, ωPauli is about 120 kJ mol−1 lower for exc-r-EDA than for CAMY-B3LYP and over 270 kJ mol−1 lower for long-range corrected functionals. All EDA contributions increase by a total of 88%, while the excitation contribution accounts for less than half of the total interaction energy for the excited state.
The findings indicate that the formation of charged fragments due to CT also enhances the electrostatic contribution. This partial CT character is evident when comparing the two variants. Unlike the benzene–TCNE bond, the stabilization of the bond here is more significantly influenced by the strengthening of orbital interactions. However, the substantial increase in attractive interactions is almost completely offset by a concurrent rise in Pauli repulsion due to the increased electron density in the bonding plane.
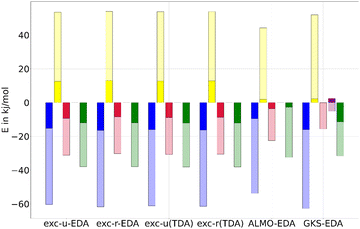
4.5. Comparison with ALMO-EDA and GKS-EDA
For comparison with ALMO-EDA and GKS-EDA, we focus on the B3LYP results, which offer reasonable outcomes both with and without TDA, as discussed in previous sections. Thereby the GKS-EDA were taken from ref. 35. In ALMO-EDA, the charge transfer ΔECT and polarization contributions ΔEPOL are combined into an orbital contribution ΔEorb, facilitating a more meaningful comparison with exc-EDA. In this context, the electrostatic term ΔECLSELEC in ALMO-EDA corresponds to the quasi-electrostatic contribution ΔEelstat, while the Pauli term ΔEPauli aligns with Pauli repulsion ΔEPauli. In GKS-EDA, the electrostatic term ΔEele is analogous to the quasi-electrostatic contribution ΔEelstat, the exchange-repulsion term ΔEexrep corresponds to Pauli repulsion ΔEPauli, and the polarization term ΔEpol relates to the orbital contribution ΔEorb for this comparison. The correlation contribution ΔEcor in GKS-EDA cannot be directly attributed to any component of exc-EDA, as it reflects the difference in XC energy and exact exchange between the system and the fragment.ALMO-EDA is applicable only within the framework of TDDFT with TDA, whereas the GKS-EDA results were computed without TDA are taken from ref. 35. The comparison of results is illustrated in Fig. 10 for the fluorenone–methanol system and detailed in Table S5 (ESI†). The excited state EDA values are dominated by the ground state contributions, which are then modestly enhanced by the excitation. An exception to this trend is observed in the GKS-EDA results, where the polarization contribution shows negligible change (less than 1 kJ mol−1), and a weakening of the ground state effect is noted for the correlation contribution. For the hydrogen bond between fluorenone and methanol, the bond strengthening due to excitation is predominantly attributed to the enhancement of the electrostatic interaction across all methods. Additionally, both ALMO-EDA and exc-EDA methods show a significant increase in orbital contribution. Despite this similarity, ALMO-EDA reports generally smaller contributions compared to exc-EDA, with a notable difference in the excitation effects and especially in the Pauli repulsion. Specifically, exc-EDA shows an increase in Pauli repulsion due to excitation that is approximately ten times greater than that observed with ALMO-EDA.
It is important to emphasize that while the absolute values of these contributions are informative, the relative magnitudes are more critical, as all EDA methods rely on comparison of trends between systems. The comparison for the fluorenone–methanol bond indicates that exc-EDA provides similar conclusions than previously published analysis methods.
4.6. Pentacene clusters
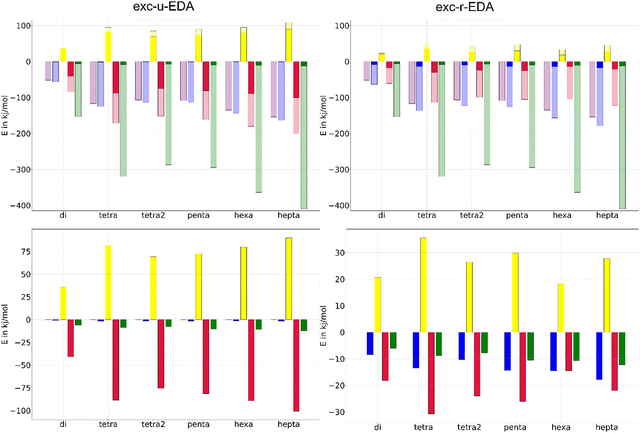
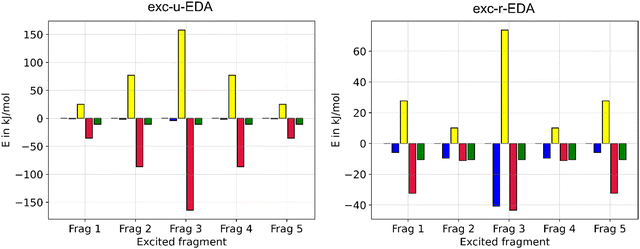
Finally, exc-EDA was applied to analyze pentacene molecular crystals in a cluster approximation. Singlet fission processes could be demonstrated for pentacene crystals,66,67 indicating it to be an interesting system for organic semiconductors and solar cells. The advantage of singlet fission lies in the spin-allowed generation of two triplet states, which facilitates charge separation while significantly hindering charge recombination due to this being a spin-forbidden process. Additionally, the Engels group demonstrated that the high-resolution experimental absorption spectra of thin films of pentacene can be reproduced with TDDFT calculations using a cluster approach.68 Consequently, exc-EDA will be employed to examine pentacene clusters. The objective of the investigation is to ascertain how the bonding between an excited pentacene and the surrounding pentacene molecules in the ground state varies with an increasing number of monomers in the cluster model. This state represents the first step of singlet fission. Consequently, the potential driving forces for this process can be identified. Additionally, the number of monomers involved in or influencing the excitation through CT effects can be examined, as shown above for the benzene–TCNE system. In this process, one monomer is initially excited, and the subsequent interaction with other monomers occurs via CT.The results of the exc-EDA calculations are shown in Fig. 11. For each cluster, sequential exc-EDA calculations were carried out, exciting one pentacene monomer at a time. Afterwards, these results were averaged.
Fig. 11 illustrates that bonding interactions in all clusters are predominantly governed by ground state contributions, with only modest changes due to excitation. The primary exception is Pauli repulsion, which shows minimal ground state contributions and a relatively pronounced change due to excitation. For exc-u-EDA, the orbital contribution in the excited state is evenly split between ground and excitation contributions. In the ground state, the electrostatic interaction exceeds the orbital interaction by approximately 30%, with this difference increasing as the cluster size grows. This trend is consistent with the long-range nature of the electrostatic interaction. The dispersion interactions determined only in the ground state are of comparable magnitude to the electrostatic contribution for all clusters. Additionally, Pauli repulsion remains very small, less than 20 kJ mol−1, or about 10% of the electrostatic interaction.
As the size of the cluster model increases, the strength of the interactions also increases. However, the results for the pentamer are anomalous, showing interaction strengths similar to those of tetramer 2 and smaller than those of tetramer 1. Despite this anomaly, the effect on the overall bonding character remains consistent across different clusters. Furthermore, there is no noticeable convergence in interaction energies up to the heptamer, with a difference of 40 kJ mol−1 observed between the hexamer and heptamer. This suggests the presence of long-range effects, indicating that additional molecules may be necessary to accurately simulate the bonding.
Fig. 11 also shows the changes in EDA contributions due to the initial excitation, highlighting the occurrence of CT. The negligible values of the electrostatic component observed in the exc-u-EDA results are indicative of this CT. In contrast, the exc-u-EDA results demonstrate a significant amplification of the orbital term compared to the exc-r-EDA results. This observation aligns with findings by Guldi et al.73,74 who reported that in pentacene dimers with weak coupling through a molecular linker, the excitation of one monomer leads to charge transfer to the other monomers. The exc-u-EDA analysis results show that the relative change in EDA contributions is consistent across all cluster structures due to excitation. The primary factor in this consistency is the substantial enhancement of orbital interactions, which contributes over 98% to the overall increase in attractive interactions. In contrast, the electrostatic contribution shows only a minor increase of 2 kJ mol−1. The larger enhancement in orbital interactions is balanced by a corresponding increase in Pauli repulsion, whereby this increase is approximately 10 kJ mol−1 smaller than by orbital interaction. As a result, the net strengthening of interactions amounts to about 10 kJ mol−1. For dimers, the enhancements are notably smaller compared to other clusters, with a 40 kJ mol−1 difference in Pauli repulsion and orbital contributions, while the interaction energy difference is only 2 kJ mol−1. The results for larger clusters are similar, differing by less than 15 kJ mol−1, except for the pentacene heptamer, which shows a 10 kJ mol−1 larger gain.
In comparison to the exc-u-EDA, the alteration in ωPauli and ωorb is smaller by 50% for exc-r-EDA. This is because CT excitation is decomposed by the exc-r-EDA. Exc-r-EDA amplifies all EDA contributions due to excitation, with the most significant increase observed in ωPauli across all clusters. ωorb is around 20 kJ mol−1, with a range from 15 kJ mol−1 for the hexamer to 31 kJ mol−1 for the tetramer. In contrast to exc-u-EDA, additional increase of the electrostatic term is found due to the generation of charged fragments by CT, with this effect increasing with cluster size. For smaller clusters, the increase in the orbital term is about 70% due to excitation. ωelstat and ωorb are approximately similar for hexamers and heptamers. Therefore, for exc-r-EDA to yield results comparable to the largest cluster, a hexamer is necessary. Only from the tetramers onwards the difference is already significantly smaller. This aligns with Engels’ findings, which suggest that a tetramer suffices for accurate absorption spectra predictions with exc-u-EDA.
Finally, we investigated the influence of different monomers on the exc-EDA contributions. Results for the pentamer are shown in Fig. 12.
Fig. 12 illustrates that the change in interaction energy due to excitation is qualitatively independent of which monomer is excited. This is because the energy difference between the pentamer and a monomer's excitation is relatively constant, regardless of fragmentation. Further, symmetry equivalent monomers yield similar results. The largest contributions are observed for the middle monomer (monomer 3) for both variants. For exc-u-EDA, the interactions are next largest for monomers 2 and 4, and smallest for monomers 1 and 5. This consistent pattern is observed across all instances. In exc-r-EDA, monomers 1 and 5 show a notably larger increase in the orbital term compared to the electrostatic contribution, whereas for the other monomers, both contributions are similarly affected. This suggests minimal CT for monomers 1 and 5, with excitation effects more pronounced compared to monomers 2 and 4. Overall, the results confirm that the exc-EDA method exhibits the expected structural characteristics since it reflects the symmetry of the clusters. In conclusion, the EDA results suggest that the initial singlet fission event in pentacene clusters involves not only two molecules but at least four. Additionally, a CT excitation is observed at this stage, indicating that the singlet fission process in pentacene occurs via a CT intermediate as proposed before.73,74
5. Conclusion
We present a novel energy decomposition analysis method for excited states, combining the Morokuma and Ziegler-Rauk EDA approach with TDDFT. The method calculates excitation energies for intermediate EDA steps and includes two variants: exc-u-EDA, which uses fixed excitation coefficients for fragments, and exc-r-EDA, which optimizes these coefficients with TDDFT. Tests showed that both variants provide reliable results, with exc-u-EDA being more robust but exc-r-EDA better suited for systems involving charge transfer. Hybrid functionals showed smaller values than range-separated GGA functionals and were less prone to artificial changes in excited states due to closely spaced excited states or numerous virtual orbitals. Smaller basis sets mitigate these issues by resulting in more distinct virtual orbitals. Comparing Pauli repulsion between the two variants can guide the choice of method, with lower Pauli repulsion indicating a better description of the system.For a test set of four exciplex complexes, exc-EDA delivered quantitative bonding insights and chemically intuitive pictures. The comparison to established methods for excited state EDA shows similar trends. We further applied exc-EDA to study singlet fission in pentacene clusters, revealing charge transfer from excited to non-excited monomers, known as CT-mediated singlet fission. The interaction between fragments was slightly enhanced by excitation, driven equally by electrostatic and orbital interactions. Accurate description of excitation effects required at least a tetramer cluster model, and the method reproduced expected structural differences within excited monomers.
The exc-EDA offers a novel perspective on bonding in the excited state. This method can provide additional insights compared to more established approaches, particularly in terms of bonding analysis. As a result, it enables a more accurate and detailed understanding of the respective excited states.
The exc-EDA method is applicable to systems where the excitation is localized on one fragment and can help analyze the effect of excitation on bonding. It works across most functional classes, though care is needed to ensure the selected functional accurately describes the excitation. Double-hybrid functionals are an exception, as they are not compatible with this method.
In the future, we will use exc-EDA to analyze chemistry in the excited state.
Data availability
The data for this article and the ESI,† including all computational data as well as the scripts to create the diagrams and the diagrams, are available at Zenodo (https://doi.org/10.5281/zenodo.14024534). The method has been implemented in the AMS program package and should be available with the 2025 version.Conflicts of interest
There are no conflicts to declare.Acknowledgements
We thank SCM/Amsterdam and specifically Dr Stan Gisbergen for providing a developer's version of the AMS code. We thank Dr Eric van Lenthe for discussions. We thank the German Science Foundation (DFG) for funding via RTG 123H (443871192).References
- (a) V. Balzani, Photochemistry and Photophysics, Wiley, 2014 Search PubMed; (b) V. Balzani, G. Bergamini and P. Ceroni, Angew. Chem., Int. Ed., 2015, 54, 11320 CrossRef CAS PubMed; (c) R. C. Evans, P. Douglas and H. D. Burrow, Applied Photochemistry, Springer, Netherlands, Dordrecht, 2013 CrossRef; (d) B. König, Eur. J. Org. Chem., 2017, 1979 CrossRef; (e) S. Reischauer and B. Pieber, iScience, 2021, 24, 102209 CrossRef CAS PubMed.
- A. Dreuw and M. Head-Gordon, Chem. Rev., 2005, 105, 4009 CrossRef CAS PubMed.
- (a) J. V. Burykina, A. D. Kobelev, N. S. Shlapakov, A. Y. Kostyukovich, A. N. Fakhrutdinov, B. König and V. P. Ananikov, Angew. Chem., Int. Ed., 2022, 61, e202116888 CrossRef CAS PubMed; (b) A. Hölzl-Hobmeier, A. Bauer, A. V. Silva, S. M. Huber, C. Bannwarth and T. Bach, Nature, 2018, 564, 240 CrossRef PubMed; (c) R. Lahmy, H. Hübner, P. Gmeiner and B. König, ChemPhotoChem, 2024, 8, e202400022 CrossRef CAS; (d) M. Leverenz, C. Merten, A. Dreuw and T. Bach, J. Am. Chem. Soc., 2019, 141, 20053 CrossRef CAS PubMed; (e) T. E. Schirmer and B. König, J. Am. Chem. Soc., 2022, 144, 19207 CrossRef CAS PubMed; (f) N. S. Shlapakov, A. D. Kobelev, J. V. Burykina, A. Y. Kostyukovich, B. König and V. P. Ananikov, Angew. Chem., Int. Ed., 2024, 63, e202314208 CrossRef CAS PubMed; (g) C. Taube, J. Fidelius, K. Schwedtmann, C. Ziegler, F. Kreuter, L. Loots, L. J. Barbour, R. Tonner-Zech, R. Wolf and J. J. Weigand, Angew. Chem., Int. Ed., 2023, 62, e202306706 CrossRef CAS PubMed; (h) A. Zech, C. Jandl and T. Bach, Angew. Chem., Int. Ed., 2019, 58, 14629 CrossRef CAS PubMed.
- S. Mai and L. González, Angew. Chem., Int. Ed., 2020, 59, 16832 CrossRef CAS PubMed.
- H. Lischka, D. Nachtigallová, A. J. A. Aquino, P. G. Szalay, F. Plasser, F. B. C. Machado and M. Barbatti, Chem. Rev., 2018, 118, 7293 CrossRef CAS PubMed.
- B. O. Roos, Advances in Chemical Physics, John Wiley & Sons, Ltd, 1987, pp. 399–445 Search PubMed.
- K. Andersson and B. O. Roos, Multiconfiguratoinal second-order perturbation theory, in Modern Electronic Structure Theory, 1995, pp. 55–109 Search PubMed.
- C. Angeli, R. Cimiraglia and J.-P. Malrieu, J. Chem. Phys., 2002, 117, 9138 CrossRef CAS.
- R. J. Buenker, S. D. Peyerimhoff and W. Butscher, Mol. Phys., 1978, 35, 771 CrossRef CAS.
- P. A. Malmqvist, A. Rendell and B. O. Roos, J. Chem. Phys., 1990, 94, 5477 CrossRef CAS.
- R. Izsák, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2020, 10, e1445 Search PubMed.
- J. Geertsen, M. Rittby and R. J. Bartlett, Chem. Phys. Lett., 1989, 164, 57 CrossRef CAS.
- C. Hättig and F. Weigend, J. Chem. Phys., 2000, 113, 5154 CrossRef.
- A. Dreuw and M. Wormit, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2015, 5, 82 CAS.
- M. E. Casida and M. Huix-Rotllant, Annu. Rev. Phys. Chem., 2012, 63, 287 CrossRef CAS PubMed.
- N. T. Maitra, J. Chem. Phys., 2016, 144, 220901 CrossRef PubMed.
- E. Pastorczak and C. Corminboeuf, J. Chem. Phys., 2017, 146, 120901 CrossRef PubMed.
- F. M. Bickelhaupt and E. J. Baerends, in Reviews in Computational Chemistry, ed. K. B. Lipkowitz and D. B. Boyd, Wiley-VCH, Inc., New York, 2000, vol. 15, pp. 1–86 Search PubMed.
- K. Kitaura and K. Morokuma, Int. J. Quantum Chem., 1976, 10, 325 CrossRef CAS.
- L. Zhao, M. von Hopffgarten, D. M. Andrada and G. Frenking, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2018, 8, e1345 Search PubMed.
- T. Ziegler and A. Rauk, Theor. Chim. Acta, 1977, 46, 1 CrossRef CAS.
- M. Raupach and R. Tonner, J. Chem. Phys., 2015, 142, 194105 CrossRef PubMed.
- A. Seidl, A. Görling, P. Vogl, J. A. Majewski and M. Levy, Phys. Rev. B:Condens. Matter Mater. Phys., 1996, 53, 3764 CrossRef CAS PubMed.
- (a) P. Maxwell, Á. M. Pendás and P. L. A. Popelier, Phys. Chem. Chem. Phys., 2016, 18, 20986 RSC; (b) M. A. Blanco, A. Martín Pendás and E. Francisco, J. Chem. Theory Comput., 2005, 1, 1096 CrossRef CAS PubMed.
- (a) Y. Mo, L. Song and Y. Lin, J. Phys. Chem. A, 2007, 111, 8291 CrossRef CAS PubMed; (b) Y. Mo, J. Gao and S. D. Peyerimhoff, J. Chem. Phys., 2000, 112, 5530 CrossRef CAS; (c) Y. Mo, P. Bao and J. Gao, Phys. Chem. Chem. Phys., 2011, 13, 6760 RSC.
- (a) P. R. Horn, E. J. Sundstrom, T. A. Baker and M. Head-Gordon, J. Chem. Phys., 2013, 138, 134119 CrossRef PubMed; (b) R. Z. Khaliullin, E. A. Cobar, R. C. Lochan, A. T. Bell and M. Head-Gordon, J. Phys. Chem. A, 2007, 111, 8753 CrossRef CAS PubMed.
- T. M. Cardozo and M. A. C. Nascimento, J. Chem. Phys., 2009, 130, 104102 CrossRef PubMed.
- (a) E. D. Glendening, J. Am. Chem. Soc., 1996, 118, 2473 CrossRef CAS; (b) E. D. Glendening and A. Streitwieser, J. Chem. Phys., 1994, 100, 2900 CrossRef CAS.
- P. Su and H. Li, J. Chem. Phys., 2009, 131, 14102 CrossRef PubMed.
- K. Szalewicz, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2012, 2, 254 CAS.
- L. Pecher and R. Tonner, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1401 Search PubMed.
- F. M. Bickelhaupt and K. N. Houk, Angew. Chem., Int. Ed., 2017, 56, 10070 CrossRef CAS PubMed.
- P. Vermeeren, T. A. Hamlin, I. Fernández and F. M. Bickelhaupt, Chem. Sci., 2020, 11, 8105 RSC.
- (a) Q. Ge, Y. Mao and M. Head-Gordon, J. Chem. Phys., 2018, 148, 64105 CrossRef PubMed; (b) Q. Ge and M. Head-Gordon, J. Chem. Theory Comput., 2018, 14, 5156 CrossRef CAS PubMed.
- Z. Tang, B. Shao, W. Wu and P. Su, Phys. Chem. Chem. Phys., 2023, 25, 18139 RSC.
- Y. Xu, R. Friedman, W. Wu and P. Su, J. Chem. Phys., 2021, 154, 194106 CrossRef CAS PubMed.
- C. P. Hettich, X. Zhang, D. Kemper, R. Zhao, S. Zhou, Y. Lu, J. Gao, J. Zhang and M. Liu, JACS Au, 2023, 3, 1800 CrossRef CAS PubMed.
- Y. X. Zhang, B. L. Mali and C. D. Geddes, Spectrochim. Acta, Part A, 2012, 85, 134 CrossRef CAS PubMed.
- P. Kimber and F. Plasser, J. Chem. Theory Comput., 2023, 19, 2340 CrossRef CAS PubMed.
- R. L. Martin, J. Chem. Phys., 2003, 118, 4775 CrossRef CAS.
- F. Weinhold and C. R. Landis, Chem. Educ. Res. Pract., 2001, 2, 91 RSC.
- N. V. Tkachenko and A. I. Boldyrev, Phys. Chem. Chem. Phys., 2019, 21, 9590 RSC.
- (a) S. A. Bäppler, F. Plasser, M. Wormit and A. Dreuw, Phys. Rev. A:At., Mol., Opt. Phys., 2014, 90, 52521 CrossRef; (b) C. Adamo, T. Le Bahers, M. Savarese, L. Wilbraham, G. García, R. Fukuda, M. Ehara, N. Rega and I. Ciofini, Coord. Chem. Rev., 2015, 304–305, 166 CrossRef CAS.
- (a) M. T. do Casal, J. M. Toldo, M. Barbatti and F. Plasser, Chem. Sci., 2023, 14, 4012 RSC; (b) F. Plasser, M. Wormit and A. Dreuw, J. Chem. Phys., 2014, 141, 24106 CrossRef PubMed.
- G. Frenking, K. Wichmann, N. Fröhlich, C. Loschen, M. Lein, J. Frunzke and V. M. Rayón, Coord. Chem. Rev., 2003, 238–239, 55 CrossRef CAS.
- (a) A. Diefenbach, F. M. Bickelhaupt and G. Frenking, J. Am. Chem. Soc., 2000, 122, 6449 CrossRef CAS; (b) M. S. Nechaev, V. M. Rayón and G. Frenking, J. Phys. Chem. A, 2004, 108, 3134 CrossRef CAS; (c) R. Tonner, G. Heydenrych and G. Frenking, Chem. – Asian J., 2007, 2, 1555 CrossRef CAS PubMed.
- (a) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, Chem. – Eur. J., 2007, 13, 6321 CrossRef CAS PubMed; (b) S. C. A. H. Pierrefixe and F. M. Bickelhaupt, J. Phys. Chem. A, 2008, 112, 12816 CrossRef CAS PubMed.
- L. de Azevedo Santos, T. C. Ramalho, T. A. Hamlin and F. M. Bickelhaupt, Chem. – Eur. J., 2023, 29, e202203791 CrossRef CAS PubMed.
- L. P. Wolters and F. M. Bickelhaupt, ChemistryOpen, 2012, 1, 96 CrossRef CAS PubMed.
- (a) M. Bortoli, S. M. Ahmad, T. A. Hamlin, F. M. Bickelhaupt and L. Orian, Phys. Chem. Chem. Phys., 2018, 20, 27592 RSC; (b) L. de Azevedo Santos, S. C. C. van der Lubbe, T. A. Hamlin, T. C. Ramalho and F. Matthias Bickelhaupt, ChemistryOpen, 2021, 10, 391 CrossRef CAS PubMed.
- L. de Azevedo Santos, T. A. Hamlin, T. C. Ramalho and F. M. Bickelhaupt, Phys. Chem. Chem. Phys., 2021, 23, 13842 RSC.
- (a) Z. Boughlala, C. Fonseca Guerra and F. M. Bickelhaupt, J. Phys. Chem. A, 2019, 123, 9137 CrossRef CAS PubMed; (b) Z. Boughlala, C. Fonseca Guerra and F. M. Bickelhaupt, Chem. – Asian J., 2017, 12, 2604 CrossRef CAS PubMed.
- (a) A. O. Ortolan, G. F. Caramori, F. Matthias Bickelhaupt, R. L. T. Parreira, A. Muñoz-Castro and T. Kar, Phys. Chem. Chem. Phys., 2017, 19, 24696 RSC; (b) A. O. Ortolan, I. Østrøm, G. F. Caramori, R. L. T. Parreira, E. H. Da Silva and F. M. Bickelhaupt, J. Phys. Chem. A, 2018, 122, 3328 CrossRef CAS PubMed.
- S. Grimme, S. Ehrlich and L. Goerigk, J. Comput. Chem., 2011, 32, 1456 CrossRef CAS PubMed.
- S. Hirata and M. Head-Gordon, Chem. Phys. Lett., 1999, 314, 291 CrossRef CAS.
- R. B. Morgan, J. Comput. Phys., 1990, 89, 241 CrossRef.
- G. te Velde, F. M. Bickelhaupt, E. J. Baerends, C. Fonseca Guerra, S. J. A. van Gisbergen, J. G. Snijders and T. Ziegler, J. Comput. Chem., 2001, 22, 931 CrossRef CAS.
- E. van Lenthe and E. J. Baerends, J. Comput. Chem., 2003, 24, 1142 CrossRef CAS PubMed.
- (a) A. D. Becke, J. Chem. Phys., 1988, 88, 2547 CrossRef CAS; (b) M. Franchini, P. H. T. Philipsen and L. Visscher, J. Comput. Chem., 2013, 34, 1819 CrossRef CAS PubMed.
- (a) J. P. Perdew, Phys. Rev. B:Condens. Matter Mater. Phys., 1986, 33, 8822 CrossRef PubMed; (b) A. D. Becke, Phys. Rev. A:At., Mol., Opt. Phys., 1988, 38, 3098 CrossRef CAS PubMed.
- J. P. Perdew, K. Burke and M. Ernzerhof, Phys. Rev. Lett., 1996, 77, 3865 CrossRef CAS PubMed.
- T. Yanai, D. P. Tew and N. C. Handy, Chem. Phys. Lett., 2004, 393, 51 CrossRef CAS.
- Y. Tawada, T. Tsuneda, S. Yanagisawa, T. Yanai and K. Hirao, J. Chem. Phys., 2004, 120, 8425 CrossRef CAS PubMed.
- E. Epifanovsky, A. T. B. Gilbert, X. Feng, J. Lee, Y. Mao, N. Mardirossian, P. Pokhilko, A. F. White, M. P. Coons and A. L. Dempwolff, et al., J. Chem. Phys., 2021, 155, 84801 CrossRef CAS PubMed.
- F. Weigend and R. Ahlrichs, Phys. Chem. Chem. Phys., 2005, 7, 3297 RSC.
- P. M. Zimmerman, Z. Zhang and C. B. Musgrave, Nat. Chem., 2010, 2, 648 CrossRef CAS PubMed.
- A. Neef, S. Beaulieu, S. Hammer, S. Dong, J. Maklar, T. Pincelli, R. P. Xian, M. Wolf, L. Rettig and J. Pflaum, et al., Nature, 2023, 616, 275 CrossRef CAS PubMed.
- L. Craciunescu, S. Wirsing, S. Hammer, K. Broch, A. Dreuw, F. Fantuzzi, V. Sivanesan, P. Tegeder and B. Engels, J. Phys. Chem. Lett., 2022, 13, 3726 CrossRef CAS PubMed.
- Y.-S. Lin, G.-D. Li, S.-P. Mao and J.-D. Chai, J. Chem. Theory Comput., 2013, 9, 263 CrossRef CAS PubMed.
- T. Oestereich, R. Tonner-Zech and J. Westermayr, J. Comput. Chem., 2024, 45, 368 CrossRef CAS PubMed.
- G.-J. Zhao and K.-L. Han, J. Phys. Chem. A, 2007, 111, 9218 CrossRef CAS PubMed.
- (a) Y. Mei and W. Yang, J. Chem. Phys., 2019, 150, 144109 CrossRef PubMed; (b) J. M. Masnovi, E. A. Seddon and J. K. Kochi, Can. J. Chem., 1984, 62, 2552 CrossRef CAS.
- B. S. Basel, J. Zirzlmeier, C. Hetzer, S. R. Reddy, B. T. Phelan, M. D. Krzyaniak, M. K. Volland, P. B. Coto, R. M. Young and T. Clark, et al., Chem, 2018, 4, 1092 CAS.
- R. Casillas, I. Papadopoulos, T. Ullrich, D. Thiel, A. Kunzmann and D. M. Guldi, Energy Environ. Sci., 2020, 13, 2741 RSC.
Footnote |
| † Electronic supplementary information (ESI) available. See DOI: https://doi.org/10.1039/d4cp04207g |
| This journal is © the Owner Societies 2025 |