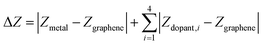Graphene-based single-atom catalysts for electrochemical CO₂ reduction: unraveling the roles of metals and dopants in tuning activity

Abstract

Discovering electrocatalysts that can efficiently convert carbon dioxide (CO₂) to valuable fuels and feedstocks using excess renewable electricity is an emergent carbon-neutral technology. A single metal atom embedded in doped graphene, i.e., single-atom catalyst (SAC), possesses high activity and selectivity for electrochemical CO₂ reduction (CO₂R) to CO, yet further reduction to hydrocarbons is challenging. Here, using density functional theory calculations, we investigate stability and reactivity of a broad SAC chemical space with various metal centers (3d transition metals) and dopants (2p dopants of B, N, O; 3p dopants of P, S) as electrocatalysts for CO₂R to methane and methanol. We observe that the rigidities of these SACs depend on the type of dopants, with 3p-coordinating SACs exhibiting more severe out-of-plane distortion than 2p-coordinating SACs. Using CO adsorption energy as a descriptor for CO₂R reactivity, we narrow down the candidates and identify seven SACs with near-optimal CO binding strength. We then elucidate full reaction mechanisms towards methane and methanol generation on these identified candidates and observe highly dopant-dependent activity and rate-limiting steps, divergent from conventional mechanistic understanding on metallic surfaces, calling into question whether previous design principles established on metals are directly transferrable to SACs. Consequently, we find that zinc embedded in boron-doped graphene (Zn–B–C) is a highly active catalyst for electrochemical CO₂R to C₁ hydrocarbons. Our work reveals the opportunities of tuning SAC reactivity via engineering dopants and metals and highlights the importance of re-elucidating CO₂R reaction mechanisms on SACs towards unearthing new design principles for SAC chemistry.

---

I. Introduction

Consumption of fossil fuels and other CO₂-emitting energy resources contributes significantly to global warming.^1,2 As energy demands are projected to increase substantially,^3,4 mitigation of CO₂ concentrations in the air will be crucial to avoiding climate-related ecological and humanitarian problems.⁵ One of the most promising solutions is the conversion of atmospheric CO₂ to valuable chemical feedstocks via electrochemical CO₂ reduction (CO₂R) using excess renewable electricity, such as solar and wind.^6–8 Various materials, including metals, metal alloys, and metal oxides, have been used to catalyze CO₂R.^9–13 Currently, copper (Cu)-based materials remain the best metal electrocatalysts for CO₂R towards generating hydrocarbon products.^14–20 However, these catalysts require high overpotentials to achieve reasonable reaction rates and exhibit poor selectivity towards valuable products, which is impractical for commercializing this technology,^9,21 motivating rational design of more efficient CO₂R catalysts with improved activity and selectivity.

Beyond conventional metal surfaces, single-atom catalysts (SACs) consisting of an isolated metal site in doped graphene (typically with nitrogen or N dopants) have become emergent catalysts for CO₂R in the past decade.^22,23 Dispersing isolated metal atoms on graphene maximizes atom utilization and suppresses competitive hydrogen evolution reaction (HER).^24–27 In addition, dopants, such as N, can stabilize active metal centers embedded on graphene, enabling proton-coupled electron transfer (PCET) to enhance CO₂R activity.^28–30 Carbon monoxide (CO) has been experimentally identified as the major product of electrochemical CO₂R for SACs on N-doped graphene. Zheng et al. synthesized nickel (Ni) SAC on N-doped graphene (Ni–N–C) and reported a nearly 100% faradaic efficiency for electrochemical CO₂ to CO conversion at an applied potential of −0.68 V vs. the reversible hydrogen electrode (RHE).³¹ Zheng et al. confirmed the superior catalytic performance of Ni–N–C in reducing CO₂ to CO with a faradaic efficiency of 98.5% and observed that Ni–N–C outperforms other SACs, including Fe–N–C, Cu–N–C, and Co–N–C, in generating CO.³² Wang et al. noted that the poor selectivity of Co–N–C for CO production comes from the undercoordinated N species in the synthesized materials and removing those undercoordinated N atoms results in a highly improved CO faradaic efficiency of 99.4% at an applied potential of −0.60 V vs. the RHE.³³ In addition to CO, hydrocarbons have also been identified as major products of CO₂R for SACs on N-doped graphene. Yang et al. reported a faradaic efficiency of 44% for methanol generation using Cu–N–C at −0.9 V vs. the RHE,³⁴ while Han et al. observed a high faradaic efficiency of 85% for methane production using Zn–N–C at −1.8 V vs. the saturated calomel electrode.³⁵ Beyond C₁ products, SACs on N-doped graphene can also generate multi-carbon hydrocarbons with notable faradaic efficiencies. Guan et al. observed production of both methane and ethylene on Cu–N–C and noted that a high Cu loading favors ethylene generation, while a low Cu loading prefers producing methane.³⁶ To improve activity and selectivity of SACs towards generating hydrocarbons, SACs incorporating dopants other than N or heteroatom dopants have been synthesized. Cai et al. achieved a high faradaic efficiency of 78% for methane production at −1.44 V vs. the RHE when mixing oxygen (O) dopants with N in Cu–N₂O₂–C SAC.³⁷ Mixing boron (B) dopants with N can also boost the catalytic performance for CO₂R to methane using Cu SACs.³⁸ In addition to SACs with 2p dopants, SACs with 3p dopants have also been successfully synthesized. For example, Co SACs with both N and sulfur (S) dopants (Co–N₂S₂–C) have been used for CO₂R to CO, outperforming Co–N–C at all overpotentials.³⁹

Despite these achievements, discovering practical SACs towards electrochemically reducing CO₂ to hydrocarbons remains a grand challenge due to the lack of in situ spectroscopy to detect atomic-scale, short-lived reaction intermediates and the existence of a large SAC chemical space that cannot be fully enumerated by experimental approaches.⁴⁰ Instead, computational modeling, typically with density functional theory (DFT), plays an important role in understanding reaction mechanisms at the electronic structure level and assessing hypothetical catalysts prior to experimental synthesis.^41–43 For example, Zhao and Liu used ab initio molecular dynamics simulations and enhanced sampling to investigate the CO₂R to CO reaction pathways via an adsorbed COOH intermediate (*COOH; * refers to an adsorption site) on Ni–N_x–C SACs (x = 0–4).⁴⁴ They found that an appropriate explicit description of solvents and surface charge can lead to the experimentally observed CO₂ chemisorption of forming *CO₂ prior to protonation and proposed that a hybrid coordination environment with one nitrogen and three carbon atoms is the most active and selective Ni–N–C SAC for CO₂R to CO. Vijay et al. also investigated the same CO₂R to CO reaction mechanisms via *CO₂ and *COOH intermediates on both Fe–N–C and Ni–N–C and determined that the rate-limiting step could be either CO₂ adsorption or the subsequent proton-coupled electron transfer step of forming *COOH.⁴⁵ Beyond CO, several computational efforts have been conducted to study CO₂R reaction pathways to hydrocarbons. Chen et al. used DFT to explain the experimentally observed high activity of Cu–N–C for CO₂R to acetone and proposed that the pyrrolic coordination environment results in an energetically favorable pathway with the rate-limiting step being the first CO₂ reduction step of forming *COOH, consistent with spectroscopic characterization of SAC structures using extended x-ray absorption fine structure.⁴⁶ Zhou et al. confirmed the favorability of pyrrolic coordination environment over the pyridinic structure for Ni–N–C SACs towards CO generation.⁴⁷ Yang et al. investigated reaction mechanisms of CO₂R to methane and methanol also on Cu–N–C and proposed that the selectivity towards different products originates from *COH reduction to *CHOH for methanol vs. to *C for methane, explaining the experimentally observed high activity of methanol production.³⁴ While still focusing on Cu–N–C, Guan et al. studied a different reaction pathway towards forming methane, i.e., through *CO to *CHO to *CH₂O, along with C–C coupling mechanism via formation of OC–*COH intermediate towards generating ethylene, and concluded that the selectivity of C₁ vs. C₂ products is dependent on Cu loading density.³⁶ In addition to mechanistic analysis, DFT simulations provide the opportunities of assessing hypothetical catalysts prior to trial-and-error experimental synthesis and verification. For example, Wang et al. investigated 23 N-doped M–N–C SACs with M ranges from 3d to 5d transition metals and concluded that their CO₂R reaction mechanisms and reactivities toward methane generation are highly dependent on the outermost d-shell electrons of the catalytically active metal centers with no ubiquitous rate-limiting step.⁴⁸ Hou et al. investigated 28 N and S co-doped SACs, M–N_xS_4−x–C SACs (M = Fe, Co, Ni, Cu), toward generating methanol and methane. They considered multiple different reaction pathways and identified Cu–N₁S₃–C as an active catalyst for CO, CH₃OH, and CH₄ production, as well as Fe–N₃S₁–C for formic acid generation.⁴⁹ Wei et al. assessed stability and catalytic performance of 10 dual metal-site SACs, M1/M2–N–C (M1, M2 = Fe, Co, Ni, Cu), for CO₂R to CO, formic acid, methanol, and methane. Considering CO₂ reduction to *COOH and *CHOH reduction to *CH as the rate-limiting-steps, they predicted that Fe/Co–N–C and Co–N–C exhibit the best activity and selectivity towards methane formation.⁵⁰

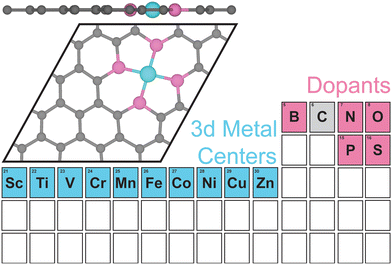
Despite previous success of using DFT to study and design graphene-based SACs for electrochemical CO₂ conversion, there is a fundamental gap in understanding the roles of metals, dopants, and coordinating environment in tuning reactivity of SACs. In addition, the reaction mechanisms of CO₂R to hydrocarbons beyond CO product on SACs remain unclear, limiting the opportunities of developing effective design principles for SACs and leaving the question whether descriptors established on metal catalysts are transferrable to SACs a puzzle. In this work, we focus on rationalizing catalytic activities of a large SAC chemical space with various metal centers (i.e., all 3d transition metals) and dopants (2p dopants: B, N, O; 3p dopants: phosphorus or P, S) as electrocatalysts for CO₂R towards generating methane and methanol. We first narrow down the selection of potential SAC candidates using CO adsorption energy, which has been previously identified as an effective descriptor for CO₂R activity on metal catalysts,⁵¹ and then elucidate full reaction mechanisms of CO₂ conversion to methane and methanol on identified SAC candidates with an CO adsorption energy close to the optimal value of −0.67 eV.⁵² Consequently, we propose promising SACs as CO₂R electrocatalysts for experimental synthesis and verification. To the best of our knowledge, no theoretical investigation exists heretofore of performing such systematic mechanistic analyses on B-, O-, P-, and S-doped SACs for electrochemical CO₂R to hydrocarbons.

II. Computational methods

We performed all spin-polarized DFT calculations within Vienna Ab initio Simulation Package (VASP)^53,54 version 6.3.1. We self-consistently simulated valence electrons of 2s and 2p electrons for B, C, N, and O, 3s and 3p electrons for P and S, and 4s and 3d electrons for first-row transition metals (Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, Zn) using the all electron, frozen-core, projector augmented-wave (PAW) method.⁵⁵ We employed the Perdew–Burke–Ernzerhof (PBE)⁵⁶ exchange–correlation functional in tandem with Grimme's D3^57,58 dispersion correction and the Becke–Johnson damping function.⁵⁹ We applied a kinetic-energy cutoff value of 800 eV for the plane-wave basis set. We obtained the initial SAC geometry, which consists of one metal atom, four dopants, and 26 C atoms in the unit cell from a previous work (Fig. 1).⁶⁰ Each clean SAC structure was fully optimized (both atomic positions and lattice parameters) until the absolute total force on each atom was less than 0.03 eV Å⁻¹. After adding adsorbates on SACs, we re-optimized atomic positions of all atoms in the supercell at fixed lattice parameters using the same convergence threshold. We confirmed that all periodic cells contain at least 15 Å of vacuum along the c-axis before and after geometry relaxation to avoid artificial interactions between the periodic images in the direction normal to the SAC surface. Locating the most stable geometries of both clean and adsorbed SACs is challenging due to the vacancies created and substitutes doped in graphene. We developed a systematic strategy to ensure that the most stable geometries were discovered in our simulations (Supplementary Method and Table S1, ESI†). In addition to full geometry optimizations, we also performed benchmark calculations of surface-constrained optimizations, in which the position of each atom in SAC along the c-axis (i.e., the direction normal to graphene plane) was fixed to maintain a planar geometry. We employed an automatic, Γ-point-centered Monkhorst–Pack⁶¹ k-point grid of 3 × 3 × 1 to sample the Brillouin zone. The chosen kinetic energy cutoff and k-point grid converge the total energies to within 1.5 meV per atom (Fig. S1 and S2, ESI†). We used a default initial magnetic moment guess of 1 on each atom. Benchmark calculations indicated that using different initial magnetic moment guesses for the metal atoms results in same final energies and magnetic moments (Tables S2 and S3, ESI†). We applied a Fermi surface smearing with first order Methfessel–Paxton method⁶² and a smearing width of 0.1 eV to integrate the Brillouin zone and aid self-consistent field convergence. Adding dipole field energy and potential corrections⁶³ yields similar CO adsorption energies with differences less than 0.01 eV on representative N-doped SACs (Table S4, ESI†). Benchmark DFT+U calculations of applying a Hubbard U value of 3.29 eV on Fe, as suggested in previous studies,^64,65 showed similar reaction energies for CO₂R to methane and methanol pathways on Fe–N–C (Fig. S3, ESI†).

Fig. 1 SAC structure side view (top) and top view (bottom) with different metal centers (Sc, Ti, V, Cr, Mn, Fe, Co, Ni, Cu, and Zn) shown in blue, dopants (B, N, O, P, and S) shown in magenta, and C shown in gray.

To quantify metal- and dopant-induced distortion within SAC, we computed displacements of metal and dopant atoms along the direction normal to the graphene surface (i.e., z-direction) using the equation,

in which Z_graphene represents the average Cartesian coordinates in the z-direction of all 26 C atoms. Similarly, Z_metal and Z_dopant,i are Cartesian coordinates in the z-direction of the metal atom and each dopant atom, respectively. Given the divergent distortions observed in dopants, we considered displacement of each dopant by summing them up. To evaluate energetic stability of SACs, we computed the complexation energy of SACs, which was used in previous work⁶⁶ to evaluate stabilization that the doped graphene provides to the metal center and is defined as the relative energy of SAC with respect to its bare and doped graphene and the gas phase metal ion,

E_complexation = E_SAC − E_graphene − E_metal

in which E_SAC, E_graphene, and E_metal are energies of SAC, bare and doped graphene, and the gas phase metal ion, respectively. We evaluated CO adsorption energies as follows:

ΔE_CO = E_CO+SAC − E_SAC − E_CO

in which E_CO+SAC and E_SAC are energies of the SAC with a CO adsorbate and the clean surface, respectively. E_CO is the energy of a gas-phase CO molecule, which was modeled as an isolated molecule in a unit cell of 15 Å × 15 Å × 15 Å. Reaction energies of PCET steps were determined using the computational hydrogen electrode⁶⁷ (CHE) model with the energy of an isolated H₂ molecule modeled in a unit cell of 20 Å × 20 Å × 20 Å.

III. Results and discussion

Dopant effects on structural stabilities of SACs

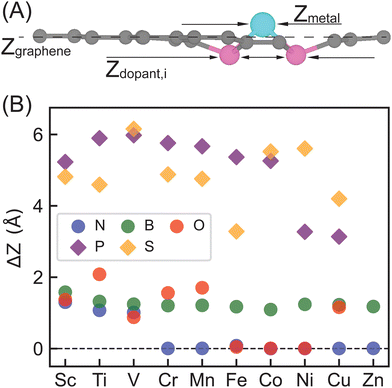
We considered a pyridinic-type SAC moiety, i.e., the central metal atom is coordinated with four pyridinic dopant atoms (Fig. 1). Other structures, such as a pyrrolic-type SAC moiety, might exist, yet how metal centers and dopants fill C vacancies in graphene is not the focus of our work. Starting from planar monolayer of SAC geometries, we fully optimized the structures and observed system-dependent out-of-plane distortion, particularly in the region of metal center and dopants (Table S1, ESI†). Local distortion among active sites is due to the capabilities of dopants to fill in C vacancies on graphene as well as symmetry and rigidity enforced by periodic boundary conditions. Overall, 2p-coordinating SACs with N, B, or O dopants exhibit distortion only among the metal site if any, while 3p-coordinating SACs with P or S dopants experience distortion among both the metal and dopant sites, regardless of the metal center.

To quantify the local out-of-plane distortion observed in SACs, we computed displacements of metal and dopant atoms along the direction normal to the graphene surface as described in the Computational methods section (Fig. 2). When performing full geometry optimizations with no constraint, we observed that SACs with 2p dopants (i.e., B, N, or O) either remain planar with a 0.0 Å distortion or exhibit a moderate distortion of less than 2.1 Å concentrated on the metal site. Though the overall structural properties remain similar across all 2p dopants, different dopants exhibit divergent local distortion sensitivities to metal sites. Within N-doped SACs, only early transition metals, Sc–N–C, Ti–N–C, and V–N–C show local distortion around the metal center with displacements of 1.0 to 1.3 Å, while the other M–N–C SACs preserve the planar structure. Interestingly, boron-doped SACs exhibit consistently local distortions with displacements in the range of 1.0 to 1.6 Å for all transition metals, indicating the crucial role of dopants in determining local metal-coordination environment. Oxygen-doped SACs show more variances in out-of-plane distortions that are sensitive to metal center valence electrons. Early and late transition metals exhibit moderate displacements, while mid-row transition metals remain planar in the same plane with graphene substrate. Switching from 2p dopants to 3p dopants (i.e., P or S), we observed out-of-plane distortion concentrated not only on metal sites, but also on dopants, increasing the degree of distortion from less than 2.1 Å for 2p dopants to 3.0 to 6.0 Å for 3p dopants. Although all 3p-coordinating SACs show severe out-of-plane distortion, P-coordinating SACs are more distorted than corresponding S-coordinating SACs for early and mid-row transition metals and vice versa for late transition metals. In addition, we noted that Zn–O–C, Zn–P–C, and Zn–S–C are not structurally stable materials since the metal centers cannot form any chemical bonds with dopants (Table S1, ESI†). Most SACs exhibit structures with all four dopants in the same side of the graphene, while two exceptions (Cu–P–C and Fe–S–C) display structures with dopants on the opposite side of graphene (Table S1, ESI†).

Fig. 2 (A) A representative model showing different coordinate values in the z-direction used to quantify out-of-plane distortion of SACs. (B) Out-of-plane distortion (ΔZ) of SACs with different 3d metals and dopants (B: green circles; N: blue circles; O: red circles; P: purple diamonds; S: orange diamonds).

These observations are consistent with previous studies performed on other graphene-based SACs that graphene's ability to accept a dopant is highly dependent on atomic radius of dopant elements,⁶⁸ and thus dopants with similar atomic radius as carbon are more suited for retaining the 2-dimensional monolayer structure of graphene.⁶⁹ Our results also indicated that 2p-coordinating systems with dopants possessing similar atomic radius to carbon favor planar configuration compared with 3p-coordinating systems with dopants possessing larger atomic radius than carbon. In addition, we generally expect longer bond distances between 3p elements with C atoms than C–C bond distances in graphene.^70,71 To enable enough space for forming 3p-C bonds and 3p-metal bonds within the rigid framework of graphene, 3p dopants and metal sites move along the direction normal to the graphene monolayer to facilitate those longer bond distances. In addition, we computed complexation energy (vide supra) to assess stabilization that the doped graphene provides to the metal center on five representative SACs, including Fe–N–C, Sc–B–C, Ni–O–C, Cu–P–C and Co–S–C (Table S5, ESI†). All SACs exhibit negative complexation energies, showing strong stabilization effects that the support provides to the active metal sites. In general, SACs with 2p pyridinic dopants are likely to be more structurally stable than SACs with 3p pyridinic dopants in experimental synthesis.

CO adsorption energy as a descriptor for CO₂R reactivity

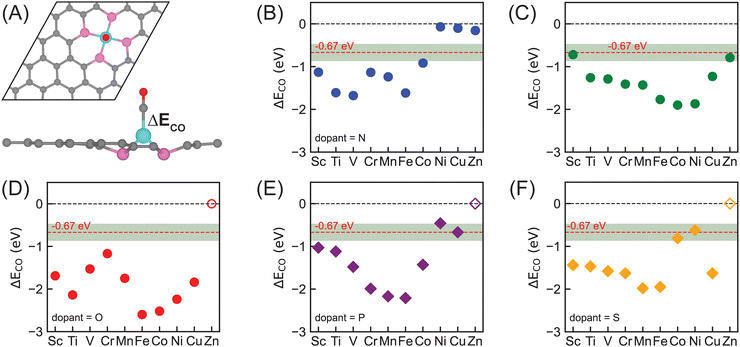
CO remains the dominant product of electrochemical CO₂R on most catalysts at lower applied potentials, leading to assumptions that *CO is a key intermediate toward further PCET steps of acquiring hydrocarbons and *CO reduction is likely to be the rate-limiting step.^72–75 *CO binding strength has recently been proposed by Liu et al. as a descriptor for CO₂R activity due to its linear correlation with reaction barriers of the *CO reduction step on multiple metallic surfaces.⁵¹ Zhong et al. further identified the optimal CO adsorption energy being −0.67 eV for CO₂R to hydrocarbons on metal catalysts.⁵² Using this descriptor, we first narrowed down potential SACs for electrochemical CO₂R within our focused chemical space, i.e., all possible combinations between 3d metals and dopants (B, N, O, P, S), by calculating CO adsorption energies on them (Fig. 3). Given the DFT errors in predicting adsorption energies,^76–78 we used a range of ±0.2 eV to the optimal value of −0.67 eV (i.e., in the range of −0.87 to −0.47 eV) in determining promising candidates for electrochemical CO₂R to hydrocarbons.

Fig. 3 (A) Top view and side view of CO-adsorbed SAC. CO adsorption energies of all 3d-transition metals embedded on (B) nitrogen-, (C) boron-, (D) oxygen-, (E) phosphorus-, and (F) sulfur-doped graphene. The red line indicates the optimal CO adsorption energy identified on metallic surfaces. A range of ±0.2 eV from the optimal line is shown in the shaded green region to indicate the promising candidates. Empty symbols indicate structurally unstable SACs.

Nitrogen-doped SACs, particularly with mid-row or late 3d transition metals, are the most widely studied SACs for electrochemical CO₂ reduction both experimentally and computationally.^25,35,43 However, unfortunately, none of those materials exhibits optimal CO binding strength within ±0.2 eV from −0.67 eV (Fig. 3B), indicating that none of them are likely to reduce CO₂ to hydrocarbons with reasonable efficiencies. Given the extensive investigations of such catalysts, we included Co–N–C with a CO adsorption energy of −0.92 eV, which is close to the optimal region, as well as the most widely studied Fe–N–C in our mechanistic analysis (vide infra). Overall, our DFT simulations predict strong CO binding strength for early and mid-row transition metals and very weak CO binding strength for late transition metals (Ni–N–C, Cu–N–C, and Zn–N–C), indicating that CO is readily desorbed from the surface once it is generated. This is consistent with multiple experimental observations that nitrogen-doped SACs with late 3d transition metals are efficient electrocatalysts for CO₂R to CO,^26,79 such as Ni–N–C being a superior electrocatalyst for CO generation with nearly 100% faradaic efficiency.^31,32

While nitrogen dopants are among the most experimentally synthesized graphene-based catalysts at atomic scale, SACs coordinated with other dopants studied in this work (i.e., B, O, P, S) are mostly hypothetical materials. Screening and narrowing down those materials in silico prior to trial-and-error experimental synthesis and verification can efficiently accelerate the catalyst design process. For boron-doped SACs, we observed a clear sensitivity of CO adsorption energy on metal center d-fillings that CO binding strength becomes stronger from Sc–B–C (−0.72 eV) to Co–B–C (−1.90 eV) and then weaker from Ni–B–C (−1.87 eV) to Zn–B–C (−0.79 eV) with increasing outer shell d electrons, resulting in two potential active and selective electrocatalysts, Sc–B–C and Zn–B–C, for converting CO₂ to hydrocarbons (Fig. 3C). Switching to another 2p dopant (i.e., O), unfortunately, we predicted that all of them bind CO too strongly and thus are unlikely effective electrocatalysts to reduce CO₂ to hydrocarbons (Fig. 3D). *CO binding strength on 3p-coordinating (i.e., with P or S) SACs exhibits more systematic dependence on d-filling, regardless of dopant type (Fig. 3E and F). We observed more negative CO adsorption energies with increasing outer shell d electrons from Sc (−1.03 eV for Sc–P–C, −1.44 eV for Sc–S–C) to Fe (−2.21 eV for Fe–P–C, −1.95 eV for Fe–S–C), and then less negative CO adsorption energies with increasing outer shell d electrons from Fe to Ni (−0.46 eV for Ni–P–C, −0.62 eV for Ni–S–C). The only exception is Cu SACs (−0.67 eV for Cu–P–C, −1.63 eV for Cu–S–C) showing stronger CO binding strength compared with Ni SACs. Unfortunately, we cannot find stable structures for Zn–P–C, Zn–S–C, and Zn–O–C. Overall, we further identified four 3p-coordinating SACs with optimal CO binding strength, namely Ni–P–C, Cu–P–C, Co–S–C, and Ni–S–C, in our following mechanistic studies.

Comparing the effect of tuning dopants on CO binding strength, we observed that the sensitivity is dependent on d-filling of metal centers (Fig. S4, ESI†). In general, early and mid-row transition metals (Sc, Ti, V, Cr, Mn, and Fe) exhibit a moderate range of CO adsorption energies when changing dopants, while late transition metals (Co, Ni, and Cu) show a larger range of CO adsorption energies. However, there is no systematic trend which dopant results in consistently strong or weak CO binding strength across all 3d transition metals. Motivated by the effects that Ni and Cu SACs have weak CO binding strength with N dopants and moderate or strong CO binding strength with other dopants, we propose a strategy of combining different dopants via heteroatom doping to tune binding energy of key adsorbates for SAC design.

For the widely studied nitrogen-doped SACs which mostly preserve planar geometries (Fig. 2), the natural approach to simulate the geometry is allowing full relaxation of atomic positions in geometry optimizations.^47,60 However, for SACs with other dopants which exhibit out-of-plane distortions, a constrained geometry optimization of restricting the movement of atoms in the direction normal to the graphene plane has been used.⁶⁶ Here, we benchmarked the accuracy of using this approach for SAC study. We constrained the movement of each atom within the graphene plane by fixing the coordinates in z-direction (i.e., direction normal to the graphene plane) in geometry optimizations for both clean and CO-adsorbed surfaces when predicting CO adsorption energies (Fig. S5, ESI†). Overall, constrained optimizations predict less negative CO adsorption energies for most SACs with several exceptions including early transition metals embedded in boron- and phosphorus-doped systems. There are larger variations in CO adsorption energy predictions between performing full and constrained geometry optimizations, ranging from −2.73 to 0.81 eV. Given the possible large discrepancies in energetics predictions, we highlight the importance of performing full relaxation when simulating SACs to incorporate the structural effects.

Reaction mechanisms of CO₂R to methane and methanol on 2p-coordinating SACs

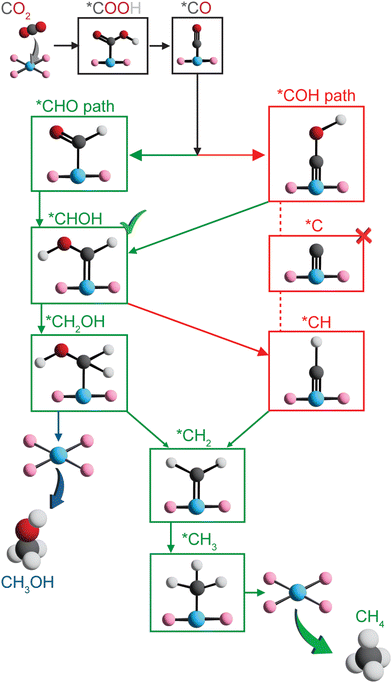
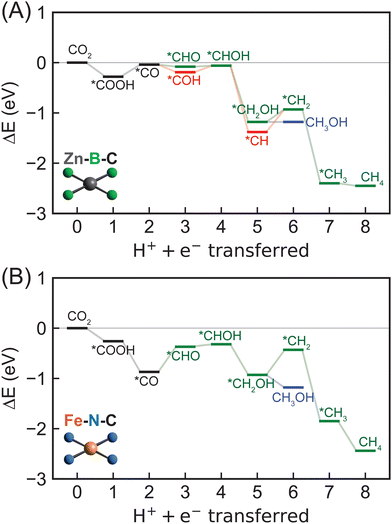
To further assess the reactivity of identified SAC candidates using CO adsorption energy as a descriptor (vide supra), we elucidated full reaction mechanisms of CO₂R to hydrocarbons. We considered eight SACs with varying metal centers and dopants in our mechanistic analysis, including Sc–B–C, Zn–B–C, Ni–P–C, Cu–P–C, Co–S–C, and Ni–S–C with optimal CO adsorption energy, as well as Co–N–C with CO adsorption energy close to optimal value and the most widely studied Fe–N–C. Given the large interatomic distances between active metal centers within SACs, C–C coupling steps toward forming C₂₊ products are extremely challenging,^36,80 and thus here we considered C₁ hydrocarbon products, i.e., methane and methanol formation. Typically, electrochemical CO₂R proceeds via *CO reduction to either *COH or *CHO, resulting in divergent reaction pathways following these two intermediates.^14,19 We focused on five possible reaction pathways towards methane formation, i.e., CO₂ → *COOH → *CO → *COH or *CHO → *C or *CHOH → *CH or *CH₂OH → *CH₂ → *CH₃ → CH₄, and two reaction pathways toward methanol formation, i.e., CO₂ → *COOH → *CO → *COH or *CHO → *CHOH → *CH₂OH → CH₃OH (Fig. 4). Unlike previous studies that only considered atop adsorption site on metal centers for intermediates,^37,48,81 we examined three possible adsorption sites: atop, bridge, and hollow around metal centers for key intermediates (Table S6, ESI†). Surprisingly, the most favorable adsorption site highly depends on both type of intermediates and metal-coordinating environments of SACs (Table S7, ESI†). Atop site is not consistently predicted to be the most favorable adsorption site for many adsorbates, indicating a complete screening of all possible adsorption sites is crucial in mechanistic study of graphene-based single atom catalysts.

Fig. 4 Possible reaction pathways considered for electrochemical CO₂R toward methane and methanol formation on graphene-based SACs. The green path denotes the most favorable reaction pathway for most SACs except for Zn–B–C.

We first considered reaction mechanisms of CO₂R to methane and methanol on Zn–B–C (Fig. 5A). The initial PECT step of CO₂ to *COOH is energetically favorable with a reaction energy of −0.28 eV (Table S8, ESI†). Subsequent PCET step from *COOH to *CO and one water molecule is predicted to have a slightly positive reaction energy of 0.24 eV. Interestingly, we observed thermodynamically favored *CO reduction to form both *CHO and *COH with reaction energies of −0.04 eV and −0.15 eV, respectively. The small quantitative energy difference, i.e., ∼0.1 eV, indicates competitive formation and thus co-existence of *CHO and *COH as key CO₂R intermediates on Zn–B–C. Considering the next PCET step, we obtained a high reaction energy of 2.86 eV for *COH reduction to form *C and one water molecule (Fig. S6 and Table S8, ESI†), indicating the infeasibility of this pathway, whereas subsequent PCET steps of both *CHO and *COH to form *CHOH are more favorable with reaction energies of 0.02 eV and 0.13 eV, respectively. Selectivity toward methane and methanol is dependent on the step of *CHOH reduction. Methanol formation proceeds through *CH₂OH intermediate with a reaction energy of −1.12 eV and the final reduction step with a reaction energy of zero. Methane is more thermodynamically favorable with a lower reaction energy for *CHOH reduction to *CH (−1.32 eV), but a higher reaction energy for subsequent reduction to *CH₂ (0.45 eV), following by favorable further reduction to form *CH₃ (−1.47 eV) and CH₄ (−0.05 eV).

Fig. 5 Energetics of CO₂R to methane via eight PCET steps and methanol via six PCET steps on (A) Zn–B–C and (B) Fe–N–C SACs predicted by DFT-PBE-D3. The green lines show the most favorable pathway toward methane or methanol formation through a *CHO intermediate identified on most SACs except for Zn–B–C. The red lines denote other favorable pathways on Zn–B–C. Blue lines indicate formation of methanol.

Overall, we found Zn–B–C SAC to be a promising electrocatalyst for CO₂R toward generating both methane and methanol. The most favorable reaction pathway proceeds via CO₂ → *COOH → *CO → *COH → *CHOH → *CH → *CH₂ → *CH₃ → CH₄ with *CH → *CH₂ (0.45 eV) as the potential rate-limiting step for methane generation. Methanol formation is also possible through CO₂ → *COOH → *CO → *COH → *CHOH → *CH₂OH → CH₃OH with *COOH → *CO (0.24 eV) as the potential rate-limiting step. Therefore, Zn–B–C SAC requires very low applied potentials, i.e., −0.45 V vs. the RHE and −0.24 eV vs. the RHE, for electrochemical CO₂R to generate methane and methanol, respectively. In addition, the identified rate-limiting steps on Zn–B–C SAC differ from conventional understanding of *CO reduction step reported previously on metallic surface,⁵¹ casting doubt whether *CO adsorption energy is an effective descriptor to screen SACs as electrocatalysts for CO₂R. To provide a more complete picture of catalytic performance of Zn–B–C SAC, we also investigated its activity for HER. We predicted that the potential rate-limiting step of HER on Zn–B–C is the Heyrovsky step with a reaction energy of 0.33 eV, which is only slightly lower than the reaction energy of 0.45 eV for the rate-limiting step of CO₂R to methane (Fig. S7, ESI†). Both reaction energies are easily surmountable with applied potentials, indicating competing CO₂R and HER on Zn–B–C.

Switching to the other boron-doped SAC, Sc–B–C, we observed consistent negative and positive reaction energies for the first two CO₂R PCET steps as on Zn–B–C, but with much larger values (−1.00 eV for CO₂ reduction to *COOH and 1.03 eV for *COOH reduction to *CO; Fig. S6, S8 and Table S8, ESI†). However, CO reduction to *CHO is favored over *COH formation by 0.89 eV (−0.52 eV for *CHO formation, 0.37 eV for *COH formation), divergent from the competing steps of *CHO and *COH formation predicted on Zn–B–C. Following *CHO formation, subsequent PCET steps involve *CHOH formation (−0.03 eV), *CH₂OH formation (−0.86 eV), leading to methanol (0.20 eV), or *CH₂ formation (0.08 eV), *CH₃ formation (−0.88 eV), resulting in methane (−0.26 eV), and thus methane is slightly more favorable than methanol on Sc–B–C. To summarize, methane proceeds via CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → *CH₂ → *CH₃ → CH₄ and methanol proceeds via CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → CH₃OH. The rate-limiting step is *COOH reduction to *CO with a high reaction energy of 1.03 eV, indicating Sc–B–C might not be an active electrocatalyst for CO₂R.

For nitrogen-doped SACs, unfortunately, none of them possesses a CO adsorption energy close to the optimal value of −0.67 eV. However, to understand how CO₂ can be electrochemically reduced to hydrocarbons catalyzed by those most widely studied graphene-based SACs, we included Fe–N–C and Co–N–C in our mechanistic analysis. Both methane and methanol production on Fe–N–C follow the same reaction pathways as on Sc–B–C, but with several different trends in energetics, including reaction energy of *COOH reduction to *CO is negative (−0.61 eV) and reaction energy of *CO reduction to *CHO reduction (0.50 eV) is positive (Fig. 5B and Fig. S6, Table S8, ESI†). In addition, the reduction of *CH₂OH to CH₃OH (−0.25 eV) is more thermodynamically favorable than to *CH₂ (0.50 eV), indicating preferred methanol formation on Fe–N–C with a rate-limiting step of *CO reduction to *CHO. The required applied potential for methanol generation on Fe–N–C is predicted to be −0.50 V vs. the RHE, suggesting that it might be an active electrocatalyst for CO₂R to hydrocarbons. However, previous experiments^82–84 suggested that Fe–N–C can only electrochemically convert CO₂ to CO with reasonable efficiencies. This is because *CO readily desorbs from the surface upon generation with a very weak *CO adsorption energy, though the required applied potentials are predicted to be low enough for methanol generation. Therefore, tuning *CO adsorption energy represents an effective strategy to strengthen the activity of Fe–N–C for CO₂R to hydrocarbons. For Co–N–C, CO₂R to methanol follows the same reaction pathway as Sc–B–C and Fe–N–C, but with a different rate-limiting step of *CHO reduction to *CHOH with a predicted high reaction energy of 0.98 eV (Fig. S6, S8 and Table S8, ESI†). Unfortunately, we were not able to locate stable structures of *CH₂ adsorbed on Co–N–C, indicating that methane formation might not be possible on Co–N–C. Our DFT predictions are consistent with experiments^33,85 that Co–N–C can only electrochemically reduce CO₂ to CO. In addition, comparing reactivity of Fe–N–C and Co–N–C for CO₂ to CO conversion, we predicted a much lower *COOH to *CO reaction energy for Fe–N–C (−0.61 eV) than for Co–N–C (0.22 eV) (Fig. S6, S8 and Table S8, ESI†), consistent with previous experiment⁸⁶ showing that Fe–N–C is more active than Co–N–C for this chemistry.

To summarize, we predicted that Zn–B–C and Fe–N–C might be active electrocatalysts for CO₂R to methane and methanol, respectively, given their surmountable energies at moderate applied potentials. However, we observed both metal- and dopant-dependent CO₂R mechanistic behaviors on 2p-coordinating SACs (Table 1). Zn–B–C favors *CO reduction to *COH, whereas the other three SACs (i.e., Sc–B–C, Fe–N–C, and Co–N–C) proceeds via *CO reduction to *CHO toward methane or methanol formation. In general, methane formation is more favorable on boron-doped SACs, while methanol generation is more preferred on nitrogen-doped SACs. Unfortunately, rate-limiting steps are fully system-dependent on 2p-coordinating SACs, indicating *CO binding strength might not be an effective descriptor for CO₂R reactivity since this proposed descriptor assumes that *CO reduction is the rate-limiting step.

Table 1 Preferred products, rate-limiting steps, and reaction energies in eV of rate-limiting steps of CO₂R to methane and methanol on Zn–B–C, Sc–B–C, Fe–N–C, Co–N–C

	Product	Rate-limiting step	Reaction energy
Zn–B–C	Methane	*CH + H^+ + e^− → *CH2	0.45
Sc–B–C	Methane	*COOH + H^+ + e^− → *CO + H2O	1.03
Fe–N–C	Methanol	*CO + H^+ + e^− → *CHO	0.50
Co–N–C	Methanol	*CHO + H^+ + e^− → *CHOH	0.98
Cu–P–C	Methanol	*CO + H^+ + e^− → *CHO	0.56
Ni–P–C	Methanol	CO2 + H^+ + e^− → *COOH	0.74
Ni–S–C	Methanol	CO2 + H^+ + e^− → *COOH	1.02
Co–S–C	Methanol	CO2 + H^+ + e^− → *COOH	1.37

---

Reaction mechanisms of CO₂R to methane and methanol on 3p-coordinating SACs

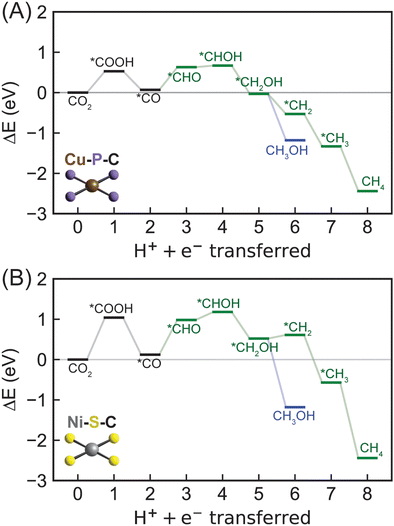
Moving from 2p-coordinating SACs to 3p-coordinating SACs, we next considered Cu–P–C (Fig. 6A), which has a CO adsorption energy (−0.67 eV) close to the optimal value (Fig. 3). Consistent with most 2p-coordinating SACs, Cu–P–C favors reaction pathways of CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → *CH₂ → *CH₃ → CH₄ and CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → CH₃OH toward methane and methanol formation, respectively (Fig. S5, ESI†). Due to the large reaction energy difference (0.65 eV) between *CH₂OH reduction to form *CH₂ (−0.49 eV) and methanol (−1.14 eV; Table S8, ESI†), Cu–P–C is predicted to exhibit a strong preference towards methanol formation with an early rate-limiting step of *CO reduction to *CHO (Table 1). To overcome the reaction energy (0.56 eV) of such step, an applied potential of −0.56 V vs. the RHE is needed for methanol generation on Cu–P–C, indicating an active electrocatalyst for CO₂R to hydrocarbons. Moving to the other phosphorous-doped SAC (Ni–P–C) with promising CO binding strength, we observed same reaction pathways for CO₂R to methane and methanol with a same preference for methanol formation (Fig. S6 and S8, ESI†). However, the rate-limiting step changes from *CO reduction to the very first PCET step of CO₂ reduction to *COOH with a reaction energy of 0.74 eV (Table 1 and Table S8, ESI†). We have identified two sulfur-doped SACs with promising CO binding strength, namely Ni–S–C and Co–S–C (Fig. 3). Their mechanistic behaviors as electrocatalysts for CO₂R are similar to Ni–P–C (Fig. 6B and Fig. S6, S8, ESI†). Unfortunately, the reaction energies of the rate-limiting step, CO₂ reduction to *COOH, are starkly high on both Ni–S–C (1.02 eV) and Co–S–C (1.37 eV; Table 1), indicating their low activities to activate CO₂.

Fig. 6 Energetics of CO₂R to methane via eight PCET steps and methanol via six PCET steps on (A) Cu–P–C and (B) Ni–S–C SACs predicted by DFT-PBE-D3. The green lines show the most favorable pathway toward methane or methanol formation through a *CHO intermediate identified on most SACs except for Zn–B–C. Blue lines indicate formation of methanol.

Overall, all 3p-coordinating SACs favor methanol formation over methane, yet Cu–P–C is the only one with surmountable energies at moderate applied potentials. 3p-coordinating SACs exhibit early rate-limiting steps, i.e., *CO reduction for Cu–P–C and CO₂ reduction for Ni–P–C, Ni–S–C, and Co–S–C. This prediction is consistent with previous computational work showing that CO₂ adsorption and reduction is critical in electrochemical CO₂R.^37,45 In addition, we observed relatively high reaction energies for the very first PCET steps, especially on sulfur-doped SACs, indicating challenges in activating CO₂ even towards generating CO, which is different from 2p-coordinating SACs and conventional metal surfaces. This discrepancy in mechanistic behavior between SACs and metal catalysts again suggests the inefficiency of using CO binding strength as a descriptor for CO₂R reactivity.

IV. Summary and conclusions

Motivated by recent experimental success in using nitrogen-doped SACs for electrochemical CO₂R to generate CO and enhancing subsequent proton-coupled electron transfer steps using other dopants, we applied computational modeling with DFT to enable a systematic understanding of the roles of metal-coordination environment in tuning SAC activity for CO₂ conversion. We screened a large chemical space containing all possible combinations of 10 active metals (i.e., 3d transition metals) and five dopants (i.e., B, N, O, P, and S). We first investigated their structural stabilities and noted dopant-dependent rigidities that 2p-coordinating SACs preserve planar geometries or at most display a minor degree of out-of-plane distortion in the metal center, while 3p-coordinating SACs exhibit severe out-of-plane distortion among the metal-coordination region. We then used *CO binding strength, which was previously identified on metal catalysts as a descriptor for CO₂R activity, to narrow down the potential SAC candidates for converting CO₂ to hydrocarbons. We identified six hypothetical SACs that might be efficient electrocatalysts for CO₂R, namely Sc–B–C, Zn–B–C, Ni–P–C, Cu–P–C, Co–S–C, and Ni–S–C.

To further assess their activity, we elucidated reaction mechanisms of CO₂R to methane and methanol on the identified SACs. Two nitrogen-doped SACs (Co–N–C and Fe–N–C) were also included in the mechanistic analysis to understand dopant effects. We observed consistent preferred reaction pathways for methane and methanol formation proceeding via CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → *CH₂ → *CH₃ → CH₄ and CO₂ → *COOH → *CO → *CHO → *CHOH → *CH₂OH → CH₃OH on most SACs except for Zn–B–C. Surprisingly, unlike metallic surfaces, the predicted rate-limiting steps on SACs are system-dependent and vary with both dopants and metals, challenging the development of efficient design principles for SACs. In addition, it indicates infeasibility of using CO adsorption energy as a descriptor for CO₂R reactivity since *CO reduction is not a consistent rate-limiting step on SACs. Regarding CO₂R selectivity, boron-doped SACs favor methane formation, while SACs with other dopants (i.e., N, P, and S) prefer methanol formation. Overall, we identified Zn–B–C as a promising electrocatalyst for CO₂R to methane, as well as Fe–N–C and Cu–P–C for CO₂R to methanol due to their surmountable energies at moderate applied potentials. We believe our systematic studies reveal fundamental insights into the role of dopants and metals in tuning SAC reactivity and inspire new design principles for CO₂R electrocatalysts. Moving forward, we are extending full mechanistic analyses of CO₂R to valuable hydrocarbons on graphene-based SACs from selected 3d transition metals to all 3d–5d transition metals, with the ultimate goal of developing new and effective descriptors to guide activity and selectivity.

Data availability

The data supporting this article have been included as part of the ESI.†

Conflicts of interest

The authors declare no competing financial interests.

Acknowledgements

The authors acknowledge support by the National Science Foundation under Award No. 2349619, by the Advanced Research Projects Agency-Energy (ARPA-E), U.S. Department of Energy, under Award Number DE-AR0001786, and by Northeastern University, Chemical Engineering Department under start-up funding. The views and options of authors expressed herein do not necessarily state or reflect those of the United States Government or any agency thereof. This work was carried out using computational resources from Discovery, Research Computing at Northeastern University.

References

1. T. R. Karl and K. E. Trenberth, Modern Global Climate Change, Science, 2003, 302, 1719–1723.
2. A. Terando, D. Reidmiller, S. W. Hostetler, J. S. Littell, T. D. Beard Jr., S. R. Weiskopf, J. Belnap and G. S. Plumlee, Using Information from Global Climate Models to Inform Policymaking—The Role of the U.S. Geological Survey, Open-File Rep., 2020, 1–32.
3. L. E. Doman, V. Arora, L. E. Singer, V. Zaretskaya, A. Jones, T. Huetteman, M. Bowman, N. Slater-Thompson, B. Hojjati, D. Peterson, et al., International Energy Outlook 2016, U.S. Energy Inf. Adm., 2016, pp. 7–17.
4. BP, BP Energy Outlook, 2017, pp. 12–21.
5. D. Panepinto, V. A. Riggio and M. Zanetti, Analysis of the Emergent Climate Change Mitigation Technologies, Int. J. Environ. Res. Public Health, 2021, 18, 6767.
6. C. Graves, S. D. Ebbesen, M. Mogensen and K. S. Lackner, Sustainable Hydrocarbon Fuels by Recycling CO₂ and H₂O with Renewable or Nuclear Energy, Renewable Sustainable Energy Rev., 2011, 15, 1–23.
7. J. L. White, M. F. Baruch, J. E. Pander, Y. Hu, I. C. Fortmeyer, J. E. Park, T. Zhang, K. Liao, J. Gu and Y. Yan, et al., Light-Driven Heterogeneous Reduction of Carbon Dioxide: Photocatalysts and Photoelectrodes, Chem. Rev., 2015, 115, 12888–12935.
8. C. E. Creissen and M. Fontecave, Solar-Driven Electrochemical CO₂ Reduction with Heterogeneous Catalysts, Adv. Energy Mater., 2020, 11, 2002652.
9. Y. Hori, I. Takahashi, O. Koga and N. Hoshi, Selective Formation of C2 Compounds from Electrochemical Reduction of CO₂ at a Series of Copper Single Crystal Electrodes, J. Phys. Chem. B, 2002, 106, 15–17.
10. Y. Chen, C. W. Li and M. W. Kanan, Aqueous CO₂ Reduction at Very Low Overpotential on Oxide-Derived Au Nanoparticles, J. Am. Chem. Soc., 2012, 134, 19969–19972.
11. C. H. Lee and M. W. Kanan, Controlling H⁺ vs. CO₂ Reduction Selectivity on Pb Electrodes, ACS Catal., 2014, 5, 465–469.
12. H. Mistry, Y. W. Choi, A. Bagger, F. Scholten, C. S. Bonifacio, I. Sinev, N. J. Divins, I. Zegkinoglou, H. S. Jeon and K. Kisslinger, et al., Enhanced Carbon Dioxide Electroreduction to Carbon Monoxide over Defect-Rich Plasma-Activated Silver Catalysts, Angew. Chem., Int. Ed., 2017, 56, 11394–11398.
13. W. Luc, C. Collins, S. Wang, H. Xin, K. He, Y. Kang and F. Jiao, Ag-Sn Bimetallic Catalyst with a Core-Shell Structure for CO₂ Reduction, J. Am. Chem. Soc., 2017, 139, 1885–1893.
14. S. Nitopi, E. Bertheussen, S. B. Scott, X. Liu, A. K. Engstfeld, S. Horch, B. Seger, I. E. L. Stephens, K. Chan and C. Hahn, et al., Progress and Perspectives of Electrochemical CO₂ Reduction on Copper in Aqueous Electrolyte, Chem. Rev., 2019, 119, 7610–7672.
15. Q. Zhao and E. A. Carter, Revisiting Competing Paths in Electrochemical CO₂ Reduction on Copper via Embedded Correlated Wavefunction Theory, J. Chem. Theory Comput., 2020, 16, 6528–6538.
16. Q. Zhao, J. M. P. Martirez and E. A. Carter, Charting C–C Coupling Pathways in Electrochemical CO₂ Reduction on Cu(111) using Embedded Correlated Wavefunction Theory, Proc. Natl. Acad. Sci. U. S. A., 2022, 119, e2202931119.
17. Q. Zhao, J. M. P. Martirez and E. A. Carter, Electrochemical Hydrogenation of CO on Cu(100): Insights from Accurate Multiconfigurational Wavefunction Methods, J. Phys. Chem. Lett., 2022, 13, 10282–10290.
18. J. Cai, Q. Zhao, W.-Y. Hsu, C. Choi, Y. Liu, J. M. P. Martirez, C. Chen, J. Huang, E. A. Carter and Y. Huang, Highly Selective Electrochemical Reduction of CO₂ into Methane on Nanotwinned Cu, J. Am. Chem. Soc., 2023, 145, 9136–9143.
19. S. Xu and E. A. Carter, Theoretical Insights into Heterogeneous (Photo)electrochemical CO₂ Reduction, Chem. Rev., 2019, 119, 6631–6669.
20. Q. Zhao, J. M. P. Martirez and E. A. Carter, Revisiting Understanding of Electrochemical CO₂ Reduction on Cu(111): Competing Proton-Coupled Electron Transfer Reaction Mechanisms Revealed by Embedded Correlated Wavefunction Theory, J. Am. Chem. Soc., 2021, 143, 6152–6164.
21. Y. Hori, A. Murata and R. Takahashi, Formation of Hydrocarbons in the Electrochemical Reduction of Carbon Dioxide at a Copper Electrode in Aqueous Solution, J. Chem. Soc., Faraday Trans. 1, 1989, 85, 2309–2326.
22. M. Li, H. Wang, W. Luo, P. C. Sherrell, J. Chen and J. Yang, Heterogeneous Single-Atom Catalysts for Electrochemical CO₂ Reduction Reaction, Adv. Mater., 2020, 32, 2001848.
23. C. Gallagher, W. Siddiqui, T. Arnold, C. Cheng, E. Su and Q. Zhao, Benchmarking a Molecular Flake Model on the Road to Programmable Graphene-Based Single-Atom Catalysts, J. Phys. Chem. C, 2024, 128, 2876–2883.
24. A. Bagger, W. Ju, A. S. Varela, P. Strasser and J. Rossmeisl, Single Site Porphyrine-Like Structures Advantages over Metals for Selective Electrochemical CO₂ Reduction, Catal. Today, 2017, 288, 74–78.
25. F. Pan, W. Deng, C. Justiniano and Y. Li, Identification of Champion Transition Metals Centers in Metal and Nitrogen-Codoped Carbon Catalysts for CO₂ Reduction, Appl. Catal., B, 2018, 226, 463–472.
26. H. Cheng, X. Wu, X. Li, X. Nie, S. Fan, M. Feng, Z. Fan, M. Tan, Y. Chen and G. He, Construction of Atomically Dispersed Cu-N₄ Sites via Engineered Coordination Environment for High-Efficient CO₂ Electroreduction, Chem. Eng. J., 2021, 407, 126842.
27. P. Wang, Z. Jin, P. Li and G. Yu, Design Principles of Hydrogen-Evolution-Suppressing Single-Atom Catalysts for Aqueous Electrosynthesis, Chem. Catal., 2022, 2, 1277–1287.
28. X. Li, H. Rong, J. Zhang, D. Wang and Y. Li, Modulating the Local Coordination Environment of Single-Atom Catalysts for Enhanced Catalytic Performance, Nano Res., 2020, 13, 1842–1855.
29. L. T. Menisa, P. Cheng, X. Qiu, Y. Zheng, X. Huang, Y. Gao and Z. Tang, Single Atomic Fe–N₄ Active Sites and Neighboring Graphitic Nitrogen for Efficient and Stable Electrochemical CO₂ Reduction, Nanoscale Horiz., 2022, 7, 916–923.
30. G. Qu, K. Wei, K. Pan, J. Qin, J. Lv, J. Li and P. Ning, Emerging Materials for Electrochemical CO₂ Reduction: Progress and Optimization Strategies of Carbon-Based Single-Atom Catalysts, Nanoscale, 2023, 15, 3666–3692.
31. T. Zheng, K. Jiang, N. Ta, Y. Hu, J. Zeng, J. Liu and H. Wang, Large-Scale and Highly Selective CO₂ Electrocatalytic Reduction on Nickel Single-Atom Catalyst, Joule, 2019, 3, 265–278.
32. W. Zheng, F. Chen, Q. Zeng, Z. Li, B. Yang, L. Lei, Q. Zhang, F. He, X. Wu and Y. Hou, A Universal Principle to Accurately Synthesize Atomically Dispersed Metal-N₄ Sites for CO₂ Electroreduction, Nano-Micro Lett., 2020, 12, 108.
33. C. Wang, Y. Liu, H. Ren, Q. Guan, S. Chou and W. Li, Diminishing the Uncoordinated N Species in Co–N–C Catalysts toward Highly Efficient Electrochemical CO₂ Reduction, ACS Catal., 2022, 12, 2513–2521.
34. H. Yang, Y. Wu, G. Li, Q. Lin, Q. Hu, Q. Zhang, J. Liu and C. He, Scalable Production of Efficient Single-Atom Copper Decorated Carbon Membranes for CO₂ Electroreduction to Methanol, J. Am. Chem. Soc., 2019, 141, 12717–12723.
35. L. Han, S. Song, M. Liu, S. Yao, Z. Liang, H. Cheng, Z. Ren, W. Liu, R. Lin and G. Qi, et al., Stable and Efficient Single-Atom Zn Catalyst for CO₂ Reduction to CH₄, J. Am. Chem. Soc., 2020, 142, 12563–12567.
36. A. Guan, Z. Chen, Y. Quan, C. Peng, Z. Wang, T.-K. Sham, C. Yang, Y. Ji, L. Qian and X. Xu, et al., Boosting CO₂ Electroreduction to CH₄ via Tuning Neighboring Single-Copper Sites, ACS Energy Lett., 2020, 5, 1044–1053.
37. Y. Cai, J. Fu, Y. Zhou, Y. C. Chang, Q. Min, J. J. Zhu, Y. Lin and W. Zhu, Insights on Forming N,O-Coordinated Cu Single-Atom Catalysts for Electrochemical Reduction CO₂ to Methane, Nat. Commun., 2021, 12, 586.
38. Y. Dai, H. Li, C. Wang, W. Xue, M. Zhang, D. Zhao, J. Xue, J. Li, L. Luo and C. Liu, et al., Manipulating Local Coordination of Copper Single Atom Catalyst Enables Efficient CO₂-to-CH₄ Conversion, Nat. Commun., 2023, 14, 3382.
39. Z. Wei, Y. Liu, J. Ding, Q. He, Q. Zhang and Y. Zhai, Promoting Electrocatalytic CO₂ Reduction to CO via Sulfur-Doped Co–N–C Single-Atom Catalyst, Chin. J. Chem., 2023, 41, 3553–3559.
40. K. S. Adarsh, N. Chandrasekaran and V. Chakrapani, In situ Spectroscopic Techniques as Critical Evaluation Tools for Electrochemical Carbon dioxide Reduction: A Mini Review, Front. Chem., 2020, 8, 137.
41. X. Zhao, J. Shi, Y. Ji and Y. Liu, The Electronic Structure Underlying Electrocatalysts of Two-Dimensional Materials, Wiley Interdiscip. Rev.: Comput. Mol. Sci., 2019, 9, e1418.
42. J. H. Montoya, C. Shi, K. Chan and J. K. Norskov, Theoretical Insights into a CO Dimerization Mechanism in CO₂ Electroreduction, J. Phys. Chem. Lett., 2015, 6, 2032–2037.
43. W. Ju, A. Bagger, G. P. Hao, A. S. Varela, I. Sinev, V. Bon, B. Roldan Cuenya, S. Kaskel, J. Rossmeisl and P. Strasser, Understanding Activity and Selectivity of Metal-Nitrogen-Doped Carbon Catalysts for Electrochemical Reduction of CO₂, Nat. Commun., 2017, 8, 944.
44. X. Zhao and Y. Liu, Unveiling the Active Structure of Single Nickel Atom Catalysis: Critical Roles of Charge Capacity and Hydrogen Bonding, J. Am. Chem. Soc., 2020, 142, 5773–5777.
45. S. Vijay, W. Ju, S. Brückner, S.-C. Tsang, P. Strasser and K. Chan, Unified Mechanistic Understanding of CO₂ Reduction to CO on Transition Metal and Single Atom Catalysts, Nat. Catal., 2021, 4, 1024–1031.
46. K. Zhao, X. Nie, H. Wang, S. Chen, X. Quan, H. Yu, W. Choi, G. Zhang, B. Kim and J. G. Chen, Selective Electroreduction of CO₂ to Acetone by Single Copper Atoms Anchored on N-Doped Porous Carbon, Nat. Commun., 2020, 11, 2455.
47. Y. Wang, L. You and K. Zhou, Origin of the N-coordinated single-atom Ni sites in heterogeneous electrocatalysts for CO₂ reduction reaction, Chem. Sci., 2021, 12, 14065–14073.
48. J. Wang, M. Zheng, X. Zhao and W. Fan, Structure-Performance Descriptors and the Role of the Axial Oxygen Atom on M–N₄–C Single-Atom Catalysts for Electrochemical CO₂ Reduction, ACS Catal., 2022, 12, 5441–5454.
49. P. Hou, Y. Huang, F. Ma, X. Wei, R. Du, G. Zhu, J. Zhang and M. Wang, S and N Coordinated Single-Atom Catalysts for Electrochemical CO₂ Reduction with Superior Activity and Selectivity, Appl. Surf. Sci., 2023, 619, 156747.
50. X. Wei, S. Cao, S. Wei, S. Liu, Z. Wang, F. Dai and X. Lu, Theoretical Investigation on Electrocatalytic Reduction of CO₂ to Methanol and Methane by Bimetallic Atoms TM1/TM2-N@Gra (TM = Fe, Co, Ni, Cu), Appl. Surf. Sci., 2022, 593, 153377.
51. X. Liu, J. Xiao, H. Peng, X. Hong, K. Chan and J. K. Nørskov, Understanding Trends in Electrochemical Carbon Dioxide Reduction Rates, Nat. Commun., 2017, 8, 15438.
52. M. Zhong, K. Tran, Y. Min, C. Wang, Z. Wang, C. T. Dinh, P. De Luna, Z. Yu, A. S. Rasouli and P. Brodersen, et al., Accelerated Discovery of CO₂ Electrocatalysts Using Active Machine Learning, Nature, 2020, 581, 178–183.
53. G. Kresse and J. Furthmüller, Efficient Iterative Schemes for Ab Initio Total-Energy Calculations Using a Plane-Wave Basis Set, Phys. Rev. B: Condens. Matter Mater. Phys., 1996, 54, 11169–11186.
54. G. Kresse and J. Furthmüller, Efficiency of Ab-Initio Total Energy Calculations for Metals and Semiconductors Using a Plane-Wave Basis Set, Comput. Mater. Sci., 1996, 6, 15–50.
55. P. E. Blochl, Projector augmented-wave method, Phys. Rev. B:Condens. Matter Mater. Phys., 1994, 50, 17953–17979.
56. J. P. Perdew, K. Burke and M. Ernzerhof, Generalized Gradient Approximation Made Simple, Phys. Rev. Lett., 1996, 77, 3865–3868.
57. S. Grimme, J. Antony, S. Ehrlich and H. Krieg, A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu, J. Chem. Phys., 2010, 132, 154104.
58. S. Grimme, S. Ehrlich and L. Goerigk, Effect of the Damping Function in Dispersion Corrected Density Functional Theory, J. Comput. Chem., 2011, 32, 1456–1465.
59. A. D. Becke and E. R. Johnson, A Density-Functional Model of the Dispersion Interaction, J. Chem. Phys., 2005, 123, 154101.
60. S. Vijay, J. A. Gauthier, H. H. Heenen, V. J. Bukas, H. H. Kristoffersen and K. Chan, Dipole-Field Interactions Determine the CO₂ Reduction Activity of 2D Fe–N–C Single-Atom Catalysts, ACS Catal., 2020, 10, 7826–7835.
61. H. J. Monkhorst and J. D. Pack, Special Points for Brillouin-Zone Integrations, Phys. Rev. B, 1976, 13, 5188–5192.
62. M. Methfessel and A. T. Paxton, High-Precision Sampling for Brillouin-Zone Integration in Metals, Phys. Rev. B:Condens. Matter Mater. Phys., 1989, 40, 3616–3621.
63. G. Makov and M. C. Payne, Periodic Boundary Conditions in ab initio Calculations, Phys. Rev. B: Condens. Matter Mater. Phys., 1995, 51, 4014–4022.
64. H. Xu, D. Cheng, D. Cao and X. C. Zeng, Revisiting the Universal Principle for the Rational Design of Single-Atom Electrocatalysts, Nat. Catal., 2024, 7, 207–218.
65. C. Y. Lin, L. Zhang, Z. Zhao and Z. Xia, Design Principles for Covalent Organic Frameworks as Efficient Electrocatalysts in Clean Energy Conversion and Green Oxidizer Production, Adv. Mater., 2017, 29, 1606635.
66. H. Jia, A. Nandy, M. Liu and H. J. Kulik, Modeling the Roles of Rigidity and Dopants in Single-Atom Methane-to-Methanol Catalysts, J. Mater. Chem. A, 2022, 10, 6193–6203.
67. J. K. Nørskov, J. Rossmeisl, A. Logadottir and L. Lindqvist, Origin of the Overpotential for Oxygen Reduction at a Fuel-Cell Cathode, J. Phys. Chem. B, 2004, 108, 17886–17892.
68. I. H. Kim, J. Lim and S. O. Kim, Discovery of Single-Atom Catalyst: Customized Heteroelement Dopants on Graphene, Acc. Mater. Res., 2021, 2, 394–406.
69. Z. Yang, Z. Yao, G. Li, G. Fang, H. Nie, Z. Liu, X. Zhou, X. Chen and S. Huang, Sulfur-Doped Graphene as an Efficient Metal-free Cathode Catalyst for Oxygen Reduction, ACS Nano, 2012, 6, 205–211.
70. F. H. Allen, O. Kennard, D. G. Watson, L. Brammer, A. G. Orpen and R. Taylor, Tables of Bond Lengths Determined by X-ray and Neutron Diffraction. Part 1. Bond Lengths in Organic Compounds, J. Chem. Soc., Perkin Trans. 2, 1987, S1–S19.
71. D. M. Chen, P. M. Shenai and Y. Zhao, Tight Binding Description on the Band Gap Opening of Pyrene-Dispersed Graphene, Phys. Chem. Chem. Phys., 2011, 13, 1515–1520.
72. A. A. Peterson and J. K. Nørskov, Activity Descriptors for CO₂ Electroreduction to Methane on Transition-Metal Catalysts, J. Phys. Chem. Lett., 2012, 3, 251–258.
73. K. J. P. Schouten, Y. Kwon, C. J. M. van der Ham, Z. Qin and M. T. M. Koper, A New Mechanism for the Selectivity to C₁ and C₂ Species in the Electrochemical Reduction of Carbon Dioxide on Copper Electrodes, Chem. Sci., 2011, 2, 1902.
74. X. Nie, W. Luo, M. J. Janik and A. Asthagiri, Reaction Mechanisms of CO₂ Electrochemical Reduction on Cu(111) Determined with Density Functional Theory, J. Catal., 2014, 312, 108–122.
75. Y. Hori, I. Takahashi, Y. Yoshinami and A. Murata, Electrochemical Reduction of CO at a Copper Electrode, J. Phys. Chem. B, 1997, 101, 7075–7081.
76. J. P. Janet, Q. Zhao, E. I. Ioannidis and H. J. Kulik, Density Functional Theory for Modelling Large Molecular Adsorbate–Surface Interactions: A Mini-Review and Worked Example, Mol. Simul., 2016, 43, 327–345.
77. Q. Zhao and H. J. Kulik, Where Does the Density Localize in the Solid State? Divergent Behavior for Hybrids and DFT+U, J. Chem. Theory Comput., 2018, 14, 670–683.
78. Q. Zhao and H. J. Kulik, Stable Surfaces That Bind Too Tightly: Can Range-Separated Hybrids or DFT+U Improve Paradoxical Descriptions of Surface Chemistry?, J. Phys. Chem. Lett., 2019, 10, 5090–5098.
79. J. Chen, Z. Li, X. Wang, X. Sang, S. Zheng, S. Liu, B. Yang, Q. Zhang, L. Lei and L. Dai, et al., Promoting CO₂ Electroreduction Kinetics on Atomically Dispersed Monovalent Zn^I Sites by Rationally Engineering Proton-Feeding Centers, Angew. Chem., Int. Ed., 2022, 61, e202111683.
80. J. Zhang, Y. Wang and Y. Li, Not One, Not Two, But at Least Three: Activity Origin of Copper Single-Atom Catalysts toward CO₂/CO Electroreduction to C₂₊ Products, J. Am. Chem. Soc., 2024, 146, 14954–14958.
81. L. Wang, Z. Liu, R. Li, H. Gao, P. Yang, W. Wang, X. Xue, S. Feng, L. Yu and G. Wang, The Intrinsic Activity Descriptor of TM–N₃–C Single-Atom Catalysts for Electrochemical CO₂ Reduction: A DFT Study, J. Mater. Chem. A, 2023, 11, 24836–24853.
82. X. Li, Y. Zeng, C.-W. Tung, Y.-R. Lu, S. Baskaran, S.-F. Hung, S. Wang, C.-Q. Xu, J. Wang and T.-S. Chan, et al., Unveiling the In Situ Generation of a Monovalent Fe(I) Site in the Single-Fe-Atom Catalyst for Electrochemical CO₂ Reduction, ACS Catal., 2021, 11, 7292–7301.
83. T. N. Huan, N. Ranjbar, G. Rousse, M. Sougrati, A. Zitolo, V. Mougel, F. Jaouen and M. Fontecave, Electrochemical Reduction of CO₂ Catalyzed by Fe–N–C Materials: A Structure–Selectivity Study, ACS Catal., 2017, 7, 1520–1525.
84. A. S. Varela, W. Ju, A. Bagger, P. Franco, J. Rossmeisl and P. Strasser, Electrochemical Reduction of CO₂ on Metal-Nitrogen-Doped Carbon Catalysts, ACS Catal., 2019, 9, 7270–7284.
85. C. Wang, H. Ren, Z. Wang, Q. Guan, Y. Liu and W. Li, A Promising Single-Atom Co–N–C Catalyst for Efficient CO₂ Electroreduction and High-Current Solar Conversion of CO₂ to CO, Appl. Catal., B, 2022, 304, 120958.
86. X.-M. Hu, H. H. Hval, E. T. Bjerglund, K. J. Dalgaard, M. R. Madsen, M.-M. Pohl, E. Welter, P. Lamagni, K. B. Buhl, M. Bremholm, M. Beller, S. U. Pedersen, T. Skrydstrup and K. Baasbjerg, Selective CO₂ Reduction to CO in Water using Earth-Abundant Metal and Nitrogen-Doped Carbon Electrocatalysts, ACS Catal., 2018, 8, 6255–6264.

---

Footnote

† Electronic supplementary information (ESI) available: Methods to locate the most stable SAC geometries; benchmark calculations of kinetic energy cutoff and k-point grid selections; initial magnetic moment guess, dipole correction, and DFT+U benchmarks; geometries of all optimized clean SACs and representative adsorption sites; comparison of dopant effects in tuning CO adsorption energies; constrained geometry optimizations for CO adsorption energy predictions; complexation energies of SACs; most favorable adsorption sites of key intermediates; energetics of HER; energetics of CO₂R to methane and methanol reaction pathways on SACs (PDF). Compressed VASP structure files (ZIP). See DOI: https://doi.org/10.1039/d4cp04212c

---